Shape Tuning in Macaque Inferior Temporal Cortex

Abstract

Neurons in the inferior temporal cortex (IT) of the macaque fire more strongly to some shapes than others, but little is known about how to characterize this shape tuning more generally, because most previous studies have used somewhat arbitrary variations in the stimuli with unspecified magnitudes of the changes. The present investigation studied the modulation of IT cells to nonaccidental property (NAP, i.e., invariant to orientations in depth) and metric property (MP, i.e., depth dependent) variations of dimensions of generalized cones (a general formalism for characterizing shapes hypothesized to mediate object recognition). Changes in an NAP resulted in greater neuronal modulation than equally large pixel-wise changes in an MP (including those consisting of a rotation in depth). There was also precise and highly systematic neuronal tuning to the quantitative variations of MPs along specific dimensions to which a neuron was sensitive. The NAP advantage was independent of whether the object was composed of only a single part or had two parts. These findings indicate that qualitative shape changes such as NAPs help explain the surplus amount of IT shape sensitivity that cannot be accounted for on the basis of metric or pixel-based changes alone. This NAP advantage may provide the neural basis for the greater detectability of NAP compared with MP changes in human psychophysics.

Introduction

Since the seminal study of Gross et al. (1972), it has been known that macaque inferior temporal (IT) neurons are shape-selective (Logothetis and Sheinberg, 1996; Tanaka, 1996). However, little is known about how to characterize this shape tuning generally, because most previous studies have used somewhat arbitrary variations in the stimuli with unspecified magnitudes of the changes. A generalized cone (GC), formed by sweeping a cross section along an axis, provides a general formalism for describing shape and volumes (Marr, 1982; Nevatia, 1982) and has been hypothesized to provide a basis for characterizing the representation of simple parts mediating object recognition (Marr, 1982; Biederman, 1987). The present investigation uses the GC formalism to study systematically the shape sensitivity of IT neurons.

The first aim was to examine the modulation of IT neurons to nonaccidental and metric variations in the dimensions of GCs. Nonaccidental property (NAP) variations are those that are primarily unaffected by rotation in depth such as whether a contour is straight or curved or whether a pair of lines is parallel. Differences in NAPs have been hypothesized to provide the basis for basic- and some subordinate-level shape classifications and to allow recognition of objects at novel orientations in depth (Biederman, 1987). In contrast, metric property (MP) variations, such as the degree of curvature of a contour or the convergence angle of a pair of nonparallel lines, are affected by rotations in depth. Vogels et al. (2001) reported that, in agreement with the human psychophysical data of Biederman and Bar (1999), IT neurons are more sensitive to NAP than to MP changes of shaded, two-part objects under rotation in depth. However, the NAP and MP comparisons of Vogels et al. (2001) were performed on different dimensions of the shapes; e.g., the NAP might have been for axis curvature, and the MP might have been for the parallelism of the sides of the part, if not on different parts. The design of the present study allowed this analysis to be performed on the same dimensions and the same shapes, having the advantage of controlling for variations in the number of local features, such as the number of vertices, that otherwise would be produced by NAP and MP variations. Apart from the scaling of the relative magnitudes of the stimulus differences, another feature of the present study consists of the reduction (Tanaka, 1996) of shaded, two-part objects, when possible, to a single part, their silhouettes, or both, making it possible to examine shape changes uncontaminated by the presence of other parts or shading. The GC formalism also allows a systematic, quantitative variation of metric shape changes along different dimensions. Thus, the second aim was to examine whether the responses of IT neurons are related in a well behaved way to changes in this multidimensional, metric shape space. Such precise tuning for metric shape variations could support discriminations of shapes that vary only in metric properties.

Materials and Methods

Subjects

Two male rhesus monkeys served as subjects. Before conducting the experiments, a head post for head fixation and a scleral search coil were implanted, under isoflurane anesthesia and strict aseptic conditions. After training in the fixation task, we stereotactically implanted a plastic recording chamber. The recording chambers were positioned dorsal to IT, allowing a vertical approach, as described byJanssen et al. (2000). During the course of the recordings, we took a structural magnetic resonance image from monkey 1, with a vitamin E tube inserted at the recording site, and a computed tomographic scan of the skull of monkey 2, with the guiding tube in situ. This, together with depth readings of the white and gray matter transitions and of the skull basis during the recordings, allowed reconstruction of the recording positions before the animals were killed. All surgical procedures and animal care was in accordance with the guidelines of the National Institutes of Health and the Katholieke Universiteit Leuven Medical School.

Apparatus

The apparatus was identical to that described by Vogels et al. (2001). The animal was seated in a primate chair, facing a computer monitor (Panasonic PanaSync/ProP110i, 21 inch display) on which the stimuli were displayed. The head of the animal was fixed, and eye movements were recorded using the magnetic search coil technique. Stimulus presentation and the behavioral task were under control of a computer, which also displayed the eye movements. A Narishige (Tokyo, Japan) microdrive, which was mounted firmly on the recording chamber, lowered a tungsten microelectrode (1–3 MΩ; Frederick Hair) through a guiding tube. The latter tube was guided using a Crist grid that was attached to the microdrive. The signals of the electrode were amplified and filtered, using standard single-cell recording equipment. Single units were isolated on line using template-matching software (SPS). The timing of the single units and the stimulus and behavioral events were stored with 1 msec resolution on a personal computer (PC) for later off-line analysis. The PC also showed raster displays and histograms of the spikes and other events that were sorted by stimulus.

Fixation task

Trials started with the onset of a small fixation target at the center of the display on which the monkey was required to fixate. After a fixation period of 300 msec, the fixation target was replaced by a stimulus for 200 msec. If the monkey's gaze remained within a 1.5° fixation window, the stimulus was replaced again by the fixation spot, and the monkey was rewarded with a drop of apple juice. When the monkey failed to maintain fixation until 100 msec after stimulus presentation, the trial was aborted, and the stimulus was presented during one of the subsequent fixation periods. As long as the monkey was fixating, stimuli were presented with an interval of ∼1 sec. Fixation breaks were followed by a 1 sec time-out period before the fixation target was shown again.

Stimuli

The stimuli consisted of gray-level rendered images of objects, composed of 1 or 2 parts selected from a set of 14 parts. Each could be readily described as a GC (some of the stimuli are illustrated in Figs.1, 2). Qualitative variations in the dimensions of GCs define different NAPs, as listed in Table 1 and illustrated in Figure 3. For example, if the cross section remains constant, the sides of the GC will be parallel; otherwise, they will be nonparallel (e.g., Fig. 3B). The axis could be straight, as in the case of the pyramid of Figure3A, or curved, producing a curved pyramid. The GC formalization allows a parametric variation of shape, and, in addition, psychophysical results suggest an independent coding of at least some of these GC dimensions by the human visual system (Stankiewicz, 2002). Also, a computer vision model by Zerroug and Nevatia (1996a,b) that assumed a GC formulation, in particular, that the cross section was orthogonal to the axis, was able to derive an accurate three-dimensional description of an object from a single gray-level image.

Fig. 1.

The 21 objects that were used to search for responsive neurons.

Fig. 2.

A, Example of stimuli used in a reduction test, including (top row) a two-part shaded object (left) and a two-part silhouette (right) and (lower row) a one-part shaded object (left) and a one-part silhouette (right). B,Top,bottom, Two-part and one-part outlines.

Table 1.

Overview of the nonaccidental and metric changes used in this study

Nonaccidental changes	Metric changes
Straight main axis versus curved main axis (Fig.3A)	Degree of curvature of the main axis
Parallel sides versus nonparallel sides (produced by expansion of the cross section) (Fig. 3B)	Amount of expansion of the cross section
Straight sides versus curved sides along the major axis (with positive or negative curvature) (Fig.3C,D)	Degree of positive or negative curvature of the sides
Curved versus straight cross section (e.g., a cylinder becomes a brick and vice versa, or a cone becomes a pyramid and vice versa)	Changes in aspect-ratio; a part of an object can vary in length or width, or it can be stretched, becoming wider and shorter or narrower and longer
The cross section ends in a point versus the cross section ends in a side (e.g., a cylinder or brick with expanding cross section becomes a cone or a pyramid or vice versa) (Fig.3E)

Fig. 3.

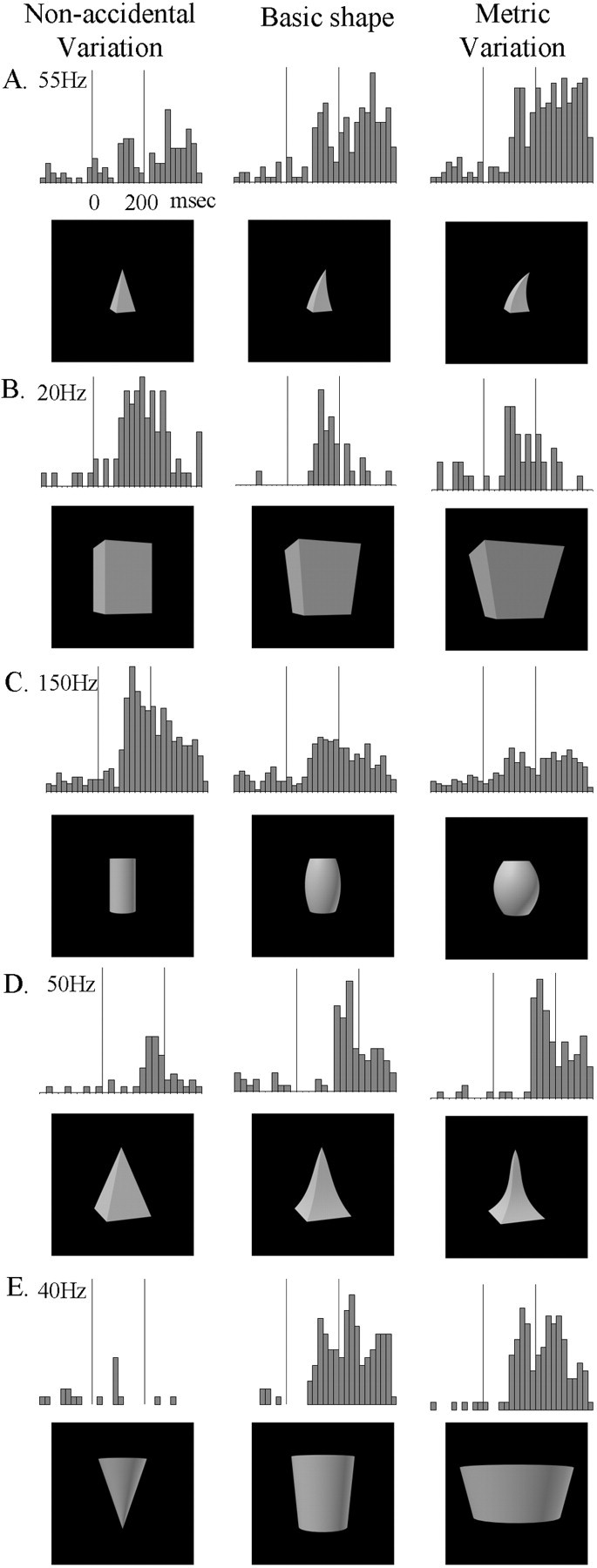
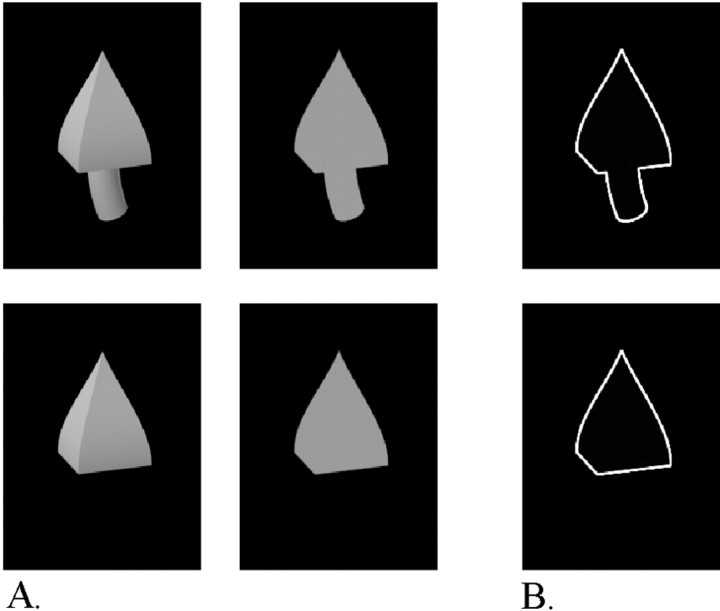
Responses of five single IT neurons to the basic object (middle), the NAP variation (left), and the equally large MP2 variation (right). A–D, Comparisons each situated on a single GC dimension within a row, but different dimensions between rows, the dimensions being (A–D, respectively) curvature of the main axis, expansion of the cross section, positive curvature of the sides, and negative curvature of the sides. In comparison E, the NAP and MP variations are situated on separate GC dimensions, the NAP change being the cross-section ending in a point versus the cross section ending on a side and the MP change being a change in aspect ratio. The vertical lines on the poststimulus time histograms indicate the stimulus onset and offset. The stimulus duration was 200 msec (see time scale oftop left histogram). Bin width is 20 msec.

The objects were rendered by 3D Studio MAX, release 2.5, on a black background. The images (size, ∼7°; mean luminance, 13 cd/m²) were shown at the center of the display.

Each shaded object had a silhouette and an “outline” counterpart. The silhouettes had the same outlines as the shaded objects, but the pixels inside the object contours had a constant luminance. The latter luminance value was equal to the mean luminance of the corresponding shaded versions of the object. The outline versions of the objects consist of line drawings (white lines, 0.1° width, on the black background) of the outer contour of the objects.

The total stimulus set consisted of 1059 gray-level shapes and their silhouette and outline counterparts. The organizational scheme behind this vast stimulus set will be described in the next sections.

Testing procedure

Search test. We searched for responsive neurons by presenting 7 two-part objects and 14 one-part objects (Fig. 1) in an interleaved manner. Each one-part object was one of the parts of the two-part objects. The same search set was used throughout the experiment. Both the one- and two-part objects will be referred to as the “basic” shape, because all other shapes were variations of these.

After isolating a neuron responsive to at least 1 of these 21 images, we conducted a reduction test and a varying number of modulation tests, using as the basic shape the shape the neuron was most sensitive to. We preferred one-part objects to two-part objects, using the former whenever the neuron responded equally or stronger to the one-part objects. The latter ensured that we were manipulating parts the neuron was sensitive to.

Reduction test. This test compared the responses to the shaded images and their silhouette versions. Using silhouettes has the advantage of eliminating the influence of shading variations (Vogels and Biederman, 2002), so we used silhouette versions instead of the shaded versions in subsequent tests whenever this was possible without lowering the activity of the neuron.

The reduction test consisted of four stimuli: the basic shape that was chosen in the search test, its two- or one-part counterpart (for, respectively, a one- or two-part basic shape), and silhouette versions of these stimuli (Fig. 2A). When the basic shape chosen in the search test was a two-part object, the reduction test used the one-part counterpart that elicited the biggest response. On the basis of the outcome of this test, we decided whether to use the silhouette or the shaded version of the basic shape and to confirm (or discard) our preference for the one- versus two-part objects. The objects were presented in an interleaved manner, and on average, five trials were conducted for each condition.

Modulation tests. These tests contained 13 shapes each, presented in an interleaved manner, and consisted of the basic shape and 12 variations of that shape. One kind of shape variation consisted of metric changes of the basic shape along a single dimension. These consisted of two series of four metric variations of the basic shape. The four variations of each series were parametrically situated along a single dimension. They are denoted MP1–MP4, with decreasing similarity with respect to the basic shape. The two series were varied on different GC dimensions as listed in Table 1 and illustrated in Figure3. Figure 4 illustrates two series of four metric variations, one for each of the two parts of a two-part object.

Fig. 4.

Conditions of a modulation test for a two-part basic object: two series of four metric variations, consisting of variations in the aspect ratio of the top part in 1 and the curvature of the axis of the bottom part in 2, two nonaccidental variations, produced by keeping constant the size of the cross section of the top part in 1 and having a straight axis of the bottom part in 2, and two rotated-in-depth versions of the basic object. When the basic object consisted of one part, the second series of metric and nonaccidental variations were along different dimensions.

A second kind of shape variation was an NAP variation of the basic shape. For each of the two series of metric variations, one NAP shape variation of the same basic shape was produced. The NAP variations used are listed in Table 1, and some are illustrated in Figures 3 and 4. Each of these was paired with a particular metric variation (see Table1 and Figs. 3 and 4). The NAP versions differed equally or less from the basic shape than did the MP2 versions (see calibration of image similarities below). When the two-part objects served as stimuli, only one part was changed at a time, and the NAP and MP changes were applied to the same part for a given comparison (Fig. 4). The NAP and MP2 shape changes were kept small, because (1) we wished to avoid floor effects in modulation, i.e., going outside the tuning range of a neuron for the NAP and MP change; and (2) we wanted to include larger MP differences to compare with the NAP modulation. Most important, very large MP changes would have often changed the relative sizes of the geons in the two-part objects, a stimulus variation (that of the relations between the two geons) that we sought to avoid in this investigation. A third kind of shape variation consisted of two rotations in depth of the basic object. The rotated versions differed in steps of 30°.

Figure 4 shows the conditions of a modulation test for a two-part, shaded basic shape: two series of four metric variations, two nonaccidental variations, and two rotated-in-depth versions.

We used one to six modulation tests for each neuron (mean, two), depending on how long we could record from that neuron. The shapes were shown to the neuron for ∼20 trials in a randomly interleaved manner. The tests were done with silhouettes or shaded objects, depending on the outcome of the reduction test. To test whether similar results were obtained when only the outlines were present, we also used outline versions of the shapes in some cells. Figure 2B shows two examples of such outline versions.

Image similarity measures

We calibrated the difference between the images by computing the Euclidean distance between the gray levels of the pixels of the image of the basic shape and the images of the nonaccidental, metrically changed or rotated shapes. Because some neurons might be mainly sensitive to low spatial frequencies, we also performed low-pass filtering on the images by using convolutions with Gaussian filters with an SD that increased from 5 to 15 pixels in steps of 5 pixels. For each of the three low-passed image versions, Euclidean distances between the gray levels for corresponding pixels were computed. We made sure that the metric shape variation MP2 differed equally or slightly more from the basic shape than the NAP variation, this at each of the four possible resolutions. The calibration was done separately for the one-part objects, the two-part objects, and the silhouettes and was followed by a γ correction.

The gray level analysis compares image similarities as present in the retinal input without making any commitment to differential sensitivities to higher-order features. Changes in the image by either nonaccidental or metric changes are treated equally. Thus, any differential sensitivity to nonaccidental versus metric changes has to originate within the visual system and cannot be an artifact of retinal image dissimilarities. We went one step further by computing image distances that were corrected for relative position (Vogels et al., 2001), assuming an (unrealistically) perfect position-invariant representation of shape (Op de Beeck and Vogels, 2000). To do this, we measured the smallest physical distance for 2500 relative positions of images in the comparison, using for each position the procedure outlined above. This minimum value was taken as the position-corrected gray-level image similarity. Even for these position-corrected similarities, the NAP changes equaled or were less than the MP2 changes.

It is worth pointing out that for the shape variations situated along the same dimension, the magnitude of the change of the values of transformations in the 3D Studio software (e.g., “curvature” and “tapering”) for the NAP and MP2 variations matched quite well; when normalizing the NAP difference with respect to the basic shape to 1 for each shape transformation, the median MP2-basic shape difference was 1.05 (first quartile, 1; third quartile, 1.05). This suggests that even for these higher-order image transformations, the NAP and MP2 changes were well matched.

Analysis

The response of the neuron was defined as the number of spikes during an interval of 200–300 msec, starting from 50–120 msec. The starting point and duration of the time interval were chosen independently for each neuron to best capture its response by inspecting the peristimulus time histograms but were fixed for a particular neuron. Each neuron responded significantly to at least one of the objects used in the experiment, which was tested by an ANOVA. Parametric (ANOVA) and, when possible, nonparametric statistical tests were used to compare responses to different stimuli.

Fitting the response with quadratic surfaces using image metrics

Many neurons were tested with at least 16 metric variations of the same basic shape, yielding, when including the basic shape, at least 17 metrically different shapes. Each of these shapes had a value according to several ad hoc defined image metrics, and multiple regression was used to fit the neural responses to the shapes in this metric image space.

The following simple image metrics proved to be valuable in fitting the single-cell responses to the one-part stimuli: (1) degree of expansion of the cross section, defined as the ratio of the smallest to the largest width of the stimulus; (2) degree of curvature, which was computed by isolating the curved segment at the left side of the stimulus and then drawing a straight line between the two end points of the curve, followed by a division of the maximal perpendicular distance between the straight line and the curve by the length of the straight line; using the right side of the stimulus instead of its left side produces correlated curvature measures; (3) average broadness, defined as the area of the image of the object divided by its maximal vertical extent; and (4) average height, defined as area divided by its maximal horizontal extent.

Only metrics that were actually varying in the set of one-part stimuli shown to that neuron were used when fitting the responses of a neuron. Average broadness and average height were used for the shape variations of all one-part stimuli. Expansion of the cross section was used for the shape variations of Figure 1, O, I,R, and U. Curvature of the main axis was used in Figure 1, H, P, J, S, andM. Curvature of the sides was used in Figure 1,K, L, N, Q, andT. Thus each one-part shape was defined by three metrics. For the two-part stimuli, average broadness and height were calculated over the entire object. The other metrics were computed for the two parts separately. Therefore, when fitting the responses to the two-part stimuli, four metrics were used: average broadness, average height, a metric specific to the top part of the stimulus, and a metric specific to the bottom part of the stimulus.

A (hyper)surface, Y = a +bX₁ +cX₁² + . . . +hX_n +iX_n², withX_i being the values of the shapes on the n (3 or 4) different metrics, was fitted to the normalized responses of a neuron to these shapes. The response of a neuron to a shape was normalized by dividing it by the response of the neuron to the basic shape. This normalization was meant to control for possible test-to-test variability in the mean response, because different variations were shown during different successive modulation tests in which the basic shape is the only constant stimulus. An iterative Gauss–Newton least square algorithm was used to fit the model to the data. The explained variance of the responses by the model was computed as the squared Pearson correlation coefficient of the actual normalized response and Y. To assess whether the observed explained variance is significantly different from the explained variance, which would be expected when the responses were randomly related to the stimuli, we randomly permuted the normalized responses and fitted these using a quadratic model with the same number of dfs as in the original model, and this procedure was executed 1000 times. We decided that the fit of model and data were significant when the explained variance of the model for the original, unpermuted responses was equal to or larger than the 95th percentile of the distribution of the explained variance of the models for the permuted responses (permutation test). A similar procedure was used to compute fits to single metrics (see Results).

Results

The data set consists of 162 responsive anterior inferior temporal (TE) neurons, 88 in monkey 1 and 74 in monkey 2. These neurons responded well to the shapes we used. Their mean best response (maximal response across the several NAP–MP shape variations, i.e., for the best stimulus for a given neuron, averaged over neurons) was 27 spikes/sec with a mean baseline activity of 5.4 spikes/sec. These values compare well with those reported in other studies using more complex images (Jagadeesh et al., 2001; Baker et al., 2002).

On the basis of the inspection of the anatomical imaging data and depth readings, we conclude that the neurons responding to these relatively simple shapes were from the ventral bank of the rostral superior temporal sulcus and, mainly, from the lateral part of anterior TE.

Comparison between the response modulation to the nonaccidental and metric variations

Table 1 and Figure 3 provide an overview of the different nonaccidental and metric variations used in this study. In Figure 3, the differences between the objects in the left column and the basic object (middle column) are nonaccidental; i.e., they remain invariant under most rotations in depth. The objects in theright column differ from the basic object in metric properties, which are continuously affected by rotation in depth. For example, in Figure 3A, the axis of the pyramid on theleft (the NAP variation) remains “straight” under all viewpoints, in opposition to the axis of the pyramid in themiddle (the basic shape) that remains curved under most viewpoints. The MP variation and the basic shape, on the other hand, differ only in their degree of curvature, a property that varies with rotation.

In each of the examples in Figure 3A–D, the different objects are situated on a single GC dimension (see Table 1, top three rows). As noted earlier, these intradimensional comparisons provide a way to compare NAP and MP differences but to hold constant the number of local features, e.g., changes in the number and type of vertices, produced by such changes. This is important because the potential difference between the response modulations to NAP and MP changes could otherwise be attributed to a change in the number of local specific features, such as vertices.

In addition to intradimensional changes, we also compared for the same neurons NAP and MP changes of the basic object when these were situated along different dimensions, as in the study by Vogels et al. (2001). Figure 3E represents an example of such a comparison between dimensions (other cross-dimensional comparisons involved the other NAP changes listed in Table 1 and aspect ratio changes as MP changes). Note that in this case, NAP and MP changes can be confounded with differences in the number of local features. Because of the important distinction between comparisons within one dimension and comparisons between dimensions, we will present the results for these comparisons separately.

Intradimensional comparisons

Figure 3, A–D, shows the responses of four different neurons to the basic shape and its NAP and MP2 variation. The image similarity between the NAP and the basic shape was equated with the similarity between the MP2 and basic shape for each NAP–MP2 pair (see Materials and Methods). Despite this equal image similarity, the four neurons show more modulation for the NAP than for the MP change.

To determine the distribution of the neuronal modulation to these changes, we computed the percent modulation for each possible comparison of NAP versus the basic shape and MP2 versus the basic shape as follows: ‖(response basic shape − response object variation)/(response basic shape)‖ ∗ 100. Overall, for all 162 neurons with 243 NAP–MP2 comparisons, the mean percent modulation to the NAP change was 34%, which was significantly higher (p < 0.000002; n = 243; Wilcoxon matched pairs test) than the 26% modulation to the physically equal MP2 change.

Figure 5A plots the frequency distributions of the response modulations for all intradimensional NAP–MP2 comparisons (n = 243, 162 neurons). The modulation for the NAP change was larger than the modulation for the MP2 change in 63% of the comparisons, which is significantly larger than 50% (binomial test, p < 0.0001).

Fig. 5.

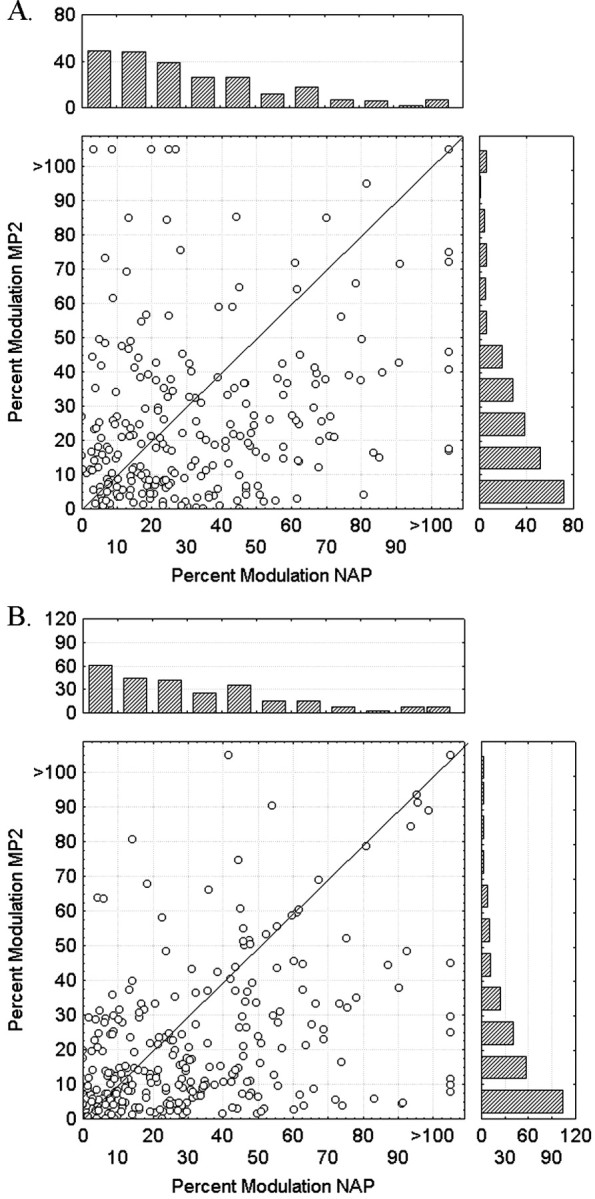
A, Frequency distributions and scatter plot of the response modulations for all intradimensional NAP–MP2 comparisons (n = 243, 162 neurons).B, Frequency distributions and scatter plot of the response modulations for all cross-dimensional NAP–MP2 comparisons (n = 268, 121 neurons).

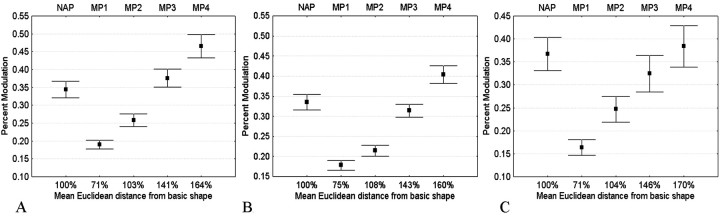
The metric change could have up to four different values (MP1–MP4), which made it possible to determine how large the MP change had to be to produce a response modulation equivalent to that produced by the NAP change. To do that, the four MP image changes were expressed in NAP image change units (the NAP change was arbitrarily set at 100%), and the percent response modulation values with respect to the basic shape were averaged across the different sorts of MP changes. Figure6A shows the resulting average response modulation for the NAP and the four different MP changes. As noted above, the mean percent modulation to the NAP change was 34%, which was significantly higher than the 26% modulation to the MP change, MP2, which was equivalent in terms of stimulus change. Figure 6A also shows that the modulation for the NAP change was similar to that obtained with the physically much larger MP3 change. Indeed, one needs a metric change that is ∼1.5 times larger in Euclidean image distance (as shown in Fig. 6A) or approximately two times larger in Manhattan distances (or City Block, sum of absolute instead of squared distances) than the nonaccidental change to have an equally large response modulation.

Fig. 6.

A, Response modulation for the NAP and the four different MP changes for all intradimensional NAP–MP comparisons, averaged over 243 cases (162 neurons). B, Response modulation for the NAP and the four different MP changes for all cross-dimensional NAP–MP comparisons, averaged over 268 cases (121 neurons). C, Response modulation for the NAP and the four different MP changes for all intradimensional NAP–MP comparisons in which the basic object is a one-part silhouette, averaged over 57 cases (57 neurons). The mean percentages of image change (mean Euclidean distance) are indicated below the label of the shape variations with the mean percent change of the NAP stimuli set at 100%. Error bars indicate SEM.

Similar results were obtained when computing absolute response differences instead of percent response modulations; the NAP change and MP2 change produced average absolute response differences of 5.3 and 3.9 spikes/sec, respectively. This NAP advantage was statistically significant (p < 0.000001; n = 243; Wilcoxon matched pairs test).

The difference between the neuronal response modulation for the NAP and MP2 change was significant in both monkeys, and there was no significant difference between the monkeys in the magnitude of their NAP effects (Kolmogorov–Smirnov two-sample test, p > 0.05). As expected when searching for responsive neurons with the basic shapes, overall, the neurons responded somewhat stronger to the basic shape than to the NAP change: the response to the basic shape was greater than the response to the NAP change in 63% of the cases, which is significantly different from 50% (binomial test, p< 0.05). It is interesting to note that the response to the MP2 change was smaller than the response to the basic shape in only 54% of the cases, which does not differ significantly from 50%.

An ANOVA on the percent modulation using NAP versus MP2 and the four different sorts of NAP–MP changes (curvature of the main axis, positive curvature of the sides, negative curvature of the sides, and expansion of the cross section) as factors produced no significant interaction of these two factors (F_(3,240) = 0.53; not significant), suggesting that the greater modulation for NAP compared with MP changes was not caused by a single dimension or a few of the dimensions we manipulated but is a general effect.

For some sorts of changes (e.g., parallelism of the sides and positive curvature of the sides), the NAP variation is smaller in size than the basic shape, which is smaller than the MP2 variation, whereas for others, the reverse is true (e.g., negative curvature of the side). The NAP advantage was significant when the NAP variation was smaller than the basic shape–MP2 variation (mean modulation, 34 vs 25%;p < 0.0005; n = 98) and when the latter was not the case (34 and 27%; p < 0.0065;n = 145). This indicates that the NAP advantage is attributable to a shape and not a size difference.

Cross-dimensional comparisons

Very similar results were obtained when comparing NAP and MP changes when these were varied along different dimensions. Figure5B plots the frequency distributions of the response modulations for all cross-dimensional NAP–MP2 comparisons (n = 268, 121 neurons). The modulation for the NAP change was larger than the modulation for the MP2 change in 65% of the comparisons, which is significantly larger than the 50% rate expected by chance (binomial p < 0.0001). The mean percent modulation to the NAP change was 33%, which is significantly higher (p < 0.000001, Wilcoxon matched pairs test) than the 21% modulation to the equally large MP2 stimulus variation (Fig. 6B). Again, one needs a metric change that is ∼1.5 or 2 times larger in Euclidean or City Block distance measures, respectively, than the nonaccidental change to have an equally large response modulation (Fig. 6B). The NAP and MP2 changes produced average absolute response differences of 6.3 and 3.9 spikes/sec, respectively. This NAP advantage was statistically significant (p < 0.000001; n = 268; Wilcoxon matched pairs test).

The greater modulation for NAP compared with MP changes was significant in both monkeys, and there was no significant difference between the monkeys in the size of the NAP effect (Kolmogorov–Smirnov two-sample test, p > 0.05).

The response to basic shape was greater than the response to the NAP and MP2 variation in 67 and 57% of the cases, respectively.

The NAP advantage was independent of the relative sizes (areas) of the NAP, MP2, and basic shape stimuli. Thus greater modulation to NAP compared with MP2 stimuli was evident (p < 0.01, Wilcoxon matched pairs test in all comparisons) when the NAP version was smaller or larger in area than both the MP2 version and the basic shape or when the NAP and MP2 versions were both smaller or larger than the basic shape.

Features possibly causing the NAP advantage

In 73% of the cases, the NAP involved a change from curved to straight lines. To determine whether the overall NAP advantage we reported above is mainly attributable to the curvature–straight edges distinction, we compared the NAP and MP2 modulations for two groups of cases, one group in which the NAP change involved a curvature–straight edge change and a second group in which it did not. The degree of modulation between the two groups was very similar (Table2), indicating that the NAP advantage is not solely attributable to the curvature–noncurvature distinction.

Table 2.

Mean modulation to nonaccidental and metric changes for different kinds of shape changes

Shape change	Modulation to NAP change (%)	Modulation to MP2 change (%)	SE, NAP (%)	SE, MP2 (%)	n	Significance level (Wilcoxon matched pairs)
Change in curvature	34	23	2	1	376	p< 0.000001
No change in curvature	34	25	2	3	135	p < 0.000092
Presence versus absence of a point	47	34	4	4	38	p < 0.005901
No presence versus absence of a point	33	23	2	1	473	p < 0.000001

Another potential feature might be the presence or absence of a point at the end of the shape, a feature manipulated in 7% of the cases. However, as for the curvature–noncurvature distinction, the NAP advantage was present whether an end point feature was manipulated (Table 2). Also, the average neuronal modulation attributable to the NAP change (29 ± 3%) was significantly larger than that for the MP2 change (21 ± 3%) in those cases in which neither a curvature nor an end point feature change was manipulated (Wilcoxon matched pairs test, p < 0.002; n = 97).

Silhouettes, outlines, and one- and two-part objects compared

To simplify the stimuli as much as possible, we reduced two-part objects to one-part objects, their silhouette, or both (see Materials and Methods, Reduction test) whenever this was possible without decreasing the neuronal response. The modulation tests were run on the reduced images. We were able to reduce the two-part objects to single parts in 50% of the neurons; i.e., in half of the neurons, the response to a single part was at least as strong as to the two-part object. In 65% of the neurons, the silhouette produced a response at least as strong as the shaded version.

In the above analysis of the NAP–MP differences, all comparisons were pooled, irrespective of whether a one- or two-part shaded object or a one- or two part silhouette was used in the test. In addition, 25 neurons were included that were tested with outlines (see Fig.2B). However, as shown in Table3, the greater neural modulation of changes in NAPs compared with MP2 changes holds within each of these image categories. There was no significant difference among shaded objects, silhouettes, and outlines or between one- and two-part objects in their greater sensitivity to NAP compared with MP differences (ANOVAs, p > 0.05).

Table 3.

Mean modulation to nonaccidental and metric changes for different kinds of shapes

Shape	Modulation to NAP change (%)	Modulation to MP2 change (%)	SE, NAP (%)	SE, MP2 (%)	n	Significance level (Wilcoxon matched pairs)
Shaded	36	27	4	3	131	p  < 0.0004
Silhouette	31	21	2	1	319	p  < 0.000001
Outline	44	32	5	4	61	p  < 0.003
One-part	36	22	2	1	232	p  < 0.000001
Two-part	32	25	2	2	279	p  < 0.00001

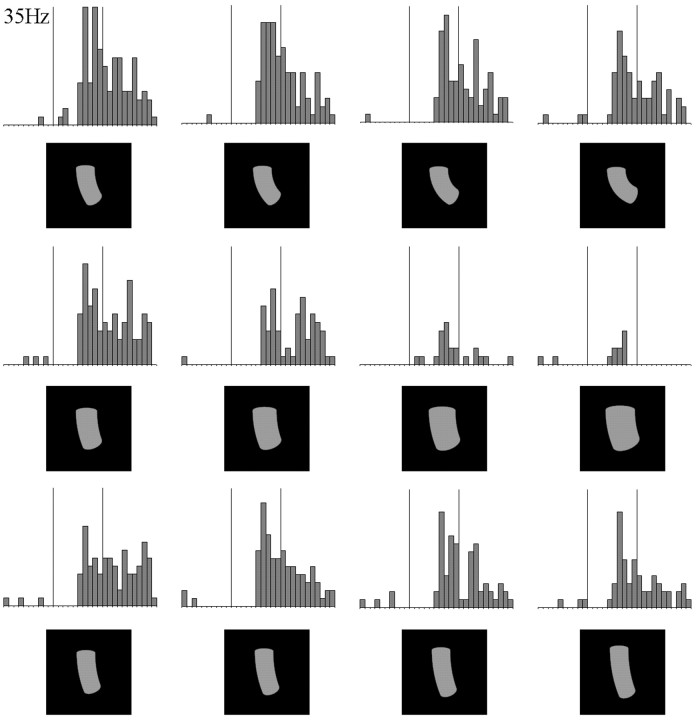
Because silhouettes lack luminance variations within their contours, and single-part object are less complex than two-part objects, the single-part silhouettes are a favorable image category to test for differential response modulations to NAP versus MP changes. Fifty-seven neurons were tested with single-part silhouettes, and the results for the intradimensional comparisons are shown in Figure 6C. For this subsample of neurons, the response modulation was significantly larger for the NAP (37%) compared with the MP2 (25%) changes (Wilcoxon matched pairs test, p < 0.0003;n = 57). This comparison rules out a possible confound of shading variations and firmly establishes that for simple one-part shapes, IT neurons are, on average, more sensitive to nonaccidental than to metric changes. Again, the average response modulation for the NAP change was at least of the same magnitude as that obtained for the physically much larger MP3 change. This is shown for a single neuron in Figure 7.

Fig. 7.

Responses of an IT neuron to one-part silhouettes illustrating an NAP change, a basic shape, and four different MP changes. The NAP and MP changes are situated on the same dimension, namely expansion of the cross section. Conventions are the same as in Figure 3. This cell shows markedly greater modulation to the NAP changes than the MP changes.

Rotation-in-depth compared with intraview shape changes

The shape changes we studied so far occurred within a single view. Given that a potential value of NAPs in representing shape derives from the invariance such properties afford to rotation in depth (Biederman and Gerhardstein, 1993; Biederman and Bar, 1999), we also tested the effect of rotating the basic object and compared this with that obtained when changing an NAP or MP without rotating the object. We will only present results of rotations of shaded or silhouette one-part objects, because those from the two-part objects are difficult to interpret. Whereas the MP and NAP changes were applied to only one of the parts of a two-part object, rotating the object usually affects both parts. We studied rotations along the vertical axis only, and the effect of this rotation was studied only for those basic objects for which the rotation affected their projected shape.

In 33 cases, the rotation changes were physically equally distant from the basic shape compared with the MP2 and NAP changes (according to the image calibration; see Materials and Methods). We made sure that in these cases, the rotation caused no nonaccidental changes (Biederman and Bar, 1999). As expected, the NAP change produced a significantly larger modulation than the MP2 change (NAP modulation, mean ± SE, 29 ± 4%; MP2, 19 ± 3%; Wilcoxon matched pair test,p < 0.005). Interestingly, the mean effect of rotation (19 ± 3%) was highly similar to that of the metric change and significantly smaller than that for the NAP change (Wilcoxon matched pair test, p < 0.03).

Because we had a larger number of MP changes (i.e., MP1–MP4) than NAP changes, and thus more opportunities to match the physical similarity with rotation changes, we performed a subsequent analysis on a much larger sample consisting of metric and rotation changes that were physically equal with respect to the basic single-part shape. In this sample of 68 cases, there was again no significant difference in response modulation when comparing the rotation (22 ± 3%) and metric changes (17 ± 2%; Wilcoxon matched pairs test,p > 0.05), although the modulations attributable to rotation tended to be larger than those obtained for the equal metric change.

Both these analyses indicate that for these simple shapes, rotation produces response modulations, but these are, on average, smaller than those produced by NAP changes and similar in size to those produced by metric property changes.

Consistent, dimension-dependent neuronal modulation to metrically varied shapes

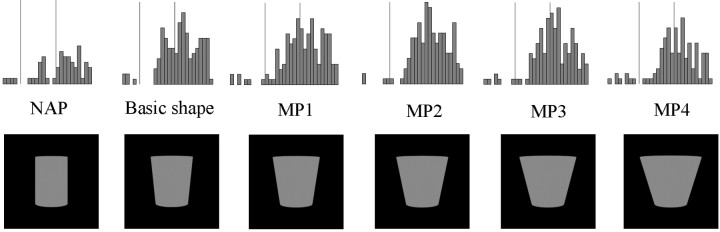
Figure 6 clearly shows that these IT neurons were sensitive to the degree of the metric change, the average modulation becoming larger with decreasing similarity between the basic shape and its metric variations. Many of these neurons were tested with at least 17 shapes that differed in metric properties. Thus the question arose of whether the responses of the neurons to these metrically varied images are related in a systematic, consistent way to simple image metrics. As explained in Materials and Methods, each of these objects could have a value on each of three (for the one-part objects) or four (for the two-part objects) ad hoc-defined image metrics. For each object, the metrics were average broadness and length, supplemented by one or two of the following: curvature of the main axis, expansion of the cross section, and curvature of the sides. These metrics can be used to define underlying dimensions along which the shapes are varied and to examine whether the responses of the neurons are related in a consistent way to changes in this multidimensional, metric shape space.

We used quadratic (hyper)surfaces (see Materials and Methods) to fit the neuronal responses to the shape space. Figure8 shows the responses of a neuron to 12 of the 25 objects with which it was tested. Each of the 25 objects has a value on each of three metric dimensions: (1) curvature of the main axis, (2) average broadness, and (3) average length (see Materials and Methods). The quadratic model using these three dimensions explained 82% of the variance of the response of this neuron to the set of 25 objects (p < 0.001; see Materials and Methods). When the fit was performed for each dimension separately, it was significant for average broadness and average length (p < 0.001) but not for curvature. Indeed, it is clear from Figure 8 that the neuron was more modulated by changes in length and width than by changes in curvature.

Fig. 8.

Responses of an IT neuron to 12 of the 25 shapes that were shown to the neuron. Conventions are the same as in Figure3.

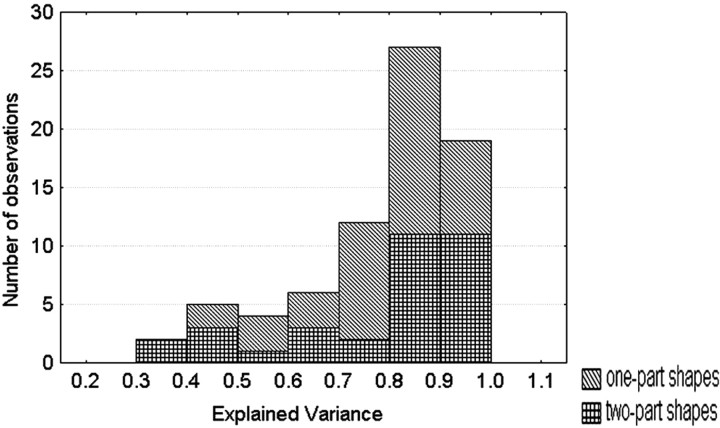
Seventy-five IT neurons were tested with 17 or 25 (average, 21) metrically varying shapes. For this set of neurons, the quadratic model resulted in a median explained variance of 85%, which is surprisingly large considering the trial-to-trial response variability of single cells. The distribution of the explained variance is shown for the one- and two-part shapes separately in Figure9. The median explained variances were 83 and 86%, respectively, for the one-part (three dimensions;n = 42 neurons) and two-part (four dimensions;n = 33) objects. The fit of the model was statistically significant in 62 (82%) of the neurons. The median explained variance of the model with randomly permuted responses was much smaller, being only 34%. Replacing broadness and length by area reduced the median explained variance from 85 to 68%, indicating that both broadness and length and not merely area (or amount of luminance) influence the responses. These excellent fits of the quadratic model show that the IT responses to a parameterized set of metrically varied shapes are highly consistent and can be systematically related to simple metric dimensions.

Fig. 9.

Distribution of the explained variance of the quadratic model fitting the responses of the neurons to 17 or 25 metrically varying shapes using three or four metric dimensions. The results are shown for the one- and the two-part stimuli separately.

The consistency in modulation was rarely equally divided between dimensions. To quantify this differential effect of dimension, we determined the explained variance for each dimension separately. When ranking within each neuron the dimensions according to their explained variance, it turned out that the best dimension had a median explained variance of 56%, and the unidimensional fit was significant in 66 (88%) of the neurons. The second-best dimension yielded a median explained variance of 30% [significant in 44 (58%) of the neurons], whereas the third-best dimension explained 16% [significant in 22 (29%) of the neurons]. Four dimensions were tested in 33 neurons. The median explained variance of the worst-ranked dimension was only 8%, and only in three (10%) of the neurons was the fit still significant.

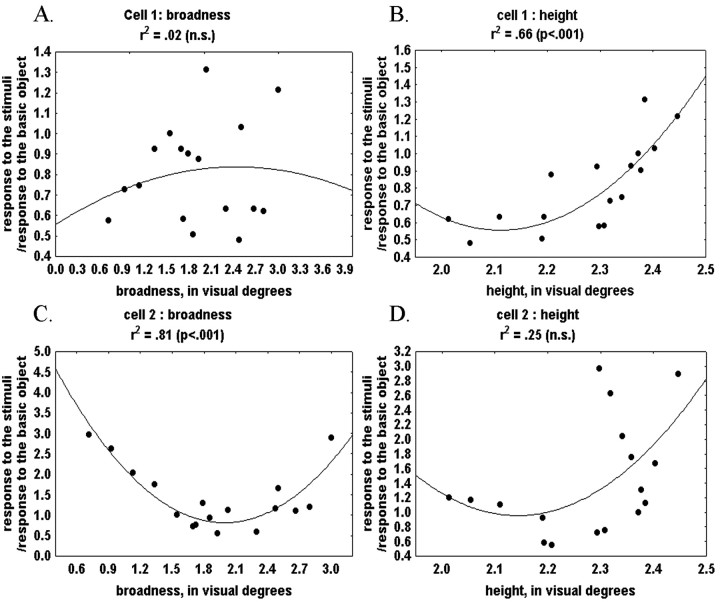
Different neurons were modulated by changes within different dimensions. Figure 10 presents the unidimensional fits for two neurons that were shown the same stimuli. The response of one neuron was strongly and consistently modulated by broadness but not length, whereas the opposite was true for the other neuron, clearly indicating that the modulation is dimension-dependent in a neuron-specific way.

Fig. 10.

Unidimensional quadratic fits for two neurons that were shown the same stimuli. A, Unidimensional fit for cell 1 based on broadness. B, Unidimensional fit for cell 1 based on height. C, Unidimensional fit for cell 2 based on broadness. D, Unidimensional fit for cell 2 based on height.

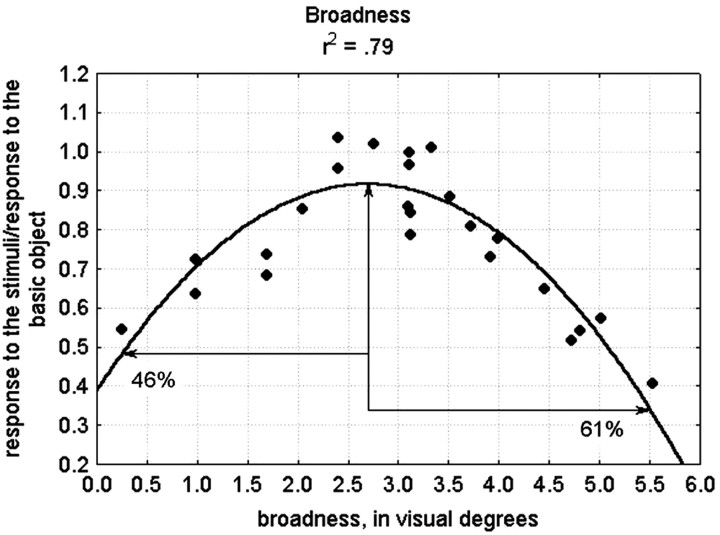
The goodness of fit for the quadratic functions does not necessarily indicate that neurons are tuned for the metric (e.g., as for orientation in primary visual cortex) but may instead reflect a monotonic increase or decrease in response with an asymptote (as seen, for example, in many contrast response functions) or an “inverted” tuning function with a minimum. This possibility can be appreciated in Figure 10B, where the responses of one neuron to 17 shapes are fitted using a single dimension. The function fitting the responses looks similar to a monotonically increasing function. However, in reality it could be an inverted tuning function with a minimum with increasing responses as the shapes become shorter than a 2° visual angle or a classical tuning function with one optimal value when the responses would show a decrease in response to longer shapes. Given the computational advantages of classical tuning functions for representing image similarities (Edelman, 1999), we assessed whether at least some of the neurons were representing the metric shape variations with a classical tuning curve by examining the fits of each dimension separately, and this for each neuron. For this, we examined 59 cases in which the image variations along a single dimension explained at least 55% of the response variance; i.e., the quadratic function fitted the responses reasonable well. We judged the function to be a tuning function when (1) its optimum or minimum was located within the sample range, and (2) the absolute difference in response between either the minimum or the maximum of the function and the points at the extremes of our sample range was at least 20% of the maximum response of the neuron. This should be true in both directions from the optimum or minimum. To avoid designating functions as tuned on the basis of just a few outliers, we added the criterion that at both sides of the minimum or maximum, it should be possible to pick out three data points that are monotonically increasing or decreasing relative to each other. Figure 11 presents a unidimensional fit for one neuron, based on the broadness dimension, which fulfilled these criteria. The maximum of the function and the two points at the extremes of our sample range are indicated with arrows. The absolute difference between the response at the left extreme and the maximum response is 46% of the maximum response, and the absolute difference between the response at the right extreme and the maximum response is 61%.

Fig. 11.

Unidimensional quadratic fit for one neuron based on broadness. The maximum of the function and the two points at the extremes of our sample range are indicated with arrows. The absolute difference between the response at the left extreme and the maximum response is 46% of the maximum response, and the absolute difference between the response at the right extreme and the maximum response is 61%.

In general, 15 (25%) of the examined functions fulfilled these criteria and were judged to be clear examples of tuning curves. Of these 15 functions, 12 had an optimum and thus corresponded to a classical tuning function, and 3 had a minimum or a inverted tuning function. The large majority of the functions resembled monotonically increasing or decreasing functions, but it is possible that when using a large range of stimulus variations, some of these neurons would also be found to be tuned to the metric dimensions.

Discussion

This study shows that the sensitivity of IT neurons to shape changes depends on the kind of shape change that is tested. IT neurons are, on average, more sensitive to NAP than to MP changes. Thus, there are feature differences, such as straight or curved and parallel or nonparallel sides, that represent important discontinuities in the representation of shape images at the level of IT. The greater modulation to NAP changes compared with MP changes is consistent with the human psychophysical finding that NAP changes are, in fact, more detectable than MP changes when the changes are of equivalent stimulus magnitudes (Biederman, 1995).

Our conclusion of the higher sensitivity to NAP versus MP changes depends critically on the calibration of the physical shape changes. Following other studies (Grill-Spector et al., 1999; Kourtzi and Kanwisher, 2000; Vogels et al., 2001; James et al., 2002; Vuilleumier et al., 2002), we scaled the image differences using pixel-wise gray-level similarities (Adini et al., 1997). Using these image similarity measures, the NAP changes were equal or smaller than the MP2 changes, leading to the conclusion that the larger IT neural sensitivity for NAP versus MP changes is not attributable to retinal image differences but instead originates in the feature sensitivity of the visual system. The magnitudes of the modulations for the NAP and MP2 changes were modest, which was to be expected given the relatively small shape changes that we used. It should be noted that modest neural response differences are meaningful, as shown by the growing literature on the relationship between perceptual discrimination thresholds and single-cell responses (for review, see Parker and Newsome, 1998).

The present results regarding the NAP–MP comparison extends those ofVogels et al. (2001), who used two-part, shaded objects for which the NAP and MP change occurred along different dimensions and, in some cases, for different parts. In the present study, we reduced the stimulus in many cases to a one-part silhouette and used intradimensional shape changes within the same view. The latter not only facilitates calibration of the image differences but also excludes possible confounding factors such as differences in shading and differences in the number of local features. We were even able to demonstrate the larger sensitivity for NAP changes using simple line drawings of the outer contours of the shapes.

Our data cannot determine where in the visual hierarchy this differential sensitivity occurs. Work in the cat (Dobbins et al., 1987;Versavel et al., 1990) and monkey (Kobatake and Tanaka, 1994; Gallant et al., 1996; Pasupathy and Connor, 1999; Hegde and Van Essen, 2000) showed that visual neurons in earlier visual areas show selectivity to curved stimuli, which is one of the features we manipulated. However, it is unclear from these studies whether the response of a population of these neurons shows a stronger modulation for straight versus curved than when changing the degree of curvature of a curved stimulus.

Whether the sensitivity bias toward NAPs is genetically determined, i.e., reflects innate, “privileged” dimensions, or instead results from experience with objects during development is unknown. During the experiment, the monkeys were exposed as frequently to the NAP as to the MP variants of a basic shape (the search for responsive neurons was done on purpose with the “neutral” basic shape), so that the bias for NAP changes cannot have resulted from differential exposure to NAPs during the experiment. However, exposure during development might have induced the NAP advantage. Indeed, single IT neurons may learn to respond similarly to temporally contiguous images (Foldiak, 1991;Wallis, 1998) (for physiological evidence, see Miyashita, 1988). Because NAPs are more robust than MPs to viewpoint variation, images of objects seen from temporally contiguous viewpoints will differ more in MPs than in NAPs, which can produce a learning-induced broader tuning for MPs compared with NAPs.

The larger modulation for NAPs is an average effect; not all neurons show it for a given dimension, and a given neuron may show it for one but not another shape dimension. Also, there is no evidence for a clear segregation between neurons responding exclusively to NAP changes and neurons responding equally to NAP and MP changes. The better tuning for NAP changes compared with MP changes is distributed among neurons: there is a more precise representation of NAP versus MP changes at the population level only. Indeed, our results also demonstrate that IT neurons show well behaved tuning for metric changes, and their responses nicely reflect at least ordinal differences in image similarity along metric dimensions, because these could be fitted remarkably well by smooth quadratic functions. The latter holds as long as no NAP changes are present, because these may lead to a larger change in response than expected from the (extrapolation of the) metric tuning function. This correspondence between neuronal modulation and the physical similarity among shapes that differ in MPs fits a similar equivalence between perceived similarity and the physical similarity of metrically varied two-dimensional (Biederman and Subramaniam, 1997) and three-dimensional shapes (Nederhouser et al., 2001). These results also accord with our previous report (Op de Beeck et al., 2001) of an ordinally faithful representation of similarities among a set of parametrized shapes at the behavioral level in primates as well as at the IT neuronal level. However, in that study, no distinctions were made between different sorts of shape changes; thus some of the discrepancies between the neuronal and physical similarities might have been attributable to a differential sensitivity of IT neurons to different kinds of shape changes.

Several studies have documented tuning of most macaque IT neurons to different views of the same object (Logothetis et al., 1995; Booth and Rolls, 1998; Vogels et al., 2001). In the present study, we compared shape changes attributable to rotating an object and intraview MP and NAP changes. For the relatively simple single-part shapes we used, rotating an object modulated the average response of IT neurons by more or less the same amount as an MP change but less than an NAP change. The latter is expected, because rotation produces (at least) MP changes, and we show that neurons are sensitive to MP changes. However, rotation in depth may also produce accidental NAP changes, as when a bent wire projects a loop at one view but not another (Biederman and Gerhardstein, 1993), and without control or specification of such changes, the degree to which the apparent effects of rotation are consequences of NAP changes is unclear.

It is generally believed that object recognition and categorization are based on the activity pattern across a set of neurons that are tuned to object features of different complexity (for review, see Riesenhuber and Poggio, 2002). The specificity of object recognition is derived from the feature selectivity of the neurons, i.e., different objects producing different activation profiles, whereas the invariance for image transformations such as position and scale is derived from an invariance to these image transformations of the feature selectivity, e.g., an object at different locations producing similar activation profiles. Some computational theories have suggested, however, that some features are more relevant than others for the categorization of objects, namely those that are affected less by changes in the object-imaging process, i.e., NAPs (Biederman, 1987), and it has been suggested that (theoretical) units would incorporate this by being more strongly tuned to the relevant than the less relevant features (Hummel and Biederman, 1992; Vetter et al., 1995). So-called view-based models of object recognition have so far incorporated only position and scale as irrelevant “features” (Edelman, 1999; Riesenhuber and Poggio, 2002), whereas the structural description model of Hummel and Biederman (1992) has units tuned to NAPs. The MP changes we used are shape changes and not changes in scale, so future view-based models have to incorporate the observed bias for NAP changes over the MP shape changes. Our results with the MPs alone even suggest that biases for different kinds of shape changes in a single neuron are commonplace, and that IT neurons can no longer be defined solely by their most preferred stimulus but also by their differential selectivity for different sorts of shape changes.

The observed NAP advantage is consistent with one of the assumptions of the geon structural description (GSD) model (Biederman, 1987; Hummel and Biederman, 1992). Geons are the shape primitives of the GSD model and are defined by contrasting NAPs, a distinction not incorporated into current view-based models. View-based models could be modified to incorporate the NAP advantage without including other assumptions of GSDs (or structural descriptions, in general), such as the explicit coding of the relationships among object parts. In general, the present work shows that the use of a computationally inspired parameterization of shapes can provide at least hints of the principles behind shape coding by primates.