The Role of the Hyperpolarization-Activated Cationic CurrentI_h in the Timing of Interictal Bursts in the Neonatal Hippocampus

Abstract

Under both pathological and experimental conditions, area CA3 of the adult or juvenile hippocampus generates periodic population discharges known as interictal bursts. Whereas the ionic and synaptic basis of individual bursts has been comprehensively studied experimentally and computationally, the pacemaker mechanisms underlying interictal rhythmicity remain conjectural. We showed previously that rhythmic population discharges resembling interictal bursts can be induced in hippocampal slices from first postnatal week mice, in Mg²⁺-free solution with GABA_Areceptor-mediated inhibition blocked. Here we show that these neonatal bursts occurred with high temporal precision and that their frequency and regularity were greatly reduced by the bradycardic agent ZD-7288 when applied at concentrations and durations that selectively block the hyperpolarization-activated, cationic currentI_h. Augmenting I_hby elevating intracellular cAMP dramatically increased burst frequency in a protein kinase A-independent manner. Burst amplitudes were strongly correlated with the preceding, but not the following, interburst intervals. The experimentally observed distribution of interburst intervals was modeled by assuming that a burst was triggered whenever the instantaneous rate of spontaneous EPSPs (sEPSPs) exceeded a threshold and that the mean sEPSP rate was minimal immediately after a burst and then relaxed exponentially to a steady-state level. The effect of blocking I_h in any given slice could be modeled by decreasing only the steady-state sEPSP rate, suggesting that the instantaneous rate of sEPSPs is governed by the level of I_h activation and raising the novel possibility that interburst intervals reflected the slow activation kinetics of I_h in the neonatal CA3.

Introduction

Area CA3 of the adult and juvenile hippocampus is a well studied generator of synchronous neuronal discharges. Under various experimental conditions, both in vivo and in vitro, it generates paroxysmal population bursts that recur at regular intervals of (depending on preparation) 2–20 sec (Ayala et al., 1973; Lebovitz, 1974; Schwartzkroin and Prince, 1978; Hablitz, 1984; Korn et al., 1987; Jensen and Yaari, 1988;Arvanov et al., 1995; Merlin et al., 1995; Avoli et al., 1996; de Curtis and Avanzini, 2001). These events resemble pathological “interictal spikes” observed in recordings from epileptic foci in human patients or from excised epileptic tissue from such patients (Cohen et al., 2002) and are therefore called interictal bursts (IBs). IBs can be recorded also in adjacent limbic regions but, in almost all cases, are found to propagate to these other regions from their site of origin in CA3 (Bragdon et al., 1992; Stoop and Pralong, 2000). Whether IBs trigger ictal epileptic episodes or, conversely, suppress them is debated (Bragdon et al., 1992; Barbarosie and Avoli, 1997; de Curtis and Avanzini, 2001); either way, IBs are closely linked with epileptogenesis, and understanding their mechanism of generation is crucial for understanding and treating epilepsy.

The intervals between IBs are highly regular: in vivo, the mean coefficient of variation of interburst intervals can be <0.1 (Lebovitz, 1979), a precision comparable with that of the normal human heartbeat (Van Hoogenhuyze et al., 1991). Whereas the ionic and synaptic mechanisms generating individual epileptiform bursts in the hippocampus have been thoroughly studied and modeled (Traub and Miles, 1991), the pacemaker mechanisms underlying the precise timing of IBs remain conjectural. In a seminal study in vivo, Lebovitz (1979) suggested that each IB generates a transient postburst period of suppression during which the system is refractory to the generation of another burst. More recent in vitro studies propose that the refractory period is attributable to synaptic depression (Staley et al., 1998). An alternative to pacing by recovery from suppression is pacing by a slow buildup of excitation, which in the heart, and in a variety of other regularly bursting neuronal networks, is mediated by the hyperpolarization-activated excitatory currentI_h (Soltesz et al., 1991) (for review, see Pape, 1996; Bal and McCormick, 1997; Luthi et al., 1998; Dickson et al., 2000). However, although I_h is expressed in the hippocampus by both pyramidal cells (Maccaferri et al., 1993) and inhibitory interneurons (Maccaferri and McBain, 1996;Strata et al., 1997), it has never been implicated in interictal rhythmogenesis.

We demonstrated recently (Wells et al., 2000) that, when GABA_A receptors (GABA_ARs) are blocked in slices of neonatal mouse hippocampus bathed in Mg²⁺-free artificial CSF (ACSF), highly rhythmic population bursts occur as early as the day of birth. Here we show that the frequency of these neonatal interictal bursts (nIBs) is strongly modulated by pharmacological manipulations that are known to affect the level of I_h activation, suggesting that I_h plays a major role in the timing of nIBs.

Materials and Methods

Slice preparation and solutions. Horizontal brain slices, 500 μm thick, including hippocampus were prepared from neonatal mice of postnatal days 1–6 (P1–P6) (P0 being the first 24 hr after birth). Except for the plane of section, procedures were as described previously (Wells et al., 2000). Slices chosen for experiments (one to two per animal, bisected along the midline to yield two hemislices each) were perpendicular to the long axis of the hippocampus or nearly so (see Fig. 1). After dissection, slices were submerged in a holding chamber with recirculated, oxygenated ACSF at room temperature. For recording, slices were transferred to a submersion chamber and continuously superfused, using a push–pull configuration of peristaltic pumps, with 2.5–3 ml/min ACSF at room temperature, saturated with a mixture of 95% O₂–5% CO₂. ACSF for dissection and for the holding chamber was composed of the following (in mm): 126 NaCl, 3 KCl, 1.2 NaH₂PO₄, 2.0 CaCl₂, 1.3 MgSO₄, 26 NaHCO₃, and 20 dextrose. In the recording chamber, slices were initially superfused with Mg²⁺-free ACSF, which was identical in composition except that equimolar CaCl₂ was substituted for MgSO₄, for a final Ca²⁺ concentration of 3.3 mm, to maintain the total divalent ion concentration. To induce paroxysmal discharges (nIBs) (see Fig.2A), 5 μm of the GABA_AR antagonist gabazine was then added to the bath. Mg²⁺-free ACSF with 5 μm gabazine will be referred to as “control ACSF.”

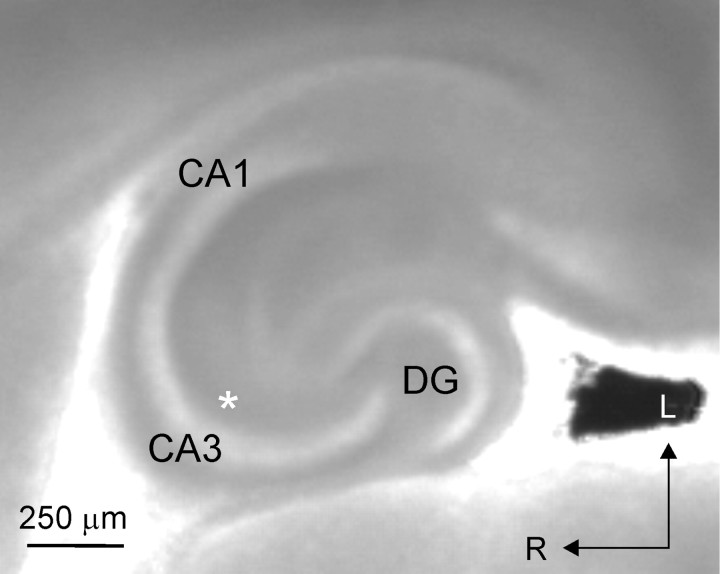
Fig. 1.

A horizontal hippocampal slice from a P4 mouse, as visualized during the experiment. CA1, CA3, and dentate gyrus (DG) are indicated; typical recording position in CA3 stratum radiatum is indicated by the asterisk. Arrows denote lateral (L) and rostral (R) directions.

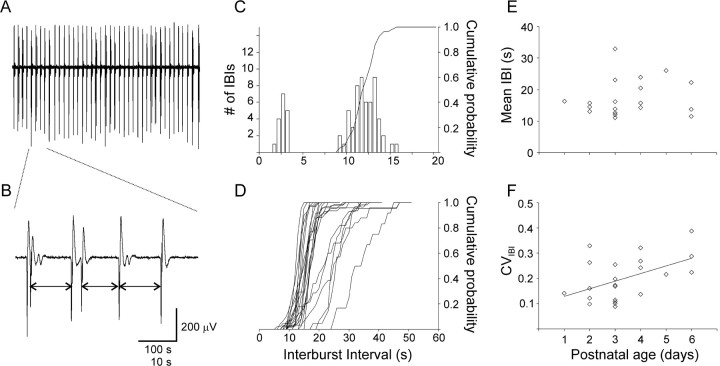
Fig. 2.

Neonatal IBs in area CA3 are highly regular. A, A 500-sec-long extracellular record from a P3 slice bathed in control ACSF (Mg²⁺-free, with 5 μm gabazine), illustrating the high regularity of nIBs.B, A segment expanded from the record inA, illustrating that intercluster intervals (two-sided arrows) but not intracluster intervals were included in the analysis in this study. C, The IBI histogram for the experiment ofA shows two well separated peaks; the peak below 5 sec consists of intracluster intervals, which were excluded in the calculation of the CIH (solid line). CV_IBI for this experiment was 0.12. D, Superimposed CIHs from all 22 slices recorded in control ACSF. Note the tight clustering and steep slope of 16 CIHs on the left side of the plot, illustrating the pacemaker-like character of nIBs. E, The mean IBI of all slices showed no change with postnatal age. F, In contrast, the CV_IBI increased significantly between P1 and P6 (note the regression line).

Drugs. SR-95531 (gabazine), 3-isobutyl-1-methylxanthine (IBMX), and staurosporine were purchased from Sigma (St. Louis, MO). Forskolin, dideoxyforskolin, and ZD-7288 were purchased from Tocris (Ballwin, MO). Drugs were prepared as stock solutions in water or DMSO, as required, at (typically) 1000-fold final concentration, divided into aliquots, and stored at −20°C. During experiments, thawed aliquots were diluted directly into control ACSF.

Electrophysiological recordings. Extracellular field potentials were recorded using thick-walled glass micropipettes broken to a final outside diameter of ∼5 μm under microscopic control and filled with 0.9% NaCl. Differential DC signals (tissue vs bath) were low-pass filtered at 1 kHz, amplified 1000× (Intronix Technologies, Bolton, Ontario, Canada), digitized at 1000 samples/sec, and streamed to disk, using custom software written (by A. Agmon) in the LabView environment (National Instruments, Austin, TX).

Data analysis. Because the raw data were highly oversampled, data records were smoothed and decimated offline by replacing successive blocks of data points with their average; the size of the averaged block (32 points) was chosen empirically to provide optimal noise reduction with minimum loss of signal amplitude and was kept the same for all analyzed records. Effects of drugs were quantified as a ratio over control conditions and are reported as geometric means ± geometric SEMs, together with the number of slices (n) and the number of animals (N) tested in each condition. To quantify drug effects on nIB frequency (see Figs. 3, 4), the number of nIBs in a 500 sec window, starting at least 1000 sec after drug arrival and spanning the period of maximal drug effect, was divided by the number of nIBs in a 500 sec window immediately preceding drug arrival. To calculate nIB amplitudes and interburst intervals (IBIs), nIBs were logged, time-stamped, and measured by custom software written in LabView (A. Agmon); each logged event was examined visually and confirmed by the user, who also checked the record to verify that no nIBs were missed by the program. The amplitude of an nIB was defined as its peak-to-peak voltage difference, and the IBI was defined as the interval between the negative peaks of two adjacent events. When bursts occurred in clusters (see Fig. 2A–C and the first paragraph of Results), each cluster was regarded as a single nIB with amplitude equal to that of the first event in the cluster (which was always the largest), and IBIs were measured from the negative peak of the last event in one cluster to the negative peak of the first event in the next cluster (see Fig. 2B, arrows). Cumulative IBI histograms (CIHs) were calculated using MathCad (MathSoft, Cambridge, MA). All slices with nIBs in control ACSF of at least 200 μV in amplitude and 20 mHz (1 every 50 sec) in frequency were included in the analysis.

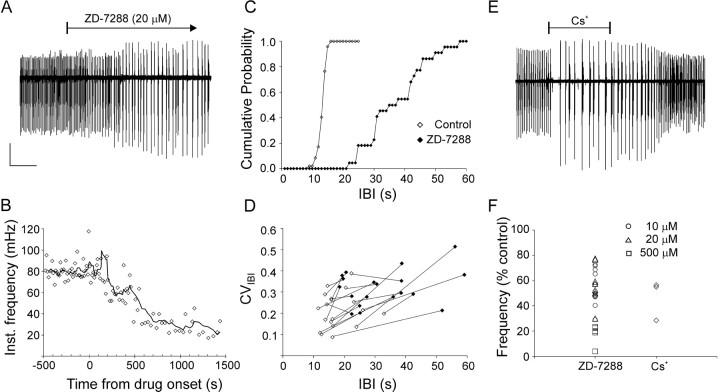
Fig. 3.

Blocking I_h strongly reduced nIB frequency and regularity. A, BlockingI_h with the specific blocker ZD-7288 caused a more than threefold reduction in nIB frequency, coupled to a pronounced increase in nIB amplitudes. B, The time course of decrease in nIB frequency for the experiment shown inA, plotted at the same time scale. Data points represent instantaneous frequency (1/previous IBI); solid line is a running average, calculated using a sliding window of five data points. Time 0 designates drug arrival in the recording chamber. C, The rightward shift and decreased slope of the CIH for the experiment ofA illustrates the drug-induced increase in the IBI and the CV_IBI, respectively. CIHs were calculated using 1 sec bins. D, CV_IBI plotted against mean IBI, with data points from the same slice before (open symbols) and after (filled symbols) adding ZD-7288 connected by lines. Note that, in the great majority of cases, the ZD-7288-induced increase in the mean IBI was coupled to a pronounced increase in the CV_IBI.E, A reduction in nIB frequency of a similar magnitude to that induced by ZD-7288 was caused by the less specific (but reversible) I_h blocker Cs⁺ (2 mm). F, Summary of the percent reduction in nIB frequency attributable to ZD-7288 (see legend for concentrations) and Cs⁺ (2 mm) in all experiments. A andE are from different P3 animals. Calibration:A, 100 μV, 300 sec; E, 150 μV, 250 sec.

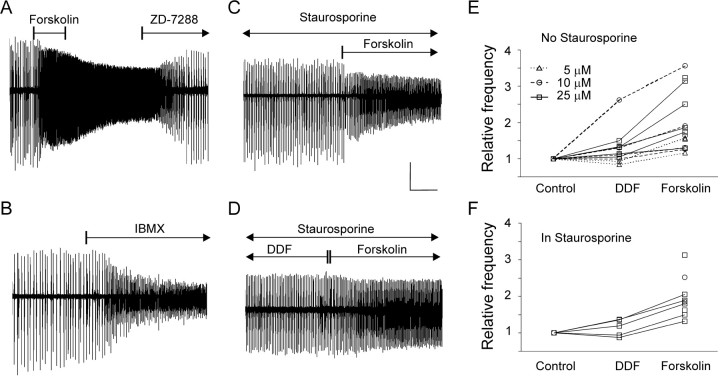
Fig. 4.

Increasing intracellular cAMP strongly accelerated nIB frequency in a PKA-independent manner. A, The adenylyl cyclase activator forskolin (25 μm) caused a threefold increase in nIB frequency and a concomitant decrease in amplitudes within minutes after application; theI_h blocker ZD-7288 (20 μm) reversed this increase and further reduced the nIB frequency to 60% of its control value before forskolin application (P1 slice).B, Application of the phosphodiesterase inhibitor IBMX (200 μm) caused a 2.5-fold increase in nIB frequency and a concomitant reduction in amplitudes (P3 slice). C, Preincubation for >1 hr with the broad-spectrum protein kinase inhibitor staurosporine (100 nm) did not prevent forskolin (20 μm) from accelerating nIBs by 1.7-fold (P3 slice).D, In the presence of staurosporine, forskolin (25 μm) still caused a 1.5-fold increase in nIB frequency over the frequency in equimolar concentration of the analog DDF, which does not activate adenylyl cyclase (P5 slice). E, Summary plot of all slices tested in DDF and forskolin without staurosporine; data points not connected by lines are from slices tested only in forskolin. Symbols and lines are coded by drug concentration (legend). F, Summary plot as inE but for slices tested in the presence of 100 nm staurosporine. Calibration: A, 100 μV, 500 sec; B, 200 μV, 400 sec; C, 200 μV, 250 sec; D, 100 μV, 250 sec.

Statistics. Statistical significance (pvalue) was computed numerically using exact permutation methods (Good, 1999); calculations were done in MathCad. Specifically, significance of drug-induced changes was computed using the binomial sign test; significance of differences between population means was computed from 10,000 random permutations of the data, and significance of linear correlations (see Fig. 2E,F) was calculated from the Pitman statistic Σ_i(i ·X_i) computed for 10,000 random permutations of the data. All reported p values are single-tailed probabilities unless noted otherwise.

Computational modeling of nIBs. All modeling was done using MathCad software; the following description uses MathCad notation. The model assumed that, on average, μ spontaneous Poissonian events (e.g., sEPSPs) occur in any given time epoch (a single time epoch in the model represented 100 msec). The probability that exactlyk events will occur in any given time epoch is given by the following Poisson distribution:

$$P(k,\mu ):=\frac{{\mu }^k}{k!}·e^{-\mu }.$$

The probability C(k,μ) that kor fewer events will occur is given by the cumulative Poisson distribution as follows:

$$C(k,\mu ):=\sum _{n=0}^{k}P(n,\mu ).$$

Assume that the occurrence of M (or more) events within a single time epoch triggers a burst. The unconditional probability B(M,μ) of burst occurrence at any given epoch is, therefore, 1 minus the probability that M − 1 or fewer events will occur, or

$$B(M,\mu ):=1-C(M-1,\mu ).$$

A normalized IBI histogram gives the probability of occurrence of an IBI of any given length. Once a burst has occurred, the probability that the next burst will occur after exactly jtime epochs is the product of the (j − 1) probabilities (1 − B(M,μ)) that a burst will not occur at any of the first (j − 1) epochs and the probability B(M,μ) that a burst will occur at the jth epoch:

$$IBI\underset{\_}{\hspace{0.5em}}{\text{histogram}}_j:=(1-B(M,\mu ){)}^{j-1}·B(M,\mu )$$

(In the limit of infinitesimally short epochs, this simply gives the interevent interval histogram of Poissonian events, which is a decaying exponential.)

Now assume that μ itself is not stationary but drops to 0 immediately after a burst and then relaxes exponentially to an asymptotic steady-state level μ_ss:

$${\mu }_j:={\mu }_{\text{ss}}·\left(1-exp\left(-\frac{j}{z}\right)\right),$$

where j is the index of the current time epoch (counting from the occurrence of the last burst), and τ is the time constant of relaxation expressed in time epochs. The expression for the normalized IBI histogram will now be as follows:

$$IBI\underset{\_}{\hspace{0.5em}}{\text{histogram}}_j:=\left(\prod _{i=0}^{j-1}(1-B(M,{\mu }_i))\right)·B(M,{\mu }_j).$$

From this vector, the mean IBI and the CV_IBI (the coefficient of variation of the IBIs) are easily calculated:

$$\text{Mean}\underset{\_}{\hspace{0.5em}}IBI:=\sum _{j}j·IBI\underset{\_}{\hspace{0.5em}}{\text{histogram}}_j,$$

$$SD\underset{\_}{\hspace{0.5em}}IBI:=\sqrt{\sum _j(j-\text{Mean}\underset{\_}{\hspace{0.5em}}IBI{)}^2·IBI\underset{\_}{\hspace{0.5em}}{\text{histogram}}_j},$$

$$CV\underset{\_}{\hspace{0.5em}}IBI:=\frac{SD\underset{\_}{\hspace{0.5em}}IBI}{\text{Mean}\underset{\_}{\hspace{0.5em}}IBI}.$$

Finally, the CIH is simply the time integral of the normalized IBI histogram, as follows:

$${CIH}_j:=\sum _{i=0}^{j}IBI\underset{\_}{\hspace{0.5em}}{\text{histogram}}_i.$$

To fit experimental CIHs with simulated curves (see Fig. 7), this vector was calculated for 1 ≤ j ≤ 1000 (equivalent to 100 sec) for different values of the three free parameters (M, μ_ss, and τ). In addition to computing CIH (see Fig. 7A), IBI, andCV_IBI values (see Fig.6E,F), the assumptions of the model were also used to simulate directly trains of nIBs (see Fig.6A–D), using the MathCad functionrpois(m, λ) which returns a vector ofm random numbers having a Poisson distribution with a mean λ.

Fig. 7.

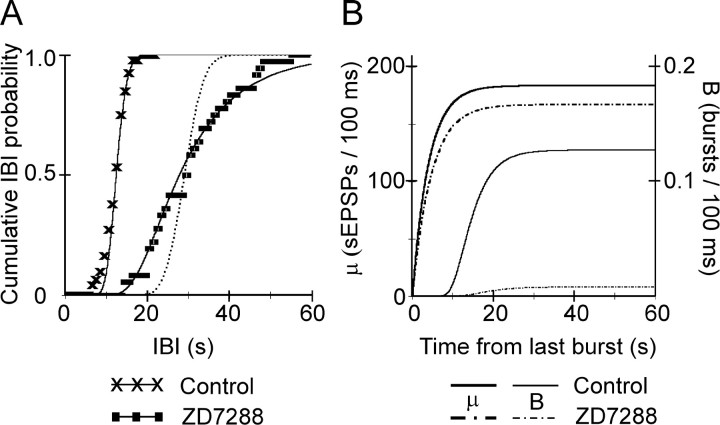
A change in μ_ss, but not in τ, can account for the effect of ZD-7288 on nIB frequency and regularity. A, CIHs of experimental nIBs from a P6 slice in control ACSF (× symbols) was fitted by a curve (solid line) computed with the parameter values μ_ss = 184 and τ = 4 sec. The effect of 20 μm ZD-7288 (squares) was well fitted (solid line) by reducing μ_ss to 167.5, with only a minor increase in τ (to 4.6 sec). With μ_ssunchanged, a 2.5-fold increase in τ (to 10.5 sec) was required to achieve the same rightward shift in the median IBI, but the resulting curve (dotted line) did not reproduce the pronounced decrease in the slope of the experimental CIH. Experimental CIHs were calculated in 1 sec bins. B, The value of the model parameter μ (lefty-axis) in control ACSF (heavy solid line) and in ZD-7288 (heavy dashed-dotted line), as a function of the time elapsed because the previous burst, for the same parameter values used inA. The relatively small reduction in μ_ssrequired to simulate the effect of the drug caused a dramatic drop in the probability of burst occurrence per 100 msec (righty-axis) in ZD-7288 (light dashed-dotted line) compared with control ACSF (light solid line), because now fluctuations around μ only rarely crossed threshold (compare with Fig.6C,D).

Fig. 6.

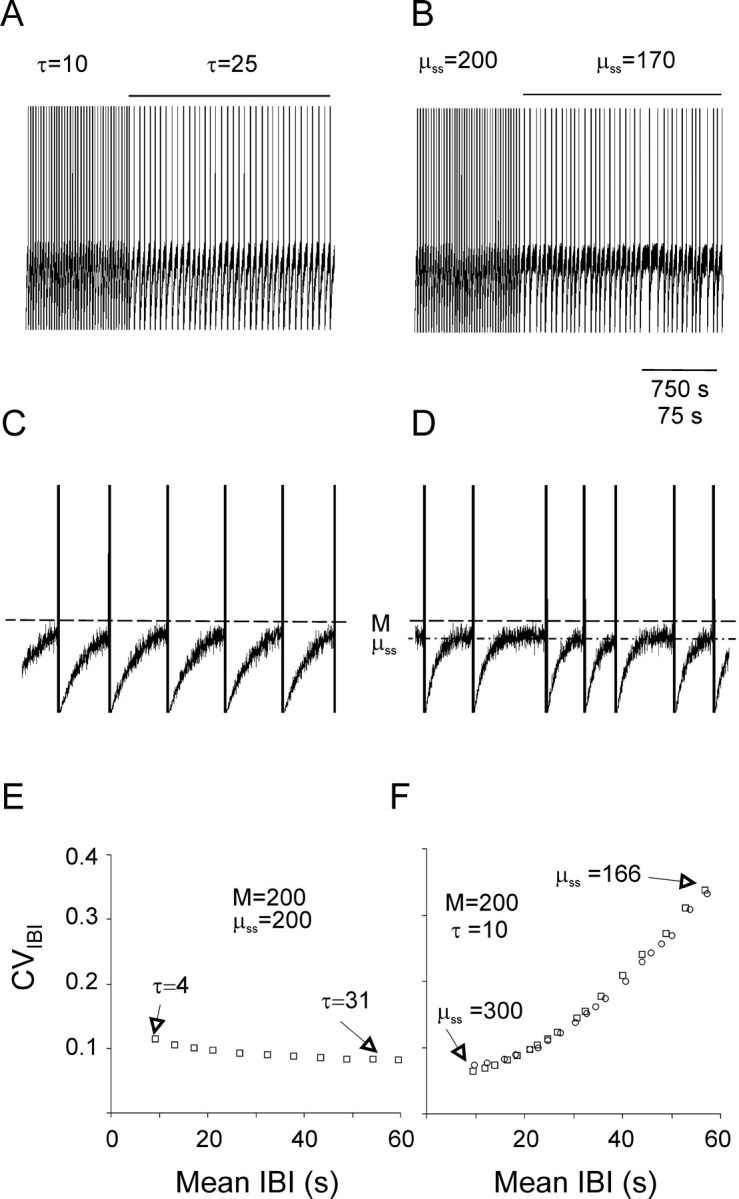
A three-parameter computational model simulated the effect of ZD-7288 on nIB frequency and regularity.A–D, Simulated sequences of nIBs are plotted at a slow (A, B) and a 10-fold faster (C, D) time base. Simulated nIBs were generated by assuming that the mean instantaneous sEPSP rate (μ) is reset to 0 after each burst and then relaxes exponentially to an asymptote (μ_ss) with a time constant τ. Fluctuations around μ were generated by a Poissonian random-number generator; each time a fluctuation crossed the thresholdM (dashed line in C andD), a burst was assumed to be triggered. InA and B, the initial part of the trace was computed using the values M = μ_ss = 200 and τ = 10 sec; during the time indicated by the horizontal lines above the trace, either τ (A, C) or μ_ss(B, D) were changed to the values indicated (μ_ss is also indicated by the dashed-dotted line in D). The traces represent the value of μ, except that the occurrence of a burst is indicated by a vertical line of arbitrary height. Note that increasing τ (A,C) reduced the frequency of bursts without affecting their regularity, whereas reducing μ_ss (B,D) affected both the frequency and the regularity of the bursts. E, The simulated CV_IBI versus the simulated mean IBI, computed using the indicated values ofM and μ_ss while varying the value of τ as indicated. Note that changing τ had very little effect on the CV_IBI. F, The simulated CV_IBIversus the simulated mean IBI, computed using the indicated values ofM and τ while varying μ_ss as indicated (squares). Note that changing μ_ss affected in parallel both the mean IBI and the CV_IBI. Changing Mfrom 140 to 238 while keeping μ_ss = 200 generated data points (circles) that fell along the same curve generated by changing μ_ss while keeping Mconstant.

Results

We monitored epileptiform population activity in area CA3 of neonatal mice, by recording extracellular field potentials from stratum radiatum in horizontal hippocampal brain slices (Fig. 1, asterisk denotes a typical recording location). As reported previously (Wells et al., 2000), superfusing the slice with Mg²⁺-free ACSF with 5 μm of the GABA_AR antagonist gabazine (control ACSF) resulted in the appearance of large-amplitude, rhythmic population discharges (Fig.2A), which will be referred to here as nIBs. An initial exposure to Mg²⁺-free ACSF alone for 20–30 min, before addition of gabazine, seemed to be required to “prime” the burst mechanism, because slices superfused directly with control ACSF often failed to burst regularly. Individual nIBs consisted of a triphasic extracellular potential (Fig. 2B), with an early, large-amplitude negative “spike,” ∼0.5 sec in duration, followed by a slower and smaller positive “wave,” and ending with an even smaller negative undershoot. In many slices, some of the nIBs occurred in doublets or triplets or (rarely) in clusters of four to five events (Fig. 2B illustrates a sequence of two doublets, followed by two single bursts). Intracluster intervals (typically <5 sec) were always much shorter than intercluster intervals and formed a clearly separable peak in the IBI histogram (Fig. 2C). Unlike intercluster intervals, intracluster intervals were not affected by our experimental manipulations (data not shown) and were likely to be under the control of a separate mechanism. Intracluster intervals were therefore excluded from analysis, and each cluster was treated as a single, prolonged event for the sake of determining IBIs (Fig. 2B, arrows demonstrate the definition of IBIs in this study) (see Materials and Methods).

Neonatal IBs exhibited pacemaker-like regularity

The bursting characteristics of each slice were quantified by calculating the mean IBI, the coefficient of variation of the IBIs (CV_IBI, i.e., the SD/mean of the IBIs), and the CIH (the normalized integral of the IBI histogram). The CIH of the slice illustrated in Figure 2A is superimposed on the IBI histogram of the same slice in Figure 2C. CIHs of all of the slices in our sample recorded in control ACSF are shown superimposed in Figure 2D. In control ACSF, nIBs occurred at highly regular intervals of 11–32 sec, with the CV_IBI averaging 0.20 ± 0.02 (n = 22; N = 17). Moreover, as illustrated in Figure 2D, the majority of our slices (73%) had CIHs tightly clustered at the left end of the range, with IBIs for this group averaging 14.2 ± 0.4 sec (n = 16) and with a mean CV_IBI of 0.18 ± 0.02. The mean IBI did not change significantly with age over the developmental period of our study (Fig. 2E) (p = 0.30; two-tailed), but the CV_IBI showed a small but significant increase (Fig. 2F) (p < 0.05; two-tailed), indicating some loss of precision with maturation. Indeed, interictal activity in slices from juvenile animals was considerably less regular than in neonatal slices (our unpublished observations).

Blocking I_h strongly reduced nIB frequency and regularity

The high regularity of nIBs prompted us to look for an underlying pacemaker mechanism. A hypothesis proposed over two decades ago (Lebovitz, 1979) suggests that each IB is followed by a postburst refractory period, during which generation of additional bursts is suppressed. This suppression was postulated to be caused by a slowly decaying inhibitory conductance activated by the burst itself; hence, this mechanism was named “autorhythmicity.” If indeed an inhibitory conductance activated by the burst was responsible for pacing nIBs, then blocking it should cause a pronounced acceleration of the rhythm. However, blocking any of the known inhibitory conductances had little or no effect on nIB frequency (our unpublished observations) (Staley et al., 1998).

An alternative to a slowly decaying inhibition is a slow buildup of excitation, for example by a slow inward “pacemaker” current. If such a current is involved in the timing of nIBs, then blocking it should decrease nIB frequency. A current implicated in pacing the heart, as well as various neuronal oscillators in the CNS, is the hyperpolarization-activated cationic currentI_h (Pape, 1996). We therefore tested the effect of ZD-7288, which, until very recently (Chevaleyre and Castillo, 2002), was considered a highly selective blocker ofI_h (Harris and Constanti, 1995;Gasparini and DiFrancesco, 1997; Satoh and Yamada, 2000), on nIB frequency. In the experiment illustrated in Figure3A, 20 μm ZD-7288 caused a threefold decrease in nIB frequency, with the mean IBI increasing from 12.0 to 35.9 sec. The time course of this effect of ZD-7288 is plotted in Figure 3B, in which the instantaneous burst rate (1/previous IBI) and its running average are plotted against time after drug arrival in the recording chamber. As illustrated by the graph, the reduction in bursting rate developed over several minutes, and the maximal effect was reached within ∼1000 sec from the moment of drug arrival. In a total of six slices in which the time course of drug action was examined in detail, on average, ∼1200 sec superfusion with 20 μmZD-7288 was required for maximal reduction in nIB frequency (range, 700–1650 sec). The time to maximal effect of ZD-7288 on nIB frequency was consistent with the time to maximal block ofI_h by ZD-7288, reported to be 10–20 min in studies using 20–100 μm of the drug (Harris and Constanti, 1995; Maccaferri and McBain, 1996; Gasparini and DiFrancesco, 1997; Chevaleyre and Castillo, 2002).

The CIHs of the experiment in Figure 3A, before and after exposure to ZD-7288, are shown in Figure 3C. In addition to the pronounced reduction in the frequency of nIBs, evident from the rightward shift of the CIH, ZD-7288 also markedly reduced their temporal precision, as evident from the pronounced decrease in the slope of the CIH (Fig. 3C). In this slice, the CV_IBI increased from 0.11 to 0.28. In Figure3D, the CV_IBI is plotted against mean IBI for all slices tested in 10–20 μm ZD-7288, with data points corresponding to the same slice before and after addition of drug connected by lines. The concomitant increase in both mean IBI and CV_IBI is clearly evident from the general upward-and-rightward direction of the connecting lines. On average, application of ZD-7288 (10–20 μm) decreased the rate of nIBs to approximately one-half of the control frequency (0.54 ± 0.03; n = 22; N= 17; p < 10⁻⁶) and increased the CV_IBI by 1.52 ± 0.14-fold over control ACSF (p < 0.001).

CsCl (2 mm), another (although less specific) blocker ofI_h (Magee, 1998), reduced nIB frequency in neonatal slices to 0.45 ± 0.10 of control (n = N = 3) (Fig. 3E). Unlike ZD-7288, the effect of Cs⁺ was readily reversed after washout. Figure 3F summarizes the effects of 10–20 μm ZD-7288 (circles and triangles, respectively) and Cs⁺ on nIB frequency in all slices tested.

Although generally considered a highly selective blocker ofI_h in various systems (BoSmith et al., 1993; Briggs et al., 1994; Harris et al., 1994; Satoh and Yamada, 2000), ZD-7288 was very recently reported to depress synaptic transmission in the hippocampus through an unknown mechanism, apparently independent of its effect onI_h (Chevaleyre and Castillo, 2002). The time course of synaptic depression was very slow compared with the effect on I_h examined in the same study, with no obvious depression occurring until at least 30 min of exposure to drug and with maximal effect requiring at least 60 min of exposure to 50 μm ZD-7288; lower concentrations of drug (10 μm) caused only a slight depression after a similar exposure time. Thus, it seemed highly unlikely that these nonspecific effects of ZD-7288 could have contributed to the pronounced reduction in nIB frequency after 20 min of exposure to 20 μm ZD-7288 in our experiments. Also, the pronounced increase in nIB amplitudes induced by ZD-7288 in our experiments seemed inconsistent with synaptic depression. Nevertheless, we tested for any synaptic depression under the conditions of our experiments by quantifying the effect of ZD-7288 on field EPSPs (fEPSPs) evoked in CA1 by stimulation of the CA3 to CA1 pathway, the same pathway tested by Chevaleyre and Castillo (2002). These control experiments were done on slices from P5–P29 mice, because, in slices from younger animals, the evoked fEPSP was too small and labile for reliable analysis. Seven slices in which the evoked fEPSP was stable (to ±20% of control amplitude) for at least 30 min before drug application were selected for analysis. In these slices, the evoked response remained virtually unchanged after 60 min of superfusion with 20–25 μm ZD-7288 (1.01 ± 0.14 of control amplitude; n = 7; N = 6; data not shown). We conclude that the typical concentration of ZD-7288 used in our study did not cause any appreciable synaptic depression within the time course of the experiments. However, very high concentrations (500 μm) of ZD-7288 caused drastic reduction in the frequency of nIBs (to 0.21 ± 0.05 of control; n = 5; N = 3; p < 0.05) (Fig.3F, squares) and, in contrast to the lower concentrations, also strongly depressed nIB amplitudes (data not shown), suggesting that high concentrations of ZD-7288 may indeed cause synaptic depression.

Increasing intracellular cAMP strongly increased nIB frequency

I_h is strongly modulated by cyclic nucleotides, which bind directly to the cytoplasmic domain of the channel (Pape, 1996; Santoro and Tibbs, 1999; Wainger et al., 2001); we therefore tested whether modulating intracellular cAMP affected nIB frequency. In the experiment illustrated in Figure4A, the adenylyl cyclase activator forskolin (25 μm) accelerated nIBs more than threefold and markedly reduced their amplitude; both effects were reversed by 20 μm ZD-7288. Overall, forskolin (10–25 μm) caused a 2.0 ± 0.5-fold increase in nIB frequency (n =N = 3). Forskolin (5–25 μm) still increased nIB frequency in the presence of ZD-7288 (15 μm), causing a 2.1- to 3-fold increase over the frequency in ZD-7288 alone (n = N = 2; data not shown); this could have represented the effect of elevated intracellular cAMP concentration on residualI_h channels, because 15 μm ZD-7288 is expected to block only ∼50% of the channels in hippocampal pyramidal neurons (Gasparini and DiFrancesco, 1997).

Because forskolin also adds to excitability by blocking K⁺ channels, we tested the effects of the analog dideoxyforskolin (DDF), which also blocks K⁺ channels but does not activate adenylyl cyclase (Hoshi et al., 1988). DDF (5–25 μm) caused a modest (1.23 ± 0.11-fold) increase in nIB frequency compared with control ACSF; however, replacing DDF by equimolar amounts of forskolin caused an additional increase (compared with the frequency in DDF) of 1.47 ± 0.09-fold (n = 11; N = 9;p < 0.001), as summarized in Figure4E. We also tested the effect on nIB frequency of IBMX, a nonselective inhibitor of the enzymatic degradation of cAMP by phosphodiesterase (Fredholm et al., 1976). Application of 200 μm IBMX caused, on average, a 1.87 ± 0.25-fold increase in nIB frequency (n = 6;N = 3; p < 0.02) (Fig.4B). Because both forskolin and IBMX are expected to increase the intracellular concentration of cAMP, we conclude that intracellular cAMP has a strong positive modulatory effect on nIB frequency.

cAMP effects on nIB frequency were protein kinase A independent

cAMP could potentially modulate nIB frequency by mechanisms independent of I_h, for example by reducing the slow I_AHP (Dunwiddie et al., 1992; Pedarzani and Storm, 1995a), by increasing synaptic efficacy (Chavez-Noriega and Stevens, 1992; Boulanger and Poo, 1999;Castro-Alamancos and Calcagnotto, 1999), or by opening gap junctions (Burghardt et al., 1995; Banoub et al., 1996; Paulson et al., 2000; van Rijen et al., 2000; Carystinos et al., 2001). All f these effects, however, are thought to be mediated by protein kinase A (PKA), whereas the effect of cAMP on I_h in CA1 and elsewhere is attributed to direct gating of the channel by cAMP (DiFrancesco and Tortora, 1991; Pedarzani and Storm, 1995b; Wainger et al., 2001). To test whether PKA-mediated effects could have contributed to the observed effect of forskolin, we superfused the slices with the broad-spectrum protein kinase blocker staurosporine (100 nm) for 30–60 min before addition of forskolin. Preincubation in staurosporine caused a variable reduction in nIB amplitude but no change in frequency (data not shown; n= 7; N = 4; p = 0.47; two-tailed). Preincubation in staurosporine did not affect the large increase in nIB frequency seen with 10–25 μm forskolin (Fig.4C) (nIB frequency increased by 2.1 ± 0.2-fold;n = 5; N = 4; p < 0.05). In the presence of staurosporine, 25 μmDDF caused a small, 1.13 ± 0.10-fold increase in nIB frequency, but replacing DDF by equimolar amounts of forskolin (Fig.4D) caused an additional increase in frequency (compared with DDF) of 1.50 ± 0.03-fold (n = 5;N = 4; p < 0.05), which was not significantly different from the effect of forskolin without staurosporine in the bath (p = 0.80; two-tailed). The effects of DDF and forskolin in the presence of staurosporine are summarized in Figure 4F. We conclude that the strong acceleration of nIBs by forskolin and IBMX was not dependent on PKA but was consistent with a direct action of cAMP on the I_h channel. This does not exclude the possibility of PKA-mediated effects onI_h (Mellor et al., 2002; Vargas and Lucero, 2002), because these indirect effects could have been occluded by the direct effects of cAMP.

[To verify that our batch of staurosporine was effective, we tested it on the cAMP-mediated presynaptic enhancement of the mossy fibers to CA3 pathway, which is PKA dependent (Weisskopf et al., 1994; Lonart et al., 1998). In two slices from two P13 mice, a 20 min application of 25 μm forskolin caused a 1.6- to 2.4-fold increase in the amplitude of the postsynaptic (but not the presynaptic) component of the field potential evoked in CA3 by a 50–80 μA stimulus in the hilus of the dentate gyrus. In a second slice from each animal, preincubation with 100 nm staurosporine for 30–45 min totally blocked this forskolin-induced potentiation (data not shown), providing evidence that our batch of staurosporine effectively blocked PKA.]

Burst amplitudes were strongly correlated with the preceding but not the following IBI

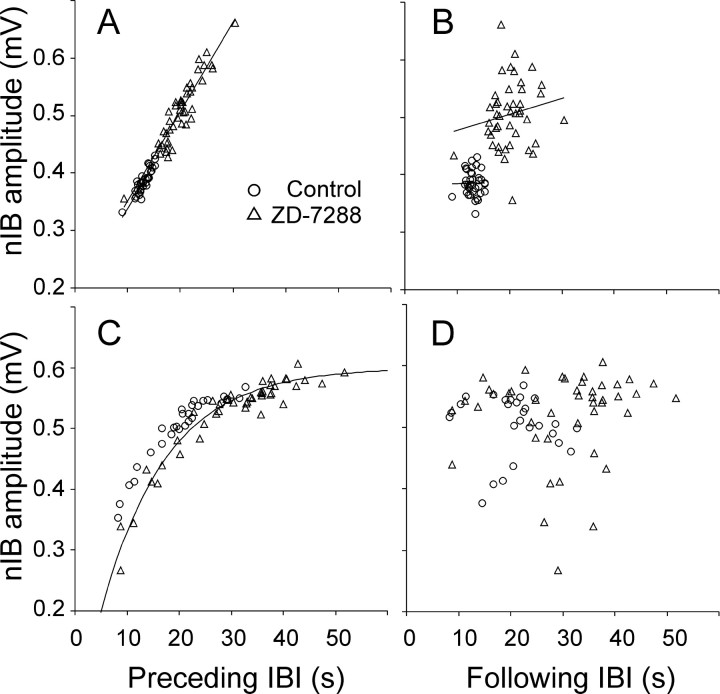
As is evident from Figures 3 and 4, drugs that reduced the frequency of nIBs also increased their amplitude, whereas drugs that accelerated the bursts reduced their amplitude. The change in amplitude could have been a result of the change in frequency; conversely, the change in frequency could have been secondary to the change in amplitude. To determine whether the primary effect of ZD-7288 was on the frequency of nIBs or on their amplitudes, we examined the correlation between event amplitudes and both the preceding and the following IBIs. If the primary effect of the drug was to increase nIB amplitude, and the increased amplitude in turn slowed down the rhythm, one would expect that nIB amplitudes would be correlated with the following, but not with the preceding, IBIs. As evident from Figure5, the opposite was the case: nIB amplitudes were strongly dependent on the IBIs preceding the events (Fig. 5A,C) and not at all on the IBIs following them (Fig. 5B,D). In slices with IBIs not exceeding 30 sec, the relationship between the amplitudes of nIBs and the preceding IBIs was well described by linear regression (Fig. 5A); the mean coefficient of determination (r²) of the linear regression line was 0.64 ± 0.04 in control and 0.78 ± 0.03 in ZD-7288 (n = 25; N = 20). When nIB amplitudes from the same slices were plotted against the following IBIs (Fig.5B), no such correlation was observed (r² = 0.04 ± 0.01 for both control and ZD-7288 conditions). In slices with IBIs longer than 30 sec, nIB amplitudes seemed to reach a ceiling at IBIs of 30–40 sec, and the relationship between nIBs and preceding IBIs was better fit by a decaying exponential (Fig. 5C); again, no such relationship was observed with the following IBIs (Fig. 5D). This analysis strongly suggested that ZD-7288 directly affected the frequency of the nIBs and that the change in amplitude was a secondary effect caused by the slowing of the rhythm and not vice versa. In most slices (e.g., the two illustrated in Fig.5A,C), data points from nIBs in control solution were distributed along or close to the same line fitted to data points collected in the presence of ZD-7288, suggesting that the drug affected only the timing of the events and did not disturb the relationship between timing and amplitude.

Fig. 5.

Amplitudes of nIBs were strongly correlated with the preceding but not the following interburst intervals. Illustrated data were recorded before (circles) and after (triangles) adding ZD-7288 to a P2 slice (A, B) and a P4 slice (C, D). In A andB, data points in control and in ZD-7288 were fitted separately with linear regression lines, illustrating a strong correlation in A(r² = 0.80 andr² = 0.87, respectively) but lack of correlation in B(r² = 5 × 10⁻⁵ and r²= 0.03, respectively). Note that the two regression lines inA nearly coincide. In C, data points in ZD-7288 were fitted by a decaying exponential with an asymptote of 0.6 mV and a time constant of 12.5 sec; note that data points in control ACSF fall along nearly the same curve

A simple computational model simulated the effect of ZD-7288 on nIB frequency and regularity

To gain insight into the mechanism by whichI_h modulates nIB rhythm, we constructed a network-level mathematical model of the pacemaker driving nIBs, which generated computed IBI distributions closely resembling experimental CIHs (for mathematical details of the model, see Materials and Methods). Our model formally resembled a model recently described by Staley et al. (2001) but differed in some of its underlying assumptions and in using Poissonian rather than binomial statistics. The model assumed that excitatory synapses in CA3 are spontaneously active at a rate that fluctuates with a Poissonian distribution around a mean instantaneous rate μ (Fatt and Katz, 1952; Rotshenker and Rahamimoff, 1970; Isaacson and Walmsley, 1995). It further assumed that μ falls to 0 immediately after an nIB and then recovers exponentially, with a time constant τ, to a steady-state level μ_ss (Staley et al., 1998, 2001). Finally, it assumed that a burst is triggered whenever the actual instantaneous rate of sEPSPs in the network exceeds a threshold M (Prida and Sanchez-Andres, 1999). A Monte-Carlo implementation of the model (based on a random number generator) was used to generate simulated trains of nIBs (Fig.6A–D), and a computational implementation was used to calculate mean IBI, CV_IBI, and CIH values of modeled nIBs (Fig.6E,F) and to fit them to experimental CIHs (Fig. 7A). It should be noted that the model made no assumptions about the underlying cellular constituents. For example, the parameter μ could be interpreted as the aggregate rate of sEPSPs in the network or it could refer to the rate of sEPSPs in a subset of cells functioning as a pacemaker “kernel.”

Although the model depended on three free parameters (M, μ_ss, and τ), within a relatively wide range of values, the simulated CIHs were sensitive mostly to the difference between M and μ_ss and not to their absolute values (Fig. 6F); we therefore effectively reduced the number of free parameters to two by fixing M at the arbitrary value M = 200 and varied the other two parameters (τ and μ_ss) independently. Varying these two parameters had very different effects on the behavior of the model. When τ was increased, the frequency of simulated nIBs was reduced, but little change in their regularity was evident (Fig.6A,C), as corroborated by calculating the mean IBI and the CV_IBI for a range of values of τ; the computed CV_IBI values slightly decreased as the computed mean IBIs increased (Fig.6E). In contrast, decreasing μ_ss also reduced the frequency of simulated nIBs but, at the same time, markedly reduced their regularity (Fig.6B,D). When CV_IBI values were plotted against corresponding IBIs computed for a range of values of μ_ss, it was evident that the CV_IBI values increased in parallel with the mean IBI (Fig. 6F, squares). When, instead of decreasing μ_ss while keeping the threshold M constant, M was increased while keeping μ_ss constant, the computed data points (Fig. 6F, circles) fell along the same line as the data points computed by varying μ_ss while holding M constant.

The effect of blocking I_h was well modeled by a reduction in the steady-state rate of sEPSPs but not by an increase in its time constant of recovery

As evident from a comparison of Figure 3D with Figure6, E and F, a reduction in μ_ss or an increase in M, but not a change in τ, could reproduce the experimental effect of blockingI_h, which was an increase in both the mean IBI and in the CV_IBI. The model would therefore be consistent with our data if blockingI_h increased the differenceM − μ_ss, but not if it changed τ. To test this directly, we fitted computed CIHs to experimentally determined ones, by keeping M = 200 and varying independently both μ_ss and τ. Figure7A illustrates experimental CIHs from a P6 slice, recorded before and after addition of ZD-7288. The superimposed solid lines were the best fit computed from our model. In control ACSF, the best fit was achieved with the parameter values μ_ss = 184 and τ = 4.0 sec. In ZD-7288, the best fit was achieved with parameter values μ_ss = 167.5 and τ = 4.6 sec, which represents a doubling of the difference M − μ_ss but only a 15% increase in the time constant τ. Increasing τ alone (by 2.5-fold), without changing μ_ss, shifted the computed control CIH to the right but did not change its slope (dotted line), corresponding to an increase in the median IBI with little or no change in CV_IBI, as demonstrated in Figure6E. On average, ZD-7288 application had no effect on the best-fit value of τ (in control, τ = 6.7 ± 0.6 sec,n = 19, N = 15; in ZD-7288, τ increased by 1.04 ± 0.05-fold and was not significantly greater than control; p = 0.23). In contrast, the best fit for the mean difference M − μ_ssnearly tripled, from 10.7 ± 3.0 in control to 28.8 ± 2 in ZD-7288 (p < 10⁻⁶).

In the example of Figure 7A, a reduction in μ_ss from 184 to 167.5 sEPSPs/100 msec, which represents a fractional reduction by <9%, caused >2.5-fold increase in the mean IBI and >1.5-fold increase in the CV_IBI. To understand why a relatively small change in the steady-state rate of synaptic activity could cause a dramatic decrease in both the frequency and the regularity of nIBs, it is instructive to examine how the probability for the occurrence of a burst (B(M,μ) in the model; see Materials and Methods) was influenced by the difference M − μ_ss. The drug-induced decrease in μ_ss is illustrated in Figure 7B, which plots μ (heavy solid line for control, heavy dashed-dotted line for ZD-7288) as a function of time elapsed from the previous burst, for the same values of the model parameters used to fit the experimental data in Figure 7A. Although the reduction in μ_ss induced by ZD-7288 was modest, the maximal probability for a burst to occur decreased from 0.127/100 msec in control ACSF (Fig. 7B, light solid line) to only 0.0088/100 msec in the presence of ZD-7288 (light dash-dotted line), which is a 14-fold decrease. The result of this large reduction in burst probability was that, by the time 20 sec have elapsed from the previous burst, a burst had occurred with near certainty (99.9% probability) in control ACSF but with only 20% probability in the presence of ZD-7288, as seen from the CIHs in Figure 7A.

Discussion

Our results indicate that the frequency and the temporal precision of spontaneous interictal bursts in the neonatal CA3 are positively modulated by the hyperpolarization-activated, cyclic nucleotide-sensitive cationic currentI_h. This conclusion is based on the pronounced decrease in nIB frequency and regularity whenI_h was blocked by either Cs⁺ or ZD-7288 (Fig. 3), a specific bradycardic agent whose only known effect, at the concentrations and exposure times we used, is to block I_h(Harris and Constanti, 1995; Gasparini and DiFrancesco, 1997; Satoh and Yamada, 2000). This conclusion was further supported by the pronounced increase in nIB frequency induced by manipulations that are expected to elevate intracellular cAMP levels (Fig. 4). The cAMP-mediated effect was not affected by blocking PKA with staurosporine, consistent with a direct action of cAMP on the I_hchannel (Pedarzani and Storm, 1995b; Wainger et al., 2001). To our knowledge, this is the first report implicatingI_h in the timing of interictal epileptiform bursts. The strong acceleration of interictal epileptiform bursts by cAMP is also demonstrated here, to our knowledge, for the first time (for modest effects in adult rats, see Boulton et al., 1993) and may need to be considered when prescribing to epilepsy-prone patients drugs that may potentially affect cAMP levels.

Blocking I_h can be modeled by either an increase in the burst threshold or a decrease in the rate of spontaneous synaptic release

How does I_h modulate burst frequency? To gain insight into this question, we developed a simple computational model based on the assumption that a burst is triggered whenever the instantaneous rate of spontaneous EPSPs exceeds a threshold M; a similar mechanism appears to determine the timing of “giant depolarizing potentials,” another form of oscillatory activity in the neonatal hippocampus (Prida and Sanchez-Andres, 1999). The rate of sEPSPs, in turn, was assumed to be a Poissonian variable, with a mean μ that dropped to zero immediately after a burst and then recovered to an asymptotic steady-state value μ_ss with a time constant τ. [A formally similar model described by Staley et al. (2001) uses binomial, rather than Poissonian, statistics and is based on somewhat different assumptions.] Once an appropriate set of parameters (M, μ_ss, and τ) was found to generate a cumulative IBI histogram that fit the experimental record from a given slice, the effect of blockingI_h in the same slice could be satisfactorily reproduced by increasing the differenceM − μ_ss, by either increasing the threshold M or decreasing the steady-state sEPSP rate μ_ss but not by increasing the time constant τ. This allows two different interpretations for the role ofI_h in the timing of nIBs.

First, I_h could be increasing neuronal excitability in general, for example by contributing to a more depolarized resting potential, as has been demonstrated in the hippocampus and elsewhere (Akasu et al., 1993; Li et al., 1993;Maccaferri et al., 1993; Travagli and Gillis, 1994; Maccaferri and McBain, 1996; Seutin et al., 2001). According to this interpretation,I_h would be contributing to a reduced threshold M but would have no effect on μ. The postburst depression and recovery of μ would then need to be explained by other mechanisms, e.g., by depletion of synaptic vesicles (caused by high-frequency firing during the burst), followed by their gradual replenishment (Zucker and Regehr, 2002). The major determinant of the time constant τ, according to this hypothesis, would be the time course of synaptic vesicle replenishment, andI_h would only be modulating the rhythm, not pacing it. Whereas recovery from synaptic depression has been successfully used to model rhythmic bursting in a variety of systems (Staley et al., 1998, 2001; Tabak et al., 2000; Tsodyks et al., 2000), the role of synaptic vesicle replenishment in pacing interictal bursts is yet to be tested directly by pharmacological or genetic manipulations that accelerate it or slow it down.

An alternative interpretation for the role ofI_h in timing nIBs, also consistent with the model, is that instead of decreasing the thresholdM, I_h increases μ_ss, the steady-state rate of sEPSPs, e.g., by directly depolarizing presynaptic terminals (Beaumont and Zucker, 2000;Southan et al., 2000; Mellor et al., 2002). Depolarization of presynaptic terminals will increase calcium influx through voltage-gated calcium channels, enhancing the probability of spontaneous neurotransmitter release (Alger et al., 1996; Frerking et al., 2001; Turecek and Trussell, 2001). This interpretation is consistent with the forskolin-induced increase in miniature GABAergic currents described in immature CA3 neurons (Sciancalepore and Cherubini, 1995) and is attractive because it also explains the postburst modulation in μ: if μ is governed byI_h, then its time course between bursts should reflect the time course ofI_h, which is expected to be inactivated immediately after the burst (attributable to the strong depolarization during the burst) and then to reactivate slowly (by the postburst hyperpolarization) to a steady-state level. The time constant of recovery τ would therefore be determined by the activation kinetics of I_h, andI_h would actually function as the pacemaker for nIBs. This interpretation is consistent with our finding that the effect of ZD-7288 could be simulated by reducing μ_ss and not by increasing τ,because ZD-7288 strongly reduces the steady-state amplitude of theI_h current with little or no change in its activation kinetics (Harris and Constanti, 1995; Satoh and Yamada, 2000).

I_h channels with the appropriate properties are expressed in the neonatal CA3

A major constraint on the alternative interpretation above is thatI_h needs to be activated with a time constant comparable with τ, which in our data averaged ∼7 sec. A very recent study of I_h in the developing mouse hippocampus (Vasilyev and Barish, 2002) indicates that activation kinetics of I_h in neonatal (P1–P5) CA3 pyramidal neurons are indeed dominated by a slow component with a time constant of 5–10 sec at physiological hyperpolarized potentials. Of the four known subunits from whichI_h channels may be assembled, pyramidal cells in the neonatal CA3 express HCN1 and HCN2 mRNA (Bender et al., 2001) and protein (Vasilyev and Barish, 2002). In heterologous expression systems, I_hchannels consisting solely of the HCN2 subunit exhibit much slower kinetics and considerably higher cAMP sensitivity compared with HCN1-only or with mixed HCN1/HCN2 channels (Santoro et al., 2000; Chen et al., 2001; Wainger et al., 2001); it is therefore tempting to speculate that the HCN2 subunit is the major contributor toI_h channels in the neonatal CA3. Regardless of molecular composition, however,I_h channels in the neonatal CA3 exhibit activation kinetics consistent with our model and with a possible role in pacing interictal bursts.

Burst amplitudes reflect recovery from synaptic depression

As shown in Figure 5, the amplitude of nIBs was correlated with the preceding, but not with the following, IBI; a similar relationship was demonstrated previously in the mature CA3 (Staley et al., 1998), in the embryonic spinal cord (Streit, 1993; Tabak et al., 2001), in the retina (Grzywacz and Sernagor, 2000), and in networks of dissociated cortical neurons (Opitz et al., 2002), suggesting that this relationship is a common feature of rhythmically bursting synaptic networks (O'Donovan, 1999). Burst intensity (which can be reflected in burst amplitude and/or in burst duration) is thought to be determined by the total number of readily releasable synaptic vesicles at the moment of burst initiation (Staley et al., 1998); this number presumably declines to near zero immediately after the burst, because virtually all synapses are activated during a paroxysmal event, and then gradually increases as vesicles are replenished from the reserve pool (Zucker and Regehr, 2002). In our experiments, burst amplitudes did not recover fully until 30–40 sec after the previous burst (Fig.5C), suggesting that the time constant of vesicle replenishment was considerably longer than the time constant τ, calculated to be ∼7 sec from our experimental data. This lends additional support to the alternative interpretation above, that the activation of I_h, and not recovery from synaptic depression, was the process pacing nIBs in the neonatal CA3.

The mechanisms of pacing by I_h are system specific

Whether I_h acts as a bona fide pacemaker of interictal activity in the neonatal hippocampus or merely modulates the rhythm by affecting overall excitability remains to be determined. Indeed, the common characterization ofI_h as a “pacemaker current” (Pape, 1996) may obscure its very different modes of action in different systems, which may oscillate at frequencies orders of magnitude apart. For example, I_h accelerates both the heartbeat (DiFrancesco and Ojeda, 1980) and the much faster oscillations in thalamocortical relay neurons (McCormick and Pape, 1990; Soltesz et al., 1991); it also accelerates nIBs in CA3, which are an order of magnitude (at least) slower than the heartbeat. In contrast, I_h actually slows down spindles in the thalamus, which oscillate at approximately the same frequency as nIBs (Luthi et al., 1998). The recent cloning of HCN channels (Ludwig et al., 1998; Monteggia et al., 2000) will no doubt be followed by the generation of knock-out mice in which the precise role of I_h in pacing oscillations in different systems could be tested directly. Note that an HCN2 knock-out mouse was reported recently by Ludwig et al. (2003).