Foveal Versus Full-Field Visual Stabilization Strategies for Translational and Rotational Head Movements

Abstract

Because we view the world from a constantly shifting platform when our head and body move in space, vestibular and visuomotor reflexes are critical to maintain visual acuity. In contrast to the phylogenetically old rotational vestibulo-ocular reflex (RVOR), it has been proposed that the translational vestibulo-ocular reflex (TVOR) represents a newly developed vestibular-driven mechanism that is important for foveal vision and stereopsis. To investigate the hypothesis that the function of the TVOR is indeed related to foveal (as opposed to full-field) image stabilization, we compared the three-dimensional ocular kinematics during lateral translation and rotational movements with those during pursuit of a small moving target in four rhesus monkeys. Specifically, we tested whether TVOR rotation axes tilt with eye position as in visually driven systems such as pursuit, or whether they stay relatively fixed in the head as in the RVOR. We found a significant dependence of three-dimensional eye velocity on eye position that was independent of viewing distance and viewing conditions (full-field, single target, or complete darkness). The slopes for this eye-position dependence averaged 0.7 ± 0.07 for the TVOR, compared with 0.6 ± 0.07 for visually guided pursuit eye movements and 0.18 ± 0.09 for the RVOR. Because the torsional tilt versus vertical gaze slopes during translation were slightly higher than those during pursuit, three-dimensional eye movements during translation could partly reflect a compromise between the two different solutions for foveal gaze control, that of Listing's law and minimum velocity strategies. These results with respect to three-dimensional kinematics provide additional support for a functional difference in the two vestibular-driven mechanisms for visual stability during rotations and translations and establish clearly the functional goal of the TVOR as that for foveal visual acuity.

Introduction

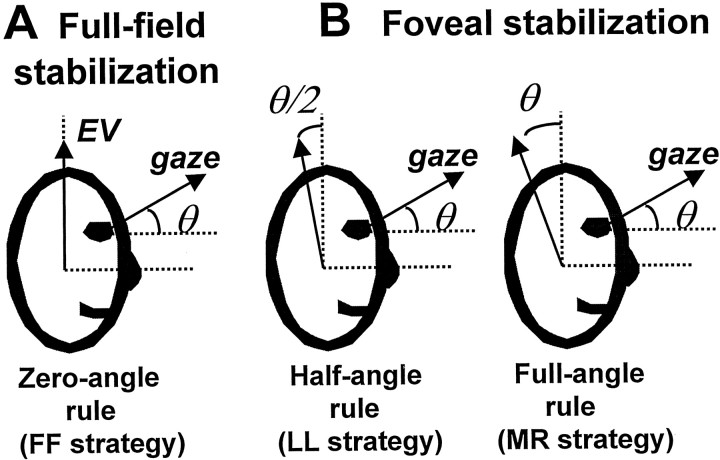
For an eye movement whose functional goal is to keep images stable on the fovea, such as during visual tracking of a small target, only the horizontal and vertical components of gaze direction need to be specified. In general, the eyes could assume an infinite number of torsional orientations and still foveate the target, because ocular torsion remains unspecified. Among the different possible orientations that the eyes could assume (each of which would have a different consequence for optic flow on the peripheral retina), three strategies have been described as providing unique, although distinct, advantages (see Fig. 1). On one extreme, the eye could always rotate about an axis that is anchored to the head and is independent of the direction of gaze. This is the optimal strategy for minimizing slip on the peripheral retina, thus providing for a full-field (FF) image stabilization solution [see Fig.1A, full-field strategy]. On the other extreme, the rotation axis of the eye could remain eye-fixed, and thus, in head coordinates, rotate similarly as gaze [see Fig. 1B,right, minimum rotation (MR) strategy]. The advantage of this solution is that the eye follows the shortest possible path to acquire the target but results in the largest slip of images on the peripheral retina. The third strategy rotates the eye about axes that are in between a head-fixed and an eye-fixed coordinate system. Its unique advantage is that, contrary to the first two solutions, ocular torsion is minimized [see Fig. 1B, left, Listing's law (LL) strategy]. It is now well established that smooth pursuit, and in general all conjugated, visually guided, foveal-specific eye movements, obey LL (Tweed and Vilis, 1987, 1990;Haslwanter et al., 1991; Tweed et al., 1992).

Fig. 1.

Geometrical expectations based on different strategies for image stabilization. A, For FF image stabilization (FF strategy), the axis of rotation of the eye [shown as the arrow indicating eye velocity (EV)] should always remain head-fixed (e.g., head horizontal) and be independent of the direction of gaze.B, For foveal image stabilization, the axis of rotation of the eye is not anchored to the head. According to the LL strategy, the axis of rotation of the eye is neither head-fixed nor eye-fixed, but rather rotates in the same direction of gaze through one-half the angle of gaze (θ/2; half-angle rule). According to the MR strategy, the axis of rotation of the eye remains eye-fixed (i.e., rotates in the same direction and through the same angle as gaze, θ; full-angle rule). Dotted lines represent the head vertical and horizontal directions.

In contrast to foveal-specific eye movements, the rotational vestibulo-ocular reflex (RVOR), whose goal is to stabilize images on the entire retina and whose sensory input can uniquely specify all three degrees of freedom of the eye, best complies with the FF strategy (Crawford and Vilis, 1991; Misslisch et al., 1994; Misslisch and Hess, 2000). However, unlike the role of the RVOR in FF visual stabilization, it has been proposed that the translational vestibulo-ocular reflex (TVOR) function is tightly coupled with foveal vision and stereopsis (Miles, 1993, 1998). To date, two experimental results have provided support for this hypothesis. First, it has been shown that the TVOR anticipates and accounts for the motion parallax associated with viewing targets at different depth planes during translation, because eye velocity changes in inverse proportion to viewing distance (Schwarz et al., 1989; Paige and Tomko, 1991;Schwarz and Miles, 1991; Telford et al., 1997; Miles, 1998). Second, the horizontal and vertical components of the evoked eye movement depend on heading (movement) direction and eye position, as expected according to the geometrical dependencies associated with keeping images stable on the fovea (McHenry and Angelaki, 2000;Angelaki and Hess, 2001).

Indeed, if the functional goal of the TVOR is to assist and extend foveal tracking, then it must be modulated as a function of gaze similar to smooth-pursuit eye movements. Thus, in the present study, we have compared the three-dimensional kinematics associated with the TVOR with those of the RVOR and pursuit eye movements as a simple test for a more general conceptual property regarding the functional role of vestibular-evoked eye movements during translation.

Materials and Methods

Binocular eye movements were recorded in four rhesus monkeys during 0.5 Hz (± 3°) pursuit, 0.5 Hz (± 0.08 gm), or 4 Hz (± 0.25 gm) lateral translation and 4 Hz (±1–3°) yaw rotation. Two of the animals were implanted with dual coils on each eye for three-dimensional eye-movement recordings (Hess, 1990). In the remaining two animals, only one eye was implanted with a dual three-dimensional coil. Because the other eye was implanted with a traditional two-dimensional coil, binocular responses were used for behavioral control (and reinforcement of the appropriate vergence angle for each target distance; see below), although quantitative analysis was performed only on the data recorded in the eye with the three-dimensional coil. All animals were trained to fixate or follow targets (<0.5°) at distances of 12, 18, 32, or 100 cm in a softly illuminated room. Targets were back-projected onto one of four screens and were presented either as single targets using a laser/mirror galvanometer system (General Scanning, Watertown, MA) in a dimly illuminated room or as a computer-generated, red target within full-field, white, random-dot patterns using a projector (Mirage 2000; Christie Digital, Cypress, CA). Eye movements were calibrated by requiring the animals to monocularly fixate far targets at different horizontal and vertical eccentricities (Angelaki et al., 2000; Angelaki and Hess, 2001).

During translation, rotation, and pursuit, the eye-position dependence of eye velocity was tested by requiring the animals to fixate targets in the midsagittal plane at different vertical eccentricities (up to ±25°). During 4 Hz motion, periods of target presentation were alternated with periods in total darkness. With the 0.5 Hz stimuli, the target was on throughout the experimental run. Trained animals were required to keep their eyes within binocular behavioral windows of <1.5° (during pursuit) or <3° (during motion), even in darkness. The vergence angle was monitored throughout the experiment. Only data for which the actual vergence angle was within 10% of the “ideal” values (based on target distance and eccentricity, as well as the monkey's interocular distance) (Angelaki et al., 2000) were included in the analyses. This was important to investigate any potential effect of different vergence angles on the kinematic rules followed by pursuit, TVOR, and RVOR.

During experiments, the monkeys were seated in a primate chair that was secured inside the inner frame of a rotator/sled motion delivery system (Neurokinetics, Pittsburgh, PA). Both stimulus presentation and data acquisition were controlled with custom-written scripts within the Spike2 software environment using the Cambridge Electronics Design(CED, model 1401; Cambridge, UK) data acquisition system. Data were anti-alias-filtered (200 Hz, six pole Bessel), and digitized by the CED at a rate of 833.33 Hz (16 bit resolution). Off-line, eye-movement data were converted into rotation vectors, using straight ahead as the reference position. In addition, angular velocity was computed and fast phases were removed from the velocity records using a semi-automated procedure based on higher derivatives of eye velocity (Hepp, 1990; Angelaki et al., 2000). Angular velocities were expressed using the right-hand rule (if you point your right thumb in the direction of the vector, then your fingers curl around in the direction of spin). Positive directions were leftward, downward, and clockwise for the horizontal, vertical, and torsional components, respectively. For example, a forward-pointing vector represents a clockwise rotation (from the animal's viewpoint). The amount of axis tilt in the animal's sagittal plane was evaluated by plotting the elicited eye-velocity vector in head coordinates and fitting a line in three dimensions. A “torsional tilt angle” was then computed from the direction cosines of the three-dimensional line, as the angle between the line and the positive horizontal axis in the sagittal plane. Subsequently, torsional tilt angles were plotted versus vertical eye position, and regression lines were used to quantitatively describe this dependence. For the 4 Hz motion stimuli, the analysis was performed separately for cycles with the target on and in total darkness. All statistical comparisons used repeated-measures ANOVA (for both the effects of distance and RVOR/TVOR/pursuit).

For a direct comparison, experimental conditions were similar during rotation, translation, and pursuit, other than the frequency of stimulation, which was 0.5 Hz for pursuit but 4 Hz for the TVOR/RVOR. We considered it important to test the TVOR at a frequency that is more functionally relevant (Paige and Tomko, 1991; Telford et al., 1997) than in the low-frequency range to be directly comparable with pursuit. Nevertheless, in two of the animals we also collected data during lower-frequency (0.5 Hz) translation. Because the results during low-frequency translation were the same as those at 4 Hz, the data presented in Results focus on the higher-frequency stimulus. Furthermore, because the orientation of Listing's plane depends on the vergence angle (Mok et al., 1992; Van Rijn and Van den Berg, 1993;Minken and Van Gisbergen, 1994; Misslisch et al., 2001), it was important that a direct comparison with pursuit be made for each viewing distance.

Results

If image stability on the peripheral retina is important for the TVOR (as is the case for the RVOR), we would expect little or no torsional eye velocity during lateral translation at vertically eccentric eye positions (“zero-angle rule”) (Fig.1A). In contrast, a kinematic requirement for both the MR and LL strategies is a specific eye-position dependence of the axis of rotation of the eye, in which the eye velocity axis is expected to tilt by the same or half the angle of gaze (“full-angle rule” and “half-angle rule,” respectively) (Fig. 1B) (Tweed and Vilis, 1987, 1990; Tweed et al., 1992; Misslisch et al., 1994). As is explained below, contrary to the RVOR, eye velocity in the TVOR exhibited a large and systematic dependence on vertical gaze position.

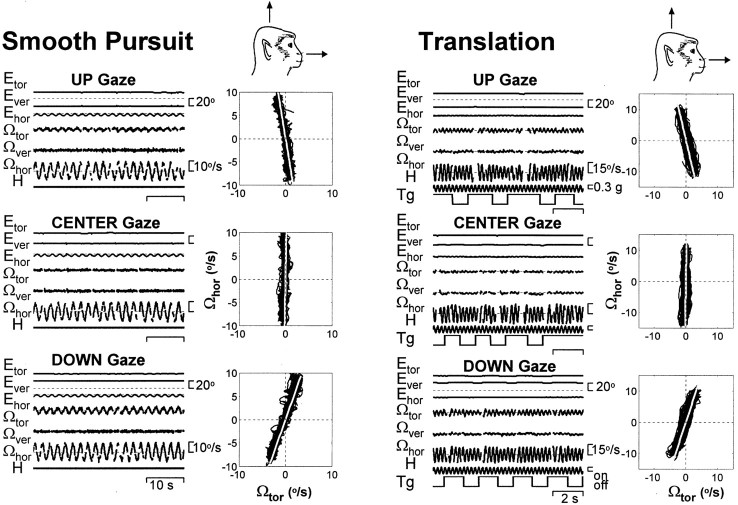
Let us first consider the three-dimensional eye velocity organization during horizontal pursuit at different vertical eccentricities. During horizontal smooth pursuit with the gaze straight ahead, for example, the elicited eye movement is purely horizontal, with negligible modulation in torsional eye velocity (Fig.2, smooth pursuit). However, because of the kinematic constraints of LL, a combination of both horizontal and torsional eye movements is observed during pursuit of a target that is moving horizontally in eccentric positions. During horizontal pursuit with gaze up, for example, a negative (counterclockwise relative to the animal, as viewed from the right ear) torsion accompanies the positive (leftward) component of pursuit. The opposite is true for down gaze (Fig. 2). As a result, the instantaneous axis of rotation of the eye tilts away from a purely head-horizontal axis in the same direction as gaze and through approximately one-half the gaze angle, as illustrated when eye velocity is plotted in head coordinates (Fig. 2, smooth pursuit).

Fig. 2.

Dependence of smooth pursuit and ocular responses during translation on vertical gaze. From top tobottom, Three-dimensional eye position (E_tor,E_ver, andE_hor) and angular velocity (Ω_tor, Ω_ver, Ω_hor) for up, center, and down gaze during 0.5 Hz (± 3°) pursuit and 4 Hz (± 0.25 gm) lateral translation (distance of 32 cm). Tg, Target on and off; H, head motion acceleration. Fast phases have been eliminated.

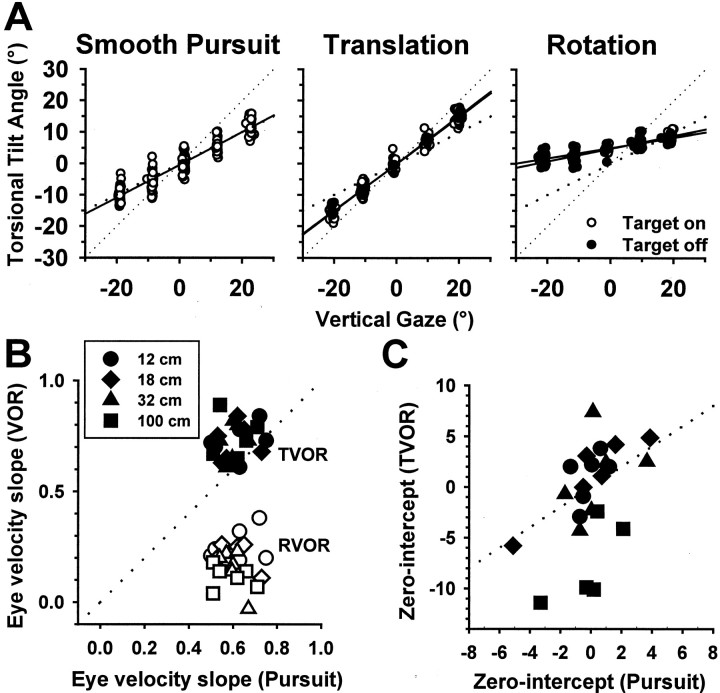
A similar dependence of eye velocity on gaze angle was also observed during lateral translation (Fig. 2, translation). Similar to pursuit responses, the amount of axis tilt was evaluated by plotting eye velocity in head coordinates and fitting a line in three dimensions (Fig. 2, white lines). The torsional tilt angle was then computed from the direction cosines of the three-dimensional line as the angle formed with the positive horizontal axis in the sagittal plane. Torsional tilt angles were plotted versus vertical gaze, and regression lines were used to describe this dependence quantitatively (Fig. 3A). Similar to pursuit, significant correlations were observed between torsional tilt angles and vertical gaze during translation. Regression lines for the gaze dependence of pursuit were consistent with the half-angle rule of LL. However, regression slopes for the TVOR were typically >0.5, as illustrated by the data points falling between the lines corresponding to half-angle and full-angle (unity) slopes (Fig. 3A,middle, dotted lines). Similar to previous reports in humans and monkeys (Misslisch et al., 1994; Misslisch and Hess, 2000), the torsional tilt angle as a function of vertical gaze during rotation was significantly lower (Fig. 3A,bottom).

Fig. 3.

A, Calculated torsional tilt angles of eye velocity as a function of vertical gaze during pursuit, translation, and rotation as the animal followed a target at a distance of 18 cm. Solid lines represent linear regressions;dotted lines illustrate the full- and half-angle rules of three-dimensional kinematics. B, The torsional eye velocity tilt versus vertical gaze angle slopes for the TVOR (solid symbols) and RVOR (open symbols) from four animals (6 eyes) at different viewing distances.Dotted lines illustrate the unity-slope line (diagonal).C, The corresponding zero-intercepts for the TVOR regressions plotted versus the corresponding values for pursuit. Other than the farthest distance (squares), data fall along the unity (dotted) line.

Data from all four animals have been summarized in Figure3B,C. For each animal, the torsional tilt versus gaze angle slope during rotation, translation, and pursuit were computed separately for four target distances (12–100 cm). When compared directly with the corresponding values during pursuit, TVOR slopes lie along or slightly above the unity-slope line (Fig. 3B,solid symbols and diagonal dotted line). The torsional tilt versus gaze angle slopes averaged 0.7 ± 0.07 during translation and 0.6 ± 0.07 (means ± SD) for visually guided pursuit eye movements (difference not significant;F_(1,4) = 0.15; p > 0.05). In contrast, RVOR slopes were smaller, averaging 0.18 ± 0.09. Results were similar during the actual fixation of either a space-fixed single target or a full-field random dot pattern, as well as in intermingled periods of complete darkness (F_(1,15) = 1.3; p > 0.05).

As shown in Figure 3B, the closer the target, the larger the RVOR slope (F_(3,24) = 11.7 ;p < 0.05). In contrast, the slopes of the eye-position dependence for the TVOR (and pursuit) were independent of viewing distance (F_(3,12) = 0.03;p > 0.05). However, the zero-intercepts of the TVOR regressions (i.e., the torsional tilt angle at zero vertical elevation) depended on viewing distance (Fig. 3C) (F_(3,12) = 33.7; p < 0.05). This was not so for pursuit, for which both the slopes and the zero-intercepts remained independent of target distance. Only for near targets (at 12, 18, and 32 cm) were the zero-intercepts for TVOR and pursuit similar (F_(1,5) = 0.04;p > 0.05). In contrast, for small vergence angles (i.e., far targets), the zero-intercept values were larger than those of pursuit (F_(1,4) = 30.6;p < 0.05; compare the squares with the unity-slope dotted line in Fig. 3C).

Discussion

Because translational displacements could result in a differential optic flow across the retina, no single eye movement could generally result in stabilization of the entire visual field. Theoretically, the brain has a choice between two extreme strategies: it can eliminate optical flow entirely over the fovea, or it can minimize the average optical flow over the entire retina, with no special concern for the fovea. Alternatively, it could do something in between, keeping optical flow over the fovea somewhat smaller than the average flow elsewhere. If the TVOR represents an eye-movement system whose function is linked to foveal image stabilization, it must also be characterized by three-dimensional kinematics that are similar to those during other foveal-specific ocular responses, such as pursuit, and different from those in the RVOR. This expectation was verified here by showing that the three-dimensional kinematics of the TVOR are more similar to those during pursuit and unlike those of the RVOR.

In a previous study in which torsion was quantified during high-frequency translation while maintaining fixation on a near target, a systematic dependence of TVOR eye velocity on vertical gaze angle was reported, with a slope of 0.7 (Angelaki et al., 2000). The possibility that TVOR might follow LL was addressed then, although because the target was visible during motion and because corresponding data for pursuit and the RVOR were not available, a direct comparison could not be made. Thus, the present study was specifically designed to compare directly the eye-position dependence of the TVOR, RVOR, and pursuit at different target distances and under different viewing conditions. The present results clearly support the hypothesis (Miles, 1993, 1998) that the RVOR and TVOR are functionally distinct processes, although they both arise from signals originating in the labyrinth. Specifically, for near-target viewing (<32 cm) when the TVOR is functionally important, we found its three-dimensional kinematics to be statistically indistinguishable from those of pursuit, in contrast to those for the RVOR. Nevertheless, because the torsional tilt versus vertical gaze slopes during translation were slightly higher than those during pursuit (means of 0.7 vs 0.6, respectively), three-dimensional eye movements during translation might partly reflect a compromise between the two different strategies for gaze control, that of LL and MR strategies (Misslisch et al., 1994).

What is the functional advantage for the eye-position dependence exhibited by the TVOR? Although several suggestions about the functional significance of LL have been made, one important aspect is keeping the eyes near the center of their motor range (by minimizing torsion), thus improving motor efficiency (von Helmholtz, 1867; Hering 1868; Hepp, 1990, 1995; Tweed and Vilis, 1990; Tweed et al., 1992). The three-dimensional kinematic rules outlined in Figure 1 also make distinct predictions about how three-dimensional visual scenes project onto the retina. Specifically, if the eye were to follow the zero-angle rule, in which eye axes remain anchored to the head and independent of gaze (Fig. 1A, FF strategy), space-horizontal lines do not remain parallel with the horizontal meridian of the eye at eccentric eye positions. A space-horizontal line appears to turn clockwise when the eye looks right and counterclockwise when it looks left (Klier and Crawford, 1998; Crawford et al., 2000). Although this geometrical problem is eliminated with a full-angle rule, in which eye axes move 100% with gaze (Fig. 1B, right), the MR strategy has never been observed for the eye. Instead, visually guided eye rotations lie in between these two extremes in terms of a mismatch between space and retinal line orientations (Crawford et al., 2000). Thus, the TVOR 0.7 angle rule might represent an efficient compromise between the need to enhance motor performance by keeping the eyes near the center of their motor range and the need to minimize the lack of correspondence between spatial and retinal coordinates.

When viewing targets at various depths, the three-dimensional rotations of the two eyes are yoked in accordance with a recently discovered geometric rule that has been referred to as the binocular extension of LL, or LL2 (Mok et al., 1992; Tweed, 1997; Misslisch et al., 2001). Briefly, the Listing's planes of the two eyes rotate temporally as the eyes converge, such that the eyes incyclorotate when looking up and excyclorotate when looking down (Mok et al., 1992; Van Rijn and Van den Berg, 1993; Minken and Van Gisbergen, 1994; Misslisch et al., 2001). The functional significance of this rotation lies in the fact that it tends to reduce torsional disparities in the two eyes: When Listing's planes rotate temporally by as much as the eyes converge, horizontal lines at the fovea stay parallel to the horizontal of the eye (Tweed, 1997). Moreover, the search zones for retinal correspondence necessary to achieve stereoscopic vision are retina-fixed and independent of gaze direction, although the epipolar lines (the retinal bands where corresponding image features project in the two eyes) migrate on the retinas when the eyes change position (Schreiber et al., 2001). Thus, the reason that the eyes twist about their lines of sight in compliance with LL2 is to reduce the motion of the epipolar lines, allowing for easier and more efficient stereopsis. Accordingly, it has been proposed that LL and LL2 represent important contributors to binocular vision (Schreiber et al., 2001).

The fact that the TVOR follows the three-dimensional kinematic strategies consistent with foveal vision and stereovision provides strong support for a phylogenetically novel role of the primate vestibular system regarding its contribution to a postulated crucial function of the oculomotor system in depth vision. How this phylogenetically novel vestibulo-ocular system is implemented within the premotor circuitry and how it interacts with the phylogenetically “old” RVOR remain unresolved. Recent neurophysiological recordings suggest a differential premotor processing of vestibular signals in the TVOR and RVOR (Angelaki et al., 2001), although details about the underlying circuitry, physiology, and computations are still in the very early stages of exploration.