A Dynamic Dendritic Refractory Period Regulates Burst Discharge in the Electrosensory Lobe of Weakly Electric Fish

Abstract

Na⁺-dependent spikes initiate in the soma or axon hillock region and actively backpropagate into the dendritic arbor of many central neurons. Inward currents underlying spike discharge are offset by outward K⁺ currents that repolarize a spike and establish a refractory period to temporarily prevent spike discharge. We show in a sensory neuron that somatic and dendritic K⁺ channels differentially control burst discharge by regulating the extent to which backpropagating dendritic spikes can re-excite the soma. During repetitive discharge a progressive broadening of dendritic spikes promotes a dynamic increase in dendritic spike refractory period. A leaky integrate-and-fire model shows that spike bursts are terminated when a decreasing somatic interspike interval and an increasing dendritic spike refractory period synergistically act to block backpropagation. The time required for the somatic interspike interval to intersect with dendritic refractory period determines burst frequency, a time that is regulated by somatic and dendritic spike repolarization. Thus, K⁺channels involved in spike repolarization can efficiently control the pattern of spike output by establishing a soma-dendritic interaction that invokes dynamic shifts in dendritic spike properties.

Introduction

The duration of an action potential is typically controlled through an active repolarization by voltage- or Ca²⁺-dependent K⁺ channels. The high K⁺ conductance driving repolarization contributes to establishing a refractory period that prevents spike discharge within a given period of time. The rate of spike repolarization and associated refractory period can thus define the maximum attainable frequency of spike discharge (Wang et al., 1998;Erisir et al., 1999). Refractory period has traditionally been considered a fixed and invariant parameter. An important recent development was the consideration of how refractory period can influence spike threshold when it overlaps with successive interspike intervals (ISIs). This can lead to a “dynamic spike threshold” that imparts a memory of previous activity to substantially improve response precision and information transfer in sensory neurons (Berry and Meister, 1998; Chacron et al., 2000, 2001; Brandman and Nelson, 2002). These results indicate the importance of understanding the factors that control spike repolarization and its influence on the pattern of spike output.

In all central neurons examined to date, the lowest threshold for initiating Na⁺ spike discharge is in the soma or axon hillock region, with spikes subsequently backpropagating over the dendritic arbor (Chen et al., 1997; Stuart et al., 1997;Williams and Stuart, 2000; Colbert and Pan, 2002). K⁺ channels repolarize both somatic and dendritic spikes and regulate the degree to which backpropagating spikes activate other voltage-dependent currents (Yuste et al., 1994;Golding et al., 1999; Magee and Carruth, 1999; Rashid et al., 2001a). A role in spike patterning becomes evident when pharmacological blockade of dendritic K⁺ channels broadens the dendritic spike sufficiently to promote burst discharge (Yuste et al., 1994;Hoffman et al., 1997; Golding et al., 1999; Williams and Stuart, 1999;Rashid et al., 2001a). A progressive broadening of dendritic spikes evoked beyond a particular frequency of spike discharge can also invoke burst output (Larkum et al., 1999; Lemon and Turner, 2000).

Pyramidal cells in the electrosensory lateral line lobe (ELL) of weakly electric fish produce burst discharge through a “conditional backpropagation” of dendritic spikes, where the pattern of spike output depends on the success of dendritic spike backpropagation (Lemon and Turner, 2000; Doiron et al., 2001). The underlying process involves a difference in the duration of somatic and dendritic spikes that allows dendritic spikes to re-depolarize the soma as a depolarizing afterpotential (DAP). We now show that somatic and dendritic K⁺ channels involved in spike repolarization exert opposite effects on the threshold for burst discharge. Moreover, during repetitive discharge, a progressive decrease in dendritic spike repolarization creates a dynamic and increasing dendritic refractory period. A leaky integrate-and-fire (LIF) model reveals that a transition from tonic to burst discharge is determined by the time of intersection between a decreasing somatic interspike interval and an increasing dendritic refractory period. The rate of progression toward this intersection is differentially controlled by somatic and dendritic spike repolarization, identifying a powerful means of controlling the pattern of spike output.

Materials and Methods

Preparation of tissue slices. Apteronotus leptorhynchus (Brown Ghost Knife fish) were purchased from local importers and maintained in fresh water aquaria at 26–28°C. Anesthesia via 0.05% phenoxy-ethanol was present during dissections, according to procedures approved by the Canadian Council of Animal Care. The techniques for preparing ELL slices have been described previously (Turner et al., 1994; Lemon and Turner, 2000). Slices were most often cut along the transverse axis of the ELL to facilitate recordings from the centromedial segment, with a limited number of slices cut on the longitudinal axis. Slices were maintained as an interface preparation at room temperature using a CSF containing (in mm): 124 NaCl, 2.0 KCl, 1.25 KH₂PO₄, 1.5 CaCl₂, 1.5 MgSO₄, 24 NaHCO₃, and 10 d-glucose, pH 7.4. Focal ejections of drugs followed the procedures of Turner et al. (1994). α-dendrotoxin and iberiotoxin were purchased from Alomone Laboratories (Jerusalem, Israel) and all other chemicals were purchased from Sigma (St. Louis, MO).

Intracellular recordings. Single intracellular recordings were obtained from within the pyramidal cell layer (n = 68) or from apical dendrites within 200 μm of the cell layer (n = 42). The input resistance was 69 ± 20.7 MΩ at the soma and 59 ± 24.5 MΩ in dendrites (n = 20 randomly selected cases; mean ± SD). Microelectrodes were backfilled with 2 m K acetate, and direct current injection of ≤0.5 nA was applied when necessary to reduce spontaneous discharge. A concentric bipolar-stimulating electrode placed in the plexiform layer was used to evoke antidromic spike discharge. Recordings were digitized (Cambridge Electronics Design, Cambridge, UK) and stored for off-line analysis (Cambridge Electronics Design; IgorPro, Lake Oswega, OR; Corel Draw, Ottawa, Canada). All average values are expressed as mean ± SD, and statistical differences were calculated using the Wilcoxin Signed Ranks test. Data plots were constructed and fit using Microcal Origin (Northampton, UK).

Burst discharge was automatically detected using a procedure written for IgorPro. Burst discharge was detected by comparing the variance (ς) of sequential afterhyperpolarization (AHP) amplitudes as ς_i = (AHP_i −AHP_{i −1})². This method was the most effective in detecting bursts, because the variance between AHPs associated with a spike doublet and burst AHP was always larger than those associated with intraburst AHPs. The time values associated with large changes in AHP variance were used to establish a threshold value for variance that marked the time of burst AHPs and thus a reference point from which other burst parameters could be calculated.

Models. A multicompartmental model of ELL pyramidal cells (Doiron et al., 2001) was used to examine the effects of varying dendritic or somatic K⁺ conductances on the properties of burst output. We recently reduced the description of the burst mechanism from continuous differential models to a two variable delay differential model (Doiron et al., 2001, 2002, 2003;Laing and Longtin, 2002). The current work used a modified version of the integrate-and-fire model to incorporate a more direct feedback from dendrite to soma, and to model dendritic refractory period as a dynamic variable linked to the duration of dendritic spikes. The modified integrate-and-fire model is as follows:

$$\frac{\text{dV}}{\text{dt}}=\left\{\begin{array}{cc}0\hfill & \hspace{0.5em}\text{if} t-t_n<r_s\hfill \\ \hspace{1em}\hfill \\ I-V+\alpha [\text{s}(\text{t}-{\text{t}}_{\text{n}},\beta \text{b}[{\text{t}}_{\text{n}}^{+}])-\text{s}(\text{t}-{\text{t}}_{\text{n}},\gamma )]\hfill & \hspace{0.5em}\text{if} t-t_n>r_s \text{and} t_n-t_{n-1}>r_d^n\hfill \\ \hspace{1em}\hfill \\ I-V\hfill & \hspace{0.5em}\text{if} t-t_n>r_s \text{and} t_n-t_{n-1}<r_d^n\hfill \end{array}\right.$$ Equation 1

$$\frac{\text{db}}{\text{dt}}=-b/\tau +(A+{\text{Bb}}^2)\sum _n \delta (t-t_n),$$ Equation 2

$$s(t,a)=\frac{{\text{te}}^{-t/a}}{a}$$

Time is measured in units of the membrane time constant.b is a second variable whose dynamics control both the width of the dendritic action potential (through the terms[t − t_n, βb(t ${}_{\text{n}}^{+}$)]) and the dendritic refractory period (through Eq. 3). I is the current injected into the soma, V is the somatic voltage, α is the conductance between the dendrite and the soma, and β and γ are parameters that control the widths of the dendritic and somatic action potentials, respectively. They are thought of as constant during a simulation but can be changed to mimic the effects of applying various pharmacological agents to either the soma (changing γ) or the dendrite (changing β). τ, A, B, D, and E are constants. r_s is the somatic refractory period (a constant). t_nis the nth firing time of the neuron (n is an integer). The firing times are those at which V = 1, at which time V is reset to 0. The function sreaches its maximum of e⁻¹ at a time a (i.e., its maximum is independent of a, but the area under it is not). Increasing a increases the width of s.

The dendritic refractory period, which is updated at each firing time, is given by:

$$r_d^n=D+\text{Eb}(t_n^{+}),$$ Equation 3

where b(t ${}_{\text{n}}^{+}$) is the value of b immediately after timet_n.r ${}_{\text{d}}^{\text{n}}$stays constant until the next firing time,t_{n + 1}, when it is updated again. Between spikes, b exponentially decays back to 0 from above, with time constant τ. At each spike it is updated:b → b + A +Bb². The value of b just after the update, b(t ${}_{\text{n}}^{+}$), is used to determine both the width of the dendritic spike and the dendritic refractory period, as both increase and decrease together.

V is fixed at 0 for a timer_s after each firing time,t_n (this is the first case in Eq. 1). If the last ISI, t_n − t_{n− 1,} was less than the refractory period of the dendrite, r ${}_{\text{d}}^{\text{n}}$, as set at the last firing time, there is no current flow from the dendrite to the soma, and the only current flowing to the soma once the somatic refractory period is over is I (this is the third case in Eq. 1). If the last ISI was longer thanr ${}_{\text{d}}^{\text{n}}$, an additional current, proportional to the “difference in voltages” between the dendrite and soma, flows into the soma: α[s(t − t_n, βb[t ${}_{\text{n}}^{+}$]) −s(t − t_n, γ)] in Equation 1. The dendritic voltage is modeled ass[t − t_n, βb(t ${}_{\text{n}}^{+}$)], and for the purposes of generating the current flow between the dendrite and the soma the somatic voltage is modeled ass(t − t_n,γ). Of course, this is not the actual somatic voltage, which follows the typical integrate-and-fire behavior of rising from 0 to 1. This is a more realistic way of modeling the feedback than that presented in the study by Laing and Longtin (2002), because the effect of the slow variable is to broaden the dendritic spike. A schematic representation of Equation 1 is given in Figure1. Simulation results are given for both tonic and bursting solutions of this model in Results (see Fig. 7).

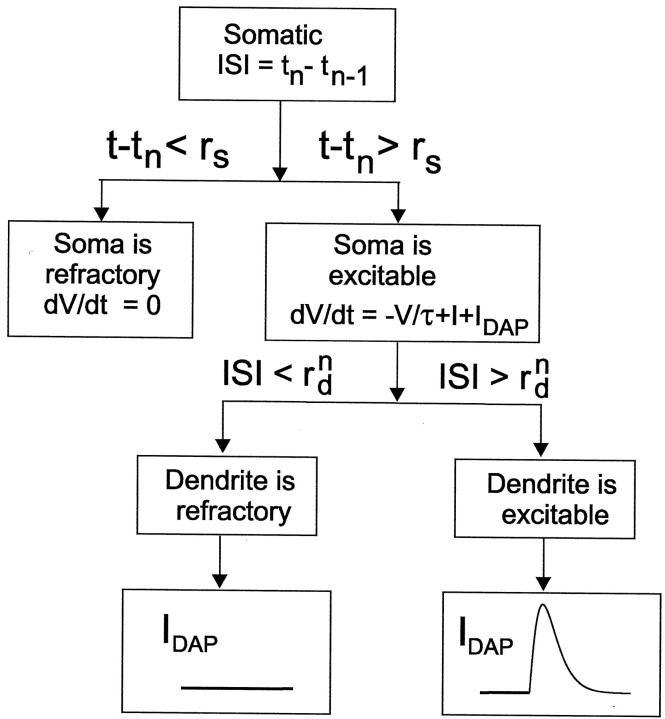
Fig. 1.

Flow diagram of the LIF burst model that links refractory period to spike width (Eq. 1). Given an ISI (t_n − t_{n − 1}), we can determine the evolution of the somatic potential, dV/dt, at time t after the second spike of the ISI. If t is less than the somatic refractory period (r_s), thendV/dt = 0, modeling the insensitivity of membrane potential to current flow during an absolute refractory state. This is case 1 in Equation 1. If t is greater than the somatic refractory period, then dV/dt =I − V/τ +I_DAP, whereI_DAP is the dendrosomatic current flow that can be one of two functions. If the ISI is greater than the dendritic refractory period, then I_DAP =s[t −t_n, βb(t ${}_{\text{n}}^{+}$)] − s(t −t_n, γ), which is the positive difference between the dendritic and somatic action potentials. A plot of this difference as a function of time is shown, where the absolute value of this function depends on the relative widths of the somatic and dendritic action potential, controlled by γ and βb(t ${}_{\text{n}}^{+}$), respectively. This is case 2 in Equation 1. Finally, if the ISI is less than the dendritic refractory period, then the second spike of the ISI does not backpropagate and the dendrite gives no current flow to the soma (i.e., I_DAP = 0). This is case 3 in Equation 1.

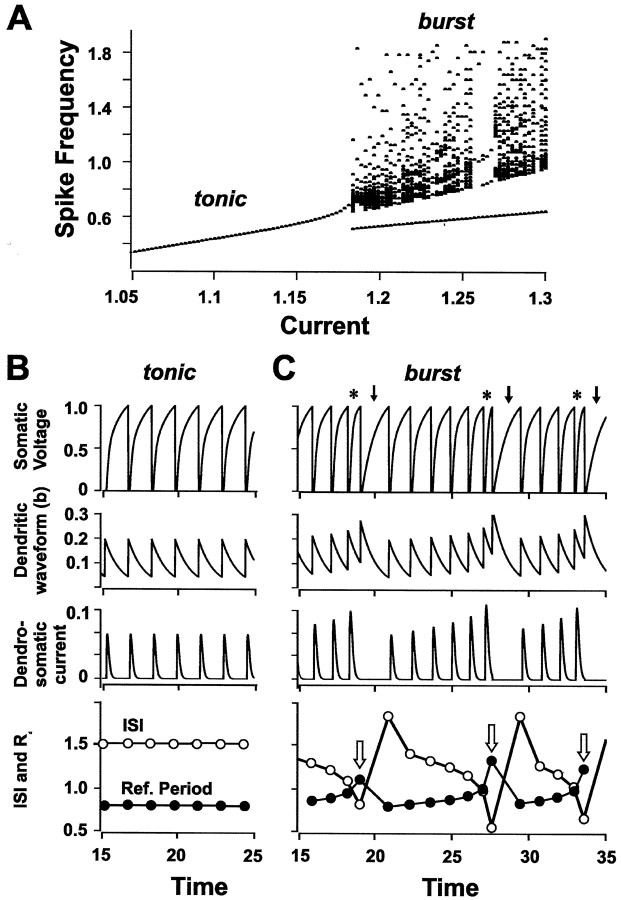
Fig. 7.

A dynamic dendritic refractory period interacts with somatic ISI to regulate burst output. A, A modified LIF model that links spike duration with refractory period reproduces an increase in spike frequency with applied current until reaching a threshold for switching from tonic to burst discharge (200 msec pulse). Frequency on the y-axis is measured in units of the inverse membrane time constant. Parameters are A = 0.15, B = 2, τ = 1,r_s = 0.1, α = 20, β = 0.35, γ = 0.05, D = 0.1,E = 3.5. B, C, Soma-dendritic interactions for applied currents that evoke either tonic discharge (B; I = 1.18) or burst discharge (C; I = 1.21). Top, Somatic voltage; second row, b, the variable used to control both dendritic spike duration and dendritic refractory period; third row, the effective spike-induced current flowing from dendrite to soma,s[t −t_n, βb(t ${}_{\text{n}}^{+}$)] − s(t −t_n, γ);bottom: somatic ISI (open circles;t_n − t_{n − 1} is plotted at t =t_n) and dendritic refractory period (r ${}_{\text{d}}^{\text{n}}$) (filled circles). In the voltage trace (C), asterisks indicate spike doublets and arrows indicate burst AHPs. Note that burst discharge is invoked at each juncture of a decreasing somatic ISI and an increasing dendritic refractory period (C,bottom, open arrows). Parameters areA = 0.15, B = 2, τ = 1,r_s = 0.1, α = 20, β = 0.35, γ = 0.05, D = 0.1,E = 3.5.

To further analyze periodic firing, we found the condition under which periodic firing was not possible, and thus established the boundary between tonic and burst firing. During periodic firing with periodT,b(t ${}_{\text{n}}^{+}$) =b* for all n, where b* is the smallest root of:

$$b*=b*e^{-T/\tau }+A+B [b*e^{-T/\tau }{]}^2$$ Equation 4

i.e.,

$$b*=\frac{1-e^{-T/\tau }-\sqrt{1-2e^{-T/\tau }+(1-4AB)e^{-2T/\tau }}}{2{\text{Be}}^{-2T/\tau }}.$$ Equation 5

b(t ${}_{\text{n}}^{+}$) is the value of b just after t_n, andb(t ${}_{\text{n}}^{-}$) is the value of b just before t_n. Equation 4is obtained by noting that ifb(t ${}_{\text{n}}^{+}$) =b*, then b(t ${}_{\text{n}+1}^{-}$) =b*e^−T/τ, because between action potentials b decays exponentially with time constant τ, and thereforeb(t ${}_{\text{n}+1}^{+}$) =b*e^−T/τ +A + B [b*e^−T/τ]².

For periodic firing, the second case in Equation 1 is always true. To find the period T, the following equation was used:

$$\frac{\text{dV}}{\text{dt}}=I-V+\alpha [s(t+r_s,\beta b*)-s(t+r_s,\gamma )]$$ Equation 6

where V(0) = 0. The period is then the amount of time needed for the solution of Equation 6 to reach the threshold of 1, plus the somatic refractory periodr_s. Using the definition ofs, Equation 6 can be rewritten as follows:

$$\frac{\text{dV}}{\text{dt}}=I-V+\alpha \left[\frac{(t+r_s)e^{-(t+r_s)/(\beta b*)}}{\beta b*}-\frac{(t+r_s)e^{-(t+r_s)/\gamma }}{\gamma }\right],$$ Equation 7

whose solution with the initial conditionV(0) = 0 is:

$$V(t)=I-\left\{I+\alpha \left[\left(\frac{r_s(\beta b*-1)-\beta b*}{(\beta b*-1{)}^2}\right)e^{-r_s/(\beta b*)}+\left(\frac{r_s(1-\gamma )+\gamma }{(1-\gamma {)}^2}\right)e^{-r_s/\gamma }\right]\right\}{e}^{-t}$$ Equation 8

$$+\alpha \left[\left(\frac{(t+r_s)(\beta b*-1)-\beta b*}{(\beta b*-1{)}^2}\right)e^{-(t+r_s)/(\beta b*)}+\left(\frac{(t+r_s)(1-\gamma )+\gamma }{(1-\gamma {)}^2}\right)e^{-(t+r_s)/\gamma }\right].$$

Thus T is a root ofV(T − r_s) = 1, or:

$$1=I-\left\{I+\alpha \left[\left(\frac{r_s(\beta b*-1)-\beta b*}{(\beta b*-1{)}^2}\right)e^{-r_s/(\beta b*)}+\left(\frac{r_s(1-\gamma )+\gamma }{(1-\gamma {)}^2}\right)e^{-r_s/\gamma }\right]\right\}{e}^{-(T-r_s)}$$ Equation 9

$$+\alpha \left[\left(\frac{T(\beta b*-1)-\beta b*}{(\beta b*-1{)}^2}\right)e^{-T/(\beta b*)}+\left(\frac{T(1-\gamma )+\gamma }{(1-\gamma {)}^2}\right)e^{-T/\gamma }\right],$$

where b* is a function of T through Equation 5. The value of I corresponding to the tonic to burst threshold can be found from Equation 9 by finding the value ofI at which two roots of Equation 9 coalesce in a saddle-node bifurcation. By following this bifurcation as either γ or β are varied, the threshold can be traced out in parameter space.

Results

Conditional backpropagation

Pyramidal cells in the ELL of weakly electric fish generate γ-frequency burst discharge in vitro through a conditional failure of dendritic spike backpropagation (Lemon and Turner, 2000;Doiron et al., 2001). Briefly, burst discharge arises through a soma-dendritic interaction that produces a DAP at the soma. We have shown that spike discharge is initiated near the soma and then actively backpropagates over only ∼200 μm of an 800 μm dendritic tree (Fig. 2A). The resulting increase in dendritic spike duration during backpropagation results in return current flow that outlasts a very narrow-duration somatic spike, producing the DAP. During repetitive discharge at spike frequencies of >100 Hz, the dendritic spike exhibits a progressive broadening that increases current flow from dendrite to soma to potentiate the DAP (Fig. 2B). The DAP finally triggers a spike doublet with an ISI that falls within a longer dendritic spike refractory period. The doublet thus abruptly terminates a spike burst when the second spike of the pair fails to backpropagate, removing the dendritic depolarization that drives a burst. A subsequent burst AHP then allows the intraburst elements to recover and the process to begin again. In this manner, pyramidal cells produce a repeating series of spike bursts, each composed of an intraburst depolarization with a decreasing ISI and an interburst pause (burst AHP). This process of bursting by conditional backpropagation is entirely intrinsic, because it proceeds unabated when synaptic transmission is blocked and can be simulated in a compartmental model (Lemon and Turner, 2000; Doiron et al., 2001).

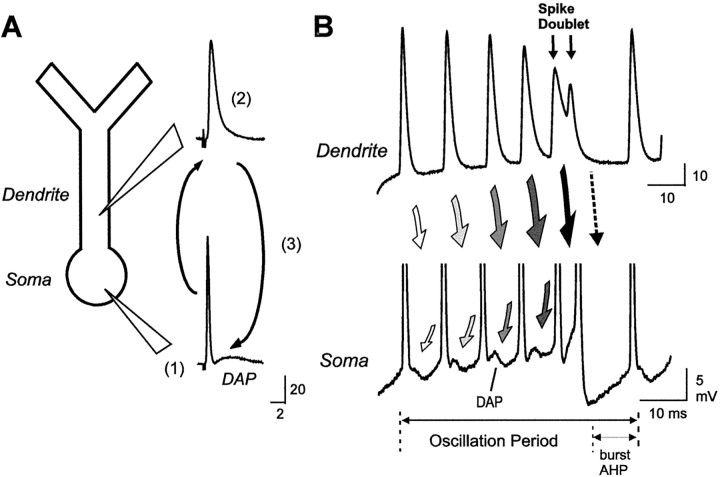
Fig. 2.

The mechanism underlying burst discharge through conditional backpropagation of dendritic spikes. A, Schematic diagram of a pyramidal cell soma and apical dendrite depicting Na⁺ spike initiation in the somatic region (1) and subsequent active backpropagation over only ∼200 μm of an 800 μm dendritic tree (2). A relatively long-duration dendritic spike compared with the soma leads to return current flow during backpropagation that generates a DAP at the soma (3). B, Schematic diagram of events during repetitive discharge that produce a spike burst. Representative traces of single spike bursts from separate dendritic (top) and somatic (bottom) recordings are shown aligned for illustrative purposes. Dendritic spikes exhibit a frequency-dependent broadening that increases current flow to the soma (indicated by shading of arrows) to potentiate DAP amplitude. Eventually a spike doublet is triggered at the soma (double-headed arrows) with an interspike interval that falls inside the dendritic refractory period. A loss of the dendritic spike removes the depolarization driving the burst (dashed arrow), and the cell returns to rest (Lemon and Turner, 2000).

Our current understanding of conditional backpropagation indicates that the relative duration of somatic and dendritic spikes, the somatic ISI, and dendritic refractory period are key variables that shape the pattern of spike output. K⁺ channels that repolarize somatic and dendritic spikes are expected to contribute to each of these parameters. This includes Kv3.3 K⁺ channels, a high threshold K⁺ channel subtype, that are expressed over the entire soma-dendritic axis of ELL pyramidal cells (Rashid et al., 2001b). Moreover, ejections of 4-AP or TEA to block dendritic Kv3 channels lower burst threshold in pyramidal cells by increasing dendritic spike duration and thus increasing DAP amplitude (Rashid et al., 2001a).

This current study further examines the identity of K⁺ channels involved in repolarizing somatic and dendritic spikes and their ability to regulate burst output, with particular emphasis on Kv3 K⁺ channels. We then examine how a change in dendritic spike repolarization during repetitive discharge affects dendritic refractory period and its contribution to conditional backpropagation.

K⁺-dependent spike responses

Spike discharge in pyramidal cells evokes distinct K⁺-dependent responses in the soma and dendrites that contribute to establishing spike repolarization, refractory period, and burst discharge (Fig.3) (Turner et al., 1994; Rashid et al., 2001a). At the soma, spike repolarization is extremely fast and is followed by both a fast AHP and a slow AHP. In apical dendrites, spike repolarization is active but occurs at a much slower rate than the soma and is followed by only a slow AHP (Fig. 3B). Individual spike bursts are followed by a long-duration burst AHP in soma and dendrites (Fig. 3D).

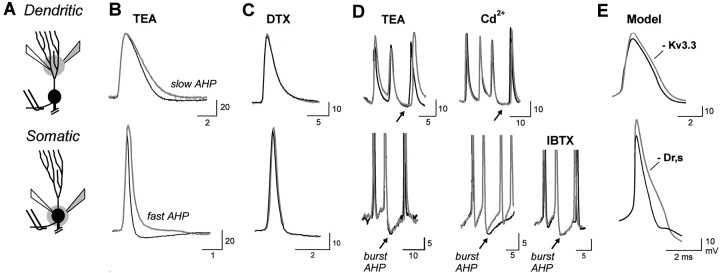
Fig. 3.

The contribution of TEA-sensitive K⁺ channels to spike repolarization and afterpotentials. A, Schematic diagrams illustrating the placement of recording electrodes and focal pressure ejection of drugs at the level of apical dendrites (B–D,top) or soma (B–D,bottom). Double wires indicate position of stimulating electrodes to evoke antidromic spike discharge. B, C, Superimposed traces of antidromic dendritic and somatic spike discharge before and after focal ejection of 1 mm TEA or 500 μm α-dendrotoxin (DTX). Control recordings are thin black traces, and postejection recordings are thick gray traces. D, Superimposed traces of current-evoked burst AHPs before (black traces) and after (gray traces) ejection of TEA, 400 μm Cd²⁺, or 200 nm iberiotoxin (IBTX).E, Superimposed voltage traces from the somatic and apical dendritic region of a multicompartmental model in which reducing dendritic g_Kv3.3 (80%) and a somatic delayed rectifier K⁺ current (g_Dr,s) (86%) simulate the change in repolarization produced by TEA ejections (compare with recordings in B).

The Kv3 class of K⁺ channels has been shown to be sensitive to TEA in the submillimolar range (Wang et al., 1998; Rudy et al., 1999; Rashid et al., 2001a). Thus, we used focal ejections of 1 mm TEA to block Kv3 channels, with accompanying tests for any affects by TEA on other K⁺ channels. Focal ejection of 1 mm TEA slowed the rate of somatic spike repolarization by 33 ± 14.6% and dendritic spike repolarization by 32 ± 10.4% (Fig. 3B) (n = 8; p< 0.05). TEA also blocked the somatic fast AHP and dendritic slow AHP (Fig. 3B) (n = 8) but had no effect on the burst AHP at either the somatic or dendritic level (Fig.3D). Bath applications of 150–300 μm TEA reproduced these effects by blocking the somatic fast AHP and slowing spike repolarization by 25 ± 12.8% (n = 3). To test for any affects by TEA on Ca²⁺-dependent large conductance (BK) K⁺ channels orShaker K⁺ channels, we focally ejected 400 μmCd²⁺, 200 nmiberiotoxin, or 500 μm α-dendrotoxin (Coetzee et al., 1999). We found that Cd²⁺ejections had no affect on the rate of somatic or dendritic spike repolarization or on dendritic AHPs (Fig. 3D) (n = 15). The only affect by Cd²⁺ was to reduce a somatic Ca²⁺-dependent slow AHP and a late component of the burst AHP (Fig. 3D). Because both the slow AHP and burst AHP were insensitive to TEA and iberiotoxin (Fig.3D), we attribute these responses to Ca²⁺-dependent small conductance (SK) K⁺ channels (Coetzee et al., 1999). Finally, focal ejections of iberiotoxin and α-dendrotoxin had no effect on somatic or dendritic spikes or any afterpotentials (Fig.3C,D) (n = 5).

To further identify K⁺ conductances involved in spike repolarization, we used a multicompartmental model that incorporates the kinetics of Kv3.3 K⁺channels (Doiron et al., 2001). Reducing dendritic Kv3.3 conductance by 80% over the first 200 μm of apical dendritic compartments was sufficient to slow the rate of dendritic spike repolarization by an amount similar to that produced by 1 mm TEA ejections (Fig.3E). In comparison, the narrow-duration somatic spike activated only enough Kv3.3 K⁺ current to account for a small percentage of spike repolarization (at least as currently modeled from Kv3.3 kinetics measured in an expression system) (Doiron et al., 2001). Instead, decreasing the density of a somatic delayed rectifier K⁺ channel (Dr,s) by 86% produced a reduction in somatic spike repolarization equivalent to that produced by TEA (Fig. 3E). The identity of this somatic delayed rectifier is currently unknown, although it could include Kv3.1 K⁺ channels, because pyramidal cells in the centromedial segment are also known to express mRNA for a homolog of Kv3.1 channels (Rashid et al., 2001a).

Therefore, we can state that focally ejected 1 mm TEA decreases the conductance of at least Kv3.3 K⁺ channels, with no contribution by Ca²⁺-dependent or dendrotoxin-sensitiveShaker K⁺ channels to spike repolarization or short-latency AHPs. No additional distinction can be made at this time given the lack of specific blockers for Kv3.3 and Kv3.1 K⁺ channels. However, with these restrictions in mind, we used focal ejections of low concentrations of TEA together with pyramidal cell models to further examine the role of K⁺ channels in modulating burst discharge.

K⁺ channels differentially control burst discharge

We have shown previously that focal ejection of 4-AP or TEA to pyramidal cell apical dendrites lowers the threshold for burst discharge, a result reflecting an increase in somatic DAP amplitude because of an increase in dendritic spike duration (Rashid et al., 2001a). To more fully establish the effects of TEA-sensitive K⁺ channels on burst output, we constructed frequency–current (F–I) plots before and after dendritic or somatic TEA ejections. Under control conditions, increasing the level of injected current evoked a gradual increase in spike frequency to a value between 20 and 250 Hz (Fig.4A,B). Focally ejecting 1 mm TEA to the dendritic region increased the frequency of spike discharge by up to 450% (n = 17), especially over the lower regions of F–I plots (Fig.4A) (n = 8; p < 0.05 for spike frequencies at the lowest injected current). As a result, near maximal frequencies of spike discharge could often be evoked at levels of current that were previously just threshold for spike discharge. There was also a significant decrease in the threshold for generating burst discharge in terms of injected current, decreasing on average from 0.8 ± 0.19 nA in control conditions to 0.48 ± 0.12 nA after TEA ejections (Fig. 4A, dashed lines) (p < 0.05; n = 8). The range of burst frequencies that could be evoked over anF–I plot also increased on average by 60% after dendritic TEA ejections (p < 0.05; n = 8), revealing an overall increase in the range of membrane depolarizations that could generate burst output.

Fig. 4.

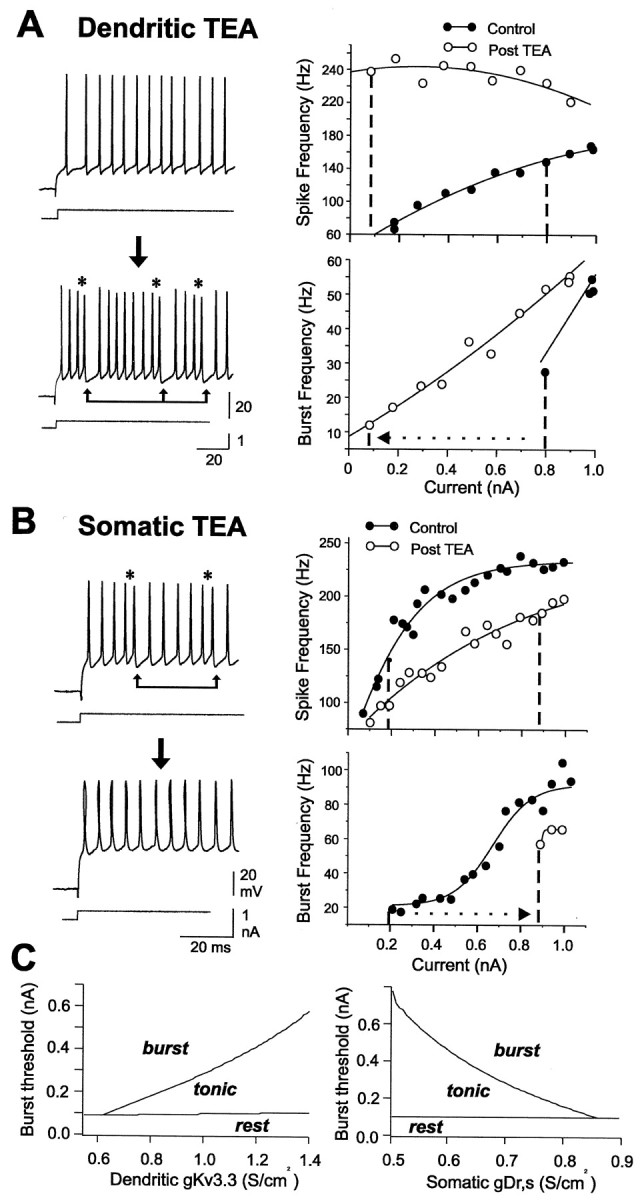
Dendritic and somatic K⁺channels differentially regulate burst discharge. A, B, Representative somatic spike recordings and frequency–current plots of mean spike frequency (top) and burst frequency (bottom). Shown are plots obtained before and after focal ejection of 1 mm TEA in either the dendritic (A) or somatic region (B). The occurrence of spike doublets is indicated byasterisks; burst AHPs are indicated by linked arrows. A, An initial frequency–current plot indicates a gradual increase in spike frequency that shifts to a burst output at 0.8 nA current injection (dashed line). Focal dendritic TEA ejection increases somatic spike frequency and lowers the threshold for burst discharge to ∼0.1 nA (dotted arrow). B, A separate somatic recording indicating that focal ejections of TEA in the cell body layer lower spike frequency and raise burst threshold from 0.2 to 0.9 nA.C, Spike output in a compartmental model is differentially regulated according to the density of somatic or dendritic K⁺ channels. Burst threshold is defined as the minimum level of applied current (I_app) required to move from tonic to burst discharge at fixed values of g_Kv3.3 or the delayed rectifier somatic K⁺ conductance (g_Dr,s). Each plot was constructed by incrementing conductance in units of 5 mS/cm² and I_app in units of 50 pA. The threshold for spike discharge, marking transitions from rest to tonic activity, is also plotted for reference.

Applications of TEA in the cell body layer produced opposite effects on burst output. Instead of lowering burst threshold, somatic TEA ejections (1 mm) or bath application of TEA (150 μm) rapidly blocked burst discharge, converting cell output to tonic spike discharge (Fig. 4B) (n = 21). This result was not attributable to a block of ion channels underlying the burst AHP, because increasing the current intensity reinstated burst discharge and evoked a burst AHP that could be superimposed on control records (Fig. 3D). Somatic TEA ejections also reduced the gain of the F–Irelationship such that a given level of current injection evoked a lower frequency of spike discharge. Interestingly, unlike dendritic TEA ejections, the effect of somatic TEA was expressed preferentially at mid–high current intensities (Fig. 4B). As a result, the current required to reach burst threshold after somatic TEA ejections was raised by a factor of 2.8–4.5X (p< 0.05; n = 7). Absolute burst frequency was significantly reduced at all current levels (p< 0.05; n = 7), with an average 75% decrease in the range of burst frequencies that could be evoked over an F–Iplot (p < 0.05; n = 7).

It is difficult to map the full contribution of K⁺ channels to spike output using focal drug ejections, because these will produce an undetermined decrease in the effective K⁺ conductance. We therefore used a compartmental model (Doiron et al., 2001) to vary the conductance of either dendritic Kv3.3 or the somatic delayed rectifier (Dr,s) in a graded manner. These studies revealed a clear partitioning of parameter space into states of resting membrane, tonic firing, and burst discharge as K⁺ conductance was varied (Fig. 4C). Importantly, a clear burst threshold was evident (boundary between tonic and burst behavior in Fig.4C). However, somatic and dendritic K⁺ channels exerted opposite effects on burst output, such that burst threshold was lowered by a decrease in dendritic Kv3.3 conductance or by an increase in somatic Dr,s conductance. In each case these changes were associated with a relative change in the rate of somatic or dendritic spike repolarization and their ability to increase the somatic DAP. A lower dendritic Kv3.3 conductance thus broadened the dendritic spike and promoted more current flow to the soma to potentiate the DAP. However, a decrease in somatic spike repolarization interfered with this process by decreasing the relative difference in somatic and dendritic spikes, and thus the ability for dendritic spikes to generate a DAP.

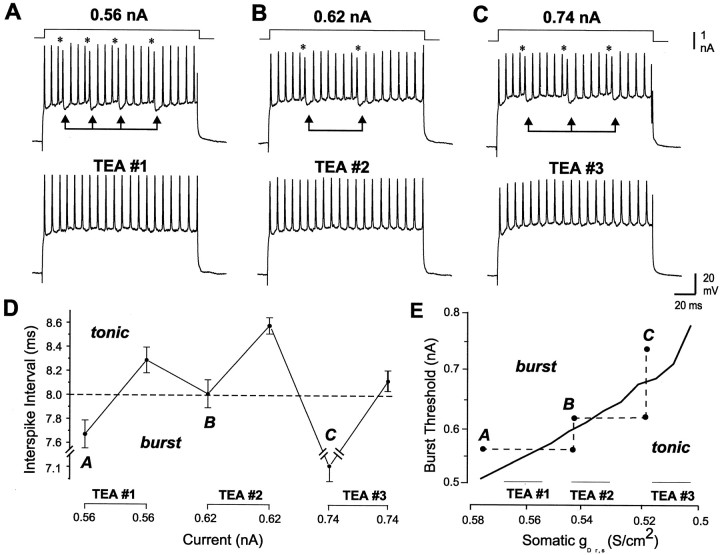
These simulations suggest that burst threshold can be shifted in a graded manner according to K⁺ channel density. To test this, we sequentially applied TEA to the somatic region by focal ejection to determine whether cell output could be alternately shifted across a burst threshold. As shown above (Fig. 4), after initial somatic TEA ejections blocked burst discharge, we could reinstate bursting by increasing the level of injected current (Fig.5). However, this process could be repeated by again ejecting TEA to block bursting and then regaining burst discharge with a higher current injection (Fig. 5A–C) (n = 3). Examining single spikes before and after each TEA ejection revealed an increase in somatic spike duration after TEA ejections.

Fig. 5.

Burst threshold is jointly determined by K⁺ conductance and somatic ISI. A–C, Burst discharge is sequentially blocked by 1 mm TEA ejections in the cell body layer but reinstated each time by higher levels of current injection (B, C).Asterisks denote the occurrence of spike doublets;linked arrows indicate burst AHPs. D, A plot of the average ISI for each of the experiments inA–C (spike doublets and burst AHP intervals omitted). Adashed line at 8 msec ISI approximates an interface between tonic and burst discharge. E, A plot of burst threshold-somatic g_Dr,s from the multicompartmental model (compare Fig. 4C).Dashed lines illustrate how TEA ejections and current adjustments sequentially shift spike output across the threshold for burst discharge. The corresponding time frames are designated by theletters A, B, and Caccording to the records shown in A–C.

To determine the relative influence of ISI on burst output during these experiments, we plotted the ISI through the course of multiple TEA ejections (Fig. 5D). We found that the initial ISI fell within the range known to be associated with dendritic spike broadening (typically ≤10 msec) (Lemon and Turner, 2000). TEA ejections raised the ISI above this level during tonic discharge. Increasing current injection repeatedly lowered the ISI back toward or below the initial value present during burst discharge (Fig. 5D). Our interpretation of how these results relate to the simulations is shown in Figure 5E, in which TEA ejections reduce the effectiveness of the dendritic spike by increasing both somatic spike duration and the ISI. Increasing the level of current injection overcomes the relative increase in somatic spike duration by forcing the ISI back to within the range required to induce dendritic spike broadening. These results emphasize the importance of a relative difference in somatic and dendritic spike duration as well as ISI in the patterning of spike output.

Dendrites exhibit a dynamic refractory period

We have shown that spike duration in pyramidal cells is correlated with refractory period, such that refractory period increases almost threefold from the soma to ∼200 μm in the apical dendrites in conjunction with dendritic spike duration (Lemon and Turner, 2000). This leads to the prediction that dendritic spike broadening during repetitive discharge could effectively shift the dendritic spike refractory period. To test this, we evoked spike discharge through antidromic stimulation and used a fixed ISI to avoid any influence of a decreasing ISI on the rate of dendritic spike broadening (Fig.6). Repetitive stimulation at ISIs of >11 msec allowed dendritic spikes to discharge on each stimulus. However, ISIs between 3 and 10 msec gradually reduced dendritic spike amplitude over three to seven stimuli until reaching a stable amplitude, short-duration prepotential (Fig. 6A) (n = 9). As shown previously, this small prepotential reflects the failure of dendritic spike discharge, leaving only a passively conducted reflection of the narrow duration somatic spike (Turner et al., 1994). Antidromically evoked somatic spikes were capable of following ISIs of ≥2.5 msec, yet ISIs of 3–8.8 msec either reduced or evoked a selective failure of the DAP during the spike train (Fig. 6B) (n = 10). This decrease in DAP amplitude has also been shown to reflect a failure of dendritic spike backpropagation (Turner et al., 1994; Lemon and Turner, 2000;Doiron et al., 2001).

Fig. 6.

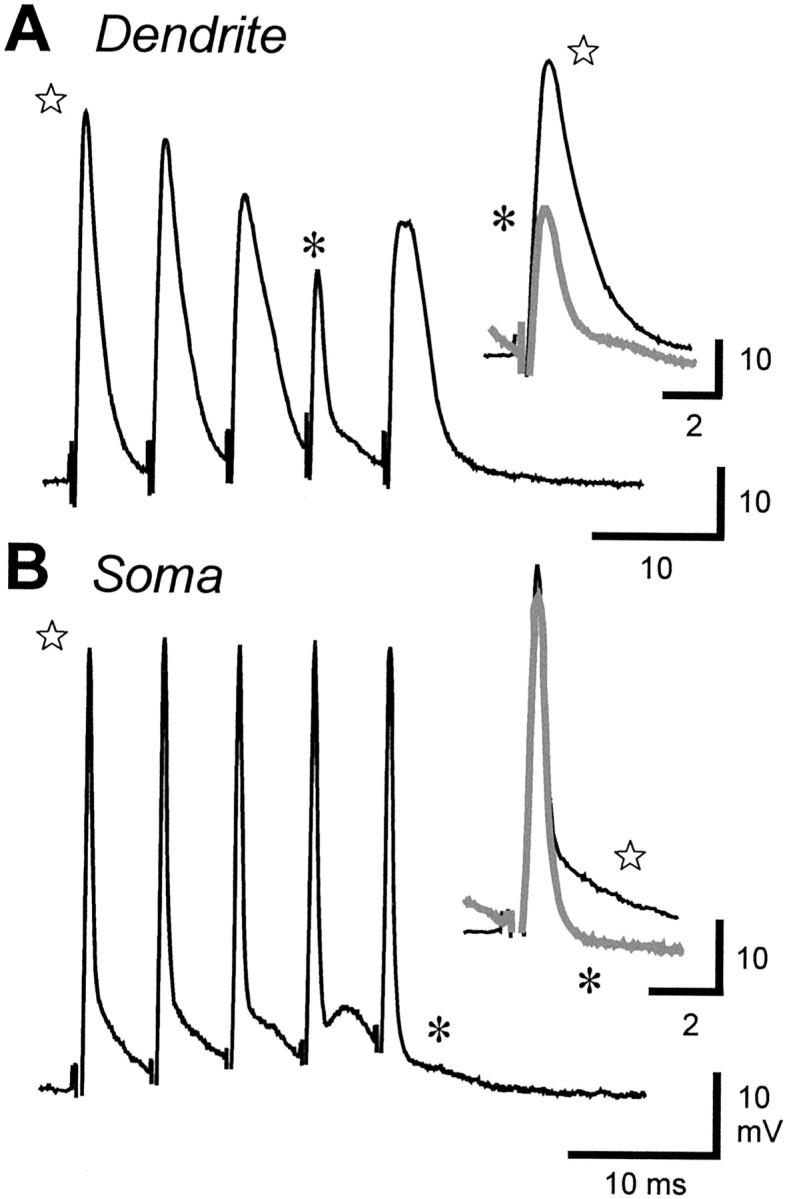
Dendritic spike refractory period increases during repetitive discharge. Dendritic (A) or somatic (B) discharge in separate recordings in response to a fixed interval of antidromic stimulation is shown.Insets superimpose the first spike (stars, dark traces) and last spike (asterisks, gray traces) of each train.A, Repetitive stimulation at 7 msec ISI progressively decreases dendritic spike amplitude and increases spike duration until the spike fails on the fourth stimulus, revealing a small prepotential associated with somatic spike discharge (asterisk) (Turner et al., 1994). B, Repetitive antidromic stimulation at 5 msec ISI potentiates the somatic DAP until achieving a selective block of the DAP on the fifth stimulus (asterisk), a result signifying a loss of dendritic spike backpropagation.

The simplest explanation for the above results is that repetitive stimulation progressively increases dendritic spike refractory period, such that dendritic spikes can no longer follow a stimulus train presented at a fixed ISI. In comparison, the somatic refractory period is essentially constant, because somatic spikes could faithfully discharge at ISIs well below that recorded in pyramidal cells (Lemon and Turner, 2000). Determining the absolute shift in dendritic spike refractory period is difficult given the gradual decline in dendritic spike amplitude and DAP during repetitive discharge. However, we estimate that an antidromic ISI of 5 msec can shift dendritic refractory period on the order of 1–2 msec. Interestingly, the ISI that invoked dendritic spike or DAP failure was variable, in that failure occurred sooner in a spike train or at longer ISIs during tonic depolarizations, revealing a voltage dependence in the shift of the dendritic refractory period. It is also important to note that a shift in dendritic refractory period became apparent even at the fixed ISI used during antidromic stimulation. Because under normal conditions the ISI steadily decreases from spike to spike, we predict even larger changes in dendritic refractory period during unconstrained repetitive discharge.

Soma-dendritic interactions control burst discharge

Our past studies indicate that backpropagation, differential somatic and dendritic refractory periods, and a cumulative inactivation of dendritic K⁺ channels are together sufficient to produce conditional backpropagation in ELL pyramidal cells (Lemon and Turner, 2000; Doiron et al., 2001, 2002; Laing and Longtin, 2002). Given that dendritic spikes in pyramidal cells also decline in amplitude during a burst, an increase in dendritic refractory period will likely also involve a direct cumulative inactivation of dendritic Na⁺ channels (Colbert et al., 1997; Mickus et al., 1999). Because we have not yet determined the extent of Na⁺ channel inactivation in pyramidal cell dendrites, we lack the requisite experimental data from which to base any detailed modeling. Therefore, for the purpose of this study, we restrict ourselves to considering the effects of K⁺ channels on dendritic spike broadening and dynamic shifts in dendritic refractory period.

To model the functional outcome of a dynamic refractory period, we modified a two variable LIF model recently introduced for ELL pyramidal cells (Laing and Longtin, 2002). This choice of model formalism is advantageous, because it allows for direct control of refractory period as an accessible model variable. This is in contrast to ionic-based modeling, in which refractory period is a measured quantity that is a consequence of both Na⁺and K⁺ channel descriptions. We thus idealized instantaneous dendritic refractory period by using a single variable to link dendritic spike width and refractory period according to the relationship described by Lemon and Turner (2000) (see Materials and Methods). Based on our experimental work, the somatic refractory period was modeled as a constant.

The modified LIF model was able to reproduce all key aspects of burst discharge in ELL pyramidal cells: spike half-width was linearly related to refractory period and spike frequency increased with current injection before reaching a defined threshold for burst output (Fig.7A). Furthermore, this burst discharge proved to be chaotic, similar to findings using ionic-based models (Doiron et al., 2002). The behavior of the model for two values of applied current that evoked a tonic or burst discharge is shown in Figure 7B,C. During tonic spike discharge, the ISI remained fairly constant, with no change in dendritic spike width or associated current flow from dendrite to soma (Fig. 7B). As a result, there was no change in dendritic refractory period over time. For current levels above burst threshold (I > 1.17), a decrease in somatic ISI was associated with an increase in the width of dendritic spikes and an increase in dendrosomatic current flow (Fig.7C). Most importantly, there was a steady approach between the decreasing values of somatic ISI and an increasing dendritic refractory period, with the intersection point signifying the time at which the ISI fell within the dendritic refractory period (Fig.7C, open arrows). This intersection point reset dendrosomatic current flow to 0, which produced a longer ISI corresponding to a burst AHP (Fig. 7C, filled arrows). Recovery of all variables after the loss of dendrosomatic current flow (the burst AHP) allowed this process to be repeated in a cyclic manner and produce oscillatory spike bursts.

These model results are highly significant, suggesting that repetitive discharge sets in motion two processes that synergistically act to increase the probability that backpropagation will fail: a decreasing somatic ISI and an increasing dendritic refractory period. These factors are interdependent, in that during repetitive discharge the somatic ISI will decrease because of dendritic re-excitation of the soma, which in turn will increase the dendritic refractory period by further broadening the dendritic spike. It is important to note that a progressive increase in dendritic refractory period is not absolutely necessary to induce the burst process itself, because the decreasing somatic ISI will eventually intersect with the longer dendritic refractory period. However, the added dimension of a dynamic dendritic refractory period greatly increases the capability for soma and dendrites to interact and regulate burst output.

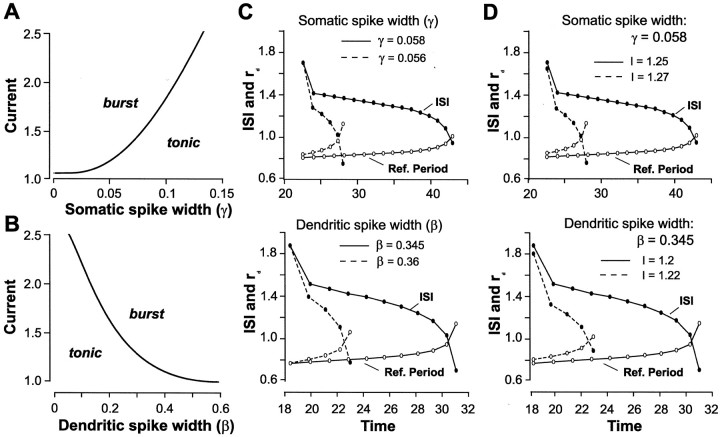
To determine the relative influence of somatic and dendritic K⁺ channels on this interaction, we examined the effects of changing the relative duration of somatic and dendritic spikes in the LIF model. We first determined that shifts in spike duration in the model (simulating a change in K⁺ conductance) reproduced the threshold boundary between tonic and burst discharge originally observed in the full compartmental model (Fig.8A,B). Note that the thresholds computed in Figure 4C are approximations because of the nature of large-scale simulations, whereas the thresholds in Figure 8A,B are exact because they are analytically calculated (see Eq. 9 in Materials and Methods). These modeling studies thus verified that an increase in somatic spike duration had an effect on burst threshold that was opposite to that seen with an increase in dendritic spike duration.

Fig. 8.

The time for somatic ISI and dendritic refractory period to intersect is modulated by spike repolarization and membrane depolarization. A, B, The threshold at which the LIF model moves from tonic to burst output increases directly with somatic spike width (A) and inversely with dendritic spike width (B) (compare Fig.4C). Parameters are β = 0.35 inA, γ = 0.05 in B,A = 0.15, B = 2, τ = 1,r_s = 0.1, α = 20,D = 0.1, E = 3.5. C, D, Burst discharge is produced at the intersection of somatic ISI (filled circles) and a dynamically shifting dendritic refractory period (open circles). Solid lines indicate control conditions; dashed linesindicate the experimental condition. The time for ISI and dendritic refractory period to intersect is reduced by changing the initial duration of somatic or dendritic spikes (C) or by increasing the level of current injection (D; γ and β are fixed). C,Top, I = 1.25; bottom, I = 1.2. Other parameters (C, D) are A = 0.15, B = 2, τ = 1,r_s = 0.1, α = 20,D = 0.1, E = 3.5.

Figure 8C,D illustrates how changes in spike duration affect the time for somatic ISI and dendritic refractory period to intersect and terminate a burst. We found that decreasing the initial duration of somatic spikes reduced the time for the ISI and dendritic refractory period to intersect (Fig. 8C). Similarly, an increase in dendritic spike duration reduced the time for somatic ISI and dendritic refractory period to intersect (Fig. 8C). Thus, changing the rate of repolarization of either somatic or dendritic spikes regulates burst threshold and frequency by controlling the dynamic interaction between somatic ISI and dendritic refractory period. This was also shown when, for a given somatic or dendritic spike duration, the intersection time was reduced by increasing the level of current injection (Fig. 8D). This resulted when a higher level of current injection induced a more rapid decrease in somatic ISI and thus a more rapid shift in dendritic refractory period.

Discussion

The results of the present study demonstrate that spike refractory period can be dynamically regulated in specific regions of a neuron. Interactions between neighboring sites can then lead to a mismatch between refractory periods that shift their relative frequency-following capabilities. In the case examined here, K⁺ channels control burst discharge in a sensory neuron by determining the relative rate of somatic and dendritic spike repolarization and dendritic refractory period. Moreover, repetitive discharge invokes a synergistic interaction between somatic ISI and a dynamically shifting dendritic refractory period to control burst threshold and frequency. The ability for K⁺ channel density and membrane depolarizations to modulate this interaction provides multiple opportunities to control spike patterning.

Spike repolarization sets the stage for burst discharge

The density of both somatic and dendritic TEA-sensitive K⁺ channels proves to be essential in establishing the difference in spike repolarization that allows a long-duration dendritic spike to generate a DAP after a narrow-duration somatic spike. TEA ejections in the cell body layer decreased the relative difference between somatic and dendritic spike durations, reducing the ability for dendritic spikes to generate a DAP. This could be overcome by increasing the level of current ejection to reduce somatic ISI to within the usual range for burst discharge. In contrast, a comparatively weak rate of dendritic spike repolarization promotes burst discharge, with any additional reduction from baseline levels shortening the ISI and promoting burst discharge over a wide range of membrane depolarizations. Our modeling data suggest that Kv3 K⁺ channels found in dendritic regions are sufficient to account for the changes induced here by focal dendritic ejection of TEA. The above interpretations were supported by two models in which applying graded shifts in K⁺channel conductance (compartmental model) or directly changing somatic and dendritic spike width (LIF model) identified an opposite relationship between somatic and dendritic spike duration to burst threshold.

A dynamic dendritic refractory period is involved in regulating burst discharge

Our results indicate that a naturally occurring increase in dendritic spike duration during repetitive discharge is associated with the important functional consequence of modifying dendritic refractory period. In comparison, the spike refractory period at the soma is either fixed or exhibits too small an increase to interfere with spike discharge at the frequencies encountered during burst discharge. The reduced LIF model indicates that this situation allows a reciprocal soma-dendritic interaction to develop in which burst discharge is generated at the intersection between a decreasing somatic ISI and an increasing dendritic refractory period. The time at which this intersection occurs determines burst duration and can be highly regulated by the density of somatic or dendritic K⁺ channels or by membrane depolarizations. In the general sense, these results are important in indicating that differences in spike refractory periods can interactively regulate spike conduction properties along a cable conductor. In the case of ELL pyramidal cells, Na⁺ spikes backpropagate only ∼200 μm before failing (Turner et al., 1994). The ionic mechanisms responsible for either a fixed or dynamic refractory period can thus be active within a distance of <200 μm. Although a dynamic refractory period is not required to produce burst discharge, it offers an important additional degree of freedom to control the threshold and frequency of burst discharge. Furthermore, this control is influenced by the past discharge history, a powerful influence in sensory systems in which stimuli are dynamic and unpredictable.

We are uncertain as to the exact identity of ion channels that allow repetitive discharge to induce a selective increase in dendritic refractory period. Modeling reveals that conditional backpropagation can be produced by a cumulative inactivation of dendritic K⁺ channels (Doiron et al., 2001). The high density of inactivating Kv3.3 K⁺channels in pyramidal cells provides a very likely candidate for a K⁺ channel subtype that could contribute to changes in dendritic spike repolarization (Rashid et al., 2001a). Given that spike broadening is accompanied by a decrease in dendritic spike amplitude, repetitive discharge is also expected to produce a cumulative inactivation of Na⁺ channels. Indeed, there is precedence for a more pronounced cumulative inactivation of Na⁺ channels in dendritic than somatic regions (Colbert et al., 1997; Jung et al., 1997; Mickus et al., 1999). ELL pyramidal cells (in the topographic map examined here) do not express Ca²⁺ currents that could contribute to spike broadening, but we have found thatI_NaP augments dendritic spikes to magnify the depolarization underlying the DAP (Doiron et al., 2003). The relative contribution of each of these factors will need to be further investigated.

It will be important to identify physiological mechanisms that can modulate K⁺ channel conductance to take advantage of such a clear potential for regulating cell output. A static modulation of spike repolarization could be achieved through second messenger pathways, some of which have been shown to be activated by ligand-gated receptors (Atzori et al., 2000; Haug and Storm, 2000; Macica and Kaczmarek, 2001; Yuan et al., 2002). Alternatively, feedback synaptic pathways known to terminate in the proximal dendritic region of pyramidal cells could inactivate dendritic K⁺ channels by producing an extended postsynaptic depolarization during repetitive activity (Berman and Maler, 1999; Berman et al., 2001). Further work will be required to characterize these interactions to determine the full potential for modulating cell output through spike repolarization.

Dynamic spike thresholds

Other models that have considered the influence of refractory period on the pattern of spike discharge have noted a dynamic shift in spike threshold that is associated with a decrease in spike train variability. Berry and Meister (1998) used a recovery function that followed spike discharge in retinal ganglion cells to temporarily increase spike threshold. This recovery function regularized spike output, which had the important effect of increasing response precision and the information transfer rate. A regularization of spike output was also reported in auditory neurons when refractory effects were considered (Gaumond et al., 1982; Miller and Mark, 1992). Recent models of electrosensory ganglion cells examined the effects of a dynamic threshold that was adjusted according to the recent history of spike discharge over several successive ISIs (Chacron et al., 2000, 2001;Brandman and Nelson, 2002). This produced cumulative refractory effects that greatly enhanced the ability of ganglion cells to estimate stimuli over time frames relevant to prey detection (hundreds of milliseconds) or electrocommunication (tens of milliseconds) (Nelson and Maciver, 1999; Chacron et al., 2001).

The exact location of a dynamic threshold has not been determined in other cells, although it is assumed to be located close to the spike output generator (i.e., presumed axon hillock or axon) (Colbert and Pan, 2002). The dynamic dendritic refractory period identified here functions in a similar manner to the dynamic threshold considered in other cells by establishing a “memory” of the recent discharge history. However, we find that a dynamic dendritic refractory period does not regularize spike output. Rather, it increases spike train variability by introducing a longer ISI in the spike train when backpropagation is blocked (burst AHPs). Therefore, our work indicates how a dynamic refractory period located at a dendritic site that is linked electrotonically to the output generator (axon hillock) can dramatically alter spike patterning. In addition, burst discharge has been reported in ELL pyramidal cells in vivo in relation to the detection, rather than estimation, of sensory stimuli (Gabbiani et al., 1996; Metzner et al., 1998; Kepecs et al., 2002; Krahe et al., 2002). A dynamic dendritic refractory period may then be one means by which pyramidal cells adjust their response to sensory stimuli and generate burst discharge for the purpose of feature extraction.

The ability to regulate spike refractory period may have widespread importance, because frequency-dependent spike broadening has been observed in somatic, dendritic, and axon terminal regions (Bourque, 1991; Quattrocki et al., 1994; Larkum et al., 1999; Shao et al., 1999;Geiger and Jonas, 2000). In hippocampal pyramidal cells, somatic spike discharge promotes a frequency-dependent decrease in dendritic spike amplitude and even failure to conduct beyond distal dendritic branchpoints (Spruston et al., 1995; Colbert et al., 1997; Jung et al., 1997). Several factors have also been identified that can modulate the properties of backpropagating spikes (Hoffman et al., 1997; Jung et al., 1997; Tsubokawa and Ross, 1997; Colbert and Johnston, 1998;Migliore et al., 1999; Gasparini and Magee, 2002; Yuan et al., 2002). It will be interesting to assess dendritic spike properties in these cells in terms of refractory period and its effects on spike patterning.