Efficient Gaussian Process-Based Modelling and Prediction of Image Time Series

Abstract

In this work we propose a novel Gaussian process-based spatio-temporal model of time series of images. By assuming separability of spatial and temporal processes we provide a very efficient and robust formulation for the marginal likelihood computation and the posterior prediction. The model adaptively accounts for local spatial correlations of the data, and the covariance structure is effectively parameterised by the Kronecker product of covariance matrices of very small size, each encoding only a single direction in space. We provide a simple and flexible framework for within- and between-subject modelling and prediction. In particular, we introduce the Hoffman-Ribak method for efficient inference on posterior processes and its uncertainty. The proposed framework is applied in the context of longitudinal modelling in Alzheimer’s disease. We firstly demonstrate the advantage of our non-parametric method for modelling of within-subject structural changes.The results show that non-parametric methods demonstrably outperform conventional parametric methods. Then the framework is extended to optimize complex parametrized covariate kernels. Using Bayesian model comparison via marginal likelihood the framework enables to compare different hypotheses about individual change processes of images.

1. Introduction

Modelling longitudinal changes in organs is fundamental for the understanding of biological and pathological processes. For instance the development of a spatio-temporal model of disease progression in Alzheimer’s disease (AD) from time series of magnetic resonance images (MRIs) would be highly valuable for the fundamental understanding of the disease process, for diagnostic purposes and individual predictions, and for testing the efficacy of disease modifying drugs in clinical trials.

The consistent modelling and prediction of spatio-temporal changes in longitudinal MRI is still an important challenge from both methodological and computational perspectives. In fact, flexible modelling instruments are required in order to robustly capture meaningful pathological accelerations specific to sensitive brain regions. Moreover, since a biological model of local brain changes is often unknown, it is important to develop optimal models in terms of statistical complexity.

Many of the previous works on spatio-temporal modelling of image time series are based on non-linear image registration, describing signal differences between images as local spatial transformations [1,2,3,4]. However, statistical inference in registration models is often limited, due to the computational complexity, and since image-registration is generally not flexible enough to perform model comparisons and clinical prediction, to account for covariates and for the within- and between subjects heterogeneity.

A statistical focus on the modeling of image time series is commonly provided by parametric linear modelling frameworks (GLM) [5]. However, GLM approaches are often limited by the choice of arbitrary model complexity and spatial resolution at which the data is analyzed. Even though flexible non-parametric models have been proposed for the analysis of spatio-temporal signals in brain images [6,7], their computational complexity still prevents the straightforward application in time series of high-resolution MRIs. Non-parametric Gaussian process (GP) models have emerged as a flexible and elegant Bayesian approach for prediction and modelling in manifold applications [8], and have been recently successfully introduced to the field of neuroimaging, e.g. in the context of single-case inference in aging [9]. However, the application of GPs to the voxel-wise modelling of image time series is to date very challenging, since the specification of the joint covariance structure of the image features is in general computationally prohibitive.

In this work we introduce a generative model of spatio-temporal changes based on GPs, to provide a flexible and computationally efficient approach to the analysis of aligned image time series by accounting for spatial and temporal correlation. In particular, by assuming a local spatial correlation model and the separability between spatial and temporal changes, we introduce a very efficient formulation based on a covariance structure parameterized by the Kronecker product of small size covariance matrices [10]. The proposed model extends GLM approaches by providing a flexible and efficient statistical tool for the analysis of image features from spatially aligned time series, for instance by allowing statistical inference on the model parameters.

The paper is organized as follows. In Section 2 we propose our generative model of longitudinal changes in image time series, while in Section 3 we provide computationally tractable optimization and prediction schemes. We also introduce a novel computational scheme based on the Hoffman-Ribak method for the statistical inference in high dimensional GP-based spatio-temporal models. Finally, in Sections 4 and 5, we apply the model in the context of longitudinal data from from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) for 1) within-subject modelling and prediction of local and regional brain longitudinal changes, and 2) group-wise joint modelling of local ventricle growth rates based on socio-demographics, genetic factors, and clinical scores.

2. A generative model for within-subject image time series

Let u = (x, y, z) be the 3-dimensional spatial coordinate system and t the temporal dimension. We consider the image time series I as a discretely sampled spatio-temporal signal of dimensions N × N × N × N_T, where N is the dimension of the sampling grid on a single spatial axis, and N_T is the number of time points³. In the following sections we represent the image time-series I as a single dimensional array of dimensions N³N_T. We model the image time series I(u, t) as a realization of a latent spatio-temporal process f (u, t) with additive noise:

$$\mathit{\text{I}}\left(u,t\right)=f\left(u,t\right)+ϵ\left(u,t\right).$$ (1)

The true signal will be modelled as a GP with zero mean and covariance Σ, while ϵ is assumed to be i.i.d. Gaussian distributed measurement noise ϵ(u, t) ~ 𝒩(0, σ²). Here we first assume that spatial and temporal processes are separable, and thus that the covariance matrix Σ can be factorised in the Kronecker product of independent spatial and temporal covariance matrices: Σ = Σ_S ⊗ Σ_T.

This is a valid modeling assumption when the temporal properties of the signal are similar across space; for instance, when analyzing within-subject time series of brain MRIs in AD the expected pathological change rates are generally mild and slowly varying across the brain. Second, a central assumption made in this paper is that the spatial dependencies of the signal are local, i.e. that the image intensities are smoothly varying and correlated within a spatial neighborhood of radius l_s. We note that our assumptions about separability and stationarity are compatible with the spatio-temporal correlation models commonly assumed by registration-based approaches.

A reasonable choice for such a local spatial covariance structure is a negative squared exponential model ${\Sigma }_S\left(u_1,u_2\right)={\lambda }_s\text{exp}(-{\frac{\Vert u_1-u_2\Vert }{2l_s}}^2),$ where λ_s is the global spatial amplitude parameter, and l_s is the length-scale of the Gaussian spatial neighborhood. We observe that such a covariance structure is stationary with respect to the space parameters. Furthermore we can exploit the separability properties of the negative exponential function to note that given two separate spatial locations u₁ = (x₁, y₁, z₁) and u₂ = (x₂, y₂, z₂) we have

$${\mathit{\text{Σ}}}_{\mathit{\text{S}}}\left(u_1,u_2\right)={\mathit{\text{λ}}}_s\text{exp}(-\frac{{\left(x_1-x_2\right)}^2}{2l_s})\text{exp}(-\frac{{\left(y_1-y_2\right)}^2}{2l_s})\text{exp}(-\frac{{(z_1-z_2)}^2}{2l_s}).$$

For this reason the covariance matrix Σ_S can be further decomposed as the Kronecker product of covariance matrices of 1-dimensional processes: Σ = K_x ⊗ K_y ⊗ K_z ⊗ Σ_T. We observe that the model is here conveniently represented by the product of independent covariances of significantly smaller size, and is completely identified by the spatial, temporal and noise parameters. In particular the proposed model is flexible with respect to the temporal covariance matrix Σ_T, which can be expressed in terms of complex mixed-effects structure, and can account for covariates and different progression models. For instance, in this work the matrix Σ_T is first specified in order to model the temporal progression observed in time series of images (Section 4), and then is used to model the influence of anatomical, genetic, clinical, and sociodemographic covariates on individual atrophy rates modelled by non-linear registration (Section 5).

3. Inference in Gaussian processes with Kronecker structure

The GP-based generative model with Kronecker covariance structure outlined in this work provides a powerful and efficient framework for prediction using image time series. Here we provide the main results concerning the marginal likelihood computation, the hyper-parameter optimization and the posterior prediction.

Let $\left(U_{K_x,}{S}_{K_x}=\text{diag}\left({\lambda }_1^x,\dots ,{\lambda }_N^x\right)\right)\text{and}\left(U_T,S_T=\text{diag}\left({\lambda }_1^t,\dots {\lambda }_{N_T}^t\right)\right)$ be the eigenvectors and eigenvalues associated to the one-dimensional spatial and temporal covariance matrices K_x and Σ_T. This eigendecomposition problem can be easily and efficiently solved beforehand offline. We further introduce the shortform notation ⊗ A = A_x ⊗ A_y ⊗ A_z.

Log-Marginal Likelihood

The marginal likelihood of the model (1) is the following:

$$\text{log}ℒ=-\frac{1}{2}{{\displaystyle \sum _{i,j,k,l}\text{log}({\mathit{\text{λ}}}_i^x{\lambda }_j^y{\lambda }_k^z{\lambda }_l^t+{\sigma }^2)-\frac{1}{2}{{{\displaystyle V}}_I}^T(\otimes S_K\otimes S_T+{\sigma }^{2}Id)}}^{-1}{V}_I+const,$$ (2)

with $const=-\frac{N^3{N}_T}{2}\text{log}\left(2\pi \right),V_1=\text{vec}\left[(U_{K_z}^T\otimes U_T^T)\tilde{I}(U_{K_x}\otimes U_{K_y})\right],$ and where Ĩ is the matricization of I into a 2 dimensional matrix of dimension N² × NN_T, and ${\lambda }_i^x,{\lambda }_j^y,{\lambda }_k^z\text{and}{\lambda }_l^t$ are the eigenvalues of respectively K_x, K_y, K_z and Σ_t. The computation of the vector V_I requires the storage and multiplication of matrices of relatively small sizes, respectively N² × N², N² × NN_T and NN_T × NN_T. The product ${(\otimes S_K\otimes S_T+{\sigma }^{2}Id)}^{-1}{V}_I$ can be finally computed as the solution of the linear system $(\otimes S_K\otimes S_T+{\sigma }^{2}Id)\mathbf{\text{X}}=V_I,$ which is straightforward since $(\otimes S_K\otimes S_T+{\sigma }^{2}Id)$ is diagonal.

Hyperparameter optimization

The derivative of the log-likelihood (2) with respect to the model parameters θ is:

$$\begin{array}{l}\frac{\text{d}}{\text{d}\mathit{\theta }}\text{log}ℒ=-\frac{1}{2}Tr\left({(\otimes K\otimes {\Sigma }_T+{\sigma }^{2}Id)}^{-1}\frac{\text{d}}{\text{d}\mathit{\theta }}(\otimes K\otimes {\Sigma }_T+{\sigma }^{2}Id)\right)\\ -\frac{1}{2}\frac{\text{d}}{\text{d}\mathit{\theta }}{I}^T{(\otimes K\otimes {\Sigma }_T+{\sigma }^{2}Id)}^{-1}I.\end{array}$$ (3)

It can be shown that formula (3) can be efficiently computed with respect to each model parameters. For instance, the gradient with respect to the noise parameter can be expressed in the form:

$$\frac{\text{d}}{\text{d}{\sigma }^2}\text{log}ℒ=-\frac{1}{2}{\displaystyle \sum _{i,j,k,l}{({\lambda }_i^x{\lambda }_j^y{\lambda }_k^z{\lambda }_l^t+{\sigma }^2)}^{-1}+\frac{1}{2}{{{\displaystyle V}}_I}^T{(\otimes S_K\otimes S_T+{\sigma }^{2}Id)}^{-2}}{V}_I.$$ (4)

Prediction

A major strength of a GP framework for image time series is that it easily enables probabilistic predictions based on given observations. The proposed generative model allows us to consider the predictive distributions of the latent spatio-temporal process at any testing locations u* and timepoints t*. Given image time series I(u, t), we now aim at predicting the image $I^{*}\text{at}{N}^{*}\times N_T^{*}$ testing coordinates {u*, t*}. Let us define Σ_I,I* = Σ(u, t, u*, t*) the cross-covariance matrix of training and testing data, and Σ_{I*, I*} = Σ(u*, t*, u*, t*) the covariance evaluated on the new coordinates. The joint GP model of training and testing data is:

$$\left(\begin{array}{l}I\left(u,t\right)\hfill \\ I^{*}\left(u^{*},t^{*}\right)\hfill \end{array}\right)\sim 𝒩\left[\left(\begin{array}{l}0\hfill \\ 0\hfill \end{array}\right),\left(\begin{array}{ll}\Sigma +{\sigma }^{2}Id\hfill & {\Sigma }_{I,I*}\hfill \\ {\Sigma }_{I*,I}\hfill & {\Sigma }_{I*,I*}+{\sigma }^{2}Id\hfill \end{array}\right)\right],$$ (5)

and it can be easily shown that the posterior distribution of I* conditioned on the observed time series I and parameters θ is [8]:

$$I^{*}|I,\left\{u^{*},t^{*}\right\},\mathit{\theta }\sim 𝒩\left({\mu }^{*},{\Sigma }^{*}\right),\text{where}{\mu }^{*}={\Sigma }_{I,I^{*}}{\Sigma }^{-1}I\text{and}{\Sigma }^{*}={\Sigma }_{I^{*},I^{*}}-{\Sigma }_{I,I^{*}}{\Sigma }^{-1}{\Sigma }_{I^{*},I}+{\sigma }^{2}Id.$$ (6)

From the practical perspective, we notice that by definition the new covariance matrices still have a Kronecker product form: Σ_I,I* = K_x,x* ⊗ K_y,y* ⊗ K_z,z* ⊗ Σ_t,t*, and Σ_I*,I* = K_x*,x* ⊗ K_y*,y* ⊗ K_z*,z* ⊗ Σ_t*,t*. The predicted mean µ* at coordinates {u*, t*} is then

$${\mu }^{*}=(K_{x,x^{*}}{U}_{K_x}\otimes K_{y,y^{*}}{U}_{K_y}\otimes K_{z,z^{*}}{U}_{K_z}\otimes {\mathit{\Sigma }}_{t,t^{*}}{U}_T){(\otimes S_K\otimes S_T+{\sigma }^{2}Id)}^{-1}{V}_I,$$

which can be computed efficiently by noting that the matrix to be inverted is diagonal and by using the product rule of the Kronecker operator. While the posterior form (6) can also be used to evaluate the posterior marginal covariance, certain considerations are necessary for a tractable approach. Indeed, the covariance matrix Σ* is computed from Σ, Σ_I*,I* and Σ_I*,I, which are evaluated on different sets of spatial and temporal coordinates. In particular, the Kronecker structure is lost and in the absence of further assumptions the matrix Σ* must therefore be explicitly computed, generally leading to impractical solutions.

Hoffman-Ribak method for posterior sampling

We propose to compute the sample distribution of (6) using the Hoffman-Ribak method (HR) introduced in the late 1990s in the astrophysics literature [11]. Given the Gaussian distribution (5) partitioned into training (observed) and testing (unobserved) components, the HR method provides a computationally efficient and exact algorithm for sampling from (6) consisting of the following two steps:

• –Sample a random observation (Y, Y*) from the joint distribution (5),
• –Compute a sample Z of the marginal posterior (6) according to Z = Y* + Σ_I*,I (Σ + σ²Id)⁻¹Y.

Despite its simple formulation, the HR method cannot be straightforwardly applied in our case as sampling from the very high dimensional joint distribution is generally prohibitive. Therefore, instead of focusing on predicting time series at arbitrary spatial and temporal coordinates, we provide here an efficient scheme for spatio-temporal prediction at arbitrary time points T* = {t*} evaluated in the same spatial coordinates of the training image time-series I. Under this assumption the matrices Σ, Σ_I*,I* and Σ_I*,I differ in the temporal part only,

$$\begin{array}{lll}\Sigma ={\Sigma }_S\otimes {\Sigma }_T+{\sigma }^{2}Id;\hfill & {\Sigma }_{I^{*},I^{*}}={\Sigma }_S\otimes {\Sigma }_{T^{*},T^{*}};\hfill & {\Sigma }_{I^{*},I}={\Sigma }_S\otimes {\Sigma }_{T^{*},T}+{\sigma }^{2}Id,\hfill \end{array}$$

and it is simple to show that the joint covariance is Σ^joint = P(Σ_S ⊗ Σ_T^j + σ²Id)P^T, where P is a structured permutation matrix, and ${\Sigma }_{T^j}=\left(\begin{array}{cc}{\Sigma }_T& {\Sigma }_{t,t^{*}}\\ {\Sigma }_{t^{*},t}& {\Sigma }_{t^{*},t^{*}}\end{array}\right).$ A sample Z from the joint distribution can thus be easily computed as Z = P(UΛ)X, where X is a standard multivariate normal distributed vector, and UΛ²U^T is the eigen-decomposition of the covariance (Σ_S ⊗ Σ_T^j + σ²Id). Eigen-decomposition and matrix multiplication can be efficiently computed by virtue of the properties of the Kronecker product.

In the following sections, after validating the proposed framework in a controlled setting, we provide a modelling application in the context of longitudinal modelling in AD.

4. Model Validation

Estimation of the Spatio-temporal Properties in Synthetic Data

Here, we test the ability of the proposed GP model to correctly estimate the underlying spatial and temporal properties prescribed in synthetic data. We chose a time-series of brain MRIs composed of 6 aligned longitudinal gray matter (GM) segment images of an example ADNI patient, and we applied Gaussian smoothing to obtain synthetic samples of a spatio-temporal process with predefined spatial correlation and signal to noise ratio. Moreover we generated synthetic longitudinal progressions of increasing temporal complexity following respectively voxel-wise linear, quadratic and cubic functions of time estimated through a general linear model (GLM). Furthermore, longitudinal changes in the synthetic time series were modelled with the proposed GP model. We applied a squared exponential model for the temporal covariance parameterized by the temporal length-scale l_t. A maximum-a-posteriori (MAP) estimate of the parameters was obtained by using Gauss-Newton optimization scheme of the log-hyperparameters, using multivariate uninformative Gaussian hyperprior with log-hyperparameters µ_h = [−2, −2, 0, 3] and Σ_h = diag([5, 5, 1, 5]) for respectively (σ², l_s, λ_s, l_t).

Table 1 shows the relationship between the spatio-temporal properties of the synthetic data and the MAP estimates of the GP parameters. Noticeably, the estimated spatial length-scale closely resembles the global smoothness parameter of the synthetic data, adaptively accounting for image smoothness properties. Additionally, we observed that the estimated temporal length-scale decreased when modeling longitudinal progressions of higher order models. Thus, the model also correctly denotes the increased complexity of the temporal changes.

Table 1.

Estimation of the global spatial and temporal properties. The estimated spatial length-scale l_s closely correspond to the global smoothness of the synthetic data, while the noise term and the signal amplitude decrease with increasingly smoother data. The estimated temporal length-scale is inversely proportional to the underlying complexity of the temporal progression.

Spatial smoothness (mm)	ls	σ2	λs
0	0.09	9e-6	0.7
0.5	0.81	5e-6	0.64
1	1.2	3e-6	0.53
2	2.3	1e-6	0.5
3	3.3	3e-10	0.48
4	4.3	7e-11	0.47

Temporal progression	lt (log-values)
linear	4.3
quadratic	1.79
cubic	1.72

Within-Subject Modelling and Prediction of Longitudinal Changes

We chose high-resolution longitudinal images of 10 AD patients, 10 patients with mild cognitive impairment (MCIc) subsequently converting to AD, and 10 healthy controls from the ADNI dataset. AD patients and healthy controls (HC) had 4 images per participant, corresponding to baseline, 6 months, 1 and 2 years scans, while for MCIc patients additional images corresponding to 3 or 4 years were available. The images were processed according to established procedures consisting of joint bias correction, tissue segmentation, alignment to the within-subject average anatomy, and non-linear normalization to a group-wise anatomical reference [12]. The final image size was of 100³ cubic voxels with isotropic resolution of 1.5 mm.

The longitudinal changes in the resulting time series of processed gray matter density maps were modelled according to the proposed GP model. The model was estimated for each subject by using 3 training images corresponding to baseline, 6 months and 1 year scans. In order to capture meaningful non-linear trends during disease progression to AD, we also applied the GP model in the MCIc group by using 4 and 5 training images, corresponding to the time range from baseline to respectively 2 and 3 years follow-up.

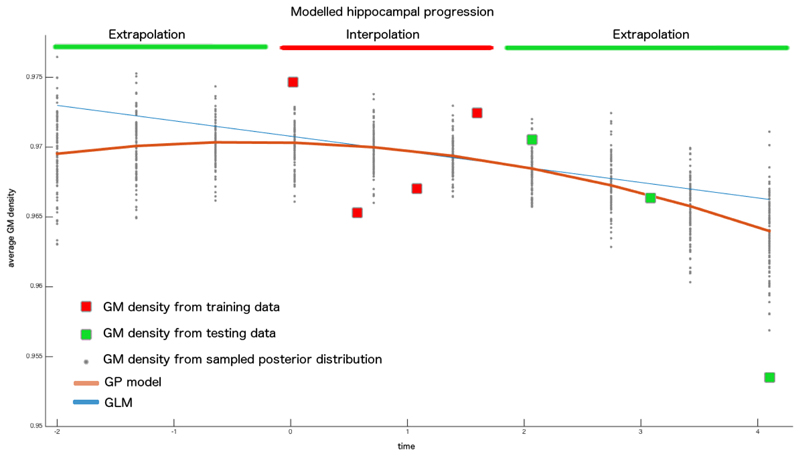
We applied the optimization scheme illustrated in Section 4 while imposing an informative prior on the temporal length-scale parameter with log-mean and -variance of 3 and 0.1 respectively. This choice was done in virtue of the experimental results illustrated in Table 1 in order to promote a moderately non-linear behaviour of the GP model, and at the same time avoid overfitting on the limited number of within-subject observations. The resulting computational time for the parameter estimation was of about 5 minutes per subject on a standard PC (with 2.6 GHz, QuadCore, 16GB RAM). The predictive accuracy of the model was then tested by voxel-wise comparison of the extrapolated image series with respect to the corresponding ground truth follow-up images, and compared with respect to a standard linear and quadratic voxel-by-voxel model using within-subject GLM. The group-wise average voxel-wise absolute differences between extrapolated images and real ones are shown in Figure 1. Errors were generally found to be proportional to the extrapolation time. Table 2 shows that the results of the GP model are comparable to those obtained by linear modelling when training on 3 time points only. However, the prediction of the GP model significantly improves the linear one when using more training points. This result indicates that the GP model is able to capture meaningful accelerations of the time process when sufficient data is provided, while it stays essentially linear otherwise. Figure 2 shows the mean hippocampal progression and associated confidence interval from the posterior latent process for a MCIc patient. We observe that the GP-based model of hippocampal loss is non-linear and fairly predicts the acceleration of volume loss observed in the follow-up testing images.

Fig. 1.

Group-wise average absolute differences between extrapolated images and real ones. The GP model was trained on scans from 3 time points corresponding to baseline, 6 months and 1 year. Errors were generally found to be proportional to the extrapolation time.

Table 2.

Mean absolute error (averaged over the whole brain and subjects) between predicted extrapolated image and real one (values are scaled by a factor 1e3). The proposed GP model significantly outperformed predictions obtained from GLM when trained on 4 and 5 time points, from baseline to 2-3 years follow-up (* for statistically significant difference, p < 0.05, paired t-test).

	AD	HC	MCI
N train points	3	3	4	5
GP	1.9	1.9	2.9*	2.5*
GLM linear	1.9	2	3.1	2.7
GLM quadratic	6.7	2.6	8.7	5.4

Fig. 2.

Predicted hippocampal progression for a sample MCIc patient. The model was estimated from 4 image time points (baseline to 2 years) in a bounding region including the hippocampus. The longitudinal sample distribution (gray dots) and mean prediction (red line) are estimated according to the marginal GP posterior of Section 3 by using the Hoffman-Ribak method.

5. Application: Between-Subjects Prediction of Individual Rates of Ventricle Growth using Multi-Kernel Learning

In this second application, we exploit the flexibility of our model to make covariate-based predictions of individual rates of atrophy in elderly subjects. In contrast to typical multivariate models which predict or classify scalar values, our GP framework allows prediction of images. In particular, we here focus on predicting the rate of volumetric growth in the lateral ventricle regions.

Firstly, we used computational morphometry to obtain the rates of atrophy in a large sample from the ADNI longitudinal dataset. To obtain these features for training and testing, we used 1143 and 569 MRI scans of 206 and 105 elderly subjects respectively (ages 59-91, age mean ± std: 76.0 ± 6.0 years). In order to enable predictions across a broad range of clinical states, the sample was pooled across clinical groups. It contained 111 healthy elderly and 108 subjects with stable and 92 subjects with progressive MCI. After longitudinal registration, tissue segmentation and inter-subject alignment [12], we calculated each subject’s ventricle growth rate from registered CSF images using a linear model.

Secondly, using the preprocessed images as features we considered a special case of generative model (1) to implement a prediction model based on individual subject’s covariates, e.g. age, cognitive scores, etc. This is realized by a different choice of covariance function Σ_T compared to the above within-subject application. In order to enable a prediction based on multiple available covariate sets e.g. genes, clinical scores, etc. we used an additive multi-kernel learning covariance

$${\Sigma }_T={\displaystyle \sum _{r=1}^4{K}_r,\text{with}{K}_r\left(c_1,c_2\right)={\alpha }_r\text{exp}(-\frac{1}{2}{\left(c_1-c_2\right)}^T{M}_r\left(c_1-c_2\right))}$$ (7)

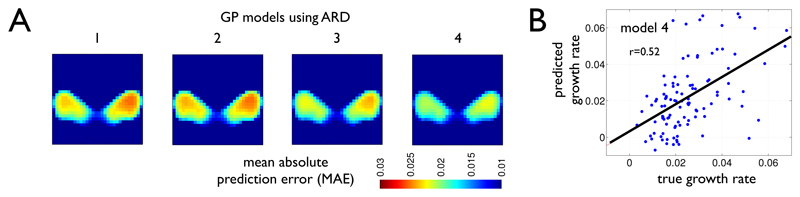
using a sum of (up to four) squared exponential covariances K_r with amplitudes α_r, and c₁, c₂ denoting pairs of covariate vectors from each of (up to four) covariate sets. The symmetric matrices M_r were chosen to be either M_ISO = ℓ⁻²Id or M_ARD = diag(ℓ)⁻². Like in typical GP regression applications, using (7) explicitly models covariance of (latent) observations f as a function of similarity of inputs c (here the covariate vectors of subjects). That implements the idea that subjects with similar covariates are expected to have similar rates of atrophy. In particular, the choice of M_r = M_ISO parametrizes an isotropic covariance assuming equal length-scale for different covariates of the same covariate set. An alternative choice of M_r = M_ARD implements automatic relevance determination (ARD) with separate length-scales estimated for each variable. We compared successively complex prediction models using (1) only global brain volumes (tgmv, twmc, tcsv) or (2) additionally using demography (age, sex, education, marital status, year of retirement), or (3) also including genetic risk in terms of the number of ApoE4 allele and (4) finally also using the clinical neuropsychological test scores MMSE, ADAS, and CDR. The models (1) to (4) step-by-step increased the amount of subject-specific information to predict maps of rates of ventricle growth. Comparison across models was performed using log marginal likelihood balancing model fit and model complexity with varying numbers of hyperparameters. We found an increasing marginal likelihood for more complex models using ARD covariance (see Table 3) and decreased model evidence for model 4 under ISO covariance. Highest marginal likelihood was observed for ARD model 4 including all predictors. This trend is also reflected in terms of mean absolute error maps demonstrating increased prediction accuracy and generalization ability during testing in an independent test sample of 105 subjects (Figure 3A). Results also showed a correlation of up to 0.52 of predicted and true growth rates (Figure 3B).

Table 3.

Log marginal likelihood (ml) of Gaussian process covariance using M_ISO and M_ARD for prediction of ventricle growth rate maps based on sets of subject’s covariates. Hyperparameters were optimized in 206 subjects training sample. Column 3 shows mean absolute error (mae) averaged across voxels in prediction of unseen 105 test subjects from independent test sample.

model	ml - ISO	ml - ARD	mae - ARD
1	1.6697	1.6769	0.0059
2	2.4309	2.0249	0.0058
3	2.4356	2.0513	0.0080
4	2.2768	2.4434	0.0057

Fig. 3.

(A) Mean absolute error (MAE) of prediction maps in an independent testing sample of 105 subjects show increasingly better predictions using more predictor sets and Gaussian process models with ARD. (B) Predicted over true growth rates using model 4 in an example voxel showing correlation of r = 0.52.

6. Conclusions

We presented a novel framework for modelling and prediction of spatio-temporal processes in image time series. It is flexible and computationally efficient thanks to the proposed Kronecker structure of the covariance, and to the use of the Hoffman-Ribak method for efficient sampling from the posterior. Our model provided promising results when tested in very different experimental scenarios concerning longitudinal modelling in AD, and opens the path to the effective use of GPs for the generative modeling of neuroimaging data. The strength of the framework relies on assuming separability of spatial and temporal processes. We show that this assumption leads to meaningful results when applied to the longitudinal modeling in AD, where the expected pathological changes are generally mild and slowly varying across brain regions. This assumption might be relaxed in future work in order to also model spatially varying processes that might underlie biological progressions with different properties. It may be indeed possible to further extend the framework to allow non-stationary correlations and noise models without compromising the computational efficiency, by accounting for local smoothly varying stationary processes as previously proposed in geostatistics [13]. Finally, further extensions of the proposed work will be devoted to the group-wise non-parametric mixed-effect modeling of disease progression in clinical cohorts such as ADNI, by exploiting the flexibility of the proposed spatio-temporal covariance structure in accounting for subject and group-specific progressions and confounders.