SKF-LDA: Similarity Kernel Fusion for Predicting lncRNA-Disease Association

Abstract

Recently, prediction of lncRNA-disease associations has attracted more and more attentions. Various computational models have been proposed; however, there is still room to improve the prediction accuracy. In this paper, we propose a kernel fusion method with different types of similarities for the lncRNAs and diseases. The expression similarity and cosine similarity are used for lncRNAs, and the semantic similarity and cosine similarity are used for the diseases. To eliminate the noise effect, a neighbor constraint is enforced to refine all the similarity matrices before fusion. Experimental results show that the proposed similarity kernel fusion (SKF)-LDA method has the superiority performance in terms of AUC values and other measurements. In the schemes of LOOCV and $5$-fold CV, AUC values of SKF-LDA achieve $0.9049$ and $0.8743\pm 0.0050$ respectively. In addition, the conducted case studies of three diseases (hepatocellular carcinoma, lung cancer, and prostate cancer) show that SKF-LDA can predict related lncRNAs accurately.

Introduction

In humans, only about 1.5% of the genome can be encoded into proteins, while the rest are extensively transcribed into non-coding RNAs (ncRNAs).1, 2, 3 Studies have shown that ncRNAs play an important role in human biological mechanisms,4, 5, 6 especially the long non-coding RNAs (lncRNAs), a kind of significant ncRNA with over 200 nt in length.7, 8, 9, 10 In the past years, lncRNAs have been found that influenced transcription, translation, cell cycle, imprinting, splicing, and protein localization;5, 11, 12 for example, intergenic 10 regulates expression of ADAM12- and FANK1-flanking genes through modulation of the chromatin structure in cis.¹³ Additionally, it has shown that the dysregulations and mutations of some lncRNAs are associated with human diseases,14, 15, 16 such as breast cancer,17, 18 intracranial aneurysm,19, 20 and $\beta$-thalassemia.21, 22 Though the detail mechanisms of lncRNA are a riddle, we can still use computational models to predict the relationship between lncRNAs and diseases, which can be helpful for disease diagnosis. Besides, the computational methods can be a powerful complementary tool to the biological experiments or can even avoid the time-consuming experiments.²³

In the past few years, many effective computational models have been built to calculate potential lncRNA-disease associations.24, 25, 26, 27 We can roughly classify the methods into two categories according to the computational model. The first category of methods predicts the lncRNA-disease associations with designed machine learning models. Chen et al.²⁸ proposed Laplacian regularized least squares for lncRNA-disease association (LRLSLDA) in the semi-supervised learning framework, which is based on the prior that similar diseases are more likely to be associated with functionally similar lncRNAs. Lan et al.²⁹ integrated multiple biological data resources to predict lncRNA-disease associations with a bagging support vector machine (SVM) classifier based on lncRNA similarity and disease similarity. The SIMCLDA³⁰ method uses an inductive matrix to predict lncRNA-disease associations. In this model, the Gaussian interaction profile kernel of lncRNAs is from known lncRNA-disease interactions, and the function similarity of diseases is based on disease-gene and gene-gene ontology associations. Also, the primary feature vectors from constructed feature matrices are used to complete the association matrix based on the inductive matrix completion framework. Another type of method predicts associations based on constructed networks. In an earlier study, Sun et al.³¹ designed a computational network framework, random walk with restart for lncRNA-disease association (RWRlncD), to predict lncRNA-disease association based on the lncRNA-lncRNA functional similarity network. RWRlncD integrates lncRNA-disease association and disease functional similarity and then uses random walk. Bi-random walks for lncRNA-disease association (BRWLDA)³² applies bi-random walks that take the structural differences into account between lncRNA similarity and disease similarity and build two networks using lncRNA functional similarity and disease semantic similarity. Then multiple the random walks method is used on both networks to predict potential lncRNA-disease associations. Paths with limited lengths for lncRNAs-diseases association (PLLDA) builds lncRNA similarity networks and disease similarity networks based on lncRNA functional similarity and disease semantic similarity.³³ PLLDA is based on the method of connecting their pathways and their length in their respective similarity networks. The depth-first search is then used to calculate the probability of lncRNA-disease association. This method is suitable for the prediction of the relation between a new disease and lncRNAs or the relation between a new lncRNA and diseases. However, since the length-based cost function is relatively simple, it is necessary to look for model substitution for machine learning. By combining lncRNA-disease association and gene and disease association, tripartite graph for lncRNAs-diseases association (TPGLDA) can effectively predict the association between lncRNA and disease, but this method relies on the structure among the three parts, and the incomplete data will limit its performance.³⁴

Although the aforementioned methods achieve relatively good results, there is still room for us to improve the accuracy of association prediction. For example, some methods only consider the similarity of lncRNA and disease in one dimension (functional or semantic) and do not fully take the multi-dimensional information into consideration. It is believed that, when more biological knowledge is applied with elaborated fusion method, we can get a more accurate prediction, as proved by previous studies on the prediction of association between microRNA (miRNA) and disease.35, 36 Recently, there are increasingly more state-of-the art computational models37, 38, 39, 40, 41 published in well-known journals that have promoted the study of the association between lncRNA and disease. For example, the integration method we used is inspired by the method of predicting miRNA and disease association.⁴² Also, the idea of using Laplacian regularization⁴³ to explore the relationship between miRNA and disease inspires us to apply similar ideas to predict the association between lncRNA and disease.

In this study, we present a similarity kernel fusion (SKF) method to predict lncRNA-disease association (SKF-LDA, for short). In the proposed method, two different similarities, the functional similarity and semantic similarity, are utilized with a new fusion approach. The fusion step is built on the refined similarity matrices by a neighbor-based constraint and iterates over the similarity matrices instead of a simply weighted addition. The final lncRNA-disease association is computed by a normal Laplacian regularized least-squares method. To demonstrate the prediction performance of the proposed SKF-LDA, the leave-one-out cross-validation (LOOCV) and 5-fold cross-validation (5-fold CV) frameworks are implemented. The experimental results showed that the proposed SKF-LDA achieves 0.9049 and 0.8743$\pm$0.0050 in terms of AUC value in the scheme of LOOCV and 5-fold CV. Furthermore, in case studies, 9, 10, and 7 out of the top 10 predicted lncRNAs for disease hepatocellular carcinoma, lung cancer, and prostate cancer, respectively, are confirmed by recent research.

Results

Overview of Proposed Method

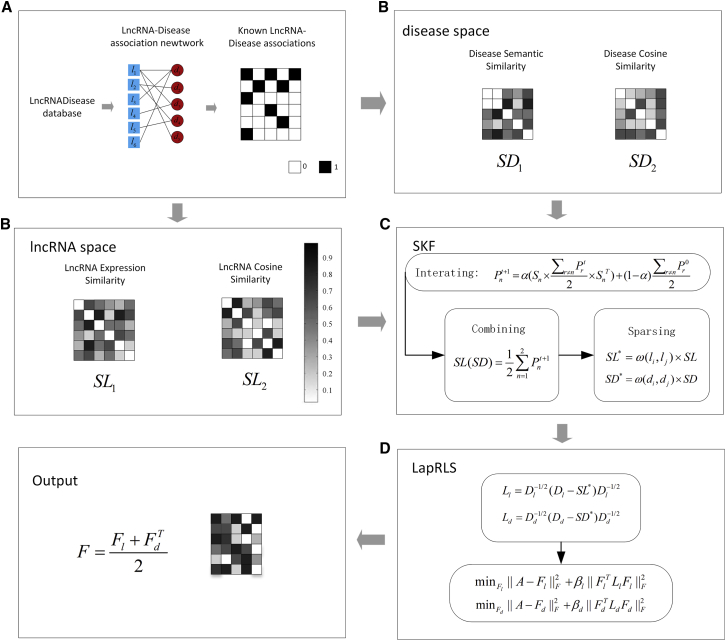
The proposed SKF-LDA method can be summarized in four steps, as shown in Figure 1. First, we construct the lncRNA-disease correlation matrix based on the known lncRNA-disease association. Second, we calculate lncRNA similarity (lncRNA expression similarity, lncRNA cosine similarity) and disease similarity (disease semantic similarity, disease cosine similarity). Third, SKF is used to integrate the two similarities of lncRNAs and diseases. Lastly, we obtain the predicted lncRNA-disease association matrix by the Laplacian regularized least-squares method.

Figure 1.

Flow Chart of SKF-LDA Applied to lncRNA-Disease Association Prediction

(A–D) SKF-LDA consists of four steps: (A) constructing the lncRNA-disease correlation matrix; (B) calculating the two similarities of lncRNA and disease similarity, respectively; (C) using SKF integration similarity; and (D) obtaining the prediction matrix by Laplacian regularized least squares.

We verify the performance of SKF-LDA by LOOCV and 5-fold CV. The idea of LOOCV is to use one of the 540 lncRNA-disease relationships as a test sample and the rest as training set. 5-fold CV randomly divides 540 lncRNA-disease associations into 5 parts; each time, one part is used as a test set and the remaining as training sets. When one dataset is used as the test set, the prior knowledge is removed before calculating the similarity, and the associations in the dataset are regarded as unknown; in other words, the initial 1 is set to be 0. When the final predicted value is higher than the threshold for those who have the associations, the prediction is correct. According to different thresholds, various false-positive rates (FPRs; 1 − specificity) and true-positive rates (TPRs; sensitivity) are obtained. Based on these data, we can plot the receiver operating characteristic (ROC) curve and get the area under the ROC curve (AUC). The prediction ability is perfect if AUC = 1, the prediction ability tends to be random if AUC = 0.5, and AUC = 0 indicates that the forecast result is negative prediction. In addition, we adopt the area under the precision-recall curve (AUPR) as another measurement. In order to verify the accuracy of SKF-LDA, the precision (PRE), sensitivity (SEN), accuracy (ACC), F1-score (F1-score) and Matthews’s correlation coefficient (MCC) are defined as follows:

$$PRE=\frac{TP}{TP+FP},$$ (Equation 1)

$$SEN=\frac{TP}{TP+FN},$$ (Equation 2)

$$ACC=\frac{TN+TP}{TP+TN+FN+FP},$$ (Equation 3)

$$F1=\frac{2\times TP}{2\times TP+FP+FN}=2\times \frac{PRE\times REC}{PRE+REC},$$ (Equation 4)

and

$$MCC=\frac{TP\times TN-FP\times FN}{\left(TN+FN\right)\times \left(TP+FP\right)\times \left(TN+FN\right)\times \left(TN+FP\right)},$$ (Equation 5)

where TP represents true positive, TN represents true negative, FP represents false positive, and FN represents false negative.

Parameter Selection

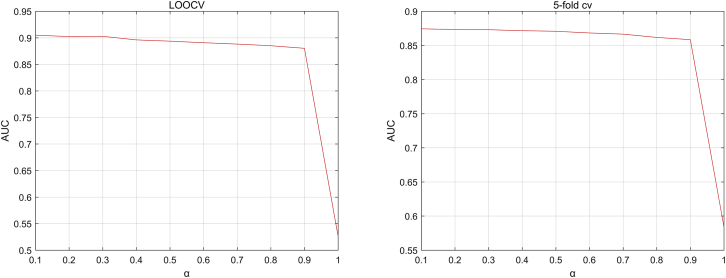
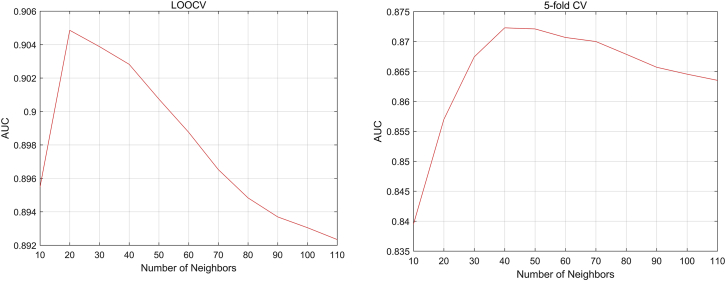
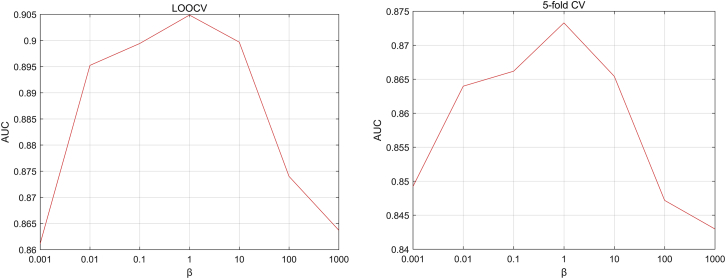
In this paper, there are five parameters: the number of iteration, $t$; the weight parameter $\alpha$; the number of neighbors, $K$, in the SKF; and the weight parameters ${\beta }_l$ and ${\beta }_d$ in Laplacian regularized least squares. In the experiments, the iteration number is set to be $t=2$, and the value of $\alpha$ is set to be 0.1 after parameter tuning. We set the value of $\alpha$ as a range from 0.1 to 1 with step 0.1. The AUC values with different $\alpha$s are shown in Figure 2 based on the LOOCV scheme and 5-fold CV scheme. As shown in Figure 2, the AUC values barely change when $\alpha$ is in the range of 0.1 to 0.9 and decay fast in the range of 0.9 to 1. Since there are 178 diseases and 115 lncRNAs in our data, the value of $K$ ranges from 10 to 110 with step 10. As shown in Figure 3, the highest AUC value is achieved at $K=20$ in the LOOCV scheme and $K=40$ in the 5-fold CV scheme. As for the weighting parameter ${\beta }_l$$\left({\beta }_d\right)$ in Laplacian regularized least squares, previous research has shown that the performance of Laplacian regularization least squares (LapRLS) is robust to the paremeters, so we set ${\beta }_l$ to be equal to ${\beta }_d$ as $\beta$, and in the experiments, the value of $\beta$ ranges from ${10}^{-3}$ to 1,000. As shown in Figure 4, the AUC values in both the LOOCV scheme and 5-fold CV scheme change in a small interval and achieve the highest value when $\beta =1$.

Figure 2.

The AUC Values with Different αs

Figure 3.

The AUC Values with Different Values of the Number of Neighbors (K)

Figure 4.

The AUC Values with Different βs

Comparison with Other Fusion Methods

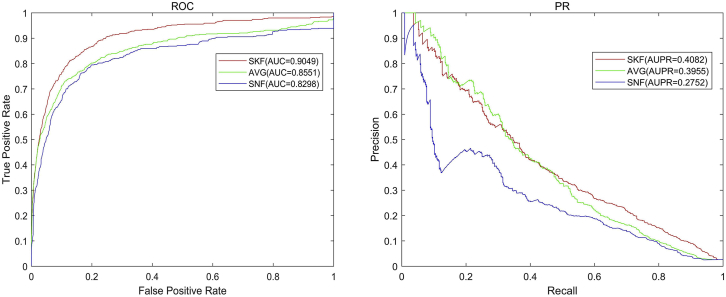
To verify the superiority of the SKF, we compared SKF with two common fusion methods: average kernel fusion (AVG) and similarity network fusion (SNF).⁴⁴ We plotted the ROC curve and the precision recall (PR) curve of three methods based on LOOCV. As shown in Figure 5, the AUC values of SKF, AVG, and SNF are 0.9049, 0.8511, and 0.8298, respectively. The AUPR values of SKF, AVG, and SNF are 0.4082, 0.3955, and 0.2752, respectively. In summary, SKF performs better than other fusion methods in terms of the prediction association accuracy between lncRNA and disease.

Figure 5.

The ROC Curve and the PR Curve of Three Integration Methods

Comparison with Single Similarity

In this paper, we combined different types of similarity for both lncRNAs and diseases. To demonstrate the benefit of the combination, we performed a series of comparison experiments, including all combinations of one single similarity for the lncRNA and the disease. The AUC values of different combinations in LOOCV and the 5-fold CV scheme are shown in Table 1, from which we can see that the proposed SKF-LDA achieves the highest AUC values.

Table 1.

The AUC Values of SKF-LDA and Other Single Similarity in LOOCV and 5-fold CV Scheme

lncRNA Similarity	Disease Similarity	LOOCV	5-fold CV
Expression	semantic	0.8512	0.8476 ± 0.0034
Expression	cosine	0.8630	0.8375 ± 0.0046
Cosine	semantic	0.8835	0.8502 ± 0.0073
Expression	cosine	0.8754	0.8519 ± 0.0070
Expression + cosine	semantic + cosine	0.9049	0.8743 ± 0.0050

Comparison with and without Neighbor Constraint

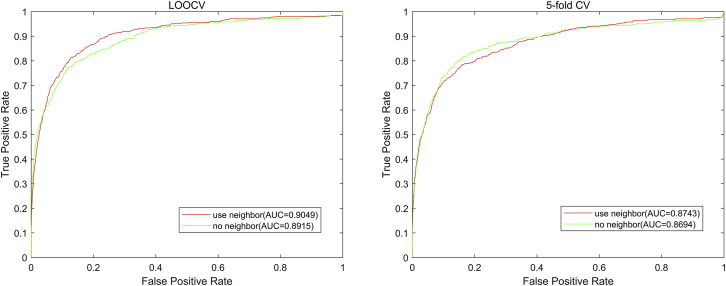
In this paper, we add a neighbor constraint to eliminate the noise effect. To demonstrate the benefit of the neighbor constraint, we tested the case without the neighbor constraint in comparison, as shown in Figure 6, which achieved 0.8915 and 0.8694$\pm$0.0035 in LOOCV and 5-fold CV, respectively; and the one with the neighbor constraint achieved 0.9049 and 0.8743$\pm$0.0050, respectively, which validates the effect of the neighbor constraint.

Figure 6.

The ROC Curve and the PR Curve When Using Neighbor and without Neighbor Constraint

Comparison with Other Methods

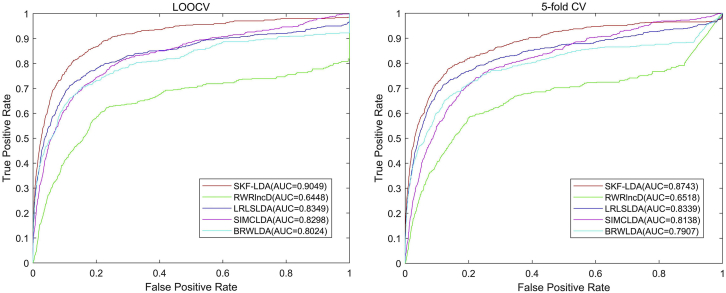
To further validate the advantage of SKF-LDA, we compared our method with four state-of-the-art methods, namely, RWRlncD,³¹ LRLSLDA,²⁸ SIMCLDA³⁰ and BRWLDA.³² As shown in Figure 7, based on the LOOCV scheme, the AUC values of RWRlncD, LRLSLDA, SIMCLDA, and BRWLDA are 0.6448, 0.8349, 0.8298, and 0.8024, respectively, while the proposed SKF-LDA method achieves 0.9049, which is much better than the others. In the 5-fold CV scheme, the AUC values of RWRlncD, LRLSLDA, SIMCLDA, and BRWLDA are 0.6518, 0.8339, 0.8138, and 0.7907, respectively, while ours is 0.8743. The AUPR measurement is also used to evaluate different methods. The AUPRs of SKF-LDA, RWRlncD, LRLSLDA, SIMCLDA, and BRWLDA are 0.4081, 0.0808, 0.3343, 0.2555, and 0.3068, respectively. Meanwhile, we set two stringency levels to evaluate predictive performance as shown in Table 2. When the stringency level of specificity is set as $Sp=95\%$, the PRE, sensitivity, accuracy, F1-score, and MCC of SKF-LDA are 0.4884, 0.3519, 0.97318, 0.5206, and 0.4013. When $Sp=99\%$, the PRE, sensitivity, accuracy, F1-score, and MCC of SKF-LDA are 0.2407, 0.5852, 0.9404, 0.7383, and 0.3501, which are higher than those of RWRlncD, LRLSLDA, SIMCLDA, and BRWLDA.

Figure 7.

The ROC Curve and AUC Values of Different Methods in LOOCV and 5-fold CV Scheme: SKF-LDA, RWRlncD, LRLSLDA, SIMCLDA, and BRWLDA

Table 2.

Results of Different Methods

Measurement	SKF-LDA	RWRlncD31	LRLSLDA28	SIMCLDA30	BRWLDA32
AUC	0.9049	0.6448	0.8349	0.8298	0.8024
AUPR	0.4082	0.0808	0.3343	0.2555	0.3068
Sp = 99%
PRE	0.4884	0.1076	0.4472	0.3539	0.4413
Sensitivity	0.3519	0.0444	0.2982	0.2019	0.2926
Accuracy	0.9732	0.9651	0.9718	0.9692	0.9716
F1-score	0.5206	0.0851	0.4593	0.3359	0.4527
MCC	0.4013	0.0532	0.3513	0.2526	0.3455
Sp = 95%
PRE	0.2407	0.1293	0.2283	0.2037	0.2100
Sensitivity	0.5852	0.2741	0.5463	0.4722	0.4907
Accuracy	0.9404	0.9321	0.9393	0.9374	0.9379
F1-score	0.7383	0.4302	0.7066	0.6415	0.6584
MCC	0.3501	0.1563	0.3271	0.2823	0.2937

Case Studies

To validate the ability of SKF-LDA to predict lncRNA-disease associations, case studies were conducted for three human diseases: lung cancer, hepatocellular carcinoma, and prostate cancer. The top 10 predicted lncRNAs of each disease are confirmed by two other databases: Lnc2Cancer⁴⁵ and MNDR.⁴⁶

Lung cancer is one of the leading cancers that cause death. The death rate for lung cancer is nearly $87\%$, as its malignancy has the highest numbers among all cancers.⁴⁷ Therefore, it is necessary to study the biological mechanism and the cause of lung cancer. Here, in our experiments, 9 of the top 10 lncRNA-lung cancer forecast results by SKF-LDA are confirmed by known databases, as shown in Table 3. GAS5 is a novel lung cancer biomarker that is related to the diagnosis and prognosis of lung cancer patients.48, 49 CCAT2 not only promotes the non-small-cell lung cancer production but also is one specific lncRNA of lung adenocarcinoma.⁵⁰ UCA1 is overexpressed in lung cancer cells, because it induces resistance to T790M in the AKT/mTOR pathway of non-small-cell lung cancer.⁵¹

Table 3.

The Top 10 lncRNA Candidates Predicted for Lung Cancer

Rank	lncRNA	Disease	Evidence
1	GAS5	lung cancer	lnc2Cancer2, MNDR
2	CCAT2	lung cancer	MNDR
3	UCA1	lung cancer	lnc2Cancer2, MNDR
4	HULC	lung cancer	unconfirmed
5	SPRY4-IT1	lung cancer	MNDR
6	CCAT1	lung cancer	MNDR
7	PVT1	lung cancer	lnc2Cancer2, MNDR
8	NEAT1	lung cancer	lnc2Cancer2, MNDR
9	XIST	lung cancer	MNDR
10	HNF1A-AS1	lung cancer	MNDR

Hepatocellular carcinoma (HCC) is one of the most often seen types of cancer in the world. Since many HCC patients are already in advanced stages of cancer when they are diagnosed, it is urgent to understand the principle of HCC and improve early diagnosis ability.⁵² Studies have shown that lncRNAs have a vital effect on human HCC.⁵³ In this study, the top 10 lncRNAs of lncRNA-HCC results based on SKF-LDA are confirmed by known databases and related literature as shown in Table 4. Studies have shown that GAS5 is downregulated in most cell cancer patients and can be regarded as an important prognostic factor for HCC.54, 55 In addition, UCA1 promotes the development of HCC by inhibiting miR-216b and activating the FGFR1/ERK signaling pathway.⁵⁶ PVT1 is upregulated during the liver development and contributes to HCC by affecting the lncRNA-hPVT1/NOP2 pathway.⁵⁷

Table 4.

The Top 10 lncRNA Candidates Predicted for Hepatocelluar Carcinoma

Rank	lncRNA	Disease	Evidence
1	GAS5	hepatocelluar carcinoma	lnc2Cancer2, MNDR
2	UCA1	hepatocelluar carcinoma	lnc2Cancer2, MNDR
3	PVT1	hepatocelluar carcinoma	lnc2Cancer2, MNDR
4	CCAT2	hepatocelluar carcinoma	lnc2Cancer2, MNDR
5	CDKN2B-AS1	hepatocelluar carcinoma	MNDR
6	CCAT1	hepatocelluar carcinoma	lnc2Cancer2, MNDR
7	BANCR	hepatocelluar carcinoma	lnc2Cancer2, MNDR
8	PTENP1	hepatocelluar carcinoma	lnc2Cancer2, MNDR
9	SPRY4-IT1	hepatocelluar carcinoma	lnc2Cancer2, MNDR
10	NEAT1	hepatocelluar carcinoma	lnc2Cancer2, MNDR

Prostate cancer is also a common form of malignancy among males and accounts for the second leading cause of cancer fatality.⁵⁸ The ability to explain the principles of prostate cancer from a genetic perspective will help us to diagnose and prevent prostate cancer. 4 of the top 5 lncRNAs are successfully found in the databases, while 7 of the top 10 lncRNAs are found in the databases based on SKF-LDA, as shown in Table 5. Different variants of CDKN2B-AS1 are associated with prostate cancer.⁵⁹ CCAT2 is upregulated in prostate cancer patients and affects the development of prostate cancer by changing the epithelial-mesenchymal transition.⁵⁰ Among prostate cancer patients, the XIST gene locus is hypomethylated. This phenomenon may contribute to a further realization of the biological mechanism of prostate cancer.⁶⁰

Table 5.

The Top 10 lncRNA Candidates Predicted for Prostate Cancer

Rank	lncRNA	Disease	Evidence
1	CDKN2B-AS1	prostate cancer	MNDR
2	CCAT2	prostate cancer	lnc2Cancer2, MNDR
3	XIST	prostate cancer	lnc2Cancer2, MNDR
4	PTENP1	prostate cancer	lnc2Cancer2, MNDR
5	LSINCT5	prostate cancer	unconfirmed
6	IGF2-AS	prostate cancer	unconfirmed
7	SPRY4-IT1	prostate cancer	lnc2Cancer2, MNDR
8	MINA	prostate cancer	unconfirmed
9	CCAT1	prostate cancer	lnc2Cancer2
10	BANCR	prostate cancer	MNDR

Discussion

Numerous literatures have shown that lncRNA is of great importance in disease. Studying the relationship between lncRNA and disease not only helps us to realize the fundamentals behind disease but also contributes to the prognosis and prevention of disease. Since the current biological experimental methods are time consuming, many lncRNA-disease predictive models have emerged. In this paper, the proposed SKF-LDA method combines both the expression similarity with cosine similarity for lncRNAs and the semantic similarity with cosine similarity for diseases with an effective fusion method. Compared with the other four methods, SKF-LDA performs better in terms of AUC and AUPR in the LOOCV and 5-fold CV schemes.

Other important reference indices show a perfect performance of SKF-LDA as well. To further validate the accuracy of the SKF-LDA, we predicted three diseases (lung cancer, HCC, prostate cancer) based on the forecast result by SKF-LDA. We found that the prediction success rates reached 90%, 100%, and 70%, respectively. The reason for the excellent performance of the SKF-LDA method is mainly due to several reasons as follows. First, SKF-LDA integrates two lncRNA similarities and two disease similarities, which provide us with rich biological information. Second, we integrate different similarities with the neighbor constraint, which will eliminate the noise data in the known dataset. Finally, the final lncRNA-disease correlation prediction matrix is obtained by solving an optimization model based on the Laplacian operator normalization, which has shown its successful application in many other related problems.

Still, the proposed method has some shortcomings. The original lncRNA-disease association matrix is a sparse matrix. There were only 540 associations for 115 lncRNAs and 178 diseases; that is to say, there are only three associations per disease, which is not enough and unstable for the forecast result. Meanwhile, there are only two similarities in the current integration, and more biological knowledge can be applied in the future.

Materials and Methods

Human lncRNA-Disease Association Dataset

The lncRNADisease database⁶¹ is used as the known lncRNA-disease association dataset, which contains 687 confirmed lncRNA-disease associations between 369 lncRNAs and 247 diseases. After eliminating lncRNAs without an expression profile⁶² and diseases without disease ontology,⁶³ 540 known lncRNA-disease associations including 115 lncRNAs and 178 diseases were obtained. From the aforementioned known associations, we can get the lncRNA-disease adjacency matrix $A\in R^{nl\ast nd}$, where $nl$and $nd$ are the number of lncRNAs and diseases, respectively, and each row of matrix $A$ represents one lncRNA, while each column denotes one disease. 0 in $A\left(i,j\right)$ indicates that the relationship between lncRNA $l\left(i\right)$ and disease $d\left(j\right)$ is still unknown, and 1 in $A\left(i,j\right)$ indicates that lncRNA $l\left(i\right)$ has some relationship to disease $d\left(j\right)$. The definition of matrix $A$ is as follows:

$$\{\begin{array}{l}A\left(l\left(i\right),d\left(j\right)\right)=1lncRNAl\left(i\right)hasassociationwithdiseased\left(j\right)\\ A\left(l\left(i\right),d\left(j\right)\right)=0lncRNAl\left(i\right)hasnoassociationwithdiseased\left(j\right)\end{array},$$ (Equation 6)

Similarity Kernels for lncRNAs and Diseases

The proposed method is based on the currently accepted hypothesis that lncRNAs with similar functionality tend to be associated with diseases with semantic or phenotypic similarities, and vice versa. Therefore, it is very important to get the similarity kernels for both the lncRNAs and the diseases, which can provide lncRNA-disease associations with more accuracy. In this paper, first, we will compute the expression similarity and cosine similarity for the lncRNAs. Second, we will get the semantic similarity and cosine similarity for the diseases. Then, a kernel fusion method is applied to all similarity kernels. At last, based on the integrated lncRNA similarity kernel matrix and the disease similarity matrix, the Laplacian regularized least-squares method is used to get the final lncRNA-disease associations.

lncRNA Expression Similarity

The expression profiles of the lncRNAs are downloaded from ArrayExpression: E-MEXP-3783,⁶⁴ in which more than 1.5 million expression profiles are collected by high-throughput sequencing. The Spearman correlation is used to calculate the expression similarity between different lncRNAs.28, 65 The matrix $S{L}_1\in R^{nl\ast nl}$ denotes the similarity of lncRNA expression, where element $S{L}_1\left(i,j\right)$ represents the similarity degree between lncRNA $l\left(i\right)$ and lncRNA $l\left(j\right)$; values range from 0 to 1.

Disease Semantic Similarity

The disease semantic is very important information in characterizing a disease. The directed acyclic graph (DAG) has been studied to calculate the semantic similarity of diseases and shows great performance.66, 67 In this paper, the semantic similarity is also used as one dimension of disease similarity. The raw data of semantic similarity are downloaded from the U.S. National Library of Medicine. Based on medical subject heading (MeSH) description information, a DAG, $G_{d_i}=\left(d_i,T_{d_i},E_{d_i}\right)$, can be constructed, where $T_{d_i}$ denotes that the ancestor node of disease $d_i$ including itself, $E_{d_i}$ is the corresponding connection of $d_i$.⁶⁸ The disease semantic similarity between disease $d_i$ and its ancestor disease $p$ is calculated as follows:

$$D_{d_i}\left(p\right)=\{\begin{array}{l}max\left\{\omega \ast D_{d_i}\left(p^{\prime }\right)|p^{\prime }\in childrenoft\right\}ifp\ne d_i\\ 1ifp=d_i\end{array},$$ (Equation 7)

where the disease $p\in T_{d_i}$, $\omega$ is the weight parameter of the semantic similarity of diseases, and $\omega =\text{ 0}\text{.}5$ by default.

Also, we can define the semantic value for each disease as follows:

$$DV\left(d_i\right)=\sum _{p\in T_{d_i}}{D}_{d_i}\left(p\right).$$ (Equation 8)

With the similarity and semantic value defined, the semantic similarity matrix $S{D}_1\in R^{nd\ast nd}$ can be calculated. The similarity between arbitrary disease $d\left(i\right)$ and disease $d\left(j\right)$ is computed as follows:

$$S{D}_1\left(d_i,d_j\right)=\frac{\sum _{p\in T_{d_i}\cap T_{d_j}}\left(D_{d_i}\left(p\right)+D_{d_j}\left(p\right)\right)}{DV\left(d_i\right)+DV\left(d_j\right)}.$$ (Equation 9)

Cosine Similarity for lncRNAs and Diseases

The expression profile similarity for lncRNAs and the semantic similarity for diseases are two commonly used similarity kernels.30, 68, 69 To better improve the similarity kernels, one more dimensional similarity is used in the proposed method. Previous studies have showed that cosine similarity is successfully applied to collaborative filtering recommendation algorithms,70, 71 which inspired us to combine such similarity into the lncRNA-disease association prediction.

The principle of lncRNA cosine similarity is based on the assumption that if lncRNA $l\left(i\right)$ and lncRNA $l\left(j\right)$ are similar to each other, then, in the lncRNA-disease association matrix, pattern $A\left(i,:\right)$ and pattern $A\left(j,:\right)$ should be similar to each other. The same assumption should also be true for diseases, and the cosine similarity between lncRNA $l\left(i\right)$ and lncRNA $l\left(j\right)$ is calculated as follows:

$$S{L}_2\left(l_i,l_j\right)=\frac{A\left(i,:\right)\cdot A\left(j,:\right)}{\Vert A\left(i,:\right)\Vert \times \Vert A\left(j,:\right)\Vert },$$ (Equation 10)

where $A\left(i,:\right)$ represents the ith row of the lncRNA-disease association matrix $A$ and contains the relationship of all the diseases to lncRNAs $l\left(i\right)$.

Similarly, the cosine similarity between disease $d\left(i\right)$ and disease $d\left(j\right)$ can be calculated as follows:

$$S{D}_2\left(d_i,d_j\right)=\frac{A\left(:,i\right)\cdot A\left(:,j\right)}{\Vert A(:,i)\Vert \times \Vert A\left(:,j\right)\Vert },$$ (Equation 11)

where $S{D}_2\in R^{nd\ast nd}$ is the cosine similarity matrix for diseases, and $A\left(:,i\right)$ represents the ith column of the lncRNA-disease association matrix $A$.

SKF for lncRNAs and Diseases

Now we have two lncRNA similarity kernels (lncRNA expression similarity and lncRNA cosine similarity) and two disease similarity kernels (disease semantic similarity and disease cosine similarity). Next, we use SKF to integrate the two lncRNA similarity kernels $S{L}_n,n=\mathrm{1,2}$. In the first step, we normalize each lncRNA similarity kernels as follows:

$$P_n\left(l_i,l_j\right)=\frac{S{L}_n\left(l_i,l_j\right)}{\sum _{l_k\in L}S{L}_n\left(l_k,l_j\right)},$$ (Equation 12)

where $L={\left\{l_i\right\}}_{i=1}^{nl}$ represents the set of lncRNAs, and $P_n$ represents the normalized kernel and satisfies $\sum _{l_k\in L}{P}_n\left(l_i,l_j\right)=1$.

In the second step, we create a neighbor-constraint kernel for two lncRNA similarity kernels as follows:

$$S_n\left(l_i,l_j\right)=\{\begin{array}{l}\frac{S{L}_n\left(l_i,l_j\right)}{\sum _{l_k\in N_i}S{L}_n\left(l_i,l_k\right)}if{l}_j\in N_i\\ 0if{l}_j\notin N_i\end{array},$$ (Equation 13)

where $S_n\left(l_i,l_j\right)$ denotes a neighbor-constraint kernel and satisfies $\sum _{l_k\in L}{S}_n\left(l_i,l_j\right)=1$. Here, the neighbor $N_i$ of lncRNA $l_i$ is defined by the most $K$ similar lncRNAs to $l_i$.

In the third step, we mix up the normalized similarity kernel $P_n$ and the neighbor-constraint kernel $S_n$ literally, as follows:

$$P_n^{t+1}=\alpha \left(S_n\times \frac{\sum _{r\ne n}{P}_r^t}{2}\times S_n^T\right)+\left(1-\alpha \right)\frac{\sum _{r\ne n}{P}_r^0}{2},$$ (Equation 14)

where $P_n^{t+1}$ denotes the nth kernel obtained after $t$th iterations, ${\mathit{P}}_r^0$denotes the initial value of $P_r^t$, and $\alpha \in \left(\mathrm{0,1}\right)$ denotes the weight parameter. After $t$th iterations, the final kernel is obtained as follows:

$$SL=\frac{1}{2}\sum _{n=1}^2{P}_n^{t+1}.$$ (Equation 15)

In the fourth step, one more weighted matrix is added to the embedding of more neighbor information. The weighted matrix is as follows:

$$\omega \left(l_i,l_j\right)=\{\begin{array}{l}1if{l}_i\in N_j\cap l_j\in N_i\\ 0if{l}_i\notin N_j\cap l_j\notin N_j\\ 0.5otherwise\end{array}.$$ (Equation 16)

Finally, we get the integrated lncRNA similarity kernel matrix $S{L}^{\ast }\in R^{nl\ast nl}$ as follows:

$$S{L}^{\ast }=\omega \left(l_i,l_j\right)\times SL.$$ (Equation 17)

Similarly, we can get the integrated disease similarity kernel matrix $S{D}^{\ast }\in R^{nd\ast nd}$.

Laplacian Regularized Least Squares for lncRNA-Disease Association

With the lncRNA similarity matrix $S{L}^{\ast }$ and the disease similarity matrix $S{D}^{\ast }$ obtained by the SKF method, LapRLS is used to predict the potential lncRNA-disease association. From the view of lncRNAs, we can build the minimization model as follows:

$${\min }_{F_l}{\Vert A-F_l\Vert }_F^2+{\beta }_l{\Vert F_l^T{L}_l{F}_l\Vert }_F^2,$$ (Equation 18)

where ${\Vert \cdot \Vert }_F$ is the Frobenius norm; $A$ is the initial known lncRNA-disease association matrix; ${\beta }_l$ is the weighting parameter of LapRLS; $F_l\in R^{nl\ast nl}$ is the correlation matrix in the lncRNA space; and $L_l=D_l^{-1/2}\left(D_l-S{L}^{\ast }\right)D_l^{-1/2}$ is the normalized similarity matrix, where $D_l\in R^{nl\ast nl}$ is the diagonal matrix obtained by summing the elements of each row of the lncRNA similarity matrix $S{L}^{\ast }$. The first objective function in Equation 18 is to make sure that the obtained new correlation matrix is similar to the known one. The second objective function is to make sure that the obtained correlation matrix is smooth over the lncRNA space. We can solve Equation 18 by calculating the derivative of the objective function as follows:⁴⁴

$$F_l=S{L}^{\ast }{\left(S{L}^{\ast }+{\beta }_l{L}_{l}S{L}^{\ast }\right)}^{-1}A.$$ (Equation 19)

Similarly, we can obtain the optimal correlation matrix $F_d$ in the disease space as follows:

$$F_d=S{D}^{\ast }{\left(S{D}^{\ast }+{\beta }_d{L}_{d}S{D}^{\ast }\right)}^{-1}{A}^T.$$ (Equation 20)

Finally, we integrate the prediction matrix $F\in R^{nl\ast nd}$ from the lncRNA and disease space and obtain the final prediction association matrix as follows:

$$F=\frac{F_l+F_d^T}{2}.$$ (Equation 21)

Author Contributions

Conceptualization, G.X. and T.M.; Formal Analysis, T.M.; Investigation and Methodology, T.M. and Y.L.; Resources, T.M.; Project Administration, G.X. and Y.L.; Supervision, G.X. and Z.L.; Visualization, T.M.; Writing – Original Draft, T.M.; Writing – Review & Editing, G.X., T.M., Y.L., and Z.L.