Investigation of Freezing Temperatures of National Bureau of Standards Aluminum Standards

Abstract

The design of a high-precision furnace for investigating the freezing points of metals up to 700 °C or higher is described. The freezing points of aluminum samples of nominally 99.999 percent purity from two batches were compared in terms of the ratio R(Al)/R(TP), the ratio of the resistance of the platinum resistance thermometer at the aluminum freezing point to that at the triple point of water. The average standard deviation of measurements of the ratio R(Al)/R(TP) obtained on six specimens corresponds to ±0.40 mK, while the average standard deviations of R(Al) and R(TP) correspond to ±0.17 mK and ±0.14 mK, respectively. (The variations in the measurements of R(TP) are amplified by 3.4 in the ratio R(Al)/R(TP).) The spread of the mean R(Al)/R(TP) obtained for five out of the six specimens corresponds to 0.51 mK; the deviation of the mean R(Al)/R(TP) of the sixth specimen from the mean R(Al)/R(TP) of the five specimens corresponds to −1.31 mK. (The sixth specimen may have been contaminated during the assembly of the freezing-point cell or the original sample bar was inhomogeneous.) The results show that aluminum can provide a freezing point (near 660 °C) that is at least as reproducible as the freezing point of antimony (near 631 °C)

1. Introduction

The upper temperature limit of the platinum resistance thermometer (prt) range of the International Practical Temperature Scale of 1968 (IPTS–68) [27]¹ is 630.74 °C and one of the reference temperatures for calibrating a standard platinum-rhodium alloy and platinum thermocouple that extends the temperature scale upward on the IPTS–68 is 630.74 °C, as determined by a prt. When no allowance is made for loss of insulation in the standard prt with mica insulation, the spread among the prt’s at 630.74 °C could be 0.01 K or more [19]. In addition, the calibration of the prt is based on the measurements at the triple point of water (TP) and the freezing points of tin and zinc; any error in calibration of the prt would be greatly amplified by the extrapolation to 630.74 °C [23]. This uncertainty could be reduced by including a fixed point at the upper temperature limit of the prt range in the definition of the temperature scale for prt’s. Furthermore, the quality of reproducibility of the IPTS–68 in the region of the upper temperature limit of the prt range can be better evaluated by employing highly reproducible fixed points in conjunction with prt’s constructed of insulators better than mica, which begins to liberate a significant amount of water starting from about 500 °C. With prt’s insulated with mica the lower reproducibility of the IPTS–68 at the higher temperatures could be principally from the loss of electrical insulation and to a lesser degree from changes in the platinum [1].

The freezing point of aluminum, a secondary reference point which is assigned 660.37 °C on the IPTS–68, has been used for many years in calibrating thermocouples [24]. The freezing point of antimony, another secondary reference point which is assigned 630.74 °C on the IPTS–68, is also used for calibrating thermocouples. Thus, the freezing point of antimony is very close and that of aluminum is not far from the junction of the prt and thermocouples ranges of the IPTS–68. As a part of the effort at the National Bureau of Standards (NBS) to maintain and develop the IPTS–68, a series of experimental studies is in progress to determine the reproducibility of the IPTS–68 and to find better means to define temperature scales. This paper presents the investigation of the reproducibility of the freezing point of aluminum. The investigation of the reproducibility of prt’s in the region of the aluminum point will be a topic for future work; better prt’s must be constructed first.

Aluminum was selected first for the investigation because it was considered superior to antimony for a number of reasons. Aluminum is much more abundant than antimony and, because of the greater technologic importance of aluminum, it is available in greater amounts at high purity and at lower cost. At the freezing point the vapor pressure of aluminum is about 2 × 10⁻⁸ torr whereas that of antimony is about 0.2 torr [21], and aluminum is less toxic than antimony. The thermal diffusivity of liquid and solid aluminum at its freezing point was estimated to be many times greater than that of liquid and solid antimony at its freezing point [2, 6, 9, 22]. Liquid aluminum supercools 1 or 2 K, while liquid antimony can supercool more than 20 K [18]; therefore, the preparation required to realize the freezing point of aluminum should be simpler than that of antimony.

2. Samples

The freezing-point investigations were conducted on aluminum samples from two batches. The samples as originally received at the Office of Standard Reference Materials (OSRM) of the NBS from the supplier were in the form of cylindrical rods about 91 cm long. Sample bars of batch 1558 were 3.2 cm diam; sample bars of batch 2571 were 3.8 cm diam. The samples had been purified by zone refining techniques and homogenized by melting together the different zone refined units. Bars of batch 1558 were made by casting in graphite molds, while those of batch 2571 were made by casting in alumina molds. The specimens of batch 1558 that were received for the freezing-point studies appeared to have in them specks of graphite. The specimens of batch 2571 appeared to contain a number of voids that were absent in specimens of batch 1558. The information supplied with batch 2571 suggests that the voids were caused by hydrogen that was dissolved in the liquid aluminum which on solidification expelled the hydrogen. The solubility of hydrogen at 1 atm pressure in aluminum at the freezing point is about 0.5 to 0.8 cm³ per 100 g of the liquid and about 0.04 to 0.05 cm³ per 100 g of the solid [2]. The solubility of hydrogen in solid aluminum is apparently less at the lower temperatures, the reported solubilities at 400 °C being about 0.003 to 0.004 cm³ per 100 g [2]. (The above volumes of hydrogen are in terms of the gas at 1 atm pressure and at 20 °C.)

The chemical analyses given in the assay certificates that accompanied the samples from the supplier are summarized in table 1. The assay is based on spectrochemical analysis. Except for Fe, the analyses of the supplier for the two batches of aluminum are about the same. The mass spectrometric analysis of batch 2571 by P. J. Paulsen of the Analytical Mass Spectrometry Section of the Bureau, summarized also in table 1, shows that Fe and Zn are present in relatively high concentrations. The spectrochemical analysis apparently also did not detect the 0.2 ppm of Na that was detected by the mass spectrometric method. No element of mass greater than zinc was detected in the aluminum by the mass spectrometric analysis; the limit of detection by the method of some of the elements are listed in table 1.

Table 1.

Chemical analysis of the aluminum samples and the estimated depression of the freezing point by the impurities

	Batch 1558	Batch 2571		Estimated effect from each impurityd
Element	Supplier ppma	Supplier ppma	NBS ppmb	mK/ppm
Ca	0.2	0.2		−0.6
Fe	0.5	0.1	1.4	−0.3
Mg	<0.1	0.1	0.2	−0.6
Mn	0.1	0.2	C⩽0.3	−0.1
Si	0.3	0.3		−0.7
Cr	0.2		⩽0.04	+ 0.2
Cu	0.2	0.1	0.1	−0.3
Ni			⩽0.2
Ti			⩽0.05
V			⩽0.04
Na			0.2	−0.7
Ga			⩽0.06
Zn			5	−0.2
Estimate of total effect of impurities	−0.57 mK	−0.47 mK	−1.7mK

^aBased on spectrochemical analysis.

^bMass spectrometric analysis by P. J. Paulsen, Analytical Mass Spectrometry Section, NBS.

^cThe values preceded by the symbol ⩽ indicate the upper limit of the elements not detected. These values were not included in determining the total change in the freezing point from the impurities.

^dEstimated from phase diagram data [11].

If the worst case is considered, the analysis given in table 1 indicates that the aluminum of batch 2571 could be about 99.9993 percent pure. The analysis on batch 1558 indicates that the material to be 99.9998 percent pure; however, the analysis on batch 1558 is not as extensive as that on batch 2571. Other impurities not detected by the spectrochemical method may be present. These SRM samples are undergoing other analyses of chemical composition and measurements of physical properties. The presence of other impurities or the presence of certain impurities in greater amounts than indicated in table 1 may be revealed by these investigations.

M. B. Kasen of the Cryogenics Division of the NBS at Boulder, Colorado, determined the residual resistivity ratios (ratio of the resistance at 0 °C to that at 4.2 K) of samples taken from the ends, middle, and outer surfaces of the aluminum bars of batch 2571 [12]. Of the total of 45 specimens from 17 bars that were examined, only two specimens were not within the residual resistivity ratio (RRR) 5000 ± 250. These two specimens were found to have scattered porosity. The RRR measurements indicate that the aluminum sample bars of batch 2571 are fairly uniform. The ultra-purity aluminum samples (SRM–RM–1R and SRM–RM–1C) have the RRR values of about 16200 or 16600 [13], which suggests that the aluminum samples used in the present freezing-point measurements could be of somewhat lower purity.

Most phase diagrams in the vicinity of the pure components are based on extrapolation of observations at relatively high impurity concentrations and, in many cases, the undetected impurity may have been the predominant source of the observed effect. Nevertheless, an attempt was made employing phase diagrams to estimate the possible effect of the impurities that were reported in the analyses of the two batches of aluminum. In estimating the effect, the effect of each impurity was assumed to be independent of the presence of the other impurities. The effect in mK/ppm of an impurity was estimated from the phase diagram data [11]. Table 1 summarizes the estimate of the freezing-point depression based on the spectrochemical analyses furnished by the supplier and on the mass spectrometric analysis. The values preceded by the symbol ⩽ indicate in principle the sensitivity of the mass spectrometric method for the given element; the effect of the impurities at these values were not considered in the depression of the freezing point. The results of the estimate suggests that the freezing points of the two batches of aluminum samples could be 2 mK lower than the freezing point of pure aluminum. (The elements Na and Zn not detected by spectrochemical analysis in the sample from batch 1558 were assumed to be present to the same degree as found in the sample from batch 2571.)

3. Preparation and Assembly of the Aluminum-Point Cells

Figures 1, 2, and 3 show schematic drawings of three aluminum freezing-point cells that were assembled for the investigations described in this paper. Special precautions were observed in the handling of the aluminum samples to avoid contamination or altering their purity. High-purity graphite components were employed in containing the samples. The samples, each about 358 g, were received from the Office of the Standard Reference Materials of the NBS in the form of cylindrical rods enclosed in polyethylene bags. The samples of 3.2 cm diam were about 16.7 cm long; the samples of 3.8 cm diam were about 11.4 cm long. These samples had been cut from bars that were about 91 cm long with a carbide tipped tool and etched in a solution at a temperature of 190 to 200 °C consisting (by volume) of reagent grade phosphoric acid (15 parts), sulfuric acid (5 parts), and nitric acid (1 part). The samples were not identified with respect to the bars from which they were cut; therefore, the samples from different bars were considered identical for the present work.

Figure 1.

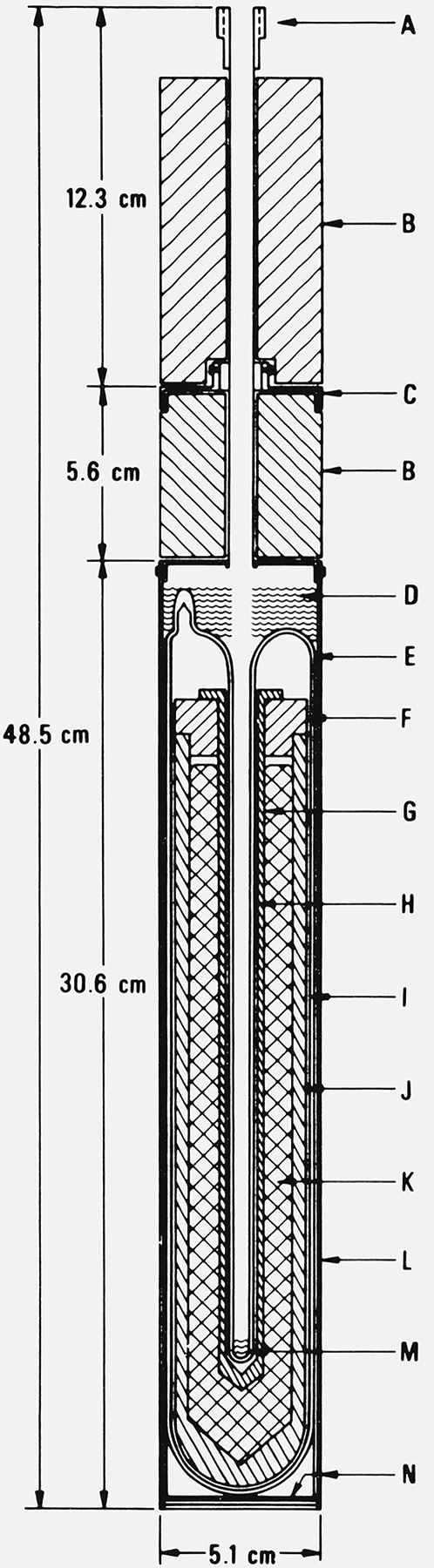
Sealed aluminum-point cell (Type 1 cell).

A. Thermometer guide tube (Inconel, 7.94 mm o.d. × 0.13 mm wall) with an adapter at the top for attaching a handle for lifting or lowering the cell into the furnace well.

B. Magnesia (MgO) block insulation.

C. Heat shunts (Inconel flange).

D. Fiberfrax insulation.

E. Fused quartz outer envelope (48 mm o.d. × 1.5 mm wall).

F. Graphite lid.

G. Graphite thermometer well.

H. Fused quartz thermometer well (precision bore (7.94 mm i.d.) and continuous with the outer envelope).

I. Fused quartz fiber, woven tape for cushioning.

J. Graphite crucible.

K. Aluminum sample.

L. Inconel case.

M. Fused quartz fiber pad for cushioning the thermometer.

N. Fiberfrax paper liner.

Figure 2.

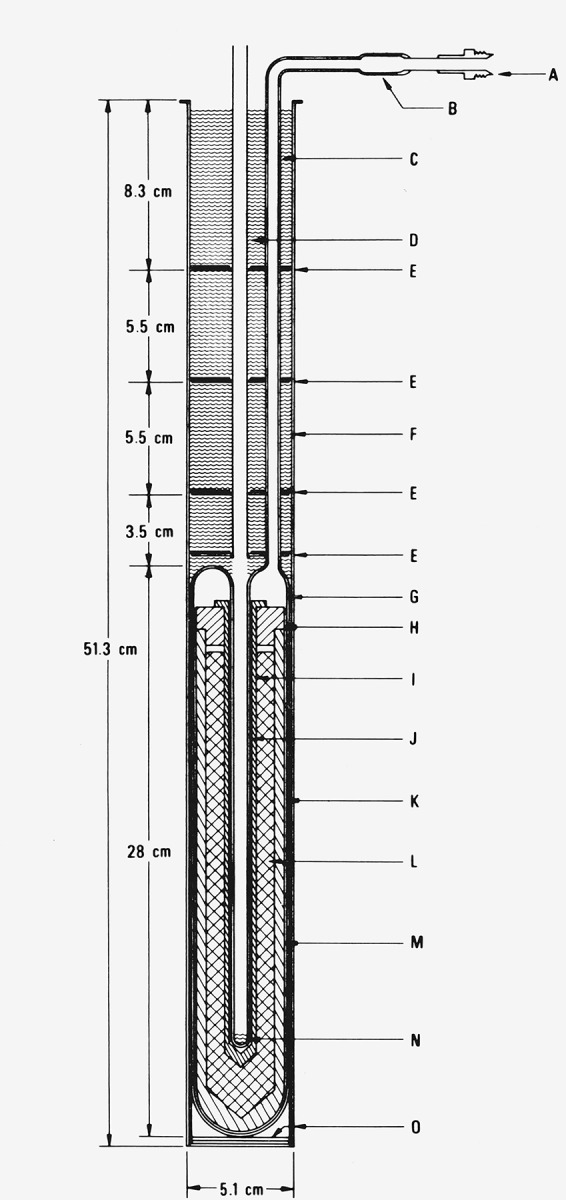
Fused quartz aluminum-point cell with Inconel casing (Type 2 cell).

A. Connection to high vacuum, purified argon gas source, and manometer (see fig. 5).

B. Fused quartz-to-Kover graded seal.

C. Fused quartz connecting tube (7.4 mm o.d. × 1 mm wall), outer surface matte finished to minimize radiation piping.

D. Thermometer guide tube (Inconel, 7.94 mm o.d. × 0.13 mm wall).

E. Heat shunts (Inconel disks).

F. Insulation, cut from Fiberfrax blanket.

G. Fused quartz outer envelope (48 o.d. × 1.5 mm wall).

H. Graphite lid.

I. Graphite thermometer well.

J. Fused quartz thermometer well (precision bore (7.94 mm i.d.) and continuous with the outer envelope).

K. Fused quartz fiber, woven tape for cushioning.

L. Aluminum sample.

M. Graphite crucible.

N. Fused quartz fiber pad for cushioning the thermometer.

O. Fiberfrax paper liner.

Figure 3.

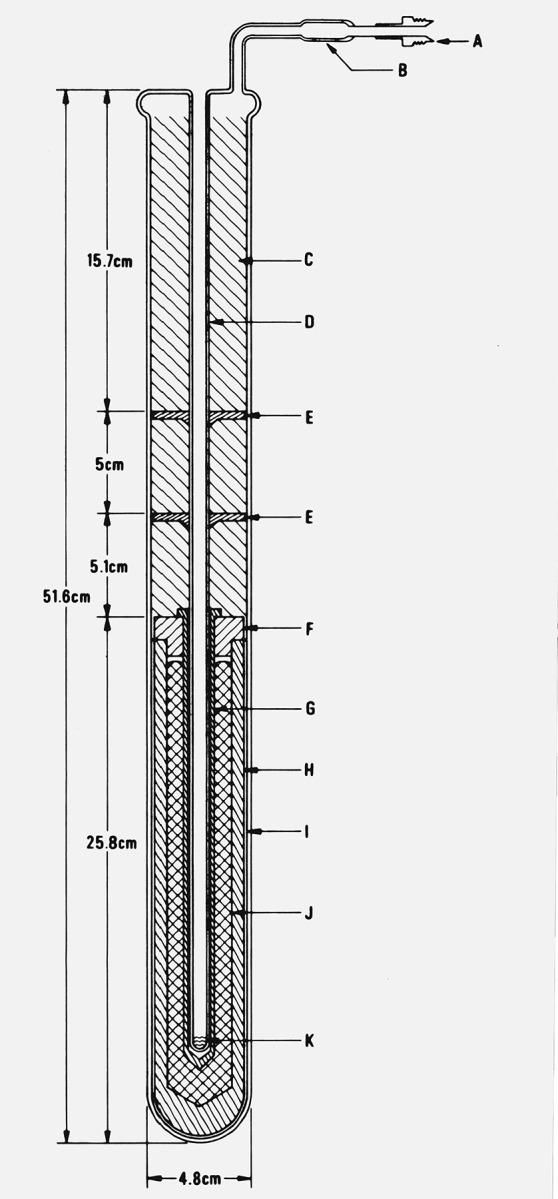
Aluminum-point cell with fused quartz casing (Type 3 cell).

A. Connection to high vacuum, purified argon gas source, and manometer (see fig. 5).

B. Fused quartz-to-Kovar graded seal.

C. Insulation, fused quartz wool.

D. Fused quartz thermometer well (precision bore 7.94 mm i.d. and continuous with the outer fused quartz envelope), outer surface matte finished to minimize radiation piping.

E. Heat shunts, graphite disks.

F. Graphite lid.

G. Graphite thermometer well.

H. Graphite crucible.

I. Fused quartz fiber, woven tape for cushioning.

J. Aluminum sample.

K. Fused quartz fiber pad for cushioning the thermometer.

The freezing-point cells were assembled as follows. The 3.2 cm diam samples were of convenient size such that they could be inserted directly in the crucible and the lid attached snugly at the top of the crucible. The graphite thermometer well, which was designed to slide slowly, under its own weight, through the central hole in the lid, was inserted by melting the sample by induction heating under vacuum. Figure 4 shows schemetically the arrangement for melting and inserting the thermometer well. The system was continuously pumped at high vacuum while gradually increasing stepwise the induction heating power. The pumping system was trapped with liquid nitrogen. The heating power was maintained constant with the crucible temperature at approximately 600 °C (a slight red glow in the graphite crucible) for about 1 h at a pressure of about 0.01 torr or lower (1 torr = 1 mm Hg at 0 °C and at the standard gravity = 133.322 N/m² [20].) The heating power was then gradually raised stepwise until the aluminum sample began to melt and the thermometer well began to “sink” into the crucible. The buoyant force of the liquid aluminum was offset by the weight of the tungsten rod, sealed in fused quartz tubing, placed in the graphite thermometer well (see D, fig. 4). After the sample started to melt, the thermometer well sank into the desired position in the crucible within about 30 min. The heating power was then turned off, the sample allowed to cool, and the crucible and its contents were removed from the assembly after filling the apparatus with dried pure argon gas. The argon gas employed was 99.999 percent (5N) pure and was dried by passing through a trap cooled to the temperature of boiling oxygen.

Figure 4.

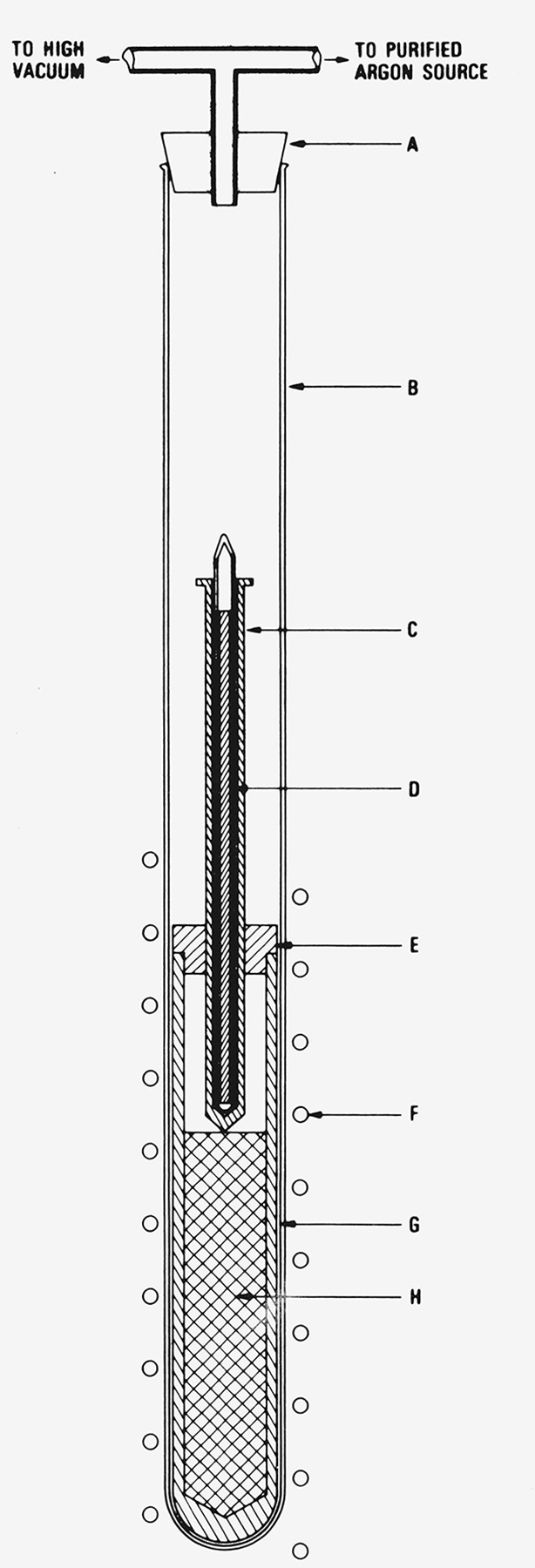
Apparatus for inserting graphite thermometer well in the graphite crucible containing the molten aluminum sample.

A. Silicone elastomer cap.

B. Fused quartz tube.

C. Graphite thermometer well.

D. Tungsten rod sealed in fused quartz tube.

E. Graphite lid.

F. Induction heater coils.

G. Graphite crucible.

H. Aluminum sample.

The 3.8 cm diam aluminum samples were too large in diameter to be inserted directly into the crucible. The samples were melted into the crucibles from a high-purity graphite funnel following a vacuum pumping and induction heating procedure similar to that outlined above for inserting the thermometer well into the crucible containing the aluminum sample. (The apparatus and procedure for filling the crucible with the aluminum samples through a graphite funnel were the same as those employed previously with tin and zinc samples [8, 23].) After the crucible was filled with the aluminum sample, it was first cooled and the thermometer well was inserted by the procedure outlined earlier for the 3.2 cm diam samples.

For protection of the samples and ease of handling, the graphite crucibles containing the samples were enclosed in three types of fused quartz cells shown in figures 1, 2, and 3. The assembly procedure was as follows. (Henceforth, for convenience these cells will be referred to as types 1, 2, and 3, respectively.) The fused quartz envelope, with the central thermometer well of precision bore fused quartz, was made first to fit the graphite crucible as closely as possible. The outer tube was sawed apart near the top. The graphite crucible was then inserted using woven fused quartz fiber tape as a cushion between the crucible and the outer fused quartz envelope. Before the outer tube was resealed, either the fused quartz thermometer well or the outer tube was shortened so that when assembled the bottom of the fused quartz thermometer well would be about 3 mm above the bottom of the graphite thermometer well. (When the aluminum is melted the buoyant force of liquid aluminum causes the bottom of the graphite thermometer well to rest against the bottom of the fused quartz well so that during operation of the cell the thermal resistance of of the 3 mm gap will no longer exist.) The above allowance for the graphite thermometer well to rise 3 mm was made to compensate for any unknown differences in the thermal expansion of the graphite used to fabricate the thermometer well and the crucible.

The completely sealed type 1 cell shown in figure 1 had the same configuration as that of type 2 cell of figure 2 when the outer tube was sealed at the sawed junction. After pumping at high vacuum (10⁻⁵ torr near the diffusion pump; see figure 5 for the general arrangement of pumping and gas handling system) for three days with the cell at 670 to 675 °C, the cell was filled with purified argon gas and maintained at slightly above atmospheric pressure until the cell cooled to the ambient temperature. The cell was then immersed in an insulated container of water at a known temperature. After the cell reached an equilibrium temperature, the argon pressure in the cell was adjusted so that its pressure would be 1 atm when heated to the melting point of aluminum; the cell was then sealed at the location shown in figure 1. These type 1 cells were employed during the initial preliminary freezing-point experiments to gain experience and to determine the best operating conditions. Because of the uncertainty of the actual pressure at the freezing point, these cells were subsequently converted to the type 2 cell configuration shown in figure 2. (Although the effect of the pressure on the freezing point is expected to be relatively small, the temperature uncertainty due to the inability to determine the actual pressure was thought unnecessary.)

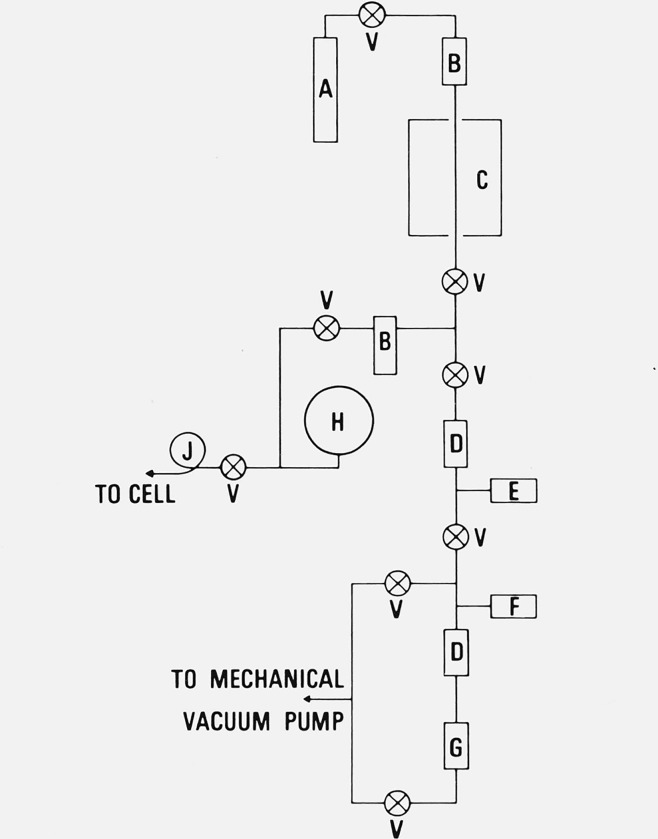
Figure 5.

Schematic arrangement of the high vacuum, argon gas purification and handling, and pressure measurement system.

A. High-purity argon gas supply cylinder.

B. Cryogenic traps, liquid oxygen.

C. Inconel tube (packed with copper metal and with copper oxide) in furnace.

D. Cryogenic traps, liquid nitrogen.

E. Vacuum gauge, cold cathode type.

F. Vacuum gauge, thermocouple type.

G. Oil diffusion pump.

H. Dial type manometer, lowest subdivision of scale: 1 mm Hg (torr).

J. Flexible loop of tubing (Inconel, 3.18 mm o.d. × 0.20 mm wall) for connecting to the aluminum-point cell.

V. Valve, bellows type.

The completely sealed type 1 cell was inserted in an Inconel² tube (5.08 cm o.d. × 0.25 mm wall) using Fiberfrax paper strips for cushioning and for alining with respect to the thermometer guide tube that is shown in figure 1. Magnesia block insulation was machined to fit around the thermometer guide tube and to fit inside the furnace well.

The type 2 cell of figure 2, similar to that of type 1 cell, is mounted inside an Inconel (5.08 cm o.d. × 0.25 mm wall) tube. The thermometer guide tube (D) is also Inconel (7.94 mm o.d. × 0.13 mm wall). Pairs of Inconel disks spaced along the assembly served as heat shunts to help temper the prt and improve its immersion characteristics [23]. One of the disks fits closely with the inside wall of the outer tube but fits rather loosely with the inner thermometer guide tube; the other disk fits closely with the thermometer guide tube but fits loosely with the outer tube. The thermometer guide tube and the fused quartz thermometer well must be assembled axially alined in the 5.08 cm o.d. Inconel case. The above design of the shunts makes allowances for any small relative misalinement of the Inconel thermometer guide tube and the fused quartz thermometer well with respect to the outer Inconel case and at the same time provides for the desired heat path between the outer and inner Inconel tubes. The disks are slotted to accommodate the cell tube (C). During assembly the disks were positioned to be in mechanical contact with the cell tube so that the tube would also be tempered. The cell tube was given a matte finish by “sand blasting” to reduce the light (heat) piping from the aluminum-point cell [17]. The space between the Inconel disks and the tubes was filled with layers of insulation (disks cut from 1.3 cm thick Fiberfrax blanket).

The type 3 cell is shown in figure 3. As described in type 1 and type 2 cells, the fused quartz envelope was also made first and sawed apart at the top. Adjustments were made to the outer fused quartz tube or to the thermometer well so that when assembled the bottom of the thermometer well would be about 3 mm above the bottom of the graphite thermometer well. Both the outer fused quartz tube and the thermometer well were sand blasted to obtain a matte finish to reduce light (heat) piping [17] from the aluminum-point cell. Fused quartz fiber tape was employed to cushion the graphite crucible inside the fused quartz envelope. Graphite disks (E) served as heat shunts between the outer tube and the inner thermometer well. Fused quartz wool was used for insulation in the space above the graphite crucible. The final seal at the top was made after “packing” the cell as shown in figure 3.

Table 2 lists the aluminum samples, the cell design, and the laboratory designation of the aluminum-point cells that were assembled.

Table 2.

Identification of aluminum samples, cell design and designation of aluminum-point cells

Cell designation	Cell type	Sample batch No.
A-1a	a1 and 2	2571
A-2a	a1 and 2	1558
A-3	3	1558
A-4	3	2571
A-5	2	2571
A-6	2	1558

^aDuring preliminary experiments to determine the best procedure to conduct the investigations on the reproducibility of the aluminum-point cells, the samples were assembled in type 1 cells. They were later converted to type 2 cells for the measurements shown in table 3 and in figure 11.

4. Vacuum, Argon Gas Handling, and Pressure Measurement System

Figure 5 shows schematically the vacuum, argon gas handling, and pressure measurement system. The vacuum pumping system consisted of the usual mechanical and oil diffusion pumps preceded by two liquid nitrogen traps (D) in series. All valves (V) preceding these two liquid nitrogen traps were packless, bellows sealed types; all connecting lines were principally stainless steel. The only component that was not stainless steel was the flexible loop of Inconel tubing (J) (3.18 mm o.d. × 0.20 mm wall) that connected the valve to the aluminum-point cell.

The argon gas that was employed to pressurize the aluminum-point cells (all three types of cells) was first purified. The 5N purity argon gas from the cylinder (A) was first passed through a trap (B) cooled to the oxygen boiling point to remove water and other condensable substances. This gas was then passed through a tube (C) containing, successively, finely divided copper metal and cupric oxide held at about 700 °C. The purpose of the copper metal was to remove any oxygen from the argon; the cupric oxide should oxidize any hydrocarbons or other organic impurities and hydrogen. Another trap (B) held at the oxygen boiling point condensed any carbon dioxide and water that may have been formed.

The argon gas pressure was determined by employing a dial type manometer (H) with a differential pressure range of 0 to 760 torr. Each division of the dial scale corresponded to 1 torr. The manometer was actuated by a sensitive bellows. The uncertainty of the pressure measurement with the dial manometer, based on comparison with a mercury ⋃-tube manometer, was estimated to be ± 0.5 torr.

5. Furnace

The furnace that was employed in the freezing-point investigation is shown schematically in figure 6. The furnace is similar in design to those used in the investigation of National Bureau of Standards – Standard Reference Material (NBS–SRM) tin standards [8]. However, there are a number of basic differences in the design. The furnace consists of an axially located Inconel alloy well (C) for the freezing-point cells. The bottom end of the Inconel well was sealed by “heliarc” welding an Inconel disk (S). An Inconel flange (B) was heliarc welded to the top end of the Inconel well. This Inconel well assembly and the furnace shell (Q) form a vacuum tight enclosure which protects the stack of four cylindrical coaxial blocks of copper (top (H), end (J), center (O), and bottom (U)) from oxidation. The space surrounding the copper blocks was packed with Fiberfrax insulation. The space was evacuated and purged with pure argon gas several times and filled with the gas at a pressure slightly above atmospheric. The four copper blocks were suspended by the Inconel well; however, the weight is partially supported by the Fiberfrax insulation at the bottom. Eight Inconel tubes (F) (3.97 mm o.d. × 0.20 mm wall), sealed at the bottom end and equally spaced on 6.668 cm diam, extend from the top of the Inconel flange (B) to the bottom of the bottom copper block (U). Small silicone elastomer “○” rings make a vacuum tight seal between these tubes and the Inconel flange. These tubes serve to contain thermocouples for controlling the furnace temperature and to contain resistance thermometers or thermocouples for determining the vertical temperature distribution of the furnace core under a given furnace control condition.

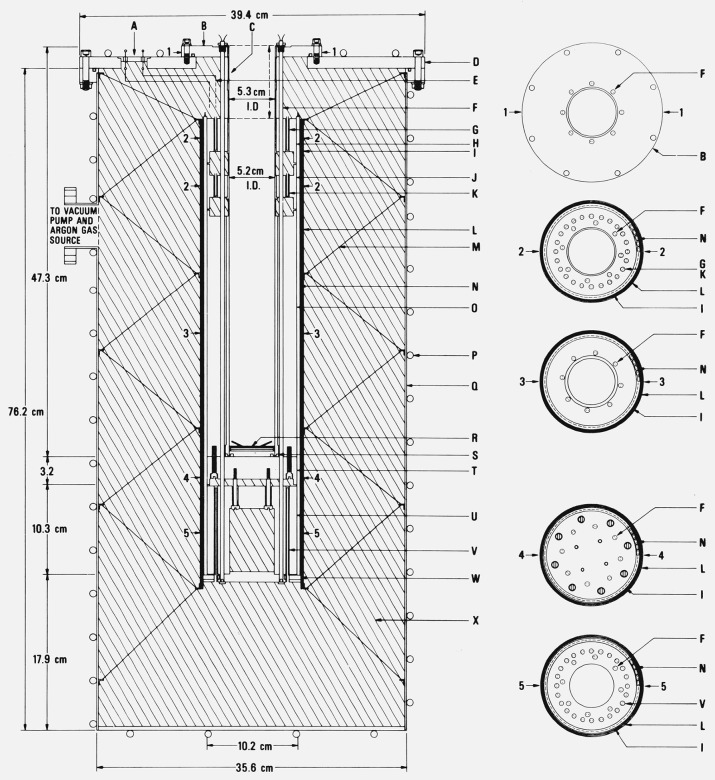
Figure 6.

Schematic of furnace core and body.

A. Hermetic insulated posts for electric leads.

B. Inconel flange welded to tube C.

C. Inconel tube furnace core.

D. Brass cover plate.

E. Electric leads (8) to control heaters.

F. Inconel tubes (8, 3.97 mm o.d. × 0.20 mm wall) with thermocouples for temperature control or for monitoring the furnace temperature.

G. Heater for the top core block.

H. Top core block.

I. Copper cylinder for holding the main heater M tightly against the copper blocks H, J, O, and U.

J. End core block.

K. Heater for the end core block.

L. Axially centered copper cylinder for receiving the furnace core.

M. Nickel-chromium alloy wire for suspending and centering copper cylinder L.

N. Main heater.

O. Center core block.

P. Coil for circulating cooling water.

Q. Stainless steel furnace shell.

R. Inconel “spider” for centering the quartz glass cell (type 3 cell) shown in figure 3.

S. Inconel disk welded to tube C.

T. End plate for the center core block.

U. Bottom core block.

V. Heater for the bottom core block.

W. Fused quartz ring for supporting the main heater N.

X. Fiberfrax insulation.

The center copper block (O) was constructed from two cylinders which were assembled by precooling the inner cylinder in liquid nitrogen and quickly inserting it inside the preheated outer cylinder. Before the cylinders were “shrunk together” eight grooves that closely fit the eight 3.97 mm o.d. Inconel tubes (F) were milled on the outside of the inner cylinder. The assembled center copper block was shrunk onto the lower end of the central Inconel tube by a process similar to that employed in assembling the block from two copper cylinders.

The top (H) and end (J) copper blocks contain circularly arranged holes (G and K) for separate control heaters. They contain also holes to accommodate the eight 3.97 mm o.d. Inconel tubes (F). The control heaters were assembled by inserting each arm of “⋃” shaped loops of 1.30 mm diameter nickel-chromium alloy wire in each of two adjacent round twin-bore alumina tubes (G and K). The lower portions of the “⋃” shaped loops were insulated with several short segments of single-bore alumina tubes. These elements were assembled successively and inserted in the holes provided in the copper blocks (G and K). The elements were heliarc welded in series to form the control heaters. These two copper blocks were also shrunk onto the central Inconel well. The wall thicknesses of the two segments of the Inconel well that separate the center, end, and top copper blocks have been reduced (to 0.8 mm) so that the temperature controls of the blocks would not interact excessively. The wall thickness of the Inconel well between the top copper block and the Inconel flange was also reduced (to 0.4 mm) to minimize the heat leak at the top of the furnace.

The bottom copper block is suspended by means of Inconel screws from the copper end plate (T) attached to the center copper block. The bottom block also contains circularly arranged holes (V) for control heaters and holes to accommodate the eight 3.97 mm o.d. Inconel tubes (F). The control heater for the bottom block was assembled from “⋃” shaped loops of nickel-chromium alloy wire in a manner similar to those used in assembling the control heaters for the end and top copper blocks.

The main heater (N) extends the whole length of the four copper blocks. It was constructed in a manner similar to the control heaters for the end, top, and bottom copper blocks from “⋃” shaped loops of 1.30 mm diam nickel-chromium alloy wire and oval-shaped twin-bore alumina tubes (4.8 × 6.4 mm o.d.). These elements were assembled tightly spaced around the four copper blocks and the “⋃” shaped loops were heliarc welded in series to form a cylindrical heater. A tightly fitting copper cylinder (I) was slipped over the “cylinder” of alumina tubes to hold them in place against the copper blocks. The main heater assembly rests on a fused quartz ring (W) at the bottom.

The “furnace core” comprises the central Inconel well assembly, the copper blocks, the control heaters, and the tightly fitting copper cylinder that holds the main heater in place. This core was assembled on a larger brass cover plate (D) which contains electrically insulated, hermetically sealed connectors for gold lead wires (E) to the main heater and to the heaters on the end, top, and bottom copper blocks. Before the furnace core which was assembled on the brass cover plate was lowered into the furnace shell (Q), the interior of the shell was packed with Fiberfrax around an axially centered copper cylinder (L). The inside diameter of this cylinder is about 0.8 mm larger than the outside diameter of the copper cylinder that held the main heaters around the copper blocks so that the furnace core would slide smoothly in place and at the same time leave relatively little space for undesirable heat convection currents.

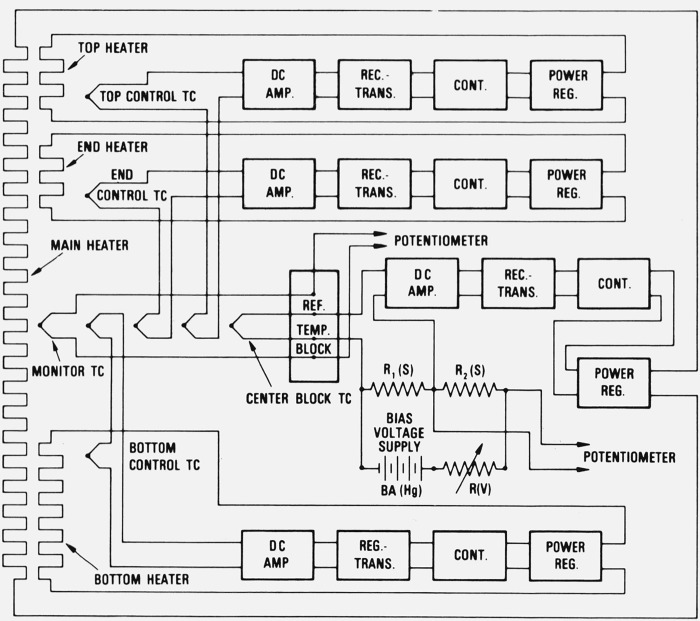
The temperature control of the parts of the furnace was achieved by utilizing Chromel-P/Alumel thermocouples and control components similar to those previously described [23], The furnace control system is shown schematically in figure 7. The control thermocouple located at the middle of the center copper block was referenced to a large aluminum block held at a constant temperature and was connected to a 10-Ω standard resistor R₁(S). The furnace control temperature was selected by adjusting the current from a pair of mercury cell batteries BA(Hg) through this standard resistor. The voltage drop across the 10-Ω standard resistor R₁(S) was accurately monitored by observing the voltage drop across a second standard resistor R₂(S), in series with the first, by means of a potentiometer. The control of the furnace temperature was monitored by observing the voltage of a separate thermocouple referenced to the previously mentioned aluminum block that was held at a constant temperature.

Figure 7.

Schematic block diagram of the furnace control system.

TC: Chromel-P/Alumel thermocouple

DC AMP: Chopper type d-c amplifier.

REC-TRANS: Strip chart recorder plus transmitting variable resistor.

CONT: Three-mode controller.

POWER REG: Solid-solid gate drive, full-wave silicon-controlled rectifier, plus transformer package.

R₁(S): Standard resistor (10 Ω) for bias voltage source.

R₂(S): Standard resistor (10 Ω) for monitoring bias voltage source.

R(V): Variable resistor for adjusting bias voltage.

BA(Hg): Mercury cells.

The control thermocouples for the end, top, and bottom copper blocks were of the differential type; their reference junctions were located at the middle of the center block and their control junctions were located about 1 cm within the respective blocks from the center block.

The voltage output of each control thermocouple was amplified by a chopper type d-c amplifier and this output was connected to a strip-chart recorder. A “transmitting variable resistor,” coupled mechanically to the recorder indicator, operated a “three-mode” controller which, in turn, operated a “solid-state gate drive” for a full-wave silicon-controlled rectifier. The rectifiers controlled the a-c power to each of the heaters. The a-c power supplies were transformers with voltage outputs and power capacities appropriate to the heaters. The total power required to hold the furnace at 660 °C was about 300 W.

The thermocouple that was employed to monitor the temperature control showed the center copper block to be stable to ±0.01 K for several hours. No miniaturized resistance thermometer suitable for use at 660 °C was available to accurately probe the vertical profile of the furnace under operating conditions. However, on the bases of the experiences with furnaces of similar design that are used at the zinc and tin points [8, 23], of the improvements in the present design to reduce heat leaks and temperature gradients, and of the results of differential thermocouples that were used to probe temperature differences in the furnace, the uniformity of the center copper block temperature is expected to be within ±0.05 K at 660 °C. (The uniformity of the center block of the furnace used with tin-point cells is shown in reference [8] to be about ±0.01 K.)

6. Thermometry

The work of Berry [1] showed that commercially available prt’s containing mica (muscovite or phlogopite) insulation begin to exhibit electrical leakage when used at temperatures above about 500 °C because of the accumulation of moisture that is liberated from the mica, the moisture being liberated faster the higher the temperature. Mica contains as a part of its chemical structure hydroxyl (OH) radicals which at high temperatures decompose irreversibly to water. The total amount of water that can theoretically be liberated on the basis of the chemical formula is about five weight-percent. As a consequence of the liberation of water mica undergoes mechanical deterioration, such as swelling and disintegration into small flakes (exfoliation). The electrical leakage of the prt becomes excessive when relatively little water is liberated from the mica; hence, the prt loses its insulation considerably before the mica begins to exhibit mechanical deterioration. The prt which has lost its insulation can be “rejuvenated” by removing the moist air in the thermometer envelope by pumping at about 200 °C (where the rate of liberation of water from the mica is negligible) and replacing with dry air. The “lifetime” of the prt, before it is necessary to replace again the moist air with dry air, is shorter the higher the temperature the prt is used. Continuous pumping of the prt envelope at the higher temperatures, where the “vapor pressure” of water of the mica is high, can cause the mica to exfoliate excessively. The results of the investigation by Berry [1] on the useful lifetimes of the gas fillings of prt’s suggest that when commercial prt’s with phlogopite mica insulation are used at the aluminum point they should be pumped and refilled with dry air whenever the accumulated exposure to the temperature reaches about one week, or even less, if high precision measurements are to be performed.

To avoid the periodic pumping and filling with dry air a “birdcage” type prt (laboratory designation: HTSS–15) with synthetic sapphire insulation [4] was obtained on loan from Sharrill D. Wood of the Temperature Section of the Bureau. The prt resistor had been assembled by threading platinum wires through holes in sapphire disks and welding them in series. The thermometer leads were also separated by sapphire disks and between the disks were sapphire rod spacers 1.3 cm long. At the upper end of the prt where the temperature would be close to the room temperature, high-purity alumina (Al₂O₃) was used instead of sapphire for lead insulation. The sheath was fused quartz. The thermometer, i.e., the platinum wire, did not contact the sheath at any point. This prt was used earlier by Mrs. Wood at temperatures up to 1100 °C and had been at temperatures in the vicinity of 1065 to 1100 °C for over 300 h [28]. For the application to the present work the external leads and thermometer “head” were replaced with another thermometer head containing BNC connectors so that the prt could be used with an a-c bridge which operated at 400 Hz [3, 23]. The two leads from one end of the prt sensor were the center terminals of the two BNC receptacles; the two leads from the other end of the prt sensor were the outer or the shield terminals of the receptacles. The prt resistance, which was nominally 0.26983 Ω, was considered somewhat low for best measurements, but no other prt that could endure the repeated use at the aluminum point was immediately available. The outer surface of the fused quartz sheath of the prt had bands of matte finish, starting from about 5.5 cm from the thermometer tip, to reduce radiation piping [17]. The matte finish had been obtained by blowing at high velocity fine particles of alumina abrasive against the surface.

The work of Evans and Wood [5] suggested that the birdcage type prt requires relatively greater depth of immersion before its indication would correspond to the equilibrium temperature of the fixed-point cell. Therefore, special precautions were taken in the design of the aluminum-point cell to temper the section of the prt well above the graphite crucible that contains the aluminum sample (see figs. 1, 2, and 3). The thermometer guide tubes were made as close fitting as practical to minimize the thermal resistance to the prt. Heat shunts were provided between these tubes and the furnace wall or the outer Inconel case.

An aluminum sleeve is generally employed in the thermometer well of the triple-point-of-water (TP) cell to improve the thermal contact of the prt with the cell [23]. With the birdcage type prt, because of the effect of inductive interaction with the sleeve, the a-c bridge method consistently yielded results that were higher with the aluminum sleeve than without the sleeve. The observed resistance at the TP was equivalent to 4.9 mK higher with one sleeve of 5.1 cm length and 3.6 mK higher with another sleeve of 4.4 cm length and slightly looser fit with the prt. The a-c bridge measurements at the TP of “standard” commercial prt’s (the platinum coil helically wound on mica crosses and with an electrical resistance of 0 °C of 25.5 Ω) with and without the aluminum sleeve have been found to be different by only 0.1 mK or less. In a similar comparison at the TP, the apparent resistance of a prt with a helically wound coil and with a resistance at 0 °C of 0.23 Ω measured with sleeve correspond to about 0.2 mK higher than without the sleeve. In the results reported in this work no aluminum sleeve was employed in the measurements with the TP cell. All a-c bridge measurements (at both the TP and the aluminum point) were performed at 3.54 and 5.00 mA currents and the resistance values were calculated for zero thermometer current. All references to values of R(Al) or R(TP) are at zero thermometer current. A strip-chart recorder was employed with the a-c bridge so that the freezing temperatures could be automatically recorded with the prt. The gains of the amplifiers of the bridge and of the recorder were adjusted so that, with a thermometer current of 3.54 mA, 1.2 mm on the recorder chart corresponded to 0.1 μΩ (or about 0.1 mK for the prt employed in this work).

The a-c bridge that was employed in this work measures the ratio of the prt resistance to that of the reference resistor. The reference was a 10-Ω resistor wound on a card and hermetically sealed in a rectangular metal case with a silicone compound to aid in the dissipation of heat that is generated in the resistor during use. The resistor case was placed in good thermal contact with an aluminum block and placed in an aluminum box thermostated at 28 °C. The variation in temperature of the aluminum block was less than 2 mK. The temperature coefficient of resistance of the resistor at 28 °C is smaller than 1 ppm per °C. The resistance of the 10-Ω reference is within about 2 × 10⁻⁵ of the nominal value. Since relative values of resistances and the resistance ratios R(Al)/R(TP) of the aluminum-point cells are being compared, the real value of the reference resistor was not considered in the results presented in this work. The reference resistor was taken to be exactly 10 Ω.

In the aluminum point cell the prt was necessarily surrounded by solid and liquid aluminum. The freezing-point experiments, to be described later, required a mantle of solid aluminum to be immediately adjacent to the graphite thermometer well. However, in every case the prt and the aluminum were separated by 1 mm of fused quartz and 2.3 mm of graphite (see figs. 1, 2, and 3). The inside diameters of the aluminum sleeves mentioned earlier that were employed with the TP cell differed by 0.3 mm; this relatively small difference in separation of the prt and the sleeve plus the difference in the length of the sleeve of 6.4 mm caused a change in the thermometer resistance corresponding to about 1.3 mK. To test the effect of any inductive interaction in the aluminum-point cell a TP cell of large inner diameter was employed to simulate the conditions. A graphite well of the same dimensions as used in the aluminum-point cell was closely fitted inside a closed-end aluminum sleeve. A closed-end fused quartz tube corresponding to the thermometer well of the fused quartz envelope was placed inside the graphite tube. The resistances observed with the above assembly inside the TP cell correspond to a temperature 2.9 mK higher than that observed without the assembly. The effect of the inductive interaction in the aluminum-point cell would probably be of this order. (The electrical conductivity of graphite at the aluminum point is, depending upon the type of graphite, two to three times that at the TP; on the other hand, the electrical conductivity of solid aluminum is approximately five times smaller at the aluminum point than at the TP [10]. Also, the electrical conductivity of graphite is about 100 to 1000 times smaller than that of aluminum at these temperatures [10]). However, in the experiments described in this paper the reproducibility of the aluminum point was to be investigated and one of the requirements was that the effect of the inductive interaction on the prt be the same among the aluminum-point cells. Since the geometry of all three types of cells was the same in the neighborhood of the aluminum sample, the effect of the inductive interaction was expected to be the same in all the cells as long as the “freezes” in the cells were prepared in the same way. (This assumption is supported somewhat by the reproducibility of the freezing points that were obtained with the aluminum-point cells, although a portion of the small deviations in the freezing points could have come from small differences in the effect of inductive interaction.)

The d-c resistance measurements employing the Mueller bridge (G–3) that was available with the prt (R(0 °C) = 0.26 Ω) were considered unwieldy and to lack the precision that is possible with the a-c bridge method. If a prt with the resistance of 2.6 or 5 Ω were available, d-c resistance measurements would have been practical for the investigations presented in this paper.

7. Experimental procedures

7.1. Freezing procedures

The aluminum liquid was found to supercool about 0.4 to 1.5 K before the nucleation of the solid started. Usually the liquid supercooled about 0.4 to 0.6 K. Several freezing procedures were tried to obtain information on the “thermal behavior” of the aluminum freezing-point cell.

To avoid quenching in defects in the prt wire by cooling rapidly from the aluminum point, it was found necessary to withdraw the prt from the aluminum-point cell in steps over a period of 30 min. Then, following the procedure described by McLaren [19], the prt was annealed at 480 °C in a tube furnace for 30 min and removed to cool at room temperature. This treatment was found to yield resistance readings at the TP that were repeatable to ±0.1 mK or better.

With the type 1 cell the freeze was initiated by withdrawing the cell from the furnace and quickly re-inserting it in the furnace when the prt indicated the onset of recalescence [8, 16]. Before the cell was withdrawn from the furnace, the furnace was set to control 1 K below the freezing point. The cell was withdrawn as soon as its temperature had decreased close to the freezing point; meanwhile, the furnace temperature continued to decrease to the lower “control point”. However, in most cases the furnace temperature was not at the control point when the cell was about to be re-inserted. The insertion of the cooled cell (outer parts) helped to lower the furnace temperature; the recalescence raised the temperature of the aluminum sample to its melting point. The input power to the furnace was sufficient to quickly compensate for any excessive cooling of the furnace by the cooled cell. (The furnace was designed to be well insulated so that relatively low input power could maintain it at any desired temperature; as a consequence, the cooling rate of the furnace was relatively slow. On the other hand, for heating a wide range of input power was readily available.) Since the presence of a mantle of solid aluminum around the thermometer well was considered essential to precision measurements, a cold fused quartz rod or a cold prt was also inserted in the thermometer well in these experiments before any temperature measurements were made. (No effort was made to determine the course of the freezing temperatures without first inducing a freeze around the thermometer well. To introduce a preheated prt into the aluminum-point cell without freezing or without changing the amount of solid aluminum around the thermometer well would require slow insertion of the prt into the cell in such a manner that the prt is preheated to the aluminum point in the thermometer guide tube.)

When a mantle of solid aluminum was frozen around the thermometer well, the freezing temperatures obtained with the freeze first induced by withdrawing the cell from the furnace were essentially the same as those obtained by a procedure, which was adopted in the experiments described in this paper, in which the freeze was initiated in the furnace without any handling of the cell. (The procedure will be described in the following paragraphs.) There was a certain degree of danger in withdrawing the hot cell from the furnace and there was always, during this operation, some “tapping” of the cell against the furnace well. (There was, in addition to possible personal injury, the danger of breaking the prt.) The type 2 and type 3 cells, which were the cell designs selected for the present investigation, could not be conveniently withdrawn from the furnace because of the connection to the gas handling system.

Since the aluminum did not supercool excessively, such as with tin [8, 16] or antimony [18], the freezing procedure that was adopted was to allow the freeze to start in the furnace in a manner similar to that employed with zinc [15, 23] which supercools only about 0.06 K. The procedure for initiating the freeze, without disturbing the cell in the furnace, was to start with the melt 4 to 6 K above the freezing point and then to reduce the furnace temperature to about 1 or 2 K, depending upon the degree of supercool, below the freezing temperature. The furnace was usually at the new “control temperature” within 15 to 20 min after the furnace controls were set to the lower temperature. Usually within the following 10 to 15 min the aluminum liquid was at the bottom of its “supercool” and in the next 5 min the temperature of the sample rose to within about 0.1 K of the freezing temperature. Although the initial temperature increase was rapid immediately after the start of recalescence, the subsequent temperature rise was slower; even after 1 h the temperature was lower by about 0.5 mK than the value that was obtained after a freeze was induced around the thermometer well by inserting a cold fused quartz rod or a cold prt.

As mentioned earlier, it was necessary to withdraw the prt from the cell in steps over a period of 30 min to avoid quenching in lattice defects and, in addition, to anneal the prt at 480 °C for 30 min. Only one suitable prt was available for these experiments. Therefore, to conserve experimental time, the time required for the sample, after the start of cooling, to go through the supercool and then recover to about 0.1 K of the freezing point was estimated from the results of preliminary experiments. At about the time when the temperature of the cell had recovered to about 0.1 K of the freezing point two fused quartz rods were successively inserted for a period of about 5 min each to induce a freeze around the thermometer well. Also, at this time, if the furnace was set to control at 2 K below the freezing point, it was raised to control at 1 K below. (Meanwhile the prt, which had previously been withdrawn from the cell, was annealed and its resistance at the TP was determined.) The rod was then removed and the cold prt inserted. About 15 to 20 min were required after insertion of the prt to be certain that the prt had come to an equilibrium temperature. The freezing temperatures were usually observed over the next 40 to 50 min, after which the sample was completely remelted for the next freeze. When the sample was allowed to freeze only for a period of time as outlined above, about 1 hour was required to melt what was frozen. However, two hours of heating were allowed before the next freeze was started. During the melting period, the prt was slowly withdrawn from the cell and annealed and its resistance at the TP was measured. Two freezes were obtained during a normal day. Usually after the second freeze, the sample was allowed to melt and remain melted overnight. In the morning, during the period of time at which the sample was cooled to initiate the freeze and later while the two fused quartz rods were inserted in the cell to freeze aluminum around the thermometer well, the prt was annealed (or annealed again depending upon whether the resistance of the prt at the TP was determined last on the previous day) and its resistance at the TP was determined.

On the basis of the results of a series of preliminary freezing experiments and the time required to prepare a cell for the experiments, it was decided to investigate the six aluminum samples successively one cell per week. Either a type 2 or a type 3 cell was investigated during the week. The schedule for the week was as follows: (Some repetition of previous descriptions are included for clarity.) On Monday, except for the first cell, the cell from the previous week was disconnected from the gas handling system and removed from the furnace. The new cell was then inserted in the furnace and connected to the gas handling system. After pumping the cell to a high vacuum, the electric power to the furnace heaters was switched on and the furnace was set to control at a temperature 4 or 6 K above the freezing point to melt the sample over night. The furnace reached the control point about 5 h after the heaters were turned on. Meanwhile the pumping of the cell at high vacuum was continued. The TP cell was also prepared on Monday. On Tuesday morning the aluminum-point cell was slowly filled (in order that impurities are reacted in the copper metal-copper oxide furnace and collected in the cold traps) to 1 atm pressure of purified argon gas and in the meantime the prt was placed in the annealing furnace at 480 °C for 30 min prior to the measurement of its resistance at the TP. After the cell was filled with argon gas to 1 atm pressure, the furnace temperature was set to cool and control at a temperature 2 K below the freezing point. Later at an appropriate time, the time at which the aluminum sample was estimated to have recovered to within about 0.1 K of the freezing point, the first fused quartz rod was inserted in the thermometer well to induce freezing around the well and the furnace temperature control was reset to control at a temperature 1 K below the freezing point. After about 5 min the first rod was removed and a second rod was inserted. Meanwhile the resistance of the prt at the TP was determined. After the second rod had been in the cell for 5 min, it was removed and the prt inserted in the cell. The measurements of the freezing point and the remelting of the aluminum sample were described earlier. By Friday, the desired number of “freezes” usually would have been obtained and on Friday afternoon the furnace and the cell were allowed to cool over the weekend.

7.2. Measurement Procedure

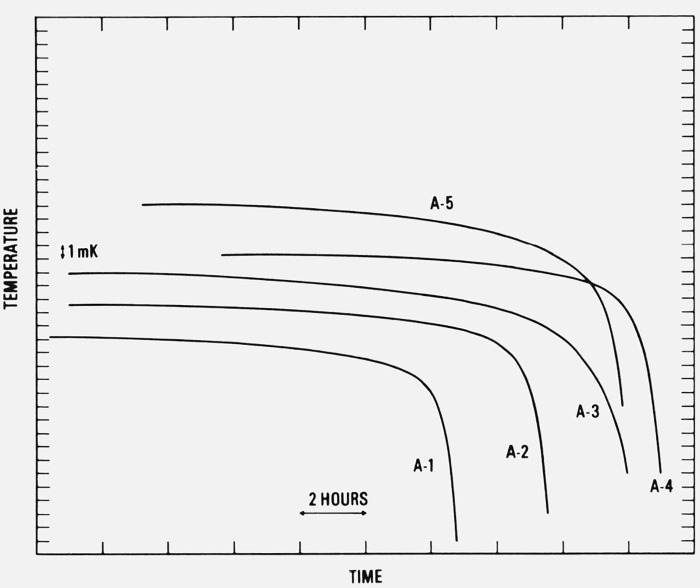
The intercomparison of the freezing temperatures of the aluminum samples was based on the analysis of the prt resistance ratios R(Al)/R(TP), the ratio of the resistance observed with the freezing aluminum sample to the resistance observed with a TP cell, reduced to zero thermometer current. The values of R(Al) were adjusted to 1 atm pressure on the liquid aluminum surface and to a common depth of immersion of the prt in the aluminum-point cell (16.7 cm from the liquid aluminum surface to the middle of the prt sensor). (The depth of immersion of the prt in the aluminum-point cell was estimated from the mass of the sample and the geometry of the graphite cell, assuming that 20 percent of the sample was solid.) The values of R(TP) were at a fixed depth of immersion in a TP cell (27.5 cm from the water surface to the middle of the prt sensor). Measurements of the resistance of the prt were made at the TP before and after each measurement in the aluminum-point cell and, except for two cases, the average R(TP) was used to determine the R(Al)/R(TP) ratios. The values of R(Al) were observed at two currents (3.54 and 5.00 mA) over a period of 40 to 50 min after the prt readings indicated that it was at an equilibrium temperature. Figure 8 shows results of experiments in which the complete freezing of the samples were recorded. (No freezing curve is shown for cell A–6; the graphite crucible containing the sample broke soon after the freezing data given in table 3 were taken.) As shown by the figure, the temperature of the aluminum-point cell changed by less than 0.1 mK during the usual 40- to 50-min period when the observations were taken. A change of 1 mK in the freezing point occurred only after over one-half (over 6 or 8 h of recorded data) of the sample was frozen.

Figure 8.

Typical freezing curves of the aluminum samples recorded starting approximately fifteen minutes after the insertion of the platinum resistance thermometer in the cell.

The curves are displaced both vertically and horizontally; they are meant to show only the relative temperatures within the individual freezing curves.

Table 3.

Observed thermometer resistance at the triple point of water and at the freezing points of the aluminum samples and the values of the ratios of the resistances

Cell A-6 (Series 1)
Date	R(AI)or R (TP)	R (TP), mean	R (AI)/R (TP)
	Ohms	Ohms
9–25-73	a,b0.269832809
	b0.269832825
9–26-73	0.269832718
	0.910413896	0.269832708	3.37399385
	0.269832699
	0.910414003	0.269832725	3.37399403
	0.269832751
	0.910413852	0.269832780	3.37399278
	0.269832810
9–27-73	0.269832621
	0.910413816	0.269832508	3.37399605
	0.269832394
	0.910413882	0.269832630	3.37399477
9–28-73	0.269832867
	0.910414020	0.269832852	3.37399250
	0.269832836
	0.9104.13930	0.269832896	3.37399162
10–2-73	0.269832955
Mean R(TP)	0.269832739	Mean 3.37399366
Std. Dev.C	±163×10-9	Std. Dev. . ±149×10-8
	±0.15 mK	:±:0.46 mK
Mean R (AI)	0.910413914
Std. Dev.	±:76×10-9	Spread 443 × 10−8
	±:0.09 mK	1.38 mK
Mean R (AI)	3.37399352	Deviation −24 × 10−8
Mean R (TP)		from the mean of five cellsd −0.07 mK
Cell A-5 (Series 2)
Date	R (AI)or R (TP)	R (TP), mean	R(AI)/R(TP)
	Ohms	Ohms
10–2-73	0.269832955
	0.910413819	0.269832995	3.37398997
	0.269833035
	0.910414069	0.269833021	3.37399057
10–3-73	0.269833007
	0.910413922	0.269832878	3.37399182
	0.269832749
	0.910413979	0.269832758	3.37399353
	0.269832768
	0.910413887	0.269832749	3.37399330
10–4-73	0.269832730
	0.910413864	0.269832674	3.37399415
	0.269832618
	0.910414088	0.269832497	3.37399720
10–5-73	0.269832376
	0.910414091	0.269832624	3.37399562
	0.269832871
Mean R (TP)	0.269832790	Mean 3.37399327
Std. Dev.	±208×10-9	Std. Dev. :±:245×10-8
	±0.19mK	±0.76 mK
Mean R(AI)	0.910413965
Std. Dev.	±109×10-9	Spread 723 × 10-8
	±0.12mK	2.25 mK
Mean R (AI)	3.37399308	Deviation from	-63×10-8
Mean R (TP)		the mean of five cellsd	−0.20 mK
Cell A-3 (Series 3)
Date	R(Al)or R (TP) Ohms	R (TP), mean Ohms	R(AI)/R(TP)
10–10-73	0.269832746
	0.910413453	0.269832848	3.37399045
	0.269832951
	0.910413741	0.269832924	3.37399057
	0.269832897
	0.910413590	0.269833058	3.37398833
	0.269833218
	0.910413735	0.269832991	3.37398971
10–11-73	0.269832764
	0.910413534	0.269832912	3.37398995
	0.269833060
	0.910413475	0.269832954	3.37398921
	0.269832848
Mean R(TP)	0.269832926	Mean 3.37398970
Std. Dev.	±168×l0-9	Std. Dev. ±81 × 10−
	±0.16 mK	±0.25 mK
Mean R(AI)	0.910413588
Std. Dev.	±126×10-9	Spread 224 × 10-8
	:±:0.15 mK	0.70 mK
Mean R(AI)	3.37398998	Deviation from	−420 × 10−8
Mean R(TP)		the mean of five cellsd	−1.31 mk
Cell A-4 (Series 4)
Date	R (AI)or R (TP)	R (TP), mean	R(AI)/R(TP)
	Ohms	Ohms
10–15-73	b0.269832848
10–16-73	0.269832782
	0.910413955	0.269832820	3.37399266
	0.269832859
	0.9]0413957	0.269832856	3.37399222
	0.269832854
10–17-73	0.269832767
	0.9104]3715	0.269832756	3.37399257
	0.269832746
	0.910414340	0.269832782	3.37399457
	0.269832819
	0.910414699	0.269832858	3.37399495
	0.269832898
	0.910414060	0.269832829	3.37399294
10–18-73	0.269832760
	0.910413952	0.269832676	3.37399445
	0.269832592
	0.910414115	0.269832684	3.37399496
10–19-73	0.269832775
	0.910414074	0.269832662	3.37399508
	0.269832548
	0.910414112	0.269832776	3.37399380
10–23-73	0.269833004
MeanR(TP)	0.269832784	Mean 3.37399382
Std. Dev.	±124X10-9	Std. Dev. ±112×10-8
	±0.12 mK	±0.35 Mk
MeanR(AI)	0.910414098
Std. Dev.	±265X10-9	Spread 286 × 10−8
	±0.31 mK	0.89 mK
Mean R (AI)	3.37399364	Deviation from	−8×10−8
Mean R(TP)		the mean of five cellsd	− 0.02 mK
Cell A-2 (Series 5)
Date	R (AI) or R (TP) Ohms	R (TP), mean Ohms	R (AI)/ R (TP)
10–24-73	0.269832938
	0.910414732	0.269832953	3.37399388
	0.269832968
	0.910414712	0.269833026	3.37399289
	0.269833085
	0.910414876	0.269832969	3.37399421
	0.269832853
10–25-73	0.269832758
	0.910414659	0.269832791	3.37399563
10–26-73	0.269832824
	0.910414540	0.269833010	3.37399246
	0.269833196
	0.910414860	0.269833048	3.37399317
	0.269832900
10–27-73	0.269832854
	0.910414727	0.269832955	3.37399384
	0.269833056
	0.910414960	0.269832953	3.37399472
	0.269832850
Mean R (TP)	0.269832935	Mean 3.37399385
Std. Dev.	±131×10-9	±103X 10-8
	±0.12 mK	±0.32 mK
Mean R (AI)	0.910414758
Std. Dev.	±134× 10-9	Spread 317×10-8
	±0.16 mK	0.99 mK
Mean R (Al)	3.37399420	Deviation from	−5×10−8
Mean R (TP)		the mean of five cellsd	− 0.02.mK.
Cell A-I (Series 6)
Date	R(AI)or R (TP)	R (TP), mean	R (AI)/ R (TP)
	Ohms	Ohms
10–30-73	0.269832882
	0.910415384	0.269833042	3.37399518
	0.269833203
	0.910415347	0.269833124	3.37399402
10–31-73	0.269833044
	0.910415434	0.269833064	3.37399509
	0.269833085
	0.910415206	0.269833022	3.37399477
	0.269832958
	0.910415621	0.269833081	3.37399557
	0.269833204
	e 0.910417677	f0.269833722	3.37399518
11–1-73	b,f0.269833722
	e 0.910417552	f0.269833722	3.37399472
	0.269833132
	0.910415657	0.269833188	3.37399437
11–2-73	0.269833245
	0.910415425	0.269833161	3.37399385
	0.269833077
	0.910415514	0.269832988	3.37399634
	0.269832898
Mean R (TP)	0.269833073	Mean 3.37399491
Std. Dev.	±128×10-9	Std. Dev. ±74× 10-8
	±0.12 mK	±0.23 mK
Mean R (AI)	0.910415448
Std. Dev.	± 147×10-9	Spread 249×10-8
	±0.17 mK	0.78 mK
Cell A-I (Series 6)
Date	R (AI) or R (TP) Ohms	R (TP), mean Ohms
Mean R (AI)	3.37399503	Deviation from	+ 101X10-8
Mean R (TP)		the mean of five cellsd	+ 0.31 mK
Average Std. Dev. Of R (TP)	±154×10-9Ω ~±0.14 mK
Spread of the mean R(TP) among the six series of observations	334×10–9Ω ~0.31 mK
Average Std. Dev. of R (AI)	± 143 ×10-9Ω ~±0.17 mK
Spread of the mean R(AI) of the six cells	1860×10-9Ω ~2.15 mK
Average Std. Dev. of R(AI)/R(TP)	±127×10-8 ~±0.40 mK
Spread of the mean R(Al)/R(TP) of the six cells	521× 10-8 ~1.62 mK
Mean of the mean R(AI)/R(TP) of the six cells	3.37399320
Spread of the mean R(AI)/R(TP) of five cells (excluding cell A-3)	164×10-8 ~0.51 mK
Mean of the mean R(AI)/R(TP) of five cells (excluding cell A-3)	3.37399390

^aThe last two figures were obtained by interpolation in the strip-chart record. On the bases of the sensitivity of the measurement system and the “noise” in the strip-chart record, the accuracy of the interpolation is estimated to be about ±3 (approximately ±0.3 mm on the chart) in the next to the last figure given. The extra figure was carried to retain an over-all consistency in the calculations.

^bThis observation was not included in computing the mean R(TP) of this series of measurements.

^cStandard deviation is defined here as [Σd²/n − 1)]^½, where d is the deviation of the individual values from the mean and n is the number of observations.

^dCell A–3 was excluded from the mean.

^eThis observation was not included in computing the mean R(Al) for this cell, but was included in computing R(Al)/R(TP).

^fThis rather high value of R(TP) was considered to be more consistent with the two adjacent exceptionally high values of R(Al) and, therefore, was employed in computing the R(Al)/R(TP) for these two values of R(Al).

8. Results

8.1. Effect of Pressure on the Freezing Temperature

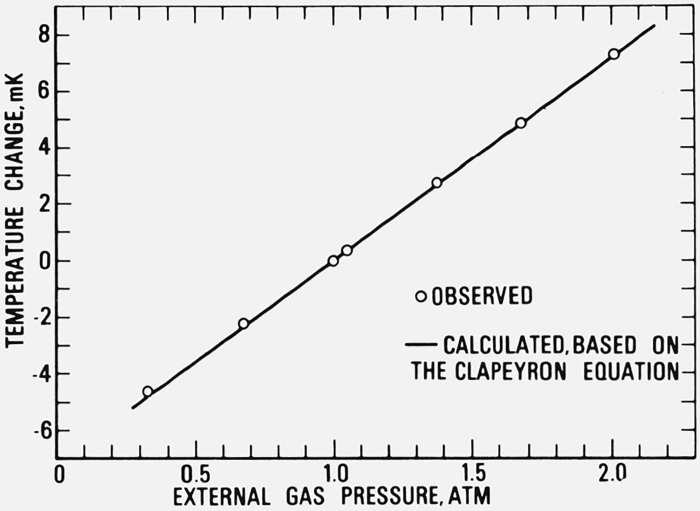
The effect of argon gas pressure on the freezing point of aluminum was investigated over the range 0.3 to 2 atm pressure. Since the differential pressure dial manometer had the range of only 0 to 760 torr, the pressure measurements above 1 atm were performed with the manometer open to the ambient atmospheric pressure (i.e., the pressure measurements were relative to the atmospheric pressure). An auxiliary dial manometer was employed to determine the atmospheric pressure. The results of the measurements are shown in figure 9. The increase in the freezing temperature of aluminum was calculated from the results to be 7.1 mK/atm. The estimated uncertainty of the value is ±0.3 mK/atm. McAllan and Ammar[14] list 6.1 mK/atm as the increase in the freezing temperature with increase in pressure.

Figure 9.

Effect of the pressure of argon gas on the freezing temperature of aluminum.

The solid linear curve, based on the Clapeyron equation, is normalized to the freezing temperature at 1 atm pressure.

The pressure effect on the freezing temperature was also calculated employing the Clapeyron relation

$$dT/dp=\frac{T_f\left(V_l-V_s\right)}{L},$$ (1)

where V_l and V_s are the specific volumes of the liquid and solid aluminum, respectively; T_f is the freezing temperature; L is the latent heat of fusion; and dT/dp is the pressure coefficient of T_f. Using 933 K (660 °C) for T_f, 10.7 kJ/mol for L reported by Stull and Prophet [26], and the densities 2.368 and 2.55 g/cm³ for the liquid and solid aluminum, respectively, given by Brandt [2], the calculated pressure coefficient of the freezing temperature becomes 7.18 mK/atm, which is close to the experimentally observed value.

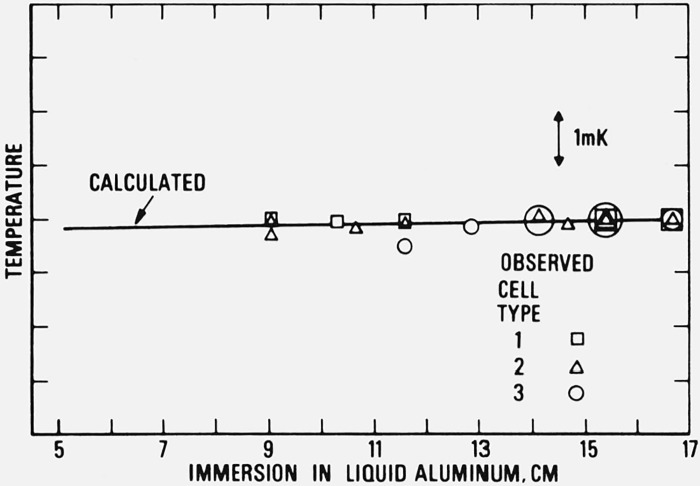
Using 7.1 mK/atm as the pressure coefficient of the freezing temperature and 2.368 g/cm³ for the density of liquid aluminum, the expected variation in the observed freezing point with the depth of immersion of the prt becomes 0.016 mK per cm of liquid aluminum. To check the adequacy of immersion of the prt, the freezing temperatures at various depths of immersion were measured for the three types of cells. The results are shown in figure 10. The solid line is the expected variation in temperature with immersion. The results show that the immersion of the prt is more than adequate for the three types of cells when the prt is fully immersed in the cell. On the basis of the results obtained with cells of type 1 and type 2, the immersion characteristics of the prt in type 3 cell can be improved by introducing better heat shunts between central thermometer guide tube and the outer case.

Figure 10.

Immersion characteristics of the platinum resistance thermometer in the aluminum point cells and the effects of the hydrostatic pressure of liquid aluminum on the vertical temperature distribution of the cell.

(The depth of immersion was estimated as the distance from the top surface of the aluminum in the cell to the mid-point of the thermometer coil. The calculated curve (straight line) is based on the Clapeyron equation. It is normalized to the reading at approximately 16.7 cm immersion when the thermometer is touching the bottom of the thermometer well of the aluminum-point cell.)

8.2. Comparison of the Freezing Temperatures

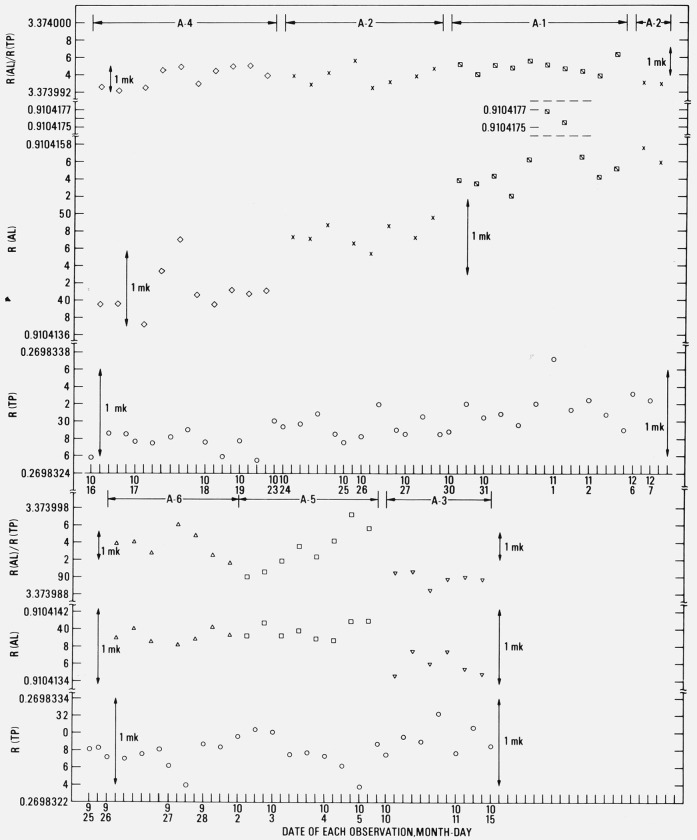
The observed values of R(Al) and R(TP) and the calculated values of the ratio R(Al)/R(TP) are summarized in table 3 and are also plotted chronologically in figure 11. In the figure, the tick marks along the abscissa indicate the occurrences of the observation of either R(Al) or R(TP). The ratios R(Al)/R(TP) are plotted where the observation of R(Al) occurred.

Figure 11.

Sequence of observed resistances (at “zero current”) of the platinum resistance thermometer (HTSS–15) at the triple point of water and in the various aluminum-point cells.

The ratios of the resistances R(Al)/R(TP) are plotted at the location (abscissa) corresponding to the observed value of R(Al).

Except in the measurements of series 4 (cell A–4), the mean R(TP) of each series of measurements tended to increase; however, there is a value (0.269833218 Ω) among those in the third series that is close to the highest value (0.269833245 Ω) of the sixth or the last series of measurements. Nevertheless, the spread of the mean R(TP) corresponds to only 0.31 mK, which shows that the overall change in the mean R(TP) was still relatively small in spite of the prt being subjected to the temperature of the aluminum point before the observations of R(TP). The average standard deviation of the six series of measurements of R(TP) corresponds to ±0.14 mK. The spread of all values (58 observations) of R(TP) is 0.81 mK. The two relatively low values of R(TP) found in the measurements of series 1 (cell A–6) and series 2 (cell A–5), without any accompanying decrease in the value of R(Al), were attributed to the ice mantle of the triple-point of water cell possibly not being completely “free” from the thermometer well. In the later measurements starting with those of series 3, the “inner melt” of the TP cell was made slightly thicker and was checked immediately before use to make certain that the ice mantle was completely free. This procedure seems to have eliminated low values of R(TP).

Except for cell A–3, the mean R(Al) also tended to increase similar to the mean R(TP) with each series of measurements. If the results on cell A-3 are included, the spread of the mean R(Al) and the average standard deviation correspond to 2.15 mK and ±0.17 mK, respectively. On the other hand, if cell A–3 is excluded, the spread of the mean R(Al) and the average standard deviation correspond to 1.77 mK and ±0.17 mK, respectively, which are not very different from the values obtained including cell A–3 in the group. Actually, the difference between the lowest mean R(Al) (i.e., cell A–3) and the next lowest mean R(Al) (cell A–6) is smaller than the differences between the highest (cell A–1) and the second highest (cell A–2), and between the second highest and third highest (cell A–4) values of mean R(Al)’s.

The values of mean R(Al)/R(TP) seem to be more random than the values of mean R(TP) or the values of mean R(Al). If the average of the mean R(Al)/R(TP)’s of cells A–6, A–5, A–4, and A–2, which have a spread that corresponds to only 0.18 mK, is compared with the values obtained with cells A–3 and A–1, the deviations correspond to −1.23 mK and +0.39 mK, respectively. However, the standard deviations of the observed values of R(Al)/R(TP) are large enough to include the results on cell A–1 with the four cells. On the other hand, the results on cell A–3 suggest that the aluminum sample in the cell may be of different purity from those of the other five cells.

The standard deviations of the values of R(TP) and R(Al) obtained for each series of measurements are considerably less than the standard deviations of the values of R(Al)/R(TP) (except in the case of cell A–4 where the standard deviations of R(Al) and of the ratio R(Al)/R(TP) are close). This deterioration in precision arises from the amplification (by about 3.4) of the variations in R(TP) when the ratio R(Al)/R(TP) is computed. In the case of cell A–4, the standard deviation (±0.31 mK) of R(Al) was sufficiently large that the deviation in R(TP) (standard deviation: ±0.12 mK) did not contribute significantly to the standard deviation of R(Al)/R(TP). When the ratio R(Al)/R(TP) was computed from the mean R(Al) and mean R(TP) and compared with the mean R(Al)/R(TP) for each cell, the maximum deviation (0.11 mK) occurred in the measurements with cell A–2. In the case of cell A–5, where the standard deviation (±0.76 mK) and the spread (2.25 mK) of the R(Al)/R(TP) values are the largest, the difference between [mean R(Al)]/[mean R(TP)] and mean R(Al)/R(TP) corresponds to only 0.06 mK. This close agreement in the values of [mean R(Al)]/[mean R(TP)] and mean R(Al)/R(TP) indicate there are no gross errors in the computations employing the observed data.

Following the above sets of measurements the freezing points of two freezes were obtained with cell A–2 (see fig. 11 at 12–6 and 12–7). The values of R(TP) and R(Al) seem to follow the general upward trend; the values of the ratio R(Al)/R(TP) are in good agreement with the earlier values. These values were not included among the earlier data used in the analysis and discussion that are presented in this paper.

9. Discussion and Conclusions

The results of the freezing-point investigations on two batches of aluminum samples of nominally 99.999 percent purity show that within the precision of the experimental method presented in this paper the two samples can not be distinguished by their freezing points. However, one specimen of batch No. 1558, which cell A–3 contains, seems to have a slightly lower freezing point than the other specimens; this suggests the possibility that contamination could have occurred during preparation of the cell or that the sample bars are not homogeneous. When the mean values of the ratio R(Al)/R(TP) for five out of the six cells (excluding cell A–3) are compared, the spread of the ratio corresponds to 0.51 mK. The mean of the ratio R(Al)/R(TP) obtained for cell A–3 deviates from the mean ratio of the above five cells by an amount that corresponds to −1.31 mK. The average standard deviation of the ratios R(Al)/R(TP) obtained for the six cells corresponds to ±0.40 mK.

The experimental procedures that have been developed in the present work and the results that have been obtained demonstrate that aluminum can provide a freezing-point that is at least as reproducible as the freezing point of antimony [19]. Since aluminum is highly reactive chemically it must be isolated in inert surroundings. Although graphite (carbon) and aluminum form a stable compound (Al₄C₃) [7], aluminum can be contained in a graphite crucible without excessive reaction, if any. Either the aluminum-carbon reaction is slow even near the temperature of the aluminum point or the aluminum carbide that is formed adheres strongly to the graphite crucible and is relatively insoluble in aluminum. (Microscopic investigations of Al₄C₃ have been reported on samples that were formed when aluminum was cast in graphite crucibles under vacuum and at temperatures above 1000 °C [25]. The Al₄C₃ crystallites that were formed in that case apparently rose to the surface of the liquid aluminum where they were observed after the sample was solidified.)

Since aluminum supercools only about 1 K, the freezing of the aluminum can be initiated in the furnace without withdrawing the hot cell from the furnace as is customarily done with antimony [18], which usually supercools over 10 or 20 K, to initiate the freeze. After the freeze starts, a fused quartz rod should be inserted in the thermometer well of the cell to induce a mantle of solid aluminum around the well and provide a liquid-solid interface close to the prt. When the aluminum-point cells were prepared to freeze as outlined above, the equilibrium freezing temperatures of five out of six cells have been found to have a range of 0.51 mK.

The work presented in this paper was performed employing a prt of an R(0 °C) of only about 0.26 Ω with an a-c bridge. The average standard deviations obtained for R(TP) and R(Al) were ±0.14 mK and ±0.17 mK, respectively. However, the values of R(Al) that were obtained included effects of inductive interaction. Therefore, proper correlation with observed resistances at the other fixed points cannot be made. At this low thermometer resistance the temperature sensitivity of d-c resistance measurements employing, for example the Mueller bridge (G–3), is only 1 mK with 10 mA thermometer current and 10 nV detector sensitivity. The steps of the lowest decade of the Mueller bridge that was available was 10 μΩ. The measurements utilizing this Mueller bridge with the above prt would be rather imprecise.³ A prt of 2.6 or 5 Ω or even slightly higher mounted on a sapphire coil form would permit d-c measurements at about 0.1 mK sensitivity using the Mueller bridge and allow proper correlation of the resistances observed at the various fixed points. The prt should have a helically wound sensor coil for use also with a-c bridges. The comparison measurements at the TP show that the inductive interaction of the prt with its metallic environment would be less if the sensor design were a helical coil instead of the bird-cage type.