Standardization of ⁶⁰Co and ¹³⁷Cs Gamma-Ray Beams in Terms of Exposure

Abstract

At the National Bureau of Standards (NBS), the exposure-rate standards for ⁶⁰Co and ¹³⁷Cs gamma rays were based for a number of years on a weighted average of measurements using a cylindrical ionization chamber and a group of small spherical chambers. Complex setup conditions for the cylindrical chamber, differences between the cylindrical and spherical chamber data, and recognition that the institution of this weighted average exposure-rate standard increased the difference between free-air-chamber and cavily-chamber measurements, led to the development of new spherical chambers. All correction factors for exposure-rate measurements were investigated and updated. Excellent agreement was achieved between independent exposure-rate measurements for six spherical chambers and, as of May 1, 1972, the exposure standards were reduced 0.7 percent for ⁶⁰Co and 0.6 percent for ¹³⁷Cs gamma rays. Recalculation of correction factors since that time indicates that the standard ¹³⁷Cs should be further reduced by 0.2 percent, and this adjustment was made on July 1, 1974.

The uncertainties associated with each of the quantities entering into the determination of exposure rate were tabulated and the overall uncertainty of the exposure rates used for instrument calibrations at NBS was found to be about 0.7 percent for addition in quadrature.

1. Introduction

The standard instrument employed for exposure measurements, for x-rays generated by potentials from ten up to a few hundred kilovolts, is the free-air ionization chamber [1, 2, 3].¹ Experimental difficulties encountered with this instrument at high energies, in fulfilling the requirement that all ionizing particles be stopped in air, cause standards laboratories to have recourse to another method of standardization. This alternate method, which obviates the necessity of a free-air chamber operated at high pressure, or with large plate spacing, employs cavity ionization chambers and relies on the principles of the Bragg-Gray theory [4] for its validity.

The exposure, X, is the quotient of dQ by dm where dQ is the absolute value of the total charge of the ions of one sign produced in air when all electrons liberated by photons in a volume element of air having mass dm are completely stopped in air [5]. The special unit of exposure is the roentgen which is equal to 2.58 × 10⁻⁴ C · kg⁻¹.

During 1959, Wyckoff [6] measured a ⁶⁰Co source and a ¹³⁷Cs source, in roentgens, using a pressurized free-air chamber. For comparison, the exposure rates were also measured using the cylindrical cavity ionization chamber of Attix [7]. The cavity-chamber measurements were performed in an open-air geometry and corrected for room scattering. Good agreement was achieved between the two methods of measurement although the cavity-chamber measurement of the ¹³⁷Cs source appeared low (see table 1, column 2).

Table 1.

Relationship of cavity-chamber and free-air-chamber source measurements, and ratios of collimated beam calibrations

Ratios of cavity-chamber exposure rate to free-air-chamber exposure rate. 60Co and 137Cs source measurements.			Ratio of weighted mean exposure rate to exposure rate based on cylindrical chamber measurements with radiation incident ⟘ to chamber axis. Calibration change in 1961.	Ratio of new weighted mean exposure rate, based on measurements with six spherical chambers, to 1961 weighted mean. Calibration change in
	Cylindrical chamber. Radiation incident ⟘ to chamber axis. (1959)	Weighted mean of cylindrical and small spherical chamber data. Cylindrical chamber axis at 45° to incident radiation. (1961)
Source				May 1972	July 1974*
60Co	1.003	1.019	1.016	0.993	0.993
137Cs	0.984	0.994	1.010	0.994	0.992
(1)	(2)	(3)	(4)	(5)	(6)

^*All new data provided in this publication reflect the July 1974 values.

The activity of the ⁶⁰Co source was determined from calorimetric measurements in 1961 by Myers [8] who calculated² ${\overline{W}}_{\text{air }}$ by combining the activity and free-air-chamber data. His value of 33.84 eV per ion pair is in good agreement with the presently accepted value of 33.73 eV [9], thus indicating consistency of the free-air-chamber measurements of exposure with other physical measurements.

The apparent good agreement between the free-air-chamber and cavity-chamber measurements was to some extent fortuitous, since subsequent comparisons between the cylindrical chamber and a group of spherical chambers showed that the cylindrical chamber response decreased, in relation to the spherical chambers, with increasing distance from the source. This characteristic of the cylindrical chamber had been observed by Attix [7] who hypothesized that the reduction was due to attenuation in the chamber end walls and who avoided the effect by orienting the axis of the chamber at an angle to the direction of the incident radiation.

The calibration of the NBS collimated gamma-ray beams, at the time of the free-air-chamber and cavity-chamber comparison, was based on measurements with the cylindrical chamber with its axis perpendicular to the direction of the incident radiation. To eliminate the distance effect in measurements with this chamber, the gamma-ray beams were recalibrated in 1961 with the chamber axis at an angle of 45° to the beam direction. At the same time, the beams were also calibrated with a small spherical chamber. The beam calibrations were then adjusted to a weighted mean of these two sets of measurements. The effect of this change on the free-air-chamber, cavity-chamber comparison is shown in table 1, column 3, and the effect on the calibrated beams is shown in table 1, column 4. The comparison of these measurements assumes that the ratios established for the directional dependence of the cylindrical chamber in a collimated beam are applicable to the open-air calibrations. All data in table 1 are for source-to-chamber distances comparable to those used in the open-air-geometry source measurements (0.8 m).

While the cavity-chamber and free-air-chamber measurements of exposure rate for high-energy gamma rays agreed to about 2 percent, the difference was still sufficiently large as to indicate that the corrections for the cavity chamber could be improved. The procedure of angling the cylindrical chamber in the beam to remove the distance effect, not only caused a divergence of the cavity-chamber, free-air-chamber exposure measurements,³ but added complexity to setup conditions for beam measurements. These difficulties prompted the development of new chambers which would not be critically directional dependent (and therefore easily set up), would allow investigation of possible variation of chamber response with chamber size, and eventually lead to the establishment of a standard based on a group of chambers of homogeneous geometry. The new chambers would also allow studies of chamber wall corrections, with the goal of improving agreement between the free-air-chamber and cavity-chamber exposure-rate measurements. To accomplish these goals, a group of eight spherical chambers was assembled. The chambers are fabricated from high-purity graphite and had special, closely fitting shells for wall-absorption measurements. The group of chambers and shells makes possible six⁴ determinations of exposure rate. The results of the measurements with these chambers, as well as some updating of calculated corrections, indicate that the exposure rates used at NBS since 1961 were too high by approximately 0.7 percent for ⁶⁰Co and 0.6 percent for ¹³⁷Cs gamma rays. The gamma-ray beams used for instrument calibrations were recalibrated on this basis as of May 1, 1972 (table 1, column 5). The adjustment in the gamma-ray standards is in a direction to improve the free-air chamber and the cavity chamber agreement for ⁶⁰Co, although it appears there is still a difference⁵ of about 1.2 percent.

The preceding discussion is based on ratios of chamber readings at different times in different radiation fields. The percentage difference between the free-air chamber and the cavity chamber for these gamma-ray energies should be considered as an estimate. Since the high-pressure free-air chamber is no longer available, confidence in the validity of the cavity-chamber determinations of exposure rate is derived from intercomparisons with other standards [12] and comparisons of cavity-chamber ionization measurements with other physical measurements such as source power [13]. Such comparisons have shown agreement in exposure-rate determinations to within several tenths percent.

2. Relationship Between Cavity Ionization and Exposure

The work of Gray was concerned with the measurement of gamma-ray energy absorbed in a small volume of material. His derivations and experiments led to the familiar expression

$$m{E}_w=J_g{\overline{W}}_g\frac{{}_m{S}_w}{{}_m{S}_g}$$ (1)

where _mE_w is the energy absorbed per unit mass of the medium, J_g is the number of ion pairs formed per unit mass of gas in a cavity in the medium, ${\overline{W}}_g$ is the average energy required to form an ion pair in the gas and _mS_w/_mS_g is the ratio of the mass collision stopping power for electrons in the medium, to that in the gas. A condition for the validity of eq (1) is that all electrons producing ionization in the cavity gas are generated in the wall of the cavity, and that the cavity does not disturb the electron flux.

For measurement of exposure, the medium in eq (1) is the wall of a cavity chamber with sufficient thickness to exclude electrons generated in other media. Any wall material and any gas can be used, provided the stopping-power ratio and the average energy required to form an ion pair in the gas are known. If the chamber wall is carbon, the energy absorbed per unit mass of air is

$${}_m{E}_{\text{air}}{=}_m{E}_c\frac{{\left(m{\mu }_{en}\right)}_{\text{air}}}{{\left(m{\mu }_{en}\right)}_c}$$ (2)

where _mμ_en is the mass energy-absorption coefficient, and

$${}_m{E}_{\text{air}}=J_g\overline{W}g\frac{m{S}_c}{m{S}_g}\frac{{\left(m{\mu }_{en}\right)}_{\text{air}}}{{\left(m{\mu }_{en}\right)}_c}.$$ (3)

If the gas in the cavity is air, the subscript g represents air. The equation for exposure computations derived from eq (3) is:

$$X=\frac{1}{2.58\times {10}^{-4}}\frac{Q_{\mathrm{air}}}{v\rho }\frac{m{S}_{\text{c}}}{m{S}_{\text{air}}}\frac{{\left(m{\mu }_{en}\right)}_{\text{air}}}{{\left(m{\mu }_{en}\right)}_c}\prod k_i$$ (4)

where 2.58 × 10⁻⁴ is the number of coulombs per kilogram of air produced by one roentgen, Q_air is the measured charge (in coulombs), v is the chamber volume (in m³) and ρ is the density (in kg/m³). $\prod k_i$ is the product of all the factors required to correct the measured charge for experimental conditions. These are: k_h the correction for water vapor in the air. k_s the correction for loss of ionization due to recombination. k_st the correction for chamber stem scatter. k_w the correction to zero wall thickness. k_CEP the reduction in the wall correction k_w, taking into account the mean center of electron production. Other corrections are required for specific experimental conditions.

3. Cavity-Chamber Description

The cavity chambers, used for studies leading to the revised (May 1, 1972) ⁶⁰Co and ¹³⁷Cs exposure-rate standards, were fabricated from reactor-grade, high-purity graphite, following the design of Wyckoff [15]. The spherical shape was chosen in order to allow the standards to be based on a homogeneous group of chambers of different volumes, to avoid the distance effect and the complexity of set up in measurements with the cylindrical chamber, and to present a uniform, symmetrical, chamber aspect to the source.

The dimensions of the spherical chambers are given in table 2. The three small-volume chambers, identified as 0.5, 1, and 2, were designed to be used as a group to determine a wall correction and provide one measurement of gamma-ray exposure. These chambers have the same nominal outside diameter but different wall thicknesses and thereby different cavity volumes. They were fabricated using ball end-mills of diameters 3/8, ½, and 5/8 in. The wall-thickness values given for these three chambers were derived from measurements of outside diameters and the diameters of the end-mills used in their fabrication.

Table 2.

Dimensions of spherical graphite ionization chambers

Nominal volume	Volume	Net volume	Outside diameter	Graphite density	Radial Wall Thickness
(cm3)	(cm3)	(cm3)	(cm)	(g·cm−3)	(cm)	(g·cm−2)
0.5	0.440	0.431	2.078	1.72	0.563	0.968
1	1.140	1.131	2.065	1.73	.398	.688
2	2.029	2.019	2.080	1.74	.246	.428
10	10.088	10.069	3.428	1.72	.3755	.647
30	30.262	30.24	4.607	1.74	.3751	.653
50–1	51.943	51.634	5.34	1.73	.3652	.632
50–2	50.425	50.089	5.58	1.73	.5085	.880
50–3	50.460	50.155	5.80	1.73	.6129	1.060

The net volumes given in table 2 are the differences between the cavity volumes and the volumes of the collection electrodes. The electrode diameter for the 50-cm³ chambers is nominally 0.3 cm but for all other chambers it is nominally 0.1 cm.

The 50-cm³ chambers have the same nominal cavity size but different wall thicknesses and can be used as a group to determine the wall correction. The wall correction can also be determined by the addition of closely fitting shells to two of the chambers. With the two methods of wall-absorption measurement available, each of the 50-cm³ chambers can be considered to provide an independent measurement of exposure.

Of all the spherical chambers, the 50-cm³ chambers are of the highest quality, great care having gone into their fabrication to insure close tolerances in all dimensions. Measurements of wall thickness at many locations on the periphery of both halves of each 50-cm³ chamber show that the range of the wall thickness variation is less than 0.025 g · cm⁻² and the largest difference between average values for the two halves is 0.016 g · cm⁻².

The fabrication of the 10-cm³ and 30-cm³ chambers was performed with less restriction on the variation of chamber wall thickness with the result that the average wall thicknesses for the two halves differ by 0.016 cm (0.025g · cm⁻²) for the 10-cm³ chamber and 0.052 cm (0.089g · cm⁻²) for the 30-cm³ chamber. Although these differences seem to infer uncertainties in the chamber wall correction of up to 0.3 percent, in fact the chamber response is related to the average wall thickness and the average is used in plotting the chamber response versus wall thickness to determine the wall correction. The wall thicknesses given in table 2 for these two chambers are the overall averages for measurements in a radial direction at a number of positions (see fig. 1), and the corrections are determined for the chambers by the addition of closely fitting spherical shells to the chamber walls.

Figure 1.

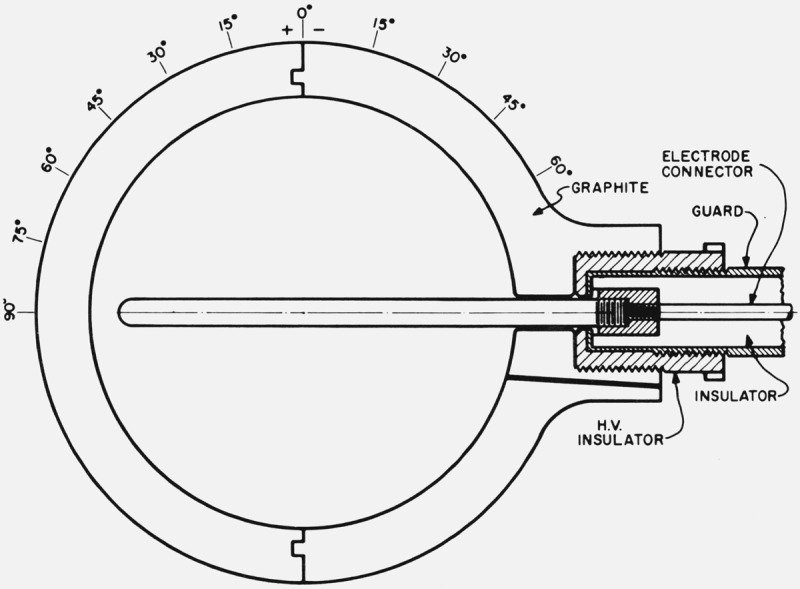
Cavity chamber design and location of wall thickness measurements.

The densities for the 0.5-cm³ and 2-cm³ chambers were measured using the principle of Archimedes, while density for the 1-cm³ chamber was inferred from measurements of another chamber fabricated from the same material. The densities for the 50-cm³ chambers were determined from a cylindrical block machined from the same material. The densities for the 10-cm³ and 30-cm³ chambers were determined using differential weighings in and out of distilled water. The differential weighing method, and mechanical measurement of dimensions and weighing of the same graphite block give densities which differ by only 0.01g · cm⁻³.

4. Wall Corrections and Volume Measurements

Ideally, the measurement of high-energy gamma radiation, in terms of exposure, should be made by sampling the ionization per unit mass of air, in a small volume surrounded by enough air to establish secondary-particle equilibrium, and removed from other sources of secondary-particle radiation. In practical situations, these conditions seldom can be met, necessitating the use of thick-walled ionization chambers.

The material chosen for the chamber wall should be sufficiently like air, with respect to its interaction with the radiation of interest that, with small corrections, the chamber wall can be considered nearly equivalent to air with a greater-than-normal density. Chambers are actually designed to have walls thick enough to exclude the highest energy secondary particles produced by interaction of the radiation with other media and this thickness is more than sufficient to achieve secondary-particle transient equilibrium [16]. Chamber ionization measurements can be plotted versus chamber wall thickness to allow extrapolation of transient-equilibrium readings to zero wall. This procedure provides an over-estimate of the corrected chamber reading as shown by Whyte [17]. The zero-wall chamber data must be reduced to account for the fact that the ionization in the chamber is being produced by electrons which are generated at some depth in the chamber wall and to bring the data into agreement with the zero-wall value for equilibrium conditions.

The amount by which the zero-wall correction for cavity chambers should be reduced can be estimated from the work of Wyckoff [6] who used, for photon attenuation corrections in a free-air chamber, a distance from the defining diaphragm to the mean position of origin of electrons producing ionization in the collecting plate region. The mean position of origin of the ionizing electrons was determined by Roesch [18] to be 0.3 times the practical electron range (350 cm-atm for ⁶⁰Co and 90 cm-atm for ¹³⁷Cs). Thus the total air path, between diaphragm and collection region, used to compute the air attenuation correction, was reduced by 105 cm-atm and 27 cm-atm for ⁶⁰Co and ¹³⁷Cs gamma rays, respectively. Since carbon and air are nearly alike as to interactions with gamma rays and electrons, the same thicknesses of material can be used for these energies. The fractional reduction calculated from the expression 1 − (μ/ρ) (ρx) is 0.995 for ⁶⁰Co and 0.999 for ¹³⁷Cs gamma rays. The values for μ/ρ (0.033 and 0.040 cm²/g) are averages from the data given in table 3. Since the correction is small, considerable latitude is allowable in each of the factors before the correction changes by 0.1 percent. This correction has been identified as k_cep since the extrapolation of the wall-absorption data is effectively carried out only to the mean center of electron production.

Table 3.

Summary of wall-absorption correction factors

Chamber	Radial wall thickness (g·cm−2)	Correction to zero wall		Correction per unit thickness (%·g−1·cm2)
		60Co	137Cs	60Co	137Cs
50–1	0.632	1.0227	1.0272	3.59	4.30
50–2	.880	1.0319	1.0384	3.63	4.36
50–3	1.060	1.0387	1.0467	3.65	4.40
30	0.653	1.0220	1.0249	3.37	3.81
10	.647	1.0216	1.0260	3.34	4.02
1	.688	1.0168	1.0199	2.44	2.89

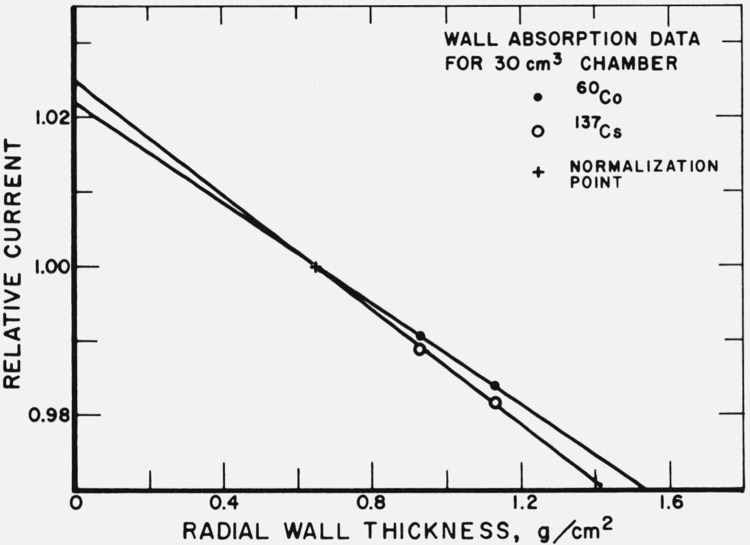
The wall corrections for ⁶⁰Co were determined by the addition of spherical graphite shells, for all chambers, and by combining data for groups of chambers designed as a set in the case of the three small-volume chambers and the three 50-cm³ chambers. The agreement between the two methods is excellent for the 50-cm³ chambers and the data are shown in figure 2. As a consequence of the close agreement between the two absorption methods, it was only necessary to use the 50-cm³ chambers as a group to determine the wall correction for ¹³⁷Cs gamma rays. These data are also shown in figure 2.

Figure 2.

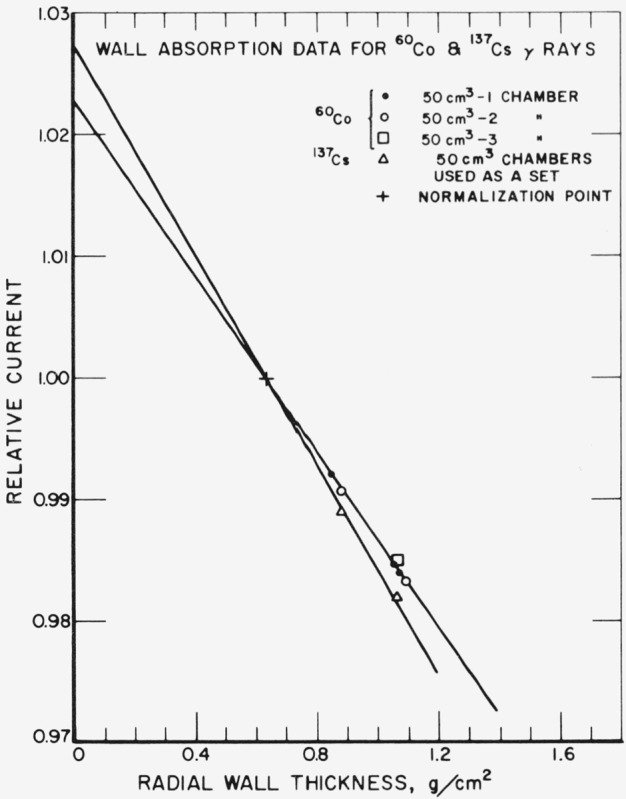
All 50-cm³ chamber absorption data for ⁶⁰Co gamma rays are combined by normalization to the data for 50–1 chamber.

The chamber group and shell addition data are shown to be consistent. The line drawn through the points was calculated using the least squares method with the data weighted according to the number of determinations for each point. The line through the points for ¹³⁷Cs gamma rays is also based on the least squares method.

The averages of several sets of measurements of chamber reading versus wall thickness for the 10- and 30-cm³ chambers are plotted in figures 3 and 4. The lines drawn through the points are least-squares regressions giving equal weight to each point. The wall-absorption corrections for all the chambers are summarized in table 3.

Figure 3.

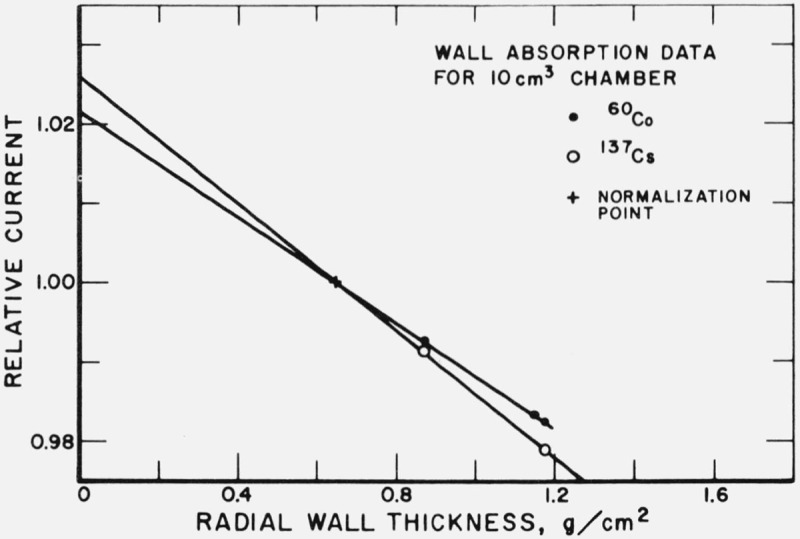
Relative ionization currents produced in the 10-cm³ chamber by ⁶⁰Co and ¹³⁷Cs gamma rays as the wall thickness is increased by the addition of graphite shells to front and back of the chamber.

Figure 4.

Relative ionization currents produced in the 30-cm³ chamber by ⁶⁰Co and ¹³⁷Cs gamma rays as the wall thickness is increased by the addition of graphite shells to front and back of the chamber.

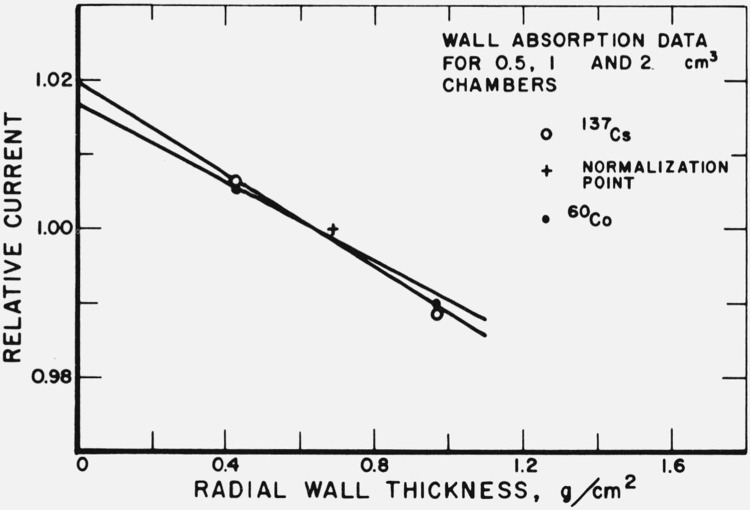
Determination of the appropriate wall-absorption correction for the set of small-volume chambers presents difficulties which are not present for the other chambers. The small chambers differ considerably in volume and when operated at the same collection potential have different field strengths. It is necessary, therefore, to apply corrections for recombination, determined for each chamber, for the exposure rate used in the experiment. An additional difficulty, and one which exacerbates the situation, is the relatively large uncertainty in the determination of the volumes for these small chambers. The differential weighing technique, i.e., weighing the chambers with and without the cavity filled with distilled water, provides volume measurements for all the large chambers with a range of only 0.02 cm³. If this range is used as a measure of the imprecision of the technique, it is obvious that for small-volume chambers such as the 0.5, 1, 2 group, the uncertainty in the volume determination can be large. Analysis of the measurements for these chambers reveals that the average volumes have the statistical parameters given in table 4. Since the confidence interval increases as the chamber volume decreases, the data for the small chambers cannot be considered to be of equal value. Weighting factors of 1, 3, and 4, based on the inverse of the 95 percent confidence intervals are therefore assigned to 0.5, 1, and 2 chambers, respectively, in the calculation of regression lines for wall absorption. The data for both gamma-ray energies are shown in figure 5 where the lines drawn through the points are determined by least squares.

Table 4.

Statistical parameters associated with volume determinations for 0.5, 1, and 2 chambers

Chamber	Average volume (cm3)	Number of measurements	Standard deviation of the mean (percent)	Weights based on 95% confidence interval
2	2.029	2	a 0.00	4
1	1.140	5	.07	3
0.5	0.440	7	.2	1

^aA series of three sets of weighings were performed for 2 and then the chamber halves were separated for inspection. The relative standard deviation of the mean, for these first weighings, is 0.035 percent. The chamber was reassembled and two more sets of weighings were performed. There was no difference (to 0.01 mg) between the last two weighings. Because the chamber halves were separated between the weighings, the volume resulting from only the last two measurements is used, however the relative standard deviation of the mean for the first series is utilized to develop weights for regression analysis.

Figure 5.

Relative ionization current per unit volume for the small chambers plotted against radial wall thickness.

Due to the different internal chamber dimensions, each measurement must be corrected for recombination. The data are weighted as described in the text and the line drawn is the regression line based on the weighted data.

The wall correction for the small-chamber set is based on the use of the chambers in combination, i.e., the current per unit volume for each chamber was plotted against chamber radial wall thickness and the data extrapolated to zero-wall. The resulting wall correction, the 1-cm³ chamber volume and other required corrections produce exposure-rate data for this chamber group which is only about 0.3 percent higher than that calculated from other spherical-chamber measurements.

Experiments designed to determine wall corrections for the small chambers, by addition of close-fitting shells to each of the chambers, show that the slopes of the chamber reading versus wall thickness curves for these chambers are consistent with those determined for the larger chambers, but greater than the slope determined by using the small chambers as a group. Since the chamber halves are joined by the tongue-in-groove method, with the juncture around the chamber middle (opposite a large fraction of the volume for the small chambers), it appears appropriate to use the chambers as a group to determine a wall correction. In this way, the effect of structural features on the small chamber exposure determinations will be minimized.

5. Recombination Corrections

For accurate measurement of gamma-ray beams with ionization chambers, it is required that all the charge produced in the chamber volume be collected and measured. This ideal is approached closely by the spherical chambers even though the geometry of the combined cylindrical electrode and spherical chamber produces nonuniform electric field strengths within the chamber volume. Tests for recombination of ions, at a particular exposure rate, are carried out by increasing the chamber collection potential until the current measured for potential V is at most only a few tenths percent greater than the current measured for V/2. Methods of treating ionization data have been developed which take into consideration the recombination mechanisms involved and which make possible the estimation of corrections in a consistent manner. Analysis of recombination characteristics for a particular chamber may be facilitated by plotting the reciprocal of the ion currents against the negative powers of the collecting potentials V^−l or V⁻² [19]. Neither provides straight-line extrapolation if small corrections, e.g., of the order of tenths of one percent, are being sought and it is often necessary to estimate the correction by extrapolating a curve. If sufficient data are available, recombination corrections for a particular operating potential can be estimated and tabulated as a function of exposure rate $\dot{X}$. These data can then be used to determine constants for an equation which includes $\dot{X}$ explicitly.

In theory, columnar and volume recombination vary as V⁻¹ and V⁻² respectively. Both effects being present, and each being small, the total correction can be considered to be the product$\left(1+\frac{C}{V}\right)\left(1+\frac{A\dot{X}}{V^2}\right)$ with only volume recombination dependent on $\dot{X}$. The values of the constants for the 50-cm³ chambers which have inside diameters of about 4.6 cm and collection electrodes 4 cm in length and 0.3 cm in diameter, are:

$$A=7200{\text{V}}^2{\text{R}}^{-1}\text{s}$$

$$C=0.66\text{V}$$

Recombination corrections for all other chambers were determined as required, by graphical extrapolation of reciprocal current versus reciprocal collection-potential curves, where intercomparisons of exposure-rate data were of interest; however, general relationships were not established as in the case of the 50-cm³ chambers. In all cases, the chambers were operated with sufficiently high collection potentials so as to make the saturation corrections not greater than a few tenths percent.

The corrections for recombination are based on the averages of chamber currents measured for both polarities of collection potential. This procedure was observed in obtaining all measurements in order to eliminate the contribution of extra-cameral ionization to the chamber ionization current.

6. Stem Leakage and Scatter Corrections

In the ideal case, the current measured by the electrometer system is generated exclusively by the electrons which ionize the gas in the chamber cavity. This ideal is not quite realized in practice since the radiation induces leakage currents in the supporting stem, and scatter from the stem adds to the chamber reading. Both of these effects are small. Studies using test stems show that induced stem-leakage currents, for the range of exposure rates used in these standardization measurements, are less than 0.1 percent of the chamber current and negligible where measurements are averaged for both positive and negative collection potentials.

The effect of stem scatter on the chamber readings is measured by using an identical stem in contact with the chamber on the side opposite the supporting stem. The stem-scatter corrections determined for all chambers are given in table 5. The corrections are small but tend to increase as the chamber size decreases. This is expected since the material immediately adjacent to the chamber is most important for this effect and the relative size and the proximity of the scatterer are greater for the smaller chambers.

Table 5.

Stem-scatter corrections for ¹³⁷Cs and ⁶⁰Co gamma rays

Chamber	137Cs	60Co
1	0.996	0.998
10	.998	.999
30 and 50	.999	.999

7. Stopping-Power Corrections

The stopping-power correction required is the ratio of the weighted mean stopping powers for carbon and for air where the weights are based on the slowing-down electron spectrum generated by the gamma rays. The value of the stopping power depends, among other things, on the mean excitation energy, I, for the material of interest. Ratios of the weighted mean stopping-power of carbon to that of air, $1/\overline{f}$, provided by Boutillon [20]⁶ are used at this time at NBS. In the calculation of $\overline{f}$, I_c = 78eV and I_air = 86.8 eV [21], and the stopping powers used in the weighting procedure are restricted to those for electrons with energies exceeding some energy limit Δ. The limiting energy is related to the cavity chamber dimensions. The energy limits were computed at NBS using the average linear intercepts [22], $\overline{L}=4/3$, for chambers with radii r, and the assumption that the projected range is about 75 percent of the “continuous-slowing-down-approximation” path length [21] for electrons in air at standard temperature and pressure. The stopping-power ratios are given in table 6 along with a value of Δ for each chamber.

Table 6.

Mass stopping-power ratios of carbon to air,$1/\overline{f}$, with I_c = 78 eV and I_air = 86.8 eV

Chamber	Δ	Stopping power ratioa
	(keV)	60Co	137Cs
1	24	1.007	1.014
10	37	1.006	1.014
30	46	1.006	1.013
50	50	1.006	1.013

^aThe stopping-power ratios used prior to May 1, 1972 were about 0.3 percent and 0.6 percent lower for ⁶⁰Co and ¹³⁷Cs respectively. The values of I used were I_c = 76.4 eV and I_air = 80.5 eV.

8. Mass Energy-Absorption Coefficient Ratio

The energy-absorption coefficient ratio converts data for photon energy absorbed in carbon to photon energy absorbed in air. The latest data published by Hubbell for _mμ_en [10] tabulates coefficients with three significant figures for carbon and for air, starting at 0.6 MeV. The ratio of the coefficients is within 0.1 percent of unity over the tabulated energy range of 0.6 to 2.0 MeV. The constancy of this ratio is, of course, one of the reasons for choosing carbon as the wall material for the cavity chamber. However, the spectra in the ⁶⁰Co and ¹³⁷Cs gamma-ray beams include energies below the minimum tabulated energy and, especially in the case of ¹³⁷Cs, weighting of _mμ_en in accord with the beam spectra could not be carried out. A special calculation, performed by Hubbell, extending the energy range down to 10 keV and increasing the number of significant figures for the coefficients, made it possible to take the entire spectrum into consideration for both ⁶⁰Co and ¹³⁷Cs. The data of Costrell [23, 24] most representative of the NBS beam spectra were used to determine weighted mean values of _mμ_en with the weighting performed in accord with the energy-fluence distribution of the photon beams. The ratios of the weighted means are 0.9995 for ⁶⁰Co and 0.9997 for ¹³⁷Cs. Hubbell’s ratios, in the energy region of interest, are given in table 7. The ratios are believed to be known only to 0.5 percent in the region from 10 keV to 100 keV while they are believed to be known to 0.1 percent or better in the region from 0.1 MeV through 1.33 MeV. Since only a negligible fraction of the total energy in the beams is below 0.1 MeV, the uncertainty for the ratios of the weighted mean energy-absorption coefficients, for ¹³⁷Cs and ⁶⁰Co gamma rays, is taken as 0.1 percent.

Table 7.

Mass energy-absorption coefficient ratio, air to carbon

Photon energy (MeV)	$\frac{\left(m{\mathit{\mu }}_{en}\right)\text{air}}{\left(m{\mathit{\mu }}_{en}\right)\text{c}}$
0.05	1.7415
.10	1.0847
.15	1.0199
.20	1.0069
.30	1.0014
.40	1.0000
.50	0.9998
.662	.9995
1.00	.9994
1.17	.9994
1.33	.9994

9. Measurements

Although beam measurements with the chambers were carried out at various times and at various source-to-chamber distances in the course of establishing the corrections required, the data which form the basis for the ⁶⁰Co and ¹³⁷Cs exposure standards were taken at 2 m from the sources.

The intercomparison of the cavity chambers was carried out under measurement conditions which minimized disturbing influences to the greatest possible extent. The beams used were uniform across the chamber dimensions to within the accuracy of careful densitometric measurement. The average film density over the smallest and largest chamber diameters was found to differ by less than 0.1 percent. The inverse square nonuniformity for the largest chamber (radius about 2.5 cm) at the measurement distance of 2 m was less than 0.02 percent in the direction perpendicular to the beam. In the direction parallel to the beam, the difference between the chamber response for a nonuniform beam (inverse square), and the chamber response assuming uniform irradiation, is 0.005 percent as calculated from the Spiers equation [25].

Although the variation of beam intensity over the range of chamber sizes is unimportant according to the criteria established above, the influence of source-chamber distance was investigated by comparing two chambers with inside diameters of 16 mm and 46 mm (2 and 50−1, respectively) at three distances from a ⁶⁰Co source. The distances chosen bracket the position used for the chamber intercomparison. The data given in table 8 show excellent agreement in the ratios of chamber readings, indicating there is no significant distance dependence due to chamber size for source-chamber distances of interest in these investigations. The geometrical center was taken as the position of the chamber for all measurements.

Table 8.

Ratios of currents for 46-mm and 16-mm diameter chambers

Distance (cm)	Current ratios	Ratio corrected for recombination
75	25.17	25.20
150	25.19	25.20
300	25.19	25.20

Two sets of intercomparisons of the six chambers were carried out in the ⁶⁰Co beam. Each was performed within one day on two separate occasions. The largest difference, 0.1 percent, between the two measurements was for the smallest-volume chamber. Intercomparisons of the chambers for ¹³⁷Cs gamma rays were carried out in the same manner as for ⁶⁰Co but the measurements occupied a longer period of time since the corrections for each chamber were determined at the same time. The longer half-life for ¹³⁷Cs reduces the importance of concurrent measurements for the intercomparison of the chambers and only small decay corrections were required. The largest difference between the two sets of ¹³⁷Cs gamma-ray measurements for each chamber was 0.06 percent.

A summary of the correction factors pertinent to each chamber for the two gamma-ray beams is given in table 9. The last column in the table is the product of all the corrections for a particular chamber. The measurements at 2 m from the sources and utilization of these factors produce exposure-rate data which are in excellent agreement as shown in table 10 where the result for each chamber is compared to the mean.

Table 9.

Summary of correction factors for each ionization chamber

137Cs gamma rays
Chamber	Wall absorption	Stopping-power ratio	Energy-absorption coefficient ratio	Stem scatter	kCEP	Product of correction factors
1	1.0199	1.0143	0.9997	0.9964	0.9990	1.0294
10	1.0260	1.0138	.9997	.9979	.9990	1.0366
30	1.0249	1.0135	.9997	.9992	.9990	1.0365
50–1	1.0272	1.0133	.9997	.9987	.9990	1.0382
50–2	1.0384	1.0133	.9997	.9987	.9990	1.0495
50–3	1.0467	1.0133	.9997	.9987	.9990	1.0578
60Co gamma rays
1	1.0168	1.0069	0.9995	0.9982	0.9950	1.0164
10	1.0216	1.0064	.9995	.9992	.9950	1.0217
30	1.0220	1.0062	.9995	.9992	.9950	1.0219
50–1	1.0227	1.0061	.9995	.9990	.9950	1.0223
50–2	1.0319	1.0061	.9995	.9990	.9950	1.0315
50–3	1.0387	1.0061	.9995	.9990	.9950	1.0383

Table 10.

Ratios of exposure rates, as determined with each ionization chamber, to the unweighted mean exposure rate (7 × 10⁻³ R · s⁻¹)

Chamber	137Cs	60Co
1	1.0033	1.0025
10	.9998	.9998
30	.9973	.9990
50–1	.9999	.9994
50–2	.9999	.9995
50–3	1.0000	.9998

If the data from each of the chambers were considered to be equally uncertain, the inverse of the ratios given in table 10 could be used as a small additional correction to bring the data for each chamber into agreement with the mean value. Since this is not the case, it appears that a weighting procedure based on the magnitude of the uncertainty for each chamber is appropriate.

An effort to quantify these uncertainties has been made by estimating upper limits for nonstatistical quantities and combining them with uncertainties based on standard deviations of the mean for data which can be treated statistically. The upper limits assigned to the uncertainties are, in most cases, arbitrary and are based on the judgment of the authors. The factors considered, and the related estimated uncertainties, are listed in table 11 where Δt and ΔV are the time and potential changes for the Townsend balance measurements. P and T are the pressures and temperatures during the measurements, v represents the chamber volumes, and the next four factors are corrections for the wall effect, stopping power, recombination and stem scatter. The last two factors are corrections for lack of reproducibility of chamber position in the direction of the beam, k_a, and for nonuniformity of the beam in a radial direction, k_R.

Table 11.

Uncertainties, S, in percent, for all factors in the intercomparison of the six NBS cavity ionization chambers. The uncertainties for Δt and v are based on standard deviations of the means brought to a 95 percent confidence level. The uncertainty for the stopping-power ratio takes into consideration only the variation with chamber size and this and all other uncertainties are estimated upper limits

Ionization chamber
Factor	1	10	30	50–1	50–2	50–3
ΔV	0.020	0.020	0.020	0.020	0.020	0.020
Δt	.056	.021	.027	.011	.015	.014
v	.200	.327	.043	.017	.052	.064
T	.03	.03	.03	.03	.03	.03
P	.01	.01	.01	.01	.01	.01
kw	.30	.10	.10	.10	.10	.10
Δksp	.04	.04	.04	.04	.04	.04
ks	.02	.02	.02	.02	.02	.02
kss	.02	.02	.02	.02	.02	.02
ka	.03	.03	.03	.03	.03	.03
kR	.00	.00	.00	.01	.01	.01

The uncertainties listed in table 11 were added in quadrature, and the reciprocals of these sums were used as relative weighting factors to compute a weighted mean exposure rate, $\overline{\dot{X}}$, at the chamber intercomparison position. The values of the relative weighting factors are given in table 12. The ratio of the weighted mean exposure rate to the exposure rate determined with a particular chamber, j, provides a correction factor, _jk_std, for that chamber to the weighted mean thus,

$${}_j{k}_{std}=\frac{\sum w_i{\dot{X}}_i}{{\dot{X}}_j}$$

Values of _jk_std are given in table 13.

Table 12.

Sums of the squares of the uncertainties in table 11, and the weighting factors, w_j, for each ionization chamber

Chamber	$\sum S_j^2$	wj
1	0.1378	0.02928
10	.1221	.03304
30	.01728	.2335
50–1	.01521	.2653
50–2	.01773	.2276
50–3	.01909	.2114

Table 13.

Chamber correction k_std required to bring exposure-rate measurements for each chamber into agreement with the weighted mean exposure rate $\overline{\dot{X}}$.

Chamber	60Co	137Cs
1	0.9970	0.9962
10	.9997	.9997
30	1.0005	1.0022
50–1	1.0002	0.9996
50–2	1.0003	.9996
50–3	0.9998	.9995

The product of the chamber corrections given in table 9, the correction to the weighted mean exposure rate given in table 13, and a recombination correction provide a total correction factor for each chamber. This factor, when used with measurement data, allows use of any of the above chambers to standardize a ⁶⁰Co or ¹³⁷Cs gamma-ray beam. The recombination correction, of course, may be rate dependent and then must be determined at the time of measurement or from previous data.

10. Accuracy

As stated above, an attempt was made to optimize all conditions which would influence the measurements. The degree of success can in part be judged by the agreement to within 0.1 percent of two sets of measurements at different times for several chambers.

Estimates of the uncertainties associated with each chamber are given in table 11 from which weights were computed based on those factors affecting the relationship of one chamber to another. Not included in this tabulation are uncertainties for factors common to all chambers such as the mass energy-absorption coefficient ratio, the reduction in the wall-absorption correction to account for the CEP effect, and the uncertainty in the stopping-power ratio, since only the uncertainty in the restricted ratio due to variation in chamber size was considered. The uncertainty for k_std must also be included in estimating the accuracy of an exposure-rate determination when any one of the chambers is used since

$$\overline{\dot{X}}{=}_j{\dot{X}}_j{k}_{std}$$

where the subscript j indicates a particular chamber. The uncertainty for _jk_std can be computed using the usual rule for the propagation of error and the relation

$${}_j{k}_{std}=\sum _i{w}_i{x}_i/x_j$$

where the x_i are proportional to the exposure rates as determined using each of the chambers. The x_i are independent and uncorrelated and $\sum _i{w}_i=1$. The general equation for the uncertainty in _jk_std is

$${}_{j}S\left(k_{std}\right)={\left[{\left(1-w_j\right)}^2{S}_j^2+\sum _i{w}_i^2{S}_i^2\right]}^{1/2}$$

where the prime on the summation sign means the sum is taken over all i except i = j. The values for S and w given in table 12 were used to compute the uncertainties for k_std given in table 14.

Table 14.

Uncertainty of k_std for each ionization chamber

Chamber	S(kstd)
1	0.37
10	.34
30	.12
50–1	.11
50–2	.12
50–3	.12

At the present time the correction for the effect of moisture in the air in the cavity chamber is considered to be equal to unity [14]. However, the work of Niatel [26] and Guiho [27] both indicate the relative humidity affects the ionization measurements. An estimate of the upper limit uncertainty for this effect is taken to be 0.3 percent.

The uncertainty in the unrestricted stopping power is estimated by Berger [21] to not exceed 2 percent. This estimate is based on a wide range of materials and energies, and the use of certain I values and a theoretical equation. Agreement between theoretical and experimentally determined stopping-power ratios is given as 0.1 percent [28] but the experimental uncertainty is given as 0.5 percent. It seems, therefore, that a conservative estimate for the upper limit of the uncertainty for the mass stopping-power ratio is 0.5 percent when the cavity gas is air and the wall material is nearly air-equivalent.

The uncertainty in the ratio of the mass energy-absorption coefficient has been estimated by Hubbell [29] to be less than 0.05 percent. His estimate is based on the difference between the coefficients calculated by the Klein-Nishina equation with and without corrections for electron binding and bremstrahlung losses. An uncertainty of 0.1 percent is arbitrarily assigned to this ratio.

The overall uncertainty in the NBS measurement of ¹³⁷Cs or ⁶⁰Co gamma radiation in terms of exposure is computed by adding in quadrature the upper limits of the non-statistical uncertainties with the standard deviations of the means of the statistical uncertainties brought to a 95 percent confidence level. The data used for this computation is given in table 15 with the statistical uncertainty for Δt taken from the data resulting from the intercomparison of the six chambers (table 11). The uncertainty for the recombination correction is for the exposure rate used in the intercomparison. The uncertainties for the chamber volumes, zero-wall corrections and stem-scatter corrections are included in the uncertainty for k_std for each chamber (values given in table 14).

Table 15.

Uncertainties in the determination of NBS exposure rates $(\overline{\dot{X}})$

Quantity or factor	Percent uncertainty (S)
Potential	0.02
Capacitance	.02
Temperature	.03
Pressure	.10
Relative humidity	.30
Stopping-power ratio	.50
Mass energy-absorption coefficient	.10
CEP correction	.20
Distance (axial)	.03
Recombination	.02
Time	(see table 11)
kstd	(see table 14)

The overall uncertainty for measurement of NBS exposure rates is determined from the data in table 15 added in quadrature. These sums are given for each chamber in table 16.

Table 16.

Overall uncertainty for NBS exposure rates

Chamber	Uncertainty (percent)
1	0.74
10	.72
30	.65
50–1	.64
50–2	.65
50–3	.65

It should be pointed out that the overall uncertainty data in table 16 have been computed using statistics derived from measurements at an exposure rate of about 7 × 10⁻³ R · s⁻¹. For other exposure-rate conditions, where the statistics for time measurement (Δt), or the uncertainty for recombination loss differs significantly from the values used, recalculation of the uncertainties might be necessary.

11. Summary and Conclusions

The foregoing provides a complete description of the cavity ionization chambers, their relationship to one another and to the weighted average of their exposure-rate data which is taken as the NBS standard. Once the correction to the standard has been established for each chamber, any of the chambers can be used to calibrate a ⁶⁰Co or ¹³⁷Cs gamma-ray beam.

The uncertainties associated with each of the factors entering into the determination of exposure rates, for ⁶⁰Co and ¹³⁷Cs gamma-ray beams, are given and the total estimated uncertainty for measurements with each of the chambers is computed for representative measurement conditions.

The ratio of the cavity-chamber to free-air-chamber exposure-rate determinations for ⁶⁰Co gamma rays may be (1.019)(0.993) = 1.012 if the ratios of measurement data given in table 1 hold. The difference of 1.2 percent is just a little less than the sum of the uncertainties for each method of measurement. A correction to the cavity chamber data for scattering in the chamber walls would reduce the cavity-chamber, free-air-chamber difference but would increase the differences between other, more recent, comparisons.

The difficulties experienced with the large cylindrical chamber have been more circumvented than solved, however the close agreement between the six spherical chambers of greatly different size gives good confidence in the new exposure standard. Moreover, the agreement of the new exposure standard for ⁶⁰Co with other standards [12] and other physical measurements [13] is within 0.4 percent.

12. Appendix

The procedure in standardizing a gamma-ray beam at NBS is to calibrate the beam at several distances from the source and then fit the data to a suitable function which will allow accurate computation of exposure rates at selected distances, or of distances for selected exposure rates. The equation used for this purpose is derived by using the inverse square law with corrections for air attenuation and buildup. A cubic equation has been found adequate for the correction terms, giving an equation of the form

$$\dot{X}{D}^2=K_1\left[1+K_{2}D+K_3{D}^2+K_4{D}^3\right]$$

where D = S + S₀. The distances read on the scale, S, are adjusted by the term S₀ to make D the distance from a point in the beam to an effective center of the source.

The values of S₀ and the K_i were determined for each calibration range using a computer program for non-linear least-squares function fitting (SAAM) developed by Berman and Weiss.⁷ The constants for each of the sources are given in table 17.

Table 17.

Constants for exposure-rate versus distance equation for five calibration ranges as of December 31, 1973

Source	S0 (cm)	K1 (mR·s−1·m2)	103K2 (m−1)	103K3 (m−2)	103K4 (m−3)
B036–137Cs	27.91	97.572	46.23	−26.05	4.898
B015A–137Cs	−0.71	2.6495	−8.945	0.8528	0
B021A–137Cs	−.41	25.328	−3.889	−.1139	0
B015B–60Co	−.14	2.5178	−2.804	−.2278	0
B021B–60Co	−.53	22.387	−0.9036	−1.279	0

Using the constants given in table 17, the agreement between exposure rates determined from the equation and the measured exposure rates is, on the average, 0.01 percent.