The Second Interaction (Cross) Virial Coefficient for Moist Air

Abstract

The results of calculations of the second interaction (cross) virial coefficient B_aw for water vapor and air, based on enhancement data obtained at NBS at 30, 40, and 50 °C, are presented. Comparisons are made with the results of calculations based on the enhancement data of Politzer and Strebel, Webster, and Goff et al. and with the results of the theoretical calculations of Mason and Monchick and of Chaddock. An empirical equation is given for interpolation and extrapolation.

The random (one standard deviation) uncertainty in the mean values of B_aw, arising from the scatter of previously obtained NBS values of the enhancement factor, is estimated to range from 0.7 percent at 30 °C to 1.4 percent of 50 °C. The estimated systematic uncertainties range from 4 percent at 30 °C to 6 percent at 50 °C, respectively.

1. Introduction

The water vapor content of real gases, and of air in particular, saturated under known conditions of pressure and temperature, is not predicted adequately by ideal gas laws [1].¹ In air, the deviations from ideality must be accounted for in order to obtain accuracies better than 0.5 percent at pressures as low as 900 millibars [2]. On any isotherm, the saturated water vapor content increases with pressure to some, as yet, undetermined limit, in a manner consistent with that described by Haar and Sengers [3]. For example, at 0 °C and 200 bars, the water vapor concentration or density in air is about twice that of the pure phase.

This increase in water vapor content with pressure is the algebraic sum of the increases in apparent vapor pressure because of the superimposed pressure of air (the Poynting effect), and the Van der Waals type interactions between different molecular species, and the decrease in apparent vapor pressure due to the solution of the air in the liquid water (the Henry’s law effect). Of the three the largest is due to the nonideality of the gas phase (the Van der Waals type interactions).

Given a real gas equation of state of a water vapor-air mixture, say an equation expressed in virial form, it is possible to derive theoretically an expression for the saturation water vapor content of the gas mixture as a function of the mole fraction of the constituents, the parameters of state, and the virial coefficients. In such a formulation, the air-water interactions are in large part characterized by the second cross virial interaction term for the air and water molecules. Unfortunately there are no definitive values for the second cross interaction virial coefficients, although previously obtained values [2] may be sufficient for some applications.

Attempts have been made to derive second cross interaction virial coefficients from statistical mechanics [4, 5]. However, the assumptions (form of potential) on which these derivations are based are far from exact so that the predicted coefficients are of limited value. What are needed are good experimental values of the second (cross) interaction coefficients. Recently, Hyland and Wexler [6] at NBS have reported precise experimental values of enhancement factors for water vapor in CO₂-free (CO₂ content on the order of 2 ppm) air at temperatures of 30, 40, and 50 °C. It is the purpose of this paper to use these new data, as well as the limited older data in the literature, in order to compute values of the second interaction virial coefficient. The formal derivations and basic experiments strictly apply to CO₂-free air. This limitation is unimportant when using the B_aw values in real air situations, as any errors introduced by the roughly 300 ppm of CO₂ molecules should be well within the limits caused by the uncertainties in B_aw.

2. Theory

2.1. General Considerations

We will derive an equation which relates the interaction virial coefficient to the enhancement factor, thermodynamic parameters of state, and several physical constants.²

Initially, it should be stated that the treatment of air as a single-component gas leads to no theoretical inconsistencies, for the following reasons: (1) Over the experimental range of temperatures, we can ignore chemical reactions. (2) The experiments involved a continuous air flow over the liquid surface, so that the molar ratios of the air components are constant, for all experimental conditions of pressure and temperature, once equilibrium has been established. (3) We deal with only the chemical potential of the water in each phase, and since the required chemical potential difference in the liquid phase depends only on the mole fraction of water (see eq (19)) and not on the amount of dissolved species, it doesn’t matter that the gas mixture dissolved in the water is of different composition than that of the gas-phase air. (This difference arises because the degree of absorption in water varies from one air component to the next.) Thus, in this paper, it will be assumed that air acts as a single component substance with a known molecular weight.

Let air be in thermodynamic equilibrium with a surface of the condensed water substance. The chemical potential μ_i of each component in the gas phase is equal to that in the condensed phase. For our purposes we need only examine the chemical potential of the water, thus

$${\mu }_w^g\left(T,P,n_w^g,n_a^g\right)={\mu }_w^c\left(T,P,n_w^c,n_a^c\right)$$ (1)

where superscripts g and c designate the gaseous and condensed phases, T is the thermodynamic temperature, P the total system pressure, $n_w^k$ (where k = g or c) is the number of moles of water, and $n_a^k$ is the number of moles of air. Water is a vapor in the gas phase, and either liquid or solid (ice) in the condensed phase.

In the equations which follow, the independent variables are always P, T, and $n_i^k$, whether stated explicitly or not. It will be understood that the variables which do not explicitly appear are being held constant, so that subscripts are unnecessary for that purpose.

Consider the difference in chemical potential in each phase between pressure states P₁ and P₂. We may write

$${\mu }_w^g\left(P_2\right)-{\mu }_w^g\left(P_1\right)={\mu }_w^c\left(P_2\right)-{\mu }_w^c\left(P_1\right).$$ (2)

We now write

$${\mu }_w^k=\frac{\partial G^k}{\partial n_w^k}$$ (3)

(see e.g., [7]) where G^k is the total Gibbs free energy of either the gas or condensed phase.

To obtain G^k we use the thermodynamic relationship

$$V^k=\frac{\partial G^k}{\partial P}$$ (4)

where V^k is the total volume of the phase. The Gibbs free energy difference between states P₁ and P₂, obtained by integrating eq (4), is

$$G^k\left(P_2\right)-G^k\left(P_1\right)=\underset{P_1}{\overset{P_2}{\int }}{V}^{k}dP.$$ (5)

Differentiating with respect to $n_w^k$ it follows that

$${\mu }_w^k\left(P_2\right)-{\mu }_w^k\left(P_1\right)=\frac{\partial }{\partial n_w^k}\left[G^k\left(P_2\right)-G^k\left(P_1\right)\right]=\left[\frac{\partial }{\partial n_w^k}\left(\underset{P^1}{\overset{P_2}{\int }}{V}^{k}dP\right)\right].$$ (6)

Substituting eq (6) into (2) yields

$$\left[\frac{\partial }{\partial n_w^g}\left(\underset{P_1}{\overset{P_2}{\int }}{V}^{g}dP\right)\right]=\left[\frac{\partial }{\partial n_w^c}\left(\underset{P_1}{\overset{P_2}{\int }}{V}^{c}dP\right)\right].$$ (7)

2.2. Gas Phase

The equation of state of a gas may be expressed in virial form as a power series in reciprocal molar volume

$$\frac{P_v}{RT}=1+\frac{B}{v}+\frac{C}{v^2}+\dots$$ (8a)

or as a power series in pressure

$$\frac{P_v}{RT}=1+B\text{'}P+C\text{'}{P}^2+\dots$$ (8b)

where P is the total pressure, T is the absolute thermodynamic temperature, ν is the molar volume, R is the gas constant, B and B′ are second virial coefficients, and C and C′ are third virial coefficients. In the enhancement measurements considered in this paper, volume is not one of the experimental parameters. For this reason eq (8b) is used in our derivation.

The virial coefficients of the pressure series are related to those of the volume series by

$$B\text{'}=\frac{B}{RT}$$ (8c)

and

$$C\text{'}=\frac{C-B^2}{{\left(RT\right)}^2}.$$ (8d)

The virial coefficients are functions only of temperature; those of eq (8a) are derivable from statistical mechanical relationships [8] if the form of the intermolecular potential is known. (A very large “if”, indeed! See, for example, Hanley and Klein [9]). The second virial coefficients may be considered to express the effects of interactions between two molecules, the third virial coefficients may be considered to express the effects of interactions among three molecules, and so forth. The number of terms or coefficients necessary to adequately represent Pv/RT will depend on the gas (or gases) involved and the PvT state.

If the gas under consideration is a mixture, then the coefficients B, C, B′, C′, etc., become mixture virial coefficients B_mix, C_mix, etc., and can be written in terms of the mole fractions of the pure components, the virial coefficients of the pure components, and quantities called interaction (cross) virial coefficients. For a two-component gas mixture, and in particular for water vapor-air mixtures, statistical mechanics shows that [8]

$$B_{\text{mix}}=x_a^2{B}_{aa}+2x_a{x}_w{B}_{aw}+x_w^2{B}_{ww}$$ (9a)

$$C_{\text{mix}}=x_a^3{C}_{aaa}+3x_a{x}_w^2{C}_{aww}+3x_a^{2}x{}_w{}^{}C{}_{aaw}+x_w^3{C}_{www}$$ (9b)

where x_a and x_w are the mole fractions of air and water vapor, B_aa and B_ww are the second virial coefficients for pure air and pure water vapor, and C_aaa and C_www are the third virial coefficients for pure air and pure water vapor. B_aw is the second interaction virial coefficient expressing the effects of interaction between an air molecule and a water molecule. C_aaw is the third interaction virial coefficient expressing the effects of interaction between two air molecules and one water molecule whereas C_aww is the third interaction virial coefficient expressing the effects of interaction between two water molecules and one air molecule.

The mole fractions of air and water vapor are given by

$$x_a=\frac{n_a}{n_a+n_w}$$ (10a)

and

$$x_w=\frac{n_w}{n_a+n_w}.$$ (10b)

The molar volume v_mix is related to the total volume V_mix by

$$V_{\text{mix}}=\left(n_a+n_w\right)v_{\text{mix}}$$ (10c)

where n_a and n_w are the number of moles of air and water vapor, respectively, in the total volume V_mix.

Substituting eqs (10), (9), (8c), and (8d) into (8b) we obtain

$$V\text{mix=}\left(n_a+n_w\right)\frac{RT}{P}+\left[\frac{n_a^2}{n_a+n_w}{B}_{aa}+\frac{2n_a{n}_w}{n_a+n_w}{B}_{aw}+\frac{n_w^2}{n_a+n_w}{B}_{ww}\right]+\left[\frac{n_a^3}{{\left(n_a+n_w\right)}^2}{C}_{aaa}+\frac{3n_a{n}_w^2}{{\left(n_a+n_w\right)}^2}{C}_{aww}+\frac{3n_a^2{n}_w}{{\left(n_a+n_w\right)}^2}{C}_{aaw}+\frac{n_w^3}{{\left(n_a+n_w\right)}^2}{C}_{www}-\frac{n_a^4}{{\left(n_a+n_w\right)}^3}{B}_{aa}^2-\frac{n_w^4}{{\left(n_a+n_w\right)}^3}{B}_{ww}^2-\frac{4n_a^3{n}_w}{{\left(n_a+n_w\right)}^3}{B}_{aa}{B}_{aw}-\frac{4n_a{n}_w^3}{{\left(n_a+n_w\right)}^3}{B}_{ww}{B}_{aw}-\frac{4n_a^2{n}_w^2}{{\left(n_a+n_w\right)}^3}{B}_{aw}^2-\frac{2n_a^2{n}_w^2}{{\left(n_a+n_w\right)}^3}{B}_{aa}{B}_{ww}\right]\frac{P}{RT}+.\dots$$ (11)

Now V_mix = V^g; therefore eq (11) may be substituted into the left-hand side of eq (7). We let P₁ be the pure phase saturation vapor pressure e_s(T) of the water substance and P₂ be any other greater total pressure P. When the total pressure P reduces to e_s, then x_a = 0 and x_w = 1. For the sake of simplicity, the superscript g will be deleted. After performing the integration and then the differentiation the left-hand side of eq (7) becomes

$$\begin{array}{l}\left[\frac{\partial }{\partial n_w}{\int }_{e_s}^P{V}_{\text{mix}}dP\right]=RT\text{ln}\frac{x_{w}P}{e_s}-x_a^2{B}_{aa}P+2B_{aw}{x}_a^{2}P+\left(P-e_s-x_a^{2}P\right)B_{ww}-\left(C_{www}-B_{ww}^2\right)\frac{e_s^2}{2RT}\\ +\left[C_{www}\frac{\left(1+2x_a\right){\left(1-x_a\right)}^2}{2}-C_{aaa}{x}_a^3+3C_{aww}{x}_a^2\left(1-x_a\right)-c_{aaw}\frac{3x_a^2\left(1-2x_a\right)}{2}-B_{ww}^2\frac{\left(1+3x_a\right){\left(1-x_a\right)}^3}{2}-B_{aa}{B}_{ww}{x}_a^2\left(1-3x_a\right)\left(1-x_a\right)+B_{aa}^2\frac{3x_a^4}{2}\right]\frac{P^2}{RT}\\ +\left[B_{aa}\frac{2x_a^3\left(2-3x_a\right)P^2}{RT}+B_{ww}\frac{6x_a^2{\left(1-x_a\right)}^2{P}^{{}^2}}{RT}\right]B_{aw}+B_{aw}^2\frac{2x_a^2\left(1-x_a\right)\left(1-3x_a\right)P^2}{RT}.\end{array}$$ (12)

The ratio $\frac{x_{w}P}{e_s}$ which appears in eq (12) will be called the “enhancement factor” and be designated by the symbol f. It has been variously called “the coefficient f,” “the function f,” and “the correction factor f” [2, 10, 11]. It is closely related to the “vapor concentration enhancement” of Haar and Sengers [3]. Thus

$$f=\frac{x_{w}P}{e_s}.$$ (13)

The quantity x_wP may be thought of as an “effective” vapor pressure of the water substance in a real gas mixture analogous to a partial pressure in an ideal gas mixture. As P approaches e_s, x_w approaches unity, and at P = e_s and x_w= 1, the enhancement factor f becomes unity.

2.3. Condensed Phase

We will confine our consideration of the condensed phase to the liquid state. Consider the right-hand side of eq (7) which expresses the difference in chemical potential for the water substance in the condensed phase between two pressure states P₁ and P₂. As before, we let P₁ be the pure phase saturation vapor pressure e_s(T) of the water substance and P₂ be any other greater pressure P. Performing the differentiation yields

$${\mu }_w^c\left(T,P,n_w^c,n_a^c\right)-{\mu }_w^c\left(T,e_s,n_w^c,0\right)=\frac{\partial }{\partial n_w^c}{\int }_{e_s}^P{V}^{c}dP$$ (14)

where V^c is the total volume of the condensed phase (i.e., liquid water containing dissolved air), and where we have emphasized that at P₁ = e_s, $n_a^c=0$. Thus

$${\mu }_w^c\left(e_s\right)={\mu }_w^1\left(e_s\right)$$ (15)

where ${\mu }_w^1\left(e_s\right)$ is the chemical potential of the pure phase liquid water substance at pressure e_s.

Consider now the pure phase (single component) liquid water substance at the same pressure states P and e_s. The difference in chemical potential is

$${\mu }_w^1\left(P\right)-{\mu }_w^1\left(e_s\right)={\int }_{e_s}^P{v}_w^{1}dP$$ (16)

where $v_w^1$ is the molar volume of pure phase liquid water.

Combining eqs (14), (15), and (16) yields

$${\mu }_w^c\left(P\right)-{\mu }_w^1\left(P\right)=\frac{\partial }{\partial n_w^c}{\int }_{e_s}^P{V}^{c}dP-{\int }_{e_s}^P{v}_w^{1}dP$$ (17a)

or

$$\frac{\partial }{\partial n_w^c}{\int }_{e_s}^P{V}^{c}dP={\int }_{e_s}^P{v}_w^{1}dP+{\mu }_w^c\left(P\right)-{\mu }_w^1\left(P\right).$$ (17b)

The laws of dilute solutions [7] predict that for a solution of dissolved air in water the chemical potential of the solvent, in this case liquid water, at pressure P differs from that of the pure phase of the same substance under the same pressure by an amount given by

$${\mu }_w^c\left(P\right)-{\mu }_w^1\left(P\right)=RT\text{ln}{x}_w^c+C$$ (18)

where $x_w^c$ is the mole fraction of water in the solution, and C is a corrective term expressing the excess chemical potential of a real solution over that predicted by the laws of ideal dilute solutions.

Substituting eqs (18) and (17b) into (14) one obtains

$${\mu }_w^c\left(P\right)-{\mu }_w^c\left(e_s\right)={\int }_{e_s}^P{v}_w^{1}dP+RT\text{ln}{x}_w^c+C.$$ (19)

Because $x_w^c+x_a^c=1$ we may write

$$\text{ln}{x}_w^c=\text{ln}\left(1-x_a^c\right).$$ (20)

For very dilute solutions³ Henry’s law may be used to calculate $x_a^c$, i.e.,

$$x_a^c=k\left(T,P\right)x_a^{g}P$$ (21)

where k(T, P) is the Henry’s law “constant” which is a function of T and P, and $x_a^g$ is the mole fraction of air in the gas phase.

The term C in eq (19) is given by [7]

$$C=W{\left(x_a^c\right)}^2$$ (22)

where W is a function of the interaction energies of the molecular species in the solution. The term C can be shown [see appendix 1] to be negligible in its contribution to B_aw and so is dropped from further consideration.

Equation (19) therefore becomes

$${\mu }_w^c\left(P\right)-{\mu }_w^c\left(e_s\right)={\int }_{e_s}^P{v}_w^{1}dP+RT\text{ln}\left(1-k{x}_a^{g}P\right).$$ (23)

Kell and Whalley [12] have shown that the specific volume of the pure liquid phase of the water substance can be represented with high accuracy by the following equation of state:

$$\frac{\overline{V}\left(t,P\right)}{\overline{V}\left(t,1\text{atm}\right)}=1+\sum _{i=0}^5\sum _{j=1}^3{\alpha }_{ij}{t}^i{\left(P-P_A\right)}^j.$$ (24)

where $\overline{V}\left(t,P\right)$ is the specific volume at temperature t (Celiuis) and pressure P, $\overline{V}\left(t,1\text{atm}\right)$ is the specific volume at temperature t and standard atmospheric pressure (1 atm), and P_A is standard atmospheric pressure. Kell [13] has shown also that

$$\overline{V}\left(t,1\text{\hspace{0.17em}atm}\right)=\frac{1+bt}{\sum _{n=0}^5{a}_n{t}^n}.$$ (25)

It therefore follows that

$$v_w^1=M_w\overline{V}\left(t,P\right)=M_w\left[1+\sum _{i=0}^5\sum _{j=1}^3{\alpha }_{ij}{t}^i{\left(P-P_A\right)}^j\right]\times \left[\frac{1+bt}{\sum _{n=0}^5{a}_n{t}^n}\right].$$ (26)

Let

$${\int }_{e_s}^P{v}_w^{1}dP=g\left(T,P\right).$$ (27)

Inserting eq (27) into (23) we obtain

$${\left[\frac{\partial }{\partial n_w^c}{\int }_{e_s}^P{V}^{c}dP\right]}_{T,n_a^c}={\mu }_w^c\left(P\right)-{\mu }_w^c\left(e_s\right)=g\left(T,P\right)+RT\text{ln}\left(1-k{x}_a^{g}P\right)$$ (28)

2.4. Second Interaction Virial Coefficient

By equating eq (12) and (28) and rearranging terms we obtain

$$\begin{array}{l}RT\text{ln}f=g\left(T,P\right)+RT\text{ln}\left(1-k{x}_{a}P\right)+B_{aa}{x}_a^{2}P-B_{ww}\left(P-e_s-x_a^{2}P\right)+C_{aaa}\frac{x_a^3{P}^2}{RT}+C_{aaw}\frac{3x_a^2\left(1-2x_a\right)P^2}{2RT}-C_{aww}\frac{3x_a^2\left(1-x_a\right)P^2}{RT}-B_{aa}^2\frac{3x_a^4{P}^2}{2RT}-C_{www}\frac{\left(1+2x_a\right){\left(1-x_a\right)}^2{P}^2-e_s^2}{2RT}-B_{aa}{B}_{ww}\frac{x_a^2\left(1-3x_a\right)\left(1-x_a\right)P^2}{RT}-B_{ww}^2\frac{e_s^2-\left(1+3x_a\right){\left(1-x_a\right)}^3{P}^2}{2RT}\\ +B_{aw}\left[-2x_a^{2}P-B_{aa}\frac{2x_a^3\left(2-3x_a\right)P^2}{RT}+B_{ww}\frac{6x_a^2{\left(1-x_a\right)}^2{P}^2}{RT}\right]-B_{aw}^2\frac{2x_a^2\left(1-x_a\right)\left(1-3x_a\right)P^2}{RT}.\end{array}$$ (29a)

For the sake of simplicity in nomenclature, all superscripts have been omitted, it being understood, however, that mole fractions x_a and x_w refer only to the gas phase. Let

$$\alpha =g\left(T,P\right)+RT\text{ln}\left(1-k{x}_{a}P\right)+B_{aa}{x}_a^{2}P-B_{ww}\left(P-e_s-x_a^{2}P\right)$$ (29b)

$$\beta =C_{aaa}\frac{x_a^3{P}^2}{RT}+C_{aaw}\frac{3x_a^2\left(1-2x_a\right)P^2}{2RT}-C_{aww}\frac{3x_a^2\left(1-x_a\right)P^2}{RT}-B_{aa}^2\frac{3x_a^4{P}^2}{2RT}-C_{www}\frac{\left(1+2x_a\right){\left(1-x_a\right)}^2{P}^2-e_s^2}{2RT}-B_{aa}{B}_{ww}\frac{x_a^2\left(1-3x_a\right)\left(1-x_a\right)P^2}{RT}-B_{ww}^2\frac{e_s^2\left(1+3x_a\right){\left(1-x_a\right)}^3{P}^2}{2RT}$$ (29c)

$$\gamma =\alpha +\beta$$ (29d)

$$D=-2x_a^{2}P$$ (29e)

$$\delta =B_{aa}\frac{2x_a^3\left(2-3x_a\right)P^2}{RT}-B_{ww}\frac{6x_a^2{\left(1-x_a\right)}^2{P}^2}{RT}$$ (29f)

$$\varphi =D-\delta$$ (29g)

$$\in =\frac{-2x_a^2\left(1-x_a\right)\left(1-3x_a\right)P^2}{RT}$$ (29h)

then

$$RT\text{ln}f=\gamma +\varphi B_{aw}+\in B_{aw}^2$$ (29i)

so that

$$B_{aw}=-\frac{\varphi }{2\in }-\frac{1}{2}{\left[{\left(\frac{\varphi }{\in }\right)}^2-\frac{4}{\in }\left(\gamma -RT\text{ln}f\right)\right]}^{1/2}$$ (30)

The quadratic term appearing in eq (29i) introduces a small correction into the calculated value of B_aw. Therefore the value of B_aw obtained from eq (29i) without that term must be nearly the same as that calculated from eq (30). It may be shown that this condition is satisfied only if the minus sign is used in front of the radical in eq (30).

3. Sources of Data

3.1. Virial Coefficients

There are several sources of data for the second and third virial coefficients of air [14, 15, 16]. Probably the best and most up to date values of B_aa are those of Sengers et al. [16] which cover the temperature range from 100 to 1400 K. Sengers et al. assign a standard deviation of 0.4 cm³/mol to B_aa. We have chosen three sigmas as our best estimate of the maximum systematic error, i.e., 1.2 cm³/mol. The Hilsenrath et al. [14] values of C_aaa are used here. These range from 90 to 1500 K. We have compared these values with those of Hall and Ibele [15] over temperatures from 0 to 100 °C, our range of interest. The two sets disagree by about 10 percent. This disparity was arbitrarily increased to 15 percent and assigned as the estimated systematic uncertainty in C_aaa.

The values given by Goff [2] are used for the second and third virial coefficients of water vapor. Wexler and Greenspan [17] recently have shown that from 0 to 100 °C the Goff values lead to highly precise correlations of theoretical and experimental values of saturation vapor pressure. Other second and third virial coefficients for water vapor are available but only those of Keyes [18] are both experimentally based and cover our experimental range of interest. Goff assigned tolerances to his values, which he stated were equal to twice his estimated probable error. These were converted to one-sigma errors, and compared to the differences between corresponding values of Keyes and Goff. For B_ww, the agreement between Keyes and Goff, below 70 °C, is better than 2 percent, while the Goff one-sigma uncertainties range from 8 to 2 percent between 30 and 60 °C. It was felt that the more conservative Goff uncertainties were appropriate here, and as estimates of the maximum systematic uncertainties in B_ww we used three-sigma errors. In the case of C_www below 70 °C, the Keyes and Goff values agree to about 45 percent, whereas the one-sigma errors computed from Goff range from 200 percent at 30 °C to 52 percent at 70 °C. These are felt to be overly conservative. Thus the difference between the Keyes and Goff values was taken as an estimate of the systematic uncertainty in Cwww.

Mason and Monchick [5] and Hyland and Mason [19] give the only known values of C_aaw and C_aww, respectively.⁴ These are theoretical calculations based on the Lennard-Jones (12–6) potential, the first covering the temperature range − 80 to + 300 °C, the second from 0 to 100 °C. For purposes of this analysis we ascribe an uncertainty of 50 percent in these values although there is no genuinely sound basis for this choice, and the errors may be larger.

Interpolation equations for the various virial coefficients are tabulated in appendix 2.

3.2. Saturation Vapor Pressure

The following equation, formulated by Wexler and Greenspan [17], is used to calculate e_s, the saturation vapor pressure of water:

$$\text{ln}{e}_s=\sum _{i=0}^5{E}_i{T}_{48}^{i-1}+B\text{ln}{T}_{48}$$ (31)

where T₄₈ is the absolute temperature on the International Practical Temperature Scale of 1948 [20, 21] and e_s is expressed in pascals.⁵ The coefficients E_i and B are given in table 1.

Table 1.

Coefficients to vapor pressure formulation eq (31)^a

E0	−7.51152 × 103
E1	9.65389644 × 101
E2	2.3998970 × 10−2
E3	−1.1654551 × 10−5
E4	−1.2810336 × 10−8
E5	2.0998405 × 10−11
B	−1.2150799 × 101

^aUnits: e_s, pascals; T, kelvins.

3.3. Function g(T, P)

The coefficients α_ij, a and b, given by Kell and Whalley [12] and Kell [13] are tabulated in table 2. These are needed in order to compute $v_w^1$ using eq (26) which, in turn, permits the computation of g(T, P) using eq (27). Kell and Whalley estimated that the standard deviation of the differences between observed values of $\overline{V}\left(T,P\right)/\overline{V}\left(t,1\text{\hspace{0.17em}atm}\right)$ and eq (24) does not exceed 10 ppm. Kell estimated that $\overline{V}\left(t,1\text{\hspace{0.17em}atm}\right)$, given by eq (25) has a standard error of 10 ppm or less for temperatures up to 100 °C.

Table 2.

Coefficients to eq (26)^a

	Coefficients αij
i╲j	1	2	3
0	−50.9769 × 10−6	8.2627 × 10−9	−9.109 × 10−13
1	3.71999 × 10−7	−1.3794 × 10−10	2.626 × 10−14
2	−7.01760 × 10−9	3.4032 × 10−12	−8.913 × 10−16
3	6.00227 × 10−11	−3.6432 × 10−14	11.467 × 10−18
4	−3.09041 × 10−13	2.0836 × 10−16	−7.102 × 10−20
5	5.93416 × 10−16	−4.1744 × 10−19	14.841 × 10−23
n	Coefficients an
0	0.9998396
1	1.8224944 × 10−2
2	−7.922210 × 10−6
3	−5.544846 × 10−8
4	1.497562 × 10−10
5	−3.932952 × 10−13
	Coefficient b
	1.8159725 × 10−2

^aUnits: t, °C; P, bar; P_A, 1.01325 bar; $v_w^1$, cm³/mol.

3.4. Constants

The solubility data of Winkler [22, 23] for air in water, as reported by Dorsey [24], was used to calculate the Henry’s law “constant” k at standard atmospheric pressure. In the absence of any known air data on the pressure dependence of this “constant,” it was assumed that the percentage changes in k between the same pressure levels at given temperatures were the same for air as for nitrogen, for which there are solubility data both at atmospheric pressure [25, 26, 27, 28], and at high pressure for temperatures above 20 °C [24, 29, 30]. Using solubility data for nitrogen in water and converting these to k, values for air were extropolated accordingly. Below 20 °C, solubilities of nitrogen in water were calculated using the method of Krichevsky and Kasarnovsky [31] and the fugacities reported by Demming and Shupe [32]. The polynomial

$${10}^{6}k=\sum _{i=0}^3{C}_i{t}^i$$ (32)

was fitted by the method of least squares to the Henry’s law “constant” for air in water at 1, 50, and 100 bars, where k is in units of mole fraction per bar, C_i are coefficients, and t is the temperature in degrees Celsius. Linear interpolations were employed between isobars. Values of k for nitrogen and air are given in table 3 and for C_i in table 4. The values of k for air are considered uncertain, at most, by 10 percent.

Table 3.

Henry’s law “constants” k for nitrogen and air dissolved in water^f

Temp. °C	Nitrogena			Air			Aire
	Pressure, bars			Pressure, bars			Pressure, bars
	1	50	100	lb	50c	100d	1	50	100
0	18.65	17.00	15.62	23.25	21.19	19.48	23.20	21.20	19.49
5	16.42	15.11	13.96	20.45	18.82	17.39	20.53	18.81	17.37
10	14.89	13.69	12.70	18.26	16.80	15.58	18.30	16.79	15.58
15	13.51	12.41	11.60	16.49	15.15	14.15	16.46	15.12	14.10
20	12.52	11.42	10.72	14.93	13.62	12.78	14.96	13.75	12.88
25	11.61	10.68	10.01	13.84	12.73	11.92	13.76	12.64	11.90
30	10.88	10.00	9.46	12.83	11.79	11.16	12.79	11.77	11.13
35	10.23	9.44	8.97	12.00	10.08	10.53	12.02	11.10	10.52
40	9.67	9.02	8.57	11.34	10.58	10.05	11.40	10.58	10.05
45	9.27	8.70	8.25	10.84	10.17	9.64	10.87	10.19	9.68
50	8.90	8.44	8.00	10.44	9.90	9.39	10.39	9.89	9.38

^aData based on solubilities in references [24, 25, 26, 27, 28, 29, 30].

^bData based on solubilities in references [22, 23, 24].

^cCalculated by assuming that the percent difference for air is the same as for nitrogen between 50 and 1 bars.

^dCalculated by assuming that the percent difference for air is the same as for nitrogen between 100 and 1 bars.

^eCalculated from eq (32).

^fUnits: k, 10⁻⁶ mole fraction per bar; P, bars.

Table 4.

Coefficients to eq (32)^a

i	Pressure, bars
	1	50	100
0	23.195	21.197	19.493
1	−0.58037	−0.51768	−0.46024
2	9.7392 × 10−3	8.2103 × 10−3	7.3781 × 10−3
3	−6.5058 × 10−5	−4.7585 × 10−5	−4.4401 × 10−5

^aUnits: t, degrees Celsius; k, mole fraction per bar.

On the unified carbon-12 scale the molecular weight of water M_w is 18.0154 g/mol with a maximum total uncertainty of 0.0009 g/mol [33]. The gas constant R is equal to 83.1434 bar cm³/mol K with a standard deviation of 0.0035 bar cm³/mol K [34].

3.5. Enhancement Factor

The NBS enhancement factor data [6] are given in table 5. It is estimated that the systematic uncertainty in f is 0.07 percent and the random uncertainty is 0.2 percent. Two 30°C runs, reported as being suspicious in [6], have not been considered for the calculation of B_aw.

Table 5.

Second interaction virial coefficients based on NBS enhancement data

Run No.	Saturation temp.	Saturation vap. press.	Total pressure	Mole fraction water vapor	Enhancement factor	Interaction virial coeff.	Normalized inter. vir. coeff.
	°C	mbar	bar			cm3/mol	cm3/mol
	t	es	P	xw	f	Baw	Baw
		Isotherm temperature, 30 °C
39	29.9994	42.4278	10.7312	0.0040827	1.0326	−29.962	−29.962
47	30.0065	42.4451	15.1088	.0029354	1.0449	−29.389	−29.392
42	29.9999	42.4290	19.9344	.0022534	1.0587	−29.115	−29.115
20	30.0112	42.4566	30.1929	.0015317	1.0893	−28.988	−28.944
40	29.9999	42.4290	35.5133	.0013201	1.1049	−28.763	−28.763
	Isotherm temperature, 40 °C
34	40.0104	73.8143	14.6417	0.0052456	1.0405	−26.286	−26.289
19	39.9969	73.7612	30.1957	.0026497	1.0847	−26.978	−26.977
27	39.9648	73.6350	40.4557	.0020231	1.1115	−26.124	−26.114
22	40.1505	74.3673	50.3962	.0016810	1.1392	−25.831	−25.876
21	40.1366	74.3122	60.9945	.0014285	1.1725	−26.158	−26.199
	Isotherm temperature, 50 °C
32	49.9898	123.3233	10.5512	0.0120190	1.0283	−23.443	−23.440
37	49.9942	123.3503	10.6310	.0119361	1.0287	−23.713	−23.711
36	50.0042	123.4115	10.7441	.0118214	1.0292	−23.915	−23.916
43	50.0047	123.4146	10.7546	.0117992	1.0282	−22.714	−22.715
46	49.9971	123.3680	10.7953	.0117446	1.0277	−21.977	−21.976
35	50.0011	123.3925	10.7989	.0117614	1.0293	−23.946	−23.946
31	49.9891	123.3191	14.6231	0.0087902	1.0423	−27.135	−27.132
33	50.0064	123.4250	14.8620	.0086263	1.0387	−23.399	−23.401
30	49.9967	123.3656	25.3585	.0051773	1.0642	−23.186	−23.185
17	50.0101	123.4477	30.1977	.0044266	1.0828	−25.846	−25.849
16	50.0050	123.4164	30.2324	.0044135	1.0811	−25.117	−25.118
29	50.0009	123.3913	36.5953	.0036782	1.0909	−22.605	−22.605
26	49.9766	123.2426	40.8462	.0033228	1.1013	−22.502	−22.495
23	50.0049	123.4158	50.3229	.0027681	1.1287	−23.227	−23.228
24	49.9784	123.2536	76.3139	.0019376	1.1997	−23.088	−23.082
28	49.9815	123.2726	96.9356	.0016749	1.2355	−22.298	−22.292
25	49.9788	123.2561	102.704	.0015264	1.2719	−22.483	−22.477

4. Results

Values of B_aw calculated from these data using eq (30) are given in table 5. The values were normalized from the experimental temperature to the nominal isotherm temperature. The changes, where they occur, are small.

Our best estimates of the magnitudes of B_aw and associated random uncertainties are represented respectively by the means of the normalized isotherm values and the standard deviations of the mean normalized values. These are reported in table 6, along with the standard deviations of the individual determinations.

Table 6.

Mean normalized second interaction virial coefficients ${\overline{B}}_{aw}$ based on NBS data

Isotherm Temp.	Mean normalized ${\overline{B}}_{aw}$	Standard deviation of single determination		Standard deviation of mean
°C	cm3/mol	cm3/mol	Percent	cm3/mol	Percent
30	−29.245	0.46	1.6	.21	0.7
40	−26.291	.41	1.6	.18	.7
50	−23.595	1.35	5.7	.33	1.4

5. Effect of Third Virial Terms

Statistical mechanics predicts that the virial coefficients are functions solely of temperature [8]. An apparent dependence of B_aw on pressure can be introduced via the calculations if a sufficient number of terms are not included in the truncated infinite series of the equation of state. If this equation were terminated at the second virial term rather than the third, the terms associated with the parameters ϵ, δ, and β would reduce to zero and from eq (29i) we would have

$$B_{aw}=\left(RT\text{ln}f-\alpha \right)/D.$$ (33)

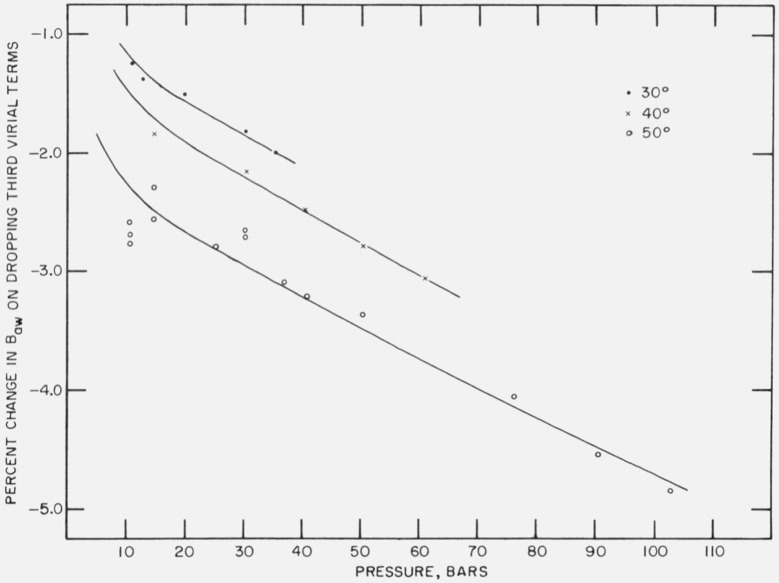
The change introduced by using eq (33) instead of (30) is significant as shown graphically in figure 1 using the NBS enhancement data. Because of this the third virial coefficients were included in the calculation of B_aw, even though there are large uncertainties associated with them. It will be shown that the accuracy in B_aw is relatively insensitive to the accuracies of the third virial coefficients.

Figure 1.

The percentage changes in calculated values of B_aw, when third virial terms are dropped from eq (30).

6. Error Analysis

An analysis was made of the effect of suspected systematic and random errors on the accuracy of the values of B_aw given in the results.

6.1. Enhancement Factor

It can be shown that the uncertainties in the experimental parameters P, e_s, and x_w contribute to the error in B_aw primarily from their appearance in the enhancement factor term and negligibility because of their presence in the other terms of eq (30).⁶ Therefore, for purposes of error analysis, the higher order virial coefficients may be neglected and eq (33) used with adequate accuracy for examining the effect of an error in f on B_aw. Differentiating B_aw with respect to f, replacing the differential with finite increments, and considering only magnitudes, we obtain

$$\mathrm{\Delta }{B}_{aw}=\frac{RT}{2P{x}_a^{2}f}\mathrm{\Delta }f\approx \frac{RT}{2P}\frac{\mathrm{\Delta }f}{f}$$ (34)

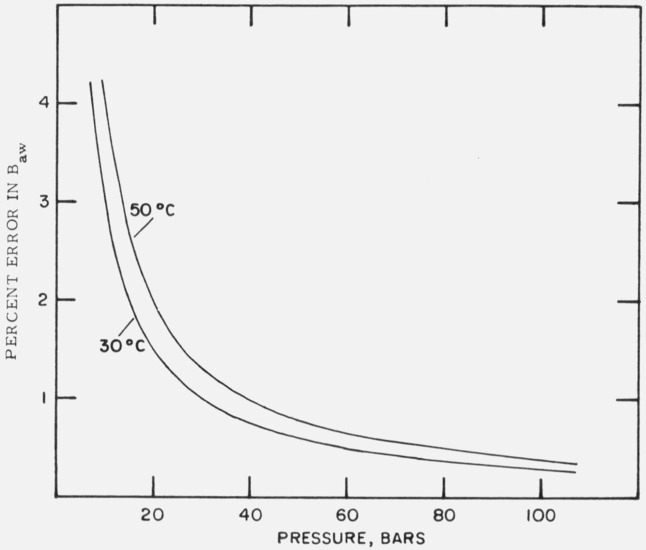
where x_a is assumed roughly equal to unity. The systematic uncertainty in the NBS values of enhancement factor is 0.07 percent [6]. By substituting this into eq (34), and using the mean values of B_aw given in table 6 to convert ΔB_aw to percent, the curves shown in figure 2 were generated. It may be noted that for a fixed relative uncertainty in f the corresponding uncertainty in B_aw decreases with increasing pressure. This relationship suggests that for interaction virial coefficient determinations it would be advantageous to perform enhancement measurements at high pressures. However, as we will show below, this gain in accuracy is offset by the increasing uncertainties contributed by the terms in eq (30) containing the third virial coefficients.

Figure 2.

Percentage errors in B_aw as a function of temperature and pressure, arising from the estimated systematic error of 7 parts in 10⁴ in the enhancement factor.

6.2. Virial Coefficients

The effects of the estimated systematic uncertainties in the virial coefficients (given in sec. 3.1) on B_aw were calculated using eq (30). The results are given in table 7 at the experimental pressures and temperatures.

Table 7.

Estimated systematic uncertainties in B_aw

Temp.	Press.	Source of error								Quadraturee
		Baa	BWW	Caaa	CWWW	Caaw	Caww	f	Other	Virial coefficient errors only	All errors
		Estimated error in parameter, percent
		(a)	(b)	15	(c)	50	50	.07	(d)
°C	bar	Estimated error in Baw, percent								Estimated error in Baw, percent
30	10.7	2.0	1.9	0.14	0.05	0.42	0.42	2.8	0.14	2.8	4.0
	19.9	2.0	1.1	.26	.03	.81	.45	1.5	.14	2.5	2.9
	35.5	2.0	.68	.47	.02	1.4	.47	0.85	.14	2.6	2.7
40	14.6	2.2	1.6	.20	.08	.62	.66	2.4	.14	2.9	3.7
	40.5	2.1	.66	.56	.04	1.7	.71	.85	.14	2.9	3.0
	61.0	2.1	.48	.84	.03	2.6	.75	.57	.14	3.6	3.6
50	10.6	2.6	2.5	.16	.21	0.46	.98	3.8	.14	3.8	5.4
	25.4	2.5	1.1	.38	.10	1.2	1.0	1.6	.14	3.2	3.6
	50.3	2.4	0.64	.76	.06	2.3	1.1	0.79	.14	3.6	3.7
	76.3	2.3	.48	1.2	.04	3.5	1.2	.52	.14	4.5	4.6
	103	2.3	.40	1.6	.04	4.8	1.2	.39	.14	5.7	5.7

^aEstimated 3σ error is 1.2 cm³/mol; error is 17, 23, and 34 percent at 30, 40, and 50 °C, respectively.

^bEstimated error is 24, 16, and 11 percent at 30, 40, and 50 °C, respectively.

^cEstimated error is nominally 43 percent at 30, 40, and 50 °C.

^dQuadrature of errors contributed by Henry’s law, gas constant, and ignoring the correction to the law of ideal solutions.

^eComputed by the square root of the sum of the squares of the individual terms.

6.3. Henry’s Law

It is shown in appendix 1 that dropping the correction term C to Henry’s law, (eq (22)), may lead to an uncertainty in B_aw of about 0.13 percent. An uncertainty is contributed also by the “constant” k. The second interaction virial coefficient may be written as follows:

$$B_{aw}\approx \frac{-RTk{x}_{a}P}{2x_{a}P}+\text{various}terms.$$ (35)

Hence, neglecting the sign,

$$\mathrm{\Delta }{B}_{aw}\approx \frac{RT}{2}\mathrm{\Delta }k\approx 13000\mathrm{\Delta }k.$$ (36)

The estimated uncertainty in k is 10 percent. Over the pressure and temperature range of the NBS data, the variation in k is small. With sufficient accuracy for this calculation, Δk = 1.1 × 10⁻⁶ and therefore ΔB_aw = 0.014 cm³/mol. Assuming a nominal magnitude of 26 cm³/mol for B_aw, k induces an uncertainty in B_aw of about 0.05 percent.

6.4. Function g(P, 7); Gas Constant

The largest contributions from the term g(P, T) to the uncertainties in B_aw arise from uncertainties in the specific volume of water $\overline{V}\left(t,P\right)$ and the molecular weight of water, while the largest contribution from the gas constant R arises through the enhancement factor term. The uncertainties in P and t in the NBS data are insignificant in their effect on$\overline{V}\left(t,P\right)$. The systematic errors in $\overline{V}\left(t,P\right)$, M_w, and R (secs. 3.3 and 3.4) likewise produce negligible uncertainties in the calculated values of B_aw.

6.5. Estimated Systematic Uncertainty in B_aw

The estimated systematic uncertainties in the individual parameters at the experimental values of P and T are summarized in table 7. These were combined by quadrature to give the estimated overall systematic uncertainty in B_aw. Two quadrature columns are shown. The left column is the estimated uncertainty in the calculated value of B_aw contributed solely by the virial coefficient terms whereas the right column is the estimated uncertainty in B_aw due to all suspected sources of systematic error. Along each isotherm, as the effect on B_aw from the fixed percentage uncertainty in enhancement factor decreases with pressure, the effect from the uncertainties in the virial coefficients increases in such a way as to keep the overall systematic uncertainty in B_aw more or less constant over the pressure range considered. The systematic uncertainty increases from 4 percent at 30 °C to 6 percent at 50 °C, and applies to the mean value of B_aw as well as to the individual values.

6.6. Estimated Random Uncertainty in B_aw

The experimental standard deviations of the single determinations and of the mean value of B_aw have been given (table 6) as our best estimates of the random uncertainties in B_aw. The random uncertainty in B_aw arises mainly from the random error in the enhancement factor. The latter, based on the residual standard deviations of fits of f to a pressure function, is 0.02 percent at 30 °C, 0.13 percent at 40, and 0.26 percent at 50 °C [6]. The corresponding calculated uncertainty in a single B_aw determination, as a function of pressure along each isotherm, is indicated in table 8. Also given for each isotherm is a mean single-determination uncertainty, based on the three tabulated values. This calculated mean value should be comparable to the experimentally determined precision of a single B_aw determination. The latter values are repeated in table 8, and it is seen that the calculated and experimental random uncertainties are in reasonably good agreement.

Table 8.

Comparison of estimated random uncertainties in a single determination of B_aw

Temp.	P	Random uncertainty in Baw
		Based on random error in fa	Based on preci-cision of Baw
°C	Bar	Percent	Percent
30	10.7	0.80
	19.9	.43
	35.5	.24
	Mean 0.49		1.6
40	14.6	4.4
	40.5	1.6
	61.0	1.1
	Mean 2.4		1.6
50	10.6	14.0
	25.4	5.8
	50.3	2.9
	76.3	1.9
	103	1.4
	Mean 5.2		5.7

^aThe standard deviation of a single determination of f is 0.02 percent at 30 °C, .13 percent at 40 °C, and 0.26 percent at 50 °C. [6].

7. Comparisons

There are three known experimental determinations of the enhancement of water vapor in air from which the interaction virial coefficient may be calculated. Politzer and Strebel [35] performed single saturation isotherm experiments at 50 and 70 °C at total pressure up to 200 bars. Webster [36] obtained values at −35, −20, 0 and 15 °C at total pressures up to 200 bars, also using the single isotherm saturation method. Goff et al. [37, 38, 39] measured a quantity closely related to the interaction virial coefficient, from 5 to 25 °C at total pressures near one bar.

Values of B_aw were computed from the Politzer and Strebel data using the same procedures, constants and virial coefficients that had been used with the NBS data. The 50 °C data of Politzer and Strebel yielded values of B_aw that appear to scatter independently of pressure around an average value, except for four points at 12 bars and below. These four points are suspect and so were discarded. The mean and the standard deviation of the mean are given in table 9. The 70 °C data of Politzer and Strebel show a strong monotonic pressure dependence, contrary to the predictions of theory. It is probable that there is a significant systematic error in the measurements although the source of this error is not obvious. Because of this, the 70 °C data were excluded from further consideration.

Table 9.

Interaction virial coefficients from literature data

Temperature °C	Source
	Webster		Politzer and Strebel		Goff		Mason and Monchick	Chaddockb
	$-{\overline{B}}_{aw}$ cm3/mola	${}^{\sigma }{\overline{B}}_{aw}$ cm3/mol	$-{\overline{B}}_{aw}$ cm3/mola	${}^{\sigma }{\overline{B}}_{aw}$ cm3/mol	−Baw cm3/mol	σ Baw cm3/mol	−Baw cm3/mol	−Baw cm3/mol
−35	64.91	7.45
−20	50.15	3.96			48.2	3.2
0	38.01	1.92			42.0	3.0	50.4	62.0
10					39.3	3.0	47.3	58.1
15	34.91	3.44			37.6	2.9	45.4	56.1
20					36.8	2.9	43.9	54.4
30					34.5	2.8	41.0	51.1
40					32.3	2.7	38.2	48.1
50			23.16	0.39	30.4	2.7	35.8	45.2
60					28.5	2.6	33.5	42.5

^a${\overline{B}}_{aw}$ = mean value along an isotherm.

^bNeither Mason and Monchick nor Chaddock assigns an uncertainty to his theoretical values of B_aw.

B_aw was computed similarly from Webster’s data for each of his isotherms. At −35 and −20 °C a minor change was introduced into the calculations to allow for the solid state ot the condensed phase. This involved the use for the Henry’s law “constant” the value for water at 0 °C and 1 bar and for e_s the appropriate values of saturation vapor pressure with respect to ice [40]. The resultant error from the choice of k is negligible; in fact, within the uncertainty of the Webster measurements the Henry’s law “constant” could be ignored. The mean value of B_aw for each temperature, and the standard deviation of the mean are given in table 9.

A set of B_aw values were calculated by an empirical equation given by Goff [2], and converted to units consistent with those employed in this paper. The standard deviation ascribed to the Goff values were derived from the tolerances he assigned, which were stated to be two times the estimated probable error. The values are given in table 9.

No attempt was made to estimate the systematic errors in the above values of B_aw. The standard deviations indicate only the precision of the measurements.

Mason and Monchick [5] and Chaddock [4] have made statistical mechanical calculations of B_aw by assuming that the forces between air and water vapor molecules can be represented by the Lennard-Jones (12–6) potential and that the separate species potential parameters ϵ₀ (the depth of the potential “well”) and σ₀ (molecular “diameter”) can be combined by simple combination rules. Their calculations have been extended to encompass our temperature range of interest and the values so obtained are given in table 9.

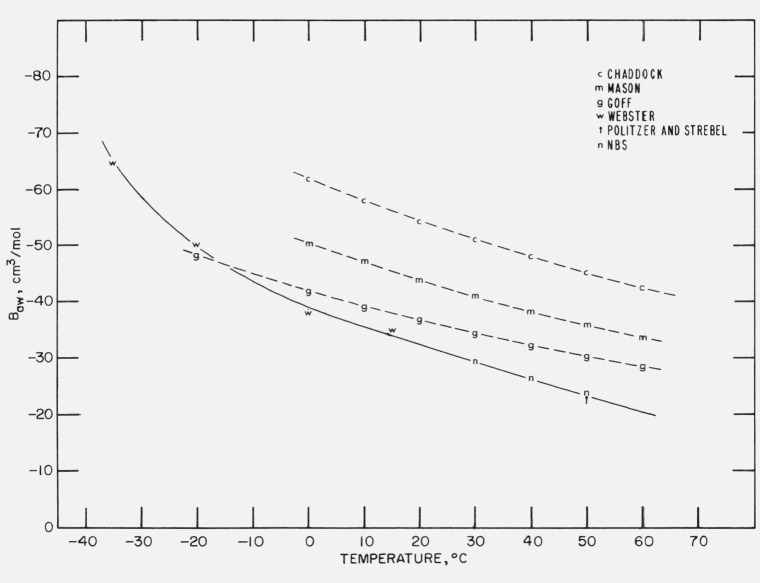
These several sets of values of B_aw are compared graphically in figure 3. The curves representing the Goff, Mason and Monchick, and Chaddock values are similar in shape but displaced from each other. It is not surprising that the curves are alike for they are based on similar theoretical formulations, but with somewhat different potential constants. Even Goff’s empirical equation is based on values calculated from a potential function similar to the Lennard-Jones that had been adjusted to yield results consistent with his experimental data [39]. The NBS values of B_aw are smaller in absolute value than these other three sets of values. Although the NBS, Webster and the 50 °C Politzer and Strebel values appear to fall on a smooth curve, this may be fortuitous. Until there is additional experimental corroboration, this apparent consistency should be viewed with reservation.

Figure 3.

B_aw versus temperature, from various investigators.

8. Smoothing Function

Given experimental values of B_aw over a reasonable temperature range, it is feasible to determine the form of the interaction potential between the water vapor and air species and therefore, to derive a theoretically based expression for interpolation and extrapolation of B_aw. Unfortunately the NBS data is too limited in temperature range to warrant this approach.

A polynomial equation was fitted, therefore, to the NBS, Politzer and Strebel, and Webster data. The resultant expression is as follows:

$$-B_{aw}=\sum _{i=0}^4{D}_i{t}^i$$ (37)

where D_i are empirical coefficients, t is the temperature in deg Celsius and B_aw is in units of cm³/mol. D_i are listed in table 10, along with the residual standard deviation of the fit. The experimental and predicted values are compared in table 11.

Table 10.

Coefficients to eq (37)

D0	38.9221
D1	−.384587
D2	+.512266 × 10−2
D3	−.117467 × 10−3
D4	+.878093 × 10−6
σres	.842 cm3/mol

Table 11.

Comparison of experimental and predicted values of B_aw

Temperature	Interaction virial coefficient		Difference		Standard deviation of mean		Source
°C	Experimental	Predicteda	Pred.—Exp.		Experimental
	cm3/mol	cm3/mol	cm3/mol	Percent	cm3/mol	Percent
−35	−64.91	−65.01	−0.11	−0.17	7.45	11.5	Webster [36].
−20	−50.15	−49.74	+0.41	+0.82	3.96	7.9	Webster ,36].
0	−38.01	−38.92	−0.91	−2.34	1.92	5.1	Webster [36].
15	−34.91	−33.95	+0.96	+2.75	3.41	9.8	Webster [36].
20		−32.48
30	−29.24	−29.53	−0.29	−0.99	0.21	0.7	NBS.
40	−26.29	−26.47	−0.17	−0.65	0.18	0.7	NBS.
50	−23.56	−23.30	+0.26	+1.10	0.33	1.4	NBS.
50	−23.16	−23.30	−0.14	−0.60	0.39	1.7	P & S [35].
60		−20.30

^aCalculated using eq (37).

The differences between the experimental and predicted values are well within the standard deviation of the mean of the experimental values. The maximum deviation of this equation from NBS values of B_aw is 1.1 percent.

Equation (37) is offered as a suitable smoothing function for B_aw that is valid from 30 to 50 °C, the temperature range of the NBS experiments. We feel confident in using it from 10 to 60 °C. Because it fits the Webster data well, and within the uncertainty of that data, the equation may be used to −35 °C. However, it should be noted that the systematic uncertainty in the Webster data is unknown so that the reliability of the predicted B_aw in the temperature range below, say, 10 °C is unresolved.

9. Appendix 1

For a two component solution of equal-size molecules, such as air dissolved in water, it can be shown [7] that

$$W\left(n_a+n_w\right)x_a{x}_w=\mathrm{\Delta }{G}_{\text{mix}}^E$$ (38)

where $\mathrm{\Delta }{G}_{\text{mix}}^E$ is the excess Gibb’s function⁷, that is, the departure from that predicted through Raoult’s law; n_a and n_w are the total number of moles of air and water; and x_a and x_w are mole fractions of air and water. The parameter W is given by [7]

$$W=\frac{Z{N}_0}{2}\left(2{\in }_{aw}-{\in }_{aa}-{\in }_{ww}\right)$$ (39)

where Z is a lattice coordination number (assuming a local crystal structure), N₀ is Avogadro’s number, ϵ_ij are interaction energies between the designated molecular species.

Let the mole fractions x_i in eq (38) be converted to moles n_i. Differentiating with respect to n_w we obtain.

$$\frac{\partial \left(\mathrm{\Delta }{G}_{\text{mix}}^E\right)}{\partial n_w}=W{x}_a^2.$$ (40)

This equation gives the excess chemical potential of the water with dissolved air over that predicted from Raoult’s law and is therefore equivalent to the term C in eqs (18), (19), and (22).

Mason and Monchick [5] and Chaddock [4] both give ϵ_aa/k = 99.2 K and ϵ_ww/k = 380 K (where k is Boltzmann’s constant). Mason and Monchick give values of 194 and 222 K for ϵ_aw/k, as determined from second virial coefficient data and viscosity data respectively whereas Chaddock gives 220.5 K. For the present purpose, assume ϵ_aw/k = 210 K. If a coordination number of 15 (which should lead to a conservatively large estimate of C) is assumed, then W is −3.69 × 10⁴ bar cm³/mol. Suppose that this is in error by a factor of 5, then W might be of the magnitude −1.84 × 10⁵ bar cm³/mol.

The mole fraction of air dissolved in water x_a may be estimated from Henry’s law using the constants in table 3. The worst case (i.e., the largest value of x_a which, in turn maximizes C) occurs at 0 °C and 100 bars. Using this value for x_a and W = −1.84 × 10⁵ atm cm³/mol, the magnitude of C is then 0.7 bar cm³/mol.

Equation (30), with the C term included, can be approximated by

$$B_{aw}\approx \left[\text{Various\hspace{0.17em}terms}\right]-\frac{g\left(T,P\right)}{2P}-\frac{C}{2P}$$ (41)

The lowest pressure present in the NBS enhancement data is 10 bars. The maximum contribution of C to B_aw, therefore, is about 0.035 cm³/mol. For B_aw of the order of 26 cm³/mol, the relative contribution of C to B_aw is about 1.3 parts in 1000, which is about one order of magnitude smaller than the estimated uncertainty in B_aw.

10. Appendix 2

The equations for the virial coefficients for water are essentially those of Goff [2]. B_ww is given here with opposite sign to conform to eq (8a). C_www is a modification of Goff’s equation to conform to eq (8a). Goff suggests the use of his equation for C_www only at temperatures 60 to 100 °C whereas we extropolate it to − 20 °C. Although this is a potentially dangerous procedure, no other alternative is available.

The equations for the virial coefficients B_aa and C_aaa were obtained by fitting the Sengers et al. data [16] and the Hilsenrath et al. data [14] respectively, over the temperature range 260 to 380 K, to polynomials.

The equations for the interaction virial coefficients C_aaw and C_aww were similarly obtained by fitting the Mason and Monchick [5] values from − 20 to + 120 °C and the Hyland and Mason [19] values from 0 to 100 °C, respectively, to polynomials.

The standard deviations of the fits for the latter four equations are given. These equations are; convenient empirical relationships and it is not intended that they be used beyond the fitted temperature ranges.

$$B_{ww}=33.97-\frac{55306}{T}\times {10}^{\frac{72000}{T^2}}{\text{cm}}^3/\text{mol}$$

$$C_{www}=2.85558\frac{B_{ww}^3}{T}+B_{ww}^2{\text{cm}}^{\text{6}}/{\text{mol}}^{\text{2}}$$

$$B_{aa}=-13.521+0.24234t-0.10022\times {10}^{-2}{t}^2+0.26880\times {10}^{-5}{t}^3{\text{cm}}^3/\text{mol;\hspace{0.17em}}\sigma \text{=0}\mathrm{.024}$$

$$C_{aaa}=1314.2-0.89453t-0.36372\times {10}^{-2}{t}^2+-.48378\times {10}^{-4}{t}^3-0.18897\times {10}^{-6}{t}^4{\text{cm}}^6/{\text{mol}}^{\text{2}};\sigma =0.17$$

$$C_{aaw}=860.79-2.4203t+0.92144\times {10}^{-2}{t}^2-0.14568\times {10}^{-4}{t}^3{\text{cm}}^{\text{6}}/{\text{mol}}^{\text{2}};\sigma =0.32$$

$$C_{aww}\times {10}^{-6}=-0.20263+0.52695\times {10}^{-2}t-0.74761\times {10}^{-4}{t}^2+0.57576\times {10}^{-6}{t}^3-0.18065\times {10}^{-8}{t}^4{\text{cm}}^{\text{6}}/{\text{mol}}^2;\sigma =0.614\times {10}^{-3}$$

$$T=t+273.16,t=\text{degrees Celsius}.$$