The Enhancement of Water Vapor in Carbon Dioxide-Free Air at 30, 40, and 50 °C

Abstract

The enhancement of water vapor in compressed atmospheric air was measured at 30, 40, and 50 °C over respective pressure ranges of 10 to 35 bars, 15 to 60 bars, and 10 to 100 bars. The data for each isotherm were fitted by the method of least squares to an empirical smoothing equation of the form ln f = a + bP where f is the enhancement factor, P is the total (absolute) pressure and a and b are constants. A detailed error analysis, necessary for the eventual use of the data in humidity standards work, shows that the calculated (predicted) values of f have an estimated limit of systematic bias of ±0.07 percent and a maximum observed standard deviation of a predicted value of ±0.2 percent.

1. Introduction

The saturation concentration of water vapor over the flat surface of its pure condensed phase is an accurately known function of temperature [1].¹ If now a second gas is introduced over the surface of the water, the saturation concentration of the water vapor is increased. At any given temperature this increase may be expressed as a ratio of the vapor concentration at the total system pressure in the presence of the second gas to the vapor concentration of the pure phase. This ratio, sometimes called the enhancement factor, is expressed by

$$f_{\rho }=\frac{{\rho }_w}{{\rho }_w^0}$$ (1)

where ρ_w is the saturation vapor concentration or density in the presence of the second gas and ${\rho }_w^0$ is the saturation vapor concentration or density of the pure phase.

The enhancement factor may also be expressed by

$$f_n=\frac{N_w}{N_w^0}$$ (2)

where N_w is the saturation molar concentration or density in the presence of the second gas and $N_w^0$ is the saturation molar density of the pure phase, and by

$$f_p=\frac{X_{w}P}{P_w^0}=\frac{X_{w}P}{e_s}$$ (3)

where X_w is the mole fraction of water vapor in the given water vapor-gas sample, $P_w^0$ is the saturation vapor pressure of the pure phase, and P is the total pressure of the system. In accordance with meteorological convention, $P_w^0$ is designated by e_s.

At any temperature, as the amount of the second gas goes to zero, the enhancement factor approaches unity. Furthermore, the expressions would be equivalent, at the same conditions of pressure and temperature, only if the ideal gas laws were valid. In this work the enhancement factor as defined by eq (3) will be used exclusively. The subscript will be dropped and the enhancement factor will be designated simply by the symbol f.

Deviations of water vapor concentrations in air from those predicted by ideal gas laws are on the order of 0.5 percent at pressures as low as 900 mb [2], making widespread use of experimentally based enhancement factors important in such areas as industrial drying processes operating at high pressures, especially in the performance of dehydration plants for compressed natural gases [3, 4, 5]. Enhancement factors are employed in hygrometry to compute the water vapor content of gases and to make accurate conversions among parameters used to express humidity [6], to calibrate hygrometers against humidity standards [7, 8], and to make precise calculations in the fields of meteorology and air conditioning [9]. From experimental enhancement factors it is possible to derive the cross-virial terms in the virial equation of state [10].

Experimental data on the enhancement of water vapor in air are meager. Politzer and Strebel [11] made measurements at 50 and 70 °C at total pressures up to 200 bars.² Webster [12] made similar measurements from −35 to +15 °C at total pressures up to 200 bars. Goff, Andersen, Gratch, and Bates [2, 10, 13, 14, 15] performed enhancement experiments from 5 to 25 °C at or near atmospheric pressure. Although enhancement measurements of water vapor in other gases have been made, the data are also very limited [3, 4, 5, 16, 17, 18].

Accurate determinations of enhancement factors are difficult to make. Dynamic rather than static experimental systems are required to avoid the insidious problems of water sorption and desorption on the walls of the system. Two approaches have been used by other researchers to obtain experimental values: the single saturation isotherm method and the double saturation isotherm method. In the first method, which we use for the work reported in this paper, the inert (indifferent) carrier gas is saturated with respect to the condensed water substance at a fixed temperature and pressure. The resultant moisture content is determined, typically, by removing the water vapor from the gas by a desiccant, weighing the collected moisture and measuring the volume or mass of the associated dry gas.

The double isotherm experiment, described by Goff and Bates [13], is basically two single isotherm experiments in series. The same air mass is used for two successive saturations at a fixed temperature but different pressures. The calculations involve a ratio from which the air mass is eliminated. The method does not give a direct measurement of enhancement factor but rather yields the “interaction constant,” a quantity closely related to the cross virial coefficient from which the enhancement factor may be calculated [13, 14].

This paper is a progress report on a continuing experimental determination of the enhancement factor for water vapor in air. Measurements have been made at three temperatures, namely 30, 40, and 50 °C, and over a range of pressures from 10 to 100 bars. Our objective, at this time, is to describe the experimental method used and to present the data obtained thus far.

2. Apparatus

For our single isotherm experiment, the apparatus consists of two basic units: a generator in which air is saturated under known conditions of temperature and pressure, and the NBS standard hygrometer which permits the determination of the ratio of the mass of water to the mass of air in the effluent from the generator. The mole fraction of water vapor is calculated from the mass ratio, while the saturation vapor pressure is obtained, from the temperature, through a mathematical formulation such as in [1]. The generator operates in a dynamic mode, producing a continuous stream of saturated air. Repeated measurements of pressure and temperature are made during a run which, coupled with the mole fraction determination, permit a value of enhancement factor to be calculated which is an average over the experimental time.

2.1. Flow and Saturation System

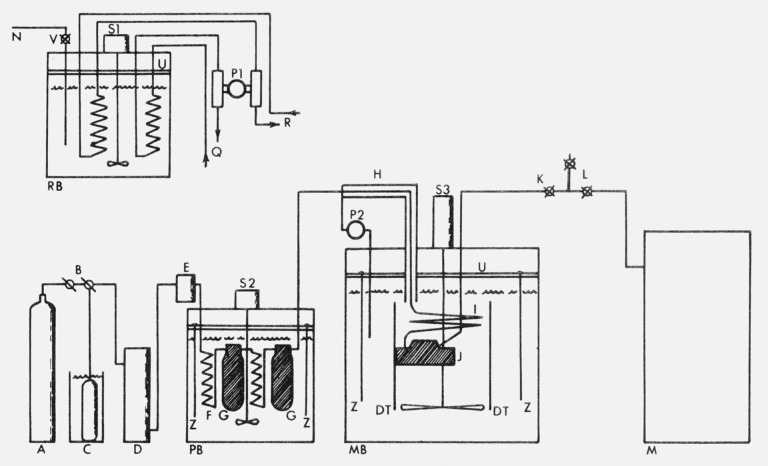
The flow chart of the apparatus is shown in figure 1. There are three baths, two of which, PB and MB, are directly involved with the air stream while the third, RB, is used in controlling the temperature of the other two. Air is supplied from cylinders A, used either singly or manifolded in parallel, and flows between components through $\frac{3}{8}$ -in o.d. stainless steel tubing. The pressure is set with two pressure-loaded (dome) reducers B in series. From these pressure reducers the air passes through a carbon dioxide removal unit D. The CO₂ is removed to prevent any possibility of the natural variability of CO₂ in the air from affecting the results. From this unit the air passes through a two-micron filter E, then into a preliminary saturation system which is immersed in a bath PB that is controlled at 3 to 5 °C above the temperature of the main bath MB.

Figure 1.

Flow diagram and apparatus arrangement; components not mentioned by Letter in the text are the preliminary bath heat exchanger (F); the preliminary saturators (G); shut-off valves (L); coolant lines to and from PB and MB (Q, R); and splash plates for each bath (U).

The wet air emerges from the preliminary bath and passes into a heated portion of the line which is maintained 20 to 30 °C above the test temperature to insure against condensation. This hot moist air is now brought to the temperature of the main bath MB. Near the main bath the tubing carrying the test gas enters a counter-current heat exchanger H in which water from the temperature-controlled main bath is pumped through a jacket surrounding the tubing. The heater, which keeps the tubing from the preliminary bath to the water jacket hot, also surrounds the water jacket to prevent the water from cooling in its course through the heat exchanger. From the counter-current heat exchanger the air enters the inlet heat exchanger coil I in the main bath. The coil is a 10-meter length of $\frac{3}{8}$ -in o.d. stainless steel tubing which fits inside a draft tube DT. From this coil the gas, which is now within several thousandths of a degree of, and very close to saturation with respect to, the main bath temperature, enters the main saturation system.

The preliminary saturation system and the main saturation system used for working pressures above 30 bars are bubbler-type systems, and are made up of one-liter capacity stainless steel cylinders filled with layers of glass beads. The preliminary system consists of two, and the main system of three, such cylinders, the cylinders of each system being interconnected with 3-meter length heat exchanger coils. (The main saturation system J of figure 1 represents the low pressure system to be discussed below.)

The general configuration of the cylinders is shown in figure 2. The particular unit illustrated is the final main saturator unit which is similar to the other configurations except for the addition of the thermometer lead-in tube E, thermometer well F, and pressure tap D. In each cylinder, water is added (and removed) through a filling tube G connected to the bottom of the cylinder. The air enters the saturator at A through an inlet tube and discharges radially through 50 orifices B near the bottom of the saturator. The air bubbles through the water and is dispersed by the glass beads for more effective saturation.

Figure 2.

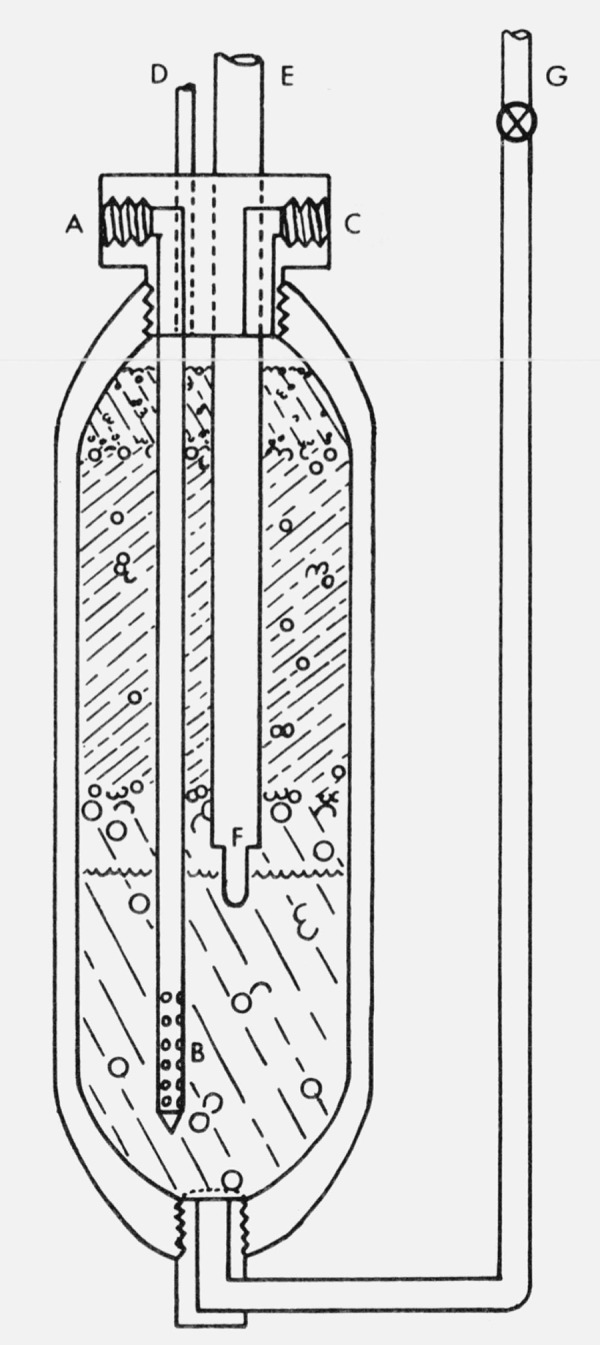
Final main bubbler saturator, indicating the three bead layers and water level as well as the inlet port (A); exit holes into the water (B); outlet port (C); pressure tap (D); thermometer lead-in tube (E); thermometer well (F); and the tube for adding and removing water (G).

A stainless steel screen prevents the beads from dropping into the filling tube.

In order to obtain optimum dispersal and eliminate splashing and spray above the bead level, a series of visual experiments was run on glass prototype saturators using various water depths, bead depths, and bead sizes before selecting the final configuration. There are two bead layers in the preliminary saturators and three in the main saturators. In each case the lower layer consists of 6-mm o.d. solid borosilicate spheres, while the second layer consists of 4-mm o.d. borosilicate glass beads, each perforated with a small hole for larger surface area. The third layer, used only in the main saturators, consists of 2-mm o.d. solid borosilicate glass spheres.

For pressures below 30 bars a single stainless steel dish or maze saturator, illustrated in figure 3, is used in lieu of the three bubbler type saturators. An interconnecting series of $\frac{7}{16}$ in (1.1 cm) wide concentric grooves is machined into the lid, so that when the lower portion, or dish, and lid are mated and water added, the grooves and water surface form channels through which the air flows on its way to the center. The air traverses a path over the water surface which is 75 cm long. The normal working condition is such that the distance between water surface and lid is about $\frac{1}{4}$ in (0.6 cm). In the central (innermost) groove, which is 2 inches (5.1 cm) in diameter, are located the pressure tap F, the thermometer well D, and the exit port for the air E; pressure and temperature measurements can be made in the region where the air leaves the saturator.

Figure 3.

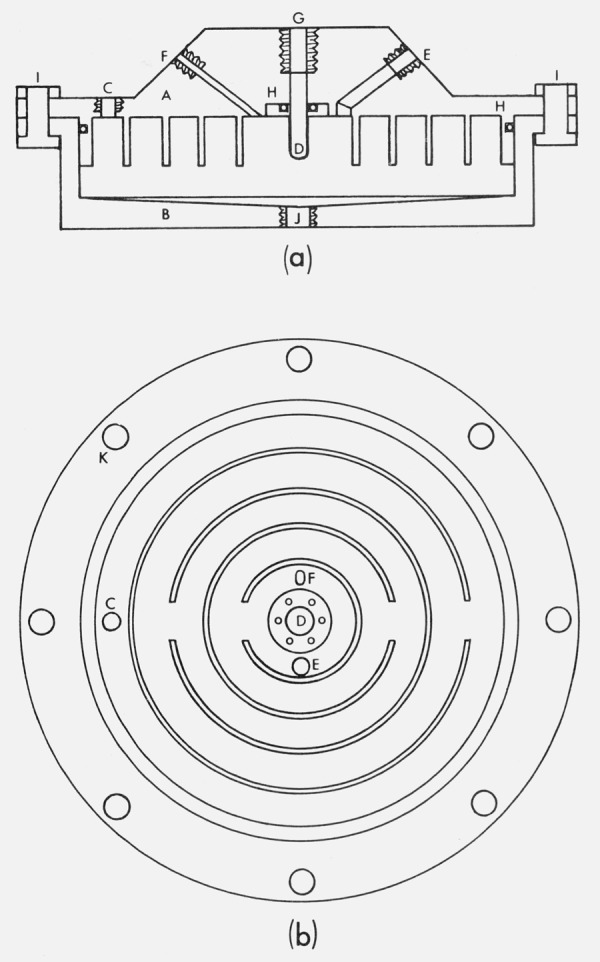
(a) Dish saturator, schematic cross section, showing lid (A); dish (B); inlet port (C); thermometer well (D); outlet port (E); pressure tap (F); thermometer lead-in port (G); O-ring seals (H); flange bolts (I); and water inlet and removal port (J). The inlet (C) is not shown in proper relation to ports (E) and (F), nor are the screws retaining the thermometer well indicated, (b) Dish saturator lid, bottom view, showing flange bolt holes (K); inlet port (C); pressure tap (F); thermometer well and its retaining screws (D); and outlet port (E). Hidden upper surfaces are not indicated, but are of circular symmetry. Bottom view rotated with respect to top view.

From the final (third) bubbler saturator unit or from the dish saturator (see fig. 1) the air enters tubing which is wrapped with an electric heater from a point prior to its emergence from the bath fluid up to a point just downstream of the expansion valve K. In the region of the expansion valve, the temperature of the test gas is maintained at or near 100 °C. The tubing downstream of the expansion valve remains warm to the touch for a distance of about 30 cm. This insures that neither heat loss to the room air nor adiabatic cooling on expansion at the expansion valve will reduce the test gas temperature to or below its dew point. Variations in temperature and pressure, provided they do not cause condensation, do not affect the ratio of water vapor mass to air mass from which the mole fraction is computed. The expansion valve reduces the test gas pressure to one bar at which pressure the test gas enters the gravimetric hygrometer M.

2.2. Pressure Measurement and Control

In the course of this work, pressure measurements were made using (a) an oil-lubricated (medium-range) piston gage with a range of 25 to 3000 psi (1.7 to 200 bars) and a weight set permitting pressure increments of 25 psi (1.7 bars), (b) a precision laboratory bourdon gage having a range of 2000 psi (140 bars) and readable to 1 psi (0.07 bar) and (c) a precision laboratory bourdon gage having a range of 3000 psi (200 bars) and readable to 1 psi (0.07 bar). The piston gage weights were augmented by a set of analytical balance gram weights and by brass washers (of known weight) so that any nominal pressure could be attained readily.

A commercial stainless steel diaphragm separator isolates the air in the saturation system from the oil in the piston gage. It has a null-detector circuit that visually indicates balance on a meter and that also provides an analog output.

Pressure is set and controlled by two air-loaded dome reducers in series. Attached to the control volume on the downstream reducer is a 1.6-liter cylinder, which initially served as a ballast volume. Subsequently, it was placed in a small water bath (C, fig. 1), the temperature of which is automatically adjusted in response to the analog output signal from the diaphragm null-detector circuit. This raises or lowers the pressure of the control volume of the downstream reducer. The latter, in turn, acts to restore the system pressure to its initial value.

2.3. Temperature Measurement and Control

The temperatures are maintained in the preliminary and main baths by balancing a slight controlled cooling with heat. The cooling is induced by circulating the water (used as the bath liquid in both baths) from the preliminary and the main baths through separate coils that are immersed in a third refrigerated bath RB (see fig. 1). The circulation rates are individually variable by means of a dual metering pump P1. The refrigerated bath fluid is industrial grade n-propyl alcohol. It is stirred with an immersed sump pump S1. A bimetallic thermoregulator controls the opening and closing of a valve V on a liquid CO₂ line N; the liquid CO₂ discharges into the bath through a small orifice, vaporizes, and abstracts heat from the alcohol. The temperature of the refrigerated bath is maintained within ±1 deg C at any selected temperature between 15 and 21 °C. The cooling capacity of the water circulated to the preliminary and main baths is adjusted by setting the temperature of the refrigerated bath and the circulation rate of the water flowing through the coils immersed in the alcohol.

The temperature of the preliminary bath PB is set and sensed with a bimetallic thermoregulator which activates an electronic relay, controlling the on-off position of an immersion heater Z. The bath liquid is stirred by a small propeller S2.

The temperature of the main bath MB is maintained within ±0.005 deg C by a time-proportioning controller with adjustable rate and automatic reset acting in response to a 4-lead platinum resistance thermometer. The controller activates a network of four electric heaters Z interconnected through switches into several optional parallel or series arrangements.

Both the preliminary and main baths have a second group of heaters for rapid warm-up and to provide a constant (adjustable) heat load.

The interior of the main bath is divided into an inner core and an outer annulus by means of an 18 in (45.7 cm)-diameter, stainless steel draft tube DT. This tube is supported by stainless steel legs and is centered by radial stainless steel brackets. The saturation system, the control thermometer, and the intake port of the water line to the counter-current heat exchanger are located within the draft tube whereas all heaters, intake and discharge lines for the water that is circulated to and from the refrigerated bath, and the discharge line from the counter-current heat exchanger are located in the annulus.

At 120 degree intervals around the interior of the draft tube, flush with the top, are vortex control vanes, 2.5 cm wide by 30 cm long. The bath water is stirred by a propeller with stabilizer ring that is located at the bottom of the draft tube and is driven by the variable speed motor S3. The bath water is forced vertically downward through the draft tube, then up through the annulus where heat is added or removed and returned to the top of the draft tube.

The main, preliminary and refrigerated baths each are insulated with styrofoam and are covered with lids. They have internal volumetric capacities of 750, 115, and 115 liters, respectively.

The temperature in the preliminary saturators is considered to be the same as that of the preliminary bath and is measured with a two-junction copper-constantan thermopile with a maximum uncertainty less that ±0.2 °C. The temperatures of the main bath and main saturation system are measured with four-lead platinum resistance thermometers and a Mueller bridge. These measurements will be discussed more fully in section 6.2.

2.4. Determination of Mole Fraction

The NBS standard (gravimetric) hygrometer is used for determining the mole fraction of the water vapor in the gas emerging from the saturation system. Because this apparatus is described in great detail in [19] only a brief description will be given here. The hygrometer yields a measurement of the mixing ratio, that is, the mass of water vapor per unit mass of dry air, from which the mole fraction is readily computed.

The saturated air from the saturation system is reduced to atmospheric pressure through the heated expansion valve K (fig. 1) and passed through a series of preweighed, desiccant-filled ⋃-tubes where the water vapor is removed. Upon completing an experiment a final weighing is made and the gain in weight gives the mass of water collected. The effluent dry air from the absorption tubes is collected in cylinders of known volume. A measurement of P and T in the volume permits the calculation of the mass of dry gas. The gravimetric hygrometer is arranged so as to permit uninterrupted gas flow through the ⋃-tubes into two alternately filled, measured, and evacuated cylinders until approximately one gram of water has been collected. The flow rate of the test gas through the hygrometer is maintained at or below 2 g per minute.

3. Materials

3.1. Air

The gas used in these experiments was low hydrocarbon content, compressed and dried atmospheric air, commercially supplied in steel cylinders. The supplier’s assays show that the methane content is usually 2 ppm by volume and never exceeds 4 ppm. The residual hydrocarbon content is about 2 ppm. The CO₂ content varies from trace quantities to 300 ppm. Analyses made at NBS agree with the supplier’s assessment of hydrocarbon content. In addition, the NBS tests indicate that 1 ppm of CO and up to 325 ppm of CO₂ are present in the air. The other normal constituents are present in the percentages usually given for atmospheric air [20]. In our experimental setup, air passes through the CO₂ removal unit previously described. The CO₂ content of the gas emerging from the generator is on the order of 2 ppm.

3.2. Water

For most of the runs (through No. 42) the water used in the saturators was first deionized, and double distilled. For the last five runs (Nos. 43 through 48) the purification process was reduced to a single distillation of tap water. The solid residuals in the deionized and doubly distilled water initially ranged between 2 and 6.5 ppm, possibly because the still had recently been installed. At a later date, measurements indicated that the solid residuals had been reduced to the parts per billion range, the major constituents being copper (4 ppb), lead (0.6 ppb), cadmium (0.02 ppb), and a trace of zinc.

Fresh water was placed in each saturator prior to all runs except in four cases, where the same water served for two successive runs. After the completion of each of 22 runs measurements of solid residuals were made on samples of water withdrawn from the final saturator unit of the main saturation system. The maximum solid residual concentration observed was 330 ppm by weight. This occurred in water that had been used for two successive runs (Nos. 23 and 24). The next highest concentration was 88 ppm (run No. 18), while the average for all runs was 48 ppm. The solid residuals tended to be lower in concentration in the water removed from the dish saturator. Qualitative spectrochemical examination of the solid residual material from the water removed from the bubbler type saturator disclosed that the principal constituents were silicon and calcium (90 to 99%) and magnesium (1 to 10%) with traces of sodium, boron, aluminum, copper, iron, titanium, silver and chromium. The calcium and sodium probably originate in the chemicals in the CO₂ removal unit and in the glass beads, whereas the silicon and boron are probably leached from the borosilicate glass beads.

Calculations based on Raoult’s law, assuming that all the solids behave as soluble ionic particles, suggest that their relative effect on the pure phase vapor pressure and, consequently, on the enhancement factor, is numerically about $\frac{1}{3}$ of the concentration in ppm. For the maximum observed concentration (330 ppm), this means the relative uncertainty should not exceed 110 ppm.

4. Experimental Procedure

In executing a run, that is, in making a single determination of enhancement factor, a desired combination of pressure and temperature at a mass flow rate of 2 g per minute was established in the generator and the entire apparatus was permitted to operate, with the effluent air from the generator exhausting into the laboratory, until equilibrium conditions were achieved. The gravimetric hygrometer was independently prepared for use by continuously flushing for three or more days with dry room-temperature air those components that would subsequently be exposed to the test gas, the intent being to eliminate any inadvertent moisture that might introduce an error. On the day of the run, the flushing process was halted briefly and the weighed desiccant-filled ⋃-tubes inserted into the absorption train. In order to minimize the possibility that traces of moisture from room air trapped in the ⋃-tube sidearms or drying train components during the insertion of the ⋃-tubes would affect the results, the flushing process was resumed. The dry gas was allowed to flow up to the sealed inlet stopcock of the first ⋃-tube and vented to the room. After sufficient time had elapsed for drying, and vent was closed and the inlet stopcock and outlet stopcock opened, the dry gas now flowing through the first tube and out the stopcock channel of the second. This procedure was repeated for the third ⋃-tube, with the flushing gas eventually exhausting downstream of the third ⋃-tube.

Equilibrium of the lines up to the ⋃-tubes, with respect to the moisture content of the test gas, was accomplished by halting the flow of the dry flushing gas through the drying train, sealing the ⋃-tubes, and permitting the test gas from the generator to flow up to the inlet stopcock of the first ⋃-tube in the drying train and vent into the room. On the initiation of the run, all stopcocks were opened thus interconnecting the gravimetric hygrometer with the generator.

The duration of a run was dictated by the requirement that nominally 1 gram of moisture be collected by the drying train. At a test gas flow rate of 2 g per minute, the elapsed time for a run varied from 1 to 10 h depending on the moisture content. During this period repeated measurements were made of generator and hygrometer variables. At the termination of the run, the ⋃-tubes were sealed, removed from the drying train, and transferred to a balance room for weighing.

5. Results

An initial group of runs was made during which system difficulties were resolved, equipment improved and apparatus redesigned. The basic experimental data for the final group of runs (Nos. 16 through 48) are given in chronological order in table 1. Run Nos. 16 through 28 utilized bubbler units in the main saturation system; the remainder of the runs employed the dish saturator. In run Nos. 21 through 27 pressure measurements were made with the bourdon gages; in the other runs, the medium-range piston gage was used. The calculated parameters and final results are given in table 2. These are arranged in groups corresponding to the three nominal test temperatures 30, 40, and 50 °C.

Table 1.

Experimental data

Run No.	Saturation temperature1 ts	Saturation vapor pressure2 es	Total pressure3 P	Mole fraction H2O Xw	Enhancement factor f	Preliminary bath temperature t	Type of saturator	Type of pressure gage
	°C	mb	bar			°C
16	50.0050	123.4164	30.2324	0.0044135	1.0811	52.67	Bubbler	Piston
17	50.0101	123.4477	30.1977	.0044266	1.0828	53.76	Bubbler	Piston
18		(contaminated U-tube; run n.g.)					Bubbler	Piston
19	39.9969	73.7612	30.1957	.0026497	1.0847	44.05	Bubbler	Piston
20	30.0112	42.4566	30.1929	.0015317	1.0893	34.40	Bubbler	Piston
21	40.1366	74.3122	60.9945	.0014285	1.1725	44.20	Bubbler	Bourdon
22	40.1505	74.3673	50.3962	.0016810	1.1392	44.20	Bubbler	Bourdon
23	50.0049	123.4158	50.3229	.0027681	1.1287	53.74	Bubbler	Bourdon
24	49.9784	123.2536	76.3139	.0019376	1.1997	52.98	Bubbler	Bourdon
25	49.9788	123.2561	102.704	.0015264	1.2719	52.56	Bubbler	Bourdon
26	49.9766	123.2426	40.8462	.0033228	1.1013	52.12	Bubbler	Bourdon
27	39.9648	73.6350	40.4557	.0020231	1.1115	42.45	Bubbler	Bourdon
28	49.9815	123.2726	90.9356	.0016749	1.2355	52.84	Bubbler	Piston
29	50.0009	123.3913	36.5953	.0036782	1.0909	52.74	Dish	Piston
30	49.9967	123.3656	25.3585	.0051773	1.0642	52.40	Dish	Piston
31	49.9891	123.3191	14.6231	.0087902	1.0423	53.49	Dish	Piston
32	49.9898	123.3233	10.5512	.0120190	1.0283	53.77	Dish	Piston
33	50.0064	123.4250	14.8620	.0086263	1.0387	52.84	Dish	Piston
34	40.0104	73.8143	14.6417	.0052456	1.0405	43.00	Dish	Piston
35	50.0011	123.3925	10.7989	.0117614	1.0293	49.44	Dish	Piston
36	50.0042	123.4115	10.7441	.0118214	1.0292	60.25	Dish	Piston
37	49.9942	123.3503	10.6310	.0119361	1.0287	52.51	Dish	Piston
38		(equipment failure; run aborted)					Dish	Piston
39	29.9994	42.4278	10.7312	.0040827	1.0326	33.68	Dish	Piston
40	29.9999	42.4290	35.5133	.0013201	1.1049	33.44	Dish	Piston
41	29.9992	42.4273	19.7704	.0023107	1.0767	32.74	Dish	Piston
42	29.9990	42.4290	19.9344	.0022534	1.0587	33.78	Dish	Piston
43	50.0047	123.4146	10.7546	.0117992	1.0282	52.65	Dish	Piston
44	(Spray trap inserted; behaved as a moisture sink; run n.g.)						Dish	Piston
45	(Spray trap inserted; behaved as a moisture sink; run n.g.)						Dish	Piston
46	49.9971	123.3680	10.7953	.0117446	1.0277	53.51	Dish	Piston
47	30.0065	42.4451	15.1088	.0029354	1.0449	33.73	Dish	Piston
48	29.9975	42.4232	15.3079	.0028727	1.0366	34.07	Dish	Piston

¹IPTS–48.

²Calculated from equation given by Wexler and Greenspan [1].

³Gage pressure plus barometric pressure.

Table 2.

Results

Run No.	Total pressure	Normalized enhancement factor1	Predicted enhancement factor2	Residual	Standard deviation of the predicted value3
	P bars	fnorm	fpred	fnorm - fpred
30 °C (all runs included)
39	10.7312	1.0326	1.0331	-0.0005	0.0053
47	15.1088	1.0449	1.0459	-.0010	.0041
48	15.3079	1.0366	1.0465	-.0099	.0041
41	19.7704	1.0768	1.0596	+ .0172	.0034
42	19.9344	1.0587	1.0601	-.0014	.0034
20	30.1929	1.0893	1.0910	-.0017	.0053
40	35.5133	1.1049	1.1074	-.0025	.0072
Residual standard deviation				.0090
30 °C (run nos. 41 and 48 deleted)
39	10.7312	1.0326	1.0325	+ 0.0001	0.0001
47	15.1088	1.0449	1.0450	-.0001	.0001
42	19.9344	1.0587	1.0589	-.0002	.0001
20	30.1929	1.0893	1.0890	+.0003	.0001
40	35.5133	1.1049	1.1050	-.0001	.0001
Residual standard deviation				.0002
40 °C
34	14.6417	1.0405	1.0410	-0.0005	0.0010
19	30.1957	1.0847	1.0832	+ .0015	.0006
27	40.4557	1.1115	1.1120	-.0005	.0006
22	50.3962	1.1393	1.1406	-.0013	.0007
21	60.9945	1.1727	1.1719	+ .0008	.0010
Residual standard deviation				.0013
50 °C
32	10.5512	1.0283	1.0294	-0.0011	0.0008
37	10.6310	1.0287	1.0296	-.0009	.0008
36	10.7441	1.0292	1.0298	-.0006	.0008
43	10.7546	1.0282	1.0298	-.0016	.0008
46	10.7953	1.0277	1.0299	-.0022	.0008
35	10.7989	1.0293	1.0300	-.0007	.0008
31	14.6231	1.0423	1.0390	+ .0033	.0007
33	14.8620	1.0387	1.0396	-.0009	.0007
30	25.3585	1.0642	1.0650	-.0008	.0006
17	30.1977	1.0828	1.0769	+ .0059	.0006
16	30.2324	1.0811	1.0770	+ .0041	.0006
29	36.5953	1.0909	1.0929	-.0020	.0006
26	40.8462	1.1013	1.1036	-.0023	.0006
23	50.3229	1.1287	1.1279	+ .0008	.0007
24	76.3139	1.1997	1.1974	+ .0023	.0012
28	90.9356	1.2355	1.2383	-.0028	.0016
25	102.704	1.2718	1.2723	-.0005	.0019
Residual standard deviation				.0026

¹Experimental enhancement factor adjusted to nominal temperature.

²Predicted enhancement factor obtained by calculation using eq (4) with appropriate coefficients from table 3.

³The method of calculation is given by Natrella [22], p. 6–12.

The experimental enhancement factors from table 1 were normalized to the nominal test temperatures given in table 2, as follows. Considerations of the theoretical aspects of f (see e.g., the papers of Goff et al., particularly eq (8) of [15]) lead to the conclusion that, along an isotherm, a smoothing expression of the form

$$\text{ln\hspace{0.17em}}f=a+bP$$ (4)

where P is the total system pressure, is nearly correct.

For the first step toward normalization, small differences between actual and nominal isotherm temperatures were ignored and plots of ln f versus pressure were made along the three isotherms. Next the slopes (ln f)/T as a function of pressure were measured from these graphs, and used to adjust the experimental values to the desired isotherm temperature. The changes in f do not exceed 2 parts in 10⁴, as can be seen by comparing the experimental values of table 1 with the normalized values of table 2. Uncertainties introduced into f by the procedure should not exceed a few parts per million and are considered negligible.

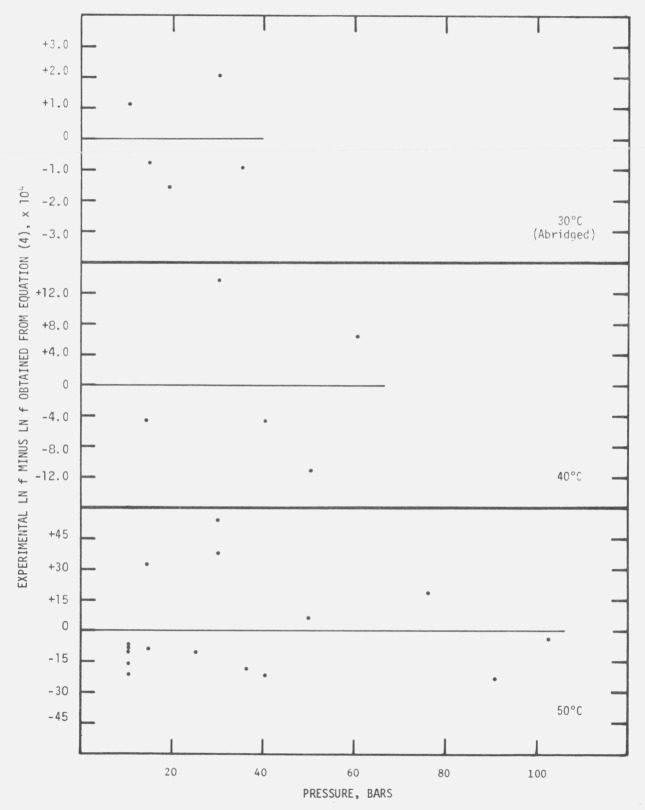
The OMNITAB computer program [21] was used for fitting eq (4), by the method of least squares, to the normalized enhancement factors for each nominal test temperature. Strictly speaking, the assumptions underlying the cited least square method are not fulfilled since f and P are both measured with errors and are correlated. However, since we are interested only in a smoothing expression for purpose of interpolation, the procedure may still be used. The computed coefficients are given in table 3. Figure 4 shows the residuals between the natural logs of the normalized f’s and the values of ln f predicted by eq (4) as a function of pressure along the three isotherms. The scatter of the deviations indicates that eq (4) is a valid approximation.

Table 3.

Coefficients for eq (4)

Source	Temperature °C	a	Standard deviation of a × 104	b	Standard deviation of b × 106
NBS	301	0.002565	87.7	0.002799	390.
	302	.002603	2.07	.002739	8.59
	40	.002745	13.7	.002556	32.2
	50	.004673	8.80	.002299	19.7
Goff	0	.00046	3.1	.00388	2.7
	10	.00072	3.0	.00362	5.0
	20	.00109	3.0	.00336	8.9
	30	.00161	3.0	.00316	15.
	40	.00229	3.0	.00297	24.
	50	.00317	3.1	.00280	39.
	60	.00430	3.4	.00264	59.
	70	.00571	3.5	.00251	89.
Webster	0	.04013	116.	.003324	116.
	15	.04076	89.2	.002701	75.1
Politzer and Strebe]	50	-.01236	82.5	.002512	66.2
	70	.02800	54.54	.002151	56.4

¹All runs included in least square fit.

²Run nos. 41 and 48 deleted from least square fit.

Figure 4.

Deviations of the ln f values predicted by eq (4) from the experimental values, as functions of pressure.

The residuals between the normalized f and the enhancement factor predicted by eq (4), f_norm − f_pred, are shown in table 2 together with the residual standard deviations and the standard deviations of the predicted values.³ The residual standard deviation may be considered an index of the precision of the measuring process whereas the standard deviation of the predicted value serves as a measure of the random uncertainty in the calculated value. The residual standard deviation for the 30 °C isotherm (±0.0090) is seven times as large as that for the 40° isotherm (±0.0013) and three times as large as that for the 50° isotherm (±0.0026). This large residual deviation can be traced to run Nos. 41 and 48 which have residuals that are grossly out of line with the others in this isotherm. Although there seems to be no experimental justification for discarding these runs, the magnitudes of the residuals are so large as to make the runs open to suspicion. If these runs are deleted and the equation refitted to the remaining data, then the residual standard deviation is reduced to ±0.0002. In our opinion this latter fit is preferable to the one based on all the data, and is the one we shall use.

6. Error Analysis

The enhancement factor is a computed quantity whose magnitude depends on three variables – the mole fraction of water vapor, the total pressure, and the saturation vapor pressure of the pure water substance. We shall estimate the uncertainty in our predicted values of enhancement factor by examining suspected sources of error in these variables.

6.1. Pressure Error

The uncertainties in the pressure measurement differ substantially from the piston gage to the bourdon gages. These are discussed separately.

a. Piston Gage

The piston gage is an instrument which measures pressure in terms of the fundamental units of force and area. However, various other factors must be considered, and Cross [23] has developed a general equation for calculating pressure which we have modified as follows for use with our gage. First, our gage is not a controlled clearance type, therefore, the relevant term in the equation reduces to unity; second, the piston is cylindrical and flat-bottomed, so that there is no fluid buoyancy correction to be considered; and third, the proportionality factor, k, for the force-mass units applicable to this gage, is the reciprocal of standard gravity, i.e., 1/g_s. Thus eq (24) given by Cross reduces to

$$P_g=\frac{\frac{M_m}{A_0}\left(1-\frac{{\rho }_a}{{\rho }_m}\right)\frac{g_1}{g_s}+\frac{\gamma C}{A_0}}{[1+a(t-25)][1+b{P}_g]}$$ (5)

where P_g is the piston gage pressure, M_m is the mass distributed over area A₀, A₀ is the effective piston area at 25 °C under zero load, ρ_α is the density of the ambient atmospheric air, ρ_m is the density of the weights, g₁/g_s is the ratio of local to standard gravity, γ is the surface tension of the oil in the gage, C is the circumference of the piston, a is the temperature coefficient of areal expansion of the piston, t is the temperature of the piston, and b is the pressure coefficient of areal expansion of the piston.

This equation is iterative. It is solved first without using the distortion term, (1 + bP_g), then with the calculated approximate value of P_g inserted into the distortion term. The difference between the two calculated values of P_g is quite small at all pressures under consideration.

For purposes of error analysis, eq (5), is rewritten as

$$P_g=\frac{\frac{M_m}{A_0}(\rho \text{'}g\text{'})+\gamma \text{'}}{a\text{'}b\text{'}}$$ (6)

where

$$\rho \text{'}=1-\frac{{\rho }_a}{{\rho }_m},$$

$$g\text{'}=g_1/g_s,$$

$$\gamma \text{'}=\frac{\gamma C}{A_0},$$

$$a\text{'}=1+a(t-25),\text{\hspace{0.17em}and}$$

$$b\text{'}=1+b{P}_g$$

The mass, M_m, which appears in eqs (5) and (6) is the sum of the individual brass weights loaded on the upper end of the piston, the auxiliary gram weights, supplementary brass washers, a copper cup (to hold the washers and analytical weights on the rotating piston), and the piston itself. The mass of each component was determined by comparison with accurately known standard weights on a precision balance. The maximum relative uncertainty in M_m for any combination of weights is 40 ppm.

The effective area, A₀, and its pressure coefficient, b, were obtained by comparison of our gage with a National Bureau of Standards reference piston gage of known characteristics. A₀ is known with a maximum relative uncertainty of 340 ppm and b is known to within a factor of 2.4. The quantity b′, calculated from b, varies in magnitude from unity at P = 0 to 1.000075 at P_g = 100 bars. The maximum relative uncertainty in b′ varies linearly from 18 ppm at 10 bars to 180 ppm at 100 bars. It is obvious that although the relative uncertainty in b is large, the corresponding relative uncertainty in b′ is small.

A precision calibrated aneroid barometer is used to measure ambient atmospheric pressure, which must be added to the gage pressure to obtain the absolute (total) pressure. The uncertainty in this atmospheric pressure measurement does not exceed ±0.07 mb, or 7 ppm and 1 ppm at 10 and 100 bars, respectively.

Table 4 indicates the small contributions of the remaining parameters to the final systematic uncertainty in pressure as determined by the piston gage. Briefly, the errors in the product ρ′g′ arise primarily from a 4 parts in 1000 error in air density ρ_α because relative humidity is neglected in its calculation, and from a 1 percent error in ρ_m because the total mass M_m is assumed to have the density of brass (8.4 g/cm³), even though the cup and piston are made of other materials. It can be shown that ρ′, which has a magnitude of about 0.9998, is known to 2 ppm, while g′, which is based on transferring the recent measurements by Tate [24] of the acceleration of gravity at the grounds of the National Bureau of Standards to the elevation of the piston gage, is known to at least 2 ppm. Thus the product ρ′g′ has a relative uncertainty, computed by quadrature (i.e., the square root of the sum of the squares of the individual independent errors), of about 3 ppm.

Table 4.

Sources of systematic piston gage errors and corresponding relative pressure uncertainties

Source of error	Symbol	Relative pressure uncertainty ppm
		Gage pressure, bars
		10	30	100
Mass of weights, etc	Mm	40	40	40
Effective piston area	A0	340	340	340
Pressure coefficient term	b’	18	54	180
Density-gravity term	P’g’	3	3	3
Surface tension term	y’	3	1	0
Coefficient of expansion term	a’	7	7	7
Diaphragm separator		1	1	1
Aneroid barometer		7	2	1
Oil head correction		13	4	1
Air head correction		4	4	4
Quadrature error		343	347	387

The quantity γ′ is of the order of 0.3 mb. Its major uncertainty arises from the uncertainty in the surface tension, γ, of the gage oil, which is assumed to be 10 percent. The equivalent relative uncertainty in P_g is 3 and 0.03 ppm at 10 and 100 bars respectively.

The temperature coefficient of areal expansion, a, is obtained from the temperature coefficient of linear expansion for steel and is conservatively estimated to be known with a relative uncertainty of 2 percent. The quantity a′ remains in the range 1.00015 to 0.9998 with a relative uncertainty arising from a of no more than 3 ppm. The thermometer which indicates piston temperature is in contact with the piston case, insulated from the ambient air. It is estimated that the piston and thermometer temperatures could differ by as much as 0.2 deg C, thereby introducing an uncertainty in a′ which may be as much as 6 ppm. The quadrature of the a′ uncertainties is thus no more than 7 ppm.

The uncertainties discussed above are associated with the parameters in eqs (5) and (6). There are several additional sources of error arising from the application of oil and air head corrections, the conversion of gage pressure to absolute pressure, the manipulation of the piston gage, and the behavior of the diaphragm separator.

A correction is applied for the difference in oil level between the diaphragm and the gage. The uncertainty in the correction is about 0.13 mb. Similarly, the uncertainty in the air head correction, which accounts for the difference in level between the measurement location in the final saturator unit and the diaphragm, is 0.04 mb at P_g = 10 bars and 0.40 mb at P_g= 100 bars.

Because all these errors arise from independent parameters and are of indeterminate sign, we have chosen to use the square root of the sum of the squares as our estimate of the systematic error in the total pressure. The sources of error and the equivalent relative uncertainty in pressure are summarized in table 4.

The piston is rotated in the cylinder of the gage by a small motor through a belt (string) drive. String slippage, wobble of the piston in the cylinder, deviation of the piston from verticality, and nonuniform distribution of weights on the loading table produce random pressure oscillations and uncertainties. The diaphragm separator introduces, in addition to a systematic uncertainty of about 1 ppm due to zero shift, random uncertainties from hysteresis, sensitivity, and repeatability.

These random uncertainties may be considered part of the randomness inferred from the pressure data of various runs. During a run the pressure was repeatedly observed and from these readings an average value was calculated. For runs where the system pressure was controlled solely by the pressure reducers, there was slight monotonic drift of pressure with time, but with a random scatter of the individual readings about the smooth drift curves. For run nos. 46 through 48, where the null detector circuit was used for improved pressure control, the pressure remained constant throughout the run, but with a random scatter about the mean value. In both cases the scatter did not exceed 210 ppm. One third of the maximum scatter, that is, 70 ppm, will be used as a measure of the precision or random error (standard deviation) of the piston gage pressure measuring process.

b. Bourdon Gages

Difficulties with the pressure measurement system were encountered after run 20, leading to the replacement of the piston gage with bourdon gages for a period spanning seven runs. The gages were compared against the calibrated medium-range piston gage over a period of several years and from the differences thus obtained between the piston gage and the bourdon gage, correction curves were constructed. A straight line was fitted to the differences for each bourdon gage. The residual standard deviation of the fit for the 2000 psi range bourdon gage was 1.8 psi (0.12 bar) and for the 3000 psi range gage was 1.5 psi (0.10 bar). Following a run, the pressures recorded from each gage were averaged. The two means were individually corrected, and the average of the corrected means was used as the mean run pressure. The individual readings on either gage seldom deviated from their respective means by any detectable amount. A precision calibrated aneroid barometer was used to measure the ambient atmospheric pressure which was added to the gage pressure to obtain the absolute (total) pressure. The uncertainty in this atmospheric pressure measurement did not exceed ±0.07 mb which is negligible and hence ignored.

In the case of the piston gage, limits were set on errors which are systematic and ordinarily of the same (but unknown) sign and magnitude in all runs. The effect of each error on either a single point, or on a curve fitted to a group of points, is the same.

A different situation exists with bourdon gages. Here, the systematic error within a given run, that is, the deviation of the gage correction from that predicted by the calibration, can vary both in sign and magnitude from run to run. When a curve is fitted to the experimental enhancement factors as a pressure function along an isotherm, the effect of the varying sign and magnitude of the individual systematic pressure errors, on the uncertainty associated with the curve, is random.

We have used the residual standard deviations of the gages’ calibration curves as measures of the systematic uncertainties within a run, and 1.6 psi (0.11 bar) as the combined systematic error of the average of the two gage readings. Thus the relative estimated systematic within run error of the average ranged from 0.37 percent at 30 bars to 0.11 percent at 100 bars. For reasons given in the previous paragraph, these are listed as random, not systematic, errors in table 6.

Table 6.

Summary of estimated errors in the enhancement factor

Source of error	Systematic error, ppm			Random error, ppm
	Pressure, bars			Pressure, bars
	10	30	100	10	30	100
Residual solids in water	110	110	110
Pressure, piston gage	343	347	387	70	70	70
Pressure, bourdon gages					3700	1110
Vapor pressure	404	404	404	35	35	35
Mole fraction	460	460	460	270	270	270
Undersaturation, dish saturator	70	20
Undersaturation, bubbler saturator		80	25
Quadrature error for:
(a) Piston gage and dish saturator	714	713		281	281
(b) Piston gage and bubbler saturators		717	733		281	281
(c) Bourdon gage and bubbler saturators		627	619		3710	1140

6.2. Saturation Temperature Errors

In the generating apparatus, a four-lead calorimetry-type (metal bulb) platinum resistance thermometer, inserted into a thermometer well, was used to measure the temperature within the saturator and a conventional (long stem glass bulb) four-lead platinum resistance thermometer, inserted into a perforated metal sheath, was used to measure the bath temperature. They were calibrated at NBS on the International Practical Temperature Scale of 1948 and subsequently checked from time to time at the triple point of water. Resistance measurements were made with a calibrated Mueller bridge, using an amplifier and d’Arsonval galvanometer for null detection. It is estimated that the uncertainty in the temperature introduced by the bridge and null detector does not exceed 1 millidegree.

The two thermometers, installed “in situ,” were compared after 8 days of undisturbed exposure to quiescent bath conditions at a nominal bath temperature of 27 °C, with static atmospheric pressure air and no water in the dish saturator. The agreement in reading was better than 1 millidegree.

Under operating flow conditions a small difference in temperature invariably existed between the two locations. With the dish saturator installed in the apparatus the bath temperature, on the average, was 3 millidegrees warmer than the temperature in the saturator well; at no time did the difference between the average bath temperature and the average temperature in the saturator well exceed 4.5 millidegrees. With the bubbler saturator units installed in the apparatus the saturator temperature, on the average, was 6 millidegrees warmer than the bath temperature; at no time did this difference exceed 12 millidegrees. These differences significantly exceed the maximum uncertainty that can be ascribed solely to the thermometer and bridge or to any mismatch in reading between thermometers. They are independent of minor periodic fluctuations in bath temperature produced by the control system, (the bath and the saturator undergo similar patterns of perturbations with time, the latter lagging the former), and also independent of the random fluctuations in temperature, which are less than 1 millidegree and which will be discussed more fully below.

On several occasions it was observed that the oil in the thermometer well of the dish saturator did not completely cover the thermometer bulb. Evidence suggests that this was generally the case, except for the last two runs (Nos. 47 and 48) where precautions were taken to insure an adequate oil supply. In these runs, the average saturator temperature and the average bath temperature agreed to a fraction of a millidegree. The baths all had plastic splash plates between the bath liquid and the lids; this space, into which the thermometer extension tube led, was slightly cooler than the liquid volume below. Apparently, when the oil was below the glass bead which seals the four leads into the metal bulb, the thermometer gave a lower temperature reading than when the oil level was fully above the bead, because the column of air above the thermometer in the extension tube tended to cool the lead wires and the bulb by convection.

Another factor probably contributing to the thermometer agreement in the last two runs was the replacement of the (0.035-in-thick wall) stainless steel well by a (0.165-in-thick wall) copper well. The conduction through this well is several times greater than that with the thinner-walled stainless steel well. By construction the dish thermometer well tends to reflect bath temperature. If the saturator interior were warmer than the bath (see below), then the increased conduction to the cooler thermometer would cause closer temperature agreement between the two thermometers.

In conjunction with the thick-walled copper well in the dish saturator, two six-junction copper-constantan thermopiles were installed, the reference junctions being sealed in holes distributed uniformly around the exterior wall of the well. This permitted measurement of temperature differences between water and well, and air and well, in circles at a radial distance of 1.2 cm from the well. Readings were taken at operating temperatures of 30 and 40 °C. The temperatures of the saturator water and the well agreed to 1 millidegree or better whereas the temperature of the test gas was higher than that of the well by as much as 3 millidegrees.

Comparable measurements on the differences between the well and test gas temperatures and the well and water temperatures in the final bubbler saturator unit were not made. The well in the bubbler saturator is completely immersed in the test gas and water in contrast to the well in the dish saturator where there is substantial direct thermal contact with the massive lid. In the dish saturator the measured temperature in the well (with adequate oil) reflects in part, if not entirely, the bath temperature. In the bubbler saturator the measured temperature may more nearly represent the actual test gas temperature, or a mean of the test gas and saturator water temperatures. If this is so then in both types of saturator the test gas is at a slightly higher temperature than the bath temperature. Let us recall that the test gas leaves the preliminary saturation system 3 to 5 deg C higher in temperature than the main bath and that it is correspondingly supersaturated with respect to the temperature of the main bath. In addition, on emerging from the preliminary bath the test gas is heated roughly 20 to 30 deg C above bath temperature (to prevent condensation). The test gas must lose considerable enthalpy and latent heat in the main bath where it asymptotically approaches bath temperature. It is understandable, therefore, that it might remain at a slightly higher temperature in the final saturator unit, even after passing through a very efficient heat exchanger coil.

The temperature of saturation was taken as the mean of the test gas temperature and the main bath temperature. With the dish saturator, the test gas temperature was obtained by adding 3 millidegrees to the measured bath temperature and with the bubbler saturator, the temperature measured in the well was assumed to be the test gas temperature.

It is estimated that the temperature of saturation may have a maximum systematic uncertainty of 7 millidegrees. With the dish saturator this arises from the maximum uncertainty inherent in the averaging of the test gas and bath temperatures (1.5 millidegrees); from the maximum uncertainty in the thermometer and bridge (1 millidegree); and from the maximum observed difference between the average well and average bath readings (4.5 millidegrees). With the bubbler saturator this arises from the maximum uncertainty due to averaging (6 millidegrees) and from the maximum uncertainty in the thermometer and bridge (1 millidegree).

During a run measurements were made at approximately 10 min intervals and from these readings means were calculated. The standard deviation of the mean for all runs, for both the bath and saturator temperature, did not exceed 0.6 millidegree. This has been used as the measure of the precision or random error of the temperature measuring process.

6.3. Saturation Vapor Pressure Errors

Recently, Wexler, and Greenspan [1] derived an equation for the saturation vapor pressure, e_s, of the pure water substance covering the temperature range 0 to 100 °C. This equation predicts values which agree with the precise experimental data of Stimson [25] to 7 ppm. Stimson’s values, in turn, have an estimated standard deviation of 20 ppm or less, except at 25 °C where it is 40 ppm. It will be assumed that the equation yields values that are uncertain by no more than 60 ppm. To this uncertainty must be added the uncertainty in vapor pressure due to the estimated systematic uncertainty in temperature of 7 millidegrees and the estimated random error (standard deviation) in temperature of 0.6 millidegrees. These are shown in table 5.

Table 5.

Uncertainties in saturation vapor pressure

Nominal temperature1	Vapor pressure2	Derivative	Systematic uncertainty					Random uncertainty
			Temperature			Vapor press eq	3	Temperature
°C	mb	mb/deg	deg C	mb	ppm	ppm	ppm	deg C	mb	ppm
30	42.43	2.435	0.007	0.017	400	60	404	0.0006	0.0015	35
40	73.77	3.933	.007	.028	380	60	385	.0006	.0024	32
50	123.38	6.122	.007	.043	350	60	355	.0006	.0037	30

¹IPTS–48.

²Wexler and Greenspan [1].

³Quadrature error.

6.4. Mole Fraction Error

The mole fraction of water, X_w, is related to the mixing ratio, r, through the equation

$$X_w=\frac{\in r}{1+\in r}$$ (7)

where ϵ is the ratio of the molecular weights of air to water. Because r is small compared to unity, and because the uncertainty in ϵ is negligible compared to that in r, the relative uncertainty in X_w is essentially the same as that in r. The mixing ratio of a moist air sample can be determined with the NBS standard reference hygrometer [19] with an estimated systematic uncertainty no greater than 460 ppm and an estimated random error (standard deviation of a single determination) no greater than 270 ppm. These same uncertainties therefore apply to X_w.

6.5. Other Considerations

In any process for generating a stream of saturated gas it is essential that the apparatus be designed to minimize the occurrence of undersaturation, supersaturation, spray, mist or aerosol. A detailed investigation was made to see whether biases from these possible sources of error are present.

a. Undersaturation

In a dynamic flow system, once saturation (or, as is the case in the preliminary saturators of our system, supersaturation) has been obtained, the necessary conditions for preventing undersaturation with respect to the desired state are that the temperature of the test gas must not fall below the desired saturation temperature and that the pressure drop, that is, expansion which decreases the water vapor concentration, must be negligible. This latter consideration necessitated use of the low pressure drop dish saturator at pressures below 30 bars.

The heating of the lines between preliminary and main baths, and between the final saturator and expansion valve, were discussed in section 2.1. In all cases these line temperatures were at or above that of the bath. Within the final saturator unit the temperature of the test gas, as discussed above, was of the order of several millidegrees higher than that of the bath. It does not appear likely that the temperature of the air at any point within the saturation system ever dropped below that of the bath.

The pressure drop across the main saturation system was measured both for the dish and for the bubbler systems. The flow rate, simulating run conditions, was 2 g per minute, at a total pressure of 3 bars. The pressure drop measurements and all enhancement factor determinations occurred under laminar flow conditions. Therefore, exclusive of the constant pressure drop through the water columns in the bubbler units, the pressure drop through the system decreases with increasing pressure.

The pressure drop through the dish saturator at the test condition was 2 mb. Thus at 10 and 30 bars, it becomes, respectively, 0.7 mb and 0.2 mb. Assuming no compensation by evaporation of water in the saturator, the maximum undersaturation would be 70 ppm at 10 bars, decreasing to 20 ppm at 30 bars.

It was shown that the total pressure drop through bubbler system was 36 mb. About 6 mb of this total occurs in the heat exchangers, while, in each of the 3 units, drops of 5 mb occur through the beads and 5 mb occurs through the nominally 5-cm water depth. The 5-mb drop through the beads decreases with increasing pressure, while the 5-mb drop through the water remains constant. The total pressure drop in each bubbler becomes 5.5 mb at 30 bars and 5.15 mb at 100 bars, indicating, in this context, the relatively unimportant role of the beads.

Compensation for the decreasing water content as the gas expands occurs both during traverse of the water column and of the damp bead layers. We will arbitrarily assign one-half the pressure drop in the water of the third bubbler unit, that is, 2.5 mb, as an upper limit to the expansion of the test gas that remains uncompensated by subsequent saturation. The ensuing undersaturation would be 80 ppm at 30 bars, decreasing to 25 ppm at 100 bars.

b. Supersaturation

The test gas temperature in the final saturator unit is, as indicated earlier, invariably slightly higher than the main bath temperature. The average of these two temperatures was used as the best value for the temperature of saturation. Because the test gas entered the saturation system with excess moisture it is possible that on leaving the final saturator unit it remained supersaturated with respect to this average temperature. The systematic uncertainty in vapor pressure from this temperature uncertainty already has been discussed in section 6.3.

c. Spray, Mist, and Aerosols

In designing the saturation system it was assumed that spray, mist or aerosols would not be generated because of the low flow rate and the absence of turbulence. Therefore, there is no separate trap or baffle in the saturation system for removal or precipitating liquid water from the test gas. Each bubbler saturator unit does have layers of small glass beads above the water surface which provide some measure of baffling, but there is no equivalent feature for the dish saturator.

Several experiments were performed in which a trap was added immediately downstream of the dish saturator. This trap was identical in design and in layers of beads to the final bubbler saturator unit. The beads were expected to remove any liquid water in the form of spray or aerosol, if such water were present. When operated dry, the trap functioned as a vapor adsorber, removing as much as 3 percent of the moisture from the test gas during 5-hour long simulated runs. When operated with the beads moistened but with the trap drained of free water, there was no apparent change in vapor concentration of the test gas.

With the trap removed from the apparatus, variations in flow rate from 0.5 to 5 g per minute also appeared to produce no change in vapor concentration, as measured with a sensitive electrical hygrometer. At higher flow rates, however, there were indications of increased moisture content.

If the moisture level in the effluent of a saturation system remains constant whether the incoming gas is super- or undersaturated with respect to the saturation system temperature, and if there is no pressure drop through the system, it indicates that saturation is being achieved and maintained. An experiment was done in which the moisture content of the test gas entering the main saturation system was varied over a wide range. The main bath temperature was set at 50 °C, the total pressure at 10 bars, and the mass flow rate at 2 g per minute. The temperature of the preliminary bath, which controls the moisture content of the test gas entering the main saturation system, was raised slowly at 5 deg per hour from 25 to 58 °C with no observable change in the water vapor concentration of the test gas emerging from the final saturator.

In summary, there is no evidence of detectable liquid water carry-over in the test gas at mass flow rates below 5 g per minute. The preliminary saturators may be operated over a wide span of temperatures without affecting the efficiency of the main saturation system. However, the preliminary saturators are normally operated at temperatures several degrees higher than that of the main bath.

6.6. Estimated Overall Accuracy

In the preceding error analysis we have examined all suspected sources of error in the measurement process. Table 6 summarizes the estimated limits to the contributing systematic errors. The estimated limit to the total systematic error has been computed by adding the contributing errors in quadrature (square root of the sum of the squares) for measurements made with (a) the piston gage and dish saturator, (b) the piston gage and bubbler saturators, and (c) the bourdon gages and bubbler saturators. The estimated total systematic error is 0.07 percent and is essentially independent of temperature, pressure, type of saturator, and type of pressure gage.

The expected precision or random uncertainty of the measurement process may be estimated either from this error analysis or from a statistical analysis of the experimental results. Both methods have been followed. Table 6 summarizes the estimated one-standard deviation magnitudes from the contributing sources. The combined (quadrature) one-standard deviation is of the order of 0.03 percent for measurements made with the piston gage; it decreases from 0.37 percent at 30 bars to 0.11 percent at 100 bars for measurements made with bourdon gages. Obviously the use of bourdon gages introduces a higher limit to the random errors. Fortunately only seven runs were made in which bourdon gages were used.

Table 2 lists the residual standard deviations of the fit for each isotherm. This statistic is used as the alternate indicator of the precision of the measurement process. The residual standard deviation is 0.02, 0.13, and 0.26 percent for the 30, 40, and 50 °C isotherms, respectively. The residual standard deviation of the 30 °C isotherm (0.02%), which is based on measurements made exclusively with the piston gage, is comparable to the calculated standard deviation (0.03%) based on the error analysis for measurements made with the piston gage. The residual standard deviations of the 40 and 50 °C isotherms are comparable to the calculated standard deviation based on the error analysis for measurements made with the bourdon gages. For the 40 °C isotherm, out of a total of 5 runs, 3 runs were made using bourdon gages; for the 50 °C isotherm out of a total of 17 runs, 4 runs were made using bourdon gages. Although there does not appear to be any statistically significant correlation between the magnitudes of the individual residuals and the type of pressure gage used for the 40 and 50 °C isotherms, it is suspected that the larger residual standard deviations for these two isotherms is due in part to the use of data obtained with the bourdon gages.

It will be assumed that the total systematic error in the measurement process derived by the error analysis (0.07%) is equally valid for the enhancement factor calculated (predicted) from eq (4). Estimates of the standard deviation of the predicted values are given in table 2. These latter estimates, which are pressure dependent, serve as our best estimates of the random uncertainty in the predicted values. In brief, the calculated (predicted) enhancement factor has an overall accuracy, for temperatures from 30 to 50 °C and pressures from 10 to 100 bars, comprised of an estimated limit of systematic bias of ±0.07 percent and a maximum observed standard deviation of a predicted value of ±0.2 percent.

7. Comparison With Other Work

Our results at 50 °C can be compared directly with the data of Politzer and Strebel [11], but there are no known measurements with which to compare our 40 and 30 °C data. Enhancement factors have been reported by Politzer and Strebel for 70 °C and by Webster [12] for 15, 0, −20 and −35 °C. The Goff, Anderson, and Gratch [14] measurements were made at 5, 15, 20, and 25 °C at or near atmospheric pressure using the double saturation isotherm method and yielded the “interaction constant,” a quantity related to the cross virial coefficient, rather than the enhancement factor.

The slopes and intercepts of eq (4), i.e., coefficients a and b, are convenient although indirect parameters for comparing our results with these other determinations, even in the absence of measurements at the same temperatures and pressures. Therefore, the data of Politzer and Strebel and of Webster were fitted by the method of least squares to eq (4). The coefficients a and b for each isotherm are given in table 3. Goff [14] presented an equation which relates ln f to P and which, by simple algebraic manipulation, has been transformed into the form of eq (4). The corresponding coefficients a and b, simply related to parameters called α and β in the Goff equation, are given in table 3.

There is too little information on the sources of error on which to base an estimate of the systematic uncertainty in the results of Politzer and Strebel and of Webster. However, the standard deviations of the coefficients a and b, which are readily calculable,⁴ can be used as an index of the precision of the basic data. These standard deviations of a and b for the 50 and 70 °C isotherms of Politzer and Strebel, for the 0 and 15 °C isotherms of Webster, and for our 30, 40, and 50°C isotherms are shown in table 3. Although similar standard deviations for the Goff, Anderson, and Gratch basic measurements cannot be computed, their reported tolerances (apparently twice the probable error) on the parameters α and β were converted to standard deviations; the standard deviation of β so obtained is used as an estimator of the standard deviation of the b’s given for Goff in table 3. The standard deviations of their α and β were combined by quadratures and used as estimators of the standard deviations of the a’s given for Goff, also in table 3.

A comparison of the intercepts a, from 30 to 50 °C, and of the slopes b, for 0 to 70 °C are shown in figure 5a and 5b respectively. The intercepts from fits to the data of Webster and Politzer and Strebel lie completely out of the range of the plot. The NBS intercepts are systematically displaced from Goff’s by about 30 percent. (All representations of Goff’s values are based on his smoothing equations, and do not reflect the precision of his raw data.)

Figure 5a.

Comparison of the intercepts obtained by fitting the relation ln f = a + b P to various data.

Figure 5b.

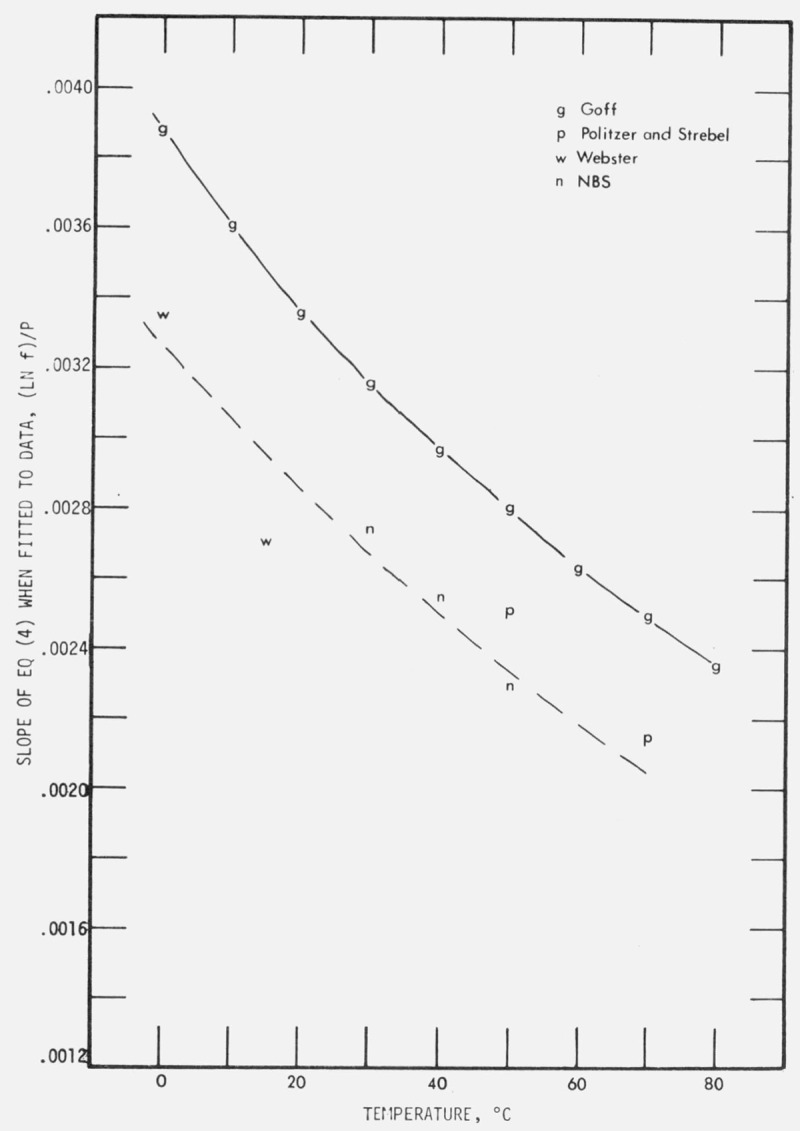
Comparison of the slopes obtained by fitting the relation ln f = a + b P to various data.

The slopes from GofFs formulation are displaced systematically from ours by about 15 percent. The slopes based on the Politzer and Strebel data and on the Webster data appear to be consistent with our extrapolated b curve. Too much significance should not be ascribed to this comparison in view of the large imprecision in the previously published data and the absence of any estimates of systematic uncertainty.