Abstract
Occupancy detection using ambient sensors has many benefits such as saving energy and money, enhancing security monitoring systems, and maintaining the privacy. However, sensors data suffers from uncertainty and unreliability due to acquisition errors or incomplete knowledge. This paper presents a new heterogeneous sensors data fusion method for binary occupancy detection which detects whether the place is occupied or not. This method is based on using neutrosophic sets and sensors data correlations. By using neutrosophic sets, uncertain data can be handled. Using sensors data fusion, on the other hand, increases the reliability by depending on more than one sensor data. Accordingly, the results of experiments applied using Random Forest (RF), Linear Discriminant Analysis (LDA), and FUzzy GEnetic (FUGE) algorithms prove the new method to enhance detection accuracy.
Keywords: Computer science, Sensors data fusion, Wireless sensor networks, Neutrosophic sets, Sensors data correlations, Heterogeneous sensors, Occupancy detection, Random forest, LDA, Fuzzy genetic
1. Introduction
Occupancy detection plays a significant role in different applications ranging from controlling energy consumption and space utilization to building security surveillance systems. Automatic occupancy detection is used to automatically control lighting and air conditioning systems based on the occupancy state. Accordingly, the world energy resources can be saved from depletion [1]. Occupancy detection is also used in risk assessment applications in cases of environmental disasters, criminal operations, or indoor pollution [2]. Security surveillance systems are another important occupancy detection application [3]. Occupancy detection is a classification problem concerned with detecting whether a certain place is occupied or not. This classification problem can be binary or multi-class. In binary classification, occupancy detection result is either the place is occupied or not, 1 or 0. On the other hand, the multi-class occupancy detection detects the number of occupants.
Occupancy detection relies on one of two different types of information sources: cameras and environmental sensors. There are many different sensors data types that have been used for occupancy detection such as, temperature, humidity, relative humidity ratio, light, Passive InfraRed (PIR) motion detectors, and CO2. The advantage of sensor-based occupancy detection over a camera-based one is maintaining the individual's privacy. Moreover, processing sensors data requires less storage and lower processing capabilities.
In spite of the advantages of using environmental sensors for occupancy detection, sensors data suffers from uncertainty and unreliability due to acquisition errors or incomplete knowledge. As a result, the accuracy of detection is affected. Most of the contemporary researches deal with occupancy classification methods such as Hidden Markov Models (HMM) [4, 5], Neural Network (NN) [6, 7], and Support Vector Machines (SVMs) [8, 9]. Nevertheless, handling data uncertainty and unreliability is not given much concern. Hence, this paper suggests a new multi-sensor data fusion method for binary occupancy detection based on neutrosophic sets. Using neutrosophic sets handles the data uncertainty, whereas fusing more than one neutrosophic sensor feature increases the reliability. Therefore, the suggested method provides better accuracy range for occupancy classification. In addition, it is computationally efficient due to using one fused feature instead of many features for training and testing. The suggested method is tested using public occupancy detection data set [3].
The rest of this paper is structured as follows. Section 2, related work, mentions recent researches on sensor-based occupancy detection. Section 3 explains the suggested method and how beneficial it is to occupancy detection. Section 4 discusses the results of using neutrosophic sets with two types of fusion, features-to-decision and features-to-feature fusions, compared to using the original data. Finally, the paper is concluded in Section 5.
2. Related work
Currently, there are many researches related to occupancy detection. These researches can be categorized into video-based [10, 11] and environmental sensor-based. Using video cameras for occupancy detection violates the privacy of individuals. Besides, video processing requires large storage and high processing capabilities. Consequently, this section focuses only on environmental sensor-based occupancy detection researches.
An occupancy behavioral pattern recognition model based on unsupervised approach was presented in [12]. The model used a variety of data such as illumination, motion, CO2, noise levels, relative humidity and temperature. The results reported maintaining indoor comfort with 30% energy saving. In [4], using HMM achieved an average of 80% accuracy in detecting the number of occupants. Data captured from CO2 and acoustic sensors was used. The work presented in [5] used the information theory for studying the correlation between the occupants number and the extracted features from CO2, relative humidity, and acoustics sensors data. It also used HMM to detect the occupancy number but with accuracy of 73% on average. In [13], accuracy of 98.4% was achieved by using a decision tree to combine multiple motion sensor features. However, the addition of power use, CO2, and sound sensors worsened the classification results. The work presented in [14] suggested an occupancy estimation model based on a Radial Basis Function (RBF) NN to predict the occupants number. Using sensors data as indoor temperature, light, sound, humidity, CO2 concentration and motion, accuracy of 64.83% was reported. NN was used to fuse multi-sensory features derived from CO2, air temperature, computer temperature, sound, relative humidity, and motion to estimate occupancy numbers [6, 7]. An accuracy of 75% was achieved in [6] and 84.59% was achieved in [7]. Using statistical correlations between occupancy levels and room temperature, CO2 concentration, and ventilation actuation signals [15], identified a dynamic model for estimating the occupancy levels with 88% accuracy. In [16], a new methodology based on the Adaptive Neuro-Fuzzy Inference System (ANFIS) algorithm was suggested to detect building occupancy. The indoor events, indoor climatic variables, and energy data were combined using a sensors fusion model. The resulting occupancy sensor was expected to improve the reliability. The work presented in [17] evaluated six machine-learning techniques performance in both single-occupancy and multi-occupancy offices using light, temperature, relative humidity, infrared, sound, motion, CO2, and door switch sensors. The decision-tree technique showed the best accuracy ranging from 96.0% to 98.2%. The work presented in [18] investigated Auto-Regressive Hidden Markov Model (ARHMM) to estimate the occupants number. The accuracy for detecting the occupants number using data from PIR, CO2, temperature, relative humidity, air speed and reed switches sensors was 76.2% and 84% for HMM and ARHMM, respectively.
In [8], non-linear multi-class SVM was used to model user occupancy and activity patterns with more than 80% accuracy in two scenarios. The statistical classification models: Gradient Boosting Machines (GBM), Linear Discriminant Analysis (LDA), Random Forest (RF), and Classification and Regression Trees (CART) were evaluated by [3] using data from light, temperature, humidity and CO2 sensors. The best accuracies ranging from 95% to 99% were obtained from LDA, CART and RF models. In [19], Feature Scaled Extreme Learning Machine (FS-ELM) algorithm was presented for estimating the number of occupants based on CO2 measurement. It provided up to 94% accuracy. In [20], a learning-based method to detect the occupancy behavior of a building was proposed. That method used a Recurrent Neutral Network (RNN) to detect the number of occupants through the temperature and/or heat source information. The error level is 0.288 at maximum with the knowledge of Heating, ventilation, and air conditioning (HVAC) powers and more than 0.5 without it. From [21], a Support Vector Regression (SVR) method was presented to detect occupancy using solar factor, working time, lights energy, and indoor/outdoor temperature features. The average error of the 4-feature SVR model and the 5-feature model are 0.638 and 0.317, respectively. Using data-driven models: Extreme Learning Machine (ELM), SVM, NN, K-Nearest Neighbors (K-NN), LDA and CART, a fusion framework for occupancy estimation was suggested [9]. The suggested framework achieved enhancements of 5–14% and 3–12% in estimation accuracy and detection accuracy (presence/absence). In [22], the decision tree and HMM algorithms were used for occupancy detection at the current/future state. The data used was CO2 concentration and electricity consumption. Accuracy of 93.2% was achieved in detecting the number of occupants. In [23], Dempster-Shafer theory was combined with HMM to predict occupancy profile. Data from dew point temperature, electrical power, and CO2 concentration was used in that work. The approach handled the periods of missing sensor data effectively. Another work suggested applying different NN algorithms to data from light, temperature, humidity and CO2 sensors [24]. The highest accuracy (99.06%) was obtained from Limited Memory Quasi-Newton (LMQN) algorithm and the lowest accuracy (80.32%) was achieved by Batch Back (BB) algorithm. In [25], Sensing by proxy (SbP) was proposed. The occupancy detection was based on “proxy” measurements such as temperature and CO2 concentrations. The proposed approach achieved 0.6 mean squared error and saved 55% of the total ventilation. The work presented in [26] applied four data mining algorithms: Naïve Bayes, SVM, K-NN and Ada boosting. Naïve Bayes and SVM resulted in an accuracy of around 94% with approximately 6% average error. K-NN and Ada boosting algorithms resulted in more than 99% average accuracy with average error less than 1% and 0.5%, respectively. A hybrid CO2/light sensor was proposed in [27] for detecting occupancy accurately.
The stacking for multi-class classification was applied to a binary occupancy classification task in [1]. NN with duo outputs was combined with the stacking. The applied approach provided 90.27% average accuracy for five input features and 70.46% average accuracy for two input features. In [2], an occupancy detection methodology based on HMM was used to infer the daily and hourly average occupancy schedules. The HMM based on the first order difference of CO2 data at 5 min time average achieved the best accuracy (90.24%). The work presented in [28] applied a rule-based method on noise, Volatile Organic Compound (VOC), PIR, temperature, relative humidity, and CO2 measurements to detect the occupancy. Accuracies of 98% and 78% in two different testing environments were reported. In [29], Fuzzy Cognitive Maps (FCM) was combined with SVM to increase the accuracy. The FCM was used at first for discovering interrelationships between variables and correlation patterns to produce a single variable. Then, the produced variable was feed to SVM to enhance prediction. The proposed SVM-FCM model achieved accuracies of 0.9790 and 0.9945 for 2 test data sets. The work presented in [30] investigated whether or not using a small random sample could produce performance that is as good as the one resulting from using a large sample. It used three classification models: Deep Feed Forward (DFF) Learning Model, RF, and K-NN. The DFF resulted in best accuracy of 98.44%. In [31], a distance sensor, CO2 and PIR motion were fused to reduce false positive and false negative, thus improving the reliability. The work in [32], however, proposed two novel feature selection algorithms: the wrapper and hybrid feature selection methods. A ranking-based incremental search was introduced in the algorithms to decrease the computation time. Accuracies of over 96% were obtained for presence detection. In [33], an ensemble learning algorithm was presented. Heterogeneous learning algorithms were used for pruning and generating diverse learners to enhance the performance of the ensemble. The proposed algorithm achieved up to 88% accuracy based on dynamic occupancy data set and 93% accuracy based on daily occupancy data set. In [34], a new control algorithm, consisting of two parts, was presented. The first part is an environmental data driven model for the occupancy status detection. The second is an integrated comfort algorithm for operating the indoor devices. Data obtained from a door sensor, CO2 concentrations, PIR sensors, and lighting electricity consumption was used by a multinomial logistic regression model to detect the occupancy status. The presented algorithm provided 94.9% accuracy. An Internet of Things (IoT)-based occupancy detection system was presented in [35]. The system used patterns change of dust concentrations to detect occupancy.
Information produced from real-world applications may be incomplete, imprecise, and inconsistent. The reason for that uncertainty may be acquisition errors, or incomplete knowledge. Some of the mentioned methods dealt with the uncertainty of decision based on probability theory [36] using HMM such as [2, 4, 5, 12, 18, 22, 23] or based on fuzzy set theory [37] such as [16, 29]. Probability is the likelihood of whether an event will occur using historical data. So, probability is related to event and not facts (historical data). In case of occupancy detection, the event is the occupancy and the facts are the sensors readings. Generally, using of the probability in occupancy detection is the probability of the place being occupied based on specific sensors reading appearing (conditional probability). It is not concerned with the validity of the sensor reading itself. On the other hand, fuzzy set theory defines set membership as a degree of truth, which is the percentage of fact (sensor reading) belonging to a specific fuzzy set. After defining the membership degree, fuzzy logic is used to combine the fuzzy sets and to make reasonings about events (occupancy) effectively. Also, fuzzy set theory deals with sensors readings as facts and is not concerned with their validity. Consequently, these two methods can deal only with one imprecision problem, which is the uncertainty of decision, without managing the problems of imprecision and uncertainty within the data. For that reason, a neutrosophy approach [38] was proposed. Neutrosophy can deal with the problem of imprecision and uncertainty as described in the following section.
3. Methods
Using environmental sensors in occupancy detection has its benefits in preserving privacy. However, sensors data is uncertain and unreliable because of acquisition errors, or incomplete knowledge. Hence, the proposed method handles this problem via using neutrosophic sets instead of the original data. For best of our knowledge, neutrosophic sets was not used before for occupancy detection.
3.1. Neutrosophic domain
Neutrosophy is a philosophy branch combining the philosophical knowledge with set theory, logics, and probability/statistics to solve the problem of imprecision and uncertainty [38]. A statement in probability/statistics is either true or false. In fuzzy logic, a statement is not necessarily true or false; rather it has a degree of truth between 0 and 1. The neutrosophic logic and intuitionistic fuzzy logic presented a percentage of “indeterminacy”. However, the neutrosophic logic allows each statement to be over or under true, over or under false and over or under indeterminate by using hyper real numbers developed in non-standard analysis theory. The hyper-real number set is an extension of the real number set. For example, the non-standard finite numbers 1+ = 1+ɛ, where “1” is its standard part and “ɛ” its non-standard part, and –0 = 0-ɛ, where “0” is its standard part and “ɛ” it's non-standard part. Neutrosophic logic represents data in a 3D space using (T, I, F), where T, I and F represent Truth, Indeterminacy, and False respectively and each is in the range of ]-0, 1+[ (Non-standard unit interval) [39]. The classical unit interval [0, 1] is used instead of non-standard unit interval for software engineering proposals [40].
3.2. Transformation to neutrosophic domain
Suppose a set of sensors S = {s1, s2…, sn} is used for occupancy detection. The sensors data is transformed to neutrosophic sets, using two methods inspired by the method applied to image data in [41]. In sensor-based transformation, each sensor data vector Sj, where 1 ≤ j ≤ n, is converted separately to a neutrosophic version using the following equations:
| (1) |
Where is the transformed neutrosophic set for the Sj sensor data. The index i refers to the ith instance in the data set. The membership values are derived as follows:
| (2) |
Where is the local mean value which is derived as follows:
| (3) |
Where is the mth data value in the sensor data vector and denotes the window size.
| (4) |
| (5) |
Where
| (6) |
The transformed data set that contains all n transformed vectors is denoted NS. In multi-sensor-based transformation, the sensors vectors are treated as one 2D matrix to give a chance for each sensor data to affect the other sensors during the conversion process. This owes to the fact that, in real world, the value of one observation may affect the value of other observations such as lighting a place may affect its temperature. Sensors vectors are arranged, either in an ascending or in a descending order, according to the readings range of each sensor. This ensures that high sensors readings do not cancel the effect of low sensors readings during occupancy detection. The 2D matrix is converted to a neutrosophic version using the following equations:
| (7) |
Where NS_all is the transformed neutrosophic set. The index i refers to the ith instance in the data set, whereas the index j refers to jth sensor vector, where 1 ≤ j ≤ n. The membership values are derived as follows:
| (8) |
Where is the local mean value and it is derived as follows:
| (9) |
Where is the data value in the sensors data matrix at the location (m, n) and denotes the window size.
| (10) |
| (11) |
Where
| (12) |
After converting the sensors data, the truth membership values for NS and NS_all are used as certain data for training and testing. To study the effect of each version of the data set on the occupancy detection, three classification algorithms, RF, LDA, and FUGE [42], are used to detect occupancy for each version of the data separately. The selection of RF and LDA is due to their achieved high accuracy in the domain of occupancy detection [3]. Also, the two algorithms are from different Machine Learning Algorithms (MLAs) categories. RF is a non-parametric algorithm, while LDA is a parametric algorithm. Besides that, LDA is a probability-based algorithm and FUGE is a fuzzy-based genetic algorithm. So, using both of them showed the effect of neutrosophy on the accuracy of probability and fuzzy based algorithms. Consequently, using these algorithms provides a chance to study the effect of neutrosophic transformation of sensors data on the results of different categories of MLAs.
3.3. Neutrosophic features fusion (NFF)
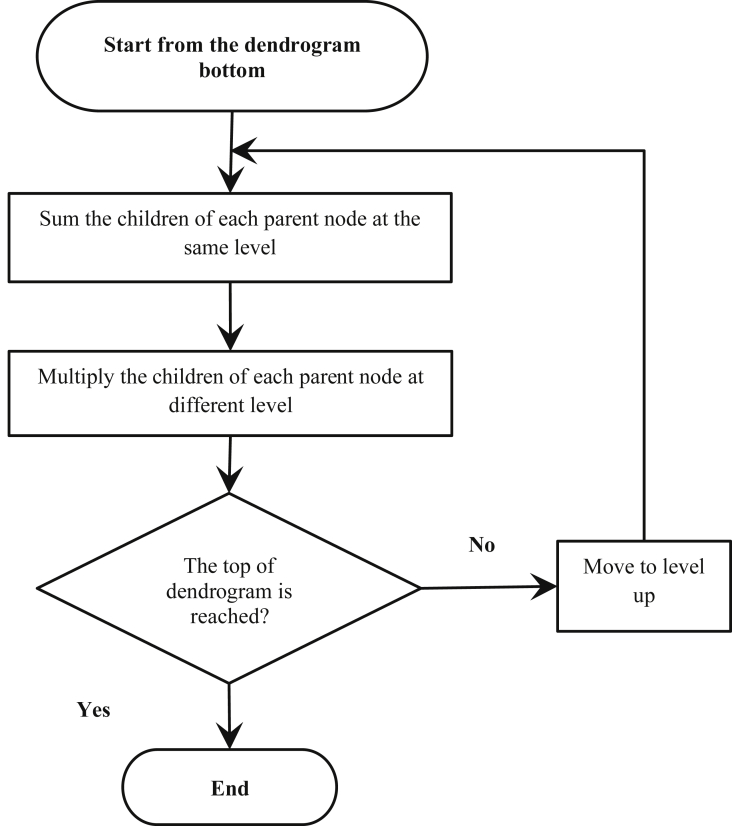
RF, LDA, and FUGE are used in this proposal to fuse the true feature of different sensors data through Features-to-Decision fusion (F2D). Despite the fact that using more than one feature can increase the accuracy of detection, it may cause over fitting [3]. Moreover, increasing the number of features increases time complexity. Using Features-to Feature (F2F) fusion produces only one feature for training, and therefore, saves some computation time. In addition, it shows better accuracy than F2D fusion as shown in detail in the next section. Thereupon, using F2F fusion can solve the mentioned problems. The proposed F2F fusion method, NFF, produces a dynamic fusion equation based on the sensors data correlation. The equation can be produced visually, using dendrogram of the training set (Fig. 1), or formed using the correlation matrix of the training set (Fig. 2). The steps to produce the fusion equation visually are illustrated using the flow chart in Fig. 1, and proceed as follows:
-
1.
Start from the bottom of the dendrogram. The bottom represents the largest correlation, because the dendrogram height represents dissimilarity which equals the ones' complement of correlation.
-
2.
Sum the children of each parent node at the same level. They can act as alternative of each other.
-
3.
Multiply the children of each parent node at different levels.
-
4.
Repeat steps 2 and 3 until the top of the dendrogram is reached.
Fig. 1.
Visual method for constructing F2F fusion equation.
Fig. 2.
Correlation-based method for constructing F2F fusion equation.
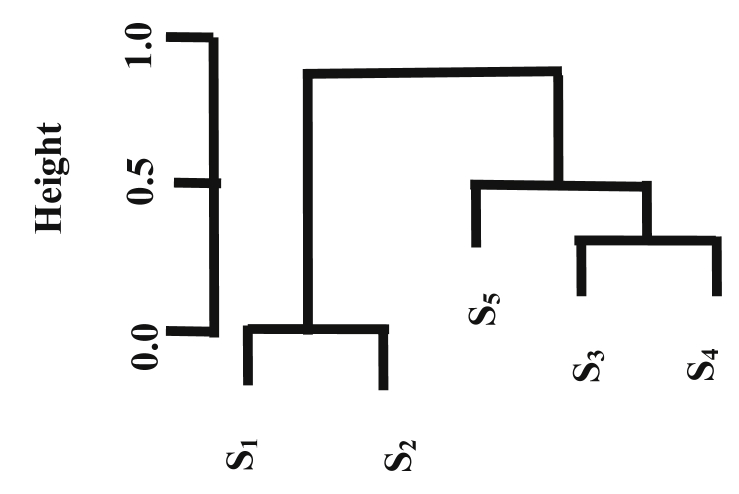
The dummy dendrogram of five sensors, S1:S5, in Fig. 3 is taken as an example. From the bottom of the dendrogram, S1 and S2 are children at the same level; hence they are summed (S1+S2). Moving up, S3 and S4 are children at the same level, thus they are summed (S3+S4). Then, (S3+S4) is multiplied by S5 which is a child of their parent at different level. (S1+S2) and S5*(S3+S4) are at a different level. Therefore, the final equation becomes (S1+S2) *S5*(S3+S4).
Fig. 3.
Dummy dendrogram.
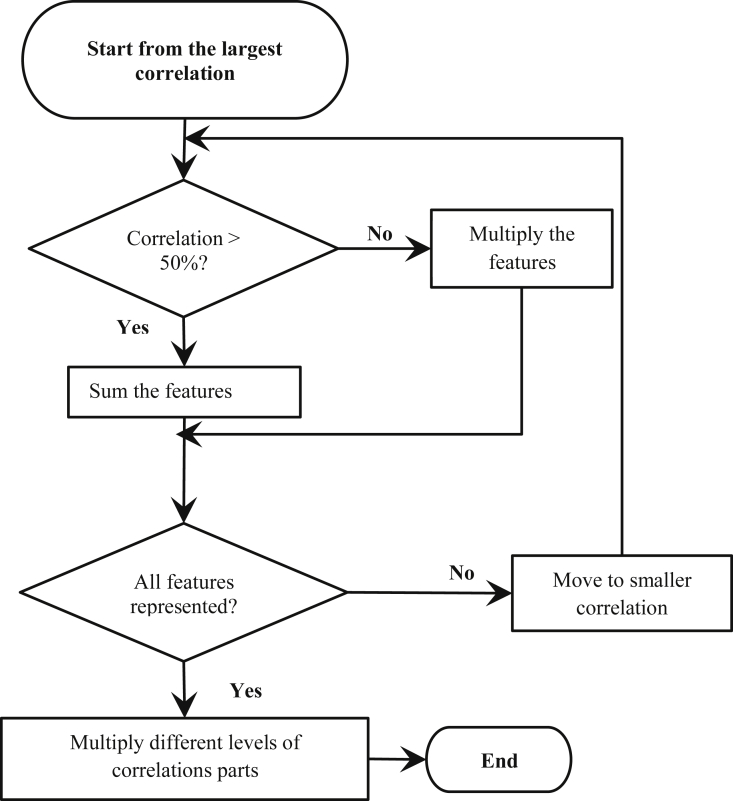
The second way, generating the equations using correlation matrix, is illustrated using the flow chart in Fig. 2 as follows:
-
1.
Start from the largest correlation value.
-
2.
If the correlation value is more than 50%, sum the two features, else multiply them.
-
3.
If the same correlation value is repeated, then sum or multiply all the involved features according to the correlation value.
-
4.
Move to a smaller correlation value and repeat steps 2 and 3 until all features are represented in the equation.
-
5.
Multiply different levels of correlations.
Using the correlation matrix in Table 1 as an example, the largest value is 0.96 and it is >0.5. So, S1 and S2 are summed (S1+S2). The smaller correlation value (0.66) is also >0.5, so S3 and S4 are summed (S3+S4). The correlation value (0.65) is for correlation between S5 and S3, but S3 is actually related to S4 by a larger correlation. Accordingly, S5 is the only feature in this level. The final equation, (S1+S2) *S5*(S3+S4), is the result of multiplying the different levels.
Table 1.
Dummy correlation matrix.
| S1 | S2 | S3 | S4 | S5 | |
|---|---|---|---|---|---|
| S1 | 1.00 | 0.96 | 0.04 | 0.44 | -0.14 |
| S2 | 0.96 | 1.00 | 0.23 | 0.63 | 0.15 |
| S3 | 0.04 | 0.23 | 1.00 | 0.66 | 0.65 |
| S4 | 0.44 | 0.63 | 0.66 | 1.00 | 0.56 |
| S5 | -0.14 | 0.15 | 0.65 | 0.56 | 1.00 |
4. Results & discussion
This section analyzes and compares occupancy detection accuracy of RF, LDA, and FUGE as F2D fusion models using the Occupancy Detection data set [3] from UCI Machine Learning Repository [43]. Also, the effect of using NFF on the occupancy detection accuracy is discussed. The motivation for using this specific data set was that the data and the data processing script were provided in [44], so the results can be compared directly. The accuracy was evaluated using the open source program R. The data set contains three sets for training and testing the classification models. They are summarized in Table 2. Each set contains: temperature (Temp), humidity (H), derived humidity ratio (HR), light (L), CO2, occupancy status (0 for non-occupied, 1 for occupied) and time stamp. The humidity ratio was not used in the experiments, because it is a ratio and the target was fusing sensors data readings. Also, the humidity is a good alternative for the humidity ratio. Different combinations from the four sensors data were used. Table 3 contains all 15 possible combinations of the four sensors data. First column is the case No. and the second is the features used, e.g. All means all features, no-CO2 means CO2 excluded and the other three sensors data are included, and H, L means only Humidity and Light are included. All cases were used for F2D fusion for occupancy detection using RF, LDA, and FUGE. Only the first 11 cases were used for F2F fusion and the reason was that one feature cannot be fused to obtain one feature. The experiments were done both by including time parameters and without including them. The time parameters are: The Number of Seconds from Midnight (NSM) and Week Status (WS). For comparison, two normalized versions of the original data were generated. The first version, Norm set, was generated using the following equation:
| (13) |
Where is the normalized set for the Sj sensor data. The index i refers to the ith instance in the data set. All normalized vectors were contained in the Norm set. The second version, Norm_all set, was generated using the following equation:
| (14) |
Where Norm_all is the normalized set. The index i refers to the ith instance in the data set, while the index j refers to jth sensor vector. Hence, five versions of the data set were used: Original, NS, NS_all, Norm, and Norm_all. NS and NS_all were produced using equations in the previous section. A window size of four was selected for producing NS because the resulted sets provided better accuracy when used for occupancy detection than the resulted sets from using window size of 2 and 6. Also, the computational time for producing the sets using window size of 4 was more than that of using window size of 2 and less than the time of using window size of 6. Thus, a window size of 4*4 was used for NS_all as well. The ascending order of sensors vectors was used before producing NS_all to ensure that high sensors readings do not cancel the effect of low sensors readings during occupancy detection.
Table 2.
Occupancy Detection data set description [3].
| Data set | Number of observations | Data Class Distribution (%) |
Comment | |
|---|---|---|---|---|
| 0 (non-occupied) | 1 (occupied) | |||
| Training | 8143 of 7 variables | 0.79 | 0.21 | Measurements taken mostly with the door closed during occupied status |
| Testing 1 | 2665 of 7 variables | 0.64 | 0.36 | Measurements taken mostly with the door closed during occupied status |
| Testing 2 | 9752 of 7 variables | 0.79 | 0.21 | Measurements taken mostly with the door open during occupied status |
Table 3.
Features combinations cases.
| # | Features | # | Features | # | Features | # | Features | # | Features | # | Features | # | Features | # | Features |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | All | 3 | no-T | 5 | no-L | 7 | T, CO2 | 9 | H, L | 11 | CO2, H | 13 | CO2 | 15 | H |
| 2 | no-CO2 | 4 | no-H | 6 | T, L | 8 | T, H | 10 | CO2, L | 12 | T | 14 | L |
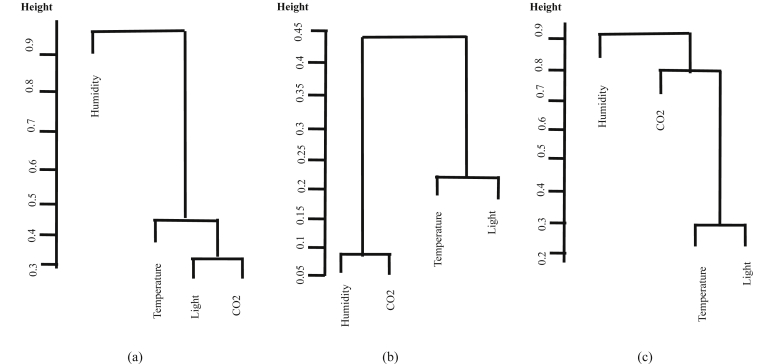
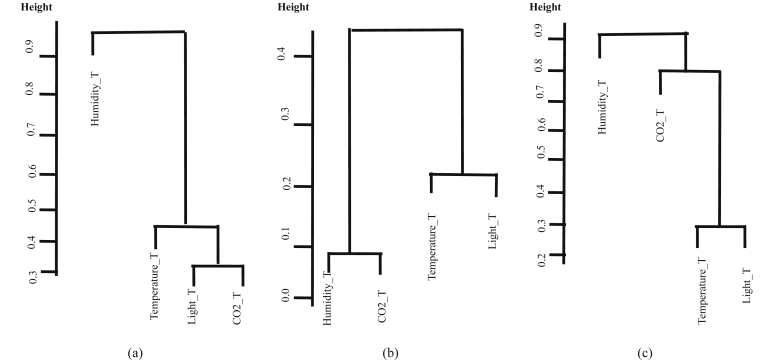
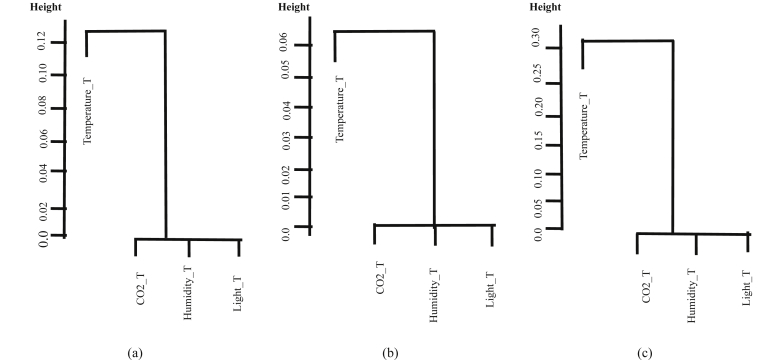
Figs. 4, 5, and 6 show dendrograms for the five versions of the data set. For NS and NS_all, the truth membership values were used for drawing the dendrograms. There are four interesting observations from these dendrograms:
-
1.
Dendrograms for Original, NS, Norm, and Norm_all are similar.
-
2.
Dendrograms for Training, Testing 1, and Testing 2 are different for Original, NS, Norm, and Norm_all.
-
3.
Dendrograms for NS_all are different from the others.
-
4.
Dendrograms for Training, Testing 1, and Testing 2 are similar for NS_all.
Fig. 4.
Original, Norm, and Norm_all sets dendrograms for (a) Training, (b) Testing 1, and (c) Testing 2.
Fig. 5.
NS set dendrograms for (a) Training, (b) Testing 1, and (c) Testing 2.
Fig. 6.
NS_all set dendrograms for (a) Training, (b) Testing 1, and (c) Testing 2.
From these observations, it is concluded that only NS_all dendrograms preserve the correlation between the four variables despite the values changes in training, testing 1, and testing 2 sets. This conclusion is drawn from dealing with four sensors vectors as one 2D matrix, which gives a chance for each sensor data to affect the other sensors during the conversion process. Changing the location of sensors in the monitored area can affect measurement readings. Hence, using NS_all version can solve the models retraining problem each time they are relocated. These dendrograms help in interpreting the results of F2D and F2F fusions results mentioned in the following sections.
4.1. F2D fusion results
Before presentation of the results, it would be convenient to explain how RF, LDA, and FUGE work. RF is an ensemble algorithm for classification and regression. It works by creating a number of decision trees at training time. While the output in regression is the mean prediction of the trees, it is the mode of the predicted classes in classification. Decision trees, as a non-parametric algorithm, suffer from the problem of overfitting which results in high variance. RF improved the problem of overfitting in decision trees by choosing a random sample of m features as split candidates rather than choosing the most optimal split-point among all features in the training data set. Hence, the predictions from the RF trees will be less correlated and this leads to a reduction in decision trees variance. As for LDA, it is a parametric probability-based method for classification. A parametric method assumes that the data follows a specific distribution which is Gaussian in case of LDA. Even though LDA assumes normality of data, it is still reliable when the multivariate normality is violated [45]. LDA representation consists of statistical properties calculated from the training data for each class. The statistical properties for a single input are the mean value for each class and the variance calculated across all classes. In case of multiple inputs, the statistical properties are the mean vector for each class and the common covariance matrix to all classes. LDA uses Bayes' theorem to estimate the probability of the output class given the input. For classifying a new data observation, a discriminate value for each class is calculated based on the statistical properties obtained from the training phase and the data is assigned to the class with the largest value [46]. Lastly, FUGE is an evolutionary algorithm for fuzzy systems. It uses a genetic algorithm to generate a random population of fuzzy systems. The fuzzy systems contain fuzzy logic rules used after that for the prediction. The generated fuzzy systems are tested using the training data. The systems with best accuracies are used to generate the population for the next generation using crossover and mutation. At the end of algorithm execution, the system with best accuracy is returned. FUGE suffers from overfitting, because the generated rules fit the training data [42].
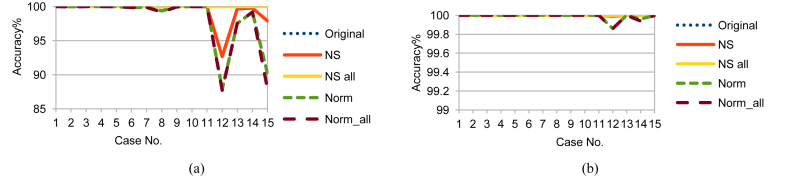
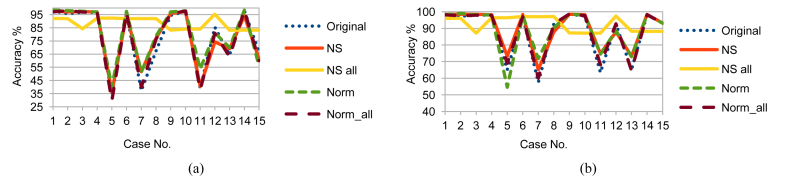
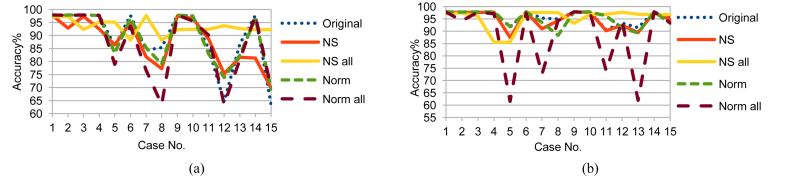
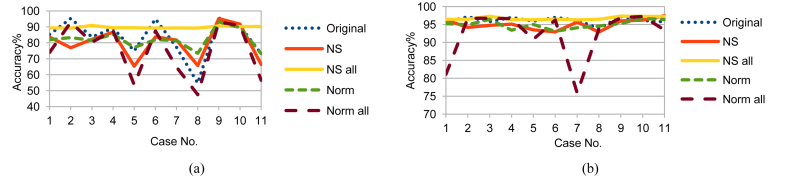
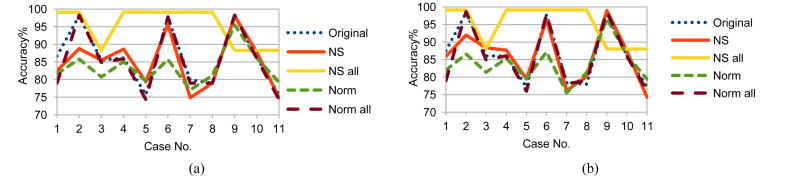
Moving on to the results, Figs. 7, 8, and 9 show the RF prediction accuracy on Training, Testing 1, and Testing 2 data with and without using the previously mentioned two time parameters: NSM and WS. Accordingly, using NS_all greatly improved the accuracy range more than the usage of any of the other sets. Not to mention that including time parameters NSM and WS enhanced accuracy even more. So, the following key points can be concluded:
-
1.
Using the time parameters, NS_all provided a stable accuracy above 96 % for all cases that included Temp feature and went down to 87.14% in accuracy for cases that excluded Temp feature. This is a logical result because, from the previous dendrograms, CO2, H, and L are alternatives, but Temp is mandatory.
-
2.
Although Testing 1 and Testing 2 data sets have different sensors measurements, NS_all provided similar accuracy ranges for them. The reason is that NS_all discovered the consistant correlation of the four variables in the Training, Testing 1, and Testing 2. Unfortunately, Original, NS, Norm, and Norm_all failed to do that.
-
3.
Using NS_all is promising for critical applications, especially security applications. Using any of CO2, L, or H with Temp provides good accuracy. If some sensors are damaged intentionally or unintentionally and the worst case happened, the accuracy of 87.14% is more acceptable than the worst cases of the other sets.
Fig. 7.
RF testing accuracy on Training data (a) without and (b) with NSM and WS.
Fig. 8.
RF testing accuracy on Testing 1 data (a) without and (b) with NSM and WS.
Fig. 9.
RF testing accuracy on Testing 2 data (a) without and (b) with NSM and WS.
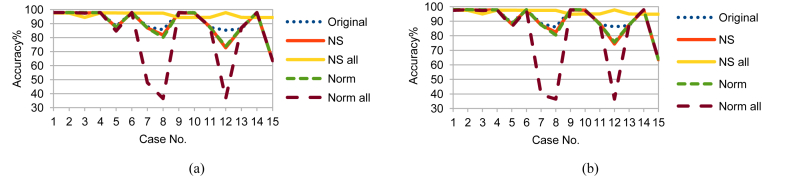
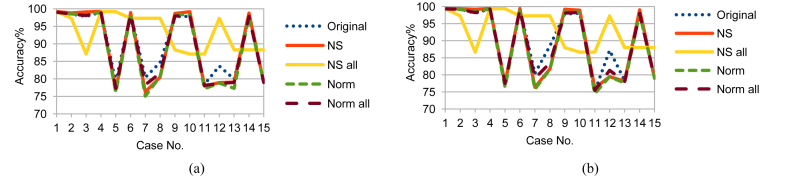
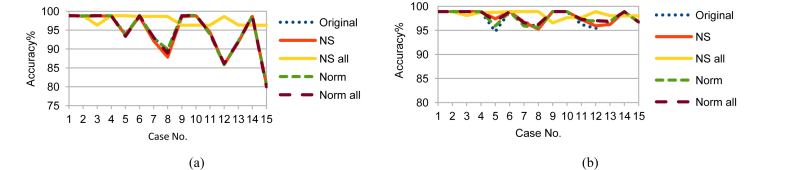
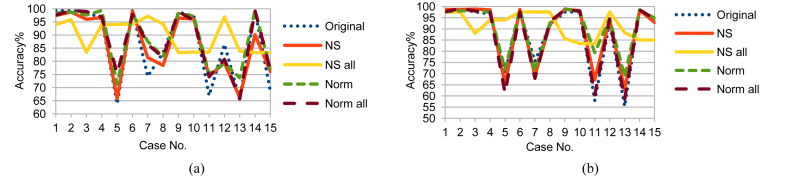
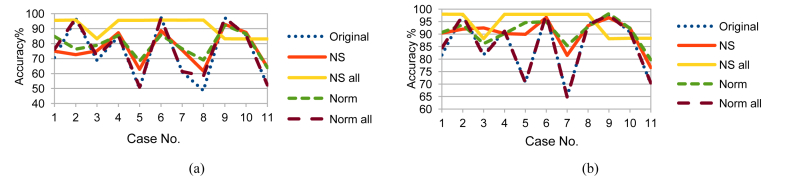
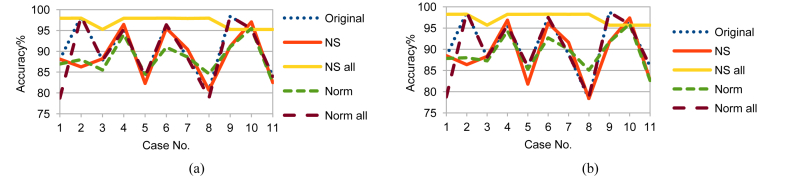
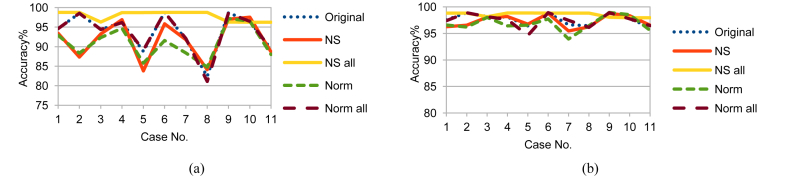
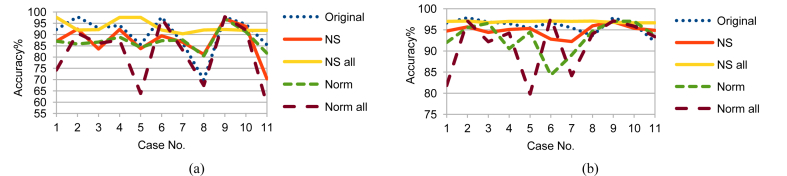
Although LDA, FUGE, and RF are from different MLAs categories, NS_all had the same effect on LDA and FUGE results as on RF ones; but with different prediction accuracy ranges as shown in Figs. 10, 11, and 12 for LDA and Figs. 13, 14, and 15 for FUGE. Using time parameters did not significantly affect the prediction accuracy of LDA. Because LDA is a parametric MLA, as mentioned in the beginning of this section; adding the time parameters to the data made a small effect on the estimated parameters (mean and covariance) calculated by LDA in the training phase. Thus, LDA has low variance in learning function estimation if training data was changed. On the contrary, RF provided better accuracy ranges using time parameters. Adding the time parameters to the input of RF changed the combinations of randomly selected split features and this in turn changed the structures of created decision trees. As a result, the predictions from the trees were less correlated and the high variance of the decision trees was reduced. Consequently, the prediction accuracy improved. Regarding the effect of using time parameters on FUGE, the latter's overfitting causes degrading in accuracy for all the data sets except for NS_all. NS_all overcomes the overfitting by preserving a consistent correlation of the four variables in the Training, Testing 1, and Testing 2. So, only NS_all provides a small enhancement through using time parameters.
Fig. 10.
LDA testing accuracy on Training data (a) without and (b) with NSM and WS.
Fig. 11.
LDA testing accuracy on Testing 1 data (a) without and (b) with NSM and WS.
Fig. 12.
LDA testing accuracy on Testing 2 data (a) without and (b) with NSM and WS.
Fig. 13.
FUGE testing accuracy on Training data (a) without and (b) with NSM and WS.
Fig. 14.
FUGE testing accuracy on Testing 1 data (a) without and (b) with NSM and WS.
Fig. 15.
FUGE testing accuracy on Testing 2 data (a) without and (b) with NSM and WS.
4.2. F2F fusion results
Based on the two NFF methods described in Section 3, the F2F fusion equation can be produced visually using dendrograms of Training sets in Figs. 4, 5, and 6 or using the correlation matrices of Training sets in Tables 4, 5, and 6. The dendrograms in Figs. 4, 5, and 6 are for all features case. For other cases, dendrograms need to be redrawn. Table 7 contains the fusion equations for all 11 possible cases. The first column is case number. The second, the third, and the fourth columns are for fusion equations.
Table 4.
Original, Norm, and Norm_all training sets correlation matrix.
| Temperature | Humidity | Light | CO2 | |
|---|---|---|---|---|
| Temperature | 1.00 | -0.14 | 0.65 | 0.56 |
| Humidity | -0.14 | 1.00 | 0.04 | 0.44 |
| Light | 0.65 | 0.04 | 1.00 | 0.66 |
| CO2 | 0.56 | 0.44 | 0.66 | 1.00 |
Table 5.
NS training set correlation matrix.
| Temperature_T | Humidity_T | Light_T | CO2_T | |
|---|---|---|---|---|
| Temperature_T | 1.00 | -0.14 | 0.65 | 0.56 |
| Humidity_T | -0.14 | 1.00 | 0.04 | 0.44 |
| Light_T | 0.65 | 0.04 | 1.00 | 0.67 |
| CO2_T | 0.56 | 0.44 | 0.67 | 1.00 |
Table 6.
NS_all training set correlation matrix.
| Temperature_T | Humidity_T | Light_T | CO2_T | |
|---|---|---|---|---|
| Temperature_T | 1.00 | 0.87 | 0.87 | 0.87 |
| Humidity_T | 0.87 | 1.00 | 1.00 | 1.00 |
| Light_T | 0.87 | 1.00 | 1.00 | 1.00 |
| CO2_T | 0.87 | 1.00 | 1.00 | 1.00 |
Table 7.
F2F fusion equations.
| Case No. | Original, Norm, Norm_all | NS | NS_all |
|---|---|---|---|
| 1 | (H)*Temp*(L + CO2) | (H)*Temp*(L + CO2) | Temp_T*(H_T + L_T + CO2_T) |
| 2 | (H)*(L + Temp) | (H)*(L + Temp) | Temp_T*(H_T + L_T) |
| 3 | (H)*(L + CO2) | (H)*(L + CO2) | (CO2_T + H_T + L_T) |
| 4 | Temp*(L + CO2) | Temp*(L + CO2) | Temp_T*(L_T + CO2_T) |
| 5 | (H)*(Temp + CO2) | (H)*(Temp + CO2) | Temp_T*(H_T + CO2_T) |
| 6 | (L + Temp) | (L + Temp) | Temp_T*(L_T) |
| 7 | (Temp + CO2) | (Temp + CO2) | Temp_T*(CO2_T) |
| 8 | (H)*(Temp) | (H)*(Temp) | Temp_T*(H_T) |
| 9 | (H)*(L) | (H)*(L) | (H_T + L_T) |
| 10 | (L + CO2) | (L + CO2) | (L_T + CO2_T) |
| 11 | (H)*(CO2) | (H)*(CO2) | (H_T + CO2_T) |
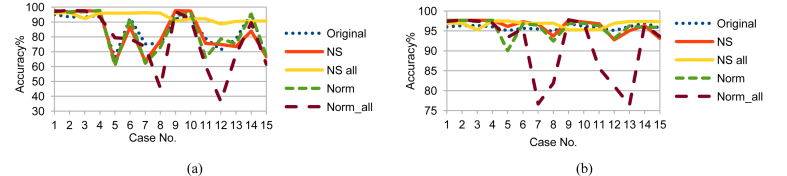
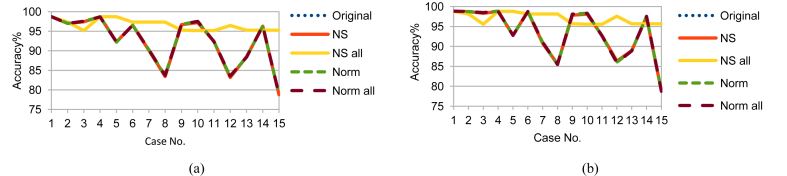
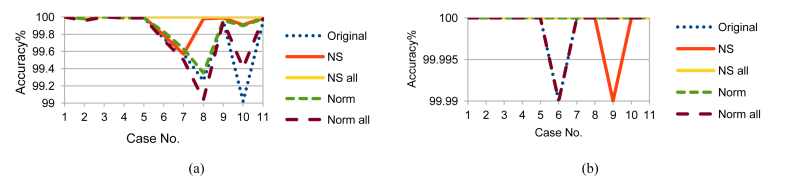
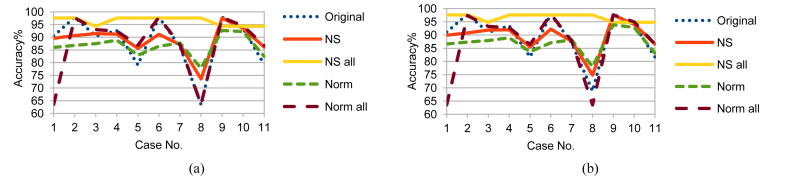
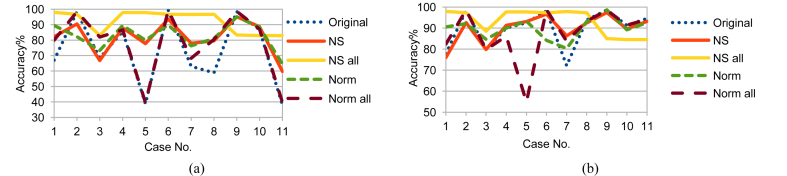
Using F2F fusion produced only one feature for training, therefore, it saved some computation time. It also showed better accuracy than F2D fusion for all the five data set versions as shown in Figs. 16, 17, 18, 19, 20, 21, 22, 23, and 24. From Figs. 16, 17, and 18, applying F2F fusion enhanced the accuracy ranges especially the minimum bound. Although using RF without time parameters showed enhancement in the other sets results, NS_all results are still the best. On using RF with time parameters, NS_all showed the best results and the minimum bound raised from 87.14 to 88.16. In case of using LDA without time parameters, Figs. 19, 20, and 21, NS_all had the best results and the minimum bound raised from 87.09 to 88.27. However, including time parameters provided similar results for NS_all and some enhancement for the other sets. Nevertheless, NS_all provided results that are better, compared to the other sets. As for using FUGE, Figs. 22, 23, and 24, with time parameters, the accuracy was higher than without using them. Also, NS_all provided the best accuracy range. The prediction accuracy ranges for F2D and F2F fusions are summarized in Table 8.
Fig. 16.
Testing accuracy of RF F2F fusion on Training data (a) without and (b) with NSM and WS.
Fig. 17.
Testing accuracy of RF F2F fusion on Testing 1 data (a) without and (b) with NSM and WS.
Fig. 18.
Testing accuracy of RF F2F fusion on Testing 2 data (a) without and (b) with NSM and WS.
Fig. 19.
Testing accuracy of LDA F2F fusion on Training data (a) without and (b) with NSM and WS.
Fig. 20.
Testing accuracy of LDA F2F fusion on Testing 1 data (a) without and (b) with NSM and WS.
Fig. 21.
Testing accuracy of LDA F2F fusion on Testing 2 data (a) without and (b) with NSM and WS.
Fig. 22.
Testing accuracy of FUGE F2F fusion on Training data (a) without and (b) with NSM and WS.
Fig. 23.
Testing accuracy of FUGE F2F fusion on Testing 1 data (a) without and (b) with NSM and WS.
Fig. 24.
Testing accuracy of FUGE F2F fusion on Testing 2 data (a) without and (b) with NSM and WS.
Table 8.
Prediction accuracy ranges summary.
| Original |
NS |
NS ALL |
Norm |
Norm ALL |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Worst | Best | Worst | Best | Worst | Best | Worst | Best | Worst | Best | |
| RF-without NSM, WS | 34.02 | 100 | 36.16 | 100 | 83.1 | 100 | 40.18 | 100 | 29.54 | 100 |
| RF-with NSM, WS | 57.51 | 100 | 65.14 | 100 | 87.14 | 100 | 54.58 | 100 | 60.08 | 100 |
| RF fusion-without NSM, WS | 48.6 | 100 | 61.66 | 100 | 83.12 | 100 | 63.96 | 100 | 47.5 | 100 |
| RF fusion-with NSM, WS | 65.1 | 100 | 76.62 | 100 | 88.16 | 100 | 79.76 | 100 | 64.74 | 100 |
| LDA-without NSM, WS | 63.53 | 99.13 | 63.53 | 99.25 | 87.09 | 99.17 | 63.53 | 99 | 36.47 | 99.05 |
| LDA-with NSM, WS | 63.53 | 99.35 | 63.53 | 99.42 | 86.66 | 99.38 | 63.53 | 99.32 | 36.47 | 99.33 |
| LDA fusion-without NSM, WS | 63.53 | 98.4 | 73.58 | 98.03 | 88.27 | 99.16 | 77.04 | 95.49 | 63.53 | 98.4 |
| LDA fusion-with NSM, WS | 68.78 | 98.74 | 74.25 | 98.98 | 88.01 | 99.16 | 75.5 | 96.67 | 63.53 | 98.74 |
| FUGE-without NSM, WS | 63.53 | 99.33 | 65.79 | 99.1 | 83.34 | 98.83 | 69.46 | 99.37 | 63.53 | 99.32 |
| FUGE-with NSM, WS | 55.38 | 98.91 | 62.87 | 98.93 | 83.45 | 98.92 | 68.68 | 98.96 | 58.43 | 99.08 |
| FUGE fusion-without NSM, WS | 37.97 | 99.32 | 59.76 | 97.54 | 82.93 | 98.76 | 64.63 | 97.21 | 39.49 | 99.32 |
| FUGE fusion-with NSM, WS | 72.14 | 98.91 | 76.02 | 98.78 | 84.55 | 98.85 | 80.33 | 98.94 | 54.91 | 98.91 |
The observations from Table 8 and Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, and 24 can be summarized as follows:
-
•
Using NS provides better accuracy range than using the original data.
-
•
NS_all provides a stable and good accuracy for all cases that include Temp feature and acceptable accuracy for cases that exclude Temp feature.
-
•
NS_all provides similar accuracy ranges for Testing1 and Testing2, despite their different data values.
-
•
Using NS_all is promising for critical applications, especially security applications; because of its acceptable accuracy in worst cases.
-
•
Using F2F based on features correlation enhances the accuracy and increases the lower bound of accuracy ranges. Also, it is computationally efficient owing to the use of one fused feature for training and testing.
-
•
All advantages provided by NS_all are due to the ability of NS_all to discover the consistent correlation among the features.
-
•
Using Neutrosophic sets, NS or NS_all, as a certain data provides better accuracy than using the original data.
5. Conclusion
This paper presented a new sensor fusion method for occupancy detection based on using neutrosophic sets and sensors correlations. This method benefited from the numerous advantages of using neutrosophic sets. One of these advantages is enhancing the occupancy detection accuracy. It is also computationally efficient which means saving energy and improving the speed of detection. Moreover, it is promising for critical applications especially security applications because of its acceptable accuracy in the worst cases. The experimental results showed that the usage of either features-to-decision or features-to-feature neutrosophic fusions provides better accuracy ranges than using the original or normalized data. However, features-to-feature fusion based on the features' correlation is more efficient and provides better accuracy than features-to-decision fusion.
Declarations
Author contribution statement
N. Fayed: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
M. Abu-ElKheir, E. El- Daydamony, A. Atwan: Conceived and designed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
Data associated with this study has been deposited at https://archive.ics.uci.edu/ml/datasets/Occupancy+Detection+.
References
- 1.Kraipeerapun P., Amornsamankul S. ACM; 2017. Room Occupancy Detection Using Modified Stacking. [Google Scholar]
- 2.Candanedo L.M., Feldheim V., Deramaix D. A methodology based on Hidden Markov Models for occupancy detection and a case study in a low energy residential building. Energy Build. 2017;148:327–341. [Google Scholar]
- 3.Candanedo L.M., Feldheim V. Accurate occupancy detection of an office room from light, temperature, humidity and CO2 measurements using statistical learning models. Energy Build. 2016;112:28–39. [Google Scholar]
- 4.Lam K.P. Occupancy detection through an extensive environmental sensor network in an open-plan office building. IBPSA Build. Simulat. 2009;145:1452–1459. [Google Scholar]
- 5.Dong B. An information technology enabled sustainability test-bed (ITEST) for occupancy detection through an environmental sensing network. Energy Build. 2010;42(7):1038–1046. [Google Scholar]
- 6.Ekwevugbe T. IEEE; 2013. Real-time Building Occupancy Sensing Using Neural-Network Based Sensor Network. [Google Scholar]
- 7.Ekwevugbe T., Brown N., Pakka V. 2013. Realt-time Building Occupancy Sensing for Supporting Demand Driven Hvac Operations. [Google Scholar]
- 8.Ortega J.G. Science and Information Conference (SAI). 2015. IEEE; 2015. A machine-learning based approach to model user occupancy and activity patterns for energy saving in buildings. [Google Scholar]
- 9.Chen Z., Masood M.K., Soh Y.C. A fusion framework for occupancy estimation in office buildings based on environmental sensor data. Energy Build. 2016;133:790–798. [Google Scholar]
- 10.Funiak S. Proceedings of the 5th International Conference on Information Processing in Sensor Networks. ACM; 2006. Distributed localization of networked cameras. [Google Scholar]
- 11.Trivedi M., Kohsia H., Mikic I. Systems, Man, and Cybernetics. IEEE International Conference on. 2000. IEEE; 2000. Intelligent environments and active camera networks. [Google Scholar]
- 12.Dong B., Andrews B. Proceedings of Building Simulation. 2009. Sensor-based occupancy behavioral pattern recognition for energy and comfort management in intelligent buildings. [Google Scholar]
- 13.Hailemariam E. Proceedings of the 2011 Symposium on Simulation for Architecture and Urban Design. Society for Computer Simulation International; 2011. Real-time occupancy detection using decision trees with multiple sensor types. [Google Scholar]
- 14.Yang Z. Proceedings of the 2012 Symposium on Simulation for Architecture and Urban Design. Society for Computer Simulation International; 2012. A multi-sensor based occupancy estimation model for supporting demand driven HVAC operations. [Google Scholar]
- 15.Ebadat A. Proceedings of the 5th ACM Workshop on Embedded Systems for Energy-Efficient Buildings. ACM; 2013. Estimation of building occupancy levels through environmental signals deconvolution. [Google Scholar]
- 16.Ekwevugbe T., Brown N., Fan D. Digital Ecosystems Technologies (DEST) 6th IEEE International Conference on. 2012. IEEE; 2012. A design model for building occupancy detection using sensor fusion. [Google Scholar]
- 17.Yang Z. A systematic approach to occupancy modeling in ambient sensor-rich buildings. Simulation. 2014;90(8):960–977. [Google Scholar]
- 18.Ai B., Fan Z., Gao R.X. American Control Conference (ACC) IEEE; 2014. Occupancy estimation for smart buildings by an auto-regressive hidden Markov model. [Google Scholar]
- 19.Jiang C. Indoor occupancy estimation from carbon dioxide concentration. Energy Build. 2016;131:132–141. [Google Scholar]
- 20.Zhao H. Circuits and Systems (ISCAS), 2016 IEEE International Symposium on. IEEE; 2016. Learning-based occupancy behavior detection for smart buildings. [Google Scholar]
- 21.Hua Q. Intelligent Human-Machine Systems and Cybernetics (IHMSC), 2016 8th International Conference on. IEEE; 2016. Occupancy detection in smart buildings using Support vector regression method. [Google Scholar]
- 22.Ryu S.H., Moon H.J. Development of an occupancy prediction model using indoor environmental data based on machine learning techniques. Build. Environ. 2016;107:1–9. [Google Scholar]
- 23.Chaney J., Owens E.H., Peacock A.D. An evidence based approach to determining residential occupancy and its role in demand response management. Energy Build. 2016;125:254–266. [Google Scholar]
- 24.Tutuncu K., çataltaş Ö., Koklu M. Occupancy detection through light, temperature, humidity and CO2 sensors using ANN. Int. J. Indus. Electronics Electrical Eng. (IJIEEE) 2017;5:63–67. [Google Scholar]
- 25.Jin M. Occupancy detection via environmental sensing. IEEE Trans. Autom. Sci. Eng. 2018;15(2):443–455. [Google Scholar]
- 26.Alghamdi D. Occupancy detection: a data mining approach. Int. J. Sci. Eng. Res. 2016;7 [Google Scholar]
- 27.Huang Q., Mao C. Occupancy estimation in smart building using hybrid CO2/light wireless sensor network. J. Appl. Sci. Arts. 2017;1(2):5. [Google Scholar]
- 28.Pedersen T.H., Nielsen K.U., Petersen S. Method for room occupancy detection based on trajectory of indoor climate sensor data. Build. Environ. 2017;115:147–156. [Google Scholar]
- 29.Christodoulou P., Christoforou A., Andreou A.S. A hybrid prediction model integrating fuzzy cognitive Maps with Support vector machines. ICEIS. 2017;1 [Google Scholar]
- 30.Improving Dalila. 2017. Prediction of Office Room Occupancy through Random Sampling.https://www.datasciencecentral.com/profiles/blogs/improving-prediction-of-office-room-occupancy-through-random cited 2018; Available from: [Google Scholar]
- 31.Luppe C., Shabani A. Electrical and Computer Engineering (CCECE), 2017 IEEE 30th Canadian Conference on. IEEE; 2017. Towards reliable intelligent occupancy detection for smart building applications. [Google Scholar]
- 32.Masood M.K., Soh Y.C., Jiang C. Occupancy estimation from environmental parameters using wrapper and hybrid feature selection. Appl. Soft Comput. 2017;60:482–494. [Google Scholar]
- 33.Hao J. Visible light based occupancy inference using ensemble learning. IEEE Access. 2018;6:16377–16385. [Google Scholar]
- 34.Kim S.H., Moon H.J. Case study of an advanced integrated comfort control algorithm with cooling, ventilation, and humidification systems based on occupancy status. Build. Environ. 2018;133:246–264. [Google Scholar]
- 35.Jeon Y. IoT-based occupancy detection system in indoor residential environments. Build. Environ. 2018 [Google Scholar]
- 36.Feller W. Vol. 2. John Wiley & Sons; 2008. (An Introduction to Probability Theory and its Applications). [Google Scholar]
- 37.Zimmermann H.J. Fuzzy set theory. Wiley Interdiscip. Rev.: Comput. Stat. 2010;2(3):317–332. [Google Scholar]
- 38.Smarandache F. 1998. Neutrosophy: Neutrosophic Probability, Set, and Logic: Analytic Synthesis & Synthetic Analysis. [Google Scholar]
- 39.Smarandache F. Neutrosophic logic-A generalization of the intuitionistic fuzzy logic. Multispace Multistructure Neutrosophic Transdisciplinarity (100 Collected Papers of Science) 2010;4:396. [Google Scholar]
- 40.Rabounski D., Smarandache F., Borissova L. Neutrosophic methods in general relativity. Inf. Stud. 2005;10 [Google Scholar]
- 41.Singala R., Agrawal A. Signal Processing and Information Technology (ISSPIT), 2014 IEEE International Symposium on. IEEE; 2014. Evaluation schema for SAR image segmentation based on swarm optimization in neutrosophic domain. [Google Scholar]
- 42.Bujard A. 2012. fugeR: FUzzy GEnetic, a Machine Learning Algorithm to Construct Prediction Model Based on Fuzzy Logic.https://rdrr.io/cran/fugeR/ Available from: [Google Scholar]
- 43.Candanedo L. 2016. UCI Machine Learning Repository: Occupancy Detection Data Set.https://archive.ics.uci.edu/ml/datasets/Occupancy+Detection+ cited 2018; Available from: [Google Scholar]
- 44.Candanedo L. 2015. Occupancy-detection-data.https://github.com/LuisM78/Occupancy-detection-data cited 2018; Available from: [Google Scholar]
- 45.Klecka W.R., Iversen G.R. Vol. 19. Sage; 1980. (Discriminant Analysis). [Google Scholar]
- 46.James G. Vol. 112. Springer; 2013. (An Introduction to Statistical Learning). [Google Scholar]