Skip to main content
PMC home page
Molecular Biology of the Cell logoLink to Molecular Biology of the Cell
. 2019 Sep 1;30(19):2458–2468. doi: 10.1091/mbc.E19-04-0227

Cell shape and intercellular adhesion regulate mitotic spindle orientation

Jingchen Li a, Longcan Cheng a, Hongyuan Jiang a,*
Editor: Alex Mogilnerb
PMCID: PMC6743358  PMID: 31411941

Abstract

Cell division orientation plays an essential role in tissue morphogenesis and cell fate decision. Recent studies showed that either cell shape or adhesion geometry can regulate the orientation of mitotic spindles and thereby the cell division orientation. However, how they together regulate the spindle orientation remains largely unclear. In this work, we use a general computational model to investigate the competitive mechanism of determining the spindle orientation between cell shape and intercellular adhesion in epithelial cells. We find the spindle orientation is dominated by the intercellular adhesion when the cell shape anisotropy is small, but dominated by the cell shape when the shape anisotropy is large. A strong adhesion and moderate adhesive size can ensure the planar division of epithelial cells with large apico-basal elongation. We also find the spindle orientation could be perpendicular to the adhesive region when only one side of the cell is adhered to an E-cadherin–coated matrix. But after the cell is compressed, the spindle orientation is governed by the cell shape and the spindle will be parallel to the adhesive region when the cell shape anisotropy is large. Finally, we demonstrate the competition between cell shape and tricellular junctions can also effectively regulate the spindle orientation.

INTRODUCTION

The orientation of the cell-division axis determines the positions of daughter cells in a tissue and thereby is crucial to the tissue morphogenesis and cell fate decisions (Théry and Bornens, 2006; di Pietro et al., 2016). Misoriented cell division can result in various developmental disorders (Gillies and Cabernard, 2011; Williams et al., 2011; Lancaster and Knoblich, 2012) and may also be responsible for the tumor progression (Caussinus and Gonzalez, 2005; Pease and Tirnauer, 2011; Nakajima et al., 2013). Cell division orientation is coupled to the mitotic spindle orientation. More than 100 years ago, the cell shape had been thought of as a determinant of spindle orientation, which is known as the "long axis rule" (Hertwig, 1884). Recent studies also confirmed the correlation between the cell shape and the spindle orientation (O’Connell and Wang, 2000; Strauss et al., 2006; Minc et al., 2011; Xiong et al., 2014; Li and Jiang, 2018). However, in many frequently used systems, the adhesion geometry (Théry et al., 2005, 2007; Matsumura et al., 2016), cell polarity (Siller and Doe, 2009; Williams and Fuchs, 2013), or extracellular mechanical force (Fink et al., 2011; Hart et al., 2017; Scarpa et al., 2018; Finegan et al., 2019) sometimes could override the cell shape to determine the spindle orientation.

In general, the long axis of the interphase cell is consistent with the principal direction of the extracellular force or anisotropic adhesion, because these factors can elongate the cell during the interphase (Théry et al., 2005; Fink et al., 2011; Wyatt et al., 2015; Bosveld et al., 2016). Therefore, the spindle orientation is usually along the long axis of the cell as well as the principal direction of extracellular force or adhesion. It is difficult to distinguish their individual influences on the spindle orientation.

However, this is not always the case. Recent experiments have found some cues about the competition between the cell shape and adhesion. For example, the division of epithelia is usually planar, that is, parallel to the monolayer plane, to maintain the single-layered tissue architecture (Ragkousi and Gibson, 2014) (Figure 1, A and B). If the cell rounding is inhibited during the mitotic phase, the spindle could orient along the apico-basal axis due to the columnar shape of the epithelial cell (Chanet et al., 2017). Furthermore, when one cell spreads on the two-dimensional substrate, the spindle orientation is usually parallel to the substrate due to the pulling of retraction fibers. When the cell is covered by another adhesive surface-coated fibronectin, the spindle orientation tends to be perpendicular to the substrate due to the symmetric distribution of traction fibers on both adhesive surfaces (Petridou and Skourides, 2014). Interestingly, if the cell is spreading on the substrate coated with E-cadherin as an artificial intercellular adhesion, the spindle orientation also becomes perpendicular to the substrate (Gloerich et al., 2017). This might be induced by coupling the spindle orientation with the intercellular adhesion through E-cadherin, which can recruit the LGN/NuMA complex and apply pulling forces on microtubules through associated dyneins (Peyre et al., 2011; Gloerich et al., 2017; Wang et al., 2018).

FIGURE 1:

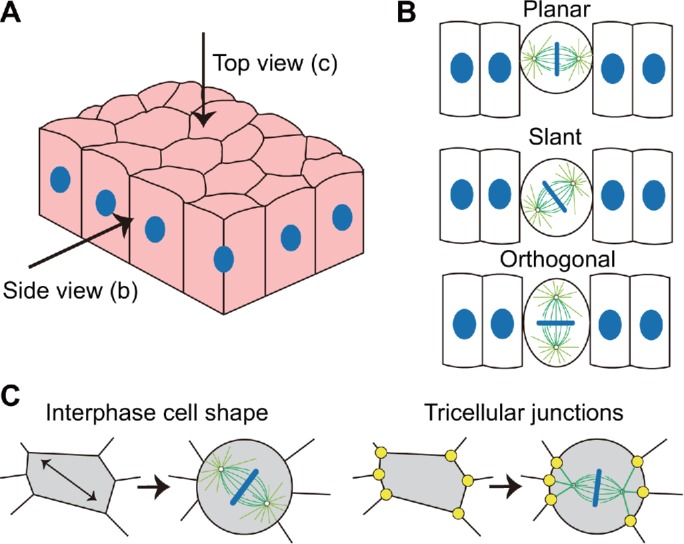
FIGURE 1:

Open in a new tab

Schematics of the epithelial tissue and the mitotic spindle orientation. (A) Schematics of the epithelial tissue. (B) The spindle orientation is planar, slant, or orthogonal in the side view. (C) The spindle orientation within the tissue plane observed in the top view. It can be regulated by either the polygonal cell shape (Wyatt et al., 2015) or the TCJs (Bosveld et al., 2016).

In addition to the competition between the planar and orthogonal directions (Figure 1B), the mitotic spindle of epithelial cells also need to select its horizontal orientation in the top view when the spindle is parallel to the tissue plane (Figure 1C). The spindles of epithelial cells, which usually have the polygonal shapes in the top view during the interphase, could orient either along their long axes (Wyatt et al., 2015) or along the tricellular junction (TCJ) polarity (Bosveld et al., 2016). The TCJs can act as force generators pulling astral microtubules and orienting cell division via the dynein-associated protein Mud (Drosophila homologue of NuMA) (Bosveld et al., 2016). If the anisotropy of interphase cell shape is large, the spindle can orient along the long axis of the cell. In contrast, the spindle orientation could be predicted by the TCJ polarity more successfully when the anisotropy of interphase cell shape is small (Bosveld et al., 2016). Moreover, when the cell monolayer is stretched, the spindle tends to orient along the long axis of the interphase cell shape (Hart et al., 2017; Wyatt et al., 2015). However, if the epithelial cell monolayer sustains a lower, more physiologically relevant uniaxial stretch (∼12% strain), a part of spindles could align with the stretch axis regardless of the long axis of the interphase cell shape (Hart et al., 2017).

These experiments suggest that the intercellular adhesion and cell shape can both regulate the spindle orientation in epithelial cells. If their polarities are different, the two mechanisms may compete with each other. It has been shown that both the intercellular adhesion (Peyre et al., 2011; Bosveld et al., 2016; Chanet et al., 2017; Gloerich et al., 2017) and the cell shape (Théry and Bornens, 2006; Minc et al., 2011; Pierre et al., 2016; Li and Jiang, 2018) could orient the spindle by exerting forces on astral microtubules. Therefore, their cooperation or competition should be actually implemented by their resultant forces on the mitotic spindle. However, how these coupling mechanisms regulate the spindle orientation is still elusive.

In this paper, we use a general computational model to investigate how the spindle orientation is determined by the competition between the intercellular adhesion and cell shape in the top view and side view of the epithelial tissue (Figure 1). Our results not only quantitatively explain many existing experiment phenomena but also provide many interesting predictions that can be verified in future experiments.

RESULTS

The model reproduces the positioning and orientation of mitotic spindles in different cell shapes and adhesion geometries

The mitotic spindle is a bipolar structure consisting of large numbers of microtubules and various molecular motors (McIntosh et al., 2012). We have developed a general model for mitotic spindles to study how cell size and cell shape regulate the positioning, orientation, and size regulation of mitotic spindles in our recent studies (Jiang, 2015; Li and Jiang, 2017, 2018). In this work, the original model is further improved (Figure 2, A and B), and we use two-dimensional (2D) simulations to investigate the orientation of mitotic spindles in different cell shapes and adhesion geometries. In brief, the model considers that microtubules are mainly nucleated from centrosomes and display dynamics, and the bipolar spindle structure can be kept stable through interactions among antiparallel microtubules and interactions between microtubules and chromosomes. Astral microtubules can interact with the cortex and generate pushing force by polymerization or pulling force by cortical dynein, so that the spindle can be positioned and oriented. Through dynamic simulation, we can reproduce the positioning and orientation of spindles (more details are provided in Materials and Methods and Supplemental Figures S1–S3 in the Supplemental Materials).

FIGURE 2:

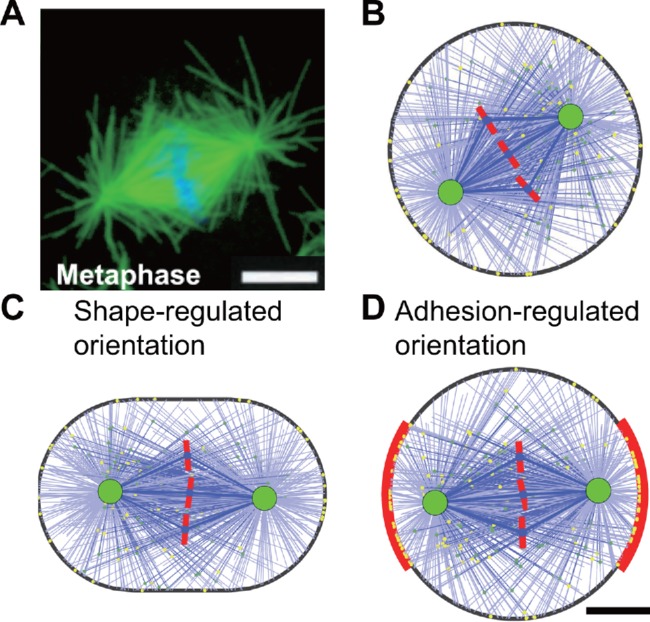
FIGURE 2:

Open in a new tab

(A) A typical metaphase mitotic spindle observed in the experiment (Rogers et al., 2002). Microtubules are labeled in green, and chromosomes are labeled in blue. (B) The simulated spindle in a round cell with the diameter of 20 µm (see also Supplemental Figure S4 and Supplemental Movie S1). (C) The simulated spindle in a stadium-shaped cell with the aspect ratio of 1.5 (see also Supplemental Figure S5 and Supplemental Movie S2). (D) The simulated spindle in a round cell with symmetric intercellular adhesion on the two sides (red region). The adhesive length L = 12 µm. The lateral adhesive region has a higher binding rate of cortical dynein than the other regions, and the ratio is k = 11 (see also Supplemental Figure S7). Scale bar: 5 µm.

First, the cell is regarded as a sphere with the diameter of 20 µm during the mitotic phase in the model. The spindles in the simulation can always be positioned to the cell center from random initial conditions, but the spindle orientation is randomly distributed since the cell shape and the cortical parameters are isotropic (Supplemental Figure S4 and Supplemental Movie S1). To define a specific orientation, we elongate the cell to a stadium shape (Figure 2C and Supplemental Figure S5) or an elliptical shape (Supplemental Figure S6), corresponding to the compression of the round cell (Fischer-Friedrich et al., 2014; Guild et al., 2017) or the stretching of the tissue (Gibson et al., 2011; Wyatt et al., 2015), respectively. The cell aspect ratio λ, that is, the ratio of the long axis to the short axis, is 1.5, and the cell volume (actually the area in the 2D simulation) is same as the round cell. In these cases, the spindle can also be positioned successfully, but always oriented along the long axis of the cell independently of the initial conditions (Supplemental Figures S5 and S6; Supplemental Movie S2). Therefore, astral microtubules can effectively sense cell shape and control the spindle orientation along the long axis.

Movie S1.

Download video file (11MB, mp4)
Open in a new tab

Positioning and orientation of simulated spindles in round cells without adhesion. Several examples show that the spindles in round cells without adhesion can always be positioned to the cell center from random initial conditions in the simulations, but the spindle orientation is randomly distributed since the cell shape and the cortical parameters are isotropic. The cell diameter is 20 µm.

Movie S2.

Download video file (12MB, mp4)
Open in a new tab

Positioning and orientation of simulated spindles in stretched-shaped cells without adhesion. In the cells with the stadium shape (left) or the elliptical shape (right), the spindles can always be positioned to the cell center and oriented along the long axis of the cell shape from random initial conditions in the simulations. The aspect ratio of the shape are all 1.5, and the area is the same as the 20 µm-diameter round cell. Two examples are provided for each shape.

Then, we define two symmetric parts of the cortex as the intercellular adhesive regions on the mitotic rounding epithelial cell (Figure 2D). The E-cadherin on the lateral adhesion can recruit the LGN/NuMA complex (Peyre et al., 2011; Gloerich et al., 2017). The Par3/Par6/aPKC complex can exclude LGN from the apical cortex to the lateral cortex, which leads to apico-basal polarity (Hao et al., 2010; Zheng et al., 2010). Both mechanisms can result in the consequence that the lateral cortex has a higher level of LGN/NuMA than the apical cortex, and thereby the lateral pulling force is larger due to more associated dyneins (Seldin et al., 2016). Therefore, we assume the lateral region has a much higher binding rate of cortical dynein than other regions (see Materials and Methods). It should also be noted that the distribution of LGN/NuMA complex can be changed by the cortical release and microtubule transport, but maintained by chromosome- and spindle-pole-derived signals after the spindle self-assembly (Kiyomitsu and Cheeseman, 2012; Zheng et al., 2013). For simplicity, we assume the parameters of the lateral region are unchanged over time. The binding rate of cortical dynein at the lateral adhesive region is assumed k = 11 times larger than at the other regions, and the size of the lateral adhesion region is assumed as L = 12 μm. More values of these two parameters and their influences will be discussed in the later sections. In this case, the spindle can also be positioned successfully, and the spindle orientation is perpendicular to the lateral adhesive region, that is, along the adhesion polarity (Figure 2D and Supplemental Figure S7). Owing to the increase of binding rate of dyneins at the adhesion region, binding microtubules will assemble there so that the pulling force generated at the adhesion region is larger than the other regions, and thus the spindle is pulled to orient along the adhesion direction. Therefore, either the cell shape or the intercellular adhesion geometry can regulate the spindle orientation in the simulation.

The competition between cell shape and bilateral intercellular adhesion determines spindle orientation in the side view of the epithelial tissue

Next, we consider the cell shape and the intercellular adhesion simultaneously to investigate the spindle orientation in the side view of Figure 1. The long axis of the columnar-shaped epithelial cell is usually along the apico-basal axis during the interphase, while the intercellular adhesion polarity is parallel to the tissue plane. If the cell rounding during the mitotic phase is inhibited, the cell shape remains elongated along the apico-basal axis, that is, perpendicular to the adhesion polarity (Chanet et al., 2017). We consider such a case in the simulation to figure out whether the spindle orientation aligns with the apico-basal cell shape or the planar adhesion polarity. Experiments showed that the cell shapes in the side view are complex, but share a common feature that the long axis is along the apico-basal axis (Chanet et al., 2017). Therefore, the cell shape is simplified as the stadium shape with a single long axis (Figure 3A).

FIGURE 3:

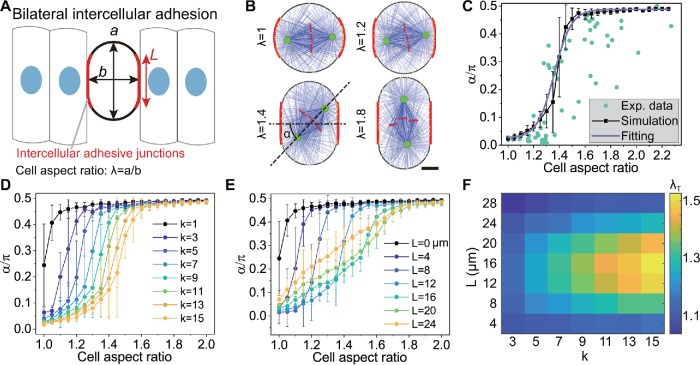
FIGURE 3:

Open in a new tab

Regulating the spindle orientation via the cell shape and the bilateral intercellular adhesion in the side view. (A) The schematic shows the cell shape and intercellular adhesion of a dividing epithelial cell in the 2D simulation. The cell is stadium-shaped, where the red segments represent the intercellular adhesion region. (B) The snapshots of simulated spindles in the cells with different aspect ratios, but the same adhesive length and adhesive strength (L = 12 µm, k = 11) (see also Supplemental Movie S3). Scale bar: 5 µm. (C) The spindle orientation quantified by the angle between the spindle axis and the adhesion polarity from (B) is plotted against the aspect ratio of the cell shape (mean ± SE, 50 simulations for each case, the same below). The green dots are the experimental data from Chanet et al. (2017). The solid line is the fitting of the simulation results by using Eq. 1. (D) The role of the adhesive strength in governing the spindle orientation. (E) The role of the adhesive length in governing the spindle orientation. The curves in D and E can also be fitted by Eq. 1 (not shown). (F) Through fitting, the critical aspect ratio λT can be obtained, and it is the function of the adhesive strength k and adhesive length L.

It should be noted that the adhesive region actually covers the lateral cylindrical surface of the cell, but the adhesive region becomes the bilaterally symmetric segments of the cortex in the 2D simulations (Figure 3A). We show that the spindle orientation transits from the horizontal to the orthogonal direction with the increase of the cell aspect ratio as the cell area is constant (Figure 3B and Supplemental Movie S3). Specifically, when the aspect ratio is small, the intercellular adhesion dominates, and the spindle orientation is horizontal (λ = 1.2 in Figure 3B). When the aspect ratio is large, the cell shape dominates, and the spindle orientation is orthogonal, that is, along the apico-basal axis (λ = 1.8 in Figure 3B). When the aspect ratio is medium, the spindle orientation is controlled by both the intercellular adhesion and the cell shape, and thereby it is slanted (λ = 1.4 in Figure 3B). When the adhesion parameters are chosen as k = 11 and L = 12 μm, the results are in agreement with the experimental data from Chanet et al. (2017), where the cell rounding was inhibited to various degrees to control the cell aspect ratio (Figure 3C). The curve can be fitted by a sigmoidal function:

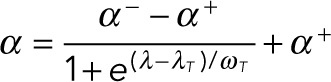graphic file with name mbc-30-2458-e001.jpg 1

where α is the spindle orientation, that is, the angle between the spindle axis and the horizontal direction (Figure 3B); λ is the aspect ratio of cell shape; α± are the limit values of the spindle orientation (α− = 0 and α+ = π/2); λT is the critical aspect ratio of cell shape, that is, the aspect ratio when α = (α− + α+)/2; and wT is a constant that reflects the width of the rising segment of the curve. Through fitting the experimental data (Chanet et al., 2017) with the numerical simulation (Figure 3C), we obtain the critical aspect ratio λT = 1.36.

Movie S3.

Download video file (11MB, mp4)
Open in a new tab

Orientation of simulated spindles in the cells with bilateral symmetric adhesion and various aspect ratios of the stadium shape. The stadium-shaped cells have the bilateral symmetric adhesion (red marked) whose parameters are k=11 and L=12 µm, and the aspect ratio is given as λ=1, 1.2, 1.4, or 2. In these cases, the stable spindle orientation transits from the horizontal to the orthogonal direction with the increase of the cell aspect ratio as the cell area is constant.

If the level of related proteins, such as E-cadherin or LGN/NuMA, is changed through the regulation of gene expression or corresponding chemical inhibitors (Peyre et al., 2011; Gloerich et al., 2017), the number of associated dyneins could be changed accordingly. To simulate this case, we can change the binding rate of cortical dyneins in the adhesive region. When the binding rate in the adhesive region is the same as the other region, that is, k = 1, the spindle orientation is completely decided by the cell shape (λT ∼1). That is, as long as the aspect ratio λ is larger than 1, the spindle tends to orient along the orthogonal direction, that is, the long axis of the cell (black line in Figure 3D). With the increase of the binding rate k in the adhesive region, the critical aspect ratio λT increases (Figure 3D), which indicates that a stronger intercellular adhesion can ensure more planar division in the epithelial tissue.

Moreover, we also change the adhesive length in the simulation to investigate the influence of the size of the adhesion area on the spindle orientation. We find that the critical aspect ratio increases with the adhesive length only when L ≤ 12 μm (∼20% of the cell perimeter; Figure 3E), but decreases if the adhesive length increases further (Figure 3E). This is because the polarity of the intercellular adhesion will be weakened when the adhesive length is too long and finally disappears when the whole cell is adhesive. Taken together, a strong adhesion and moderate adhesive length can generate a large critical aspect ratio λT, leading to more planar divisions in the epithelial tissue (Figure 3F).

Besides, we have investigated the role of other cortical parameters in the orientation process without adhesion in our recent work (Li and Jiang, 2018). To further investigate how the cortical parameters impact the spindle orientation when cell adhesion exists, we changed the unbinding rate of cortical dyneins as an example (Supplemental Figure S8). We find that the critical aspect ratio increases with the decrease of the unbinding rate. This is because the decrease of unbinding rate of dynein leads to the increase of the pulling–pushing ratio of cortical microtubules (Li and Jiang, 2018), and the adhesion polarity can have a stronger effect. Previously, we have also studied the spindle length regulation (Li and Jiang, 2017). Here we found that the critical aspect ratio increases with the spindle length through increasing the binding rate of cross-linking kinesins (Supplemental Figure S8). This indicates the adhesion polarity can have a stronger influence on the longer spindle.

It should be noted that the lateral adhesion region can be asymmetric due to the apico-basal cell polarity, that is, it is closer to the apical cortex during the interphase (Bergstralh et al., 2013). During the mitotic phase, the asymmetry in the lateral adhesion region may remain the same if the cell rounding is inhibited. Therefore, we further assume the adhesive region is asymmetric with 75% of the adhesion region closer to the apical cortex (Supplemental Figure S9). We found the results are similar to the symmetric cases as expected.

The competition between unilateral cell adhesion on E-cadherin–coated substrate and compressed cell shape determines spindle orientation

Above, we have shown that the competition between the bilateral intercellular adhesion and the cell shape can determine the spindle orientation. We then wondered how the spindle orientation is determined if only one side of the cell adheres to others. Previous studies showed that when the cell adheres to the E-cadherin–coated wall as an artificial intercellular adhesion, the mitotic spindle orientation is perpendicular to the wall (Gloerich et al., 2017). To study this phenomenon, we assumed only the bottom of the cell is the adhesive region (Figure 4A). On the basis of the experimental observation (Gloerich et al., 2017), we assumed that the adhesive length of the round cell is L = 7 μm. Simulations show the spindle orientation can be perpendicular to the substrate, which is in good agreement with the experimental result (Gloerich et al., 2017) (the case λ = 1 in Figure 4B; Supplemental Movie S4). This result also confirms that the unilateral adhesion is enough to control the spindle orientation.

FIGURE 4:

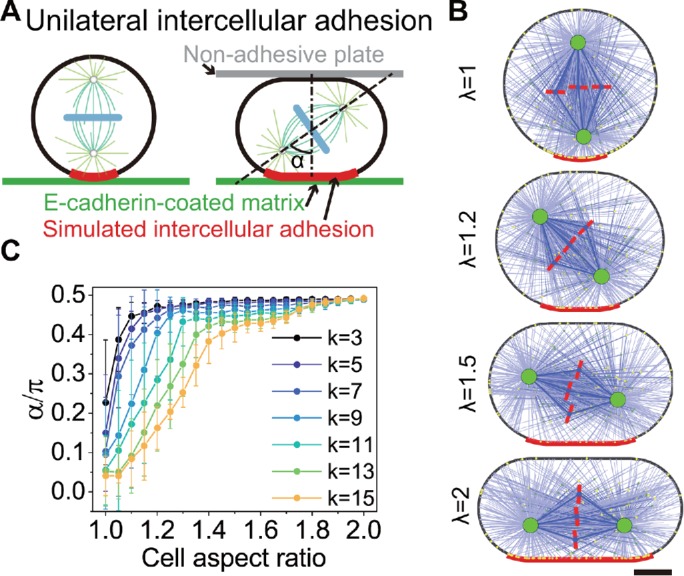
FIGURE 4:

Open in a new tab

Regulating the spindle orientation via cell compression vs. unilateral intercellular adhesion in the side view. (A) The schematic shows the cell shape and the artificial intercellular adhesion on the E-cadherin–coated matrix in the 2D simulation. The compressing plate above is nonadhesive. The matrix below (green color) is E-cadherin–coated. The cell is stadium-shaped, where the adhesive length (red color) increases with the compression degree. (B) The snapshots of the simulated spindles in the cells with various aspect ratios but the same adhesion strength (k = 11) (see also Supplemental Movie S4). Scale bar: 5 µm. (C) The spindle orientation is plotted against the aspect ratio of the cell with various adhesive strengths.

Movie S4.

Download video file (12.5MB, mp4)
Open in a new tab

Orientation of simulated spindles in the cells with unilateral adhesion and various aspect ratios of the stadium shape. The stadium-shaped cells have the unilateral adhesion (red marked) whose parameters are k=11 and that L increases with the aspect ratio, and the aspect ratio is given as λ=1, 1.2, 1.5, or 2. In these cases, the stable spindle orientation transits from the perpendicular to the parallel direction to the adhesion region with the increase of the cell aspect ratio.

Then, we investigated the competition between the unilateral intercellular adhesion and cell shape. If we further use a nonadhesive surface, such as the cantilever beam of the atomic force microscope or microplates, to compress the cell, the cell can elongate in the planar direction and the cell shape polarity could become perpendicular to the vertical adhesion polarity (Figure 4A). We assume that the adhesion area increases with the compression of the cell and further assume the adhesive region of the cell includes the cell surface whose distance to the substrate is less than 0.6 μm (Figure 4, A and B).

Similar to Figure 3, we also find the critical aspect ratio increases with the adhesive strength (Figure 4C). In other words, the stronger adhesion can orient more spindles perpendicular to the adhesion region. Unexpectedly, we find the spindle orientation angle α increases with the cell aspect ratio initially and then approaches two platforms one after the other (Figure 4C), especially for large k. After the first platform is reached, the cell shape dominates, with the result that the spindle tends to be parallel to the substrate. However, only one spindle pole is mainly pulled by the adhesive region due to the asymmetry of the adhesion, and thereby the spindle is slightly tilted (λ = 1.5 in Figure 4B). The first platform is slightly less than π/2. Until the adhesive length is longer than the spindle length, the two spindle poles are equally pulled by the adhesive region (λ = 2 in Figure 4B), and thus the spindle orientation can be parallel to the substrate completely and the second platform is reached. Compared with the bilateral adhesion (Figure 3), the spindle orientation with the unilateral adhesion is dominated by cell shape with a smaller aspect ratio, which indicates that the unilateral adhesion is relatively weaker to overcome the influence of cell shape than the bilateral adhesion.

As a comparison, we can also assume the adhesive length is independent of the cell shape (Figure 5). When the fixed adhesive length is small, the results are similar to Figure 4, that is, the spindle orientation can transit from vertical to parallel direction depending on the degree of the compression of cell shape (L = 12 μm in Figure 5A, L ≤ 16 μm in Figure 5B, and Supplemental Figure S11). We can also use Eq. 1 to fit the results to obtain the critical aspect ratio (Figure 5C) and then also find that a strong adhesion and moderate adhesive length can result in more adhesion-regulated spindle orientations, that is, perpendicular orientations. However, when the fixed adhesion length is large (up to one-half of cell perimeter), the spindle orientation will always be parallel to the substrate no matter what compression degree of the cell shape is (L = 24 μm in Figure 5A, L = 20 and 24 μm in Figure 5B). This is because the adhesive length is always longer than the spindle length in this case, leading to equal pulling on both spindle poles by the unilateral adhesion (Figure 5A).

FIGURE 5:

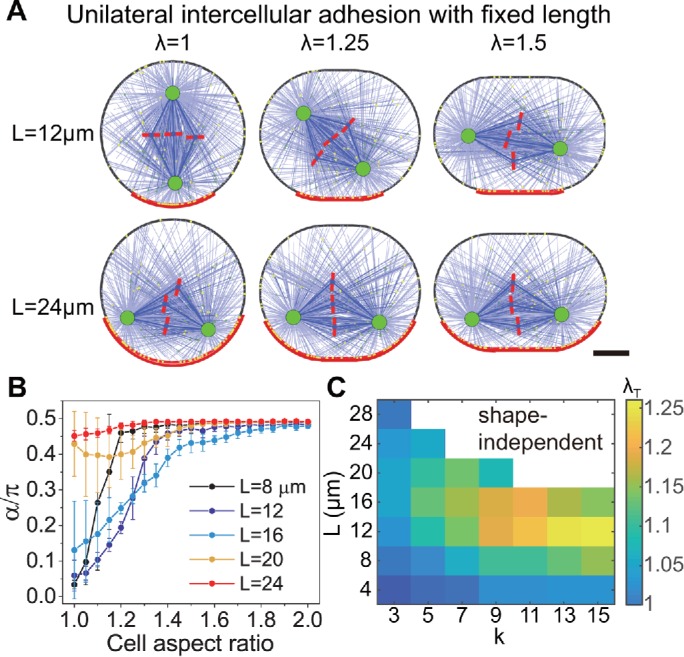
FIGURE 5:

Open in a new tab

Regulating the spindle orientation via cell compression vs. unilateral intercellular adhesion with the fixed adhesive length. (A) Examples of the simulated spindles in the cells with short and long adhesive regions and various aspect ratios. The adhesive strength is k = 11. Scale bar: 5 µm. (B) The spindle orientation is plotted against the aspect ratio of the cell with various adhesive lengths. (C) The curves of spindle orientation vs. cell aspect ratio can also be fitted by Eq. 1, and then the critical aspect ratios λT as the function of adhesive length and strength can be obtained. When the adhesive length is very large, the spindle orientation is always parallel to the substrate independently of the cell shape (white region).

In addition, we also simulate the case of bilateral adhesion when the adhesive length increases with the cell elongation, and the results are qualitatively the same as the case of bilateral adhesion with the fixed length (Figure 3; Supplemental Figures S11 and S13). We also perform simulations in elliptical cells under the above conditions and find that the results are similar to the stadium-shaped cells (see the Supplemental Materials and Supplemental Figures S10–S13 for details).

The competition between the epithelial TCJs and cell shape determines the spindle orientation in the planar surface

Next, we consider the spindle orientation within the tissue plane (Figure 1C). During the interphase, epithelial cells usually have the polygonal shapes in the top view. In our recent work (Li and Jiang, 2018), we found that the final orientation of spindle is not necessarily along the longest axis in the polygonal cells, but is determined by the radial profile and the symmetry of the cell shape. This general rule can accurately predict the experimental results, in which the sea urchin embryos were forced into microchambers with various shapes (Minc et al., 2011). However, since the epithelial cells in tissues become round during the mitotic phases, the cell shape would not be the main determinant of the spindle orientation. Bosveld et al. (2016) found that cells can memorize their interphase shapes by TCJs, which can also act as force generators pulling astral microtubules and orienting cell division via the dynein-associated protein Mud (Drosophila homologue of NuMA in mammals) (Bosveld et al., 2016). Therefore, similar to the lateral adhesion, we assume the binding rate of dyneins at the TCJs is higher. Since the astral microtubules are distributed uniformly in the model, the number of microtubules that can reach TCJs are limited and less than the other cortical region. To ensure the sufficient influence of TCJs, we slightly increase the nucleation rate in the direction pointing to TCJs (see Materials and Methods). Since the cell completely adheres to surrounding cells from the top view, all the cell cortex except the TCJs are defined as the intercellular adhesion region (k = 11) as above.

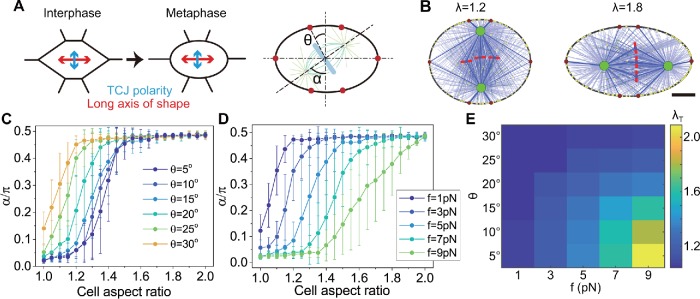
To test the modified model, we select two typical cell shapes from the experiment (Bosveld et al., 2016), in which the TCJ polarity and the cell shape polarity are consistent and inconsistent, respectively (Figure 6A). The definition of the TCJ polarity and the cell shape polarity is given in the Supplemental Materials (Bosveld et al., 2016). Our simulations show that the spindle can orient along the cell shape polarity without the TCJ mechanism, but along the TCJ polarity with the TCJ mechanism (Figure 6A and Supplemental Movie S5). We further generate 1000 random polygons with the same area and compute the direction angles of the TCJ polarity θTCJ and the cell shape polarity θshape of these shapes. The variance of their difference θTCJ −θshape decreases with the shape anisotropy, while the mean of θTCJ −θshape keeps zero (Figure 6B). Through simulating the spindle orientation in these shapes, we find the TCJ polarity gives better predictions of the spindle orientation than the cell shape when the TCJ mechanism exists (Figure 6D), which is in agreement with the experimental data (Bosveld et al., 2016). Instead, if the TCJ mechanism is not considered, it is better to use the cell shape to predict the spindle orientation (Figure 6C).

FIGURE 6:

FIGURE 6:

Open in a new tab

Modification of the model with the epithelial TCJs. (A) The comparison between experiments (Bosveld et al., 2016) and simulations with and without the TCJ mechanism (also see Supplemental Movie S5). The blue, red, and green lines in the experimental images indicate the directions of the cell shape polarity, the TCJ polarity, and the actual spindle orientation, respectively. Scale bar: 5 µm. (B) We randomly generated 1000 polygonal cells and computed the directions of the cell shape polarity and the TCJ polarity. The distribution of the difference between the two directions (θTCJ−θshape) is in good agreement with the experimental data (Bosveld et al., 2016). (C, D) The difference between the spindle orientation and the cell shape polarity (blue) or the TCJ polarity (red) obtained from the simulations with and without the TCJ mechanism.

Movie S5.

Download video file (11.3MB, mp4)
Open in a new tab

Orientation of simulated spindles in typical polygonal cells with and without the mechanism of tricellular junctions. Two typical cell shapes are selected, in which the tricellular junction polarity (red dotted) and the cell shape polarity are consistent and inconsistent, respectively. The simulated spindle can orient along the cell shape polarity without the tricellular junction mechanism, but along the tricellular junction polarity with the tricellular junction mechanism.

We did not consider the cell rounding during the mitotic phase in the simulations above, because other detailed mechanism is needed to determine the junction positions after the cell rounding. Ideally, the cell shape polarity disappears after the cell rounding. However, in previous experiments, there exist some elliptical cells during the metaphase in the epithelial tissue (Nakajima et al., 2013; Bosveld et al., 2016; Wang et al., 2017; Scarpa et al., 2018) mainly due to the anisotropic distribution of mechanical stress on the mitotic cells (Gibson et al., 2011; Wyatt et al., 2015). For instance, in Figure 3C of Gibson et al. (2011), the spindle orientation is along the TCJ polarity, but perpendicular to the long axis of the elliptical cell. This showed that in this case, the TCJs dominate the spindle orientation when the cell shape polarity and the TCJ polarity are inconsistent. However, what if the cell shape anisotropy is larger?

To answer this question, we select a typical shape that the long axis of the ellipse is perpendicular to the TCJ polarity (Figure 7A). The anisotropy of TCJs can be changed by the distribution of the TCJs. As shown in Figure 7A, the TCJs are distributed symmetrically, the increase of the angle θ (θ ≤ 30°) can result in the decrease of the TCJ anisotropy, and the anisotropy decreases to 0 when θ = 30° (see the Supplemental Materials). We find that for the same TCJ anisotropy, if the anisotropy of the cell shape is small, the spindle orientation tends to be along the TCJ polarity; but if the anisotropy of the cell shape is large, the spindle orientation tends to be along the long axis of the cell (Figure 7A and Supplemental Movie S6).This indicates that the TCJs only dominate the spindle orientation for small anisotropy of the cell shape, which is similar to the circumstance of intercellular adhesion (Figure 3). In the experiments, for example, in Figure 3C of Gibson et al. (2011), the anisotropy of the cell shape is small (λ∼1.25), and thus the spindle orientation is along the TCJ polarity. As expected, when the TCJ anisotropy is decreased (i.e., θ is increased), or the pulling force generated at the TCJ is decreased, the critical aspect ratio of the cell decreases, that is, there are fewer spindles oriented along the TCJ polarity (Figure 7, C–E). The results of the stadium-shaped cells are also similar to the results of elliptical cells (Supplemental Figure S14).

FIGURE 7:

FIGURE 7:

Open in a new tab

Regulating the spindle orientation via cell shape and TCJs in the top view. (A) When subjected to anisotropic stress, the rounding cell could exhibit an elliptical shape during the mitotic phase (Wyatt et al., 2015), probably leading to the inconsistency of the TCJ polarity and the cell shape polarity. The schematic shows an example that the long axis of the elliptical cell is perpendicular to the TCJ polarity. (B) The snapshots of the simulated spindles in the cells with different aspect ratios but the same force and anisotropy of the TCJs (f = 5 pN, θ = 15°). Scale bar: 5 µm. (C) The spindle orientation is plotted against the aspect ratio of the cell shape with various anisotropy of the TCJs. (D) The spindle orientation is plotted against the aspect ratio of the cell shape with various forces generated at the TCJs. (E) The critical aspect ratio λT as the function of the anisotropy and the pulling force at the TCJs is obtained by using Eq. 1 to fit the curves in C and D and other cases.

Movie S6.

Download video file (7.7MB, mp4)
Open in a new tab

Orientation of simulated spindles in the cells with tricellular junctions and various aspect ratios of the stadium shape. The stadium-shaped cells have the tricellular junctions (red dotted), and the aspect ratio is given as λ=1.2 or 1.8. In these cases, the stable spindle orientation transits from the tricellular junction polarity to the cell shape polarity with the increase of the cell aspect ratio as the cell area is constant.

DISCUSSION

In this work, we focused on the epithelial cell and considered both the cell shape and adhesion geometry to investigate the mitotic spindle orientation in the side view and top view of the epithelial tissue (Figure 1). The positioning and orientation of spindles are mainly driven by cortical forces on astral microtubules, including pushing force and pulling force. The combination of pushing force and pulling force can provide a more robust mechanism for positioning (Zhu et al., 2010; Pavin et al., 2012) and orientation (Li and Jiang, 2018). The cytoplasmic pulling by motors along microtubules can also drive the positioning and orientation, but this mechanism is only significant in very large cells during early embryonic development (Wühr et al., 2010; Minc et al., 2011; Li and Jiang, 2018). In normal body cells, the cytoplasmic pulling is negligible. With uniformly distributed astral microtubules, cortical forces on astral microtubules can generate a torque to rotate the spindle to the minimal torque orientation, that is, the long axis of the cell. The larger the cell shape anisotropy is, the stronger the torque becomes. In contrast, the cell adhesion, including the E-cadherin adhesion and TCJs, can induce preferential distribution of microtubules and generate a larger pulling force on microtubules in the adhesion region. The preferential pulling force can also generate torque to rotate the spindle to the direction of adhesion polarity. Shape-generated and adhesion-generated torques can be cooperative or competitive to control the spindle orientation. Therefore, we found that in epithelial cells, the intercellular adhesion dominates the spindle orientation for small anisotropy of the cell shape, but the cell shape dominates for large anisotropy of the cell shape (Figures 3 and 8A). When the cell adheres to the E-cadherin–coated wall as an artificial intercellular adhesion, the mitotic spindle orientation is perpendicular to the wall (Gloerich et al., 2017) since the adhesion to the E-cadherin–coated surface leads to more pulling force pointing to the adhesion region (Figure 8B). However, if a nonadhesive plate is used to compress the cell, the mitotic spindle may tilt or even become parallel to the surface due to the increase of anisotropy of the cell shape (Figures 4 and 8B). Therefore, the spindle orientation is determined by the competition between cell shape and the nonuniformly distributed force on the spindle induced by intercelluar adhesion.

FIGURE 8:

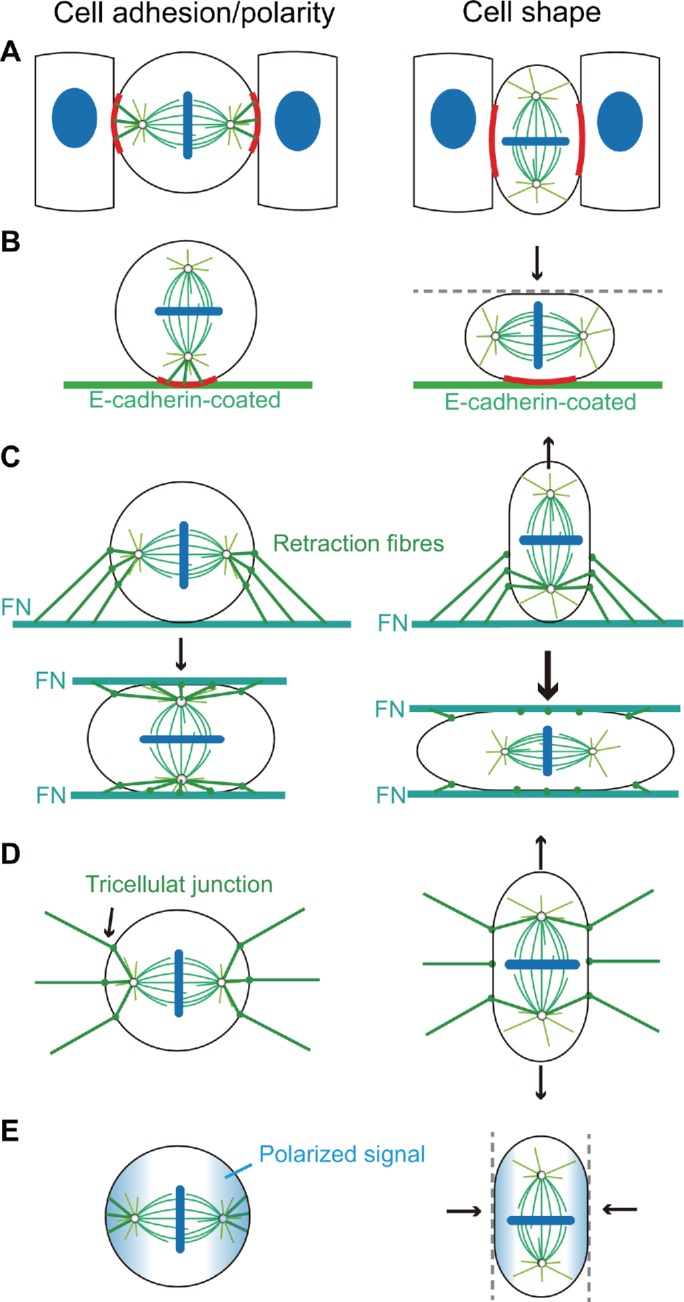
FIGURE 8:

Open in a new tab

Mitotic spindle orientation is regulated by the competition between cell shape and cell adhesion geometry (or cell polarity) in various mechanical microenvironments, including (A) cells in the epithelium are adhered by surrounding cells; (B) cells are adhered on the E-cadherin–coated matrix; (C) cells are adhered on FN-coated matrix with retraction fibers; (D) cells are pulled by TCJs; (E) cells are polarized by chemical signals.

Compared to the E-cadherin–coated matrix (Gloerich et al., 2017), cells that adhered to the FN-coated matrix (Petridou and Skourides, 2014) have different spindle orientations. In this case, the lateral retraction fibers can generate larger lateral pulling forces on astral microtubules after the cell rounding and thereby the spindle orientation parallels to the surface (Figure 8C). However, when the cell is covered by another FN-coated surface, the spindle orientation tends to be perpendicular to the substrate due to the symmetric distribution of traction fibers on the both adhesive surfaces (Petridou and Skourides, 2014). No matter whether the cells adhere to one or two parallel FN-coated surfaces, the spindle orientation can also be tuned by the cell shape if the cell shape is further changed by external forces (Figure 8C). Similarly, when cells adhere to various fibronectin micropatterns, although the cells still remain spherical after the mitotic cell rounding, the spindle orientation can be regulated effectively since the direction of the pulling force generated by the retraction fibers can be designed (Théry et al., 2005).

Another way to induce the nonuniformly distributed astral microtubules and pulling forces is TCJs (Figures 7 and 8D), through which cells can memorize their interphase shapes via the dynein-associated protein Mud (Bosveld et al., 2016). Finally, when the spindle is oriented by some polarized chemical signal (Siller and Doe, 2009; Williams and Fuchs, 2013), we speculate that the spindle orientation can also be changed if the cell is elongated perpendicular to the direction of polarization (Figure 8E). Therefore, the competition between cell shape and cell adhesion could exist under various mechanical microenvironments.

Our results are in agreement with some existing experiment observations (Bosveld et al., 2016; Chanet et al., 2017; Gloerich et al., 2017). Moreover, we also provided more predictions that could be verified in future experiments. Among currently available experimental methods, the position and size of the adhesion can be controlled by microcontact printing (Théry et al., 2005, 2007); the adhesive strength can be changed by inhibitors or regulation of gene expression; and the cell shape can be manipulated by microfabricated chambers (Minc et al., 2011), atomic force microscope, or microplates (Petridou and Skourides, 2014). Therefore, based on the combination of these methods, our predictions can be further tested, and the competition between the cell shape and the adhesion geometry can be observed and investigated more directly and quantitatively.

The computational model used in this paper was developed based on our recent work (Jiang, 2015; Li and Jiang, 2017, 2018), and the new version is more general and robust after improvement. Most of the previous models for spindle orientation considered the spindle structure as a bipolar rigid body (Théry et al., 2007; Gibson et al., 2011; Minc et al., 2011; Pierre et al., 2016). In contrast to these phenomenological assumptions, we considered the formation of bipolar spindle structure and the capture and positioning of chromosomes based on the search-and-capture mechanism (Mogilner and Craig, 2010). Therefore, our model is more general. Although the formation of spindle structure is not necessary to the main conclusion of this paper, it is probably useful in future studies. For example, if the spindle size is changed by the pushing force generated by kinesin-5 or the pulling force on kinetochores, what is the influence on the spindle orientation? Besides, to improve computational efficiency, we used 2D simulations with minimal simplification from the 3D model. The competition we considered is between the planar and orthogonal orientation in Figure 3, or between the parallel direction and perpendicular direction to the substrate in Figures 4 and 5. Furthermore, the spindle orientation has already been confined to the tissue plane in Figures 6 and 7. Therefore, 2D simulation is enough for the problems we studied. We did not consider the deformation of microtubules explicitly and only recorded the state and force of microtubules as some previous models (Zhu et al., 2010; Pavin et al., 2012), which also largely increased the computational efficiency. Recent studies also found some new forces and structure in spindles, including the bridge, twist, and rotational forces (Kajtez et al., 2016; Novak et al., 2018; Tolíc et al., 2019), which we did not consider in the current model. In the future, we can include them in our model by considering the deformation of the microtubules.

MATERIALS AND METHODS

We have developed a general computational model for mitotic spindles in our recent work (Li and Jiang, 2017, 2018). In the model, microtubules are mainly nucleated from two centrosomes and grow or shrink by the polymerization or depolymerization of their positive ends (Zhu et al., 2010). Thus, they display the dynamic instability to search the kinetochores on the chromosomes (Mogilner and Craig, 2010). The polymerization of microtubules can generate pushing forces on the cortex or chromosome arms (Civelekoglu-Scholey et al., 2006; Pavin et al., 2012), and the depolymerization can generate pulling forces on the kinetochore (Civelekoglu-Scholey et al., 2006; Banigan et al., 2015). In the meantime, microtubules can be bound by cortical motors (Mogilner and Craig, 2010), chromokinesins (Campas and Sens, 2006), cytoplasmic motors (Wu¨hr et al., 2010), and sliding motors (Nédélec, 2002; Goshima et al., 2005b; Channels et al., 2008; Loughlin et al., 2010), all of which can generate various forces on the microtubules (Supplemental Figure S1). Relying on these forces, the spindle can be self-assembled, positioned to the cell center, and oriented along the cell long axis (Li and Jiang, 2017, 2018). Here, we further improved the model to investigate the spindle orientation.

Nucleation and dynamic instability of microtubules

During the self-assembly of mitotic spindles, microtubules can be nucleated from the centrosome, or near the chromosomes (Karsenti and Nédélec, 2004), or from existing microtubules as branches in the spindle region (Petry et al., 2013) (Inset 1 of Supplemental Figure S1). The microtubules nucleated near the chromosomes are converged to the spindle pole by minus end-directed motor proteins, dynein and Ncd (Goshima et al., 2005a), and the branching microtubules have the same polarity with their mother microtubules (Petry et al., 2013). Therefore, all microtubules have interactions with the spindle poles. For simplicity, we assume all microtubules are nucleated from the centrosomes as we did before (Li and Jiang, 2017), and there is a higher nucleation rate in the direction from the centrosome to chromosomes. Specifically, in the 2D model, we first assume that each centrosome has a nucleation rate of k0 and the nucleation direction is uniformly distributed. Therefore, the density of nucleation rate is k0/(2π). Second, we assume that the density of nucleation rate in the direction from the centrosome to chromosomes is higher as knk0/(2π), where kn is a constant parameter and larger than 1 (Inset 1 of Supplemental Figure S1). This assumption is more reasonable than the original model in which we assumed the extra nucleation in a range of 60° (Li and Jiang, 2017). The positioning and orientation of spindles are regulated by astral microtubules, which are mainly generated by the nucleation rate of k0 in the model, and the extra nucleation can ensure the bipolar spindle structure is stable.

Microtubules can randomly switch between slowly growing state and fast shrinking state, which is named the dynamic instability and crucial to searching the kinetochore (Mogilner and Craig, 2010). Here, we assume that the microtubules elongate at a speed of v1 in the growing state and shorten at a speed of v2 in the shrinking state. The rescue rate (from shrinking to growing) and catastrophe rate (from growing to shrinking) of microtubules are k1 and k2, respectively. These four parameters determine the dynamics of microtubules and are considered as constants in the cytoplasm.

Microtubules interact with cortex

When a growing microtubule reaches the cortex, its polymerization is blocked, and a pushing force is generated on the cortex (Pavin et al., 2012) (Inset 3 of Supplemental Figure S1). The pushing force equals the stall force of microtubules fstall. Since the microtubules are very slender (length ∼10 µm, diameter 25 nm), they can be buckled by the pushing force easily (Pavin et al., 2012). If we neglect the lateral limitation, the critical force is given by the Euler buckling formula fc = π2κ/l2, where κ and l denote the bending rigidity and the length of the microtubule, respectively (Pavin et al., 2012; Jiang, 2015; Li and Jiang, 2017). After buckling, the growth of the micro­tubule only brings a little increase of the pushing force, thus we assume the pushing force equals the critical buckling force when the microtubule is buckling (Jiang, 2015). Therefore, the pushing force induced by microtubule polymerization is given as

graphic file with name mbc-30-2458-e002.jpg 2

When the microtubules are applied with a pushing force by the cortex, they have a higher catastrophe rate 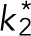Inline graphic (Howard, 2006; Kozlowski et al., 2007).

Besides the pushing force, the cortex can also apply pulling force on microtubules generated by cortical dynein (Inset 3 of Supplemental Figure S1), and the pulling force is crucial to the positioning and orientation of mitotic spindles (Laan et al., 2012; Bosveld et al., 2016; Gloerich et al., 2017). The cortical dynein can bind to microtubules touching the cortex at a rate of kb−, which is usually thought to be proportional to the density of unbound motors. We assume the density of cortical dyneins is uniform, so that kb− is constant on the cortex. When the cortical microtubule is bound by cortical dynein, the dynein can walk to the minus-end direction of the microtubule driven by the energy of the hydrolysis of ATP and thus generate a pulling force on the microtubule. The force is velocity-dependent as (Jiang, 2015; Li and Jiang, 2017)

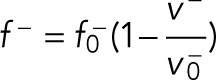graphic file with name mbc-30-2458-e004.jpg 3

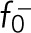where Inline graphic and Inline graphic are the stall force and the unloaded velocity of dynein; 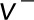Inline graphic is the walking velocity of the motor. If we neglect the poleward flux of microtubules, the velocity here equals the velocity component of the centrosome in the microtubule direction. It should be noted that the velocity is positive when the microtubule is shortening, while it is negative when the microtubule is elongating.

The binding dynein can unbind from the microtubule at a rate of ku−, which is load-dependent (Campas and Sens, 2006; Jiang, 2015; Li and Jiang, 2017), as

graphic file with name mbc-30-2458-e008.jpg 4

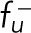where Inline graphic is a characteristic force representing the sensitivity of the unbinding rate to the load, and k0− is the unloaded unbinding rate of dynein. After the unbinding of dynein, the microtubules are in the state of depolymerization (Laan et al., 2012).

Force generated by cytoplasmic dyneins

Besides above-mentioned motors, some motors walk along the microtubules to carry cargoes in the cytoplasm (Inset 6 in Supplemental Figure S1). These motors mainly generate pulling forces and also play an important role in the positioning and orienting of mitotic spindles (Wühr et al., 2010; Minc et al., 2011; Li and Jiang, 2018). This cytoplasmic pulling force is thought as microtubule length-dependent because more motors can bind to a longer microtubule. It should be noted that the number of binding motors is large, but the velocity of one motor carrying a cargo and walking along the microtubule almost equals the unloaded velocity, which indicates the pulling force generated by a single motor is very small (Eq. 3). Therefore, we simply assume the pulling force induced by the cytoplasmic motors on a microtubule is

graphic file with name mbc-30-2458-e010.jpg 5

where η is the pulling force per unit microtubule length and l is the total length of the microtubule (Li and Jiang, 2017, 2018).

Force generated at the intercellular adhesion region

Experiment studies have found that the E-cadherin can recruit the LGN/NuMA complex (Gloerich et al., 2017; Wang et al., 2018). They can bind more astral microtubules and apply larger pulling forces through associated dyneins (Seldin et al., 2016). Since we have assumed the binding rate of dyneins is proportional to the density of unbound motors, we can assume that the intercellular adhesion region has a higher binding rate of dyneins, which is k times higher than that on the other cortex region. The forces generated on microtubules and the other changes of microtubule state are the same as described above (Eqs. 2–4).

Force generated at TCJs

The TCJs can also act as force generators to pull astral microtubules and orient cell division via the dynein-associated protein Mud (Bosveld et al., 2016). When microtubules arrive at the TCJ, defined as the region where the distance from the node is less than 0.25 µm, they can bind to dyneins at the TCJs at a larger binding rate of kb,a. However, microtubules are distributed uniformly, and microtubules that can reach the TCJs are limited and less than the other cortex region. Under such conditions, the influence of TCJs on the spindle is little. Therefore, we assume there is an extra nucleation rate klk0 along the existing microtubules that have been bound to TCJs to increase the number of microtubules there. Since the extra nucleation rate is much smaller than k0, the total number of cortical microtubules is almost unchanged. The force generated by TCJs on microtubules is also similar to the cortical dynein, 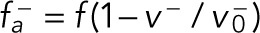Inline graphic. Here, f is the stall force generated by the motor at TCJs and will be regulated as a controlling parameter in the simulations. Besides, this binding can also unbind at a load-dependent rate as Eq. 4.

Bipolar spindle structure and other simulation details

Based on these mechanical interactions above, the spindle can be positioned and oriented by the cortical cues. Besides, through the interaction between antiparallel microtubules, and the interaction between microtubules and chromosomes based on the search-and-capture mechanism (Mogilner and Craig, 2010), the bipolar spindle structure can keep stable. More details of model and simulation methods can be seen in the Supplemental Materials.

Compared with the original model, the new version mainly has three improvements. First, in the original 2D model, chromosomes could hinder most of the microtubules from forming antiparallel structures. Therefore, we computed the chromosomes and antiparallel microtubules separately and then superposed them. However, in the 3D case, chromosomes have a finite thickness and thus can only hinder a fraction of microtubules. Thus, we can directly simulate the antiparallel microtubules. Considering the computational feasibility, we still use 2D simulation with a quasi-3D assumption that microtubules can bypass the chromosome. Therefore, they cannot only bind to chromosomes by chromokinesins or kinetochores but also bind to antiparallel microtubules by cross-linkers (Supplemental Figure S1). Second, microtubules can be nucleated from centrosomes, chromosomes (Karsenti and Nédélec, 2004), or existing microtubules as branches in the spindle region (Petry et al., 2013). The latter two nucleation sites can induce more polar microtubules between the centrosome and chromosomes. For simplicity, we still assume all microtubules are nucleated from centrosomes (Li and Jiang, 2017, 2018), but the nucleation rate is given higher in the range where the microtubule can meet the chromosomes. In this way, the simulated spindle has a higher density of polar microtubules than that of astral microtubules (Supplemental Figure S2), which is more consistent with the real spindle. Third, we add the microtubule bundling mechanism that the minus-end-directed molecular motor kinesin-14 can cooperate with the plus-end tracker EB1 to guide the growing plus end along the existing microtubule (Molodtsov et al., 2016) (Supplemental Figure S1). We assume the microtubule connected on the kinetochore can induce this bundling mechanism. After these improvements, we can perform the dynamic Monte Carlo simulation (Supplemental Figure S3). More details of the model, simulation methods, and parameters (Supplemental Table S1) are provided in the Supplemental Materials.

Supplementary Material

Click here for additional data file. (20.1MB, pdf)

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grants No. 11622222, 11872357, and 11472271), the Thousand Young Talents Program of China, Fundamental Research Funds for the Central Universities, and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB22040403).

Abbreviations used:

2D

two dimensional

3D

three dimensional

TCJ

tricellular junction.

Footnotes

This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E19-04-0227) on August 14, 2019.

REFERENCES

  1. Banigan EJ, Chiou KK, Ballister ER, Mayo AM, Lampson MA, Liu AJ. (2015). Minimal model for collective kinetochore-microtubule dynamics. Proc Natl Acad Sci USA , 12699–12704. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bergstralh DT, Lovegrove HE, St Johnston D. (2013). Discs large links spindle orientation to apical-basal polarity in drosophila epithelia. Curr Biol , 1707–1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bosveld F, Markova O, Guirao B, Martin C, Wang Z, Pierre A, Balakireva M, Gaugue I, Ainslie A, Christophorou N, et al. (2016). Epithelial tricellular junctions act as interphase cell shape sensors to orient mitosis. Nature , 495–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Campas O, Sens P. (2006). Chromosome oscillations in mitosis. Phys Rev Lett , 128102. [DOI] [PubMed] [Google Scholar]
  5. Caussinus E, Gonzalez C. (2005). Induction of tumor growth by altered stem-cell asymmetric division in drosophila melanogaster. Nat Genet , 1125–1129. [DOI] [PubMed] [Google Scholar]
  6. Chanet S, Sharan R, Khan Z, Martin AC. (2017). Myosin 2-induced mitotic rounding enables columnar epithelial cells to interpret cortical spindle positioning cues. Curr Biol , 3350–3358. [DOI] [PubMed] [Google Scholar]
  7. Channels WE, Nédélec FJ, Zheng Y, Iglesias PA. (2008). Spatial regulation improves antiparallel microtubule overlap during mitotic spindle assembly. Biophys J , 2598–2609. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Civelekoglu-Scholey G, Sharp D, Mogilner A, Scholey J. (2006). Model of chromosome motility in drosophila embryos: adaptation of a general mechanism for rapid mitosis. Biophys J , 3966–3982. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. di Pietro F, Echard A, Morin X. (2016). Regulation of mitotic spindle orientation: an integrated view. EMBO Rep , 1106–1130. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Finegan TM, Na D, Cammarota C, Skeeters AV, Na´dasi TJ, Dawney NS, Fletcher AG, Oakes PW, Bergstralh DT. (2019). Tissue tension and not interphase cell shape determines cell division orientation in the drosophila follicular epithelium. EMBO J , e100072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Fink J, Carpi N, Betz T, B´etard A, Chebah M, Azioune A, Bornens M, Sykes C, Fetler L, Cuvelier D, et al. (2011). External forces control mitotic spindle positioning. Nat Cell Biol , 771–778. [DOI] [PubMed] [Google Scholar]
  12. Fischer-Friedrich E, Hyman AA, Jülicher F, Müller DJ, Helenius J. (2014). Quantification of surface tension and internal pressure generated by single mitotic cells. Sci Rep , 6213. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Gibson WT, Veldhuis JH, Rubinstein B, Cartwright HN, Perrimon N, Brodland GW, Nagpal R, Gibson MC. (2011). Control of the mitotic cleavage plane by local epithelial topology. Cell , 427–438. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Gillies TE, Cabernard C. (2011). Cell division orientation in animals. Curr Biol , R599–R609. [DOI] [PubMed] [Google Scholar]
  15. Gloerich M, Bianchini JM, Siemers KA, Cohen DJ, Nelson WJ. (2017). Cell division orientation is coupled to cell-cell adhesion by the e-cadherin/lgn complex. Nat Commun , 13996. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Goshima G, Nédélec F, Vale RD. (2005a). Mechanisms for focusing mitotic spindle poles by minus end-directed motor proteins. J Cell Biol , 229–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Goshima G, Wollman R, Stuurman N, Scholey JM, Vale RD. (2005b). Length control of the metaphase spindle. Curr Biol , 1979–1988. [DOI] [PubMed] [Google Scholar]
  18. Guild J, Ginzberg MB, Hueschen CL, Mitchison TJ, Dumont S. (2017). Increased lateral microtubule contact at the cell cortex is sufficient to drive mammalian spindle elongation. Mol Biol Cell , 1975–1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hao Y, Du Q, Chen X, Zheng Z, Balsbaugh JL, Maitra S, Shabanowitz J, Hunt DF, Macara IG. (2010). Par3 controls epithelial spindle orientation by apkc-mediated phosphorylation of apical pins. Curr Biol , 1809–1818. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hart KC, Tan J, Siemers KA, Sim JY, Pruitt BL, Nelson WJ, Gloerich M. (2017). E-cadherin and lgn align epithelial cell divisions with tissue tension independently of cell shape. Proc Natl Acad Sci USA , E5845–E5853. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hertwig O. (1884). Das problem der befruchtung und der isotropie des eies. eine theorie der vererbung. Jenaische Zeitschrift für Naturwissenschaft , 276–318. [Google Scholar]
  22. Howard J. (2006). Elastic and damping forces generated by confined arrays of dynamic microtubules. Phys Biol , 54. [DOI] [PubMed] [Google Scholar]
  23. Jiang H. (2015). Cell size modulates oscillation, positioning and length of mitotic spindles. Sci Rep , 10504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kajtez J, Solomatina A, Novak M, Polak B., Vukušic´ K, Rüdiger J, Cojoc G, Milas A, Šestak IŠ, Risteski P, et al. (2016). Overlap microtubules link sister k-fibres and balance the forces on bi-oriented kinetochores. Nat Commun , 10298. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Karsenti E, Nédélec F. (2004). The mitotic spindle and actin tails. Biol Cell , 237–240. [DOI] [PubMed] [Google Scholar]
  26. Kiyomitsu T, Cheeseman IM. (2012). Chromosome- and spindle-pole-derived signals generate an intrinsic code for spindle position and orientation. Nat Cell Biol , 311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kozlowski C, Srayko M, Nedelec F. (2007). Cortical microtubule contacts position the spindle in C. elegans embryos. Cell , 499–510. [DOI] [PubMed] [Google Scholar]
  28. Laan L, Pavin N, Husson J, Romet-Lemonne G, Van Duijn M, López MP, Vale RD, Jülicher F, Reck-Peterson SL, Dogterom M. (2012). Cortical dynein controls microtubule dynamics to generate pulling forces that position microtubule asters. Cell , 502–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Lancaster MA, Knoblich JA. (2012). Spindle orientation in mammalian cerebral cortical development. Curr Opin Neurobiol , 737–746. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Li J, Jiang H. (2017). Geometric asymmetry induces upper limit of mitotic spindle size. Biophys J , 1503–1516. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Li J, Jiang H. (2018). Regulating positioning and orientation of mitotic spindles via cell size and shape. Phys Rev E , 012407. [DOI] [PubMed] [Google Scholar]
  32. Loughlin R, Heald R, Nédélec F. (2010). A computational model predicts Xenopus meiotic spindle organization. J Cell Biol , 1239–1249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Matsumura S, Kojidani T, Kamioka Y, Uchida S, Haraguchi T, Kimura A, Toyoshima F. (2016). Interphase adhesion geometry is transmitted to an internal regulator for spindle orientation via caveolin-1. Nat Commun , ncomms11858. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. McIntosh JR, Molodtsov MI, Ataullakhanov FI. (2012). Biophysics of mitosis. Q Rev Biophys , 147–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Minc N, Burgess D, Chang F. (2011). Influence of cell geometry on division-plane positioning. Cell , 414–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Mogilner A, Craig E. (2010). Towards a quantitative understanding of mitotic spindle assembly and mechanics. J Cell Sci , 3435–3445. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Molodtsov MI, Mieck C, Dobbelaere J, Dammermann A, Westermann S, Vaziri A. (2016). A force-induced directional switch of a molecular motor enables parallel microtubule bundle formation. Cell , 539–552. [DOI] [PubMed] [Google Scholar]
  38. Nédélec F. (2002). Computer simulations reveal motor properties generating stable antiparallel microtubule interactions. J Cell Biol , 1005–1015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nakajima YI, Meyer EJ, Kroesen A, McKinney SA, Gibson MC. (2013). Epithelial junctions maintain tissue architecture by directing planar spindle orientation. Nature , 359–362. [DOI] [PubMed] [Google Scholar]
  40. Novak M, Polak B, Simunic´ J, Boban Z, Kuzmic´ B, Thomae AW, Tolic´ IM, Pavin N. (2018). The mitotic spindle is chiral due to torques within microtubule bundles. Nat Commun , 3571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. O’Connell CB, Wang YL. (2000). Mammalian spindle orientation and position respond to changes in cell shape in a dynein-dependent fashion. Mol Biol Cell , 1765–1774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Pavin N, Laan L, Ma R, Dogterom M, Jülicher F. (2012). Positioning of microtubule organizing centers by cortical pushing and pulling forces. New J Phys , 105025. [Google Scholar]
  43. Pease JC, Tirnauer JS. (2011). Mitotic spindle misorientation in cancer-out of alignment and into the fire. J Cell Sci , 1007–1016. [DOI] [PubMed] [Google Scholar]
  44. Petridou NI, Skourides PA. (2014). Fak transduces extracellular forces that orient the mitotic spindle and control tissue morphogenesis. Nat Commun , 5240. [DOI] [PubMed] [Google Scholar]
  45. Petry S, Groen AC, Ishihara K, Mitchison TJ, Vale RD. (2013). Branching microtubule nucleation in xenopus egg extracts mediated by augmin and tpx2. Cell , 768–777. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Peyre E, Jaouen F, Saadaoui M, Haren L, Merdes A, Durbec P, Morin X. (2011). A lateral belt of cortical lgn and numa guides mitotic spindle movements and planar division in neuroepithelial cells. J Cell Biol , 141–154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Pierre A, Sall´e J, Wühr M, Minc N. (2016). Generic theoretical models to predict division patterns of cleaving embryos. Dev Cell , 667–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Ragkousi K, Gibson MC. (2014). Cell division and the maintenance of epithelial order. J Cell Biol , 181–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Rogers SL, Rogers GC, Sharp DJ, Vale RD. (2002). Drosophila eb1 is important for proper assembly, dynamics, and positioning of the mitotic spindle. J Cell Biol , 873–884. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Scarpa E, Finet C, Blanchard GB, Sanson B. (2018). Actomyosin-driven tension at compartmental boundaries orients cell division independently of cell geometry in vivo. Dev Cell , 727–740. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Seldin L, Muroyama A, Lechler T. (2016). Numa-microtubule interactions are critical for spindle orientation and the morphogenesis of diverse epidermal structures. Elife , e12504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Siller KH, Doe CQ. (2009). Spindle orientation during asymmetric cell division. Nat Cell Biol , 365–374. [DOI] [PubMed] [Google Scholar]
  53. Strauss B, Adams RJ, Papalopulu N. (2006). A default mechanism of spindle orientation based on cell shape is sufficient to generate cell fate diversity in polarised xenopus blastomeres. Development , 3883–3893. [DOI] [PubMed] [Google Scholar]
  54. Théry M, Jiménez-Dalmaroni A, Racine V, Bornens M, Jülicher F. (2007). Experimental and theoretical study of mitotic spindle orientation. Nature , 493–496. [DOI] [PubMed] [Google Scholar]
  55. Théry M, Racine V, Pépin A, Piel M, Chen Y, Sibarita JB, Bornens M. (2005). The extracellular matrix guides the orientation of the cell division axis. Nat Cell Biol , 947–953. [DOI] [PubMed] [Google Scholar]
  56. Théry M, Bornens M. (2006). Cell shape and cell division. Curr Opin Cell Biol , 648–657. [DOI] [PubMed] [Google Scholar]
  57. Tolic´ IM, Novak M, Pavin N. (2019). Helical twist and rotational forces in the mitotic spindle. Biomolecules , 132. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Wang X, Dong B, Zhang K, Ji Z, Cheng C, Zhao H, Sheng Y, Li X, Fan L, Xue W, et al. (2018). E-cadherin bridges cell polarity and spindle orientation to ensure prostate epithelial integrity and prevent carcinogenesis in vivo. PLoS Genet , e1007609. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Wang MF, Hunter MV, Wang G, McFaul C, Yip CM, Fernandez-Gonzalez R. (2017). Automated cell tracking identifies mechanically oriented cell divisions during drosophila axis elongation. Development , 1350–1361. [DOI] [PubMed] [Google Scholar]
  60. Williams SE, Beronja S, Pasolli HA, Fuchs E. (2011). Asymmetric cell divisions promote notch-dependent epidermal differentiation. Nature , 353–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Williams SE, Fuchs E. (2013). Oriented divisions, fate decisions. Curr Opin Cell Biol , 749–758. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Wühr M, Tan ES, Parker SK, Detrich HW, Mitchison TJ. (2010). A model for cleavage plane determination in early amphibian and fish embryos. Curr Biol , 2040–2045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Wyatt TP, Harris AR, Lam M, Cheng Q, Bellis J, Dimitracopoulos A, Kabla AJ, Charras GT, Baum B. (2015). Emergence of homeostatic epithelial packing and stress dissipation through divisions oriented along the long cell axis. Proc Natl Acad Sci USA , 5726–5731. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Xiong F, Ma W, Hiscock TW, Mosaliganti KR, Tentner AR, Brakke KA, Rannou N, Gelas A, Souhait L, Swinburne IA, et al. (2014). Interplay of cell shape and division orientation promotes robust morphogenesis of developing epithelia. Cell , 415–427. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Zheng Z, Wan Q, Liu J, Zhu H, Chu X, Du Q. (2013). Evidence for dynein and astral microtubule–mediated cortical release and transport of gα;i/lgn/numa complex in mitotic cells. Mol Biol Cell , 901–913. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Zheng Z, Zhu H, Wan Q, Liu J, Xiao Z, Siderovski DP, Du Q. (2010). Lgn regulates mitotic spindle orientation during epithelial morphogenesis. J Cell Biol , 275–288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Zhu J, Burakov A, Rodionov V, Mogilner A. (2010). Finding the cell center by a balance of dynein and myosin pulling and microtubule pushing: a computational study. Mol Biol Cell , 4418–4427. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file. (20.1MB, pdf)

Articles from Molecular Biology of the Cell are provided here courtesy of American Society for Cell Biology

RESOURCES