Paramagnon drag in high thermoelectric figure of merit Li-doped MnTe

Neutrons spot magnetic fluctuations that propel charges in a novel class of paramagnetic thermoelectrics.

Abstract

Local thermal magnetization fluctuations in Li-doped MnTe are found to increase its thermopower α strongly at temperatures up to 900 K. Below the Néel temperature (T_N ~ 307 K), MnTe is antiferromagnetic, and magnon drag contributes α_md to the thermopower, which scales as ~T³. Magnon drag persists into the paramagnetic state up to >3 × T_N because of long-lived, short-range antiferromagnet-like fluctuations (paramagnons) shown by neutron spectroscopy to exist in the paramagnetic state. The paramagnon lifetime is longer than the charge carrier–magnon interaction time; its spin-spin spatial correlation length is larger than the free-carrier effective Bohr radius and de Broglie wavelength. Thus, to itinerant carriers, paramagnons look like magnons and give a paramagnon-drag thermopower. This contribution results in an optimally doped material having a thermoelectric figure of merit ZT > 1 at T > ~900 K, the first material with a technologically meaningful thermoelectric energy conversion efficiency from a spin-caloritronic effect.

INTRODUCTION

Thermal fluctuations of the long-range ordered structure of localized spins in ferromagnetic (FM) and antiferromagnetic (AFM) materials form magnons. Magnons interact strongly with itinerant electrons in metals and semiconductors via magnetic scattering. In the presence of a temperature gradient ∇T, the free electrons in metals and semiconductors develop a gradient in chemical potential ∇μ_e, and the diffusion thermopower is α_d = ∇μ_e/∇T. The temperature gradient also excites a gradient in the magnon chemical potential ∇μ_m, giving a magnonic thermopower α_m = ∇μ_m/∇T, which equals the specific heat per magnon (1). The resulting magnon flux drags the free electrons along by exchange of linear momentum, an advective transport process, giving rise to a second contribution to the thermopower α, the magnon-drag thermopower α_md. Magnon drag was first discussed in the 1960s as contributing strongly to the thermopower of the AFM semiconductor MnTe (2) and FM Fe (3). Recently, it was identified as a branch of spin-based thermal effects called spin caloritronics (4). Both hydrodynamic and spin-dynamic theories have been developed for the thermopower of Fe, Co, and Ni, and these provide guidance to the field (5). The spin-dynamic model was refined further to include the effects of both localized and itinerant spins (6). In many magnetic materials, α_md ≫ α_d and dominates the thermopower, just as magnetic scattering is the dominant mechanism that limits the resistivity. The reason for this originates in the statistical distribution functions of electrons (fermions) and magnons (bosons): α_d is inversely correlated with carrier density because states below the Fermi level do not contribute due to the Pauli exclusion principle, while for α_m, the full density of magnon states is available (1).

Here, we extend the observation of magnon drag in magnetically ordered materials to paramagnets in which the local thermal fluctuations of the magnetization (paramagnons) have a finite lifetime, τ_L, and a spin-spin correlation length, ξ. We argue that when τ_L ≫ τ_me, the electron-on-magnon scattering time, and the spatial extent of the fluctuations ξ are larger than the electron de Broglie wavelength λ_dB and effective Bohr radius a^*, paramagnons look like magnons to the conduction electrons and give rise to the drag thermopower α_md.

We worked with Li-doped MnTe, a p-type AFM semiconductor with an ordering temperature T_N ~ 307 K, a Curie-Weiss temperature of T_C ~ −585 K (7), and a direct band gap of Eg ~ 1.2 eV. MnTe crystallizes in the hexagonal NiAs structure and is known to be a good thermoelectric material (8, 9, 10). Previous work (2) on resistivity, Hall, and thermopower identified a strong magnon-drag effect in the AFM state, but no predictive model was given, and the thermopower in the paramagnetic (PM) regime remained unexplained (11, 12). Here, the hole concentration is tuned (2.5 × 10¹⁹ < n < 2 × 10²¹ cm⁻³) by varying the Li concentration. Like Wasscher and Haas (2), we report a large magnon-drag contribution to the thermopower at T < T_N and model it using the theory of (5) using only one adjustable parameter for all dopant concentrations and temperatures. The paramagnons are identified using neutron spectroscopy, and their lifetime τ_L (~3 × 10⁻¹⁴ s) is measured up to 450 K. The paramagnon-drag thermopower is important at least up to temperatures that reach 3 × T_N. This thermopower results in optimally doped (4.5 × 10²⁰ cm⁻³) MnTe to develop a thermoelectric figure of merit ZT that exceeds unity (ZT ≡ α²σT/κ, where σ is the electrical conductivity and κ is the thermal conductivity) at 850 K. This is the first example of a material in which a spin-based effect gives rise to a technologically meaningful ZT.

For completion, we show the resistivity and thermopower of a sample of binary MnTe that contains no Li in the supplement. The trends are the same for the Li-doped material, again providing evidence of magnon drag at T < T_N and paramagnon drag above that. The high vapor pressure of Mn and Te, the tendency of Mn to oxidize, and the complex defect chemistry of chalcogenide semiconductors (13) do not allow control of the carrier concentration at the 10¹⁷ cm⁻³ level that is necessary to obtain the same degree of sample-to-sample reproducibility that is achieved in the Li-doped samples. This fact, and the fact that the ZT of the non-intentionally doped material is much lower than that of the Li-doped material, limits the amount of discussion given the binary compound in the study.

RESULTS

Six polycrystalline Li_xMn_1−xTe samples were prepared with doping level x = 0.003, 0.01, 0.02, 0.03, 0.04, and 0.06. From Hall measurements at 80 K (see below), these correspond to hole concentrations of 5.5 × 10¹⁹, 15 × 10¹⁹, 29 × 10¹⁹, 45 × 10¹⁹, 35 × 10¹⁹, and 100 × 10¹⁹ cm⁻³, respectively. Figure 1A shows the temperature dependence of thermopower for all six samples. All the curves share the same feature: After a phonon-drag peak near 30 K [Supplementary Materials], the thermopower follows a slow increase at T < 150 K, an abrupt increase that follows approximately the sum of a T³ plus a T law at 150 K < T ≤ T_N, and an increase in the PM regime that follows approximately a T¹ law. Each curve increases monotonically for 150 K < T < 750 K, without anomaly near T_N.

Fig. 1. Transport properties of Li-doped MnTe.

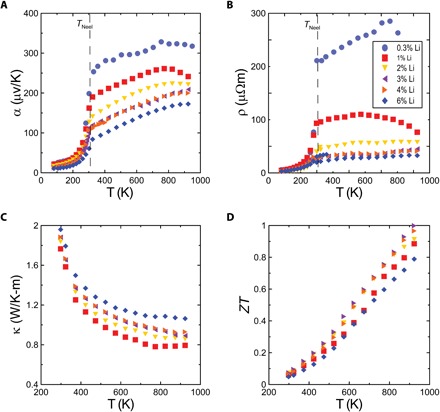
(A) Thermopower, (B) resistivity, (C) thermal conductivity, and (D) thermoelectric figure of merit ZT. The Li concentrations for all frames are shown in the inset of frame (B).

Figure 1 (B and C) shows the resistivity and thermal conductivity data, which are used to calculate the figure of merit reported in Fig. 1D. The value ZT = 1 is reached for x = 0.03 at T = 850 K. Several batches of samples have been prepared, and the measurements have been carried out at Chinese Academy of Sciences (CAS), North Carolina State University (NCSU), and The Ohio State University (OSU) with consistent results: In all cases, ZT values at or above 1 were achieved.

The T³ law observed in the thermopower at T ≤ T_N is characteristic of the magnon specific heat in an AFM and, as we will show below, of magnon drag. However, the excess thermopower does not vanish at T > T_N, which hints at an excess magnon-like contribution to the thermopower in the PM regime. Therefore, neutron scattering measurements were carried out to investigate the remnants of the magnetic structure of the x = 0.03 sample in the PM regime. This is particularly important, as the high value of ZT is obtained in the PM regime. The data are given in Fig. 2. In the AFM phase at 250 K, orientation-averaged magnon scattering is observed emanating from the magnetic Bragg peaks at 0.92 and 1.95 Å⁻¹. The magnon bands extend up to a maximum energy of ~30 meV [see data from the ARCS (wide angular-range chopper spectrometer) in Fig. 2A], in agreement with the observed and modeled magnon structure in MnTe (14).

Fig. 2. Inelastic neutron scattering result.

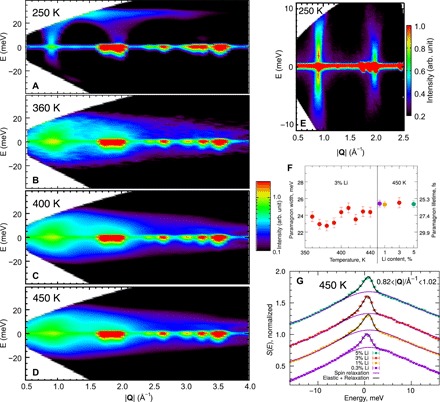
Inelastic neutron scattering data S(Q,E) obtained on MnTe doped with 3 at % Li at ARCS, SNS, in the AFM phase (A) and PM phase (B to D). Magnon bands visible in (A) are transformed into a paramagnon relaxation spectrum in the PM phase. The S(Q,E) obtained at HYSPEC in the AFM phase (E) reveals low-energy features of the magnon scattering and the pseudogap of ~0.6 meV at Q = 0.92 Å⁻¹. The paramagnon full width at half maximum (FWHM) and lifetime (F) is obtained from fits to a slice in S(Q,E) (G). Data at 450 K were gathered on MnTe doped with 0.3, 1, 3, and 5 at % Li: No dependence of the FWHM (G) or lifetime (F) is observed with Li concentration.

Above ~350 K, we observe evident paramagnon scattering at 0.92 Å⁻¹, and the magnon band at 30 meV disappears. The paramagnon scattering is essentially constant with temperature in intensity and energy distribution up to 450 K, the highest measured temperature (see Fig. 2, B to D). It is also independent of Li concentration in the range studied, 0.3 to 5 atomic % (at %) (see Fig. 2, F and G). Note that the data measured with a 1-min run shown in Fig. 2B exhibit the same features as those measured for 1 hour in Fig. 2 (C and D). The high-resolution data obtained on HYSPEC (Hybrid Spectrometer) provide too narrow an energy range to characterize the paramagnon scattering. However, these data reveal the existence of a pseudogap in the magnon scattering with AFM excitations gapped at ~1 meV and nongapped FM excitations (see Fig. 2F), consistent with (14).

DISCUSSION

AFM regime

Below the ordering temperature of FMs and AFMs, the magnon-drag thermopower is shown (5) to be proportional to the magnon specific heat C_m and inversely proportional to the number of free electrons or holes n, following the equation

$${\mathrm{\alpha }}_{\text{md}}=\pm \frac{2}{3}\frac{C_{\mathrm{m}}}{\mathit{ne}}\cdot \frac{1}{1+{\mathrm{\tau }}_{\text{em}}/{\mathrm{\tau }}_{\mathrm{m}}}$$ (1)

The second factor in the right-hand side of Eq. 1 contains magnon relaxation times. A summary of the different relaxation times and lifetimes used in this paper follows:

1) τ_m is the total momentum relaxation time for magnons. It accounts for all magnon interactions, e.g., 4-magnon Umklapp processes, magnon-phonon, or magnon-electron interactions.

2) τ_em is the magnon momentum relaxation time limited by magnon-electron interactions, which enters Eq. 1. Thus, the second factor in Eq. 1 represents the fraction of magnon scattering events that impel momentum to electrons.

3) τ_L is the magnon lifetime in the AFM (τ_L,AFM) and PM (τ_L,PM) regimes, as measured from neutron scattering. It does not a priori concern momentum exchange, because neutron scattering measures the spin pair correlations. The linewidth is a measure of how the spin-spin pair correlation function decays with time at a specific value of magnon momentum q. However, because τ_m is a measure of the perturbations in q and the relaxation mechanisms that limit τ_m are those that limit τ_L, it is reasonable to assume that τ_L ≈ τ_m, just as the phonon lifetime measured by neutron spectroscopy is a measure of phonon scattering times.

4) τ_e quantifies the electron momentum relaxation by all scattering mechanism; it is the relaxation time that enters the electron mobility.

5) τ_me quantifies the electron momentum relaxation in electron-magnon interactions; because the resistivity of magnetic materials is often limited mostly by magnetic scattering, this is likely the dominant term in τ_e.

The sign of α_md is determined by the polarity of the majority carriers (5, 6). The theory is confirmed at low temperature (<½ T_Curie) in FM Fe, Co, and Ni (5), where the second factor, with the relaxation times, can be assumed to be unity. This is not an assumption that can be made in a semiconductor, where the concentration of electrons is smaller than in metals.

The carrier concentration n is determined experimentally from the Hall effect measurements (Fig. 3A) in the AFM regime. The Hall coefficient shows an anomaly at T_N and, in some samples, can give a different value in the PM regime from that in the AFM regime. This is discussed in (15) and attributed to magnetic scattering; the value in the AFM regime, reported here, is accepted as representative of the true carrier concentration (15). Because the carrier concentration is determined by the Li-doping level, which does not depend on T, it is reasonable to assume that it is essentially temperature independent for n > 6 × 10¹⁹ cm⁻³.

Fig. 3. Hole concentration, mobility and relaxation time, and specific heat of Li-doped MnTe.

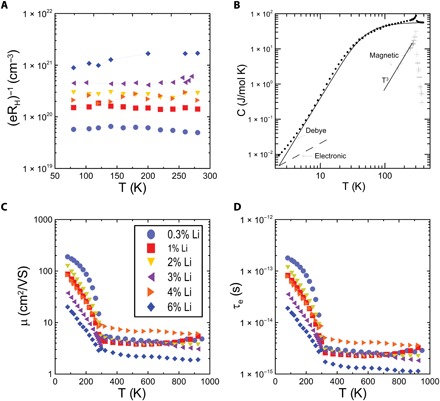
(A) Carrier concentration of all samples from Hall measurements. (B) Specific heat analysis of 6% Li-doped sample. The black dots are measured specific heat; the dashed line at low temperature is electron specific heat. Assuming that the high-temperature plateau is the Dulong-Petit high-temperature limit, a Debye model is fitted to the data to calculate the phonon contribution. The difference between measured specific heat and Debye model plus electronic specific heat is then the magnetic contribution. (C) Sample mobility μ. (D) Electron relaxation time τ_e from mobility. The legend for all frames is shown in frame (C).

The magnon specific heat C_m is determined experimentally from the total specific heat measurements. The specific heat (C) of all six samples has an identical temperature-dependence curve and shows no field dependence up to 7 T. The specific heat of 6% Li-doped sample is shown in Fig. 3B (black dots); it consists of a Debye contribution, an electron contribution at T < 6 K, and a magnetic contribution. The electronic part at low temperature follows a T¹ law, the phonon part follows a Debye function, and the magnetic part follows a T³ law, except very close to T_N. At low temperature, both phonon and magnon specific heat is proportional to T³, while electron specific heat is proportional to T. Therefore, at low temperature, the specific heat can be expressed as C_p = γ ⋅ T + A ⋅ T³ or

$$\raisebox{1ex}{$C_{\mathrm{p}}$}\!\left/ \!\raisebox{-1ex}{$T$}\right.=\mathrm{\gamma }+A\cdot T^2$$ (2)

Equation 2 is solved graphically by plotting C_p/T as a function of T² to yield γ = 2.07 μJ/mol-K². After subtracting the linear term, a Debye model is fitted to the difference of measured specific heat and the electron specific heat (Fig. 3B, solid line). The plateau above T_N is set to be the Dulong-Petit high-temperature limit; the fit gives a Debye temperature of Θ = 223 K. The magnetic contribution C_m is then the measured specific heat subtracted by the Debye model and electron specific heat (Fig. 3B, cross marks). At T < T_N, it follows a T³ law, as expected from AFM magnons, which have a linear dispersion (16). This is the value of C_m that we will combine with the experimental data for n to calculate α_md.

It is informative to compare the order of magnitude of different relaxation times τ_m, τ_em, and τ_me. However, we have not found a way to estimate the second factor in Eq. 1 quantitatively, especially as a function of temperature and doping level. An order-of-magnitude estimate comes from the following considerations. We can estimate τ_m assuming τ_L ≈ τ_m. The neutron spectroscopy data on polycrystalline samples permit only a coarse estimate of the magnon lifetime in the dispersion-less region of the spectrum, where the bandwidth ~3 to 5 meV is an upper bound (T = 250 K). Thus, τ_{L, AFM} is of the order of 1 × 10⁻¹³ to 2 × 10⁻¹³ s. τ_me is related to τ_em via mutual scattering of the charge carriers and magnons. The electron scattering time τ_e can be estimated from the Hall mobility according to τ_e = m^*μ/e, where m^* and μ are the hole effective mass and mobility, respectively. The mobility is shown in Fig. 3C, and τ_e is calculated using a value of m^* = 0.53 m_e (the free electron mass) (11) in Fig. 3D. If magnetic scattering dominates the mobility, τ_me is expected to be of the same order of magnitude as τ_e. This relation is valid only if we can ignore the second-order effect, i.e., the momentum transferred from the carriers to magnons is randomized before it can be transferred back to another carrier (17). Furthermore, magnons and charge carriers must have similar drift velocity provided that the effects of other scattering mechanisms are small, like the case of phonon-electron drag (18). On the basis of this argument, one can show that in the degenerate regime, ${\mathrm{\tau }}_{\text{em}}={\mathrm{\tau }}_{\text{me}}\raisebox{1ex}{$k_{\mathrm{B}}T$}\!\left/ \!\raisebox{-1ex}{$m*c^2$}\right.$, where c is the magnon group velocity (11, 15). The original calculation of this relation by Zanmarchi and Haas (15) is smaller by a factor of 2, because they assumed a single magnon mode. However, the magnon modes in AFMs are usually doubly degenerate, resulting in τ_em two times larger. From these considerations and the value of τ_L, we derive that the range for the ratio τ_em/τ_m falls in the bracket ~2 to 200 in the AFM regime; we will treat this ratio as the sole adjustable parameter in the thermopower.

The total thermopower is given by the sum of the magnon-drag and diffusion thermopower (5)

$$\mathrm{\alpha }={\mathrm{\alpha }}_{\text{md}}+{\mathrm{\alpha }}_{\mathrm{d}}$$ (3)

with, for metals (assuming acoustic phonon scattering) (5)

$${\mathrm{\alpha }}_{\mathrm{d}}=\frac{2}{3}{\left(\frac{\mathrm{\pi }}{3}\right)}^{2/3}\frac{k_{\mathrm{B}}}{e}\frac{m^{*}}{{\mathrm{\hslash }}^2}\frac{k_{\mathrm{B}}T}{n^{2/3}}$$ (4)

Except for the ratio 1 + τ_em/τ_m in Eq. 1, all the quantities are known, and the experimental thermopower can be fit to Eq. 3. We set 1 + τ_em/τ_m = 100 for all temperatures and all doping levels. The resulting values for the calculated thermopower are compared to the data in Fig. 4 for x = 0.01, 0.03, and 0.06. The agreement in the AFM regime is within a factor of 2. Thus, the thermopower in the AFM regime fits quite well to a model that includes a diffusion term (T¹ law) plus a magnon-drag term (T³ law).

Fig. 4. Comparison between calculated thermopower and measured thermopower.

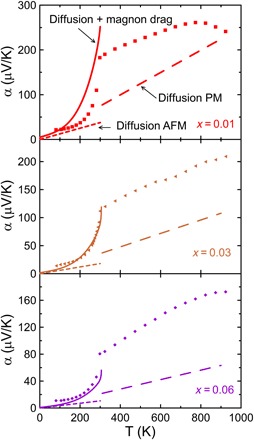
The experimental temperature dependence of the thermopower of the samples doped with Li concentrations x = 0.01, 0.03, and 0.06 is compared to the calculated values. The low-temperature dashed line is the diffusion thermopower α_d in the AFM regime; the full line is the sum of the calculated magnon-drag and diffusion thermopowers α = α_d + α_md. In the PM regime, the lower dashed line is the calculated diffusion thermopower α_d. The difference between this dashed line and the experimental data is attributed to paramagnon drag.

PM regime

In the PM region, the transport data suggest that the total thermopower also has two terms: a diffusion thermopower (T¹ law) and an additional thermopower that is T independent up to 800 K. The diffusion thermopower again can be calculated from Eq. 2, and the density of states effective masses of holes derived from the band structure in the PM regime (m^* = 1.05 m_e) [Supplementary Materials]. α_d is represented in Fig. 4 by the slope of the dashed line at T > T_N, which is rather parallel to the data, confirming the origin of the increase in thermopower with increasing T in the PM regime. However, the experimental value of α is offset by a significant amount compared to the calculated α_d. This amount equals the value of the magnon-drag thermopower at T_N. It is that offset, α_md (T_N), that we attribute to magnon drag, now extended in the PM regime and therefore labeled paramagnon drag. This term appears to be essentially temperature independent up to 800 K and to continue to 900 K, i.e., 3 × T_N.

Neutron scattering provides evidence for the existence of paramagnons (Fig. 2, B to D). The paramagnon scattering observed above 360 K can be characterized by modeling the spectral response, S(Ε), with a Lorentzian relaxation term of width Γ, corrected for thermal population factors

$$S(E)=\frac{c\mathrm{\Gamma }}{E^2+{\left(\raisebox{1ex}{$\mathrm{\Gamma }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)}^2}\cdot \frac{E}{1-\text{exp}(-E/k_{\mathrm{B}}T)}$$ (5)

and including the elastic scattering term convoluted with the instrumental resolution function (see, e.g., Fig. 2E for the fit to the data obtained at 440 K). The scattering data were integrated in the 0.82 < |Q|/Å⁻¹ < 1.02 momentum transfer (Q) range. The Lorentzian full width at half maximum obtained from the fit to this model is 24.0(0.7) meV at 440 K and does not exhibit a resolvable Li concentration or temperature dependence between 360 and 450 K. This width translates to a paramagnon average lifetime of τ_L,PM = ℏ/24 meV ~ 27 ± 1 fs. The scattering data also provide a Q width of the paramagnons, from which a spatiotemporal correlation/relaxation scale is derived. At 400 K, a cut of the elastic scattering near 0.92 Å⁻¹ reveals that the correlations extend spatially to about ξ ~ 2 to 2.5 nm.

We can compare the paramagnon correlation length, ξ, to the electron de Broglie wavelength λ_dB and the effective Bohr radius. The band structure calculation [Supplementary Materials] shows that the Fermi surface (x = 0.06) fills roughly ²/₃ of the Brillouin zone along the Γ-M and Γ-Z directions so that λ_dB ~ ³/₂ of a lattice constant or 0.6 to 1 nm. The effective Bohr radius is $a_{\mathrm{B}}^{*}=a_{\mathrm{B}}\raisebox{1ex}{${\mathrm{\epsilon }}^{*}$}\!\left/ \!\raisebox{-1ex}{$(m^{*}/m_e)$}\right.\approx 0.5 \text{nm}$, where a_B is the Bohr radius (5.3 × 10⁻¹¹ m), m^* is given above, and ε^* = 11 is the relative permittivity (19). The paramagnon lifetime, τ_L,PM, can be compared to the electron-magnon scatting time τ_me. Assuming that magnetic scattering is the mechanism that dominantly limits the mobility, we approximate τ_me ~ τ_e ~ 1 to 5 fs (see Fig. 3D). Because both a^*_B and λ_dB ≪ ξ and because τ_me ≪ τ_L,PM, one can conclude that, from the point of view of conduction electrons, the paramagnons behave like real magnons in the ordered AFM state. Therefore, we expect that paramagnons exert a drag thermopower. Experimentally, the paramagnon-drag thermopower appears to be temperature independent in degenerately doped samples. While no quantitative model is offered for that observation, one can point out that, in the measurement range accessible to the present experiment, both τ_L,PM and τ_e are approximately T independent (T < 800 K). From these observations, we conclude that the paramagnon heat capacity must also be temperature independent.

Conclusions

To summarize, we have measured the thermoelectric properties of Li-doped MnTe. The calculated magnon-drag thermopower in the magnetically ordered state matches well with measurement. We offer evidence for the existence of paramagnons in the PM state of MnTe and submit the thesis that these give a strong drag contribution to the thermopower. These spin-mediated effects lead to an optimized ZT of 1 at 900 K in a 3% Li-doped sample, which demonstrates that paramagnons offer a new path toward the exploration of high-performance thermoelectric materials. Considering only electronic charge effects, α, σ, and κ are correlated inversely with one another and therefore present a significant difficulty in optimizing ZT. Our results show that adding spin dynamics to the problem of finding high-ZT materials gives an additional degree of freedom that breaks this inverse correlation and opens a new route toward the design of thermoelectric materials.

MATERIALS AND METHODS

Synthesis and structural characterization

Samples with the nominal compositions of Mn_1−xLi_xTe (x = 0, 0.003, 0.01, 0.03, 0.04, and 0.06) were synthesized by ball milling the raw elements (Mn powder, 99.99%; Li chunks, 99.9%; Te chunks, 99.999%) within an argon-filled stainless steel jar using a high-energy ball-milling machine (SPEX 8000D). We milled the materials for 8 hours and then hot pressed them at 1173 K for 20 min by spark plasma sintering under an axial pressure of 40 MPa with a heating rate of 50 K/min. The densities of the obtained samples were not less than 97% relative to the theoretical values. The samples were disc shaped, 12.7 mm in diameter, and ~2 mm in thickness. We performed the resistivity and thermopower measurements on samples cut both perpendicularly and parallel to the press direction and verified to be isotropic. We performed the phase analysis by x-ray diffraction (XRD) (X'Pert PRO PANalytical) using Cu-Kα radiation and operating under 40 kV and 40 mA. We obtained the XRD of all the samples by quick scanning. We carried out slow scanning of pristine MnTe and Mn_0.97Li_0.03Te for structure refinement.

Measurements

Neutron scattering

Inelastic neutron scattering data were recorded at the HYSPEC and ARCS spectrometers of the Spallation Neutron Source (SNS), with incident neutron energies of 15 and 60 meV, respectively. Data at HYSPEC were collected at 250, 350, and 450 K. Data at ARCS were collected between 250 and 450 K upon heating in increments of 10 K. Every 50 K, data were collected for 1 hour, whereas intermediate data collection every 10 K was carried out for about 1 min. The sample was a polycrystalline cylindrical pellet of MnTe doped with 3% Li with 12.7 mm diameter and 25.4 mm height. All data are represented as a function of neutron energy transfer, E, and momentum transfer, |Q|, where |Q| = 4πsin(θ)/λ, with θ as the scattering angle and λ as the neutron wavelength (2.335 and 1.168 Å at HYSPEC and ARCS, respectively). The energy resolution was of the order of 0.5 and 1.8 meV at HYSPEC and ARCS, respectively.

Low-temperature electrical properties

Below 420 K, we measured the electrical conductivity, thermopower, and Hall coefficient in a homemade cryostat. We mounted the bar-shaped samples (dimensions, ~6 mm by 2 mm by 0.5 mm) onto a piece of alumina working as a heat sink. We attached copper wires and copper-constantan thermocouples (25 μm in thickness) to the samples with silver epoxy and connected a resistive heater assembly to the sample’s top surface. We attached the entire sample setup to a cryostat and conducted the measurement under vacuum from 78 to 420 K in increments of 20 K with a sweeping magnetic field up to 1.4 T, controlled by a LabVIEW program. We converted the Hall coefficient R_H for each sample into a carrier concentration using n = 1/R_H.e (Fig. 3A). At T > 250 K, the Hall coefficient displays an anomaly near T_N, as previously observed in MnTe (20) and many other AFMs (21, 22), so that only the low-temperature Hall coefficient was used for carrier concentration calculation. Geometrical errors due to contact placements dominate the error bars; they were of the order of 5% for resistivity and 3% for thermopower and Hall measurements.

High-temperature electrical properties

For 300 K < T < 1000 K, several runs of data were taken both at the CAS and OSU; these were consistent. We measured the Seebeck coefficient and electrical conductivity simultaneously from room temperature to 923 K under a low-pressure helium atmosphere by using an LSR-3 instrument (Linseis, Germany) and the Physical Property Measurement System (PPMS) (Quantum Design) for the temperature range from 4 K to room temperature. We also performed room temperature Hall measurements on a Nanometrics Hall instrument. We loaded samples on a boron nitride (BN) substrate and attached four probes to the edge of the sample. We placed the sample in a vacuum chamber with a magnetic field (up to ±0.5 T) perpendicular to its surface. Last, we also measured the resistivity ρ and Hall coefficient R_H (along the in-plane direction) using the Van de Pauw method.

Specific heat

We measured the low-temperature heat capacity from 2 to 400 K using the specific heat option to the PPMS, both in zero fields and at 7 T. At higher temperatures, we measured the specific heat capacity by differential scanning calorimetry (DSC) from 300 to 625 K and used these values of C_p hereunder. Last, we measured the specific heat capacity by DSC from 300 to 625 K and used these values of C_p to derive the thermal conductivity from the diffusivity, as described hereunder.

Thermal conductivity

We calculated the thermal conductivity from κ = DC_Pd, where the thermal diffusivity coefficient (D) was measured with Linseis LFA-1000 from room temperature to 873 K, the density (d) was determined by using the Archimedes drainage method, and the specific heat was obtained as described above. We measured the low-temperature thermal conductivity (not reported) using a PPMS (Quantum Design) from 4 K to room temperature and also in the homemade cryostat used for the thermopower and electrical measurements.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/9/eaat9461/DC1

Fig. S1. Band structures of paramagnetic and antiferromagnetic hexagonal MnTe.

Fig. S2. Comparison of the resistivity (left frame) and thermopower (right frame) of non-intentionally doped binary MnTe (black diamonds) and MnTe doped with 3% Li (red squares).

Fig. S3. Phonon drag in Li-MnTe.