Thermal biology of mosquito‐borne disease

Abstract

Mosquito‐borne diseases cause a major burden of disease worldwide. The vital rates of these ectothermic vectors and parasites respond strongly and nonlinearly to temperature and therefore to climate change. Here, we review how trait‐based approaches can synthesise and mechanistically predict the temperature dependence of transmission across vectors, pathogens, and environments. We present 11 pathogens transmitted by 15 different mosquito species – including globally important diseases like malaria, dengue, and Zika – synthesised from previously published studies. Transmission varied strongly and unimodally with temperature, peaking at 23–29ºC and declining to zero below 9–23ºC and above 32–38ºC. Different traits restricted transmission at low versus high temperatures, and temperature effects on transmission varied by both mosquito and parasite species. Temperate pathogens exhibit broader thermal ranges and cooler thermal minima and optima than tropical pathogens. Among tropical pathogens, malaria and Ross River virus had lower thermal optima (25–26ºC) while dengue and Zika viruses had the highest (29ºC) thermal optima. We expect warming to increase transmission below thermal optima but decrease transmission above optima. Key directions for future work include linking mechanistic models to field transmission, combining temperature effects with control measures, incorporating trait variation and temperature variation, and investigating climate adaptation and migration.

Introduction

Pathogens transmitted by biting arthropods – vector‐borne diseases – comprise a major burden of human, animal, and plant diseases worldwide. Transmission of these pathogens is tightly linked to the ecology of vector populations, including biting behaviour, competence for transmitting the pathogen, survival, and life history. This vector ecology depends in part on climate, habitat, and host density (Gatton et al. 2005; Bi et al. 2009; Paaijmans et al. 2010b, 2011; Werner et al. 2012; Mordecai et al. 2013; Stewart Ibarra et al. 2013; Mordecai et al. 2017; Paull et al. 2017; Shapiro et al. 2017; Thomson et al. 2017; Shocket et al. 2018; Tesla et al. 2018). Since the turn of the 20th century, when scientists and physicians discovered that mosquitoes transmit malaria and yellow fever, biologists have recognised that temperature drives vector‐borne disease transmission. Ambient temperatures alter mosquito lifespan and the period after ingesting an infectious blood meal before a mosquito becomes infectious (the extrinsic incubation period); these traits in turn affect the rate of pathogen transmission (Cox 2010; Smith et al. 2012). Medical entomologists have since characterised how temperature also affects the rates of biting, reproduction, development, and survival across vector life stages, and the probability of becoming infectious after biting an infectious host (i.e., vector competence) (Thomas & Blanford 2003; Shapiro et al. 2017). Temperature shapes transmission via its effects on all of these traits, promoting transmission at intermediate optimal temperatures and suppressing it beyond lower and upper thermal limits (Craig et al. 1999; Lafferty 2009).

Although temperature affects the transmission of all arthropod‐borne pathogens, here we focus on mosquito‐borne diseases because they pose a major worldwide health burden and because the effects of temperature are perhaps best recognised in these pathogens, particularly in light of climate change (Martens et al. 1997; Craig et al. 1999; Pascual et al. 2006; Pascual & Bouma 2009; Parham & Michael 2010; Alonso et al. 2011; Rohr et al. 2011; Stewart Ibarra et al. 2013; Siraj et al. 2014; Ryan et al. 2019). Several important gaps limit our ability to understand the effect of temperature on mosquito‐borne disease (Parham et al. 2015). In this paper, we summarise scientific knowledge about the role of temperature in mosquito‐borne disease transmission, identify critical gaps, and chart a course for future research in the context of changing climate and emerging diseases. First, we outline fundamental concepts in vector thermal biology. Then, we illustrate how these concepts can be applied by synthesising recent trait‐based research on the effects of temperature on multiple mosquito‐borne parasites and viruses and by making quantitative comparisons. Finally, we discuss implications and predictions for transmission under climate change, open questions to shape future research on the thermal biology of mosquito‐borne disease (Box 1), and extensions to other types of arthropod vectors. We aim to identify generalities in the effects of temperature on mosquito‐borne disease transmission, leaving more system‐specific processes such as precipitation, immature vector habitat, host distribution and behaviour, immune dynamics, socioeconomic factors, and vector control for future work.

Box 1. Key open questions to guide the future of vector‐borne disease thermal biology research.

Building on over a century of progress on climate‐driven vector‐borne disease research, several important questions remain to guide the next century of research.

• Across species and populations, what tradeoffs constrain the evolution and acclimation of thermal performance curves?

• Is variation in thermal performance curves greatest in the magnitude, optimum, breadth, or limits?

• How does variation in climate extremes interact with changes in climate means and variances to affect trait performance and transmission?

• What is the potential for thermal performance to adapt to warming temperatures, and which aspects of thermal performance have the most adaptive potential: thermal optima, performance breadth, or heat or cold tolerance?

• What physiological, genetic, and environmental pathways drive variation in thermal performance among individuals, populations, species, and traits, and how predictable is this variation?

• How accurately can thermal performance curves that are derived from constant temperature experiments be integrated across temperature variation to predict performance under varying temperatures?

• How can trait‐based model predictions best be combined with observed dynamics of human cases to infer and predict the role of temperature in disease dynamics?

• At what geographic and temporal scales is temperature most useful as a predictor for vector‐borne disease dynamics? What drivers interact with temperature to drive disease dynamics?

• Are warming‐driven declines in transmission in formerly optimal ranges already occurring? How do we isolate putative temperature‐driven declines from the impacts of public health interventions, rainfall, humidity, land use, human immunity, and human behaviour?

• How well matched are species’ thermal response curves to their environments and how well are thermal responses of vectors and parasites matched to each other? How important is this matching or mismatching?

Foundational concepts in thermal biology

Temperature limits the geographic range and magnitude of mosquito‐borne disease transmission via its effects on mosquito and pathogen traits (Martens et al. 1997; Craig et al. 1999; Thomas & Blanford 2003; Parham & Michael 2010; Mordecai et al. 2013, 2017; Paull et al. 2017; Shapiro et al. 2017; Shocket et al. 2018; Tesla et al. 2018). Transmission cannot occur at temperatures that prohibit mosquito or pathogen survival, development, reproduction, or metabolism. Within the range of permissive temperatures, the nonlinear influence of temperature on mosquito and pathogen traits affects the magnitude of transmission (Thomas & Blanford 2003). Determining the effects of temperature on transmission requires identifying temperatures that optimise the tradeoffs between different temperature‐dependent traits of mosquitoes and pathogens.

Extensive empirical and theoretical work has established that most physiological and life history traits respond nonlinearly to temperature – increasing from zero at a thermal minimum approximately exponentially up to an optimum before declining back to zero at a thermal maximum (Huey & Berrigan 2001; Angilletta 2009; Dell et al. 2011) (Fig. 1). This unimodal or hump‐shaped relationship is nearly universal across measured responses from ectotherm taxa and traits (Dell et al. 2011) and is predicted from first principles of enzyme kinetics and physiology (Huey & Berrigan 2001; Angilletta 2009; Kingsolver 2009; Huey & Kingsolver 2011; Amarasekare & Savage 2012). Moreover, the rates of increase and decline in performance with temperature are tightly constrained for many traits. From the metabolic theory of ecology (Brown et al. 2004), the approximate exponential rate of increase (the Boltzmann–Arrhenius constant) ranges from 0.6 to 0.7 eV for most metabolically related traits and taxa, while the constant for exponential decline above the optimum is approximately 1.2 eV (Brown et al. 2004; Dell et al. 2011). Metabolic theory of ecology has predicted host and parasite traits that affect parasite dynamics in microsporidia and helminths (Hechinger 2013; Molnár et al. 2013; Kirk et al. 2018, 2019; O’Connor & Bernhardt 2018). Whether these canonical values from metabolic theory apply to the traits of mosquitoes and pathogens that drive vector‐borne disease transmission is unknown (Molnár et al. 2013, 2017).

Figure 1.

The trait‐based approach to understanding effects of temperature on vector‐borne disease transmission. In this approach, we derive trait thermal performance curves from experimental data, synthesise their combined temperature‐dependent effect on R₀, validate the model with independent field observations, and project predicted temperature suitability for transmission onto current and future climates.

Thermal optima for traits like development, survival, and reproduction affect organismal fitness, and vary with the profile of the environmental temperature (Deutsch et al. 2008; Kingsolver 2009). As temperature varies over time, organisms experience temperatures below and above their thermal optima, affecting fitness. Such temperature variation may limit species range boundaries (Overgaard et al. 2014). The cost of exceeding thermal optima are higher than the costs of undershooting thermal optima when trait thermal performance curves are cold‐skewed (Bernhardt et al. 2018). Since daily and seasonal temperature variation is large in temperate regions, many temperate species have evolved thermal performance curves with optima well above the mean environmental temperature (Deutsch et al. 2008; Martin & Huey 2008). This ‘thermal safety margin’ buffers individual and population fitness against temperature fluctuations, particularly the disproportionate cost of temperatures exceeding thermal optima. By contrast, many tropical species, that experience less variation in temperature have low thermal safety margins (Deutsch et al. 2008). As a result, climate warming is expected to push environmental temperatures above thermal optima for many organisms, particularly in the tropics (Deutsch et al. 2008; Kingsolver 2009). The emergent effect of climate change depends on a population’s thermal performance relative to the current environment, thermal stress tolerance, and ability to adapt or migrate, and the speed and magnitude of climate change (Loarie et al. 2009; Paaijmans et al. 2013).

From theory and empirical studies, we derive four key thermal biology principles for mosquito‐borne disease:

1. Mosquito and pathogen traits related to survival, development, and reproduction are temperature sensitive.

2. These traits generally respond to temperature unimodally, with lower and upper limits and optima potentially adapted to local environments.

3. Climate change will affect many mosquito and pathogen traits that govern mosquito distribution, abundance, and pathogen transmission.

4. Climate change has the potential to increase, decrease, or have minimal effect on transmission depending on organismal thermal responses, the changing climate regime, and the rate of migration or adaptation.

Temperature defines one dimension of the fundamental ecological niche for mosquito‐borne disease transmission – the range of conditions that is required for transmission to be possible – which also includes immature vector habitat and humidity. Within this fundamental niche, the realised ecological niche for transmission additionally depends on host factors including density, movement, behaviour, demography, susceptibility, control strategies, and exposure to mosquito bites (Gething et al. 2010; Rodriguez‐Barraquer et al. 2011; Paaijmans & Thomas 2011a; Parham et al. 2015; Wesolowski et al. 2015; Krisher et al. 2016; Metcalf et al. 2017; Salje et al. 2017, 2018; Jaramillo‐Ochoa et al. 2019). Mosquito and pathogen physiological responses to temperature determine fundamental transmission potential, but the realised impact of climate change on disease dynamics also depends on these host population processes, socio‐economics, disease control efforts, or other mitigation measures (Gething et al. 2010; Paaijmans & Thomas 2011a; Parham et al. 2015; Wesolowski et al. 2017). Shared physiological mechanisms imply that mosquito thermal biology is likely to apply generally across systems and scales, whereas host population biology may be more responsive to context‐dependent behavioural or technological adaptation. For these reasons, we focus here on how physiological effects of temperature on mosquito and pathogen traits affect transmission.

To illustrate one approach for applying principles of thermal biology to vector‐borne disease transmission, we synthesise the results of previous research that used trait‐based models derived from experimental data to understand how temperature affects mosquito‐borne disease transmission. This is one application – with several strengths and limitations – of thermal biology concepts that apply more generally across research approaches. We also highlight important caveats that correspond to key extensions and directions for future research (Table 1).

Table 1.

Challenges and future research directions for the temperature‐dependent R₀ approach

Challenge	Future research directions
(1) Data quality and gaps. Trait thermal response data are often sparse, requiring models to estimate trait thermal responses from related species or limited numbers of data points or temperatures. What is the quality of data that is truly needed?	Use sensitivity and uncertainty analyses on models to identify key data gaps to prioritise for experiments (Johnson et al. 2015; Parham et al. 2015).
(2) Generalities across thermal performance curves. How much do differences across species matter, given the other sources of variation in transmission in the field?	Use sensitivity analyses on models to identify which traits most influence differences in transmission among species. Increase model validation efforts to measure the degree to which predicted species differences are borne out in the field.
(3) Relative versus absolute thermal performance curves. Although the relative R0 approach synthesises how the relative shapes of trait thermal performance curves affect transmission, differences in absolute trait magnitudes could also affect temperature‐dependent transmission. How do relative magnitudes of traits like lifespan, biting rate, and extrinsic incubation rate affect transmission?	Measure traits and/or entomological inoculation rate (EIR) across temperatures in the field to determine how, for example, the relative magnitudes of biting rates, extrinsic incubation rates, and lifespan vary across temperature. Model the effects of absolute differences in trait values on transmission rates, across temperatures.
(4) Interactive versus additive effects of temperature and other factors on traits. Humidity, food quality, and other factors affect vector traits simultaneously with temperature. Are these effects additive (scaling the magnitude of the trait thermal performance curve) or interactive (changing the shape, limits, or optimum of the thermal performance curve)?	Experimentally vary temperature and other environmental factors in a factorial design and measure vector and parasite traits (e.g. Bayoh 2001; Murdock et al. 2014). Use theory based on physiological mechanisms underlying trait performance to generate hypotheses for additive versus interactive effects of temperature and other factors (Kearney et al. 2009).
(5) Translation of thermal performance curves from laboratory to field. Vector traits can vary substantially between the laboratory and the field, including longevity, biting, and egg‐laying. Are the laboratory‐estimated thermal performance curves proportional to trait thermal responses in the field?	Validate mechanistic models and laboratory trait measurements in the field. Incorporate field‐based trait estimates into mechanistic models to understand their impacts on transmission.
(6) Trait interactions across life stages. Larval rearing conditions such as food availability and temperature can affect body size and physiological condition, which affect adult traits such as longevity, biting rate, and vector competence. How does trait covariance across life stages affect transmission?	Use physiological ecology to model mechanistic linkages among traits based on joint dependence on metabolism, body size, and body condition. Empirically estimate trait covariation across life stages, and incorporate joint distributions of trait thermal performance curves into mechanistic models.
(7) Relative importance of temperature versus other drivers of traits and transmission. Temperature is one component in a complex network of causality linking environmental conditions to vector traits and disease transmission. What is the relative importance of these drivers, and how does it vary across transmission settings?	Systematically review epidemiological studies that estimate the importance of temperature and other factors (e.g. Stewart‐Ibarra & Lowe 2013) to see how their importance varies across settings, diseases, and scales (Cohen et al. 2016). Use species distribution models (SDMs) to estimate the relative importance of different factors for explaining current distributions of vectors and diseases. Use mechanistic and statistical models to estimate when temperature is expected to be an important driver (e.g. near thresholds) and when it is not (Parham et al. 2015).
(8) Microclimates and habitats vary in temperature. While studies often focus on constant or mean temperatures, in the field vectors can preferentially occupy habitats with favourable microclimates (Paaijmans et al. 2010b; Paaijmans & Thomas 2011b; Murdock et al. 2017). How much do microhabitat availability and preferences moderate the effects of average temperatures on transmission?	Collect mosquitoes in their preferred resting and breeding habitats in the field. Experimentally measure traits in different microclimates in the field (Murdock et al. 2017). Adapt mechanistic models to incorporate temperatures from relevant microclimates, rather than averages over larger spatial scales.
(9) Temperature varies over time. Temperature varies across hours, days, weeks, seasons, and years. Because of Jensen’s inequality, temperature variation has nonlinear effects on trait performance and transmission. What are the most important time scales of temperature variation, and how do they influence transmission?	Adapt approaches for nonlinear averaging (Savage 2004; Bernhardt et al. 2018) to understand how temperature variation affects traits and transmission (Paaijmans et al. 2010a; Lambrechts et al. 2011; Blanford et al. 2013). Experimentally test how well nonlinear averaging across thermal performance curves estimated at constant temperatures can predict trait performance at variable temperatures.
(10) Thermal performance curves vary across individuals, populations, and species. Trait thermal responses are expected to vary due to genetic variation, phenotypic plasticity (e.g. acclimation), environmental conditions, and chance (Cator et al. 2019). How much variation exists, at what scales (individual, population, species), and how does it affect transmission? Are differences in thermal performance curves among species predictable based on phylogenetic, geographic, or ecological factors?	Use physiological models and trait databases to predict variation in thermal responses (Rohr et al. 2018; Cator et al. 2019). Experimentally measure trait thermal performance curves across different field‐derived populations. In thermal response experiments, measure traits at the individual level to quantify individual trait variation and covariation among traits. Use metabolic theory of ecology to identify systematic differences in trait performance curves that vary with phylogenetic and ecological predictors.
(11) Time lags between climate and transmission. Transmission requires multiple developmental processes to occur in the mosquito and parasite, resulting in time lags that vary with temperature. How do these temperature‐dependent lags affect our ability to measure and infer the effects of climate on transmission?	Incorporate time‐ (or temperature‐) dependent biological lags into dynamical models, an ongoing area of mathematical biology research. Quantitatively review statistical studies that estimate time lags between climate and vector or disease dynamics (e.g., Mordecai et al. 2017; Lowe et al. 2018; Shocket et al. 2018), to assess how these lags vary geographically and with climate.
(12) Relative versus absolute limits on transmission. Our R0 approach estimates the relative temperature suitability physiological limits for transmission (where R0 = 0) but not the stability of the disease‐free equilibrium (where R0 = 1). Other factors are expected to scale the overall magnitude of transmission (e.g., EIR for malaria in Africa varied between 0 and ~ 700 infectious bites per person per year at optimal temperatures of 25ºC) (Mordecai et al. 2013). How much do the precise temperature limits at which R0> 1 vary with the suitability of other conditions for transmission?	Quantify the absolute temperature dependence of transmission by measuring R0 as a disease invades a novel environment (e.g. for an emerging epidemic like Zika (Duffy et al. 2009)) or by estimating a temperature‐dependent force of infection after accounting for susceptible depletion (e.g., Perkins et al. 2015). For endemic or seasonally epidemic pathogens, use dynamic transmission models to mechanistically incorporate trait thermal performance curves (e.g., Huber et al. 2018).
(13) Potential for thermal performance curves to adapt to warming temperatures. Vectors and parasites are expected to respond to selective pressures, including rising temperatures, through plasticity and adaptation. How much can thermal performance curves adapt, and how much have they already adapted, to varying climates?	Experimentally measure trait thermal performance curves across populations originating from different climates (Zouache et al. 2014; Ruybal et al. 2016). Conduct artificial selection experiments on diverse populations to measure potential for adaptation to changing temperature mean, variance, and extremes. Identify candidate genes for thermal adaptation using conserved genetic regions studied in other species (e.g., Drosophila spp.) and study their population genetics in the field.

Approach

Insights from trait‐based mechanistic models

Here, we synthesise our previous research that applied a trait‐based modelling approach (Fig. 1) to incorporate the empirical effects of constant temperature on mosquito and parasite traits, and in turn transmission, for a variety of mosquito‐borne pathogen systems (Table 2) (Mordecai et al. 2013, 2017; Johnson et al. 2015; Shocket et al. 2018, 2019; Tesla et al. 2018). By comparing previous model results – developed with consistent methodology – we investigate how temperature differentially affects transmission across vector‐borne diseases and examine the implications for climate change. Temperature affects all traits of mosquitoes and pathogens that are tied to biological rates, times, and probabilities via metabolism, including many traits that drive transmission. Transmission is a dynamic, nonlinear process that depends on the density of infected vectors and the availability of susceptible hosts. Time lags arise between climate and transmission because temperature affects mosquito development rates in immature stages, the oviposition cycle, and pathogen extrinsic incubation period (Stewart Ibarra et al. 2013; Huber et al. 2016). Temperature varies at multiple time scales – daily, seasonally, yearly – that affect these traits in different ways (Paaijmans et al. 2010a, 2013). As a result, effects of temperature on transmission are nonlinear, dynamic, and complex at multiple biological scales.

Table 2.

Thermal optima and limits for temperature‐dependent R₀ models across systems

System	Topt (CIs)	Tmin (CIs)	Tmax (CIs)
EEEV | Ae. triseriatus	22.7 (22.0–23.6)	11.7 (8.8–16.3)	31.9 (31.1–33.0)
WEEV | Cx. tarsalis	23.0 (22.0–24.7)	8.6 (6.3–13.0)	31.9 (30.3–35.2)
SINV | Cx. pipiens	23.2 (21.7–24.6)	9.4 (6.9–13.3)	33.8 (28.2–37.0)
WNV | Cx. univittatus	23.8 (22.7–25.0)	11.0 (8.0–15.3)	33.6 (31.2–36.9)
WNV | Cx. tarsalis	23.9 (22.9–25.9)	12.1 (9.6–15.2)	32.0 (30.6–38.6)
SLEV | Cx. tarsalis	24.1 (23.1–26.0)	12.9 (11.0–14.8)	32.0 (30.6–38.5)
WNV | Cx. pipiens	24.5 (23.6–25.5)	16.8 (14.9–17.8)	34.9 (32.9–37.6)
WNV | Cx. quinquefasciatus	25.2 (23.9–27.1)	19.0 (14.1–20.9)	31.8 (31.1–32.2)
P. falciparum | Anopheles	25.4 (23.9–27.0)	19.1 (16.0–23.2)	32.6 (29.4–34.3)
RVFV | Ae. taeniorhynchus	25.9 (23.8–27.1)	10.6 (8.6–14.4)	37.8 (34.4–39.1)
SINV | Ae. taeniorhynchus	26.0 (23.9–27.3)	9.7 (8.3–13.6)	37.8 (34.4–39.2)
DENV | Ae. albopictus	26.4 (25.4–27.6)	16.2 (13.0–19.8)	31.4 (29.5–34.0)
RRV | Cx. annulirostris	26.4 (26.0–26.6)	17.0 (15.8–18.0)	31.4 (30.4–33.0)
MVEV | Cx. annulirostris	26.4 (26.2–26.8)	17.0 (16.0–19.2)	31.4 (30.4–33.0)
ZIKV | Ae. aegypti	28.9 (28.2–29.6)	22.8 (20.5–23.8)	34.5 (34.1–36.2)
DENV | Ae. aegypti	29.1 (28.4–29.8)	17.8 (14.6–21.2)	34.5 (34.1–35.8)

Posterior estimates of mean optimal temperatures, lower thermal limits and upper thermal limits (with 95% credible intervals in parentheses) for each of our temperature‐dependent R₀ models. Models are named for the predominant vector and pathogen species from which trait thermal responses were derived, but models occasionally filled in missing traits with the most conservative estimates available from closely‐related species (Mordecai et al. 2013, 2017; Johnson et al. 2015; Shocket et al. 2018; in prep; Tesla et al. 2018). The parasite abbreviations are as follows: Eastern equine encephalitis virus (EEEV), Western equine encephalitis virus (WEEV), Sindbis virus (SINV), West Nile virus (WNV), St. Louis encephalitis virus (SLEV), Rift Valley fever virus (RVFV), dengue virus (DENV), Ross River virus (RRV), Murray Valley encephalitis virus (MVEV), and Zika virus (ZIKV). The vectors are abbreviated as Culex (Cx.) and Aedes (Ae.).

To capture nonlinearity and complexity in a simple, easily‐used model, we have ignored temperature variation and dynamic time lags (Table 1) in this work and represented the effects of temperature on transmission by focusing on a common summary of transmission, the basic reproduction number R₀, at constant temperatures. This number describes the average number of secondary cases that result from a single infected individual introduced into a fully susceptible population. Critically, R₀ can incorporate all the temperature‐dependent mosquito and pathogen traits that control transmission, providing a simple metric for examining emergent, nonlinear effects of temperature. Reproduction numbers can be calculated using multiple methods, with differing interpretations (Heesterbeek 2002; Heffernan et al. 2005; Diekmann et al. 2009), although their direct application is limited in realistically variable environments (Bacaër & Guernaoui 2006; Bacaër & Ait Dads 2012). Because several non‐temperature factors that vary across transmission settings can influence the absolute magnitude of R₀, our work has focused on the relative temperature suitability for transmission, a version of R₀ rescaled from zero to one derived exclusively from temperature relationships. The aim is to identify (constant) temperature limits on transmission (where R₀ = 0, so transmission is impossible) and the optimal temperature for transmission (where R₀ peaks) as metrics that can be compared across mosquito–pathogen systems, transmission settings and climate scenarios. Temperature variation can then be incorporated into these models in the future (see Table 1 and Limitations to the R₀(T) approach).

This approach begins with a commonly used derivation based on dynamical susceptible–infected–recovered (SIR) models and leading‐eigenvalue calculation (Dietz 1993), an extension of the Ross–Macdonald framework (Smith et al. 2007b; Reiner et al. 2013):

$$R_0\left(T\right)=\sqrt{\frac{a{\left(T\right)}^{2}b\left(T\right)c\left(T\right)exp\left(-\mathrm{\mu }\left(T\right)/PDR\left(T\right)\right)M\left(T\right)}{Nr\mathrm{\mu }\left(T\right)}},$$ (1)

where r is the host recovery rate, N is the density of hosts, and T indicates the temperature dependence of the following parameters (traits): mosquito biting rate, a; mosquito adult mortality rate, μ (the inverse of lifespan, lf); parasite development rate, PDR (the inverse of the extrinsic incubation period); and vector competence (the product of the proportion of exposed mosquitoes that acquire a disseminated infection, c and the proportion of infected mosquitoes that become infectious with pathogens in their salivary glands, b).

Temperature should also affect mosquito abundance, M, because it affects mosquito life‐history traits. Parham & Michael (2010) extended eqn (1) to incorporate effects of temperature on mosquito abundance via its effects on egg‐to‐adult development rate (MDR) and survival probability (p_EA), and lifetime fecundity (B, which we approximate as eggs per female per day, EFD, times lifespan, 1/μ). Following Parham & Michael (2010), our work has modelled temperature‐dependent mosquito abundance as follows:

$$M\left(T\right)=\frac{EFD\left(T\right)p_{\mathit{EA}}\left(T\right)MDR\left(T\right)}{\mathrm{\mu }{\left(T\right)}^2}$$ (2)

Incorporating M(T) into the R₀(T) model, we obtained the full temperature‐sensitive R₀ expression (Mordecai et al. 2013, 2017; Johnson et al. 2015; Shocket et al. 2018; Tesla et al. 2018):

$$R_0\left(T\right)=\sqrt{\frac{a{\left(T\right)}^{2}b\left(T\right)c\left(T\right)exp\left(-\mu \left(T\right)/PDR\left(T\right)\right)EFD\left(T\right)p_{\mathit{EA}}\left(T\right)MDR\left(T\right)}{Nr\mathrm{\mu }{\left(T\right)}^3}}$$ (3)

To estimate the effect of temperature on R₀, in previous work, we parameterised thermal response functions for each of the temperature‐dependent parameters using laboratory experiments that measure mosquito or pathogen traits at three or more constant temperatures. Based on data availability, for some mosquito species, we used alternative measurements of immature survival and fecundity (Table S1) and adjust eqn (3) accordingly (Shocket et al. 2019).

This approach is simple, mechanistic, analytical and broadly applicable across the vector‐borne disease systems for which eqns ((1), (2), (3)) apply (i.e. mosquito‐ and fly‐borne pathogens). In this framework, we have used sensitivity analyses to examine the effects of different temperature‐dependent traits on transmission, and Bayesian inference to assess how uncertainty in traits affects uncertainty in R₀ across temperatures, pinpointing critical traits and temperatures for further data collection (Johnson et al. 2015). We have applied this approach to a variety of mosquito vectors and pathogens to estimate temperature‐dependent transmission functions that can be field‐tested and compared across systems (Mordecai et al. 2013, 2017; Shocket et al. 2018, 2019; Tesla et al. 2018) (Table 2).

Limitations to the R₀(T) approach

This approach has several important limitations, some of which can be addressed by extending the models – making them less general – while others represent priorities for future research (summarised in Table 1). One limitation of constant‐temperature models is that in nature temperature varies daily, seasonally, interannually, and spatially. Because trait thermal responses are nonlinear, trait performance under varying temperatures deviates from performance at constant temperatures due to Jensen’s inequality (Table 1) (Martin & Huey 2008; Paaijmans et al. 2010a; Lambrechts et al. 2011). Performance at variable temperatures exceeds performance at a constant temperature for concave‐up regions of thermal performance curves (near thermal limits), and vice versa for concave‐down regions of thermal performance curves (near thermal optima) (Bernhardt et al. 2018). For example, parasites may complete development within the mosquito under varying temperatures centred on constant temperatures at which development would never be completed, near thermal limits (Blanford et al. 2013). Because of nonlinear thermal performance curves, the optimal mean temperature in a variable environment depends on the amount of temperature variation (Martin & Huey 2008; Paaijmans et al. 2010a; Lambrechts et al. 2011; Blanford et al. 2013). Future work could incorporate variance and higher‐order terms for fluctuation in temperature across different time scales to estimate its effect on transmission (Table 1) (Savage 2004; Cohen et al. 2019).

Nonlinearities also make many traits difficult to measure even at constant temperatures, especially near thermal limits (Table 1). For cold‐skewed thermal performance curves, trait performance can drop steeply from peak to zero over a few degrees, so experiments must span wide ranges of temperatures in small increments to fully capture nonlinear thermal responses. Rates can be difficult to measure near lower thermal limits because they are exceedingly slow (Waite et al. 2019). Near upper performance limits, constant temperature estimates may not capture non‐lethal and time‐dependent effects of heat stress (Kingsolver & Woods 2016; Sinclair et al. 2016). Traits are most easily and accurately measured near thermal optima, while uncertainty is highest near thermal limits (Johnson et al. 2015). For composite traits such as vector competence, measuring the underlying physiological responses may be important for understanding thermal responses, particularly under varying temperatures (Table 1).

Keeping these empirical limitations in mind, we have applied R₀(T) estimated from constant‐temperature trait thermal performance experiments as a consistent metric of relative temperature suitability across vector‐borne diseases. This metric captures the emergent, nonlinear effects of temperature on disease transmission, allowing us to investigate general patterns in thermal responses. The models could be extended to include temperature variation, individual‐ or population‐level trait variation, differences in performance between the laboratory and the field, and mosquito and human behaviour (Table 1), gaining explanatory power while losing generality.

Synthesising previous results

We empirically parameterised thermal performance curves for traits and R₀ for a suite of 15 ecologically important mosquito species that transmit 11 different pathogens: Western and Eastern Equine Encephalitis virus (WEEV and EEEV), Sindbis virus (SINV), Rift Valley Fever virus (RVFV), West Nile virus (WNV), St. Louis Encephalitis virus (SLEV), Plasmodium falciparum malaria, Ross River virus (RRV), Murray Valley Encephalitis virus (MVEV), dengue virus (DENV) and Zika virus (ZIKV) (Figs 2, 3, 4, 5; Table 2, Table S1). In total, we empirically estimated thermal performance curves for 88 traits, resulting in 16 temperature‐dependent R₀ models (in some cases, we estimated separate R₀ models for different pathogens in the same vector or different vectors for the same pathogen) (Mordecai et al. 2013, 2017; Johnson et al. 2015; Shocket et al. 2018, 2019; Tesla et al. 2018). With these thermal performance curves, we compare temperature responses across vector–pathogen systems and estimate potential effects of climate change on disease transmission.

Figure 2.

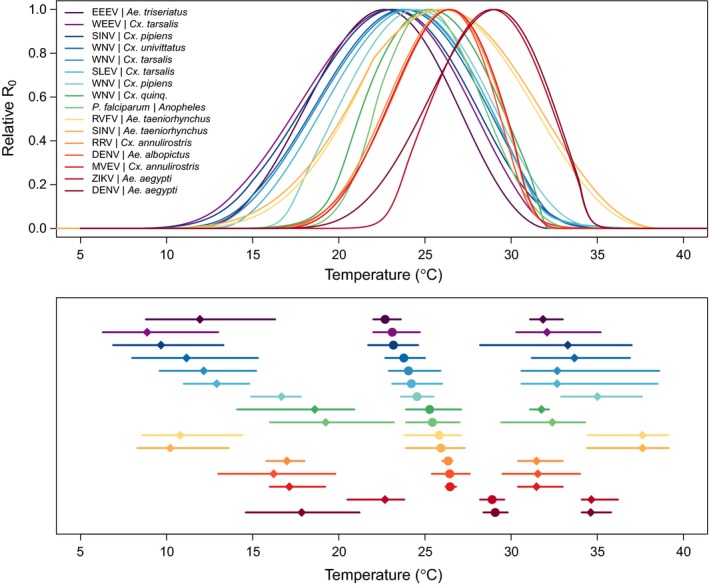
Temperature‐dependent R₀ models are consistently unimodal with differing thermal optima and limits across systems. Top panel: temperature‐dependent R₀ models for 16 vector–pathogen systems; bottom panel: R₀ thermal optima (temperature where R₀ peaks; circles) and lower and upper limits (temperature where R₀ = 0; diamonds), with 95% credible intervals (lines). Curves depict empirically parameterised temperature‐dependent R₀ models for each vector – pathogen pair, normalised so the y‐axis ranges from 0 to 1 because other factors that affect the absolute magnitude of R₀ vary by system. Colors designate different vector – pathogen systems, ordered by thermal optima for R₀ in the both panels. Abbreviations for all vectors and parasites are given in Table S1.

Figure 3.

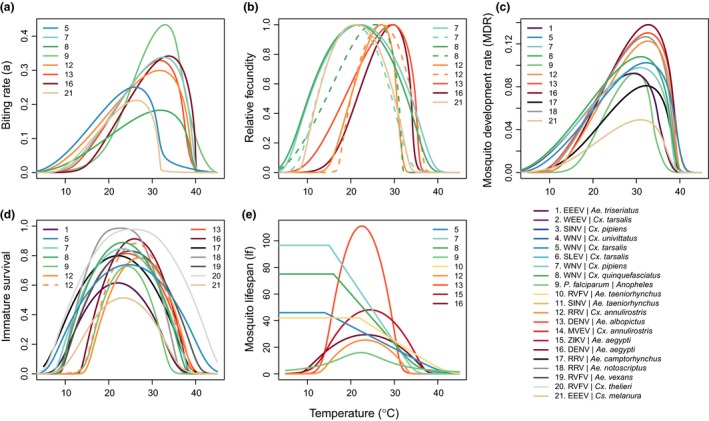
Trait thermal performance curves for vector life history traits vary by species. Thermal performance curves estimated from laboratory experimental data across different vector species that transmit different pathogens (systems are numbered in each panel; overall system numbering key and color scheme are in the main legend). Color scheme is consistent with Fig. 2, i.e., ordered by thermal optima for R₀; systems for which no R₀ model was calculated are listed last. Vector traits are (a) biting rate (a); (b) relative fecundity; (c) mosquito development rate (MDR); (d) immature survival; and (e) mosquito lifespan (lf). Fecundity is rescaled to range from zero to one because it is alternatively measured as eggs per female per day (EFD; Ae. aegypti, Cx. annulirostris), eggs per female per oviposition cycle (EFOC; Ae. albopictus, Cx. pipiens), number of larvae per raft (n_LR; Cx. annulirostris [dashed line]), eggs per raft (EPR; Cx. quinquefasciatus), or proportion ovipositing (p_O; Cx. pipiens [dashed line], Cx. quinquefasciatus [dashed line], Cs. melanura). Immature survival probability is measured as egg‐to‐adult survival probability (p_EA; Ae. aegypti, Ae. albopictus, An. gambiae), larva‐to‐adult survival probability (p_LA; Ae. camptorhynchus, Ae. notoscriptus, Ae. triseriatus, Ae. vexans, Cx. annulirostris, Cx. pipiens, Cx. quinquefasciatus, Cx. tarsalis, Cs. melanura), proportion of egg rafts that hatch (p_RH; Cx. annulirostris [dashed line]), or egg viability (EV; Cx. thelieri). To be conservative, for three temperate vectors that can undergo diapause and therefore survive cold temperatures (Cx. tarsalis, Cx. pipiens, Cx. quinquefasciatus), lifespan (lf) was assumed to be constant from 0ºC to the lowest temperature measured in the experiments (14‐16ºC), because a decline at low temperatures was not observed in the data. Abbreviations for all vectors and parasites are given in Table S1.

Figure 4.

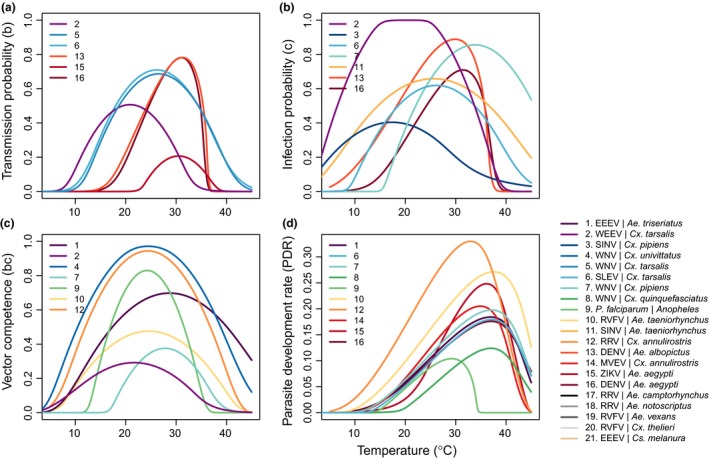
Trait thermal performance curves for pathogen transmission traits within the vector vary by species. Thermal performance curves estimated from laboratory experimental data across different pathogens and vectors (systems are numbered in each panel; overall system numbering key and color scheme are in the main legend). Color scheme is consistent with Figs 2 and 3. Traits are (a) transmission probability (b); (b) infection probability (c); (c) vector competence (bc); and (d) parasite development rate (PDR). Abbreviations for all vectors and parasites are given in Table S1.

Figure 5.

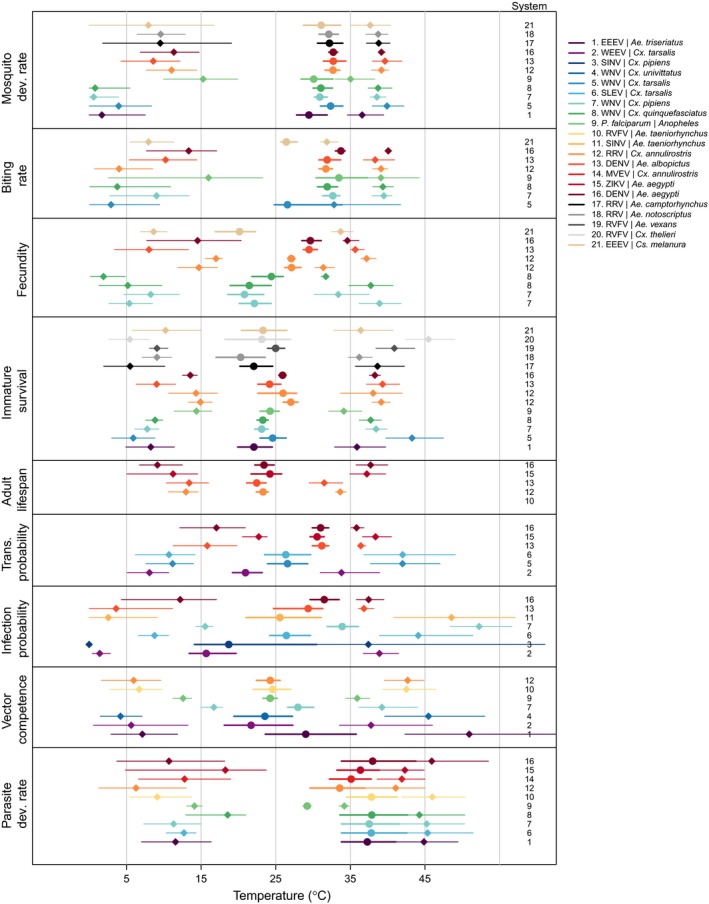
Traits vary in thermal minimum, optimum, and maximum across species. For each vector and/or pathogen for which a trait was measured, points show the mean thermal optimum (circles) and lower and upper thermal limits (diamonds) along with their 95% credible intervals (lines). Traits are mosquito development rate (MDR), biting rate (a), fecundity (EFD, EFOC, n_LR, EPR, p_O), immature survival (p_EA, p_LA, p_RH, EV), adult mosquito lifespan (lf), transmission probability (b), infection probability (c), vector competence (bc), and parasite development rate (PDR). Traits for which minima, optima, or maxima were not estimated are not shown. Not all traits were measured in all species. Color scheme is consistent with Figs 2 and 3. Systems are numbered to the right of each trait; overall system numbering key and color scheme are in the main legend. Abbreviations for all vectors and parasites are given in Table S1.

As expected, all of the mosquito and pathogen traits we examined were temperature‐sensitive and generally respond unimodally, peaking from 15.7 to 38.0°C (mean thermal optimum = 28.4°C; Figs 3, 4, 5). (One exception is lifespan for three temperate mosquitoes, discussed below; Fig. 3.) These traits were estimated to decline to zero at thermal minima ranging from 0 to 22.7°C (mean = 9.5°C) and maxima ranging from 31.4 to 56.6°C (mean = 39.5°C; Fig. 5). Mosquito immature survival and adult lifespan had the lowest thermal optima, while pathogen development rate had the highest thermal optima (Fig. 5). Vector competence often peaked at much lower temperatures than pathogen development rate (Fig. 5), emphasising the importance of measuring both trait thermal responses (Paaijmans et al. 2011). Temperate mosquito species had notably higher immature survival at temperatures below 10°C than the sub‐tropical and tropical species (Fig. 3), suggesting that this trait is important for persistence in temperate climates. Consistent with previous ectotherm physiology work (Amarasekare & Savage 2012), rate traits usually exhibited asymmetric unimodal thermal responses with higher optima, while probability traits were more symmetrical with lower optima (Figs 3 and 4). Asymmetric curves for rates such as immature development, fecundity, biting, and parasite incubation can be well fit by Brière and modified Arrhenius functions, while symmetrical curves for probability traits such as survival and vector competence are well described by quadratic or Gaussian functions (Figs 3 and 4) (Johnson & Lewin 1946; Briere et al. 1999; Amarasekare & Savage 2012; Molnár et al. 2013, 2017).

In contrast to the unimodal responses for other traits, the lifespans of three temperate mosquitoes – Culex pipiens, Cx. tarsalis, and Cx. quinquefasciatus – monotonically declined across the temperature ranges measured (above 14°C). These species may differ in their biological responses to low temperature because of their ability to diapause as an adaptation to survive cold winters (Shocket et al. 2019). Further research in species like Ae. albopictus, which differ geographically in the ability to diapause, could test the hypothesis that diapause affects the shape of the thermal performance curve for lifespan (Table 1) (Thomas et al. 2012). Nonetheless, theory predicts that exposure to more extreme cold temperatures would eventually limit lifespans even for diapausing mosquitoes, suggesting a unimodal response over a wider temperature range.

Synthesising the overall influence of temperature on disease transmission (R₀), we found several commonalities in the thermal performance curves and thermal limits from our trait‐based models. First, we estimated that transmission peaked at intermediate temperatures between 22.7 and 29.1°C (mean optimal temperature = 25.2°C; Fig. 2). Lower thermal limits for modeled R₀ under constant temperatures ranged from 8.7 to 22.7°C and upper thermal limits ranged from 31.5 to 37.8°C (Fig. 2). As expected, several temperate mosquito species had relatively cool thermal ranges for transmission, although the lower thermal limits are more divergent than the thermal optima and upper limits (Fig. 2; Table 2). Tropical mosquito‐borne diseases had intermediate thermal optima within the environmentally relevant range of temperatures, ranging from 25.4°C for P. falciparum malaria in Anopheles gambiae to 29.1°C for DENV in Ae. aegypti. At the same time, many temperate vectors and pathogens (e.g., Cx. pipiens, Cx. tarsalis, and Cx. quinquefasciatus and WNV, EEEV, WEEV, SLEV, and SINV), had R₀ thermal limits up to 32–35°C, similar to those of tropical diseases (Fig. 2; Shocket et al. 2019). Finally, the temperature response of R₀ – particularly the lower thermal limit and optimum – varied across multiple pathogens transmitted by a single mosquito species (e.g. DENV and ZIKV in Ae. aegypti; WNV, WEEV, and SLEV in Cx. tarsalis; WNV and SINV in Cx. pipiens) and across multiple mosquito species transmitting a single pathogen (e.g. DENV in Ae. albopictus and Ae. aegypti; WNV in Cx. tarsalis, Cx. pipiens, Cx. quinquefasciatus, and Cx. univittatus) (Fig. 2; Table 2). This implies that the thermal response of transmission depends on the effects of temperature on traits of both the mosquito and the pathogen.

Sensitivity analyses conducted in previous work showed that all mosquito and pathogen traits limit the thermal response of transmission – including traits regularly incorporated into temperature‐dependent models like mosquito lifespan, extrinsic incubation rate, and biting rate as well as less‐recognised temperature‐dependent traits like vector competence and demographic rates (Mordecai et al. 2013, 2017; Johnson et al. 2015; Shocket et al. 2018; Tesla et al. 2018). Adult mosquito lifespan consistently limited R₀ at warm temperatures while pathogen development rate (i.e., extrinsic incubation rate) and mosquito biting rate limited R₀ at low temperatures (Mordecai et al. 2013, 2017; Shocket et al. 2018, 2019). However, in some systems other traits determined lower and upper thermal limits, and optima for transmission varied across systems. For RRV in Cx. annulirostris, fecundity and immature survival determined the upper and lower limits, respectively (Shocket et al. 2018). For WNV in Cx. pipiens, vector competence determined the lower limit (Shocket et al. 2019). For WNV in Cx. quinquefasciatus, oviposition rate determined the upper limit, and for WNV, WEEV, and SLEV in Cx. tarsalis, biting rate was important for the upper limits (Shocket et al. 2019). Because R₀ models were sensitive to different traits for different systems, it is critical to include empirically‐estimated thermal responses for the full suite of traits in transmission models. Models based on more limited thermal response assumptions often predict very different effects of temperature on transmission, which align poorly with field data.

Discussion

Strengths and limitations of mechanistic and statistical approaches

Research on the effects of temperature on mosquito‐borne disease has taken either mechanistic (trait‐based) or statistical (correlative) approaches (Rogers & Randolph 2006). Mechanistic approaches are most suitable for characterising the multivariate, nonlinear effects of temperature on disease transmission across broad temperature and geographic ranges, for estimating the fundamental environmental limits on transmission, and for extrapolating into future climate regimes and novel settings, for which statistical approaches have limited applicability (Parham et al. 2015). However, statistical models are often more appropriate for locally predicting disease dynamics, for describing or forecasting transmission over smaller spatial or temporal scales, for understanding the relative explanatory power of multiple drivers of transmission, and for describing current patterns of disease transmission (Parham et al. 2015).

Mechanistic models rely on our understanding of the dominant processes that underlie organismal fitness to predict geographic range, population size, or transmission rate (Helmuth et al. 2005; Kearney et al. 2009, 2010; Kearney & Porter 2009), and therefore require experiments on multiple traits of pathogens, vectors, and their interactions across environmental conditions. Synthesising heterogeneous data sources from the literature, including filling in parameter values from related species where necessary (e.g., Mordecai et al. 2013), introduces methodological and biological differences that can add error to parameter estimates. Unlike statistical approaches, such as species distribution models (SDMs), mechanistic models often do not jointly capture many biotic and abiotic constraints that limit observed ranges.

The value of mechanistic models is their flexibility and extensibility, which are particularly important for predicting distributions and dynamics in novel environments (Williams & Jackson 2007). Because experiments can capture mechanistic responses to both current and anticipated climatic conditions, they are more appropriate than SDMs for predicting species responses to novel or non‐equilibrium contexts, such as climate change (Helmuth et al. 2005; Kearney & Porter 2009). Moreover, many statistical models have several key limitations: limited geographic and/or temporal extent (Table S2), limited capacity to separate effects of multiple interacting and covarying environmental, population, and behavioural factors, and the assumption that the processes currently limiting ranges have set range limits in the past and will continue to do so in the future, despite entering unprecedented regimes of climate, population movement, and interventions. Direct comparisons of statistical and mechanistic models revealed that they performed similarly at predicting current distributions, but predicted differential responses of species to a uniform warming (Buckley et al. 2010).

These approaches are complementary because of their differing strengths, applications, and data requirements (Parham et al. 2015). Thermal biology principles that govern mosquito‐borne disease transmission – i.e., that temperature, and therefore climate change, has nonlinear effects on multiple traits and on transmission as a whole – apply to both mechanistic and statistical approaches.

Comparing our results with other mechanistic models

The assumption that warmer, wetter conditions universally promote mosquito‐borne disease is pervasive in the literature (Ermert et al. 2012; Morin et al. 2015; Caminade et al. 2017; Thomson et al. 2017). Yet our trait‐based work (Figs 2, 3, 4, 5) has highlighted the importance of applying rigorous thermal biology in mosquito‐borne disease models to accurately estimate nonlinear effects of temperature. Many models assume that only mosquito longevity, extrinsic incubation period, and sometimes biting rate are temperature‐sensitive, measure either temperature‐dependent vector competence or extrinsic incubation period but not both, and/or assume monotonic thermal responses that do not account for unimodal effects of temperature (e.g. Martens et al. 1997; Craig et al. 1999; Fros et al. 2015; Morin et al. 2015; Perkins et al. 2016; Vogels et al. 2016; Paull et al. 2017; Siraj et al. 2017). Even when they predict that the effects of temperature on transmission are unimodal overall, these models with limited thermal biology often predict very different thermal optima and limits for transmission than models that include the full suite of nonlinear trait thermal responses (Table 3).

Table 3.

Thermal optima and limits vary substantially across previous mechanistic models of vector‐borne disease transmission

System	Topt	T min	T max	Study
Falciparum malaria (Anopheles spp.)	25	16	34	Mordecai et al. (2013)
Falciparum malaria (Anopheles spp.)	31	18	38	Martens et al. (1997)
Falciparum malaria (Anopheles gambiae)	30	18	40	Craig et al. (1999)
Falciparum malaria (Anopheles spp.)	32–33	20	39	Parham & Michael (2010)
Falciparum malaria (Anopheles stephensi)	29	12	38	Shapiro et al. (2017)
DENV, CHIKV, ZIKV (Ae. aegypti)	29	18	35	Mordecai et al. (2017)
DENV, CHIKV, ZIKV (Ae. albopictus)	26	16	32	Mordecai et al. (2017)
CHIKV (Ae. aegypti)	30	–	–	Johansson et al. (2014)
DENV (Ae. aegypti)	29	12	32	Liu‐Helmersson et al. (2014)
DENV (Ae. aegypti)	35	21	36	Morin et al. (2015)
DENV (Ae. aegypti)	29	13	33	Wesolowski et al. (2015)
ZIKV (Ae. aegypti)	36	–	–	Caminade et al. (2017)
ZIKV (Ae. albopictus)	29	–	–	Caminade et al. (2017)
DENV (Ae. aegypti)	33	–	–	Siraj et al. (2017)
ZIKV (Ae. aegypti)	29	23	35	Tesla et al. (2018)
WNV (Cx. pipiens)	25	17	35	Shocket et al., (2019)
WNV (Cx. tarsalis)	24	12	32	Shocket et al., (2019)
WNV (Cx. quinquefasciatus)	25	19	32	Shocket et al. (2019)
WNV (Aedes and Culex spp)	35	18	*	Kushmaro et al. (2015)
WNV (Cx. tarsalis, Cx. pipiens, Cx. quinquefasciatus)	24‐25	15‐17	–	Paull et al. (2017)
WNV (Cx. pipiens, biotypes pipiens, molestus, hybrid)	28	18	*	Vogels et al. (2017)

For each vector‐borne disease and study, estimated thermal optima (Topt) and lower and upper thermal limits (T _min and T _max, respectively) in degrees Celsius were taken from the original papers or by plotting the models. Models include R₀, vectorial capacity, and other related measures of transmission. Dashes (‐) indicate that thermal limits were not reported. Asterisks (*) indicate that models were not unimodal. Models presented in this paper (Table 2) are shown in bold for comparison. The parasite abbreviations are as follows: dengue virus (DENV), chikungunya virus (CHIKV), Zika virus (ZIKV), and West Nile virus (WNV). Note: Johnson et al. (2015) used Bayesian inference refit the models for falciparum malaria in Anopheles spp. from the original formulation in Mordecai et al. (2013) and reported similar Topt, T _min and T _max estimates of approximately 25, 19, and 33 degrees Celsius, respectively, depending on the choice of priors.

For falciparum malaria, our published R₀ model predicted a suitable temperature range of 17–34ºC and an optimum of 25ºC (Mordecai et al. 2013; Johnson et al. 2015), while earlier models with more limited thermal biology assumptions predicted 3–15ºC wider temperature ranges and 5–7ºC higher optimal temperatures (Table 3) (Martens et al. 1997; Craig et al. 1999; Parham & Michael 2010). Independent field data on the number of malaria‐infectious mosquitoes per person per year (entomological inoculation rate; EIR) across Africa strongly support our predicted optimum of 25ºC and declines in transmission above 28ºC, providing little support for previous predictions (Fig. S1) (Mordecai et al. 2013). Similarly, for dengue, chikungunya, and Zika viruses in Ae. aegypti, previous models with more limited thermal biology assumptions predicted thermal optima for transmission up to 6ºC higher than our published R₀ model, which peaked at 29ºC (Table 3) (Johansson et al. 2014; Liu‐Helmersson et al. 2014; Morin et al. 2015; Wesolowski et al. 2015; Caminade et al. 2017; Siraj et al. 2017). We found a strong positive relationship between predicted temperature‐dependent R₀ and human incidence of dengue (> 85% accuracy) and chikungunya and Zika (> 66% accuracy) across the Americas in 2014–2016 (Fig. S2) (Mordecai et al. 2017). From a more recently published version of our Ae. aegypti R₀ model updated with Zika‐specific traits (which also peaked at 29ºC), 71.5% of cases in Colombia fell within municipalities with 1–12 months of predicted temperature suitability (mismatches were often due to spatial grain of the data), strongly supporting our predicted relationship (Tesla et al. 2018). Finally, for West Nile virus, previous models predicted thermal optima up to 11ºC higher than our predicted optima of 24–25ºC (Table 3) (Kushmaro et al. 2015; Paull et al. 2017; Vogels et al. 2017), which matched the unimodal thermal response of human neuroinvasive West Nile incidence that also peaked at 24ºC (Fig. S3; Shocket et al. 2019).

Together, these examples illustrate the importance of both accurately incorporating a full suite of empirically derived, nonlinear trait thermal responses into mechanistic models and validating the models against field data. Other published mechanistic models did not directly report the inferred relationship between temperature and transmission nor validate the relationship with independent field data (e.g., Brady et al. 2014; Perkins et al. 2016; Li et al. 2019), making model comparison difficult.

Model validation

Connecting mechanistic model predictions to independent field data – model validation – is critical for comparing different models and for assessing their applicability in the field (Hooten & Hobbs 2015). Although several potential approaches exist, including simulating data from mechanistic models to compare with observed vector abundance or case incidence (e.g., Morin et al. 2015; Kramer et al. 2016), or testing the accuracy of models fit to a training dataset when predicting a separate testing dataset (e.g. Smith et al. 2007a; Ren et al. 2016), few studies have applied existing methods to validate vector‐borne disease models (but see Tompkins & Ermert 2013; Wesolowski et al. 2015).

Several challenges have limited model validation (Table 1). First, the relationship between R₀ and incidence of human cases – the most commonly available data for validation – is nonlinear (Smith et al. 2007b), so their similarity may be difficult to assess. Second, in local time series data, temperature ranges may cover only a subset of globally relevant temperatures and covary with other environmental factors, but larger‐scale datasets that span a wider range of temperatures introduce error from spatial aggregation and confounding variation in other factors that affect transmission. Third, because environmental drivers affect transmission at varying time lags, the time scales on which to compare temperature and transmission are not obvious. Validation of mechanistic temperature‐dependent transmission models therefore remains a critical gap in theory, statistical approaches, and data availability (Table 1).

In light of these challenges, we have taken several approaches to validating mechanistic models, depending on the type and scale of data available. First, we graphically compared predicted temperature‐dependent R₀ with entomological inoculation rate (EIR, a metric closely related to R₀ (Smith et al. 2007b)) for malaria plotted against average transmission season temperature from data spanning 30 years across Africa (Hay et al. 2000). We showed that the maximum EIR within data subsets binned by temperature were closely correlated with predicted R₀, though EIR varied greatly within temperature bins (Fig. S1) (Mordecai et al. 2013). With incidence data, we graphically compared seasonal and geographical patterns with predicted temperature‐dependent R₀. Ross River virus incidence in Australia from 1992 to 2013 closely aligned with predicted average seasonal temperature‐dependent R₀ across cities weighted by population size, with a 2‐month lag (Fig. S4) (Shocket et al. 2018). As described above, our mechanistic model predictions corresponded closely with monthly county‐level West Nile neuroinvasive disease incidence in the US from 2001 to 2016 (Fig. S3) (Shocket et al. 2019), weekly dengue, chikungunya, and Zika incidence across countries in the Americas from 2014 to 2016 (Fig. S2) (Mordecai et al. 2017), and Zika occurrence across municipalities in Colombia from 2015 to 2017 (Tesla et al. 2018). Together, this diverse set of field data and approaches shows that temperature‐dependent R₀ is often strongly associated with observed patterns of disease, despite the known limitations of the models and data.

Comparison with previous statistical models

In contrast to mechanistic models, statistical models have directly inferred relationships between climate and vector abundance, occurrence, or disease incidence from field data at local, regional, and global scales. In particular, species distribution models (SDMs) use statistical analyses of geographic records of vector or disease occurrence and climate and other environmental covariates to predict species geographic distributions and their ecological determinants (Table S2). These methods are appealing because they can infer current climate relationships using presence‐only data from health departments or surveillance records, along with remotely sensed or ground‐based climate data.

Most SDMs for vectors and vector‐borne diseases find at least one aspect of temperature (e.g., mean, range, variability) to be an important predictor of occurrence (Table S2). Differences among models may arise because of the difficulty of inferring nonlinear, dynamic effects of temperature in noisy data and the limited range of environmental conditions represented in many studies. Direct model comparison with mechanistic models is not feasible because most SDMs do not directly report either the inferred relationships between climate variables and probability of occurrence or the occurrence probabilities as spatially explicit datasets. This is an important problem because individual SDMs are often difficult to reproduce, externally validate, or apply to new research settings. Without such improvements (Qiao et al. 2016; Sloyer et al. 2019), the majority of published SDMs cannot contribute substantially to our understanding of the drivers and projected changes in vector‐borne disease transmission. Recent efforts in model comparison and ensemble modelling for mosquito‐borne disease (Yamana et al. 2016; Little et al. 2017; Carlson et al. 2018) highlight how multi‐model synthesis can move the field forward when model assumptions and results are transparent and reproducible. Nonetheless, SDMs provide evidence that temperature is a strong statistical predictor of the occurrence of vector‐borne diseases and vectors, supporting principles from vector thermal biology.

Evidence of unimodal temperature responses in the field

A key principle of thermal biology, supported by mechanistic models (Fig. 2), is that the effects of temperature on mosquito‐borne disease transmission are unimodal. This implies that relationships observed across more limited temperature ranges are expected to range from negative to positive to null. Field‐based empirical support for positive temperature – disease relationships is widespread (e.g., Alonso et al. 2011; Mena et al. 2011; Stewart‐Ibarra & Lowe 2013; Siraj et al. 2014; Lowe et al. 2018), but support for unimodal responses or declines at high temperatures is more limited. However, emerging field evidence supports unimodal relationships with temperature, including declines at high temperatures, for dengue incidence and Aedes aegypti abundance in Colombia (Peña‐García et al. 2016, 2017), for chikungunya incidence in the Americas (Perkins et al. 2015), for malaria incidence in Kenya and across Africa (Mordecai et al. in review; Shah et al. in press), for West Nile disease in the United States (Fig. S3; Shocket et al. 2019), and for the vectors of malaria, dengue, chikungunya, yellow fever, Zika, leishmaniasis, and Chagas disease in Ecuador (Escobar et al. 2016). Ambiguous or spatially variable relationships between temperature and incidence (e.g., for Ross River virus, Gatton et al. 2005; Bi et al. 2009; Hu et al. 2010; Werner et al. 2012; Koolhof et al. 2017) may be explained by unimodal thermal responses. In other cases, for example, for malaria in sub‐Saharan Africa, effects of climate are attributed to temperature in cooler, highland areas and to drought in warm, semi‐arid regions, without recognising that high temperatures alone could limit transmission (Ermert et al. 2012; Thomson et al. 2017). However, recent work has shown negative effects of locally high temperatures on urban malaria transmission in a semi‐arid city in India (Santos‐Vega et al. 2019). Mechanistic temperature‐based models are important for predicting effects on disease when climate change alters the covariation among temperature, humidity, rainfall, and drought. We find growing support for unimodal relationships between mosquito‐borne disease and temperature in the field from the few studies that have investigated nonlinear responses, supporting thermal biology principles and mechanistic model predictions (Fig. 2).

Implications and predictions for climate change

Our synthesis of previous research on the effects of temperature on mosquito‐borne disease transmission provides a clear set of case studies to support the universal importance of nonlinear thermal responses for vector‐borne diseases more generally. From these case studies, we derive four key implications for climate change:

1. Changes in temperature may locally increase, decrease, or have no effect on transmission (Fig. 2). The direction and relative magnitude of these effects are predictable from mechanistic models (Fig. 1) but would otherwise appear idiosyncratic.

2. Accurately estimating the thermal optima and limits for transmission is critical for predicting effects of temperature change on transmission. Models derived from incomplete assumptions for mosquito and pathogen thermal biology can incorrectly estimate both the direction and magnitude of effects of climate change (Table 3).

3. Enhanced climate data products and projections (Thomson et al. 2006, 2011, 2017; Caminade et al. 2014; Tjaden et al. 2018) are only as valuable as the models that link climate to disease transmission, which vary widely in their assumptions, predicted relationships, and field validation (Tables 2‐3).

4. Climate warming may increase the geographic and seasonal ranges of mosquito‐borne diseases with high thermal optima and upper limits relative to their current distributions, including Ross River, dengue, and Zika viruses (Mordecai et al., 2017; Shocket et al. 2018; Tesla et al. 2018; Ryan et al. 2019). However, climate warming is more likely to shift or contract the geographic and seasonal ranges of diseases with lower thermal optima and upper limits, including malaria and West Nile virus (Mordecai et al. 2013; Johnson et al. 2015; Ryan et al. 2015, 2019; Shocket et al. 2019).

The trait‐based thermal biology approach illustrated here for mosquito‐borne diseases can be applied more broadly to understand the effects of climate change on many other types of vector‐borne diseases, including plant diseases transmitted by aphids, flies, and psyllids (Taylor et al. 2016, 2018) and human and livestock diseases transmitted by biting midges, fleas, and flies (Akey et al. 1978; Carpenter et al. 2011; Moore et al. 2012; Alsan 2015), and tick‐borne diseases (Ostfeld & Brunner 2015; Cheng et al. 2017). However, differences in vector and host biology, including the effects of vector life history and biting behaviour and how they interact with host activities and life cycles, can cause major differences between the models presented here (eqns (1), (2), (3)) and the transmission models most appropriate for other systems. For example, in some tick‐borne disease systems the most important effects of climate on human disease risk arise from effects on tick questing behaviour, non‐human host community composition, seasonal phenology of feeding, and human exposure to ticks (Randolph 2010; Estrada‐Pena et al. 2012; Gilbert et al. 2014; Ostfeld & Brunner 2015). Despite the variation among different types of vector‐borne diseases, the trait‐based approach applied here is broadly applicable across many diseases (Molnár et al. 2017). The nonlinearity of ectotherm trait thermal responses implies that effects of climate change on nearly all infectious diseases will be globally nonlinear but may be locally positive, negative, or neutral depending on host, vector, and parasite trait responses. Crucially, these shifts in disease transmission and burden should be predictable using the type of trait‐based approach presented here (Gehman et al. 2018).

In contrast to transmission within suitable environments, current and future geographic range limits on transmission may depend primarily on the capacity of organisms to tolerate heat and cold stress, as well as factors like water availability, land use and vector control (Kearney et al. 2009; Overgaard et al. 2014; Parham et al. 2015). Climate warming may release populations from cold stress near cool range margins (particularly with warming winter temperatures), allowing latitudinal and altitudinal range expansions. By contrast, populations near upper thermal margins will experience increased heat stress that could restrict future geographic ranges (Kingsolver & Woods 2016; Gehman et al. 2018). However, many diseases are already much more geographically constrained than their physiological thermal limits (e.g., malaria is now restricted to the tropics but historically occurred throughout temperate and tropical zones), implying that climate change may not expand their range boundaries (Gething et al. 2010). Moreover, changes in temperature extremes may have a greater impact on range limits than changes in mean temperatures. Incorporating changes in temperature means and variation is critical for understanding how climate change will impact vector‐borne disease transmission (Savage 2004; Paaijmans et al. 2010a; Lambrechts et al. 2011; Rohr et al. 2011; Blanford et al. 2013; Waite et al. 2019).

The potential for vectors and pathogens to adapt, via plasticity or evolution, to warming climates is an important empirical and theoretical gap (Table 1) (Thomas & Blanford 2003; Kearney et al. 2009; Sternberg & Thomas 2014). Pathogens experience different temperature‐driven selective pressures than vectors. For example, for mosquito‐borne disease transmission to occur at warm temperatures, a minimal requirement is that mosquito lifespan, which has consistently low thermal optima and upper limits, must be long enough to complete the extrinsic incubation period, which decreases dramatically at warm temperatures (Fig. 3). Therefore, as the climate warms, mosquito‐borne disease transmission will require mosquitoes to adapt for longer lifespans at high temperatures, currently the main limitation on transmission near upper thermal limits. Yet mosquitoes could maintain high fitness at high temperatures via rapid oviposition cycles and high reproduction rates despite short lifespans, resulting in diverging selective pressures on mosquitoes and pathogens. Moreover, thermal stress tolerance traits that often determine species range boundaries (Kearney et al. 2009; Overgaard et al. 2014) do not directly affect transmission and may trade off with other fitness‐ and transmission‐relevant traits. The potential for climate adaptation depends on the amount of standing genetic variation and phenotypic plasticity for survival and other traits at high temperatures, the correlations between these traits and of traits with fitness, the velocity of climate change relative to generation times, and the impact of other selective forces (e.g. insecticide resistance) (Sternberg & Thomas 2014; Lefevre et al. 2018; Ohm et al. 2018).

While physiological effects of temperature on vectors may be relatively predictable, climate‐driven changes in host population size, movement, behaviour, and immunology are much more idiosyncratic. Human populations may respond to climate change via changes in land use and agricultural practices, housing type and density, water storage practices, seasonal migration, relocation between regions, and demographic shifts (Parham et al. 2015; Wesolowski et al. 2017), which will inevitably vary geographically. As a result, the realised impact of climate change on disease dynamics will depend on physiological changes in vectors and pathogens as well as on behavioural and demographic changes in host populations (Parham et al. 2015; Metcalf et al. 2017; Wesolowski et al. 2017).

Although direct and indirect effects of temperature on vectors, parasites and hosts have a profound effect on transmission, temperature is only one component of a complex network of causality. Our goal is to predict conditions that favour and disfavor transmission. By analogy, warming oceans tend to increase the intensity of hurricanes, yet warm oceans alone do not generate hurricanes. Likewise, steroid use in baseball players makes hitting home runs more likely, but steroids alone do not cause home runs. In the same way, increasing temperature suitability does not cause disease outbreaks, but it can increase their probability and intensity when other necessary conditions align: it is a threat multiplier (Department of Defense 2014).

Physiological effects of temperature on transmission predict that cool locations and seasons are most vulnerable to warming‐driven increases in vector‐borne disease transmission, while warmer regions may see climate‐driven declines or seasonal shifts in transmission. Urbanisation, land conversion, and other landscape changes may act in concert with climate to drive shifts in the burden of vector‐borne disease from cooler‐adapted diseases like An. gambiae‐transmitted malaria to warmer‐adapted diseases like Ae. aegypti‐transmitted dengue, chikungunya, and Zika (Mordecai et al. in review). Already, in the last two decades malaria has declined in Africa (Bhatt et al. 2015) and Latin America (Carter et al. 2015), which may be attributable to interactive effects of climate and malaria control programs (Thomson et al. 2017), while dengue and other viruses transmitted by warm‐adapted Ae. aegypti mosquitoes have risen dramatically (Mitchell 2016; Stanaway et al. 2016; PAHO WHO & | Chikungunya | Statistic Data 2016), consistent with the combined effects of climate, urbanisation, and declining vector control.

Conclusions

Temperature is a fundamental, complex and nonlinear driver of vector‐borne disease transmission. Its physiological effects are consistent across a variety of ectotherm vectors and pathogens because of the underlying constraints of ectotherm physiology. Combining these effects into a unified trait‐based transmission framework can facilitate qualitative predictions for the effects of climate change and comparison across systems. For any vector – pathogen system, a limited range of temperatures permits transmission and intermediate temperatures within this range are optimal. Across systems, thermal limits and optima vary. In a changing climate, the transmission of specific diseases may experience seasonal and geographic shifts that include declines, increases, and minimal effects, which are predictable from trait‐based models. At the same time, because thermal limits and optima vary across vectors and pathogens, the relative suitability for transmission of different diseases is expected to change with the climate. Finally, seasonal and inter–annual variation in temperature, variation in rainfall and weather events, changing land use and urbanisation, and human population changes may mitigate or exacerbate the influence of climate change on vector‐borne disease transmission in many settings. Integrative research that builds on thermal physiology as a backbone and incorporates additional drivers of vector, pathogen, and host ecology is critical for understanding the changing ecology of vector‐borne disease.

Authorship

EAM conceived of, designed and wrote the manuscript. EAM, LRJ, JRR, SJR, VS, MSS, AMSI and MBT contributed to model parameterisation and validation. EAM, LRJ, MN, JRR, SJR, VS, AMSI and MBT obtained funding for the study. All authors contributed to literature reviews in the studies. All authors revised the manuscript and approved of its final version.

Supporting information

‐

Data accessibility statement

All data used in this paper are either already published elsewhere or included within the tables.