Evaluating the predictions of the protein stability change upon single amino acid substitutions for the FXN CAGI5 challenge

Abstract

Frataxin (FXN) is a highly-conserved protein found in prokaryotes and eukaryotes that is required for an efficient regulation of cellular iron homeostasis. Experimental evidence associates amino acid substitutions of the frataxin to Friedreich Ataxia, a neurodegenerative disorder. Recently, new thermodynamic experiments have been performed to study the impact of somatic variations identified in cancer tissues on protein stability. The Critical Assessment of Genome Interpretation (CAGI) data provider at the University of Rome measured the unfolding free energy of a set of variants (frataxin challenge dataset) with far-UV circular dichroism and intrinsic fluorescence spectra. These values have been used to calculate the change in unfolding free energy between the variant and wild-type proteins at zero concentration of denaturant (ΔΔG^H2O). The frataxin challenge dataset, composed of eight amino acid substitutions, was used to evaluate the performance of the current computational methods for predicting the ΔΔG^H2O value associated with the variants and to classify them as destabilizing and not destabilizing. For the fifth edition of CAGI, six independent research groups from Asia, Australia, Europe and North America submitted 12 sets of predictions from different approaches. In this paper we report the results of our assessment and discuss the limitations of the tested algorithms.

Introduction

The human frataxin is a protein localized in the mitochondria and cytoplasm of the cells that promotes the heme biosynthesis, the assembly and repair of iron-sulfur clusters by delivering Fe²⁺ to proteins involved in these pathways. Frataxin may play a role in the protection against iron-catalyzed oxidative stress (Lupoli, Vannocci, Longo, Niccolai, & Pastore, 2018).

Frataxin (FXN) single-nucleotide variants have been associated to Friedreich Ataxia (MIM# 229300), a degenerative disorder primarily affecting the nervous system (Pandolfo, 2008). Moreover, frataxin might play a role in cancer as previous studies have shown that it protects tumor cells against oxidative stress and apoptosis, but also acts as a tumor suppressor (Guccini et al., 2011; Schulz et al., 2006). The COSMIC (Catalog of Somatic Mutations in Cancer) database (Tate et al., 2019) collects a set of FXN somatic variations identified in cancer tissues. To investigate the possible thermodynamic effect of those variations on protein stability a subset of eight variants were expressed as soluble recombinant protein in E.coli (Petrosino et al., 2019). For this dataset of amino acid substitutions the stability of the variant proteins is experimentally measured with circular dichroism and fluorescence and compared with wild-type. These measures have been used for the frataxin challenge of the fifth edition of the Critical Assessment of Genome Interpretation (CAGI5). For the frataxin challenge participants were asked to predict the variation of free energy change at zero concentration of denaturant (ΔΔG^H2O) upon single-point protein variation. During the last decades several methods have been developed to predict the impact of amino acid variants on protein stability (Compiani & Capriotti, 2013). These available algorithms are mainly based on energy functions designed to assess the stability free energy of the protein and its variants and/or machine-learning-based methods trained to predict the stability changes upon variation. In this manuscript we scored the performance of six research groups in predicting the measured ΔΔG^H2O value (regression task) and its class (classification task) for eight frataxin single amino acid variants. The performances of all the groups are compared with those achieved by state-of-the-art methods (Capriotti, Fariselli, & Casadio, 2005; Guerois, Nielsen, & Serrano, 2002) to estimate the possible improvement with respect to previously developed algorithms. For the calibration of the predictions, previous experimental thermodynamic data on a different set of variants (Faraj, Gonzalez-Lebrero, Roman, & Santos, 2016) were used as a reference.

Material and methods

Dataset and classification

The CAGI5 frataxin challenge dataset consists of 8 coding variants of the FXN gene. These variants encode for single amino acid substitutions reported in the COSMIC database. A representation of the variation sites in the three-dimensional structure of frataxin (PDB: 1EKG) is provided in Fig.1.

Figure 1.

Mapping of the eight variation sites of the frataxin challenge data set on the three-dimensional structure of the protein (PDB: 1EKG)

For each protein variant, the unfolding free energy change (ΔG_u) at different denaturant concentrations was experimentally determined with circular dichroism and fluorescence. These measures were used to calculate the unfolding free energy at zero concentration of denaturant (ΔG^H2O). Finally, the change of ΔG^H2O of the variant protein (ΔΔG^H2O) was calculated using the following equation:

$$\mathrm{\Delta }\mathrm{\Delta }{G}^{H_{2}O}=\mathrm{\Delta }{G}_{mut}^{H_{2}O}-\mathrm{\Delta }{G}_{wt}^{H_{2}O}$$ [1]

The average experimental values of the ΔΔG^H2O obtained by circular dichroism and fluorescence (Supporting Table S1) were used for the challenge. An exception to this procedure is the case of the variant p.W173C which does not fold. In this case, we assumed its unfolding free energy equal to 0 kcal/mol and the ΔΔG^H2O equal to the negative of the ΔG^H2O of the wild-type protein.

We also assessed the quality of the predictions by calculating the performance of the methods in classification mode. For this task we selected a threshold of −1.0 kcal/mol to discriminate between destabilizing (ΔΔG^H2O <−1.0 kcal/mol) and not destabilizing variants (ΔΔG^H2O ≥−1.0 kcal/mol). With this assumption, five variations in the dataset were classified as destabilizing and the remaining three as not destabilizing. A visual representation of the similarity between the ΔΔG^H2O obtained by different experimental techniques (circular dichroism and fluorescence) and the classification of the variations is shown in Fig. S1.

The final set of 8 variations with the relative average ΔΔG^H2O and their experimental errors are reported in Table 1.

Table 1.

Frataxin challenge dataset of amino acid substitutions. The mean variation of unfolding free energy change at zero solvent concentration (ΔΔG^H2O) is calculated as the mean ΔΔG^H2O values of Fluorescence and Circular Dichroism experiments (see Supporting Table S1). The standard deviation (σ) is obtained summing the errors associated to both types of measures. Destabilizing are the variants with ΔΔG^H2O < −1.0 kcal/mol.

DNA (hg38)	mRNA (NM_000144.4)	Protein (NP_000135.2)	ΔΔGH20 kcal/mol	Destabilizing
chr9:g.69053187A>G	c.311A>G	p.D104G	0.4±0.4	No
chr9:g.69053196C>T	c.320C>T	p.A107V	0.0±0.6	No
chr9:g.69053201T>C	c.325T>C	p.F109L	−2.8±0.4	Yes
chr9:g.69053244A>C	c.368A>C	p.Y123S	−5.1±0.3	Yes
chr9:g.69065035G>T	c.482G>T	p.S161I	−3.1±0.4	Yes
chr9:g.69072648G>T	c.519G>T	p.W173C	−9.5±0.3*	Yes
chr9:g.69072671C>T	c.542C>T	p.S181F	−3.0±0.4	Yes
chr9:g.69072734C>T	c.605C>T	p.S202F	−0.2±0.4	No

^*The variant p.W173C does not fold into a three-dimensional. Thus, for calculating the ΔΔG^H2O of p.W173C we assumed that its ΔG^H2O = 0 kcal/mol. It follows that ΔΔG^H2O is equal to −ΔG^H2O of the wild-type, which is −9.50 kcal/mol.

Experimental measures

Human frataxin (FXN) variants were obtained with specific mutagenesis primers with PCR, using wild-type as a template. Wild-type and variants were then expressed in E. coli and purified. The structural conformation of the variants was compared to that of the wild-type by monitoring the near and far-UV circular dichroism and intrinsic fluorescence spectra. The thermodynamic stability was measured at different concentrations of denaturant (Urea) by monitoring the spectral changes (far-UV circular dichroism and intrinsic fluorescence emission) induced by urea. The spectral changes were extrapolated to zero denaturant concentration (ΔΔG^H2O). For equilibrium transition studies, FXN wild-type and variants were incubated at 20 °C at increasing concentrations of urea (0−9 M). After 10 min, equilibrium was reached and both intrinsic fluorescence emission and far-UV CD spectra were recorded in parallel at 20 °C. To test the reversibility of the unfolding, FXN wild type and variants were unfolded at 20 °C in 9.0 M urea. After 10 min, refolding was started by 10-fold dilution of the unfolding mixture at 20 °C into solutions of the same buffer used for unfolding containing decreasing urea concentrations. After 24 h, intrinsic fluorescence emission and far-UV CD spectra were recorded at 20 °C. All denaturation experiments were performed in triplicate. For thermal denaturation studies, FXN wild-type and variants were heated from 20°C to 95°C and then cooled from 95°C to 20°C. The dichroic activity at 222 nm was continuously monitored every 0.5°C. Melting temperature (T_m) values were calculated by taking the first derivative of the ellipticity at 222 nm with respect to temperature. All denaturation experiments were performed in triplicate. More details about the procedure for the calculation of the ΔΔG^H2O and the analysis of the thermodynamic data are described in supplementary materials.

Challenge participants and prediction methods

Six groups participated to the CAGI5 frataxin challenge by submitting a total or 12 sets of predictions using different procedures. The Lichtarge Lab at the Baylor College of Medicine, referred as Group 1, submitted one set of predictions (G1–1) using Evolutionary Action (EA) method (Katsonis & Lichtarge, 2014). The output of the program was normalized to return ΔΔG^H2O values between 0 and −3 kcal/mol. The Biocomputing Group (Group 2) from the University of Bologna provided one batch of predictions (G2–1) using INPS-3D (Savojardo, Fariselli, Martelli, & Casadio, 2016). For this challenge the 1EKG structure from the Protein Data Bank was considered as wild-type. The Zhou Lab at the Griffith University, labelled as Group 3, submitted three sets of predictions (G3–1, G3–2, G3–3) using EASE-MM (Evolutionary, Amino acid, and Structural Encodings with Multiple Models) algorithm (Folkman, Stantic, Sattar, & Zhou, 2016). For the assessment we considered only one set of predictions (G3–1) because the three batches of predictions returned the same ΔΔG^H2O values. The Shen Lab at the Texas A&M University (Group 4) submitted two groups of predictions (G4–1, G4–2) using iCFN (interconnected Cost Function Network) (Karimi & Shen, 2018). This method was modified to fit the experimental ΔΔG^H2O values for frataxin variants from a previous work (Correia, Pastore, Adinolfi, Pastore, & Gomes, 2008). The Pal Lab at the Indian Institute of Science in Bangalore, labelled as Group 5, submitted two batches of unscaled predictions (G5–1, G5–2) using GROMACS (Van Der Spoel et al., 2005). This approach uses molecular dynamics simulations to estimate the stability of unfolded and native conformations for the wild-type and variants. The Kim Lab at the University of Toronto (Group 6) submitted three batches of predictions (G6–1, G6–2, G6–3) using the ELAPSIC algorithm (Berliner, Teyra, Colak, Garcia Lopez, & Kim, 2014; Witvliet et al., 2016). ELAPSIC is a meta-predictor that combines predictions from other methods with sequence and structure-based features using a gradient boosting algorithm. During the assessment we observed that predictions submitted by Group 6 showed strong negative correlation with the experimental data. This is due to the difference between the challenge’s request of predicting the variation of unfolding free energy change (ΔΔG_u) and the predictions of folding free energy change (ΔΔG_f) submitted by Kim’s Lab. For this reason, we also scored the inverse of the three sets of Group 6 predictions (G6–R1, G6–R2, G6–R3).

Finally, to estimate the improvement of the performance between more recent algorithms and state-of-the-art methods, we included in our assessment the performance of FoldX (Guerois et al., 2002) and I-Mutant2.0 (Capriotti et al., 2005).

In the supplementary materials we described more in detail the methods and procedures used by each group to perform their predictions. A summary of all the submissions is reported in Supporting Table S2.

Prediction assessment

For the evaluation of the predictions we considered eight measures of performance for the regression and classification tasks defined in supplementary materials (section Measures of performance). Comparing the predicted and experimental values of ΔΔG^H2O of each protein variant, we calculated three types of correlations (Person, Spearman and Kendall-Tau) and two types of errors (Root Mean Square Error and the Mean Absolute Error). Furthermore, we considered a threshold of −1.0 kcal/mol for classifying variants in destabilizing (ΔΔG^H2O <−1.0 kcal/mol) and not destabilizing variants (ΔΔG^H2O ≥−1.0 kcal/mol). Using this threshold for the binary classification task, we scored the predictions calculating the balanced accuracy (BQ₂), the Matthews correlation coefficient (MCC) and the Area Under ROC Curve (AUC). Finally, we ranked all the submissions considering each one of the eight measures of performance and calculating the average value of the ranks which is used to select the best predictions.

In the second part of the assessment, we determined the significance of the differences between the performance of two methods with the Kolmogorov-Smirnov (KS) test. The KS test was used to compare the distribution of the ranks for each measure of performance.

Another important issue in the evaluation of the most reliable predictions is the presence of outliers in the experimental dataset. With outlier, we refer to an experimental measure that, for different reasons, is considered to be less accurate or reliable than others. In general, it is expected that most of the methods will fail in the prediction of the outliers. According to this assumption, in our assessment we also scored the performance of the algorithms removing the outliers from the initial frataxin challenge dataset. In particular for this calculation we removed from the dataset the variant p.W173C for which the ΔG^H2O was set to 0 kcal/mol because it was not folding properly.

The definitions of the eight measures of performance considered for this assessment are reported in supplementary materials.

Results

Assessment and performance evaluation

In our assessment we first evaluated the success of the participants in predicting the value of ΔΔG^H2O. For this task, we calculated five performance measures, three of which score the correlations between experimental and predicted data (r_P, r_S and r_KT) and two the prediction errors (RMSE and MAE). The performance in the regression task for the best predictions of each group are reported in Fig. S2. According to the calculated scores, Group 3 resulted in the best predictions reaching the highest Pearson correlation coefficient (r_P=0.84) and lowest root-mean-square-deviation (RMSE=2.94 kcal/mol). Our analysis also showed that Group 6 resulted in negative values of the Pearson correlation coefficient close to −1 (r_P=−0.89). Assuming that Group 6 predicted the variation of the ΔΔG^H2O of folding instead of the unfolding, we decided to include in our assessment the opposite of the predictions submitted by Group 6. The performances of participants were compared with those achieved by state-of-the-art methods by including in our assessment the predictions returned by FoldX and I-Mutant2.0. Furthermore, we combined the regression measures with three classification scores (BQ₂, MCC and AUC) obtained using a threshold of −1.0 kcal/mol for discriminating between destabilizing and not destabilizing variants. The assessment, including eight scores of performance sorted by the average of the rank orders of each method, is summarized in Table 2.

Table 2.

Assessment of the predictions of the 6 groups and the state-of-the-art methods (FoldX and I-Mutant2.0). The eight measures of performance are defined in supplementary materials. Zhou Lab submitted three set of predictions with the same ΔΔG^H2O values. For this reason we reported only the measure of performance for submission 1.

Group	Submission	rP	rS	rKT	RMSE	MAE	BQ2	MCC	AUC	<Rank>
Kim Lab	G6–R1*	0.82	0.69	0.50	2.4	1.7	0.80	0.60	0.93	1.75
FoldX	-	0.84	0.64	0.57	2.2	1.7	0.73	0.47	0.87	2.00
Zhou Lab	G3–1	0.85	0.64	0.64	3.0	2.3	0.70	0.45	0.80	2.88
Kim Lab	G6–R2*	0.71	0.57	0.43	2.7	2.0	0.63	0.26	0.80	4.13
Biocomp	G2–1	0.74	0.52	0.36	3.2	2.3	0.80	0.60	0.80	4.25
Lichtarge Lab	G1–1	0.46	0.60	0.50	3.1	2.2	0.63	0.26	0.87	4.38
I-Mutant2.0	-	0.75	0.55	0.43	3.3	2.5	0.70	0.45	0.73	4.75
Kim Lab	G6–R3*	0.89	0.57	0.50	3.9	3.7	0.50	0.00	0.80	5.25
Shen Lab	G4–2	−0.02	0.12	0.07	4.1	2.6	0.70	0.45	0.60	7.00
Shen Lab	G4–1	−0.09	0.17	0.07	3.9	2.7	0.60	0.29	0.60	7.25
Pal Lab	G5–1	0.57	0.43	0.29	41	36	0.63	0.26	0.67	7.88
Kim Lab	G6–2	−0.71	−0.57	−0.43	6.2	4.4	0.50	0.00	0.20	9.13
Kim Lab	G6–1	−0.89	−0.57	−0.50	10.9	9.5	0.50	0.00	0.20	10.00
Kim Lab	G6–3	−0.82	−0.69	−0.50	6.4	4.5	0.50	0.00	0.07	10.00
Pal Lab	G5–2	−0.42	−0.64	−0.50	1441	1378	0.50	0.00	0.27	10.13

^*The submissions of the Kim’s Lab that were reversed. Confusion matrices for the binary classification are reported in Supporting Table S3.

The results showed that the opposite predictions of submission 1 from Kim Lab (G6–R1) achieved the top average rank calculated over the eight measures of performance. It is worth noting that FoldX scored second in the ranking achieving on average lower performance on the binary classification task and better results in the prediction of the ΔΔG^H2O value with respect to the Kim’s Lab R1 submission. Additional details about the comparison between Kim’s Lab R1 submission and the prediction of the state-of-the-art methods are shown in Fig. 2.

Figure 2.

Comparison between the performance achieved in the regression task by the top ranking submission from Kim Lab (G6-R1), FoldX, and I-Mutant2.0. rP, rS, rKT, RMSE, and MAE are defined in Supporting Information Materials. MAE, mean absolute error; RMSE, root mean square error

Dataset outlier

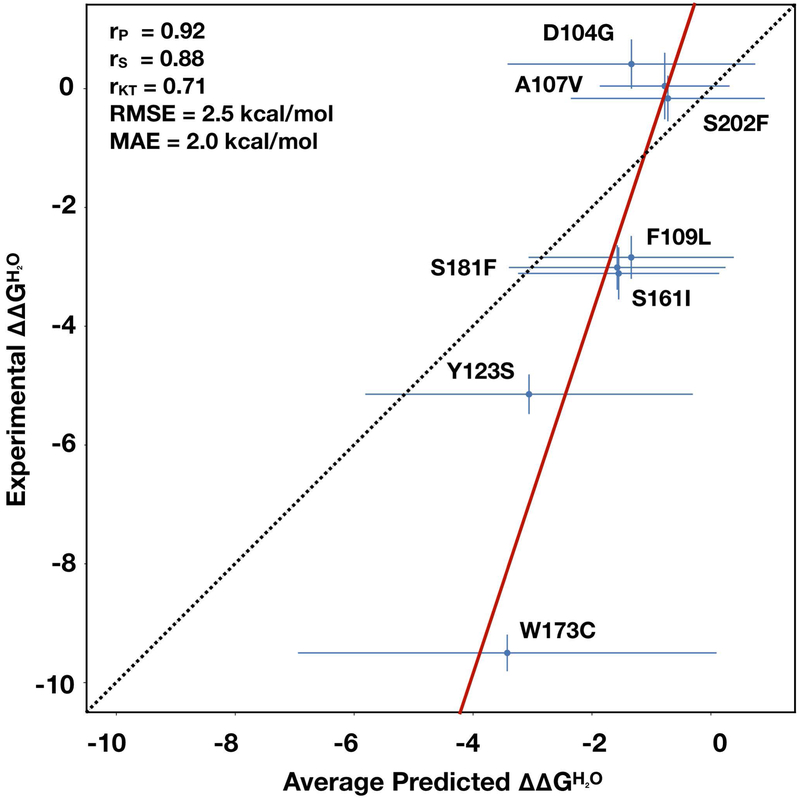
The analysis of all the submitted predictions revealed that on average all the groups failed in the prediction of the ΔΔG^H2O for the variant p.W173C. Excluding Group 5, for this variant the difference between the average predicted and experimental ΔΔG^H2O is ~6 kcal/mol (see Fig 3). A possible motivation of the strong discrepancy between predicted and experimental ΔΔG^H2O values is the partial indetermination of the ΔG^H2O of the unfolding of the p.W173C variant. Indeed, this protein variant did not fold into a three-dimensional structure. For this reason, we arbitrarily assigned to the p.W173C variant a ΔG^H2O equal to 0 kcal/mol, which implies an equal fractions of folded and unfolded protein at equilibrium. According to this observation, the protein variant p.W173C was considered an outlier and we performed a second assessment of the predictions removing it from the frataxin challenge dataset. Sorting all the predictions, according to the average ranking based on the eight measures of performance, we observed that the G6–R1 from Kim’s Lab and FoldX predictions scored in the first and second position respectively. The difference with respect to the previous assessment including all the frataxin variants is the third position in the ranking achieved by the Biocomputing Group. As expected for all the submissions the RMSE and MAE values decreased. Thus, removing the variant p.W173C from the dataset, the average RMSE for the top four ranking submissions was ~1.7 kcal/mol while it was ~2.6 kcal/mol for all the variants.

Figure 3.

Linear regression between the average predicted and experimental urn:x-wiley:10597794:media:humu23843:humu23843-math-0044. The average predictions are calculated excluding the prediction from Group 5 and considering only one submission from Group 3. rP, rS, rKT, RMSE, and MAE are defined in Supporting Information Materials. MAE, mean absolute error; RMSE, root mean square error

Methods and predictions similarity

In the last part of our assessment we compared all the submissions to calculate the level of similarity among the predictions. For the comparison we assigned to each submission a ranking vector based on the eight measures of performance defined in supplementary materials. The statistical difference among such vectors was calculated with the Kolmogorov-Smirnov test. In Fig. 4 we summarized our analysis assigning a blue color to the submissions that had significantly different ranking distributions (p-value<0.05). Contrarily, red spots are assigned to the pairs of submissions which were statistically indistinguishable. The results showed that R1 (the reverse of submission 1 from Kim’s Lab) is not statistically different from FoldX. This observation is consistent with the fact that ELAPSIC algorithm, used by Kim’s group, includes the calculation of ΔΔG values with FoldX. Our analysis also revealed that after Kim’s lab and FoldX predictions, the submissions from the Zhou Lab, Biocomputing Group and Lichtarge Lab were statistically indistinguishable. The performances of methods from the previous groups are comparable with those achieved by I-Mutant2.0. These observations, which are valid for the whole frataxin dataset (Fig. 4 panel A), are partially confirmed after removing the p.W173C variant. In this case the ranking of the predictions from Kim’s Lab are statistically different from FoldX (Fig. 4 panel B) while the second group of submissions (Biocomputing Group, Zhou Lab and Lichtarge Lab) remain statistically indistinguishable.

Figure 4.

Similarity between the predictions based on the Kolmogorov–Smirnov test among the ranking vectors from the eight measures of performance. The color of each cell is proportional to the −log10 of the Kolmogorov–Smirnov p value. Similarities calculated considering the whole frataxin data set and excluding the variant p.W173C are plotted in panels (a) and (b), respectively

Discussion

The assessment of the frataxin challenge of the CAGI5 experiment provided an opportunity to evaluate the performance of the available variant annotation methods for predicting the impact of single amino acid variations on protein stability. In detail, we scored each submission by considering the performance of the corresponding method in predicting the ΔΔG^H2O values (regression task) and by correctly classifying the variants in destabilizing and not destabilizing (classification task). The results showed that, in the regression task, the best methods achieved a Pearson correlation coefficient higher than 0.8 and a root mean square error (RMSE) lower than 2.4 kcal/mol (see Table 2). After removing from the dataset p.W173C, which represents an outlier with respect to all the other variants, the RMSE values of the best submissions decrease below 1.5 kcal/mol (see Table 3). For the classification task, we select a ΔΔG^H2O threshold of −1.0 kcal/mol for discriminating between destabilizing (ΔΔG^H2O <−1.0 kcal/mol) and not destabilizing variants (ΔΔG^H2O ≥−1.0 kcal/mol). Using such threshold, the best predictions (reversed submission 1 from Kim’s Lab) achieved remarkable balanced accuracy (BQ₂), Matthews correlation coefficient (MCC) and area under the Receiving Operator Characteristic curve (AUC) scoring 0.80, 0.60 and 0.93 respectively (see Table 2). Slightly lower performance was obtained when the p.W173C variant was removed from the frataxin dataset. The evaluation of the similarities among the submissions showed that although the reverse submission 1 (R1) from ELAPSIC scores better than FoldX for the classification task, the difference between the ranking distributions of the two methods is not significant (Kolmogorov-Smirnov p-value=0.19). A significant difference between the ranking distribution of G6–R1 Kim’s Lab and FoldX predictions is found when the p.W173C variant is removed from the dataset. In this case, the Kim’s Lab R1 submission ranks in the first position for seven over eight measures of performance considered in our assessment. Comparing the ranking distribution of the second block of groups we found that the predictions from Zhou Lab, Biocomputing Group and Lichtarge Lab are statistically indistinguishable. Finally, the analysis of the predictions from Group 5, which adopted a molecular dynamics-based approach, shows the largest ΔΔG^H2O resulting in the highest RMSE values. As suggested by the Group 5 submitters, their predictions could have been improved by normalizing the energies obtained from the simulations.

Table 3.

Assessment of the predictions submitted by the 6 groups and returned by state-of-the-art methods (FoldX and I-Mutant2.0) excluding the p.W173C variant. The eight measures of performance are defined in supplementary materials. Zhou Lab submitted three set of predictions with the same ΔΔG^H2O values. For this reason we reported only the measure of performance for submission 1.

Group	Submission	rP	rS	rKT	RMSE	MAE	BQ2	MCC	AUC	<Rank>
Kim Lab	G6–R1*	0.75	0.57	0.43	1.5	1.2	0.75	0.55	0.92	1.13
FoldX	-	0.73	0.46	0.43	1.5	1.3	0.71	0.42	0.83	2.13
Biocomp	G2–1	0.72	0.32	0.24	1.9	1.6	0.75	0.55	0.75	3.50
Kim Lab	G6–R2*	0.65	0.39	0.33	1.8	1.4	0.58	0.17	0.75	3.75
Zhou Lab	G3–1	0.57	0.46	0.52	2.1	1.8	0.63	0.35	0.75	4.25
Lichtarge Lab	G1–1	0.20	0.46	0.43	2.1	1.6	0.58	0.17	0.83	4.38
Shen Lab	G4–1	0.50	0.50	0.33	2.2	1.8	0.63	0.35	0.67	4.88
I-Mutant2.0	-	0.58	0.36	0.33	2.3	1.9	0.63	0.35	0.67	5.25
Shen Lab	G4–2	0.22	0.07	0.05	2.5	1.6	0.75	0.55	0.58	5.63
Kim Lab	G6–R3*	0.66	0.36	0.33	4.1	3.8	0.50	0.00	0.75	6.00
Pal Lab	G5–1	0.09	0.14	0.05	38	33	0.58	0.17	0.58	8.13
Kim Lab	G6–2	−0.65	−0.39	−0.33	4.5	3.1	0.50	0.00	0.25	8.50
Kim Lab	G6–3	−0.66	−0.36	−0.33	8.4	7.8	0.50	0.00	0.25	9.13
Kim Lab	G6–1	−0.75	−0.57	−0.43	4.5	3.2	0.50	0.00	0.08	9.50
Pal Lab	G5–2	−0.51	−0.54	−0.43	1472	1404	0.50	0.00	0.33	9.63

^*The submissions of the Kim’s Lab that were reversed. Confusion matrices for the binary classification are reported in Supporting Table S4.

In conclusion, the assessment of the predictions submitted for the frataxin challenge confirmed that the methods for predicting the protein stability change upon variation achieved a good level of performance especially in the classification task. For the prediction of the ΔΔG^H2O values, the best methods achieved good performance in terms of correlation coefficient but the error is still high (RMSE ~2.0 kcal/mol). Finally, we observed that all the algorithms fail to predict the ΔΔG^H2O of p.W173C. variant which has a high impact on protein stability. Our hypothesis is that the high error level is due to the low number of experimental data for highly destabilizing variants in the training set. This hypothesis is consistent with the observation that machine learning-based methods such as INPS3D and EASE-MM resulted in higher RMSE than FoldX which implements an energy-functions-based approach.

Although the selection of a single protein and the limited number of variants in frataxin challenge dataset do not allow to generalize the results of our assessment, nevertheless it is noteworthy that the most accurate methods achieved good performance in terms of correlation coefficient and RMSE.