Predicting changes in protein stability caused by mutation using sequence- and structure-based methods in a CAGI5 blind challenge

Abstract

Predicting the impact of mutations on proteins remains an important problem. As part of the CAGI5 frataxin challenge, we evaluate the accuracy with which Provean, FoldX, and ELASPIC can predict changes in the Gibbs free energy of a protein using a limited data set of eight mutations. We find that different methods have distinct strengths and limitations, with no method being strictly superior to other methods on all metrics. ELASPIC achieves the highest accuracy while also providing a web interface which simplifies the evaluation and analysis of mutations. FoldX is slightly less accurate than ELASPIC but is easier to run locally, as it does not depend on external tools or datasets. Provean achieves reasonable results while being computational less expensive than the other methods and not requiring a structure of the protein. In addition to methods submitted to the CAGI5 competition, and with the aim to inform about other methods with high accuracy, we also evaluate predictions made by Rosetta’s ddg_monomer protocol, Rosetta’s cartesian_ddg protocol, and thermodynamic integration calculations using Amber package. ELASPIC still achieves the highest accuracy, while Rosetta’s catesian_ddg protocol appears to perform best in capturing the overall trend in the data.

Introduction

Advances in DNA sequencing technology have led to an enormous growth in the amount of available genomic data. Interpreting this wealth of data to provide meaningful and actionable insights remains a challenge. One important aspect of genome interpretation involves predicting the effect of missense mutations on the structure of proteins. Evaluating the structural impact of a mutation, and the associated change in the Gibbs free energy of protein folding (ΔΔG), can assist in predicting the deleteriousness of a mutation (Glusman et al., 2017, p.), can offer a mechanism explaining how a particular mutation produces a particular phenotype (Nielsen et al., 2017), and could potentially guide the selection of treatment strategies and the development of targeted therapeutics to combat mutation effects (Albanaz, Rodrigues, Pires, & Ascher, 2017). While many tools exist for predicting the ΔΔG of mutations (Barlow et al., 2017; Baugh et al., 2016; Capriotti, Fariselli, & Casadio, 2005; Dehouck, Kwasigroch, Gilis, & Rooman, 2011; Kellogg, Leaver-Fay, & Baker, 2011; Park et al., 2016; Pires, Ascher, & Blundell, 2014b; Schymkowitz et al., 2005), the accuracy of those tools is difficult to ascertain. Most of the tools have been trained and validated on the same dataset of experimentally-measured ΔΔG values (Bava, Gromiha, Uedaira, Kitajima, & Sarai, 2004), and while they generally report good accuracies on that dataset, the results are more varied when it comes to new mutations that had not been evaluated previously (Buß, Rudat, & Ochsenreither, 2018; Geng, Xue, Roel-Touris, & Bonvin, 2019; Khan & Vihinen, 2010; Kroncke et al., 2016; Potapov, Cohen, & Schreiber, 2009).

Critical Assessment of Genome Interpretation (CAGI) is a competition which allows for the objective evaluation and comparison of different methods at tasks relating to the interpretation of genomic variation. At the beginning of the competition, data providers release mutations, or entire genomes, for which they have experimental measurements, and research groups from around the world are invited to submit their predictions for those experimental measurements. At the end of the competition, independent assessors evaluate the submissions made for each challenge and use a pertinent set of metrics to select submissions that are the most accurate. The goal of the CAGI5 frataxin challenge was to predict changes in the Gibbs free energy of protein folding (ΔΔG) for eight mutations in human frataxin (FXN) protein. We made three submissions to this challenge, containing predictions made by Provean (Choi et al., 2012), FoldX (Guerois et al., 2002), and ELASPIC (Witvliet et al., 2016), with submission identifiers G6–3, G6–2, and G6–1, respectively. Predictions made by ELASPIC, a computational framework developed in our lab, were selected as the winning submission by the independent assessor.

In this article we give a brief overview of different approaches for predicting the ΔΔG of mutations and describe the three submissions that we had made to the CAGI5 frataxin challenge. We also describe predictions made by three alternative methods: Amber Thermodynamic Integration (Amber TI) (Case et al., 2005), Rosetta’s ddg_monomer protocol (Kellogg et al., 2011), and Rosetta’s cartesian_ddg protocol (Park et al., 2016). While the latter predictions were not evaluated in the blind challenge and therefore have more potential for bias, we believe that including those predictions in our analysis is necessary in order to provide a comprehensive overview of the most widely-used methods.

Provean is a sequence-based method which uses the conservation pattern of amino acids to predict whether a given mutation is likely to be deleterious. Other examples of sequence-based methods include SIFT (Ng & Henikoff, 2003), PolyPhen-2 (Adzhubei, Jordan, & Sunyaev, 2001), and CADD (Kircher et al., 2014). While sequence-based methods do not predict the ΔΔG of mutations directly, predictions made by sequence-based methods often correlate well with experimental ΔΔG measurements, since deleterious mutations are much more likely to destabilize the structure of a protein than benign mutations (Berliner, Teyra, Colak, Garcia Lopez, & Kim, 2014; Kroncke et al., 2016).

FoldX and Rosetta are two examples of structure-based tools which use statistical potentials, in combination with various sampling techniques, to predict the ΔΔG of mutations. Statistical potentials are comprised of a diverse set of features, including energies calculated using molecular mechanics force fields, probabilities of finding specific backbone conformations and rotamers in high-resolution crystal structures, and outputs of custom routines designed to improve the concordance between experimental and predicted values. Those features are integrated together in various ways to make the final predictions. Existing methods using statistical potentials do not attempt to model large changes in protein conformation, either assuming that the backbone of a protein remains fixed or allowing only local movements around the site of the mutation.

ELASPIC is a meta-predictor, developed by our lab, which uses the gradient-boosted decision tree algorithm (Friedman, 2002) to integrate predictions made by Provean, empirical energy terms calculated using FoldX, as well as other features, in order to predict the ΔΔG of mutations. ELASPIC falls in the category of methods which use both sequence and structural information to predict the ΔΔG of mutations, with examples of other methods in this category being DUET (Pires, Ascher, & Blundell, 2014a), VIPUR (Baugh et al., 2016), and STRUM (Quan, Lv, & Zhang, 2016). In every case, sequence and structural features are integrated using machine learning algorithms trained on datasets of experimentally-measured ΔΔG values (Bava et al., 2004; Moal & Fernández-Recio, 2012).

Amber TI is a protocol which uses Amber’s pmemdGTI module (Lee, Hu, Sherborne, Guo, & York, 2017) to simulate the transition from the wild type to the mutant protein and to calculate the ΔΔG of that transition. It falls in the category of methods performing “alchemical” free energy calculations, where molecular dynamics is used to model the transition from the wild type to the mutant protein and the energy of the transition is calculated using thermodynamic integration (TI), multistate Bennett Acceptance Ratio (mBAR), or other techniques (Gapsys, Michielssens, Seeliger, & de Groot, 2015; Lee et al., 2017). The primary advantage of methods using alchemical free energy calculations is that they can be applied to a much broader set of problems, such as predicting the effect of mutations on the binding of small molecules (Lee et al., 2017) and on the stability of D-amino acid peptides (Garton, Sayadi, & Kim, 2017). The primary disadvantage of alchemical free energy calculations is that they are much more computationally expensive than the other methods.

While one must exercise extreme caution when drawing conclusions from the small dataset of only eight mutations, we believe it is still beneficial to discuss the strengths and limitations of different methods belonging to each of those four categories. Additional blind assessments, with a larger number of mutations, are required to either corroborate or disprove our findings.

Methods

FXN protein and mutations

FXN is a mitochondrial protein involved in iron-sulfur (Fe-S) cluster assembly, heme biosynthesis, and the oxidation of Fe²⁺ to Fe³⁺ (Bridwell-Rabb, Winn, & Barondeau, 2011; O’Neill et al., 2005). Disruption of the FXN gene can lead to Friedreich’s ataxia, a neuro- and cardio-degenerative disease with an autosomal recessive mode of inheritance and an estimated prevalence of 1 in 50,000 in the European population (Campuzano et al., 1996). The majority of patients with Friedreich’s ataxia are homozygous for a GAA repeat expansion in the first intron of the FXN gene, which causes a decrease in the amount of FXN that is transcribed (Campuzano et al., 1996). The remaining patients are heterozygous for a GAA repeat expansion and a point mutation, with over 20 distinct mutations known to cause the disease (Cossée et al., 1999; Galea et al., 2016; McCormack et al., 2000). Patients who are heterozygous for a GAA repeat expansion and a point mutation can exhibit a variety of phenotypes, depending on the mutation that is present (Cossée et al., 1999). In the case of missense mutations, it has been suggested that the phenotype depends the effect that the mutation has on the stability of FXN, the affinity of FXN for the iron-sulfur assembly complex (SDU), and the ability of FXN to allosterically activate this complex to promote iron-sulfur cluster biosynthesis (Bridwell-Rabb et al., 2011; Correia, Pastore, Adinolfi, Pastore, & Gomes, 2008).

For the CAGI5 frataxin challenge, thermodynamic effects of eight mutations in human FXN (NP_000135.2) were evaluated using far-UV circular dichroism and intrinsic fluorescence spectra (Petrosino et al., n.d.). Those experimental measurements were used to calculate changes in free energy of protein folding (ΔΔG) associated with the mutations. The goal of the challenge was to use computational tools to accurately predict those ΔΔG values.

ELASPIC web server

Provean scores (G6–3), FoldX ΔΔG values (G6–2), and ELASPIC ΔΔG values (G6–1) were obtained by submitting mutations from the frataxin challenge to the ELASPIC web server (Witvliet et al., 2016). Predictions made by ELASPIC for all mutations in the challenge are available at http://elaspic.kimlab.org/result/a5393e/ and Supp. Table S1. The ELASPIC web server uses FoldX version 3.0 beta 6.1, Provean version 1.1.5, and ELASPIC version 0.1.42, to make its predictions. For a larger set of mutations, predictions could also have been obtained using the ELASPIC command-line utility (Strokach, Corbi-Verge, Teyra, & Kim, 2019). Since experimental and FoldX ΔΔG values are provided as changes in the Gibbs free energy of protein unfolding rather than protein folding, the sign of those values was reversed. The sign of the Provean scores was also reversed, since Provean predicts smaller values for deleterious mutations than for benign mutations, and deleterious mutations are more likely to be destabilizing.

Rosetta

Two Rosetta protocols exist for predicting the ΔΔG of mutations: the ddg_monomer protocol (Kellogg et al., 2011) and the cartesian_ddg protocol (Park et al., 2016). The ddg_monomer protocol uses flexible backbone design with the soft_rep_design energy function to generate 50 models of the wild type protein and 50 models of the mutant protein. The ΔΔG of the mutation is calculated as the difference in Rosetta energies between the 3 top-scoring wild type structures and the 3 top-scoring mutant structures (Kellogg et al., 2011). The cartesian_ddg protocol optimizes the wild type and mutant structures in cartesian space, rather than in torsion space, using the beta_nov16_cart energy function. The backbone of the protein is optimized for only those residues that are within 6 Angstroms or 3 amino acids of the mutated residue. The ΔΔG of the mutation is calculated as the energy difference between the refined mutant structure and the refined wild type structure, multiplied by an energy-function-specific scaling factor (Park et al., 2016). Predictions by both the ddg_monomer protocol and the cartesian_ddg protocol were generated using Rosetta version 2017.26.59567. System commands used to generate predictions by the two protocols are presented in Supp. Table S2.

Thermodynamic integration

Thermodynamic integration (TI) estimates the free energy of a physical process between two different states where the Hamiltonian H is linked to a parameter λ which is used to shift a system from a state A (λ = 0) to a state B (λ = 1) (Seeliger and de Groot, 2010). The free energies obtained are additively combined through the concept of closed thermodynamic cycles to obtain calculated free energies (Mitchell and McCammon, 1991). Folding free energy differences are obtained by the combination of the free energies between the unfolded state simulations and the free energies computed for the mutations in the folded protein. Although the unfolded state of a protein is challenging to model, different approaches have been proposed to approximate the reference state. Here, the unfolded states have been approximated by creating a model where the flanking residues of the position of interest are substituted by Glycines. This approach is widely used to mimic the unfolded state during a simulation (Seeliger and de Groot, 2010).

A pre-equilibrated structure tends to generate more stable ensembles and therefore more accurate estimations of the free energy (Garton et al., 2018). To that end, all water and ions atoms were removed from the structure with PDB code 1EKG. Correct protonation states were identified and annotated. Using TLEAP in AMBER16 (Case et al., 2005) and AMBER ff14SB force field (Maier et al., 2015), the structure was solvated by adding a 12 nm³ box of explicit water molecules, TIP3P. Next, Na+ and Cl- counterions were added to neutralize the overall system net charge, and periodic boundary conditions were applied. Following this, they were minimized, equilibrated and heated over 100 ps to 300 K and positional restraints were gradually removed. Bonds to hydrogen were constrained using SHAKE (Ryckaert, Ciccotti, & Berendsen, 1977) and a 2 fs time step was used. The particle mesh Ewald (Toukmaji, Sagui, Board, & Darden, 2000) algorithm was used to treat long-range interactions. Restraints were completely removed and full equilibration was achieved after 5 ns. Then, the most representative structure was identified by clustering using the MMTSB toolset (Feig, Karanicolas, & Brooks, 2004) to be used as the initial structure for the subsequent TI.

All TI simulations were carried out using similar conditions. With the only exception of 1 step was used for the integration of the equations of motion and SHAKE algorithm was deactivated during the heated and pre-equilibration steps. And, a cutoff of 9 Å was used for long-range electrostatic interactions with the particle-mesh Ewald method (PME). The transformation between λ=0 and λ=1 was divided into 11 windows where the λ value changed from 0.0 to 1.0 with Δλ=0.1. The whole mutated residues were treated with softcore potentials, and the electrostatic and van der Waals forces were modified simultaneously. All the starting structures were first minimized and relaxed at 300 K in the NVT ensemble. The initial conformations for each λ window were sequentially generated with 1 ns pre-equilibration for each λ-value. 15 ns of MD simulations were performed for each λ window for every mutation. The first 1 ns data were discarded and the last 14 ns data were collected for data analysis at a sampling frequency of 500 fs. Each simulation was repeated 5 times to calculate the ensemble-averaged values. More information on the recommended setup protocol found in the references (Garton et al., 2018; Lee et al., 2017; Seeliger & de Groot, 2010). Input files and scripts can be found here: https://gitlab.com/kimlab/rapid.

Metrics

The lines of best fit shown in Figure 1 were calculated using ordinary least squares. Mean absolute errors were calculated by taking the average of the absolute differences between expected and actual values. Pearson’s and Spearman’s correlation coeffiients were calculated using SciPy’s stats.pearsonr and stats.spearmanr functions (Jones, Oliphant, & Peterson, 2014). Balanced accuracy and area under the receiver operator characteristic were calculated using scikit-learn’s metrics.balanced_accuracy_score and metrics.roc_auc_score functions (Buitinck et al., 2013). When calculating balanced accuracy and the area under the receiver operator characteristic, mutations with an experimental ΔΔG greater than 1 kcal / mol were categorized as destabilizing and assigned a value of 1 while mutations with an experimental ΔΔG less than or equal to 1 kcal / mol were categorized as neutral and assigned a value of 0. When calculating balanced accuracy, we used a threshold of 1 kcal / mol to classify mutations as neutral or destabilizing.

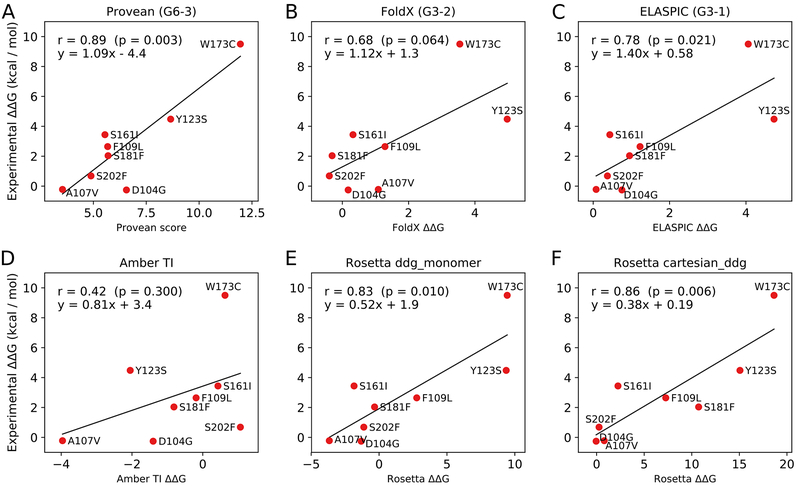
Figure 1.

(A-C) Correlation between predicted and experimental values for Provean, FoldX, and ELASPIC, which formed our three submissions to the CAGI5 frataxin challenge (submission identifiers G6–3, G6–2, and G6–1, respectively). (D-F) Correlations between predicted and experimental values for Amber TI, Rosetta’s ddg_monomer protocol, and Rosetta’s cartesian_ddg protocol. Those predictions were not submitted to the CAGI5 frataxin challenge and did not undergo blind assessment. The ΔΔG values shown in the plots correspond to changes in the Gibbs free energy of protein folding.

Results

Comparing predictions

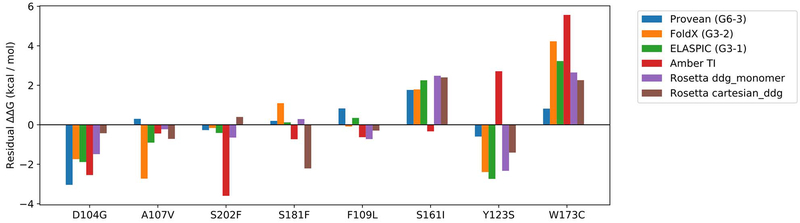
The correlations between predicted and experimental values for Provean (G6–3), FoldX (G6–2), ELASPIC (G6–1), Amber TI, Rosetta’s ddg_monomer protocol and Rosetta’s cartesian_ddg protocol are presented in Figure 1, while the residuals from the lines of best fit are displayed in Figure 2. Provean scores have the strongest correlation with experimental ΔΔG values, with a Pearson’s correlation coefficient of 0.89 and a p-value of 0.003 (Figure 1). The primary reason for the strong correlation is that Provean correctly captures the trend for mutations p.Y123S and p.W173C, while other methods either overestimate or underestimate the impact of p.Y123S and underestimate the impact of p.W173C (Figure 2). The experimental ΔΔG for mutation p.Y123S is 4.48 kcal / mol, which is close to the ΔG of folding for FXN, reported to be 5.6 kcal / mol (Correia et al., 2008). However, Provean predicts that p.Y123S is less deleterious than p.W173C, which suggests that p.Y123S mutants still retain some residual function and are less detrimental to an organism than p.W173C mutants. Structure-based methods struggle with assigning a ΔΔG to mutations p.Y123S and p.W173C because they do not model large changes in the conformation of the protein that are caused by those mutations. Furthermore, most structure-based methods are either trained or optimised using datasets of experimentally measured ΔΔG values, such as Protherm (Bava et al., 2004), and those datasets contain only few mutations with a ΔΔG above 5 kcal / mol. Amber TI predictions have the worst correlation with experimental ΔΔG values, with a Pearson’s correlation coefficient of 0.42 and a p-value of 0.3 (Figure 1D).

Figure 2.

Residuals between actual and predicted values after predictions have been adjusted using lines of best fit displayed in Figure 1.

All methods, except for Rosetta’s cartesian_ddg protocol, overestimate the destabilizing impact of mutation p.D104G (Figure 2), which is only mildly destabilizing with a ΔΔG of 0.255 kcal / mol. Mutation p.D104G introduces a glycine inside of an alpha helix, and glycines are strongly depleted inside alpha helices because of the high entropic cost associated with constraining the relatively large region of phi-psi space that glycines can occupy to the small region that is amenable to alpha-helix formation (Pace & Scholtz, 1998; Serrano, Neira, Sancho, & Fersht, 1992). In the case of mutation p.D104G, it is possible that this entropic cost is smaller than average because of other structural features, such as additional constraints introduced by the set of negative residues protruding from the alpha helix of FXN. Existing structure-based tools would not be able to evaluate the impact of such features on the entropic cost of alpha-helix formation because they do not model the full ensemble of conformations that a protein can occupy in the folded and unfolded states. Provean also predicts mutation p.D104G to be more deleterious than would be expected based purely on its ΔΔG value. Since mutation p.D104G removes an aspartic acid from a patch of negative residues on the surface of FXN, it is likely to have a negative effect on the role that FXN plays in the delivery of Fe²⁺ to proteins involved in heme biosynthesis and in the oxidation of Fe²⁺ to Fe³⁺. This acquired functional deficit would be consistent with the prediction made by Provean.

Evaluating method performance

We used several different metrics to quantify the accuracy of predictions made by the six methods and to provide an indication for their suitability for different applications (Figure 3). Different properties of the methods may make them more well-suited to some applications than others. Therefore, we evaluate the performance of the six methods on three different subproblems. First, we evaluate the ability of the methods to predict with high accuracy the exact value of the ΔΔG caused by a mutation. Predicting the ΔΔG of individual mutations may be important when parametrizing thermodynamic models or when attempting to elucidate the mechanism by which a mutation causes a particular phenotype. Second, we evaluate the ability of the methods to capture the overall trend in ΔΔG values for a set of mutations. Capturing the correct trend in the data is important for applications such as protein design, where computational methods are often used to select mutations that are the most likely to stabilize a protein or increase its affinity to a target. Finally, we evaluate the ability of the methods to distinguish between neutral mutations and destabilizing mutations. Good performance on this task may be important if we want to predict when a mutation is likely to cause loss of function or result in disease.

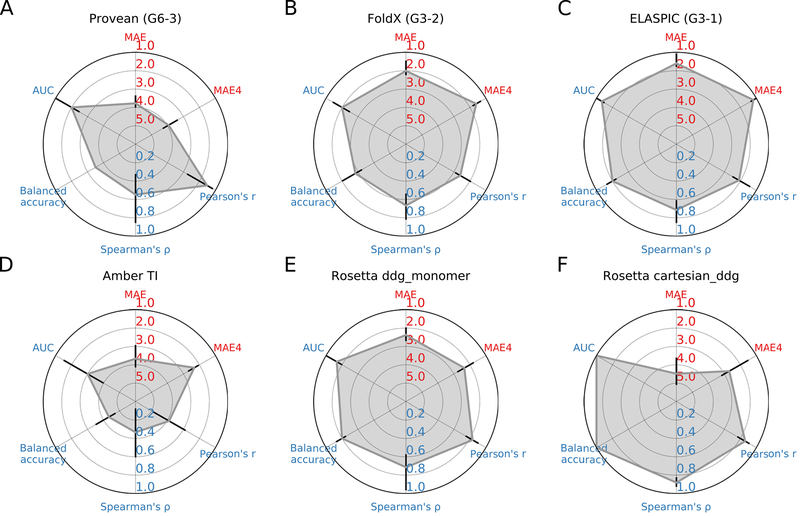
Figure 3.

Accuracy of predictions made by Provean, FoldX, ELASPIC, Amber TI, Rosetta ddb_monomer, and Rosetta cartesian_ddg characterised using 6 different metrics. The error bars correspond to the minimum and maximum scores that are obtained when the analysis is repeated removing one of the mutations in turn (see Supp. Figure S1). Predictions made by Provean, FoldX, and ELASPIC formed our three submissions to the CAGI5 frataxin challenge (submission identifiers G6–3, G6–2, and G6–1, respectively). Predictions made by Amber TI, Rosetta ddb_monomer, and Rosetta cartesian_ddg were not submitted to the CAGI5 frataxin challenge and did not undergo blind assessment. MAE: Mean absolute error. MAE4: Mean absolute error considering only those mutations that have an experimental ΔΔG less than 4 kcal / mol. Pearson’s r: Pearson’s correlation coefficient. Spearman’s ⍴: Spearman’s correlation coefficient. Balanced Accuracy: Average of the recall for neutral mutations and for destabilizing mutations. AUC: Area under the receiver Receiver Operating Characteristic Curve.

In order to evaluate how well different methods can predict ΔΔG values of individual mutations, we calculated the mean absolute error between predicted and experimental values (MAE) and the mean absolute error considering only those mutations that have an experimental ΔΔG less than 4 kcal / mol (MAE4). Mutations with a ΔΔG greater than 4 kcal / mol are likely to produce either misfolded proteins or proteins with a substantially different structure, and predicting the exact ΔΔG of those mutations is not necessary for many applications. Predictions made by ELASPIC have the lowest MAE of 1.60 kcal / mol and the lowest MAE4 of 1.18 kcal / mol. FoldX has the second-lowest MAE of 2.01 and the second lowest MAE4 of 1.60. One reason why predictions made by ELASPIC have a lower MAE than predictions made by FoldX may be that, while FoldX uses a linear regression model to predict ΔΔG values from its energy terms, ELASPIC uses a gradient-boosted decision tree algorithm which can fit more complicated functions with less bias. Rosetta’s cartesian_ddg protocol has the highest MAE of the six methods compared in this study and an MAE4 that is higher than all methods except for Provean. This was surprising since the authors of the cartesian_ddg protocol report explicitly calibrating predicted values to match the ΔΔG values reported in the Protherm dataset (Park et al., 2016).

In order to evaluate how well different methods can capture the overall trend in the data, we calculated Pearson’s correlation coefficient (Pearson’s r), which describes how closely the predicted and experimental values are related by a linear model with Gaussian noise (it is easily swayed by outliers), and Spearman’s correlation coefficient (Spearman’s ⍴), which describes how well the methods can order mutations from least destabilizing to most destabilizing. Surprisingly, Provean has the highest Pearson’s r, with a value of 0.89, followed by Rosetta’s cartesian_ddg protocol, with a Pearson’s r value of 0.86. However, while Rosetta’s cartesian_ddg protocol has the highest Spearman’s ⍴ (0.88), Provean’s Spearman’s ⍴ is second last (0.54), largely because Provean assigns a higher score to p.D104G, mutation with the lowest experimental ΔΔG, than to five other mutations (Figure 1A).

In order to evaluate how well the methods can distinguish between mutations that are neutral and mutations that are destabilizing we calculated the balanced accuracy and the area under the receiver operator characteristic. We defined mutations with experimental ΔΔG between −1 and 1 kcal / mol as neutral, and mutations with experimental ΔΔG greater than 1 kcal / mol as destabilizing, which is consistent with previous studies (Park et al., 2016). The balanced accuracy score, or the average recall for positive and negative examples, measures how well each method can distinguish between neutral and destabilizing mutations when using a threshold of 1 (Buitinck et al., 2013). Rosetta’s cartesian_ddg protocol achieves a balanced accuracy of 1, since all mutations with a Rosetta ΔΔG less than 1 are neutral, and all mutations with a Rosetta ΔΔG greater than 1 are destabilizing (Figure 1F). Provean and Amber TI have the worst balanced accuracies, since Provean assigns a score greater than 1 to all mutations and Amber TI assigns a ΔΔG that is less than 1 to all but one mutation. In order to evaluate how well each method can distinguish between neutral and deleterious mutations using an adjusted threshold, we calculated the area under the receiver operator characteristic curve (AUC), which captures the relationship between the true positive rate and the false positive rate at different thresholds. Rosetta’s cartesian_ddg protocol achieves an AUC of 1, followed by ELASPIC with an AUC of 0.93.

Discussion

As part of the CAGI5 competition, the frataxin challenge gave us an opportunity to do an unbiased assessment of Provean (G6–3), FoldX (G6–2), and ELASPIC (G6–1) in their ability to predict the effects of mutations on protein stability, albeit on a very limited dataset. After the challenge, we also evaluated predictions made by Amber TI, Rosetta’s ddg_monomer protocol, and Rosetta’s cartesian_ddg protocol, in order to have a reference for the accuracies that are achieved using other widely-used methods. There are two major applications for predicting the ΔΔG of mutations, and the implications of our findings differ for each.

First, in the context of predicting mutations that cause disease (or other phenotypes), the ultimate goal when evaluating the impact of mutations on the structure of proteins is to provide some mechanistic insight into how a given mutation produces its phenotypic effects. While existing methods can provide some insight, they still fall short of this goal. ELASPIC, the method that achieves the best accuracy in predicting the ΔΔG of individual mutations, still has a mean square error in its predictions that is close to 1 kcal / mol. This means that any explanation that is based on the predicted ΔΔG of a mutation will come with a relatively large degree of uncertainty. Furthermore, impacting the stability of a protein is only one of many ways by which a mutation can produce a phenotypic effect. Mutations can impair the activity of a protein without changing its stability (or with a minor change to it), for example by blocking the catalytic site of an enzyme, and they can alter the affinity of proteins to their interaction partners, disrupting the formation of macromolecular complexes and altering the signaling pathways of a cell. ELASPIC was aiming to address the latter challenge by constructing homology models of interacting proteins and predicting the effect of mutations on the stability of those interactions. However, the fraction of protein-protein interactions which are known and for which a homology model can be constructed is still limited (Mosca, Céol, & Aloy, 2013), and the predicted ΔΔG of binding is not likely to be more accurate than the predicted ΔΔG of folding. In fact, while FXN is known to interact with NFS1, ISD11, and ISCU proteins to form the SDUF complex (Bridwell-Rabb et al., 2011), structural templates required to model those interactions are not available. It is conceivable that, at some point in the future, we may be able to mutate a protein inside a computational model of a cell, including all interacting partners, and observe the resulting phenotype (Karr et al., 2012; Bordbar et al., 2015), but at the moment, the accuracy of the predictors remains too low, and the structural coverage of protein-protein interactions too limited, for this to be possible.

Second, in the context of protein optimization and design, the goal is usually to generate a list of candidate mutations which are likely to stabilize a protein, improve the function of a protein under inhospitable conditions, or increase the affinity or specificity of a protein to an interaction partner. For this goal, existing methods appear to produce more promising results. Predictions made using Rosetta’s cartesian_ddg protocol show a Spearman’s correlation coefficient of 0.88 with experimental measurements and are able to distinguish between the 3 neutral mutations and the 5 destabilizing mutations with perfect accuracy (Figure 3). However, it is important to note that FXN is a well-studied protein, with both changes in melting temperatures and the ΔΔG of mutations having been previously reported in the literature (Adinolfi et al., 2004; Correia et al., 2008). Those measurements may have been included in the training and optimization of statistical potentials and machine learning algorithms, which would make the scoring of mutations in FXN more accurate than the scoring of mutations in less-studied proteins.

FXN is a highly conserved protein that is found in both prokaryotes and eukaryotes. This makes it possible to construct extensive and high-quality multiple sequence alignments, which, in turn, helps sequence-based tools such as Provean in making accurate predictions. It is likely that the Provean score would show a weaker correlation with experimental ΔΔG values for proteins that evolved more recently, thus having less extensive sequence alignments. Nevertheless, Provean provides a useful signal for predicting the ΔΔG of mutations and it is computationally inexpensive relative to structure-based methods. Most of the structural features that ELASPIC uses to make its predictions are generated by FoldX, and the fact that ELASPIC makes more accurate predictions can be attributed, at least in part, to the incorporation of sequence information, including the Provean score, into its model.

The primary strength of alchemical free energy calculations is that they can be applied to a wide range of problems, including those for which statistical potentials and training data are not available. Amber’s TI module produced the least accurate results, both in terms of raw accuracy and in its ability to capture the correct trend in the data. It seems likely that the particular protocol used did not sufficiently sample the conformational space and utilized an inaccurate approximation for the energy of the unfolded state. In addition, some alchemical free energy studies suggest that prediction performance is system dependent (Christ & Fox, 2014; Homeyer, Stoll, Hillisch, & Gohlke, 2014). Consequently, any system evaluated with this approach should need additional work to identify the optimal parameters and sampling time. Furthermore, It is possible that alternative approaches, for example using Gromacs and the multistate Bennett Acceptance Ratio (Gapsys et al., 2016), would achieve better results.

One consistent finding regarding mutation ΔΔG prediction is that sequence-based methods, which evaluate the evolutionary conservation of residues, are surprisingly accurate in predicting the ΔΔG of mutations, while methods which use structural information alone, or in addition to sequential information, add relatively little additional information while being much more computationally expensive (Kroncke et al., 2016). This finding is also observed in methods which predict the deleteriousness of mutations, where tools which use sequential and structural information are only marginally better than methods which use sequential information alone (Baugh et al., 2016).

While ΔΔG prediction methods achieve promising results in some applications, there remains considerable room for improvement. One of the biggest factors limiting the performance of existing methods, as well as the application of modern machine learning techniques (such as deep learning), is the lack of large and high-quality training datasets of experimentally measured ΔΔG values. A number of high-throughput approaches for obtaining such measurements have been developed, but as of yet no consistent large-scale set has emerged (Findlay, Boyle, Hause, Klein, & Shendure, 2014; Fowler & Fields, 2014; Sahni et al., 2015; Weile et al., 2017).

We believe that with continuous improvement of current methods, as well as with the generation of larger datasets and thus application of data-driven methods, much better accuracies will be achieved in the not too distant future.