CAGI experiments: modeling sequence variant impact on gene splicing using predictions from computational tools

Abstract

Improving predictions of phenotypic consequences for genomic variants is part of ongoing efforts in the scientific community to gain meaningful insights into genomic function. Within the framework of the Critical Assessment of Genome Interpretation (CAGI) experiments, we participated in the Vex-seq challenge, which required predicting the change in the percent spliced in measure (ΔΨ) for 58 exons caused by more than 1000 genomic variants. Experimentally determined through the Vex-seq assay, the Ψ quantifies the fraction of reads that include an exon of interest. Predicting the change in Ψ associated with specific genomic variants implies determining the sequence changes relevant for splicing regulators, such as splicing enhancers and silencers. Here we took advantage of two computational tools, SplicePort and SPANR, that incorporate relevant sequence features in their models of splice sites and exon-inclusion level, respectively. Specifically, we used the SplicePort and SPANR outputs to build mathematical models of the experimental data obtained for the variants in the training set, which we then used to predict the ΔΨ associated with the mutations in the test set. We show that the sequence changes captured by these computational tools provide a reasonable foundation for modeling the impact on splicing associated with genomic variants.

1. Introduction

Improving the functional predictions associated with genomic variants is subject to an ongoing effort in the genomics community to help with functional annotation of the rising number of variants produced by an increasing number of sequencing projects. Gene splicing is just one of the many molecular mechanisms through which genomic variants, either germline or somatic, can impact gene function. Mutations that affect gene splicing can have serious phenotypic consequences, including disease phenotypes. For example, diseases caused by splicing mutations include Duchenne muscular dystrophy (Habara et al., 2009), neurofibromatosis type 1 (Fang et al., 2001; Xu, Yang, Hu, & Li, 2014), cystic fibrosis (Ramalho et al., 2003; Scott, Petrykowska, Hefferon, Gotea, & Elnitski, 2012), and xeroderma pigmentosum (Khan et al., 2010). Furthermore, complex diseases are also likely to be affected by splicing misregulation, as illustrated by SNVs present in autism spectrum disorder cases (Xiong et al., 2015). Despite these compelling examples, the impact of many splice-disrupting events has yet to be fully appreciated as such events are only considered when relevant missense mutations are not discovered in exome or genome sequencing projects. Many missense coding mutations may have been overlooked for a role in splicing regulation because they affect protein function at the amino acid level (Xiong et al., 2015), albeit with minor functional consequences in many cases. Furthermore, synonymous substitutions have recently gained attention for a role as cancer driver mutations through alteration of splicing regulatory sites (Supek, Minana, Valcarcel, Gabaldon, & Lehner, 2014). In addition to coding variants, there is growing evidence that deep intronic mutations affect mRNA splicing to a greater degree than previously appreciated (Anna & Monika, 2018; Xiong et al., 2015). It thus becomes clear that an improved methodology to predict the impact of sequence variants on gene splicing would benefit clinical interpretation of variants discovered through various sequencing projects.

In light of this goal, we participated in the challenge of predicting the splicing impact of sequence variants that were experimentally assessed through the Vex-seq approach (Adamson, Zhan, & Graveley, 2018). This experimental approach uses barcoding of variant-containing plasmids that are transfected into cultured cells, which parallelizes the assessment of splicing effects of many sequence variants by quantifying the percent spliced in (PSI or Ψ) for each exon in the presence and absence of the variant. The Vex-seq challenge within the 2018 CAGI experiment required participants to predict the ΔΨ values associated with 1098 sequence variants. Of these, 1058 were single nucleotide variants (SNVs), 40 were insertions and deletions (indels) and they were located in and around a total of 58 exons. Reference Ψ were provided for all exons. The training set for this challenge consisted of 957 variants (913 SNVs and 44 indels) located in and around a total of 52 exons different from the ones in the test set. Experimentally determined reference Ψ values were provided for all exons, along with ΔΨ values associated with the presence of each variant. Here we describe a mathematical approach to model the experimentally determined ΔΨ associated with sequence variants based on the output of two existing computational tools previously developed to evaluate different aspects related to the splicing process.

2. Background

2.1. Conceptual approach.

In order to link the presence of specific genomic variants to altered splicing patterns one needs to connect those variants with alteration of sequence features that are relevant for the splicing process. Such features include not only canonical dinucleotides located at the splice junctions, but also more distant features such as exonic and intronic splicing enhancers and silencers. Here we take advantage of existing computational tools that have taken into account such sequence features in the context of splicing, and which could thus be used to link the presence of sequence variants with relevant disturbances of the splicing mechanism.

2.2. SplicePort.

One of the tools, SplicePort (Dogan, Getoor, Wilbur, & Mount, 2007), was designed to score the strength of splice sites (SSs), a method popularized by MaxEntScan (Yeo & Burge, 2004). The maximum entropy-based model used by MaxEntScan uses 9-bp sequences to score donor (5’) SSs and 23-bp sequences to score acceptor (3’) SS and is dominated by the presence of the consensus dinucleotides located at exon junctions (GT for donor and AG for acceptor SSs). SplicePort extended this model to incorporate sequence features located further away from the splice junctions. By using 80 bps on each side of the consensus dinucleotide, the SplicePort model, trained on 4000 pre-mRNA human RefSeq sequences, captures splicing enhancers and silencers that can function in intra-exonic and shallow intronic positions. Features evaluated by SplicePort are both compositional, such as the presence of k-mers (with k ranging from 1 to 6) upstream and downstream of the splice site, as well as positional features (e.g. position-specific k-mers) and conjunctive positional features that capture correlation between nucleotides at non-consecutive positions. Within the context of this extended sequence environment (162 bps centered on the canonical junction dinucleotides), variant-induced sequence changes influence the SS score computed by SplicePort. We make use of this property to quantify the impact of sequence variants up to 80 bps away from SSs by scoring the same SS in the context of both the reference and mutated sequences.

2.3. SPANR.

To complement a tool whose model is purely sequence based, we also used SPANR (Xiong et al., 2015), which used Bayesian deep learning to generate a comprehensive model of the splicing code that can be used to predict exon inclusion. Specifically, it uses RNA-Seq data from 16 human tissues together with 1393 sequence features extracted from 10,689 exons, extending to neighboring introns and exons, to model Ψ for each exon. Provided with a specific SNV, SPANR estimates ΔΨ determined by the presence of the variant across each of the 16 tissue types and provides the maximum value among those. SPANR can predict the impact of mutations located up to 300 bps away from exons annotated in the RefSeq database.

Given the output of these two complementary tools we could link relevant sequence-based disturbances with the experimental data provided for the training set through a mathematical model, which we could then use to predict ΔΨ associated with the variants in the test set.

3. Methods

3.1. Evaluating mutation impact on SSs with SplicePort.

In order to evaluate the mutation impact on SSs, we first used SplicePort to compute the scores of the acceptor and donor splice sites with the reference sequence (refS_acc and refS_don, respectively) associated with each exon. For this purpose, we extracted 162 bps from the hg19 assembly of the human genome centered on the consensus dinucleotides. Using custom Perl scripts, we modified the corresponding sequences for each variant, SNVs and indels, located within 80 bps of the consensus dinucleotide and recomputed corresponding SS scores (mutS_acc and mutS_don for acceptor and donor SSs, respectively). We then calculated the changes in SS scores associated with each variant (ΔS_acc = mutS_acc - refS_acc; ΔS_don = mutS_don - refS_don). If a mutation was found further than 80 bps from a given splice site, the score of the splice site associated with the variant was assigned the same score calculated with the reference sequence (i.e. mutS_don = refS_don or mutS_acc = refS_acc), which consequently would lead to a 0 change in score. Of note, SplicePort was not designed to compute scores for SSs that do not have GT or AG consensus dinucleotide for donor and acceptor SSs, respectively. Because of this, if a mutation disrupted the canonical dinucleotide, mutS_acc or mutS_don, as appropriate, was assigned a score of −10 under the assumption that such a change would significantly disrupt the SS function. Also, two exons in the training dataset have a non-canonical GC dinucleotide for their donor SS instead of GT. For those exons, we replaced the GC with the canonical GT dinucleotide in order to be able to compute the scores with SplicePort because of the aforementioned limitation. This solution was implemented under the assumption that score changes calculated this way would still be relevant since they would represent changes in features that are not located at the consensus dinucleotide. All SplicePort computations were performed with the standalone version of SplicePort.

3.2. Evaluating mutation impact on splicing using SPANR.

For this purpose, we used the online SPANR tool available at http://tools.genes.toronto.edu/, where we provided the chromosome, position, reference and variant alleles for each SNV. Of note, SPANR cannot evaluate the impact of indels. The output provided by the online tool includes an accession number for the affected transcript, a reference Ψ value for the exon affected, a ΔΨ associated with the mutation and a percentile value associated with the ΔΨ. This percentile value indicates how the change estimated for a given variant compares to changes induced by a collection of common SNVs. Depending on the context and the gene annotation database used by SPANR, a specific mutation could impact none, one, or more exons. If more than one exon was affected, separate estimates are provided for each exon. However, the SPANR output does not contain coordinates for the exons evaluated. For this reason, we matched the identity of the exons with those provided for the Vex-seq challenge using the exon coordinates from the RefSeq database corresponding to the specific transcript and exon number provided by the SPANR output. For transcripts utilized by SPANR but no longer included in the current RefSeq release, we used older versions of the RefSeq database. We only retained SPANR predictions associated with a given variant if we could find a perfect match for the exon coordinates provided for the Vex-seq challenge.

3.3. Mathematical modeling.

All modeling analyses were performed using the R statistical software (R Core Team, 2018). In order to predict changes in the Ψ measure associated with variants in the test set ($\widehat{\text{ΔΨ}}$) we used two modeling approaches. In the first, we built a model for the Ψ values associated with reference and variant alleles in the training set, which we then used to predict Ψ values for the reference and variant alleles in the test set ($\widehat{{\text{Ψ}}_{var}}$ and $\widehat{{\text{Ψ}}_{ref}}$). The prediction for $\widehat{\text{ΔΨ}}$ would then be computed as a difference between the predicted values for the variant and reference alleles. A second approach involves building a model for experimental ΔΨ values, model that can be then used to predict $\widehat{\text{ΔΨ}}$ directly.

Approach based on modeling Ψ.

We modeled experimental Ψ values using three mathematical models based on SplicePort and SPANR data. The full model based on the output from both tools is a weighted linear regression model to fit logit-transformed, thresholded Ψ as a function of SplicePort acceptor and donor scores, denoted S_acc and S_don, respectively, and SPANR Ψ predictions, denoted ψ_SPANR:

$$\ln \left(\frac{\text{max}\left\{\text{Ψ},1\right\}}{100-\text{Ψ}}\right)={\beta }_0+{\beta }_1{S}_{acc}+{\beta }_2{S}_{don}+{\beta }_3\ln \left(\frac{\text{max}\left\{{\text{ψ}}_{SPANR},1\right\}}{100-{\text{ψ}}_{SPANR}}\right)+\epsilon .$$ (Equation 1)

Models based on SplicePort or SPANR data alone are equivalent to the full model when β₃ is set to 0 for the former and β₁ and β₂ are set to 0 for the latter. We note that Ψ and ψ_SPANR can vary between 0 and 100%. Using these models, we predicted for each reference and variant allele in the test set a logit-transformed $\widehat{\text{Ψ}}$ value (together with its standard error), which was then transformed to $\widehat{\text{Ψ}}$. A predicted $\widehat{\text{ΔΨ}}$ for each variant allele was computed by taking the difference between the $\widehat{\text{Ψ}}$ values associated with the corresponding variant and reference alleles:

$$\widehat{\text{ΔΨ}}=\widehat{{\text{Ψ}}_{var}}-\widehat{{\text{Ψ}}_{ref}}.$$ (Equation 2)

The standard error of the two predicted ψ values (reference and variant alleles) were modified accordingly, and the standard error of their difference was also computed.

Approach based on modeling ΔΨ.

This approach consisted in fitting a multiple linear regression model directly to the experimental ΔΨ as a function of score differences:

$$\mathrm{\Delta }\text{Ψ}={\gamma }_1\mathrm{\Delta }{S}_{acc}+{\gamma }_2\mathrm{\Delta }{S}_{don}+{\gamma }_3\mathrm{\Delta }{\text{ψ}}_{SPANR}+\epsilon .$$ (Equation 3)

We used this model to predict ΔΨ values, as well as associated standard errors, associated with variants in the test set. In the case of the model based on SplicePort alone the model in Equation 3 is simplified by setting γ₃ to 0. For the SPANR-based model, parameters γ₁ and γ₂ are set to 0 instead.

Imputation of missing SPANR predictions.

Because SPANR did not produce predictions for 208 (21.7%) variants in the training set and 147 (13.4%) variants in the test set and their associated reference values, we imputed these values using a model of ψ_SPANR values based on SplicePort scores for acceptor and donor SSs associated with each exon:

$${\text{ψ}}_{SPANR}={\alpha }_0+{\alpha }_1{S}_{acc}+{\alpha }_2{S}_{don}+\epsilon .$$ (Equation 4)

The model was fitted separately for SPANR values in the training and test sets, as well as separately for reference and variant alleles. The imputed values were used in downstream analyses as genuine ψ_SPANR for the purpose of predicting $\widehat{\text{Ψ}}$ and $\widehat{\text{ΔΨ}}$.

Comparison of mathematical models.

To compare the performance of different models within each approach, we used Akaike’s An Information Criterion (AIC) (Akaike, 1973) as implemented in the AIC function from the stats R package.

4. Results

4.1. SplicePort analysis.

The native SplicePort tool was designed to calculate SS scores for canonical exon junction dinucleotides in provided sequences, and it does not have innate capabilities to evaluate the impact of variants on SS strength. We adapted the tool to calculate changes in SS scores by first computing the score with the reference and then with the mutated sequence (see Methods). Of note is the fact that we were able to evaluate the score changes for both SNVs and indels, whereas other tools designed to evaluate the impact of mutation on splicing only deal with SNVs. A decrease in SS score can be interpreted as weakening of the SS and consequently as a potential decrease in Ψ for a given exon, whereas a score increase would be associated with a strengthening of the SS and consequently an increase in Ψ.

Most mutations (52.7%) in the training set are located within the exon of interest, with the rest being located in flanking intronic regions. Almost a third of mutations (32.7%) are located up to 49 bps away into the upstream intronic region, and just 14.6% of them are located up to 32 bps downstream of the donor SS. Since all variants, both from the training and test sets, are located within 80 bps of at least one of the two SSs, we were able to evaluate the impact of all mutations using the SplicePort tool, with more than 40% of mutations affecting scores of both SSs (Table 1). We note that for 638 out of 957 variants (66.6%) in the training set the score change determined with SplicePort in at least one SS is consistent with experimental data, i.e. decrease of score is consistent with a negative value of the experimentally determined ΔΨ, whereas a score increase is consistent with a positive ΔΨ. We found that for mutations evaluated for impact on a single SS (i.e. those located more than 80 bps away from the other SS), those with predictions concordant with experimental observations tend to be located closer to the corresponding SS than those with discordant predictions (Figure 1A, B). In the case of mutations located within 80 bps from either SS, mutations with exclusive 3’ SS prediction agreement are not located significantly closer to the 3’ SS (Figure 1C), but those with exclusive 5’ SS prediction agreement are closer to the 5’ SS (Figure 1D). It is also notable that variants with no experimentally consistent prediction are not located further from either SS compared to variants whose predictions for that SS are consistent with experimental data (P=0.3 for acceptor and P=0.6 for donor SSs, one-sided Wilcoxon rank-sum test). This observation suggests that however extensive a sequence-based model of SSs is, it is inevitably lacking additional biologically relevant information that is not encoded in the sequence itself, such as, for example, the tissue-specific availability and/or abundance of splice factors.

Table 1.

Summary of mutations’ impact on splice sites of targeted exons as evaluated with the SplicePort tool.

Mutation set	Count	Affect 3’ SS	Affect 5’ SS	Affect both SSs
Training	957	767	599	419
Test	1098	885	710	503

Figure 1.

Distances from splice sites to variants in the training set in relation to agreement of their associated computational predictions with corresponding experimental data (i.e. predicted and experimental ΔΨ have the same sign). Numbers above graphs indicate mutation counts in each category. A, B) Variants scored by SplicePort for their effect on only one SS (A: 3’, acceptor; B: 5’, donor), as they are located more than 80 bps away from the other SS. In both cases, variants with computational predictions that agree with experimental data are located closer to the corresponding SS than variants with discordant predictions (A: P=2.2×10⁻⁴; B: P=6.1×10⁻⁴, one-sided Wilcoxon rank sum test). C, D) Variants evaluated for impact on both SSs (they are located within 80 bps from both SSs). Mutations are divided in four groups based on predictions agreement with experimental data: “3’SS” and “5’SS” - only one prediction agrees with experimental evidence (the prediction for the other SS is discordant), “Both” – predictions associated with both SSs are concordant with experimental data, “No” – predictions for both SSs are discordant with experimental evidence. Only variants with exclusive experimental agreement for their 5’ SS prediction are located closer to the corresponding SS (D: P=0.01, one-sided Wilcoxon rank sum test). E, F) Variants evaluated for their impact on gene splicing by SPANR. Variants with predictions concordant with experimental data are not located closer to either SS than variants with discordant predictions (P > 0.1 for both comparisons, one-sided Wilcoxon rank sum test).

4.2. SPANR analysis.

The SPANR tool provides an easy-to-use interface, requiring as input the genomic location of the variants of interest and the reference and variant alleles. Since it is limited by design to evaluate only SNVs, we were not able to evaluate directly the impact of indels. Overall, we were able to evaluate the impact of 749 (78.3%) variants in the training set, and 951 (86.6%) variants in the test set. The missing predictions are due to indels (44 variants from the training set and 40 from the test set) and variants located in exons not present in the pre-computed annotation used by SPANR (164 variants from the training set located in 17 exons and 107 variants from the test set located in 14 exons). For the variants in the training set, we found that SPANR predictions are consistent with experimental data in 63.4% of cases, comparable to SplicePort predictions. Also similar to SplicePort is the fact that variants with predictions opposite to the experimental data do not tend to be located further from either SS than variants with experimentally consistent predictions (Figure 1E,F).

4.3. Linking computational predictions to experimental observations.

The availability of sequence-based computational predictions for splicing impact together with experimental data for the variants in the training set allowed us to mathematically model experimental observations. In a first approach, we built models of experimentally determined Ψ that allowed us to predict Ψ values associated with the reference and variant alleles. These further allowed us to compute the required ΔΨ (see Methods). In a second approach, we built models of ΔΨ, which enabled us to directly predict ΔΨ values associated with the variant alleles (see Methods). In each case, we built a model that incorporated data from both SplicePort and SPANR, as well as two separate models with data from each tool individually. For this step designed to identify the better performing models, we used only variants for which we had predictions from both tools, specifically 749 SNVs. We fitted the experimental observations for these variants using the full models indicated by equations 1 and 3, as well as individual tool-based models (see Methods, Figure 2). We then compared the performance of these models using the AIC measure. In both modeling approaches (see Methods), models incorporating data from both SplicePort and SPANR showed smaller (better) AIC values than the subset models. For the first approach, i.e. prediction of Ψ, the SplicePort-only and SPANR-only models had AIC increases of 4.8 and 293, respectively. For the second approach, i.e. prediction of ΔΨ, the increases relative to the corresponding full model were 22.7 and 148. Models with higher AIC values can be considered less likely to minimize information loss, thus having a worse performance. For example, a model with an AIC higher by 4.8 can be considered as 11 times less likely to minimize information loss (i.e. being worse) compared to the model with the smaller AIC value. Larger differences translate into even smaller relative likelihoods, but we note here that AIC values for models that predict different variables (i.e. Ψ and ΔΨ) are not directly comparable. We have retained the full models from either approach for producing predictions for the test set since they are conceptually different. These models also exhibit higher correlation values (Pearson and Spearman) between predicted values and experimental observations than respective models based on data from one individual tool only (Figure 3).

Figure 2.

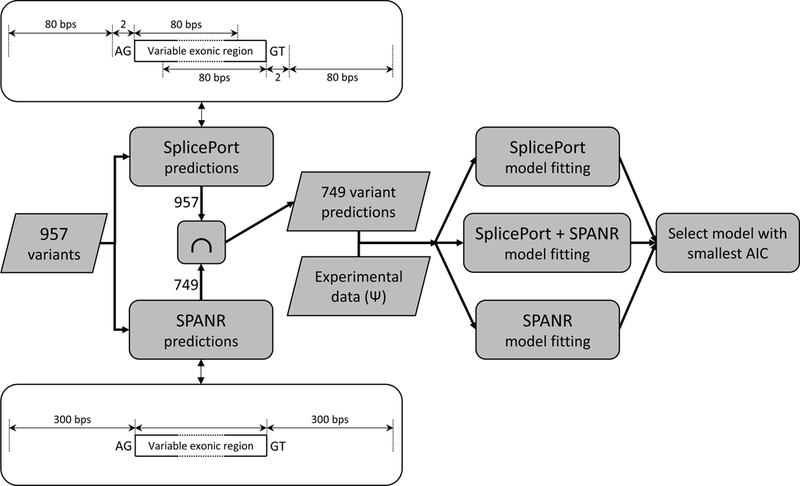
Flowchart representation of the computational steps performed for selection of the mathematical model to be used for predicting splicing impact of variants in the test set. The schematic representations associated with the SplicePort and SPANR prediction steps indicate the genomic regions containing mutations for which their impact can be evaluated by each tool. Specifically, SplicePort can evaluate the impact on variants located within 80 bps of either splice site (AG indicates the 3’ or the acceptor site, whereas GT indicates the 5’ or donor splice site). SPANR can evaluate the impact of exonic mutations as well as mutations located up to 300 bps away. Exon lengths in the Vex-seq dataset vary between 69 and 98 bps, and are illustrated as “Variable exonic region”.

Figure 3.

Predictions of the tested models for the 749 variants from the training set evaluated by both SplicePort and SPANR in relation to experimental data. A) Correlation coefficients between experimental data and predictions for all tested models. Name of tool(s) below each graph indicate the corresponding models used for training purposes, whereas Ψ and ΔΨ refer to the modeling approaches. B) Predictions for the 749 variants obtained using the full model (SP&SPANR) and the Ψ modeling approach in relation to experimental data. Correlation coefficients are 0.535 (Pearson) and 0.374 (Spearman). C) Predictions for the 749 variants obtained using the full model (SP&SPANR) and the ΔΨ modeling approach in relation to experimental data. Correlation coefficients are 0.512 (Pearson) and 0.384 (Spearman). Dashed lines represent lines of best fit obtained using the least squares method.

4.4. Predictions for the test set variants.

Similar to the case of variants in the training set, not all variants in the test set were evaluated by SPANR, with 147 (13.3%) of them (107 SNVs and 40 indels) missing SPANR predictions. In order to be able to use the full models selected in the previous step, we had to impute the missing SPANR values for 147 variants. This motivated us to also train the full models on the entire set of 957 variants in the training set with missing SPANR values imputed as well. We therefore imputed the missing SPANR data for 208 variants based on SplicePort scores associated with reference and variant alleles (Equation 4; see Methods, Figure 4). While potentially problematic because of the use of inferred value, this approach also has the advantage that it makes use of the SplicePort predictions for the entire set of variants, which appear to be the stronger individual predictors (Figure 3).

Figure 4.

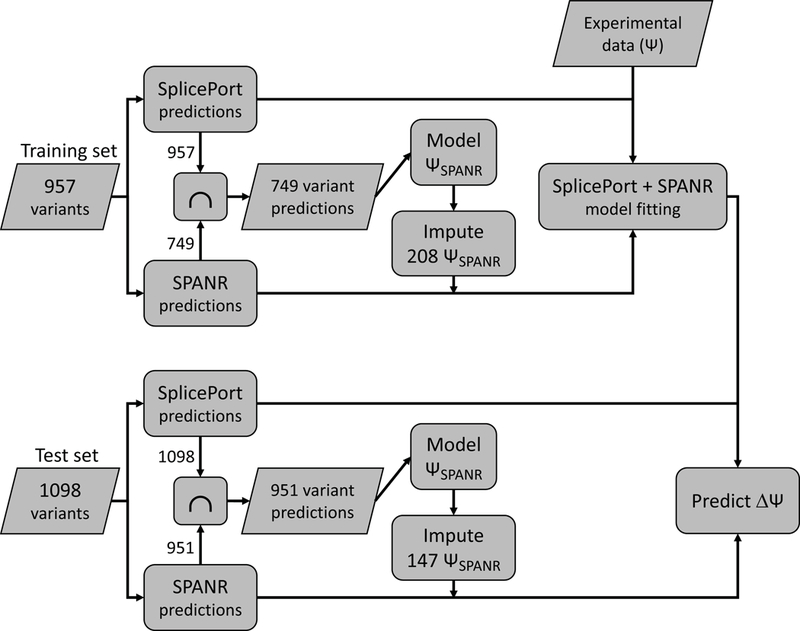
Flowchart representation of the computational pipeline used for predicting the splicing impact of variants in the test set. First, the full model (i.e. the mathematical model based on predictions from both SplicePort and SPANR) is trained on predictions from all variants in the training set. SPANR predictions for the 208 variants not evaluated by SPANR are imputed based on SplicePort predictions. This model is further used to perform predictions for variants in the test set based on their corresponding computational predictions. Similarly to the training step, SPANR predictions for the 147 variants not evaluated by SPANR are imputed based on a SplicePort-based model.

To infer the missing SPANR values for 147 variants in the test set, we used the same method as for the training set, specifically we predicted them with models based on SplicePort scores (Equation 4). We then used the full models developed on the entire set of variants in the training set (including 208 variants with inferred SPANR values) to predict changes in Ψ for all variants in the test set (Supp. Table S1). The Pearson’s correlation coefficient between observed experimental data and predictions was 0.500 (P = 1.5×10⁻⁷⁰) for the approach based on predicting Ψ (Figure 5A), variants with predictions concordant with experimental data being located slightly closer to the 5’ SS than variants with discordant predictions (Figure 5B,C). The Pearson’s correlation coefficient was 0.454 (P = 8.3×10⁻⁵⁷) for the approach based on predicting ΔΨ (Figure 5D), with concordant variants being similarly located closer to the 5’ SS (Figure 5E,F).

Figure 5.

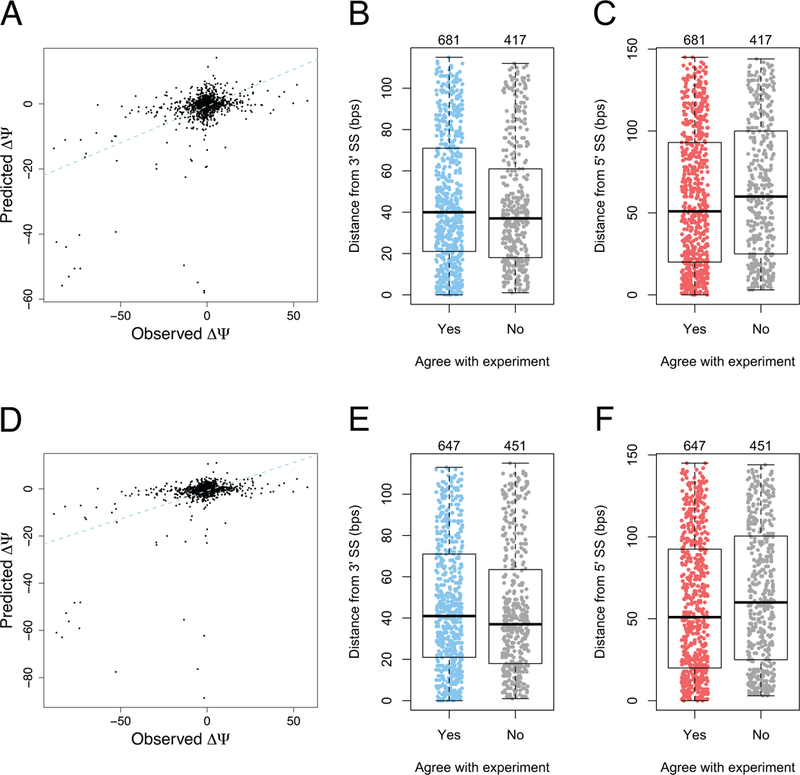
Predictions for the 1098 variants in the test set compared to corresponding experimental observations. A) Predictions produced by modeling Ψ and obtaining ΔΨ as a difference between values for variant and reference alleles. Pearson’s ρ = 0.5, Spearman’s ρ = 0.321. B, C) Distributions of distances from splice sites of variants in the test set in relation to prediction agreement for the Ψ modeling approach with experimental data. Variants with concordant predictions appear to be located slightly closer to the 5’ SS than variants with discordant predictions (the difference between distribution medians is 9 bps, P=5.6×10⁻³, one-sided Wilcoxon rank sum test). D) Predictions produced by modeling ΔΨ directly. Pearson’s ρ = 0.454, Spearman’s ρ = 0.294. E, F) Distributions of distances from splice sites of variants in the test set in relation to prediction agreement for the ΔΨ modeling approach with experimental data. Similarly to the Ψ modeling approach, variants with concordant predictions appear to be located slightly closer than variants with discordant predictions (the difference between distribution medians is 9 bps, P=6×10⁻³, one-sided Wilcoxon rank sum test). Dashed lines in panels A, D represent the lines of best fit obtained using the least squares method.

We note that less than 8% of variants determine a large Ψ change (> 20% in absolute value). Moreover, less than 2% (21 variants) cause a Ψ change larger than 50%, most of which (18 out of 21) are located at or very close to exon junctions. Our model predicts large impacts for these variants as well, mainly owing to large SS score deviations determined by SplicePort. If variants with large (> 50% in absolute value) changes are removed, Pearson’s correlation coefficients drop below 0.3 suggesting that numerical prediction for small ΔΨ values is more difficult. However, we note that our model correctly predicts the direction of change (i.e. exon skipping or retention) for 62% (P = 7.6×10⁻¹⁶, one-sided binomial test) of variants in the case of the Ψ-based model, and 60% (P = 1.8×10⁻⁹, one-sided binomial test) in the case of the ΔΨ-based model.

5. Discussion

The 2018 CAGI Vex-seq experiment offered the challenge of predicting the impact on splicing of 58 exons for more than 1,000 genomic variants experimentally assessed through a high-throughput, in vitro splice analysis assay. Here we tested a relatively simple modeling approach based on data produced by two well-known tools, SplicePort and SPANR, that evaluate different splicing-related aspects. Among the many tools developed for splicing-related analyses, we chose SplicePort for its ability to score SSs based on sequence features located both close and further (up to 80 bps) away from exon junctions. Given that all exons considered are shorter than 100 bps, and all intronic variants are within 50 bps of exon junctions, SplicePort allowed us to computationally evaluate the impact of all variants included in this challenge, although this required development of custom software to facilitate SplicePort computations for large sets of genomic variants. The second computational tool, SPANR, was chosen for its deep learning approach, which incorporates extensive sequence-based features along with expression data from 16 tissues. It provides coverage for all variants located in and around (up to 300 bps away) of all exons in the RefSeq database. We incorporated these predictions into two mathematical models that use two slightly different approaches. In one approach we predicted Ψ values associated with variant and reference alleles and compute the change in Ψ as a difference between the two. In the second approach, we modeled and predicted directly the change in Ψ associated with genomic variants relative to the reference genome sequence. We show that both these approaches produce meaningful predictions, albeit far from perfect. Despite the underlying simple mathematical models, the performance of these approaches is likely due to the comprehensive computational models that both SplicePort and SPANR incorporate.

We note here that using the full models (i.e. models based on data from both SplicePort and SPANR) we had to infer missing SPANR data for 208 variants in the training set and 147 variants in the test set. Interestingly, performing predictions on test set variants with models trained only on the 749 variants with data produced by both tools do not result in vastly different Pearson’s correlation coefficients with the experimental observations (0.499 for the Ψ-based model and 0.457 for the ΔΨ-based model compared to original values of 0.500 and 0.454, respectively). Similarly, if we perform predictions with models based only on SplicePort data, Pearson’s correlation coefficients remain largely the same (0.499 and 0.463, respectively), whereas the Spearman correlations coefficients are slightly larger (0.324 and 0.322, respectively, compared to 0.321 and 0.294, respectively, of the full models). These results indicate that the changes in SS scores computed with SplicePort are the main predictors for variant impact in splicing of the examined exons.

The limitations of our modeling approach are several-fold. First, experimental data provided were obtained by using HepG2 cells, a liver cancer cell line. SplicePort is tissue-agnostic, as it was trained solely on sequence features of 4000 pre-mRNA sequences. SPANR somewhat complements this deficiency owing to its training on RNA-Seq data from 16 tissue types. However, its output that contains a maximum ΔΨ computed across these tissue types but does not provide tissue information, so that output for different variants could well be originating in different tissue types, with obvious confounding effects. Because splicing is dependent on splice factors both ubiquitous and tissue specific, the cell type may have a large influence on the splicing results, and predictions could be improved by using tissue-specific models. Furthermore, splicing typically happens in a co-transcriptional manner, which may not be strictly parallel with the exon order, therefore the plasmid-based construction of the VEX-seq splicing vectors may not fully recapitulate the effects of variants in the endogenous setting.

Additional confounding effects not readily addressed by this modeling approach include variations of splicing interference not limited to exon skipping or retention, such as exon truncation or elongation. Such scenarios could have dramatic phenotypic effects, depending on the specific exon and gene affected, and thus their accurate prediction is equally important. To that effect, the prediction of change in directionality, i.e. exon skipping or retention, is equally important, since these two opposite scenarios have very different consequences. The loss of exons is typically detrimental by removing functional domains or changing the open reading frame and generating premature stop codons that truncate the protein. The impact of increased exon retention is more difficult to interpret and/or measure, but it can lead to increase protein stability, alteration of splicing order, or increase in amounts of translation products without an increase in gene expression. The importance of directionality of splicing changes would warrant using the correct prediction of directionality as a separate criterion for evaluation of predictions.

In summary, we are encouraged that a simple modeling approach using computational predictions of two off-the-shelf tools has produced meaningful predictions that are likely to be improved, provided more data for the training step. At the same time, our modeling approach could benefit from improvements if separate models for variants causing small changes in Ψ are developed separately from variants causing large changes. We hope that our approach could provide ideas for further improvement of computational tools that evaluate various aspects of gene splicing.