Abstract
Quickly growing genetic variation data of unknown clinical significance demand computational methods that can reliably predict clinical phenotypes and deeply unravel molecular mechanisms. On the platform enabled by CAGI (Critical Assessment of Genome Interpretation), we develop a novel “weakly supervised” regression (WSR) model that not only predicts precise clinical significance (probability of pathogenicity) from inexact training annotations (class of pathogenicity) but also infers underlying molecular mechanisms in a variant-specific fashion. Compared to multi-class logistic regression, a representative multi-class classifier, our kernelized WSR improves the performance for the ENIGMA Challenge set from 0.72 to 0.97 in binary AUC (Area Under the receiver operating characteristic Curve) and from 0.64 to 0.80 in ordinal multi-class AUC. WSR model interpretation and protein structural interpretation reach consensus in corroborating the most probable molecular mechanisms by which some pathogenic BRCA1 variants confer clinical significance, namely metal-binding disruption for p.C44F and p.C47Y, protein-binding disruption for p.M18T, and structure destabilization for p.S1715N.
Keywords: Genome medicine, genetic variation, clinical significance, machine learning, weak supervision, model interpretability, molecular mechanism
1. INTRODUCTION
Quickly growing genomic data, largely attributed to next-generation sequencing and high-throughput genotyping, hold great promise for precision medicine. However, a major challenge remains making the stride from genomic variation and other dsata to diagnostic and therapeutic decision-making. Therefore, there has been a critical need to develop computational methods to predict and understand phenotypic impacts of genetic variants at various biological scales (Cline and Karchin, 2011; Karchin and Nussinov, 2016).
The method development has seen excellent opportunities created by the growing public databases (such as TCGA (Weinstein et al., 2013), dbSNP (Sherry et al., 2001), ClinVar (Landrum et al., 2016) and dbNSFP (Liu et al., 2016)), benchmark studies (Martelotto et al., 2014; Guidugli et al., 2018), and community experiments (in particular, CAGI (Hoskins et al., 2017)). Indeed, some algorithms are widely and successfully applied for functional prediction of genetic variants, such as SIFT (Ng and Henikoff, 2003), PolyPhen2 (Adzhubei et al., 2013), MutationTaster2 (Adzhubei et al., 2013), SNAP (Bromberg and Rost, 2007; Hecht et al., 2015), MutPred (Li, et al., 2009; Pejaver et al., 2017a,b), and Evolutionary Action (Katsonis and Lichtarge, 2014, 2017). In addition, the data-driven approach for unraveling genotype-phenotype relationships will continue absorbing the artificial intelligence (AI) and machine learning technologies that have been quickly reshaping other fields (Krizhevsky et al., 2012; Silver et al., 2017).
In this paper, building on our participation in the ENIGMA Challenge in the 5th CAGI experiment, we introduce and assess our novel methods developed for predicting clinical significance and inferring molecular mechanisms for missense variants (single nucleotide variants or SNVs that change resulting amino acids). Specifically, our weakly-supervised machine learning models achieve probability prediction, multiclass classification, confidence (uncertainty) estimation, and mechanistic interpretation of cancer pathogenicity by addressing central questions and making novel contributions in the following two aspects.
First, in the aspect of precision medicine, our central question is how to construct clinical significance predictors that are generally interpretable for diagnosis and potentially actionable for therapeutics. In this study, we combine interpretable and actionable features that describe molecular impacts of SNVs (specifically, impacts on protein structure, dynamics, and function here) and expert-curated labels that accurately summarize clinical significance of SNVs (specifically, the posterior probability of pathogenicity, PoP, and corresponding 5-tier classification by the ENIGMA consortium (Cline et al., 2019)) in supervised machine learning. We examine to what extent molecular-level impacts of SNVs can predict organism- and population-level clinical significance to facilitate the often-expensive clinical phenotyping. We also examine to what extent molecular mechanisms underlying clinically significant SNVs can be uncovered from important features of molecular impacts to help identify potentially actionable therapeutics, which is further probed by structural modeling for some variants.
Compared to some other features commonly used in the field (Martelotto et al., 2014), molecular impacts carry direct causal effects on clinical phenotypes (Pejaver et al., 2017b; Reeb et al., 2016), thus enabling model interpretability; they are available for many genes thanks to relatively inexpensive yet accurate bioinformatics tools (such as MutPred2 (Pejaver et al., 2017b) and others used in this study), thus enabling broad applicability; and they apply to non-synonymous variants beyond SNVs studied here (such as in-frame or frame-shift indels), thus enabling model generalizability.
Second, in the aspect of machine learning, our central question is how to solve a new type of “weakly supervised” machine learning problems (Zhou, 2018) where the desired label (PoP here) has to be regressed from training data without the exact labels. Such inexact supervision can be observed in many real world applications where only coarse- grained labels are available because exact labels are too hard or/and too expensive to generate (for instance, in computer vision, annotating bird breeds in images by crowd-sourcing or experts). Particularly in our case, whereas the desired label (PoP) is continuous, the only available labels in the publicly-accessible data are five ordered classes which are categorized based on pre-determined PoP ranges (see more details in Sec. 2.1). We develop weakly supervised regressors with tailored loss functions to directly predict PoP. Our first model, a linear one developed during CAGI, used parabola- shaped polynomials for loss functions to penalize predicted PoP values based on their supposed classes (equivalently, PoP ranges here). As the parabola-shaped polynomials as loss functions are too structured and rigid, we continue after CAGI to develop linear and nonlinear (kernelized) models with flexible flat-bottomed loss functions directly learned from data.
Other methods participating in the challenge treat the problem as classification (Cline et al., 2019) and assign PoP afterwards (a non-trivial challenge), among which multi-class logistic regression is compared as a representative in this study. From the perspective of machine learning, they do not consider the order among classes when making classifications (for which a representative of ordinal regression is compared in this study as well) and have to make strong assumptions about the distribution of PoP, albeit implicitly, when converting class category or probability into PoP.
The rest of the paper is organized as following. We first introduce in Materials and Methods the ENIGMA challenge, our training data and feature engineering. We then introduce three types of machine learning models, the first two for multi-class pathogenicity classification whereas the last – weakly supervised regression – newly developed by us for direct prediction of the probability of pathogenicity (PoP). In Results, we start with examining the value of gene type-specific rather than gene-specific data as well as variants data with less confident clinical annotations. We proceed to compare prediction performances among the machine learning models and integrate model interpretation and (protein) structural interpretation to infer molecular mechanisms by which some BRCA1 missense variants could confer pathogenicity.
2. MATERIALS AND METHODS
2.1. The ENIGMA Challenge
One of the 14 challenges in the 5th CAGI experiment, the ENIGMA Challenge presented 430 BRCA1 and BRCA2 variants (326 exonic and 104 intronic ones) whose clinical significance was newly annotated or recently updated by the ENIGMA Consortium (Cline et al., 2019) and not available in the public domain during the challenge. Specifically, a posterior probability of pathogenicity (PoP) was produced for each variant by multifactorial likelihood analysis (Goldgar et al., 2008) that integrates clinically-calibrated bioinformatics information and clinical information in a Bayesian network. Based on calibrated ranges of PoP shown in Table 1, variants have been classified according to the IARC (International Agency for Research on Cancer) 5-tier classification scheme: Benign, Likely Benign, Uncertain, Likely Pathogenic, and Pathogenic (Classes 1–5).
Table 1.
The 5-tier ENIGMA classification of variants based on the ranges in the probability of pathogenicity (PoP).
| Class | 1. Benign | 2. Likely Benign |
3. Uncertain | 4. Likely Pathogenic |
5. Pathogenic |
|---|---|---|---|---|---|
| PoP range | <0.001 | 0.001–0.049 | 0.05–0.949 | 0.95–0.99 | >0.99 |
Participants were asked to predict for each variant PoP according to the ENIGMA classifications as well as confidence level (measured by standard deviation, SD). They were also told that the assessment would be against predicted classes based on PoP ranges (Table 1) instead of PoP and predictions for classes 1 and 5 would be weighted more without the exact formula given. We only submitted predictions for all the 318 missense variants.
2.2. Data
To approach the task with supervised learning, we collected missense variants data similarly classified using the five-tier clinical significance system and publicly available in the ClinVar database (https://www.ncbi.nlm.nih.gov/clinvar/) (Landrum et al., 2016). In other words, no exact values but ranges of PoP (equivalently, classes) are publicly available, creating a weakly supervised learning scenario. The five terms of clinical significance used in ClinVar, following the guidelines from ACMG/AMP (the American College of Medical Genetics and Genomics and the Association for Molecular Pathology) (Richards et al., 2015), are consistent with those used by ENIGMA, following the IARC guidelines. Some ClinVar entries are even submitted by ENIGMA. A slight inconsistency was disregarded, namely that the uncertain range in the ACMG/AMP guideline is 0.10~0.899 rather than 0.05~0.949.
Consistent with the practice during the challenge, during our post-CAGI replication we retrieved missense variants from ClinVar with the last-interpreted date no later than June 29, 2017, around 6 months before the challenge was released. We also set two cutoffs on the review status which ranges from zero to four stars suggesting increasingly reliable interpretation: at least three stars (reviewed by expert panel) or at least two stars (reviewed by multiple qualified submitters without conflict), thus generating two data sets denoted G2 and G3 (a subset of G2), respectively. The exact query filters used for ClinVar can be found in Supp. Table S1.
Besides BRCA1/2 variants, we also collected missense variants of other tumor suppressor genes from ClinVar following the same procedure as described above. Even though the challenge was exclusive to BRCA genes, our rationale is to develop predictors that are not just gene-specific but gene type-specific. One benefit from the machine learning perspective is to access more training data and allow for more complex models for accuracy. We used the STRING database (https://string-db.org/) (Szklarczyk et al., 2017) to identify other genes whose protein products interact with BRCA1 and BRCA2 proteins and the OncoKB (https://oncokb.org/) (Chakravarty et al., 2017) database to filter the resulting genes for tumor suppressor genes only. We ended up with 21 other tumor suppressor genes, 17 of which have variant interpretation in ClinVar and are referred to as non-BRCA in short. Details about data-collection procedures and resulting data statistics can be found in the Supp. Sec. 1 and 2, respectively.
A stratified split considering the frequencies of the five classes was used to create a held-out ClinVar BRCA test set (one sixth) and a training set (five sixths) from G2. The same test set was used when testing G3-trained models, whereas the G3 training set is the subset of the G2 training set with three stars or more in review status. When other genes are considered, their variants would be added to corresponding training sets.
When we finally generalize our study in Sec. 3.5, we similarly collected missense variants of 325 more genes from ClinVar as described in Supp. Sec. 1.3 and Sec. 2.
2.3. Feature Engineering
When calculating features for each variant collected for training or validation, we restricted the choices to molecular impacts for interpretable and actionable models. These impacts are often predicted from sequence-level features, which is a great challenge itself. We used MutPred2 (Pejaver et al., 2017b) that predicts the posterior probabilities of loss or gain, whichever is greater, for a wide range of properties induced by amino acid substitutions. These properties, capturing mutational impacts on protein structure, dynamics, and function, are grouped hierarchically into a custom oncology based on their inherent relationships (Pejaver et al., 2017b). To help model interpretability, we only chose those numeric properties on the 3rd level of the ontology because, unlike their parent or child properties, they are not directly related in calculation and more or less “orthogonal” in molecular mechanism. Therefore, we used as features the posterior probabilities of alteration in 9 properties summarized in Table 2. More features (conservation scores and pathogenicity predictions) are also used in a generalization study and summarized in Supp. Table S2.
Table 2.
The list of properties whose MutPred2-predicted alteration probabilities are used as features.
| Feature Index | Property/Molecular Impact |
|---|---|
| 1 | Relative solvent accessibility |
| 2 | Allosteric site |
| 3 | Catalytic site |
| 4 | Secondary structure |
| 5 | Stability and conformation flexibility |
| 6 | Special structural signatures |
| 7 | Macromolecular binding |
| 8 | Metal binding |
| 9 | PTM site |
2.4. Machine Learning
2.4.1. Mathematical Description
We consider examples each represented by features, i.e., . Although each has a continuous label [PoP (probability of pathogenicity), or here], the exact label is not available. Rather, a categorized class of is given according to a customized K-tier system: if where threshold parameters are increasing in . Without loss of generalizability, and , echoing the range of . In our study, and ’s are set according to Table 1.
All vectors are column vectors unless stated otherwise and are denoted in bold-faced lower-case italics. Matrices are denoted in bold-faced upper-case italics.
2.4.2. Models Overview
We describe three types of machine learning models. The first two do not predict PoP ( ) directly but classify pathogenicity ( ) instead: multi-class logistic regression (MLR), a representative multi-class classification method used by other participants in the challenge (Cline et al., 2019), disregard the order among the five classes; and cumulative logit model (CLM) (Agresti, 2003), a representative of ordinal regression, treat the classes as ordered albeit on an arbitrary scale. In contrast, the last, including three “weakly supervised” regressors (WSR) developed by us, directly predict PoP ( ) for variant i by training models on inexact labels (not PoP but PoP ranges encoded by pathogenicity class ) while utilizing both the order and the scale among the classes. A quick summary is provided in Table 3.
Table 3.
Overview of two types of baseline machine learning models compared in this study as well as our model weakly supervised model.
| Model | Target Label | Learning Type | Ordered Classes | Scaled Classes |
|---|---|---|---|---|
| Multi-class Logistic Regression | Pathogenicity Class | Classification | ✘ | ✘ |
| Cumulative Logit Model | Pathogenicity Class | Classification | ✔ | ✘ |
| Weakly Supervised Regression | Pathogenicity Probability | Regression | ✔ | ✔ |
2.4.3. Multi-class Logistic Regression (MLR)
MLR (Böhning, 1992), a multi-class classification model, is an extension of binary logistic regression. We consider a linear model with parameters for each class . Let denote the column vector stacking all ’s. The conditional probability that a sample belongs to class is thus given by softmax: . The model parameters are trained by minimizing the following objective function:
| (1) |
where the loss function is negative weighted log-likelihood, the regularization term is L2 regularization for controlling model complexity, and is a hyper-parameter for balancing the two terms. Throughout this study, we set , the relative weight of training examples from Class , at the reciprocal of their portion in the training set for the sake of class balance. One could also use other weighting schemes for class prioritization (for instance, penalizing more for pathogenic examples).
2.4.4. Cumulative Logit Model (CLM)
CLM (Agresti, 2003) is a multi-class classification model that, unlike MLR, considers the order among classes on an arbitrary scale. It is a representative for the type of classification problems called ordinal regression (Gutierrez et al., 2016). Specifically, CLM models the cumulative distribution function by a logistic function : . Therefore, the conditional probability is now simply the difference between the cumulative distribution functions at two consecutive classes: . Compared to qK parameters in MLR, a total of q + K parameters including and are trained here by minimizing a similar objective function (negative weighted log-likelihood with L2 regularization):
| (2) |
Both baseline models above just calculate the conditional probability that a variant is classified as each of the K = 5 classes: . To calculate the probability of pathogenicity , we assume that its probability density function is a constant over each class range as specified in Table 1. As such, we estimate by its expectation: .
2.4.5. Weakly Supervised Regression (WSR)
In contrast to using multi-class classification followed by somewhat ad hoc assignment of the probability of pathogenicity or PoP ( for variant i), we developed weakly supervised regression that predicts PoP directly while training data only contains inexact version of PoP, i.e., the pathogenicity class . Specifically, we designed various loss functions that measure the inconsistency between predicted PoP and its supposed class and trained models by minimizing the L2-regularized loss function:
| (3) |
Whereas the regularization term is to prevent overfitting, the loss function is a weighted sum of individual loss . The design rationales for the loss include the following. First, it should (only) penalize a prediction when it is outside the supposed range of class . Second, it should incur more penalty when is further away from the range (for instance, it is worse to predict a pathogenic variant to be benign than uncertain). Last, besides the concerns in the application domain, a good loss function should correspond to optimization problems easy to solve.
Based on aforementioned rationales, we introduce three versions of weakly supervised regressors of various loss functions. We summarize them in Table 4 before we describe each in details.
Table 4.
Comparing the three versions of weakly supervised regression (WSR) models on their loss functions, thresholds, label transformation, and feature embedding.
| Model | Loss function | Threshold | Label Transformation | Feature Embedding |
|---|---|---|---|---|
| WSR1 | Fixed polynomial | Constant b | ✘ | Linear |
| WSR2 | Parameterized ε–insensitive | Parameter τ | ✔ | Linear |
| WSR3 | Parameterized ε–insensitive | Parameter τ | ✔ | Nonlinear (Kernelized) |
●. WSR1: Fixed, parabola-shaped polynomial loss function
We introduced this model during the challenge and submitted its predictions. Here the PoP predictor is a logistic function whose decision score is linear in . And the loss function is a pre-determined parabola-shaped polynomial centered around the midpoint of its supposed range :
| (4) |
As illustrated in Figure 1A, the shape of the loss function in Eq. 4 is very particular, which can be both unnecessary and biased thus prevents better accuracy. Although the WSR1 loss function being convex and smooth is easy to optimize, it also has clear drawbacks. Specifically, it pushes each prediction to the center of its supposed range and increases the penalty with a peculiar slope (that depends on the range) as the prediction is further away from the range. We thus proceeded to develop much-improved models after the challenge, as elaborated next.
Figure 1:
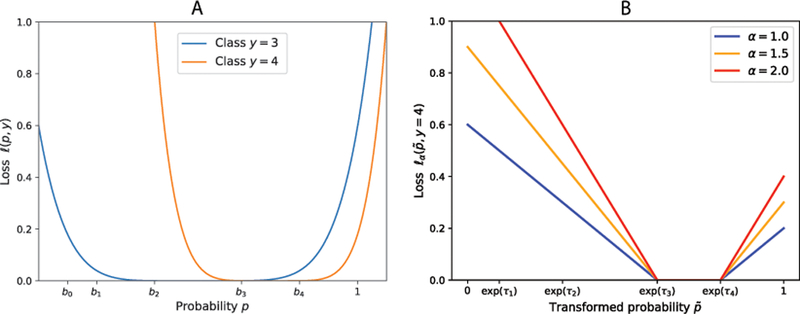
Illustration of loss functions used in weakly supervised regressors (WSR). A. Parabola-shaped loss functions for WSR1 and B. ε-insensitive loss functions for WSR2 and WSR3.
●. WSR2: Parameterized ε-insensitive loss function
Considering the aforementioned drawbacks of the WSR1 loss function used during the Challenge, we further developed two more weakly supervised regressors (WSR2 and WSR3) afterwards. As illustrated in Figure 1B, we allow the class-specific loss function to be flat bottomed (rather than parabola-shaped) in a corresponding parameterized scale (rather than the original, fixed scale) and the label to be transformed (rather than staying in the original space). In other words, these new loss functions do not penalize a prediction when it resides anywhere in the supposed range (no longer pushed to the center); and they give a parameterized penalty otherwise.
Specifically, we first transformed the original scale of fixed thresholds b over [0, 1] (Table 1) into a new scale of parameterized thresholds exp(τ) (including ) to be learned from training data. Note that the use of exp(τ) rather than its logarithm form was designed for the numerical optimization reason (Antal and Csendes, 2016). Correspondingly we had the following transformation between the desired, original label for instance i and the transformed label to be predicted:
| (5) |
We then used in the transformed -space flat-bottomed ε-insensitive loss functions (Vapnik, 2013) that can be regarded as the sum of two hinge loss functions h(·). We used class-specific hyperparameters to control the slope of a hinge function . The higher the , the higher the penalty a prediction would receive if it is outside its supposed range; and no penalty would a prediction receive otherwise. Therefore, for an example of class with predicted probability , we define its loss as:
| (6) |
The above expression applies to all classes including the two borders when or by introducing constants and .
As we did for WSR1, we use logistic functions for the predictor of the transformed label , with a linear decision score . With the loss for each example redefined in Eq. 6, following the general formula for our weakly supervised regression in Eq. 3, our WSR2 models can be learned by solving the following optimization problem:
| (7) |
Note that class-specific for penalizing out-of-the-range predictions are treated as hyperparameters to be optimized on grid search (see more details in Sec. 2.4.6).
●. WSR3: Kernelized WSR2
The decision score function , based on which we used a logistic function to predict transformed label , was linear in (features) for both WSR1 and WSR2, i.e., . Therefore, we further introduce nonlinearity of the decision score function to WSR2 following a “kernel trick” (Aizerman et al., 1964; Theodoridis and Koutroumbas, 2008) that maps the original feature space to a high-dimensional implicit one and finds linear decision boundary there. Noticing that parameters enter the WSR2 formulation (Eq. 7) in the form of the inner-product with the feature vector , but parameter do not, and we have constraints on . We build on the Representer Theorem (Wahba, 1990) (Supp. Lemma 1) and prove a theorem (Supp. Theorem 1) before we apply a kernel trick. A short proof can be found in Supp. Sec. 3.
Based on Theorem 1, we can kernelize the objective function in the WSR2 formulation (Eq. 7) to reach the following formulation for WSR3:
| (8) |
where is now logistic in the kernel space, i.e., .
As such, the kernel trick maps the original feature space into an infinite-dimensional space without the need of calculating the exact mapping between them. This trick will enable our model to deal with the non-linear situation, which could significantly increase our model accuracy. In this paper, we use radial basis function (RBF) kernels with bandwidth . The hyperparameter is optimized by cross-validation with more details given next.
2.4.6. Model Training and Uncertainty Estimation
In order to obtain the uncertainty measure we randomly split the training set into 5 folds and trained 5 models on 5 combinations of 4 folds. This random split was fixed across all types of machine learning models in the study. The predictions of the five models on the test set are used to calculate the mean and the standard deviation of both the label and the assessment metrics. We then trained on all the 5 folds of the training set to obtain the final model for interpretation.
The hyperparameters are optimized using grid search through 4-fold and 5-fold cross validation respectively for uncertainty estimation and final PoP prediction. Specifically, the grid for regularization coefficient consists of 25 points, for which the log2 of them are uniformly distributed on . We use this grid for the regularization constant in all models mentioned before. For WSR2 and WSR3, class-specific slope of the ε-insensitive loss function, , is sampled on the grid of 4 points: . For WSR3, the bandwidth of the RBF kernel, , is sampled on a grid of 25 points, for which their log2 values are evenly distributed between −3 and 2.
For each combination of hyperparameter values, we find model parameters by solving the corresponding optimization problem. Except that MLR (multiclass logistic regression) is already implemented in Python-sklearn (Pedregosa et al., 2011), we implemented all other models in Python 2.7 with optimizers provided in SciPy (Jones et al., 2001-). CLM (cumulative logit model) involves a convex optimization problem and was solved by the optimizer ‘BFGS’.
WSR1 (weakly supervised regressor 1) involves a nonconvex, unconstrained optimization problem and was solved by BFGS with multi-start. Similarly, WSR2 and WSR3 involve nonconvex, constrained optimization problems and were solved by the optimizer ‘L-BFGS-B’ with multi-start. Specifically, we sampled 100 initial coordinates for and , where ’s are uniformly sampled from , and are uniformly sampled from with the constraint of . The rationales for these ranges are the following. First, the standard logistic function saturates quickly when becomes large and, since our features are all MutPred2 property probabilities between 0 and 1, large would push transformed PoP values ( ) close to 0 or 1. Second, since is a threshold in the scale of the exponential function saturates quickly when becomes far negative, which pushes all ’s to become numerically close. We analyze the detailed optimization results in Supp. Sec. 4.
2.4.7. Model Interpretation
We further ask how our model makes a certain pathogenicity prediction for each pathogenic or likely pathogenic variants (Class 4&5) in the ENIGMA Challenge (denoted the set of ). In other words, for each variant we would like to find the most contributing features (and their underlying molecular mechanisms) that place the predicted PoP for the variant above those for the set of benign and likely benign examples (Class 1&2; denoted the set of ). We chose model WSR2 for its balance of accuracy and interpretability.
From Eq. 5 and the expression of a logistic function, we know that the PoP is monotonically increasing with respect to the decision score : the higher the decision score the variant has, the more pathogenic it is. Therefore, given all benign or likely benign variants’ decision scores for each variant with decision we calculate the following differences for the -th feature: (where i is given in and ). With the differences defined above, we perform the one-tailed one-sample t-test for each variant i’s feature and calculate corresponding P-values, where the null hypothesis is that the expected value of the differences, treated as a random variable, is bigger than 0. Finally, for each variant we rank all its features based on their P-values in an increasing order, where the smallest P-value corresponds to the most important feature.
Our model interpretability is enabled by both the MutPred2 features that are interpretable and our decision scores that are linear in feature values. As we rank features for each variant based on the absolute differences between and the data-learned weight in a variant -specific way, determines the direction (positive or negative) and the magnitude (large or small) of feature ’s contribution toward predicted probability of pathogenicity.
2.5. Assessment Metrics
Due to the unavailability of ground-truth PoP values, we use two metrics to assess multi-class classification performances. The first is the multi-class area under the curve (AUC) of receiver operating characteristic (ROC) curve (Hand and Till, 2001), which is simply the unweighted average of binary AUC between all pairs among K classes:
| (9) |
where denotes the binary AUC between class i and j.
As the metric disregards orders among classes, we adopted a second metric, ordinal which estimates the joint probability that randomly picked instances, one from each class, are scored in the supposed order (Waegeman et al., 2008).
| (10) |
where denotes the binary AUC between two partitions of all classes: the first k and the rest.
As the official assessment did (Cline et al., 2019), we also assess performances on binary classification when classes 1 and 2 are merged to a negative class and classes 4 and 5 are merged to a positive. We use binary AUC as well as RMSD (root mean squared deviation) in PoP. Since ground-truth PoP values are not available, they are approximated to be 0.025 and 0.975 in the assessment.
2.6. Protein Modeling for Structural Interpretation
We investigate the impact of pathogenic missense mutations on BRCA1/2 proteins through structural modeling. There are only ten pathogenic BRCA variants (class 5) in the ENIGMA Challenge (also referred to as the CAGI test set) including seven for BRCA1 and three for BRCA2. Furthermore, among these pathogenic variants, only five BRCA1 variations occur in available 3D structures (Bateman et al., 2017), including four in the RING (Really Interesting New Gene) domain [NP_009225.1:p.Met18Thr (p.M18T), NP_009225.1:p.Cys44Phe (p.C44F), NP_009225.1:p.Cys47Tyr (p.C47Y), NP_009225.1:p.Arg71Gly (R71G)] and one [NP_009225.1:p.Ser1715Asn (p.S1715N)] in the BRCT (The BRCA1 C-terminal) domains.
Following various mechanistic hypotheses (such as mutational impacts on folding stability and binding affinity), these five variants are structurally modeled by re-designing wild-type structures using multi-state protein design method iCFN (Karimi and Shen, 2018). Residues within 5 Å from the mutation site were allowed to be flexible (as discrete rotamers) in all designs except that they were extended to those within 8Å when modeling the mutational effect of p.S1715N on BRCT-protein binding as the mutation site is at the second layer of the binding interface.
For modeling the effect of four RING-domain mutations (p.M18T, p.C44F, p.C47Y, p.R71G) on folding stability, we used the single state design (positive only) with substate ensembles where substates were defined as the BRCA1 RING domain in 14 NMR structures in complex with BARD1 (PDB ID: 1JM7). Substate energies were folding energies of the RING domain only that include Coulomb electrostatics, van der Waals, internal energies (Geo term), and a nonpolar contribution to the hydration free energy based on solvent accessible surface area (SASA) (Shen et al., 2015, 2013; Shen, 2013). A positive-substate stability cutoff and positive-versus-negative substate specificity were essentially not mandated with a cutoff of 1,000 kcal/mol.
For modeling the effect of the four RING-domain mutations on interactions with BARD1 (RING domain as well), we used multi-state design (positive and negative) with protein-complex substate ensembles defined in the same PDB entry 1JM7. Positive-substate energies were the total folding energies of the RING domain and BARD1 separately and negative-substate energies were folding energies of the complex of RING domains of BRCA1 and BARD1. A positive-substate stability cutoff was set at 10 kcal/mol and positive-versus-negative substate specificity was essentially not mandated with a cutoff of 1,000 kcal/mol.
Similarly, for modeling the effect of one BRCT-domain mutation (p.S1715N) on the stability and protein interaction of BRCT, we did the same as described above except that there was only a single substate available in the crystal structure. For modeling protein interaction, we used BRCT interacting with Bach1 Helicase (PDB ID: 1T29) and for modeling the stability, we used the unbound structure of BRCT domain (PDB ID: 1JNX).
For either folding stability or binding affinity, top conformations of each designed sequence in each substate (backbone conformation here) generated from iCFN for either state were geometrically grouped into representatives. Later, folding stabilities (G) and binding affinities (ΔG) of the top sequence-conformation ensembles were re-evaluated and re-ordered with a higher-resolution energy model where continuum electrostatics replaced Coulombic electrostatics (Karimi and Shen, 2018). Lastly, the representative conformation at either state was chosen based on the best binding affinity or folding stability (lowest ΔG or G) for modeling the binding or folding respectively. Each calculated relative binding energy to wild type (WT), ΔΔG, and relative folding energy to WT, ΔG, was further decomposed into contributions of van der Waals (vdW), continuum electrostatics (elec), SASA-dependent nonpolar solvation interactions (SASA), and internal energy (Geo).
3. RESULTS
3.1. The Value of Gene Non-specific Data and Less Confident Clinical Annotations
We first assess the value of more abundant albeit less confident variant annotations. When restricted to those at least reviewed by panel (‘review status’ being at least 3 stars, or G3), the number of BRCA1/2 variants accessible from ClinVar was 201, which increased to 699 when the review status was relaxed to at least 2 stars, or G2 (at least reviewed by multiple qualified submitters without conflict). Detailed gene list and class distribution for the G2 and G3 dataset are provided in Supp. Table S3 and S4, respectively. The larger G2 training set, even though their annotations are less confident, actually led to no worse multi-class logistic regressor (MLR). As shown in Table 5, mAUC (ordinal mAUC) was improved by 6% (4%) for the ClinVar test set and even more 8% (9%) for the CAGI test set in the posterior analysis, respectively.
Table 5.
The classification performance of multi-class logistic regression trained on various datasets.
| Dataset for training | ClinVar Test Set | CAGI Test Set | ||
|---|---|---|---|---|
| mAUC | Ordinal mAUC | mAUC | Ordinal mAUC | |
| G3 with BRCA only | 0.572 ± 0.025 | 0.588 ± 0.017 | 0.532 ± 0.034 | 0.512 ± 0.015 |
| G2 with BRCA only | 0.639 ± 0.009 | 0.623 ± 0.005 | 0.610 ± 0.004 | 0.603 ± 0.011 |
| G2 with non-BRCA genes | 0.542 ± 0.010 | 0.535 ± 0.008 | 0.503 ± 0.014 | 0.521 ± 0.008 |
| G2 with all genes | 0.640 ± 0.012 | 0.632 ± 0.008 | 0.611 ± 0.010 | 0.636 ± 0.006 |
We also examine to what extent a gene non-specific predictor can rival a gene specific one for pathogenicity prediction. We desire a predictor specific to the same type of genes whose encoded proteins function similarly with possibly similar structural bases. As such structural and functional knowledge is not always easily accessible, we simply restrict the consideration to 17 other tumor suppressor genes interacting with BRCA1/2. There were 895 G2 non-BRCA variants much more heavily skewed toward Class 3 (uncertain significance) compared to BRCA variants in the ClinVar set (Supp. Table S3). The BRCA variants in the CAGI set turned out to be heavily skewed toward Class 2 (likely benign) instead (Supp. Table S5). Compared to that trained on the BRCA-only data, the MLR model trained on the non-BRCA data had slightly worse performance (8%∼11%), whereas that trained on both data (nearly 60% are non-BRCA variants) performed equally.
We extend the aforementioned comparisons using cumulative logit model and a version of our weakly supervised regressor (WSR1). And we have observed the same trend as seen in Supp. Table S8. Taken together, these results indicate the value of less confident albeit more abundant variant data for pathogenicity prediction. They also show the promise of gene type-specific pathogenicity predictors that can access more variant data of more genes and allow for more complex machine learning models with more parameters. We thus use the G2 dataset with the 19 pooled tumor suppressors thereinafter except when we generalize the study to more genes in Sec. 3.5.
3.2. Comparing Machine Learning Models
We next compare three types of machine learning models, as previously summarized in Table 3, for the task of pathogenicity prediction: multi-class logistic regression (MLR), a representative of multi-class classification used by other participants in the Challenge (Cline et al., 2019); cumulative logit model (CLM), a representative of multi-class classification that considers the order among classes (ordinal regression); and our three weakly supervised regression (WSR) models that directly predict the probability of pathogenicity from training pathogenicity classes using designed loss functions, summarized and compared in Table 4. Due to the lack of ground-truth PoP values, we were only able to assess classification performances. The comparison using multi-classification metrics (mAUC and ordinal mAUC) is given in Table 6 whereas that using binary classification metrics (binary AUC and RMSD) can be found in Table 7.
Table 6.
Pathogenicity-prediction performance comparison (5-class evaluations) among MLR (multi-class logistic regression), CLM (cumulative logit model), and our WSR (weakly supervised regression) variants.
| ClinVar Test Set | CAGI Test Set | |||
|---|---|---|---|---|
| Model | mAUC | Ordinal mAUC | mAUC | Ordinal mAUC |
| MLR | 0.640 ± 0.012 | 0.632 ± 0.008 | 0.611 ± 0.010 | 0.636 ± 0.006 |
| CLM | 0.673 ± 0.016 | 0.691 ± 0.005 | 0.635 ± 0.009 | 0.684 ± 0.026 |
| WSR1 | 0.646 ± 0.016 | 0.682 ± 0.012 | 0.623 ± 0.011 | 0.666 ± 0.008 |
| WSR2 | 0.754 ± 0.015 | 0.782 ± 0.011 | 0.763 ± 0.010 | 0.778 ± 0.023 |
| WSR3 (Kernelized WSR2) | 0.791 ± 0.008 | 0.826 ± 0.014 | 0.781 ± 0.010 | 0.802 ± 0.017 |
Table 7.
Pathogenicity-prediction performance comparison (2-class evaluations) among MLR (multi-class logistic regression), CLM (cumulative logit model), and our WSR (weakly supervised regression) variants.
| ClinVar Test Set | CAGI Test Set | |||
|---|---|---|---|---|
| Model | Binary AUC | RMSD | Binary AUC | RMSD |
| MLR | 0.751 ± 0.004 | 0.251 ± 0.005 | 0.720 ± 0.011 | 0.277 ± 0.003 |
| CLM | 0.853 ± 0.006 | 0.220 ± 0.004 | 0.854 ± 0.008 | 0.213 ± 0.005 |
| WSR1 | 0.801 ± 0.010 | 0.212 ± 0.012 | 0.780 ± 0.005 | 0.234 ± 0.010 |
| WSR2 | 0.971 ± 0.001 | 0.201 ± 0.004 | 0.961 ± 0.003 | 0.198 ± 0.004 |
| WSR3 (Kernelized WSR2) | 0.982 ± 0.003 | 0.131 ± 0.004 | 0.968 ± 0.002 | 0.161 ± 0.003 |
By comparing MLR, CLM, and WSR1, we found that they had very similar performances for both the ClinVar and the CAGI sets in mAUC that disregards orders among classes; and CLM and WSR1, both respecting class order in their models, improved for both sets ordinal mAUC that addresses class order. WSR1 did not improve against CLM, a representative ordinal regression model, because WSR1 suffers from its very peculiar loss function that is fixed to penalize predicted PoP on the fixed, original scale (thresholds b).
Building upon WSR1, we used in WSR2 flat-bottomed ε-insensitive loss functions and b-transformed thresholds τ that are flexibly parameterized and jointly learned along with other parameters from data. Furthermore, in WSR3 we replaced the linear decision score function with an RBF-kernelized one. Accordingly WSR2 and WSR3 drastically improved the performance compared to WSR1 for both mAUC and ordinal mAUC as well as for both test sets. In particular, compared to WSR1, WSR3 improved for the ClinVar test set by 0.14 (0.14) and did so for the CAGI set by 0.16 (0.14) in mAUC (ordinal mAUC). Compared to the baseline MLR widely used in the Challenge, WSR3 improved for the ClinVar test set by 0.15 (0.19) and did so for the CAGI set by 0.17 (0.17) in mAUC (ordinal mAUC).
We found similar trends in the case of merged two-class evaluations (Class 1&2 vs. Class 4&5). Compared to MLR for the CAGI set, WSR3 increased binary AUC from 0.72 to 0.97 and reduced RMSD from 0.28 to 0.16. Speaking of binary AUC, WSR3, using only 9 features, did on a par with the best performer for the Challenge, LEAP (Lai et al., 2018) even though LEAP used many more features and patient information (Cline et al., 2019).
We also provide the confusion matrices of all 5 models for the two test sets in Supp. Table S9 and S10. Obviously WSR3 outperformed the other 4 models in such analyses as well. Specifically, among a total of 36 likely pathogenic or pathogenic cases (classes 4 and 5), WSR3 only mis-classified 3 cases to be non-pathogenic (classes 1 through 3), whereas MLR, CLM, WSR1, and WSR2 did so for 19, 20, 19, and 14 cases, respectively. Compared to WSR2 and CLM that mis-classified nearly all such failed cases only to be uncertain (class 3), MLR and WSR1 had 14/19 and 9/19 mis-classified respectively to be benign or likely benign (classes 1 and 2).
3.3. Mutation-Specific Interpretation of Machine Learning Models
We went on to interpret our weakly supervised regressors, in particular WSR2 whose decision score function is linear in x and model is easily interpretable. As variants can impact disease severity through different molecular and cellular mechanisms, we ranked for each pathogenic or likely pathogenic variant their individual important features (P-value below 0.01) by P-values found by our model-interpretation procedure in Sec. 2.4.7.
As shown in Table 8, the more interpretable WSR2 correctly predicted 9 of 16 pathogenic or likely pathogenic to be so compared to WSR3 that correctly did so for 14 of those 16, which shows the trade-off between interpretability and accuracy. Detailed confusion matrices are provided in Supp. Table S10. We focused on the 6 correctly predicted pathogenic variants and found that the most important features (and likely most probable molecular mechanisms) are related to 2 - allosteric site [NP_009225.1:p.Met18Thr (BRCA1 p.M18T)], 8 - metal binding [NP_009225.1:p.Cys44Phe and NP_009225.1:p.Cys47Tyr (BRCA1 p.C44F and p.C47Y)], 5 - stability and conformational flexibility [NP_009225.1:p.Ser1715Asn (BRCA1 p.S1715N)], and 3 - catalytic site [NP_000050.2:p.Arg2659Gly and NP_000050.2:p.Asn3124Ile (BRCA2 p.R2659G and p.N3124I)]. More detailed results on mutation-specific mechanistic interpretation can be found in Supp. Sec. 7.
Table 8.
Summarized results of WSR2 model interpretation for 16 pathogenic and likely pathogenic BRCA variants. Important features are retained with a P-value cutoff of 1E-02 and ranked from left to right in increasing P-values. PoP predictions of WSR3, more accurate yet less interpretable, are also reported. Bold-faced are correctly predicted (likely) pathogenic.
| Variants | WSR2 | WSR3 | ||
|---|---|---|---|---|
| Predicted PoP | Indices of important features | Predicted PoP | ||
| Class 5 | BRCA1 (NP_009225.1) | |||
| p.M18T | 0.988 ± 0.003 | 2 5 6 9 8 7 | 0.953 ± 0.004 | |
| p.C44F | 0.981 ± 0.002 | 8 7 2 6 5 9 1 | 0.957 ± 0.010 | |
| p.C47Y | 0.953 ± 0.015 | 8 2 7 6 5 | 0.956 ± 0.004 | |
| p.R71G | 0.803 ± 0.002 | 7 4 2 5 9 | 0.050 ± 0.002 | |
| p.R1495T | 0.501 ± 0.020 | 1 5 2 | 0.990 ± 0.008 | |
| p.E1559K | 0.501 ± 0.016 | 5 7 1 | 0.990 ± 0.009 | |
| p.S1715N | 0.959 ± 0.003 | 5 2 6 9 7 4 | 0.953 ± 0.007 | |
| BRCA2 (NP_000050.2) | ||||
| p.R2659G | 0.981 ± 0.004 | 3 2 4 5 8 9 | 0.960 ± 0.005 | |
| p.Q2829R | 0.697 ± 0.009 | 6 5 2 7 9 | 0.953 ± 0.009 | |
| p.N3124I | 0.964 ± 0.005 | 3 2 6 9 4 5 7 | 0.953 ± 0.004 | |
| Class 4 | BRCA1 (NP_009225.1) | |||
| p.V1736G | 0.565 ± 0.002 | 2 8 3 7 6 | 0.953 ± 0.009 | |
| p.G1738E | 0.991 ± 0.001 | 2 8 3 7 6 5 | 0.952 ± 0.007 | |
| p.D1739V | 0.996 ± 0.001 | 3 2 8 6 4 | 0.963 ± 0.008 | |
| p.G1748D | 0.996 ± 0.004 | 3 2 8 7 6 4 | 0.952 ± 0.001 | |
| BRCA2 (NP_000050.2) | ||||
| p.T2607P | 0.681 ± 0.006 | 6 5 9 2 4 | 0.820 ± 0.010 | |
| p.S2670L | 0.501 ± 0.004 | 2 7 | 0.954 ± 0.009 | |
As will be shown next, four of these six variants with predicted mechanisms reside in available 3D protein structures and can be structurally modeled. The predicted molecular mechanisms by which mutations might confer clinical significance were thus verified to be metal binding for p.C44F and p.C47Y, stability for p.S1715N, and protein binding (feature 7, a top but not the first-ranked feature) for p.M18T.
3.4. Protein Structural Interpretation of Some BRCA1 Pathogenic Variants
BRCA1 is known to be required in several cellular processes including transcription, cell-cycle check point control, DNA damage repair and control of centrosome number (Kais et al., 2012). Five pathogenic variants of BRCA1 occur at sites with available protein structure data (p.M18T, p.C44F, p.C47Y, and p.R71G in the RING domain and p.S1715N in the BRCT domain). In addition biological experiments have shown that p.M18T, p.C44F and p.C47Y are deleterious for both homologous recombination process and centrosome number, but p.R71G, being similar to the wild type, is deleterious for neither (Kais et al., 2012).
We performed structural modeling and energetic analysis for these variants to assess their impacts on protein folding stability and binding affinity, features found in the WSR2 model to be the most important features for correctly predicting pathogenicity of these variants.
3.4.1. Structural modeling reproduces destabilization effects of p.M1775R
To validate our structural modeling protocol first, we first tried to replicate the known structure (PDB ID: 1N5O) of a pathogenic BRCA1 mutant, p.M1775R, by re-designing a wild-type (WT) structure (PDB ID: 1JNX). The results in Supp. Fig.S1 displayed an accurate replication of mutant’s ground-truth structure. Moreover, our structural modeling provided the agreement that p.M1775R leads to conformational instability, a causal mechanism for its pathogenicity (Williams and Glover, 2003).
3.4.2. Disrupted metal binding: p.C44F and p.C47Y
Highly conserved C44 and C47 interact with zinc ions that coordinate the stability of the RING domain (Ransburgh et al., 2010). Mutating the cystine residues would disrupt the strongly favorable sulfur-zinc interaction, which has been shown in our structural modeling as well. For both of these mutation zinc-coordinated stability has been disrupted and electrostatics is a main, disrupted molecular force based on energy decomposition (Supp. Fig. S2). Consistently shown in Table 8, feature 8 (Metal Binding) was deemed significant and ranked the first for both p.C44F and p.C47Y, which echoes our structural interpretation.
3.4.3. Disrupted protein binding: p.M18T
Heterodimerization of the RING domains of BRCA1 and BARD1 comprise an E3 ubiquitin ligase. The stability of the heterodimer is crucial for the stability of the full-length BRCA1. Mutants that do not dimerize result in defects in HDR and loss-of-tumor suppression (Starita et al., 2015). Residue M18 is at BRCA1’s interface with BARD1 and the mutation p.M18T is very likely to disrupt the binding with BARD1 (Morris et al., 2002). Based on structural modeling, we found that M18 of BRCA1 WT and M104 of BARD1 WT form a intermolecular sulfur-oxygen interaction which is known to be important for protein-protein binding (Zhang et al., 2015). We also found from structural modeling that this interaction is disrupted upon mutation p.M18T, which is shown in Figure 2. From binding energy decomposition (Supp. Fig. S2), electrostatics is the main reason for the binding disruption. Consistently shown in Table 8, feature 7 (Macromolecular Binding) was deemed significant (although not ranked the first) for p.M18T, which agrees with our structural interpretation.
Figure 2:
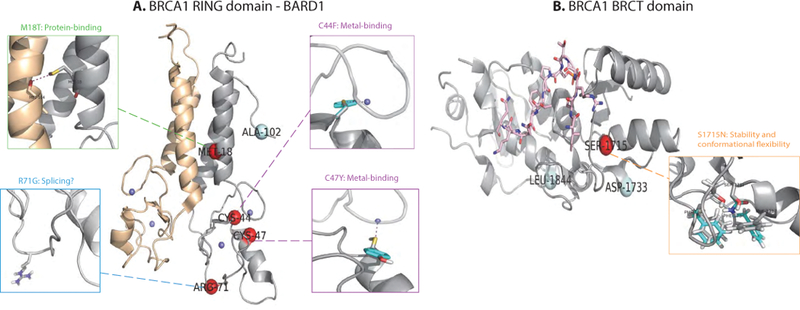
Structural interpretation of pathogenicity mechanisms for several BRCA1 variations at structurallyavailable RING and BRCT domains. Pathogenic (Class 5) and benign (Class 1) variation sites are shown in red and pale cyan spheres. Zoomed-in illustrations of molecular mechanisms have been shown for individual variants in smaller side boxes, where crystal wild-type residues are in gray sticks and modeled mutant residues are in cyan sticks. A. RING domain complex of BRCA1-BARD1 in PDB structure 1JM7 where RING domain of BRCA1 is shown in gray cartoon, BARD1 wheat cartoon, and Zn2+ ions small blue sphere. B. BRCT domain of BRCA1 interacting with Bach1 helicase in PDB structure 1T29 PDB where BRCT is shown in grey cartoon and Bach1 helicase in pink sticks.
3.4.4. Aberrant splicing: p.R71G
The mutation p.R71G was found to affect the splicing process rather than homologous recombination process and the centrosome number (Vega et al., 2001; Kais et al., 2012). The aberrant splicing of BRCA1 mRNA would result in premature translation and truncated proteins, which is beyond the capability of structural modeling. Indeed, the mutation was not found to destabilize BRCA1 (Supp. Fig. S2). Interestingly, the top-performing LEAP team found that splicing information, such as the distance to the nearest splice site, was also important for correctly annotating the clinical significance of some variants (Cline et al., 2019).
3.4.5. Decreased stability: p.S1715N
The BRCT domain of BRCA1 displays an intrinsic transactivation activity. S1715 is an evolutionarily conserved residue and pathogenic mutations in the BRCA domain including p.S1715N have shown the loss of such activity in yeast and mammalian cells (Vallon-Christersson et al., 2001). p.S1715N has been shown unable to complement BRCA1 deficiency for homologous recombination and leading to high instability (Petitalot et al., 2019). Our structural modeling confirms that p.S1715N is structurally destabilizing (Supp. Fig. S2). Specifically, van der Waals clashes was found the main reason for the destabilization effect, as shown in Supp. Fig. S2. Of course, the extent of such clashes could be alleviated by improving the modeling of structure flexibility. Consistently show in Table 8, feature 5 (Stability and Conformational Flexibility) was ranked the most important for p.S1715N, echoing our structural interpretation.
To summarize, we have found for these pathogenic BRCA1 variants the consensus of our machine learning-based and structure modeling-based mechanistic interpretations. Although we do not have structure data to start with for some mutation sites, our machine learning-based interpretations could generate actionable hypotheses of the causal mechanisms that can be tested experimentally, potentially suggesting therapeutic candidates accordingly.
3.5. Generalization of Weakly Supervised Regressors for More Genes
With the 9 MutPred2 features we also test the WSR2 and WSR3 models on 325 more genes as described in the Supp. Sec. 1.3. 4,834 missense variants annotated in ClinVar were collected and their class distributions are detailed in a supplemental Excel sheet (SI_new_genes_stat.xlsx at https://github.com/Shen-Lab/WSR-PredictPofPathogenicity/). We use two schemes to split the data into training (five sixths) and test sets (one sixth). The first scheme allows for overlapping genes between the two sets whereas the second does not, thus testing within- and across-gene predictions, respectively. From Table 9, we conclude that these models achieved similar performances for the 325 additional genes as they did for the BRCA test sets (ClinVar and CAGI in Sec. 3.1). Impressively, WSR3 achieved an ordinal mAUC value over 0.75 even when training and test sets do not overlap in genes. Note that hyper-parameters were not optimized particularly and kept the same as for the BRCA set.
Table 9:
The performance of WSR2 and WSR3 on 325 more genes with different data split frameworks (within/across genes).
| Data Split | Within Genes | Across Genes | ||
|---|---|---|---|---|
| Model | mAUC | Ordinal mAUC | mAUC | Ordinal mAUC |
| WSR2 | 0.713 ± 0.004 | 0.734 ± 0.005 | 0.678 ± 0.004 | 0.683 ± 0.013 |
| WSR3 (Kernelized WSR2) | 0.781 ± 0.011 | 0.801 ± 0.003 | 0.735 ± 0.011 | 0.754 ± 0.004 |
4. CONCLUSION
Starting with interpretable and actionable features that capture molecular impacts of genetic variants and expert-curated albeit inexact labels that only annotate variants using their ranges in the probability of pathogenicity (PoP), we have developed novel weakly-supervised regression models that can directly predict the probability of pathogenicity. By considering the order among pathogenicity classes, penalizing PoP prediction with novel loss functions, and embedding the original feature space into a kernel space, our weakly supervised regressor 3 – WSR3 – has significantly improved the predictive performance for a CAGI challenge set compared to a representative multi-class classification model: binary AUC increased from 0.72 to 0.97 and ordinal multi-class AUC increased from 0.64 to 0.80. WSR3 even improved the predictive performances compared to a representative ordinal regression model CLM (again, a multi-class classifier) that respects class order. Note that our pathogenicity predictors generalize well to additional genes, which could access more variant data and employ more advanced machine learning models.
We further developed methods to interpret our weakly-supervised regressor by assessing the statistical significance of feature importance in supporting individual model predictions. We identified and ranked important features (each corresponding to a mechanism of molecular impacts upon amino-acid substitution) for newly annotated or updated, pathogenic or likely pathogenic BRCA1/2 variants. Our structural modeling of mutational effects on protein folding stability and binding affinity has corroborated the machine learning-predicted molecular mechanisms by which genetic variants lead to diseases. Namely, validated in structural modeling, metal binding for BRCA1 p.C44F and p.C47Y was predicted by our machine learning model interpretation as the most important feature for the pathogenic calling of the variants. So was stability for p.S1715N. And protein binding was predicted to be a statistically significant but not the first-ranked feature for p.M18T. These promising results indicate that these models could generate experimentally-testable mechanistic hypotheses and lead to therapeutic candidates accordingly.
Throughout the study, we only used nine features out of over 50 property probabilities from MutPred2. The main reason was that other highly dependent or not directly causal features could hurt model interpretability. Nevertheless, when 14 more features were used, including 8 conservation scores and 6 pathogenicity predictions (see Supp. Table S2), the predictive power of our weakly supervised regressors was strengthened (see Supp. Table S11). In particular, the ordinal multi-class AUC of WSR3 improved from around 0.80 to 0.85 for the CAGI test set.
One limitation about the current feature set though is the entire focus on molecular impacts of genetic variation without the consideration of cellular contexts or systems-level impacts. On one hand, some variants significantly impacting protein functions may not lead to clinical significance. On the other hand, splicing information for some missense variants is found important for their pathogenicity prediction (Cline et al., 2019). Therefore, it would be of great value to include endophenotypes (Masica and Karchin, 2016) encoding causal mechanisms across hierarchical subsystems (Yu et al., 2016) at various biological scales. Although endophenotype predictors are not adequate for the purpose yet, increasingly available big data and empowering artificial intelligence methods (Ma et al., 2018) are stimulating their development and making the goal of precision medicine more attainable than ever.
Supplementary Material
4.1. ACKNOWLEDGEMENTS
We thank the CAGI organizers, data providers, challenge assessors, and fellow participants for the insightful challenges, data, analysis, and tools which made this study possible. We also thank Dr. Vikas Rao Pejaver for the help on generating MutPred2 features. Part of the computing support was provided by the Texas A&M University High Performance Research Computing.
Funding information This project is in part supported by the National Institute of General Medical Sciences of the National Institutes of Health (R35GM124952 to YS). The CAGI experiment coordination is supported by NIH U41 HG007346 and the CAGI conference by NIH R13 HG006650.
Abbreviations:
- CAGI
Critical Assessment of Genome Interpretation
- ENIGMA
Evidence-based Network for the Interpretation of Germline Mutant Alleles
- PoP
Probability of Pathogenicity
- WSR
Weekly Supervised Regression
- MLR
Multi-class Logistic Regression
- CLM
Cumulative Logit Model
- AUC
Area Under the Curve
Footnotes
Availability Source codes and data are provided at https://github.com/Shen-Lab/WSR-PredictPofPathogenicity
4.1. CONFLICT OF INTEREST
The authors declare no conflict of interest.
4.3. REFERENCES
- Adzhubei I, Jordan DM and Sunyaev SR (2013) Predicting functional effect of human missense mutations using polyphen-2. Current protocols in human genetics, 76, 7–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agresti A (2003) Categorical data analysis, vol. 482. John Wiley & Sons. [Google Scholar]
- Aizerman MA, Braverman EA, Rozonoer L (1964) Theoretical foundations of the potential function method in pattern recognition learning. Automation and Remote Control, 25, 821–837. [Google Scholar]
- Antal E and Csendes T (2016) Nonlinear symbolic transformations for simplifying optimization problems. Acta Cybernetica, 22, 5–23. [Google Scholar]
- Bateman A, Martin MJ, O’Donovan C, Magrane M, Alpi E, Antunes R, Bely B, Bingley M, Bonilla C, Britto R, Bursteinas B, Bye-A-Jee H, Cowley A, Silva AD, Giorgi MD, Dogan T, Fazzini F, Castro LG, Figueira L, Garmiri P, Georghiou G, Gonzalez D, Hatton-Ellis E, Li W, Liu W, Lopez R, Luo J, Lussi Y, MacDougall A, Nightingale A, Palka B, Pichler K, Poggioli D, Pundir S, Pureza L, Qi G, Renaux A, Rosanoff S, Saidi R, Sawford T, Shypitsyna A, Speretta E, Turner E, Tyagi N, Volynkin V, Wardell T, Warner K, Watkins X, Zaru R, Zellner H, Xenarios I, Bouguel- eret L, Bridge A, Poux S, Redaschi N, Aimo L, Argoud-Puy G, Auchincloss A, Axelsen K, Bansal P, Baratin D, Blatter M-C, Boeckmann B, Bolleman J, Boutet E, Breuza L, Casal-Casas C, Castro E. d., Coudert E, Cuche B, Doche M, Dornevil D, Duvaud S, Estreicher A, Famiglietti L, Feuermann M, Gasteiger E, Gehant S, Gerritsen V, Gos A, Gruaz-Gumowski N, Hinz U, Hulo C, Jungo F, Keller G, Lara V, Lemercier P, Lieberherr D, Lombardot T, Martin X, Masson P, Morgat A, Neto T, Nouspikel N, Paesano S, Pedruzzi I, Pilbout S, Pozzato M, Pruess M, Rivoire C, Roechert B, Schneider M, Sigrist C, Sonesson K, Staehli S, Stutz A, Sundaram S, Tognolli M, Verbregue L, Veuthey A-L, Wu CH, Arighi CN, Arminski L, Chen C, Chen Y, Garavelli JS, Huang H, Laiho K, McGarvey P, Natale DA, Ross K, Vinayaka CR, Wang Q, Wang Y, Yeh L-S and Zhang J (2017) UniProt: the universal protein knowledgebase. Nucleic Acids Research, 45, D158–D169. URL: https://academic.oup.com/nar/article/45/D1/D158/2605721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Böhning D (1992) Multinomial logistic regression algorithm. Annals of the institute of Statistical Mathematics, 44, 197–200. [Google Scholar]
- Bromberg Y and Rost B (2007) SNAP: predict effect of non-synonymous polymorphisms on function. Nucleic Acids Res, 35, 3823–3835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakravarty D, Gao J, Phillips S, Kundra R, Zhang H, Wang J, Rudolph JE, Yaeger R, Soumerai T, Nissan MH, Chang MT, Chandarlapaty S, Traina TA, Paik PK, Ho AL, Hantash FM, Grupe A, Baxi SS, Callahan MK, Snyder A, Chi P, Danila DC, Gounder M, Harding JJ, Hellmann MD, Iyer G, Janjigian YY, Kaley T, Levine DA, Lowery M, Omuro A, Postow MA, Rathkopf D, Shoushtari AN, Shukla N, Voss MH, Paraiso E, Zehir A, Berger MF, Taylor BS, Saltz LB, Riely GJ, Ladanyi M, Hyman DM, Baselga J, Sabbatini P, Solit DB and Schultz N (2017) OncoKB: A Precision Oncology Knowledge Base. JCO Precision Oncology, 1, 1–16. URL: http://ascopubs.org/doi/full/10.1200/PO.17.00011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cline MS and Karchin R (2011) Using bioinformatics to predict the functional impact of SNVs. Bioinformatics, 27, 441–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cline MS, Babbi G, Bonache S, Cao Y, Casadio R, de la Cruz X, … ENIGMA Consortium (2019) Assessment of blind predictions of the clinical significance of BRCA1 and BRCA2 variants. Human Mutation, 10.1002/humu.23861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldgar DE, Easton DF, Byrnes GB, Spurdle AB, Iversen ES, Greenblatt MS, Boffetta P, Couch F, de Wind N, Easton D, Eccles D, Foulkes W, Genuardi M, Goldgar D, Greenblatt M, Hofstra R, Hogervorst F, Hoogerbrugge N, Plon S, Radice P, Rasmussen L, Sinilnikova O, Spurdle A and Tavtigian S (2008) Genetic evidence and integration of various data sources for classifying uncertain variants into a single model. Hum. Mutat, 29, 1265–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guidugli L, Shimelis H, Masica DL, Pankratz VS, Lipton GB, Singh N, Hu C, Monteiro ANA, Lindor NM, Goldgar DE, Karchin R, Iversen ES and Couch FJ (2018) Assessment of the Clinical Relevance of BRCA2 Missense Variants by Functional and Computational Approaches. Am. J. Hum. Genet, 102, 233–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutierrez PA, Perez-Ortiz M, Sanchez-Monedero J, Fernandez-Navarro F and Hervas-Martinez C (2016) Ordinal regression methods: survey and experimental study. IEEE Transactions on Knowledge and Data Engineering, 28, 127–146. [Google Scholar]
- Hand DJ and Till RJ (2001) A Simple Generalisation of the Area Under the ROC Curve for Multiple Class Classification Problems. Machine Learning, 45, 171–186. URL: 10.1023/A:1010920819831. [DOI] [Google Scholar]
- Hecht M, Bromberg Y and Rost B (2015) Better prediction of functional effects for sequence variants. BMC Genomics, 16 Suppl 8, S1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoskins RA, Repo S, Barsky D, Andreoletti G, Moult J and Brenner SE (2017) Reports from CAGI: The Critical Assessment of Genome Interpretation. Hum. Mutat, 38, 1039–1041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones E, Oliphant T, Peterson P et al. (2001. –) SciPy: Open source scientific tools for Python. URL: http://www.scipy.org/ [Online; accessed <today>].
- Kais Z, Chiba N, Ishioka C and Parvin J (2012) Functional differences among BRCA1 missense mutations in the control of centrosome duplication. Oncogene, 31, 799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karchin R and Nussinov R (2016) Genome Landscapes of Disease: Strategies to Predict the Phenotypic Consequences of Human Germline and Somatic Variation. PLoS Comput. Biol, 12, e1005043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karimi M and Shen Y (2018) iCFN: an efficient exact algorithm for multistate protein design. Bioinformatics, 34, i811–i820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katsonis P and Lichtarge O (2014) A formal perturbation equation between genotype and phenotype determines the Evolutionary Action of protein-coding variations on fitness. Genome Res, 24, 2050–2058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katsonis P— (2017) Objective assessment of the evolutionary action equation for the fitness effect of missense mutations across CAGI-blinded contests. Hum. Mutat, 38, 1072–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krizhevsky A, Sutskever I and Hinton GE (2012) ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems 25 (eds. F. Pereira, C. J. C. Burges, L. Bottou and K. Q. Weinberger), 1097–1105. Curran Associates, Inc URL: http://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf. [Google Scholar]
- Lai C, O’Connor R, Topper S, Ji J, Stedden W, Homburger J, Van den Akker J, DeSloover D, Zhou A, Z. A and Mishne G. (2018) Using Machine Learning to Support Variant Interpretation in a Clinical Setting. Presented at the Advances in Genome Biology and Technology (AGBT). Retrieved from https://static.getcolor.com/pdfs/research/Color_AGBT_PH_Poster_2018.pdf [Google Scholar]
- Landrum MJ, Lee JM, Benson M, Brown G, Chao C, Chitipiralla S, Gu B, Hart J, Hoffman D, Hoover J, Jang W, Katz K, Ovetsky M, Riley G, Sethi A, Tully R, Villamarin-Salomon R, Rubinstein W and Maglott DR (2016) ClinVar: public archive of interpretations of clinically relevant variants. Nucleic Acids Research, 44, D862–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Biao, Krishnan VG, Mort ME, Xin F, Kamati KK, Cooper DN, Mooney SD, Radivojac P (2009) Automated inference of molecular mechanisms of disease from amino acid substitutions. Bioinformatics, 25(21), 2744–2750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Wu C, Li C and Boerwinkle E (2016) dbNSFP v3.0: A One-Stop Database of Functional Predictions and Annotations for Human Nonsynonymous and Splice-Site SNVs. Hum. Mutat, 37, 235–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J, Yu MK, Fong S, Ono K, Sage E, Demchak B, Sharan R and Ideker T (2018) Using deep learning to model the hierarchical structure and function of a cell. Nat. Methods, 15, 290–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martelotto LG, Ng CK, De Filippo MR, Zhang Y, Piscuoglio S, Lim RS, Shen R, Norton L, Reis-Filho JS and Weigelt B (2014) Benchmarking mutation effect prediction algorithms using functionally validated cancer-related missense mutations. Genome Biology, 15 URL: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4232638/. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masica DL and Karchin R (2016) Towards Increasing the Clinical Relevance of In Silico Methods to Predict Pathogenic Missense Variants. PLoS Comput. Biol, 12, e1004725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris JR, Keep NH and Solomon E (2002) Identification of residues required for the interaction of bard1 with brca1. Journal of Biological Chemistry, 277, 9382–9386. [DOI] [PubMed] [Google Scholar]
- Ng PC and Henikoff S (2003) Sift: Predicting amino acid changes that affect protein function. Nucleic acids research, 31, 3812–3814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M and Duchesnay E (2011) Scikit-learn: Machine learning in Python. Journal of Machine Learning Research, 12, 2825–2830. [Google Scholar]
- Pejaver V, Mooney SD and Radivojac P (2017. a) Missense variant pathogenicity predictors generalize well across a range of function-specific prediction challenges. Hum. Mutat, 38, 1092–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pejaver V, Urresti J, Lugo-Martinez J, Pagel KA, Lin GN, Nam H-J, Mort M, Cooper DN, Sebat J, Iakoucheva LM, Mooney SD and Radivojac P (2017b) MutPred2: inferring the molecular and phenotypic impact of amino acid variants. bioRxiv, 134981. URL: https://www.biorxiv.org/content/early/2017/05/09/134981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petitalot A, Dardillac E, Jacquet E, Nhiri N, Guirouilh-Barbat J, Julien P, Bouazzaoui I, Bonte D, Feunteun J, Schnell JA et al. (2019) Combining homologous recombination and phosphopeptide-binding data to predict the impact of brca1 brct variants on cancer risk. Molecular Cancer Research, 17, 54–69. [DOI] [PubMed] [Google Scholar]
- Ransburgh DJ, Chiba N, Ishioka C, Toland AE and Parvin JD (2010) The effect of brca1 missense mutations on homology directed recombination. Cancer research, 70, 988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reeb J, Hecht M, Mahlich Y, Bromberg Y and Rost B (2016) Predicted Molecular Effects of Sequence Variants Link to System Level of Disease. PLoS Comput. Biol, 12, e1005047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Richards S, Aziz N, Bale S, Bick D, Das S, Gastier-Foster J, Grody WW, Hegde M, Lyon E, Spector E, Voelkerd-ing K and Rehm HL (2015) Standards and Guidelines for the Interpretation of Sequence Variants: A Joint Consensus Recommendation of the American College of Medical Genetics and Genomics and the Association for Molecular Pathology. Genetics in medicine: official journal of the American College of Medical Genetics, 17, 405–424. URL: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4544753/. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y (2013) Improved flexible refinement of protein docking in capri rounds 22–27. Proteins: Structure, Function, and Bioinformatics, 81, 2129–2136. [DOI] [PubMed] [Google Scholar]
- Shen Y, Altman MD, Ali A, Nalam MN, Cao H, Rana TM, Schiffer CA and Tidor B (2013) Testing the substrate- envelope hypothesis with designed pairs of compounds. ACS chemical biology, 8, 2433–2441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen Y, Radhakrishnan ML and Tidor B (2015) Molecular mechanisms and design principles for promiscuous inhibitors to avoid drug resistance: Lessons learned from hiv-1 protease inhibition. Proteins: Structure, Function, and Bioinformatics, 83, 351–372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sherry ST, Ward MH, Kholodov M, Baker J, Phan L, Smigielski EM and Sirotkin K (2001) dbSNP: the NCBI database of genetic variation. Nucleic Acids Res, 29, 308–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silver D, Schrittwieser J, Simonyan K, Antonoglou I, Huang A, Guez A, Hubert T, Baker L, Lai M, Bolton A, Chen Y, Lillicrap T, Hui F, Sifre L, van den Driessche G, Graepel T and Hassabis D (2017) Mastering the game of Go without human knowledge. Nature, 550, 354 URL: 10.1038/nature24270. [DOI] [PubMed] [Google Scholar]
- Starita LM, Young DL, Islam M, Kitzman JO, Gullingsrud J, Hause RJ, Fowler DM, Parvin JD, Shendure J and Fields S (2015) Massively parallel functional analysis of brca1 ring domain variants. Genetics, genetics–115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szklarczyk D, Morris JH, Cook H, Kuhn M, Wyder S, Simonovic M, Santos A, Doncheva NT, Roth A, Bork P, Jensen LJ and von Mering C (2017) The STRING database in 2017: quality-controlled protein-protein association networks, made broadly accessible. Nucleic Acids Research, 45, D362–D368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theodoridis S and Koutroumbas K (2008) Pattern Recognition, Fourth Edition. Orlando, FL, USA: Academic Press, Inc., 4th edn. [Google Scholar]
- Vallon-Christersson J, Cayanan C, Haraldsson K, Loman N, Bergthorsson JT, Brøndum-Nielsen K, Gerdes A-M, Møller P, Kristoffersson U, Olsson H et al. (2001) Functional analysis of brca1 c-terminal missense mutations identified in breast and ovarian cancer families. Human molecular genetics, 10, 353–360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vapnik V (2013) The nature of statistical learning theory. Springer science & business media. [Google Scholar]
- Vega A, Campos B, Bressac-de Paillerets B, Bond PM, Janin N, Douglas FS, Domènech M, Baena M, Pericay C, Alonso C et al. (2001) The R71G BRCA1 is a founder spanish mutation and leads to aberrant splicing of the transcript. Human Mutation, 17, 520–521. [DOI] [PubMed] [Google Scholar]
- Waegeman W, De Baets B and Boullart L (2008) ROC analysis in ordinal regression learning. Pattern Recognition Letters, 29, 1–9. URL: http://www.sciencedirect.com/science/article/pii/S0167865507002383. [Google Scholar]
- Wahba G (1990) Spline Models for Observational Data. CBMS-NSF Regional Conference Series in Applied Mathematics. Society for Industrial and Applied Mathematics. URL: https://epubs.siam.org/doi/abs/10.1137/1.9781611970128. [Google Scholar]
- Weinstein JN, Collisson EA, Mills GB, Shaw KR, Ozenberger BA, Ellrott K, Shmulevich I, Sander C, Stuart JM, Chang K, Creighton CJ, Davis C, Donehower L, Drummond J, Wheeler D, Ally A, Balasundaram M, Birol I, Butter- field SN, Chu A, Chuah E, Chun HJ, Dhalla N, Guin R, Hirst M, Hirst C, Holt RA, Jones SJ, Lee D, Li HI, Marra MA, Mayo M, Moore RA, Mungall AJ, Robertson AG, Schein JE, Sipahimalani P, Tam A, Thiessen N, Varhol RJ, Beroukhim R, Bhatt AS, Brooks AN, Cherniack AD, Freeman SS, Gabriel SB, Helman E, Jung J, Meyerson M, Ojesina AI, Pedamallu CS, Saksena G, Schumacher SE, Tabak B, Zack T, Lander ES, Bristow CA, Hadjipanayis A, Haseley P, Kucherlapati R, Lee S, Lee E, Luquette LJ, Mahadeshwar HS, Pantazi A, Parfenov M, Park PJ, Pro-topopov A, Ren X, Santoso N, Seidman J, Seth S, Song X, Tang J, Xi R, Xu AW, Yang L, Zeng D, Auman JT, Balu S, Buda E, Fan C, Hoadley KA, Jones CD, Meng S, Mieczkowski PA, Parker JS, Perou CM, Roach J, Shi Y, Silva GO, Tan D, Veluvolu U, Waring S, Wilkerson MD, Wu J, Zhao W, Bodenheimer T, Hayes DN, Hoyle AP, Jeffreys SR, Mose LE, Simons JV, Soloway MG, Baylin SB, Berman BP, Bootwalla MS, Danilova L, Herman JG, Hinoue T, Laird PW, Rhie SK, Shen H, Triche T, Weisenberger DJ, Carter SL, Cibulskis K, Chin L, Zhang J, Getz G, Sougnez C, Wang M, Saksena G, Carter SL, Cibulskis K, Chin L, Zhang J, Getz G, Dinh H, Doddapa- neni HV, Gibbs R, Gunaratne P, Han Y, Kalra D, Kovar C, Lewis L, Morgan M, Morton D, Muzny D, Reid J, Xi L, Cho J, DiCara D, Frazer S, Gehlenborg N, Heiman DI, Kim J, Lawrence MS, Lin P, Liu Y, Noble MS, Stojanov P, Voet D, Zhang H, Zou L, Stewart C, Bernard B, Bressler R, Eakin A, Iype L, Knijnenburg T, Kramer R, Kreisberg R, Leinonen K, Lin J, Liu Y, Miller M, Reynolds SM, Rovira H, Shmulevich I, Thorsson V, Yang D, Zhang W, Amin S, Wu CJ, Wu CC, Akbani R, Aldape K, Baggerly KA, Broom B, Casasent TD, Cleland J, Creighton C, Dodda D, Edgerton M, Han L, Herbrich SM, Ju Z, Kim H, Lerner S, Li J, Liang H, Liu W, Lorenzi PL, Lu Y, Melott J, Mills GB, Nguyen L, Su X, Verhaak R, Wang W, Weinstein JN, Wong A, Yang Y, Yao J, Yao R, Yoshihara K, Yuan Y, Yung AK, Zhang N, Zheng S, Ryan M, Kane DW, Aksoy BA, Ciriello G, Dresdner G, Gao J, Gross B, Jacobsen A, Kahles A, Ladanyi M, Lee W, Lehmann KV, Miller ML, Ramirez R, Ratsch G, Reva B, Sander C, Schultz N, Sen-babaoglu Y, Shen R, Sinha R, Sumer SO, Sun Y, Taylor BS, Weinhold N, Fei S, Spellman P, Benz C, Carlin D, Cline M, Craft B, Ellrott K, Goldman M, Haussler D, Ma S, Ng S, Paull E, Radenbaugh A, Salama S, Sokolov A, Stuart JM, Swatloski T, Uzunangelov V, Waltman P, Yau C, Zhu J, Hamilton SR, Getz G, Sougnez C, Abbott S, Abbott R, Dees ND, Delehaunty K, Ding L, Dooling DJ, Eldred JM, Fronick CC, Fulton R, Fulton LL, Kalicki-Veizer J, Kanchi KL, Kandoth C, Koboldt DC, Larson DE, Ley TJ, Lin L, Lu C, Magrini VJ, Mardis ER, McLellan MD, McMichael JF, Miller CA, O’Laughlin M, Pohl C, Schmidt H, Smith SM, Walker J, Wallis JW, Wendl MC, Wilson RK, Wylie T, Zhang Q, Burton R, Jensen MA, Kahn A, Pihl T, Pot D, Wan Y, Levine DA, Black AD, Bowen J, Frick J, Gastier-Foster JM, Harper HA, Helsel C, Leraas KM, Lichtenberg TM, McAllister C, Ramirez NC, Sharpe S, Wise L, Zmuda E, Chanock SJ, Davidsen T, Demchok JA, Eley G, Felau I, Ozenberger BA, Sheth M, Sofia H, Staudt L, Tarnuzzer R, Wang Z, Yang L, Zhang J, Omberg L, Margolin A, Raphael BJ, Vandin F, Wu HT, Leiser- son MD, Benz SC, Vaske CJ, Noushmehr H, Knijnenburg T, Wolf D, Van ‘t Veer L, Collisson EA, Anastassiou D, Ou Yang TH, Lopez-Bigas N, Gonzalez-Perez A, Tamborero D, Xia Z, Li W, Cho DY, Przytycka T, Hamilton M, McGuire S, Nelander S, Johansson P, Jornsten R, Kling T and Sanchez J (2013) [Google Scholar]
- The Cancer Genome Atlas Pan-Cancer analysis project. Nat. Genet., 45, 1113–1120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams RS and Glover JM (2003) Structural consequences of a cancer-causing brca1-brct missense mutation. Journal of Biological Chemistry, 278, 2630–2635. [DOI] [PubMed] [Google Scholar]
- Yu MK, Kramer M, Dutkowski J, Srivas R, Licon K, Kreisberg J, Ng CT, Krogan N, Sharan R and Ideker T (2016) Translation of Genotype to Phenotype by a Hierarchy of Cell Subsystems. Cell Syst, 2, 77–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X, Gong Z, Li J and Lu T (2015) Intermolecular sulfur···oxygen interactions: Theoretical and statistical investiga- tions. Journal of chemical information and modeling, 55, 2138–2153. [DOI] [PubMed] [Google Scholar]
- Zhou Z-H (2018) A brief introduction to weakly supervised learning. National Science Review, 5, 44–53. URL: 10.1093/nsr/nwx106. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


