BRCA1- and BRCA2-specific in silico tools for variant interpretation in the CAGI 5 ENIGMA challenge

Abstract

BRCA1 and BRCA2 (BRCA1/2) germline variants disrupting the DNA protective role of these genes increase the risk of hereditary breast and ovarian cancers. Correct identification of these variants then becomes clinically relevant, because it may increase the survival rates of the carriers. Unfortunately, we are still unable to systematically predict the impact of BRCA1/2 variants. In this article, we present a family of in silico predictors that address this problem, using a gene-specific approach. For each protein, we have developed two tools, aimed at predicting the impact of a variant at two different levels: functional and clinical. Testing their performance in different datasets shows that specific information compensates the small number of predictive features and the reduced training sets employed to develop our models. When applied to the variants of the BRCA1/2 (ENIGMA) challenge in CAGI 5 we find that these methods, particularly those predicting the functional impact of variants, have a good performance, identifying the large compositional bias towards neutral variants in the CAGI sample. This performance is further improved when incorporating to our prediction protocol estimates of the impact on splicing of the target variant.

1. Introduction

Germline variants disrupting the DNA protective role of BRCA1 and BRCA2 (BRCA1/2) result in an increased risk of developing hereditary breast and ovarian cancers (HBOC) (Roy, Chun, & Powell, 2012; Venkitaraman, 2014). Identification of the carriers of these variants is clinically relevant because it allows channeling these individuals to surveillance, prevention programs and targeted therapies (Paluch-Shimon et al., 2016). As a result, these patients increase their survival rates; however, not all of them will benefit equally, because we lack an exact knowledge of the functional impact of BRCA1/2 variants. In these cases, a straightforward decision can only be taken when the variant is overtly deleterious (insertions, deletions, and substitutions codifying truncated proteins). When the variant has an uncertain effect on protein function (e.g., missense, synonymous, intronic, and 5’UTR or 3’UTR variants) the best course of action becomes unclear. Solving this problem is not easy because experimentally measuring the impact of these variants on the activity of BRCA1 and BRCA2 (BRCA1/2), requires complex cell-based assays (reviewed in (Guidugli et al., 2013; Millot et al., 2012)) that are technically challenging for a systematic application (Starita et al., 2015).

In these circumstances, in silico pathogenicity predictors of missense substitutions -Align-GVGD (Tavtigian et al., 2006), PolyPhen-2 (Adzhubei et al., 2010), SIFT (Kumar, Henikoff, & Ng, 2009), PON-P2 (Niroula, Urolagin, & Vihinen, 2015) etc.- are employed as an inexpensive, easy-to-use alternative. The predictions obtained are applied for prioritizing variants for experimental evaluation and as a contribution to decision models that integrate different sources of evidence (Karbassi et al., 2016; Lindor et al., 2012; Moghadasi, Eccles, Devilee, Vreeswijk, & van Asperen, 2016; Vallée et al., 2016). However, the moderate success rate of these tools is an obstacle for their extended use in a clinical environment (Riera, Lois, & de la Cruz, 2014). In the specific case of BRCA1/2, Ernst et al. (Ernst et al., 2018) suggest, after testing the performance of Align-GVGD, SIFT, PolyPhen-2, MutationTaster2 on a set of 236 BRCA1/2 variants of known effect, that in silico results cannot be used as stand-alone evidence for diagnosis. In terms of molecular effect, two independent, massive functional assays of BRCA1 variants (Findlay et al., 2018; Starita et al., 2015) show that in silico predictors provide only a limited view of the functional impact of these variants. In summary, we need to improve the predictive power of these tools, if we want to increase their usage in the clinical setting and augment their value for healthcare stakeholders.

The slow progression in performance displayed by pathogenicity predictors along time shows that ameliorating them is a difficult task (Riera et al., 2014). In this scenario, the use of rigorous performance estimates becomes an important factor, since improvements are expected to be small and hard to establish. Generally, these estimates are obtained using a standard N-fold cross-validation procedure (Baldi, Brunak, Chauvin, Andersen, & Nielsen, 2000; Riera et al., 2014; Vihinen, 2012). However, given the increasing availability of variant data, independent testing of predictors is emerging as a valuable option to complement cross-validated performance estimates. Sometimes this testing is done in specific systems for which new variants with impact annotations become available, either at specific/general databases or through experimental testing of their function. For example, Riera et al. (Riera et al., 2015) cross-validate their Fabry-specific predictor with a set of 332 pathogenic and 48 neutral variants, and provide an independent validation, using a set of 65 pathogenic variants obtained from an update of the Fabry-specific database. Wei et al. (Wei & Dunbrack, 2013) test five in silico predictors using an independent set of 204 variants (79 deleterious, 125 neutral) of the human cystathionine beta-synthase whose impact they establish with an in vitro assay. Large variant sets, including data from different genes, are also frequently used to assess and compare the performance of several predictors simultaneously (reviewed in (Niroula & Vihinen, 2016)). While relevant, the value of these approaches to validation is limited by different factors, such as the fact that the standard of performance evaluation may vary between works, the manuscripts may not always be easy to find, etc. In this situation, CAGI (Critical Assessment of Genome Interpretation) (Hoskins et al., 2017), a community experiment where developers can assess the performance of their methods in specific challenges, offers an excellent opportunity to obtain an independent view on their work. For users, it allows having an idea on the state of the art for a protein or disease of their interest.

In this manuscript we present: (i) a novel family of pathogenicity predictors for scoring BRCA1 and BRCA2 missense variants; and (ii) their performance in the recently held CAGI 5 community experiment.

The four tools described in this work (two for BRCA1 and two for BRCA2) are protein-specific (Crockett et al., 2012; C. Ferrer-Costa, Orozco, & de la Cruz, 2004; Pons et al., 2016; Riera, Padilla, & de la Cruz, 2016), that is, only variants for a given protein are used to train its two predictors. These two predictors differ on their objective: one is trained to estimate the molecular-level impact of variants and the other their clinical impact (neutral/pathogenic). Technically, for the first predictor we employed a standard multiple linear regression approach and for the second, a neural network model with no hidden layers.

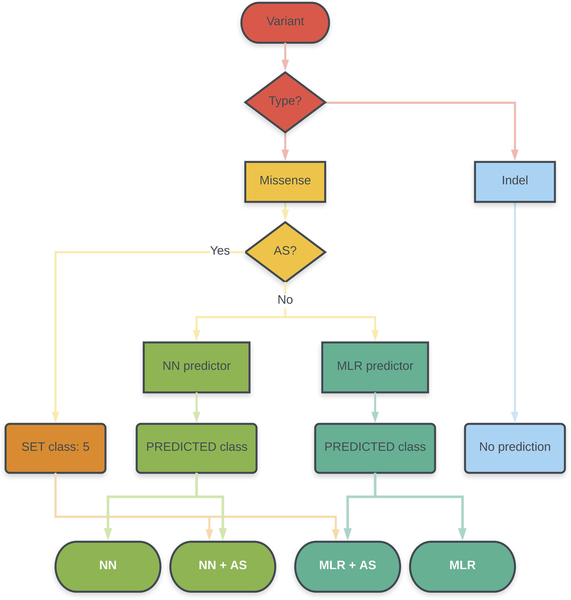
Once obtained, these predictors were applied to the variants constituting the BRCA1/2 (ENIGMA) challenge in CAGI 5. This was done following a protocol that combined predictions of affected splicing and protein impact and was the same for both proteins (Figure 1). Evaluating these two effects of genetic variants (on splicing and protein function) is routine in general diagnostic procedures (Richards et al., 2015) and there are specific tools in the case of BRCA1/2 variants ((Vallée et al., 2016), http://priors.hci.utah.edu/PRIORS/). In our protocol, given an unknown variant, it was first tested for its effect on the splicing pattern, using a recently developed approach (Moles-Fernández et al., 2018). If the variant had no detectable effect, it was subsequently tested for its impact on protein function, using the predictors here presented. Our results show that all our protein-specific predictors can discriminate (with different degrees of success) between neutral and pathogenic variants, both for BRCA1 and BRCA2. For this binary discrimination problem (neutral/pathogenic) their performances are comparable to, or better than, those of general predictors (CADD, PolyPhen-2, PON-P2, PMut, SIFT). When applied to the variants of the CAGI challenge, where the goal is to classify them in one of the IARC 5-tier classes (or a reduced version with three classes) we see the same trend. In spite of a decrease in performance, our methods are able to predict the biased composition of the dataset, mainly our predictors trained using data from the HDR assay. Most of the neutral variants are correctly identified by these predictors and, for pathogenic variants, in silico prediction of affected splicing enhances the final success rate.

Figure 1. Prediction protocol.

In this article, we present a protocol for the prediction of missense variants that includes assessment of the impact of this variant on splicing and protein function. This protocol has been used to interpret the variants of the ENIGMA challenge in the CAGI 5 community experiment. MLR and NN refer to our two protein-specific predictors, based on a Multiple Linear Regression model and a neural network model, respectively. AS refers to the procedure to predict variants resulting in Affected Splicing (Moles-Fernández et al., 2018).

Note on terminology.

We have italized the gene symbols (BRCA1 and BRCA2) and not the protein symbols (BRCA1 and BRCA2). In general, because we are presenting protein-specific predictors, when referring to them, to the training variants, etc, we have utilized the non italized version. However, we are aware that at some points it is unclear which option is preferable and our decision may be arbitrary.

2. Materials and Methods

In this work, we present: (i) the development of a family of predictors for BRCA1/2 missense variants, and (ii) the use of these tools to predict the pathogenicity of the ENIGMA variants in the CAGI challenge. We first describe the overall prediction protocol (Figure 1), which integrates predictors of splicing and protein impact, and then focus on the description of the specific predictors.

NOTE.When referring to a variant regarding its impact on protein function, we will speak of ‘functional’, ‘intermediate’ or ‘non-functional’ variants, as those that result in a protein that preserves its function, has lost part of it or has lost all of it, respectively. We will preserve the terms ‘neutral’, ‘unknown’ (or ‘uncertain’) and ‘pathogenic’ to refer to the clinical phenotype of the variant.

2.1. Overall prediction protocol

In this section and in Figure 1, we describe the protocol followed in our contribution to the CAGI 5 experiment, an experiment that presents participants with different challenges revolving around a central theme (Hoskins et al., 2017): the prediction of variant pathogenicity and its applications. We focused our efforts on the set of BRCA1 and BRCA2 variants provided by the ENIGMA consortium (Spurdle et al., 2012), and we submitted four sets of predictions per protein (Supp. Table S1). These four sets correspond to different combinations of our approaches for the prediction of variants leading to affected splicing (AS, one method) (Moles-Fernández et al., 2018) or affecting protein function/structure (two methods: multiple linear regression –MLR- and neural network –NN). They are the following:

1.- Set MLR+AS: AS impact + Protein impact with MLR

2.- Set NN+AS: AS impact + Protein impact with NN

3.- Set MLR+nAS: Predict protein impact with MLR, no AS predictions used

4.- Set NN+nAS: Predict protein impact with NN, no AS predictions used

The submission format was the same for each set and was provided by the organizers. It comprised the following information per variant: three fields for the identification (DNA variant; Gene; protein variant), three fields for the prediction (predicted IARC 5-tier class; probability of the variant being pathogenic, which we call ‘p’; confidence of each prediction probability, which we call ‘sd’), and one field for ‘Comments’.

For the sets MLR+AS and NN+AS, any variant predicted as ‘pathogenic’ by the AS predictor was arbitrarily assigned values of p=1 and sd=0, and the ENIGMA class ‘5’. Otherwise, the variant was annotated using our protein impact predictors, which were obtained as explained below. That is, the protein impact was estimated only if the variant had no predicted effect on AS. One can distinguish these situations by the text in the ‘Comments’ column: (i) ‘splicing’, which means that the variant is annotated with the AS predictor; (ii) ‘protein’, which means that the variant is annotated with the protein-based predictors (MLR or NN); (iii) ‘arbitrary’, which is only used for variants for which we have not a predictor (annotation is arbitrarily set to the following: ENIGMA class=5, p=0.5, and sd=0.5).

For the sets MLR+nAS and NN+nAS we did not use AS predictors. All the variants are annotated using our protein impact predictors (obtained as explained below). As before, these situations are distinguished in the ‘Comments’ field with the labels ‘protein’, if the variant is annotated with the protein-based predictors (MLR or NN).

NOTE. The five ENIGMA classes used correspond to the IARC 5-tier classification system (Goldgar et al., 2008; Plon et al., 2008) (1=‘Not pathogenic’, 2=‘Likely not pathogenic’, 3=‘Uncertain’, 4=‘Likely pathogenic’, 5=‘Pathogenic’) and were taken from CAGI’s website for the BRCA1 and BRCA2 challenge (https://genomeinterpretation.org/content/BRCA1_BRCA2).

2.2. Prediction of AS variants

To score the effect on splicing of the CAGI variants from the ENIGMA challenge, we have used the results of our recent work (Moles-Fernández et al., 2018) where we identified the best combination of in silico tools for predicting splice site alterations, among those predictors available in the package Alamut Visual v2.10. More precisely, we showed that the HSF+SSF-like combination (with Δ−2% and Δ−5% as thresholds, respectively) for donor sites and the SSF-like (Δ−5%) for acceptor sites, exhibited an optimal performance in a benchmark combining RNA in vitro testing and a dataset of variants retrieved from public databases and reported in the literature. For the CAGI challenge (Figure 1), a variant predicted to produce splice site alterations was arbitrarily assigned class 5, p=1 and sd=0; in the comments column it was identified as ‘splicing’. Variants giving no signal for splice site alterations were directly channeled to the protein predictors.

2.3. Protein-based predictors

We have developed two methods for predicting the impact of protein sequence variants of BRCA1 and BRCA2. One is based on a neural network (NN) and is trained to produce a binary output reflecting the pathogenic nature -cancer risk (high/low)- of a cancer variant. The other method is based on a multiple linear regression (MLR) and is trained to predict the values of the HDR assay for a variant. Both methods are protein-specific: there is a version of MLR for BRCA1 and another for BRCA2, and the same for NN. We describe them below; we start with the NN because it employs more predictive features (6) than the MLR, which only uses a subset of these (3).

2.3.1. The NN method

We have followed our approach to produce protein-specific predictors (Riera et al., 2016), which comprises the three steps described below: (i) obtention of a variant dataset true to the prediction goal; (ii) labeling of variants with chosen features; and (iii) obtention of the NN model.

2.3.1.1. Obtention of BRCA1 and BRCA2 variants

Missense variants in this dataset were selected with clinical impact in mind. This was done by manually reviewing several gene-specific databases that collect BRCA1 and BRCA2 variants along with published literature: Leiden Open Variation Database describing functional studies of specific BRCA1 and BRCA2 variants (LOVD; http://databases.lovd.nl/shared/genes/BRCA1;http://databases.lovd.nl/shared/genes/BRCA2), LOVD-IARC dedicated to variants that have been clinically reclassified using an integrated evaluation (http://hci-exlovd.hci.utah.edu/home.php?select_db=BRCA1), BRCA Share™ (formerly Universal Mutation Database UMD-BRCA mutations database http://www.umd.be/BRCA1/; http://www.umd.be/BRCA2/), CLINVAR, that provides clinical relevance of genetic variants (https://www.ncbi.nlm.nih.gov/clinvar/), and BRCA1 CIRCOS which compiles and displays functional data on all documented BRCA1 variants (https://research.nhgri.nih.gov/bic/circos/). Finally, each variant was validated by combining different sources of evidence.

Variants for which the pathogenic role was attributable to splice site alterations (assessed using Alamut Visual biosoftware 2.6, from Interactive Biosoftware) were eliminated. This was done to ensure, as far as possible, that our model was trained using variants whose damaging/neutral nature was a consequence of their impact in protein function/structure only.

The final datasets (Supp. Table S1) were constituted by (Table 1):

Table 1A.

Size of the datasets used in this work (CAGI: missense + AS)

	NN	MLR	CAGI	SGE†
BRCA1	226 (P=77/N=149)‡	28	144	1837
BRCA2	141 (P=36/N=105)‡	56	174	-

^†Dataset extracted from Findlay et al., 2018. SGE: saturation genome editing.

^‡P: pathogenic; N: neutral

.- BRCA1: 77 ‘pathogenic’ and 149 ‘neutral’ variants.

.- BRCA2: 36 ‘pathogenic’ and 105 ‘neutral’ variants.

2.3.1.2. Features

We used a total of six features to label the variants for the predictor training. We have previously used them for the development of protein-specific predictors (Riera et al., 2016). We describe them below for the benefit of the reader.

Two features are based on the use of multiple sequence alignments (MSA): Shannon’s entropy and position-specific scoring matrix element. Shannon’s entropy is equal to -Σ_ip_i.log(p_i), where the index i runs over all the amino acids at the variant’s MSA column. Position-specific scoring matrix element for the native amino acid (pssm_nat) is equal to log(f_nat,i/f_nat,MSA), where f_nat,i is the frequency of the native amino acid at the locus i of the variant and f_nat,MSA is the frequency of the same amino acid in the whole MSA. We used two different MSA, psMSA and oMSA, which resulted in two versions of the NN predictor. psMSA were obtained using the same protocol utilized for the protein-specific predictors (Riera et al., 2015, 2016) which, briefly, consists of two steps: (i) recovery of BRCA1/2 homologs using a query search of UniRef100; (ii) elimination of remote homologs (<40% sequence identity); alignment of the remaining sequences with Muscle (Edgar, 2004). The resulting MSA are available on demand from the authors. The oMSA, available from the group of Sean Tavtigian (Tavtigian, Greenblatt, Lesueur, & Byrnes, 2008), comprise only orthologs of BRCA1 and BRCA2, and are publicly available at the web of the Huntsman Cancer Institute, University of Utah (http://agvgd.hci.utah.edu/alignments.php). The NN predictions submitted to CAGI were those obtained with the method developed using the psMSA, although results for the second predictor are mentioned below.

Three features, each measuring the difference between native and mutant amino acids for a single physicochemical property: Van der Waals volume (Bondi, 1964), hydrophobicity scale (estimated from water/octanol transfer free energy measurements) (Fauchere & Pliska, 1983) and the element of the Blosum62 matrix (Henikoff & Henikoff, 1992) corresponding to the amino acid replacement.

Finally, a sixth feature that is binary (1/0) and summarizes the information available on the functional/structural role of the native residue at the UniProt database. It is set to “1” when the native residue has a functional annotation on that database, and “0” if this is not the case.

2.3.1.3. Neural network predictor

The NN predictor was built using WEKA (v3.6.8) (Hall et al., 2009). Following our experience in the development of protein-specific predictors with small datasets (Riera et al., 2016), we employed the simplest neural network model: a single-layer perceptron. Sample imbalances in the training set were corrected with SMOTE (Chawla, Bowyer, Hall, & Kegelmeyer, 2002).

The NN model gives two outputs: (i) a binary prediction for the variant, either pathogenic or neutral; (ii) a continuous score, comprised between 0 and 1, that reflects the probability of pathogenicity.

A Leave-one-out cross-validation (LOOCV) of the model was done also using the WEKA (v3.6.8) (Hall et al., 2009) package.

2.3.1.4. CAGI output

As mentioned above, the CAGI submission requires three pieces of information for each variant prediction: the predicted IARC 5-tier class, p (probability of pathogenicity) and sd (reliability). We took as ‘p’ the output from the NN: it varies between 0 (minimal probability of pathogenicity) and 1 (maximal probability of pathogenicity). For the sd value, we used the following formula (C. Ferrer-Costa et al., 2004): sd= 0.5-|0.5-p|. It goes from 0 (maximal reliability) to 0.5 (minimal reliability). Finally, the predicted IARC 5-tier class was obtained from the p, using the ENIGMA conversion table at the CAGI site (class 5: p>0.99; class 4: 0.95<p<0.99; class 3: 0.05<p<0.949; class 2: 0.001<p<0.049; class 1: p<0.001).

2.3.2. The MLR method

This method aims to predict the values of the HDR (homology-directed DNA repair) assay for a given variant, which is a measure of the impact of this variant on BRCA1/2 molecular function. Since the output of the HDR assay is a continuous value, we opted for using a multiple linear regression as a modeling tool, as implemented in the python package Scikit-learn (Pedregosa et al., 2011). The LOOCV of the model was done with the same package. For a given variant, the output of our model is HDR_pred, the predicted value of the HDR assay.

To develop our method we used experimental HDR results available from the literature: 44 variants for BRCA1 (Starita et al., 2015) and 185 variants for BRCA2 (Guidugli et al., 2013, 2018) proteins. However, to reinforce the strength of the signal, relative to experimental noise, we did not employ the full data sets. The BRCA1 training dataset was constituted by those variants used to build the NN predictor (see the previous section) for which HDR values were available; for BRCA2 we followed the same approach. The final number of HDR values was 28 for BRCA1. For BRCA2, we worked with 92 HDR values that corresponded to 56 variants (some had been tested twice (Guidugli et al., 2013, 2018)).

Given the small size of these variant datasets, to try to minimize overfitting problems, we used only three of the previous features (see section 3.1.2, Shannon’s entropy, pssm_nat, and Blosum62 element) as independent variables in the regression model. Like for NN methods, the MSA-based features were computed with the psMSA and the oMSA, thus leading to two versions of the MLR. Only the predictions for the oMSA-based MLR where submitted to CAGI; however, the results for the second predictor are also provided in this manuscript.

NOTE. When obtaining the HDR predicted values using this method, in a few cases the result was a slightly negative number. In these cases, the predicted value was set to 0, since the output of the HDR experiment is always a positive number.

2.3.2.1. CAGI output

To adapt the MLR predictions to the CAGI format, we used the following steps:

1.- Obtain HDR_pred, the MLR predictions for the variants in the BRCA1 and BRCA2 training datasets.

2.- Separately for BRCA1 and BRCA2, compute the mean and standard deviations of the HDR values of the known ‘pathogenic’ and ‘neutral’ variants. At this point, we have four values for each protein: m_P, sd_P, m_N, sd_N.

3.- After the ‘pathogenicity’ assignment, we computed CAGI’s ‘p’ as follows: N(x; m_P, sd_P)/(N(x; m_P, sd_P)+N(x; m_N, sd_N)), where N(x; m, sd) represents a normal probability distribution of mean m and standard deviation sd. The resulting value is comprised between 0 (‘neutral’) and 1 (‘pathogenicity’) and reflects the probability of a variant being ‘pathogenic’, according to our model.

4.- The sd value was obtained, as for the NN methods, using the following formula (C. Ferrer-Costa et al., 2004): sd= 0.5-|0.5-p|.

2.4. Performance Assessment

As mentioned before, during the development process predictor performance was estimated using a standard LOOCV procedure for each predictor (Riera et al., 2016), regardless of whether it was MLR or NN.

The parameters used to measure the success rate of the predictors vary depending on the number of classes predicted. During the development process, the NN method predicted only two classes: pathogenic and neutral; in subsequent validations, including that of the CAGI submissions, three and five classes were considered. We describe below the performance parameters employed in each case.

2.4.1. Binary performance assessment

Here success rate was measured with four commonly employed parameters for binary predictions (Baldi et al., 2000; Vihinen, 2013): sensitivity, specificity, accuracy, and Matthews Correlation Coefficient (MCC). They are computed as follows:

.- Sensitivity:

$$\frac{TP}{TP+FN}$$

.- Specificity:

$$\frac{TN}{TN+FP}$$

.- Accuracy:

$$\frac{TP+TN}{TP+FP+TN+FN}$$

.- Matthews Correlation Coefficient:

$$\frac{TP\cdot TN-FP\cdot FN}{\sqrt{(TP+FN)\cdot (TN+FP)\cdot (TP+FP)\cdot (TN+FN)}}$$

where TP and FN are the numbers of correctly and incorrectly predicted pathological variants; TN and FP are the numbers of correctly and incorrectly predicted neutral variants, respectively.

2.4.2. Multiclass performance assessment

In our case, we need to evaluate the performance of our methods when their score is transformed into a five or three class prediction; e.g., this happens when assessing the CAGI submission (we predict five classes) and the application of our MLR to the recently published exhaustive, functional assay of BRCA1 variants (Findlay et al., 2018), where we predict three classes. For multiclass problems, the number of options available is smaller than for binary problems (Baldi et al., 2000; Vihinen, 2013). Here we have utilized the following: the confusion matrices, the accuracies per class, the overall accuracy, and the multiclass Matthews Correlation Coefficient (Gorodkin, 2004; Jurman, Riccadonna, & Furlanello, 2012).

For a multiclass problem with M classes the confusion matrix, C=(c_ij), is an (MxM) matrix where c_ij is the number of times a class i input is predicted as class j. The sum of the c_ij corresponds to the sample size N, which in our case is the total number of variants predicted. This matrix provides the simplest description of the performance of a predictor; its diagonal and off-diagonal elements correspond to the predictor’s successes and failures, respectively. If we normalize each diagonal element by its row total (c_ii/ Σ_jc_ij, where j=1,M) we obtain the accuracy of the predictor for class i. If we add all the diagonal elements and divide the result by N (Σ_ic_ii/N, where i=1,M), we obtain the overall accuracy.

The multiclass MCC (Gorodkin, 2004; Jurman et al., 2012) was obtained using the implementation in the python package Scikit-learn (Pedregosa et al., 2011).

3. Results

In this article, we describe the obtention of a novel family of pathogenicity predictors specific for BRCA1/2 proteins (MLR and NN) and their application to the variants in the CAGI challenge, within a protocol that also includes AS predictions (Figure 1). Sections 3.1 to 3.5 correspond to the first part, and section 3.6 corresponds to the second part.

As we have seen in the Materials and Methods section, we have considered the use of different MSA (psMSA and oMSA) to develop our predictors. However, we center our descriptions on the versions employed for the CAGI challenge: MLR based on oMSA and NN based on psMSA. For completeness, we also provide the performance of our methods when developed using psMSA (for MLR) and oMSA (for NN).

3.1. The variant datasets

In Table 1A we give the size of the datasets employed in this work. In Table 1B, we report the overlap between the CAGI and the remaining datasets. Note that the CAGI class information on each variant was made public only after the challenge was closed.

Training datasets for NN and MLR.

The number of missense variants in the NN training sets (BRCA1: 226; BRCA2: 141) is comparable to that used for developing protein-specific predictors with the same neural network model and variant features (Riera et al., 2016). The situation is different for the MLR training sets, which were small (BRCA1: 28; BRCA2: 56), thus imposing a severe limitation in the number of features that can be used in the model (see Materials and Methods).

Validation dataset for BRCA1 MLR.

This set is obtained from the results of a recently published (Findlay et al., 2018) experiment for BRCA1. The authors functionally score a large number of single nucleotide variants (SNVs); we retrieved the 1837 cases corresponding to missense variants. We refer to this dataset as SGE (from ‘saturation genome editing’). We used SGE to further test the performance of our BRCA1 MLR because Findlay et al. find that there is a correspondence between their functional score and the score of the HDR assay (Findlay et al., 2018).

CAGI datasets.

Their size (BRCA1: 144; BRCA2: 174) is of the same magnitude as that of the NN training datasets. In Table 2 we provide two partitions of these datasets, corresponding to: (i) the original, 5-class ENIGMA partition; and (ii) a reduced, 3-class partition. For the latter, the ‘Pathogenic’ and ‘Likely pathogenic’ classes have been unified into a single ‘Pathogenic’ class, and the ‘Likely not pathogenic’ and ‘Not pathogenic’ classes have been unified into a single ‘Neutral’ class. The ‘Uncertain class’ (or ‘Unknown’) has been left untouched. It must be noted the high compositional imbalance of the CAGI dataset, with the total of classes 1 and 2 being 10 and 25 times higher than that of the remaining classes, for BRCA1 and BRCA2, respectively. In particular, the absolute numbers of variants for classes 3, 4 and 5 are so low that they can hardly lead to reliable estimates for class-dependent parameters. For example, there are only two variants of class 3 for both BRCA1 and BRCA2; two and three variants for classes 4 and 5, respectively, in BRCA2; and four and seven variants for classes 4 and 5, respectively, in BRCA1.

Table 2.

Composition of the ENIGMA dataset in the CAGI 5 challenge

(A) BRCA1
IARC 5-tier class	1 (<0.001)	2 (0.001–0.049)	3 (0.05–0.949)	4 (0.95–0.99)	5 (>0.99)
CAGI	31	100	2	4	7
Three Class†	Neutral		Unknown	Pathogenic
CAGI	131		2	11

(B) BRCA2
IARC 5-tier class	1 (<0.001)	2 (0.001–0.049)	3 (0.05–0.949)	4 (0.95–0.99)	5 (>0.99)
CAGI	31	136	2	2	3
Three Class†	Neutral		Unknown	Pathogenic
CAGI	167		2	5

^†This classification is a simplified version of the IARC 5-tier scheme (see manuscript) where the Neutral class corresponds to IARC classes 1 and 2, the Pathogenic class corresponds to IARC classes 4 and 5, and Unknown corresponds to IARC class 3.

3.2. Predicting the functional impact of BRCA1/2 variants: the MLR predictor

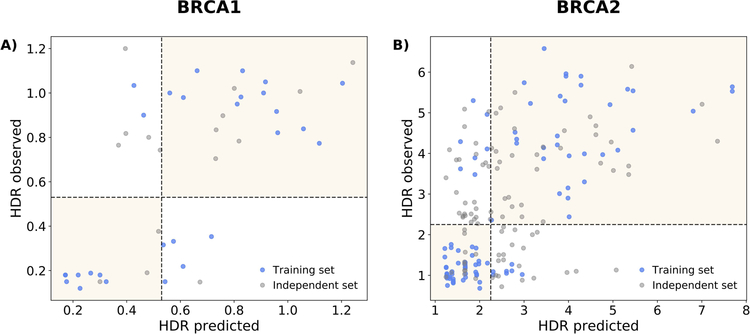
We have developed two MLR methods, one per protein. The goal of these methods is to predict the impact of a given variant on protein function, as measured by the HDR experiment. To this end, they were trained with a set of variants with known experimental values for the HDR assay and the features chosen are related to the effect variants can have on protein structure, protein-protein interactions, etc. (Carles Ferrer-Costa, Orozco, & de la Cruz, 2002; Riera et al., 2014). In Figure 2, we see that there is a statistically significant correlation between observed vs. predicted (LOOCV) HDR values (BRCA1: 0.72, p-value=1.5×10⁻⁵; BRCA2: 0.73, p-value=3.3×10⁻¹⁷). Visual inspection reveals that the variants tend to group into two clusters, showing that MLR predictions approximately reproduce the bimodal pattern of HDR assays (Guidugli et al., 2013; Starita et al., 2015). We also show (grey color), the predictions for the variants which were left outside the training set, after applying the pathogenicity condition (see Materials and Methods); they are more scattered than those forming the training set, illustrating how the filtering worked.

Figure 2. Observed vs. predicted HDR values for (A) BRCA1 and (B) BRCA2.

In blue, we show the variants used for the training/testing of our MLR method (the version trained with oMSA, used to generate CAGI predictions). The HDR predicted values are cross-validated (LOOCV, see Materials and Methods). For completeness, we show in grey the points from the original HDR experiments that were excluded from the training process after applying our filtering procedure (see Materials and Methods).

We explored how good this level of accuracy is for a standard two-class (pathogenic/neutral) prediction of the variant’s pathogenicity. To this end we discretized the predictions applying a decision boundary: a variant was called pathogenic or neutral when its predicted HDR score was below or above a given threshold, respectively. These thresholds, taken from the experimental papers, where: 0.53 for BRCA1 (Starita et al., 2015) and 2.25 for BRCA2 (Guidugli et al., 2013). In Table 3 we give the parameters measuring the success rate of the discretized MLR methods. Their accuracies, 0.75 for BRCA1 and 0.86 for BRCA2, fall within the 0.79–0.99 accuracy range for protein-specific predictors (Riera et al., 2016); the same happens for the MCC, 0.50 for BRCA1 and 0.71 for BRCA2. We detect that specificity (0.85) and sensitivity (0.86) are closer for BRCA2 than for BRCA1 (spec: 0.87; sens: 0.62). Actually, for BRCA1 sensitivity tends to be small when compared to that of protein-specific predictors (Riera et al., 2016). Overall, these results indicate that the continuous HDR predictions of our MLR model can be transformed into binary predictions preserving a non-random prediction power, comparable to that of predictors trained with binary encodings (pathogenic/neutral) of the variant impact.

Table 3.

Two-class (binary) performance of our predictors. ‘CAGI’ identifies the predictors used for this challenge

Protein	Method	SN	SP	ACC	MCC
BRCA1	MLR (psMSA)	0.692	0.933	0.821	0.651
	MLR-CAGI (oMSA)	0.615	0.867	0.75	0.502
	NN (oMSA)	0.922	0.852	0.876	0.746
	NN-CAGI (psMSA)	0.857	0.718	0.765	0.546
BRCA2	MLR (psMSA)	0.828	0.741	0.786	0.571
	MLR-CAGI (oMSA)	0.862	0.852	0.857	0.714
	NN (oMSA)	0.75	0.867	0.837	0.592
	NN-CAGI (psMSA)	0.75	0.771	0.766	0.473

3.3. Validation of the BRCA1 MLR predictor with functional data

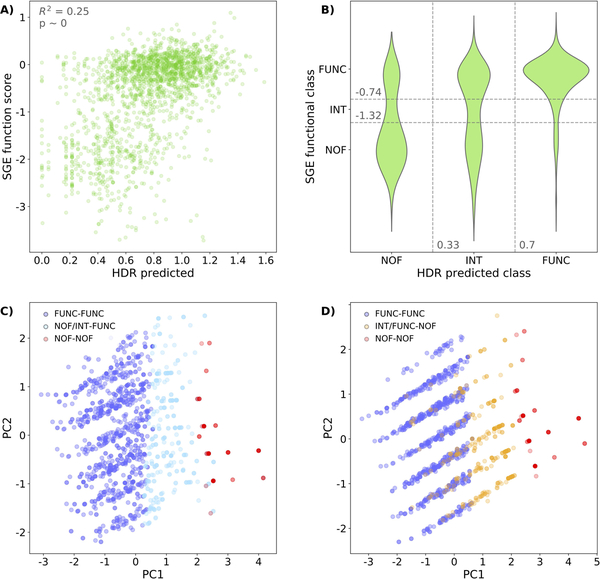
The recent publication (Findlay et al., 2018) of a massive functional assay of BRCA1 variants has given us the opportunity to check the performance of our MLR model on a set of 1837 variants. The output of this experiment is a continuous value measuring the impact of sequence variants on BRCA1 function. When we represent these values against our HDR predictions (Figure 3A) we observe two clusters of points (below and above SGE=−1) that reflect the bimodal behavior of both assays, with a statistically significant rank correlation (Spearman’s ρ=0.47, p-value~0). This overall coincidence is limited by a substantial scatter. Part of it may be due to technical/biological (inter-exon normalization procedures, impact of RNA levels, etc.) differences between the SGE and HDR experiments that introduce some dispersion in the comparison between both experiments (see Figure 9m from Extended Data Section in (Findlay et al., 2018)). Another part of the scatter is due to limitations of our model. To better understand these, we divided the SGE-HDR plane into 9 regions, corresponding to the 3×3 combinations of SGE (‘functional’, ‘intermediate’ and ‘non-functional’) (Findlay et al., 2018) and HDR (‘High’, ‘Int’, ‘Low’) (Starita et al., 2015) equivalent, functional classes. The main blocks of outliers correspond to the two top-left and the two bottom-right regions. We separately used the variants inside each block for a principal component analysis (PCA), using as variables the three features in our model (Shannon’s entropy, pssm_nat, and Blosum62 element). As a reference, for each PCA we also included the variants from the upper (‘functional’) and lower (‘non-functional’) diagonal regions. In the plane of the first two principal components (PC1 and PC2 in Figures 3C and 3D) the chosen variants adopt a three-layered disposition, where we successively find the ‘functional’, the outliers and the ‘non-functional’ ones. This disposition reflects the contrast between the bimodal nature of the SGE experiment and the smoother nature of our model.

Figure 3. Prediction of the ‘saturation genome editing’ (SGE) experiment in BRCA1.

We use our impact prediction to check the correspondence between our HDR predictions and the results of the SGE experiment (Findlay et al., 2018). (A) Scatterplot representing SGE values vs. HDR predictions for the 1837 missense variants from (Findlay et al., 2018) (Spearman’s ρ=0.47, p-value~0). (B) Violin plot showing the distribution of variants for the different combinations of SGE and HDR functional categories: ‘functional’ (FUNC), ‘intermediate’ (INT) and ‘non-functional’ (NOF). Points in the off-diagonal quadrants correspond to outliers: points whose SGE (observed) and HDR (predicted) functional classes do not coincide. (C) Principal component analysis of three variant populations (HDR-SGE classes): FUNC-FUNC (dark blue), NOF-NOF (red) and the outliers NOF-FUNC plus INT-FUNC (light blue). (D) Principal component analysis of three variant populations (HDR-SGE classes): FUNC-FUNC (dark blue), NOF-NOF (red) and the outliers INT-NOF plus FUNC-NOF (yellow). PC1 and PC2 refer to the first two principal components (those which accumulate the highest variance).

In fact, in Supp. Figure S1 we can see that those outlier variants indeed tend to have intermediate values (comprised between those of the ‘functional’ and ‘non-functional’ populations’) for the features in our model. This suggests that for these variants we need to improve our representation of protein impact with new properties, to reproduce more accurately the results of the SGE experiment. However, it may also indicate the need to consider the effect of variants on other aspects of gene function, like RNA levels (Findlay et al., 2018).

3.4. Predicting the clinical impact of BRCA1/2 variants: the NN predictors

We have developed two NN methods, one per protein. These methods were trained with the idea of predicting the clinical impact of a given variant. To this end, during the training process, each variant was labeled with a binary version of this clinical impact: pathogenic/neutral. Here, the larger amount of data (Table 1A) allowed us to work with three additional features, fully adhering to our protocol for the obtention of protein-specific predictors (Riera et al., 2016). As for the MLR predictors, the results obtained (Table 3) are comparable to those of other protein-specific predictors. Their accuracies, 0.77 for both BRCA1 and BRCA2, are almost within the 0.79–0.99 accuracy range for protein-specific predictors; the same happens for the MCC, 0.55 for BRCA1 and 0.47 for BRCA2. The sensitivities and specificities are more balanced for both BRCA1 (spec: 0.72; sens: 0.86) and BRCA2 (spec: 0.77; sens: 0.75) when compared with what happened for the MLR predictors.

Overall, as in the case of MLR, the results indicate that the more clinically flavored NN predictors have a prediction power comparable to that of other protein-specific predictors (Riera et al., 2016).

3.5. Comparison with general pathogenicity predictors

To put in context the results of our protein-specific predictors, we give the performance, on our training datasets, of a representative set of general predictors: CADD (Kircher et al., 2014), PolyPhen-2 (Adzhubei et al., 2010), SIFT (Kumar et al., 2009), PON-P2 (Niroula et al., 2015) and PMut (López-Ferrando, Gazzo, de la Cruz, Orozco, & Gelpí, 2017). Care must be exercised when considering the results of this comparison, since the variants in our datasets can be found in databases, like UniProt (Bateman et al., 2017), commonly used to develop pathogenicity predictors (Riera et al., 2014). Therefore, it is likely that some of these variants have been used in the training of the general methods, thus leading to optimistic estimates of their performance. An additional limitation of the comparison is the small sample size involved, e.g., training of BRCA1 MLR was done using only 28 variants.

In general, we observe (Figure 4) that our specific methods have success rates comparable to those of general methods. For MCC, our methods are only surpassed by PMut. For BRCA2, our NN is slightly surpassed by PON-P2 (MCC of 0.47 vs. 0.49), but our MLR surpasses PON-P2 (MCC of 0.71 vs. 0). The sensitivities and specificities of our methods are generally smaller and larger, respectively, than those of other methods. However, our methods have an equilibrated performance for pathogenic and neutral variants (Figures 4E, 4F), since they display the smallest differences between sensitivity and specificity, 0.14 (BRCA1) and 0.021 (BRCA2) for NN, respectively, and 0.25 (BRCA1) and 0.01 (BRCA2) for MLR. Only PMut has closer values for the MLR training set of BRCA1, 0.06.

Figure 4. Binary, cross-validated performance of the predictors.

We represent the performance of our MLR and NN methods, as well as that of general predictors (CADD, PolyPhen-2, PMut, PON-P2 and SIFT), using four parameters: accuracy and MCC (radar plots (A), (B), (C) and (D)) and sensitivity and specificity (scatterplots, (E) and (F)). The methods labeled MLR-CAGI and NN-CAGI are those used to generate our CAGI predictions; for completeness, we give the performance of the other versions: MLR-psMSA (entropy and pssm_nat values were obtained from psMSA-based parameters) and NN-oMSA (entropy and pssm_nat values were obtained from oMSA-based parameters). In (E) and (F) points are colored according to the set in which sensitivity and specificity were estimated: blue and orange for the MLR and NN sets, respectively.

3.6. Results of the predictors in the CAGI experiment

In this section, we present the results of applying our prediction protocol (Figure 1) to the CAGI variants. For each protein, we submitted to the CAGI challenge the results of four versions of this protocol (Figure 1): MLR+AS, NN+AS, MLR, and NN. For simplicity, we will restrict our analysis to the complete protocols (MLR+AS, NN+AS), mentioning protein predictions (MLR, NN) only for discussing the contribution of the AS predictors. Performance was assessed using the class assignments provided by the CAGI organizers after the challenge was closed. More precisely, we computed the ability of our protocols to correctly assign a variant to its class in two different classification schemes. One is the IARC 5-tier classification system (Goldgar et al., 2008; Plon et al., 2008), which was the one requested by the organizers; the other is a 3-class version of this system (see Materials and Methods).

The fact that we must consider the performance for more than two classes makes the evaluation problem more difficult: in multiclass problems confusion matrices retain their explanatory power, but summary measures are not easy to generalize, nor to interpret (Baldi et al., 2000; Vihinen, 2012). In our case, the severity of this problem is augmented by the compositional imbalance in the CAGI dataset (Table 2). For these reasons, we focus our analysis mainly on the confusion matrices (represented as heatmaps) because they provide the basal information in any prediction process and allow a direct interpretation. More concretely, we consider: (i) the diagonal elements to see how good our predictions are; and (ii) the off-diagonal elements to see how incorrect predictions distribute among classes. We treat separately BRCA1 and BRCA2 cases because the performance of specific and general pathogenicity predictors is gene-dependent (Riera et al., 2016).

3.6.1. BRCA1 variants

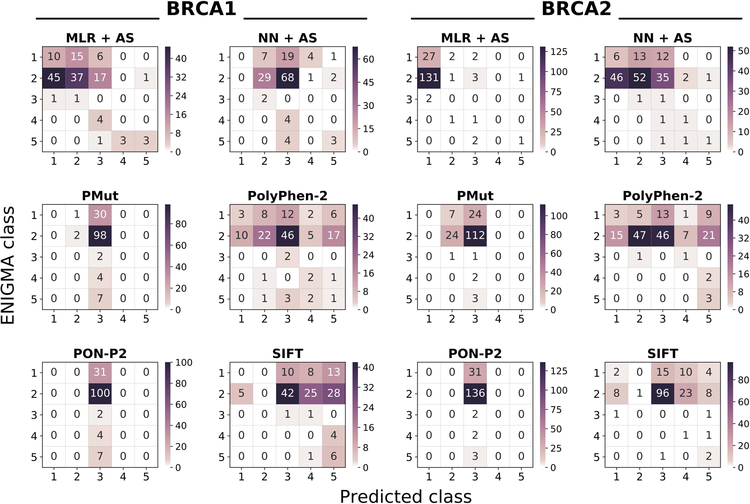
Looking at the diagonals of their confusion matrices (Figure 5), we observe that MLR+AS and NN+AS can recognize, with varying accuracies, members from three (1,2,5) and two classes (2,5), respectively. This overall trend is reflected in the class accuracies, which are higher for MLR-based protocols than for NN-based ones (Table 4). If AS predictions are not included, the two methods also fail to recognize class 5 variants (Table 4). In fact, for MLR+AS and NN+AS protocols AS predictions are responsible for the accuracy of class 5, which is 0.43 (3 out of 7 correctly predicted variants) in both cases; AS predictions lead to a single failure, for a class 2 variant.

Figure 5. Heatmap of the predictor performances on the CAGI datasets.

Each heatmap represents the confusion matrix of a predictor. We provide six heatmaps per protein, two for our predictors (MLR+AS and NN+AS) and four for the general predictors (PolyPhen-2, PON-P2, PMut, and SIFT). In all the plots, the vertical and horizontal axes correspond to the observed (provided by CAGI organizers) and predicted IARC 5-tier classes, respectively. Diagonal and off-diagonal elements correspond to successful and failed predictions, respectively. NOTE: given the range differences in the predictions, each plot has its color scale.

Table 4.

Class accuracies for the CAGI variants (IARC 5-tier and 3-class unified classes). The color shading reflects the correspondence between the two class systems.

(A) BRCA1
IARC 5-tier	1 (<0.001)	2 (0.001–0.049)	3 (0.05–0.949)	4 (0.95–0.99)	5 (>0.99)
MLR	0.323	0.37	0	0	0
MLR +AS	0.323	0.37	0	0	0.429
NN	0	0.29	0	0	0
NN + AS	0	0.29	0	0	0.429
Three Class	Neutral		Unknown	Pathogenic
MLR	0.817		0	0.273
MLR +AS	0.817		0	0.545
NN	0.275		0	0
NN + AS	0.275		0	0.273

(B) BRCA2
IARC 5-tier	1 (<0.001)	2 (0.001–0.049)	3 (0.05–0.949)	4 (0.95–0.99)	5 (>0.99)
MLR	0.871	0.007	0	0	0
MLR +AS	0.871	0.007	0	0	0.333
NN	0.194	0.382	0.5	0.5	0
NN + AS	0.194	0.382	0.5	0.5	0.333
Three Class	Neutral		Unknown	Pathogenic
MLR	0.97		0	0
MLR +AS	0.964		0	0.2
NN	0.701		0.5	0.4
NN + AS	0.701		0.5	0.6

To understand the distribution of incorrect predictions among classes, we consider the off-diagonal elements of the confusion matrices (Figure 5). For MLR+AS, incorrect predictions mostly group at positions adjacent to the diagonal, with only 9 out of 144 variants breaking this trend. For NN+AS this number grows to 31 and predictions (both correct and incorrect) seem to cluster around class 3 column.

If we analyze the predictions within the unified 3-class framework, we find that the class accuracies increase for MLR+AS: 0.82 and 0.56 for ‘Neutral’ and ‘Pathogenic’, respectively. For NN+AS, this is not the case, due to the previously mentioned clustering of predictions around class 3. Accuracy for the ‘Unknown’ class is the same as that for IARC 5-tier class 3, because the classes are the same.

Finally, we compare the performance of our predictors with that for the general predictors for which the output directly corresponded to a probability of pathogenicity (we only excluded CADD, because the score has another scale) (Figure 5). For the chosen predictors (PMut, PolyPhen-2, PON-P2, and SIFT) their score is a probability of pathogenicity that can be transformed into an equivalent of the IARC 5-tier classes, using the ENIGMA conversion table (see Materials and Methods). Focusing on the most frequent CAGI variants (31 from class 1; 100 from class 2), we see that MLR+AS performs better than general methods; for class 5, all general methods, except SIFT, identify fewer correct variants. The case of SIFT is of interest since some of the class 5 variants appear to be splicing variants according to our AS predictions: at this point, and without further evidence, it is unclear which is the correct view, the amino acid view provided by SIFT or the nucleotide view provided by AS predictions. For classes 3 and 4, the size of the sample, two and four variants, respectively, limits the value of the results, which are: for the two variants of class 3, MLR+AS performs worse than general methods; for the four variants of class 4, only PolyPhen-2 correctly identifies two of them. A remarkable feature of MLR+AS, relative to general methods, is that its predictions form a band around the diagonal, while general methods either scatter their predictions (PolyPhen-2, SIFT) or cluster them around class 3 (PON-P2 and PMut). Comparison of NN+AS with general methods (Figure 5) shows similarities with PON-P2 and PMut, and a failure to identify members of class 1 that is shared with all general methods, except PolyPhen-2; again, AS predictions favor our method for class 5, except in the case of SIFT.

The comparison within the three-class framework (Supp. Figure S2) confirms the previous trends, with MLR+AS having the largest class accuracy for ‘Neutral’, 0.82, well over that of general methods (0.33 for PolyPhen-2; 0.04 for SIFT, 0.02 for PMut and 0 for PON-P2). MLR+AS displays the second best accuracy for ‘Pathogenic’, together with PolyPhen-2 and behind SIFT. NN+AS again shows a performance below that of these two general methods, but above that of PON-P2 and PMut.

3.6.2. BRCA2 variants

For BRCA2, the situation is somewhat different. The diagonal elements of the confusion matrix (Figure 5) show that NN+AS can recognize variants from the five classes, with varying accuracies (Table 4), while MLR+AS recognizes only variants from classes 1, 2 and 5. Additionally, for the most frequent classes (1, 2) NN+AS is more balanced than MLR+AS (Figure 5, Table 4): 0.19 (1) and 0.38 (2) vs. 0.87 (1) and 0.01 (2), respectively. Inspection of the off-diagonal elements shows that wrong predictions are more spread for NN+AS than for MLR+AR. For example, for MLR+AS, essentially all (97%) the incorrect predictions of class 2 go to class 1, while this figure drops to 55% for NN+AS. As before, the tiny number of variants in the remaining classes reveals no clear trends. The AS predictions result in one correctly identified member of class 5 for the two versions of our protocol; AS predictions lead to a single failure, for a class 2 variant.

As for BRCA1, reduction of the five IARC 5-tier classes to a 3-class system reveals a reversion in the previous trend, with a high class accuracy for ‘Neutral’, higher for MLR+AS (0.96) than for NN+AS (0.70). Accuracy for the ‘Unknown’ class is the same as that for IARC 5-tier class 3, because the classes are the same. For the ‘Pathogenic’ class, NN+AS still performs better than MLR+AS (Figure 5, Table 4).

Finally, we compare the performance of our predictors with that for the general predictors for which the output directly corresponded to a probability of pathogenicity (we only excluded CADD, because the score has another scale) (Figure 5). Focusing on the most frequent CAGI variants (31 from class 1; 136 from class 2), we see that NN+AS performs better than general methods; MLR+AS is only better for class 1; for class 2 its accuracy is low, the same as SIFT, and below that of PolyPhen-2 and PMut. For classes 3, 4 and 5, the sample size is smaller than that of BRCA1 (2, 4, 7 vs. 2, 2, 3 variants for BRCA1 and BRCA2, respectively); for this reason, we believe that for these variants it is preferable to wait for next rounds of the CAGI challenge to assess the performance of the different in silico tools, including ours.

The comparison within the three-class framework (Supp. Figure S2) confirms the previous trends, showing that for the ‘Neutral’ class (167 out of 174 CAGI variants) both MLR+AS and NN+AS surpass general methods (Supp. Figure S2). For the ‘Pathogenic’ class (5 variants), PolyPhen-2 and SIFT have the best performances, while our methods rank third (MLR+AS) and fourth (MLR+AS).

4. Discussion

Obtaining good estimates of the functional impact and cancer risk of BRCA1 and BRCA2 sequence variants plays a vital role in the diagnosis and management of inherited breast and ovarian cancers (Eccles et al., 2015; Findlay et al., 2018; Guidugli et al., 2018; Moreno et al., 2016; Paluch-Shimon et al., 2016). A priori, in silico tools can be used to obtain these estimates; however, their moderate success rate restricts their applicability (Ernst et al., 2018). In this work, we have addressed this issue focusing on the problem of predicting the pathogenicity of BRCA1/2 missense variants using protein-specific information (Riera et al., 2014). This approach has been validated in different proteins (Crockett et al., 2012; Riera et al., 2016); recent results (Hart et al., 2019) show that it can improve the identification BRCA1/2 pathogenic variants. Here, we present a new family of BRCA1- and BRCA2-specific tools that we validate in two different ways: (i) in isolation, using manually curated sets of functionally and clinically annotated variants; and (ii) in combination with predictors of splicing impact (Figure 1), to interpret the variants from the ENIGMA challenge of the CAGI 5 experiment.

4.1. The performance of BRCA1- and BRCA2-specific predictors in isolation

When tested in isolation, we find that our two methods (MLR and NN) are competitive when compared with general methods (Section 3.5, Table 3 and Figure 4), for both BRCA1 and BRCA2. In particular, their specificities are among the best, a property desirable from the point of view of HBOC diagnosis requirements (Ernst et al., 2018); they also have the best balances between specificity and sensitivity, with the only exception of PMut in BRCA1, which has slightly better figures for the MLR training set. General methods also show good success rates in our training sets (Figure 4), in contrast with the usually lower performance estimates cited in the literature. For example, the last version of PMut displays an MCC of 0.31 for both BRCA1 (63 variants) and BRCA2 (104 variants) (López-Ferrando, Gazzo, De La Cruz, Orozco, & Gelpí, 2017). In the same work, we find MCC values for other tools, computed on the same dataset: for BRCA1 they vary between 0.17 (PROVEAN) and 0.38 (LRT); for BRCA2 they vary between 0.01 (PROVEAN) and 0.19 (Mutation Assessor). In a previous study, using a small dataset of BRCA2 variants, Karchin et al. (Karchin, Agarwal, Sali, Couch, & Beattie, 2008) find that general tools display good sensitivities but low specificities. A similar trend has been recently reported by Ernst et al. (Ernst et al., 2018), after testing PolyPhen-2, SIFT, AlignGVGD and MutationTaster2 in a set of 236 BRCA1/2 variants. These authors express concern about the moderate performance observed, particularly about the low specificities observed relative to HBOC diagnosis requirements (e.g., PolyPhen-2: 0.67 and 0.72 for BRCA1 and BRCA2, respectively). We believe that our higher estimates for general predictors (Table 3 and Figure 4), relative to those in the literature, may partly result from the overlap between their training sets and our manually curated dataset.

Presently, stand-alone use of in silico methods for HBOC diagnosis is discouraged (Ernst et al., 2018). Nonetheless, it is considered that these methods can be fruitfully combined with the results of functional assays, to provide an alternative to multifactorial models in the absence of family information (Guidugli et al., 2018). The tools presented in this work are amenable to this type of approach because of their extreme simplicity and interpretability. This is a consequence of the small number of features utilized (3 and 6 for MLR and NN, respectively) and of the low complexity of our models (Riera et al., 2014). Additionally, our MLR models allow a direct interpretation of a variant’s impact at the molecular level, because they produce estimates of the HDR assay for the target variant. In this sense, the MLR approach resembles that of Starita et al. (Starita et al., 2015) who estimate HDR values using the results of other functional assays (E3 ligase scores and BARD1-binding scores). In our case, we use instead a few sequence-based features, with two conservation measures (Shannon’s entropy and psssm_nat) standing among them given their recognized predictive power (C. Ferrer-Costa et al., 2004). Conceptually, this makes MLR methods an implementation of the idea of addressing pathogenicity prediction problems focusing on endophenotypes, rather than on clinical phenotypes. Endophenotypes are quantitative measures of intermediate phenotypes with clinical relevance (Masica & Karchin, 2016); they are closer to the genotype and, for this reason, may result in predictors with high success rates, given the small contribution of genetic background and environmental effects to the outcome of the variant. In general, this is the case when looking at clinical performance (Table 3, Figure 4). However, for BRCA1, the sensitivity (0.62) is low compared to specificity (0.87); while this may be a consequence of the discretization of the HDR prediction, it may also be a consequence of the extreme simplicity of our model. When testing the MLR model with SGE data we observe a significant correlation (Spearman’s ρ=0.47, p-value~0), comparable to that of Align-GVGD (ρ=0.46) and better than that of CADD (ρ=0.40), PhyloP (ρ=0.36), SIFT (ρ=0.36) and PolyPhen-2 (ρ=0.28) (values obtained from (Findlay et al., 2018), Extended Data Figure 9). However, visual inspection shows the presence of substantial deviations from a monotonic relationship (Figures 3A, 3B). If we analyze the population of outliers using PCA and value distributions of the features in our model (Supp. Figure S1) we see that, generally, they have an intermediate behavior between ‘functional’ and ‘non-functional’ variants for all features. This points to an aspect of the variant’s impact that is poorly represented by our present set of features, like the effect of the mutation in RNA levels.

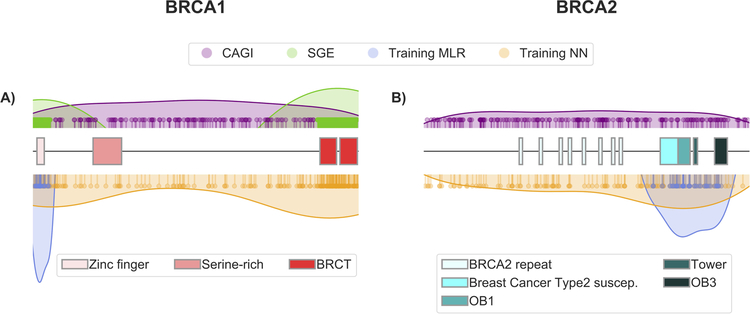
Finally, it is worth mentioning that our MLR predictors have been trained with small sets of variants that are concentrated in a reduced region of BRCA1 and BRCA2 (Figure 6). This is in contrast with the broader range of positions covered by the NN and the CAGI datasets. The fact that, in spite of this situation, the MLR tools are competitive suggests that they capture some general effect of variants on protein function/structure, like impact on stability (Yue, Li, & Moult, 2005).

Figure 6. Distribution of the variants along the BRCA1 and BRCA2 sequences.

Each variant dataset used in this work is represented with a set of pins (indicating the location of each variant) and a colored surface that provides a general, smoothed view of the distribution. The different functional domains in each structure are represented with boxes; for representation purposes, BRCA1 (1863 aa) and BRCA2 (3418 aa) are displayed with the same length. The color codes for the different sets are: CAGI (lilac), SGE (green), MLR training (blue) and NN training (orange).

4.2. The performance of BRCA1- and BRCA2-specific predictors in the CAGI 5 experiment

The ENIGMA challenge within the CAGI experiment provides a good opportunity to independently validate the performance of pathogenicity predictors for BRCA1/2. Two aspects are specific of the ENIGMA challenge. First, if some of the target variants are pathogenic, the participants do not know what molecular effect originates their pathogenicity: it can be the impact on protein function, but it can also be the impact on splicing (Eccles et al., 2015). For this reason, we decided to combine predictions for these two effects in our protocol (Figure 1). A second, distinctive aspect of the challenge is that the submissions had to provide the predicted IARC 5-tier class for each variant (see Section 2.1). This is relevant since this classification is strongly related to the clinical actions associated to each class (Goldgar et al., 2008; Moghadasi et al., 2016; Plon et al., 2008) which are in turn related to factors such as impact on the counselee or cost to the healthcare system. Collective consideration of these factors crystallizes into five decision regions (Plon et al., 2008) that are applied to the posterior probability of pathogenicity, a probability obtained after integrating different sources of clinical/biomedical evidence. In our case, this probability was estimated using only molecular information; nonetheless, to adapt our output to the CAGI requirements we directly applied the ENIGMA boundaries (Section 2.3.1.4 and 2.3.2.1). We computed our performances on the basis of this assignment; however, we also obtained the performances for a simplified version of the ENIGMA classification, separately collapsing its neutral and pathogenic classes (Table 2).

Assessment of the results obtained (Figure 5, Supp. Figure S2, Tables 4 and 5) shows some clear trends. For the 5-class problem, all the methods (both ours and the general methods) have poor per class performances; however, our methods are more successful at reproducing the compositional bias of the sample and outperform general methods for the most abundant classes (1 and 2) in BRCA1/2, with only one exception, for class 2 in BRCA2, both PolyPhen-2 and PMut surpass MLR+AS; our methods also have a better distribution of wrong predictions among classes, because they tend to cluster nearby the correct class. These trends are reinforced when reducing the number of classes from five to three. Overall, the results for the CAGI challenge show that our methods can identify low-risk variants with an accuracy higher than that of general methods, a desirable property for HBOC diagnosis (Ernst et al., 2018). Part of this improved performance could be attributed to an unequal effect of applying the ENIGMA decision boundaries to the posterior probability generated by general methods. We believe that this mapping procedure may play a role, but not a determining one since comparison of the original, binary predictions of the general methods with those of the binary versions of our tools (MLR scores binarized as explained in Section 3.2) gives a similar result (Table 6) again. MLR+AS has the top specificities for BRCA1/2 and high sensitivities; NN+AS has the same sensitivities but lower specificities, nonetheless these are only surpassed by PMut.

Table 5.

Overall accuracies (ACC) and MCC for our two methods (MLR and NN, with and without splicing) and the general methods (PMut, PolyPhen-2, PON-P2, and SIFT) in the CAGI dataset.

(A) BRCA1
IARC 5-tier	MLR	MLR+AS	NN	NN+AS	PMut	PolyPhen-2	PON-P2	SIFT
ACC	0.326	0.347	0.201	0.222	0.028	0.208	0.014	0.049
MCC	−0.041	0.006	0.015	0.056	−0.002	0.031	0	0.021
Three Class	MLR	MLR+AS	NN	NN+AS	PMut	PolyPhen-2	PON-P2	SIFT
ACC	0.764	0.785	0.25	0.271	0.035	0.354	0.014	0.118
MCC	−0.237	0.354	−0.012	0.055	0.026	0.136	0	0.123

(B) BRCA2
IARC 5-tier	MLR	MLR+AS	NN	NN+AS	PMut	PolyPhen-2	PON-P2	SIFT
ACC	0.161	0.167	0.345	0.351	0.144	0.305	0.011	0.034
MCC	−0.109	−0.068	−0.017	−0.006	−0.029	0.078	0	0.017
Three Class	MLR	MLR+AS	NN	NN+AS	PMut	PolyPhen-2	PON-P2	SIFT
ACC	0.931	0.931	0.69	0.695	0.184	0.431	0.011	0.086
MCC	0.18	0.277	0.185	0.213	−0.013	0.125	0	0.022

Table 6.

Binary performances (sensitivities and specificities) for our predictors and the general predictors (PMut, PolyPhen-2, PON-P2, SIFT).

(A) BRCA1
	MLR+AS	NN+AS	CADD	PMut	PolyPhen-2	PON-P2	SIFT
Sensitivity (P = 11)†	0.909	0.909	1	0.818	0.727	1	1
Specificity (N = 131)‡	0.977	0.718	0.456	0.817	0.557	0.188	0.435

(B) BRCA2
	MLR+AS	NN+AS	CADD	PMut	PolyPhen-2	PON-P2	SIFT
Sensitivity (P = 5)†	0.8	0.8	1	0.6	1	1	0.8
Specificity (N = 167)‡	0.97	0.886	0.533	0.958	0.653	0.625	0.731

^†P: pathogenic;

^‡N: neutral

In summary, we have applied the protein-specific approach to building a pathogenicity predictor for BRCA1/2 variants, using either clinical phenotypes or endophenotypes. The results obtained from our methods indicate that this approach can contribute to improve our ability to discriminate between high- and low-risk variants for BRCA1/2. Of particular interest is the MLR+AS tool, because it gives an estimate of the molecular impact of a sequence replacement that is easy to interpret since it corresponds to an in silico version of the HDR assay. Participation in the CAGI experiment has allowed us to obtain independent estimates of the performance of our predictors, to compare them with other predictors and to help us clarify the classification level at which in silico tools could be useful for HBOC diagnosis. This participation has also underlined the role that splicing predictions can play in the correct annotation of BRCA1/2 variants, particularly when integrated in protocols that combine different views of a variant’s impact.

Table 1B.

Overlap between datasets (CAGI: missense + AS)

	NN-CAGI	MLR-CAGI	MLR-SGE†
BRCA1	18 (P=7/N=11)‡	2	28
BRCA2	5 (P=2/N=3)‡	4	-

^†Dataset extracted from Findlay et al., 2018. SGE: saturation genome editing.

^‡P: pathogenic; N: neutral