Anisotropic magnetocaloric effect in Fe_3−xGeTe₂

Abstract

We present a comprehensive study on anisotropic magnetocaloric porperties of the van der Waals weak-itinerant ferromagnet Fe_3−xGeTe₂ that features gate-tunable room-temperature ferromagnetism in few-layer device. Intrinsic magnetocrystalline anisotropy is observed to be temperature-dependent and most likely favors the long-range magnetic order in thin Fe_3−xGeTe₂ crsytal. The magnetic entropy change ΔS_M also reveals an anisotropic characteristic between H//ab and H//c, which could be well scaled into a universal curve. The peak value $-\mathrm{\Delta }{S}_M^{\mathit{max}}$ of 1.20 J kg⁻¹ K⁻¹ and the corresponding adiabatic temperature change ΔT_ad of 0.66 K are deduced from heat capacity with out-of-plane field change of 5 T. By fitting of the field-dependent parameters of $-\mathrm{\Delta }{S}_M^{\mathit{max}}$ and the relative cooling power RCP, it gives $-\mathrm{∆}{S}_M^{\mathit{max}}$ ∝ Hⁿ with n = 0.603(6) and RCP ∝ H^m with m = 1.20(1) when H//c. Given the high and tunable T_c, Fe_3−xGeTe₂ crystals are of interest for fabricating the heterostructure-based spintronics device.

Introduction

Intrinsic long-range ferromagnetism recently achieved in two-dimensional-limit van der Waals (vdW) crystals opens up great possibilities for both studying fundamental two-dimensional (2D) magnetism and engineering novel spintronic vdW heterostuctures^1–5. Fe₃GeTe₂ is a promising candidate since its Curie temperature (T_c) in bulk is high and depends on the concentration of Fe atoms, ranging from 150 to 230 K^6–11. Intrinsic magnetocrystalline anisotropy in few-layer counteracts thermal fluctuation and favors the 2D long-range ferromagnetism with a lower T_c of 130 K⁵. Most significantly, the T_c can be ionic-gate-tuned to room temperature in few-layers which is of high interest for electrically controlled magnetoelectronic devices¹².

The layered Fe_3−xGeTe₂ displays a hexagonal structure belonging to the P6₃/mmc space group, where the 2D layers of Fe_3−xGe sandwiched between nets of Te ions are weakly connected by vdW bonding [Fig. 1(a)]⁶. There are two inequivalent Wyckoff positions of Fe atoms which are denoted as Fe1 and Fe2. The Fe1-Fe1 dumbbells are situated in the centre of the hexagonal cell in the honeycomb lattice, composed of covalently bonded Fe2-Ge atoms. No Fe atoms occupy the interlayer space and Fe vacancies only occur in the Fe2 sites¹³. Local atomic environment is also studied by the Mössbauer and X-ray absorption spectroscopies^14,15. Partially filled Fe d orbitals results in an itinerant ferromagnetism in Fe_3−xGeTe₂¹⁶, which exhibits exotic physical phenomena such as nontrivial anomalous Hall effect^17–19, Kondo lattice behavior²⁰, strong electron correlations²¹, and unusual magnetic domain structures^22,23. A second-step satellite transition T^* is also observed just below T_c, and is not fully understood^10,15.

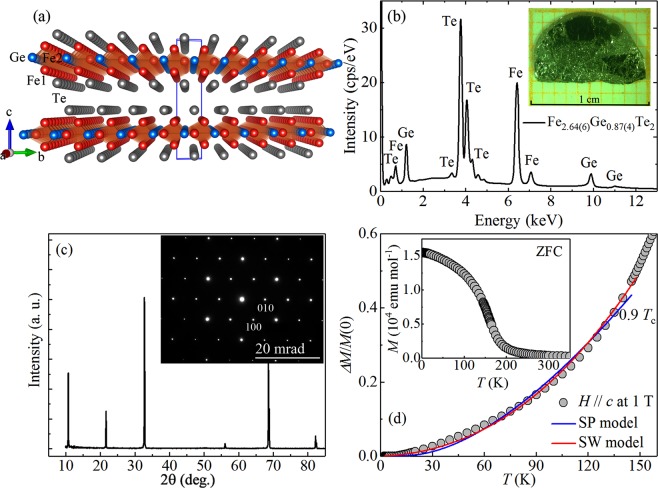
Figure 1.

(a) Crystal structure and (b) X-ray energy-dispersive spectrum of Fe_3−xGeTe₂ single crystal. Inset shows a photograph of Fe_3−xGeTe₂ single crystal on a 1 mm grid. (c) X-ray diffraction (XRD) pattern of Fe_3−xGeTe₂. Inset shows the electron diffraction pattern taken along the [001] zone axis direction. (d) Temperature dependence of the reduced magnetization with out-of-plane field of Fe_3−xGeTe₂ fitted using spin-wave (SW) model and single-particle (SP) model. Inset shows the temperature dependence of zero-field-cooling (ZFC) magnetization of Fe_3−xGeTe₂ measured at H = 1 T applied along the c axis.

Here we address the anisotropy in Fe_3−xGeTe₂ as well as the magnetocaloric effect investigated by heat capacity and dc magnetization measurements. The magnetocrystalline anisotropy is observed to be temperature-dependent. The magnetic entropy change ΔS_M(T, H) also reveals an anisotropic characteristic and could be well scaled into a universal curve. Moreover, the $-\mathrm{\Delta }{S}_M^{\mathit{max}}$ follows the power law of Hⁿ with n = 0.603(6), and the relative cooling power RCP depends on H^m with m = 1.20(1).

Methods

High quality Fe_3−xGeTe₂ single crystals were synthesized by the self-flux technique¹⁴. The element analysis was performed using energy-dispersive X-ray spectroscopy (EDX) in a JEOL LSM-6500 scanning electron microscope (SEM). The selected area electron diffraction pattern was taken via a double aberration-corrected JEOL-ARM200F operated at 200 kV. The dc magnetization and heat capacity were measured in Quantum Design MPMS-XL5 and PPMS-9 systems with the field up to 5T.

Results and Discussion

The average stoichiometry of our flux-grown Fe_3−xGeTe₂ single crystals was determined by examination of multiple points. The actual concentration is determined to be Fe_2.64(6)Ge_0.87(4)Te₂ [Fig. 1(b)], and it is referred to as Fe_3−xGeTe₂ throughout this paper. The as-grown single crystals are mirror-like and metallic platelets with the crystallographic c axis perpendicular to the platelet surface with dimensions up to 10 millimeters [inset in Fig. 1(b)]. In the 2θ X-ray diffraction pattern [Fig. 1(c)], only the (00l) peaks are detected, confirming the crystal surface is normal to the c axis. The corresponding electron diffraction pattern [inset in Fig. 1(c)] also confirms the high quality of single crystals.

Figure 1(d) presents the low temperature thermal demagnetization analysis for Fe_3−xGeTe₂ with out-of-plane field using both spin-wave (SW) model and single-particle (SP) model. The temperature dependence of zero-field-cooling (ZFC) magnetization M(T) for Fe_3−xGeTe₂ measured in H = 1 T applied along the c axis is shown in the inset of Fig. 1(d). Localized-moment spin-wave excitations can be described by a Bloch equation^24–26:

$$\frac{\mathrm{\Delta }M}{M(0)}=\frac{M(0)-M(T)}{M(0)}=A{T}^{3/2}+B{T}^{5/2}+\cdots ,$$ 1

where A and B are the coefficients. The M(0) is the magnetization at 0 K, which is usually estimated from the extrapolation of M(T). The T ^3/2 term stems from harmonic contribution and the T^5/2 term is a high-order contribution in spin-wave dispersion relation. In an itinerant magnetism, it is a result of excitation of electrons from one subband to the other. The single-particle excitation is²⁴:

$$\frac{\mathrm{\Delta }M}{M(0)}=\frac{M(0)-M(T)}{M(0)}=C{T}^{3/2}exp\frac{-\mathrm{\Delta }}{k_{B}T},$$ 2

where C, Δ and k_B are fit coefficient, the energy gap between the Fermi level and the top of the full subband and the Boltzmann constant, respectively. It can be seen that the SW model gives a better fit than the SP model up to 0.9 T_c [Fig. 1(d)], indicating possible localized moment, in agreement with the bad-metallic resistivity of Fe_3−xGeTe₂¹⁵. It is also understandable that the SP model fails due to strong electron correlation in Fe_3−xGeTe₂²¹. The fitting yields A = 8.4(7) × 10⁻⁵ K^−3/2, B = 1.24(5) × 10⁻⁶ K^−5/2, C = 3.4(1) × 10⁻⁴ K^−3/2 and Δ = 3.9(4) meV.

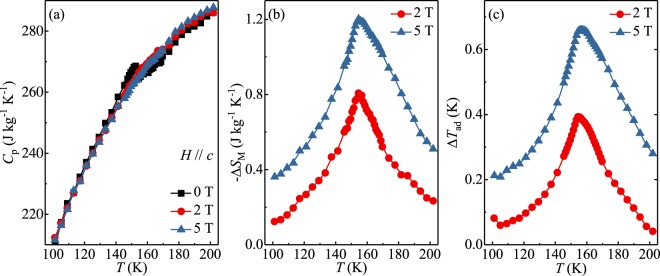
Figure 2(a) shows the temperature dependence of heat capacity C_p for Fe_3−xGeTe₂ measured in zero-field and out-of-plane field of 2 and 5 T, respectively. The ferromagnetic order anomaly at T_c = 153 K in the absence of magnetic field is gradually suppressed in fields. The entropy S(T, H) can be determined by

$$S(T,H)={\int }_0^T\frac{C_p(T,H)}{T}dT.$$ 3

Figure 2.

Temperature dependences of (a) the specific heat C_p, (b) the magnetic entropy change −ΔS_M, and (c) the adiabatic temperature change ΔT_ad for Fe_3−xGeTe₂ with out-of-plane field changes of 2 and 5T.

The magnetic entropy change ΔS_M(T, H) can be approximated as ΔS_M(T, H) = S_M(T, H) − S_M(T, 0). In addition, the adiabatic temperature change ΔT_ad caused by the field change can be derived by ΔT_ad(T, H) = T(S, H) − T(S, 0) at constant total entropy S(T, H). Figure 2(b,c) present the temperature dependence of −ΔS_M and ΔT_ad estimated from heat capacity with out-of-plane field. They are asymmetric and attain a peak around T_c. The maxima of −ΔS_M and ΔT_ad increase with increasing field and reach the values of 1.20 J kg⁻¹ K⁻¹ and 0.66 K, respectively, with the field change of 5 T. Since a large magnetic anisotropy is observed in Fe_3−xGeTe₂, it is of interest to further calculate its anisotropic magnetic entropy change.

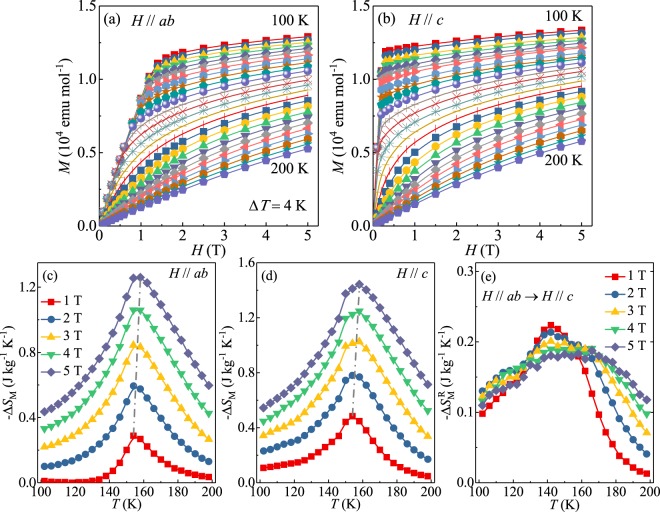
Figure 3(a,b) present the magnetization isotherms with field up to 5 T applied in the ab plane and along the c axis, respectively, in temperature range from 100 to 200 K with a temperature step of 4 K. The magnetic entropy change can be obtained from dc magnetization measurement as²⁷:

$$\mathrm{\Delta }{S}_M(T,H)={\int }_0^H{\left[\frac{\partial S(T,H)}{\partial H}\right]}_{T}dH.$$ 4

Figure 3.

Initial isothermal magnetization curves from T = 100 to 200 K with temperature step of T = 4 K measured with (a) in-plane and (b) out-of-plane fields. Temperature dependence of magnetic entropy change −ΔS_M obtained with (c) in-plane and (d) out-of-plane field changes, and (e) the difference −$\mathrm{\Delta }{S}_M^R$.

With the Maxwell’s relation ${\left[\frac{\partial S(T,H)}{\partial H}\right]}_T$ = ${\left[\frac{\partial M(T,H)}{\partial T}\right]}_H$, it can be rewritten as²⁸:

$$\mathrm{\Delta }{S}_M(T,H)={\int }_0^H{\left[\frac{\partial M(T,H)}{\partial T}\right]}_{H}dH.$$ 5

When the magnetization is measured at small temperature and field steps, ΔS_M(T, H) is approximated:

$$\mathrm{\Delta }{S}_M(T,H)=\frac{{\int }_0^{H}M(T+\mathrm{\Delta }T)dH-{\int }_0^{H}M(T)dH}{\mathrm{\Delta }T}.$$ 6

Figure 3(c,d) show the calculated −ΔS_M(T, H) as a function of temperature in various fields up to 5 T applied in the ab plane and along the c axis, respectively. All the −ΔS_M(T, H) curves feature a pronounced peak around T_c, similar to those obtained from heat capacity [Fig. 2(b)], and the peak broadens asymmetrically on both sides with increase in field. Moreover, the value of −ΔS_M(T, H) increases monotonically with increase in field; the peak −ΔS_M reaches 1.26 J kg⁻¹ K⁻¹ with in-plane field change and 1.44 J kg⁻¹ K⁻¹ with out-of-plane change of 5 T, respectively. We calculated the rotating magnetic entropy change $\mathrm{\Delta }{S}_M^R$ as

$$\mathrm{\Delta }{S}_M^R(T,H)=\mathrm{\Delta }{S}_M(T,H_c)-\mathrm{\Delta }{S}_M(T,H_{ab}).$$ 7

The asymmetry of −ΔS_M(T, H) is more apparent in the temperature dependence of −$\mathrm{\Delta }{S}_M^R$ [Fig. 3(e)]. Furthermore, there is a slight shift of −ΔS_M maximum towards higher temperature when the field varies from 1 to 5 T [Fig. 3(c,d)]. This shift of T_peak excludes the mean field model but could be reproduced by the Heisenberg model due to its discrepancy with T_c²⁹.

Around the second order phase transition³⁰, the magnetic entropy maximum change is $-\mathrm{\Delta }{S}_M^{\mathit{max}}$ = aH^n 31, where a is a constant and n is³²

$$n(T,H)=dln|\mathrm{\Delta }{S}_M|/dln(H).$$ 8

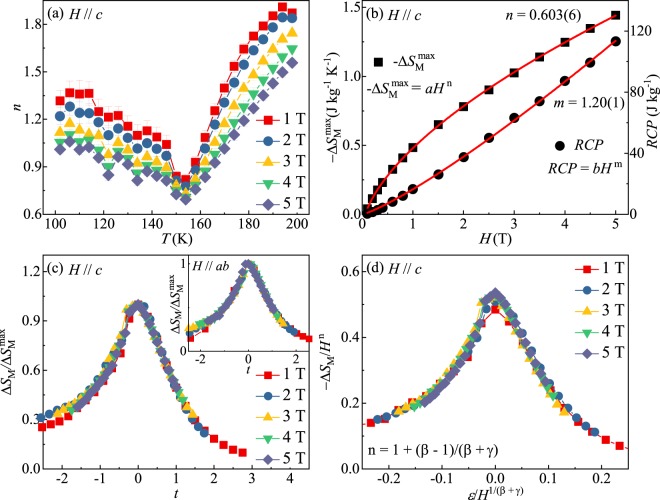
Figure 4(a) shows the temperature dependence of n(T) in various fields. All the n(T) curves follow an universal behavior³³. At low temperatures, n has a value close to 1. At high temperatures, n tends to 2 as a consequence of the Curie-Weiss law. At T = T_c, n has a minimum. Additionally, the exponent n at T_c is related to the critical exponents³⁰:

$$n(T_c)=1+\left(\frac{\beta -1}{\beta +\gamma }\right)=1+\frac{1}{\delta }\left(1-\frac{1}{\beta }\right),$$ 9

Figure 4.

(a) Temperature dependence of n in various fields. (b) Field dependence of the maximum magnetic entropy change $-\mathrm{\Delta }{S}_M^{\mathit{max}}$ and the relative cooling power RCP with power law fitting in red solid lines. (c) The normalized ΔS_M as a function of the rescaled temperature t with out-of-plane field and in-plane field (inset). (d) Scaling plot based on the critical exponents β = 0.372 and γ = 1.265¹⁴.

where β, γ, and δ are the critical exponents related to the spontaneous magnetization M_s below T_c, the inverse initial susceptibility H/M above T_c, and the isotherm M(H) at T_c, respectively.

Relative cooling power (RCP) could be used to estimate the cooling efficiency³⁴:

$$RCP=-\mathrm{\Delta }{S}_M^{max}\times \delta T_{FWHM},$$ 10

where $-\mathrm{\Delta }{S}_M^{\mathit{max}}$ is the entropy change maximum around T_c and δT_FWHM is the width at half maximum. The RCP also depends on the field as RCP = bH^m, where b is a constant and m is related to the critical exponent δ:

$$m=1+\frac{1}{\delta }.$$ 11

Figure 4(b) presents the field-dependent $-\mathrm{\Delta }{S}_M^{\mathit{max}}$ and RCP. The RCP is 113.3 J kg⁻¹ within field change of 5 T for Fe_3−xGeTe₂. This is one half of those in manganites and much lower than in ferrites^35,36. Fitting of the $-\mathrm{\Delta }{S}_M^{\mathit{max}}$ and RCP gives n = 0.603(6) and m = 1.20(1), which are close to the values estimated from the critical exponents (Table 1).

Table 1.

Critical exponents of Fe_3−xGeTe₂¹⁴. The MAP, KFP and CI represent the modified Arrott plot, the Kouvel-Fisher plot and the critical isotherm, respectively.

Technique	β	γ	δ	n	m
$-\mathrm{\Delta }{S}_M^{\mathit{max}}$				0.603(6)
RCP					1.20(1)
MAP	0.374(1)	1.273(8)	4.404(12)	0.620(1)	1.227(1)
KFP	0.372(4)	1.265(15)	4.401(6)	0.616(2)	1.227(1)
CI			4.50(1)		1.222(1)

The scaling of magnetocaloric data is constructed by normalizing all the −ΔS_M curves against the maximum $-\mathrm{\Delta }{S}_M^{\mathit{max}}$, namely, ΔS_M/$\mathrm{\Delta }{S}_M^{\mathit{max}}$ by rescaling the temperature t below and above T_c as defined in:

$$t_{-}=(T_{peak}-T)/(T_{r1}-T_{peak}),T<T_{peak},$$ 12

$$t_{+}=(T-T_{peak})/(T_{r2}-T_{peak}),T>T_{peak},$$ 13

where T_r1 and T_r2 are the temperatures of two reference points corresponding to $\mathrm{\Delta }{S}_M(T_{r1},T_{r2})=\frac{1}{2}\mathrm{\Delta }{S}_M^{max}$³⁷. All the −ΔS_M(T, H) curves collapse onto a single curve regardless of temperature and field, as shown in Fig. 4(c). In the phase transition region, the scaling analysis of −ΔS_M can also be expressed as

$$\frac{-\mathrm{\Delta }{S}_M}{a_M}=H^{n}f\left(\frac{\epsilon }{H^{1/\mathrm{\Delta }}}\right),$$ 14

where a_M = T_c⁻¹A^δ+1B with A and B representing the critical amplitudes as in M_s(T) = A(−ε)^β and H = BM^δ, Δ = β + γ, and f(x) is the scaling function³⁸. If the critical exponents are appropriately chosen, the −ΔS_M(T) curves should be rescaled into a single curve, consistent with normalizing all the −ΔS_M curves with two reference temperatures. By using the values of β = 0.372 and γ = 1.265 obtained by the Kouvel-Fisher plot¹⁴, we have replotted the scaled −ΔS_M for Fe_3−xGeTe₂ [Fig. 4(d)]. The good overlap of the experimental data points clearly indicates that the obtained critical exponents for Fe_3−xGeTe₂ are not only in agreement with the scaling hypothesis but also intrinsic.

Then we estimated the magnetocrystalline anisotropy of Fe_3−xGeTe₂. By using the Stoner-Wolfarth model a value for the magnetocrystalline anisotropy constant K_u can be estimated from the saturation regime in isothermal magnetization curves [Fig. 5(a)]³⁹. Within this model the magnetocrystalline anisotropy in the single domain state is related to the saturation magnetic field H_s and the saturation moment M_s with μ₀ is the vacuum permeability:

$$\frac{2K_u}{M_s}={\mu }_0{H}_{sat}.$$ 15

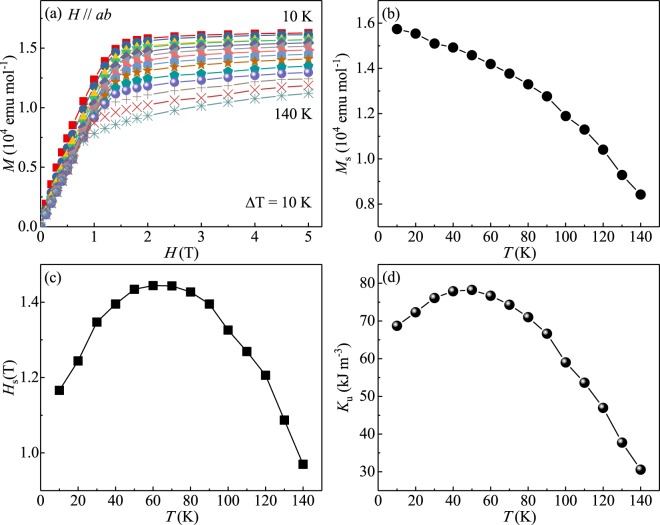
Figure 5.

(a) Initial isothermal magnetization curves from T = 10 to 140 K with in-plane fields. Temperature evolution of (b) the saturation magnetization M_s, (c) the saturation field H_s, and (d) the anisotropy constant K_u.

When H//ab, the anisotropy becomes maximal. We estimated the saturation magnetization M_s by using a linear fit of M(H) above a magnetic field of 2.5 T with in-plane field [Fig. 5(b)], which monotonically decreases with increasing temperature. Then we determined the saturation field H_s as the intersection point of two-linear fits, one being a fit to the saturated regime at high fields and one being a fit of the unsaturated linear regime at low fields. The value of H_s increases at low temperature, which is possibly related to a spin reorientation transition¹⁵, and then decreases with increasing temperature [Fig. 5(c)]. Figure 5(d) presents the temperature evolution of K_u for Fe_3−xGeTe₂, which can not be described by the l(l + 1)/2 power law^40,41. The value of K_u for Fe_3−xGeTe₂ is about 69 kJ cm⁻³ at 10 K, slightly increases to 78 kJ cm⁻³ at 50 K, and then decrease with increasing temperature, which are comparable to those for CrBr₃, but smaller than those for CrI₃⁴². The decrease of K_u with increasing temperature is also observed in CrBr₃ and CrI₃⁴², arising from a large number of local spin clusters^43,44. In a pure two-dimensional system, materials with isotropic short-range exchange interactions can not magnetically order. The long-range ferromagnetism in few-layers of Fe_3−xGeTe₂ could possibly be favored by the large magnetocrystalline anisotropy.

Conclusion

In summary, we have investigated in detail the magnetocaloric effect of Fe_3−xGeTe₂ single crystals. The large magnetocrystalline anisotropy is found to be temperature-dependent and probably establishes the long-range ferromagnetism in few-layers of Fe_3−xGeTe₂. The magnetic entropy change −ΔS_M also reveals an anisotropic characteristic and could be well scaled into a universal curve independent on temperature and field. By fitting of the field-dependent parameters of $-\mathrm{\Delta }{S}_M^{\mathit{max}}$ and the relative cooling power RCP, it gives $-\mathrm{\Delta }{S}_M^{\mathit{max}}$∝Hⁿ with n = 0.603(6) and RCP ∝ H^m with m = 1.20(1) when H//c. Considering its tunable room-temperature ferromagnetism and hard magnetic properties in nanoflakes, further investigation on the size dependence of magnetocaloric effect is of interest.

Author Contributions

Y.L. and C.P. designed this study and synthesized crystals; Y. L. performed magnetization and heat capacity measurements. J.L., J.T. and Y.Z. contributed TEM measurement. Y.L. and C.P. organized and wrote the paper with input from all collaborators. This manuscript reflects the contribution and ideas of all authors.

Competing Interests

The authors declare no competing interests.