S(-) and R(+) species derived from antihistaminic promethazine agent: structural and vibrational studies

Abstract

Structural and vibrational properties of free base, cationic and hydrochloride species derived from both S(-) and R(+) enantiomers of antihistaminic promethazine (PTZ) agent have been theoretically evaluated in gas phase and in aqueous solution by using the hybrid B3LYP/6-31G* calculations. The initial structures of S(-) and R(+) enantiomers of hydrochloride PTZ were those polymorphic forms 1 and 2 experimentally determined by X-ray diffraction. Here, all structures in aqueous solution were optimized at the same level of theory by using the polarized continuum (PCM) and the universal solvation model. As was experimentally reported, variations in the unit cell lead to slight energy, density, and melting point differences between the two forms but, this behavior is not carried through in isotropic condition, like in solution with non-chiral solvents. Hence, the N–C distances, Mulliken, atomic natural population (NPA) and Merz-Kollman (MK) charges, bond orders, stabilization and solvation energies, frontier orbitals, some descriptors and their topological properties were compared with the antihistaminic cyclizine agent. The frontier orbitals studies show that the free base species of both forms in solution are more reactive than cyclizine. Higher electrophilicity indexes are observed in the cationic and hydrochloride species of PTZ than cyclizine while the cationic species of cyclizine have higher nucleophilicity index than both species of PTZ. The presences of bands attributed to cationic species of both enantiomers are clearly supported by the infrared and Raman spectra in the solid phase. The expected 114, 117 and 120 vibration normal modes for the free base, cationic and hydrochloride species of both forms were completely assigned and the force constants reported. Reasonable concordances among the predicted infrared, Raman, UV-Vis and Electronic Circular Dichroism (ECD) with the corresponding experimental ones were found.

1. Introduction

Species containing in their structures the N–CH₃ group presenting a wide range of pharmacological and medicinal properties such as tropane alkaloids whose known biologics effects can cause from pain cure up to addiction [1, 2, 3, 4, 5, 6, 7]. However, there are another groups of species that also contain that group but that present other different biological properties such as, diphenhydramine and cyclizine, where both species are broadly used in pharmacology as antihistaminic agents [8, 9]. Nevertheless, the most remarkable differences among the free base, cationic and hydrochloride species of those two antihistaminic agents are that in the species derived from diphenhydramine their two N–CH₃ groups are not linked to rings while in the cyclizine species those groups are linked to piperazine rings [8, 9]. Previous theoretical studies on structures and properties of alkaloids have evidenced that when the N–CH₃ group is linked to fused rings as in scopolamine, cocaine and tropane some properties are slightly different from those where the N–CH₃ group is linked to only one ring as in heroin and morphine [1, 2, 3, 5, 6, 7]. Besides, the stabilities of these series of alkaloids are strongly dependent on the N–C distances [6, 7]. On the other hand, the reactivities predicted for the three species of diphenhydramine practically are the same than that reported for cationic form of cocaine [3, 7] while lowest solvation energy value was observed for the free base of cyclizine, as compared with the corresponding to tropane alkaloids [9]. Evidently, there is an important connection between the quantity of N–CH₃ groups and the type of groups linked to N atom, that is, >N- tertiary or >N< quaternary. Consequently, the biological activities and effects of these types of species on human health are obviously resulted of their nature and structural, electronic and topological properties. Hence, the interest to study another antihistaminic agent, in this case promethazine (PTZ) [10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33], which has two N–CH₃ groups (as diphenhydramine) linked to a chiral carbon and, as a consequence two enantiomeric S and R structures are expected for their three free base, cationic and hydrochloride species. PTZ hydrochloride is a drug used to treatment of nausea, vomiting, and dizziness associated with motion sickness and, besides possesses anti-pruritic, anti-allergic, anticholinergic, antihistaminic, central nervous system depressant, and with general anaesthetics effects. Their metabolic and clinic effects were studied from long time together with their side effects [13, 29, 30, 31, 32, 33]. Some known chemical names of promethazine are proazamine, diphergan, phenargan or phensedyl while its IUPAC name is N,N-dimethyl-1-phenothiazin-10-ylpropan-2-amine. PTZ has structurally two >N–CH₃ groups, three fused six members rings (two phenyl and one phenothiazine) and a chiral carbon and where experimentally Borodi et al [19] have determined by X-ray diffraction two enantiomeric disordered structures of promethazine hydrochloride but, so far, the structural properties and vibrational assignments of those three species of PTZ were not published. The vibrational analyses of the three species of PTZ are actually of great interest and significance taking into account that the infrared, Raman and SERS spectroscopies are practically the most used spectroscopic techniques to identify these species in different systems and preparations [10, 12, 15, 17, 22, 23, 24, 25, 26, 27, 28]. Hence, the aims of this work are: (i) to study the structural, electronic, topological and vibrational properties of free base, cationic and hydrochloride species of S(-) and R(+)-PTZ, (ii) to find some correlations between their properties that can explain the differences between its biological properties, as compared with alkaloids and other antihistaminic agents, (iii) to perform the complete vibrational assignments of those three species of PTZ because, so far, these are not reported. In accordance to previous studies, the infrared spectra of many hydrochloride species show clearly the presence of their cationic forms in the solid phase and in aqueous solution [1, 2, 3, 5, 7, 8]. To achieve those purposes, the theoretical structures of free base, cationic and hydrochloride species of both S(-) and R(+)-PTZ enantiomers were optimized in gas phase and in aqueous solution by using the hybrid B3LYP/6-31G* method [34, 35] while experimental infrared and Raman spectra available from the literature were used to perform the vibrational analyses [17, 24, 25, 26, 27, 28]. The studies in solution were performed with the integral equation formalism variant polarised continuum method (IEFPCM) because it scheme contemplates the solvent effects while the solvation energies were computed with the universal solvation model [36, 37, 38]. Hence, for those three S(-) and R(+)-PTZ species, atomic charges, molecular electrostatic potential, bond orders, frontier orbitals and topological properties were calculated together with the harmonic force fields by using the scaled quantum mechanical force field (SQMFF) and transferable scaling factors [39, 40]. Then, the complete assignments for the three species were performed by using the corresponding force fields, internal normal coordinates and the experimental available vibrational spectra of PTZ hydrochloride [41] together with the Molvib program [42]. Taking into account the wide range of biological activities that presents PTZ, the reactivities and behaviours of those three S(-) and R(+)-PTZ species were predicted in both media by using the frontier orbitals [43, 44] and global descriptors [45, 46, 47, 48, 49, 50, 51, 52, 53]. Finally, the predicted properties of both enantiomeric series of S(-) and R(+)-PTZ were evaluated and then compared with the available data reported for alkaloids, diphenhydramine and cyclizine [1, 2, 3, 4, 5, 6, 7, 8, 9].

2. Methodology

2.1. Ab-initio calculations

The initial structure of S(-) enantiomer of PTZ hydrochloride was that experimental polymorphic form 1 determined by X-ray diffraction by Borodi et al [19] and taken from the available CIF file. The corresponding cationic and free base species were modelled respectively by using the GaussView program [54] where the Cl atom was first removed from that initial structure of PTZ hydrochloride and, later, the H atom. A similar procedure was employed to obtain the three species of R(+) enantiomer but in this case the structures were built from that experimental polymorphic form 2 determined by X-ray diffraction by Borodi et al [19]. The Revision A.02 of Gaussian program was employed to optimize those six species in both media [55] by using the hybrid B3LYP/6-31G* method [34, 35]. In solution, the three species were optimized by using PCM and SMD calculations [36, 37, 38] while their volumes changes were evaluated with the Moldraw program [56]. In Fig. 1 can be seen the six S(-) and R(+)-PTZ structures as free base, cationic and hydrochloride together with the atoms labelling and the identifications of their three rings. The solvation energies corrected by zero point vibrational energy (ZPVE) were computed for all species of S(-) and R(+)-PTZ with the universal solvation model [36, 37, 38]. Besides, atomic natural population (NPA), Mulliken and Merz-Kollman (MK) charges [57], molecular electrostatic potentials, bond orders and topological properties were calculated by using the NBO program [58] and with the Bader's theory of atoms in molecules (AIM) by using AIM2000 program [59, 60]. On the other hand, the evaluation of reactivities and behaviours of S(-) and R(+)-PTZ species were performed calculating the gap values [43, 44] and some useful and known global descriptors with the frontier orbitals [45, 46, 47, 48, 49, 50, 51, 52, 53]. The harmonic force fields and force constants in gas phase and in aqueous solution were computed at the B3LYP/6-31G* level by using the normal internal coordinates and transferable scaling factors with the scaled quantum mechanical force field (SQMFF) and the Molvib program [39, 40, 42]. Here, the predicted Raman activities for all species were corrected to intensities by using recommended equations [61, 62] while the scale factors used were those reported for the B3LYP/6-31G* method. At this point, it is necessary to clarify that all studied properties were computed for six S(-) and R(+)-PTZ species by using only the B3LYP/6-31G* level because they are compared with properties reported at the same level of theory for other species containing N–CH₃ groups, such as alkaloids, diphenhydramine and cyclizine [1, 2, 3, 6, 7, 8, 9].

Fig. 1.

Theoretical molecular structures of free base, cationic and hydrocloride species of both S(-) and R(+) enantiomers of promethazine.

3. Results and discussion

3.1. Properties of species of S(-) and R(+)-PTZ in both media

The structural studies in solution of these species are of great interest because the >N–CH₃ group can present fast N-methyl inversion in this medium, as suggested by Lazni et al [63]. Here, in Table 1 are summarized calculated total uncorrected and corrected by ZPVE energies, dipole moments and volumes (V) of three species of both enantiomers S(-) and R(+)-PTZ in gas and aqueous solution phases by using the B3LYP/6-31G* method. Analyzing deeply the results, it is observed that the total energy values corrected by ZPVE decrease for all species in both media while the dipole moment and volume values increase in solution, as expected because these species are possibly hydrated in solution. The exception is observed only for the cationic form of S(-)-PTZ because the E and V values decrease in solution. Here, the imaginary frequencies obtained for that species could justify clearly these differences. Note that the cationic species of both enantiomers have higher dipole moments in solution while the hydrochloride forms present the higher volumes in both media having the S(-) species slightly the higher values in the two media. In Table 2 can be observed corrected and uncorrected solvation energies by the total non-electrostatic terms and by zero point vibrational energy (ZPVE) of free base, cationic and hydrochloride species of S(-) and R(+)-PTZ by using the B3LYP/6-31G* method. The variations observed experimentally in the unit cell lead to small displacements of the molecules in the crystal structures and, consequently, to slight energy, density, and melting point differences between the forms. Note that these obtained values are closer to those observed in the study of interaction of gelatin with promethazine hydrochloride [64]. These values are compared in the same table with morphine, cocaine, scopolamine, heroin and tropane alkaloids and with cyclizine [1, 2, 3, 4, 5, 6, 7, 9]. In particular, due to the imaginary frequencies predicted for the cationic form of cyclizine in solution the value for cyclizine was obtained by using B3LYP/6-31+G* calculations while for S(-)-PTZ in solution the value of -14,48 kJ/mol was obtained directly from Table 1. The ΔG_c values for the three species of tropane were calculated in this work. Fig. 2 shows clearly the variations of ΔG_c for all compared species by using the solvation model [38]. In general, it is observed that all cationic species have more negative values while the free bases the less negative values. The cationic forms of morphine, scopolamine and heroin have the most negative values while the S(-) form of PTZ the most low ΔG_c value. Probably, this resulted change if other basis set is used. Interesting results are observed for cyclizine (-244,36 kJ/mol) and tropane (-244,33 kJ/mol) because their cationic forms have practically the same values. In both species, the N–CH₃ groups are linked to rings, in cyclizine to piperazine ring while in tropane a two fused piperidine and pyrrolidine rings. The heroin hydrochloride species present the most negative ΔG_c value while the R(+)-PTZ the lower value. On the other hand, the free base of heroin presents the most negative ΔG_c value while the tropane species the lowest value. Evidently, the acetyl groups in heroin increase the solvation energies of their three species, as compared with morphine. Obviously, these comparisons show easily why the hydrochloride species are highly used in pharmacology, as compared with their free base and cationic ones. Besides, the hydrochloride species in solution are in their cationic forms and show clearly high solubility in this medium. Evidently, the solubility limits visibly the drug absorption, as mentioned by Bohloko studying the formulation of an intranasal dosage form for cyclizine hydrochloride [65].

Table 1.

Calculated total energies (E), dipole moments (μ) and volumes (V) of three species of S(-) and R(+)-promethazine in gas and aqueous solution phases.

B3LYP/6-31G* Method
Medium	E (Hartrees)	ZPVE	μ (D)	V (Å3)
S(-)-Free base
GAS	-1167.5298	-1167.1923	2.18	312.7
PCM	-1167.5383	-1167.2000	3.75	314.2
S(-)-Cationic
GAS	-1167.9143	-1167.5615	14.62	316.3
PCM#	-1167.9121	-1167.5588	15.20	315.1
S(-)-Hydrochloride
GAS	-1628.3493	-1627.9992	9.33	342.1
PCM	-1628.3849	-1628.0312	14.16	342.8
R(+)-Free base
GAS	-1167.5263	-1167.1907	1.92	312.3
PCM	-1167.5277	-1167.1894	3.03	312.2
R(+)-Cationic
GAS	-1167.9127	-1167.5599	14.77	315.9
PCM	-1168.0075	-1167.6532	19.73	319.0
R(+)-Hydrochloride
GAS	-1628.3509	-1628.0002	7.50	338.6
PCM	-1628.3836	-1627.9920	11.72	341.4

^#Imaginary frequencies.

Table 2.

Corrected and uncorrected solvation energies by the total non-electrostatic terms and by zero point vibrational energy (ZPVE) of three species of S(-) and R(+)-promethazine by using the B3LYP/6-31G* method compared with other similar species.

B3LYP/6-31G* methoda
Solvation energy (kJ/mol)
Condition	ΔGun#	ΔGne	ΔGc
Free base
S(-)-Promethazinea	-20.19	15.88	-36.07
R(+)-Promethazinea	-3.41	14.46	-17.87
Cyclizineb	-23.60	5.93	-29.53
Morphinec	-47.74	13.17	-60.91
Cocained	-42.75	28.51	-71.26
Scopolaminee	-56.66	18.81	-75.47
Heroinf	-59.54	29.13	-88.67
Tropanea,g	-11.80	0.75	-12.55
Cationic
S(-)-Promethazinea	-7.08	7.40	-14.48
R(+)-Promethazinea	-255.22	7.59	-262.81
Cyclizineb,#	-238.43	5.93	-244.36
Morphinec	-282.23	26.96	-309.19
Cocained	-216.66	38.58	-255.24
Scopolaminee	-279.87	30.47	-310.34
Heroinf	-280.13	43.01	-323.14
Tropanea,g	-228.99	15.34	-244.33
Hydrochloride
S(-)-Promethazinea	-101.25	30.81	-70.44
R(+)-Promethazinea	-21.51	30.51	-52.02
Cyclizineb	-81.57	23.49	-105.06
Morphinec	-118.82	25.92	-144.74
Cocained	-99.94	38.20	-138.14
Scopolaminee	-95.19	27.55	-122.74
Heroinf	-118.56	43.38	-161.94
Tropanea,g	-72.13	15.05	-87.18

ΔG_un^# = uncorrected solvation energy: defined as the difference between the total energies in aqueous solutions and the values in gas phase. ΔG_un = Solvation energy (kJ/mol) corrected by ZPVE.

ΔG_ne = total non electrostatic terms: due to the cavitation, dispersion and repulsion energies.

ΔG_c = corrected solvation energies: defined as the difference between the uncorrected and non-electrostatic solvation energies.

^aThis work.

^bFrom Ref [9].

^cFrom Ref [1].

^dFrom Ref [3].

^eFrom Ref [7].

^fFrom Ref [5].

^gFrom Ref [2].

^#Cation cyclizine: 6-31+G*.

Fig. 2.

Corrected solvation energies of free base, cationic and hydrocloride species of both S(-) and R(+) enantiomers of promethazine by using the B3LYP/6-31G* method.

3.2. Geometries of species of S(-) and R(+)-PTZ in both media

Calculated geometrical parameters for three species of S(-) and R(+)-PTZ in both media are compared with the corresponding experimental polymorphic forms 1 and 2 [19] in Tables 3 and 4, respectively by using the root-mean-square deviation (RMSD) values. Despite theoretical B3LYP/6-31G* calculations show visibly overestimated values, as compared with the corresponding experimental ones, the results for all species of S(-)-PTZ forms show very good correlations for bond lengths (0.020–0.012 Å) but the three species of R(+)-PTZ evidence the better correlations for bond (1.7–1.3°) and dihedral angles (6.1–3.7°) than the S(-) ones. On the other hand, the higher differences in dihedral angles are predicted for the three species of S(-) form (176.1–137.9°), as can be seen in Table 3. Here, it is necessary to remember that those two polymorphic conformations found by Borodi et al [19] are experimentally the same where the two forms are present in the unit cell but our theoretical calculations show slight differences in the dihedral angles of both S(-) and R(+)-PTZ forms. Thus, the calculated bonds N2–C6 and N2–C7 lengths of phenothiazine rings belong to the three species of both S(-) and R(+) enantiomers are practically predicted with same values but different from the bond N2–C5 lengths of side chain. In the same way, the calculated S1–C9 bonds of phenothiazine rings are approximately the same than the S1–C10 bonds while the predicted N3–C11 bonds are practically the same than the N3–C12 bonds. The predicted values for both pairs bonds are different from the corresponding experimental ones.

Table 3.

Comparison of calculated geometrical parameters for three species of S(-)-promethazine in both media with the corresponding experimental ones.

B3LYP/6-31G* Methoda						Form 1
Parameter	Free base		Cation	Hydrochloride		Experimentalb
	Gas	PCM	Gas	Gas	PCM
Bond lengths (Å)
S1–C9	1.783	1.786	1.786	1.783	1.786	1.772
S1–C10	1.783	1.786	1.785	1.784	1.786	1.781
N2–C5	1.464	1.471	1.445	1.457	1.465	1.435
N2–C6	1.416	1.419	1.427	1.420	1.420	1.422
N2–C7	1.416	1.418	1.424	1.420	1.419	1.418
C6–C9	1.406	1.409	1.404	1.407	1.408	1.379
C7–C10	1.406	1.409	1.406	1.407	1.409	1.389
C4–C5	1.553	1.552	1.547	1.545	1.543	1.545
N3–C4	1.472	1.482	1.550	1.511	1.525	1.513
N3–C11	1.454	1.463	1.505	1.485	1.495	1.502
N3–C12	1.456	1.465	1.505	1.484	1.495	1.491
C6–C13	1.401	1.405	1.399	1.402	1.404	1.398
C9–C15	1.392	1.395	1.395	1.395	1.396	1.394
C13–C17	1.393	1.396	1.396	1.395	1.396	1.396
C15–C19	1.393	1.396	1.395	1.395	1.396	1.392
C17–C19	1.391	1.394	1.394	1.393	1.395	1.366
C7–C14	1.401	1.404	1.400	1.402	1.404	1.402
C14–C18	1.393	1.396	1.397	1.396	1.396	1.387
C16–C10	1.392	1.395	1.395	1.394	1.395	1.394
C16–C20	1.393	1.396	1.395	1.395	1.396	1.382
C18–C20	1.391	1.395	1.394	1.393	1.394	1.379
RMSDb	0.020	0.019	0.014	0.012	0.013
Bond angles (°)
C9–S1–C10	97.8	97.8	98.2	98.0	98.0	96.4
C6–C9–S1	118.6	118.5	118.8	118.7	118.6	119.0
C7–C10–S1	118.6	118.5	118.7	118.6	118.6	117.9
C5–N2–C6	119.5	118.7	120.2	119.5	119.0	118.9
C5–N2–C7	119.3	119.2	119.8	119.6	119.3	119.1
C6–N2–C7	117.5	117.0	118.3	117.9	117.7	115.6
N2–C5–C4	112.7	113.2	108.6	111.3	110.6	108.9
C5–C4–N3	113.1	113.0	111.8	111.6	111.1	106.9
C4–N3–C11	114.3	112.4	113.1	114.3	113.2	111.7
C4–N3–C12	116.2	114.1	114.4	115.8	114.9	112.1
C11–N3–C12	111.9	109.8	111.2	111.2	110.7	111.4
N2–C7–C14	122.5	122.5	122.6	122.5	122.5	122.4
N2–C6–C13	122.6	122.6	122.5	122.6	122.5	121.9
S1–C10–C16	120.4	120.3	120.8	120.6	120.3	120.0
S1–C9–C15	120.4	120.3	120.7	120.5	120.3	120.0
RMSDb	2.4	2.1	1.8	2.0	1.6
Dihedral angles (°)
C11–N3–C4–C5	75.9	72.8	75.7	71.0	73.8	167.0
C12–N3–C4–C5	-56.6	-53.1	-53.0	-60.3	-54.9	-67.0
N3–C4–C5–N2	-168.3	-167.7	-165.4	-169.6	-165.2	175.4
C4–C5–N2–C6	-137.3	-142.2	-127.8	-135.3	-136.5	-68.6
C4–C5–N2–C7	63.8	63.4	66.3	64.2	66.2	140.3
C14–C7–N2–C6	-135.8	-134.5	-134.5	-135.2	-136.0	-129.1
C15–C9–S1–C10-	-144.8	-144.5	-144.2	-144.7	-144.8	-139.1
C8–C4–C5–N2	65.1	66.0	69.7	64.9	70.4	-65.9
RMSDb	138.9	139.5	137.9	176.1	223.0

The letters bold indicated RMSD values.

^aThis work.

^bRef [19].

Table 4.

Comparison of calculated geometrical parameters for three species of R(+)-promethazine in both media with the corresponding experimental ones.

B3LYP/6-31G* Methoda							Form 2 Experimentalb
Parameter	Free base		Cation		Hydrochloride
	Gas	PCM	Gas	PCM	Gas	PCM
Bond lengths (Å)
S1–C9	1.783	1.785	1.786	1.785	1.784	1.785	1.772
S1–C10	1.783	1.786	1.785	1.786	1.782	1.785	1.781
N2–C5	1.464	1.470	1.443	1.462	1.457	1.464	1.435
N2–C6	1.418	1.418	1.427	1.420	1.423	1.421	1.422
N2–C7	1.417	1.418	1.425	1.420	1.418	1.421	1.418
C6–C9	1.408	1.409	1.404	1.408	1.407	1.409	1.379
C7–C10	1.408	1.409	1.406	1.408	1.409	1.409	1.389
C4–C5	1.551	1.549	1.554	1.547	1.552	1.548	1.545
N3–C4	1.479	1.486	1.551	1.533	1.520	1.527	1.513
N3–C11	1.460	1.468	1.508	1.502	1.487	1.496	1.502
N3–C12	1.460	1.468	1.508	1.503	1.486	1.496	1.491
C6–C13	1.403	1.404	1.399	1.403	1.402	1.404	1.398
C9–C15	1.394	1.395	1.395	1.396	1.395	1.395	1.394
C13–C17	1.395	1.396	1.396	1.396	1.395	1.396	1.396
C15–C19	1.395	1.396	1.395	1.396	1.395	1.395	1.392
C17–C19	1.393	1.395	1.394	1.395	1.393	1.394	1.366
C7–C14	1.403	1.404	1.400	1.403	1.403	1.403	1.402
C14–C18	1.395	1.396	1.397	1.396	1.396	1.396	1.540
C16–C10	1.394	1.395	1.395	1.395	1.394	1.395	1.540
C16–C20	1.395	1.396	1.396	1.396	1.395	1.396	1.540
C18–C20	1.393	1.395	1.394	1.394	1.393	1.394	1.325
RMSDb	0.060	0.059	0.058	0.015	0.058	0.058
Bond angles (°)
C9–S1–C10	97.8	97.8	98.2	98.0	98.0	98.0	96.4
C6–C9–S1	118.6	118.5	118.7	118.6	118.8	118.7	119.0
C7–C10–S1	118.6	118.4	118.7	118.6	118.7	118.7	117.9
C5–N2–C6	119.2	119.3	120.0	118.9	119.1	118.7	118.9
C5–N2–C7	119.4	119.1	119.7	119.2	119.4	119.1	119.1
C6–N2–C7	117.6	117.3	118.2	117.8	118.0	117.6	115.6
N2–C5–C4	113.1	112.4	109.5	111.2	110.9	111.2	108.9
C5–C4–N3	107.7	109.1	109.4	108.2	108.6	108.6	106.9
C4–N3–C11	114.8	111.9	113.6	113.5	114.5	113.5	112.1
C4–N3–C12	111.9	110.5	112.8	112.8	113.2	112.7	111.7
C11–N3–C12	108.9	107.2	109.2	108.8	109.6	108.9	111.4
N2–C7–C14	122.5	122.5	122.7	122.5	122.6	122.5	122.4
N2–C6–C13	122.5	122.6	122.6	122.5	122.5	122.5	121.9
S1–C10–C16	120.4	120.3	120.8	120.3	120.5	120.2	121.0
S1–C9–C15	120.4	120.3	120.8	120.3	120.3	120.1	120.0
RMSDb	1.6	1.7	1.4	1.3	1.4	1.3
Dihedral angles (°)
C11–N3–C4–C5	157.1	165.9	165.5	164.2	160.7	163.5	167.0
C12–N3–C4–C5	-77.8	-74.4	-69.3	-71.2	-72.5	-71.9	-67.0
N3–C4–C5–N2	172.2	165.7	170.5	171.6	171.4	166.4	175.4
C4–C5–N2–C6	137.0	136.7	130.3	137.3	133.5	137.6	139.9
C4–C5–N2–C7	-64.6	-66.7	-65.9	-65.5	-67.5	-66.7	-69.0
C14–C7–N2–C6	135.9	135.5	134.3	136.0	136.5	136.0	131.7
C15–C9–S1–C10-	144.6	144.1	144.1	144.7	144.7	144.8	140.1
C8–C4–C5–N2	-64.5	-71.0	-65.8	-65.7	-65.9	-70.7	-62.7
RMSDb	6.1	5.8	4.6	3.7	4.8	5.4

The letters bold indicated RMSD values.

^aThis work.

^bRef [19].

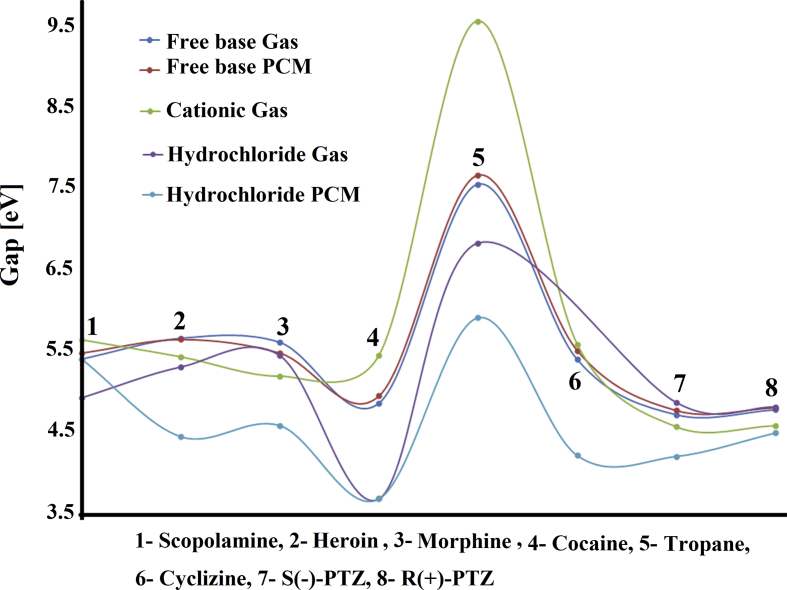
Another interesting comparisons are observed in the average bond N–C lengths of the N–CH₃ groups belonging to the three species of S(-) and R(+)-PTZ with those observed for cyclizine, morphine, heroin, cocaine, scopolamine and tropane where the results in gas phase and in aqueous solution by using B3LYP/6-31G* calculations can be seen in Table 5. Here, due to the presence of two N–CH₃ groups the average of N–C distances between both groups were considered. In Fig. 3 are easily observed the behaviours of N–C distances of all compared species in both media. In gas phase, the comparisons between the free base and cationic species show that cationic form of cyclizine has the lowest value (1.453 Å) while the highest value is observed in the cationic species of R(+)-PTZ (1.508 Å). In solution, it is observed that the free base species have low values and different from the hydrochloride ones. Evidently, the presence of charged cationic species and electronegative Cl atoms in all hydrochloride species produce increase in the N–C distances. The tropane hydrochloride has the shorter value while the species corresponding to R(+)-PTZ the higher value.

Table 5.

Bond lengths observed between the N and C atoms of the N–CH₃ bonds belonging to the three S(-) and R(+)-promethazine species in gas phase and in aqueous solution by using B3LYP/6-31G* calculations.

N–CH3 bonds ()
Species	Gas phase			Aqueous solution
	Free base	Cationic	Hydrobromide	Free base	Cationic	Hydrobromide
R(+)-promethazineγ	1.460	1.508	1.487	1.468	1.501	1.496
S(-)-Promethazineγ	1.455	1.505	1.485	1.464	#	1.495
Cyclizine	1.453	1.453	#	1.459	#	1.489
Scopolamine	1.462	1.492	1.491	1.466	1.491	1.493
Heroin	1.453	1.501	1.483	1.460	1.498	1.492
Morphine	1.453	1.500	1.483	1.460	1.497	1.493
Cocaine	1.459	1.493	1.487	1.467	1.492	1.494
Tropane	1.458	1.496	1.478	1.467	1.491	1.486

^#Imaginary frequencies.

^γaverage.

Fig. 3.

Calculated N–C distances corresponding to N–CH₃ groups of free base, cationic and hydrocloride species of both S(-) and R(+) enantiomers of promethazine in both media by using the B3LYP/6-31G* method.

3.3. Atomic charges, molecular electrostatic potentials and bond orders

Mulliken, Merz-Kollman (MK) and atomic natural population (NPA) charges, molecular electrostatic potentials (MEP) and bond orders (BO), expressed as Wiberg indexes were calculated for the three forms of S(-) and R(+)-PTZ in gas phase and in aqueous solution by using B3LYP/6-31G* calculations. The resulted only for the S1, N2, N3, C8, C11 and C12 atoms can be seen in Table 6 because these atoms present the higher variations in all species while the behaviours of MK charges on these atoms are represented in Fig. 4. Analyzing first the MK charges for the free base species of S(-) and R(+)-PTZ we observed from Fig. 4 that: (i) the MK charges on the N2, C8 and C11 atoms of all free base species undergoes important changes, presenting the highest change on N2 of free base of R(+)-PTZ in solution and (ii) the charges on the S1, N3 and C12 atoms of all species in both media have practically the same values. In the cationic species, the lower MK charges values are observed on those five atoms of S(-)-PTZ in gas phase while on N2 atoms of R(+) species in the two media are observed the higher changes. Different behaviours are observed on the MK charges of those five atoms corresponding to the hydrochloride species in both media. Hence, the charges on the N3 atoms have the higher values, as expected due to the presences in these species of electronegative Cl atoms. The Mulliken charges on those five atoms of free base species show practically the same behaviours but, in particular, on the N2 and C8 atoms are observed the most negative values while the NPA charges on C8 atoms of free base, cationic and hydrochloride species show the lower values in both enantioners. The Mulliken charges in the cationic and hydrochloride species present basically the same behaviours but on the N2 atoms are observed the lower values.

Table 6.

Mulliken, Merz-Kollman and NPA charges, molecular electrostatic potentials (MEP) and bond orders, expressed as Wiberg indexes for three forms of S(-) and R(+)-promethazine in gas phase and in aqueous solution by using B3LYP/6-31G* calculations.

S(-)-Free base
GAS						PCM
Atoms	MK	Mulliken	NPA	MEP	BO	MK	Mulliken	NPA	MEP	BO
S1	-0.120	0.157	0.330	-59.182	2.335	-0.118	0.156	0.328	-59.182	2.333
N2	-0.311	-0.581	-0.452	-18.312	3.305	-0.360	-0.581	-0.449	-18.311	3.305
N3	-0.346	-0.365	-0.506	-18.356	3.127	-0.357	-0.367	-0.501	-18.354	3.115
C8	-0.272	-0.455	-0.685	-14.757	3.844	-0.267	-0.455	-0.685	-14.756	3.844
C11	-0.222	-0.300	-0.468	-14.719	3.819	-0.266	-0.305	-0.473	-14.719	3.820
C12	-0.138	-0.308	-0.475	-14.719	3.819	-0.124	-0.311	-0.479	-14.720	3.820
S(-)-Cationic
GAS						PCM
Atoms	MK	Mulliken	NPA	MEP	BO
S1	-0.097	0.186	0.348	-59.085	2.343
N2	-0.122	-0.587	-0.471	-18.197	3.264
N3	-0.025	-0.492	-0.450	-18.052	3.469
C8	-0.279	-0.498	-0.718	-14.593	3.809
C11	-0.335	-0.348	-0.475	-14.519	3.713
C12	-0.368	-0.351	-0.479	-14.519	3.715
S(-)-Hydrochloride
GAS						PCM
Atoms	MK	Mulliken	NPA	MEP	BO	MK	Mulliken	NPA	MEP	BO
S1	-0.106	0.171	0.340	-59.167	2.339	-0.101	0.174	0.340	-59.164	2.338
N2	-0.215	-0.583	-0.456	-18.291	3.291	-0.257	-0.586	-0.453	-18.283	3.294
N3	0.370	-0.481	-0.497	-18.250	3.341	0.452	-0.480	-0.483	-18.223	3.383
C8	-0.212	-0.488	-0.708	-14.733	3.816	-0.180	-0.490	-0.711	-14.725	3.811
C11	-0.400	-0.321	-0.477	-14.673	3.756	-0.357	-0.328	-0.474	-14.660	3.745
C12	-0.348	-0.325	-0.481	-14.673	3.759	-0.337	-0.334	-0.479	-14.658	3.748
R(+)-Free base
GAS						PCM
Atoms	MK	Mulliken	NPA	MEP	BO	MK	Mulliken	NPA	MEP	BO
S1	-0.344	0.155	0.329	-59.182	2.334	-0.126	0.154	0.327	-59.183	2.332
N2	-0.344	-0.584	-0.455	-18.313	3.303	-0.018	-0.583	-0.454	-18.312	3.304
N3	-0.344	-0.387	-0.511	-18.354	3.112	-0.336	-0.390	-0.504	-18.353	3.104
C8	-0.330	-0.484	-0.695	-14.753	3.836	-0.341	-0.484	-0.694	-14.752	3.837
C11	-0.255	-0.296	-0.472	-14.723	3.815	-0.215	-0.300	-0.476	-14.723	3.816
C12	-0.123	-0.306	-0.469	-14.720	3.821	-0.127	-0.309	-0.473	-14.720	3.822
R(+)-Cationic
GAS						PCM
Atoms	MK	Mulliken	NPA	MEP	BO	MK	Mulliken	NPA	MEP	BO
S1	-0.106	0.188	0.349	-59.085	2.343	-0.090	0.190	0.351	-59.088	2.341
N2	0.033	-0.586	-0.471	-18.197	3.263	-0.048	-0.591	-0.460	-18.193	3.276
N3	0.046	-0.495	-0.449	-18.050	3.470	0.033	-0.490	-0.447	-18.047	3.471
C8	-0.145	-0.499	-0.722	-14.597	3.805	-0.155	-0.492	-0.719	-14.593	3.806
C11	-0.308	-0.343	-0.476	-14.521	3.708	-0.298	-0.343	-0.476	-14.519	3.707
C12	-0.384	-0.351	-0.473	-14.519	3.713	-0.358	-0.353	-0.473	-14.517	3.711
R(+)-Hydrochloride
GAS						PCM
Atoms	MK	Mulliken	NPA	MEP	BO	MK	Mulliken	NPA	MEP	BO
S1	-0.129	0.158	0.331	-59.173	2.335	-0.122	0.160	0.332	-59.170	2.335
N2	-0.132	-0.588	-0.457	-18.299	3.295	-0.226	-0.588	-0.456	-18.292	3.293
N3	0.407	-0.481	-0.492	-18.244	3.353	0.454	-0.482	-0.479	-18.221	3.389
C8	-0.208	-0.496	-0.710	-14.725	3.818	-0.190	-0.497	-0.712	-14.715	3.816
C11	-0.319	-0.315	-0.476	-14.671	3.753	-0.314	-0.322	-0.475	-14.660	3.743
C12	-0.448	-0.324	-0.472	-14.668	3.760	-0.415	-0.332	-0.471	-14.657	3.749

Fig. 4.

Calculated Merz-Kollman charges of free base, cationic and hydrocloride species of both S(-) and R(+) enantiomers of promethazine by using the B3LYP/6-31G* method.

The bond orders (BO) expressed as Wiberg indexes in the three species of both enantiomers in the two media have approximately the same values and behaviours, observing the higher values in the C8, C11 and C12 atoms and the lower values in the S1 atoms. In general, higher values are observed for the N2 atoms of the free base and hydrochloride species of both S(-) and R(+)-PTZ in the two media than for the N3 atoms and only in the cationic species are observed higher values in the N3 atoms.

The molecular electrostatic potentials (MEP) presented in Table 6 show practically the same values and behaviours in the three species of both enantiomers, however, when the surfaces of these species are mapped the colorations show important differences among them, as can be seen in Fig. 5. Thus, the cationic species of both enantiomers in gas phase show blue colours on the entire surface but, in particular, strong blue colours it is observed on the protonated N–H region. In the free base species the strong red colours are observed on the N3 atoms and S1 atoms while in the hydrochloride species the strong red colours are observed on the Cl atoms. Hence, the typical nucleophilic sites are clearly identified with red colours while the electrophilic sites with blue colours, as observed in other species [6, 7, 8, 9].

Fig. 5.

Calculated electrostatic potential surfaces on the molecular surfaces of the free base, cationic and hydrochloride species of both S(-) and R(+) enantiomers of promethazine. B3LYP functional and 6-31G* basis set. Isodensity value of 0.005.

3.4. NBO study

For the three species of both S(-) and R(+)-PTZ enantiomers the main delocalization energies in gas and aqueous solution were calculated by using B3LYP/6-31G* calculations with the NBO program [58]. The resulted for the three species of S(-) and R(+)-PTZ are summarized in Tables 7 and 8, respectively. Different interactions can be observed in the three species and, especially in the hydrochloride species due to the presence of Cl atoms where in particular, the π*→π* and π→π* interactions present the higher values in the S(-) and R(+)-PTZ forms, respectively. Thus, the free base (3509.36–3522.22 kJ/mol) and hydrochloride (6253.53–5840.28 kJ/mol) species present higher total energies than the cationic ones (1541.01 kJ/mol) and, for these reasons, these two species are most stable than the cationic ones. However, the hydrochloride species of R(+)-PTZ have higher values in both media than the corresponding to other enantiomer (7527.88–7332.02 kJ/mol). Nevertheless, the free base of R(+)-PTZ present lower values than the corresponding to S(-)-PTZ (3484.4–3193.04 kJ/mol) while the cationic form of R(+)-PTZ is most stable than the corresponding to S(-)-PTZ (1540.08–1612.71 kJ/mol). These studies shows clearly that the hydrochloride species are most stable than the other two species of both forms and in the two media studied but, in particular the species of R(+)-PTZ show higher total energy values evidencing a slight higher stability than the S(-) one. The three PTZ species show higher stabilities than the corresponding to cyclizine [9].

Table 7.

Main delocalization energies (in kJ/mol) for three species of S(-)-promethazine in gas and aqueous solution by using B3LYP/6-31G* calculations.

B3LYP/6-31G*a
Delocalization	Free base		Hydrochloride
	Gas	PCM	Gas	PCM
πC6-C13→ π*C9–C15	74.32	74.28	73.40	73.19
πC6-C13→ π*C17–C19	88.41	88.49	85.98	85.77
πC7-C14→ π*C10–C16	74.49	74.61	72.73	72.02
πC7-C14→ π*C18–C20	88.28	88.49	85.23	85.19
πC9-C15→ π*C6–C13	83.56	83.39	85.27	85.27
πC9-C15→ π*C17–C19	71.18	71.27	72.02	71.98
πC10-C16→ π*C7–C14	83.81	83.60	85.90	86.19
πC10-C16→ π*C18–C20	71.52	71.60	72.23	72.10
πC17-C19→ π*C6–C13	79.59	79.59	81.34	81.97
πC17-C19→ π*C9–C15	93.84	93.67	94.09	94.26
πC18-C20→ π*C7–C14	80.05	80.21	82.05	82.26
πC18-C20→ π*C10–C16	93.75	93.67	94.26	94.30
Σπ→π*	982.8	982.87	984.5	984.5
LP(2)S1→ π*C9–C15	45.98	45.44	46.27	46.02
LP(2)S1→ π*C10–C16	45.98	45.23	46.36	46.27
LP(1)N2→ π*C6–C13	99.86	99.36	92.96	94.89
LP(1)N2→ π*C7–C14	100.74	99.44	94.30	97.56
ΣLP→π*	292.56	289.47	279.89	284.74
π*C9–C15→ π*C17–C19	1106.65	1113.09
π*C10–C16→ π*C18–C20	1127.35	1136.79
π*C6–C13→ π*C17–C19			1101.14	978.58
π*C7–C14→ π*C18–C20			909.65	805.44
π*C9–C15→ π*C17–C19			1057.33	1045.67
π*C10–C16→ π*C18–C20			1040.23	1046.42
Σπ*→π*	2234	2249,88	4108,35	3876,11
σN3-C4→ LP(1)*H41			44,60	62,57
σN3-C11→ LP(1)*H41			50,08	62,82
σN3-C12→ LP(1)*H41			47,61	60,19
Σσ→LP*			142,29	185,58
LP(1)N3→ LP(1)*H41			1158,49	1456,02
LP(1)Cl42→ LP(1)*H41			46,94	16,51
LP(4)Cl42→ LP(1)*H41			797,46	306,06
ΣLP→LP*			2002,89	1778,59
ΣTOTAL	3509.36	3522,22	6253,53	5840,28
Cationica
Delocalization	Gas
πC13-C17→ π*C6–C9	47.86
πC15-C19→ π*C6–C9	43.22
πC15-C19→ π*C13–C17	46.98
Σπ→π*	138.06
πC7-C10→ LP(1)*C16	93.51
πC18-C20→ LP(1)*C16	107.22
Σπ→LP*	200.73
LP(1)C14→ π*C7–C10	171.17
LP(1)C14→ π*C18–C20	125.57
LP(1)C16→ π*C7–C10	176.65
LP(1)C16→ π*C18–C20	133.97
ΣLP→π*	607.36
π*C6–C9→ π*C13–C17	361.99
π*C6–C9→ π*C15–C19	232.87
Σπ*→π*	594.86
ΣTOTAL	1541.01

The letters bold indicated RMSD values.

^aThis work.

Table 8.

Main delocalization energies (in kJ/mol) for three species of R(+)-promethazine in gas and aqueous solution by using B3LYP/6-31G* calculations.

B3LYP/6-31G*a
Delocalization	Free base		Hydrochloride
	Gas	PCM	Gas	PCM
πC6-C13→ π*C9–C15	74.70	74.65	76.53	76.07
πC6-C13→ π*C17–C19	88.41	88.49	86.23	85.65
πC7-C14→ π*C10–C16	74.65		72.48	72.23
πC7-C14→ π*C18–C20	88.45		86.82	86.57
πC9-C15→ π*C6–C13	83.43	83.35	83.06	82.51
πC9-C15→ π*C17–C19	71.18	71.14	70.56	70.30
πC10-C16→ π*C7–C14	83.68		84.98	85.77
πC10-C16→ π*C18–C20	71.44		72.15	72.56
πC17-C19→ π*C6–C13	79.80	79.88	82.26	82.93
πC17-C19→ π*C9–C15	93.97	93.97	95.89	96.14
πC18-C20→ π*C7–C14	80.09			80.59
πC18-C20→ π*C10–C16	93.84			93.13
Σπ→π*	983.64	491.48	810.96	984.45
πC10-C16→ LP(1)*C7		202.39
πC10-C16→ LP(1)*C20		167.07
πC14-C18→ LP(1)*C7		219.66
πC14-C18→ LP(1)*C20		183.38
Σπ→LP*		772.5
LP(2)S1→ π*C9–C15	45.73	45.02	44.73	44.77
LP(2)S1→ π*C10–C16	45.81	45.27	47.23	47.02
LP(1)N2→ π*C6–C13	99.32	99.44	91.37	92.13
LP(1)N2→ π*C7–C14	101.03		101.78	100.74
LP(1)C20→ π*C10–C16		337.28
LP(1)C20→ π*C14–C18		305.43
ΣLP→π*	291.89	832.44	285.11	284.66
LP(1)*C7→ π*C10–C16		267.60
LP(1)*C7→ π*C14–C18		258.91
ΣLP*→π*
π*C9–C15→ π*C17–C19	1084.83
π*C10–C16→ π*C18–C20	1123.92
π*C6–C13→ π*C17–C19			1247.39	1083.04
π*C7–C14→ π*C18–C20			1071.67	978.87
π*C9–C15→ π*C17–C19		1096.62	843.40	817.61
π*C10–C16→ π*C18–C20			1184.32	1207.85
Σπ*→π*	2208.87	1096.62	4346.78	4087.37
σN3-C4→ LP(1)*H41			49.70	61.65
σN3-C11→ LP(1)*H41			49.16	59.73
σN3-C12→ LP(1)*H41			46.48	57.85
Σσ→LP*			145.34	179.23
LP(1)N3→ LP(1)*H41			1234.86	1491.17
LP(1)Cl42→ LP(1)*H41
LP(4)Cl42→ LP(1)*H41			704.83	305.14
ΣLP→LP*			1939.69	1796.31
ΣTOTAL	3484.4	3193.04	7527.88	7332.02
Cationica
Delocalization	Gas	PCM
πC13-C17→ π*C6–C9	47.90	46.98
πC15-C19→ π*C6–C9	43.30	43.43
πC15-C19→ π*C13–C17	47.07	47.61
Σπ→π*	138.27	138.02
πC7-C10→ LP(1)*C16	93.63	94.47
πC18-C20→ LP(1)*C16	107.30	107.05
Σπ→LP*	200.93	201.52
LP(1)N2→ π*C6–C9		42.72
LP(1)N2→ π*C7–C10		44.68
LP(1)C14→ π*C7–C10	171.67	168.95
LP(1)C14→ π*C18–C20	125.57	125.69
LP(1)C16→ π*C7–C10	176.65	177.86
LP(1)C16→ π*C18–C20	133.72	133.84
ΣLP→π*	607.61	693.74
π*C6–C9→ π*C13–C17	361.78	356.18
π*C6–C9→ π*C15–C19	231.49	223.25
Σπ*→π*	593.27	579.43
ΣTOTAL	1540.08	1612.71

The letters bold indicated RMSD values.

^aThis work.

3.5. AIM studies

According to the Bader's theory the topological properties are interesting parameters to predict different types of interactions, such as intra or inter-molecular, ionic and hydrogen bonds interactions [59]. Hence, these properties can be easily computed in the bond critical points (BCPs) and in the ring critical points (RCPs) with the AIM2000 program [60]. Here, the electron density, ρ(r), the Laplacian values, ∇²ρ(r), the eigenvalues (λ1, λ2, λ3) of the Hessian matrix and, the |λ1|/λ3 ratio calculated by using the B3LYP/6-31G* method for the three forms of both S(-) and R(+)-PTZ enantiomers can be observed from Tables 9, 10 and 11. Note that the ionic and hydrogen bonds interactions are observed when λ1/λ3< 1 and ∇²ρ(r) > 0 [9]. Here, RCPN1, RCPN2 and RCPN3 are new RCPs formed as a consequence of C⋯H and H⋯H interactions while RCP1, RCP2 and RCP3 are RCPs corresponding to the R1, R2 and R3 rings, as defined in Fig. 1. In all species, the topological properties of RCP1 and RCP3 are practically the same in the two phenyl rings but different from RCP2 because this ring is the phenothiazine ring. First, analyzing the free bases species of both enantiomers, we observed that S(-)-PTZ present two C14⋯H21 and H⋯H interactions in both media but the involved atoms change of H24--H32 in gas phase to H23--H33 in solution. In R(+)-PTZ, the free base presents in gas phase the C14⋯H21 and H22⋯H31 interactions while in solution are observed three different H⋯H interactions. In the cationic species of S(-)-PTZ are not observed interactions while in R(+)-PTZ is observed a H⋯H interaction in gas phase while in solution are observed two C⋯H and a H⋯H interactions. The hydrochloride species of S(-)-PTZ present two interactions in gas phase and three different in solution while in the R(+)-PTZ enantiomer in gas phase (Table 11) are observed five interactions and only three in solution. In the hydrochloride species the Cl⋯H are ionic interactions where in S(-)-PTZ the Cl–H distances are 1.716 Å in gas phase and 2.032 Å in solution while in R(+)-PTZ the distances change to 1.748 Å in gas phase and 2.029 Å in solution. Evidently, both hydrochloride species are the most stable due to the higher values of their topological properties. These results are in agreement with those analyzed by NBO studies. The hydrochloride species of both forms of PTZ reveals higher stabilities than the corresponding to cyclizine [9].

Table 9.

Analysis of the Bond Critical Points (BCPs) and Ring critical point (RCPs) for three species of S(-)-promethazine in gas and aqueous solution by using the B3LYP/6-31G* method.

B3LYP/6-31G* Method
Free base
Gas phase
Parameter#	C14--H21	RCPN1	H24--H32	RCPN2	RCP1	RCP2	RCP3
ρ(r)	0.0088	0.0088	0.0095	0.0095	0.0198	0.0170	0.0198
∇2ρ(r)	0.0333	0.0357	0.0400	0.0421	0.1580	0.1104	0.1580
λ1	-0.0043	-0.0036	-0.0084	-0.0080	-0.0146	-0.0055	-0.0145
λ2	-0.0011	0.0013	-0.0014	0.0015	0.0815	0.0552	0.0813
λ3	0.0388	0.0379	0.0500	0.0485	0.0910	0.0608	0.0911
|λ1|/λ3	0.1108	0.0950	0.1680	0.1649	0.1604	0.0905	0.1592
Distances (Å)	2.693		2.190
Aqueous solution
Parameter#	C14--H21	RCPN1	H23--H33	RCPN2	RCP1	RCP2	RCP3
ρ(r)	0.0093	0.0090	0.0133	0.0133	0.0198	0.0169	0.0198
∇2ρ(r)	0.0344	0.0398	0.0626	0.0656	0.1573	0.1103	0.1572
λ1	-0.0049	-0.0026	-0.0084	-0.0077	-0.0145	-0.0055	-0.0144
λ2	0.0035	0.0050	-0.0019	0.0020	0.0809	0.0569	0.0808
λ3	0.0429	0.0375	0.0729	0.0712	0.0909	0.0590	0.0908
|λ1|/λ3	0.1142	0.0693	0.1152	0.1081	0.1595	0.0932	0.1586
Distances (Å)	2.646		2.086
Cationic
Gas phase
Parameter#	RCP1	RCP2	RCP3
ρ(r)	0.0199	0.0173	0.0199
∇2ρ(r)	0.1584	0.1084	0.1586
λ1	-0.0146	-0.0050	-0.0146
λ2	0.0832	0.0469	0.0835
λ3	0.0896	0.0665	0.0896
|λ1|/λ3	0.1629	0.0752	0.1629
Hydrochloride
Gas phase
Parameter#	Cl42--H25		Cl42--H41	RCPN1	RCP1	RCP2	RCP3
ρ(r)	0.0080		0.0804	0.0080	0.0198	0.0171	0.0198
∇2ρ(r)	0.0263		0.0866	0.0284	0.1582	0.1100	0.1582
λ1	-0.0062		-0.1359	-0.0062	-0.0146	-0.0053	-0.0145
λ2	-0.0017		-0.1357	0.0018	0.0822	0.0530	0.0820
λ3	0.0342		0.3583	0.0327	0.0905	0.0624	0.0906
|λ1|/λ3	0.1813		0.3793	0.1896	0.1613	0.0849	0.1600
Distances (Å)	2.908		1.716
Aqueous solution
Parameter#	C13--H23	RCPN1	H22---28	RCPN2	Cl42--H41	RCP1	RCP2	RCP3
ρ(r)	0.0134	0.0133	0.0090	0.0090	0.0416	0.0198	0.0169	0.0198
∇2ρ(r)	0.0617	0.0666	0.0384	0.0398	0.0764	0.1574	0.1094	0.1574
λ1	-0.0093	-0.0081	-0.0079	-0.0074	-0.0534	-0.0145	-0.0056	-0.0145
λ2	-0.0031	0.0036	-0.0014	0.0014	-0.0532	0.0813	0.0552	0.0811
λ3	0.0742	0.0711	0.0476	0.0458	0.1828	0.0906	0.0597	0.0907
|λ1|/λ3	0.1253	0.1139	0.1660	0.1616	0.2921	0.1600	0.0938	0.1599
Distances (Å)	2.508		2.189		2.032

^# This symbol implies values in a.u. units.

Table 10.

Analysis of the Bond Critical Points (BCPs) and Ring critical point (RCPs) for free base and cationic species of R(+)-promethazine in gas and aqueous solution by using the B3LYP/6-31G* method.

B3LYP/6-31G* Method
Free base
Gas phase
Parameter#	C14--H21	RCPN1	H22--H31	RCPN2	RCP1	RCP2	RCP3
ρ(r)	0.0084	0.0084	0.0120	0.0110	0.0198	0.0170	0.0198
∇2ρ(r)	0.0315	0.0332	0.0483	0.0571	0.1580	0.1105	0.1580
λ1	-0.0037	-0.0033	-0.0127	0.0078	-0.0146	-0.0055	-0.0145
λ2	-0.0008	0.0009	-0.0083	0.0107	0.0815	0.0551	0.0813
λ3	0.0362	0.0355	0.0694	0.0542	0.0911	0.0609	0.0911
|λ1|/λ3	0.1022	0.0930	0.1830	-0.1439	0.1603	0.0903	0.1592
Distances (Å)	2.727		2.024
Aqueous solution
Parameter#	H31--H34	H22--H31	RCPN1	H23--H33	RCPN2	RCP1	RCP2	RCP3
ρ(r)	0.0057	0.0128	0.0057	0.0132	0.0132	0.0198	0.0170	0.0198
∇2ρ(r)	0.0212	0.0511	0.0208	0.0605	0.0656	0.1573	0.1103	0.1572
λ1	-0.0041	-0.0137	-0.0038	-0.0093	-0.0080	-0.0145	-0.0055	-0.0144
λ2	-0.0022	-0.0092	0.0029	-0.0033	0.0039	0.0809	0.0559	0.0807
λ3	0.0275	0.0742	0.0216	0.0732	0.0697	0.0909	0.0598	0.0909
|λ1|/λ3	0.1491	0.1846	0.1759	0.1270	0.1148	0.1595	0.0920	0.1584
Distances (Å)	2.353	1.995		2.072
Cationic
Gas phase
Parameter#	H22--H31	RCPN1	RCP1	RCP2	RCP3
ρ(r)	0.0120	0.0108	0.0199	0.0173	0.0199
∇2ρ(r)	0.0478	0.0533	0.1584	0.1084	0.1588
λ1	-0.0131	-0.0087	-0.0146	-0.0049	-0.0146
λ2	-0.0086	0.0107	0.0832	0.0472	0.0836
λ3	0.0696	0.0513	0.0897	0.0664	0.0896
|λ1|/λ3	0.1882	0.1696	0.1628	0.0738	0.1629
Distances (Å)	2.008
Aqueous solution
Parameter#	C14--H21	RCPN1	C13--H23	RCPN2	H22--H31	RCPN3	RCP1	RCP2	RCP3
ρ(r)	0.0085	0.0085	0.0131	0.0131	0.0124	0.0112	0.0198	0.0169	0.0198
∇2ρ(r)	0.0326	0.03369	0.0617	0.0639	0.0495	0.0556	0.1576	0.1095	0.1575
λ1	-0.0033	-0.0030	-0.0085	-0.0080	-0.0135	-0.0090	-0.0145	-0.0056	-0.0145
λ2	-0.0006	0.0006	-0.0014	0.0015	-0.0087	0.0108	0.0815	0.0553	0.0811
λ3	0.0366	0.0360	0.0716	0.0704	0.0717	0.0538	0.0906	0.0598	0.0908
|λ1|/λ3	0.0902	0.0833	0.1187	0.1136	0.1883	0.1673	0.1600	0.0936	0.1597
	2.718		2.520		1.996

^# This symbol implies values in a.u. units.

Table 11.

Analysis of the Bond Critical Points (BCPs) and Ring critical point (RCPs) for three species of R(+)-promethazine in gas and aqueous solution by using the B3LYP/6-31G* method.

B3LYP/6-31G* Method
Hydrochloride
Gas phase
Parameter#	C5⋯H34	RCPN1	C13⋯H23	RCPN2	H22⋯H31	RCPN3	Cl42⋯H23	Cl42⋯H41	RCPN3	RCP1	RCP2	RCP3
ρ(r)	0.0112	0.0112	0.0130	0.0130	0.0120	0.0109	0.0093	0.0746	0.0082	0.0198	0.0170	0.0199
∇2ρ(r)	0.0508	0.0508	0.0624	0.0624	0.0484	0.0548	0.0311	0.0935	0.0343	0.1580	0.1096	0.1584
λ1	-0.0092	-0.0092	-0.0090	-0.0090	-0.0130	-0.0087	-0.0072	-0.1220	-0.0057	-0.0146	-0.0055	-0.0146
λ2	-0.0005	-0.0005	-0.0006	-0.0006	-0.0085	0.0107	-0.0051	-0.1219	0.0068	0.0815	0.0535	0.0820
λ3	0.0606	0.0606	0.0720	0.0720	0.0699	0.0528	0.0435	0.3374	0.0331	0.0910	0.0615	0.0909
|λ1|/λ3	0.1518	0.1518	0.1250	0.1250	0.1860	0.1648	0.1655	0.3616	0.1722	0.1604	0.0894	0.1606
Distances (Å)	2.637		2.520		2.008		2.814	1.748
Aqueous solution
Parameter#	C13⋯H23	RCPN1	H22⋯H31	RCPN2	Cl42⋯H41	RCP1	RCP2	RCP3
ρ(r)	0.0134	0.0134	0.0122	0.0111	0.0418	0.0198	0.0169	0.0198
∇2ρ(r)	0.0633	0.0668	0.0494	0.0558	0.0771	0.1575	0.1093	0.1576
λ1	-0.0094	-0.0085	-0.0131	-0.0088	-0.0536	-0.0145	-0.0057	-0.0145
λ2	-0.0023	0.0025	-0.0085	0.0106	-0.0535	0.0813	0.0557	0.0808
λ3	0.0750	0.0726	0.0711	0.0537	0.1843	0.0907	0.0592	0.0911
|λ1|/λ3	0.1253	0.1171	0.1842	0.1639	0.2908	0.1599	0.0963	0.1592
Distances (Å)	2.507		1.999		2.029

^# This symbol implies values in a.u. units.

3.6. Frontier orbitals and global descriptors studies

To predict reactivities and behaviours of both S(-) and R(+)-PTZ forms are of interest to understand why the presence of two N–CH₃ groups in their structures present the same biological activities than cyclizine despite those two groups in PTZ are not linked to rings. Hence, from the frontier orbitals and their differences is possible to compute the gap values [43, 44] and later, by using known equations the chemical potential (μ), electronegativity (χ), global hardness (η), global softness (S), global electrophilicity index (ω) and global nucleophilicity index (Ε) descriptors can be calculated by using the hybrid B3LYP/6-31G* level of theory [45, 46, 47, 48, 49, 50, 51, 52, 53]. The gap and descriptors values for both PTZ enantiomers in the two media are presented in Table 12. The evaluation of gap values for the three species show easily that the hydrochloride species of both S(-) and R(+)-PTZ forms in solution have low gap values and, for these reasons, the two species are more reactive but the S(-) form is most reactive than the R(+)-PTZ one, as expected because this latter form presents higher stability by NBO analysis (>Total energy). Moreover, the free base and cationic species of S(-) form are most reactive than the corresponding to the R(+) form. Comparisons of these results with the observed for similar species containing N–CH₃ groups, as scopolamine, heroin morphine, cocaine, tropane and cyclizine are presented in Table 13 while their behaviours can be seen in Fig. 6. This figure shows that the hydrochloride species of cocaine in both media present the lower gap values and, obviously, are the most reactive species while in all media the tropane species are the less reactive being, the cationic one in gas phase the less reactive. Note that the free base and cationic species of two forms of PTZ are most reactive than the corresponding to cyclizine, however, the hydrochloride species of cyclizine is most reactive than both forms of PTZ. If now the descriptors are analyzed it is observed from Table 12 that the three species of S(-)-PTZ have higher electrophilicity indexes than the corresponding to R(+) form while, on the contrary, the species of R(+) form have higher nucleophilicity indexes than the species of S(-)-PTZ. The only exception is the hydrochloride species in gas phase of S(-) form because it present a higher value (-7.6061 eV) than the corresponding to R(+) form (7.1020 eV). If both electrophilicity and nucleophilicity indexes of the two S(-) and R(+)-PTZ are compared with other species from Table 14 the behaviours can easily be seen in Fig. 7. Higher electrophilicity indexes are observed in the cationic and hydrochloride species of PTZ than cyclizine while the cationic species of cyclizine have higher nucleophilicity index than both species of PTZ. The higher electrophilicity indexes are observed for all cationic forms in gas phase and, in particular, for cocaine while tropane in both media presents the lowest values. In relation to nucleophilicity indexes, the cationic species of tropane in gas phase presents the highest negative value indicating probably that for these two reasons, this species is the less reactive than the other ones (see Table 13).

Table 12.

Frontier molecular HOMO and LUMO orbitals , gap values and descriptors for the three species of S(−) and R(+)-promethazine (in eV) in gas and aqueous solution by using the B3LYP/6-31G* level of theory.

Orbitals	Free base		Cationic		Hydrochloride
	Gas	PCM	Gas	PCM	Gas	PCM
S(-)-promethazine
HOMO	-5.0096	-5.0559	-7.943		-5.5593	-5.0151
LUMO	-0.2939	-0.2857	-3.3769		-0.6939	-0.8109
∣GAP∣	4.7157	4.7702	4.5661		4.8654	4.2042
Descriptors
χ	-2.3579	-2.3851	-2.2831		-2.4327	-2.1021
μ	-2.6518	-2.6708	-5.6600		-3.1266	-2.9130
η	2.3579	2.3851	2.2831		2.4327	2.1021
S	0.2121	0.2096	0.2190		0.2055	0.2379
ω	1.4911	1.4954	7.0158		2.0092	2.0184
Ε	-6.2524	-6.3701	-12.9219		-7.6061	-6.1234
R(+)-promethazine
HOMO	-5.0504	-5.0776	-7.9403	-5.5593	-5.3579	-5.1538
LUMO	-0.2748	-0.2748	-3.3633	-0.6939	-0.5469	-0.6612
∣GAP∣	4.7756	4.8028	4.5770	4.8654	4.8110	4.4926
Descriptors
χ	-2.3878	-2.4014	-2.2885	-2.4327	-2.4055	-2.2463
μ	-2.6626	-2.6762	-5.6518	-3.1266	-2.9524	-2.9075
η	2.3878	2.4014	2.2885	2.4327	2.4055	2.2463
S	0.2094	0.2082	0.2185	0.2055	0.2079	0.2226
ω	1.4845	1.4912	6.9790	2.0092	1.8118	1.8817
Ε	-6.3578	-6.4266	-12.9341	-7.6061	-7.1020	-6.5311

χ = - [E(LUMO)- E(HOMO)]/2; μ = [E(LUMO) + E(HOMO)]/2; η = [E(LUMO) - E(HOMO)]/2.

S = ½η; ω = μ²/2η; Ε = μ*η.

Table 13.

Frontier molecular HOMO and LUMO orbitals and gap values for the three species of S(-) and R(+)-promethazine compared with other species in gas and aqueous solution phases by using the B3LYP/6-31G* level of theory.

Orbital	Scopolamine#,b	Heroinc	Morphined	Cocainee	Tropanef	Cyclizineg	Promethazinea
							S(-)	R(+)
Free base/Gas phase
∣GAP∣	5.4004	5.6563	5.6044	4.8580	7.5506	5.3946	4.7157	4.7756
Free base/Aqueous solution
∣GAP∣	5.4758	5.6414	5.4750	4.9487	7.6611	5.5067	4.7702	4.8028
Cationic/Gas phase
∣GAP∣	5.6356	5.4268	5.1889	5.4468	9.5595	5.5823	4.5661	4.5770
Hydrochloride/Gas phase
∣GAP∣	4.9239	5.3024	5.4417	3.6813	6.8246		4.8654	4.8110
Hydrochloride/Aqueous solution
∣GAP∣	5.4026	4.4469	4.5840	3.6813	5.9119	4.2159	4.2042	4.4926

^#Hydrobromide.

^aThis work.

^bFrom Ref [7].

^cFrom Ref [5].

^dFrom Ref [1].

^eFrom Ref [3].

^fFrom Ref [2].

^gFrom Ref [9].

Fig. 6.

Calculated gap values of free base, cationic and hydrocloride species of both S(-) and R(+) enantiomers of promethazine in both media by using the B3LYP/6-31G* method compared with reported values for alkaloids and antihistaminic agents.

Table 14.

Global electrophilicity(ω) and nucleophilicity (E) indexes for the three species of S(-) and R(+)-promethazine compared with other species in gas and aqueous solution phases by using the B3LYP/6-31G* level of theory.

Descriptor	Scopolamine#,b	Heroinc	Morphined	Cocainee	Tropanef	Cyclizineg	Promethazinea
							S(-)	R(+)
Free base/Gas phasea
ω	1.7393	1.5083	1.3639	2.5183	0.3914	1.6777	1.4911	1.4845
Ε	-8.2756	-8.2606	-7.7475	-8.4959	-6.4905	-8.1146	-6.2524	-6.3578
Free base/Aqueous solutiona
ω	1.7504	1.5180	1.2339	2.5297	0.4429	1.7288	1.4954	1.4912
Ε	-8.4763	-8.2545	-7.1153	-8.7546	-7.0557	-8.4953	-6.3701	-6.4266
Cationic/gas phasea
ω	6.4529	6.7459	6.8155	7.9799	6.9598	6.5083	7.0158	6.9790
Ε	-16.9925	-16.4174	-15.4288	-17.9548	-38.9872	-16.8238	-12.9219	-12.9341
Hydrochloride/Aqueous solutiona
ω	0.9799	1.9667	1.8414	2.6828	0.6421	1.9053	2.0184	1.8817
Ε	-6.2154	-6.5755	-6.6589	-5.7845	-5.7592	-5.9742	-6.1234	-6.5311

ω = μ²/2η; Ε = μ*η.

^#Hydrobromide.

^aThis work.

^bFrom Ref [7].

^cFrom Ref [5].

^dFrom Ref [1].

^eFrom Ref [3].

^fFrom Ref [2].

^gFrom Ref [9].

Fig. 7.

Calculated electrophilicity indexes of free base, cationic and hydrocloride species of both S(-) and R(+) enantiomers of promethazine in both media by using the B3LYP/6-31G* method.

3.7. Vibrational study

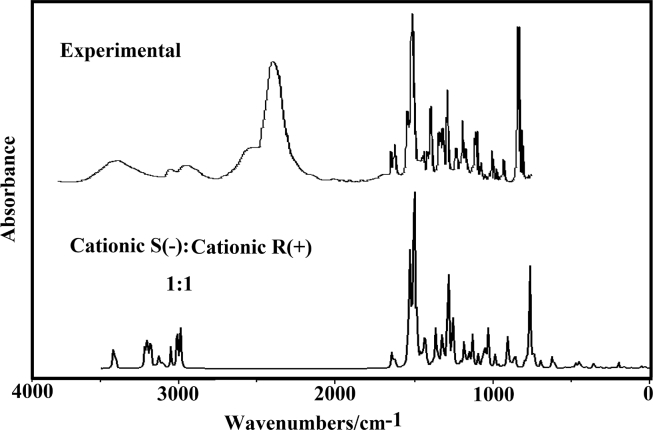
B3LYP calculations have optimized the three species of S(-) and R(+)-PTZ forms with C₁ symmetries. The normal vibration modes expected for the free base, cationic and hydrochloride species are respectively 114, 117 and 120 and, where all modes are active, in both spectra. The experimental available infrared and Raman spectra for promethazine hydrochloride were taken from Refs [10] and [66]. The experimental IR from Ref [66] was compared with the corresponding predicted for the three species of both enantiomers in Fig. 8 while the comparisons of the corresponding predicted Raman spectra with the experimental one are given in Fig. 9. Evidently, the hydrochloride forms of both enantiomers are not present in the experimental IR spectrum because the predicted intense IR bands of both S(-) and R(+) forms at 1625 and 1713 cm⁻¹ respectively are not observed in the experimental one with the same intensities. Besides, the predicted IR spectra in the 2000-500 cm⁻¹ region show strong differences between the intensities of IR bands at 1459 and 759 cm⁻¹ in the three species of both S(-) and R(+)-PTZ enantiomers but when only the average of cationic forms by using frequencies and intensities Lorentzian band shapes for a 1:1 population ratio of each species the ratio between those two bands decreases notably, as shown in Fig. 10. Note that in the higher wavenumbers region the predicted IR spectra for both cationic species are similar to the corresponding experimental ones. Hence, it is evident the presence of both cationic species of S(-) and R(+)-PTZ in the solid phase, as revealed by Borodi et al [19]. The normal internal coordinates, the SQMFF methodology [39] and the Molvib program [42] were used to calculate the harmonic force fields in order to perform the complete vibrational assignments of all species of DHC. The scale factors used were those reported in the literature [40]. In Table 15 are presented the experimental and calculated wavenumbers together with the assignments of three species of S(-) and R(+)-PTZ forms, respectively. Below, discussions of assignments for some groups are presented.

Fig. 8.

Experimental infrared spectrum of hydrocloride promethazine compared with the corresponding predicted for the free base, cationic and hydrochloride species of both S(-) and R(+) enantiomers by using B3LYP/6-31G* level of theory.

Fig. 9.

Experimental Raman spectrum of hydrocloride promethazine compared with the corresponding predicted for the free base, cationic and hydrochloride species of both S(-) and R(+) enantiomers by using B3LYP/6-31G* level of theory.

Fig. 10.

Experimental infrared spectrum of hydrocloride promethazine compared with the corresponding average predicted for the cationic species of both S(-) and R(+) enantiomers by using frequencies and intensities Lorentzian band shapes for a 1:1 population ratio of each species at B3LYP/6-31G* level of theory.

Table 15.

Observed and calculated wavenumbers (cm⁻¹) and assignments for the three species of S(-) and R(+)-promethazine in gas phase by using B3LYP/6-31G* level of theory.

Experimental			B3LYP/6-31G* Methoda
			S(-)-PTZ						R(+)-PTZ
			Free base		Cationic		Hydrochloride		Free base		Cationic		Hydrochloride
IRc	IRd	Ramane	SQMb	Assignmentsa	SQMb	Assignmentsa	SQMb	Assignmentsa	SQMb	Assignmentsa	SQMb	Assignmentsa	SQMb	Assignmentsa
3391w,br	3448w	3411vw			3295	νN3-H41					3273	νN3-H41
		3104w							3092	νC14-H34	3092	νC19-H39
											3091	νC20-H40
		3104w									3090	νaCH3(C11)	3090	νC13-H33
									3087	νC13-H33	3088	νaCH3(C12)	3087	νC14-H34
													3081	νC15-H35
									3079	νC20-H40	3080	νC17-H37	3080	νC20-H40
									3078	νC19-H39	3078	νC16-H36	3078	νaCH3(C11)
											3073	νC15-H35	3071	νaCH3(C12)
			3071	νC14-H34							3072	νC18-H38	3070	νC17-H37
			3066	νC13-H33	3069	νC20-H40	3067	νC14-H34	3066	νC15-H35	3067	νaCH3(C12)	3067	νC16-H36
					3069	νC19-H39	3065	νC19-H39	3066	νC16-H36	3063	νaCH3(C11)	3060	νC19-H39
		3058sh	3059	νC20-H40	3057	νC17-H37					3059	νC13-H33	3058	νC18-H38
		3058sh	3058	νC19-H39	3056	νC16-H36 νC18-H38	3060	νC20-H40	3057	νC18-H38
					3051	νaCH3(C12)	3057	νC13-H33	3056	νC17-H37	3055	νC14-H34
					3050	νC16-H36 νC15-H35	3049	νC16-H36
			3046	νC16-H36	3050	νC15-H35	3047	νC15-H35
			3045	νC15-H35	3044	νaCH3(C11)	3040	νC18-H38
3046w,br		3044m			3039	νC13-H33	3039	νC17-H37					3039	νaCH3(C12)
			3037	νC17-H37	3037	νC14-H34							3036	νaCH3(C11)
					3035	νaCH3(C12)
		3035sh	3037	νC18-H38	3031	νaCH3(C11)	3032	νaCH3(C12)			3030	νaCH3(C8)	3031	νaCH2
							3019	νaCH3(C11)	3021	νaCH3(C11)			3025	νaCH3(C8)
							3006	νaCH3(C11)	3013	νaCH3(C8)			3014	νaCH3(C8)
		3018w					3004	νaCH3(C12)	3012	νaCH2	3012	νaCH3(C8)
			2986	νaCH3(C8)	2995	νaCH3(C8)	2999	νaCH3(C8)	3000	νaCH3(C12)	2989	νC4-H21
		2980w	2984	νaCH2	2984	νaCH2	2986	νaCH2	2999	νaCH3(C8)	2982	νsCH3(C12)
	2966sh		2978	νaCH3(C12)	2974	νaCH3(C8)	2979	νaCH3(C8)			2978	νsCH3(C11)
		2948w	2968	νaCH3(C8)	2955	νC4-H21			2962	νaCH3(C11)			2958	νsCH3(C12)
			2962	νaCH3(C11)	2952	νsCH3(C12)	2953	νC4-H21	2957	νaCH3(C12)			2956	νsCH3(C11)
2938w,br		2930sh	2928	νC4-H21	2947	νsCH3(C11)	2931	νsCH3(C12)			2974	νaCH2	2945	νsCH3(C8)
			2925	νsCH3(C12)			2926	νsCH3(C11)	2929	νsCH3(C8)	2933	νsCH3(C8)	2941	νC4-H21
			2918	νsCH3(C11)			2913	νsCH3(C8)	2915	νsCH2			2926	νsCH2
		2907sh	2907	νsCH3(C8)	2908	νsCH3(C8)
2872sh	2888sh	2887sh	2875	νsCH2	2863	νsCH2	2872	νsCH2	2837	νC4-H21	2894	νsCH2
	2824m		2793	νaCH3(C12)					2820	νsCH3(C12)
	2747m		2782	νaCH3(C11)					2812	νsCH3(C11)
		2673w
2370s		2508w
	1688w						1625	νN3-H41					1713	νN3-H41
1638vw	1633w	1630vw							1600	νC13-C17	1596	νC13-C17 νC14-C18	1599	νC14-C18
1596w	1586w	1581sh	1581	νC14-C18			1580	νC14-C18	1581	νC18-C20 νC17-C19	1584	νC17-C19 νC18-C20	1581	νC17-C19 νC15-C19
		1558s			1577	νC13-C17 νC14-C18			1577	νC14-C18	1578	νC7-C14	1578	νC13-C17
1573w	1582sh	1558s	1561	νC7-C14	1566	νC17-C19	1564	νC7-C14	1570	νC17-C19 νC18-C20	1573	νC18-C20 νC17-C19	1571	νC7-C14
		1558s	1556	νC13-C17	1558	νC7-C14	1557	νC13-C17
	1550w	1552sh	1550	νC17-C19 νC18-C20	1554	νC17-C19	1552	νC17-C19 νC18-C20					1498	ρN3-H41
1489m	1500w								1489	βC13-H33 βC16-H36	1486	δaCH3(C8)	1488	βC14-H34
	1480sh								1483	δaCH3(C8)	1484	δaCH3(C8)	1480	δaCH3(C8)
1466sh		1470w					1473	ρN3-H41	1474	δCH2	1478	δaCH3(C12)	1476	δCH2 δaCH3(C8)
1466sh		1470w					1470	βC16-H36 βC14-H34	1471	δaCH3(C11) δaCH3(C12)			1473	δaCH3(C8)
1466sh		1470w	1469	βC16-H36 βC14-H34 βC13-H33	1467	βC15-H35 βC13-H33 βC14-H34			1468	δaCH3(C8)	1468	δaCH3(C8)
1459vs	1454sh								1463	δaCH3(C12)	1463	δaCH3(C11)	1464	δaCH3(C11) δaCH3(C12)
1459vs	1454sh		1456	δaCH3(C12) δaCH3(C11)	1456	δaCH3(C11)			1458	δaCH3(C11)	1460	βC14-H34 βC13-H33	1461	δaCH3(C12)
1459vs	1454sh				1452	δaCH3(C11)	1454	δCH2	1455	δCH2	1453	δCH2	1454	δCH2
	1451sh		1451	δCH2	1451	δaCH3(C12)	1451	δaCH3(C8)	1450	δaCH3(C12)	1451	δaCH3(C11)	1449	δaCH3(C11)
1447sh	1447sh		1444	δaCH3(C8)	1446	δaCH3(C8) δaCH3(C12)	1449	δaCH3(C11)			1447	βC20-H40 βC18-H38	1447	βC20-H40 βC18-H38
1447sh	1447sh		1440	δaCH3(C8)	1444	δaCH3(C12)	1442	βC13-H33	1446	βC20-H40 βC18-H38	1446	βC19-H39	1446	βC19-H39
1433sh	1438sh		1437	δaCH3(C12) δaCH3(C8)	1440	δCH2	1438	δaCH3(C8)	1444	βC19-H39	1442	δaCH3(C12)	1443	δaCH3(C11) δaCH3(C12)
1433sh	1438sh	1435sh	1435	δaCH3(C8)	1432	βC19-H39	1438	δaCH3(C12)
			1430	δaCH3(C12)	1431	βC20-H40 βC17-H37	1430	βC20-H40	1435	δsCH3(C12) δsCH3(C11)
			1429	βC17-H37 βC19-H39	1429	δaCH3(C11) δaCH3(C12)	1429	βC19-H39			1427	δsCH3(C12)	1425	wagCH2 ρ′N3–H41
		1421sh	1427	βC19-H39	1423	δaCH3(C8)	1426	δaCH3(C12)	1406	wagCH2	1407	wagCH2	1420	wagCH2
	1419sh		1417	δaCH3(C11)	1411	δsCH3(C12)	1420	δaCH3(C11)			1400	ρN3-H41	1408	δsCH3(C11)
1408vw		1403sh	1406	δsCH3(C11)	1400	δaCH3(C8)	1408	ρ′N3–H41	1402	wagCH2 δsCH3(C11)	1397	δsCH3(C11)	1401	δsCH3(C12)
1390vw	1395sh				1392	ρ′N3–H41 wagCH2	1394	wagCH2			1394	ρ′N3–H41
1378w		1387w	1388	wagCH2	1381	ρN3-H41	1376	δsCH3(C11) δsCH3(C12)	1375	δsCH3(C8) ρ′C4–H21	1380	δsCH3(C8)	1379	δsCH3(C8)
	1364sh	1374vw	1376	δsCH3(C12)	1379	δsCH3(C11)	1360	δsCH3(C8)
1354w			1362	ρC4-H21	1361	δsCH3(C8)	1355	νN3-H41 δsCH3(C12)	1357	δsCH3(C8)	1350	ρ′C4–H21 ρCH2	1356	ρ′C4–H21
1342sh	1347sh	1340w	1342	δsCH3(C8)	1349	ρC4-H21	1351	ρC4-H21
1334m	1327sh	1326sh	1323	ρ′C4–H21					1335	ρ′C4–H21	1330	ρC4-H21 νN2-C6	1327	ρCH2 νN2-C6
		1320w			1319	ρCH2 νN2-C6	1320	ρ′C4–H21	1318	ρC4-H21	1320	ρ′C4–H21	1313	ρC4-H21
1292sh	1312sh	1315sh	1309	νN2-C6 ρCH2	1307	ρ′C4–H21	1315	νN2-C6	1301	νC6-C13	1300	νC6-C13	1301	νC6-C13
1285m	1294s	1296sh							1286	βC15-H35 νC16-C10	1282	νC9-C15 νC6-C9 νC7-C10	1288	βC15-H35 βC13-H33
1285m	1294s	1296sh	1283	νC6-C13	1282	νC6-C13	1283	νC6-C13	1285	νC9-C15 νC6-C9	1286	βC15-H35	1285	νC16-C10 νC7-C10 νC6-C9
1270m	1279sh	1289m	1273	βC15-H35 νC16-C10	1274	νC16-C10 νC9-C15	1275	νC16-C10	1270	νN3-C4 ρCH3(C12)
		1274sh	1267	νC9-C15 νC6-C9 νC7-C10
1256m		1253sh	1265	νN3-C4	1264	νC7-C10 νC6-C9	1266	νC9-C15 νC7-C10 νC6-C9	1267	ρCH2	1266	ρCH2	1269	ρCH2 βC16-H36
1249sh		1247m	1253	ρCH2	1255	ρCH2 βC16-H36	1260	ρCH2
1228m	1233sh	1236sh			1233	νN2-C5 νN2-C7	1234	νN2-C5 νN2-C7	1243	νN2-C6 βC14-H34 νC7-C14	1248	νN2-C5 νN2-C7	1242	νN2-C6
1228m		1223sh	1228	νN2-C6			1228	ρ′CH3(C12) ρ′CH3(C11)	1224	νN3-C12	1226	ρCH3(C12)	1238	ρCH3(C12)
1218sh	1208s	1218w	1217	νN2-C7	1216	ρ′CH3(C12)			1221	νN2-C7	1216	ρ′CH3(C11)	1223	νN2-C7
1218sh	1208s	1209sh			1210	νN2-C6	1211	νN2-C7 βC15-H35
1170w	1189vs	1209sh	1187	νN3-C11	1187	ρ′CH3(C11)	1181	ρCH3(C11) δC8C4N3			1178	ρ′CH3(C12)	1200	ρ′CH3(C11)
1170w	1189vs	1171sh							1166	βC17-H37	1167	βC17-H37	1172	ρCH3(C11)
1162sh	1167sh	1164m	1153	βC18-H38 βC20-H40	1156	βC17-H37	1155	βC17-H37	1164	ρCH3(C11) ρ′CH3(C12)	1166	βC18-H38 βC20-H40	1167	βC17-H37
	1156sh	1157sh	1151	βC17-H37	1155	βC18-H38 βC20-H40	1153	βC18-H38	1163	βC18-H38	1157	ρ′CH3(C11) ρCH3(C11)	1164	βC18-H38 βC20-H40
1142w			1143	ρCH3(C11) ρCH3(C12)	1141	ρ′CH3(C12)	1138	ρCH3(C12)	1137	βC20-H40	1138	βC19-H39	1138	νC15-C19
1128m		1129sh	1126	βC19-H39 βC20-H40	1128	νC15-C19	1128	βC19-H39 βC20-H40	1120	βC19-H39 βC20-H40	1121	νC15-C19	1121	νC16-C20
1106w	1117sh	1118m	1109	νC15-C19	1111	νC16-C20 νC15-C19	1111	νC16-C20	1111	ρCH3(C8)	1100	ρCH3(C8) νN2-C5
1091sh	1103m	1105m	1097	ρ′CH3(C8)			1094	ρ′CH3(C8)	1103	ρCH3(C11) ρ′CH3(C12)	1095	ρCH3(C8)	1107	ρCH3(C8)
1091sh	1103m	1105m	1084	ρCH3(C12) ρCH3(C11)	1089	νN2-C5			1089	νN2-C5 νC7-C10			1091	νN2-C5
1082sh	1075sh	1088sh	1080	νN2-C5 νC9-S1	1084	νN2-C5	1082	νN2-C5	1079	ρ′CH3(C8)			1079	νC4-C8
1066vw	1066sh		1073	νC4-C8			1069	νC4-C8	1067	νC4-C8	1072	νC4-C8
1059vw		1058sh	1060	ρ′CH3(C11)	1057	ρ′CH3(C8)	1052	βR1(A3)			1057	βR1(A3)	1057	ρ′CH3(C12)
1048sh			1047	βR1(A3)	1054	βR1(A1)	1050	ρCH3(C11)	1052	βR1(A3)			1053	βR1(A3)
1043m	1040sh	1044sh	1043	βR1(A1)	1048	βR1(A3)	1048	βR1(A1)	1048	βR1(A1)	1051	βR1(A1)	1051	βR1(A1)
1034m		1027vs	1030	ρ′CH3(C12) νN3-C11	1023	νC17-C19 ρCH3(C12)	1040	βR1(A3)	1036	ρ′CH3(C11) νN3-C11	1031	νC17-C19	1034	νC4-C8 βR1(A3)
1034m		1027vs	1023	νC17-C19	1020	ρCH3(C11) ρCH3(C12)			1033	νC17-C19 νC15-C19	1029	νC18-C20 νC16-C20	1033	νC17-C19 νC18-C20
1034m		1027vs	1021	νC18-C20 νC16-C20	1019	νC18-C20 νC16-C20	1024	νC17-C19	1031	νC18-C20 νC16-C20	1025	ρCH3(C11)	1032	νC18-C20 νC17-C19 νC15-C19
1009sh	1012s	1008sh			1015	νC4-C8 νC4-C5	1021	νC18-C20 νC15-C19
1005w	1012s	1008sh									1006	ρ′CH3(C8)	1002	νN3-C11
	987s	996sh			987	γC19-H39 γC17-H37	988	νN3-C11 νN3-C12			981	γC19-H39 γC17-H37
988vw			973	γC18-H38 γC20-H40							980	γC20-H40
976w		971vw	971	γC17-H37	986	γC20-H40	976	γC20-H40 γC18-H38	968	νN3-C12 νN3-C11			971	γC17-H37
							975	γC19-H39 γC17-H37	964	γC17-H37
957sh	955s		957	νN3-C12					963	γC18-H38	958	νN3-C11 νN3-C12	965	γC20-H40 γC18-H38
950w		949vw			949	νN3-C11 νN3-C12
935sh	941sh		935	γC16-H36	943	γC15-H35	937	γC15-H35			937	γC15-H35	939	ρCH3(C8)
930w	930sh		934	γC15-H35	941	γC16-H36 γC18-H38	936	γC16-H36	928	γC15-H35 γC13-H33	930	γC16-H36 γC18-H38	932	γC15-H35
924sh		929w			924	ρCH3(C8)	928	νN3-C4 ρCH3(C8)	923	γC16-H36	928	ρCH3(C8) γC15-H35	922	γC16-H36
902w	893m	917sh	915	ρCH3(C8)			918	ρCH3(C8)	920	γC15-H35			915	νN3-C12
884vw	893m				875	νN3-C4			866	νC4-C5	873	νC4-C5	867	γC13-H33 νC4-C5
874vw		873sh	854	γC13-H33	856	γC13-H33	862	νC4-C5			861	γC13-H33
859w	856s	856w	851	γC14-H34	854	γC14-H34	853	γC14-H34	856	γC13-H33	854	γC14-H34	857	γC13-H33 γC15-H35
852w	832sh	842sh	847	νC4-C5	852	γC14-H34 γC16-H36	850	γC13-H33	852	γC14-H34	844	νN3-C11 νN3-C12	850	γC14-H34
807vw	817sh	808m	803	τwCH2	808	τwCH2	813	τwCH2	816	τwCH2	811	τwCH2	813	τwCH2
778sh	775sh	775sh	778	βR2(A1)	774	βR2(A1)	777	βR2(A1)	794	δC5C4N3	787	νN3-C4	803	νN3-C4 δC5C4N3
759vs	758s	761w	752	γC19-H39	756	γC19-H39 γC17-H37	754	νN3-C4	760	νN3-C4	760	γC19-H39 γC17-H37	762	βR2(A1)
759vs	758s	761w							756	γC19-H39	755	γC20-H40 γC14-H34	757	γC19-H39
759vs	758s	754sh	751	γC20-H40	751	γC20-H40 γC18-H38	752	γC20-H40	751	γC20-H40			752	γC20-H40 γC18-H38
752sh	742sh		745	γC20-H40 γC19-H39			746	γC20-H40 γC18-H38			747	νN3-C4
734m		737sh	722	τR1(A1)	723	τR1(A3) τR1(A1)	722	τR1(A1)	723	τR1(A3)	722	τR1(A3)	722	τR1(A3)
		729m			720	τR1(A1)
712vw	718m		714	τR1(A3)	713	τR1(A3)	714	τR1(A3)	716	τR1(A1)	716	τR1(A1)	715	τR1(A1)
695w	687m	688sh	686	βR2(A3)	683	τR1(A3) τR1(A1)	686	βR2(A3)	688	βR2(A3)	685	τR1(A3) τR1(A1)	688	τR1(A3) τR1(A1)
675w	655m	672s	676	βR3(A1)	675	βR3(A1) βR2(A3)	677	βR3(A1)	677	βR3(A1)	676	βR3(A1)	677	βR3(A1) βR2(A3)
	646s	616vw	623	βR3(A3)	619	βR3(A3)	631	βR3(A3)	623	βR3(A3)	619	βR3(A3)	622	βR3(A3)
	613w	594vw	609	βR2(A1)	611	βR2(A1)	613	βR2(A1)	605	βR2(A1) βR1(A2)	601	βR1(A2) βR2(A1)	604	βR2(A1) βR1(A2)
	567s	540w	539	τR1(A2) τR3(A1)	534	τR3(A1)	546	τR2(A3) τR1(A2)	537	τR1(A2) τR3(A1)	532	τR1(A2) τR3(A1)	538	τR1(A2) γN2-C5
			524	βR1(A2)	526	βR1(A2)	530	βR1(A2)	524	τR3(A1)	519	τR3(A1)	525	τR3(A1)
	510vw	518sh	520	τR3(A3)	517	τR3(A3)	520	τR3(A3) τR3(A1)	522	τR3(A3)	514	τR3(A3)	520	τR3(A3)
	486sh	508w	502	δC8C4N3			497	τR3(A1)	490	δC8C4N3	494	δC5C4C8 δC11N3C12	503	δC5C4C8 νH41-Cl42
	486sh	508w			486	δC4N3C12 τR2(A1)	489	δC8C4N3	479	δC5C4C8			475	δC11N3C12 δC4N3C11
	482s	479sh			473	δC8C4N3					466	δC11N3C12 δC4N3C11	471	δC4N3C12
		470w	451	δC4N3C11	444	τR2(A3)	447	τR2(A3) τR2(A1)	445	τR2(A3) τR2(A1)			441	τR2(A3)
	440s	440sh	439	δC11N3C12					439	τR2(A3) ButtC6-C9	438	τR2(A3)
			435	τR2(A3)	432	τR2(A1)	434	τR2(A1)	434	τR2(A1)	434	τR2(A1)	434	τR2(A1)
	423sh	423m	426	τR2(A1) νC10-S1	427	νC9-S1 νC10-S1	429	νC9-S1	427	νC9-S1 νC10-S1	427	νC10-S1 νC9-S1 βR2(A3)	429	νC10-S1 νC9-S1
	423sh	423m	421	δC5C4N3	417	δC11N3C12	424	νC10-S1			418	δC8C4N3 δC4N3C12
	392w	394sh	402	βR2(A2) βR3(A2)	401	βR2(A2)	404	βR2(A2)	407	βR2(A2) βN2-C5	402	βR2(A2)	407	βR2(A2)
	392w	394sh									382	δC5C4C8	395	δC5C4C8
	370w	370sh	360	γN2-C5			375	δC11N3C12	379	δC4N3C11			377	δC8C4N3
	357sh	357sh	352	δC5C4C8	358	βR3(A2)	356	βR3(A2) δC5C4C8	356	γN2-C5 βR3(A2)	357	βR3(A2)	356	βR3(A2)
	357sh	357sh			349	δC5C4C8			346	δC4N3C12	347	δC4N3C12 δC4N3C11
		340sh	333	βR2(A2)	331	τR2(A3)	332	τR2(A3)
		337s					325	βN2-C5	337	τR2(A3)	336	τR2(A3)	340	τR2(A3) γN2-C5
	320sh	325sh	319	τR2(A3) δC11N3C12	315	βN2-C5							318	βN2-C5
	303m	294vw							302	δC11N3C12	305	βN2-C5 δC5C4N3
	278sh		281	βN2-C5 δC4N3C12			288	δC4N3C12 δC4N3C11	280	τR2(A2)
	278sh				273	δC4N3C12	272	τR2(A2)	272	τwCH3(C8)	273	τR2(A2)	284	τR2(A2)
	245sh		266	τR2(A2)	263	δC4N3C11					257	τwCH3(C8)	267	τwCH3(C8)
	235m						232	νH41-Cl42	233	ButtC7-C10			232	ButtC7-C10 ButtC6-C9
	235m		227	ButtC6-C9 ButtC7-C10	228	ButtC6-C9 ButtC7-C10	228	ButtC6-C9 ButtC7-C10
					220	τwCH3(C11)			225	τwCH3(C11)	226	ButtC7-C10 ButtC6-C9	222	νH41-Cl42
	215s		211	τwCH3(C11) τwCH3(C12)	214	τwCH3(C8)			213	τwCH3(C12)	218	τwCH3(C11)
			209	τwCH3(C12)			209	τwCH3(C8)
	204sh		203	τwCH3(C11)					201	δN2C5C4	201	δN2C5C4	206	δN2C5C4
					198	δN2C5C4	197	δN2C5C4
	195sh		194	τwCH3(C8)	196	τwCH3(C12)							194	τwCH3(C11)
	188sh						188	τwCH3(C11)
							178	τwCH3(C12)	177	τR2(A2) τR1(A2)	178	τR2(A2) τwCH3(C12)	180	τR2(A2) τR1(A2)
			155	τR1(A2)	159	δC5C4N3	157	τR1(A2) τR2(A2)
							140	τR1(A2)			164	τwCH3(C12)	154	τwCH3(C12)
									144	τR1(A2)	143	τR1(A2)	143	τR1(A2)
			136	τR3(A1)	139	τR1(A2)
			118	τR3(A2)	115	τR3(A2)	119	τR3(A2)	122	τR3(A2) τR3(A3)	119	τR3(A2)	119	τR3(A2)
							105	τN3-H41
			80	τN3-C4			80	δN3H41Cl42					83	δN3H41Cl42 ρ′N3–H41
			62	τR2(A2) γN2-C5	72	τN3-C4	66	τN3-C4	72	τR3(A2)			70	τN3-C4 τN3-H41
			54	τR2(A2) δN2C5C4	58	τR2(A2)	57	τR2(A2)	60	τR2(A2)	61	γN2-C5 τwN2-C5	62	τN3-H41
			42	γN2-C5 τwN2-C5	52	γN2-C5 τN3-C4			47	τN3-C4	58	τR2(A2)	54	τR2(A2) τR2(A2)
					36	τC4-C5	31	γN2-C5	37	τC4-C5	35	τC4-C5	37	γN2-C5 τwN2-C5
			31	τwN2-C5 τC4-C5			27	τN3-C4 τC4-C5	27	τwN2-C5	32	τN3-C4 γN2-C5	31	τC4-C5
					24	γN2-C5 τwN2-C5	21	τC4-C5 τwN2-C5			18	τN3-C4	18	τN3-C4

Abbreviations: ν, stretching; β, deformation in the plane; γ, deformation out of plane; wag, wagging; τ, torsion; βR, deformation ring; τR, torsion ring; ρ, rocking; τw, twisting; δ, deformation; a, antisymmetric; s, symmetric; (A1), Ring 1.

^aThis work.

^bFrom scaled quantum mechanics force field.

^cFrom Ref [66].

^dFrom Ref [10].

^eFrom Ref [10].

3.7.1. Band assignments

3.7.1.1. N–H modes

For both PTZ forms, the NH stretching modes are expected only for the cationic and hydrochloride species. For instance, in monomer and dimer of clonidine hydrochloride [67] these modes are assigned at 3427/3341 and 2584cm⁻¹, respectively while in those two forms of diphenhydramine [8] these modes are predicted respectively at 3150 and 1748 cm⁻¹. Here, in the cationic and hydrochloride species of S(-) form of DHC these modes are predicted to 3295 and 1638 cm⁻¹ and in the R(+) form they are predicted to 3273 and 1713 cm⁻¹. Then, they can be assigned in the same region. Here, the group of bands observed in IR spectrum of DHC between 2800 and 2200 cm⁻¹ with a strong band centered at 2370 cm⁻¹ could be assigned to the N–H stretching modes due to H bonds, as was also reported for clonidine hydrochloride [67]. The N–H rocking modes for both cationic and hydrochloride forms are predicted in different regions, as observed in Table 15. Later, these modes are assigned in accordance. The torsion τN3-H41 modes expected only in both hydrochloride forms are predicted by calculations to 105 and 70 cm⁻¹ and they cannot be assigned because there are not observed bands in this region.

3.7.1.2. CH modes

In the three species of both S(-) and R(+)-PTZ enantomers, eight aromatics C–H stretching modes are expected and only one stretching mode (C4–H21) with aliphatic characteristic. Hence, they are predicted by the SQM/B3LYP/6-31G* calculations in different regions. Evidently, the aromatics modes are assigned at higher wavenumbers than the other ones, as shown in Tables 15 and 16. Besides, the in-plane deformation or rocking and out-of-plane deformation modes expected only for these C–H aromatics are predicted respectively between 1489/1120 and 987/745 cm⁻¹. Hence, they can be assigned in these regions. These modes in carquejol [50] are assigned between 1483/1121 and 972/746 cm⁻¹.

Table 16.

Scaled internal force constants for the free base, cationic and hydrochloride species of S(-) and R(+)- prometazine in gas phase by using the B3LYP/6-31G* method compared with the corresponding to cyclizine.

Force constant	Promethazinea						Cyclizineb
	S(-)			R(+)
	Free base	Cationic	HCl	Free base	Cationic	HCl	Free base	Cationic	HCl/PCM
f(νN-H)		6.02	2.47		5.94	2.60		5.91	4.61
f(νN-CH3)	4.67	3.92	4.25	4.70	3.94	4.94	4.85	4.06	4.33
f(νC-N)	4.97	4.65	4.82	5.05	4.74	4.96	4.54	4.13	4.19
f(νCH2)	4.74	4.72	4.74	4.85	4.76	4.89	4.62	4.82	4.87
f(νCH3)	4.82	4.83	4.85	4.90	4.94	4.95	4.69	5.06	5.07
f(νC-H)R	5.11	5.11	5.11	5.18	5.19	5.19	5.15	5.17	5.18
f(νC-H)	4.73	4.82	4.81	4.45	4.90	4.78	4.31	4.44	4.74
f(νC=C)							6.50	6.50	6.46
f(νC-C)	3.40	3.57	3.65	3.70	3.56	3.69
f(δCH2)	0.78	0.79	0.79	0.81	0.82	0.81	0.74	0.73	0.73
f(δCH3)	0.53	0.53	0.53	0.56	0.56	0.57	0.58	0.56	0.55

Units are mdyn Å⁻¹ for stretching and mdyn Å rad⁻² for angle deformations.

^aThis work.

^bFrom Ref. [9].

3.7.1.3. CH₃ modes

The three species of both S(-) and R(+)-PTZ enantiomers present three CH₃ groups, where two of them are linked to N3 atoms and the other one to C4 atoms. Then, these modes are predicted in different regions and, thus, they can be easily assigned in accordance to the calculations. In carquejol [50] these stretching modes are assigned between 3031 and 2919 cm⁻¹ while in this case these modes are assigned to the IR and Raman bands between 3411 and 2747 cm⁻¹. Note that the symmetrical stretching modes corresponding to CH₃ groups linked to N3 atoms of two free base species of both S(-) and R(+)-PTZ are predicted at lower wavenumbers and, hence, they are assigned to the IR bands at 2824 and 2747 cm⁻¹. The CH₃ deformation, rocking and twisting modes in carquejol [50] are respectively assigned between 1587/1436, 1084/1026 and 220/171 cm⁻¹. Here, those three vibration modes are assigned to the IR and Raman bands to 1500/1340, 1289/902 and 267/154 cm⁻¹. These latter modes between 178 and 154 couldn't be assigned due to that there are not observed bands in these regions.

3.7.1.4. CH₂ modes

All PTZ species have only one CH₂ group, for which, the expected antisymmetrical and symmetrical stretching, deformation, wagging, rocking and twisting modes are clearly assigned as predicted by the calculations. For the free base and hydrochloride species of R(+)-PTZ the antisymmetrical modes are predicted at higher wavenumbers than the other species of S(-) form, hence, those modes are assigned to the groups of IR and Raman bands at 3037/2872, 1470/1433, 1421/1387, 1354/1247 and 817/808 cm⁻¹. Those vibration modes of the two CH₂ groups of Carquejol are assigned in approximately the same regions [50].

3.7.1.5. Skeletal modes

In the three species of both S(-) and R(+)-PTZ enantiomers are very important the N3–C11 and N3–C12 stretching modes because their corresponding bonds are predicted by B3LYP/6-31G* calculations longer than the corresponding to N3–C4 bonds, as was experimentally observed by X-ray diffraction [19]. Therefore, the strong IR bands at 1012, 987, 955 and 893 cm⁻¹ could be associated to the N3–C11 and N3–C12 stretching modes. Note that the IR band of medium intensity at 1256 cm⁻¹ could be also attributed to the N3–C4 stretching mode of free base of S(-)-PTZ while the strong IR band at 1189 cm⁻¹ could be assigned to the N3–C11 stretching mode of free base of that form. Moreover, the very strong IR band at 759 cm⁻¹ and the band at 893 cm⁻¹ could be associated to N3–C4 stretching modes of both forms. The IR bands at 1128, 1208 and 1105 cm⁻¹ could be assigned to other N–C stretching modes (N2–C5, N2–C6 and N2–C7) expected for all species of PTZ because the calculations predicted these modes in those regions. The C=C stretching modes are usually assigned between 1680 and 1659 cm⁻¹ [[1], [2], [3], [5], [6], [7], [8], [9], [45], [47], [48], [49], [50], [52], [53], [67]]; thus, the strong IR bands at 1558 cm⁻¹ is without difficulty associated to these vibration modes of three species of both enantiomeric forms. Here, a very important result is the very strong Raman band observed at 1027 cm⁻¹ which is attributed to C–C stretching modes of both phenyl rings of both forms, as was reported for identification of PTZ by Assi [22]. In the IR spectrum that band is observed with medium intensity at 1034 cm⁻¹. The two C9–S1 and C10–S1 stretching modes expected in all species of both enantiomers can be associated to the IR band of medium intensity at 423 cm⁻¹ because all species, with exception of free base of S(-) form, are predicted in this region. In the free base of S(-) form the C9–S1 stretching mode is predicted at 1080 cm⁻¹ coupled with the N2–C5 stretching mode. The remaining skeletal modes including the deformation and torsion modes of both phenyl rings are assigned in the regions predicted by SQM calculations and according the assignments for similar compounds [1, 2, 3, 5, 6, 7, 8, 9, 45, 47, 48, 49, 50, 52, 53, 67], as detailed in Table 15.

3.8. Force fields

Both S(-) and R(+)-PTZ enantiomers have evidenced differences in the positions of IR bands because differences in their geometrical parameters are observed. Hence, it is necessary to investigate if the harmonic force constants present some changes since these parameters are also strongly dependent of their structures. Hence, the force fields for all species of both forms are calculated in gas phase by using B3LYP/6-31G* level of theory. These parameters are compared in Table 16 with the reported for the three species of cyclizine [9]. In general, the force constants for the R(+)-PTZ enantiomer have higher values than the corresponding to the S(-) form. Comparing the f(νN-H) force constants of all species, we observed that the cationic species of both forms of PTZ and cyclizine are higher than the hydrochloride ones because the presence of electronegative Cl atoms linked to H atoms generate a enlargement of N–H bonds with the consequent reduction of their f(νN-H) force constants. Note that in hydrochloride cyclizine the presence of N–CH₃ group linked to two rings produces a higher value in its force constant (4.61 mdyn Å⁻¹), as compared with both forms of PTZ. Probably, for this same reason, the f(νN-CH₃) force constants of free base and cationic species of cyclizine have higher values than the corresponding to PTZ. On the other hand, the hydrochloride species of R(+) has higher value than the other ones because the distances observed for both N–CH₃ groups are lower in the R(+) form than the S(-) one, as observed in Tables 3 and 4. Note that the f(νC-H) force constants corresponding to the aromatic rings in general are higher in all species than the aliphatic ones and, moreover, these values are similar to those published for the species of diphenhydramine [8]. The remaining constants have similar values in the two compared species, as is observed in Table 16.

3.9. Ultraviolet-visible spectrum

The electronic spectra of free base, cationic and hydrochloride species of both S(-) and R(+)-PTZ enantiomers were predicted in aqueous solution with the TD-DFT method and the Gaussian program [55] by using the B3LYP/6-31G* level of theory. The experimental UV-Vis spectrum of a racemic mixture of hydrochloride species of both enantiomers in ethanol solution was taken from Ref. [68] where in each enantiomer it is observed one intense band at c. a. 250 nm and where one of them is slightly most intense than the other one. In all theoretical spectra are observed one intense band, whose positions are respectively in free base, cationic and hydrochloride species of S(-) form at 247.0 (shoulder at 283.2 nm), 290.8 and 290.2 nm while and in the R(+) form the positions of those bands change at 245.7 (shoulder at 280.0 nm), 292.7 and 284.4 nm, respectively. The shifting of the bands observed in the experimental UV spectra from 250 to 290 nm, in relation to the theoretical ones, can be attributed to the different solvents. All UV spectra are compared in Fig. 11 with the corresponding experimental one. Here, it is evident that the free base species of both forms are protonated, as suggested by the shoulders at higher wavelengths and closer to the values for the cationic species. Also, the proximities between the maxima of both hydrochloride forms show that these species are as cationic species. Hence, these spectra evidence clearly the presence of both cationic S(-) and R(+) forms in solution. Obviously, the π→π* transitions due to the C=C double bonds justify the intense bands observed in the experimental spectra, as supported by NBO calculations.

Fig. 11.

Experimental electronic spectrum of hydrocloride promethazine in ethanol solution compared with the corresponding predicted for the free base, cationic and hydrochloride species of both S(-) and R(+) enantiomers in aqueous solution by using B3LYP/6-31G* level of theory.

3.10. Electronic circular dichroism (ECD)

The experimental ECD spectrum of hydrobromide prometazine was taken from Ref [66] which shows two bands with opposite polarity, one of them with cotton effect and the other one positive. This ECD spectrum is similar to that recorded in the 190–240 nm region by Rub et al. in the study of interaction of gelatin with promethazine hydrochloride [64]. On the other hand, the predicted ECD spectra for the free base of R(+) shows one positive band while in the S(-) form one negative in the same position. In the same region, in the cationic species of R(+) form can be observed two bands one positive and other negative while in the S(-) form two bands negative. The hydrochloride species of S(-) and R(+) forms show one band positive and two negative in different positions, hence, these forms evidently are not present in the experimental spectrum in solution. Here, only the predicted ECD spectra in solution for the cationic species of both enantiomers present similarity with the experimental one, for which, both species are present in a racemic sample of hydrochloride promethazine in aqueous solution. Then, the two negative and positive bands observed in the experimental spectrum at 250 nm could be assigned to π→π* transitions.

4. Conclusions

In this work, the molecular structures of free base, cationic and hydrochloride species of both S(-) and R(+)- enantiomers of promethazine antihistaminic agent were theoretically studied in gas phase and in aqueous solution by using the hybrid B3LYP/6-31G* method. The initial structures of S(-) and R(+) enantiomers of PTZ hydrochloride were those polymorphic forms 1 and 2 experimentally determined by X-ray diffraction. In solution, all species were optimized with the SCRF methodology by using the PCM and SD models. The corrected solvation energies (ΔG_c) by the total non-electrostatic terms and by zero point vibrational energy (ZPVE) were computed for all species showing the higher value the cationic species of R(+) form. The comparisons of geometrical parameters with the corresponding experimental ones have showed slight differences in the dihedral angles of both S(-) and R(+)-PTZ forms that later they are evidenced in the different vibrational assignments of their infrared and Raman spectra and in the calculated force constants. Here, the studied MK, Mulliken and NPA charges have evidenced variations in the three species of both enantiomers observing the higher MK charges on N2 atoms of the cationic species of R(+) species in the two media. The cationic and hydrochloride species present basically the same behaviours in the Mulliken charges where the lower values are observed on N2 atoms. The mapped surfaces MEP have clearly evidenced nucleophilic sites in the free base on the N3 and S1 atoms and in the hydrochloride species on the Cl atoms. The NBO and AIM studies reveal clearly that the hydrochloride species are most stable than the other two species of both forms and in both media and, in particular, the species of R(+)-PTZ evidence a slight higher stability than the S(-) one. The frontier orbitals studies show that the free base species of both forms in solution are more reactive than cyclizine. Higher electrophilicity indexes are observed in the cationic and hydrochloride species of PTZ than cyclizine while the cationic species of cyclizine have higher nucleophilicity index than both species of PTZ. The predicted infrared, Raman, UV-Visible and ECD have showed a reasonable concordance with the corresponding experimental available spectra. The presences of cationic species of both enantiomers are clearly supported by the infrared, Raman, UV-Vis and ECD spectra. The increase in the volume of cationic and hydrochloride species in solution could suggest the H bonds formation, as supported by AIM study. The force fields were computed by using the SQMFF approach and Molvib program which were used to perform the complete vibrational analysis. Here, the 114, 117 and 120 vibration normal modes expected for the free base, cationic and hydrochloride species were assigned and the force constants reported and compared with other reported from the literature.

Declarations

Author contribution statement

María Eugenia Manzur: Performed the experiments; Contributed reagents, materials, analysis tools or data.

Silvia A. Brandán: Conceived and designed the experiments; Performed the experiments; Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data; Wrote the paper.

Funding statement

This work was supported by grants from CIUNT Project Nº 26/D608 (Consejo de Investigaciones, Universidad Nacional de Tucumán).

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.