Abstract
Mixing of initially distinct substances plays an important role in our daily lives as well as in ecological and technological worlds. From the continuum point of view, which we adopt here, mixing is complete when the substances come together across smallest flow scales determined in part by molecular mechanisms, but important stages of the process occur via the advection of substances by an underlying flow. We know how smooth flows enable mixing but less well the manner in which a turbulent flow influences it; but the latter is the more common occurrence on Earth and in the universe. We focus here on turbulent mixing, with more attention paid to the postmixing state than to the transient process of initiation. In particular, we examine turbulent mixing when the substance is a scalar (i.e., characterized only by the scalar property of its concentration), and the mixing process does not influence the flow itself (i.e., the scalar is “passive”). This is the simplest paradigm of turbulent mixing. Within this paradigm, we discuss how a turbulently mixed state depends on the flow Reynolds number and the Schmidt number of the scalar (the ratio of fluid viscosity to the scalar diffusivity), point out some fundamental aspects of turbulent mixing that render it difficult to be addressed quantitatively, and summarize a set of ideas that help us appreciate its physics in diverse circumstances. We consider the so-called universal and anomalous features and summarize a few model studies that help us understand them both.
Keywords: turbulent mixing, universal features, anomalous features, ramp model, model studies
From supernovae to cream in coffee, and numerous circumstances in between, the mixing of two initially distinct substances plays an important role in our daily lives and in the evolution and sustenance of life itself. A simple case is the mixing of scalars (i.e., the mixing substances have no identifying labels other than their concentrations) that are chemically neutral with initially flat and stationary interfaces separating them, and forces such as surface tension and gravity are absent. Molecular diffusion causes the separating interface to encroach increasingly into both substances by thickening with time, thus eroding the concentration gradients and tempering the effectiveness of diffusion. One way to sustain the concentration gradients and thus the effectiveness of diffusion is to constantly push the substances toward each other by an external flow. A flow also destabilizes, distorts, and sharpens an interface while increasing its surface area and enhancing diffusion effects. In the simplest case, the mixing of scalars does not affect the flow itself; this is the so-called passive scalar mixing, which is the subject of this article. In practice, there will be practically important complications such as chemical reactions, density differences, multiple species, externally applied forces, and so forth, but the essence of mixing (for small diffusivity) is the interplay between the flow of substances and their intrinsic capacity to diffuse and mix molecularly. The literature on more complex instances of mixing is rather large but a useful entry can be made via refs. 1–4 and references therein. The flow itself could be smooth or turbulent (i.e., temporally and spatially stochastic); for the most part, we consider the latter.
We particularly keep in mind the following situation. We deposit a blob of a passive scalar such as a neutral dye within a tank of stirred fluid and observe its evolution. Experience shows that the blob will be stretched, folded, and fragmented and eventually dispersed and diluted in the fluid volume. The fragmentation and stretching of the blob enhance the area of the interface and the scalar gradients across it, thus putting diffusion and molecular mixing into new action. This role of diffusion is essentially secondary at this stage. However, two thin fragments of the stretched pieces of the scalar with opposing gradients will often come together and coalesce into a single entity. This act changes the local topology of the stretched fragments and allows diffusion to play more than that secondary role. For the somewhat more complex case of the blob in which the scalar gradient is prescribed initially as a Gaussian distribution, Fig. 1 shows the evolution of isoconcentration contours soon after the background turbulent flow launches the mixing process (5); the timescales noted in the bottom left corners are multiples of the Kolmogorov timescales (defined below). The isoconcentration contours acquire a fractal-like character (6) during some part of their evolution.
Fig. 1.
Mixing of an initially Gaussian scalar blob in a homogeneous isotropic statistically stationary turbulent flow. Reprinted with permission from ref. 5. Just one blob of the dye is introduced at . The timescale corresponding to each panel is indicated at each bottom left corner.
If one measures the probability density function (PDF) of the scalar concentration in a completely unmixed state, it will initially show two delta functions, one corresponding to 0 of the background fluid with no scalar and the second corresponding to 1, say, of the unmixed scalar blob. No matter how strongly the blob gets stretched and contorted by the flow, the shape of the PDF as two delta functions will remain unchanged without diffusivity; it is only by diffusive action that the PDF changes in shape. It then develops an intermediate peak between 0 and 1, corresponding to the mixed fluid, and the two peaks at 0 and 1 gradually diminish in magnitude even as the middle peak becomes dominant. The area under the middle peak is the fraction of the mixed fluid. Ultimately, one observes mostly the middle peak (see Anomalous Behaviors); this can be seen clearly in the numerical simulations of ref. 7 in a related context. The nature of the middle peak depends on the specifics of the flow.
Since the equations governing turbulent mixing do not have general solutions, the path to progress has been to deduce specific results on the basis of broad paradigms and compare their results with experiments and numerical solutions of the equations. There have been many insightful experiments but they do not always cover an adequate range of parameters or have the needed spatial and temporal resolutions; and they are often made in complex flow geometries that add new conceptual problems. On the other hand, direct numerical simulations of the equations, run on machines that are fast (several petabytes) and massively parallel (of the order of 1 million cores), have allowed increasingly sharper conclusions to be drawn. We exploit the computational results while also using experiments where possible. We particularly comment on homogeneous and isotropic turbulence in a periodic cube for which statistically stationary states have been computed with adequate resolution over a wide range of Reynolds and Schmidt numbers. Many of these results come from the frontier simulations by Yeung and coworkers (8–13), Schumacher and coworkers (14–18), Gotoh and coworkers (19–23), and others.
Equations and Classical Paradigms
The Velocity Field.
As already noted, the role of fluid flows is central to mixing. The flows of interest to us obey the Navier–Stokes (NS) equations
| [1] |
supplemented by the mass conservation condition for incompressible flows, given by
| [2] |
Here, is the velocity vector (usually in three dimensions) and is the pressure. Eqs. 1 and 2 are equally valid for smooth and turbulent flows. Since NS equations are nonlinear and no explicit turbulent solutions are known, one’s physical intuition and understanding of turbulence is based on particular paradigms with testable outcomes. For later reference, it is useful to summarize the most important such paradigm, named after Kolmogorov (24), although other illustrious names such as Obukhov, Onsager, Heisenberg, von Weizsäcker, Fermi, and von Neumann are associated with it. This paradigm is not valid for all commonly known flows, but it is helpful toward framing proper questions.
The effect of the pertinent boundary conditions is replaced in this paradigm by a steady stirring at some large scale and a characteristic velocity . Since the Reynolds number , where is the kinematic viscosity of the fluid, is regarded as large, a series of instabilities generates successively smaller scales, which increasingly lose the organization of the stirring scale. When these scales are small enough, viscosity will act directly on them (because of their large gradients) and dissipate the kinetic energy transmitted and initiated by the stirring action. The dissipation occurs at scales of the order of the Kolmogorov length scale , where is the energy dissipation rate (in units of kinetic energy per unit mass and unit time). The corresponding velocity and timescales are and . In the intermediate range of scales called the inertial range, a typical scale is small compared with but large with respect to so the details of stirring and viscosity are both irrelevant, and the only factor that controls the dynamics of turbulence is the rate of energy transfer across its scales; in a statistically steady state, this energy transfer rate equals the rate of kinetic energy introduction by stirring at scales and also the rate of energy dissipation around scales . The inertial range is thus expected to be universal because it is independent of both the stirring and dissipative mechanisms. A concrete result is that the so-called longitudinal structure functions, which are moments of velocity component differences, chosen along a prescribed direction, across a separation distance in the same direction in the inertial range, obey the form
| [3] |
for all integers , where are constants and the angular brackets imply a suitable average. Only for is the result known to be exact (25). The Fourier representation of the case is that the energy spectral density of the form being a constant. The inertial range in the wavenumber space corresponds to , where the wavenumber is the inverse of the length scale and the subscripts and indicate that the wavenumbers refer to length scales and , respectively.
The Advection–Diffusion Equation.
The classical equation for studying passive-scalar mixing is the advection–diffusion (AD) equation
| [4] |
where is the scalar concentration and its molecular diffusion coefficient, and is the velocity advecting . Since the scalar is passive, is prescribed by the operator and defines, along with and , the Reynolds number of the flow. Beyond that, the ratio , called the Schmidt number, , matters. In practice, could be as small as in the Sun’s interior, of the order unity when the scalar of interest is a modest amount of heat in air and of the order of for a water-soluble dye in water. Its magnitude makes a considerable difference to details of molecular mixing. Another quantity that matters is the ratio of to that at which the scalar is introduced (acting again as the surrogate for the effect of boundary conditions). The AD equation has a number of limitations as the model for mixing, as has been emphasized in ref. 26, sections 49, 50, 58, and 59, but it is a good model for a wide range of applications in technology, the atmosphere, and the oceans; other models with more specific goals are discussed briefly in Anomalous Behavior of Large-Scale Quantities and Some Model Equations.
Eq. 4 is linear in and the boundary conditions, which sustain the scalar concentration from being eroded by diffusion, are also almost always linear (although perhaps mixed), but difficulties are caused by the turbulent nature of . Turbulence converts the AD equation into a stochastic differential equation, for which we may seek only statistical averages such as the mean, the mean square, etc. While linearity holds for each realization of , the averaging process introduces new terms because of , and the equation becomes statistically nonlinear. As for the velocity field, we develop paradigms and compare their outcomes with experiment to infer their veracity.
It is helpful to recast the AD equation in Lagrangian terms. Eq. 4 is equivalent to stochastic advection of Lagrangian particles
| [5] |
where and is the vectorial Brownian motion, statistically independent in its three components. Here, the particle trajectories following the NS velocity are perturbed by the white noise of strength .
Consideration of Lagrangian trajectories clarifies some interesting issues (e.g., refs. 27 and 28), but one has to treat the twin limits on and carefully; we will not be too formal here. The NS velocities are analytic (i.e., space differentiable or “smooth”) for distances and smaller, above which, in the inertial range, they are only Hölder continuous (or “rough”). This simply means that a velocity increment over a distance is of the form , (29). The Hölder exponent, which is for Kolmogorov turbulence (24), assumes a distribution in practice (30). This is the multiscaling property of turbulence that sets it apart from standard scaling problems in critical phenomena. If with , we get and two Lagrangian particles which are close at one time separate explosively. That is, two Lagrangian fluid particles that are advected by the fluid velocity follow wildly different paths even if they start at the same position . This nonuniqueness is apparent in Richardson’s law of diffusion (31), which is thought to govern how particle pairs in turbulent motion separate in time (32–36). If is the separation distance between a pair of particles, we have
| [6] |
This is the special case of above. We stress again that the right-hand side of Eq. 6 is independent of the initial separation, so this power-law separation, much more explosive than for temporal chaos, is in principle applicable even for two initially coincident particles.
Universality in Second-Order Statistics of the Scalar.
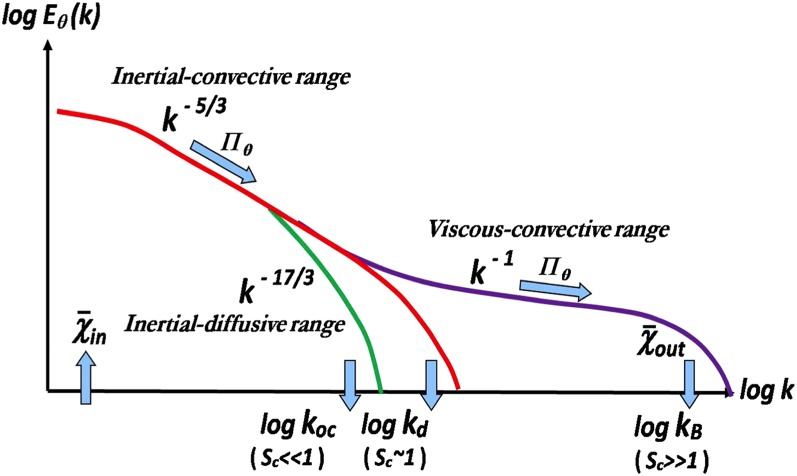
The spectral density fluctiation, of the scalar fluctuation, whose integral over all yields the scalar variance, has a rich structure that depends on , which is described briefly below. Denote by (which may be different from ) the scale at which scalar fluctuations are introduced into the flow that eventually mixes them; let be the smallest scalar scale around which diffusion evens out all fluctuations.
i) The inertial–convective range, : When , . In the so-called inertial–convective region sandwiched between the smaller of and , on the one hand, and , on the other, the spectral density depends on neither the viscosity nor the scalar diffusivity; its structure, determined by the spectral flux of scalar variance at the constant rate (Fig. 2, see ref. 37), is given by dimensional arguments similar to those in ref. 24, as
| [7] |
where is the Obukhov–Corrsin constant (38, 39) and is the rate at which the scalar variance gets smeared out by diffusion. The cutoff occurs at the scale .
Fig. 2.
Schematic of scalar spectrum for (red), (green), and (purple). Reprinted with permission from ref. 37.
Both simulations and experiments show that a spectral region exists within which the slope is roughly and that, for the 3D spectrum, (9), consistent with experiments (40), which gave the constant for the 1D spectrum to be about 0.40. (The 1D constant is three-fifths the 3D value.)
i.a) The fast roll-off part at higher wave numbers: For , within the spectrum in the fast roll-off range (the part of the red curve that drops off faster than the power), fluid viscosity and the scalar diffusivity are both important. Only recently have we begun to understand the energy spectrum in the viscous range (41), and it is fair to say that we do not yet know the scalar spectrum in this region.
ii) The viscous–convective range: When , the scalar diffusivity becomes effective at much smaller scales than those at which viscosity becomes effective; there is a spectral range called the viscous–convective range (42) within which diffusion is not important but viscosity prevails; instead of appearing directly, the viscosity appears only through the small-scale rate-of-strain . This is the purple curve in Fig. 2 with the power-law scaling part. Dimensional analysis shows that the spectrum has the shape
| [8] |
where is the Batchelor constant. Batchelor (42) derived this law from dynamical considerations and deduced the constant , as well, so this law rests on a theory. Batchelor considered the stretching effects of the velocity field to be stationary in time. Kraichnan (43) considered the opposite limit of infinitely oscillating strain rate and also found the −1 power in the viscous–convective range, which probably speaks to its robustness. Past evidence for the −1 power has been mixed: while refs. 44–46 found support for it, refs. 47 and 48 claimed the opposite. Only recently have we found convincing evidence that the −1 region does exist and becomes better defined with increasing (Fig. 3). However, is numerically determined to be about 5.5 (8, 11, 22), compared with Batchelor’s theoretical estimate of about 2, so there is still a missing piece of the puzzle.
Fig. 3.
Time-averaged 3D scalar spectrum obtained from direct numerical simulations for multiple Schmidt numbers, with the arrow in the direction of increasing Sc; sloped dotted line is proportional to . Reprinted with permission from ref. 65.
ii.a) The rapid roll-off part at higher wave numbers: Batchelor (42) had deduced the nature of the spectrum as it rolls off in the so-called viscous–diffusion range (the part of the purple curve that drops off fast toward the right end, where viscosity and diffusion are both important), but ref. 11 has shown that the data fit Kraichnan’s (43) formula much better.
iii) If , scalar diffusivity becomes important within the inertial range toward the high wavenumbers where the viscosity does not act. The power is truncated at a larger scale than at the so-called scalar dissipation length (38, 39) ; this truncated inertial range is called the inertial convective range (49, 50), in which the wavenumbers are such that , while . The theory of ref. 49 showed the expected power-law exponent to be . This part (the green curve in Fig. 2) had not been observed for many years because it is hard to obtain experimental data for high Reynolds number and low Schmidt number simultaneously, and the numerical simulations also place great demands on the time resolution—but it has finally been confirmed (51, 52). Nothing definitive is known about how the roll-off occurs at wavenumbers to the right of .
The Yaglom Relation in the Inertial–Convective Range.
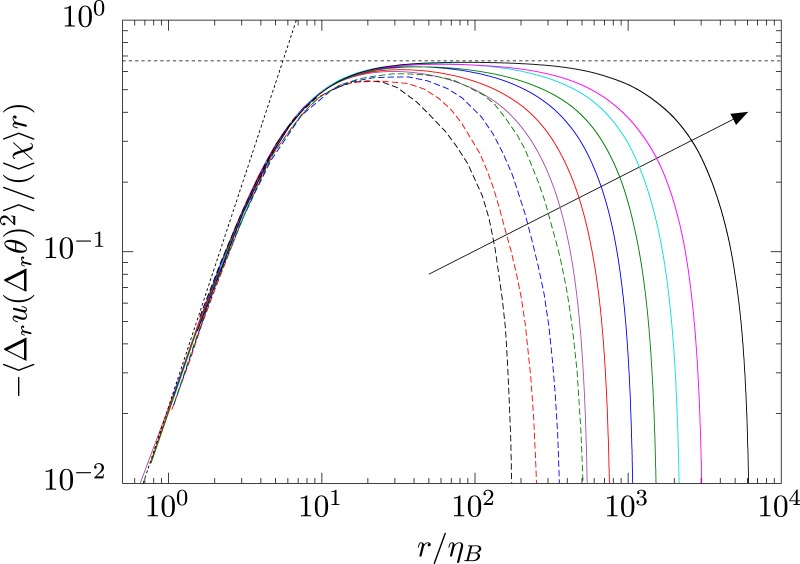
In analogy to Eq. 3, which is exact for the special case of , the cross-correlation between velocity and scalar increments was shown by Yaglom (53) to be exact in the inertial–convection region:
| [9] |
Here, again, the velocity increment , where the spatial distance is along the direction of and is contained in the inertial–convective range, and the scalar increment also corresponds to the inertial–convective range. This work has been extended in ref. 54 for a refined similarity hypothesis (55) and in refs. 56 and 57 for nonstationary forcing conditions. Its verification was attempted experimentally in ref. 54 as well as in ref. 58, but the wait was considerably longer (Fig. 4) before the support became clear for a variety of Reynolds and Schmidt numbers (8–23). See also ref. 59 for similar work for low Schmidt numbers.
Fig. 4.
Mixed velocity–scalar structure function with scaling according to Yaglom’s relation. Various curves correspond to various values of , with the arrows indicating the direction of increasing valkues. The slope at the smallest values of corresponds to , expected from the smoothness condition at small . Reprinted with permission from ref. 65.
Scalar Dissipation Rate.
In the above discussion, it has been assumed that the flux of scalar variance across wavenumbers, equal in steady state to the scalar dissipation rate, stays fixed even as the diffusivity goes to zero. This seems counterintuitive because the scalar dissipation rate defined (from the AD equation) as
| [10] |
depends directly on the diffusivity. The anomaly is that is independent of as .
The direct evidence for this behavior, which often surprises the uninitiated, can be found in ref. 10 where , normalized by large-scale quantities in the flow (not involving ), is plotted against the Peclet number, (the Peclet number is the product of the Reynolds and Schmidt numbers). For , the scalar dissipation rate indeed seems to be independent of (and thus ). We have already discussed, in describing the swift separation of two Lagrangian particles, a physical mechanism that may allow diffusion not to play a direct role. As long as the diffusivity is small (i.e., ), it is only an agent whose action appears to be slaved to the explosively dispersive effect of the particle trajectories. We thus have , where is a constant of the order unity. From ref. 10, it is about 0.7 for ; this constancy holds for nonunity as well, with perhaps depending weakly on .
Summary So Far.
The major point of the account so far is not to cover all subregions of the spectra or the “universality” arguments thoroughly, but to illustrate that we have come a long way in assessing past theories and are able to conclude that they perform reasonably well at the level of second-order statistics; such corrections as may arise from intermittency, to which we return in Anomalous Behaviors, are ignored here. The broad agreement with the theory has been tested primarily in cases where an isotropic and homogeneous velocity field is generated in a periodic cube, maintained stationary by forcing at a few of the lowest wavenumbers, and the scalar field is maintained stationary by a mean scalar gradient. Thus, it seems that, by virtue of the work that has taken some 70 y to complete, the physics for the second-order quantities are founded on solid enough ground to believe that they hold well as a working approximation (although with a few gaps). Concurrently, however, work of the last four decades has also shown that this approach, as well as the concepts behind it, breaks down for higher-order moments and that the notion of universality is fundamentally at peril. This is the topic in Anomalous Behaviors.
Anomalous Behaviors
Anomaly Due to Shear.
The first major anomalous behavior concerns the persistence of anisotropy at high Reynolds numbers in scales that are nominally regarded as small. This would suggest that the physics of universal behavior is incorrect at the basic level; the fact that it may work well for second-order quantities does not negate this thought. We now discuss an example of such properties and their place in scalar mixing.
Recall that the vector , being a derivative, is regarded as a small-scale property. If small scales are universal, they are also statistically isotropic; rotational symmetry of an isotropic vector would need its odd moments, in particular the third one, to vanish at high Reynolds number. However, one finds that the derivative skewness, the ratio of the third derivative moment to the power of the mean-square derivative, assumes values of the order unity with no tendency to decrease with Reynolds number (60) and has been reaffirmed multiple times in the last 40 y (61, 62). If it remains a constant of about unity at all moderate Reynolds numbers, small-scale isotropy appears to be violated, with the possible implication that we should not expect any universality to emerge. Does it mean that we have to discard the paradigm that seemed quite successful for second-order quantities?
The ostensible reason for this anomalous behavior is the ramp–cliff structure of Fig. 5, which shows the time trace of temperature fluctuations in a heated jet (60). The heating is only slight so that the temperature is passive. The so-called Taylor’s hypothesis (the equivalence of the transformation , where is the velocity with which turbulent features are advected) implies that these are also 1D spatial cuts of the temperature field. The ramp–cliff structure shows that the temperature builds up rather sharply but falls rather gradually.
Fig. 5.
The ramp–cliff structure in the temperature trace in a slightly heated jet. Reproduced with permission from ref. 60. Below the trace is shown a schematic of the large eddy structure that could create the ramp–cliff. The scales are indicated on the schematic.
A plausible physical reason for the ramp–cliff signature is this: Imagine large structures in the flow that are moving at a speed that is different from the local value. For example, in a boundary layer, it has been shown in ref. 63 that large structures travel nearly everywhere in the outer boundary layer with approximately the speed of the free stream. One can imagine then that there will be some stagnation regions toward the front of such structures where the jump of a property such as its temperature will be rather steep, but the fall-off toward the back of the structure will be rather gradual because of the diffuse nature in the wake; see ref. 64 for an average of streamline patterns around such structures. The basic notion is that the temperature jump across the stagnation region will be on the order of the maximum value possible, that is, the maximum overheat in a jet. Let us denote this maximum temperature jump by . The longer leg of the ramp is on the order of , and the shorter leg is on the order of the shortest scalar scale; what is true of the temperature trace is also true of any scalar field, so the shortest scale will be on the order of the Batchelor scale when . On each ramp are the superimposed fluctuations coming from all other scales of the temperature. These are the parts essentially unaffected by the mean gradients and other inhomogeneities in the flow, contributing most to low-order even moments of the scalar derivative such as its mean square; and the contributions of the cliffs to even-order statistics are intrinsically small, but are important for odd and high-order moments, both odd and even.
The ramp–cliff model can be used to calculate the skewness of the scalar derivative in a straightforward manner. The nonvanishing part of the third moment of the scalar derivative within a ramp is on the order of , and its average value over the ramp is . This forms the numerator for the skewness. Noting that the even moments are largely coming from fluctuations superimposed on the ramp, the denominator for the skewness is the power of (by isotropy, valid for even-order moments) and can be substituted using dissipative anomaly as . It follows that —that is, the skewness is independent of but varies as the power of . In arriving at the above result, we have used only standard relations valid in turbulence.
We can indeed verify the dependence on . Fig. 6, reproduced from the thesis of Clay (65), shows the skewness as a function of . Its variation is only slightly smaller than the power (but this minor difference can be addressed by a modestly more sophisticated analysis). These considerations can be used to predict the behavior of the normalized fifth moment, or the hyperskewness, , of the scalar derivative. The result for . Data bear out these predictions. The nonvanishing of odd-order structure functions occurs in the inertial–convective range and can be understood the same way.
Fig. 6.
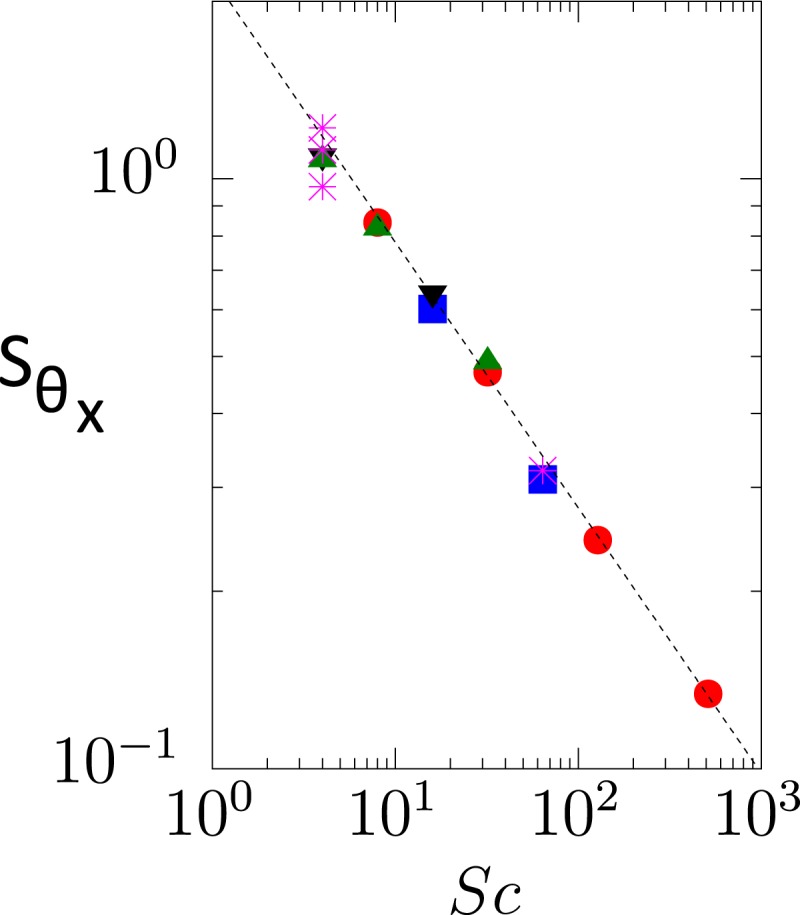
The decay of the scalar derivative skewness as a function of the Schmidt number. Most data from ref. 65. The line corresponds to a slope close to the prediction of the ramp–cliff model.
What we have shown is that the skewness and the hyperskewness, which are ostensibly small-scale properties, are actually large-scale properties, and so their anomalous behavior need not in itself negate the likelihood that small scales are universal at low-order even moments. Thus, our earlier conclusion that small-scale properties at the second-order level are essentially consistent with the paradigm of universal theories is quite reasonable. In reality, second-order statistics are also influenced by the large scale “somewhat” and are thus only approximately universal, because the large scale is somehow imprinted on the small scale. Thus, all moments of the small scale are susceptible to the influence of the large scale, the ramp–cliff structure being a manifestation of this effect. This structure has the important consequence that the mixing in shear flows is never complete (which means, in principle, that the PDFs of the scalar discussed in the Introducton will never attain a state at which the two delta functions at 0 and 1 disappear entirely). We discuss this feature in the next subsection by considering structure functions of the scalar.
Anomalous Scaling of Structure Functions.
For simplicity, we discuss . Define the structure functions of order for the scalar as . For , these objects are independent of the large scale; they are also independent of diffusivity when . In the intermediate scales , the properties of depend only on the energy and scalar fluxes across the scale range. This is the inertial–convective region we have already encountered. Dimensional reasoning says that
| [11] |
This dependence on is the normal scaling. Although experiments and simulations are susceptible to many shortcomings (such as inadequate scaling range, uncertain convergence of statistics, inadequate repeatability from one flow to another, dependence on the method of forcing the large scale, etc.), new developments have given us confidence that the measured scaling exponents and, in fact, saturate with respect to (66) for moment orders of the order 10. This saturation is the extreme case of anomalous scaling and implies that there are always some regions in the flow where the scalar concentration varies from the maximum possible to the minimum possible, or between 0 and 1, in quick succession, as the ramp–cliff model has already suggested.
The Kraichnan Model.
All this strong evidence for anomalous scaling suggests the need for a good theoretical understanding. Since it has not yet been possible to obtain this for the AD equation, it is helpful to have a nontrivial model. Kraichnan’s model (43, 67) is one such.
The crucial element of this model is that it replaces the velocity in the AD equation by a stochastic Gaussian field with a time correlation that decays infinitely rapidly (“white in time”) and a spatial correlation that has the expected power law with a prescribed scaling exponent, . That is,
| [12] |
with
| [13] |
where and , is a diffusivity and and are constants, and corresponds to advection in a very rough flow and to a smooth flow (see ref. 27 for an introduction). This power-law scaling on is similar to the NS case (although the scaling exponent here assumes a more general value between 0 and 2), but the temporal scaling is conceptually different by being a delta function. For statistical stationarity, a random forcing has to be added to the right-hand side of the AD equation, with the property that
| [14] |
The function decays rapidly to zero for small scales. Kraichnan’s insight was that this model possesses the essential elements of the scalar mixing while retaining analytical tractability. Indeed, it has been possible to establish anomalous scaling (see ref. 68 for a review) for this model even though the idealized advecting flow itself does not exhibit any anomaly. In other words, the scaling exponents for the Eulerian structure functions of the scalar increments differ from the classical form (with ) and depend on the order of the moment. We come to the conclusion that the anomalous behavior is imprinted on it by the scalar itself and does not need an anomalous velocity field.
We must stress, however, that no explicit solution has been found for all values of , but only expansions in the limits of and have been found (e.g., refs. 69–72). However, accurate numerical solutions have been obtained for the general case (73–75). One important feature of these calculations is that the scaling exponents asymptote to a constant instead of increasing with moment order (76), just as happens for real flows (66).
The physical picture that has emerged from the Kraichnan model is this: To understand the third-order scaling exponent , it is obvious that one needs to study the properties of objects generated from the scalar at three different positions in space. The triangle formed by these positions is described by the length scale —which, for specificity, can be taken as the geometric mean of the lengths of the sides of the triangle—and two of the three angles, say and (77, 78). As the three particles advect, the triangles change in shape and size. If we rescale the triangles to the same at each time step, the dynamics reduce to the evolution of shapes of triangles, or to a suitable function of the two angles and . The important result obtained for the Kraichnan model is that the three-point statistics are governed by those trajectories for which the change in the length scale is compensated by the change in shape of the triangles such that the product is a constant. In general, as particles move in the Kraichnan flow, an -particle cloud grows in size but fluctuations in the cloud shape decrease in magnitude. This happens because the correlation between particles—which arises, in the first place, because they are contained within the integral scale of the velocity field—weakens with the separation distance. Therefore, as mentioned above, one looks for suitable functions of size and shape that have the property of being conserved via the balance between the growth in size and the decrease of shape fluctuations.
An important qualitative lesson from this work is that certain types of Lagrangian characteristics, conserved only on the average, determine the statistical scaling of Eulerian structure functions. This may mean that there are certain statistically conserved laws which determine the anomalous exponents (79). Clearly, in this instance the Lagrangian point of view has given a better understanding of Eulerian quantities—a conclusion that may have broad validity in systems with strong fluctuations. While there are several differences between the predictions of the Kraichnan model and the behavior of a passive scalar in NS turbulence (5), it has advanced our understanding of anomalous scaling.
An interesting observation concerns the ramp–cliff structure discussed earlier. One may think that the ramp–cliff structure arises because the shear persistently acts on the scalar, which is not the feature of the Kraichnan model because it reshuffles the flow at every instant. Despite this, simulations in ref. 75 suggest that ramp–cliff features are possible even in the Kraichnan model, leading to the saturation of the scaling exponents: The scalar will occasionally undergo the largest possible fluctuation over a very short length scale, these being and in our ramp model.
A Consequence of Anomalous Scaling: Length-Scale Fluctuations.
We pointed out earlier that velocity increments in the inertial–convective range are Hölder continuous; for small , the magnitudes of velocity increments change greatly from one spatial position to another. This intermittent feature shows up even more conspicuously in energy and scalar dissipation rates, and , for which fluctuations increase with increasing Reynolds number. These intermittent properties of and have been studied extensively—in refs. 10, 30, and 80–84 among others.
One property of intermittency is that the magnitude fluctuations are accompanied by length-scale fluctuations as well. Since the instantaneous and local values of and fluctuate rather wildly (tens of thousands of times the mean value are likely even at modest Reynolds numbers), it can be expected that, if one defined local Kolmogorov scale based on the local values of , that scale would fluctuate as well; and would fluctuate too, and both smaller and larger values than the mean values would result (6). The result would be similar if one defined (85, 86) the fluctuating dissipation scale through the intermittency of the structure functions via as (i.e., by requiring the corresponding Reynolds number to be unity). The two definitions, although not identical, illustrate the same basic phenomenon.
These length-scale fluctuations imply, for example, that will be significantly different from the definition . The same situation would arise with the timescale. Data show that the mean timescale . This means that a measure of the eddy diffusive time/molecular diffusive time could well be , which exceeds unity only when [the so-called mixing transition (86)].
Anomalous Behavior of Large-Scale Quantities and Some Model Equations
Instances exist when the observed large-scale behaviors cannot be explained from the AD equation directly, so various model studies have been proposed. As in the Kraichnan model, these models replace the NS velocity by an artificial field satisfying the condition . A collection of such models is discussed in ref. 87. A broad-brush summary of the large-scale, long-time results is given below.
-
i)
For smooth velocity fields (e.g., periodic and deterministic), homogenization is possible. That is, , where the effective diffusivity can be determined. See, for example, ref. 88.
-
ii)
Velocity is a homogeneous random field, but a scale separation exists between the velocity and scalar fields: (i.e., the scalar is injected at a much larger scale than the kinetic energy). Homogenization is possible here as well.
-
iii)
Velocity is a homogeneous random field but delta correlated in time, ; eddy diffusivity can be computed here as well.
-
iv)
For the special case of shearing velocity (with and without transverse drift), the problem can be solved essentially completely: Eddy diffusivity and anomalous diffusion can be calculated without any scale separation (89–91).
We now cite two specific examples where such models have been helpful:
i) Decay rates: For the case of turbulent flow behind grids, there is no source of turbulent energy except the grid itself; the turbulent energy thus decays with distance from the grid, and the rate of decay for the energy follows ∼ −1.2 power of the distance (ref. 92 and references therein). The turbulence-generating grid itself, or a secondary grid just downstream, can be heated to generate temperature fluctuations [for which ]. Initial studies (93, 94) showed that the scalar variance decays as a power law with nonunique exponents. It was shown (95) by a simple model that all of the decay exponents collapse when the length-scale ratio is taken into account. This insight would not have been possible without the model.
ii) The PDF of the scalar variable: The decaying scalar described in the previous paragraph possesses a self-similar Gaussian PDF (94); the PDF in simulations of the stationary case with stochastic scalar driving is Gaussian or only slightly sub-Gaussian (19). Also when driven by a mean scalar gradient, the PDF assumes a nearly Gaussian form (96–98). However, some experiments have yielded exponential tails (99), consistent with the Kraichnan model, for which the tails of the PDF are super-Gaussian or exponential (100). At present, we do not fully understand the circumstances for which the passive scalar mixed by NS turbulence assumes an exponential PDF, but some insight comes from model studies (101) which suggest that the PDF is exponential when and Gaussian (when ).
The shape of the PDF in inhomogeneous shear flows is understood even less (102).
Concluding Remarks
This article has attempted to provide a perspective on the state of turbulent mixing essentially after the process is complete, focusing on passive scalars. Many basic aspects of mixing, relating to the transient process, are omitted. Also omitted, by necessity, are aspects such as mixing time, efficiency of mixing, and other bulk measures (103, 104). We did not likewise explore the effect of rotation (105), compressibility (106), buoyancy (107), chemical reactions (108), chaotic mixing (109), and other external effects and the mixing of non-Newtonian fluids. The views taken here are entirely continuum in character. Nevertheless, we hope that this article is a useful background for understanding these richer contexts.
While we need not deny the usefulness of universality at the spectral level for scalar variance, it is clearly the case that not everything falls within the cloak of universality; indeed, we discussed several examples of anomaly. Our view is that a good understanding of turbulent mixing is possible only if we understand the value and limitations of the universality paradigms while being aware of the causes of anomalies. Our attempt in a nutshell has been to show that there are underpinnings of decent theory but they have yet to be strung together to create a full-fledged narrative. To go deeper than the continuum, using molecular dynamics, and establish specific results, for example, the Schmidt number effects, would be spectacular.
Acknowledgments
This report has been inspired by many colleagues over the years, and I particularly cite P. K. Yeung, D. A. Donzis, and J. Schumacher from whose computer simulations I have learned much of the material presented; G. Eyink, V. Yakhot, T. Gotoh, and S. I. Abarzhi for many insightful comments and discussions; K. P. Iyer for his help in preparing the LaTeX file; and M. Clay for permission to use his figures.
Footnotes
The author declares no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Abarzhi SI, Sreenivasan KR. Turbulent mixing and beyond. Phil Trans Roy Soc Lond A. 2010;368:1539–1546. doi: 10.1098/rsta.2010.0021. [DOI] [PubMed] [Google Scholar]
- 2.Abarzhi SI. Review of theoretical modeling approaches of Rayleigh-Taylor instabilities and turbulent mixing. Phil Trans Roy Soc Lond A. 2010;368:1809–1828. doi: 10.1098/rsta.2010.0020. [DOI] [PubMed] [Google Scholar]
- 3.Abarzhi SI, Gauthier S, Sreenivasan KR. Turbulent mixing and beyond: Non-equilibrium processes from atomistic to astrophysical scales I. Phil Trans Roy Soc A. 2013;371:20120435. doi: 10.1098/rsta.2012.0435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Abarzhi SI, Gauthier S, Sreenivasan KR. Turbulent mixing and beyond: Non-equilibrium processes from atomistic to astrophysical scales II. Phil Trans Roy Soc Lond A. 2013;371:20130268. doi: 10.1098/rsta.2013.0268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sreenivasan KR, Schumacher J. Lagrangian views on turbulent mixing of passive scalars. Philos Trans R Soc Lond A. 2010;368:1561–1577. doi: 10.1098/rsta.2009.0140. [DOI] [PubMed] [Google Scholar]
- 6.Sreenivasan KR. Fractals and multifractals in fluid turbulence. Annu Rev Fluid Mech. 1991;23:539–600. [Google Scholar]
- 7.Yeung PK, Xu J. Effects of rotation on turbulent mixing: Nonpremixed passive scalars. Phys Fluids. 2014;16:93–103. [Google Scholar]
- 8.Yeung PK, Xu S, Donzis DA, Sreenivasan KR. Simulations of three-dimensional turbulent mixing for Schmidt numbers of the order 1000. Flow Turbul Combust. 2004;72:333–347. [Google Scholar]
- 9.Yeung PK, Donzis DA, Sreenivasan KR. High-Reynolds-number simulation of turbulent mixing. Phys Fluids. 2005;17:081703. [Google Scholar]
- 10.Donzis DA, Sreenivasan KR, Yeung PK. Scalar dissipation rate and dissipative anomaly in isotropic turbulence. J Fluid Mech. 2005;532:199–216. [Google Scholar]
- 11.Donzis DA, Sreenivasan KR, Yeung PK. The Batchelor spectrum for mixing of passive scalars in isotropic turbulence. Flow Turbul Combust. 2010;85:549–566. [Google Scholar]
- 12.Donzis DA, Yeung PK. Resolution effects and scaling in numerical simulations of passive scalar mixing in turbulence. Phys D. 2010;239:1278–1287. [Google Scholar]
- 13.Donzis DA, Aditya K, Sreenivasan KR, Yeung PK. The turbulent Schmidt number. J Fluids Eng. 2014;136:060912. [Google Scholar]
- 14.Schumacher J, Sreenivasan KR, Yeung PK. Schmidt number dependence of derivative moments for quasi-static straining motion. J Fluid Mech. 2003;479:221–230. [Google Scholar]
- 15.Schumacher J, Sreenivasan KR. Geometric aspects of the passive scalar mixing at high Schmidt number. Phys Rev Lett. 2003;91:174501. doi: 10.1103/PhysRevLett.91.174501. [DOI] [PubMed] [Google Scholar]
- 16.Schumacher J, Sreenivasan KR. Statistics and geometry of passive scalar fields in turbulence. Phys Fluids. 2005;17:125107. [Google Scholar]
- 17.Schumacher J, Sreenivasan KR, Yeung PK. Very fine structures in scalar mixing. J Fluid Mech. 2005;531:113–122. [Google Scholar]
- 18.Kumar B, Schumacher J, Shaw RA. Lagrangian mixing dynamics at the cloudy-clear air interface. J Atmos Sci. 2014;71:2564–2580. [Google Scholar]
- 19.Watanabe T, Gotoh T. Statistics of a passive scalar in homogeneous turbulence. New J Phys. 2004;6:40. [Google Scholar]
- 20.Watanabe T, Gotoh T. Intermittency in passive scalar turbulence under the uniform mean scalar gradient. Phys Fluids. 2006;18:058105. [Google Scholar]
- 21.Watanabe T, Gotoh T. Inertial-range intermittency and accuracy of direct numerical simulation for turbulence and passive scalar turbulence. J Fluid Mech. 2007;590:117–146. [Google Scholar]
- 22.Gotoh T, Watanabe T, Miura H. Spectrum of passive scalar at very high Schmidt number in turbulence. Plasma Fusion Res. 2014;9:3401019. [Google Scholar]
- 23.Gotoh T, Watanabe T. Power and non-power laws of passive scalar moments convected by isotropic turbulence. Phys Rev Lett. 2015;115:114502. doi: 10.1103/PhysRevLett.115.114502. [DOI] [PubMed] [Google Scholar]
- 24.Kolmogorov AN. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl Akad Nauk SSSR. 1941;30:9–13. [Google Scholar]
- 25.Kolmogorov AN. Dissipation of energy in the locally isotropic turbulence. Dokl Akad Nauk SSSR. 1941b;32:16–18. [Google Scholar]
- 26.Landau LD, Lifshitz EM. 1987. Hydrodynamics by Fluid Mechanics (Pergamon Press, Burlington, MA, Vol 6.
- 27.Bernard D. 2000. Turbulence for (and by) amateurs. arXiv:cond-mat/0007106. Preprint, posted July 6, 2000.
- 28.Eyink GL, Drivas TD. Spontaneous stochasticity and anomalous dissipation for Burgers equation. J Stat Phys. 2015;158:386–432. [Google Scholar]
- 29.Parisi G, Frish U. On the singularity structure of fully developed turbulence. In: Ghil M, Benzi R, Parisi G, editors. Turbulence and Predictability in Geophysical Fluid Dynamics. North-Holland, Amsterdam: 1983. pp. 84–87. [Google Scholar]
- 30.Chen SY, Dhruva B, Kurien S, Sreenivasan KR, Taylor MA. Anomalous scaling of low-order structure functions of turbulent velocity. J Fluid Mech. 2005;533:183–192. [Google Scholar]
- 31.Richardson LF. Atmospheric diffusion shown on a distance-neighbor graph. Proc R Soc Lond A. 1926;110:709–733. [Google Scholar]
- 32.La Porta A, Voth GA, Crawford AM, Alexander J, Bodenschatz E. Fluid particle accelerations in fully developed turbulence. Nature. 2001;409:1017–1019. doi: 10.1038/35059027. [DOI] [PubMed] [Google Scholar]
- 33.Mordant N, Metz P, Michel O, Pinton JF. Measurement of Lagrangian velocity in fully developed turbulence. Phys Rev Lett. 2001;87:214501. doi: 10.1103/PhysRevLett.87.214501. [DOI] [PubMed] [Google Scholar]
- 34.Boffetta G, Sokoloff IM. Relative dispersion in fully developed turbulence: The Richardsons law and intermittency corrections. Phys Rev Lett. 2002;88:094501. doi: 10.1103/PhysRevLett.88.094501. [DOI] [PubMed] [Google Scholar]
- 35.Biferale L, et al. Multifractal statistics of Lagrangian velocity and acceleration in turbulence. Phys Rev Lett. 2004;93:064502. doi: 10.1103/PhysRevLett.93.064502. [DOI] [PubMed] [Google Scholar]
- 36.Bourgoin M, Ouellette NT, Xu H, Berg J, Bodenschatz E. The role of pair dispersion in turbulent flow. Science. 2006;311:835–838. doi: 10.1126/science.1121726. [DOI] [PubMed] [Google Scholar]
- 37.Gotoh T, Yeung PK. Passive scalar transport in turbulence: A computational perspective. In: Davidson PA, Kaneda Y, Sreenivasan KR, editors. Ten Chapters in Turbulence. Cambridge Univ Press; Cambridge, UK: 2012. [Google Scholar]
- 38.Obukhov AM. Structure of the temperature field in turbulent flows. Izv Geogr Geophys. 1949;13:58–69. [Google Scholar]
- 39.Corrsin S. On the spectrum of isotropic temperature fluctuations in isotropic turbulence. J Appl Phys. 1951;22:469–473. [Google Scholar]
- 40.Sreenivasan KR. The passive scalar spectrum and the Obukhov-Corrsin constant. Phys Fluids. 1996;8:189–196. [Google Scholar]
- 41.Khurshid S, Donzis DA, Sreenivasan KR. Energy spectrum in the dissipative range. Phys Rev Fluids. 2018;3:082601(R). [Google Scholar]
- 42.Batchelor GK. Small scale variation of convected quantities like temperature in a turbulent fluid. Part 1. General discussion and the case of small conductivity. J Fluid Mech. 1959;5:113–133. [Google Scholar]
- 43.Kraichnan RH. Small-scale structure of a scalar field convected by turbulence. Phys Fluids. 1968;11:945–953. [Google Scholar]
- 44.Gibson CH, Schwarz WH. The universal equilibrium spectra of turbulent velocity and scalar fields. J Fluid Mech. 1963;16:365–384. [Google Scholar]
- 45.Sreenivasan KR, Prasad RR. New results on the fractal and multifractal structure of the large Schmidt number passive scalars in fully turbulent flows. Phys D. 1989;38:322–329. [Google Scholar]
- 46.Holzer M, Siggia ED. Turbulent mixing of a passive scalar in two dimensions. Phys Fluids. 1994;6:1820–1837. [Google Scholar]
- 47.Miller PL, Dimtakis PE. Measurements of scalar power spectra in high Schmidt number turbulent jets. J Fluid Mech. 1996;308:129–146. [Google Scholar]
- 48.Williams BS, Marteau D, Gollub JP. Mixing of a passive scalar in magnetically forced two-dimensional turbulence. Phys Fluids. 1997;9:2061–2080. [Google Scholar]
- 49.Batchelor GK, Howells ID, Townsend AA. Small-scale variation of convected quantities like temperature in turbulent fluid. Part 2. The case of large conductivity. J Fluid Mech. 1959;5:134–139. [Google Scholar]
- 50.Howells ID. An approximate equation for the spectrum of a conserved scalar quantity in a turbulent fluid. J Fluid Mech. 1960;9:104–106. [Google Scholar]
- 51.Yeung PK, Sreenivasan KR. Spectrum of passive scalars of high molecular diffusivity in turbulent mixing. J Fluid Mech. 2013;716:R14. [Google Scholar]
- 52.Yeung PK, Sreenivasan KR. Direct numerical simulation of turbulent mixing at very low Schmidt number with a uniform mean gradient. Phys Fluids. 2014;26:015107. [Google Scholar]
- 53.Yaglom AM. Local structure of the temperature field in a turbulent field. Dokl Akad Nauk SSSR. 1949;69:743–746. [Google Scholar]
- 54.Stolovitzky G, Kailasnath P, Sreenivasan KR. Refined similarity hypotheses for passive scalars mixed by turbulence. J Fluid Mech. 1995;297:275–291. [Google Scholar]
- 55.Kolmogorov AN. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J Fluid Mech. 1962;13:82–85. [Google Scholar]
- 56.Danaila L, Anselmet F, Zhou T, Antonia RA. A generalization of Yaglom’s equation which accounts for the large-scale forcing in heated decaying turbulence. J Fluid Mech. 1999;391:359–372. [Google Scholar]
- 57.Orlando P, Antonia RA. Dependence of the non-stationary form of Yaglom’s equation on the Schmidt number. J Fluid Mech. 2002;451:99–108. [Google Scholar]
- 58.Mydlarsky L. Mixed velocity-passive scalar statistics in high-Reynolds-number turbulence. J Fluid Mech. 2003;475:173–203. [Google Scholar]
- 59.Iyer KP, Yeung PK. Structure functions and applicability of Yaglom’s relation in passive-scalar turbulent mixing at low Schmidt numbers with uniform mean shear. Phys Fluids. 2014;26:085107. [Google Scholar]
- 60.Sreenivasan KR, Antonia RA, Britz D. Local isotropy and large structures in a heated jet. J Fluid Mech. 1979;94:745–775. [Google Scholar]
- 61.Sreenivasan KR, Tavoularis S. On the skewness of the temperature fluctuation in turbulent flows. J Fluid Mech. 1980;101:783–795. [Google Scholar]
- 62.Sreenivasan KR. On local isotropy of passive scalars in turbulent shear flows. Proc R Soc Lond A. 1991;434:165–182. [Google Scholar]
- 63.Kovasznay LSG, Kibens V, Blackwelder RF. Large-scale motion in the intermittent region of a turbulent boundary layer. J Fluid Mech. 1970;41:283–325. [Google Scholar]
- 64.Antonia RA, Chambers AJ, Britz D, Browne LW. Organized structures in a turbulent plane jet: Topology and contribution to momentum and heat transport. J Fluid Mech. 1986;172:211–229. [Google Scholar]
- 65.Clay M. 2017. Strained turbulence and low-diffusivity turbulent mixing using high performance computing. PhD thesis (School of Aerospace Engineering, Georgia Institute of Technology, Atlanta)
- 66.Iyer KP, Schumacher J, Sreenivasan KR, Yeung PK. 2018. Steep cliffs and saturated exponents in three dimensional scalar turbulence. arXiv:1807.01651v1. Preprint, posted July 4, 2018.
- 67.Kraichnan RH. Anomalous scaling of a randomly advected scalar. Phys Rev Lett. 1994;72:1016–1019. doi: 10.1103/PhysRevLett.72.1016. [DOI] [PubMed] [Google Scholar]
- 68.Falkovich G, Gawedzki K, Vergassola M. Particles and fields in fluid turbulence. Rev Mod Phys. 2001;73:913–975. [Google Scholar]
- 69.Bernard D, Gawedzki K, Kupiainen A. Anomalous scaling of the N-point functions of a passive scalar. Phys Rev E. 1996;54:2564–2572. doi: 10.1103/physreve.54.2564. [DOI] [PubMed] [Google Scholar]
- 70.Chertkov M, Falkovich G. Anomalous scaling exponents of a white-advected passive scalar. Phys Rev Lett. 1996;76:2706–2709. doi: 10.1103/PhysRevLett.76.2706. [DOI] [PubMed] [Google Scholar]
- 71.Shraiman BI, Siggia ED. Anomalous scaling of a passive scalar in turbulent flow. C R Acad Sci Paris IIB. 1995;321:279–284. [Google Scholar]
- 72.Arad I, Biferale L, Celani A, Procaccia I, Vergassola M. Statistical conservation laws in turbulent transport. Phys Rev Lett. 2001;87:164502. doi: 10.1103/PhysRevLett.87.164502. [DOI] [PubMed] [Google Scholar]
- 73.Frisch U, Mazzino A, Vergassola M. Intermittency in passive scalar advection. Phys Rev Lett. 1998;80:5532–5535. doi: 10.1103/PhysRevLett.84.2385. [DOI] [PubMed] [Google Scholar]
- 74.Gat O, Procaccia I, Zeitak R. Anomalous scaling in passive scalar advection: Monte Carlo Lagrangian trajectories. Phys Rev Lett. 1998;80:5536–5539. [Google Scholar]
- 75.Chen SY, Kraichnan RH. Simulations of a randomly advected passive scalar field. Phys Fluids. 1998;10:2867–2884. [Google Scholar]
- 76.Balkovsky E, Lebedev V. Instanton for the Kraichnan passive scalar problem. Phys Rev E. 1998;58:5776–5795. [Google Scholar]
- 77.Pumir A, Shraiman BI, Chertkov M. Geometry of Lagrangian dispersion in turbulence. Phys Rev Lett. 2000;85:5324–5327. doi: 10.1103/PhysRevLett.85.5324. [DOI] [PubMed] [Google Scholar]
- 78.Celani A, Vergassola M. Statistical geometry in scalar turbulence. Phys Rev Lett. 2001;86:424–427. doi: 10.1103/PhysRevLett.86.424. [DOI] [PubMed] [Google Scholar]
- 79.Falkovich G, Sreenivasan KR. Lessons from hydrodynamic turbulence. Phys Today. 2006;59:43–49. [Google Scholar]
- 80.Meneveau C, Sreenivasan KR. The multifractal nature of turbulent energy dissipation. J Fluid Mech. 1991;224:429–484. [Google Scholar]
- 81.Yeung PK, Zhai XM, Sreenivasan KR. Extreme events in computational turbulence. Proc Natl Acad Sci USA. 2015;112:12633–12638. doi: 10.1073/pnas.1517368112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Sreenivasan KR, Antonia RA. The phenomenology of small-scale turbulence. Annu Rev Fluid Mech. 1997;29:435–472. [Google Scholar]
- 83.Yeung PK, Zhai XM, Sreenivasan KR. Extreme events in computational turbulence. Proc Natl Acad Sci USA. 2016;112:12633–12638. doi: 10.1073/pnas.1517368112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Schumacher J, et al. Small-scale universality in fluid turbulence. Proc Natl Acad Sci USA. 2014;111:10961–10965. doi: 10.1073/pnas.1410791111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Paladin G, Vulpiani A. Degrees of freedom of turbulence. Phys Rev A. 1987;35:1971–1973. doi: 10.1103/physreva.35.1971. [DOI] [PubMed] [Google Scholar]
- 86.Yakhot V. Dissipation-scale fluctuations and mixing transition in turbulent flows. J Fluid Mech. 2008;606:325–337. [Google Scholar]
- 87.Majda AJ, Kramer PR. Simplified models for turbulent diffusion: Theory, numerical modelling, and physical phenomena. Phys Rep. 1999;314:237–574. [Google Scholar]
- 88.Stroock DW, Varadhan SRS. Diffusion processes with continuous coefficients I. Commun Pure Appl Math. 1969;22:345–400. [Google Scholar]
- 89.Glimm G, Lundquist B, Pereira F, Peierls R. The multifractal hypothesis and anomalous diffusion. Mat Aplic Comput. 1992;11:189–207. [Google Scholar]
- 90.Avellaneda M, Majda AJ. Simple examples with features of renormalization for turbulent transport. Philos Trans R Soc Lond A. 1994;346:205–233. [Google Scholar]
- 91.Ben Arous G, Owhadi H. Super-diffusivity in a shear flow model from perpetual homogenization. Commun Math Phys. 2002;227:281–302. [Google Scholar]
- 92.Sinhuber M, Bodenschatz E, Bewley GP. Decay of turbulence at high Reynolds numbers. Phys Rev Lett. 2015;114:034501. doi: 10.1103/PhysRevLett.114.034501. [DOI] [PubMed] [Google Scholar]
- 93.Warhaft Z, Lumley JL. An experimental study of the decay of temperature fluctuations in grid-generated turbulence. J Fluid Mech. 1978;88:659–684. [Google Scholar]
- 94.Sreenivasan KR, Tavoularis S, Henry R, Corrsin S. Temperature fluctuations and scales in grid-generated turbulence. J Fluid Mech. 1980;100:783–795. [Google Scholar]
- 95.Durbin P. Analysis of the decay of temperature fluctuations in isotropic turbulence. Phys Fluids. 1982;25:1328–1332. [Google Scholar]
- 96.Overholt MR, Pope SB. Direct numerical simulation of a statistically stable turbulent reacting flow. Combust Theor Model. 1999;3:371–408. [Google Scholar]
- 97.Ferchichi S, Tavoularis S. Scalar probability density function and fine structure in uniformly sheared turbulence. J Fluid Mech. 2002;461:155–182. [Google Scholar]
- 98.Schumacher J, Sreenivasan KR. Statistics and geometry of passive scalars in turbulence. Phys Fluids. 2005;17:125107. [Google Scholar]
- 99.Jayesh WZ. Probability distribution, conditional dissipation and transport of passive temperature fluctuations in grid-generated turbulence. Phys Fluids A. 1992;4:2292–2307. [Google Scholar]
- 100.Balkovsky E, Fouxon A. Universal long-time properties of Lagrangian statistics in the Batchelor regime and their application to the passive scalar problem. Phys Rev E. 1999;60:4164–4174. doi: 10.1103/physreve.60.4164. [DOI] [PubMed] [Google Scholar]
- 101.Bourlioux A, Madja AJ. Elementary models with probability distribution function intermittency for passive scalars with a mean gradient. Phys Fluids. 2002;14:881–897. [Google Scholar]
- 102.Kailasnath P, Sreenivasan KR, Saylor J. Conditional scalar dissipation rates in turbulent wakes, jets and boundary layers. Phys Fluids A. 1993;5:3207–3215. [Google Scholar]
- 103.Doering CR, Thiffeault J-L. Multiscale mixing efficiencies for steady sources. Phys Rev E. 2006;74:025301. doi: 10.1103/PhysRevE.74.025301. [DOI] [PubMed] [Google Scholar]
- 104.Thiffeault J-L. Using multiscale norms to quantify mixing and transport. Nonlinearity. 2012;25:R1–R44. [Google Scholar]
- 105.Pouquet A, Rosenberg D, Marino R, Herbert C. Scaling laws for mixing and dissipation in unforced rotating stratified turbulence. J Fluid Mech. 2018;844:519–545. [Google Scholar]
- 106.Jagannathan S, Donzis DA. Reynolds and Mach number scaling in solenoidally-forced compressible turbulence using high-resolution direct numerical simulations. J Fluid Mech. 2016;789:669–707. [Google Scholar]
- 107.Gibson CH. Buoyancy effects in turbulent mixing: Sampling turbulence in the stratified ocean. AIAA J. 1981;19:1394–1400. [Google Scholar]
- 108.Baldyga J, Makowski L, Orciuchi W. Interaction between mixing, chemical reactions, and precipitation. Chem Eng Res Des. 2015;85:745–752. [Google Scholar]
- 109.Aref H, et al. Frontiers of chaotic advection. Rev Mod Phys. 2017;89:025007. [Google Scholar]