Abstract.
Volume-of-interest (VOI) imaging is a strategy in computed tomography (CT) that restricts x-ray fluence to particular anatomical targets via dynamic beam modulation. This permits dose reduction while retaining image quality within the VOI. VOI-CT implementation has been challenged, in part, by a lack of hardware solutions for tailoring the incident fluence to the patient and anatomical site, as well as difficulties involving interior tomography reconstruction of truncated projection data. We propose a general VOI-CT imaging framework using multiple aperture devices (MADs), an emerging beam filtration scheme based on two binary x-ray filters. Location of the VOI is prescribed using two scout views at anterior–posterior (AP) and lateral perspectives. Based on a calibration of achievable fluence field patterns, MAD motion trajectories were designed using an optimization objective that seeks to maximize the relative fluence in the VOI subject to minimum fluence constraints. A modified penalized-likelihood method is developed for reconstruction of heavily truncated data using the full-field scout views to help solve the interior tomography problem. Physical experiments were conducted to show the feasibility of noncentered and elliptical VOI in two applications—spine and lung imaging. Improved dose utilization and retained image quality are validated with respect to standard full-field protocols. We observe that the contrast-to-noise ratio (CNR) is 40% higher compared with low-dose full-field scans at the same dose. The total dose reduction is 50% for equivalent image quality (CNR) within the VOI.
Keywords: fluence field modulation, volume-of-interest imaging, model-based iterative reconstruction
1. Introduction
Computed tomography (CT) has found wide applications in disease diagnosis, monitoring,1,2 interventional guidance,3,4 and radiotherapy guidance.5–7 There has been increasing concern about cumulative dose to patient populations as well as dose to single patients over longitudinal studies. Such concerns have encouraged investigations of protocols and strategies for dose reduction. Because interior volume-of-interest (VOI) imaging utilizes a relatively narrow area of x-ray coverage compared with traditional full field-of-view (FOV) CT, there is great potential for dose reduction.8 Such VOI-CT has been proposed for single organ/tissue studies, e.g., cardiac imaging,9,10 as well as in follow-up studies for specific prescribed locations, e.g., in interventional monitoring11 or in image-guided radiotherapy.12,13 Despite the promise of VOI imaging for various clinical applications, a main challenge in VOI imaging is appropriate hardware to reduce or block fluence outside the VOI. Clinical CT systems generally employ a static bowtie filter that cannot efficiently tailor the incident fluence for specific tasks, especially for noncentered targets. Chityala et al.14 implemented a VOI-imaging system using a static regional filter to decrease the fluence outside the VOI permitting a regional scan with a fixed, centered, and cylindrical VOI. Other studies took advantage of the orbital flexibility of C-arm systems to find a C-arm trajectory enabling noncentered cylindrical VOI.15,16 For more general noncentered, noncircular VOIs, a more flexible fluence field modulation that can translate the fluence position and modulate the beam width is required. Various methods have been proposed including split bowtie filters and dynamic collimators.17,18 In this work, we investigate the use of multiple aperture devices (MADs) that have been previously investigated for x-ray beam shaping as a dynamic bowtie filter.19
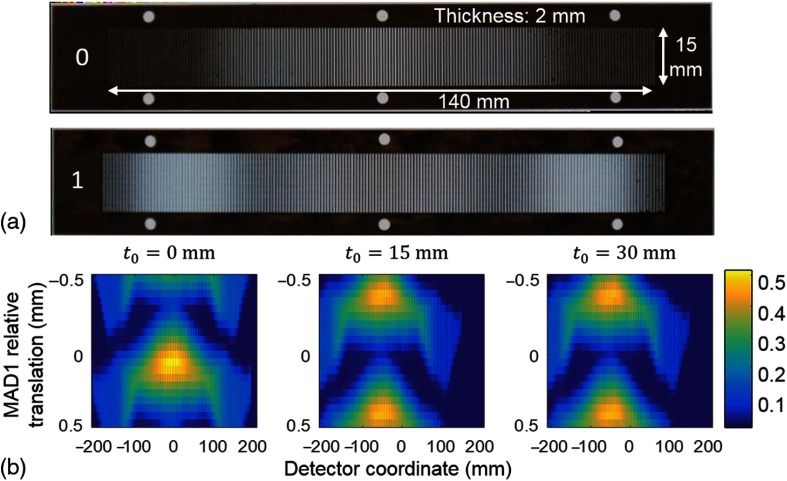
MADs [Fig. 1(a)] are (dual) sequential binary filters that provide a new strategy for dynamic fluence field modulation in a compact design since the filters can be made very thin from an appropriate high-density material (e.g., tungsten). Specifically, each filter is made of slit-shaped apertures with a periodic grating-like structure. In each MAD pitch length (one period), x-ray photons are either blocked by the structure or passed through the slit unattenuated controlling the local fluence. The varying widths of blockers determine the overall transmission within each pitch. The MAD pitch can be designed to be sufficiently small so that the extended x-ray focal spot blurs the binary pattern to achieve relatively smooth fluence profiles. Moreover, since the filter is essentially binary, there is also minimal change to the beam spectrum. Dynamic modulation is achieved through motion of the MADs. Two linear actuators translate each MAD separately. Absolute translation of both MADs as a whole shifts the fluence pattern in the lateral direction, whereas relative translations between the two filters modulate the fluence distribution, e.g., changing the width of the filtered x-ray beam as shown in Fig. 1(b). In essence, the effective local transmission is the composition of the effects of the two filters and increasing local overlap of the blockers will reduce transmission. The local spacing and slit widths can be designed to admit a range of fluence patterns with smooth transitions. Such filtration has provided adequate flexibility for fluence modulation for noncircular19 and off-centered20 object imaging. In this work, we seek to apply this filtration scheme for VOI imaging.
Fig. 1.
(a) Optical (backlit) photos of tungsten MADs featuring spatial modulation of light. Filter thickness: 2 mm; MAD pitch size: 0.9 mm. (b) Measured fluence patterns achieved by dual-MAD filtration for three different absolute translations of both MADs (0, 15, and 30 mm from center). Each subfigure shows the lateral beam profile (rows) as a function of the relative displacement between MADs at 20 discrete locations within an MAD pitch. Absolute motion shifts the center of the beam profile while relative MAD motion changes the beam shape, e.g., from a narrow to a wide beam. Note narrowing of the x-ray beam with absolute motion due to obliquity effects.
The three aforementioned general VOI techniques (split filters, dynamic collimation, and MAD filters) each have a different set of advantages and disadvantages. For example, split bowtie filters are capable of smooth modulation within and at the edges of the FOV allowing for control of fluence within the patient and avoiding hard truncation and an interior tomography type reconstruction problem. In contrast, dynamic collimation tends to have a step-like beam at the edge of the FOV with potential reconstruction issues due to the hard truncation. Dynamic collimation has a potential advantage in that the beam blockers can be made very thin with a high-density material, whereas most bowties use a thicker lower density material, which leads to a potentially less compact design. The MAD filtering approaches provide an alternative set of trade-offs with a thin design and the potential to shape the beam within the FOV. The MAD filters studied in this work exhibit near complete blockage of fluence at the edges of the FOV but with a smooth transition (though future designs may eliminate such truncation). We do not explicitly compare these various approaches in this work. Instead we provide an initial investigation demonstrating the feasibility of MAD-based VOI imaging.
In addition to hardware challenges, reconstruction in interior tomography demands special attention. Extrapolation21–23 is widely used when truncation in projection data occurs to alleviate artifacts at the edge of FOV. However, extrapolation cannot generally provide an exact solution and is likely to suffer significant artifacts in cases with severe truncation. For cases where limited x-ray fluence is permitted outside the VOI, statistical reconstruction may be applied.14,16 Differentiated backprojection methods have been developed that exactly reconstruct the VOI along with the addition of a priori knowledge.12,24–29
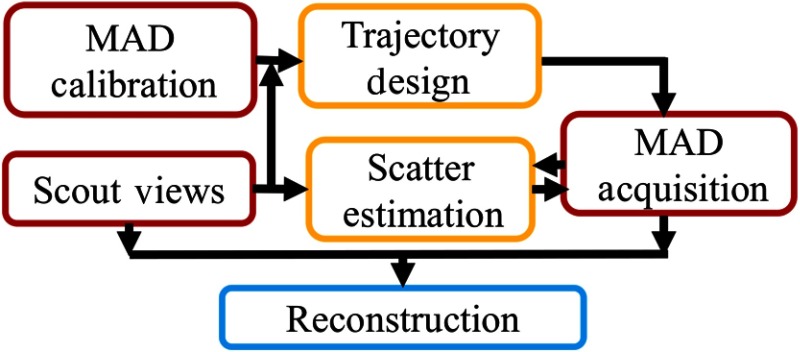
In this study, we propose a workflow for VOI imaging using MAD-based fluence field modulation as summarized in Fig. 2. Two full-field scout views are acquired at anterior–posterior (AP) and lateral perspectives to determine the VOI. Trajectories of MADs are designed to maximize the ratio of exposure through the VOI. A model-based iterative reconstruction algorithm is designed for fully truncated projections but uses the AP and lateral scout views to augment the data. Scatter correction is designed to equalize the CT measurements between the full-field and VOI projection data. Physical experiments were conducted to validate MAD-based VOI-CT feasibility for spine and single lung imaging applications using two anthropomorphic phantoms. Image quality and dose were compared with standard full-field scans.
Fig. 2.
MAD-based VOI imaging framework.
2. Methods and Materials
2.1. Filter Trajectory Design for VOI Fluence Field Modulation
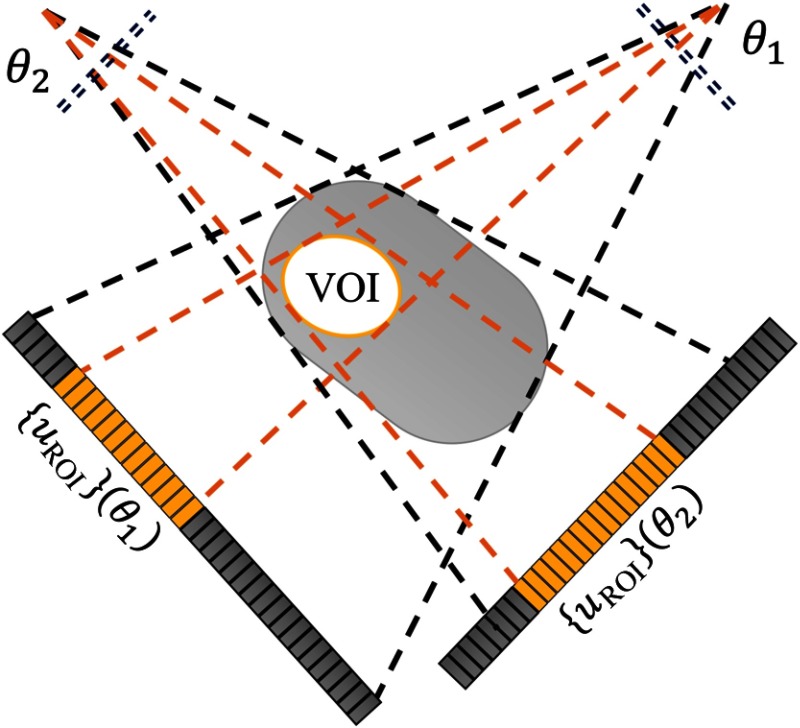
MADs provide a large range of fluence patterns as a function of absolute and relative displacement. To design a dynamic fluence field modulation scheme for a specific VOI task, one must identify the position and size of the VOI, find the range of projection data required to cover the VOI, and find the optimal MAD trajectories that induce fluence patterns that illuminate the detector accordingly (Fig. 3).
Fig. 3.
MAD-based VOI imaging diagram and notations.
In this work, we focus on VOIs of a general elliptical cylindrical shape, i.e., VOIs that are elliptical (or circular) in axial cross section for all slices. Two scout scans that cover the whole support at AP and lateral views are acquired to permit localization of the VOI with respect to patient anatomy. Specifically, we estimate the central position and width of the ellipse in transverse plane that circumscribes the VOI. Mathematically, we define the VOI with a two-dimensioanl (2-D) binary mask, , that has value 1 within the ellipse and 0 outside. The forward projection of the binary image mask in a fan-beam system (central slice of cone-beam system) is calculated for each projection view ,
| (1) |
where is the system matrix that projects a 2-D (central) axial image to a one-dimensional projection profile at angle and denotes the horizontal detector index. The logical operator, , returns 1 if the input statement is true such that has value 1 where the VOI mask projection is nonzero. The set of masks over all represents the projection support required for obtaining the desired VOI. We denote the set of VOI mask projection indices at projection as . The beam width and center column index at projection are calculated as follows:
| (2) |
Fluence field design for VOI imaging using MAD-based dynamic filtration follows two goals: (1) seek maximum (relative) exposures within the VOI region while limiting exposure outside the VOI and (2) constrain minimum fluence within VOI projections to be higher than a threshold (i.e., to maintain data fidelity at the edge of the VOI). A calibration of all possible MAD-based fluence patterns is acquired through an exhaustive sweep of absolute and relative MAD translations to form a look-up table relating MAD positions and corresponding fluence patterns. We denote as the lateral transmissivity profile of the dual-MAD filters with individual MAD0 and MAD1 filter positions labeled and , respectively. Note that represents a shift of MAD1 relative to MAD0. Due to the periodic nature of MAD structure, the modulated fluence patterns change periodically over relative displacement approximately equal to the pitch of the MADs. For simplicity, only one period is measured in the calibration process.
A coarse optimization of MAD positions for each view by simply matching center position and fluence width to find approximate fits. From the fluence modulation calibration , we may write
| (3) |
| (4) |
where denotes the minimum required transmissivity. While one could potentially use these metrics directly in the optimization, such fitting discounts the particular shape of the beam profile. However, these metrics do provide a good guide for candidate positions. For example, for each projection, a set of actuations “close” to these candidate positions may be specified where the filtered fluence approximately matches center and width:
| (5) |
where is a threshold to constrain filtration center deviation from the desired center. We may then constrain our optimization to solutions close to this coarse optimization improving robustness of design. In our physical experiments, we select and pixels empirically.
In particular, we pose the optimization problem as
| (6) |
| (7) |
where Eq. (6) seeks a solution with the greatest ratio of fluence inside the projected VOI to the total fluence. The solution is constrained to the set of fluence patterns with at least a specific level () inside the projected VOI and also within the coarse constraints [Eq. (5)]. This optimization problem is solved via exhaustive evaluation of all candidates selected through the coarse optimization.
Since the measured transmissivity profiles are noisy and contain the slit patterns from the MADs, there is potential to find nonsmooth trajectories. To eliminate such solutions and to obtain a smooth trajectory design, we follow the initial optimization with a sinusoidal fitting of the MAD0 trajectory , which is then fixed and used as an input to a second pass optimization of MAD1 trajectory alone, using the same objective function above.
2.2. Reconstruction of Truncated Data
As discussed in previous work,19 reconstruction of MAD-modulated data requires appropriate gain correction methods to account for a number of effects, including initial incident fluence, detector sensitivity, focal-spot variations, and spectral effects. This preprocessed data are used as an input to a modified reconstruction pipeline.
The MAD settings designed for VOI-CT effectively block most of the fluence outside the VOI. Such lateral projections have very low data fidelity, which results in severely truncated data. To obtain accurate reconstruction within the VOI, additional prior knowledge of the entire support is needed.27,28 Reshef et al.30 proved that exact interior VOI reconstruction is achievable with the addition of untruncated projections. In this work, we adapt a penalized-likelihood (PL) method that reconstructs the interior VOI using MAD-VOI data along with supplementary untruncated scout views obtained as part of the workflow of VOI identification.
2.2.1. Scatter correction
X-ray scatter is dependent on many factors including patient anatomy and x-ray protocol. Scatter by the MADs themselves is expected to be low and highly smoothed due to the large distance between the MADs and the detector as well as the extended focal spot. (Thus, we do not model or correct scatter from the filters.) However, the spatial fluence modulation (e.g., varying beam width) can change the scatter due to the patient more significantly. Similarly, the scatter fraction varies between the truncated data and the untruncated scout views. While perfect scatter correction is desired, practical scatter correction often leaves residual scatter in the data. This effect is often minor; however, scatter differences between the truncated and untruncated data result in mismatched CT measurements between scans. Such mismatches can result in artifacts including DC offsets within the VOI and truncation-like artifacts at the edge of the VOI. In this work, we implemented a scatter correction method based on analytical models of the MAD acquisition with particular attention to equalization of scatter in the matched AP and lateral views of the truncated and untruncated projections.
We presume that the untruncated AP and lateral projections have a standard scatter correction method applied. Various approaches exist, but in this work, we presume an “oracle” best constant scatter value is subtracted from each of these two views.31 It remains to develop a strategy for scatter estimation in the truncated data.
In the gain-corrected MAD projection data, the additive scatter distribution, denoted with , is related to both the absolute fluence behind the phantom and the MAD transmissivity profile (e.g., a wider beam has a different profile than a narrow beam). We observe in Monte-Carlo simulation on anthropomorphic phantoms that the scatter distribution in beam-modulated scans is roughly matched with a scaled square-root MAD transmissivity profile. (This is an empirical fit that may only be applicable to objects with similar size and shape.) In gain-corrected projection data, the scatter distribution is therefore proportional with an inverse square-root MAD transmissivity profile.
| (8) |
In the scatter model, represents the constant used in full-field data scatter correction where . Such scatter ratios in a bare-beam scan are modulated by the phantom and approximately linear with the minimum transmissivity behind the phantom.
To integrate the scatter-corrected scout views into the subsequent reconstruction, one must match the MAD projection data with the scout views. The scatter estimation in the truncated data is generalized in the following steps.
-
1.Scatter ratios and are estimated by minimizing the mean-square error between the scatter-corrected MAD projection data at the corresponding views and the full-view data presuming the linear relationship in minimum transmissivity.
(9) -
2.To evaluate the scatter distribution in the rest of the scan where the full-view scan is not collected, the minimum projection behind the patient is estimated with an uniform elliptical scout , modeled with axes lengths, central offset, in-plane rotation, and attenuation coefficient, through matching pursuit in projections based on the two scout views.
(10) -
3.Combining the scatter ratios and the estimated minimum projection , scatter ratio for each view is linearly estimated. For an elliptical scout,
If the scout estimation is nearly circular [], is estimated with the mean of and as a constant with respect to view angle .(11) -
4.
Substituting in Eq. (8), the scatter estimation is subtracted from the projections frame by frame.
2.2.2. Penalized-likelihood model and reconstruction
Reconstruction requires a forward model for the data. We adopt the following vectorized model with a uniform (prefiltration) bare-beam fluence magnitude and a variable gain/transmissivity of the MADs given by the diagonal matrix :
| (12) |
where denotes the system matrix and represents the entire three-dimensional (3-D) volume. Note that specifies the geometric projection of all truncated data views as well as the two full-field scout views. Moreover, the diagonal gain term also accommodates the beam modulation in the AP and lateral views. Since no MAD filters are used in the scout images, the transmissivity term is enforced to 1 in the two full-field frames. For the MAD-filtered projection data, is fixed to 0 outside the VOI. With the gain- and scatter-corrected projection data (scaled with incident x-ray counts ) and the presumption of Poisson distributed noise, we can form the following PL objective function:
| (13) |
where is the image estimate. The regularization term and regularization strength are introduced to control the resolution-noise trade-off. In this work, we adopt a quadratic penalty term based on pairwise differences of the six nearest neighbors in each (3-D) axial direction:
| (14) |
The objective function was solved iteratively using the separable paraboloidal surrogates (SPS) method.32
2.3. Experimental Setup
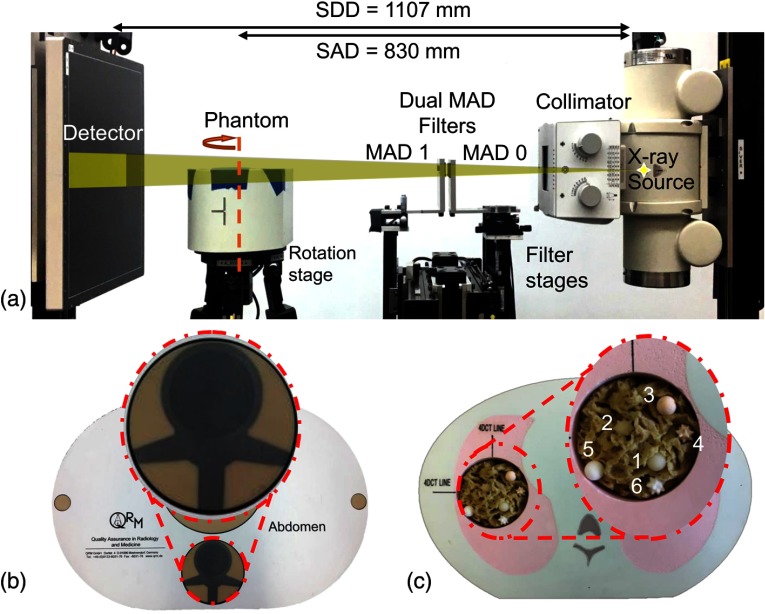
Physical experiments were conducted on a cone-beam CT test bench equipped with MAD filters manufactured from 2-mm-thick tungsten plates with a pitch size of 0.9 mm [Fig. 4(a)]. Two different experiments were conducted using anthropomorphic phantoms. (1) A spine imaging scenario was conducted wherein a cylindrical VOI centered on the spine in a QRM abdomen phantom [Fig. 4(b)] was investigated and (2) a lung imaging nodule surveillance scenario, e.g., emulating a single organ follow-up scan, wherein an elliptical cylindrical VOI around the left lung in a CIRS Xsight phantom with six subsolid nodules (Kyoto Kagaku) [Fig. 4(c)] was studied. MAD trajectories were designed based on prescribed VOIs for MAD-VOI scans for each phantom. For comparison, standard full-view scans (without beam modulation) were acquired at relatively high () and low exposure () settings. The low exposure setting is intended to approximately match both the incident exposure and deposited dose in the MAD-VOI protocol. Projection data used 720 frames and 360 frames for the abdomen phantom and the lung phantom, respectively, with equiangular steps over one full rotation. The bare-beam fluence, , was estimated to be photons/pixel in the high-dose cases and photons/pixel in the low-dose cases, and averaged photons/pixel within the VOI in the MAD scans.
Fig. 4.
(a) Test bench experiment setup. The source-to-axis distance (SAD) and source-to-detector distance (SDD) are specified. (b) Abdomen QRM phantom with a noncentered cylindrical VOI. (c) CIRS Xlight lung phantom with a noncentered elliptic VOI. (VOIs circumscribed by red dashed lines.)
For all the experiments, projections are reconstructed using PL method. About 300 iterations of the SPS algorithm are used with 20 subsets for the first 5 iterations, 10 for the following 5, and 1 for the remaining.33 All reconstructions used separable footprints projectors/backprojectors.34 A volume of , 0.5-mm cubic voxels was used to cover the entire patient support in reconstruction. Reconstructions were truncated to the VOI support of voxels and in abdomen and lung phantom phantoms, respectively, for analysis. In all reconstruction, we used a uniform quadratic roughness penalty with first-order neighborhood and pairwise voxel differences. Regularization strength, , was scaled with the (average) fluence for fair comparison between protocols, and was , , and in full-field high-dose, MAD-VOI, and full-field low-dose cases, respectively.
Dose distributions were estimated using Monte-Carlo simulation for all protocols.35 The incident fluence in MAD-VOI scan was estimated with MAD transmissivity profiles scaled by bare-beam fluence . Contrast-to-noise ratios (CNRs) and accumulative dose were reported for all protocols.
3. Experimental Results
3.1. MAD-VOI Fluence Field Modulation
MAD trajectory design for the spine and lung imaging scenarios as well as the achieved fluence field modulation are shown in Fig. 5. The red solid lines show the trajectory of MAD0 translation, and the blue dashed lines show the displacement of MAD1 to MAD0 from frame to frame. The highest absolute translation of MAD0 from the reference point was 26 mm for spine imaging and 33 mm for lung imaging. Relative displacement between MAD0 and MAD1 was constrained within corresponding to a single period of the MAD pitch. The stepping pattern in MAD1 trajectories results from the phase wrapping effects, which is more significant in a lung imaging case, where the phase shift from view to view is larger for varying fluence width for an elliptical VOI. The largest absolute displacement of both MADs between frames was 1 mm—again, a relatively short actuation distance.
Fig. 5.
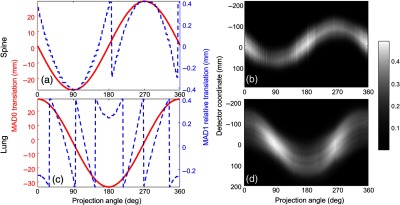
(a), (c) MAD trajectory designs for round and elliptical VOI imaging. The red solid lines show the trajectory of MAD0 translation. The blue dashed lines show the displacement of MAD1 to MAD0. (b), (d) Achieved fluence field modulation. (a), (b) Spine imaging experiment. (c), (d) Single lung imaging experiment.
In the spine imaging scenario, the fluence width was approximately constant over all projection angles since the prescribed VOI was a circular cylinder (though minor magnification and obliquity effects are present for an off-center VOI). In the lung imaging case, which has an elliptical axis region of interest, the fluence width reached the highest at 90 deg and 270 deg views, where the long-axis of the prescribed elliptical VOI is parallel to the detector panel. In both cases, since the VOI was off-center, the beam was sinusoidally shifted in the lateral direction to track the center of the VOI. The relative displacements between two MADs components also changed sinusoidally with respect to projection angle though wrapping is present due to constraint within one MAD period. We note some nonsmoothness of the estimated fluence patterns. We conjecture that this is due to inherent variabilities in the calibration scans and optimizer selecting particular solutions among fluence patterns of similar width. This variability is more pronounced for narrow beams and is more evident in the spine imaging scenario.
3.2. Image Quality Analysis
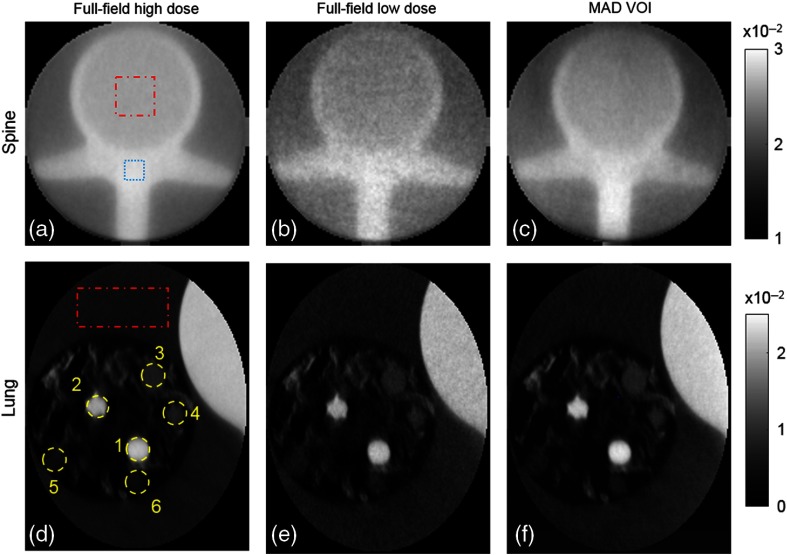
PL reconstructions of VOIs in full-field high-dose, low-dose, and MAD-VOI scans are shown in Fig. 6. To minimize the bias due to residual scatter mismatch and low fluence level, the CT values were matched between protocols with a linear fit in two constant regions for a fair comparison. Detailed structures were well-preserved within the VOI in the proposed protocol, and the noise was significantly reduced compared with the full-field low-dose scan that used a similar exposure. The CNRs of each nodule placed in the lung phantom and the spine phantom were calculated and summarized in Table 1. The noise is measured through standard deviation calculation in a flat background region circumscribed with a red dashed line. The contrast in the spine phantom is computed using the difference between the vertebral bone tissue (circumscribed with blue dashed line) and the interior of the vertebra (circumscribed with red dashed line). The CNRs in MAD-VOI scans are higher compared to the full-field low-dose scans, except for nodule 5, which was very close to the boundary of the elliptical VOI. Because the regularization strength is scaled according to the average incident photon counts to enforce similar spatial resolution between reconstructions, the dose is approximately proportional to the square of noise. To conduct a fair comparison of dose usage between the full-field and MAD-VOI scans, a noise-adjusted dose that can achieve the same CNR as the MAD-VOI scan with the full-field scan is computed as 1.96 times of the low-dose scan dose. Thus, the overall dose reduction of the MAD-VOI protocol is to achieve the same CNR within the VOI.
Fig. 6.
Reconstructions with different acquisition protocols. (a), (d) The high-dose full-field reconstructions. (b), (e) Low-dose full-field. (c), (f) MAD-VOI images. (a)–(c) Spine imaging experiment and (d)–(f) lung imaging experiment. The attenuation coefficient unit is .
Table 1.
CNR.
| Protocol | Nodule 1 | Nodule 2 | Nodule 3 | Nodule 4 | Nodule 5 | Nodule 6 | Spine |
|---|---|---|---|---|---|---|---|
| Full-field high dose | 116.5 | 108.0 | 40.38 | 40.55 | 20.30 | 21.70 | 20.30 |
| Full-field low dose | 48.67 | 45.27 | 16.71 | 16.59 | 9.30 | 9.71 | 9.10 |
| MAD-VOI | 67.96 | 62.09 | 24.62 | 22.87 | 10.30 | 12.86 | 16.38 |
3.3. Dose Calculation
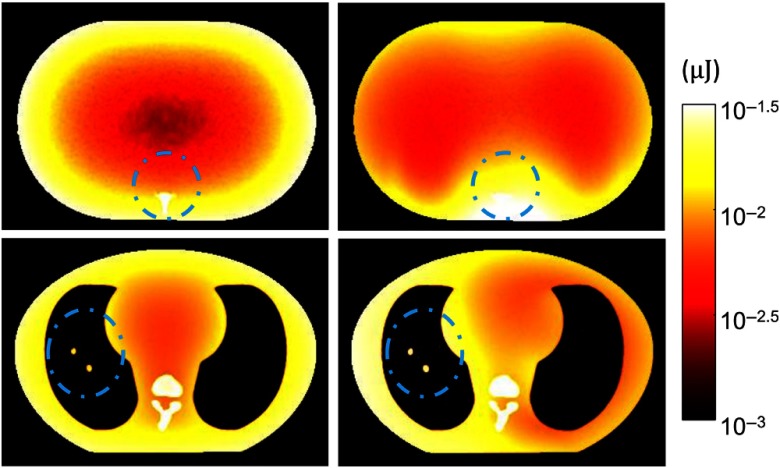
The results of Monte-Carlo estimated dose distributions in full-field low-dose scans and MAD-VOI scans are shown in Fig. 7. As expected, we observe that the MAD-VOI scan delivered more dose to the VOI region, whereas the full-field scan delivered dose more widely in the phantom, especially near the edges of the phantoms. Accumulative dose within the VOI, outside the VOI, and the total in all protocols are summarized in Table 2. In the spine imaging case, the total dose in MAD-VOI scan was 11.9% of the total dose in full-field high-dose scan and 67.2% of the total dose in low-dose scan. In the lung scan, the total dose was 18.6% of full-field high-dose scan, and approximately the same as low-dose scan. The dose within the VOIs was, on the other hand, higher than in the low-dose protocols. In Table 1, the CNRs in MAD-VOI scans are higher than in full-field low-dose scan. Because the regularization strength is scaled according to the average incident photon counts to enforce similar spatial resolution between reconstructions, the dose is approximately proportional to the square of noise. To conduct a fair comparison of dose usage between the full-field and MAD-VOI scans, a noise-adjusted dose that can achieve the same CNR as the MAD-VOI scan with the full-field scan is computed as 1.96 times of the low-dose scan dose. The overall dose reduction of MAD-VOI protocol is that retains image quality within the VOI.
Fig. 7.
Monte-Carlo simulated dose distribution maps in (a), (c) full-field low-dose scan and (b), (d) MAD-VOI scan. Prescribed VOIs are circumscribed with blue dashed lines. (a), (b) Spine imaging experiment and (c), (d) lung imaging experiment. The colormap is shown in log-scale for optimal variation display.
Table 2.
VOI, peripheral, and total dose.
| Protocols | Spine imaging dose (mJ) | Lung imaging dose (mJ) | ||||
|---|---|---|---|---|---|---|
| VOI | Peripheral | Total | VOI | Peripheral | Total | |
| Full-field high dose | 4.56 | 45.84 | 50.40 | 2.94 | 19.02 | 21.96 |
| Full-field low dose | 0.68 | 6.84 | 7.52 | 0.53 | 3.42 | 3.95 |
| MAD-VOI | 1.40 | 4.60 | 6.00 | 0.75 | 3.34 | 4.09 |
| Full-field noise-adjusted | 1.33 | 13.41 | 14.74 | 1.04 | 6.70 | 7.74 |
4. Discussion
We have proposed a VOI-CT imaging protocol using an MAD filtration scheme and validated the feasibility with physical experiments. The protocol includes a general approach for MAD trajectories for a prescribed VOI and a truncated data reconstruction method implemented using a PL framework. Two scout views are required for identifying the VOI, aiding in scatter correction, and adding a priori knowledge to condition the reconstruction problem and eliminating interior reconstruction artifacts. Off-center and elliptical VOIs were realized and explored in physical experiments. Image quality and radiation dose are reported and compared with full-field scans without standard static bowtie filtration or tube-current modulation design. The approach permits overall reduction of radiation dose while maintaining image quality within the VOI. Such performance suggests potential practical benefits for dose reduction in scenarios such as disease screening for specific organs or tissues, follow-up examinations, or interventional procedures where known anatomical targets can be specified a priori.
In this work, we have demonstrated the potential for VOI imaging with MADs, but we have not made explicit comparisons to other VOI methods, such as split bowtie filters and dynamic collimators. It is important to explore the balance between various specifications, including speed requirements, filter thickness, ability to perform beam shaping, and degree of truncation for practical implementation. The optimality of different approaches is potentially tied to clinical applications and target anatomies, as well as more general capabilities (e.g., ability to perform both full-field beam shaping and dynamical filtering as well as VOI imaging). Future studies should also include comparisons with standard static bowtie systems and current modulation since these features also have the potential to improve dose efficiency.
The investigated MAD-VOI approach is flexible for any prescribed single VOI imaging since current MADs were designed to achieve single peak transmissivity profiles of varying widths. However, the MADs we used in this work were designed for dynamic fluence field modulation that flatten the detected signal behind the AP and lateral views of a uniform acrylic phantom of the same shape as the QRM phantom. The achievable fluence modulation patterns are not optimized for VOI imaging task. Due to the limited maximum transmissivity of the MADs, tube loading is a practical concern. The MADs used in this work have a maximum transmission of 50%. More recent designs have improved this to around 85% using the same fabrication methods.19 Future versions of MADs can be further improved for better transmission characteristics. Maximum transmissivity is determined by the minimum slit width, and investigation of better fabrication methods would improve tube loading. Moreover, new MAD designs that are thinner or made from lower density material could allow a targeted minimum fluence level at the edges avoiding full data truncation36 and hard data truncation. Additional investigations may include new MAD designs that allow multimodal patterns for multiple VOI imaging tasks. The MAD filters in this work were designed for a relatively small cone-angle. However, it should be possible to extend the height of the MADs for large cone-angle CBCT. To do so will require study of the MAD fabrication limits. Specifically, larger slit and blocker heights will require additional support structure to avoid flex and breakage of the MAD structure. Possible solutions include use of interstitial low-density support materials in the slots and designs with lateral support structures (e.g., two-dimensional designs). Such engineering challenges would require additional investigation in future work. Moreover, dose utilization can be further optimized considering noise and dose objectives including organ sensitivity to radiation.37 Such scenarios are the subject of future work.
Acknowledgments
This work was supported, in part, by the U.S. National Institutes of Health under Grant No. U01EB018758.
Biographies
Wenying Wang received her BE degree in engineering physics from Tsinghua University in Beijing, China. Currently, she is a PhD candidate in biomedical engineering at Johns Hopkins University. Her studies involve advanced acquisition and reconstruction methods for CT including dynamic beam modulation and analysis of imaging properties in model-based iterative reconstruction in CT, cone-beam CT, and spectral CT systems.
Grace J. Gang obtained her PhD in biomedical engineering from the University of Toronto in 2014. Currently, she is an assistant research professor of biomedical engineering at Johns Hopkins University. Her research interests involve image quality modeling, assessment, and optimization for advanced technologies in CT and cone-beam CT.
Jeffrey H. Siewerdsen received his PhD in physics from the University of Michigan, in 1998. He is the John C. Malone Professor of biomedical engineering, computer science, radiology, and neurosurgery and the director of the Carnegie Center for Surgical Innovation at Johns Hopkins University. His research focuses on the physics of image quality in digital x-ray, CT, and cone-beam CT, and the development of systems to improve precision, accuracy, and safety in image-guided interventions.
Reuven Levinson received his BS degree in physics from Hebrew University in Jerusalem, Israel, and his MS degree in bioengineering from University of Pennsylvania in 1982. He is a senior staff scientist in the Advanced CT Development Business Unit at Philips Healthcare in Haifa, Israel. His work in medical CT systems has focused on the design of detectors for multislice acquisition and spectral CT, and optimizing the dose efficiency of commercial CT systems using dynamic beam-shaping filters.
Satomi Kawamoto received her MD from Gunma University in Japan with distinction (cum laude), in 1988. She completed her residency training in internal medicine at St. Luke’s International Hospital in Tokyo, Japan, and in diagnostic radiology at Johns Hopkins University, where she has been an associate professor of radiology since 2009. Her research focuses on body CT and biopsy, and particularly imaging of the genitourinary and gastrointestinal systems.
J. Webster Stayman received his PhD in electrical engineering from the University of Michigan, in 2003. He is an associate professor of biomedical engineering at Johns Hopkins University and the principal investigator of the Advanced Imaging Algorithms and Instrumentation Laboratory. His research interests include tomographic reconstruction, statistical reconstruction approaches, regularization design, prior-image-based reconstruction, task-driven and adaptive acquisitions, and cone-beam CT modeling and analysis.
Disclosures
Mr. Levinson was an employee of Philips Medical Systems at the time of this research.
References
- 1.Parr D. G., et al. , “Validation of computed tomographic lung densitometry for monitoring emphysema in -antitrypsin deficiency,” Thorax 61(6), 485–490 (2006). 10.1136/thx.2005.054890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Anzidei M., et al. , “Longitudinal assessment of carotid atherosclerosis after radiation therapy using computed tomography: a case control study,” Eur. Radiol. 26(1), 72–78 (2016). 10.1007/s00330-015-3753-9 [DOI] [PubMed] [Google Scholar]
- 3.Jaffray D. A., et al. , “Flat-panel cone-beam computed tomography for image-guided radiation therapy,” Int. J. Radiat. Oncol. Biol. Phys. 53(5), 1337–1349 (2002). 10.1016/S0360-3016(02)02884-5 [DOI] [PubMed] [Google Scholar]
- 4.Morimoto M., et al. , “C-arm cone beam CT for hepatic tumor ablation under real-time 3D imaging,” Am. J. Roentgenol. 194, W452–W454 (2010). 10.2214/AJR.09.3514 [DOI] [PubMed] [Google Scholar]
- 5.Jaffray D. A., “Emergent technologies for 3-dimensional image-guided radiation delivery,” Semin. Radiat. Oncol. 15(3), 208–216 (2005). 10.1016/j.semradonc.2005.01.003 [DOI] [PubMed] [Google Scholar]
- 6.Balter J. M., Kessler M. L., “Imaging and alignment for image-guided radiation therapy,” J. Clin. Oncol. 25(8), 931–937 (2007). 10.1200/JCO.2006.09.7998 [DOI] [PubMed] [Google Scholar]
- 7.Jaffray D. A., “Image-guided radiotherapy: from current concept to future perspectives,” Nat. Rev. Clin. Oncol. 9(12), 688–699 (2012). 10.1038/nrclinonc.2012.194 [DOI] [PubMed] [Google Scholar]
- 8.Wang G., “The meaning of interior tomography,” in IEEE Int. Conf. Acoust., Speech and Signal Process., pp. 5764–5767 (2011). 10.1109/ICASSP.2011.5947670 [DOI] [Google Scholar]
- 9.Hoffmann M. H. K., “Noninvasive coronary angiography with multislice computed tomography,” JAMA 293(20), 2471–2478 (2005). 10.1001/jama.293.20.2471 [DOI] [PubMed] [Google Scholar]
- 10.Ziegler A., Nielsen T., Grass M., “Iterative reconstruction of a region of interest for transmission tomography,” Med. Phys. 35(4), 1317–1327 (2008). 10.1118/1.2870219 [DOI] [PubMed] [Google Scholar]
- 11.Lee J., et al. , “Volume-of-change cone-beam CT for image-guided surgery,” Phys. Med. Biol. 57(15), 4969–4989 (2012). 10.1088/0031-9155/57/15/4969 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yu L., et al. , “Region of interest reconstruction from truncated data in circular cone-beam CT,” IEEE Trans. Med. Imaging 25, 869–881 (2006). 10.1109/TMI.2006.872329 [DOI] [PubMed] [Google Scholar]
- 13.Chen L., et al. , “Feasibility of volume-of-interest (VOI) scanning technique in cone beam breast CT—a preliminary study,” Med. Phys. 35, 3482–3490 (2008). 10.1118/1.2948397 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chityala R., et al. , “Region of interest (ROI) computed tomography (CT): comparison with full field of view (FFOV) and truncated CT for a human head phantom,” Proc. SPIE 5745, 583–590 (2005). 10.1117/12.595430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kolditz D., Kyriakou Y., Kalender W. A., “Volume-of-interest (VOI) imaging in C-arm flat-detector CT for high image quality at reduced dose,” Med. Phys. 37(6), 2719–2730 (2010). 10.1118/1.3427641 [DOI] [PubMed] [Google Scholar]
- 16.Cho S., et al. , “Region-of-interest image reconstruction with intensity weighting in circular cone-beam CT for image-guided radiation therapy,” Med. Phys. 36(4), 1184–1192 (2009). 10.1118/1.3085825 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Parsons D., Robar J. L., “An investigation of kV CBCT image quality and dose reduction for volume-of-interest imaging using dynamic collimation,” Med. Phys. 42(9), 5258–5269 (2015). 10.1118/1.4928474 [DOI] [PubMed] [Google Scholar]
- 18.Pearson E., Pan X., Pelizzari C., “Dynamic intensity-weighted region of interest imaging for conebeam CT,” J. X-Ray Sci. Technol. 24, 361–377 (2016). 10.3233/XST-160550 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gang G. J., et al. , “Dynamic fluence field modulation in computed tomography using multiple aperture devices,” Phys. Med. Biol. 64(10), 105024 (2019). 10.1088/1361-6560/ab155e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mao A., et al. , “Dynamic fluence field modulation for miscentered patients in computed tomography,” J. Med. Imaging 5(4), 043501 (2018). 10.1117/1.JMI.5.4.043501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chityala R., et al. , “Artifact reduction in truncated CT using sinogram completion,” Proc. SPIE 5747, 2110–2117 (2005). 10.1117/12.595450 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Zhao S., Yang K., Yang X., “Reconstruction from truncated projections using mixed extrapolations of exponential and quadratic functions,” J. X-Ray Sci. Technol. 19(2), 155–172 (2011). 10.3233/XST-2011-0284 [DOI] [PubMed] [Google Scholar]
- 23.Hsieh S. S., et al. , “An algorithm to estimate the object support in truncated images,” Med. Phys. 41(7), 071908 (2014). 10.1118/1.4881521 [DOI] [PubMed] [Google Scholar]
- 24.Noo F., Clackdoyle R., Pack J. D., “A two-step Hilbert transform method for 2D image reconstruction,” Phys. Med. Biol. 49(17), 3903–3923 (2004). 10.1088/0031-9155/49/17/006 [DOI] [PubMed] [Google Scholar]
- 25.Defrise M., et al. , “Truncated Hilbert transform and image reconstruction from limited tomographic data,” Inverse Prob. 22(3), 1037–1053 (2006). 10.1088/0266-5611/22/3/019 [DOI] [Google Scholar]
- 26.Pan X., Zou Y., Xia D., “Image reconstruction in peripheral and central regions-of-interest and data redundancy,” Med. Phys. 32(3), 673–684 (2005). 10.1118/1.1844171 [DOI] [PubMed] [Google Scholar]
- 27.Kudo H., et al. , “Tiny a priori knowledge solves the interior problem,” in IEEE Nucl. Sci. Symp. Conf. Rec., Vol. 6, pp. 4068–4075 (2007). 10.1109/NSSMIC.2007.4437021 [DOI] [Google Scholar]
- 28.Courdurier M., et al. , “Solving the interior problem of computed tomography using a priori knowledge,” Inverse Prob. 24(6), 065001 (2008). 10.1088/0266-5611/24/6/065001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Li L., et al. , “A general region-of-interest image reconstruction approach with truncated Hilbert transform,” J. X-Ray Sci. Technol. 17(2), 135–152 (2009). 10.3233/XST-2009-0218 [DOI] [PubMed] [Google Scholar]
- 30.Reshef A., et al. , “Parallel-beam ROI reconstruction with differentiated backprojection and angularly subsampled complementary sinograms,” HAL Id: hal-01807413 (2018).
- 31.Bertram M., Wiegert J., Rose G., “Potential of software-based scatter corrections in cone-beam volume CT,” Proc. SPIE 5745, 259–270 (2005). 10.1117/12.595032 [DOI] [Google Scholar]
- 32.Fessler J., Erdogan H., “A paraboloidal surrogates algorithm for convergent penalized-likelihood emission image reconstruction,” in IEEE Nucl. Sci. Symp. Conf. Rec. IEEE Nucl. Sci. Symp. and Med. Imaging Conf., IEEE, Vol. 2, pp. 1132–1135 (1998). 10.1109/NSSMIC.1998.774361 [DOI] [Google Scholar]
- 33.Erdogan H., Fessler J. A., “Ordered subsets algorithms for transmission tomography,” Phys. Med. Biol. 44(11), 2835–2851 (1999). 10.1088/0031-9155/44/11/311 [DOI] [PubMed] [Google Scholar]
- 34.Long Y., Fessler J. A., Balter J. M., “3D forward and back-projection for x-ray CT using separable footprints,” IEEE Trans. Med. Imaging 29(11), 1839–1850 (2010). 10.1109/TMI.2010.2050898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sisniega A., et al. , “Monte Carlo study of the effects of system geometry and antiscatter grids on cone-beam CT scatter distributions,” Med. Phys. 40(5), 051915 (2013). 10.1118/1.4801895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yu Z., et al. , “How low can we go in radiation dose for the data-completion scan on a research whole-body photon-counting computed tomography system,” J. Comput. Assisted Tomogr. 40(4), 663–670 (2016). 10.1097/RCT.0000000000000412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bartolac S., et al. , “Fluence field optimization for noise and dose objectives in CT,” Med. Phys. 38(Suppl. 1), S2 (2011). 10.1118/1.3574885 [DOI] [PubMed] [Google Scholar]