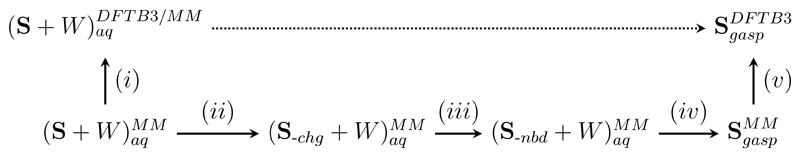On the use of interaction energies in QM/MM free energy simulations

Abstract

The use of the most accurate (i.e., QM or QM/MM) levels of theory for free energy simulations (FES) is typically not possible. Primarily, this is because the computational cost associated with the extensive configurational sampling needed for converging FES is prohibitive. To ensure the feasibility of QM-based FES, the “indirect” approach is generally taken, necessitating a free energy calculation between the MM and QM/MM potential energy surfaces. Ideally, this step is performed with standard free energy perturbation (Zwanzig’s equation) as it only requires simulations be carried out at the low level of theory; however, work from several groups over the past few years has conclusively shown that Zwanzig’s equation is ill-suited to this task. As such, many approximations have arisen to mitigate difficulties with Zwanzig’s equation. One particularly popular notion is that the convergence of Zwanzig’s equation can be improved by using interaction energy differences instead of total energy differences. Although problematic numerical fluctuations (a major problem when using Zwanzig’s equation) are indeed reduced, our results and analysis demonstrate that this “interaction energy approximation” (IEA) is theoretically incorrect, and the implicit approximation invoked is spurious at best. Herein, we demonstrate this via solvation free energy calculations using IEA from two different low levels of theory to the same target high level. Results from this proof-of-concept consistently yield the wrong results, deviating by ~1.5 kcal/mol from the rigorously obtained value.

1. Introduction

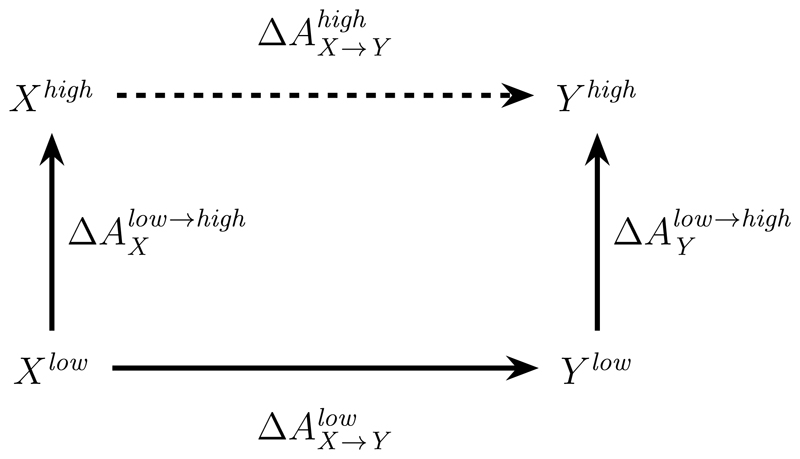
For many applications, the use of (S)QM/MM¹ Hamiltonians is essential.^2–7 Unfortunately, when implementing molecular dynamics (MD) based methods for computing free energy differences (i.e., free energy simulations, FES), direct use of (S)QM/MM Hamiltonians causes two major problems. First, particularly for ai-QM methods, the computational cost for the requisite configurational sampling quickly becomes prohibitive. Second, many crucial techniques frequently employed in FES using MM force fields, most notably the use of soft-core potentials^8,9 are incompatible with (S)QM/MM Hamiltonians.³ Many of these limitations can be circumvented by the so-called “indirect” approach to (S)QM/MM FES.^10–15 The key idea is outlined in Fig. 1. The goal is to compute the free energy difference between two states X and Y at a high level of theory $(\Delta A_{X\to Y}^{high},\text{dashed}\text{arrow}),$ where high denotes an accurate, but expensive method; e.g., ai-QM/MM. Similarly, the label low denotes a computationally affordable method that may not be accurate enough for the intended application. Often, the low level of theory is a standard MM force field, but it could also be a sufficiently fast SQM/MM method (although at the cost of most alchemical tricks). Since the free energy difference along any closed path is zero, the identity

$$\Delta A_{X\to Y}^{high}=-\Delta A_X^{low\to high}+\Delta A_{X\to Y}^{low}+\Delta A_Y^{low\to high}$$ (1)

follows immediately from Fig. 1.

Figure 1.

Thermodynamic cycle underlying the “indirect” scheme in FES employing (S)QM/MM potential energy functions.

Eq. 1 is the foundation of indirect FES using (S)QM/MM Hamiltonians. This is has recently re-emerged as a very active area of research as this is both an attractive approach and littered with potential pitfalls.^16–35 For example, the challenge is to compute ΔA^low→high for states X and Y; the free energy difference at the respective low level of theory, $\Delta A_{X\to Y}^{low},$ is assumed to be easy to compute. In the majority of past applications of the indirect scheme, ΔA^low→high was computed using Zwanzig’s equation, often called free energy perturbation (FEP),^36,37 i.e.

$$\Delta A^{\mathit{\text{low}}\to \mathit{\text{high}}}=-k_{B}T\text{ln}{\langle \text{exp}\left[\frac{-\Delta U^{\mathit{\text{low}}\to \mathit{\text{high}}}}{k_{B}T}\right]\rangle }_{\mathit{\text{low}}}$$ (2)

Since the term “free energy perturbation” encompasses also, e.g., Bennett’s acceptance ratio method, we will preferentially refer to Eq. 2 as Zwanzig’s equation in this work. Here k_B and T are Boltzmann’s constant and temperature; ΔU^low→high = U^high – U^low is the difference in energy of the system evaluated at the low and high levels of theory, and 〈. . .〉_low denotes an ensemble average of configurations sampled at the low level of theory. Use of Eq. 2 has the advantage that MD simulations need to be carried out only at the low level of theory and the energy U^high is computed only for selected configurations during a post-processing step.

Recent evidence, however, shows that attempts to compute ΔA^low→high by Zwanzig’s equation converge poorly, if at all.^{18,19,21,38–42} Analysis carried out by various groups suggests that this is mostly caused by differences in the internal energy at the two levels of theory, in particular bond lengths and angles. E.g., in MM simple harmonic terms approximate the bond stretching energy, whereas the true functional dependence is more complicated. Thus, configurations generated with MM Hamiltonians are always “slightly wrong” at the (S)QM level of theory. By “slightly wrong” we mean that a bond length, which is perfectly reasonably at the MM level of theory, may actually be quite off from the minimum geometry at the (S)QM/MM level of theory. In principle, the same can happen between two (S)QM/MM levels of theory, employing different quantum chemical techniques, but the harmonic terms used in force fields likely acerbate this. These individually small “configurational mismatches” sum up to large fluctuations of the central quantity entering Zwanzig’s equation, the energy difference ΔU^low→high, and, thus, failure of Zwanzig’s equation to converge.³⁷ Given sufficiently large differences between the potential energy surfaces of two states, such problems can occur even for diatomic molecules.^28,43 In the context of indirect (S)QM/MM FES we have observed this for quantum regions as small as 10 atoms.⁴⁴ This configurational mismatch between levels of theory only compounds with growing system size, and by proxy so will the observed fluctuations in ΔU^low→high, i.e., σ_{ΔU^low→high} becomes large, easily exceeding several kcal/mol.

Usually, convergence problems in Zwanzig’s equation are mitigated by the use of intermediate states with Hamiltonian H(λ), where λ is the so-called coupling parameter.³⁷ However, under the specific circumstances H(λ) = (1 – λ)H^low + λH^high, so simulations at any intermediate state λ > 0 require energy/force evaluations at the high level Hamiltonian. Thus, any performance gain of the indirect scheme is lost. The same problem arises in the other standard methods to compute free energy differences. For Bennett’s acceptance ratio (BAR) method⁴⁵ simulations at both the low and the high level of theory are needed. In thermodynamic integration^46,47 by construction several MD simulations at intermediate Hamiltonians H(λ), all of which require force evaluations at the high level of theory, are needed. It has been pointed out very recently that the introduction of (S)QM intermediate states might still improve the overall performance of the free energy simulation if it can significantly improve the phase space overlap between levels of theory, thus reducing the computational effort to achieve convergence when computing ΔA^low→high.²⁸

In recent years, a growing number of studies attempted to circumvent the poor convergence of Zwanzig’s equation in connection with (S)QM/MM FES by taking into account changes in interaction energies, rather than full energies.^{16,21,27,38,39,48–59} We will refer to this practice as the interaction energy approximation (IEA). To clarify the term interaction energy, consider a solute, S, in water, W. The interaction energy U_inter of such a system is defined as

$$U_{\mathit{\text{int}}er}=U_{total}({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W)-U_S({\mathbf{\text{r}}}_S)-U_W({\mathbf{\text{r}}}_W)$$ (3)

where U_total (r_S, r_W) is the total potential energy of the solute–solvent system, with r_S, r_W denoting solute and solvent coordinates. U_S(r_S) and U_W(r_W) are the potential energies for just the solute and solvent coordinates, respectively. The separation of energy terms in Eq. 3 is always possible, even in the case of non-pairwise interactions, such as a (S)QM/MM description of interactions. The interaction energy between a protein and a ligand can be defined analogously. The IEA consists of replacing total energies in Zwanzig’s equation by interaction energies. Thus, the free energy difference between a system described at the low and high level of theory becomes

$$\Delta A_{\mathit{\text{int}}er}^{low\to high}=-k_{B}T\text{ln}{\langle \text{exp}\left[\frac{-\Delta U_{\mathit{\text{int}}er}^{low\to high}}{k_{B}T}\right]\rangle }_{low}.$$ (4)

Since the interaction energy difference $\Delta U_{\mathit{\text{int}}er}^{low\to high}=U_{\mathit{\text{int}}er}^{high}-U_{\mathit{\text{int}}er}^{low}$ does not contain contributions from “mismatches” in intramolecular terms, in particular bond stretching and angle bending terms, ${\sigma }_{\Delta U_{\mathit{\text{int}}er}^{low\to high}}\ll {\sigma }_{\Delta U^{low\to high}}.$

An early use of interaction energies is a study by Wood et al. from 1999.⁵⁴ Using Zwanzig’s equation, they sought to account for changes in interaction energies in solute–solvent systems between classical and quantum levels of theory. Specifically, they considered a classical solvated solute system, then perturbed to a state where both solute and solvent were treated classically, but the solute-solvent interactions were obtained with DFT. Within the well-defined scope of this study ΔU^low→high is identical to $\Delta U_{\mathit{\text{int}}er}^{low\to high}.$ The work focused on the averages and fluctuations of ΔU^low→high, with the goal of refining solvent nonbonded parameters in a way that minimized those quantities. In follow-up work, Wood and co-workers used this approach, referred to as “ABC-FEP”, in several applications ranging from solvation to potential of mean force (PMF) calculations.^54–59 More recently, Essex and co-workers adopted the notion of using interaction energy rather than total energy difference.^16,21,38,39 Unlike in the earlier work by Wood et al., however, the approach appears more and more as a workaround to avoid the use of total energies as required by the cycle in Fig. 1 and Eq. 2, whilst researchers maintain results are full QM/MM free energy differences.

Based on statistical mechanics (see also Theory), Eq. 4 as replacement for Eq. 2 in the context of the indirect thermodynamic cycle (i.e., Fig. 1) cannot be justified rigorously. In fact, in their first use of the IEA, Essex and co-workers stated that use of $\Delta U_{\mathit{\text{int}}er}^{low\to high}$ constitutes an approximation.¹⁶ However, the nature of the approximation was not analyzed; the argument given in favor of interaction energies is that their use captures polarization between solute and solvent, or protein and ligand, and, hence, includes types of interactions not accounted for by, e.g., MM force fields. Essex and co-workers also showed conclusively that Eq. 2 (i.e., Zwanzig’s equation with the full energy difference ΔU^low→high) led to an incorrect result, as convergence could not be achieved.³⁹ Lately, the improved convergence seems to have become the main justification for use of interaction energies.^39,49 On the other hand, there are cases when use of interaction energies is not appropriate. One obvious counter example would be the calculation of a PMF along a reaction coordinate when studying a chemical reaction. Clearly, during bond breakage and formation, changes in intramolecular geometries and interactions will lead to an essential contribution to the PMF; hence, they cannot be omitted. Given the increasing use of the IEA, we are not aware of any detailed investigation into the approximation(s) implied by the use of interaction energies, and no systematic comparison of results obtained with $\Delta U_{\mathit{\text{int}}er}^{low\to high}$ instead of ΔU^low→high for computing ΔA^low→high is available.

Providing such an analysis and comparison is the goal of this work. Until recently, this would have been challenging because of the failure of Zwanzig’s equation to converge when using energy differences ΔU^low→high in all but the simplest applications. In recent studies, however, we have demonstrated that Jarzynski’s equation (JAR)⁶⁰ can be used to obtain converged values for ΔA^low→high via non-equilibrium fast switching work simulations.^24,61 Since the mismatches in bond lengths and bond angles correct themselves during even short (less than 100 fs) switching simulations, this source of error is removed easily, regardless of the size of the quantum region. While the method may be too expensive in large scale applications, it can provide reference results in select applications. Several examples are presented in this work, which is organized as follows. In the Theory section we work out in detail the differences between the use of full energies and interaction energies, providing indications when use of the latter may or may not be appropriate. In addition, we briefly summarize the use of non-equilibrium work methods to compute ΔA^low→high. The theoretical considerations are illustrated by numerical results for several model tasks, all concerned with the determination of solvation free energies. In Methods we present the rationale behind the choice of model problems and provide the technical details of the calculations. The Results section is followed by a discussion in which we point out similarities between the IEA and the role of “self-terms” or “intraperturbed-group interactions” in alchemical FES.^62,63

2. Theory

2.1. Interaction vs. total energies

2.1.1. Brief recapitulation of Zwanzig’s equation

At the risk of belaboring the obvious, we start by briefly outlining the derivation of Zwanzig’s equation. The customary starting point is two systems (or alternatively, energetic states) X and Y, having potential energies U_X and U_Y. Here and in the following, we assume that the kinetic energy part of the Hamiltonian can always be decoupled and, thus, can be ignored. This holds true even when (S)QM/MM Hamiltonians are considered as the equations of motion are treated classically. Defining ΔU_X→Y = U_Y – U_X, one can obviously write U_Y = U_X + ΔU_X→Y. Further, the free energy of system X, A_X is assumed to be known. Thus, to determine A_Y it suffices to compute the free energy difference

$$\Delta A_{X\to Y}=A_Y-A_X=-k_{B}T\text{ln}\frac{Z_Y}{Z_X},$$ (5)

where $Z={\int }_{\Gamma }d\mathbf{\text{r}}\text{exp}[-U(\mathbf{\text{r}})/k_{B}T]$ is the configurational partition, with the integration being carried out over all configuration space Γ in the canonical ensemble of the two systems X and Y, respectively. Employing the identity 1 = exp[+U_X(r)/k_BT] exp[−U_X(r)/k_BT] and the definition of the expectation value ${\langle \Theta \rangle }_X={\int }_{\Gamma }d\mathbf{\text{r}}\Theta (\mathbf{\text{r}})P_X(\mathbf{\text{r}})={\int }_{\Gamma }d\mathbf{\text{r}}\Theta (\mathbf{\text{r}})\frac{\text{exp}[-U_X(\mathbf{\text{r}})/k_{B}T]}{{\displaystyle {\int }_{\Gamma }d\mathbf{\text{r}}\text{exp}[-U_X(\mathbf{\text{r}})/k_{B}T}]}$ for some observable Θ with the Boltzmann probability distribution of state X, P_X, leads to

$$\Delta A_{X\to Y}=-k_{B}T\text{ln}{\langle \text{exp}[-\Delta U_{X\to Y}/k_{B}T]\rangle }_X;$$ (6)

i.e., the general form of Eq. 2. The subscript X emphasizes that the average 〈…〉_X is sampled using the potential energy function of state X. When analyzing what contributes to a free energy difference obtained by Zwanzig’s equation (Eq. 2 or 6), one has to consider both the details of ΔU, as well as the (energy function of the) ensemble at which configurations are sampled.

While the exponentials within the integral can be rearranged in various manners, the integral in the ensemble average 〈exp(−ΔU/k_BT)〉_X cannot be split into two (or more) additive terms in a unique manner. Specifically, the energy difference between the two states may consist of two or more distinct terms, e.g., differences in electrostatic (elec) and Lennard-Jones (LJ) interactions, i.e., ΔU = ΔU_elec + ΔU_LJ. While separable at the level of energies, it is not possible in an unambiguous fashion to split the exponential average 〈exp[−(ΔU_elec + ΔU_LJ)/k_BT]〉_X, and, hence, the corresponding free energy difference, into contributions from ΔU_elec and ΔU_LJ.^64–66 In other words, $\Delta A_{X\to Y}\ne \Delta A_{X\to Y}^{elec}+\Delta A_{X\to Y}^{LJ}$ since $-k_{B}T\text{ln}{\langle \text{exp}[-\Delta U_{X\to Y}/k_{B}T]\rangle }_X\ne -k_{B}T\text{ln}{\langle \text{exp}[-\Delta U_{X\to Y}^{elec}/k_{B}T]\rangle }_X-k_{B}T\text{ln}{\langle \text{exp}[-\Delta U_{X\to Y}^{LJ}/k_{B}T]\rangle }_X.$ ⁶⁷

2.1.2. The special case of solvation free energies — definitions

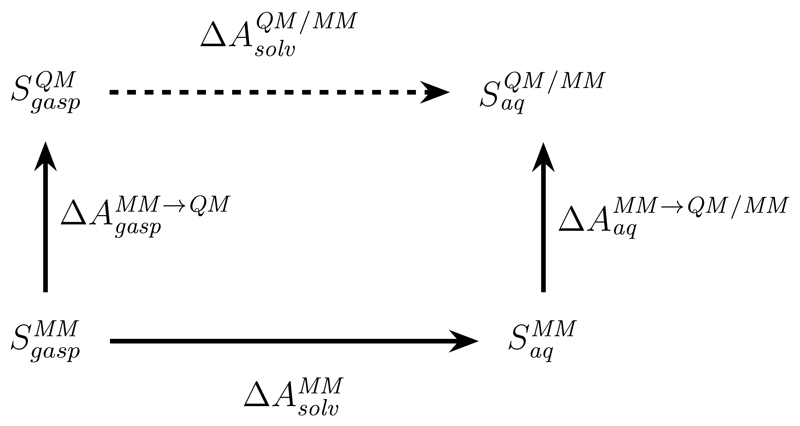
For the following analysis we focus on the calculation of a solvation free energy for some solute S by an indirect QM/MM FES (Fig. 2). We assume that a solvation free energy has been computed using a MM force field $\left(\Delta A_{solv}^{MM}\right);$ this result is to be refined by a QM/MM method. The IEA has been used in such scenarios;^48–50 also, all model problems considered in this work are related to solvation free energies. The considerations given below can be straightforwardly extended to other situations, such as the calculation of binding affinities of protein–ligand interactions.

Figure 2.

Indirect scheme to refine a MM solvation free energy at a QM/MM level of theory.

In other words, we are interested in the following specialization of Fig. 1, i.e., the computation of the free energy difference $\Delta A_{solv}^{QM/MM}$ for transferring solute S from the gas phase (gasp) into aqueous solution (aq). In the full indirect scheme, instead of following the dotted arrow in Fig. 2, we would use Eq. 1 and compute

$$\Delta A_{solv}^{QM/MM}=\Delta A_{solv}^{MM}+\left(\Delta A_{aq}^{MM\to QM/MM}-\Delta A_{gasp}^{MM\to QM}\right).$$ (7)

Using the IEA, i.e., using Eq. 4 instead of Eq. 2, we would instead compute

$$\Delta A_{solv\left(\mathit{\text{inter}}\right)}^{QM/MM}=\Delta A_{solv}^{MM}+\left(\Delta A_{aq,\mathit{\text{inter}}}^{MM\to QM/MM}\right)$$ (8)

since by construction there is no (solute-solvent) interaction energy in the gas phase. The central question we want to address is how $\Delta A_{solv}^{QM/MM}$ and $\Delta A_{solv\left(\mathit{\text{inter}}\right)}^{QM/MM}$ differ and whether one can expect that $\Delta A_{solv}^{QM/MM}\approx \Delta A_{solv\left(\mathit{\text{inter}}\right)}^{QM/MM}$, i.e., whether use of Eq. 8 instead of Eq. 7 will lead to an identical or, at least, comparable result. As a shorthand for later, we add a conditional expression for the MM → QM /MM (low → high) correction encompassing both cases:

$$\Delta A_{corr}^{MM\to QM/MM}\{\begin{array}{ll}=\Delta A_{aq}^{MM\to QM/MM}-\Delta A_{gasp}^{MM\to QM}\hfill & :\text{full}\text{cycle}\left(\text{Fig. 2}\right)\hfill \\ \approx \Delta A_{aq,\mathit{\text{inter}}}^{MM\to QM/MM}\hfill & :\text{IEA}\hfill \end{array}$$ (9)

We start by writing down, in a schematic way, the various potential energy functions needed to compute the terms in Eqs. 7 and 8. The gas phase is straightforward, the solute (S) is described either by a MM $\left(U_{gasp}^{MM}\left({\mathbf{\text{r}}}_S\right)\right)$ or QM potential energy function $\left(U_{gasp}^{QM}\left({\mathbf{\text{r}}}_S\right)\right).$ For the aqueous solution, we assume that water (W) is always treated classically, i.e., by a MM force field $\left(U_W^{MM}\left({\mathbf{\text{r}}}_W\right)\right).$ Here r_S and r_W denote the coordinates of the solute and water, respectively. Therefore, the potential energy describing the solute in water at the MM and QM/MM levels of theory is given by

$$U_{aq}^{MM}=U_{S,S-W}^{MM}\left({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W\right)+U_W^{MM}\left({\mathbf{\text{r}}}_W\right)=U_S^{MM}\left({\mathbf{\text{r}}}_S\right)+U_{S-W}^{MM}\left({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W\right)+U_W^{MM}\left({\mathbf{\text{r}}}_W\right)$$ (10)

and

$$U_{aq}^{QM/MM}=U_{S,S-W}^{QM/MM}\left({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W\right)+U_W^{MM}\left({\mathbf{\text{r}}}_W\right).$$ (11)

We assume an additive MM force field; hence, in Eq. 10 we have separated intra-solute $U_S^{MM}\left({\mathbf{\text{r}}}_S\right)$ and solute–solvent interactions $U_{S-W}^{MM}\left({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W\right).$ For QM/MM this is not possible, as reflected by the combined term in $U_{S,S-W}^{QM/MM}\left({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W\right)$ Eq. 11.

In preparation for the analysis of the IEA, we also need to give matching expressions for the interaction energies at the two levels of theory:

• $$U_{aq,\mathit{\text{inter}}}^{MM}=U_{aq}^{MM}-U_S^{MM}-U_W^{MM}=U_{S-W}^{MM}\left({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W\right)$$ (12)
• $$U_{aq,\mathit{\text{inter}}}^{QM/MM}=U_{aq}^{QM/MM}-U_S^{QM}-U_W^{MM}=U_{S,S-W}^{QM/MM}\left({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W\right)-U_S^{QM}\left({\mathbf{\text{r}}}_S\right)$$ (13)

Eqs. 12 and 13 follow directly from Eqs. 10 and 11 above; U_S denotes the potential energy of the solute at either the MM or QM level of theory, computed as if the waters were not present.

2.1.3. Analysis of using interaction energy differences

We now turn to the analysis of the free energy differences involved in computing a solvation free energy when using the exact thermodynamic cycle (Fig. 2) and when using the IEA. For the former, the difference in total energies between the MM and QM/MM levels of theory is needed. In the gas phase one trivially has

$$\Delta U_{gasp}^{MM\to QM}=U_{gasp}^{QM}\left({\mathbf{\text{r}}}_S\right)-U_{gasp}^{MM}\left({\mathbf{\text{r}}}_S\right).$$ (14)

In aqueous solution, subtracting Eq. 10 from Eq. 11 one obtains

$$\begin{array}{l}\Delta U_{aq}^{MM\to QM/MM}=U_{aq}^{QM/MM}-U_{aq}^{MM}\\ =U_{S,S-W}^{QM/MM}\left({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W\right)-U_S^{MM}\left({\mathbf{\text{r}}}_S\right)-U_{S-W}^{MM}\left({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W\right).\end{array}$$ (15)

Since interactions between waters are always treated classically, the term $U_W^{MM}({\mathbf{\text{r}}}_W)$ present in both Eqs. 10 and 11 cancels from the difference Eq. 15. If interaction energies are used instead, the corresponding interaction energy difference (subtracting Eq. 12 from Eq. 13) is

$$\begin{array}{l}\Delta U_{aq,\mathit{\text{inter}}}^{MM\to QM/MM}=U_{aq,\mathit{\text{inter}}}^{QM/MM}-U_{aq,\mathit{\text{inter}}}^{MM}\\ =U_{S,S-W}^{QM/MM}({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W)-U_S^{QM}({\mathbf{\text{r}}}_S)-U_{S-W}^{MM}({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W)\end{array}$$ (16)

Eqs. 14, 15, and 16 are the energy differences entering Zwanzig’s equation to compute $\Delta A_{gasp}^{MM\to QM},\Delta A_{aq}^{MM\to QM/MM},\text{and}\Delta A_{aq,\mathit{\text{inter}}}^{MM\to QM/MM},$ respectively.

We first focus on comparing $\Delta A_{aq}^{MM\to QM/MM}\text{and}\text{Δ}{A}_{aq,\mathit{\text{int}}er}^{MM\to QM/MM}.$ These two quantities are obtained from the same underlying simulation of the solute in water, modeled at the low level of theory (MM). Its potential energy $U_{aq}^{MM}$ is given by Eq. 10. Recall from the recapitulation of Zwanzig’s equation that, given an initial state X, the energy of the final state Y can be written as U_Y =U_X + ΔU_X→Y. Here, $U_X=U_{aq}^{MM}$ and is given by Eq. 10 One can easily convince oneself that adding $\Delta U_{aq}^{MM\to QM/MM}$ (Eq. 15) to $U_{aq}^{MM}$ (Eq. 10) leads to the potential energy function $U_{aq}^{QM/MM}$ of the QM/MM description (Eq. 11), as expected.

Repeating this seemingly trivial exercise for the IEA, we add $\Delta U_{aq,\mathit{\text{int}}er}^{MM\to QM/MM}$ (Eq. 16) to the potential energy $U_{\mathit{\text{aq}}}^{MM}$ (Eq. 10) of the reference state. This leads to

$$\begin{array}{ll}{\tilde{U}}_{aq}^{QM/MM}=U_{S,S-W}^{QM/MM}({\mathbf{\text{r}}}_S,{\mathbf{\text{r}}}_W)+U_W^{MM}({\mathbf{\text{r}}}_W)\hfill & +\left[U_S^{MM}({\mathbf{\text{r}}}_S)-U_S^{QM}({\mathbf{\text{r}}}_S)\right]=\hfill \\ =U_{aq}^{QM/MM}\hfill & +\left[U_S^{MM}({\mathbf{\text{r}}}_S)-U_S^{QM}({\mathbf{\text{r}}}_S)\right].\hfill \end{array}$$ (17)

where the tilde ˜ is used to distinguish this result from the true $U_{aq}^{QM/MM}$ (Eq. 11). The difference between Eq. 11 and Eq. 17, $U_S^{MM}({\mathbf{\text{r}}}_S)-U_S^{QM}({\mathbf{\text{r}}}_S),$ reflects that the difference in intramolecular energies between the two levels of theory is excluded when using interaction energies. However, we can go further. Eq. 17, after all, is the effective potential energy function corresponding to the high level of theory when using the IEA. What is the nature of a system described by ${\tilde{U}}_{aq}^{QM/MM}?$ The intramolecular energy of the solute in this hypothetical state is described by the low level of theory (MM), whereas solute–water interactions are treated at the desired high level of theory (QM/MM). Thus, when using the IEA $\Delta A_{corr}^{MM\to QM/MM}$ (Eq. 9) is the free energy difference between the MM representation of the system and a hybrid representation in which the intramolecular interactions of the solute, our quantum region, are described by MM, and only the solute–water interactions correspond to a QM/MM treatment.

In the special case of solvation free energies, there is a second aspect worth pointing out in connection with the IEA. In the full indirect cycle (Fig. 2), the correction ΔA^{MM →QM} is computed both for the gas phase, as well as for solution. Since in the gas phase there are by definition no interaction energies, any contributions from the gas phase are not taken into account when the IEA is employed. For flexible molecules the minimum energy conformation(s) in the gas phase and in solution need not be the same. Clearly, any free energy contribution from such conformational preferences is omitted in the IEA. This constitutes an additional source of error that goes beyond the earlier considerations, where we identified the chimeric high level state employed by the IEA. Assume a solute–solvent system for which the low-level (MM) description of intra-solute molecular forces in solution is comparable to that of the high-level description; i.e., the solute’s behavior in aqueous solution in the MM simulation is very similar to what it would be during a true QM/MM simulation. Since in this case the remaining difference between the two levels of theory is the solute–solvent interaction, the use of IEA would seem justified. However, just because the intra-solute molecular forces are adequately described in solution, this does not mean that this is true in the gas phase as well. E.g., biomolecular force fields often sacrifice gas phase properties in order to describe interactions in and with water correctly.⁶⁸ Since the gas phase is not even considered in the IEA, any such free energy contributions are overlooked. An alternative way of viewing this is to state that in the IEA the properties of the solute, in particular its conformational preferences, are assumed to be identical in the gas phase and in aqueous solution.

Thus, two assumptions are made when applying the IEA to the calculation of solvation free energy differences. (1) The IEA connects the low level of theory (MM in our analysis) with a hypothetical high level state, in which the solute is described by MM and only the solute-solvent interactions obey the QM/MM potential energy function. (2) Further, the IEA implicitly requires that the solute’s conformational preferences are identical in the gas phase and in aqueous solution.

2.2. A brief summary of Jarzynski’s and Crook’s equation

Next, we briefly describe the theoretical basis of non-equilibrium work methods to accurately compute ΔA^{MM →QM /MM} corrections even in cases when Zwanzig’s equation fails to converge. Approximately twenty years ago, Jarzynski ⁶⁰ showed that Zwanzig’s equation is merely a limiting case of a much more general identity, i.e.,

$$\Delta A^{X\to Y}=-k_{B}T\text{ln}{\langle \text{exp}\left[\frac{-W^{X\to Y}}{k_{B}T}\right]\rangle }_X$$ (18)

Here, W^X→Y is the non-equilibrium work (NEW) of transforming state X into Y in finite time. We refer to a simulation, during which the potential energy function is changed between two states and the corresponding work W is recorded, as ‘switch’. The average 〈…〉_X is carried out over multiple such switches, each starting from an equilibrium configuration and velocity set obtained at state X. Zwanzig’s equation is recovered when carrying out the switch instantaneously, in this case W^X→Y reduces to ΔU^X→Y = U^X – U^Y. Similarly, thermodynamic integration can be viewed as Jarzynski’s equation in the limit of infinitely slow switching times, thus keeping the system at each intermediate step in equilibrium.

Jarzynski’s equation has become an indispensable tool to model biophysical/biochemical processes that range from pulling experiments to ligand (un)binding; more recently it is also used in alchemical FES.^69,70 As we showed in earlier work,^24,61 it is also well suited for the problem at hand, the reliable computation of ΔA^low→high. Even short switching protocols (50–100MD steps) can ameliorate mismatches between the low and high level description of the system, in particular disparity in bonded degrees of freedom. While quite costly, in particular if ai-QM methods are used, the switches are a post-processing step, and hence any number of switching simulations can be trivially carried out in parallel.

Just as Jarzynski’s equation is the non-equilibrium extension of Zwanzig’s equation, its two-sided equilibrium variant, BAR, can also be generalized to averages of forward and backward non-equilibrium work values. In particular, Crooks⁷¹ proved the general theorem

$$\text{exp}\left(-\beta \Delta A\right)=\frac{{\langle f\left(W\right)\rangle }_X}{{\langle f\left(-W\right)\text{exp}\left(-\beta W\right)\rangle }_Y}$$ (19)

Eq. 19 is true for any function f (W), where, as in the above discussion of Jarzynski’s equation, W denotes a non-equilibrium work value. The average 〈. . .〉 is taken over multiple work values, starting from equilibrated configurations corresponding to state X or Y (as indicated by the subscript). By minimizing the statistical variance with respect to the arbitrary function f (W), Bennett was the first to show that the choice

$$f\left(W\right)={[1+\frac{n_{X\to Y}}{n_{Y\to X}}\text{exp}\left(\beta (W-\Delta A\right)]}^{-1}$$ (20)

minimizes the variance in the free energy estimate. ⁴⁵ Here n_X→Y, n_Y→X are the number of forward and backward switches, respectively. While Bennett’s derivation was carried out for the equilibrium case, Eq. 20 can also be used to compute free energy difference from Crooks’ theorem. Additional details about using Jarzynksi’s and Crooks’ equation to compute ΔA^low→high can be found in our earlier work; for general background we refer the reader to a recent review of NEW methods by Dellago and Hummer. ⁷²

In principle, BAR and Crooks are problematic methods for computing ΔA^low→high since in both cases simulations at the high level of theory are required (cf. the Introduction). However, both in previous work,^24,61 as well as in this study SQM/MM was/is employed as the high level of theory for model problems. For these systems, simulations at an SQM/MM level of theory are feasible. Being able to use two-sided free energy perturbation methods, such as BAR or Crooks serves as a stringent test whether free energy differences obtained by one-sided methods (i.e., Jarzynski’s equation) have indeed converged.

3. Methods

Overview of model calculations

Validating the IEA is challenging due to the poor convergence of Zwanzig’s equation when computing ΔA^low→high. Specifically, it is difficult to obtain reference results for the full thermodynamic cycle (Fig. 2) for all but the simplest systems. E.g., Ref. 39 convincingly demonstrated the convergence failure of Zwanzig’s equation, but because of the practical impossibility to achieve convergence, it could not be shown that the use of interaction energies instead of the full thermodynamic cycle would lead to identical results. In contrast, ΔA^low→high with NEW methods is much more robust as compared to Zwanzig’s equation; thus, we will rely heavily on these to obtain reference results.

Although (S)QM/MM calculations are the ultimate target, it seems instructive to start with purely MM test cases. For such systems reference results and results based on the IEA can be calculated with high precision. The application we will be studying is the solvent affinity of blocked amino acids using three CHARMM force fields to describe the solute with the TIP3 water model employed in all three cases. We arbitrarily consider one force field the low level of theory, and the two others high levels of theory.

Our proof-of-concept work demonstrating the utility of Jarzynski’s equation to compute ΔA^low→high contained examples of varying complexity.^24,61 Thus, we will use some of these earlier results for ΔA^low→high as reference values and compare them to values obtained with the IEA. First, we chose the zeroth order test application of FES, the solvation free energy differences of ethane and methanol, and refine MM results at the SQM/MM level of theory (see below for details), using both the full indirect cycle as shown in Fig. 2, as well as the approximation based on interaction energies. For these systems, we expect the use of interaction energies to suffice. Second, we report results for the blocked amino acids alanine (N-acetyl-alanine-methylamide, Ala) and serine (N-acetyl-serine-methylamide, Ser). These are flexible systems, with different conformational preferences in the gas phase and in aqueous solution, as well as when described by force fields and at the SQM/MM level of theory. Thus, they contain all the potential complications discussed in the Theory section which might result in incorrect results relying on interaction energies.

In Ref. 61 we also reported results for bis-2-chloro diethyl ether (2CLE) in the gas phase. This rather small molecule proved quite difficult since MM parameters obtained from the CHARMM generalized (CGenFF) force field ⁷³ led to rather different conformational preferences compared to SQM. While we could obtain converged results for ΔA^low→high using Jarzynski’s equation, the low to high correction could be obtained more easily using reoptimized force field parameters. Here, we present results not only for the gas phase but for 2CLE’s full free energy of solvation calculation, using two different MM representations as the low and SQM/MM as the high level of theory according to Fig. 2. The result obtained with the full indirect cycle will be compared to the use of the IEA.

Free energy differences between force fields

The first generation of the CHARMM all-atom protein force field⁷⁴ was revised in 2004 by the introduction of the so-called crossterm correction (“CMAP”).⁶⁸ We consider the initial protein force field, ⁷⁴ referred to here as C22,noCMAP, to be the low level of theory, and the revised force field,⁶⁸ referred to as C22, a possible “high” level of theory. The two parameter sets differ only by the absence / presence of the cross-term correction. The CMAP force field term is an intramolecular energy term and would pertain only to the solute. Hence, using the interaction energy approach, the free energy difference of solvation between any system described with the C22,noCMAP and the C22 force fields will be, by definition zero, as the interaction energies are the same in both cases. We will compare this theoretical result based on the IEA with the true relative solvation free energy difference for Ala and Ser when using the two force fields. Further, we will repeat this comparison for C22,noCMAP and the current CHARMM36 protein force field (C36).^75,76 In this case, there are several differences between the two parameters sets, some also directly affecting protein–water interactions.⁷⁷ Hence, both corrections $\Delta \Delta A_{solv}^{low\to high},$ the one based on the IEA and the one on the full thermodynamic cycle Fig. 2, need to be computed.

Specifically, MD simulations of blocked Ala and Ser were carried out in the gas phase and in aqueous solution, using the three force fields C22,noCMAP, C22, and C36. Trajectories were saved and energies recomputed at the respective other states. E.g., configurations saved during simulations with C22 were reevaluated with C22,noCMAP, and C36. Based on these energy time series, BAR was used to compute the free energy differences between force fields in a single step, in analogy to Ref. 78. Trajectories generated in aqueous solution were further used to compute interaction energies (the energy of the solute and water-water energies were subtracted from the full energies). Then, Zwanzig’s equation was used to compute the free energy difference corrections based on the IEA. Error bars for the BAR and Zwanzig’s equation free energy difference were obtained as follows. Dividing the full data set (here 100,000 ΔU values) into ten sequential blocks, we computed ΔA_i (i = 1, . . . 10) for each block independently. The standard deviation s of these ten ΔA_i is reported as statistical error estimate ($s=\sqrt{1/(N-1){\displaystyle {\sum }_{i=1}^N(\Delta A_i-\overline{\Delta A}}{)}^2},$ where in this work N = 10). The approach just outlined was motivated by an approach of Wood et al.⁷⁹ to estimate “sample size hysteresis” and was also used in Refs. 44, 61. Simulation details are provided in SI.

Ethane/methanol, Ala/Ser

We take results from Ref. 61 for ΔA^low→high, with low referring to the C36 force field and high to the semi-empirical SCC-DFTB method^80–84 with the 3ob-3-1 parameter set^85–88 and third order corrections (herein referred to as DFTB3). The trajectories saved during earlier work⁶¹ were used to compute interaction energy differences and to compute ΔA^low→high according to the IEA. In particular, we report results for ethane (ETHA), methanol (MEOH), blocked Ala and Ser, for which we had computed values for ΔA^low→high both in the gas phase and in aqueous solution. The details of the underlying simulations can be found in Ref. 61.

Solvation free energy of bis-2-chloro diethyl ether (2CLE)

Finally, we carried out a full solvation free energy calculation for 2CLE. As reported for the gas phase earlier,⁶¹ for this molecule the CGenFF force field parameters generated by PARAMCHEM^89,90 turned out to lead to very different conformational sampling than at the DFTB3 level of theory. Using refined force field parameters obtained with GAAMP⁹¹ resulted in more similar conformational sampling and facilitated convergence of $\Delta A_{gasp}^{low\to high}.$⁶¹ Results using this parameterization will be referred to as “GAAMP”. Here we again use the CGenFF and GAAMP force field parameters as low levels of theory and refine results obtained with them to the DFTB3 level of theory.⁹²

Fig. 3 depicts the individual steps used to compute the solvation free energy of 2CLE, using either the CGenFF or the GAAMP force field, and to refine the classical results to the DFTB3 level of theory. The calculation of the classical solvation free energy $\Delta A_{solv}^{MM}$ consists of three steps, denoted (ii)–(iv) in the figure: First, in step (ii) the charges of the solute atoms were turned off in five steps. Next, step (iii), all Lennard-Jones interactions of the solute were turned off (six steps, see below for details). In the PERT module of CHARMM, one cannot selectively turn on/off solute–solvent interactions, so steps (ii) and (iii) also removed solute intramolecular nonbonded interactions. This contribution was calculated in step (iv), in which nonbonded intramolecular interactions were turned on again (vide infra). Steps (i) and (v) are the corrections steps ΔA^low→high for aqueous solution and the gas phase, respectively. Simulation details for the five steps can be found in SI.

Figure 3.

Detailed thermodynamic cycle to compute the solvation free energy of 2CLE, including an overview of the purely classical steps. S denotes the solute, W water.

Given the relatively small system size and the semi-empirical level of theory chosen, we could afford to carry out MD simulations at the high level of theory. Thus, we used Crooks’ equation (Eqs. 19 and 20) to compute the free energy difference ence between the high and low level of theory (steps (i) and (v) in Fig. 3). Non-equilibrium switches in the two directions were carried out using the MSCALE⁹³ facility of CHARMM combined with the slow-growth mode of the PERT module; cf. Refs. 24, 61 for further details. In the gas phase, 10,000 forward (low → high) and backward (high → low) switches were carried out; only every fourth of the 40,000 restart files saved at the low level of theory were used. Switches were started from the restart files saved during the production simulations at the two levels of theory and were carried out during 1000 steps of Langevin dynamics (friction coefficient 5 ps^–1 on all atoms, 0.5 fs timestep). The same switching protocol was also used in solution. Out of the 40,000 restart files collected during simulations using the CGenFF and GAAMP force field, as well as the SQM/MM simulation (see SI), every second was used, resulting in 20,000 forward and backward work values.

Finally, all coordinates saved during the force field simulations in aqueous solution (CGenFF, GAAMP) were also used to compute interaction energies, U_inter, at the low and high levels of theory, respectively. The interaction energy differences, $\Delta U_{\mathit{\text{inter}}}^{low\to high},$ were then inserted into Eq. 4 to compute $\Delta A_{\mathit{\text{inter}}}^{low\to high}$ according to the IEA.

4. Results

Free energy differences between force fields

Table 1 summarizes results for the differences in solvation free energies for Ala and Ser using three generations of CHARMM protein force fields C22,noCMAP, C22, and C36. As described in Methods, these were computed exactly and employing the IEA. The case C22,noCMAP vs. C22 is of particular interest, as it is clear in this case that the free energy resulting from the IEA has to be exactly zero (cf. Methods). By contrast, as one sees in Table 1, the exact result is approximately 0.5 kcal/mol for both Ala and Ser. A similar discrepancy is obtained for C22 vs. C36. For Ala, the IEA again suggests a free energy difference of zero, whereas the correct value is 0.4 kcal/mol. For Ser, the exact result is 0.1 kcal/mol, whereas the IEA leads to a value of –0.2 kcal/mol. While the discrepancy in results is not large, it clearly is not negligible.

Table 1.

Toy problems based on purely classical mechanical force fields. All free energy differences are in kcal/mol.

	Ala		Ser
	fulla	IEAb	fulla	IEAb
$\Delta A_{gasp}^{C\mathit{22},noCMAP\to C\mathit{22}}$	-0.57±0.01		-0.82±0.06
$\Delta A_{aq}^{C\mathit{22},noCMAP\to C\mathit{22}}$	-0.12±0.11		-0.27±0.07
$\Delta A_{corr}^{C\mathit{22},noCMAP\to C\mathit{22}}$c	0.45±0.11	0.00d	0.55±0.09	0.00d
$\Delta A_{gasp}^{C\mathit{22},noCMAP\to C\mathit{36}}$	-0.04±0.01		2.85± 0.10
$\Delta A_{aq}^{C\mathit{22},noCMAP\to C\mathit{36}}$	0.39±0.07		2.93±0.08
$\Delta A_{corr}^{C\mathit{22},noCMAP\to C\mathit{36}}$c	0.43±0.07	-9×10–4±0.00	0.08±0.13	-0.18±0.00

^aCorrections ΔA^low→high (low = C22, noCMAP, high = C22 or C36) computed separately in gas phase and in solution, cf. Fig. 2.

^bCorrection $\Delta A_{aq,\mathit{\text{int}}er}^{low\to high}$ (low = C22, noCMAP, high = C22 or C36) computed according to the IEA.

^cEq. 9.

^dTheoretical result — there is no change in interaction energy between C22,noCMAP and C22

The cross-term (CMAP) correction modifies the ϕ/ψ backbone angle distribution sampled by peptides and proteins. Thus, there are two ways in which its presence / absence contributes to the solvation free energy. First, as the average conformation of the peptide is different with and without the CMAP term, solute–solvent interactions are changed, even though the nonbonded force fields terms are identical in both cases. Since in the framework of the IEA the respective other state is never simulated, this contribution is not accounted for. Second, the effect of the CMAP correction on the preferred φ/ψ values is different in the gas phase and in water. As the gas phase is not even considered in the IEA, any free energy contributions resulting from this cannot be accounted for. Thus, although the numerical discrepancy for these purely classical systems is not large, it nicely illustrates the types of contributions ignored by the IEA, in line with the earlier theoretical analysis.

Ethane/methanol, Ala/Ser

Table 2 summarizes several results from Ref. 61 concerning MM → SQM(/MM) corrections which are required to compute solvation free energies. In addition, we used our raw data to compute the corrections using the IEA. For two model systems, ethane and methanol, the results are in quite good agreement. Both systems have little conformational flexibility, and the MM force field can be expected to describe intramolecular, as well as interactions with water well; hence, this findings is not surprising. For Ala and Ser, on the other hand, the deviations between the two approaches (exact thermodynamic cycle Fig 2 vs. IEA) are considerable. In both cases, the MM→SQM/MM correction obtained from the IEA is too negative, –1.9 kcal/mol for Ala, and –1.2 kcal/mol for Ser. Given the flexibility of the two peptides and their different conformational preferences observed when described by MM and by SQM/MM,^24,61 these findings are not too surprising. As outlined in the Theory section, use of the IEA implicitly relies on the assumption that the simulations at the low level of theory result in configurational and conformational sampling that is also representative for the high level of theory. Our earlier results showed this not to be the case; hence, the expected failure.

Table 2.

Test of IEA in an SQM/MM setting. All free energy differences are in kcal/mol.

	Etha		Meoh
	fullb	IEAc	fullb	IEAc
$\Delta A_{gasp}^{C\mathit{36}\to DFTB\mathit{3}}$a	-86.49±0.01		-8.64±0.01
$\Delta A_{aq}^{C\mathit{36}\to DFTB\mathit{3}}$a	-86.83±0.01		-6.82±0.01
$(\Delta )\Delta A^{C\mathit{36}\to DFTB\mathit{3}}$d	-0.34±0.01	-0.18±0.01	1.82±0.01	1.92±0.01
	Ala		Ser
$\Delta A_{gasp}^{C\mathit{36}\to DFTB\mathit{3}}$a	-46.09±0.04		-27.31±0.17
$\Delta A_{aq}^{C\mathit{36}\to DFTB\mathit{3}}$a	-56.97±0.03		-36.06±0.09
$\Delta A_{corr}^{C\mathit{36}\to DFTB\mathit{3}}$d	-10.88±0.05	-12.79±1.01	-8.75±0.19	-9.98±0.81

^aFor better readability, free energies listed in the table are offset by +4, 100 (Meoh), +3, 500 (Etha), +16, 400 (Ala) and +18, 500 kcal/mol (Ser). All ’full’ results taken from Tables 2 and 3 of Ref. 61.

^bCorrections ΔA^C36→DFTB3 computed separately in gas phase and in solution, cf. Fig. 2.

^cCorrection $\Delta A_{aq,\mathit{\text{inter}}}^{C\mathit{36}\to DFTB\mathit{3}}$ computed according to the IEA.

^dEq. 9.

Finally, the Ala/Ser results of Table 2 are worrisome in a second regard. One main justification for the IEA is that the modified Zwanzig equation (Eq. 4) is expected to converge more quickly than the exact expression, Eq. 2. Indeed, we showed in Refs. 24,61 that attempts to compute ΔA^MM→SQM/MM for Ala and Ser by Zwanzig’s equation fail to converge, both in the gas phase and in solution. Using non-equilibrium work methods, on the other hand, the exact correction can be computed, though in aqueous solution relatively long switching protocols were required. The interaction energy results for Ala and Ser in Table 2 have relatively high standard deviations, almost ±1 kcal/mol. Further, they fail several of the criteria we recently suggested to gauge convergence of Zwanzig’s equation. ⁴⁴ Despite being computed from 200,000 interaction energy differences each, the Π value,⁹⁴ which ideally should be > +0.5, is only –0.26 for Ala and –0.15 for Ser. The standard deviation of the interaction energy differences themselves is ≈ 4k_BT in both cases, the absolute upper limit we found for Zwanzig’s equation to lead to correct results. Thus, while the use of interaction energies helps convergence and makes it possible to use somewhat larger quantum regions, it does not remove all of the underlying diffculties hindering convergence. In Ref. 61 we pointed out that the solute’s charge distribution was quite different for MM and SQM; hence, water configurations appropriate for a MM charge distribution may be quite “incorrect” for a SQM solute. Clearly, this factor hampering convergence is also present when using interaction energies.

Solvation free energy of bis-2-chloro diethyl ether (2CLE)

Finally, we report solvation free energies of 2CLE at the SQM/MM level of theory. Two MM force field were used as the low level of theory; the MM results were refined either by the full thermodynamic cycle Fig. 2, or according to the IEA. All results are summarized in Table 3.

Table 3.

IEA compared to full free energy correction (Fig. 2) as applied to the computation of the solvation free energy ΔA_solv of bis-2-chloroethylether (2CLE). All free energies in kcal/mol. The experimental solvation free energy is –4.23 kcal/mol.⁹⁵

	fullb	IEAc
$\Delta A_{gasp}^{C\mathit{36}\to DFTB\mathit{3}}$a	-27.34±0.20
$\Delta A_{aq}^{C\mathit{36}\to DFTB\mathit{3}}$a	-27.54±0.53
$\Delta A_{corr}^{C\mathit{36}\to DFTB\mathit{3}}$d	-0.20±0.57	1.73±0.26
$\Delta A_{solv}^{C\mathit{36}}$e	-3.26±0.08	-3.26±0.08
$\Delta A_{solv}^{DFTB\mathit{3}/MM}$f	-3.46±0.57	-1.53±0.27
$\Delta A_{gasp}^{GAAMP\to DFTB\mathit{3}}$a	-33.55±0.13
$\Delta A_{aq}^{GAAMP\to DFTB\mathit{3}}$a	-35.79±0.04
$\Delta A_{corr}^{GAAMP\to DFTB\mathit{3}}$d	-2.24±0.14	-0.88±0.20
$\Delta A_{solv}^{GAAMP}$e	-0.81±0.03	-0.81±0.03
$\Delta A_{solv}^{DFTB\mathit{3}/MM}$f	-3.05±0.14	-1.69±0.20

^aFor better readability, free energies listed in the table are offset by +12,200 kcal/mol.

^bCorrections ΔA^MM→DFTB3 (MM is C36 or GAAMP) computed separately in gas phase and in solution, cf. Fig. 2. Results as reported were computed using non-equilibrium work methods, specifically Crook’s equation.

^cCorrection $\Delta A_{aq,\mathit{\text{inter}}}^{MM\to DFTB\mathit{3}}$ (MM is C36 or GAAMP) computed according to the IEA; cf. Eq. 4

^dEq. 9, MM is C36 or GAAMP.

^eClassical solvation free energy for 2CLE computed using the C36 or GAAMP force field parameters for the solute. This corresponds to the horizontal arrow at the bottom of Fig 2. For details of the computational protocol see SI.

^fSolvation free energy for 2CLE corrected to the DFTB3/MM level of theory: $\Delta A_{solv}^{DFTB\mathit{3}/MM}=\Delta A_{solv}^{MM}+\Delta A_{corr}^{MM\to DFTB\mathit{3}},$ where MM is C36 or GAAMP.

With the regular CHARMM CGenFF force field (C36), one obtains a solvation free energy difference $\Delta A_{solv}^{MM}$ of –3.26 kcal/mol, deviating slightly less than 1 kcal/mol from the experimental value of –4.23 kcal/mol. ⁹⁵ When this MM result is refined through the indirect cycle Fig. 2, the solvation free energy $\Delta A_{solv}^{SQM/MM}$ becomes –3.46 kcal/mol, in slightly better agreement with experiment. If one does the same with the IEA (column ’IEA’ in Table 3), the agreement with experiment becomes much poorer. The “corrected” solvation free energy $\Delta A_{solv(\mathit{\text{inter}})}^{SQM/MM}=-1.53\text{kcal}/\text{mol},$ which deviates by almost 3 kcal/mol from the experimental value.

Since the C36 MM simulations led to conformations of 2CLE which were rather different from those obtained with SQM,⁶¹ we repeated the MM simulations with parameters obtained from GAAMP (lower half of Table 3). Somewhat surprisingly, the MM solvation free energy is in much poorer agreement with experiment than the one obtained using the C36 force field (see below). Correcting to the SQM/MM level of theory improves this result considerably, although the deviation of ≈ 1.2 kcal/mol from the experimental result remains higher than for the SQM/MM corrected result based on C36 (deviation ≈ 0.8 kcal/mol). In hindsight, this result is not as surprising as first thought as recent work has clearly shown that solvation free energies are very sensitive to differences in (S)QM levels of theory (i.e., differences in local intermolecular interactions with waters in the first solvation shell).^22,26,96 Using the IEA, the “corrected” number is close to the one based on C36 and is far off the experimental value. Thus, we have two clear cases where the use of the IEA leads to a poor result and in one case even makes the MM result worse. The “performance” of the IEA here is particularly treacherous, as the results appear well converged (pass all our usual convergence criteria). Further, the “corrected” solvation free energy differences obtained from the two MM representations agree almost perfectly.

Two aspects of the results merit additional consideration. First, we remind the reader of the goal of the GAAMP re-parameterization, which is to make the configurations / conformations sampled more high-level like. We already showed that this is the case in Ref. 61, and this is also reflected by the much lower statistical uncertainty of $\Delta A_{corr}^{MM\to SQM/MM},$ ±0.14 for GAAMP vs. ±0.57 for C36. One should keep in mind the role of the low level in indirect (S)QM/MM FES. The purpose of the low level is to act as a bridge, helping to generate configurations/conformations which are also meaningful at the desired high level of theory.

The second observation worth mentioning is that the two corrected SQM/MM results do not fully agree, though, given the rather high statistical uncertainty of the C36 based result, stemming from the difficulty to converge the ΔA^{MM →SQM/MM} corrections, the two final results are statistically indistinguishable. Further, the GAAMP re-parameterization led to changes of some Lennard-Jones parameters. In CHARMM based (S)QM/MM calculations, electrostatic interactions between the (S)QM and the MM region are computed based on the (S)QM charge distribution; however, the apolar interactions are still calculated using the classical Lennard-Jones parameters for the (S)QM region. Since these are different in the two parameterization, differences in solvation free energies are to be expected.

5. Discussion

In this section we address several topics related to the IEA. First, the rationale for its use is to avoid the configurational mismatch between the two levels of theory, i.e., the mismatch between bond lengths and angles sampled at the MM level of theory, which are “slightly wrong” at the desired (S)QM level of theory. Since by definition interaction energies do not consider bonded degrees of freedom, this issue and the resulting poor convergence are avoided. We note, however, that our results for Ala and Ser (Table 2) suggest that IEA it is still susceptible to other sources of poor convergence. In addition, we argued in the Theory section that when applied to solvation free energies use of the IEA removes any considerations of the gas phase. If, e.g., a solute adopts different conformational states in the gas phase and in solution, the resulting free energy contributions are not accounted for.

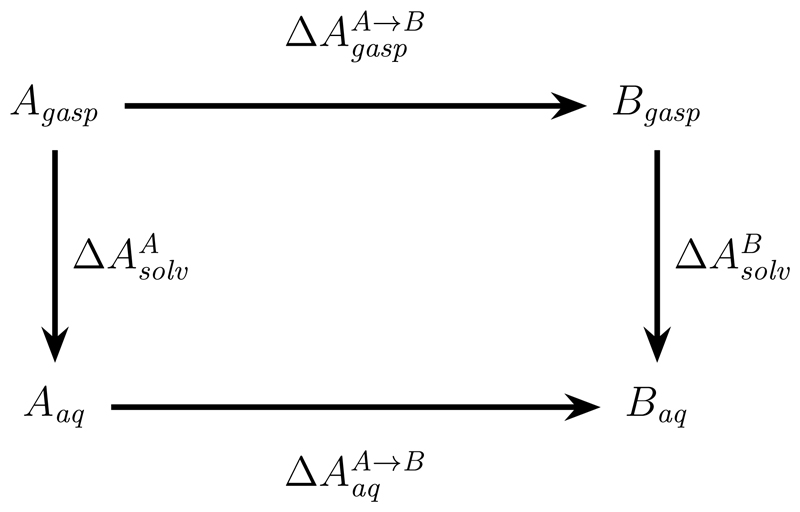
Curiously, this last issue bears resemblance to a 20+ year old question in classical alchemical FES, specifically, whether the so-called “self-terms” or “intra-perturbed group interactions” cancel from relative free energy differences.^62,63,97 As a reminder, consider the thermodynamic cycle used to compute a relative free energy difference of solvation. Along the alchemical, horizontal paths, identical changes in intra-molecular interactions occur in the gas phase and in aqueous solution. The resulting contributions to the free energy changes $\Delta A_{gasp}^{A\to B}\text{and}\Delta A_{aq}^{A\to B}$ have been called self-terms (intra-perturbed group interactions). However, while, at least in additive force fields, the changes in potential energy are always separable, the additivity of interactions is not mirrored by an additivity of free energy differences, i.e., in general

$$\Delta A_{aq}^{A\to B}\ne \Delta A_{gasp}^{A\to B}+\Delta A_{aq,\mathit{\text{inter}}}^{A\to B}.$$ (21)

Nevertheless, several free energy codes in wide use 20 years ago excluded or made it possible to exclude intramolecular energy terms from the calculations of free energies, assuming that $\Delta A_{gasp}^{A\to B}$ would approximately cancel out of Eq. 21. This approach had the added advantage that no gas phase calculations were required. E.g., the alchDecouple option of NAMD still makes it possible to exclude self-terms.⁹⁸ Boresch and Karplus investigated this question in detail,^62,63 taking into account the underlying differences between a single or a dual topology approach to carry out the alchemical transformation.⁹⁹ It was concluded at the time that “the present results indicate that selected terms of the energy function might be omitted from the free energy formalism unless single free energy differences are required”.⁶³ In particular, it could be derived that contributions from changes in stiff, bonded degrees of freedom, i.e., bond stretching and angle bending terms, canceled more or less completely from parallel legs of a thermodynamic cycle. For the soft bonded terms, dihedral angles etc. the theoretical considerations were less conclusive, though for the model systems investigated any errors were negligible. However in a later study focused on computing the relative solvation free energy differences between leucine and asparagine, it was concluded that “. . . because of the different conformations adopted by the two molecules in the gas phase and in solution . . ., the contributions to ΔA_gasp and ΔA_aq from changes in the potential energy function that are identical along the alchemical portions of the thermodynamic cycle (i.e., all intramolecular energy terms of leucine and asparagine affected by the alchemical mutation) are not the same”.¹⁰⁰ Thus, there is very concrete evidence in the context of classical FES that (indirectly) “omitting” different conformational preferences in two parallel legs of a thermodynamic cycle can lead to systematic errors.

In MM simulations it is customary to constrain some or all bond lengths through SHAKE^101,102 or a similar algorithm. Fixing bond lengths (and angles) may, in principle, provide a different route to avoid the “configurational mismatch” problem, though it is not immediately clear whether constraining internal degrees of freedom is appropriate at (S)QM/MM levels of theory. Recently, König and Brooks outlined how to separate approximately hard and soft bonded degrees of freedom in (S)QM/MM FES; the low level simulations employ SHAKE and the loss of vibrational entropy is accounted for in a post-processing step.⁴⁰

It seems appropriate to comment on the relative computational cost of the full indirect cycle vs. the use of IEA, as well as provide an overview of available toolchains. First, if inserting full energy differences into Zwanzig’s equation led to converged free energy differences, then use of the IEA would actually increase the computational cost. In addition to recomputing the total energy of the system at the (S)QM/MM level of theory, one has to compute the (S)QM energy of the intended high level region in order to extract interaction energies. However, in practical terms the overhead is relatively small; extracting interaction energies from trajectories is more tedious than costly. Carrying out NEW switching simulations is computationally more demanding, though overall there are mitigating factors. As already pointed out in Refs. 24,61, the switching simulations are a post-processing step and are completely independent; hence, they are trivial to parallelize. Further, we typically carry out much fewer switches compared with using Zwanzig’s equation or, in the context of the present study, employing the IEA. E.g., the full results for ethane, methanol, Ala and Ser (Table 2) were obtained from 10,000 NEW switches, whereas the IEA results were computed from 100,000 coordinate sets. The investigation into optimal switching lengths/protocols, as well as finding criteria how many switches are needed is work in progress. Finally, carrying out NEW switches may seem daunting. As described in Methods/SI, we employed the MSCALE module of CHARMM,⁹³ with which such calculations can be set up in a straightforward manner, though details remain tricky (c.f. 10.5281/zenodo.2328952).¹⁰³ Very recently, Wang et al.³⁴ carried out NEW switching simulations using the AMBER SQM/MM code.¹⁰⁴

One key result of the present study is highlighting that use of the IEA amounts to employing a chimeric potential energy function as the high level of theory: interactions between the MM and (S)QM/MM regions are modeled at the high level of theory, whereas interactions withing the “S(QM)/MM” region continue to be modeled at the low level. The use of chimeric potential energy functions in (S)QM/MM is actually not uncommon. Already in the 1990s Gao worked out (S)QM/MM methods, intended for the calculation of free energy profiles along a reaction coordinate, in which the treatment within the (S)QM region itself and the treatment of (S)QM/MM interactions could be described at different levels of theory.^105,106 Such dual-level strategies, refined, e.g., by the groups of Moliner and Tuñón,¹⁰⁷ are essential in several applications of (S)QM/MM methods. A review of such approaches applied to the study of kinetic isotope effects was published recently.¹⁰⁸ An important difference between these dual-level strategies and IEA, however, is the fact that the former employ a higher level of theory for the (S)QM region itself, whereas IEA, as shown in this work, employs the low level of theory.

6. Conclusions

The data just presented clearly indicate that the IEA may lead to erroneous results, or, at least, to results which deviate systematically from a full correction to a (S)QM/MM level of theory. We showed that the use of the IEA corresponds to a ‘chimeric’ potential energy function: the interactions within the high level region (in our cases the intramolecular energy of the solute) are described at the low level of theory, and only the interactions between the high level region of interest and the remainder of the system are computed at the high level of theory. If one looks back to the initial use of interaction energies by Wood and co-workers,⁵⁴ this is the exact construction of the Hamiltonian they employed. However, in recent applications of the IEA this distinction became blurred, and use of interaction energy differences rather than differences in total energy was suggested as a means to improve convergence.^39,49 Our data also show that IEA only mitigates convergence problems, but does not resolve them. Based on the theoretical considerations and the results reported here, we advise against the IEA.

Overall, the free energy community at large needs to refocus on improving ways to rigorously compute indirect free energies as opposed to finding ways to “cut corners” with theoretically unjustified approximations. Our own work is based on a two-pronged approach: on the one hand, we explore more powerful methods to compute ΔA^low→high, such as NEW based techniques.^24,61 Recent work by Ryde and co-workers is moving in this direction as well.^33,34 On the other hand, we are searching for ways to make the low level of theory more high level like, as reflected in present work focusing on using force matching as a means to reparameterize force-fields to better provide accurate indirect free energy calculations. ^30,31,109 Additionally, we are very interested in machine learning approaches that facilitate more quantum-like treatment of systems at a fraction of the computational cost.^110–113

Supplementary Material

The following can be found in the supporting information: simulation details for the force field model calculations, as well as the 2CLE calculations; and the parameters of 2CLE from both CGenFF and the modified ones from GAAMP.

Figure 4.

Thermodynamic cycle used to compute the relative free energy difference of solvation $\Delta \Delta A_{solv}^{A\to B}=\Delta A_{solv}^B-\Delta A_{solv}^A=\Delta A_{aq}^{A\to B}-\Delta A_{gasp}^{A\to B}$ for two solutes X and Y.