Predictive Models of Protease Specificity based on Quantitative Protease-Activity Profiling Data

Abstract

Bioinformatics-based prediction of protease substrates can help to elucidate regulatory proteolytic pathways that control a broad range of biological processes such as apoptosis and blood coagulation. The majority of published predictive models are position weight matrices (PWM) reflecting specificity of proteases towards target sequence. These models are typically derived from experimental data on positions of hydrolyzed peptide bonds and show a reasonable predictive power. New emerging techniques that not only register the cleavage position but also measure catalytic efficiency of proteolysis are expected to improve the quality of predictions or at least substantially reduce the number of tested substrates required for confident predictions. The main goal of this study was to develop new prediction models based on such data and to estimate the performance of the constructed models. We used data on catalytic efficiency of proteolysis measured for eight major human matrix metalloproteinases to construct predictive models of protease specificity using a variety of regression analysis techniques. The obtained results suggest that efficiency-based (quantitative) models show a comparable performance with conventional PWM-based algorithms, while less training data are required. The derived list of candidate cleavage sites in human secreted proteins may serve as a starting point for experimental analysis.

Graphical Abstract

1. Introduction

Regulatory proteolysis, or proteolytic processing, the main topic of this study, is a process of activation or deactivation of a target protein substrate via site-specific hydrolysis by a specialized regulatory protease. The fidelity of this process is driven by high specificity of regulatory proteases [1], which allows them to selectively recognize and process their substrates, thus modulating (suppressing or enhancing) functional activity. While large amounts of experimental data have been collected [2], the entire spectrum of possibilities may not be covered in experiment, and hence it is essential to be able to accurately predict plausible proteolytic events for the entire set of human proteases and their cognate substrate. Such predictions rely on large data collections, especially those generated by high-throughput techniques such as phage display, synthetic libraries, and genome-scale proteomics [3–8].

The protease specificity toward its cognate substrates is largely driven by the amino acid sequence context around the cleaved peptide bond. The positional weighted matrix (PWM) [9] is the method of choice for modeling the protease specificity because the binding regions of any given protease are usually of the same length (hidden Markov [10] models are more appropriate in the case of variable-size regions). A PWM-based model is essentially a table with frequencies of occurrence of amino acids in positions around the cleavage site. It is typically used for calculating the probability (or some normalized score) of a peptide to be cleaved at a particular site. Parameters of the model, i.e. positional frequencies of amino acids, are obtained from protease profiling experiments such as phage display or peptide libraries [11,12].

Most of these experimental techniques yield qualitative information about proteolytic events. Recent and emerging methods enable high-throughput quantitative kinetic assessment [13] delivering both cleavage site positions and proteolytic efficiency for each cleavage site. Although a PWM matrix can be constructed from both types of data, in the latter case the required number of tested substrates is expected to be much lower. Construction of predictive models from qualitative data is relatively straightforward [14], whereas bioinformatics methods for building predictive models from the quantitative data have been less explored.

Recently, both qualitative and quantitative protease profiling studies had been performed for the Matrix metalloproteinase (MMP) family [13]. MMPs are a family of zinc-dependent endopeptidases playing a crucial role in tissue remodeling, organ development, regulation of inflammation, and various diseases such as rheumatoid arthritis and cancer [15]. Cells exports MMPs to the extracellular matrix, where they can potentially act on other secreted proteins [16].

Twenty three structurally related MMPs expressed in human share some substrate preferences, but at the same time they are distinct by the primary specificity and physiological role. Since their discovery in 1962 [17], MMPs have been subject of extensive studies, including high-throughput experiments [18,19]. Hence MMPs represent a challenging, but interesting and informative case for development and validation of computational methods. Previously qualitative data from [13], i.e. the information about cleavage site positions, has been used to construct MMP specificity models [20]. Here we apply a variety of regression methods to develop MMP specificity models based on quantitative data from the same study [13]. The obtained models are compared with each other and with prediction models constructed from the qualitative data. This analysis demonstrates comparable overall performance of both approaches, proving that the quantitative (kinetic) approach is useful, as it provides reasonable predictive efficiency after training on a relatively small number of substrates. Finally, we applied the developed methods to human secreted proteins.

2. Material and methods

2.1. Quantitative protease-activity profiling data and problem formulation

The catalytic efficiency of proteolytic cleavages on a set of 1363 peptides for eight members of the matrix metalloproteinase family, MMP2, MMP9, MMP14, MMP15, MMP16, MMP17, MMP24, and MMP25, was taken from ref. [13]. The peptide sequence, proteolytic site position, and calculated catalytic efficiency of the proteolytic event for 1363 peptides are given in Supplemental File 1. For each cleaved peptide we concatenated the 6-aa variable part with the 4-aa constant adapter sequences GGSG (left) and TASG (right) and then extracted five amino acids on both sides of the cleavage site. The obtained 10-aa sequences were thus aligned by the position of the cleavage site in the middle, yielding multiple alignments of the cleaved regions of substrates for eight studied proteases (Supplemental File 1).

We formulate the problem as the search for a function f: X; → R; which predicts the catalytic efficiency for a given peptide, where X is the space of peptides and R is the set of real numbers. To construct this function, we applied regression analysis methods including multiple linear regression, ridge regression, and applied specially designed approaches for the dimensionality reduction and the sample size expansion. At that, the catalytic efficiency values of proteolytic cleavage obtained in experiment may be considered, in terms of the regression analysis, as a response or dependent variable, while the indicator variables reflecting the presence of particular amino acids at positions close to the cleaved peptide bond serve as predictors, or independent variables. In the linear regression model the response variable is the sum of the independent variables multiplied by coefficients estimated from the data. The matrix of coefficients obtained after fitting of the model is equivalent in size and usage to a PWM obtained from qualitative data (Fig. 1a). This matrix can be applied for prediction of the proteolytic efficiency at a given peptide bond.

Figure 1.

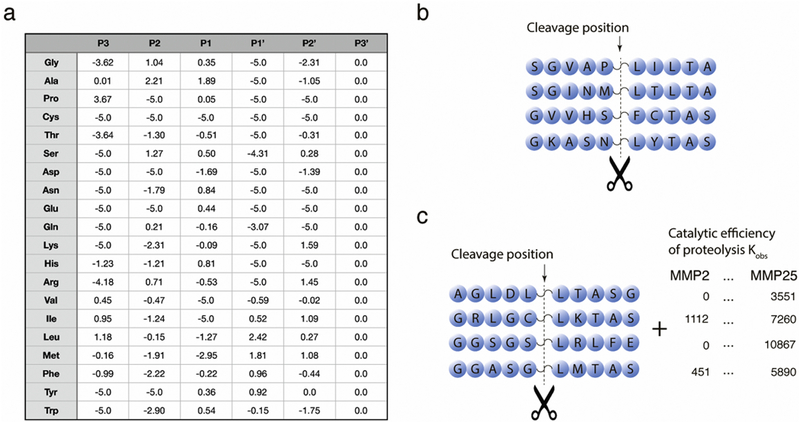
(a) Example of a Position Weight Matrix (PWM) for Matrix metalloproteinase-2 (MMP2). Columns represent positions of the peptide in the active-site cleft. Rows show logarithms of amino acid frequencies in the active-site positions. The score of a possible proteolytic cleavage for a particular peptide bond is calculated as $S={\prod }_{i=P3}^{P{3}^{\prime }}{f}_{ij}$, where i is the position, j is the amino acid, f_ij is the logarithm of the frequency of amino acid j in position i. (b) Phage-display experimental data provides information only about the position of the proteolytic cleavage in the peptide. In contrast, data considered in this study (c) provides also the measured catalytic efficiency of the proteolytic event.

2.2. Multiple linear and ridge regression

To build a multiple linear regression model, we first assign each peptide with an associated K-dimensional vector X of binary variables indicating the presence of each of twenty amino acids at a particular position of the peptide relative to the cleavage site. The vector length is K = n_aa × L, where n_aa is the number of possible amino acids and L is the peptide length. The multiple linear regression model is then defined as:

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k+\epsilon$$

where y is the response variable, i.e., in our case, the catalytic efficiency of proteolysis, {x_i} are independent indicator variables of the presence of amino acids in peptide positions, {β_j} are regression coefficients, and ε is a normally distributed error. A conventional method for estimation of the regression coefficients {β_j} is the least squares method (OLS). We have used an ad-hoc Java implementation of this method based on the Gauss method of covariation matrix inversion.

Linear regression with the Tikhonov regularization (known as the ridge regression), which penalizes the sum of the squared regression coefficients, minimizes the following function:

$$L={\sum }_{i=1}^n{\left(y_i-{\sum }_{j=1}^k{\beta }_j{x}_{ij}\right)}^2+\alpha {\sum }_{j=1}^k{\beta }_j^2$$

where y_i is the cleavage catalytic efficiency of the i-th peptide, x_ij is the j-th indicator variable of the i-th peptide, $\left\{{\beta }_j\right\}$ are the regression coefficients, and α is the regularization parameter. An implementation of the ridge regression has been derived from our OLS implementation by adding α to all diagonal elements of the covariation matrix.

2.3. Selection of important position around the cleavage site

We applied the Forward Feature Selection (FFS) algorithm [21] to estimate the importance of amino acid positions around the cleavage site. For each studied protease, the FFS algorithm with linear regression was applied to the dataset of cleaved peptides with measured catalytic efficiency of proteolysis. The FFS algorithm is a sequential evaluation of the feature fixed-size subsets, which begins with single-variable subsets and ends with the all-variable subset. At the first iteration, the linear regression is applied to all possible single-variable subsets {x₁}, {x₂},…{x_K}, allowing us to select the best individual variable x₍₁₎. At the next step we find the best subset consisting of two variables, x₍₁₎ and one other feature from the remaining K–1 variables. Then, the subsets with three, four and more features are evaluated. As our indicator variables reflect amino acids occupying a particular position of the peptide, we modified the FFS algorithm in the following way: at each iteration, if any of twenty indicator amino acid variables for a particular position had been selected, we considered this position as selected entirely, i.e. all twenty indicator variables for that position were added to the selected variable set. Totally 80 cycles of the FFS algorithm were executed and the probability of selecting a position at particular iteration was calculated. The FFS algorithm was implemented in Java without specialized libraries.

2.4. Regression with grouping of rare amino acids

Another known approach of improving the quality of regression models is grouping of rare levels of a categorical variable to a single new level. In our case it implies introducing of a single indicator variable of a particular position of the peptide that groups indicator variables for amino acids that are rare in this position. Let $A_{\text{rare}}^i$ be the subset of amino acids occurring at the i-th substrate position with frequencies less than a threshold T:

$$A_{\text{rare}}^i=\left\{a{a}_j:f_i\left(a{a}_j\right)<T\right\}$$

where aa_j is the j-th amino acid out of 20, f_i is the frequency at position i. Then the new variables, which replace the old variables for rare amino acids, are defined as:

$$x_{\text{rare}}^i=\left\{\begin{array}{c}1,\text{if}\hspace{0.33em}\exists \hspace{0.33em}j:x_j=1\hspace{0.33em}\text{and}\hspace{0.33em}{x}_j\in A_{\text{rare}}^i\\ 0,\text{otherwise}\end{array}\right.$$

where x_j is the j-th indicator variable. Note that the introduced grouping variables are position-dependent.

2.5. Amino acid parametrization

Let f(x_aa) be a mapping of the amino acid domain into real numbers R:

$$f:x_{aa}\to R$$

Let k be the number of such mappings (k ≤ 20) in the model. Then, the model with amino acid parametrization has the following form:

$$y=\sum _{i=1}^n\sum _{j=1}^k{\alpha }_{ij}{f}_j\left(x_i\right)$$

where i is a position, j is the mapping number, α_i,j is the impact of the j-th mapping at the i-th position of the peptide, x_i is the amino acid at the i-th position of a peptide. Fitting of the model on training data implies fitting of the α_i,j coefficients, as well as the number of mappings k and the mapping itself, i.e. a set of real values defined for each of twenty amino acids. The form and the number of mappings have been optimized simultaneously for all studied MMPs.

2.6. Regression with addition of presumably uncleaved peptides

As the number of possible peptides strongly exceeds the number of possible proteolysis substrates, there is a very low probability to obtain a real protease substrate among randomly generated peptides. Thus, it is reasonable to expand the dataset by generating random peptide sequences and assigning these peptides with some negligible value of the proteolysis catalytic efficiency. A larger training dataset may improve the quality of prediction.

Firstly, we generated a set {U}_m of random 10-aa peptides, not intersecting with the cleaved peptide set {C}_n. Then, we modified the conventional regression loss function to include a term responsible for the random peptide set. We defined the loss as zero if the predicted cleavage catalytic efficiency was less than all cleavage efficiencies from the set {U}_m. Otherwise, we calculated the deviation from the minimal value of the cleavage catalytic efficiency from {U}_m:

$$L=\sum _{i=1}^n{\left(y_i-\sum _j^k{\beta }_i{x}_{ij}\right)}^2+\sum _{i=1}^m{\left(y_{min}-\sum _{j=1}^k{\beta }_i{x}_{ij}\right)}^2$$

where n is the size of the cleaved peptide set, m is the size of the random peptide set, y_min is the minimal cleavage catalytic efficiency in the cleaved peptide set {C}_n; [x] = x if x < 0, otherwise [x] = 0.

2.7. Evaluation of model performance on CutDB dataset

To collect a testing set for the comparison of prediction models, we extracted all proteolytic events registered for three studied matrix metalloproteinases, MMP2, MMP9, and MMP14, from the CutDB database [22]. We applied the MMP2, MMP9, and MMP14 prediction models to peptides from the testing set and calculated the standard metrics of the prediction quality, the Receiving Operation Curve (ROC) and the Area Under the ROC curve (AUC).

2.8. Prediction of cleavage sites in human secreted proteins

The list of human secreted proteins was downloaded from the Uniprot [23] database by applying the following filter condition: organism=“Homo sapiens”, keyword=“Secreted”. All prediction methods developed here were applied to the obtained set of proteins, resulting in the cleavage scores calculated by each method for every peptide bond of each protein. The obtained predictions are available at http://sector3.iitp.ru/files/MMPsecretomePredictions.zip. To estimate the prediction reliability, the set of secreted proteins was intersected with known MMP substrates from the MEROPS database [24] for three out of eight considered MMPs, MMP2, MMP9, and MMP14. These families were selected because they had a sufficiently large number of known proteolytic sites. The prediction scores were sorted by decrease for each protein, producing (separately for each method) the rank for each peptide bond. Then the ranks O_ij of peptide bond i in protein j were normalized by the total number N_j of peptide bonds in protein j and inverted so that the normalized rank of the highest score in a protein was equal to 1 and that of the lowest score was equal to 0:

$$0_{ij}^{\text{norm}}=1-\left(0_{ij}-1\right)/\left(N_j-1\right).$$

The distribution of the normalized ranks of predicted cleavage score was approximated by the exponential distribution and the distribution parameter λ_exp was estimated (the higher is the value of this parameter, the stronger is the prediction power of the method).

3. Results

3.1. Estimating the number of important positions around the cleavage site

Prior to building the prediction models, we identified substrate positions around the cleavage site that significantly influence the catalytic efficiency of each studied protease. To this end, we applied a feature selection approach to independent indicator variables corresponding to a large number of positions in both directions from the cleaved peptide bond. We used the Forward Feature Selection algorithm (FFS) [21], at each step iteratively selecting a single position that, upon addition to the current position set, yielded the best prediction result among all remaining positions. At each iteration of the FFS algorithm, we applied linear regression and calculated the prediction quality. As seen in Figure 2a, the prediction quality improves with addition of new positions until five or six positions have been selected. After that the quality of prediction stabilizes or even decreases. In agreement with earlier observations [25,26], the P1’ subsite position (in the Schechter–Berger notation [27]) has been always selected as the most important one (Figure 2b). The P3 subsite position was also selected with 100% frequency at the second iteration and the P1 position dominated at the third iteration. At the fourth and fifth iteration, either P2 or P2’ were most frequently selected depending on the considered protease. Specifically, at the fourth iteration, the P2 subsite position was selected most frequently for MMP2, MMP9, MMP14, and MMP16, while P2’ was selected for MMP15, MMP17, MMP 24, and MMP25. The P3’ position was most frequently selected at the sixth iteration. Other subsite positions, P5, P4, P4’, P5’, were selected at iterations 7–10 without any consistent order.

Figure 2.

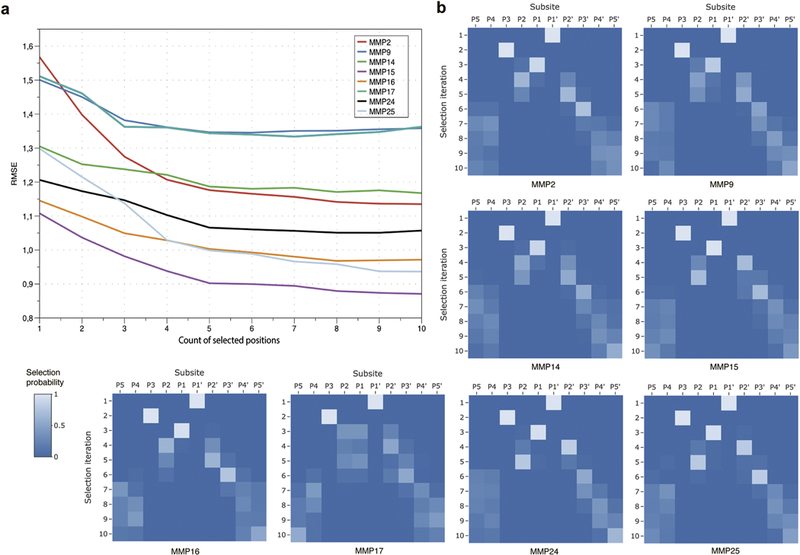
(a) Selection of substrate positions around the cleavage site using the FFS algorithm with linear regression. (b) Frequency of selection of subsite positions at different iterations of the FFS algorithm.

3.2. Performance of regression models is comparable with PWM models of protease specificity

Using the optimal set of positions around the cleavage site, we applied a variety of regression approaches for building models from the quantitative protease activity data. We compared their performance with phage-display derived PWM models built using information about the frequencies of occurrence of amino acids around the cleavage position. We obtained models of protease specificity for eight matrix metalloproteinases, MMP2, MMP9, MMP14, MMP15, MMP16, MMP17, MMP24, and MMP25. The number of peptides in the training set used for construction of the models was 1363 (Supplemental File 1). Using proteolytic event data taken from the CutDB database (see Methods), we compared the prediction quality of the constructed models with PWM matrices derived from the phage-display experiment [20]. (Figure 3,4, Supplemental File 2). As shown in Figure 4, although the prediction quality estimated by AUC for the linear regression (LR) model built on quantitative date is less than the prediction quality of the phage-display derived PWM model (PD), their performance is comparable for MMP2, and slightly smaller for MMP9 and MMP14: 0.76 versus 0.8 for MMP2, 0.68 versus 0.85 for MMP9 and 0.59 versus 0.75 for MMP14, respectively.

Figure 3.

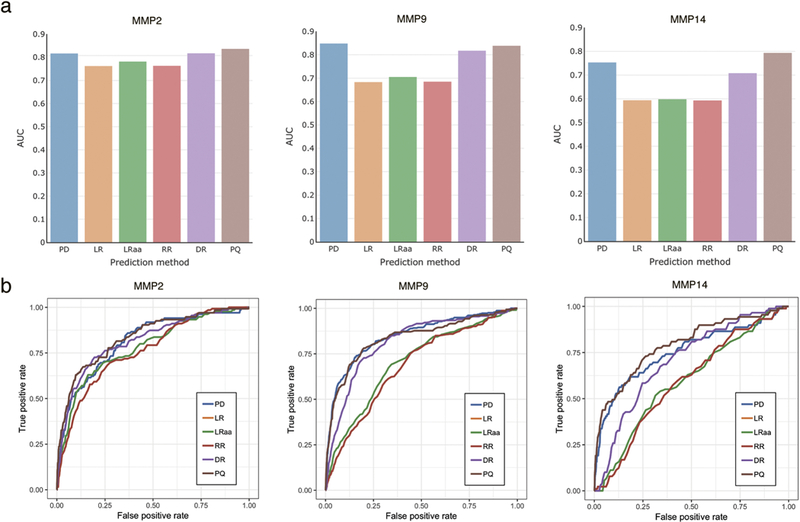
(a) Comparison of the prediction quality of the considered regression methods by ROC curves on CutDB proteolytic events. (b) Area Under ROC Curves (AUC) calculated for the considered regression methods on the CutDB data. Abbreviations: PD – phage-display derived PWM, LR – linear regression, LRaa – linear regression with grouping of rare amino acids, RR – ridge regression, DR - regression with amino acid parametrization, PQ – regression with random peptides.

Figure 4.

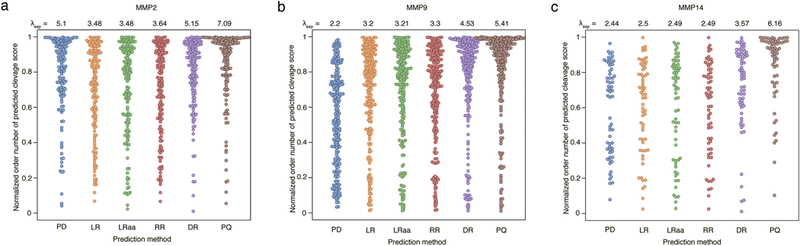
Distributions of the normalized ranks of predicted cleavage scores (best is 1, worst is 0) for peptide bonds corresponding to known proteolytic sites of MMP2, MMP9, MMP14 for human secreted proteins from the MEROPS database. Abbreviations of prediction methods as in Figure 3. All distributions were approximated by the geometric distribution and parameter p_geom was calculated and shown in plots (higher values of p_geom indicate stronger shift of distributions toward 1, i.e. greater prediction power of a method).

Application of ridge regression (RR) improved prediction for two out of three tested matrix metalloproteinases, MMP2 and MMP9 (Figures 3, Supplemental File 2).

3.3. Dimension reduction

We then attempted to reduce the problem dimension by grouping rare amino acids (LRaa) and by applying a newly developed method of amino acids parametrization (DR). Grouping of rare amino acids improved prediction for all tested proteases (MMP2, MMP9, MMP14), compared to the linear and ridge regression (Figures 3,4, Supplemental File 2). The AUC metric calculated for MMP2 was 0.78, which is 2.4% and 2.3% more than that for the linear and ridge regression, respectively. Similarly, the AUC calculated for MMP9 was 0.71, which is 3.2% and 2.9% more, and the AUC calculated for MMP14 was 0.60, 0.7% and 0.8% more than that for the linear and ridge regression, respectively. We also introduced a novel amino acids parametrization method, which transforms the input variables into a relatively small set of real-valued functions {f(x)} on the amino acid domain (see Methods).These functions may be interpreted, for example, as approximations of physicochemical properties of amino acids such as hydrophobicity, charge, or size. The number of functions and their definitions, together with the weighted impact of the functions at each position of the peptide are derived from the training data. At that, while the same set of functions is considered for all positions, the weight of a function at a given position may vary, reflecting positional preferences towards amino acid properties. Here, we defined these functions as linear and optimized their number iteratively increasing it from 1 to 20. The optimal fitted number of functions f(x) was six. Figure 3 features the improvement of the prediction quality for the three considered proteases. The AUC calculated for MMP2 was 0.82, that is 7.2%, 7%, and 4.6% more than for the linear regression, ridge regression, and grouping of rare amino acids, respectively. The same value of AUC, 0.82, was obtained for MMP9, which improves the prediction performance in comparison with the specified methods by 19.6%, 19.3% and 15.9%, respectively. The AUC value for MMP14 was 0.71, that is 19.2%, 19.4%, and 18.4% more than for the LR, RR, and LRaa methods, respectively.

3.4. Extension of the dataset size with the random peptides increases the predictive power of the models

For each of eight protease-specific datasets, in addition to the registered cleaved substrates, we generated the same number of random peptides and considered these peptides as if their values of cleavage catalytic efficiency were below all values of catalytic efficiency for the cleaved peptides (see Methods). We further assigned a quadratic loss penalty to random peptides when their catalytic efficiency values were predicted to be higher than at least one of the cleaved peptides. The ROC-curves (Figures 3, Supplemental File 2) for such prediction models (PQ) demonstrate better prediction quality compared to all above approaches. Hence, the AUC calculated for MMP2 was 0.84, that is 9.7% more than for linear regression, 9.6% more than for ridge regression, 7% more than for grouping of rare amino acids, and 2.8% more than for parametrization of amino acid. The improvements for MMP9 were 0.84, 22.7%, 22.3%, 18.9%, and 2.6%, and for MMP14 they were 0.79, 33.5%, 33.7%, 32.6%, and 11.7%, respectively.

3.5. Application to human secreted proteins

We applied the prediction models to all human proteins known to be secreted, and estimated the prediction quality by comparing the predictions with known proteolytic sites from the MEROPS database [24]. A substantial number of secreted substrates in MEROPS was found only for MMP2, MMP9, and MMP14, and thus we limited our quality estimation to substrates of these three proteases. Figure 4 shows the distribution of normalized ranks of predicted cleavage scores for peptide bonds corresponding to known proteolytic cleavages. All distributions are shifted to 1, proving that all models have predictive power. The best quality of prediction was demonstrated by the PQ method, with λ_exp being 7.09 for MMP2, 5.41 for MMP9, and 6.16 for MMP14. The second best predictive power was demonstrated by DR (5.15, 4.53 and 6.16, respectively). For LR, RR, and LRaa, the predictive power it is approximately the same for all three proteases, with λ_exp in the range [3.48, 3.64] for MMP2, [3.2, 3.3] for MMP9 and [2.49, 2.5] for MMP14 (Supplemental File 2). It is lower than that of the PWM method (PD) for MMP2 (5.1), almost the same for MMP14 (2.44), and better for MMP9 (2.2).

3.6. Estimation of the minimal required size of the training set

We also identified the minimum number of substrates required for the efficient training of the regression models for protease specificity based on the catalytic efficiency by training the models on reduced datasets and comparing their performance with the frequency-based models trained on the whole set of substrates (PWM models), and also with the position weight matrices obtained from the phage-display experimental data [13] (PD models). The top performing PQ model was trained using 10%, 20%, …, 90% of the initial data. As shown in Figure 5 and Supplemental File 2, the PQ models outperform the PWM model for each of the three proteases after inclusion of 30–60% of the training data. For two out of three considered proteases, the PQ models based on reduced training sets outperformed the PD models constructed with considerably larger numbers of training substrates [13]. Thus, we conclude that in practice, training of six-position protease specificity regression models requires around 400–800 substrates with measured catalytic efficiency of proteolysis.

Figure 5.

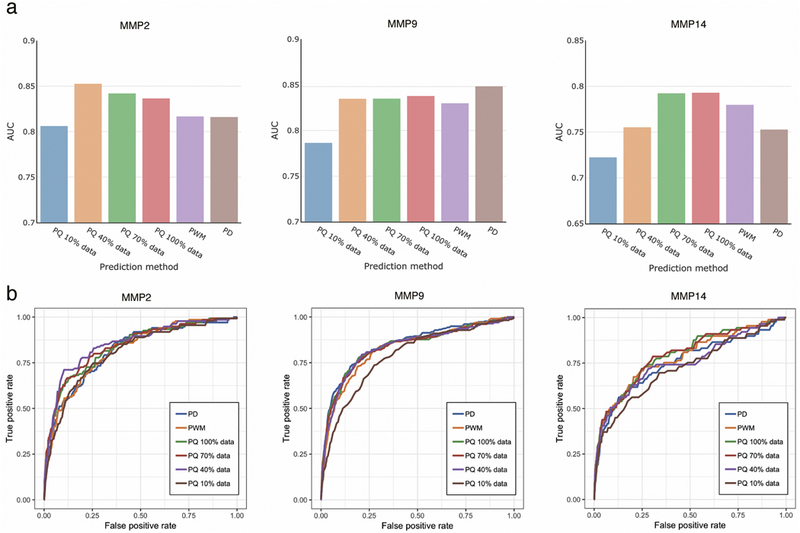
Comparison of the prediction quality by the AUC metric (a) and ROC cirves (b) for PQ models, constructed using increased fractions of the training data, the position weight matrix build based on the whole training set (PWM) and phage-display experiment data derived model (PD). Abbreviations PQ and PD as in Figure 3.

4. Discussion

Until recently, protease activity profiling data were largely qualitative, reflecting proteolytic events but not proteolytic efficiency. Computational models derived from such data required large samples to estimate the frequency of proteolytic sites given amino acid context of cleaved bonds. Here, we have used quantitative data providing catalytic efficiency for each proteolytic event. Theoretically, to estimate the impact of all amino acids at each position of a peptide of length L, assuming their independency, it is sufficient to have 20×L independent measurements of the catalytic efficiency. Therefore, with the quantitative (kinetic) approach much less substrates need to be analyzed to construct a prediction model.

Here we demonstrate that linear regression methods can be successfully applied to the prediction of protease specificity using quantitative protease-activity profiling data. The predictive models constructed in this study for eight MMP enzymes demonstrate comparable performance with PWM models derived from larger qualitative data. Three special techniques incorporated into the regression methods may improve the predictive quality. These methods are dimensionality reduction by grouping of (positionally) rare amino acids and by transformation of the input data into a set of real-valued functions on the amino acid domain. The third technique, specific for protease-activity profiling studies, implies inclusion of random peptides to the training set under assumption that most of them would not be cleaved. The latter approach showed the best performance among the methods tested in this study. In addition, ridge regression also proved to be useful.

All predictive models constructed in this study are available at Supplemental File 3. Currently, dozens of protease specificity prediction models are available from MEROPS [24] and other resources [28]. However, these collections do not cover the entire repertoire of important regulatory proteases. With advances in modern experimental techniques, new quantitative type of data from protease-activity profiling experiments will become widely available. Here, we have shown that this type of data could be successfully used for construction of protease specificity predictive models using regression methods. These models demonstrate comparable or superior performance (depending on the testing dataset) to qualitative data-based models while requiring less peptide substrates. The obtained list of predicted MMP proteolytic sites, available at http://sector3.iitp.ru/files/MMPsecretomePredictions.zip, may serve as a starting point for experimental validation.

Highlights.

• Protease specificity models can be built from quantitative protease profiling data

• Regression methods is applicable for the building of such predictive models

• These models perform at least as well as traditional quantitative PWMs

• Significantly smaller number of peptide substrates are required for training data

Abbreviations:

PWM

position weight matrices

MMP

matrix metalloproteinases

LR

linear regression

LRaa

linear regression with grouping of rare amino acids

RR

ridge regression

DR

regression with amino acid parametrization

PQ

regression with random peptides