Abstract
The micellar structure of six alkyl trimethylammonium halides was studied via conductivity. It was found that the aggregation number increased with the decreasing carbon chain length. Furthermore, Br− significantly enhanced the micellar formation over Cl−. However, the aggregation number and ionization degree remain similar for both anions. The modelling results validate that the counter-anions affect micellar formation via equilibrium constants, instead of their hydration size. In particular, the association constants between surfactant (both monomer and micelle) and Br− are significantly higher than Cl−. This is consistent with the qualitative description of hydrated Br− in the literature. The experimental and modelling results confirm that micelles are formed via “ion-paring/hydration” structure, instead of the conventional “packing” concept.
Keywords: Chemical engineering, Physical chemistry, Surfactants, Micelles, Conductivity
1. Introduction
Cationic surfactants are critical reagents for many industrial processes. Some important usages of cationic surfactants are fabric softeners in the textile industry, anticaking agents for fertilizers, corrosion inhibitors for metal surfaces, pigments dispersants and microorganism germicides [1]. Since the early 20th century, it has been well-evidenced that ionic surfactants can form aqueous aggregates [2], which were subsequently described as spherical micelles [3]. However, our understanding of the size, aggregation number, ionisation degree and water content of the micelles remains unsatisfactory. Critically, the correlation between these properties and the surfactant structure is not established. The knowledge deficits hinder a proper understanding of and prediction for surfactant applications [4].
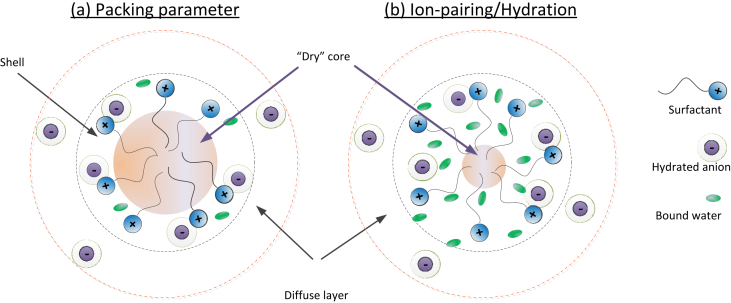
In the literature, there are two conceptual structures of micelles [5], as demonstrated in Fig. 1. The first approach is based on packing parameters, in which the micelles are determined mostly by the volume of the surfactant tails [6]. The approach implies that counter-ions and water can only penetrate the outer “shell” of micelles, which is dominated by the head-groups. The second approach is based on the hydration/ionic pairing interactions and is referred to as the “ion-pairing/hydration” model [7]. This approach designates a much smaller dry core, which contains only a few carbons, and was originated from an observation of the high water content within the micelle [8]. It should be highlighted that the water molecules within the micelles contain non-hydrogen-bonded –OH groups, due to interaction with hydrophobic molecules. The existence of this water condition (hereafter referred to as “bound” water) have been confirmed at air/water surface [9], alkane/water interface [10], and in hydrophobic hydration shells of alkanols [11]. The equilibrium between the bound water and “free” water (which have normal water-water H-bonds) have been validated for many aggregation systems [12]. The hydration shells around halides [13] and hydrophilic heads [14] are also more rigid than the “free” water, and constitute other types of hydration layer. A recent simulation showed that the structure of hydrophobic hydration is different from the water arrangement around ionic groups [15]. Dielectric spectra of water have revealed that the water number of the hydration layer can be more than 10 for both anionic and cationic surfactants [16]. The quantities of “bound” water would be a critical factor for the 2nd concept, as these water molecules affect the binding probability. In both structures, the micelles have fewer counter-ions than surfactants and formed charged aggregates. Similar to other charged aggregates, the counter-ions are located within a thin electrical layer, the diffuse layer [12]. The diffuse layer forms an inseparable counterpart of the micelle and plays a critical role in the experimental quantification of micellar structure [17].
Fig. 1.
Conceptual description of micelle structure: (a) packing approach and (b) ion-pairing/hydration approach.
The two concepts lead to vastly different quantification. In the packing approach, the micelle size and aggregation are controlled by the volume of the hydrocarbon tail [18]. In the hydration model, however, the aggregation is determined by binding equilibrium constants, which involve surfactant heads, surfactant tail/water and hydrated ions. The mechanisms result in contrasting relationships between the micellar core size and surfactant length. The “dry” core in the 1st model contains most carbons of the surfactant tails and would decrease with decreasing surfactant length. On the other hand, the “dry” core in the 2nd model should be independent of the surfactant length.
A consequence of the conceptual approaches is the predicted correlation between surfactant length and micellar aggregation, for instance, a surfactant series with the same ionic head-and decreasing length. The 1st approach would imply a decreasing volume of the “dry” core and thus decreasing aggregation number [18]. The 2nd model, in contrast, envisions a decreasing number of the bound water [5], and thus decreasing binding probability with the hydrated anion. The net result could be an increment in aggregation number. Similarly, the two approaches imply different impacts of counter-ion. The 1st approach would indicate that the counter-ions influence micellar structure via their molecular size. In the 2nd structure, in contrast, counter-ion influence micelles by controlling the ionic binding constants.
The aggregation number of alkyl trimethylammonium halides has been reported by various experimental methods, including steady-state-fluorescence (SSF) [23], time-resolved fluorescence quenching (TRFQ) [27], electron paramagnetic resonance (EPR), neutron diffraction (NF) [25] or small-angle neutron scattering (SANS) [22]. However, some of these methods require additional probing agents. For example, C16PC are needed in TRFQ [28]. Similarly, EPR employs 16-doxylstearic acid methyl ester (16DSE) as a spin probe. While NF and SANS do not require additional probes, these methods are only feasible for high-contrasting solute-solvent systems, such as a hydrogenated surfactant in D2O or a deuterated surfactant in water. It should be highlighted that the data from these methods need to be interpreted in combination with theoretical models to get the aggregation number. A comparative study has shown that the three methods can result in different aggregation numbers, depending on the interpretation [22]. Furthermore, one of the priory assumptions is that the probes have no effect on the micelles and ionization degree. For polar probes, the assumption implies that the probe located in the Stern layer of micelles and nowhere else [17]. On the other hand, more complicated distribution of the probe between the “core”, the “shell” and the Stern layer of the micelles remains a possibility [12].
Hence, an experimental method without the use of additional probes is critically required. The study investigates the micelle formation by a combination of conductivity [29, 30, 31] and modelling, without using additional probing agents. A series of well-known cationic surfactants, alkyl trimethyl ammonium (CnTA+) with either Cl− or Br−, were used. The conductivity will be modelled via chemical equilibria between surfactants/counter-ions and micelles. The aggregate size is also measured by 1H NMR DOSY and provides qualitatively verification for the model. Ultimately, the study aims to clarify the structure of micelles and shred new insights into micellar formation/surfactant structure relationship. Furthermore, the new insights can clarify the inconsistency in the literature on the micellar aggregation numbers.
2. Theory
For a dilute solution of a mixture of ionic moieties, the conductivity is given by the Kohlrausch's law of independent migration of ions:
| (1) |
where λi is limiting molar conductivity of species i. It should be noted that the above formula was obtained for 1st order analysis and is only applied to the low concentrations. For aqueous solutions, the applicable limits are typically in the range of linearity and ∼10 mM [32]. For strong electrolytes, such as NaCl and KBr, the limits are well known [33], as demonstrated by the linear correlation between conductivity and concentration. For cationic surfactants, the limits are around the critical micelle concentration (CMC) and within 10 mM.
For the concentration above the CMC, the conductivity is governed by counter-ions, monomer and micelles. The concentration of the micelles can be obtained from the total surfactant concentration with chemical equilibria [34]. The equilibrium between monomer (Mo) and micelles (Mi) and counter-ions (In) [35] is governed by a chemical reaction. Assuming that each micelle consists of m surfactants and n counter-ions, micellization reaction is given by:
| (2) |
The reaction equilibrium is:
| (3) |
where cion is the concentration of the dissociated ions, cmo and cmi are concentrations of monomer and micelles, respectively. The reaction constant, km, has a unit of M1−m-n.
The ratio n/m is the degree of micellar ionization. Collective results in the literature have indicated that the degree of ionization varies from 0.1 to 0.7 depending on the surfactant and quantification method [1]. Since surfactants are strong electrolytes, the monomer can also associate with counter-ions to form associated surfactant (Si). The association of monomer and counter-ion is given by a similar reaction and equilibrium constant:
| (4) |
| (5) |
where the reaction constant, ks, has a unit of M−1. The total surfactant in the solution, cb, is given by:
| (6) |
For 1:1 ionic surfactants, the total number of ions equals to cb and hence:
| (7) |
It should be noted that the above model doesn't include the interactions between charged species, the electrophoretic and relaxation effects [36], which can be significant at high micellar concentrations. Near the CMC, however, the available model showed that these effects were not significant. Furthermore, one needs to obtain the aggregation and ionization degree before modelling these two effects.
2.1. Numerical solution
The above system of equations (Eqs. (3), (5), (6) and (7)) has four unknowns: cSi, cion, cmo and cmi. Substitute Eqs. (6) and (7) into Eqs. (3) and (5), one obtains a system of two equations and two unknowns:
| (8) |
| (9) |
Eq. (8) can be expressed in the quadratic form:
| (10) |
The above equation has 2 positive roots. However, the larger root is greater than cb, which is physically infeasible. Hence, we can take the smaller root:
| (11) |
Where
| (12) |
One can substitute the above function into Eq. (8) to obtain a non-linear equation. The equation can be solved via a bisection algorithm for cmi at any given value of cb. Subsequently, other concentrations (cSi, cion and cmo) are determined. Hence, the conductance of the surfactant solution is given by:
| (13) |
The calculated K can be fitted against experimental data by changing the reaction constants.
Below the CMC, with significant monomer association and negligible micelles formation, the above system reduced to:
| (14) |
| (15) |
Eqs. (14) and (15) can be applied at low concentration range to determine ks.
2.2. Fitting procedure
Since the conductivity of the solutions contained monomer, ions and micelles, several fitting steps are applying in the following sequence:
-
1
- the molar conductivities of ions (Na+, K+, Cl−, Br−) are obtained from data of the four salts.
-
2
- λmo of CnTA+ are obtained from lower limits (<1.5 mM) of CnTACl and CnTABr solutions
-
3
- Ks are obtained by fitting to the lower part, up to CMC, the data to Eq. (15)
-
4
- λmi, km, m and n are obtained by fitting Eq. (11) with data from low to above CMC.
By applying the above procedure to a series of surfactant, with two different counter-anions (Cl− and Br−), we aim to quantify the role of surfactant length and counter-ions on the micellar formation.
3. Experimental
Three alkyl surfactants (C14H29(CH3)3N+, C12H25(CH3)3N+ and C10H21(CH3)3N+) and two common halides (Cl− and Br−) were selected for the study. Tetradecyltrimethylammonium chloride (C14H29(CH3)3N+Cl−, 98%), tetradecyltrimethylammonium bromide (C14H29(CH3)3N+Br−, 99%), dodecyltrimethylammonium chloride (C12H25(CH3)3N+Cl−, 98%) and decyltrimethylammonium bromide (C10H21(CH3)3N+Br−, >97%) were purchased from Wako Pure Chemical and used without further purification. Dodecyltrimethylammonium bromide (C12H25(CH3)3N+Br−, ≥98%) and decyltrimethylammonium chloride (C10H21(CH3)3N+Cl−, >98%) were obtained from Sigma-Aldrich and Tokyo Chemical, respectively, and were used as received. Sodium chloride (NaCl, 99.5%), potassium chloride (KCl, 99%) and sodium bromide (NaBr, 99.5%) were obtained from Wako Pure Chemical and potassium bromide (KBr, 99%) was obtained from Kishida Chemical and used without further purification. Deionized water was used to prepare the solutions.
It should be noted that the longer surfactants, C16H33(CH3)3N+Br− and C16H33(CH3)3N+Cl−, have solubility close to the CMC, and thus were not included in the study. The shorter surfactant, C8H17(CH3)3N+, has very high CMC and thus also become unsuitable. As shown in the result section, the CMC of C10H21(CH3)3N+Cl− is too high for effective modelling.
3.1. Conductivity
In this study, practically low temperature was selected to reduce molar conductivity and thus increase the reliability of Kohlrausch's law. Hence, 17 °C was applied for all measurements.
The conductivity was measured using a Horiba LAQUAact ES-71 conductivity meter equipped with 3551-10D conductivity cell (submersible type). The temperature of the solution was controlled by using a circulating water bath (EYELA NCB 1200). Experiments were started with pure water and the subsequent concentrated solutions were obtained by adding a previously prepared stock solution into the measurement cell. After each addition, the solution was stirred to maintain homogeneity before measuring the conductance. The CMC values were determined from the breakpoint in the conductance-versus-concentration plot. All the measurements were performed two or three times until reproducible data were found.
3.2. Diffusion-ordered NMR spectroscopy
The samples were prepared in deionized water with conductivity near about 1 μS/cm. The concentration of the sample was maintained above the CMC of the surfactants. To observe self-diffusion of micelle 1H diffusion-ordered NMR spectroscopy (DOSY) measurements with solvent suppression were performed. The measurements were conducted on a Bruker DRX-500 spectrometer. The DOSY spectrum was acquired at 19.5 °C. To obtain the diffusion coefficient (D), data was analyzed with Topspin 1.3 software [37]. Consequently, the hydrodynamic radius of the aggregates can be calculated via the Stokes-Einstein equation:
| (16) |
where D is diffusion coefficient, η is solvent viscosity, Rh is the hydrodynamic radius, kB is Boltzmann's constant and T is temperature. The radii were then extrapolated to the zero concentration to estimate the aggregate size.
4. Results
4.1. Molar conductivity of ions and dissociated surfactants
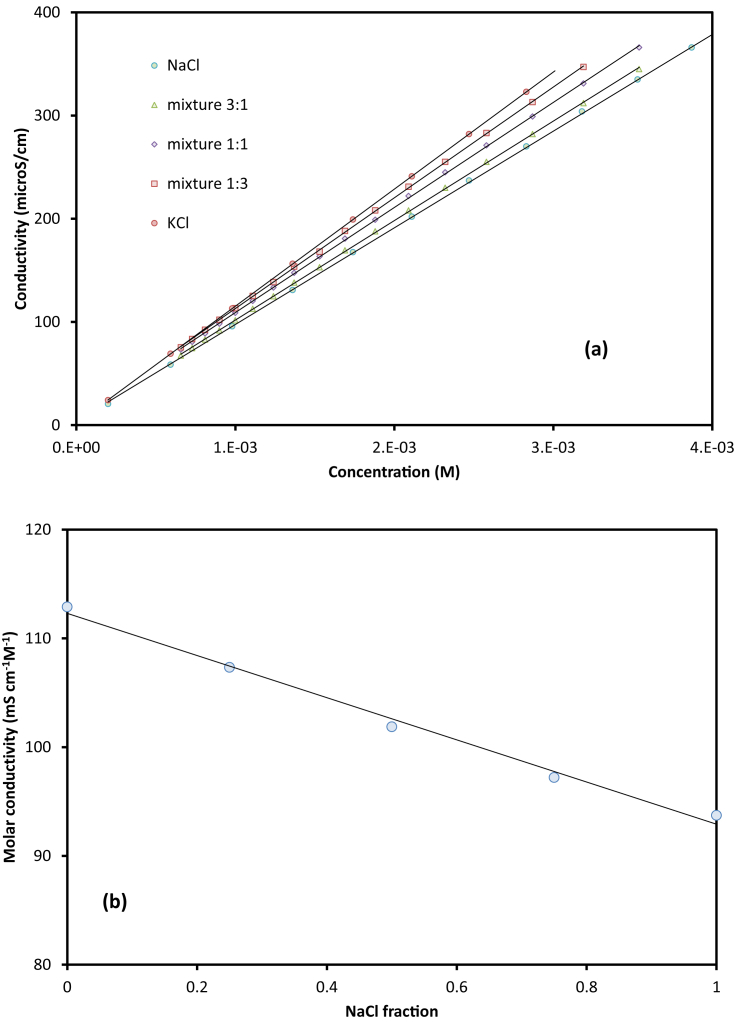
To obtain the limiting molar conductivity λo for surfactant and counter-ions, the following steps were applied in sequence. First, NaCl/KCl and their mixtures were analysed. The slopes of these data (Fig. 2a and b), λo were obtained for Na+, K+, and Cl−. Second, the molar conductivity of Br− was calculated from the average gradient of NaBr and KBr solutions. It can be seen that the deviation between the two calculations (from NaBr and KBr) is less than 0.3%. It should be noted that all concentration range was less than 4 mM, so that all ions can be assumed fully dissociated.
Fig. 2.
(a) Conductivity of NaCl and KCl solutions. (b) Molar conductivity as the function of NaCl fraction (of NaCl–KCl mixtures).
The increment between the cations (from Na+ to K+) was much higher than increment from Cl− to Br−, which is consistent with the reported λmo for these ions [38].
It can be seen that the obtained conductivities were larger than the literature values for the cations and smaller for the anions. It should be noted that the literature values were based on Cl− conductivity, at 66 mS cm−1 M−1 which was obtained by interpolating data from the Landolt-Börnstein Tabellen [39]. The deviation in Table 1 can be explained by the selection of the first referenced value. On the other hand, the differences between Cl− and Br− from the two sets were consistent. The value of λmo increased ∼2 mS cm−1 M−1, from Cl− to Br−. Since our study concerns with the impact of anions on the micellar formation, we employed both data for the subsequent analysis.
Table 1.
Limiting molar conductivities of surfactant monomers (mS cm−1 M−1), using anionic conductivity from this study and from Robison and Stokes data.
| Ionic species | This study | Previous anionic conductivity (18 °C) | Note |
|---|---|---|---|
| C14H29(CH3)3N+ | 30.649 ± 0.772 | 3.8 ± 1.0 | From C14H29(CH3)3N+ Cl− and C14H29(CH3)3N+ Br− solutions |
| C12H25(CH3)3N+ | 32.272 ± 0.500 | 5.5 ± 0.3 | From C12H25(CH3)3N+Cl− and C12H25(CH3)3N+Br− solutions |
| C10H21(CH3)3N+ | 32.607 ± 0.739 | 5.8 ± 0.5 | From C10H21(CH3)3N+Cl− and C10H21(CH3)3N+ Br− solutions |
The molar conductivities of alkyl trimethyl-ammonium were calculated from the slope within the lower limit (1.5 mM). Consequently, the average data from Cl− and Br− solutions were obtained for each surfactant. It can be seen that λmo was consistent between the corresponding two pairs (with standard deviations of less than 1 mS cm−1 M−1). The consistency also indicated that within the range, the association with halides is negligible. The values indicated an insignificant influence of alkyl chain on the molar conductivity of dissociated surfactants. The observation was consistent with the charged allocation within the surfactant.
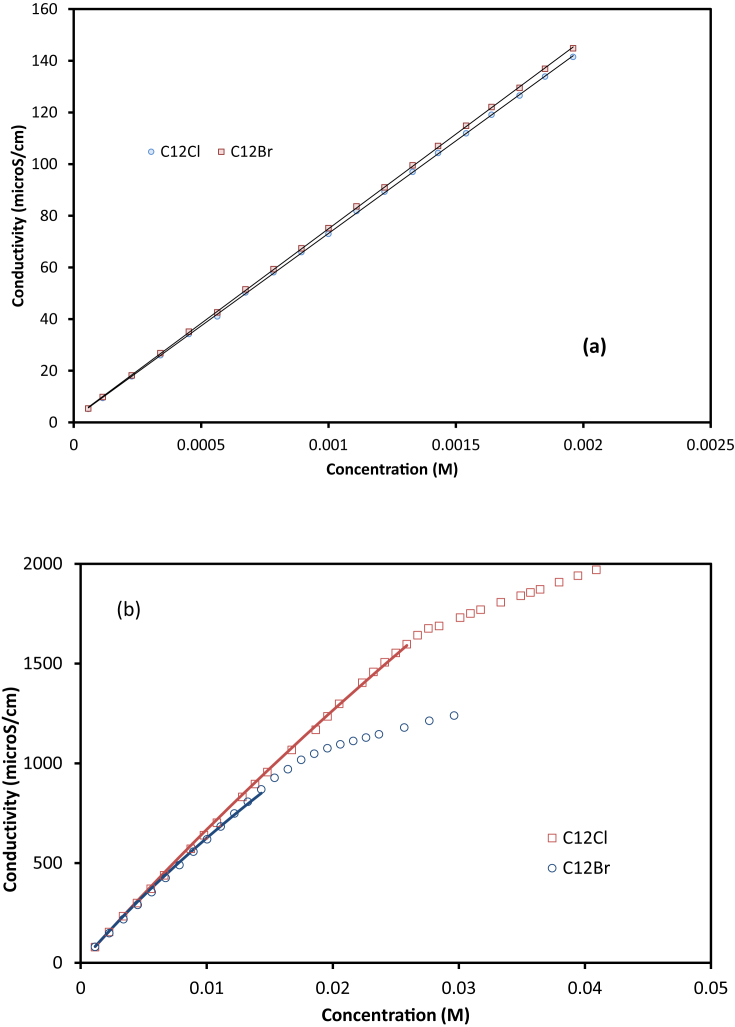
At higher concentrations, up to CMC (Fig. 3b), Cl− and Br− produced a clear deviation, which indicated a significant association. The values of ks were calculated by fitting to the simplified form of equations [14] and [15]. Since these equations use the sum of conductivity of dissociated surfactant and anion, the usage of either new or previous anionic conductivity in Table 2 yielded the same ks. In Fig. 3a, C12TABr has a higher conductivity than C12TAC, due to higher atomic conductivity (Table 2). However, Fig. 3b shows an opposite trend: C12TAB has a lower conductivity than C12TAC from 0.01 M. The relative change is due to association of at the higher concentration range, as quantified by ks in Table 3.
Fig. 3.
Modelling conductivities of C12H25(CH3)3N+: (a) lower concentration ranges for determining λmo (b) below CMC range for determining ks (lines are best-fitted predictions).
Table 2.
Limiting molar conductivities of ions (mS cm−1 M−1).
| Ionic species | This study (17.5 °C) | Note | From the literature, 18 °C [39] |
|---|---|---|---|
| Na+ | 53.123 | From mixtures of NaCl and KCl | 42.8 |
| K+ | 73.379 | 63.9 | |
| Cl- | 39.018 | 66.0 | |
| Br- | 41.365 ± 0.123 | From NaBr and KBr solutions | 68.0 |
Table 3.
Association constants, ks (M−1), between surfactant monomer and counter-ions.
| Surfactant | Br- | Cl- |
|---|---|---|
| C14H29(CH3)3N+ | - | 9.774 |
| C12H25(CH3)3N+ | 19.759 | 7.152 |
| C10H21(CH3)3N+ | 11.324 | 5.885 |
| (CH3)4N+ (from literature) | 0.83 | 0.29 |
The values of ks (Table 3) are consistent the physical trends. First, the selective impact of the anion is consistent with the current understanding. The increment is expected due to changes in water properties within the hydration shell of Br− over Cl−. It has been well-reported that the H-bonds switching dynamics of the hydration shell can vary significantly between halides [13]. As Br− hydration shell has a higher switching rate, with a vibrational relaxation time at 4.3 ps [40], the probability of pairing with bound water of surfactants increased. For tetramethylammonium (CH3)4N+, it has been shown that ks increased from 0.29 with Cl− to 0.83 M−1 with Br− [41]. The similar trend has been demonstrated with many cationic surfactants systems [7].
The second correlation with carbon length is also expected. As confirmed in the literature, increasing hydrocarbon length exponentially increases the number of bound water [5]. The increased number of bound water will increase the probability of interaction [42] with hydration shells of the anions (which are also isolated from water H-bonds network in the bulk). Consequently, ks decreased with decreased alkyl length. The interaction also explains the higher ks for Br−.
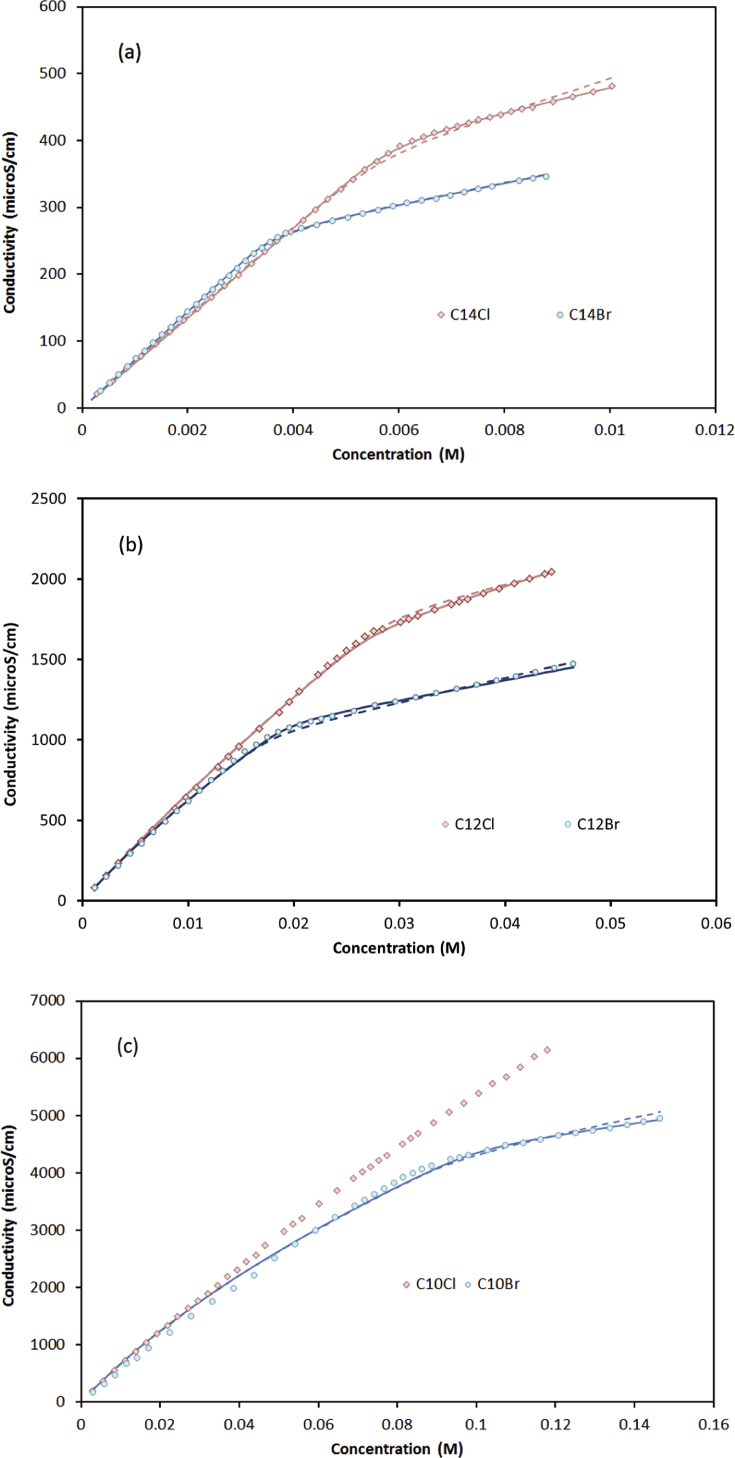
It should be noted that the two reactions (micellization in Eq. (2) and association in Eq. (4)) are competing against each other. Depending on the relativity of equilibrium constants, one reaction may start at lower concentration and dominate over the other reaction. The data for C14TA+Br− indicated that micellization dominates the system, as such ks was not measurable. On the opposite extreme, C10H21(CH3)3N+ Cl− has a dominant association, as shown in the next section.
The two short surfactants, C10H21(CH3)3N+ Cl− and C10H21(CH3)3N+ Br−, have a large transition width from monomer to micelles regions. Furthermore, the data of C10H21(CH3)3N+ Cl− demonstrated a small shift between the pre- and post-micellization regressions (Fig. 4c) and thus not sufficient for the fitting purpose. As a result, we could not get a reliable aggregation number for C10H21(CH3)3N+ Cl−.
Fig. 4.
Conductivity of CnTABr and CnTACl: (a) 14, (b) 12 and (c) 10 carbons. Broken lines present model with literature anionic conductivity, solid lines represent model with new anionic conductivity.
4.2. DOSY
Diffusion coefficients for the surfactants were measured at various concentrations above the CMC. An example of the fitting function is showed in Fig. 5.
Fig. 5.
A fitting function for the DOSY measurement of C14H29(CH3)3N+Cl− at 0.1M concentration.
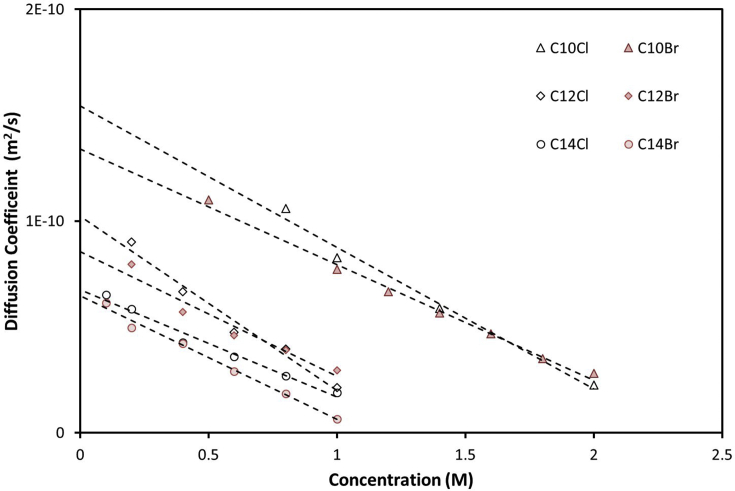
The obtained diffusion coefficients for the six surfactants are presented in Fig. 6. The aggregate sizes were obtained by extrapolation to zero concentration and tabulated in Table 4. The data will be used to verify the modelling results.
Fig. 6.
Diffusion coefficients estimated from DOSY.
Table 4.
Rh value obtained by extrapolating diffusion coefficient to zero concentration.
| Surfactants | Diffusion coefficient (m2/s) | Rh (nm) |
|---|---|---|
| C14H29(CH3)3N+ Br- | 6.49×10−11 | 3.25 |
| C14H29(CH3)3N+ Cl- | 6.74×10−11 | 3.13 |
| C12H25(CH3)3N+ Br- | 8.59×10−11 | 2.48 |
| C12H25(CH3)3N+ Cl- | 1.02×10−10 | 2.09 |
| C10H21(CH3)3N+ Br- | 1.33×10−10 | 1.82 |
| C10H21(CH3)3N+ Cl- | 1.55×10−10 | 1.37 |
5. Discussion
5.1. Critical micellar concentration
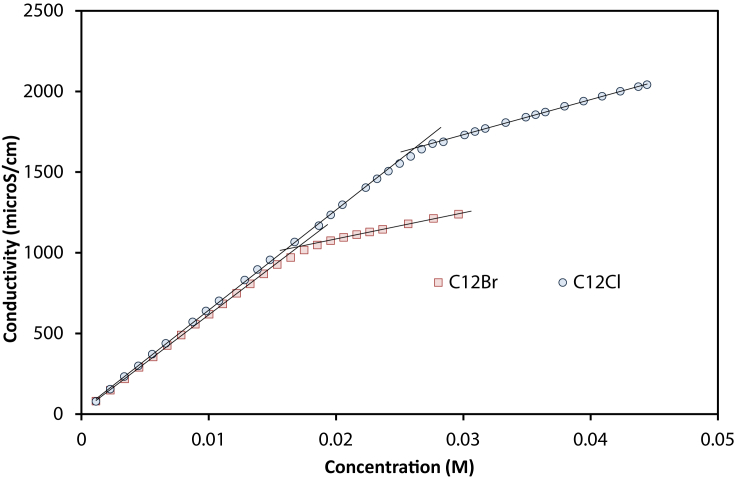
The CMC of surfactants were also obtained by linear regressions for all surfactants (see Fig. 7). As seen in Table 5, the obtained CMC is comparable with literature values. Our values are slightly different from the previously reported values due to the lower temperature. Most significantly, the two correlations with anions and alkyl length were consistent. The linear relationship between ln(CMC) and carbon number has been recognized for all ionic surfactants in the literature. Similarly, the anion can have a clear influence: Br− has lower CMC than Cl− [36]. The apparent CMC of Br− surfactant was much lower (∼30%) than that of the corresponding Cl− surfactant. The same ratio was reported with C14TACl/C14TABr [36], and C16TACl/C16TABr [43].
Fig. 7.
CMC determination of C12TACl and C12TABr.
Table 5.
CMC of alkyl-trimethyl ammonium halide (× 10−3 M).
| Surfactant | This study (Conductivity, 17 °C) | Literature value | Temperature |
|---|---|---|---|
| C14H29(CH3)3N+ Br- | 3.7 | 3.6 [44] 3.2 [45] 3.5 [20] 3.8 [36] |
20 °C 22 °C 24 °C 25 °C |
| C14H29(CH3)3N+ Cl- | 6.1 | 6 [46] 5.53 [47] 4.5 [20] 5.5 [36] |
25 °C 25 °C 25 °C 25 °C |
| C12H25(CH3)3N+ Br- | 18 | 14.4 [44] 15.5 [20] |
20 °C 25 °C |
| C12H25(CH3)3N+ Cl- | 25.8 | 21 [46] 21.5 [47] 22 [20] |
25 °C 25 °C 25 °C |
| C10H21(CH3)3N+ Br- | 64 | 64.3 [48] 65 [44] 58.8 [45] |
30 °C 20 °C 22 °C |
| C10H21(CH3)3N+ Cl- | 82 | 86.9 [47] | 25 °C |
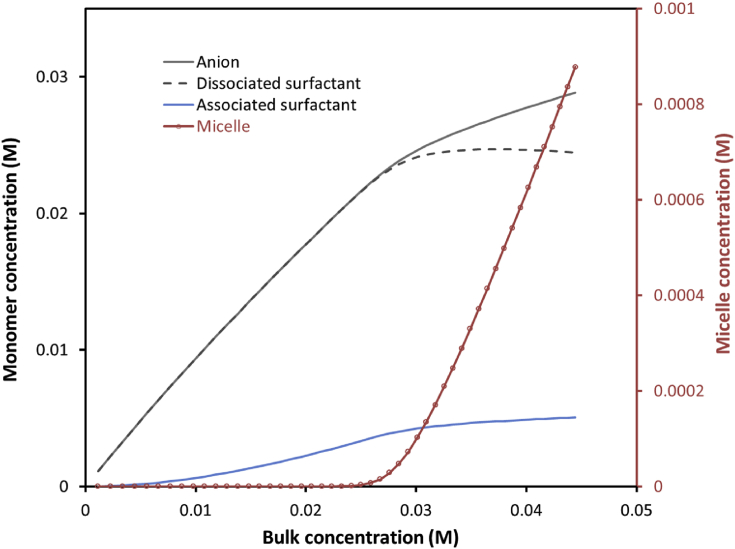
As recognized by Tanfold [4], CMC is a conveniently measurable quantity without detailed insights to the solution composition. Physically, micelles, associated/dissociated monomers, and dissociated anions co-exist over a large concentration range and need to be calculated via reaction constants. As seen in Fig. 3, the transition range can vary significantly from one surfactant system to another. Even the two extreme cases (C14TABr and C10TACl), at least 3 species coexist over the transition. From our model, the composition of all species can be obtained (example for C12TACl is shown in Fig. 8). It can be seen that micellar concentration remains very small in comparison with monomers and counter-ions. Consequently, our modelling is insensitive to λmi. The data also shows that associated surfactant decreases slightly over the CMC. However, the total monomer concentration (associated and dissociated) remains constant.
Fig. 8.
Composite concentrations of C12TACl (the unit of micellar concentration is microM).
5.2. Aggregation number
It can be seen that the limiting conductivity of anions affected the aggregation and ionic constants (Table 6), not the fitness of the model (Fig. 4). More importantly, the correlations with alkyl branch and anion were the same for both models. A critical finding in the modelling results was that m was much smaller than reported values in the literature (Table 7) and follows the opposite trend. The discrepancy can be explained by the theoretical interpretation.
Table 6.
Aggregation parameters.
| Surfactants | Using new conductivity |
Using previous conductivity |
||||
|---|---|---|---|---|---|---|
| m | n | km(Mm+n−1) | m | n | km(Mm+n−1) | |
| C14H29(CH3)3N+ Br- | 16 | 8 | 1.25×1054 | 14 | 8 | 1.59×1054 |
| C14H29(CH3)3N+ Cl- | 16 | 8 | 1.21×1049 | 14 | 8 | 3.35×1045 |
| C12H25(CH3)3N+ Br- | 20 | 11 | 3.14 ×1052 | 17 | 12 | 6.65×1049 |
| C12H25(CH3)3N+ Cl- | 20 | 7 | 9.79 ×1039 | 17 | 12 | 6.51×1042 |
| C10H21(CH3)3N+ Br- | 24 | 14 | 8.30×1042 | 23 | 16 | 5.58×1044 |
| C10H21(CH3)3N+ Cl- | - | - | - | - | - | - |
Table 7.
Micelle aggregation numbers (m) of alkyl trimethylammonium halides from the literature.
| Surfactant | m | Methods |
|---|---|---|
| C14H29(CH3)3NBr | 122 106 97 78 |
SANS at 10 °C [19] SANS at 20 °C [19] Fluorescence at 24 °C [20] SANS at 25 °C [21] |
| C14H29(CH3)3NCl | 82 55 |
Fluorescence at 15 °C [20] SANS at 25 °C [21] |
| C12H25(CH3)3NBr | 71 73 82 65 47 |
SANS in presence of additional NaBr [22] TRFQ [22] SSF [23] Fluorescence at 20 °C [20] SANS at 25 °C [21] |
| C12H25(CH3)3NCl | 63 60 56 32 |
SANS in presence of additional NaCl [22] TRFQ [22] Fluorescence at 15.3 °C [20] SANS at 25 °C [21] |
| C10H21(CH3)3NBr | 48 45 38 63 |
DLS 25 °C, in presence of 0.5 M NaBr [24] NF with partially deuterated alkyl [25] Theoretical prediction [26] SSF [23] |
Previously, the aggregation numbers [22] were calculated with simplifying assumptions on the “core” and “shell” sections of the micelles. Most these studies assumed that the “core” contains no water. The “dry core” assumption led to an overestimation of m. The assumption is been questioned by other studies. For example, some studies estimated up to 10 to 15 water molecules per surfactant [16], and up to ∼50% of the micellar volume [5]. If the core has a high water content, then m will be significantly less for the same volume.
We can reconcile the aggregation number in Table 6 and hydrodynamic size by considering the size of the head group. A simulation has revealed that the trimethyl ammonium (TA) group has a hydration radius of ∼0.625 nm [49]. Consequently, a C14TA+ micelle with a radius of 3.25 nm would have an inner radius (radius of the core in Fig. 1a) of 2 nm. The area of such a sphere is 50 nm2. With a cross-section area of TA group at 1.23 nm2, the “shell” can accommodate a maximum of 41 head-groups only. This maximum has not accounted for the space occupied by counter-ions (with a hydration radius between 0.3 to 0.4 nm) nor the bound water in the shell [16]. For trimethylammonium halides, the dielectric spectra have confirmed that the ionic association followed the solvent-shared type [16], which means there is a significant number of water between the associated pairs. Furthermore, it has been demonstrated that the hydrodynamic shear layer of micelles should include the Stern layer [50]. Hence, the actual aggregation should be much less than 41. An aggregation number of ∼20 surfactants is more reasonable.
The decreasing trend from the literature and DOSY analysis (Table 4) can be explained by the relative quantity between monomer and micelle. Above CMC, the DOSY spectra contain signals from both micelles and monomeric surfactants. The total concentration of monomeric surfactants remains around CMC values. As the alkyl chain gets shorter, the CMC increased and thus the signal from monomers gets more dominant. Consequently, the obtained hydrodynamic radius was reduced. Replacing Br with Cl also increased the CMC and lead to a similar effect. The evidence was clearest with C10TABr and C10TACl. With the length of C10H21 at ∼ 0.8 nm and hydration radius of TA group at 0.625 nm, a hydrodynamic radius of 1.82 nm is more consistent with a monomeric surfactant than a micelle. To precisely model the hydrodynamic radius of mixed micelles/monomer, one would require more information on the diffusion of the electrical layer [34] and mutual diffusion coefficients [51].
In summary, a volume analysis based on the head-group and DOSY indicated a maximum aggregation of 41 of trimethyl-ammonium surfactants. Hence, the obtained m via the model is physically feasible. The higher m in the literature might come from the assumption on the water content of the micellar core. Furthermore, these studies employed polar probes. As discussed earlier, the possibility of the probe penetrating the micelles, even the core, remains debatable [17]. More critically, these polar probes might interfere with ionic binding and potentially affect the aggregation. It should be noted that the previous model, with the electrophoretic and relaxation effects on C12TABr [52] and C12TACl [36], employed larger aggregation numbers and excluded the formation of associated monomer. With the new values, the influence of these interactions can be re-quantified.
5.3. Micellar structure and formation
The most significant, and somewhat counter-intuitive, result in Table 6 was that m increases with decreasing carbon length and independent on counter-ions. The values of n were mostly 50% of m for both anions. The binding constants, ks and km, of Br− are much higher than those of Cl−. The usage of different anionic conductivities does not affect these trends.
The influence of counter-ions on parameters validated the micellar conceptual structures. First, the ionic arrangement within micelles is governed by electrostatic attraction with the head and available space within the micelles. Since Cl− and Br− have a similar hydration size, ∼ 0.3 nm [53], their hydration volume and thus values of n should be very similar. The values of m and n indicated that anions have an insignificant role in determining the micellar composition. On the other hand, the CMC with Br− was dramatically lower than that with Cl−, which was also evidenced by the increased equilibria constants. Hence, the properties (not quantity) of the water in the hydrated anions play a critical role. Various studies have indicated the increased activities of the hydration shell of Br-over Cl−, including the rate of water bonds switching [40], the strength of electric fields [53] and the average orientated angle [54]. Consequently, Br− has a higher probability to associate with bound water, of both monomer and micelles, than Cl−. A similar trend was observed on the interaction between hydrated halides and the bound water of alcohol [42]. As a result, both ks and km of Br− are higher.
The same mechanism readily explains the correlation with the carbon length. With decreasing length, the number of bound water decreases, and the probability of association decreases. As a result, both ks and km decrease with the decreasing surfactant length. It should be noted that the number of bound water is not a linear function of carbon length. Indeed, the accumulative effect due to the interactions between neighbouring bound waters has been demonstrated in the literature [5, 11]. Simulations have qualitatively confirmed that the hydrophobic hydration is enhanced at the end of surfactant tails and weakened near the middle part of surfactants [15]. Consequently, the correlation between reaction constants and carbon length is highly non-linear.
In summary, the modelling results indicated that anions and alkyl length affect the micellar formation via their binding probability rather than their molecular volumes. The ionic pairing probabilities (measured by ks and km) are governed by water interactions. The mechanism overwhelmingly supports the 2nd conceptual structure over the 1st one.
6. Conclusion
In this study, we developed a model to calculate the aggregation number of surfactants. The model, which incorporates both association and micellization, was successfully validated for a series of alkyl trimethylammonium halides. The results revealed systematic insights into the molecular origins of the micellar formation. First, the association constant between monomer and counter-ion increased significantly from Cl− to Br−. Second, the aggregation number increased with decreasing carbon length. Third, the degree of ionisation remains mostly 50% for all surfactant/anion systems.
The experimental and modelling results confirmed the role of reaction equilibria, and the “ion-paring/hydration” micellization concept. Specifically, the reaction constants are controlled by the “bound” water around surfactants and the hydration shell of the anion. As a result, both counter-ions and carbon length have a deterministic role on the equilibria constants. On the other hand, the role of their molecular size seems less significant. The impacts of these two factors were systematically validated in this study. The model provides a consistent description of the micellar formation of trimethyl-ammonium halides and can be extended to other ionic surfactants.
Declarations
Author contribution statement
Komol Sharker: Performed the experiments; Analyzed and interpreted the data.
Shin-ichi Yusa: Conceived and designed the experiments; Contributed reagents, materials, analysis tools or data; Analyzed and interpreted the data.
Minh Chi Phan: Conceived and designed the experiments; Analyzed and interpreted the data; Wrote the paper.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- 1.Rosen M.J., Kunjappu J.T. Wiley; 2012. Surfactants and Interfacial Phenomena. [Google Scholar]
- 2.McBain J.W., Cornish E.C.V., Bowden R.C. CCXV.—studies of the constitution of soap in solution: sodium myristate and sodium laurate. J. Chem. Soc. Trans. 1912;101:2042–2056. [Google Scholar]
- 3.Hartley G.S. Hermann; Paris: 1936. Aqueous Solutions of Paraffin-Chain Salts: a Study in Micelle Formation.https://trove.nla.gov.au/work/32755308?q&sort=holdings+desc&_=1524720615581&versionId=210958879 [Google Scholar]
- 4.Tanford C. Micelle shape and size. J. Phys. Chem. 1972;76:3020–3024. [Google Scholar]
- 5.Long J.A., Rankin B.M., Ben-Amotz D. Micelle structure and hydrophobic hydration. J. Am. Chem. Soc. 2015;137:10809–10815. doi: 10.1021/jacs.5b06655. [DOI] [PubMed] [Google Scholar]
- 6.Maibaum L., Dinner A.R., Chandler D. micelle formation and the hydrophobic effect. J. Phys. Chem. B. 2004;14:6778–6781. [Google Scholar]
- 7.Geng Y., Romsted L.S., Menger F. Specific ion pairing and interfacial hydration as controlling factors in gemini micelle morphology. Chemical trapping studies. J. Am. Chem. Soc. 2006;128:492–501. doi: 10.1021/ja056807e. [DOI] [PubMed] [Google Scholar]
- 8.Menger F.M., Jerkunica J.M., Johnston J.C. The water content of a micelle interior. The Fjord vs. Reef models. J. Am. Chem. Soc. 1978;100:4676–4678. [Google Scholar]
- 9.Du Q., Freysz E., Shen Y.R. Surface vibrational spectroscopic studies of hydrogen bonding and hydrophobicity. Science (80-.) 1994;264:826–828. doi: 10.1126/science.264.5160.826. [DOI] [PubMed] [Google Scholar]
- 10.Moore F.G., Richmond G.L. Integration or segregation: how do molecules behave at oil/water interfaces? Acc. Chem. Res. 2008;41:739–748. doi: 10.1021/ar7002732. [DOI] [PubMed] [Google Scholar]
- 11.Davis J.G., Rankin B.M., Gierszal K.P., Ben-Amotz D. On the cooperative formation of non-hydrogen-bonded water at molecular hydrophobic interfaces. Nat. Chem. 2013;5:796–802. doi: 10.1038/nchem.1716. [DOI] [PubMed] [Google Scholar]
- 12.Bagchi B. Water dynamics in the hydration layer of biomolecules and self-assembly. Chem. Rev. 2005;105:3197–3219. doi: 10.1021/cr020661+. [DOI] [PubMed] [Google Scholar]
- 13.Heisler I.A., Meech S.R. Low-frequency modes of aqueous alkali halide solutions: glimpsing the hydrogen bonding vibration. Science (80-.) 2010;327 doi: 10.1126/science.1183799. http://science.sciencemag.org/content/327/5967/857.abstract 857 LP-860. [DOI] [PubMed] [Google Scholar]
- 14.Pal S., Bagchi B., Balasubramanian S. Hydration layer of a cationic micelle, C10TAB: structure, rigidity, slow reorientation, hydrogen bond lifetime, and solvation dynamics. J. Phys. Chem. B. 2005;109:12879–12890. doi: 10.1021/jp0510793. [DOI] [PubMed] [Google Scholar]
- 15.Jimenez-angele F., Firoozabadi A. Hydrophobic hydration and the effect of NaCl salt in adsorption of hydrocarbons and surfactants on hydrate surface. ACS Cent. Sci. 2018 doi: 10.1021/acscentsci.8b00076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Baar C., Buchner R., Kunz W. Dielectric relaxation of cationic surfactants in aqueous solution. 2. Solute relaxation. J. Phys. Chem. B. 2001;105:2914–2922. [Google Scholar]
- 17.Lebedeva N., Zana R., Bales B.L. A reinterpretation of the hydration of micelles of dodecyltrimethylammonium bromide and chloride in aqueous solution. J. Phys. Chem. B. 2006;110:9800–9801. doi: 10.1021/jp060516q. [DOI] [PubMed] [Google Scholar]
- 18.Maibaum L., Dinner A.R., Chandler D. 2004. Micelle Formation and the Hydrophobic Effect; pp. 6778–6781. [Google Scholar]
- 19.Gorski N., Kalus J. Temperature dependence of the sizes of tetradecyltrimethylammonium bromide micelles in aqueous solutions. Langmuir. 2001;17:4211–4215. [Google Scholar]
- 20.Malliaris A., Le Moigne J., Sturm J., Zana R. Temperature dependence of the micelle aggregation number and rate of intramicellar excimer formation in aqueous surfactant solutions. J. Phys. Chem. 1985;89:2709–2713. [Google Scholar]
- 21.Berr S., Jones R.R.M., Johnson J.S. Effect of counterion on the size and charge of alkyltrimethylammonium halide micelles as a function of chain length and concentration as determined by small-angle neutron scattering. J. Phys. Chem. 1992;96:5611–5614. [Google Scholar]
- 22.Griffiths P.C., Paul A., Heenan R.K., Penfold J., Ranganathan R., Bales B.L. Role of counterion concentration in determining micelle aggregation: evaluation of the combination of constraints from small-angle neutron scattering, electron paramagnetic resonance, and time-resolved fluorescence quenching. J. Phys. Chem. B. 2004;108:3810–3816. [Google Scholar]
- 23.Menger F.M., Shi L. Exposure of self-assembly interiors to external elements. A kinetic approach. J. Am. Chem. Soc. 2006;128:9338–9339. doi: 10.1021/ja062807i. [DOI] [PubMed] [Google Scholar]
- 24.Geer R.D., Eylar E.H., Anacker E.W. Dependence of micelle aggregation number on polar head structure. J. Phys. Chem. 1971;35:369–374. [Google Scholar]
- 25.Hargreaves R., Bowron D.T., Edler K. Atomistic structure of a micelle in solution determined by wide Q-range neutron diffraction. J. Am. Chem. Soc. 2011;133:16524–16536. doi: 10.1021/ja205804k. [DOI] [PubMed] [Google Scholar]
- 26.Nomura H., Koda S., Matsuoka T., Hiyama T., Shibata R., Kato S. Study of salt effects on the micelle-monomer exchange process of octyl-, decyl-, and dodecyltrimethylammonium bromide in aqueous solutions by means of ultrasonic relaxation spectroscopy. J. Colloid Interface Sci. 2000;230:22–28. doi: 10.1006/jcis.2000.7067. [DOI] [PubMed] [Google Scholar]
- 27.Pisárčik M., Devínsky F., Pupák M. Determination of micelle aggregation numbers of alkyltrimethylammonium bromide and sodium dodecyl sulfate surfactants using time-resolved fluorescence quenching. Open Chem. 2015;13:922–931. [Google Scholar]
- 28.Bales B.L., Zana R. Characterization of micelles of quaternary ammonium surfactants as reaction media I: dodeclytrimethylammonium bromide and chloride. J. Phys. Chem. B. 2002;106:1926–1939. [Google Scholar]
- 29.Shanksf P.C., Franses E.I. Estimation of micellization parameters of aqueous sodium dodecyl sulfate from conductivity data. J. Phys. Chem. 1992;96:1794–1805. [Google Scholar]
- 30.Paul B.C., Islam S.S., Ismail K. 1998. Effect of Acetate and Propionate Co-ions on the Micellization of Sodium Dodecyl Sulfate in Water. [Google Scholar]
- 31.Dar A.A., Bhat M.A., Rather G.M. Application of mixed electrolyte mass-action model to the micellization of 1-dodecylpyridinium chloride in aqueous medium. Colloids Surfaces A Physicochem. Eng. Asp. 2004;248:67–74. [Google Scholar]
- 32.Vink H. Electrolytic conductivity of mixed electrolyte solutions. Berichte Der Bunsengesellschaft Für Phys. Chemie. 1994;98:1039–1045. [Google Scholar]
- 33.Plewa A., Kalita M., Siekierski M. Estimation of ion pair formation constants of lithium salts in mixtures of glymes and 1,4-dioxane. Electrochim. Acta. 2007;53:1527–1534. [Google Scholar]
- 34.Danov K.D., Kralchevsky P.A., Ananthapadmanabhan K.P. Micelle–monomer equilibria in solutions of ionic surfactants and in ionic–nonionic mixtures: a generalized phase separation model. Adv. Colloid Interface Sci. 2014;206:17–45. doi: 10.1016/j.cis.2013.02.001. [DOI] [PubMed] [Google Scholar]
- 35.Anacker E.W., Geer R.D. Dependence of micelle aggregation number on polar head structure. II. Light scattering by aqueous solutions of decyldiethylammonium bromide and related heterocyclic surfactants. J. Colloid Interface Sci. 1971;35:441–446. [Google Scholar]
- 36.Durand-Vidai S., Jardat M., Dahirel V., Bernard O., Perrigaud K., Turq P. Determining the radius and the apparent charge of a micelle from electrical conductivity measurements by using a transport theory: explicit equations for practical use. J. Phys. Chem. B. 2006;110:15542–15547. doi: 10.1021/jp062956n. [DOI] [PubMed] [Google Scholar]
- 37.Groves P. Diffusion ordered spectroscopy (DOSY) as applied to polymers. Polym. Chem. 2017;8:6700–6708. [Google Scholar]
- 38.Benson G.C., Gordon A.R. A reinvestigation of the conductance of aqueous solutions of potassium chloride, sodium chloride, and potassium bromide at temperatures from 15° to 45°C. J. Chem. Phys. 1945;13:473–474. [Google Scholar]
- 39.Robinson R.A., Stokes R.H. second ed. Butterworths; London: 1965. Electrolyte Solutions. [Google Scholar]
- 40.Timmer R.L.A., Bakker H.J. Vol. 113. 2009. Hydrogen Bond Fluctuation of the Hydration Shell of the Bromide Anion; p. 6104. [DOI] [PubMed] [Google Scholar]
- 41.Geng Y., Romsted L.S. Ion pair formation in water. Association constants of bolaform, bisquaternary ammonium, electrolytes by chemical trapping. J. Phys. Chem. B. 2005;109:23629–23637. doi: 10.1021/jp0546195. [DOI] [PubMed] [Google Scholar]
- 42.Rankin B.M., Hands M.D., Wilcox D.S., Fega K.R., Slipchenko L.V., Ben-Amotz D. Interactions between halide anions and a molecular hydrophobic interface. Faraday Discuss. 2013;160:255–270. doi: 10.1039/c2fd20082a. [DOI] [PubMed] [Google Scholar]
- 43.Zhang C., Geng T., Jiang Y., Zhao L., Ju H., Wang Y. Impact of NaCl concentration on equilibrium and dynamic surface adsorption of cationic surfactants in aqueous solution. J. Mol. Liq. 2017;238:423–429. [Google Scholar]
- 44.Buckingham S.A., Garvey C.J., Warr G.G. Effect of head-group size on micellization and phase behavior in quaternary ammonium surfactant systems. J. Phys. Chem. 1993;97:10236–10244. [Google Scholar]
- 45.Gilányi T., Varga I., Stubenrauch C., Mészáros R. Adsorption of alkyl trimethylammonium bromides at the air/water interface. J. Colloid Interface Sci. 2008;317:395–401. doi: 10.1016/j.jcis.2007.10.007. [DOI] [PubMed] [Google Scholar]
- 46.Mehta S.K., Bhasin K.K., Dham S., Singla M.L. Micellar behavior of aqueous solutions of dodecyldimethylethylammonium bromide, dodecyltrimethylammonium chloride and tetradecyltrimethylammonium chloride in the presence of α-, β-, HPβ- and γ-cyclodextrins. J. Colloid Interface Sci. 2008;321:442–451. doi: 10.1016/j.jcis.2008.02.030. [DOI] [PubMed] [Google Scholar]
- 47.Roger G.M., Bernard O., Perger P.T., Bes M., Turq P. 2008. Interpretation of Conductivity Results from 5 to 45 ° C on Three Micellar Systems below and above the CMC Interpretation of Conductivity Results from 5 to 45 ° C on Three Micellar Systems below and above the CMC; pp. 16529–16538. [DOI] [PubMed] [Google Scholar]
- 48.Bakshi M.S. Micelle formation by sodium perfluorooctanoate and decyltrimethylammonium bromide in 18-crown-6+beta-cyclodextrin plus water systems. J. Incl. Phenom. Macrocycl. Chem. 1999 [Google Scholar]
- 49.Garcia-Tarrés L., Guardia E. Hydration and dynamics of a tetramethylammonium ion in water: a computer simulation study. J. Phys. Chem. B. 1998;102:7448–7454. [Google Scholar]
- 50.Stigter D. Micelle formation by ionic surfactants. III. Model of stern layer, ion distribution, and potential fluctuations. J. Phys. Chem. 1975;79:1008–1014. [Google Scholar]
- 51.Galantini L., Giampaolo S.M., Mannina L., Pavel N.V., Viel S. Study of intermicellar interactions and micellar sizes in ionic micelle solutions by comparing collective diffusion and self-diffusion coefficients. J. Phys. Chem. B. 2004;108:4799–4805. [Google Scholar]
- 52.Jardat M., Durand-Vidal S., Da Mota N., Turq P. Transport coefficients of aqueous dodecyltrimethylammonium bromide solutions: comparison between experiments, analytical calculations and numerical simulations. J. Chem. Phys. 2004;120:6268–6273. doi: 10.1063/1.1652427. [DOI] [PubMed] [Google Scholar]
- 53.Smith J.D., Saykally R.J., Geissler P.L. The effects of dissolved halide anions on hydrogen bonding in liquid water. J. Am. Chem. Soc. 2007;129:13847–13856. doi: 10.1021/ja071933z. [DOI] [PubMed] [Google Scholar]
- 54.Soper A.K., Weckström K. Ion solvation and water structure in potassium halide aqueous solutions. Biophys. Chem. 2006;124:180–191. doi: 10.1016/j.bpc.2006.04.009. [DOI] [PubMed] [Google Scholar]