Anisotropic Singlet Fission in Single Crystalline Hexacene

Summary

Singlet fission is known to improve solar energy utilization by circumventing the Shockley-Queisser limit. The two essential steps of singlet fission are the formation of a correlated triplet pair and its subsequent quantum decoherence. However, the mechanisms of the triplet pair formation and decoherence still remain elusive. Here we examined both essential steps in single crystalline hexacene and discovered remarkable anisotropy of the overall singlet fission rate along different crystal axes. Since the triplet pair formation emerges on the same timescale along both crystal axes, the quantum decoherence is likely responsible for the directional anisotropy. The distinct quantum decoherence rates are ascribed to the notable difference on their associated energy loss according to the Redfield quantum dissipation theory. Our hybrid experimental/theoretical framework will not only further our understanding of singlet fission, but also shed light on the systematic design of new materials for the third-generation solar cells.

Graphical Abstract

Highlights

• •Remarkable anisotropy of the overall singlet fission along different crystal axes
• •The correlated triplet pair emerges on the same timescale along both crystal axes
• •The quantum decoherence is predominantly driven by electron-phonon coupling
• •The anisotropic decoherence is due to the directional difference of its energy loss

Spectroscopy; Theoretical Photophysics; Quantum Phenomena

Introduction

Singlet fission has recently attracted extensive attention from both experimentalists (Busby et al., 2015, Chan et al., 2011, Chan et al., 2012, Congreve et al., 2013, Musser et al., 2015, Walker et al., 2013) and theoreticians (Berkelbach et al., 2013a, Berkelbach et al., 2013b, Berkelbach et al., 2014, Tiago et al., 2003, Yost et al., 2014, Zimmerman et al., 2010, Zirzlmeier et al., 2015), since it has the potential to circumvent the Shockley-Queisser limit for solar energy utilization. Many materials have exhibited singlet fission, and they range from small molecules to polymers, and from isolated molecules, thin films, to polycrystalline materials (Burdett et al., 2010, Busby et al., 2014, Busby et al., 2015, Cook et al., 2016, Johnson et al., 2010, Jundt et al., 1995, Katoh et al., 1997, Marciniak et al., 2009, Michl et al., 2007, Najafov et al., 2010, Pensack et al., 2016, Schwob and Williams, 1972, Takeda et al., 1996, Tayebjee et al., 2013, Walker et al., 2013, Watanabe et al., 2006, Wen et al., 2013, Wilson et al., 2011, Zenz et al., 1999). Singlet fission is a spin-conserving process, in which a photo-generated singlet exciton is converted into two individual triplet excitons (Smith and Michl, 2010). This unique photophysical phenomenon is usually considered to proceed in two steps, namely, the formation of a correlated triplet pair, ¹(T₁T₁), and its subsequent quantum decoherence to engender a decoupled triplet dimer, T₁+T₁. A generic model often employed to describe the mechanism of singlet fission is given by (Merrifield et al., 1969):

$$S_0+S_1\stackrel{k_F}{\to }{}^1\left(T_1{T}_1\right)\stackrel{k_Q}{\to }{T}_1+T_1$$ (Equation 1)

where S₀ is a ground state, S₁ is a singlet excited state, and k_F and k_Q denote the rate constants for the formation of ¹(T₁T₁) and its quantum decoherence, respectively. Despite recent tremendous efforts, the mechanisms of these two constituent steps of singlet fission (Bakulin et al., 2016, Chan et al., 2011, Chan et al., 2012, Miyata et al., 2017, Musser et al., 2015, Stern et al., 2017) are still not well understood.

Previous studies were primarily focused on the first step (Berkelbach et al., 2013b, Chan et al., 2013, Monahan and Zhu, 2015, Schwerin et al., 2010, Smith and Michl, 2010, Yost et al., 2014, Zimmerman et al., 2010, Zimmerman et al., 2011) and have invoked three mechanisms so far to rationalize the formation of ¹(T₁T₁). They are the direct mechanism (Zimmerman et al., 2010, Zimmerman et al., 2011, Zimmerman et al., 2013), the charge-transfer (CT)-mediated mechanism (Beljonne et al., 2013, Busby et al., 2015, Chan et al., 2013, Monahan and Zhu, 2015, Smith and Michl, 2010), and the sequential mechanism (Berkelbach et al., 2013b, Nakano et al., 2016). On the other hand, the quantum decoherence of ¹(T₁T₁) is rarely explored, particularly from the theoretical perspective (Casanova, 2018). As a matter of fact, quantum decoherence plays a key role in singlet fission by decoupling ¹(T₁T₁) through vibronic coupling. Therefore, a rapid decoherence of correlated ¹(T₁T₁) is highly desired for an efficient production of decoupled T₁+T₁, the final product of singlet fission. Otherwise, the reverse of the singlet fission could be mediated by fusion of two triplets via triplet-triplet annihilation (Yong et al., 2017), thereby decreasing the photon-to-exciton conversion efficiency. The fundamental driving force for the quantum decoherence of ¹(T₁T₁) is its interaction with its dissipative environment, which is typically described by a thermalized phonon path at finite temperature (Tao, 2014). This system-environment interaction varies greatly from amorphous, or polycrystalline, to ordered crystalline structures. Singlet fission materials in the form of single crystal are anticipated to exhibit pronounced collective characteristics in molecular vibrations because of their ordered crystalline structures.

In this work, we investigated the quantum decoherence of ¹(T₁T₁) states in single crystalline hexacene by polarized transient absorption spectroscopy in conjunction with ab initio quantum mechanics simulations. Our results showed that both ¹(T₁T₁) and T₁+T₁ states are of anisotropic origin owing to triplet Davydov splitting in hexacene, leading to distinctive quantum decoherence rates along crystal a and b axes. This notable anisotropy can be principally ascribed to the difference on the energy gap between ¹(T₁T₁) and T₁+T₁ according to the Redfield quantum dissipation theory (Ishizaki and Fleming, 2009). Moreover, through our functional mode analysis, the anisotropic quantum decoherence is predominantly driven by some slow phonon modes with an effective frequency ω_p < 50 cm⁻¹.

Results

Singlet Davydov Splitting in Hexacene

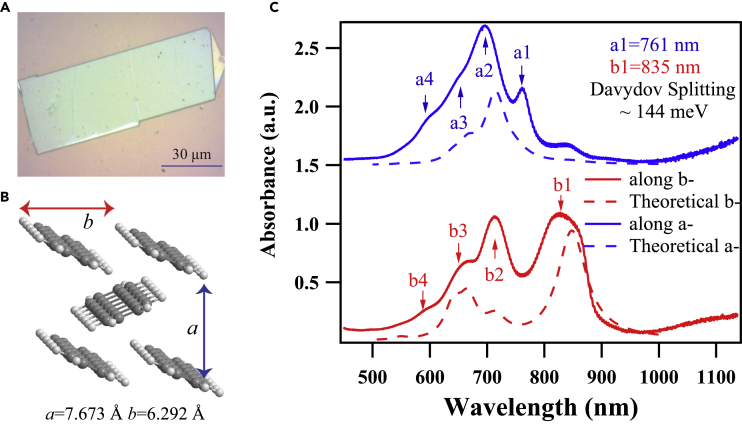
Hexacene single crystals used in our experiments were grown with physical vapor transport by following a recently developed method (Laudise et al., 1998, Watanabe et al., 2012). Their typical lateral size was on the order of 20 μm × 40 μm (Figure 1A), whereas their thickness was estimated to be 0.5 μm as detailed in Supplemental Information. The triclinic unit cell of hexacene shown in Figure 1B is defined by experimental in-plane crystal lattice constants (Watanabe et al., 2012) of a = 7.673 Å (long axis) and b = 6.292 Å (short axis) (Yamagata et al., 2011). A home-built microscopy was coupled with a tungsten-halogen light source for polarization-dependent optical transmission measurements of hexacene single crystal (Figure S1), and its polarization-resolved linear absorption spectra for the ab plane is presented on Figure 1C. Interestingly, the polarized measurements exhibit different absorption features along these two lattice axes. The lowest resonant peak at 835 nm was assigned to be the transition along the short b axis and is called b₁. On the other hand, the lowest transition at 761 nm was attributed to the transition along the long a axis and is named a₁. Apparently, b₁ is redshifted by 144 meV (1,160 cm⁻¹) with respect to a₁. This notable energy difference is due to the splitting of electronic excitations, the so-called singlet Davydov splitting (Davydov, 1948, Davydov, 2013) that stems from dipole-dipole interactions of two non-equivalent molecules in a hexacene unit cell (Chernikov et al., 2014, Hestand et al., 2015).

Figure 1.

Polarized Linear Absorption Spectra of Single Crystalline Hexacene

(A) Optical image of one of hexacene single crystals in our experiments.

(B) The schematic of a unit cell of hexacene single crystal.

(C) Polarization resolved linear absorption spectra in the a-b plane of hexacene single crystals along the a (upper) and b (lower) axes. The dotted curves are the theoretical results. The lowest transition along the a axis is located at 761 nm, whereas the lowest transition along the b axis is located at 835 nm. The singlet Davydov splitting exhibits a large value of 144 meV in hexacene single crystals.

Calculated Anisotropic Energy Levels in Hexacene Single Crystals

To explore the energy levels of all singlet-fission participating states in single crystalline hexacene, we performed computer simulations under periodic boundary conditions. Specifically, the single crystalline hexacene was modeled as a 9 × 9 × 3 supercell with a total of 20,412 atoms (Figure 2A). For a compromised balance between numerical efficiency and physical accuracy, the hybrid quantum mechanics/molecular mechanics approach (Warshel and Levitt, 1976) was adopted. A detailed description of the computational calculations can be found in Supplemental Information. As shown in Figure 2B, we denote the ground state, singlet excited state, charge-transfer state, correlated triplet pair, and decoupled triplet dimer as ¹(S₀S₀), ¹(S₁S₀), CT, ¹(T₁T₁), and T₁ + T₁, respectively, and their constituent spin configurations were illustrated in our previous studies (Elenewski et al., 2017a, Elenewski et al., 2017b). Geometry optimization was carried out on all spin states before their relative energies are determined. The only exception is ¹(S₁S₀)*, which assumes the same geometry as ¹(S₀S₀), such that $\Delta E\left(S_0{S}_0\to S_1{S}_0^{\ast }\right)$ reflects the vertical optical gap of hexacene crystal. In particular, the linear-response time-dependent density functional theory(Casida and Huix-Rotllant, 2012) was utilized to delineate the ¹(S₁S₀) and ¹(S₁S₀)* states, whereas the constrained density functional theory (CDFT) (Kaduk et al., 2012) was used to construct the reference orbitals needed for the multi-configurational CT, ¹(T₁T₁), and T₁ + T₁ states. As for the T₁ + T₁ dimer, a correction term of −k_bTln(3 × 3) ≈ −56 meV was added to account for the electronic spin entropy. Interestingly, we found that the ¹(T₁T₁) and T₁ + T₁ states along the short b axis are more thermodynamically stable than their counterparts along the long a axis, suggesting possible directional heterogeneity of quantum decoherence.

Figure 2.

Supercell and Energy Diagram of all Spin States for Hexacene Single Crystal

(A) 9 × 9 × 3 supercell of a hexacene single crystal. The tetramer designated as the singlet fission reaction center is highlighted. The molecular pair along the crystal a axis is colored blue, whereas the one along the crystal b axis is colored red. Moreover, all nearest neighbors of the tetramer are colored green.

(B) Energy diagram of all spin states participating in the single-fission process. The ground state, singlet excited state, charge-transfer state, correlated triplet pair, and uncorrelated triplet dimer are denoted as S₀S₀, S₁S₀, CT, ¹(T₁T₁), and T₁ + T₁, respectively. Their subscripts of a and b refer to the corresponding crystal axes. For instance, ¹(T_1aT_1a) represents a correlated triple pair whose constituents are along the [100] crystal axis.

Spectroscopic Signatures of Triplet Davydov Splitting

Transient absorption spectroscopy is a proven tool to investigate singlet fission in solution and in thin film. We have designed and constructed a polarization-resolved transient absorption microscopy to examine anisotropic singlet fission in hexacene single crystals. A detailed description of our experimental setup is presented in Figure S1. In short, a regenerative amplifier Ti:Sapphire laser system operating at 795 nm and 1 kHz repetition rate was used for our measurements. A small portion of the laser pulse was taken as a pump light, and its fluence on samples was kept below 200 μJ/cm² to avoid exciton-exciton annihilation (Figure S3) by using a half-wave plate and a polarizer. Another small part of the laser pulse with a pulse energy of ca. 1 μJ was focused onto a sapphire crystal to generate white light supercontinuum as a probe. The pump and probe beams were combined to become collinear with a pellicle beam splitter. They were then focused onto samples through a 10× microscope objective. The polarizations of the pump and probe beams were independently adjusted with two individual half-wave plates.

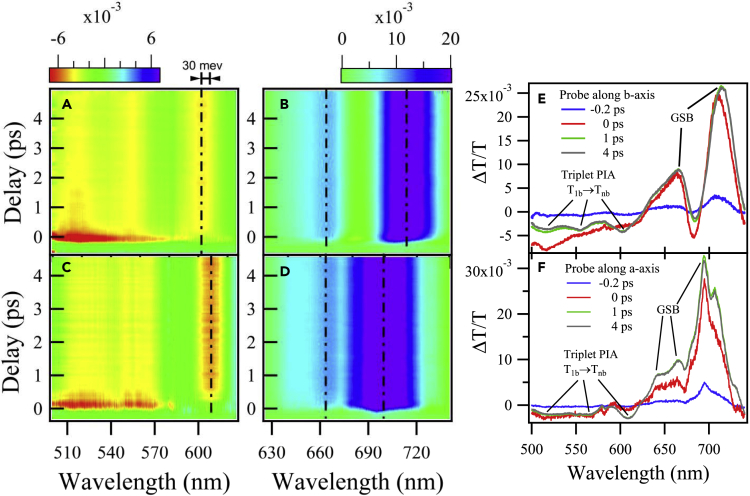
To explore anisotropic spectral kinetics in hexacene single crystals, polarization-resolved transient absorption measurements were performed along both axes using a pump along b axis under the near lowest photo-excitation of 795 nm. Their results were presented as pseudo-color plots of transient absorption spectra (ΔT/T) along b axis (Figures 3A and 3B) and a axis (Figures 3C and 3D). We chose two different color scales to highlight the difference on relaxation between the perturbed ground state and the newly populated excited states. The strong positive changes in ΔT/T between 729 and 620 nm were primarily due to the ground state bleaching and recovery. As expected, these positive responses ΔT/T in spectra are similar to those of the linear absorption spectra in hexacene as shown in Figure 1C. The negative spectral changes in ΔT/T between 496 and 620 nm were attributed to the photo-induced absorption of the excited states (Figures 3E and 3F). The transient spectra along both axes have broad, featureless, and short-lived bands from 496 to 577 nm (Figures 3E and 3F). The fast process dominated in this spectral region can be ascribed to the excited state absorption S₁ to a higher singlet state S_n (S₁→ S_n). By contrast, long-lived peaks appear in the range between 590 and 620 nm, as well as in the range between 508 and 544 nm. The latter even overlaps with the short-lived bands. We attributed these long-lived peaks to triplet transitions in hexacene. Again, a strong anisotropicity was observed on the triplet transitions. The peak along b axis is at 599 nm, whereas the one along a axis is redshifted by 9 nm. Since the redshift is an indicator of triplet Davydov splitting, we expect a coexistence of two kinds of triplet excitons with a splitting energy of 30 meV. Note that the correlated triplet pair, ¹(T₁T₁), is a dark state in our case and did not show appreciable spectral feature in the transient spectra. Therefore, the 9-nm redshift must be induced by the energy difference between the decoupled triplet dimers, i.e., T_1a + T_1a and T_1b + T_1b. Interestingly, T_1b + T_1b was found to be energetically more stable than T_1a + T_1a probably due to the stronger Davydov splitting between two spatially closer triplet excitons. Nevertheless, the long-lived spectral features between 500 and 620 nm were assigned to the T₁ → T_n transitions along both axes (Busby et al., 2014, Lee et al., 2013).

Figure 3.

Polarized Transient Absorption Spectra of Hexacene Single Crystal

(Left) Pseudo-color plots of polarized transient absorption spectra from hexacene single crystal excited at 795 nm along the b crystalline axis and probing along the b axis (A and B) and along the a axis (C and D). Note that the color scales for (B) and (D) (ground state bleaching, 620 nm–738 nm) and (A) and (C) (excited state absorption, 500 nm–626 nm) are comparison sake. For a better contrast, the color scale for (D) has been multiplied by 1.75. (Right) Transient absorption spectra at several time delays probing the b axis (E) and along the a axis (F).

Moreover, we measured the anisotropic transient spectra using pumps along both axes to further verify the independence of triplet Davydov splitting on pump polarization. The independence was confirmed by Figure S4, which does not manifest appreciable change when the pump polarization is varied. Furthermore, we changed the excitation wavelengths to 400 nm and again observed distinctive triplet Davydov splitting (Figure S12). Therefore, the anisotropy of the triplet states and their derivatives is an intrinsic property of crystalline hexacene regardless of external electromagnetic perturbations.

Singlet Fission Kinetics along the Long and Short Crystal Axes

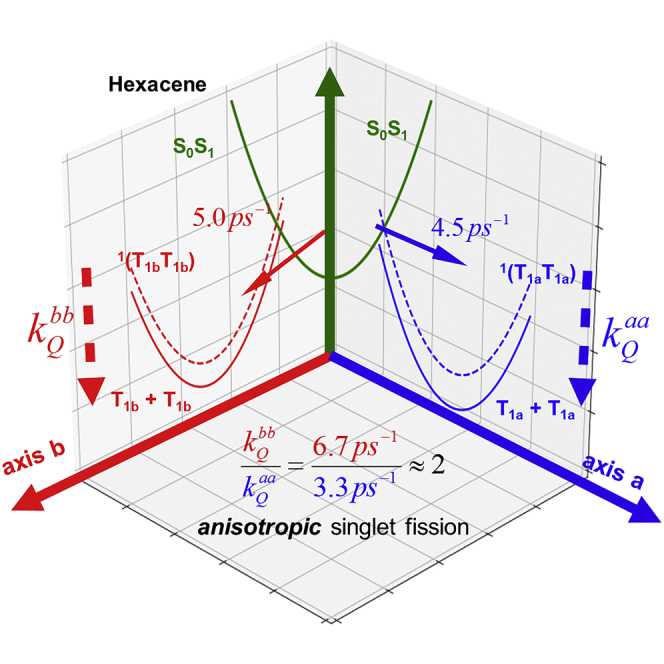
Figure 4 shows kinetic traces of hexacene in terms of ΔT/T after pumps are applied along b axis with the following wavelengths: (1) 525 ± 18.0 nm for S₁→S_n; (2) 599 ± 8.7 nm for T_1b →T_nb; (3) 608 ± 9.0 nm for T_1a →T_na. A kinetic model (Johnson et al., 2010, Monahan et al., 2017, Wan et al., 2018) was used to derive the generation and dissociation rates of ¹(T₁T₁) state from the experimental data shown in Figure 4. The detailed fitting procedure can be found in Supplemental Information. A global fitting of the kinetic traces affords the formation (k_F) and decoherence (k_Q) rates along b axis as k_{F, bb} = 4.5 ± 0.2 ps⁻¹ and k_{Q, bb} = 6.7 ± 0.2 ps⁻¹, respectively. Similarly, their counterparts along a axis are given by k_F,aa = 5.0 ± 0.2 ps⁻¹ and k_{Q, aa} = 3.3 ± 0.2 ps⁻¹. Apparently, k_F remains nearly unchanged, whereas k_Q has more than doubled after the probe polarization rotates from a axis to b axis. Once again, our experimental data suggest that the mechanism of singlet fission is of anisotropic nature in single crystalline hexacene.

Figure 4.

Kinetics Traces in the Transmission Change ΔT/T along the a and b Axes

(A and B) (A) At 525 ± 18.0 and 599 ± 8.7 nm probing along the b axis and (B) at 525 ± 18.0 and 608 ± 9.0 nm probing along the a axis, under 795 nm with a pump polarization along the b axis. Global fittings of the kinetic traces to the two-step model described in the context yield the generation and dissociation rates for the ¹(T₁T₁) along the b axis (k_F,b = 4.5 ± 0.2 ps⁻¹, k_Q,b = 6.7 ± 0.2 ps⁻¹) and the a axis (k_F,a = 5.0 ± 0.2 ps⁻¹, k_Q,a = 3.3 ± 0.2 ps⁻¹), respectively. The instrumental response function was 130 fs.

Discussion

Our studies of single crystalline hexacene have three main traits: (1) a large triplet Davydov splitting of 30 meV; (2) a homogeneous ¹(T₁T₁) formation rate regardless of molecular directionality; (3) a notable anisotropy of ¹(T₁T₁) quantum decoherence rate. We have also proposed a unified vibronic model for singlet fission by treating the formation of a correlated triplet pair and its quantum decoherence on the same footing using our non-adiabatic functional mode approach (Chen, 2014, Elenewski et al., 2017b). As clearly depicted in Scheme 1, the optical excitation results in anisotropic structural and dynamical properties for both the ¹(T₁T₁) and T₁ + T₁ states, allowing us to gain more insights into the intrinsic directional heterogeneity of triplet excitons in single crystalline hexacene.

Scheme 1.

Schematic for Anisotropic Singlet Fission in Hexacene Single Crystal

Anisotropic ¹(T₁T₁) states are formed along the short b and long a axes directly from the hot S₁S₀ state. The rate for quantum decoherence along the short b axis is almost twice that along the long a axis. ¹(T_1aT_1a) and ¹(T_1bT_1b) represent correlated triplet pair states along the a and b axes, whereas T_1a + T_1a and T_1b + T_1b are triplet states along the a and b axes.

Formation of ¹(T₁T₁) Directly from ¹(S₁S₀)^∗

The formation of ¹(T₁T₁) is generally considered as the rate-determining step of singlet fission under the assumption of ultrafast quantum decoherence of ¹(T₁T₁). Surprisingly, our results show that the formation of ¹(T₁T₁) outpaces its quantum decoherence in hexacene, making the overall singlet fission rate predominantly decided by the latter. More interestingly, the formation rates of ¹(T₁T₁) were found to be similar along b axis (k_{F, bb} = 4.5 ± 0.2 ps⁻¹) and a axis (k_F,aa = 5.0 ± 0.2 ps⁻¹). As previously discussed, the formation of ¹(T₁T₁) could proceed through the direct, the CT-mediated, and the sequential mechanisms. To reconcile which mechanism is responsible for the fast and isotropic formation of ¹(T₁T₁) in hexacene, we employed our functional mode vibronic theory that has been successfully applied to investigate singlet fission in tetracene and pentacene (Elenewski et al., 2017a, Elenewski et al., 2017b). If the direct mechanism is followed, ¹(T₁T₁) is formed without the aid of any CT intermediate. By contrast, the sequential mechanism demands a thermodynamically stable CT state with an energy lower than the hot ¹(S₁S₀)^∗. Similarly, the mediated mechanism entails a virtual CT state, whose energy should be close to ¹(S₁S₀)^∗ for an ideal vibrational wave-function mixing between them. Since our calculated energy diagram in Figure 2 manifests a relatively large energy gap of over 0.25 eV between the CT and ¹(S₁S₀)^∗ states, both the sequential and mediated mechanisms should be effectively blocked. In this regard, we assume that the ¹(T₁T₁) pair production in single crystalline hexacene only proceeds through the direct mechanism (Elenewski et al., 2016, Elenewski et al., 2017b):

$$k_F=\frac{J^2}{{ћ}^2}\underset{-\infty }{\overset{+\infty }{\int }}{e}^{\frac{i\left(\Delta G_0+\lambda -ћ\text{Ω}n\left(0\right)e^{-\Gamma \left|t\right|}\right)t}{ћ}}{e}^{-\frac{1}{2}{\text{Ω}}^2{t}^2}{e}^{-n\left(0\right)e^{-\Gamma \left|t\right|}{\text{Ω}}^2{t}^2}dt$$ (Equation 2)

where J is the electronic strength between ¹(S₁S₀)^∗ and ¹(T₁T₁), $\Delta G_0=E_{S_0{S}_1}-E_{\left(TT\right)}$ is the driving force of singlet fission, λ is the associated reorganization energy, Ω is the angular frequency of the effective singlet-fission driving vibrational mode, Γ is its thermal relaxation rate, and $n\left(0\right)=E_{inc}-E_{S_0{S}_1}/ћ\text{Ω}$ is the optically populated initial vibrational quanta where E_inc is the incident light energy, which is 795 nm in the present study. We can then apply Equation 2 to calculate the ¹(T₁T₁) formation rate k_F under non-thermalized condition. It was found that k_F,aa of 0.93 ps⁻¹ is nearly the same as k_F,bb of 0.83 ps⁻¹, in spite of a modest disparity in energetic parameters such as ΔG₀ and λ. The diminished difference on k_S along a and b axes primarily arises from their fast Ωs, whose zero-point energies become much more overwhelming for vibrational quantum tunneling. As suggested by Busby et al., 2014, almost all singlet excitons in hexacene crystal undergo singlet fission, resulting in a triplet quantum yield of nearly 200% that also affords a negligible fluorescence quantum yield. If so, the overall decay rate, k_D, of ¹(S₁S₀)^∗ is simply k_F + Γ, leading to k_D,aa of 1.86 ps⁻¹ and k_D,bb of 2.08 ps⁻¹. These computed rates are in good agreement with those obtained from our experimental measurements, indicating a direct formation of ¹(T₁T₁) from the vibrationally “hot” ¹(S₁S₀)^∗ in hexacene. In fact, previous studies of hexacene thin films attributed a slower singlet fission to multi-phonon relaxations, as compared with pentacene and tetracene (Busby et al., 2014). For example, ultrafast vibronic spectroscopies of pentacene and its derivatives showed that the singlet fission process is a single-molecular internal conversion via a conical intersection due to strong coupling between nuclear and electronic motions (Musser et al., 2015). As a result, the thermal relaxation of the ¹(S₁S₀)^∗ state should be taken into account when its decay rate is probed by transient spectroscopy techniques.

Anisotropic Nature of T₁ + T₁ and ¹(T₁T₁)

Triplet Davydov splitting exhibits a difference in energy as high as 30 meV along the a and b axes in hexacene single crystals, indicating that the T₁ + T₁ states remain strong dipole-dipole interactions in the anisotropic environment. The energy level of T_1b + T_1b is lower than that of T_1a + T_1a in the case of hexacene. This energy alignment is opposite to that of pentacene (Figure S5) and tetracene (Schwoerer and Birech, 2014), both of which have T_1b + T_1b higher than T_1a + T_1a as reported. Since the anisotropic lowest spin-correlated triplet T₁ + T₁ states arises from the decoherence of ¹(T₁T₁), it is legitimate to surmise that the ¹(T₁T₁) states should be anisotropic in hexacene single crystals. We further hypothesized that the energy level for ¹(T_1bT_1b) is lower than that for ¹(T_1aT_1a) in hexacene single crystals from the measured triplet Davydov splitting.

To reveal the nature of the anisotropic ¹(T₁T₁) and T₁ + T₁ states, we need to address the anti-ferromagnetic electron correlation in acenes as revealed by a complete active space simulation using the density matrix renormalization group algorithm (Hachmann et al., 2007). This anti-ferromagnetism was later corroborated by a spin-polarized density functional theory study (Jiang and Dai, 2008), which discovered spatially separated magnetizations in acenes. Similarly, electron spins in hexacene favor anti-ferromagnetic correlation, resulting in the notable presence of diradical covalence resonance structures. For example, a pair of adjacent hexacene molecules along a axis had been extracted from the crystal structure before a complete active space self-consistent field calculation (Aquilante et al., 2016) with an active space of CAS(6,6) was conducted to reveal an enthalpy difference, $E_{{\left(T_1+T_1\right)}_{aa}}-E_{{\left(T_1{T}_1\right)}_{aa}}$, of 16.7 meV. In fact, a similar value of 13.5 meV was also achieved by our employed CDFT method that had been demonstrated to achieve a comparable accuracy against the multireference configuration interaction MRCI + Q level of theory on polyacenes (Kubas et al., 2014). Since a T₁ + T₁ dimer has less anti-ferromagnetic characteristics than its parental ¹(T₁T₁) pair in spite of more available spin microstates, its relative energetic stability is determined by a direct competition between enthalpy and entropy, i.e., E_HS→LS  versus  k_BTln9. It turns out that entropy is a more dominant factor than enthalpy for crystalline hexacene at room temperature, making T₁ + T₁ thermodynamically more stable than ¹(T₁T₁) as shown in Figure 2. By the same token, the ¹(T_1aT_1a) pair is expected to have a higher energy than its counterpart along axis b owing to diminished anti-ferromagnetic coupling strength over distance. Nevertheless, the difference on the spin-flip energy between the two axes is not strong enough to override their gap on the ¹(T₁T₁) pair, thus sustaining the relative stability of T_1b + T_1b over T_1a + T_1a.

In polycrystalline singlet fission materials, the anisotropy of the ¹(T₁T₁) states may preserve within individual crystalline grains. The random orientation of those grain boundaries, however, is bound to suppress the global expression of the anisotropy. Very uniquely, our studies in the form of single crystals allow us to unravel the anisotropic nature of the ¹(T₁T₁) state without ambiguity. Previous studies of polycrystalline acenes and other singlet fission materials showed that the energy level of a triplet pair ¹(T₁T₁) is higher than that of a decoupled triplet dimer(Basel et al., 2019, Yong et al., 2017). Recently, a triplet pair ¹(T₁T₁) was reported to be bound relative to free triplets with an energy of ca. 30 meV, which is largely material independent (Yong et al., 2017). Our results not only demonstrated a higher energy of ¹(T₁T₁) than T₁ + T₁, but also exhibit their anisotropic features in hexacene.

Anisotropic Quantum Decoherence of ¹(T₁T₁)

The transition dipole strength for the triplet pair ¹(T₁T₁) state is generally too weak to be detected so that its quantum decoherence is usually assumed to be much faster than its formation (Berkelbach et al., 2014, Chan et al., 2013, Coto et al., 2015, Mirjani et al., 2014, Tamura et al., 2015, Yost et al., 2014). Nevertheless, some studies implied that the quantum decoherence rate of the ¹(T₁T₁) state could be as slow as its formation rate (Feng and Krylov, 2016, Kolomeisky et al., 2014, Monahan et al., 2017, Pensack et al., 2016). In the present study, we found that k_Q is even slower than k_F along the long a axis, whereas k_Q along the short b axis is comparable with k_F. Our results indicate that the relatively slow quantum decoherence is as important as triplet pair formation for the overall singlet fission rate in hexacene. According to the Redfield quantum dissipation theory (Ishizaki and Fleming, 2009), the quantum decoherence rate, k_Q, due to system-bath coupling is given by:

$$k_Q\approx \frac{2\lambda {\omega }_p\text{Δ}E}{\text{Δ}{E}^2+{ћ}^2{\omega }_p^2}\left(\frac{e^{\frac{\text{Δ}E}{k_{b}T}}}{e^{\frac{\text{Δ}E}{k_{b}T}}-1}\right)$$ (Equation 3)

where ΔE is the energy gap between the initial and final states of quantum decoherence, λ is the corresponding reorganization energy, and ω_p is the system-bath coupling frequency. If the quantum decoherence of ¹(T₁T₁) pair in hexacene crystal is assumed to be driven by vibronic coupling only, ω_p can be ascertained by the functional mode analysis (Hub and de Groot, 2009), which projects the diabatic energy gaps between ¹(T₁T₁) and T₁ + T₁ onto the dimer's vibrational normal modes for 5,000 snapshots extracted from our MD trajectory. It was found that the quantum decoherence is predominantly driven by a few slow vibrational modes with ω_p < 50 cm⁻¹ (Figure S11). Thus, the quantum decoherence is mediated by the electron-phonon interaction in crystalline hexacene. Even if we account for the small contributions from other vibrational modes that are usually much faster, the calculated effective driving mode, ${\omega }_p=\left(\sum _{i=1}^{N_{vib}}{c}_i^2{\omega }_i^{-1}\right)$, is still as slow as ∼40 cm⁻¹ (Table S3). Therefore, ω_p is an important factor for the quantum decoherence of ¹(T₁T₁) pair in hexacene because of its notable mismatch with ΔE, i.e., ћω_p≪ΔE→k_Q∝ω_pλΔE⁻¹. Interestingly, the $\Delta E$ along a axis is nearly two times as large as its counterpart along b axis, resulting in a remarkable directional heterogeneity of k_D, i.e., $\frac{k_{Q,bb}}{k_{Q,aa}}\approx 1.7$. Besides the experimentally consistent heterogeneity factor, our calculated values of k_Q along the two crystal axes are also well in line with the results from our ultrafast spectroscopy studies (Table S2).

Previous studies of singlet fission in pentacene and hexacene were performed on their polycrystalline films (Bakulin et al., 2016, Busby et al., 2014, Chan et al., 2011, Kandada et al., 2014, Rao et al., 2011, Wilson et al., 2011, Wilson et al., 2013). Fission rates of the films are, in general, the averaged result over different orientations of the polycrystalline structures, leading to a loss of intrinsically anisotropic features in these materials. Transient absorption microscopy experiments found that long-lived correlated triplet pairs exist and triplet interaction and binding could be induced by a π-staked geometry in crystalline pentacene derivative (Folie et al., 2018). Polarization measurements of tetracene demonstrated that there was no difference in kinetics along the long and short axes (Schwoerer and Birech, 2014, Wan et al., 2015, Zhang et al., 2014). By contrast, our results showed that the anisotropic quantum decoherence of ¹(T₁T₁) occurs in single crystalline hexacene. This decoherence process is driven by the vibronic coupling between the ¹(T₁T₁) state and some low-frequency phonon modes of hexacene crystal. Owing to the directional asymmetry of the crystal, this quantum decoherence process might be intrinsically anisotropic as governed by the energy gap between ¹(T₁T₁) and T₁ + T₁.

In summary, we discovered anisotropic singlet fission in single crystalline hexacene and have revealed its mechanism by deciphering its two constituent steps. For the first step that gives rise to correlated triplet pairs through the so-called direct mechanism, no anisotropy was found as they were formed on the same timescale of ∼200 fs along the two crystal axes. In the second step that involves quantum decoherence of the correlated triplet pairs, the rate along the short b axis is nearly two times as fast as that along the long a axis. The difference on the rate might be ascribed to the directional heterogeneity of the hexacene crystal that results in distinct thermodynamic stabilities between the initial and final states of the quantum decoherence, which is driven by system-bath coupling with a slow effective frequency of ω_p < 50 cm⁻¹. Our findings not only corroborated the importance of quantum decoherence in fission process, but will also guide future experimental and theoretical endeavors of exploring anisotropic photophysical properties in novel materials for multiple exciton generation.

Limitations of the Study

From a fundamental point of view, one of the most challenging tasks for the singlet fission community is the characterization and monitoring of the optically dark ¹(T₁T₁) state due to its small absorption cross section and short lifetime upon photo-excitation. Although the transient absorption spectra of the ¹(T₁T₁) state were presented in recent experiments (Burdett and Bardeen, 2012, Korovina et al., 2016, Lukman et al., 2015, Lukman et al., 2016, Stern et al., 2015, Stern et al., 2017), those results are limited to intramolecular singlet fission or intermolecular one for dimers in solution (Rao and Friend, 2017) with unusually long ¹(T₁T₁) lifetime. Therefore, it is not surprising that the optical identification of the short-lived ¹(T₁T₁) state in hexacene has not been reported yet with the transient absorption spectroscopy method. More recently, the two-dimensional optical spectroscopy was employed to demonstrate the existence of ¹(T₁T₁) state in thin film pentacene and its derivatives (Bakulin et al., 2016). Nevertheless, this technique has to be coupled with a microscopy approach for small-size samples such as single crystalline hexacene, our system of interest.

Methods

All methods can be found in the accompanying Transparent Methods supplemental file.

Published: September 27, 2019