Abstract
The proximity of a transition-metal dichalcogenide (TMD) to graphene imprints a rich spin texture in graphene and complements its high-quality charge/spin transport by inducing spin–orbit coupling (SOC). Rashba and valley-Zeeman SOCs are the origin of charge-to-spin conversion mechanisms such as the Rashba–Edelstein effect (REE) and spin Hall effect (SHE). In this work, we experimentally demonstrate for the first time charge-to-spin conversion due to the REE in a monolayer WS2-graphene van der Waals heterostructure. We measure the current-induced spin polarization up to room temperature and control it by a gate electric field. Our observation of the REE and the inverse of the effect (IREE) is accompanied by the SHE, which we discriminate by symmetry-resolved spin precession under oblique magnetic fields. These measurements also allow for the quantification of the efficiencies of charge-to-spin conversion by each of the two effects. These findings are a clear indication of induced Rashba and valley-Zeeman SOC in graphene that lead to the generation of spin accumulation and spin current without using ferromagnetic electrodes. These realizations have considerable significance for spintronic applications, providing accessible routes toward all-electrical spin generation and manipulation in two-dimensional materials.
Keywords: Rashba−Edelstein effect, spin Hall effect, Rashba spin−orbit coupling, valley-Zeeman, proximity effect
Spin-orbitronics is a promising field of research that serves the future of spintronic devices, which is based on the manipulation and control of spins and is enabled by spin–orbit coupling (SOC). Graphene is known to be a superior material for long-distance spin transport;1−3 however, it has intrinsically weak SOC.4 The control of the spin signal that is necessary for spin-based devices becomes possible in graphene by inducing SOC that can be realized via the proximity of materials with large SOC. Recent theoretical5−9 and experimental10−18 studies have shown that the proximity of transition-metal dichalcogenides (TMD) can induce SOC with the strength of a few millielectronvolts in graphene.19 This leads to a large spin lifetime anisotropy7,13,16,18 due to the suppression of the in-plane spin lifetime and/or spin absorption.20,21
A few orders of magnitude larger SOC in a monolayer TMD,22 compared with graphene, together with its inversion symmetry breaking, provides this semiconductor with the theoretically predicted large intrinsic spin Hall angle.23 Moreover, spin-torque24 and spin-pumping25 experiments have shown the possibility of charge-to-spin conversion by the Rashba–Edelstein effect in TMDs. However, for the injection/detection and transfer of the spin information, the short spin relaxation time in TMDs presents a major obstacle.
The hybridization of TMD to graphene is an effective way to complement the properties of these materials. Theory predicts that the band structure of graphene in the proximity of TMD is spin-split by the presence of Rashba and valley-Zeeman spin–orbit fields.5,6 These spin–orbit fields are the origin of charge-to-spin conversion mechanisms such as the Rashba–Edelstein effect (REE) and the spin Hall effect (SHE) that generate spin accumulation and spin-polarized currents, respectively.9,26−31 More importantly, the strength of these spin–orbit fields and also the efficiency of the charge-to-spin conversion mechanisms are dependent on the position of the Fermi energy within the band structure of the TMD-graphene heterostructure. For the first time, we show in this work that this is indeed the case for a WS2-graphene heterostructure where the Rashba–Edelstein effect, in particular, creates a spin accumulation within the graphene channel which is detectable up to room temperature and is tunable by a gate transverse electric field.
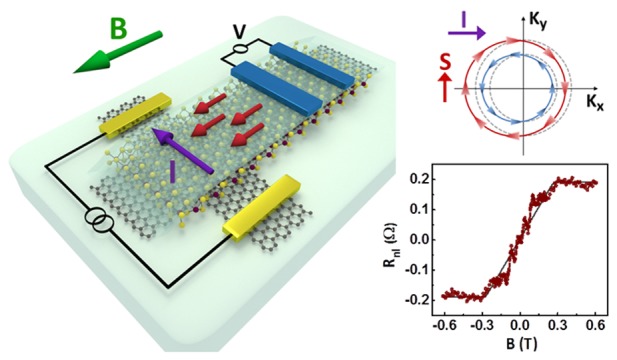
The Rashba SOC in graphene originates from breaking the out-of-plane symmetry due to the proximity of the TMD.27 The resulting out-of-plane effective electric field (E = Eẑ) generates an in-plane Rashba spin–orbit field (∼E × p) that is perpendicular to the momentum (p) of the electrons within the Dirac cone and ultimately creates a tangential winding spin texture of the electron states in momentum space. Because of the Rashba–Edelstein effect, a charge current (density) J generates a nonzero spin density (∝ẑ × J), polarized perpendicular to the current direction.26,27
The winding Rashba spin–orbit field in the graphene changes sign between the spin-split Dirac cones of the conduction (or valence) band (Figure 1a). Therefore, the current-driven spin densities of the spin-split bands have opposite sign, which reduces the total spin density at the Fermi energy. However, the energy gap between the spin-split Dirac cones is enhanced by the presence of the valley-Zeeman field (calculated to be about 2.2 meV for WS2-graphene6). This results in considerably different magnitudes of the (current-driven) spin densities associated with each of the cones for low-energy states. This avoids compensation of the spin accumulation from the bands with opposite spin winding and helps to optimize the efficiency of the charge-to-spin conversion.9
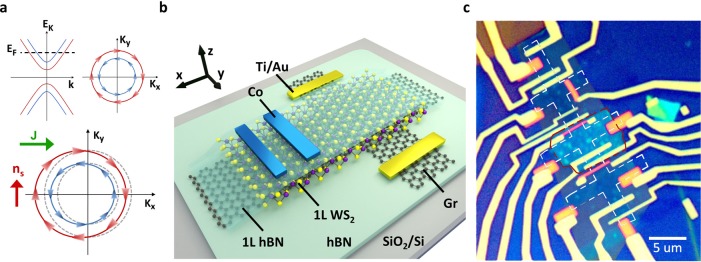
Figure 1.
(a) TMD-graphene band structure, consisting of spin-split Dirac cones with opposite spin helicity. The charge current (J) shifts the Fermi-level contours from equilibrium (gray dashed lines) and induces a nonequilibrium electron spin density (ns) by the Rashba–Edelstein effect. (b) Sketch of the van der Waals heterostructure of 1L WS2-graphene encapsulated with the top monolayer hexagonal boron nitride (hBN) and bottom bulk hBN (with a thickness of 14 nm). The device is made with Ti/Au and Co electrodes on a SiO2/doped Si substrate. The sketch illustrates the central region of the sample including the electrodes that are used for our measurements. (c) Optical microscope image of the fabricated device. The red and white dashed lines show the edges of the WS2 and etched graphene flake, respectively.
Here we observe clear evidence of the charge-to-spin conversion in TMD-graphene heterostructures due to the REE, which is accompanied by the SHE. Different directions of the spins generated from these two effects make their contributions distinguishable by their distinct symmetries as a function of the magnitude and direction of the magnetic field in our (oblique) Hanle precession measurements. The SHE has recently been observed in multilayer MoS2/multilayer graphene,31 where the SHE signal in graphene is superimposed by an additional spin-to-charge conversion mechanism which is mainly associated with SHE in the bulk MoS2. However, the measurements in this work are performed on a vdW heterostructure of a single layer of WS2 and graphene. The two-dimensionality of monolayer (1L) TMD compared to bulk TMD32 eliminates the vertical charge transport inside the 1L TMD. Therefore, a possible contribution from the SHE in bulk TMD is largely suppressed in our system. Stronger induced SOC in graphene by 1L TMD, as compared to bulk,17 in addition to the theoretical prediction of the largest SHE signal, specifically, in a 1L WS2-graphene heterostructure,30 makes the vdW stack of our sample an optimal choice.
In Figure 1b, we show the device geometry consisting of 1L WS2/1L graphene that is encapsulated between 1L hexagonal boron nitride (hBN) and bulk hBN. The device is fabricated on a 300 nm SiO2/doped Si substrate with Ti/Au and Co electrodes, made by shadow mask evaporation and e-beam lithography, respectively (Methods section). The 1L hBN acts as a tunnel barrier for the spin injection/detection by the Co electrodes. Represented by the white dashed line in the optical image (Figure 1c), the graphene channel is etched into a Hall bar which allows for the nonlocal detection of the induced spin density, generated by both effects. Note that for the fabrication of the vdW stack we do not have control over the crystallographic alignment of the TMD, graphene, and hBN flakes which can affect the strength of the spin–orbit fields as compared to the calculations that assume (super)lattice matching.33,41
REE and SHE Measurements with an In-Plane Magnetic Field (x–y Plane)
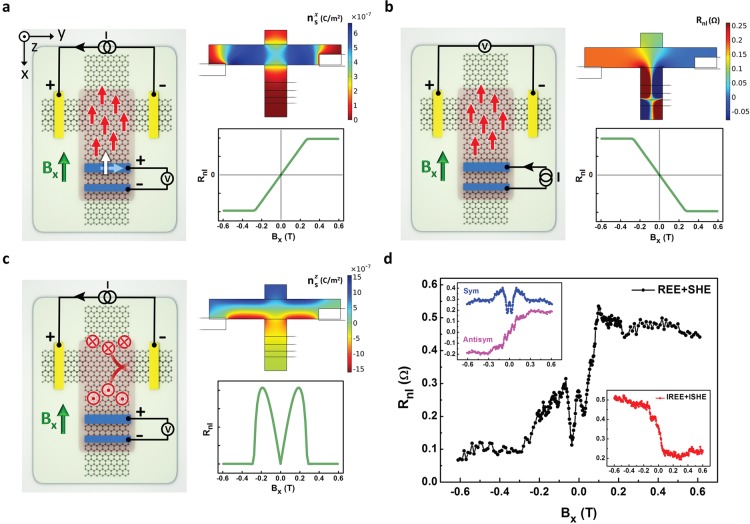
Our main focus in this work is on the TMD-covered graphene region of this device. As shown in the device sketch in Figure 2a, using the Ti/Au contacts on graphene we apply charge current (I), and with ferromagnetic Co electrodes, we measure the nonlocal voltage (Vnl) as a function of an applied magnetic field (B). With an applied charge current along the y axis and in the presence of REE, one should expect the generation of nonzero spin density polarized along the x axis, nsx. We formulate our theoretical model of coupled charge-spin transport in the presence of REE. By numerically solving Bloch diffusion equations (COMSOL; details in section 6 of the SI), we obtain a distribution of ns over the full sample shown as a color map in Figure 2a. Using these solutions at any applied field B, one can estimate the signal between the spin-sensitive Co contacts, shown in the bottom right corner of Figure 2a.
Figure 2.
Rashba–Edelstein effect (REE) and inverse REE (IREE) and spin Hall effect (SHE). (a) Device sketch and measurement geometry for REE. A current source (I) is applied to the Ti/Au electrodes, and the voltage (V) is measured across the Co electrodes. Red arrows represent the accumulation of in-plane spins polarized along the x axis. The color map is the magnitude of the spin density polarized along the x axis (nsx) at zero magnetic field (Bx = 0 T) over the sample. The plot shows the modulation of the nonlocal resistance (Rnl) vs Bx, calculated by considering the Stoner–Wohlfarth model for the behavior of the Co contacts. The white arrows in the sketch represent the Co magnetization direction. (b) Inverse REE (IREE) measurement geometry, color map for the voltage distribution at Bx ≥ 0.3 T when contact magnetization is fully aligned with Bx, and the corresponding expected modulation of the Rnl vs Bx. (c) Measurement geometry for SHE and generation of out-of-plane polarized spin current, resulting in an accumulation of out-of-plane spins (polarized along the z axis). The color map shows the density of the out-of-plane spins (ns) at Bx = 0 T. The plot shows the modulation of Rnl, expected from Hanle precession of the out-of-plane spins, resulting in symmetric behavior vs Bx (considering that the y component of the Co contact magnetization is oriented along with the y component of the magnetic field direction). (d) Rnl versus Bx, experimentally measured in the geometry of the REE and SHE (with I = 5 μA). The measurement is performed at 4.2 K with a charge carrier density of +1.5 × 1012 cm–2. The inset at the top left shows the symmetric and antisymmetric components of the signal, separately. The inset at the bottom right is the Rnl measured in IREE geometry (with I = 2 μA).
At B = 0 T, the magnetization of the Co contacts is along their easy axis (y direction), implying that the nonlocal resistance (Rnl) should be zero. Applying a magnetic field in the x direction (Bx) changes the direction of the contact magnetization, in accordance with the Stoner–Wohlfarth model.34 The component of the contact magnetization along the x axis increases linearly with Bx while the REE-induced spin density stays unaffected. This results in a linear increase in the nonlocal resistance until the contact magnetization direction is completely saturated along the x axis (at Bx ≈ 0.3 T, for our Co electrode geometry). A negative magnetic field causes the alignment of the contact magnetization in the opposite direction. This results in a negative signal because the polarization of the REE spin density stays unchanged. Therefore, antisymmetric behavior of the nonlocal signal versus B is a direct signature of REE and can be used to extract the REE-related signal from the experimental results.
By the inverse of the REE (IREE), the generation of charge current becomes possible as a result of the nonzero spin density in graphene.35 In this geometry (shown in Figure 2b), the detection of the nonlocal voltage drop is across the Ti/Au contacts, while Co electrodes are used to apply the current required for the injection of in-plane spins. IREE is the Onsager reciprocal of REE, implying that the detected nonlocal signal should be the same but with a reversed sign of B (Rij,kl(B) = Rkl,ij(−B), with ij and kl being the indices of current and voltage terminals).
In Figure 2c, we illustrate the mechanism for creating a spin current and the resulting accumulation of spins by SHE. In this case, a spin current with out-of-plane polarization is generated perpendicular to the direction of the charge current.36 In the color map of Figure 2c, we show the out-of-plane spin density (nsz) produced by the SHE all over the sample. The out-of-plane spins cannot generate a nonlocal voltage across the in-plane-magnetized Co electrodes unless they precess around the applied magnetic field. Therefore, the detected signal develops from zero at B = 0 T to a finite value as the spins precess to the in-plane direction along the y axis. Furthermore, the Rnl drops back to zero above the saturation field of the Co contact because the Co magnetization and spin alignment are again perpendicular to each other. The sign of the SHE signal depends on the orientation of the Co magnetization (Figure 1c). In our calculations, we assume that the y component of the contact magnetization is oriented along with the y component of the magnetic field direction (details in SI section 5). This results in the symmetric behavior of the SHE component versus B, which is thus easily distinguishable from the antisymmetric REE component.
We show our experimental result in Figure 2d, obtained by applying a current source of 5 μA and measuring Rnl with the Co electrode located 2 μm from the center of the graphene cross. The graphene width is about 1.8 μm. These measurements are performed at 4.2 K with a charge carrier density of +1.5 × 1012 cm–2. The observed result contains signals from both REE and SHE effects. The top-left inset shows the antisymmetric and symmetric components that are extracted from the measured data in order to discriminate the spin signal dominated by the REE and SHE, respectively. The magnitude of the measured REE spin signal is ΔRnl ≈ 200 mΩ, defined as half of the difference between the Rnl values measured at the two saturation levels.
The bottom-right inset shows the IREE spin signal measured with the inverse geometry that shows similar behavior but with reversed sign versus B, confirming the spin-to-charge conversion and preservation of the reciprocity in the linear regime. The very small background resistance in these measurements affirms that in our nonlocal geometry the current path is well-separated from the voltage probes.
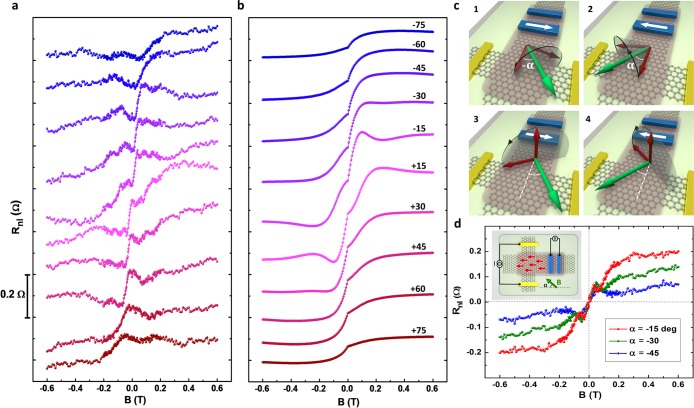
The magnitude and modulation of the measured spin signal is strongly dependent on the direction of the applied magnetic field. In Figure 3a, we evaluate how the nonlocal resistance changes as we apply the in-plane magnetic field at certain angles with respect to the x axis (α ≈ −75 to +75°). All of the measurements are performed by aligning the contact magnetization at high fields, meaning that the y component of the Co magnetization is always collinear with the y component of the magnetic field. In panel b, we show the corresponding modeled dependences that closely reproduce our experimental results.
Figure 3.
Precession of REE and SHE spins under an α-angled magnetic field. (a) Rnl measured versus B applied under an angle of α ≈ −75 to +75°. The unknown component is subtracted from this data set. (b) Closest fit to the data, obtained for τ∥ ≈ 3.5 ps and τ⊥≈ 90 ps, considering the spin Hall angle (ΘSH) of 0.13 and an REE conversion efficiency (αRE) of 2.8 (defined as the ratio of the spin density over the charge current density nsx/(2vFJy), with vF being the Fermi velocity). (c) Device sketch with symmetries of the Hanle signal vs the angle, considering the precession of the in-plane spins (panels 1 and 2) and the out-of-plane spins (panels 3 and 4). (d) Measurement geometry for REE. Antisymmetric component of Rnl versus B, applied under angles of α ≈ −15, −30, and −45°.
The behavior of Rnl is understood by considering the precession of the in-plane and out-of-plane spins around the α-angled magnetic field and the corresponding symmetries versus α. As shown in Figure 3c, REE-induced spins result in the same positive projection on the Co magnetization direction for both +α and −α, meaning that the REE spin signal is symmetric versus angle α. On the other hand, the precessed out-of-plane SHE spins generate signal projections on the contact magnetization with opposite signs for +α and −α, implying the antisymmetric contribution of SHE spins versus the angle. This means that the REE contribution to the signal does not change whereas the SHE contribution changes from peaks (dips) to dips (peaks) when the angle is changed from +α to −α.
Specifically, in Figure 3d we show the REE spin signal (antisymmetric vs B and symmetric vs α) measured under angled B. As expected for the Co magnetization behavior, we observe the shift of the saturation fields under different angles, together with the change in the magnitude of the spin signal. In the following table, we summarize the symmetries for the in-plane Hanle precession measurements as
| vs | REE | SHE |
| B | antisym | sym |
| α | sym | antisym |
Note that in the measured nonlocal signal there is an additional component that does not comply with the symmetries of the REE and SHE. This component is subtracted from the experimental data, resulting in Figure 3a. (For details and discussions, see the SI, section 4).
The closest fit to the data (Figure 3b) gives an estimate of the in-plane spin lifetime of τ∥ ≈ 3.5 ps with a spin lifetime anisotropy of τ⊥/τ∥ ≈ 26, considering the spin Hall angle (ΘSH) of 0.13 and REE conversion efficiency (αRE) of 2.8 (defined as the ratio of the spin density over the charge current density nsx/(2vFJy), with vF as the Fermi velocity. (See ref (9) and the SI, sections 7 and 8, for details.) We formulate the spin Hall angle and the REE efficiency as ΘSH = SHρ and αRE = 2REvFρτ∥, where ρ is the resistivity of the TMD-covered graphene channel and SH and RE are the strengths of the two effects. The ratio between the strengths is defined as SH/RE = 2ΘSHvFτ/αRE ≃ 0.33 μm. Because in our analysis the Co contact polarizations cannot be extracted independently from the REE and SHE strengths, their ratio is more accurate compared to their individual values. For comparison, the reported value for ΘSH in bulk MoS2-graphene is about 0.05 (with undefined charge carrier density).31
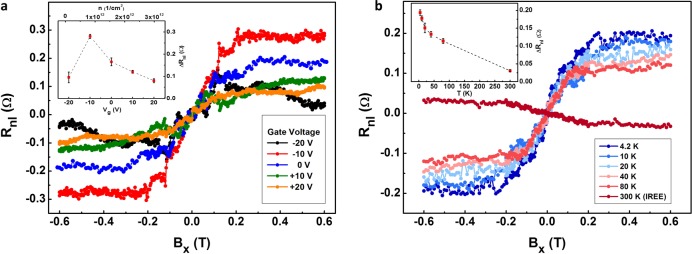
One of the most important requirements for the spin-based devices is the possibility to tune the spin signal by a gate electric field. Here we demonstrate the modulation of the REE efficiency with a gate. The REE is theoretically predicted to be gate-tunable9 because of its strong dependence on the spin-split band structure of the TMD-graphene heterostructure. We evaluate this by comparing it to our measurements in REE geometry at different back-gate voltages (Vg), shown in Figure 4a. Electrical characterization of the graphene channel shows n-type doping with the charge neutrality point at Vg = −22 V (SI section 2). Measurements performed close to the Dirac point are difficult to interpret because of the presence of inhomogeneity originating from disorder. In addition, in this regime the contact resistance becomes comparable to the channel resistance, which can suppress spin transport considerably. Therefore, we exclude measurements performed at the Dirac point from our consideration. However, we observe that the increase in the gate voltage from −10 to +20 V (corresponding to a change in Fermi energy from 100 to 200 meV) results in a considerable decrease in the spin signal, ∼70%.
Figure 4.
Gate and temperature dependence of the REE spin signal. (a) Hanle precession measured with respect to Bx (antisymmetrized Rnl vs B) at gate voltages of −20 to +20 V (at T = 4.2 K). The inset is the magnitude of the REE spin signal versus Vg. (b) Antisymmetric component of Rnl vs Bx, measured at different temperatures in the REE geometry. The signal shown at room temperature is measured in IREE geometry. The inset is the temperature dependence of the REE spin signal.
This behavior can be associated with the fact that Vg shifts the Fermi energy from the charge neutrality point into the conduction band, at which both of the spin-split Dirac cones (with opposite spin-winding directions) are available. The opposite winding of the spin texture of the two bands reduces the efficiency of the REE to a large extent, leading to a lower in-plane spin density. We observe that the measured REE spin signal decays as a function of gate voltage, which is in agreement with the theoretically predicted decay in the REE efficiency versus the position of the Fermi energy.9
The preservation of the charge-to-spin conversion mechanism at room temperature is a prerequisite for potential applications. We evaluate the temperature dependence of the REE (Figure 4b) and observe that the spin signal generated by the REE and the IREE is preserved up to room temperature; however, it decays by about 80% from 4 K up to RT. This behavior indicates the robustness of the REE charge-to-spin conversion mechanism, which is in agreement with theoretical predictions.9 We observe that the features associated with SHE in our system, together with the unknown component in the Hanle precession measurements, vanish at temperatures above 20 K. This indicates that the SHE has a stronger dependence on temperature than does the REE.
REE Measurements with an Out-of-Plane Magnetic Field (x–z Plane)
We further characterize the spin transport by applying the magnetic field in the x–z plane, under an angle (θ) with respect to the normal to the sample plane (shown in the sketch of Figure 5). First, the θ-angled B brings the contact magnetization direction out of plane, and second, it precesses the in-plane spins in the out-of-plane direction, which are then detected by the contacts with a tilted magnetization. The symmetry table for the non-precessing SHE and REE components for the out-of-plane field measurements is
| vs | REE | SHE |
| B | antisym | antisym |
| θ | antisym | sym |
Figure 5.
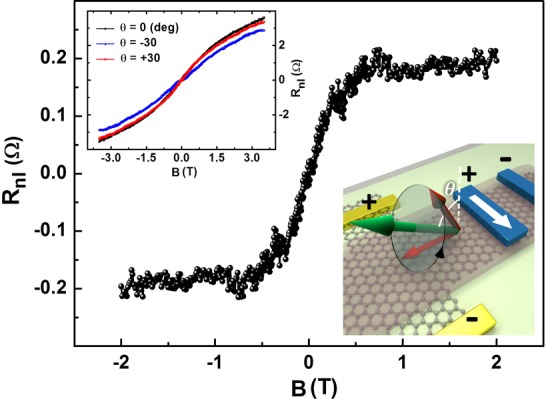
Observation of REE by out-of-plane Hanle precession measurements. The device sketch shows the precession of the in-plane REE spins about the applied magnetic field, angled by θ with respect to the normal to the plane. The curve is the antisymmetric component of the subtraction of the signal measured under angles of θ = ±30° (attributed to the REE spin signal), measured at 300 K. The inset is the antisymmetric component of the nonlocal resistance as a function of B, measured with respect to the θ-angled magnetic field.
SHE is symmetric vs angle and is antisymmetric vs B, thus having the same symmetries as the ordinary Hall effect. The nonlocal sample geometry minimizes the local charge current contribution to the detection voltage to a large extent. However, the detection electrodes in our sample are close to the current path, which results in a (small) Hall effect contribution of an order of magnitude similar to that of the SHE contribution. This implies that we are not able to extract the SHE component. Nevertheless, by antisymmetrizing the measured signal with respect to the angle we eliminate both SHE and the regular Hall effect, thus leaving only the REE contribution. In Figure 5, we show the resulting dependence of the described procedure which gives an ∼200 mΩ REE spin signal, measured at RT. Note that this is considerably larger than the REE-associated spin signal obtained via the in-plane geometry at RT, which is consistent with an increase in REE efficiency with a lower carrier density (estimated for holes from charge transport at 10 K, SI section 2). More importantly, taking into account the change in the sign convention of the current source electrodes (compared with the in-plane measurements, Figure 2a), we observe that the sign of the REE signal remains the same. This is because of the fact that the REE spin polarization associated with holes should have a sign opposite to that of electrons.27
Note that in the nonlocal geometry of the measurements in such graphene Hall bars there is the possibility for a finite contribution of a Hall effect, locally generated by the stray field of the ferromagnetic electrodes, in both in-plane and out-of-plane magnetic field measurements. This contribution of the Co stray fields in the nonlocal voltage as well as the regular Hall effect (by the out-of-plane external magnetic field) is dependent on the current distribution in the graphene channel in the region in between the Co voltage probes. However, in this sample, we observe that the linear change in the Rnl (associated with the regular Hall effect, shown in the inset of Figure 5) is about 1 order of magnitude smaller than the Hall voltage expected from the modeled current distribution in the region of Co detectors. This discrepancy can be related to the inhomogeneities in the graphene channel that may lead to smaller current flow in the region of the Co probes. Considering also the possible uncertainties in the determination of sample geometry, we quantify the magnitude of the nonlocal voltage generated by the stray fields to be about 1 order of magnitude smaller than the measured signal in both in-plane and out-of-plane measurements associated with the REE spins. Therefore, the effect of the stray field in these measurements is unlikely to explain our results. (For further details, see SI section 11.)
In this work, we also observe modulations of the second harmonic signal (Vnl/I2). The results show a considerable dependence on the applied magnetic field and gate electric field which is a signature of thermally driven spin polarization in the TMD-graphene heterostructure. This observation (results are shown in SI section 13) could be an indication of spin-Nernst or spin-Seebeck effects37 in this system; however, it requires further studies.
Our experimental observations are unambiguous evidence for the presence of both Rashba–Edelstein and spin Hall charge-to-spin conversion mechanisms in a monolayer TMD-graphene heterostructure. This is the direct proof of the effective imprint of the Rashba and valley-Zeeman spin–orbit fields in graphene, while its charge-transport properties are preserved. In this work, we comprehensively addressed the charge-induced nonequilibrium spin density, generated by the REE, and we employed strategies in order to discriminate this effect from SHE by symmetries of the Hanle precession measurements as a function of oblique magnetic fields. The ability to address the individual effects in one heterostructure allows for a valid comparison of their strengths. Moreover, the observed strong dependence of the REE spin signal on the position of Fermi energy shows the efficient tunability of spin generation by a transverse electric field. This observation, in addition to the fact that the spin signal remains considerable up to room temperature, confirms that the monolayer TMD-graphene heterostructure is a promising choice for the future of two-dimensional spin transistors without the need for bulk ferromagnetic electrodes.
Methods
Device Fabrication
The monolayers of WS2 and graphene and hBN (1L and bulk) are mechanically cleaved from their bulk crystals (provided by HQ graphene) on SiO2/Si substrates, using adhesive tapes.38 The monolayer flakes are identified by their optical contrast with respect to the substrate.39 The thicknesses of the flakes are verified by atomic force microscopy (AFM). Using a dry pick-up technique,40 we transfer the graphene on the bulk hBN flake. By a prepatterned PMMA mask, we etch the graphene-bulk hBN by oxygen-plasma into an H-bar geometry. We finalize the fabrication of the vdW stack by the transfer of the 1L hBN-WS2 on top of the etched graphene-bulk hBN. We proceed with the fabrication of electrodes on the vdW stack by shadow-mask evaporation and an e-beam lithography technique (using PMMA as the e-beam resist). Because of the complications of the fabrication process, there is a high chance of breaking the graphene channel. In the sample studied in this work, the presence of a few cracks in our graphene channel has caused the TMD-covered graphene region to be electrically disconnected from the rest of the sample. Therefore, our analysis is focused only on the TMD-covered graphene region, shown in the device sketch of Figure 1b.
Electrical Measurements
The charge and spin transport measurements are performed by using a standard low-frequency (<20 Hz) lock-in technique with an ac current source of 100 nA to 5 μA. A Keithley source meter is used as the dc voltage source for the gate. Rotatable sample stages (separate for the in-plane and out-of-plane measurements) are used to apply the magnetic field by a (superconducting) magnet in all possible directions.
Acknowledgments
We kindly acknowledge Josep Ingla-Aynés for insightful discussions, and we thank T. J. Schouten, H. Adema, Hans de Vries, and J. G. Holstein for technical support. This research has received funding from the Dutch Foundation for Fundamental Research on Matter (FOM) as part of The Netherlands Organisation for Scientific Research (NWO), FLAG-ERA (15FLAG01-2), the European Unions Horizon 2020 research and innovation programme under grant agreement nos. 696656 and 785219 (Graphene Flagship Core 1 and Core 2), NanoNed, the Zernike Institute for Advanced Materials, and the Spinoza Prize awarded in 2016 to B.J.v.W. by NWO.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.9b01611.
Further details on device fabrication, AFM characterization, charge transport, (anti)symmetrization of Hanle prcession measurements, contact magnetization behavior, modelings, fittings and determination of REE and SHE coefficients, y–z and x–z plane Hanle precession measurements, the effect of stray fields, gate dependence of the nonlocal measurements, and second-harmonic measurements (PDF)
Author Contributions
‡ T.S.G. and A.A.K. contributed equally to this work.
The authors declare no competing financial interest.
During the publication procedure, we became aware of very recent work on a similar system, where the ISHE and IREE are observed in a bulk WS2-graphene heterostructure.42
Supplementary Material
References
- Tombros N.; Jozsa C.; Popinciuc M.; Jonkman H. T.; Van Wees B. J. Electronic spin transport and spin precession in single graphene layers at room temperature. Nature 2007, 448, 571. 10.1038/nature06037. [DOI] [PubMed] [Google Scholar]
- Drogeler M.; Franzen C.; Volmer F.; Pohlmann T.; Banszerus L.; Wolter M.; Watanabe K.; Taniguchi T.; Stampfer C.; Beschoten B. Spin lifetimes exceeding 12 ns in graphene nonlocal spin valve devices. Nano Lett. 2016, 16, 3533–3539. 10.1021/acs.nanolett.6b00497. [DOI] [PubMed] [Google Scholar]
- Han W.; Kawakami R. K.; Gmitra M.; Fabian J. Graphene spintronics. Nat. Nanotechnol. 2014, 9, 794–807. 10.1038/nnano.2014.214. [DOI] [PubMed] [Google Scholar]
- Gmitra M.; Konschuh S.; Ertler C.; Ambrosch-Draxl C.; Fabian J. Band-structure topologies of graphene: Spin-orbit coupling effects from first principles. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 80, 235431. 10.1103/PhysRevB.80.235431. [DOI] [Google Scholar]
- Gmitra M.; Fabian J. Graphene on transition-metal dichalcogenides: A platform for proximity spin-orbit physics and optospintronics. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 155403. 10.1103/PhysRevB.92.155403. [DOI] [Google Scholar]
- Gmitra M.; Kochan D.; Högl P.; Fabian J. Trivial and inverted Dirac bands and the emergence of quantum spin Hall states in graphene on transition-metal dichalcogenides. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 155104. 10.1103/PhysRevB.93.155104. [DOI] [Google Scholar]
- Cummings A. W.; Garcia J. H.; Fabian J.; Roche S. Giant spin lifetime anisotropy in graphene induced by proximity effects. Phys. Rev. Lett. 2017, 119, 206601. 10.1103/PhysRevLett.119.206601. [DOI] [PubMed] [Google Scholar]
- Gmitra M.; Fabian J. Proximity Effects in Bilayer Graphene on Monolayer WSe 2: Field-Effect Spin Valley Locking, Spin-Orbit Valve, and Spin Transistor. Phys. Rev. Lett. 2017, 119, 146401. 10.1103/PhysRevLett.119.146401. [DOI] [PubMed] [Google Scholar]
- Offidani M.; Milletarì M.; Raimondi R.; Ferreira A. Optimal Charge-to-Spin Conversion in Graphene on Transition-Metal Dichalcogenides. Phys. Rev. Lett. 2017, 119, 196801. 10.1103/PhysRevLett.119.196801. [DOI] [PubMed] [Google Scholar]
- Avsar A.; Tan J. Y.; Taychatanapat T.; Balakrishnan J.; Koon G.; Yeo Y.; Lahiri J.; Carvalho A.; Rodin A.; O’Farrell E.; Eda G.; Castro Neto A.; Özyilmaz B. Spin-orbit proximity effect in graphene. Nat. Commun. 2014, 5, 4875. 10.1038/ncomms5875. [DOI] [PubMed] [Google Scholar]
- Wang Z.; Ki D.-K.; Chen H.; Berger H.; MacDonald A. H.; Morpurgo A. F. Strong interface-induced spin–orbit interaction in graphene on WS 2. Nat. Commun. 2015, 6, 8339. 10.1038/ncomms9339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z.; Ki D.-K.; Khoo J. Y.; Mauro D.; Berger H.; Levitov L. S.; Morpurgo A. F. Origin and magnitude of designerspin-orbit interaction in graphene on semiconducting transition metal dichalcogenides. Phys. Rev. X 2016, 6, 041020. 10.1103/PhysRevX.6.041020. [DOI] [Google Scholar]
- Ghiasi T. S.; Ingla-Aynés J.; Kaverzin A. A.; van Wees B. J. Large proximity-induced spin lifetime anisotropy in transition-metal dichalcogenide/graphene heterostructures. Nano Lett. 2017, 17, 7528–7532. 10.1021/acs.nanolett.7b03460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang B.; Lohmann M.; Barroso D.; Liao I.; Lin Z.; Liu Y.; Bartels L.; Watanabe K.; Taniguchi T.; Shi J. Strong electron-hole symmetric Rashba spin-orbit coupling in graphene/monolayer transition metal dichalcogenide heterostructures. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 041409. 10.1103/PhysRevB.96.041409. [DOI] [Google Scholar]
- Avsar A.; Unuchek D.; Liu J.; Sanchez O. L.; Watanabe K.; Taniguchi T.; Ozyilmaz B.; Kis A. Optospintronics in graphene via proximity coupling. ACS Nano 2017, 11, 11678–11686. 10.1021/acsnano.7b06800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benítez L. A.; Sierra J. F.; Torres W. S.; Arrighi A.; Bonell F.; Costache M. V.; Valenzuela S. O. Strongly anisotropic spin relaxation in graphene–transition metal dichalcogenide heterostructures at room temperature. Nat. Phys. 2018, 14, 303. 10.1038/s41567-017-0019-2. [DOI] [Google Scholar]
- Wakamura T.; Reale F.; Palczynski P.; Guéron S.; Mattevi C.; Bouchiat H. Strong Anisotropic Spin-Orbit Interaction Induced in Graphene by Monolayer WS 2. Phys. Rev. Lett. 2018, 120, 106802. 10.1103/PhysRevLett.120.106802. [DOI] [PubMed] [Google Scholar]
- Zihlmann S.; Cummings A. W.; Garcia J. H.; Kedves M.; Watanabe K.; Taniguchi T.; Schönenberger C.; Makk P. Large spin relaxation anisotropy and valley-Zeeman spin-orbit coupling in WSe 2/graphene/h-BN heterostructures. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 97, 075434. 10.1103/PhysRevB.97.075434. [DOI] [Google Scholar]
- Garcia J. H.; Vila M.; Cummings A. W.; Roche S. Spin transport in graphene/transition metal dichalcogenide heterostructures. Chem. Soc. Rev. 2018, 47, 3359–3379. 10.1039/C7CS00864C. [DOI] [PubMed] [Google Scholar]
- Yan W.; Txoperena O.; Llopis R.; Dery H.; Hueso L. E.; Casanova F. A two-dimensional spin field-effect switch. Nat. Commun. 2016, 7, 13372. 10.1038/ncomms13372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dankert A.; Dash S. P. Electrical gate control of spin current in van der Waals heterostructures at room temperature. Nat. Commun. 2017, 8, 16093. 10.1038/ncomms16093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu Z.; Cheng Y.; Schwingenschlögl U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84, 153402. 10.1103/PhysRevB.84.153402. [DOI] [Google Scholar]
- Feng W.; Yao Y.; Zhu W.; Zhou J.; Yao W.; Xiao D. Intrinsic spin Hall effect in monolayers of group-VI dichalcogenides: A first-principles study. Phys. Rev. B: Condens. Matter Mater. Phys. 2012, 86, 165108. 10.1103/PhysRevB.86.165108. [DOI] [Google Scholar]
- Shao Q.; Yu G.; Lan Y.-W.; Shi Y.; Li M.-Y.; Zheng C.; Zhu X.; Li L.-J.; Amiri P. K.; Wang K. L. Strong Rashba-Edelstein effect-induced spin–orbit torques in monolayer transition metal dichalcogenide/ferromagnet bilayers. Nano Lett. 2016, 16, 7514–7520. 10.1021/acs.nanolett.6b03300. [DOI] [PubMed] [Google Scholar]
- Mendes J.; Aparecido-Ferreira A.; Holanda J.; Azevedo A.; Rezende S. Efficient spin to charge current conversion in the 2D semiconductor MoS2 by spin pumping from yttrium iron garnet. Appl. Phys. Lett. 2018, 112, 242407. 10.1063/1.5030643. [DOI] [Google Scholar]
- Edelstein V. M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 1990, 73, 233–235. 10.1016/0038-1098(90)90963-C. [DOI] [Google Scholar]
- Dyrdał A.; Barnaś J.; Dugaev V. Current-induced spin polarization in graphene due to Rashba spin-orbit interaction. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 075422. 10.1103/PhysRevB.89.075422. [DOI] [Google Scholar]
- Manchon A.; Koo H. C.; Nitta J.; Frolov S.; Duine R. New perspectives for Rashba spin–orbit coupling. Nat. Mater. 2015, 14, 871. 10.1038/nmat4360. [DOI] [PubMed] [Google Scholar]
- Milletarì M.; Offidani M.; Ferreira A.; Raimondi R. Covariant conservation laws and the spin Hall effect in Dirac-Rashba systems. Phys. Rev. Lett. 2017, 119, 246801. 10.1103/PhysRevLett.119.246801. [DOI] [PubMed] [Google Scholar]
- Garcia J. H.; Cummings A. W.; Roche S. Spin Hall effect and weak antilocalization in graphene/transition metal dichalcogenide heterostructures. Nano Lett. 2017, 17, 5078–5083. 10.1021/acs.nanolett.7b02364. [DOI] [PubMed] [Google Scholar]
- Safeer C.; Ingla-Aynés J.; Herling F.; Garcia J. H.; Vila M.; Ontoso N.; Calvo M. R.; Roche S.; Hueso L. E.; Casanova F. Room-Temperature Spin Hall Effect in Graphene/MoS2 van der Waals Heterostructures. Nano Lett. 2019, 19, 1074–1082. 10.1021/acs.nanolett.8b04368. [DOI] [PubMed] [Google Scholar]
- Wang Q. H.; Kalantar-Zadeh K.; Kis A.; Coleman J. N.; Strano M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 2012, 7, 699. 10.1038/nnano.2012.193. [DOI] [PubMed] [Google Scholar]
- Gmitra M.; Kochan D.; Högl P.; Fabian J. Trivial and inverted Dirac bands and the emergence of quantum spin Hall states in graphene on transition-metal dichalcogenides. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 155104. 10.1103/PhysRevB.93.155104. [DOI] [Google Scholar]
- David A.; Rakyta P.; Kormanyos A.; Burkard G. Induced spin-orbit coupling in twisted graphene–transition metal dichalcogenide heterobilayers: Twistronics meets spintronics. Phys. Rev. B: Condens. Matter Mater. Phys. 2019, 100, 085412. 10.1103/PhysRevB.100.085412. [DOI] [Google Scholar]
- Stoner E. C.; Wohlfarth E. P. A mechanism of magnetic hysteresis in heterogeneous alloys. Philos. Trans. R. Soc., A 1948, 240, 599–642. 10.1098/rsta.1948.0007. [DOI] [Google Scholar]
- Shen K.; Vignale G.; Raimondi R. Microscopic theory of the inverse Edelstein effect. Phys. Rev. Lett. 2014, 112, 096601. 10.1103/PhysRevLett.112.096601. [DOI] [PubMed] [Google Scholar]
- Sinova J.; Valenzuela S. O.; Wunderlich J.; Back C.; Jungwirth T. Spin hall effects. Rev. Mod. Phys. 2015, 87, 1213. 10.1103/RevModPhys.87.1213. [DOI] [Google Scholar]
- Bauer G. E.; Saitoh E.; Van Wees B. J. Spin caloritronics. Nat. Mater. 2012, 11, 391. 10.1038/nmat3301. [DOI] [PubMed] [Google Scholar]
- Novoselov K.; Jiang D.; Schedin F.; Booth T.; Khotkevich V.; Morozov S.; Geim A. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. U. S. A. 2005, 102, 10451–10453. 10.1073/pnas.0502848102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H.; Wu J.; Huang X.; Lu G.; Yang J.; Lu X.; Xiong Q.; Zhang H. Rapid and reliable thickness identification of two-dimensional nanosheets using optical microscopy. ACS Nano 2013, 7, 10344–10353. 10.1021/nn4047474. [DOI] [PubMed] [Google Scholar]
- Zomer P. J.; Guimarães M. H. D.; Brant J. C.; Tombros N.; van Wees B. J. Fast pick up technique for high quality heterostructures of bilayer graphene and hexagonal boron nitride. Appl. Phys. Lett. 2014, 105, 013101. 10.1063/1.4886096. [DOI] [Google Scholar]
- Benitez L. A.; Torres W. S.; Sierra J. F.; Timmermans M.; Garcia J. H.; Roche S.; Costache M. V.; Valenzuela S. O.. Tunable room-temperature spin galvanic and spin Hall effects in van der Waals heterostructures. 2019, arXiv:1908.07868v1. arXiv.org e-Print archive. https://arxiv.org/abs/1908.07868. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.