Understanding Gas Storage in Cuboctahedral Porous Coordination Cages

Abstract

Porous molecular solids are promising materials for gas storage and gas separation applications. However, given the relative dearth of structural information concerning these materials, additional studies are vital for further understanding their properties and developing design parameters for their optimization. Here, we examine a series of isostructural cuboctahedral, paddlewheel-based coordination cages, M₂₄(^tBu-bdc)₂₄ (M = Cr, Mo, Ru; ^tBu-bdc²⁻ = 5-tert-butylisophthalate), for high-pressure methane storage. As the decrease in crystallinity upon activation of these porous molecular materials precludes diffraction studies, we turn to a related class of pillared coordination cage-based metal-organic frameworks, M₂₄(Me-bdc)₂₄(dabco)₆ (M = Fe, Co; Me-bdc²⁻ = 5-methylisophthalate; dabco = 1,4-diazabicyclo[2.2.2]octane) for neutron diffraction studies. The five porous materials display BET surface areas from 1,057 – 1,937 m²/g and total methane uptake capacities of up to 143 cm³(STP)/cm³. Both the porous cages and cage-based frameworks display methane adsorption enthalpies of −15 to −22 kJ/mol. Also supported by molecular modeling, neutron diffraction studies indicate that the triangular windows of the cage are favorable methane adsorption sites with CD₄-arene interactions between 3.7 and 4.1 Å. At both low and high loadings, two additional methane adsorption sites on the exterior surface of the cage are apparent for a total of 56 adsorption sites per cage. These results show that M₂₄L₂₄ cages are competent gas storage materials and further adsorption sites may be optimized by judicious ligand functionalization to control extra-cage pore space.

Graphical Abstract

INTRODUCTION

Three-dimensional porous materials have been widely investigated for gas storage applications. Although these have included carbon dioxide,¹ oxygen,² ammonia,³ acetylene,⁴ sulfur dioxide,⁵ ethylene oxide,⁶ ethylene,⁷ and nitrogen,⁸ they have most commonly been studied for the high-pressure storage of small molecules of consequence to energy.⁹ Indeed, the storage of hydrogen^10–12 and methane^13–15 in metal-organic frameworks has been the topic of recent review articles. In the case of the former, many MOFs have displayed high H₂ storage capacities at cryogenic temperatures, although these are greatly diminished near 298 K. Methane storage capacities approaching DOE targets have been recently reported for a number of metal-organic frameworks.¹⁶ When considering the deliverable capacities of these materials, along with their actual densities (as opposed to crystallographic densities which are often utilized for total adsorption calculations), MOF capacities fall significantly short of targets.¹⁷ Although flexible MOFs have been touted as a means to elevate deliverable capacities of these materials,¹⁵ (i) flexible frameworks also suffer from a large discrepancy between bulk and crystallographic density and (ii) a complicated tank design is required to accommodate its dramatic expansion/collapse.¹⁸ Though, it is clear that significantly altered strategies must be employed to meet storage and delivery targets. Molecular adsorbents may show utility in this regard, as they offer novel strategies for precise pore design and enhanced control over crystallite size and morphology.¹⁹

Porous molecular solids have shown considerable promise for gas separation,²⁰ catalysis,²¹ chiral separations,²² sensing,²³ and as soluble designer pores for porous liquids.²⁴ In addition to the benefits of three-dimensionally connected porous materials, molecular solids have the additional advantage of solubility and significantly increased molecular-level control. These can aid in the design, synthesis, characterization, and utilization of these adsorbents. However, understanding and optimizing porosity in these solids can be challenging as it can exist as a result of surface area intrinsic to the individual molecule or can arise from void space present from inefficient packing of molecules that need not display porosity.²⁵ Regardless, molecular materials have displayed BET surface areas in excess of 3,500 m²/g.²⁶ All-organic porous molecules encompass various molecular species; the organic molecule to first display porosity was Dianin’s compound (4-p-hydroxyphenyl-2,2,4-trimethylchroman).²⁷ Similarly, calixarenes,²⁸ cucurbiturils,²⁹ Noria,³⁰ phthalocyanines,³¹ boronic ester cages,³² alkyne-based cages,³³ and imine-based cages have all shown considerable porosity.³⁴ Hybrid metal-organic cages—also known as metal organic polyhedra³⁵ have been shown to adopt analogous structures, such as octahedral and cuboctahedral cages (Figure 1), but have displayed relatively limited porosity.^36,37,38 We aim to both expand the scope of porous metal-organic molecular materials and utilize spectroscopic, computational, and diffraction methods to better understand adsorption phenomena in them. In addition to the benefits of porous molecules mentioned above, the cation sites in hybrid metal-organic porous molecules could serve as sites for selective gas adsorption, gas storage, small molecule activation, or redox chemistry.

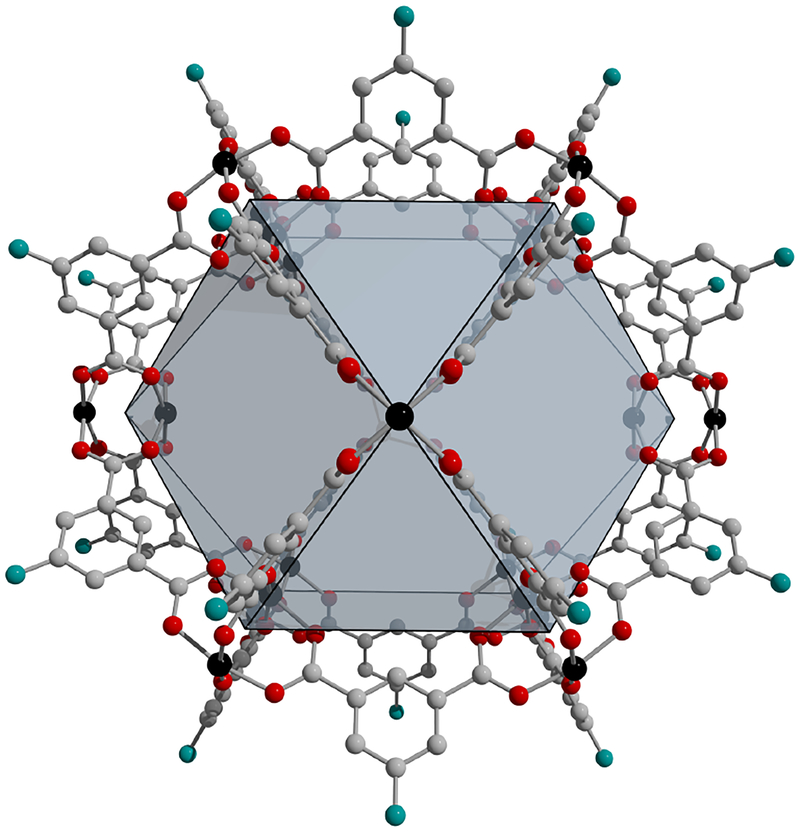
Figure 1.

M₂₄(R-bdc)₂₄ cuboctahedral cage featuring bimetallic paddlewheel units. This pore structure, which is isolable as molecular species, is also pervasive in isophthalic acid-based MOFs. Black, gray, and red spheres represent metal (M), carbon, and oxygen atoms, respectively. The blue spheres represent functional groups (R) that can include hydroxy, alkyl, amino, and others.

Although some coordination cages have shown moderate levels of porosity, the most widely studied porous cages have been based on bimetallic paddlewheel building blocks. This is likely a result of the relative ease with which paddlewheel-based materials assemble and their compatibility with a wide variety of ligand functional groups. Indeed, in the vast area of metal-organic frameworks, a very large number of paddlewheel-based MOFs have been reported, from one- to two- to three-dimensional frameworks.³⁹ For porous coordination cages, paddlewheel building units often assemble into cuboctahedral and octahedral structures. These have been reported for a variety of transition metal cations and ligand functional groups. Cuboctahedral cages are an intriguing set of compounds as they have been isolated for Cr, Ni, Cu, Mo, Ru, and Rh.^40–45 Although some of these materials have been reported to possess high surface areas, specifically Cr₂₄(^tBu-bdc)₂₄ (^tBu-bdc²⁻ = 5-tert-butylisophthalic acid) with a BET surface area of 1135 m²/g,⁴⁶ porosity is often overlooked in coordination cages. Relatedly, there is a lack of structural studies on porous cages upon activation or gas adsorption.

Adsorption properties of porous cages can be partially inferred from analogous metal-organic frameworks, as the cuboctahedral cage serves as the building block for many well-known MOFs. For example, one of three pore types in the canonical MOF, HKUST-1, is a cuboctahedral cage.⁴⁷ Showing the versatility of paddlewheel building units, HKUST-1 analogues have been prepared using a wide variety of transition metal cations including Cr, Fe, Co, Ni, Cu, Zn, Mo, and Ru.⁴⁸ Many of the members of the PCN and NOTT/MFM families of frameworks similarly contain copper paddlewheel-based cuboctahedral pores, including PCN-11,⁴⁹ −12,⁵⁰ and −61⁵¹ as well as NOTT/MFM-112,⁵² −115,⁵³ −122⁵⁴ (also known as NU-125),⁵⁵ and −132.⁵⁶ The high surface areas and crystallinities displayed by these materials have spurred numerous adsorption and diffraction studies.^39,57 Although some of these have shown the importance of the triangular windows of the cuboctahedral pores in the MOFs as gas storage sites, the presence of additional smaller pores and ligand-based binding sites complicates structural studies. We have recently shown that a family of MOFs based on coordination cages and dabco pillars can be used to glean insight into gas adsorption sites in porous cages.⁵⁸ These frameworks feature cuboctahedral cages connected in three dimensions via dabco molecules. Frameworks of this type, which have been reported for Fe, Co, Cu, and Zn, display BET surface areas in excess of 2,000 m²/g. Further, the arrangement of cuboctahedral cages in the MOFs is nearly identical to those found in M₂₄(^tBu-bdc)₂₄ cages.

Herein, we report the synthesis and characterization of two novel dabco-pillared metal-organic frameworks based on cobalt and iron cuboctahedral cages. Detailed structural analysis of these solids suggest 5-functionalization of isophthalic acid is sterically limited to methyl substituents. The structures of these MOFs are analogous to a family of tert-butyl functionalized cuboctahedral molecules. We assess the Cr, Mo, and Ru analogs of these cages, in addition to the dabco-pillared MOFs, for high-pressure methane storage. Given the high surface areas and crystallinities of the frameworks, we investigated neutron diffraction as a means to infer the adsorption sites in the molecular solids, which display high volumetric methane uptakes and deliverable capacities. Additionally, we conducted molecular simulations of methane adsorption to confirm the analogous nature of methane binding sites in the materials.

EXPERIMENTAL SECTION

Materials and Methods.

With the exception of Ru₂(OAc)₄Cl,⁵⁹ metal salts and organic ligands were obtained from commercial sources and used without further purification. For the syntheses of Co₂₄(Me-bdc)₂₄(dabco)₆ and Ru₂₄ (^tBu-bdc)₂₄Cl₁₂ N,N-dimethylformamide (DMF), methanol (MeOH), and chloroform were obtained from commercial sources and used without further purification. Where syntheses and/or solvent exchanges are performed in a glovebox, solvents were obtained from a solvent drying system and stored in a glovebox on the appropriately sized molecular sieves.

Synthesis of Co₂₄(Me-bdc)₂₄(dabco)₆.

In a 100 mL media bottle, CoCl₂·6H₂O (2.365 g, 9.941 mmol), and H₂Me-bdc (1.801 g, 9.999 mmol) were dissolved in DMF (100 mL) and left to sit at room temperature for five days. In a separate 100 mL media bottle, dabco (1.116 g, 9.949 mmol), was dissolved in DMF (100 mL). The resulting cobalt/ligand stock solution (10 mL) was pipetted into five 20 mL glass scintillation vials. The dabco solution (10 mL) was layered onto the cobalt/ligand solution. The resulting solution was capped and heated at 365 K for 12 hours. The sample was allowed to cool to room temperature before removing excess solvent. Resulting dark purple cubic crystals were removed from the bottle with fresh DMF and a Pasteur pipette. Solvent exchange was completed by soaking the product in fresh DMF at 383 K for 3 days with the solvent replaced every 12 hours. The DMF washed solid was isolated by removing excess solvent with a Pasteur pipette and then soaked in chloroform at 333 K for three days with the solvent replaced every 12 hours. Activated material was obtained by evacuation at 348 K.

Synthesis of Fe₂₄(Me-bdc)₂₄(dabco)₆.

In an N₂ glovebox, FeCl₂ (0.100 g, 0.789 mmol) and H₂Me-bdc (0.142 g, 0.788 mmol) were dissolved in DMF (12 mL) in a capped 20 mL scintillation vial and heated at 393 K for two hours. Dabco (0.177 g, 1.578 mmol) was then dissolved in acetonitrile (4 mL) and layered on top the DMF solution. The reaction was allowed to stand for one week, after which the reaction mixture was gently swirled and decanted to remove suspended product from larger, higher-density impurities. The light-yellow solid was then isolated by centrifugation and soaked in DMF at room temperature for three days replacing the solvent with fresh DMF every 8 hours. After DMF washing the solid was washed with benzene by a similar procedure. Over the course of benzene washes, the solid turns a lime-green color. Activated material was obtained by evacuation of frozen benzene at 273 K for two days followed by heating under vacuum at 323 K for two days. The resulting light green solid is incredibly air sensitive, turning dark brown upon exposure to O₂.

Synthesis of M₂₄(^tBu-bdc)₂₄ compounds.

These compounds were prepared as previously reported.^41,42,46 However, as surface areas of the Ru²⁺ and Mo²⁺ analogs were not previously reported or were low, respectively, modified solvent exchange and activation procedures were followed. For these, the solids (~200 mg) were soaked in 20 mL of anhydrous, air-free methanol for 48 hours, with the solvent replaced by fresh methanol every 8 hours. The solids were isolated by vacuum filtration and placed in gas adsorption tubes. The materials were activated under dynamic vacuum with a turbomolecular pump and a heating ramp rate of 0.1 K/min up to their final activation temperatures (Mo = 298 K, Ru = 398 K).

Optimized Synthesis of Mo₂₄(^tBu-bdc)₂₄.

In an N₂ glovebox, Mo₂(OAc)₄ (0.10 g, 0.234 mmol) and tert-butylisophthalic acid (0.052 g, 0.234 mmol) were dissolved in 10 mL of DMPU with 5 drops of pyridine and heated at 383 K for 1 day to yield large red crystals. The material was solvent exchanged and activated as reported above.

Gas Adsorption Measurements.

Gas adsorption measurements up to 1.1 bar were recorded on a Micromeritics 3Flex gas adsorption analyzer. Surface area measurements were recorded in a liquid nitrogen bath. 298, 308, and 318 K isotherms were recorded in an isothermal bath. Ultrahigh purity gas was used for both the free-space measurements (He) and analyses (N₂ or CH₄). Prior to measurements, samples were considered activated when their outgas rate under static vacuum was ≤ 2 μbar/min. High-pressure isotherms were collected on a Sieverts’ apparatus (PCT-Pro-2000 from Hy-Energy Scientific Instruments) using ultrahigh purity gases. Total adsorption was calculated using NIST Thermochemical Properties of CH₄ and the pore volume of each material, as determined via 77 K N₂ adsorption experiments.

Single-Crystal X-Ray Diffraction.

Crystals were mounted using viscous oil onto a plastic mesh and cooled to the data collection temperature. Data were collected on a Bruker-AXS APEX II DUO CCD diffractometer with graphite-monochromated Mo-Kα radiation (λ=0.71073 Å) for Co₂₄(Me-bdc)₂₄(dabco)₆ and with Cu-Kα radiation (λ = 1.54178 Å) focused with Goebel mirrors for Mo₂₄(^tBu-bdc)₂₄.⁶⁰ Unit cell parameters were obtained from 36 data frames, 0.5 ° ω, from three different sections of the Ewald sphere. The polarized optical properties of the crystal, unit cell parameters, systematic absences and equivalent reflections in the diffraction data are consistent with F432 (209), F-43m (216) and Fm-3m (225) for Co₂₄(Me-bdc)₂₄(dabco)₆; and, uniquely, with P2₁/n (14) for Mo₂₄(^tBu-bdc)₂₄. The centrosymmetric space group option for Co₂₄(Me-bdc)₂₄(dabco)₆ yielded chemically reasonable and computationally stable results of refinement. The data were treated with multi-scan absorption corrections. The structures were solved using intrinsic phasing methods⁶¹ and refined with full-matrix, least-squares procedures on F².⁶²

The cage in Co₂₄(Me-bdc)₂₄(dabco)₆ is located at the intersection of two orthogonal mirror planes and a three-fold rotoinversion axis. The dabco ligand in Co₂₄(Me-bdc)₂₄(dabco)₆ was treated as an idealized rigid group with rigid bond anisotropic restraints and equal atomic displacement parameters for chemically equivalent atoms. The cage in Mo₂₄(^tBu-bdc)₂₄ is located at an inversion center. Although initial solutions for Mo₂₄(^tBu-bdc)₂₄ suggested disordered DMPU molecules at the central void as well as between polyhedra, only some of the DMPU molecules coordinated on the outer surface of the cage could be modeled satisfactorily. The t-butyl groups in Mo₂₄(^tBu-bdc)₂₄ were restrained such that the quaternary carbon to methyl carbon distance is 1.534(5) Å and the methyl carbon to methyl carbon distance is not allowed to be shorter that 2.451(5) Å. Three t-butyl groups in Mo₂₄(^tBu-bdc)₂₄ were given additional idealized geometry with the aromatic carbon to t-butyl carbon distance restrained to 1.527(16) Å. The atoms in Mo₂₄(^tBu-bdc)₂₄ were treated with global three-dimensional anisotropic displacement rigid bond constraints.

The protons on the water molecule at the center of the cage in Co₂₄(Me-bdc)₂₄(dabco)₆ could neither be geometrically calculated nor located and were ignored. All other hydrogen atoms were treated as idealized contributions with geometrically calculated positions and with U_iso equal to 1.2 (or 1.5 for methyl) U_eq of the attached atom. Remaining electron density that cannot be localized as atoms was treated as a diffused contribution.⁶³ The structures have been deposited at the Cambridge Structural Database as CCDC 1881620 and 1891146.

Neutron Diffraction.

Experiments were performed on 0.4495 g Co₂₄(Me-bdc)₂₄(dabco)₆ and 0.7061 g Fe₂₄(Me-bdc)₂₄(dabco)₆ at the National Institute of Standards and Technology Center for Neutron Research (NCNR). Data was collected at the high-resolution neutron powder diffractometer, BT1, utilizing a Ge(311) monochromator with an in-pile 60’ collimator, corresponding to a neutron wavelength of 2.0775 Å. Activated samples were loaded into vanadium sample cans in an He environment glovebox, and sealed with an indium o-ring onto a copper heating block containing a valved outlet for gas loading. After mounting samples onto a bottom-loaded closed cycle (CCR) refrigerator, samples were cooled to base temperature for measurement. For CD₄ gas doses, the sample was connected to a fixed-volume gas manifold, heated to T = 120 K, and cooled back to base temperature for measurement. Each of the two samples were dosed with ~ 0.5 and ~1.5 CD₄ per M, per formula unit. Adsorption was verified barometrically prior to cooling to avoid condensation of the vapor phase for each gas dosage, with each sample dosed twice with CD₄.

Neutron powder diffraction data was analyzed using Topas Academic.⁶⁴ The space group $Fm\overline{3}m$ was chosen based on analogous previously reported structures.^58,65 Initial Pawley refinements were first conducted to determine a background function, lattice parameters, and peak shapes.⁶⁶ The position and orientation of molecules was then solved using rigid bodies with the global optimization method of simulated annealing (SA) in real space.⁶⁷

Rigid bodies were refined similarly to our previous work, using a full methyl-isophthalic acid (bdc) centered and refined on a 96k (x, x, z) position (with two orientations of methyl group), and a full dabco molecule allowed to rotate along a 48i (x, 0.5, −x) position. Using trigonometric constraints, both only required one variable for rotational movement. As before, activated materials required an additional Me-bdc molecule, as well as DMF molecule, refined on a 96k (x, x, z) and a 32f (x, x, x) sites respectively, with the additional Me-bdc allowed to freely move and the DMF molecule to rotate around a fixed axis using one degree of freedom. The refined positions of these two molecules represents their disordered, occupied space, rather than absolute positions. Once a reasonable solution was found, the number of atoms and their Wyckoff positions were corrected, followed by refining occupancies and thermal parameters separately. Additionally, occupancies which refined within error of unity were fixed and thermal parameters were fixed across each rigid body.

Once activated structures were determined, SA refinements were conducted on CD4 gas loaded data. Initial positions were determined using Fourier difference maps in both Topas Academic and GSAS.^64,68 This involved the addition of four CD₄ molecules; one at the open metal site on a 48i (x, x, 0.5) position, one in the corners of triangular windows on a 96k (x, x, z) site, one in the corners of square windows on a 96j (0, y, z) site, and one between four triangular windows on a 32f (x, x, x) site. Initially the orientation of each molecule was fixed according to known methane interactions,^69,70 which additionally mapped each CD₄ molecule onto itself. Each molecule was then allowed to freely rotate, which keeping as many variables fixed as possible, then additionally allowed to refine off each Wykoff position, all while adjusting occupancies as needed. Final CD₄ positions/orientations were chosen based on how each additional freedom of movement improved the refinement. Where possible the activated structure was fixed throughout this process. Once final CD₄ positions were obtained occupancies, thermal parameters, and lattice parameters were refined.

The resulting refinements from this process are shown in Figures S1–6. Despite numerous attempts at deuteration on these compounds, dabco molecules contained 10–25 % hydrogen, and Me-bdc molecules contained 65–85 % hydrogen. Given that complete removal of excess DMF and Me-bdc was not possible without structural degradation, there is considerable incoherent scattering due to hydrogen. However, Weller et al.,^71,72 as well as our previous MOF work,⁷³ has shown that neutron powder diffraction is quite possible with various amounts of hydrogen in crystalline materials, with hydrogen positions readily accessible due to their negative contrast. It is understandable that due to the amount of hydrogen, as well as the large unit cell, that the patterns do not contain much information beyond Q = 2 Å⁻¹, despite containing sharp crystalline peaks. The Rietveld analysis indicates that there is a good agreement between the data and the models (Figures S1 and 2), with the resulting activated materials being commensurate with previously reported analogous materials. The model CD₄ dosed structures are additionally in exceptional agreement with the neutron data (Figures S3–S6).

Computational Methodology.

We used our open-source software for classical molecular modeling in nanoporous crystals, PorousMaterials.jl. The Julia code and input files to reproduce our calculations are available on Github.⁷⁴

Molecular Model.

We approximate the material as crystalline and rigid, using the experimentally determined crystal structures (with disorder repaired to arrive at chemically valid structures) as input to our molecular simulations. We model the potential energy of a microstate of gas molecules in the material as pairwise additive interatomic interactions described by 12–6 Lennard Jones potentials. We model a methane molecule as a single, “united-atom” interaction site with parameters taken from the Transferable Potentials for Phase Equilibria (TraPPE) force field;⁷⁵ molecular simulations using these parameters accurately reproduce the normal boiling point and critical properties of methane. For the atoms composing the materials, we take Lennard Jones parameters for C, H, N, and O from the Dreiding Force Field⁷⁶ and for Co and Mo from the Universal Force Field⁷⁷ since they are missing from Dreiding. The non-bonded Dreiding force field parameters were tuned to reproduce crystal structures and sublimation energies of a large set of compounds. Parameters for cross-atomic-species interactions follow from the Lorentz-Berthelot mixing rules. We truncate the Lennard-Jones potentials at a cutoff distance of 14 Å and apply periodic boundary conditions to the simulation box consisting of a supercell of the crystal (box in Figure 6).

Figure 6.

Binding site elucidation via molecular modeling and simulation. Visualization of the spatial probability density of methane in Mo₂₄(^tBu-bdc)₂₄ during grand-canonical Monte Carlo simulations at 298 K and 1 bar (a), 5 bar (b), 35 bar (c), and 65 bar (d). Methane primarily adsorbs in the center of the triangular window at low pressure. At higher pressures, the corners of the triangular and square windows become populated. (e) Level surfaces of the potential energy of a methane molecule in the cage at −16 kJ/mol (orange) and −14 kJ/mol (white) highlight the triangular window and four corners of the square window as the most favorable binding sites.

Potential Energy Contours.

To generate the visualizations in Fig. 6 of the level surfaces of the potential energy V = V(x) of an isolated methane molecule at position x in the crystal, of we first superimpose on the supercell a regular grid points with less than 0.1 Å grid spacing. Then, we compute the potential energy of a methane molecule at each grid point and store it in a 3D array. We visualize the level surfaces of V(x), represented as a .cube file, using the VisIt visualization tool.⁷⁸

Molecular Simulations of Methane Adsorption.

We obtained the simulated methane adsorption isotherms at 298 K in Fig. S88 by conducting a set of Markov chain Monte Carlo simulations of the grand-canonical (μVT) statistical mechanical ensemble⁷⁹ at different chemical potentials. The simulation volume V is a supercell of the crystal. We relate the bulk gas pressure to a corresponding chemical potential using the Peng-Robinson equation of state for methane. As Markov chain transitions, we propose particle insertions, deletions, translations, and re-insertions with probability 0.35, 0.35, 0.25, and 0.tr05, respectively. A proposal to transition to a new microstate is accepted with probabilities governed by the Metropolis-Hastings rules so as to sample the grand-canonical statistical ensemble. Initiating the system with zero adsorbed molecules, we conducted 100,000 Monte Carlo burn-in cycles, then 100,000 Monte Carlo production cycles during which we collected statistics to compute e.g. the average number of adsorbed gas molecules in the system. A Monte Carlo cycle is defined as max(20,n) Markov chain transition proposals, where n is the number of molecules in the system immediately before a new cycle begins. Figs. S88 and S89 compare the simulated and experimental methane adsorption isotherms and heats of adsorption; the simulations over-estimate adsorption but agreement with the heats of adsorption is good.

Methane Spatial Probability Density.

We characterized the spatial probability density of methane molecules in the material during our grand-canonical Monte Carlo simulations as follows. First, we partition the simulation box (the supercell of the crystal) into a regular grid of voxels whose centers are less than 0.5 Å apart. Then, during the simulation, at the end of each Monte Carlo production cycle, we effectively count the number of methane molecules that belong to each voxel (“take a snapshot”). At the end of the simulation, we have a 3D histogram (normalized by the number of snapshots) of the positions of the methane molecules observed during the simulation. Because the voxels are too small to host two methane molecules, this gives an approximation to the integral of the spatial probability density of methane over the voxel. We visualize the spatial probability density, represented as a .cube file, using the VisIt visualization tool. We use the same scale to determine color for each pressure so the visualized densities can be readily compared across pressures. We used 100,000 burn-in cycles and 200,000 production cycles-- thus, taking 200,000 snapshots of methane molecules-- to generate the probability density plots for methane adsorption simulations at 1 bar, 5 bar, 35 bar, and 65 bar of pressure.

RESULTS AND DISCUSSION

Although metal-organic framework surface areas can often be optimized regardless of the exact nature of the synthesis, solvent exchange, and activation procedures, we have recently shown that these factors are vitally important for realizing maximal surface area in coordination cages.⁷⁰ The lack of three-dimensional connectivity in molecular systems often results in significant structural rearrangement upon solvent exchange and evacuation. Cages can also display differing porosity depending on the space group into which they crystallize. For one of the coordination cages displaying the highest surface area, Cr₂₄(^tBu-bdc)₂₄, the solid undergoes two phase changes upon activation, from P42/mnm to C2 to C2/c. In spite of this, the solid displays both high surface area and thermal stability. Encouraged by this, we sought to reinvestigate the reported M₂₄(^tBu-bdc)₂₄ (M = Cu²⁺, Mo²⁺, Ru^2+/3+) family of cages. For these adsorbents, surface areas are either entirely lacking (Ru) or reported to be significantly lower than the chromium(II)-based material (Cu = ~225 m²/g, Cr = 1135 m²/g, Mo = 437 m²/g).⁸⁰

Regardless of synthesis, solvent exchange, or activation conditions, we were unable to improve upon the surface area of Cu₂₄(^tBu-bdc)₂₄. This was similarly the case for Cu₁₂(cdc)₁₂ (cdc²⁻ = carbazoledicarboxylic acid), an octahedral coordination cage that displayed significantly diminished surface areas as compared to its chromium(II) and molybdenum(II) counterparts.⁷⁰ Ru₂₄(^tBu-bdc)₂₄Cl₁₂ displayed a comparable surface area to Cr₂₄(^tBu-bdc)₂₄ by utilizing specific solvent exchange and activation methods. To achieve this, as-synthesized solid was thoroughly exchanged with anhydrous, air-free methanol. Upon activation at 348 K, the solid displays a BET (Langmuir) surface area of 1057 (1540) m²/g (Figure 2). This value is in relatively good agreement with the value expected based on change in formula unit mass as compared to the Cr²⁺ cage (962 m²/g BET, 1522 m²/g Langmuir). The infrared spectrum of the activated material indicates the absence of metal- or pore-bound DMF or methanol, confirming complete desolvation of the cage (Figure S19). Despite demonstrating good porosity, powder X-ray diffraction reveals major structural rearrangement to the point of amorphization upon solvent evacuation (Figure S20), suggesting ordered cuboctahedra cages which are rotationally disordered relative to one another.

Figure 2.

N₂ adsorption isotherms collected at 77 K for the three M₂₄L₂₄ cages and two analogous pillared cage-based metal-organic frameworks.

In order to optimize the surface area of Mo₂₄(^tBu-bdc)₂₄, a significantly altered strategy was employed. Solvent exchange and activation of a sample that was prepared via the previously reported route (1,2-dichlorobenzne/pyridine mixture) afforded surface areas consistently below 800 m²/g.⁸⁰ For Mo₁₂(cdc)₁₂ we previously showed that surface area is significantly affected by synthetic conditions with higher symmetry space groups affording higher surface area materials.⁷⁰ Although varying synthetic conditions, including solvent, co-solvent, acid addition, and reaction temperature typically afforded cage that crystallized in the same space group as the previously reported solid, I4/m, utilization of a pyridine/N,N’-dimethylpropyleneurea (DMPU) mixture for the synthesis afforded an optimally porous material that crystallized in P2₁/n. Interestingly, the cage synthesized via this route adopts the same cuboctahedral structure arranged in the same orientation as the reported structure but displays a significantly increased surface area. Here, after room temperature methanol exchanges and activation, Mo₂₄(^tBu-bdc)₂₄ is shown to have a BET (Langmuir) surface area of 1321 (2105) m²/g. This value is significantly higher than the value predicted based on the increased formula mass of the cage as compared to Cr₂₄(^tBu-bdc)₂₄ (BET = 977 m²/g) and, to the best of our knowledge, represents a new record value for porous coordination cages.

Close investigation of the crystal structures of all three porous M₂₄(^tBu-bdc)₂₄ materials reveals multiple possible structural factors contributing to their high porosity (Figures S21–S40). The structures contain solvent-solvent interactions between metal-bound solvent molecules on adjacent cages. Given the ease at which solvent is removed from Cr²⁺, Mo²⁺, and Ru^2+/3+ paddlewheels, and as confirmed via infrared spectroscopy, these interactions are likely no longer present in the activated phases of these solids. It has been previously posited that paddlewheel-paddlewheel interactions account for their high surface areas and stabilities.⁴⁴ These types of interactions are relatively common with acetic acid-based paddlewheels. Here, the axial site of the paddlewheel cation coordinates to a carboxylate oxygen on an adjacent paddlewheel. This interaction is propagated throughout the structure to essentially form one-dimensional chains. However, examples of this are relatively rare for Cr²⁺ and Mo²⁺ paddlewheels.⁸¹ Further, the necessity of a charge balancing anion in Ru^2+/3+ structures prevents this interaction. The cage-cage interactions that are most likely predominantly involved are the van der Waals contacts between tert-butyl groups on adjacent molecules. Here, each tert-butyl group interacts with two groups from neighboring cages. The body centered cubic packing arrangement of cuboctahedra facilitates this interaction. As a result, all 24 tert-butyl groups on each cage feature these interactions. In all three structures, the average distance between adjacent methyl groups on tert-butyl functionalities is ~4.0 Å. This value is consistent with the van der Waals radius of a methyl group of 2.0 Å. Ultimately, rather than solvent-solvent interactions or paddlewheel-paddlewheel interactions, it is the large number of ligand-ligand interactions that endow the solids with sufficient thermal stabilities to survive solvent removal/activation.

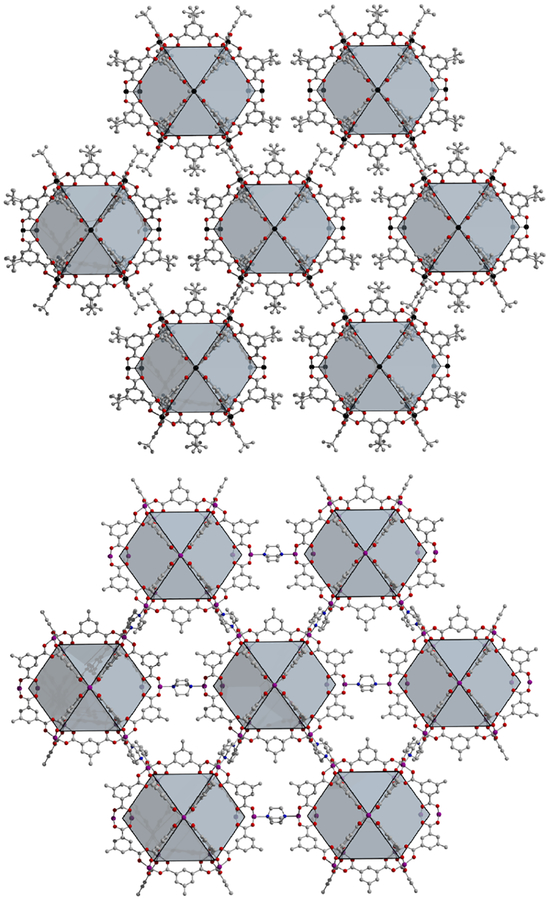
In order to better understand surface areas of tert-butyl-functionalized cuboctahedral cages, it is useful to compare them to the previously reported dabco-pillared MOFs, the structures of which are highly similar. For these, cuboctahedral cages are similarly arranged in a body centered cubic arrangement (Figure 3). Dabco molecules coordinated to the exterior sites of the cages connect them in three dimensions. Analogous to the structures of the molecular materials, the 5-position of the ligands of three cages are pointed to the same position. However, in the MOF the ligands are in much closer proximity. This is a result of the dabco pillar bringing the cages in closer contact as compared to the molecular case. The paddlewheel–paddlewheel distance in the pillared MOF is approximately 6.75 Å whereas this is expanded to 7.42 Å for the cages. This again points to the importance of ligand functionalization in designing and synthesizing these metal-organic cages. Close inspection of M₂₄(bdc)₂₄(dabco)₆ (M = Fe, Co, Cu, Zn) suggests the structure will be incompatible with large functional groups. In order to interrogate this, we turned to the synthesis of new members of the M₂₄(R-bdc)₂₄(dabco)₆ family with various metal cations and ligand functional groups.

Figure 3.

Structures of Mo₂₄(^tBu-bdc)₂₄ (top) and Co₂₄(Me-bdc)₂₄(dabco)₆ (bottom) illustrating the similarities between the cage and MOF structures, respectively. In the former, van der Waals contacts between tert-butyl groups give rise to three-dimensional pseudo-connectivity, whereas in the latter, metal-coordinated dabco ligands pillar the cages into three dimensions. Black, purple, red, gray, and blue atoms represent Mo²⁺, Co²⁺, O, C, and N, respectively. Solvent molecules and hydrogen atoms have been omitted.

Although Cu₂₄(OH-bdc)₂₄(dabco)₆ can be isolated via the addition of dabco to a solution of pre-synthesized cage, these materials are typically prepared via one-pot solvothermal reaction as the cages that comprise them are neither soluble nor synthetically accessible. The typically soluble Cr²⁺- and Mo²⁺-based cages lack the metal acidity to strongly coordinate dabco, a result of the presence of M–M quadruple bonds for these cations. To prepare new pillared cages, we screened the reaction of various Mn, Fe, Co, Ni, Cu, Zn, and Mo salts with R-bdc (R = methyl, alkoxides, tert-butyl, hydroxy, amino, cyano, nitro, and bromo) in the presence of dabco in various amide-based solvent systems. Consistent with the lack of pore space for bulky functional groups, we were only able to isolate crystalline product for M₂₄(Me-bdc)₂₄(dabco)₆ (M = Fe, Co, Cu) and Fe₂₄(OH-bdc)₂₄(dabco)₆, as confirmed by powder X-ray and neutron diffraction. Of these, only M₂₄(Me-bdc)₂₄(dabco)₆ (M = Fe, Co) displayed high levels of porosity, even after precise activation conditions, with BET (Langmuir) surface areas of 1937 (2264) and 1727 (2252) m²/g for the iron and cobalt analogs, respectively. These numbers essentially represent the upper limits of surface areas for analogous cage materials, as in the pillared MOFs both the interior and exterior surfaces of the cages are potentially accessible to probe molecules. Porous or potentially porous cages that lack directional ligand functional groups that can interact tend to close pack, exemplified by the low surface area of Cu₂₄(bdc)₂₄.⁴⁰ When all of the pore windows are blocked off, the solids are inaccessible to nitrogen or carbon dioxide. Often these materials display low levels of porosity as only the interior surface of the cages are nitrogen assessible. However, this should be highly tunable based on judicious ligand functionalization.

Given the nearly isostructural nature of the tert-butyl-based porous cages and the dabco-pillared MOFs (Figure 3), the latter offer a unique and powerful opportunity to further understand the former in terms of the storage of small molecules. At 298 K, all five materials display similar methane uptake up to one bar, ranging from 0.4 to 0.7 mmol/g (Figures S67–S72). At low pressures and correspondingly low uptake values, the one bar gravimetric capacities do not trend with BET or Langmuir surface areas. Temperature dependence of adsorption indicates adsorption enthalpies ranging from −15 to −21 kJ/mol and following the trend Ru < Mo < Cr < Fe < Co. This range of adsorption enthalpies is well within the range of values typically seen for porous solids.⁸² Methane adsorption enthalpies in the two MOFs are lower as their metal cations, which have been shown to be highly polarizing adsorption sites, are blocked on the exterior surface with pillaring dabco and on the interior surface with DMF. This effectively lowers the average adsorption enthalpy of the materials.

To further evaluate the methane storage properties of all five materials, high pressure adsorption isotherms were collected at 298 K (Figures S74–S85). At both 35 and 65 bar, the total gravimetric capacities generally correlate with BET surface areas with the up-take values following the trend Ru ~ Cr < Mo < Fe < Co. The gravimetric capacities, which range from 138 to 216 cm³/g, are generally comparable to many MOFs with similar surface areas.⁸² Given the greatly varying crystallographic densities of the solids, the volumetric uptakes of the solids are significantly altered with Cr (88 cm³(STP)/cm³) < Ru ~ Mo < Fe < Co (144 cm³(STP)/cm³) (Figure 4). In terms of the porous cages, the gravimetric uptakes of these three materials at 35 and 65 bar are actually lower than expected based on their surface areas and as compared to our previously reported M₁₂(cdc)₁₂ cages (M = Cr²⁺, Cu²⁺, Mo²⁺; cdc^2- = carbazoledicarboxylate). This is accentuated when comparing their volumetric capacities. For example, Mo₁₂(cdc)₁₂ displays 298 K volumetric capacities of 111.5 and 150.0 cm³(STP)/cm³ at 35 and 65 bar, respectively. Under these same conditions, Mo₂₄(^tBu-bdc)₂₄ shows uptakes of 97 and 120 cm³(STP)/cm³, despite having a BET surface area that is 20 % higher than the carbazole-based cage. This discrepancy is likely a result of the absence of highly favorable CH₄ binding sites in Mo₂₄(^tBu-bdc)₂₄.

Figure 4.

(Top) Isosteric heats of CH₄ adsorption calculated from fits to variable temperature low-pressure uptake experiments. (Bottom) High-pressure total methane adsorption in M₂₄(^tBu-bdc)₂₄ (black = Mo, blue = Ru, green = Cr) and M₂₄(Me-bdc)₂₄(dabco)₆ (orange = iron, purple = cobalt) at 298 K.

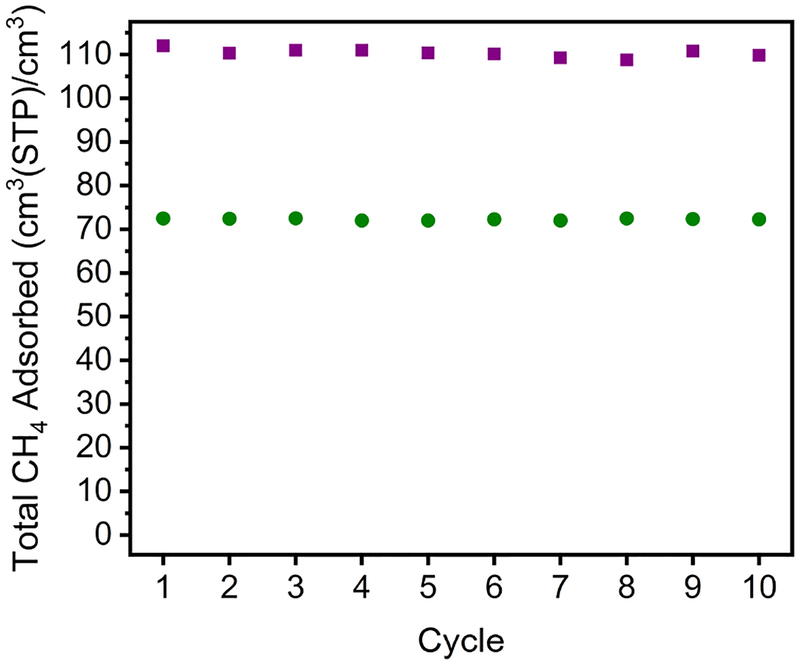
As methane storage materials, deliverable capacity, cyclability and adsorption/desorption kinetics are important considerations. As shown in Figure 5, two representative adsorbents-Cr₂₄(^tBu-bdc)₂₄ and Co₂₄(Me-bdc)₂₄(dabco)₆ display no loss in capacity at 298 K over 10 adsorption/desorption cycles. Under these conditions, the kinetics of both ad/desorption are very rapid, with 35 bar adsorption equilibria achieved in under two minutes. Desorption was carried out by placing the materials under dynamic vacuum at 298 K for five minutes. For a pressure swing from 35 to 5.8 bar, deliverable capacities of all five solids range from 45 (Cr) to 80 (Co) cm³(STP)/cm³. Increasing the adsorption uptake pressure to 65 bar increases the deliverable capacities to up to 102 cm³(STP)/cm³ (Full table of deliverable capacities for these materials and comparable MOFs are listed in Tables S8 and S9). Although these fall short of the record values of the best performing metal-organic frameworks (up to 200 cm³(STP)/cm³),⁸³ they are nearly on par when taking actual bulk density (rather than crystallographic density) into consideration. With this in mind, both Mo₂₄(^tBu-bdc)₂₄ and Co₂₄(Me-bdc)₂₄(dabco)₆ have 65–5.8 bar working capacities of 72 cm³(STP)/cm³ as compared to 83 cm³(STP)/cm³ for HKUST-1.⁸² The molecular nature of the cages reported here may offer an advantage in this regard, as their solubility may afford a means to tune phase and thus bulk density.

Figure 5.

Methane cycling in Cr₂₄(^tBu-bdc)₂₄ (green circles) and Co₂₄(Me-bdc)₂₄(dabco)₆ (purple squares) at 298 K and a final adsorption pressure of 35 bar. Between cycles, the samples were reactivated under dynamic vacuum for 5 minutes.

We next conducted molecular simulations of methane adsorption in both the MOF Co₂₄(Me-bdc)₂₄(dabco)₆ and the cage Mo₂₄(^tBu-bdc)₂₄. Our aims were to (i) elucidate the methane adsorption sites in the structures and the sequence in which they are occupied as pressure increases and (ii) juxtapose the hierarchy of adsorption sites in these two structures that harbor iso-structural cuboctahedral cages. To characterize the spatial probability density of methane, we first partitioned the simulation box into a regular grid of voxels. Then, we took snapshots during grand-canonical Monte Carlo simulations of methane adsorption and counted the methane molecules that belonged to each voxel. Fig. 6a–6d visualizes the spatial probability density of methane in Mo₂₄(^tBu-bdc)₂₄ at 298 K and 1 bar, 5 bar, 35 bar, and 65 bar. At low pressures, methane adsorbs primarily at the center of the triangular window. At higher pressures, the corners of the triangular windows and square windows are populated. Fig. 6e shows level surfaces of the computed potential energy of a methane molecule in the cage, confirming that the strongest binding sites are offered by the triangular window, followed by the corners of the square windows. The spatial probability density of methane in Co₂₄(Me-bdc)₂₄(dabco)₆ (Fig. S86) show a similar trend, where the triangular windows are filled first, then the corners of the square windows.

To confirm the mechanism of CH₄ binding in these materials, we turned to neutron powder diffraction. The lack of long-range order and low crystallinity in porous cages often precludes the use of diffraction methods for in-depth characterization. Given the structural similarities of the cages and frameworks, diffraction experiments on the porous frameworks can be used to infer information about adsorption sites, as our computational modeling confirms the similar nature of the adsorption sites between the framework and cage materials. Detailed powder neutron diffraction experiments performed on Fe₂₄(Me-bdc)₂₄(dabco)₆ and Co₂₄(Mebdc)₂₄(dabco)₆ allowed us to precisely determine CD4 binding sites and occupancies. For both frameworks, methane doses of 0.5/M²⁺ and 1.5 CD₄/M²⁺ were utilized. In Fe₂₄(Me-bdc)₂₄(dabco)₆ this corresponds to adsorption uptakes (pressures) of 36.8 cm³/g (4.2 bar) and 110.0 cm³/g (17.9 bar). As Co₂₄(Me-bdc)₂₄(dabco)₆ exhibits similar methane uptakes and a similar molar mass, the loadings correspond to 36.5 cm³/g (3.5 bar) and 109.4 cm³/g (16 bar).

In both materials at both loadings, four different methane binding sites are apparent (Table 1), three of which show loading-dependent occupancies (Figures S90–S101). The highest occupancy site in both frameworks is the center of the six triangular windows in the cage (Figure 7). Methane adsorbs in the bowl that is formed by three paddlewheel sites and three Me-bdc ligands. The CD4-arene distances for the iron and cobalt frameworks are 4.12(7) and 4.15(4) Å, respectively. Together with the methyl groups of the ligand, this center site forms the basis for additional adsorption sites at the triangular window that is disordered over three positions. These sites involve CD₄–CD₄ distances of ~3.6 Å and CD₄–methyl distances of approximately 4 Å. It is of interest to note that the pillaring dabco ligands are adjacent to this site and within van der Waals contact of the CD₄ molecule. As a result, dabco displays less rotational disorder as compared to the bare structures. The metal site on the interior surface of the cuboctahedron is the second highest occupancy site in both materials (~0.28 and 0.21 for Fe and Co, respectively). The occupancy of this site, with a M-C distance of approximately 2.3 Å, is loading independent. This is likely a result of the presence of metal-coordinated DMF and unreacted ligand on the interior surface of the cage, which was also observed in the IR spectra of the material. The corner of the square windows of the cuboctahedral cages serve as the final binding sites at these loadings. At this site methane is interacting with the carboxylate group of the ligand with CD₄–C distances of ~3.4 Å. These binding sites have also been observed in the cuboctahedral pore of HKUST-1 with similar ligand–CD₄ and CD₄–CD₄ distances (Figures S102–S103).⁶⁹ Between the six square windows and eight octahedral windows in the cuboctahedron, these account for 56 adsorption sites. Full population of these adsorption sites would afford gravimetric uptake capacities of 192, 165, and 154 cm³/g for Cr₂₄(^tBu-bdc)₂₄, Mo₂₄(^tBu-bdc)₂₄, and Ru₂₄(^tBu-bdc)₂₄Cl₁₂, respectively. On average, the cages achieve 90 % of these uptake values at 65 bar. Previous studies at higher methane loadings in HKUST-1 indicate additional methane binding sites on the interior surface of the cuboctahedral cage.⁶⁹

Table 1.

Methane occupancies in M₂₄(Me-bdc)₂₄(dabco)₆ (M = Fe, Co) at various loadings.

Site	0.5 CD4/Fe2+	1.5 CD4/Fe2+	0.5 CD4/Co2+	1.5 CD4/Co2+
Center of triangle	0.51(4)	0.62(4)	0.59(2)	0.62(2)
Metal	0.28(2)	0.29(2)	0.21(2)	0.21(1)
Top of triangle	0.20(2)	0.77(2)	0.14(2)	0.92(1)
Corner of square	0.13(1)	0.66(2)	0.13(1)	0.69(1)

Figure 7.

Methane binding sites in Co₂₄(Me-bdc)₂₄(dabco)₆ as determined by powder neutron diffraction. At loadings up to 1.5 CD4/M²⁺, four binding sites are apparent: the center of the triangular window, corners of the triangular window, corners of the square window, and open metal coordination sites on the interior surface of the cage. Black, red, gray, and blue spheres represent cobalt, oxygen, and carbon, and deuterium, respectively. The pink, yellow, and teal spheres represent carbon atoms of adsorbed methane.

The higher-loading powder neutron diffraction data shed light on the large discrepancy between the gravimetric and volumetric uptakes of M₂₄(^tBu-bdc)₂₄ and M₁₂(cdc)₁₂ materials. At a pressure of approximately 30 bar, the entire center of the cuboctahedral cage remains essentially empty, whereas the corresponding octahedral, carbazole-based cage displays negligible wasted volume. Further, the twelve-metal carbazole cages display minimal extra-cage pore volume. Comparison of pore size distribution plots for both cages reveals the presence of significant pore size greater than 15 Å in the cuboctahedral cage. In terms of volumetric gas storage, this wasted pore space is detrimental to the overall deliverable capacity of an adsorbent. However, the molecular nature of these cages can be utilized in this regard by judicious ligand functionalization to tune the extra-cage pore space. Further, their solubility and propensity to crystallize into a number of space groups and crystal morphologies renders them completely tunable for small molecule storage applications.

CONCLUSIONS

By optimizing synthesis, solvent exchange, and activation conditions, surface areas of porous coordination cages can approach those displayed by three-dimensional metal-organic frameworks. We have shown this to be the case for a family of tert-butyl-functionalized cuboctahedral coordination cages. The Cr²⁺, Mo²⁺, and Ru^2+/3+ analogs of these molecules display high BET surface areas, with Mo₂₄(tBu-bdc)₂₄ having a porous cage record surface area of 1320 m²/g. Additionally, calculations demonstrated molecular gas interactions are analogous in nature to pillared cuboctahedra coordination cages. Although the methane storage properties of these materials are not remarkable when compared to flexible, or ultra-high surface area metal-organic frameworks, the fact that they are molecular renders them significantly more tunable than their MOF counterparts. Further, in terms of deliverable capacities based on bulk as opposed to crystallographic densities, Mo₂₄(tBu-bdc)₂₄ boasts 87 % the methane capacity of HKUST-1, despite having a surface area that is approximately 40 % lower. Moving forward, this insight will aid in the development of future porous metal-organic materials. In particular, by precisely tuning both the pore size and shape of the cage, in addition to the pore space between cages, adsorbents with true molecular level control are attainable.