Points and lines inside human brains

Abstract

Starting from the tenets of human imagination, i.e., the concepts of lines, points and infinity, we provide a biological demonstration that the skeptical claim “human beings cannot attain knowledge of the world” holds true. We show that the Euclidean account of the point as “that of which there is no part” is just a conceptual device produced by our brain, untenable in our physical/biological realm: currently used terms like “lines, surfaces and volumes” label non-existent, arbitrary properties. We elucidate the psychological and neuroscientific features hardwired in our brain that lead us humans to think to points and lines as truly occurring in our environment. Therefore, our current scientific descriptions of objects’ shapes, graphs and biological trajectories in phase spaces need to be revisited, leading to a proper portrayal of the real world’s events: miniscule bounded physical surface regions stand for the basic objects in a traversal of spacetime, instead of the usual Euclidean points. Our account makes it possible to erase of a painstaking problem that causes many theories to break down and/or being incapable of describing extreme events: the unwanted occurrence of infinite values in equations. We propose a novel approach, based on point-free geometrical standpoints, that banishes infinitesimals, leads to a tenable physical/biological geometry compatible with human reasoning and provides a region-based topological account of the power laws endowed in nervous activities. We conclude that points, lines, volumes and infinity do not describe the world, rather they are fictions introduced by ancient surveyors of land surfaces.

Throughout the centuries, different skeptical claims have been proposed, from doubts about the possibility of knowledge/certainty, to the doctrine that true knowledge is uncertain, to concerns about the limitations of human mind. Here we will focus on the skeptical tenet that “human beings cannot attain knowledge of the external world”. Throughout the centuries, such skeptical claim has been just tackled through logical weapons (for a survey, from Pyrrho to Erasmus, from Montaigne to Feyerabend and Fogelin, see: Popkin and Maia Neto 2007). However, logic does not describe the world, rather the human interpretation of the world. Indeed, our brain works with models. Demarcation among objects and things is somewhat arbitrary, because our mind tends to exclude the continuity among the world’s structures. We tend to draw a line of separation among things that we judge different, arbitrarily excluding or including issues in our description, to achieve positive demarcations that allow a pragmatic treatment of the world based on regularity and uniformity (Bonzon 2017; Kim and Lim 2017). In touch with set theory, our mind, equipped with logic weapons, tends to split the set of the entire world in different, arbitrary subsets that do not really stand, in terms of quantum dynamics, for different things (Mizraji and Lin 2017; Peters et al. 2017). The same scientific concept of “observable” is based on the choice of variables in an experimental setting: scientists, putting aside most of the variables, focus their efforts on a few features. For example, elementary particles are fully defined just in terms of three experimental observables, i.e., charge, spin and mass (Seiden 2005), putting aside, for practical purposes, less “useful” features.

We will proceed as follows. In the first section, we will describe how the most successful description of the world, i.e., mathematics, is based on Euclidean geometry. Then, we will show how Euclidean geometry is intrinsically unable to describe the physical and biological world surrounding us. In the sequel, we will analyze feasible alternatives to Euclidean points and lines, in order to quantitatively describe the world. Then, in Sect. 2, we will provide an example of the feasible use of such novel techniques, tackling the issue of removing the troublesome concept of infinity from mathematical formulas.

Mining the authority of mathematics

Our physical and biological world can be described in terms of mathematical definitions, postulates, relations, theorems, formulas, equations and algorithms. Despite the claims that math is a collection of abstractions invented by our minds, it is astonishingly successful in order to explain and quantify a lot of issues of our world (Wigner 1960). Indeed, math elucidates many physical phenomena, such as the interaction of photons and physical surfaces, the diffraction of light with prisms, the apparent influence of speed on moving masses, and so on. Novel branches of math—such as algebraic topology, group theory and functional analysis—leading to far-flung approaches that include nonlinear dynamics in physics and chemistry—start to unveil also the mysteries of otherwise previously unclassifiable issues, such as weather, thrust, interactions and structure of neuro-systems (albeit minds) and the collective behaviors of societies.

A huge portion of our mathematics of the physical world is based on the amazingly simple Euclidean geometry. Indeed, starting from very straightforward assumptions and theorems such as those found in Euclid’s geometry, it is feasible to build also non-Euclidean geometries with the convergence of parallel lines (Aleksandrov 1969) and complex manifolds able to explain issues such as those in quantum mechanics. One of the main components of Euclidean geometry is the point, that stands for the most fundamental object. The first definition of a point (prior to Euclid) is given by the Pythagoreans: a point is a monad having position. Euclid begins his geometry with the definition of a point [that of which there is no part] (Def. 1, Euclid 300 BCE) and the extremities of a line are points (Def. 2). Euclid’s Def. 1 is interpreted by T.L. Heath to mean that a point is that which is indivisible in parts. Therefore, we are confronted with a primitive notion defined only by axioms that it must satisfy, i.e., the point upon which the whole apparatus is built, meaning that geometry cannot be described in terms of previously defined real objects or structures. Here we ask whether the zero-substance point holds true in our physical world and extend our analysis also to other Euclidean objects, such as lines, surfaces, volumes and so on.

The physical unfeasibility of Euclidean points and surfaces

Despite the huge influence of the Euclidean geometry in current scientific approaches, its internal framework is fatally flawed from the very beginning, if we want to use it to describe physical (and also biological) phenomena. The geometric points described by Euclid, originally defined as “that which have no part”, are not equipped with any diameter, area, volume, or other physical features such as height, density, weight. Many constructs of Euclidean geometry are represented by a set of points, that stand for infinite collections of objects that conform to certain axioms. In particular, the Euclidean point is posited as something which has location but zero diameter. However, it is widely recognized that our world is quantized, and that a minimum length does exist, i.e., the Planck size. Instead of a Euclidean point, we arrive at a region-based view of points in which every point is a spatial region (Peters 2016b) with measurable diameter as well as location of its centroid. The quantization of matter leads to one of the hallmarks of spacetime, namely, Planck’s constant. This allowed scientists to formulate frameworks, such as string theories (Duff 1996; de Haro et al. 2013) and quantum gravity (Rovelli and Smolin 1988; Muxin 2011), in which our reality is quantized, and therefore discontinuous. Thus, a real manifold must be made of separable units, and is not a continuum with no holes. However, such an approach does not hold true for the Euclidean manifolds. In the sequel, we will show how and why an Euclidean geometric structure (such as points, lines, surfaces, volumes) cannot display a real counterpart, and are therefore useless in the description of our physical world.

Paraphrasing Aristotle’s account of continuity and indivisibility (ARISTOTLE PHYSICS Book VI, Part 1), things are said to be “continuous” if their extremities are one, “in contact” if their extremities are joined together, and “in succession” if there is nothing of their own kind intermediate between them (Bradwardine 1330). Nothing that is termed “continuous” can be composed of “indivisibles”: to make an example, an Euclidean line cannot be composed of points, the line being continuous and the point indivisible. Indeed, the extremities of two Euclidean points can neither be one (since of an indivisible there can be no extremity as distinct from some other part), nor together (since that which has no parts can have no extremity, the extremity and the thing of which the extremity is distinct). Moreover, if that which is continuous is composed of Euclidean points, these points must be either continuous, or in contact with one another. Therefore, indivisibles cannot be continuous: one thing can be in contact with another only if whole is in contact with whole or part with part or part with whole. But since indivisibles have no parts, they must be in contact with one another as whole with whole. And if they are in contact with one another as whole with whole, they will not be continuous. For Euclid, that which is continuous has distinct parts, and these parts into which it is indivisible need to be spatially separate. In particular, concerning the line, an Euclidean point cannot be in succession to another in such a way that length can be composed of points. Indeed, things are in succession, provided there is nothing of their own kind intermediate between them, whereas that which is intermediate between points is always a line, or a region of a surface. Again, if the Euclidean length (i.e., the line) could be composed of indivisibles, it could be divided into indivisibles, since each is divisible into the parts of which it is composed. But, as stated above, no continuous thing is divisible into things without parts. Nor can there be anything of any other kind intermediate between the parts: if there could be any such thing, it must be either indivisible or divisible, and if it is divisible, it must be divisible either into indivisibles or into divisibles that are infinitely divisible, in which case it is continuous.

In sum, because the Euclidean line is either continuous or depicted as an infinite set of zero-mass points, it does not describe real lines, that are made of a set of contiguous multi-mass regions.

The problem of a physical continuum becomes more murky, if we consider what means mathematically for a mapping between spatial regions to be continuous. Let $f:X\to Y$ be a mapping on $X$ into $Y,$ so that $f(x)\in Y\text{for}x\in X.$ In the context of proximity spaces, a point x is near a region or set of points A, provided $f(x)$ is near $f(A)$(Naimpally and Warrack 1970). In other words, a function proximally continuous, provided the function preserves pairs of sets so that whenever $\left\{x\right\},A$ are near (in the same proximity), so too $f(x),f(A)$ are near (Peters 2014). Put another way, a function $f$ is continuous, provided the image $f(x)$ of every point of adherence $x\in X$ is a point of adherence in the set $f(A)$(Smirnov 1952).

Again from a mathematics perspective, it is an axiom in proximity space theory that the closeness of a point to a cell complex that is a collection of 0-cells (vertexes) implies that the point is either on the boundary or within the cell complex. By contrast, a physically continuous mapping from a computational proximity perspective (Peters 2016a) imply that the closeness of a physical region such as an atom $\chi$ to another physical region such as a collection of atoms $A$ means that $\chi$ is the in the neighbourhood of A, not that $\chi$ is in A.In other words, as anticipated by old philosophers too (Autrecourt and About 1340), closeness of points and sets in mathematics is quite different from the closeness of points and sets in the physical world. Instead of the conventional closeness of points and sets, the axiomatic foundations of the descriptive closeness of points and sets has been recently introduced (Di Concilio et al 2018). In the context of descriptive proximity, the closeness of points and cell complexes is viewed in terms of overlapping descriptions of the points and the sets. In other words, a feature vector that describes a point and the feature vector that describes a cell complex overlap without requiring that the descriptive closeness of a point x and cell complex A implies the inclusion of the point x in the cell complex.

As for the line, the same applies also for other Euclidean structures, such as two-dimensional surfaces and three-dimensional volumes. Indeed, every continuous Euclidean manifold (whatsoever its dimensions may be) is divisible into divisibles that are infinitely divisible: if it were divisible into indivisibles, we should have an indivisible in contact with an indivisible, since the extremities of closed manifolds that are continuous with one another are one and are in contact. This means that a collection of n-dimensional Euclidean structures cannot give rise, when joined together, to a n + 1 dimensional manifold. Therefore, the Euclidean points, lines, surfaces, volumes cannot exist in the real world. In particular, considering that physical space is quantized and that the minimum possible length is the Planck one, a real “point” cannot exhibit zero mass. Furthermore, at Planck length, another problem arises for an hypothetical basic “point”: many theories predict that the minimum separable structure, i.e., the string, lies in 10–11 dimensions, rather than being a dimensional. Therefore, in the real world, also the simplest structure, i.e., the real point, must be a spatial region that displays nonzero mass in spacetime, otherwise it cannot exist. Furthermore, as stated above, it is also difficult to talk about real lines, surfaces, volumes, given the indefiniteness and vagueness of their Euclidean definition and structure.

Further possibilities to cope with the physical reality

In the previous paragraph, we showed that the concept of Euclidean points and n-dimensional manifolds do not hold true for the description of our real world, because every physical structure cannot be built starting from nonzero mass ones. An Euclidean line does not exist in the real world, because a real line must be composed of spatial subregions, and this is not compatible with the Euclidean tenets. It might be objected that a line could be made of points made of bosons, that, satisfying the Bose–Einstein condensate theory, can be described as superimposed. However, a real line in our world must be composed of matter, i.e., fermions that are subject to the principle of locality: therefore, a point made of fermions cannot be superimposed to another one, because they must occupy different locations in space. It might also be objected that a line could be made of different points that are not superimposed, rather they are separated by a small void, but it is not the case of the Euclidean line’s description.

Our results suggest that it’s time to change our approach. It is clear, from our account, that the Euclidean axiomatic system cannot hold in the real world. The Euclidean point is just a conceptual device, and the same holds for its consequences: lines, surfaces, volumes. The physical impossibility of points holds also for “surfaces”. For example, in weighting, since many years, there is the problem to take into account where the mass surface ends, because there are always, without solution of continuity, “layers” of air molecules more or less interacting with the “solid”, part of which does influence the “weighted mass” also in the most accurate measurements. That is already a fact long since in precision metrology: “the non-uniqueness in these cases comes from thickness of the adherent interface layer(s), having an effect different from zero on the actual dimensions of the object, i.e., adding additional mass to the object with possibly time-dependent variability” (Pavese and Charki 2016).

Is it feasible to provide definitions of points and manifolds other than the Euclidean ones, in order to overtake its fatal limitations in the description of physical matters?

Despite there exist several regions-based accounts of space/time, due to Roeper, Menger, Tarski and others (Shapiro and Hellman 2017), the most of them, contrary to our approach, follow the Aristotelian theme that continua are not composed of points. A more recent view of a point by M. Simon (1901) moves closer to physical points. According to such an approach, a point is the limit of localization. More in keeping with the contemporary view of a point as a property of duration, a theory of extensive connection and atomicity of actual entities has been built (Whitehead 1929). The notion of extensive connection brings us full circle to an expansion of cellular topology and physical proximity space theory, in which a point stands for the minimal part of overlapping regions of physical space, such as overlapping perimeters of vortex atoms that live together in motion continua with limited duration. In other words, a point is a finite region of space with non-zero area, while a line is drawn from one region to another (Peters 2016a).

One region A includes another region B, whenever every region connected to B is also connected to A (Whitehead 1929). In other words, region A is connected to region B, provided there is a path from any subregion of B to a subregion of A. The extremity of a connecting path between subregions is itself a subregion with measurable area, albeit a tiny subregion that has the appearance of a point in Euclides’ surveyer-like geometry.

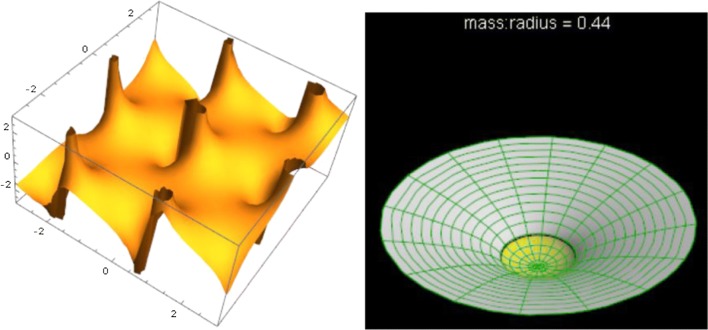
We may state that a region of space is the maximum distance between subregions (intervals) of its bounding edge. This definition allows the description of a point as a single abstract spatial vertex: in other words, our physical reality can be described in terms of multiple surface spacetime vortices, in which each vortex is a funnel reaching down to a physical limit, called a vertex. Examples are provided in Fig. 1. This approach permits us to remove the unwanted Euclidean geometry from the quantitative assessment of our world.

Fig. 1.

Examples of sample vortices. Left: a Weierstrass-Zeta mathematical model for multiple surface spacetime vortices, in which each vortex is a funnel reaching down to a physical limit called a vertex. Right: black hole vortex (initial mass radius 0.44 km) formation. It results from steadily increasing strong gravitational force that pulls neighboring chunks of matter into its funnel winding down to the squish level. Therefore, massive chunks of matter are squeezed to the diameter of a vortex

A humanly reasonable Euclidean geometry

Despite the usefulness of Euclidean geometry, our results suggest that it’s time to change our approach to the geometry of physical surfaces, because Euclid describes totally abstract surface regions. It is also feasible to deliver a psychological explanation for the Euclid’s successful mathematical description of the world. Indeed, taking into account recent neuroscientific findings, we are allowed to hypothesize why our mind seems to recognize in the surrounding environment Euclidean points, lines, surfaces, volumes, despite the fact that they cannot, according to our account, exist in reality. Over the last few years, studies of receptive field properties in several mammalian visual brain structures, such as the lateral geniculate nucleus and the primary sensitive cortex, have suggested the existence of cell classes with unique functional response properties (Van Hooser et al. 2005; Viswanathan and Nieder 2017). To make an example, the cells of the cortical visual area V1 display basic receptive field properties, such as orientation selectivity, direction selectivity, bar length and end-stopping (Duffy and Hubel 2007). Further, similar to the primary visual cortex, orientation sensitivity was closely reflected by the receptive fields properties also in extracortical structures, such as the lateral geniculate nucleus (Li et al. 2018). Therefore, many experimental suggestions dating back just a few years suggest that our brain is equipped with neurons, located in cortical and extra-cortical areas, that selectively fire when our sight perceives angles, surfaces, lines, contours. And such angles, surfaces, lines, contours do not exist in the real world, provided that the borders of the objects cannot be as well sharply delimited as suggested by Euclidean geometry.

Our perception is perhaps an evolutionary mechanism that permits us to cope with our external, rather visual, world, in order to avoid dangers and harms. The detection by sight of geometrical issues in the environment (such as points, lines, contours and so on) does not necessarily describe the real world, but rather stands for a sort of internal map based on species-specific, innate interpretations of the physical reality. We are rather firmly wired, if not actually hardwired, to think of the abstractions represented by such programs as realities. The whole idea in biology is after all to respond to survival situations quickly and effectively, rather than to question or contemplate their deeper nature. In Karl Friston’s terms (2010), the brain is an inferential machine that compares the real world with an internal map, pre-existent in our mind. Therefore, it might be suggested that what we see is just partially real: indeed, we might ask whether other animals, such as, e.g., an ant equipped with olfactive-tactile perceptions rather than our visual ones, or a bat (Nagel 1974), are able to recognize points and lines. Indeed, some response properties, such as linearity of spatial summation, contrast gain, dependence of receptive field size on eccentricity and interlaced arrangement of cortical neurons, vary from species to species (Van Hooser et al. 2005; Mazade and Alonso 2017). To make an example, despite the fact that a squirrel has greater visual acuity and a physically larger V1 than some mammals that have orientation maps in V1, it is not provided of such maps (Van Hooser et al. 2005). In turn, electrophysiological recordings in awake and anesthetized turtles reveal that their dorsal cortex is sensitive to the spatial structure of natural images, and their receptive fields are not entirely uniform across space (Fournier et al. 2018). Therefore, the mapping and representation of visual space in turtle’s three-layered cortex differ from those found in mammalian primary visual cortex. This means that, contrary to the mammalian primary visual cortex, the turtle dorsal cortex performs a global, rather than local, analysis of the visual scene (Fournier et al. 2018). This means that, in animals different from us, spatial information can be found both at the single-neuron and population scales and a clear retinotopic mapping of thalamocortical projections is not detectable.

Our sensations and perceptions (and therefore our world) depend on the activity of our cortex. A recent study points towards this hypothesis. Indeed, Armenta Salas et al. (2018) showed that intracortical microstimulation in primary somatosensory cortex (S1) is a method of inducing discriminable artificial sensation. In a tetraplegic human with microelectrode arrays implanted in S1, the Authors reported replicable elicitations of sensations in both the cutaneous and proprioceptive modalities. Therefore, the direct activation of the cortex is able to achieve naturalistic percepts that closely mimic the body’s natural physiological capabilities.

Tackling the problem of infinity in physics and biology

We showed, in the previous paragraphs, that infinity does not exist in our physical and biological world, rather it is a technical device correlated with our mathematical formulations of the world issues. In their theories and models dealing with formulas that describe finite, measurable quantities, physicists do not appreciate the occurrence of unwished infinite values. Indeed, with the exception of various forms of conformal infinity (Frauendiener 2000; Sommers 1978), mathematical infinity—indeterminate infinite results in which, for example, solutions of the gravitational field equations cannot be continued (Bergmann 1989)—prevents scientific issues to provide practical formulas that correspond to, or at least approximate, the real observables. For example, in case of bodies with infinite gravitational mass and/or energy, equations become intractable and useless, since their results would be always the same, regardless of objects’ position, mass and movement. In some cases, infinite results mean that the used theory is approaching the point where it fails. A classic example is the black holes’ mathematical singularity: the commonest solutions of the general relativity’s equations allow for zero-size finite mass distributions, leading to infinite density, e.g., a point where general relativity breaks down and is incapable of appropriately describing events. Other examples are the Newtonian gravity and Coulomb’s law of electrostatics at r = 0. Although infinity can be used in physics, scientists require for practical purposes the final result being physically meaningful: e.g., in quantum field theory, infinities are treated through procedures such as renormalization (‘t Hooft 1971).

The concept of infinity is a painful concern also, e.g., in fullerenic issues. To make an example, Chan et al. (2016) carried out large-scale computational quantum chemistry calculations to obtain heats of formation for C60 and some higher fullerenes, using the DSD-PBE-PBE/cc-pVQZ double-hybrid density functional theory method. However, they noticed a slow convergence to the graphene limit, which they attributed to the relatively small proportion of fullerene carbons that are in “low-strain” regions. Indeed, it would take tens, if not hundreds, of thousands of carbons for a fullerene to roughly approach the limit. Other problems linked with infinity arise when researchers try to assess asymptotic shapes of symmetrical fullerene ball, that is a flat-sided polyhedron whose edges have an average curvature radius of order R^2/3 (Witten and Li 1993).

Here we propose a different way to cope with the enigmatic results of the infinity in the description of physical equations, holding out the possibility of a physical geometry (Peters 2016a) that is region-based instead of point-based. This approach leads to a form of Desarguesian affine space in which locally parallel lines converge (Zaka and Peters 2019). We infer scaling of the shape and energy of a space-enclosing elastic sheet such as a large fullerene ball of linear dimension R. Stretching deformation is crucial in determining the optimal shape, in conjunction with bending. The asymptotic shape of a symmetrical fullerene ball is a flat-sided polyhedron whose edges have an average curvature radius of order R2/3. The predicted asymptotic energy is concentrated in these edges and is of orderR1/3. Analogous edges with this scaling property should occur generally in elastic sheets with discrete disclinations.

Infinity as the continuation of a straight line in affine geometry

As stated above, unqualified infinity cannot be any of the physical observables which we either can assess or measure: when we set out to investigate the infinity, we must leap beyond simple physical concepts and use mathematics. Inspired by Nicholas de Cusa’ treatment of infinity (de Cusa 1440; Tozzi and Peters 2017a), here we illustrate how to use mathematical and geometrical features to undertake physical infinity. If one wants to assess finite physical measurements leading to infinity, one needs at first to consider finite mathematical figures and topological manifolds, together with their features and relations. Next, one must apply these relations in a projective way. Thirdly, one must thereafter, in a still more highly transformed way, apply the relations of these infinite figures to the general concept of mathematical infinity, which is altogether independent even of all figures and manifolds.

Let us start, in touch with de Cusa’s accounts, with the picture of mathematical infinite, which will be represented by a straight line. One can maintain that, if there were an infinite line, it would be a straight one, or, for example, an infinite triangle, circle or sphere. Since the latter three figures display infinite sides, as will be shown, they can also be described in terms of infinite lines. First of all, an infinite line would be a straight one. The circle’s diameter is a straight line, and its circumference is a curved line greater than the diameter. If the curved line becomes less curved in proportion to the increased circle’s circumference, then the maximum circle’s circumference, which cannot be greater, is minimally curved and therefore maximally straight (Fig. 2a). Indeed, in the Figure, the arcs of the larger circle are less curved than the smaller ones. Therefore, the straight line will be the arc of the maximum circle, which cannot be greater. An infinite line is necessarily the straightest; and to it no curvature is opposed. In the same way, every manifold with positive curvature, such as, for example, a triangle, or a circumference, or a sphere, can be described in terms of an infinite line standing for a maximum triangle, or a maximum circle, or a maximum sphere. Indeed, an infinite line is whatever is present in the curvature of a finite line: a line finite in length can be longer and straighter, therefore the maximum line is the longest and straightest. If figures are describable by a finite line, and if an infinite line is all-the-things-with-respect-to-which a finite line is in infinity, then it follows that an infinite line stands also for a triangle, a circle, and a sphere.

Fig. 2.

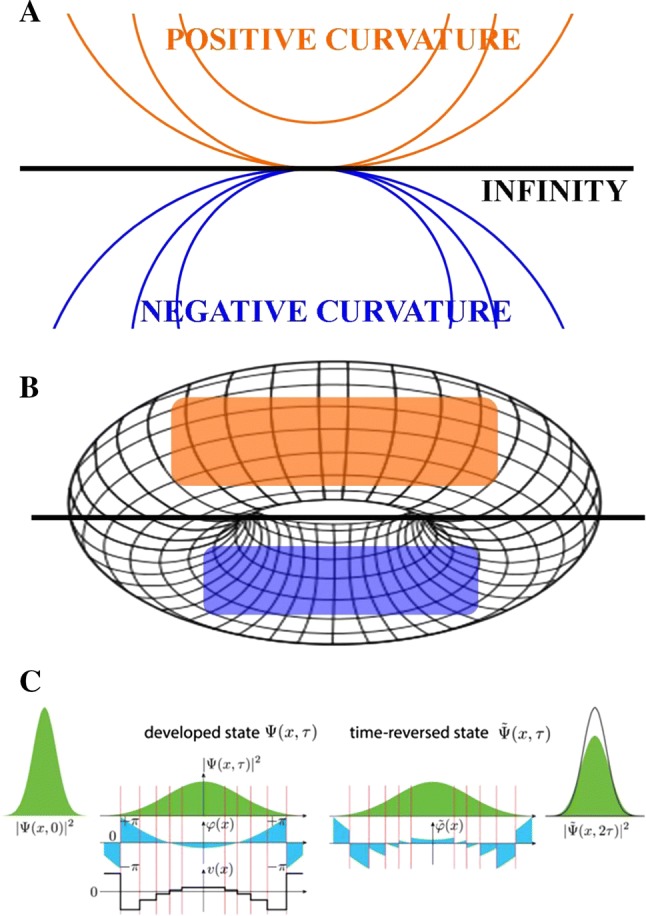
Curvature changes in biological and physical systems. a given a physical system described by progressively increasing curves on a positive-curvature manifold, the occurrence of infinity (straight line) can be removed by taking into account progressively decreasing curves on a negative-curvature manifold. b by placing physical observables on a toroidal manifold, one achieves a correspondence between positive and negative curvatures, thus erasing the unwanted occurrence of infinity. c Time-reversal according to Lesovik et al. (2019). From the second (“developed state”) to the third (“time-reversed state”) panel, the Authors modified the phase of the wave-function in every tiny area, so that the lines with positive curvatures in the second panel become lines with negative curvatures in the third one

How is it possible that an infinite line is a side of a triangle? Since any two sides of any triangle cannot, if conjoined, be shorter than the third, this means that, in the case of a triangle whose one side is infinite, the other two sides are not shorter, i.e., they are both infinite. Since there cannot be more than one infinite thing, an infinite triangle cannot be composed of a plurality of lines, even though it is the greatest and simplest triangle. And because it is a triangle—something which it cannot be without three lines—it will be necessary that the one infinite line be three lines, and that the three lines be one most simple line. And similarly, regarding the angles: for there will be only one infinite angle; and this angle is three angles, and the three angles are one angle. Nor will this maximum triangle be composed of sides and angles; rather, the infinite line and angle are one and the same thing, so that the line is the angle, because the triangle is the line. The larger the one angle, the smaller are the other two. Now, any one angle can be increased almost but not completely up to the size of two right angles. Nevertheless, let us hypothesize that it is increased completely up to the size of two right angles, while the triangle remains nonetheless a triangle. In that case, it will be obvious that the triangle has one angle that comprises the three angles and that the three angles are one. In the same manner, one can state that a triangle is a line, and an infinite line is a maximum triangle. For any two sides of a quantitative triangle are, if conjoined, as much longer than the third side as the angle which they form is smaller than two right angles. Hence, the larger the angle, the less the lines and the smaller its surface. Therefore, if, by hypothesis an angle could be two right angles, the whole triangle would be resolved into a simple line. Hereby it is evident that an infinite line is a maximum triangle. Next, by applying the same reasoning and the proper rotations, it is feasible to show that an infinite triangle is also an infinite circle and an infinite sphere.

In sum, an infinite line has been shown to be all that which is in the possibility of every finite line and manifold: a triangle is extracted from a line, and an infinite line from an infinite triangle. Hence, an important speculative consideration can be inferred: infinity is correlated with finite manifolds. Because infinite curvature is infinite straightness, this means that an infinite manifold can be described in opposite terms: it is not a thing and is not any other thing; it is not here and is not there; it is unqualifiedly free from all things and is beyond all things; is above the negation of all things. By a physicist’s standpoint, this explains why physical theories leading to infinite values are awfully problematic and difficult to cope with. In the next paragraph, starting from the above-mentioned de Cusa’s account, we propose a geometrically-framed method to solve the problem of infinity in physical systems.

Geometric removal of infinity in physical and biological formulas: an example

In the previous section, the result was reached that infinity can be expressed by a straight line with zero-curvature. How to use this observation, in the mathematical treatment of physical finite systems whose equations lead to the unwanted infinity? When one has a physical system of equations, he may project it into a positive-curvature manifold through well-described geometrical procedures (Frankel 2011). If the equations tend towards infinity, and therefore give meaningless results, one is allowed to remove the infinity by projecting the same physical equations on a negative-curvature manifold. Given equations’ trajectories moving in a convex phase space, when they tend to converge towards a zero-curvature manifold, the undesirable infinity is approximated. To remove the obstacle, we could describe the same equations on an opposite, concave phase space. Indeed, recent work has shown that the appropriate isometric space for embedding complex networks—and in particular the neural multidimensional ones, such as the human connectome (Tozzi 2019)—is not the flat Euclidean space, but rather a negatively curved hyperbolic space (Sengupta et al. 2016; Tozzi et al. 2018). Hyperbolic space has the property that power-law degree distributions, strong clustering and hierarchical community structure emerge naturally when random graphs are embedded in positive-curvature manifolds. It is therefore logical to exploit the structure of the hyperbolic space for useful embeddings of complex networks: in touch with this claim, it has been demonstrated that, when applied to the task of classifying vertices of complex networks, hyperbolic space embeddings outperform the Euclidean space ones (Chamberlain et al. 2017). To provide an operational example, the steps of the Langevin equation (Langevin 1908) experimentally detected in the three-dimensional (plus time) Euclidean space can be transported to a hyperbolic manifold, though, e.g., Levi–Civita or Ehresmann connections (Levi–Civita 1917; Ehresmann 1950). This allows us to assess dynamics inside abstract negative-curvature manifolds that mimic the real physical phase space where such processes occur. This procedure has been tackled by Tozzi et al. (2018), who showed that biophysical activities, including cellular metabolic pathways, protein folding and brain function, can be described in terms of curved trajectories in hyperbolic spaces which are constrained by energetic requirements. The transition and the relationships between the positive- and negative-curvature manifolds are described in Fig. 2b, for sake of simplicity, as taking place on the opposite sides (one convex, one concave) of a single multidimensional torus. A recent, very interesting approach shows that changes in curvatures, apart from removing infinity from physical equations, are able to reverse time too. Indeed, Lesovik et al. (2019) used variations in curvatures to reverse the arrow of time (Fig. 2c). This means that, once again in touch with the 1440 de Cusa’s account, a trajectory taking place on a positive-curvature manifold can be counteracted by one taking place on a negative-curvature manifold.

Other solutions to the problem of infinity were introduced in Geroch et al. Kronheimer Geroch, Penrose (1972), leading to computable solutions (Frauendiener 2000; Zenginoglu 2007). The basic approach is to rewrite metrics defined in terms of points at infinity with tractable, computable metrics that sidestep infinite planes and points at infinity such as those shown in Fig. 3.

Fig. 3.

Conformable infinity at computable points near, but not at ideal points. Left side: Tractable point on spheres in spacetime that are sliced by an infinite plane. Ideal points on the infinite plane are replaced with non-ideal points that are computable. Right side: Those parts of a sheaf of infinite places that intersect with computable lines are computable up to but not including the ideal points

Here is an example. The Minkowski spacetime metric in polar coordinates is $g=d{t}^2-d{r}^2-r^{2}d{\sigma }^2,$ where $d{\sigma }^2$ is the metric of the unit sphere. To achieve confomal rescaling of $g,$ the null coordinates $u=t-r$ and $v=t+r$ are introduced, to obtain

$$g=dudv-\frac{1}{4}{\left(v-u\right)}^{2}d{\sigma }^2.$$

The coordinates u and v range over the complete real line, provided $v-u\ge 0.$ This infinite range is compactified, using $u=tanU,v=tanV,$ and new null coordinates ranging over $\left(-\frac{\pi }{2},\frac{\pi }{2}\right),$ resulting in

$$g=\frac{1}{4{cos}^{2}U{cos}^{2}V}\left[4dUdV-{sin}^2(V-U)d{\sigma }^2\right],$$

which is not defined at $U=\pm \frac{\pi }{2},V=\pm \frac{\pi }{2}.$ To resolve this problem, a new metric is extracted from $g,$ namely,

$$g_{\mathit{new}}=4dUdV-{sin}^2(V-U)d{\sigma }^2.$$

$g_{\mathit{new}}$ is the tractable metric of the Einstein cylinder, which means that Minkowski space is now conformable embedded into the Einstein cylinder (Frauendiener 2000).

A foremost topic: nervous fractals and power laws

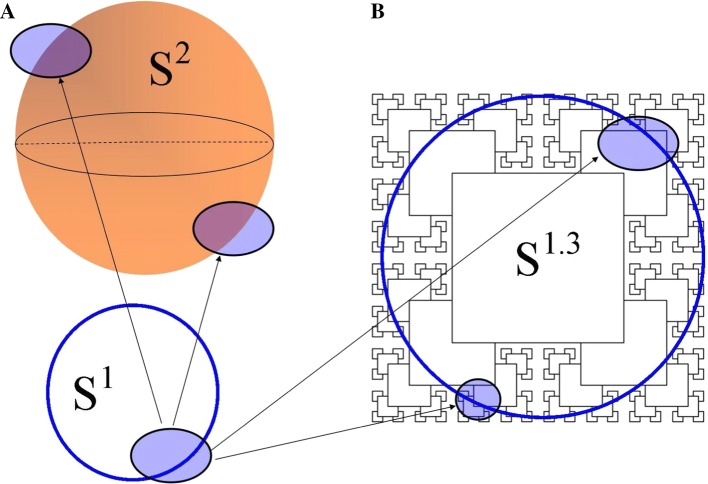
In this paragraph, we will tackle the issue of a point-free description of (spatial) fractals and (temporal) power laws. Scale-invariant behaviors have been shown to be ubiquitous in nature, as well as in the brain, and explain well the underlying dynamics of many natural phenomenon, and how we perceive the surrounding environment (Papo 2014; Fox et al. 2015; de Arcangelis et al. 2006; Lübeck 2004). It is noteworthy that fractals display an astonishing analogy with de Cusa’s logical concept of “coincidentia oppositorum”, both displaying self-similarity at all scales and magnitudes of observation. The frequency spectrum of cerebral activity exhibits a scale-invariant behavior S(f) = 1/fⁿ, where S(f) is the power spectrum, f is the frequency and n is the power spectral density. The latter is termed fractal “dimension” and equals the negative slope of the line in a log power versus frequency scatter plot (Milstein et al. 2009; Pritchard 1992). Power law distributions contain information on how large-scale physiological and pathological outcomes arise from the interactions of many small-scale processes. leading also to self-organized criticality (de Arcangelis and Herrmann 2010; Jirsa et al. 2014). A recently introduced version of the Borsuk-Ulam theorem (BUT), termed re-BUT, states that there is a continuous mapping between regions in topological spaces (Peters 2016a). In simpler words, a single region in lower dimensions maps to two matching regions in higher dimensions, provided the function is continuous (Tozzi and Peters 2016). Note that, instead of the canonical points described in the standard BUT, in re-BUT a point-free description (i.e., based on regions) is provided (Fig. 4a). Is it suitable to make use of re-BUT (and therefore of point-free geometry) in the description of fractals and power laws? Tozzi and Peters (2016) showed that the dimensions involved in BUT and re-BUT could be Hausdorff (fractal) as well as spatial (Fig. 4b). Indeed, the fractal account gives rise to a dimension greater than the “classical” one-dimension which is generally attributed to the “normal” curves embedded in a standard Euclidean space. In Fig. 4b, we used, as an example, a dimension corresponding to the value of 1.3.

Fig. 4.

A point-free topology allows description of fractals. a the novel BUT variant, termed re-BUT, describes a pointless feature (blue shape) on a two-dimensional circle S¹. When projected onto a sphere S², two pointless features with matching description are achieved (blue shapes). b the pointless feature on S¹ can be projected not just to S², but also to the fractal structure S^1.3. Therefore, we achieve two pointless features in S^1.3 (blue shapes): they stand for two matching descriptions, because they depict the same fractal structure, self-similar at different magnifications and coarse-grained scales. (Color figure online)

In sum, point-free descriptions, through the use of topological weapons such as the re-BUT, can be extended to encompass the description of brain’s fractal dynamics too.

Conclusions: removing points, lines and infinity

Here we ask whether one of the basic building blocks of Euclidean geometry, i.e., the point, holds true in our physical world. Given our negative answer, we concluded that the Euclidean manifolds cannot properly describe the real world. Our observation suggests the need for a viable alternative to Euclidean geometry, despite its current utmost importance in the description of the reality surrounding us. Indeed, the Euclidean geometry, after many centuries from its first formulation, still stands for the main tenet of the ensuing mathematical and physical developments. Starting from its postulates and theorems, it has been feasible to consider exception conditions, such as curved space, that are more in keeping with the relativistic spacetime. Furthermore, Euclidean geometry allowed to work our way toward non-Euclidean geometries (Johnstone 1983), R. Descartes’s vortex geometry, sweeping comprehensive cellular complexes in Whiteheadean closure finite weak topology, V.G. Boltyanskii and V.A. Efremovich intuitive combinatorial topology, Edelsbrunner-Harer computational topology, Cech-Efremovich-Lodato-Naimpally-DiConcilio proximity spaces (Di Concilio 2013), K. Borsuk shape theory (Borsuk 1958, 1969), P.G. Tait’s knots (1877). Such improvements led to J.S. Birman’s braids, links, knots and mapping class groups that allow amazingly simple solutions to problems in quantum mechanics and to W.T. Kelvin’s knotted and knitted vortex atoms (Kelvin 1867). This also led to a deep understanding of Helmholz’s discovery (Helmholz 1858) of simple vortex rings and the vexing problem of vortex motion in perfect liquids, as well as the elucidation of thermodynamic properties of gases.

Further, we showed that points and lines are programs running in mammalian brains, able to capture predictable consistencies in the external world, in forms that are both compact and supportive of fast, first-level approximations even in slow, neuron-based brains. So, while a ball is not much like a point, it is enough like a point for a human or canine brain to use a point-like approximation of it to move a hand (or snout) to the right location to catch it when thrown (Bollinger 2018). Even though quantum uncertainty adamantly informs us that higher levels of detail always requires higher energy costs, our mammalian-brain mathematics treat this paradox as “minor detail” that can be overlooked in our formal treatments of the physical world (Barranca et al. 2018).

It is assumed by physicists, due to pragmatic issues, that no measurable quantity or event might have infinite values. Indeed, any physical theory needs to provide operational formulas that correspond, to or at least approximate, reality (e.g., Iyer and Petters 2007). As an example, if any object of infinite gravitational mass were to exist, any use of the formula in order to quantify the gravitational force would lead to a useless infinite result. The formula would be useful neither to compute the force between two objects of finite mass, nor to compute their motions. Sometimes, an infinite result of a physical quantity may mean that the theory being used is approaching the point where it fails. We provided a novel conceptual framework to theoretically solve the problem of the occurrence of infinity in physical equations. We compared (a) finite quantities to curved lines endowed in positive-curvature manifolds, and (b) intractable infinity to a straight line. In order to restore the equations and erase the straight line of infinity, we project the quantities onto curved lines endowed in negative-curvature manifolds.

We achieved at first a physical system’s description on, say, the convex surface of a manifold. In order to avoid the occurrence of infinite when the curvature approaches the zero, we projected such description to the concave surface of a manifold, through a long list of available and well-studied procedures of vectorial and tensorial transport: e.g., Ehresmann connections (Tozzi et al. 2017), parallel transport on Riemannian manifolds (Sengupta et al. 2016), and so on. In other words, we need at first to project a physical phenomenon which tends to intractable infinity onto a positive-curvature manifold, such as a triangle, or a sphere, or a donut-like manifold, arriving at a physical geometry useful in the physical sciences (see, e.g., Peters 2016a; Tozzi and Peters 2017b). Indeed, when the phenomenon’s calculations tend towards infinity, we achieve an unwanted flat line. To go back to a tractable description, we need now to introduce a negative-curvature manifold, corresponding to a modified physical phenomenon, where finite operations might take place.

We would like to bring to an end with a prediction: an intellectually satisfying and experimentally meaningful resolution of the apparent conflicts between quantum mechanics and classical physics, including general relativity, will not be possible until the Euclidean conceptual barrier we have described in our paper is fully overcome (Bollinger, personal communication). In particular, recognizing that “time” must also be “unEuclidified” should rather dramatically alter how we perceive and use to represent both quantum and classical time, making them more of a continuum in which the level of temporal detail once again depends on the resources applied. By then, using mathematical abstractions that no longer relegate spatial and temporal uncertainty “only” to the quantum domain, many of the seemingly insurmountable barriers between quantum and classical quite likely will disappear.