Scale-free behaviour and metastable brain-state switching driven by human cognition, an empirical approach

Abstract

We developed a framework to study brain dynamics under cognition. In particular, we investigated the spatiotemporal properties of brain state switches under cognition. The lack of electroencephalography stationarity is exploited as one of the signatures of the metastability of brain states. We correlated power law exponents in the variables that we proposed to describe brain states, and dynamical properties of non-stationarities with cognitive conditions. This framework was successfully tested with three different datasets: a working memory dataset, an Alzheimer disease dataset, and an emotions dataset. We discuss the temporal organization of switches between states, providing evidence suggesting the need to reconsider the piecewise model, in which switches appear at discrete times. Instead, we propose a more dynamically rich view, in which besides the seemingly discrete switches, switches between neighbouring states occur all the time. These micro switches are not (physical) noise, as their properties are also affected by cognition.

Introduction

The study of the dynamics and integration of information in the brain reveals fascinating coordination mechanisms. Take for instance the integration of low level visual information during the well-known feature binding process (Treisman 1996; Schneegans and Bays 2017; Fitousi 2018). We will not describe in detail feature binding here, but rather take enough elements from it to illustrate our point. When perceiving an object, information from different sensory modalities is registered in physically separated brain areas (Robertson 2003; Kondo et al. 2017). Even considering only the visual modality, colour, shapes, sizes and motion are registered in parallel at different locations. Ungerleider and Mishkin [cited in Treisman (1998)] proposed a ventral pathway registering colour and shapes, and a dorsal pathway coding motion and space. Our visual field is populated by a collection of objects that usually change over time. It can be concluded then that as objects or their properties change in our visual field, different brain regions engage and disengage in transient states of coordination. In addition, visual perception does not only involve low level signals, but also top-down effects. The mere concept of an object requires us to identify properties such as manipulability or topological connectedness (Taraborelli 2002). Beyond the visual modality, the environment that we perceive consists of a broadband, high temporal resolution stream of information. Furthermore, generally speaking cognitive functions require the interaction of low level and high level information, external and internal. Emotions, external stimuli, intentions and memories all interact in a coordinated fashion in our brain, and the mind can be thought of as the workspace in which these interactions occur. Writing down an idea (in a syllabic writing system), a simple everyday task, can illustrate this intricate set of interactions. To accomplish this task, an abstract idea needs to be phrased in words in our mind, and further decomposed into its constituent phonemes. The graphemes corresponding to the phonemes must be retrieved from memory, and visual, motor and haptic information must be integrated to perform the actual writing.

How does the brain manage to self organise to create and annihilate these transient coordination involving low and high level information? As early as 1974, Katchalsky et al. [cited in Werner (2007)] wrote “waves, oscillations, macrostates emerging out of cooperative processes, sudden transitions, patterning, etc. seem made to order to assist in the understanding of integrative processes of the nervous system”. More recently, the concept of metastability, or in general that of transient spatio-temporal patterns has attracted attention. Lehmann and his colleagues (Lehmann 1971; Milz et al. 2016) developed the concept EEG micro-states, temporary patterns of electric activity observed in EEG recordings. These EEG micro-states remain quasi-stable at the sub-second scale, to later give rise quickly to other patterns. EEG micro-states do not only appear during ongoing activity, but they are known to be modulated by cognitive activity (König et al. 1998; Lehmann et al. 2004), or conditions such as depression (Strik et al. 1995) or schizophrenia (Strelets et al. 2003). In the context of perception, Freeman and Holmes (2005) describes metastability in the neocortex with the recurrence of spatial patterns of phase and amplitude, or frames. These frames (Freeman and Kozma 2010; Kozma and Freeman 2017) carry the meaning of sensory information in spatial patterns of cortical activity that resemble discrete film frames. Buzsaki (2006, Chapter 5) suggests that the brain is in a high complexity, critical state, as might be evidenced by the power law (pink noise, in particular) in the EEG power spectral density. He proposes as well that the most important property of cortical brain dynamics is the ability to rapidly switch between metastable pink noise and oscillatory behaviour. Under this view, sensory or motor activity are perturbations (which we will refer to as disturbances) that can temporarily reorganize the effective connectivity to induce “transient stability by oscillations”. An oscillatory, short-lived regime can hold information required for psychological constructs, whereas the critical state allows for an efficient switching between states. Coordination dynamics (Kelso 2012; Bressler and Kelso 2016) is a theoretical framework in which complex systems theory is used to model this transient coordination. Metastability in this framework is a dynamical regime for the relative phase of coupled oscillators in which all stable fixed points have disappeared. Phase trapping, temporarily convergent dynamics, and phase scattering, temporarily divergent dynamics, are the result of competing tendencies. On the one hand, segregation, or modularity, promoting independent behaviour and local coupling; on the other hand, integration, a global attempt for cooperation. One of the reasons why the author proposes metastability is that, unlike multistability (where stable fixed points still exist), metastability does not require disengage mechanisms (such as stochastic noise or energy flow) for state switching. Tognoli and Kelso (2014) point out that although the concept of phase locking1 has gained increasing relevance in the study of neural assemblies’ synchronization, transients have not received an adequate attention due perhaps to the lack of truly dynamical approaches. According to them metastability has yet to be demonstrated and fully treated from a spatiotemporal perspective. To go a step further in that direction, we propose the framework presented in this study.

We propose that a suitable candidate to study brain metastability is the lack of EEG stationarity. EEG is known to be non stationary (Barlow 1985; Shin et al. 2015), it is considered however that it is composed of a succession of locally stationary segments. Kaplan et al. (2005) suggest that these non stationarities might arise from the switching of the metastable states of neural assemblies during brain functioning. Surprisingly, although EEG non stationarity might result from normal brain functioning, few researchers investigate directly whether non stationarities can convey relevant information about cognition, or about brain functioning in general. Most of the times, EEG nonstationarity is either not discussed at all, or considered as problem to circumvent given that many techniques such as power spectral density estimations, complexity measures and autoregressive models require stationarity. Common approaches are signal segmentation into stationary epochs (Agarwal and Gotman 1999; Florian and Pfurtscheller 1995; Azami et al. 2015), or the use of techniques that do not assume stationarity (Hazarika et al. 1997; Krystal et al. 1999). To list a few exceptions, Kaplan et al. (2005) developed a technique estimating synchrony between any two channels (operational synchrony) as the degree to which they undergo simultaneous switches. Cao and Slobounov (2011) studied the change of the dominant frequency of the EEG signal over time, and used this measure to detect residual abnormalities in concussed individuals. Kreuzer et al. (2014) found in a study regarding depth of anaesthesia, that during loss of consciousness stationarity is heavily influenced by the anaesthetic used. Fingelkurts and Fingelkurts further developed operational synchrony to propose the framework of operational architectonics (Fingelkurts and Fingelkurts 2001), aiming at characterizing the temporal structure of information flow in functionally connected neural networks.

Most of the above cited research, from EEG micro-states to EEG non-stationarity, assumes discrete timing. Switches occur in an abrupt manner, and the region remains in the same state until the next switch. Fingelkurts and Fingelkurts (2006) discuss the differences between the concepts of elements of thought and stream of consciousness. They review psychophysical, electrophysiological, neurophysiological and computational support for either discreteness or continuity of timing in cognition. Lehman and his colleagues postulate as well that the seemingly continuous stream of consciousness is actually a concatenated sequence of building blocks (Lehmann 1990). While acknowledging the existence of such discrete, abrupt changes, we investigate the time scale at which transitions happen, and whether small fluctuations around these states are noise or, alternatively, driven by cognition, which would be more compatible with continuous timing.

We take an empirical approach. We take a set of minimal assumptions about the spatiotemporal organization of brain dynamics under cognition, and derive from them a set of measurable properties. With said set of properties we train a classifier and classify data recorded from subjects undergoing specific (and known) aspects of cognition. If the assumptions are true and the specific aspect of cognition targeted affects the proposed measurable properties, then these properties will carry information about cognition. This information will allow classification with better accuracy than a random classifier. Our datasets consist of EEG recordings regarding Working Memory (WM), Alzheimer Disease (AD) and emotional valence.

Methods

We are interested in finding measurable physiological variables that are related to brain states, in characterizing the spatio-temporal properties of these variables, and in correlating these properties with cognition. EEG micro-states could be a candidate framework to study empirically the dynamics of transient coordination and spatio-temporal pattern formation under cognition. However, instead of using directly voltage values that are expected to be erratic individually, metastability can provide a hint to define surrogate variables directly related to brain states.

In statistical physics, a metastable system is a system out of equilibrium, with several available states (for instance liquid, solid and gas for water), and near the boundary between a subset of them. External inputs (energy, noise, matter...) can drive the system into one state or the other. As long as the system stays in a given state, the state variables (the distribution of molecular velocities in the case of water) of the system remain stationary, that is, the underlying distribution of the state variables does not change over time. Therefore, by definition, metastable systems are piece-wise stationary. In the case of the brain, ideally, we should take the electric activity of single neurons as state variables, but due to this impossibility, EEG measurements will be considered the state variables. It is possible then to divide the brain into regions corresponding to the EEG channels, and, assuming metastability, define the appearance of a state switch as the time at which the underlying EEG distribution changed.

Having identified the times at which switching occurs, the next question is how to characterise a state. When a statistical distribution changes, its statistical moments (mean, variance, skewness, kurtosis, ...) change as well. If, by definition, during the course of a state the underlying distribution of the system remains constant, then the collection of statistical moments can be used to characterise a state. A statistical distribution has an infinite number of moments, however, we suppose just as Von Bünau et al. (2009) that changes in EEG stationarity are already visible in the first statistical moments. To study these changes in statistical properties, for a given channel, at a given time t, we compute v(t), s(t), and k(t): the estimations of the variance, skewness and kurtosis over a short time window2 centred at t. The length of the window depends on the frequencies to be investigated, as will be explained in the “Methods” section. The vector v(t), s(t), and k(t) is a trajectory parametrised by time. During the course of a state, the elements of this vector are expected to remain constant, and hence the system will remain in one point of the three-dimensional space where the trajectory is embedded. When the underlying distribution changes, the system will move to another region of that space. We have then constructed variables that are sensitive to metastable state switches.

As a graphical example, take a random variable drawn from a normal distribution $\mathcal{N}(-3,1)$. After a certain time $t_0=0$, the underlying distribution changes to $\mathcal{N}(2,3)$, as we observe in Fig. 1a. Using a sliding window, we can compute the estimation of the first two statistical moments: the mean in blue, and the variance in red, in Fig. 1b. The time series of the estimation of the mean and variance can be considered a 2-dimensional trajectory, as shown in Fig. 1c. In this 2-dimensional space, a point is a state, and evidently there is estimation noise arising from the fact that the window has a finite length. If switches occur in a discrete manner, fluctuations in Fig. 1b at times other than $t_0$ are artifacts due to this noise only. We will show in “Method 1: Temporal structure of the switches” section that as these fluctuations correlate with cognition they are not only estimation noise, and therefore the assumption that switches occur at discrete times must be questioned.

Fig. 1.

a A synthetic signal. The underlying statistical distribution changes in the middle. b The time series of the evolution of the estimation of the two statistical moments over time, when using a window of 50 time points. c The process viewed as a trajectory in the space of states. Each dimension of this space is the estimation of a statistical moment

We have shown that above trajectory is affected by metastable state switching, and our working hypothesis is that if these states are representative of cognitive operations, then cognition should affect the properties of the trajectory in a predictable manner. In other words, we expect these states to reflect the local underlying dynamical regime, and how it changes to support different cognitive requirements. The methods described in this work aim at capturing these changes induced by cognition.

Data acquisition

Three datasets were used, a WM dataset, an AD dataset and an emotions related dataset. All recordings performed by us followed the principles outlined in the Declaration of Helsinki. All participants were given explanations about the nature of the experiment and signed an informed consent form before the experiment started.

WM dataset

20 subjects performed a WM task as described in Mora-Sánchez et al. (2015). The dataset consists of 530 trials lasting 10 s each. 281 of them correspond to low WM load and the rest to high WM load. All the artifacted trials were discarded, and eye blinks were removed with Independent Component Analysis (Bell and Sejnowski 1995). The sampling rate was 500 Hz, and 16 channels of the international 10–20 system were used: Fp1, Fp2, F7, F3, Fz, F4, F8, Cz, CP5, CP6, P3, Pz, P4, O1, Oz, and O2.

AD dataset

We used the same dataset as Vialatte et al. (2005). Recordings from 61 subjects were collected, 23 of which were AD patients, and the rest healthy, age-matched controls. For each subject 20 s of continuous recordings were available. Data was sampled at 200 Hz, using 21 channels: Fp1, Fp2, F3, F4, C3, C4, P3, P4, O1, O2, F7, F8, T7, T8, P7, P8, Fz, Cz, Pz, FPz, and Oz. Each 20 s recording was divided into 8 epochs. In total 488 epochs were analysed, 184 corresponding to AD patients and the rest to healthy controls.

Emotions dataset

We used the processed version of the DEAP dataset for emotions (Koelstra et al. 2012). 32 participants watched videos and rated them based on valence, arousal and dominance, in an integer scale from 1 to 9. EEG data was recorded while the subjects watched the videos, and our objective was to classify valence in two classes, one corresponding to the first half of the range of the scores, and a second class corresponding to the second half. Data was sampled at 128 Hz, using 32 channels: Fp1, AF3, F3, F7, FC5, FC1, C3, T7, CP5, CP1, P3, P7, PO3, O1, Oz, Pz, Fp2, AF4, Fz, F4, F8, FC6, FC2, Cz, C4, T8, CP6, CP2, P4, P8, PO4, and O2. EOG artifacts were removed as indicated in Koelstra et al. (2012). The original 60-s trials were divided into 10-s epochs, which gave rise to 7680 epochs, 3876 of which corresponded to negative valence.

The framework

For a schematic representation of the type of measures that we want to derive, we can imagine that we divide the brain into N regions: $r_1,r_2,\dots ,r_N$. We consider the state of region $r_i$ at time t to be $s_i(t)$. Whenever $s_i(t_1)\ne s_i(t_2)$, at least one switch is said to have occurred for a given t in the interval $[t_1,t_2]$. We want these states to represent a particular operation, for the sake of concreteness, $s_i(t)$ might be for instance registering colour red in brain regioniat timet. Suppose for simplicity that we study only 3 regions, that time is discrete and that region 1 has access to states A, B and C; region 2 has access to states D, E and F; and region 3 has access to states G, H and I. Now imagine two different cognitive conditions (see the “Methods” section for more details about what we call cognitive conditions), for instance low WM load and high WM load. If we follow the dynamics for a few time steps, we might observe something similar to what is depicted in Fig. 2:

Fig. 2.

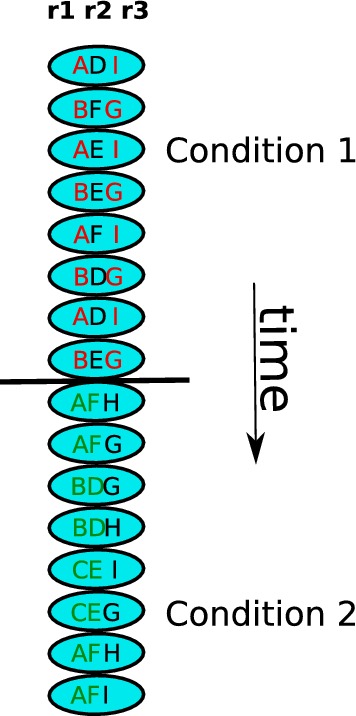
A simplified illustration of the spatiotemporal organization that we expect to capture. There are three regions: $r_1$, $r_2$ and $r_3$. Each region has three available states. If we follow the state of r1 over time, we will observe that not only did the temporal behaviour change when condition 2 started, but also r1 engaged in joint activity with a different region

Evidently in the brain the number of accessible states is not necessarily finite and time is not necessarily discrete. Nonetheless, this toy example allows us to observe the behaviour that we expect to capture. We can follow over time any of the regions, let us take $r_1$. At the boundary between conditions a dynamical change occurs, the succession of states becomes slower, and more states become available (state C in particular). In addition, while $r_1$ was engaged with $r_3$ in condition 1 (they had similar dynamics), in condition 2 it disengages from $r_3$ and engages with $r_2$.

We ask the following questions:

1. Do regions experience state switches more often in one cognitive condition than in the other? Do state switches occur in a discrete manner, or continuously?

2. Are pairs of regions more or less engaged depending on the cognitive condition?

3. Is there some underlying criticality affecting state switching dynamics? Do critical parameters depend on cognition?

4. Does the cognitive condition affect the available states and the time spent in each state?

A way to address these questions is to construct spatially localized variables that represent the time evolution of brain states in the region of the cortex whose activity was inferred by the scalp recordings. We will then derive measurable properties from the above questions. We hypothesize that the vector $(v(t),s(t),k(t))\in {\mathbb{R}}^3$ described in “Methods” section can be seen as a three-dimensional feature vector sensitive to brain-state switches. In general, by considering n moments, each trajectory is embedded in an n-dimensional space, and we expect to test whether cognition affects the spatiotemporal structure of these trajectories. We will call this vector time series the channel state surrogate time series (CSS(t), or simply CSS). There are references throughout this text to small or large transitions, and the distance between states (or switch size) can be defined as being proportional to the norm of the velocity of the CSS (the speed time series$∥v_{\mathit{el}},(t)∥=∥\frac{d}{\mathit{dt}},C,S,S,(t)∥=\sqrt{v^{\prime }{(t)}^2+s^{\prime }{(t)}^2+k^{\prime }{(t)}^2}$ ), because the signal is sampled at a constant rate and the window size remains constant over time. Therefore the more the next states differs in its statistical properties from the current one, the larger the value of the speed time series will be at every time point. Another important property of the speed time series is that, as the CSS remains constant over the course of a state, the speed time series vanishes except around state-switching time points.

Once a biologically plausible way to numerically characterize states and transitions has been developed, we can go back to the questions. All of them, except the one about discreteness or continuity, can be rephrased as does cognition affect propertyX? In the next section we will derive from each property X a measurement, or feature (feature being taken here in its machine learning sense, not to be confused with the feature binding problem discussed above). Then we will investigate the potential of each of these properties to correctly classify cognitive conditions.

Regarding the question of continuity versus discreteness, we will assume discreteness and provide inconsistent evidence in the following way. We will only keep the switches considered spurious (due to estimation noise) if discreteness holds, and assess whether we are still able to classify cognitive conditions with performance above random classification.

For methods 1, 2 and 4, before computing the CSS, the EEG signal spectrum was segmented into the usual physiological bands: delta (1–4 Hz), theta (4–8 Hz), alpha (8–12 Hz), lower beta (12–20 Hz), upper beta (20–30 Hz) and lower gamma (30–45 Hz). For bandpass filtered data, we computed the CSS using a sliding window of length $L=1/f_{\mathit{min}}$ s, where $f_{\mathit{min}}$ is the minimum frequency of the corresponding band, so that each window contains at least one full oscillation of the smallest frequency. Method 3 did not involve bandpass filtering, as its purpose is to estimate the shape of the power spectrum of the CSS. For method 3 the window length was 0.1 s, considering the length of stationary EEG segments reported in the literature (Klonowski 2009).

For every method, after feature extraction, relevant features are selected by Gram–Schmidt Orthogonalization. In particular, we implemented the algorithm described in citepstoppiglia2003ranking, where features are ranked in order of decreased relevance to the output. The selected features were then feed to a Linear Discriminant Analysis (LDA) (Fisher 1936) classifier. The task of the classifier is to discriminate between cognitive conditions: high versus low WM load in the first dataset, AD versus control in the second dataset, and positive versus negative valence in the third dataset. If, after cross-validation, the performance of the classifier is better than that of a random classifier, we can conclude that the features carry information about cognition and hence are modulated by cognition. The results of the process are the classification performance estimated by cross-validation, and the set of most informative features.

Due to the imbalance of the AD dataset, the Area Under the Curve (AUC) (Hanley and McNeil 1982) of a Receiver Operating Characteristic (ROC) curve was used as the measure of classification performance. A ROC curve is not influenced by the imbalance of the classes, and its AUC value is typically 0.5 for a random classifier, and 1 for a perfect classifier. Values larger than 0.5 indicate performance better than random. The statistical significance of the performance of the classifier was estimated by replacing the features with random numbers and iterating the classification process 300 times. We counted the fraction of times that the performance with the random features was higher than the observed performance. For cross-validation using the AD dataset, when classifying a subject, the whole subject data was left out of the learning set, given that in a real-life diagnosis task, there is no available information about the subject to be diagnosed. On the other hand, only half of the subject data was left out for the WM and emotions datasets, simulating the calibration process common in brain-computer interfaces. Half of the subject data was left in the learning dataset for calibration, however, classification was done always on EEG epochs that had not been “seen” by the classifier.

The implementations of all the algorithms were written by us in Matlab 2017b, except for the following built-in Matlab functions: fitcdiscr for the LDA classifier, filtfilt and butter for creating a third order Butterworth filter for the signal, and perfcurve to estimate the AUC.

Each of the following sections is an attempt to address one of our main questions.

Method 1: Temporal structure of the switches

The motivation behind Method 1 is to investigate the temporal structure of brain state switches. In particular, whether these switches occur at discrete or continuous times, and to what extent cognition affects such continuous or discrete dynamics. Discrete switching assumes that small transitions are noise, whereas large transitions are the result of brain functioning.

For each channel and for each band, the speed time series (that, as it was mentioned before, vanishes except at state-switching time points) was sorted by amplitude. Only the fraction F of the samples for which the velocity was smallest was used to compute the mean speed, and mean speeds were used as features for classification. The performance of the classifier was studied as a function of F. For small values of F, we would pick only noise under the assumptions of discreteness (and hence piece-wise stationarity), and transition size larger than noise. As F increases, if these assumptions are true, the classification performance should start gradually improving and be better than random classification above a certain threshold value. Method 1 therefore consisted in using the parameter F that maximises the performance of the classifier under cross-validation. To compare how small transitions behave as compared to large transitions, we studied also the performance of the classifier when F represents the fraction of the samples for which the velocity was largest.

Results specific to Method 1

Figure 3 shows the performance of the classifier using Method 1, as a function of the fraction F, for the WM dataset when using only the upper beta and lower gamma bands (combined, for simplicity, to use a single window). Only high frequencies were considered in order to use a small sliding window, and only the WM dataset was used for this figure due to its high sampling rate. The window size used was $L=1/20$ s, or 25 points. The blue dots correspond to the classification performance obtained using only the fraction F of transitions that had the smallest velocities. For the red dots, we used the fraction F that had the largest velocities.

Fig. 3.

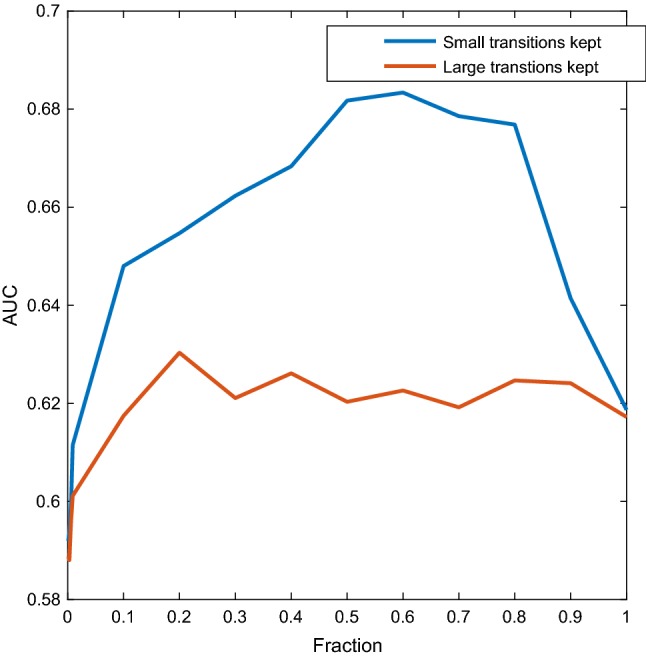
WM dataset using only upper beta and lower gamma ranges. The mean speeds of the CSSs were used as features. To compute the mean, the smallest (blue) and largest (red) F fraction of amplitudes were used. The classification performance is studied as a function of F. (Color figure online)

Figures 4, 5 and 6 show the performance of the classifier, using Method 1, as a function of the fraction F when using all the bands, for the three datasets. For each band and for each channel there was a time series whose amplitudes were sorted by size, hence the total number of features of the classifier in these cases equals the number of channels multiplied by the number of bands.

Fig. 4.

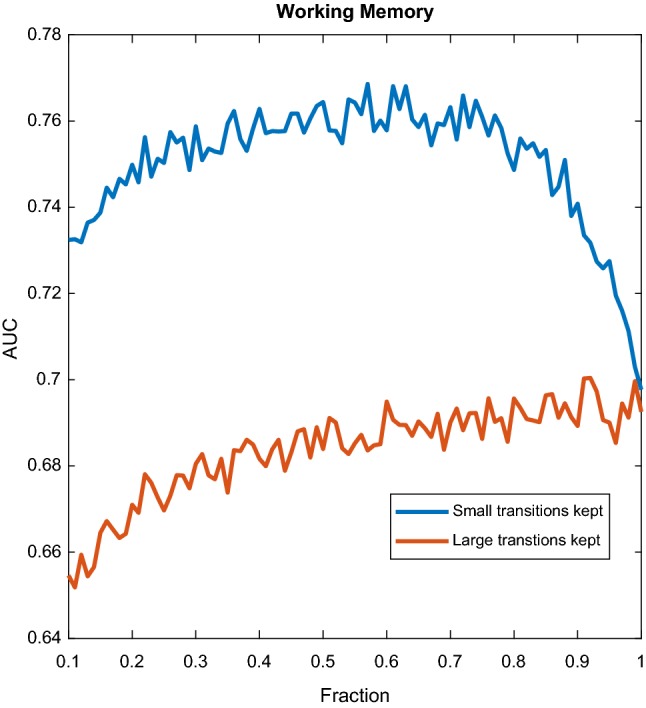
WM dataset. Performance of the classifier as a function of the fraction of transitions kept. In blue, keeping small transitions only, in red, keeping large transitions only. (Color figure online)

Fig. 5.

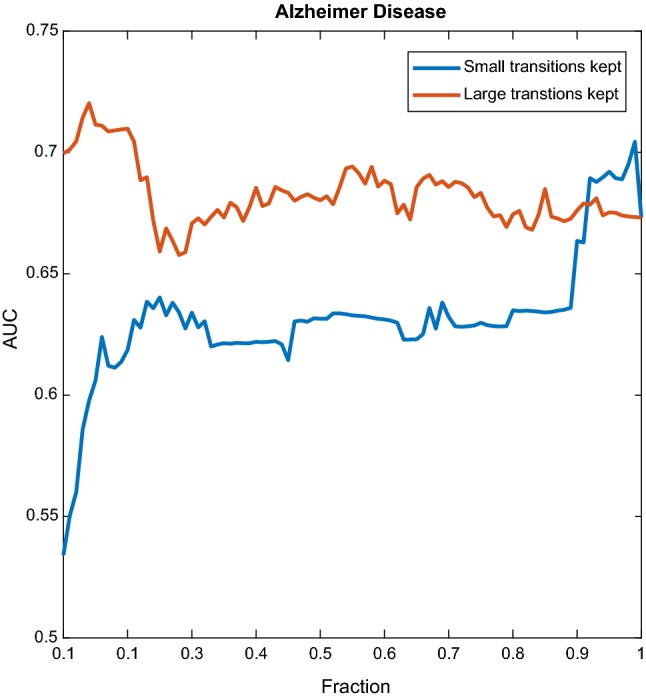
AD dataset. Performance of the classifier as a function of the fraction of transitions kept. In blue, only the small transitions were kept, in red, only the large ones. (Color figure online)

Fig. 6.

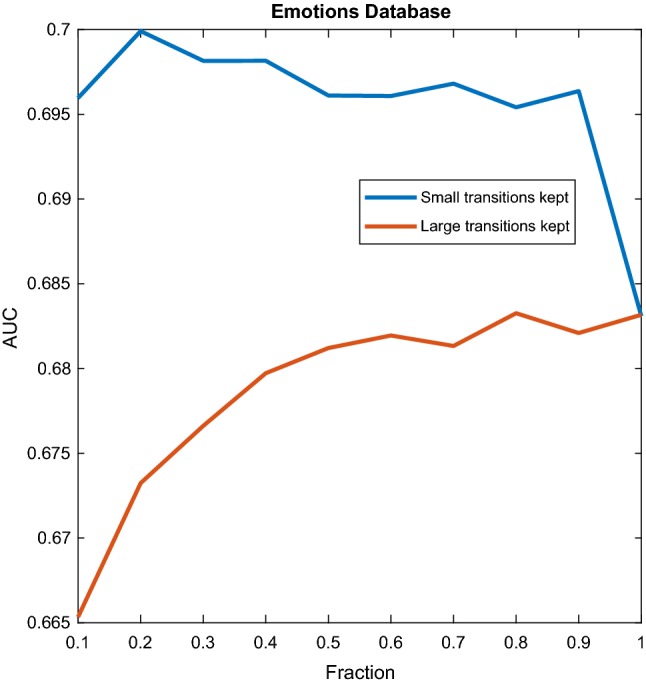
Emotions dataset. Performance of the classifier as a function of the fraction of transitions kept. In blue, small transitions, in red, large transitions. Due to the large size of the dataset, the performance of the classifier was computed for a smaller number of values of F as compared with the other datasets, and hence the figure is less smooth. (Color figure online)

Discussion specific to Method 1

The blue lines of Figs. 3, 4 and 6 show that even for small values of F, classification performance is well above random, which means that small transitions are not noise. Furthermore, not only these transitions are not noise, but they are better predictors of cognition than large transitions. To further elaborate on this we can analyse Fig. 3. The blue curve reflects the behaviour when the fraction F concerns the smallest transitions, while for the red curve the fraction F pertains to the largest transitions. We can observe two things. First, already in the left part of the blue curve classification performance is above random and therefore small transitions are not noise. Second, the blue curve is always above the red curve, which means that given any fraction F, it is always more informative to take the F smallest transitions than the F largest transitions. As we gradually increase F following the blue curve, we pick larger transitions and classification performance increases, up to a point, at which performance starts decreasing when we add larger and larger transitions. As it was mentioned in the previous section, only the $\beta$ range was used, and the window size used was $L=1/20$ s, or 25 points. If all the points are informative, it means that there are at least 20 switches per second, because the sampling rate is 500 Hz. More than twenty switches per second means that the inter-switch duration (the lifespan of a state) is smaller than the wavelength, and therefore the switching could be effectively considered as continuous. We decided to focus only on high frequencies aiming at contrasting the results with the reported lengths of stationary segments, usually larger than 1/20 s. Figure 4 reveals the same behaviour when considering all the bands. Figure 6 shows a similar mechanism for the emotions dataset. The exception to this behaviour in which small transitions are more informative was the AD dataset, as shown in Fig. 5, suggesting that for diagnosing AD large transitions are more relevant. The latter could be explained by the fact that patients in this database were not performing any cognitive task, therefore localized activity of brain circuits during processing (likely to cause the small transitions) was not present. Furthermore, it is compatible with findings of “slowing” of the brain rhythms found on AD patients, for which has been reported a decrease of the alpha power, and an increase in the delta and theta power (slow rhythms) as compared to healthy controls (Schreiter-Gasser et al. 1993). With dominant slower rhythms, it would be expected that most of the information is carried by slow transitions.

It seems clear that the temporal structure of the statistical properties of EEG carry information about cognition. This in turn provides evidence supporting the claim that these metastable states correspond to brain states driven by cognition. On the other hand, as mentioned in the introduction, theoretical considerations such as the stability required to sustain oscillations led other researchers to postulate discrete timing. Based on this hypothesis they found evidence that large transitions between states, as observed by large changes in the EEG properties (rapid transition processes or phase resetting events), correlate with cognition. In this study, we provide evidence showing that not only do small transitions convey information, but indeed they seem to carry more information than large ones under certain circumstances.

Method 2: Spatial synchrony between states

If regions engage and disengage in joint activity depending on cognition, we can compute synchrony between pairs of CSSs and test whether synchrony values are different for different cognitive conditions. The CSS is 3-dimensional, and therefore the norm of the CSS was used as a proxy-CSS (pCSS) whenever a method required, for clarity, a 1-dimensional representation of the state. For each EEG epoch, we computed the mutual information between pairs of pCSSs, and these values were used as features to build the classifier. Having six series per channel, and 16 (WM dataset), 21 (AD dataset) or 32 (emotions dataset) channels, the potential number of combinations are in the order of several thousands. To prevent overfitting, only the CSSs whose time derivatives provided the best features for Method 1 were taken into account for measuring the spatial synchrony in terms of their mutual information estimation. The number of combinations considered was set by cross-validation, but was required to be lower than 10. While Method 1 is meant to capture regularities in the temporal structure of the proposed variables for each condition, Method 2 aims to capture spatial structure by using mutual information between selected pCSSs as features.

The results and discussion concerning this method will be part of the global section.

Method 3: Power law of the power spectra

Power laws are not sufficient to guarantee criticality (Newman 2005), however, scale-free behaviour, like power laws, emerges from self-organized criticality. If indeed the brain is in a critical state that allows effective switching in the proposed states, we would expect a power law in the Power Spectral Density (PSD) of the pCSS. If there is some functional meaning of this power law, its properties should be affected by cognition. An important property to look at is the scaling factor of the power law, as it determines its memory properties (Miramontes and Rohani 2002): the extent to which past events affect the present, and hence the extent to which disturbances (sensory or motor, in this context) propagate.

A power law was fitted to the PSD of the pCSS. The CSS used for the power law was not filtered in any particular band, as we are studying the whole spectrum, therefore there is only one pCSS per channel. A linear fit in a log–log plot of the PSD of the pCSS was performed and the slope was used as a feature. The power law hypothesis was tested using the criteria of Clauset et al. (2009). For a given sample, the test developed by Clauset et al. fits the sample to a power-law, and generates synthetic samples drawn from the same power-law distribution. Afterwards, a Kolmogorov–Smirnov test is used to decide whether the real and the synthetic samples belong to the same distribution (null hypothesis). The null hypothesis was accepted when the Kolmogorov–Smirnov test yielded a p-value larger than 0.1. The estimation of the coefficient suggested by the same article was not used, given that it provided significant, yet lower classification performance. As mentioned before, this method is meant to test whether there is cognitive-driven scale-free behaviour in the proposed variables, and hence the slope of the fit was fed to the classifier.

Results specific to Method 3

The Kolmogorov–Smirnov test failed to reject the null hypothesis (power law) 98% of the time for the WM dataset, 83% of the time for the AD dataset, and 62% of the time for the emotions dataset. The fit of a randomly chosen AD trial is shown in Fig. 7, x values are the amplitudes of the PSD of the pCSS.

Fig. 7.

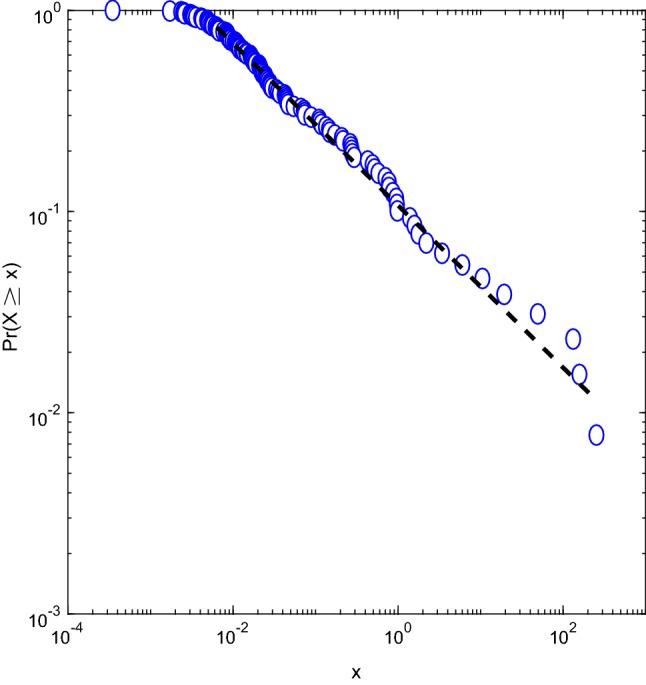
Power law fit of a randomly selected AD trial. The x values are the amplitudes of the PSD of the pCSS

Discussion specific to Method 3

It is important to remember here that for Method 3 we computed the PSD of the CSS, not the one of the raw EEG. Therefore, high frequencies mean small transitions. EEG is a particularly noisy signal, and for high frequencies the noise might be larger than the signal. A power law fit however allows us to infer the behaviour at the tail (large frequencies, or small transitions in this case) by studying more accessible regions of the system. In addition, the power-law hypothesis supports the claim of criticality, where information (such as sensory or motor) is optimally transferred, as discussed in the introduction. Furthermore, cognition modulates power law exponents, and therefore the propagation of information.

Method 4: Most visited states, and how many of them are available

Having variables that represents local brain states, it is interesting to ask whether certain cognitive conditions impose a richer set of states, and if these states are equally present or not.

As we are in a dynamical framework, we can borrow the concept of phase space. For an n-dimensional system, the phase space is a 2n-dimensional space able to express all the possible positions and velocities of all of the n components. A point in the phase space is a particular dynamical state: a specific value of all the n positions and velocities, that completely captures the instantaneous dynamical properties. We will analyse each CSS separately, in particular, the 1-dimensional pCSS, so that our phase space is two-dimensional. To clarify, a dynamical state is not exactly the same as the above mentioned brain states. Here, a dynamical state is the 2-dimensional combination of the pCSS(t) and its time derivative. In other words, it is the surrogate of the current brain state plus dynamical information about it.

We discretized the phase space in the following way. The full range of the pCSS was divided into 20 bins, the range was from 0 to 25. Its time derivative was divided into 20 bins, ranging from – 2 to 2. The ranges were chosen after analysing the intervals in which the pCSS and its time derivative usually fell. The number of bins was not thoroughly optimized, given that results were robust to different number of bins. For each pCSS, such discretization scheme produced a 20 × 20 grid (see Fig. 8) spanning the phase space. The element i, j of the grid is a dynamical state $s_{i,j}$.

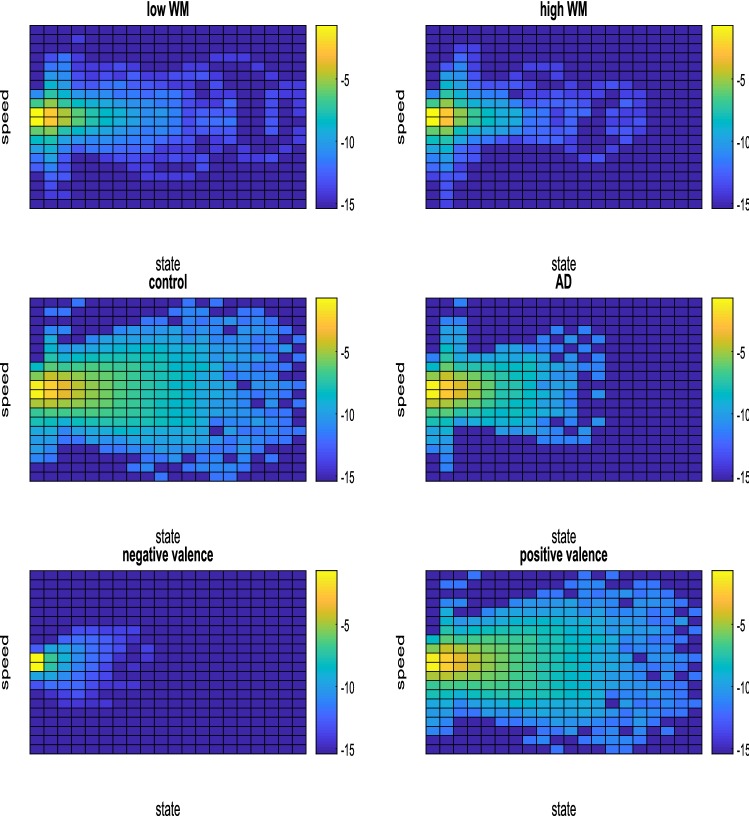
Fig. 8.

Visual representation of the most visited states of the (discretized) phase pace for each condition, for each dataset. The feature (a specific channel at a specific band) ranked first by OFR was selected to generate the image

With the discretised version of the phase space, we used an entropy measure to characterize it:

$$\begin{array}{c}\hfill H=-\sum _{i=1}^{20}\sum _{j=1}^{20}p(s_{i,j})log\left(p,(,s_{i,j},)\right)\end{array}$$

where $p(s_{i,j})$ is the probability of dynamical state $s_{i,j}$, measured as the fraction of time that the system spent in dynamical state $s_{i,j}$.

The above measure is small when, for a given period of time, the dynamical system is found only in a small set of dynamical states. It is large on the other hand when the set of states is large and the probability of observing each of the states is similar. The values of H for each of the pCSS were used as features for this method.

Results specific to Method 4

Figure 8 provides visual information of how the dynamical states are visited for each cognitive condition. For generating the figure, we selected for each dataset only the feature ranked first by the OFR algorithm, i.e, the feature that carries the largest amount of information about the output. In this case, it is the particular channel and the particular band at which the entropy measure related to the phase space changed the most across cognitive conditions. For the WM dataset the best feature was channel F4 filtered in the lower beta range, for the AD dataset the best feature was channel Oz filtered in the alpha range; finally, for the emotions dataset, the best feature was electrode T8 in the lower gamma range. For a given condition we performed the grand average with data from all the subjects, and plotted how the discretised phase space was visited as a logarithmic heatmap. Red tones represent states that were more visited. For the sake of visual clarity, for generating the images the ranges were slightly modified as compared to the above description of method 4. The pCSS was divided into 20 bins as before, but for each dataset, the discretisation range was chosen as the interval ranging from the minimum value to the maximum value of all the pCSSs (from all the subjects and all the trials). The discretisation range for the time derivative of the pCSS was chosen in the same manner.

Discussion specific to Method 4

The OFR method selected, for each dataset, features consistent with other studies in the literature. Occipital alpha activity had been reported as a marker of AD (Huang et al. 2000; Prinz and Vitiell 1989), lateralised activity elicited by valence had been reported as well (Harmon-Jones and Allen 1998) (Khalfa et al. 2005). However, a dynamical approach allows us to go a bit further. Consider occipital activity in AD disease. Healthy controls have access to a richer set of dynamical states. Furthermore, if we ignore the dynamical part (velocity-axis), and observe only how the distribution of brain states changes across conditions, the available number of states turns out to be also richer for the healthy controls, suggesting loss of functions (both dynamic and in terms of available brain states) related to AD disease. It is important to consider that subjects recorded for this dataset were not performing any particular task, and therefore the observed states are due to spontaneous ongoing activity. By contrast, the other two datasets were collected while subjects performed specific tasks, and therefore the observed states might be task-specific. The WM figures show that the low WM condition has the richer set of states. The low WM condition did not require full engagement, and subjects reported performing various mental activities while completing the task: from planning their evening activities to be attentive to possible background conversations. The high WM condition on the other hand required full engagement, and the small set of states may be specifically related to WM. Regarding valence, let us observe the third row of images, corresponding to the T8 electrode, located in the right hemisphere. The dynamical richness of the right hemisphere is much higher for positive valence, as compared to negative valence. It has been proposed that negative emotions are processed in the right hemisphere (Ahern and Schwartz 1979). The right hemisphere could be engaged in a small set of task-specific states while exposed to negative valence material. On the other hand, the observed large set of states related to the positive valence condition could be ongoing activity. Evidently the right hemisphere does not devote all its resources to the processing of emotions. We observe in the figures only the most visited states, not the totality of them. The same reasoning applies to the WM dataset. The above findings can be summarized by stating that task-related activity seems to elicit a small, perhaps more specific set of states. The task-free AD dataset on the other hand suggests that AD decreases the dynamical richness of ongoing activity. Steyn-Ross et al. extended mean-field models3, that consider only chemical synapses, to include diffusive effects via electrical synapses (Steyn-Ross et al. 2009). They found different patterns of self-organisation depending on the time-scale of somatic and dendritic dynamics. If soma voltage remains almost constant during dendritic integration, their model displays patterns consistent with ongoing activity. On the other hand, if both time-scales are comparable, they observe faster dynamics, consistent with cognitive activity. They provide clinical evidence supporting the findings of their model. In their model as well as in our empirical analysis, patterns of self-organisation are different in nature for ongoing and for cognitive activity; in addition, cognition-driven activity exhibits faster dynamics (with small, more frequent transitions being more informative in our analysis).

Baseline: power spectral density

Although the aim of the study is not to develop a feature extraction method, but rather to address questions about brain dynamics, spectral features were used as a baseline to compare classification performance. Spectral features included power in the delta (1–4 Hz), theta (4–8 Hz), alpha (8–12 Hz), lower beta (12–20 Hz), upper beta (20–30 Hz) and lower gamma (30–45 Hz) ranges. The frequency bands used were the same as in Methods 1 and 4, to maintain an equal number of features. Table 3 shows the comparison between methods, using power spectral density as baseline.

Table 3.

Performance of the different methods

Dataset	Method 1	Method 2	Method 3	Method 4	Baseline
AD	0.70 (126)	0.71 (126)	0.48 (21)	0.71 (126)	0.54 (126)
WM	0.76 (96)	0.74 (96)	0.68 (16)	0.75 (96)	0.75 (96)
Emotions	0.70 (192)	0.70 (192)	0.64 (32)	0.76 (192)	0.68 (192)

Spectral properties of the signal (power at different frequency ranges) were used as a baseline. The number of features is indicated in parentheses

Control tests

Control test 1: Destroying temporal structure and assessing statistical significance

A large part of the motivation of this work is to investigate the temporal structure of brain state switches. To provide more convincing evidence that what we are measuring is indeed a result of the time organization, we used shuffled variables. We computed the CSS, and before computing its time derivative we shuffled it. Then we applied Methods 1, 3 and 4 and tested whether classification power disappeared. Method 4 is a mixture of static (distribution of states) and dynamic (states having a certain speed) information, and therefore using shuffled data should not necessarily destroy all the information. Method 2 is about spatial synchrony and therefore is not concerned: in fact, mutual information is not affected by the temporal structure of the data. We iterated the above procedure 300 times for each dataset for each method, and observed how often classification results were better than the ones we observed with no shuffling. In addition to the shuffled data, random features drawn from a uniform distribution were used too. 300 iterations were performed with random data, and we computed the fraction of the iterations for which classification performance was higher than the observed results. While random features helped assess the statistical significance of the methods, by shuffling the data we explore the validity of a particular claim, namely, that the observed results arise from the temporal organization of the switches. In the next section we further refine the control tests by targetting not the general temporal structure of the variables, but rather events that might be considered as switches in the discrete model.

Control test 2: removing known discrete events

Models based on discrete switches assume that switches between states occur at precise instants that can be tracked. In Freeman’s work these points correspond to phase resetting in the original EEG signal (Ruiz et al. 2010). In Kaplan’s work they are the Rapid Transition Processes (RTP) (Kaplan et al. 2005). To find candidates of RTPs, two moving averages are created from the EEG time series. One moving average uses a small sliding window, to track, rapid cortical processes; and the other uses a larger sliding window, to represent slower cortical processes. The times at which the time series from both moving averages cross are candidates to be a RTP. Further statistical testing is required to discard false positives.

In general, for the control test 2, any segmentation technique could be used as well. These transitions can be removed from the time series, to assess their contribution to classification performance. If classification is not substantially degraded, we could be even more confident in saying that the majority of information comes from the small transitions that occur continuously. We removed points associated with phase resetting and rapid transition processes with severe criteria, to reduce the risk of failing to remove the postulated events. Due to the latter, more than 80% of the signal was removed, as shown in Table 2. We removed not only the phase resetting points but also their neighbours. As for the rapid transition processes, the segmentation algorithm proposed by Kaplan finds first a large set of pre-candidates to be rapid transition processes. The elements of this set are further tested and considered rapid transitions processes only if they fulfil the remaining criteria [for details see (Kaplan et al. 2005)]. We decided to remove the whole set of pre-candidates to increase certainty. This test was performed in the WM dataset because it had the highest temporal resolution.

Table 2.

Control test 2

Target	Percentage of data removed (%)	Decrease in classification performance (%)
Phase resetting points	80.8	3.8
Rapid transition processes	80	14.4

Results of removing known discrete events. Specific points associated with transition events acknowledged in the literature were removed. The decrease in classification performance is shown in the third column

Results specific to control tests

The results concerning Control test 1 are shown in Table 1. For each cell, the first value corresponds to the percentage of iterations for which random features outperformed real features. The second number reflects the percentage of the iterations for which shuffled data outperformed non-shuffled data. As mentioned in “Control test 1: Destroying temporal structure and assessing statistical significance” section, the shuffled data is not expected to completely destroy all the information provided by Method 4, as it also involves static information about the distribution of states.

Table 1.

Results of control test 1

Dataset	Method 1	Method 2	Method 3	Method 4*
AD	0%/0%	0%/NA	89%/34%	0%/0%
WM	0%/18%	0%/NA	0%/0%	0%/18%
Emotions	0%/0%	0%/NA	0%/ 0%	0%/0%

Out of the 300 iterations, fraction of times in which random features outperformed real data (first number of the cell), and fraction of times in which shuffled data outperformed real data (second number of the cell). Method 2 was not considered for generating shuffled data because it deals with spatial synchrony, not with temporal structure. *Shuffled data is not expected to destroy all the information provided by Method 4

Table 2 shows the results of Control test 2.

Global results

The summary of the performance of all the methods for all the datasets is presented in this section. Table 3 shows classification results reported as the area under the ROC curve. As a reference, the baseline technique (spectral properties of the EEG signal) is displayed for comparison. The performance on the WM and emotions dataset was non-deterministic, as the calibration step involved adding noisy copies of the data. For all the non-deterministic estimations of performance, 20 realizations were executed, and the results displayed correspond to the average. The number of features encompassed by each method is displayed in parentheses.

Discussion

We proposed and successfully tested certain assumptions about brain dynamics motivated by the way different areas of the brain engage in joint activity and disengage on demand. First, we assume, as other authors do, metastability driven by cognition. Following the definition of metastability, we propose local variables that reflect the time evolution of brain states, and develop a framework to study how cognition affects different properties of the spatiotemporal organization of these variables. To our knowledge this is the first time that the switching between metastable brain states driven by cognition is investigated in a fully data-driven manner for a range of cognitive functions.

We can conclude by looking at Tables 1 and 3 that the proposed properties of the spatiotemporal structure of the proposed variables are affected by cognition in a manner that cannot be explained by chance. An exception is Method 3 in the AD dataset. However, it is worth noting that the number of features computed for Method 3 is six times lower than the number of features in the other methods, and therefore we cannot directly compare them. As mentioned in “Baseline: power spectral density” section, the main goal was not to develop a feature extraction technique, therefore the hyper-parameters of the model (e.g. size of the window length, number of statistical moments) were not optimised. The latter would imply losing statistical significance, and being the first time that this techniques are applied, we favoured statistical power over performance.

Concerning the debate of discreteness versus continuity, we can observe in Table 2 that targeting specific events recognised as candidates for state switching did not substantially degrade the quality of the information. Our conservative approach, that removed as well neighbours and false positives, discarded more than 80% of the data, with only a small decrease in the classification performance: 3.8% when removing phase resetting points, and 14.4% when removing rapid-transition-process points.

We suggest two possible explanations. The first explanation is that although the spatiotemporal structure of the statistical properties of EEG, and in particular their dynamics are relevant to predict cognitive conditions, switches do not occur in a discrete manner. The brain undergoes large transitions at seemingly discrete times, however it keeps fluctuating between neighbouring states in a way that is affected by cognition. In other words, these small fluctuations are not artifacts due to any source of noise, but rather induced by cognition. Computations in the brain are analogue, and even under continuous switching, the neighbourhood of a state could provide enough stability to induce the oscillations thought to be required for psychological constructs. Werner (2007) suggested that metastability can be given an operational meaning: instead of considering integration-segregation as two poles, a continuous range of tendencies of neural coordination seems more appropriate. This continuum, according to him, seems to be supported at the neuronal dynamics level by the flexibility of coupling coefficients amongst different neuron groups. Assuming continuity might be thought of as rejecting the existence of metastable states, as there are no states of finite duration with constant statistical properties. It is possible still to draw on the less restrictive concept of metastable regimes in the dynamical systems point of view (Tognoli and Kelso 2014): dynamics takes place in a region where all attractors have disappeared.

A second explanation is that switches are discrete, but due to volume conduction the recordings reflect the influence of neighbouring regions: continuity would be then an artifact of the lack of spatial resolution of the measurements. The further the region, the less its changes in statistical properties affect the local recording. EEG source localization could be used to either support or rule out this possibility. The CSS can be computed using the EEG sources instead of the EEG raw recordings. If timing is discrete, we should observe, at the level of the sources, piecewise continuity in the statistical properties.

An argument favouring the first explanation is that the power law fit of the PSD of the CSS demonstrates a fractal temporal structure of the CSS. As mentioned above, the power law coefficient is a parameter that expresses the extent to which disturbances propagate. We showed that this parameter is affected by cognition, which makes sense if we consider, as other authors do, sensory and motor information as disturbances in this context. The second explanation requires an extra hypothesis then. The inter-switch duration of a particular brain source should be influenced by the neighbouring sources, as their joint switching dynamics should still be fractal in time. In other words, we require to translate the fractal time structure of a single region (first explanation) into spatial organization of sub-regions (second explanation). Postulating the latter should involve postulating as well a mechanism producing this spatial organization. Such mechanism should be at least as parsimonious biologically as the one in which dynamics evolve for allowing an efficient propagation of disturbances under the first explanation.

The above discussion might be theoretically relevant at different levels. We have discussed the biological implications of continuity and discreteness, however, other aspects are concerned as well. Phenomenologically, a fragmented flow of perception or consciousness is essentially different from a continuous flow. Whereas a thought, an action or perceiving an object might seem granular after a quick exercise of introspection, microcognitive science, or neurophenomenology at the sub-second level, suggests otherwise. Petitmengin et al. (2013) investigate how elicitation techniques provide access to micro-states (not to be confused with EEG micro-states), at the sub-second level, where boundaries across sensory modalities and between object and subject begin to blur. They advocate finding correlations between these sub-second, first person experiences and third-person, objective measurements. The proposed spatiotemporal analysis of brain-state switches is a possible candidate tool to investigate such correlations. In addition, regarding the mathematical description of natural systems, discrete and continuous mathematical models may have very different properties. As a simple case in point, we can consider the logistic map, one of the simplest discrete dynamical systems able to exhibit chaos. Its continuous version on the other hand, is never chaotic. For a discrete system there is always a “next” value, whereas for a continuous system this is not the case. On the other hand, if continuity is an artifact of volume conduction, the presented framework has proven useful still. If the temporal organization turns out being spatial organization disguised, we have no reason to discard the information obtained from small (far?) transitions. Evidently, the next step would be to identify and investigate the biological mechanisms generating this spatial organisation.

A continuous perspective is more compatible with an analogue computer metaphor, and in this regard, our proposals are compatible with the work of Spivey (2008). He suggests that if we could take the activity of single neurons as variables, cognition would be a continuous trajectory in a high dimensional space, where each coordinate is the activity of a neuron. He suggests as well abandoning the digital computer metaphor in favour of a dynamical framework. In his proposal a specific cognitive task would be a point in this space, and performing such task would be a trajectory moving towards this point. Perceiving a face for instance, would be moving towards the point that corresponds to that particular face. Interestingly, he claims that we spend more time near such points than at them. Experimentally, Chang and Tsao (2017) were able to accurately reconstruct human faces by reading the activity of 205 neurons in primates. Each neuron codes for a particular face feature, and the joint activity of the the 205 neurons, ie, a point in a space of dimension 205, represents a specific face. While face recognition is so important that evolution might have given it a sparse representation, in the general case of cognition we do not have the experimental and computational means to explore such points and trajectories. Nevertheless, using a low number of statistical moments and a few scalp recordings, we showed that the idea of cognition as a continuous trajectory in an abstract space is worth further investigation.

Our framework aims at producing evidence that can enrich theoretical discussions about brain dynamics. As it is important for us to show that cognition is driving these phenomena, we developed tools for classifying cognitive conditions on a single-trial basis, and therefore practical applications such as cognitive brain-computer interfaces can benefit too from these methods. In addition, the predictive power of this framework resides in a signal property often overlooked, or even considered as a problem to overcome: the lack of stationarity.

Compliance with ethical standards

Conflict of interest

We declare that we have no conflict of interest.