Abstract
Memristor is a nanoscale circuit element with nonvolatile, binary, multilevel and analog states. Its conductance (resistance) plasticity is similar to biological synapses. Information sparse coding is considered as the key mechanism of biological neural systems to process mass complex perception data, which is applied in the fields of signal processing, computer vision and so on. This paper proposes a soft-threshold adaptive sparse coding algorithm named MMN-SLCA based on the memristor, neural network and sparse coding theory. Specifically, the memristor crossbar array is used to realize the dictionary set. And by leveraging its unique vector–matrix operation advantages and biological synaptic characteristic, two key compositions of the sparse coding, namely, pattern matching and lateral neuronal inhibition are realized conveniently and efficiently. Besides, threshold variability further enhances the adaptive ability of the intelligent sparse coding. Furthermore, a hardware implementation framework of the sparse coding algorithm is designed to provide feasible solutions for hardware acceleration, real-time processing and embedded applications. Finally, the application of MMN-SLCA in image super-resolution reconstruction is discussed. Experimental simulations and result analysis verify the effectiveness of the proposed scheme and show its superior potentials in large-scale low-power intelligent information coding and processing.
Keywords: Memristor, Adaptive sparse coding, Lateral neuronal inhibition, Super resolution, Image reconstruction
Introduction
Leon Chua proposed the theoretical concept of “memristor” for the first time and pointed out that its resistance can be adjusted by external stimulation (1971). In 2008, researchers at HP laboratory in the United States reported in Nature that the memristive effect could be achieved with a nanometer double-layered TiO2-based structure, confirming the physical existence of the memristor (see Strukov et al. 2008). Since then, the memristor has attracted great attention from scientific research, education and industry. For instance, oxide memristors including TiO2–TiO2−x-based, HfOx-based and WOx-based (see Strukov et al. 2008; Long et al. 2013; Chen et al. 2013) memristors, exhibit superior device performance and excellent compatibility with complementary metal oxide semiconductor (CMOS). Furthermore, more and more physical memristor models based on different materials and mechanisms have been proposed, such as the solid electrolyte Si–Ag memristor with simple operating voltage (see Muenstermann et al. 2010), the spintronic memristor based on spin characteristic (see Wang et al. 2009), the flexible memristor with the organic gel (see Zakhidov et al. 2010), the new grounded memristor emulator based on MOSFET-C (see Yesil 2018), as well as the new one with ultra-high temperature tolerance (see Wang et al. 2018), etc. Compared with the conventionally charge-based switching electronic devices, the conduction state of the memristor is determined by the internal ion channels under the external stimulation. Furthermore, the formation and disconnection of the conductive channel has a regulating effect on its resistivity and overall performance (see Yang et al. 2014). This programmable resistance ability is similar to the variable biological synapse strength, therefore the memristor becomes an ideal component of miniature artificial electronic synapses. Meanwhile, Kawahara et al. have successfully developed memristor crossbar array models at different nanometer scales and memory levels (2013) to explore new integrated circuit technologies based on memristors. At present, the memristor crossbar array has been widely used in digital logic and analog circuits (see Pershin and Di Ventra 2010). It can provide parallelism and high density required by large-scale signal processing and provide a highly integrated implementation scheme for the synaptic connection, which will greatly simplify the circuit design and implementation of neural networks (see Yang et al. 2013). Snider team developed a new implementation method of STDP learning rule using memristors (2011). Consequently, scholars designed various types of memristive neural networks and discussed their applications. For example, Itoh and Chua (2014) studied passive nonlinear cellular automata based on the memristor and discrete time cellular neural network. Hu et al. (2017) developed the multilayer cellular neural networks with memristor crossbar array synapses. Bao et al. (2017, 2018, 2019) designed many memristor-based circuits, and artificial electronic synapses. It can be seen that, based on the great similarity between memristors and biological synapses, as well as the unique storage and operation mechanism, memristor crossbar array can facilitate realizing various neural networks (see Zhang et al. 2017; Yan et al. 2018). On the basis of neurobiology, this paper proposes a new hardware-friendly and low-power intelligent sparse coding scheme by combining the memristor network with the sparse coding technology for the requirement of efficiently mass information processing.
Sparse coding originally refers to the significant sensitivity in the receptive field of primary visual cortex cells, where a single neuron responds to stimulus within its receptive field, such as edges, line segments, stripes, and other image features in a specific direction (see Field 1987). Mathematically, sparse coding is the way to describe multidimensional data. Since 1961, people began to study sparse coding and put forward many coding theories. Field (1989) proposed the sparse distributed coding method. Olshausen and Field (1997) developed a sparse coding algorithm based on overcomplete basis and successfully modeled the receptive field model of V1 simple cells, by utilizing basis function and the probability density model of coefficients. In recent years, many new sparse coding algorithms have been proposed by researchers (see Li et al. 2004; Donoho and Elad 2003); meanwhile, it has been widely used in signal processing (see Candès and Wakin 2008), neural computing systems (see Jo and Chang 2010), pattern recognition (see Wright et al. 2010), etc. However, the processing efficiency could be further improved and the low-power hardware implementation and acceleration is still in urgent need (see Sheridan et al. 2017). Fortunately, the appearance of memristor brings opportunities for the design of hardware-friendly, low-power consumption and large-scale bionic sparse coding.
By combining the memristor crossbar array characteristics and the principle of biological sparse coding, this paper proposes a memristive neural network-based soft-threshold adaptive sparse coding (MMN-SLCA) algorithm. Specifically, two memristor crossbar array synapses are constructed to realize the dictionary. Along with the input and output neurons, these crossbar arrays can conveniently execute pattern matching and lateral neuron inhibition, efficiently achieving the sparse coding. On this basis, the application of MMN-SLCA in the super resolution reconstruction of natural images is discussed, which is effectively verified by experimental simulation and result analysis.
Memristor model and crossbar array
The threshold adaptive memristor model
Memristor is a kind of nonlinear device with variable resistance, which can be defined by charge and flux flowing through the memristor:
| 1 |
where M(q) is the memristor resistance. The typical HP memristor is composed of a two-layer TiO2–TiO2−x film sandwiched between two Pt electrodes. Up to now, the corresponding mathematical models include linear, nonlinear, exponential, adaptively piecewise linear model and so on. There are also some models based on experimental data, such as the Simmons tunnel potential barrier model. However, due to the lack of ports and state equations, these experimental models are not suitable for programming simulation and mathematical derivation. Subsequently, the threshold adaptive memristor model (TEAM) is obtained through appropriate simplification of the Simmons tunnel barrier model (see Kvatinsky et al. 2013). It has a relatively simple mathematical expression but also can reflect the actual physical device characteristics. Consequently, our work is carried out based on the TEAM because of its reasonable accuracy and computational efficiency. The TEAM is shown in Fig. 1a, whose resistance depends on the tunnel barrier resistance and a resistance Rs. The equivalent circuit is shown in Fig. 1b.
Fig. 1.
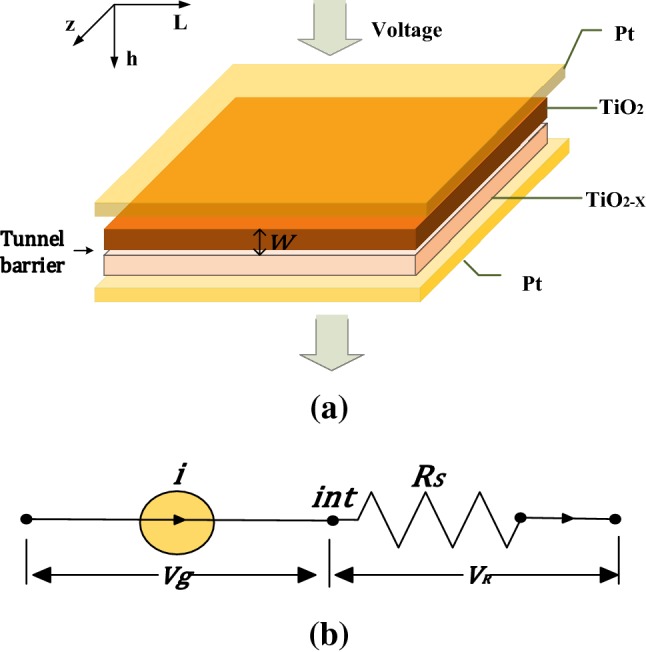
The threshold adaptive memristor model (a) and equivalent circuit (b)
Its internal state variable is defined as the width of the tunnel by Kvatinsky et al. (2013):
| 2 |
where koff denotes the amplitude parameter; koff is positive and kon is negative. The matching parameters von and voff represent the current threshold at switching time, respectively. A typical set of parameter values are koff = 0.091 m/s, kon= − 216.2 m/s, voff= 0.2 V and von= − 1.45 V. foff(w) and fon(w) are two window functions characterizing ions drifting:
| 3 |
| 4 |
where aoff = 1.2 ± 0.02 nm, aon = 1.8 ± 0.01 nm, wc = 107 ± 4 pm and b = 0.2 V. The relationship between voltage and current of the TEAM memristor can be expressed as:
| 5 |
where RL and RH are the low and high memristor resistance state, respectively. Then memristor resistance M(w) changes linearly with inner state w:
| 6 |
The internal state variable w can be changed accordingly with external excitations. The programmability and threshold characteristics of the TEAM provide theoretical and experimental support for the synapse construction. At the same time, the TEAM responses quickly at the order of nanoseconds and has strong anti-interference ability. With appropriate thresholds, it can effectively prevent the accidental disturbance of feeble non-writing signal on its resistance.
Memristor crossbar array
The memristor crossbar array is an expandable regular structure, which is considered as a promising technology to realize ultra-high-density non-volatile memory and ultra-large-scale neural computing chip with low-power consumption. As shown in Fig. 2, in the 4 × 4 crossbar array schematic diagram, the horizontal and vertical lines transmit the input and output signal, respectively. On the one hand, the memristor is non-volatile, it can realize low-power even zero-power weight storage by representing the weight in memductance (memristor conductance). When the input signal Vm is applied to the horizontal lines of the memristor crossbar array, the total charge collected on the n-th column line is linearly proportional to the weighted input signal passing through the column, which can be expressed as:
| 7 |
where Gmn is the memductance in m-th row and n-th column (= 1/Mmn). Therefore, the crossbar array can realize the dot product of input and weight vectors by a simple reading operation. Furthermore, the crossbar array can efficiently execute matrix multiplication operation by leveraging its parallel structure advantage, which is very high time-and power-consumption in traditional computing architecture and technology. On the other hand, the programmability of the memristor is very similar to the plasticity of biological synapses and thus facilitate realizing the flexible weight updates. Therefore, it greatly improves the adaptability and generalization ability of the computing architecture.
Fig. 2.
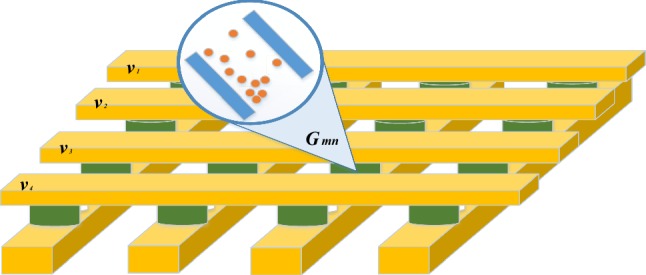
Memristor crossbar array
The adaptive sparse coding based on memristive neural network
Sparse coding
Sparse coding can effectively reduce the complexity of input signals and improve the efficiency of signal processing and storage. Particularly, it has been widely used in feature extraction and pattern recognition. The purpose of sparse coding is to obtain a set of sparse coefficients representing an input image based on the feature dictionary Dmn. And by using linear combination of the dictionary and sparse coefficients, the original input x can be reconstructed later. Meanwhile, the number of non-zero coefficients should be as few as possible. As a whole, the sparse coding target can be expressed as (see Rozell et al. 2008; Sheridan et al. 2017):
| 8 |
where is the L2-norm and is the L0-norm, respectively. represents signal reconstruction errors, that is, the errors between x and the reconstruction signal . reflects the sparsity, which denotes the number of active elements in the sparse coefficient vector. It can be seen that this target not only requires the difference between the reconstructed signal and original signal to be smaller, but also requires the coefficient vector to be sparser.
The combined constraint result is just the optimal solution of sparse coding. It is worth noting that in this work the L0-norm is adopted instead of the L1-norm used in classical sparse coding algorithm (see Wright et al. 2010). For most of the traditional mathematical problems, the initial values of the parameters are greater than zero, so the optimal process is to gradually reduce to close to zero. Therefore, the L1-norm denoting the summation of the absolute value of elements can achieve sparsification. However, in our MNN-SLCA, all coefficient parameters start from zero and only a few will increase, therefore, the L0-norm calculating the number of non-zero elements is more suitable. Different from many compression algorithms that only focus on reconstruction errors, the MNN-SLCA can not only realize sparsity of the input, but also characterize its hidden component features, which is conducive to advanced data analysis such as pattern recognition.
The memristive neural network based adaptive SLCA sparse coding algorithm
Adaptive soft-threshold locally competitive algorithm (SLCA) is one of the important sparse coding algorithms, which can code temporal and spatial signals. It has plasticity, adaptability, and compatibility with the crossbar array structure. In this paper, the SLCA algorithm is used to optimize the energy function (8), and implemented based on the memristive neural network. In specific, the image pixel values are converted to appropriate voltage pulse vector x, applied on the memristors at the cross points via the input neurons on the row lines, and weighted by the memristor synaptic weights (Dmn). Based on the accumulation–stimulation learning rule, the current accumulation of each vertical line determines the membrane potential, namely activity state of the corresponding output neuron, which is expressed as the sparse coefficient .
Theoretically, the dynamic change of output neuron membrane potential is jointly affected by a leakage term and inhibition term from other active neurons, which can be expressed as (see Rozell et al. 2008; Sheridan et al. 2017):
| 9 |
| 10 |
where ui and are membrane potential and activity coefficient associated with the i-th output neuron, respectively; is the threshold of output neuron membrane; is the soft threshold function and r is the parameter controlling threshold conversion speed; dm and dn are m-th and n-th column vectors of the dictionary, respectively. It is worth noting that the activity coefficient will approximately be zero unless ui(t) exceeds the threshold according to Eq. (10). And when ui(t) exceeds the threshold, the activity coefficient will change slightly instead of jumping, which makes the whole algorithm more adaptive and robust (see Rozell et al. 2008). Take r = 1, the soft-threshold function (10) exhibits the characteristic shown in Fig. 3 and its circuit realization based on memristors is designed in next part.
Fig. 3.
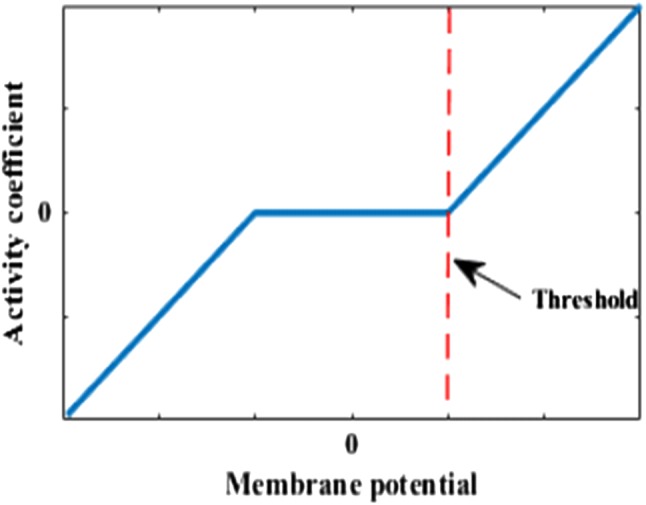
Characteristic curve of Soft-threshold function (10) (r = 1)
In Eq. (9), calculates the similarity of the receptive field between the active neurons and the rest neurons (Fig. 4). When it multiplies the activity coefficient, they can be rewritten as:
| 11 |
where I is identity matrix; is also the inhibition term, and it reflects the effect of lateral neuron inhibition of the biological visual system.
Fig. 4.
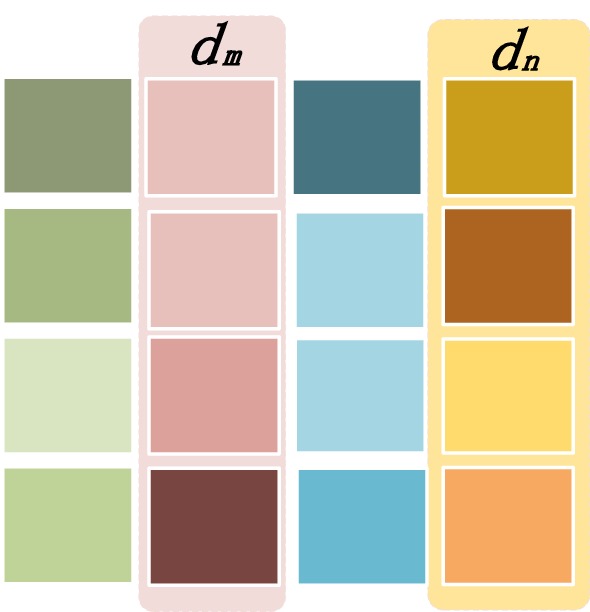
The similarity of the receptive field
The inhibition intensity is proportional to the similarity of the receptive fields. Based on the inhibition feature, the SLCA is able to guarantee the sparsity of coding, by preventing simultaneous neuron activation with the similar receptive fields. However, if based on the traditional hardware computing architecture, the computational intensity of the inhibition item is large and the memory occupation is very high. Therefore, the Eq. (9) can be rewritten into Eqs. (12) and (13) to effectively reduce the computational complexity (see Sheridan et al. 2017). They are given as follow:
| 12 |
| 13 |
where is the reconstructed signal represented by neuron activity coefficient and dictionary set Dmn. Traditional sparse coding algorithm realizes de-duplication by inhibiting synapses, while the SLCA sparse coding directly inhibits activity of neurons to inhibit repeated expression with similar neurons. Equation (12) redefines the inhibition term as the difference between the original signal and the reconstructed signal, and then the difference will be taken as the input signal for the new iteration. This is equivalent to deleting the similar characteristic information between input and reconstruction, and thus it can inhibit the activity of other neurons with similar receptive fields. In addition, it transforms the matrix–matrix product into the vector–matrix product. The computational intensity is thus reduced to some extent. By taking advantage of the unique crossbar structure, it can conveniently perform the vector–matrix dot multiplication, significantly cutting down the computational complexity and improving the efficiency.
The equilibrium point of the sparse coding network will appear after some iterations. When ui(t) is approximately equal to ui(t + 1), the iteration is completed, which means that the membrane change rate approximately equals to zero. Now extremely matches x and the network is in stable state. Consequently, according to (10), the final coefficients associated with the output neurons will be obtained and the sparse representation of the original input signal can be achieved.
Sparse coding with hardware-friendly MNN-SLCA
Combining the characteristics of the adaptive SLCA coding theory and the memristor network, the sparse coding can be achieved by repeated forward matching and backward inhibition, where we use one memristor to achieve forward pass, meanwhile, another one is used to realize backward inhabition. The schematic diagram is shown in Fig. 5. In each iteration, the forward matching of the input signal can be represented as (Fig. 5a). Then, the membrane potential of the output neuron with integral ability substantially changes in the continuous iteration. Meanwhile, the coding coefficient representing the activity state of the output neurons is obtained based on (10). After that, the current signal is transmitted back again to reconstruct the signal (). The new input signal () deleting the residual term of the already matched feature inhibits the neurons with similar receptive field in the following iteration. Finally, after several forward–backward iterations, the stable activity state of the output neurons can be obtained and sparse coding is completed.
Fig. 5.
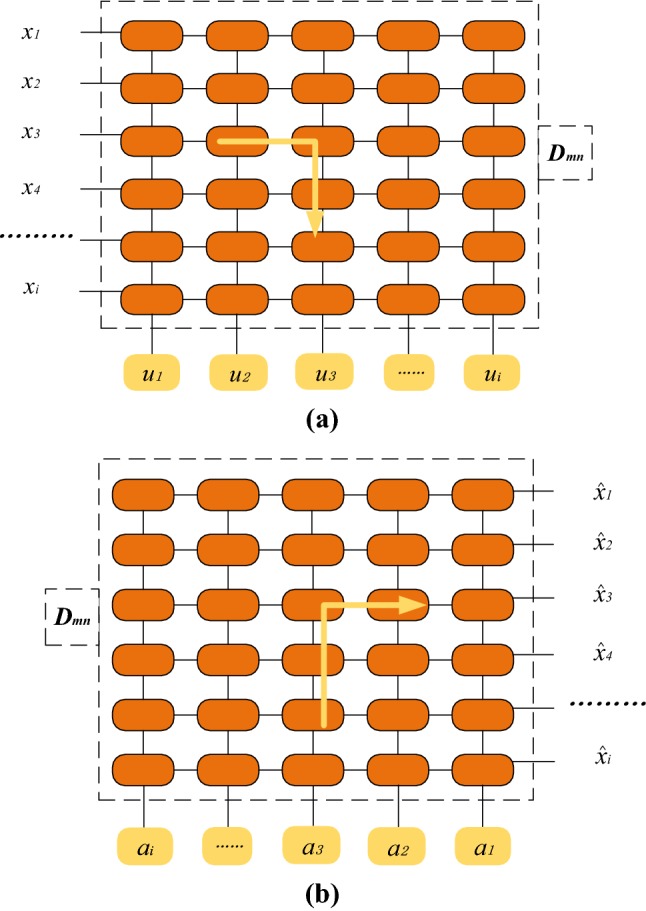
Sparse coding with SLCA and the memristor network. a The forward matching updates the neuron membrane potentials. b The backward inhibition updates the residual input
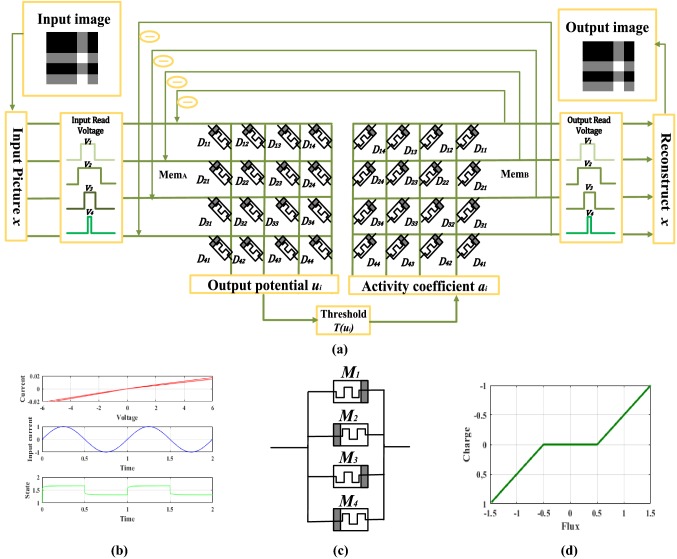
Furthermore, the adaptive SLCA sparse coding (10–13) based on the memristive neural network (MNN-SLCA) is designed. As shown in Fig. 6a, the memristor crossbar network A (MemA) and B (MemB) store the same dictionary set for realizing forward-pattern matching and backward-inhibition reconstruction, respectively, where the dictionary elements are the synaptic weights (memductance) (). The dictionary set is implemented by using two memristor crossbar arrays mainly for two reasons. Firstly, the effect of reading process can be minimized and the system’s robustness can be enhanced. Secondly, forward and backward operations can be performed simultaneously, improving the processing speed.
Fig. 6.
Implementation of the proposed MNN-SLCA. a The complete simplified schematic diagram. b The characteristic curves of the TEAM model. c The circuit realization of the soft-threshold function in (10) based on four memristors connected in reverse parallel and its circuit characteristics in (d)
After converting the original image to the appropriate voltage pulse (the same amplitude, different widths), the voltage signal is input into the array MemA, then the current runs through every memristor synapses. The charge flowing a memristor is proportional to the product of input signal and memristor conductance (). In addition, based on the Kirchhoff’s current theory, the total charge of flowing through the n-th column memristor synapses is . Since the input signal is converted into the voltage signal, it can also be written as , where GT is the memductance; V is input voltage pulse amplitude and t is pulse width. In other words, the charge accumulated on the output neuron corresponding to each column is proportional to the sum of dot product of the input signal x and the receptive field Dn. It reflects the degree of matching between the input vector and the feature vector. Therefore, pattern matching can be achieved efficiently in a reading operation. At the same time, the accumulated membrane potential (xTDn) of the output neuron is obtained by in each iteration. If the output neuron’s membrane potential exceeds threshold value , the neuron will be excited, and then the sparse coding network will adjust adaptively with the change of the threshold value . The threshold will directly affect the sparsity of coding, which will be precisely analyzed later in experiment part. It is noticed that the membrane potential has the same unit as the charge. After forward matching is completed, the membrane potential vector of all output neuron will be obtained, and then the sparse coefficient vector will be got.
Next, the backward inhibition iteration is implemented. The sparse coefficient vector is converted into the corresponding current signal, which is input into the MemB network. Similarly, the flux accumulated in each row line is equal to the flux flowing through all the related memristor synapses (). Since is converted into current amplitude I, it could be redefined as , where t is the current pulse width. Therefore, the backward reading operation performs the weighted sum between the output neuron signal and its receptive field. In addition, the final output column vector is obtained, which is the reconstructed signal (). After backward iteration is completed, the reconstructed signal is fed back to the MemA input terminal, whose difference with the original input signal () is taken as the input of the next new iteration.
In the new iteration, as the input signal is the residual term, the membrane potential of neurons with similar receptive fields is inhibited. Specifically, due to the elimination of similar signals, the related output neuron’s membrane potential accumulates a little (). At the same time, because of the attenuation term, the membrane potential of these neurons will become smaller and smaller, realizing inhibition effect. After a certain number of bidirectional iterations and threshold adjusting, the network will be stable. At this moment, the final coefficient vector is anticipated optimal sparse codes.
It should be noted that before sparse coding, the dictionary is stored in the memristor synapses by one-to-one transform. Based on the TEAM, the input signal (reading signal) should be set to be lower than the memristor writing-threshold value. Therefore, the memristor conductance can remain almost unchanged during each working iteration. In conclusion, the memristor has nanoscale size and non-volatility, and the crossbar array structure possesses the advantages of parallel computing and easy of expansion. Hence, the implementation scheme (MNN-SLCA) can satisfy the requirements of large-scale image sparse coding and low-power consumption.
Circuit design of the soft-threshold function
Figure 6b shows the characteristic curves of the adopted memristor model. Furthermore, four memristors (M1, M2, M3 and M4) are connected in reverse parallel (Fig. 6c) as a combinational circuit (see Adhikari et al. 2012). Then, through two transformations, i.e., ( is flux) as the input and qout= 100q − 1 (q is charge) as the output. The combinational memristor circuit can approximately realize the soft-threshold function in (10) with characteristic curve presented in Fig. 6d. Here, relevant peripheral differential and integral modules, amplification modules and conversion modules are commonly-used and thus omitted.
Dictionary training and storage
Dictionary is a key part of realizing information sparse coding. At present, dictionary construction methods are generally divided into two kinds: analysis-based method and learning-based method. The analysis-based dictionary is constructed by harmonic analysis method and some predefined mathematical transformation, where each element in the dictionary can be described by a mathematical function and a small number of parameters. Compared with the dictionary from analysis-based method, the number of dictionary elements obtained by learning-based method can be determined adaptively. The learning-based dictionary has richer morphology and better matches the memristive network structure. Certainly, MNN-SLCA can also be used to train the dictionary set but could cause overfitting problem like other sparse coding based training methods (see Olshausen and Field 1997). Therefore, in this paper, the Winner-take-all and Oja’s Rule are used to train the dictionary set. (see Lazzaro et al. 1989). Specifically, the theoretical expression of the learning-based method is given as follows:
| 14 |
| 15 |
where DW is dictionary set; is change of the dictionary set during training; y is output neurons of Winner-take-all; is training rate and s is the training set. After offline training, a proper image dictionary set can be obtained.
Theoretically, due to its synaptic behavior and non-volatility, the memristor can realize analog storage with infinite precision. However, based on the current process and controlling accuracy, it has reported only two states, four states, 128 states and 256 states. Hence, for nature image, this paper chooses 256-state memristors to store dictionary by one-to-one transform shown as in Fig. 7a–d. When the reading-writing circuit is in writing state, the converter output is writing voltage correspondingly and applied to memristors. When the reading–writing circuit is in reading sate, the corresponding reading voltage is applied, then the current data can be read out. Through the reading/writing operations, the pixel of the dictionary image can be realized in the form of the corresponding memristor resistance (conductance) and store here. The detailed descriptions are given as follows.
-
Transform function
In digital image processing, the gray value of the initial image is usually preprocessed with a pre-set transform function. For gray pixel, the relation between gray value and corresponding voltage pulse width are designed as follows:
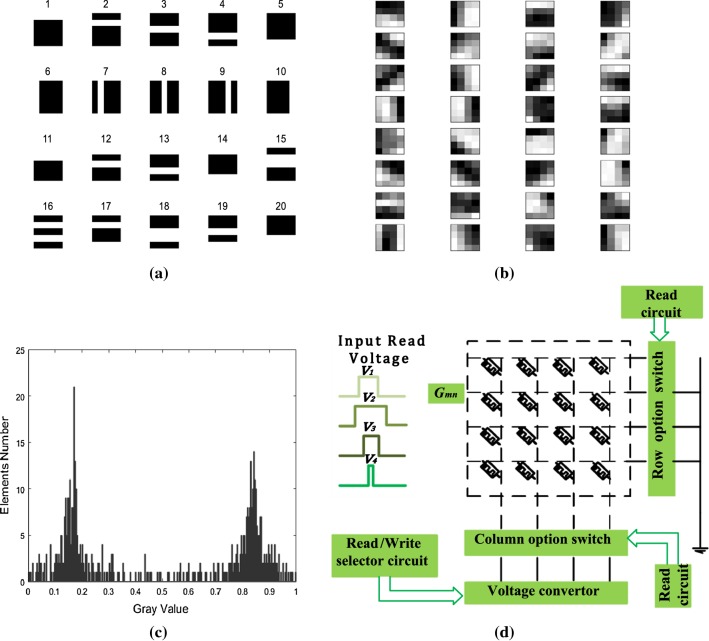
where Wwrite is writing voltage pulse width; is initial pulse width; is pulse width coefficient and g is gray value. According to the corresponding linear relation, 256 gray values in the range [0,1] are transformed into writing voltage pulse width successively. The gray values are correspondingly converted to the write voltage pulse width, as shown in Fig. 7d. It should be noticed that each voltage amplitude is greater than the memristor writing threshold of the TEAM to change the memristor conductance.16 Dictionary Storage (the binary dictionary set shown as Fig. 7a: 25 × 20 and the gray shown as Fig. 7b: 16 × 32)
Step_1 Apply the refresh voltage (Vref> von) onto both terminals of the memristor, then keep the memristor resistances in high resistance state.
Step_2 Read a dictionary, and then select a memristor size correspondingly.
Step_3 Enable writing state of the reading–writing circuit, then employ the writing voltage to obtain the gray value comparison current, which is used for later reading operation. Convert each element of the dictionary matrix to different voltage pulses according to Eq. (16).
Step_4 Under the writing voltage, the memristor resistance in the crossbar array will change correspondingly. When memristor resistance keeps stable, one of memristors is written down.
Step_5 Repeat the above steps to write the two memristors (due to bi-memristor scheme).
Fig. 7.
The procedure of memristor crossbar array storage. a Binary dictionary set. b Gray value dictionary set. c The distribution of dictionary elements set. d The voltage vector of input and the theory of memristor crossbar array storage
Figure 8 demonstrates an example of applying a writing voltage pulse sequence (with the same amplitude, different pulse widths) to a memristor. Theoretically, it is possible to use the memristor crossbar array to store dictionary sets of any size. Meanwhile, with the programmability of memristor, the dictionary set can be updated flexibly without changing the circuit structure. Consequently, the scheme based on memristor crossbar array has better adaptability and generalization ability.
Fig. 8.
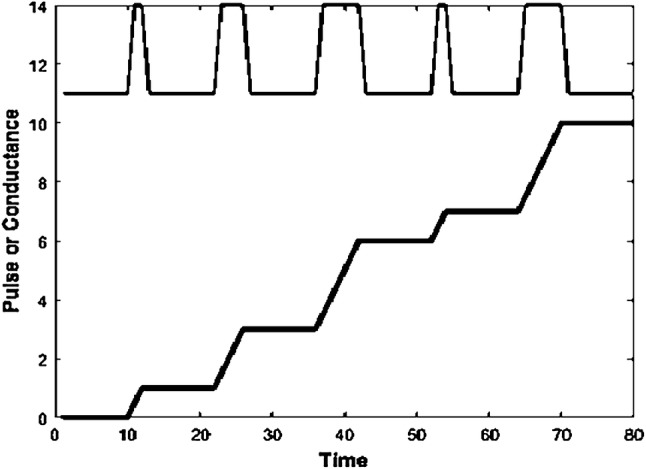
The relationship between input voltage pulse width and conductance in time domain
Super resolution image reconstruction
In the previous sections, the proposed MNN-SLCA algorithm and hardware implementation scheme are interpreted in the above. Next, its application in super resolution (SR) image reconstruction will be further explored.
The flow chart of super resolution image reconstruction based on MNN-SLCA is shown in Fig. 9. The SR reconstruction is an optimizing process in entire learning sample space, through sparsely representing the Low Resolution (LR) and High Resolution (HR) training images samples and decreasing their dimensions. Compared with compression and perception process, the proposed sparse representation exhibits more advantages. On the one hand, sufficient prior knowledge can be guaranteed, which is useful to reduce the amount of data for reconstruction and to improve process efficiency. On the other hand, overfitting and underfitting can effectively overcome.
Fig. 9.
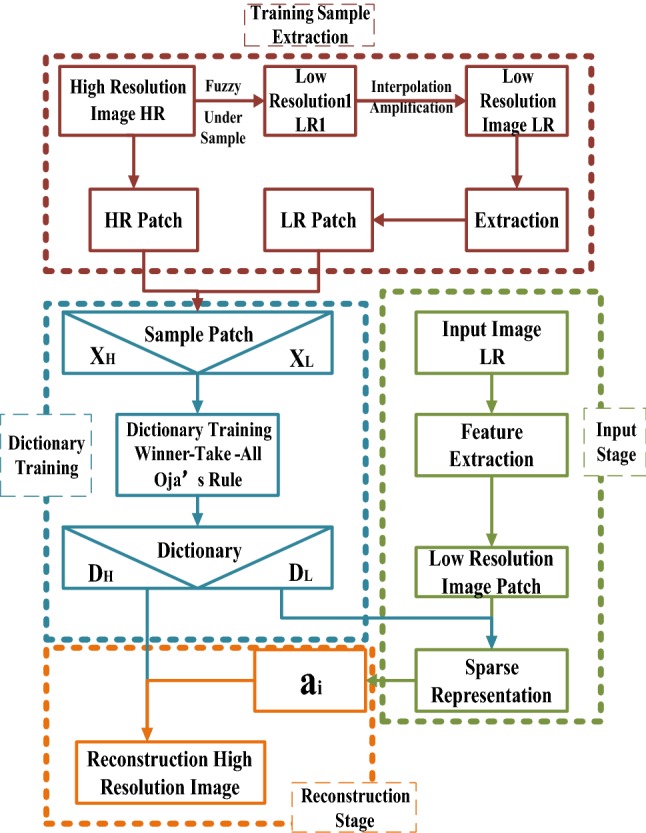
Flow chart of super resolution image reconstruction based on MNN-SLCA
Firstly, for each HR sample image, the corresponding LR image is obtained by under sampling and fuzzy processing. The problem to be solved in super resolution reconstruction is how to reconstruct the corresponding HR image based on a given single LR image. The reconstruction model is given as follows:
| 17 |
| 18 |
| 19 |
| 20 |
where Y is a complete reconstructed super-resolution image; h represents the fuzzy operator; k is under-sampling operator; v is additive noise; X represents the complete HR reconstruction image; is HR image patch. According to the relation between HR image dictionary set DH and image patch , as well as LR image dictionary set DL and image patch , the two dictionaries can be obtained (DH and DL) by the local sparsity relation model (Eqs. 19, 20). The input LR image is divided into patches, and each image patch can be represented by DL sparsely. That means, each patch of a single LR image can be represented by sparse coefficients and a LR overcomplete dictionary. The HR image patch is represented similarly. Finally, the complete HR image is combined by the HR reconstruction image patches. The premise of the basic idea is that the LR and HR overcomplete dictionaries need to be jointly trained to ensure the sparse representation consistency. Therefore, as long as the images are jointly trained to obtain the common sparse representation coefficient, the HR image can be reconstructed using DH and LR image coefficient . It is noticed that a LR image can lead to more than one HR images based on the HR dictionaries. Therefore, in this work, the reconstruction solution is obtained by using the sparse prior knowledge above to construct the relationship between LR image patches sparse coding and HR dictionary. Then the SR reconstruction based on local sparse representation model is established. Specifically, the detail of local high frequency information is reconstructed by Eq. (20), and each HR image patch can be represented by HR image dictionary DH and activity coefficient that is obtained by Eq. (19). Combining the global restriction (Eq. 17) makes the output image more natural and smoother. Finally, a complete super resolution reconstruction image (Y) is obtained.
Experiment simulation and analysis
Parameter analysis and setup
SLCA-λ selection analysis
As the threshold value (λ) changes, the number of active neurons in sparse coding will change adaptively. In order to achieve the optimal sparse target (8), we use different thresholds for contrastive analysis. For the experiment analysis, we set the threshold gradient to be 10, and the threshold range is between 0 and 140. As shown in Fig. 8, the parameter λ is the variable threshold, and N represents the number of active neurons. Figure 10a, b show the simulation results under different thresholds. When the threshold is lower, the number of active neurons increases. As the threshold increases, the number of active neurons decreases. In the case of low threshold, the input signal is expressed by more neurons and more redundant information is reconstructed. In the case of high threshold, the input signal will be reconstructed by fewer neurons and the reconstruction distortion might appear. For the reconstruction shown in Fig. 10b, when the threshold value λ is 40, the reconstruction efficiency is the best. This phenomenon is also the adaptive feature of SLCA. Therefore, the selection of λ will directly influence the reconstructed signal, namely the solution of sparse target (8).
Fig. 10.
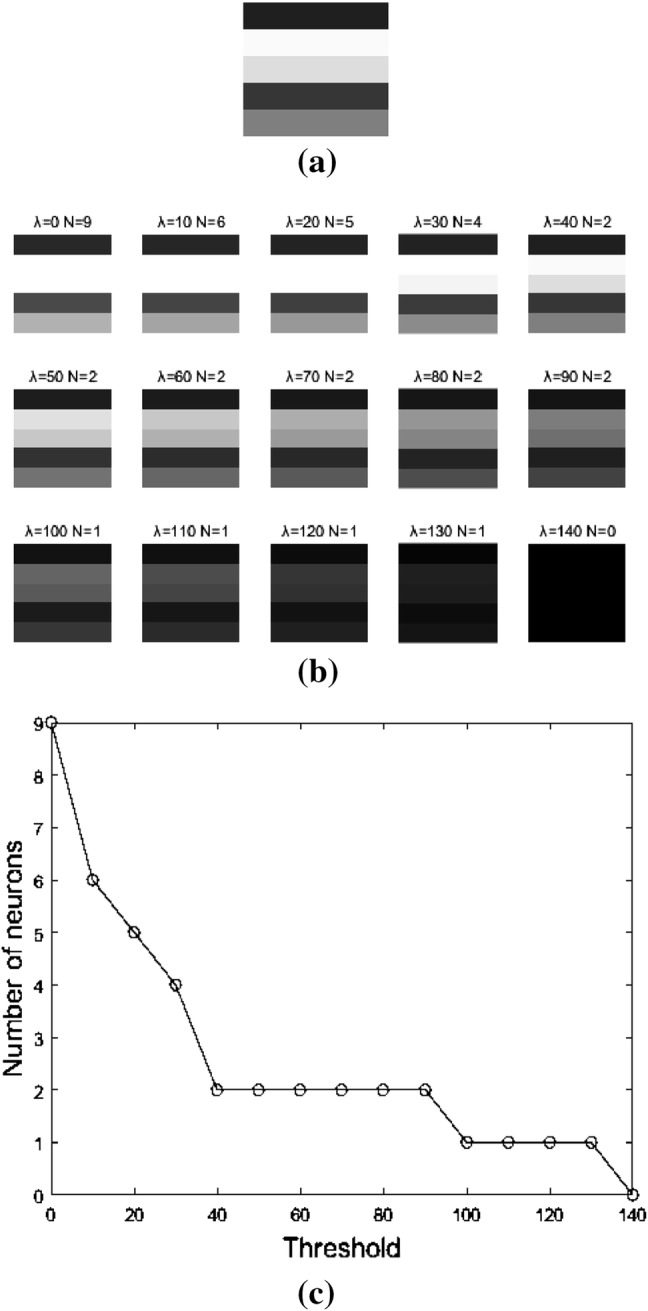
Binary image reconstruction with different thresholds. a The original input. b The output reconstruction images with different thresholds. c The relationship between the number of neurons and the thresholds
Binary image sparse coding with MNN-SLCA
Simple image refers to the image that can be constructed by binary dictionary set. Firstly, a simple image is read and its numerical matrix will be obtained, which is a size of 5 × 5 numerical matrix. The binary value of the simple image matrix is converted into the corresponding voltage pulse signal. Then the voltage pulse signals are applied into the memristor crossbar array storing the binary dictionary set (Fig. 7a). After a certain number of iterations, the memristor networks are stable. Only a small number of output neurons are active whose membrane potential is greater than the threshold. The active neuron coefficient is just the goal anticipated sparse code. Then,by combing the coefficient and binary dictionary set through the proposed reconstruction scheme, the reconstructed image of the input will be achieved.
As shown in Fig. 11a, the different binary image is reconstructed by the same way. Among the 12 groups of images, the front one is the input image, and the back one is the reconstructed image obtained by the MNN-SLCA. Figure 11b shows the iterative curve of the No. 7 input image corresponding to the membrane potential of output neurons. It can be seen that the neurons (U(3) and U(9)) are in active state finally. Certainly, the MNN-SLCA algorithm can be also used in sparse coding and reconstruction of other digital signals with its adaptability and versatility.
Fig. 11.
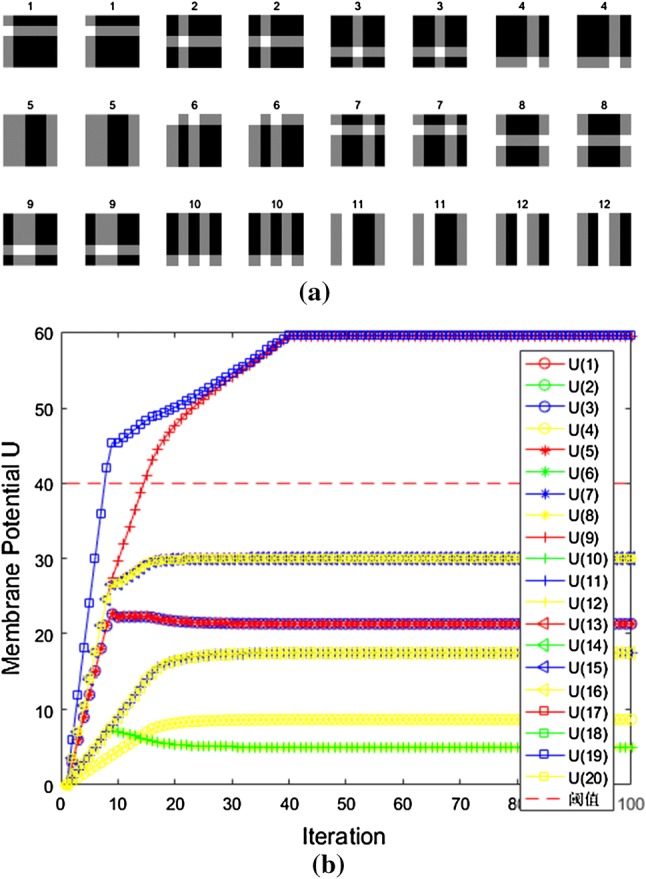
Binary image reconstruction. a The sample of input and output. b The seventh neuron membrane potential iteration
Table 1 shows the performance estimation and comparison between the novel MNN-SLCA solution and the traditional CMOS circuits, which includes time, MSE and energy (see Sheridan et al. 2017). It can be seen the advantages of MNN-SLCA. Certainly, the measurement of the practical performance will be more accurate on physical hardware circuits, but by leveraging the nanometer memristor and efficient vector–matrix operation based on memristor crossbar array, the hardware acceleration and low power consumption are fully expectable.
Table 1.
Performance estimation and comparison between the novel MNN-SLCA and traditional CMOS circuit
| Method/index | Time | MSE | Energy |
|---|---|---|---|
| MNN-SLCA | 0.0059 s | 1.26e − 3 | 876.5 uJ |
| CMOS | 0.0097 s | 3.12e − 3 | 3.45 mJ |
Gray image with MNN-SLCA
Then, the grayscale image (Fig. 12a) is processed similarly. However, the pixel of the entire grayscale image relative to a dictionary set is not homologous, so we split the input image matrix into smaller patches to match the requirement. According to the corresponding dictionary set (Fig. 7b), image should be divided into patches with size of 4 × 4 (Fig. 12c). Then, according to the above, the integrated dictionary set (Fig. 12d) is stored in 16 × 32 memristor crossbar array.
Fig. 12.

Gray input image and dictionary. a Input image. b Segmentation. c Patch. d Overcomplete set of the dictionary (4 × 4×32)
According to the above, we know there are 32 neurons associated with 32 receptive fields. Therefore, neurons are numbered from 1 to 32 for conveniently observing their membrane potential change.
The reconstruction detail of one patch is shown as Fig. 13a, where the membrane potentials of 32 output neurons are continuously iterated. When these active neurons keep on stable, the iteration is completed with stable network. The reconstruction of the whole gray image is sparsely coded in this way. Then, the reconstruction images patches are combined, achieving the whole reconstruction gray image (Fig. 13b). Furthermore, color images can also be reconstructed by three RGB dictionaries that are trained by the same way, respectively. According to the above sample, the size of the segmentation patch corresponds to the dictionary set. The dictionary set with different dimensions can sparse the gray image to different degrees. Therefore, it should be selected according to the actual needs. If requires high reconstruction, one can choose the overcomplete dictionary set with larger dimensions.
Fig. 13.
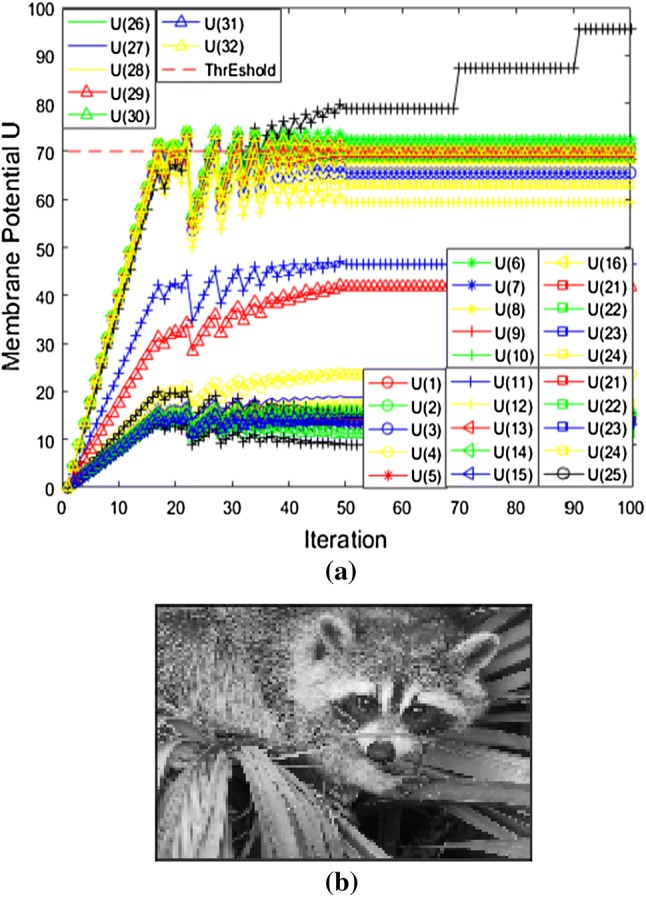
The procedure of gray image reconstruction. a The iteration of neurons membrane potential. b The reconstruction output image
Super resolution image reconstruction with MNN-SLCA
It can be known from the sparse coding for the natural images, the resolution of the reconstructed HR image is determined by the dictionary set DH. According to the flow of Fig. 9, the dictionary set DH and DL are trained. Then, the MNN-SLCA and Classical sparse coding (Classical SC) were used to prosses the input LR gray image and HR gray image (Fig. 14), respectively.
Fig. 14.

The samples of super-resolution image reconstruction. a House-SC. b House-MNN-SLCA. c Girl-SC. d Girl-MNN-SLCA
Furthermore, we used PSNR and SSIM measurement methods to evaluate image quality in Fig. 14, respectively. According to the selected test samples, the PSNR and SSIM value results are obtained as shown in Table 2. It can be seen from the table, the HR image quality obtained by the MNN-SLCA method is better (the PSNR and SSIM values of the Classical SC are lower). On the one hand, the main reason may be that the Classical SC method cannot effectively simulate the visual complexity of natural images. If the number of input training images is insufficient, the performance will be affected badly in Classical SC. On the other hand, different dictionary learning methods also affect the quality of HR images. Therefore, the final effect of super resolution reconstruction depends on dictionary quality and specific sparse coding algorithm. By using MNN-SLCA, the accuracy of image reconstruction is improved, and the image quality of super resolution reconstruction is higher. Therefore, the effectiveness and superiority of the whole scheme proposed can be verified.
Table 2.
The PSNR and SSIM of the images
| Methods | PSNR(dB) | SSIM | ||
|---|---|---|---|---|
| House | Girl | House | Girl | |
| MNN-SLCA | 31.68 | 33.57 | 0.9201 | 0.9535 |
| Classical SC | 29.36 | 31.69 | 0.8354 | 0.8723 |
Conclusion and discussion
Combing the characteristic of memristor crossbar array and the principle of biological sparse coding, this paper proposes an adaptive sparse coding algorithm based on memristive neural network with soft-threshold local competition (MNN-SLCA). The scheme uses programmable and non-volatile memristor crossbar array to realize dictionary training and storage. It provides key technical support for large-scale sparse coding. With the unique advantages of vector–matrix operation and bionic synapse characteristics, the efficient pattern matching and lateral neuronal inhibition of biology can be achieved. Therefore, neurons with impulse accumulation–stimulation mechanism are constructed, and the sparse coding information can be represented by the activity state of output neurons. The hardware scheme of adaptive SLCA sparse coding based on bi-memristor networks is fully designed. It is expected to further realize hardware acceleration of sparse coding algorithm and improve real-time processing capacity of complex tasks. Finally, the application of the MNN-SLCA in super resolution image reconstruction is explored. A series of experimental results of image reconstruction and objective analysis verify the effectiveness of the scheme. With its superior potential in intelligent information coding, it will be widely used into large-scale and low-power consumption information-processing applications.
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant No. 61601376, 61672436), Fundamental Research Funds for the Central Universities (XDJK2019C034), Fundamental Science and Advanced Technology Research Foundation of Chongqing (cstc2016jcyjA0547), China Postdoctoral Science Foundation Special Funded (2018T110937), Chongqing Postdoctoral Science Foundation Special Funded (Xm2017039), Student’s Platform for Innovation and Entrepreneurship Training Program (201810635017).
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Adhikari SP, Yang C, Kim H. Memristor bridge synapse-based neural network and its learning. IEEE Trans Neural Netw Learn Syst. 2012;23(9):1426–1435. doi: 10.1109/TNNLS.2012.2204770. [DOI] [PubMed] [Google Scholar]
- Bao B, Jiang T, Wang G. Two-memristor-based Chua’s hyperchaotic circuit with plane equilibrium and its extreme multistability. Nonlinear Dyn. 2017;89(2):1157–1171. doi: 10.1007/s11071-017-3507-0. [DOI] [Google Scholar]
- Bao H, Wang N, Bao B. Initial condition-dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria. Commun Nonlinear Sci Numer Simul. 2018;57:264–275. doi: 10.1016/j.cnsns.2017.10.001. [DOI] [Google Scholar]
- Bao H, Liu W, Hu A. Coexisting multiple firing patterns in two adjacent neurons coupled by memristive electromagnetic induction. Nonlinear Dyn. 2019;95(1):43–56. doi: 10.1007/s11071-018-4549-7. [DOI] [Google Scholar]
- Candès EJ, Wakin MB. An introduction to compressive sampling. IEEE Signal Process Mag. 2008;25(2):21–30. doi: 10.1109/MSP.2007.914731. [DOI] [Google Scholar]
- Chen L, Li C, Huang T. A synapse memristor model with forgetting effect. Phys Lett A. 2013;377(45–48):3260–3265. doi: 10.1016/j.physleta.2013.10.024. [DOI] [Google Scholar]
- Chua L. Memristor-the missing circuit element. IEEE Trans Circuit Theory. 1971;18(5):507–519. doi: 10.1109/TCT.1971.1083337. [DOI] [Google Scholar]
- Donoho DL, Elad M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc Natl Acad Sci. 2003;100(5):2197–2202. doi: 10.1073/pnas.0437847100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Field DJ. Relations between the statistics of natural images and the response properties of cortical cells. J Opt Soc. 1987;4(12):2379–2394. doi: 10.1364/JOSAA.4.002379. [DOI] [PubMed] [Google Scholar]
- Field DJ. What the statistics of natural images tell us about visual coding. Hum Vis Vis Process Digit Disp. 1989;1077:269–277. doi: 10.1117/12.952724. [DOI] [Google Scholar]
- Hu X, Feng G, Duan S. A memristive multilayer cellular neural network with applications to image processing. IEEE Trans Neural Netw Learn Syst. 2017;28(8):1889–1901. doi: 10.1109/TNNLS.2016.2552640. [DOI] [PubMed] [Google Scholar]
- Itoh M, Chua L (2014) Memristor cellular automata and memristor discrete-time cellular neural networks. In: Memristor networks. Springer, Cham, pp 649–713
- Jo SH, Chang T. Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett. 2010;10(4):1297–1301. doi: 10.1021/nl904092h. [DOI] [PubMed] [Google Scholar]
- Kawahara A, Azuma R, Ikeda Y. An 8 Mb multi-layered cross-point ReRAM macro with 443 MB/s write throughput. IEEE J Solid-State Circuits. 2013;48(1):178–185. doi: 10.1109/JSSC.2012.2215121. [DOI] [Google Scholar]
- Kvatinsky S, Friedman EG, Kolodny A. TEAM: threshold adaptive memristor model. IEEE Trans Circuits Syst I Regul Pap. 2013;60(1):211–221. doi: 10.1109/TCSI.2012.2215714. [DOI] [Google Scholar]
- Lazzaro J, Ryckebusch S, Mahowald M A (1989) Winner-take-all networks of O(n) complexity. In: Advances in neural information processing systems, pp 703–711
- Li Y, Cichocki A, Amari S. Analysis of sparse representation and blind source separation. Neural Comput. 2004;16(6):1193–1234. doi: 10.1162/089976604773717586. [DOI] [PubMed] [Google Scholar]
- Long S, Perniola L, Cagli C. Voltage and power-controlled regimes in the progressive unipolar RESET transition of HfO 2-based RRAM. Sci Rep. 2013;3:2929. doi: 10.1038/srep02929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muenstermann R, Menke T, Dittmann R. Coexistence of filamentary and homogeneous resistive switching in Fe-doped SrTiO3 thin-film memristive devices. Adv Mater. 2010;22(43):4819–4822. doi: 10.1002/adma.201001872. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Sparse coding with an overcomplete basis set: A strategy employed by V1? Vis Res. 1997;37(23):3311–3325. doi: 10.1016/S0042-6989(97)00169-7. [DOI] [PubMed] [Google Scholar]
- Pershin YV, Di Ventra M. Practical approach to programmable analog circuits with memristors. IEEE Trans Circuits Syst I Regul Pap. 2010;57(8):1857–1864. doi: 10.1109/TCSI.2009.2038539. [DOI] [Google Scholar]
- Rozell CJ, Johnson DH, Baraniuk RG. Sparse coding via thresholding and local competition in neural circuits. Neural Comput. 2008;20(10):2526–2563. doi: 10.1162/neco.2008.03-07-486. [DOI] [PubMed] [Google Scholar]
- Sheridan PM, Cai F, Du C. Sparse coding with memristor networks. Nat Nanotechnol. 2017;12(8):784. doi: 10.1038/nnano.2017.83. [DOI] [PubMed] [Google Scholar]
- Snider G, Amerson R, Carter D. From synapses to circuitry: using memristive memory to explore the electronic brain. Computer. 2011;44(2):21–28. doi: 10.1109/MC.2011.48. [DOI] [Google Scholar]
- Strukov DB, Snider GS, Stewart DR. The missing memristor found. Nature. 2008;453(7191):80–83. doi: 10.1038/nature06932. [DOI] [PubMed] [Google Scholar]
- Wang X, Chen Y, Xi H. Spintronic memristor through spin-torque-induced magnetization motion. IEEE Electron Device Lett. 2009;30(3):294–297. doi: 10.1109/LED.2008.2012270. [DOI] [Google Scholar]
- Wang M, Cai S, Pan C. Robust memristors based on layered two-dimensional materials. Nat Electron. 2018;1(2):130. doi: 10.1038/s41928-018-0021-4. [DOI] [Google Scholar]
- Wright J, Ma Y, Mairal J. Sparse representation for computer vision and pattern recognition. Proc IEEE. 2010;98(6):1031–1044. doi: 10.1109/JPROC.2010.2044470. [DOI] [Google Scholar]
- Yan B, Chen Y, Li H (2018) Challenges of memristor based neuromorphic computing system. Sci China Inf Sci 61(6):060425
- Yang JJ, Strukov DB, Stewart DR. Memristive devices for computing. Nat Nanotechnol. 2013;8(1):13. doi: 10.1038/nnano.2012.240. [DOI] [PubMed] [Google Scholar]
- Yang Y, Chang T, Lu W (2014) Memristive devices: switching effects, modeling, and applications. In: Memristors and memristive systems. Springer, New York, NY, pp 195–221
- Yesil A. A new grounded memristor emulator based on MOSFET-C. AEU-Int J Electron Commun. 2018;91:143–149. doi: 10.1016/j.aeue.2018.05.004. [DOI] [Google Scholar]
- Zakhidov AA, Jung B, Slinker JD. A light-emitting memristor. Org Electron. 2010;11(1):150–153. doi: 10.1016/j.orgel.2009.09.015. [DOI] [Google Scholar]
- Zhang F, Duan S, Wang L. Route searching based on neural networks and heuristic reinforcement learning. Cogn Neurodyn. 2017;11(3):245–258. doi: 10.1007/s11571-017-9423-7. [DOI] [PMC free article] [PubMed] [Google Scholar]