Abstract
Human leukocyte antigen (HLA) genes provide useful information on the relationship between cancer and the immune system. Despite the ease of obtaining these data through next-generation sequencing methods, interpretation of these relationships remains challenging owing to the complexity of HLA genes. To resolve this issue, we developed a Bayesian method, ALPHLARD-NT, to identify HLA germline and somatic mutations as well as HLA genotypes from whole-exome sequencing (WES) and whole-genome sequencing (WGS) data. ALPHLARD-NT showed 99.2% accuracy for WGS-based HLA genotyping and detected five HLA somatic mutations in 25 colon cancer cases. In addition, ALPHLARD-NT identified 88 HLA somatic mutations, including recurrent mutations and a novel HLA-B type, from WES data of 343 colon adenocarcinoma cases. These results demonstrate the potential of ALPHLARD-NT for conducting an accurate analysis of HLA genes even from low-coverage data sets. This method can become an essential tool for comprehensive analyses of HLA genes from WES and WGS data, helping to advance understanding of immune regulation in cancer as well as providing guidance for novel immunotherapy strategies.
Keywords: Bayesian model, HLA genotyping, HLA mutation calling, whole-exome sequencing, whole-genome sequencing
1. Introduction
Human leukocyte antigen (HLA) genes are essential components of the immune system, which present peptides to immune cells to facilitate recognition of nonself antigens. HLA genes must be highly polymorphic to effectively carry out this function, with many types or alleles recognized, resulting in high individual variation in immune responses. Therefore, HLA genotyping, in which the specific pair of HLA types is identified for each HLA locus, is essential to understand the immune system. Recently, the interaction between cancer and the immune system has attracted attention (Grivennikov et al., 2010; Schreiber et al., 2011; Kreiter et al., 2015; Rooney et al., 2015; Marty et al., 2017), and somatic mutations in HLA genes have been shown to accumulate in specific cancer types (The Cancer Genome Atlas Research Network, 2014; Testoni et al., 2015; The Cancer Genome Atlas Network, 2015; Giannakis et al., 2016; McGranahan et al., 2017). Therefore, HLA genotyping can further help to understand the link between cancer and immunity, which would benefit personalized medicine.
There are several approaches currently available for HLA genotyping. Conventional approaches use polymerase chain reaction-based methods with sequence-specific oligonucleotides (Saiki et al., 1986), sequence-specific primers (Olerup and Zetterquist, 1992), and sequence-based typing (Santamaria et al., 1992); however, these methods are time consuming and labor intensive, and can only provide information on targeted HLA genes. New methods for HLA genotyping have been developed more recently with advances in molecular techniques, including whole-exome sequencing (WES), whole-genome sequencing (WGS), and RNA sequencing (Boegel et al., 2012; Warren et al., 2012; Kim and Pourmand 2013; Liu et al., 2013; Bai et al., 2014; Szolek et al., 2014; Nariai et al., 2015; Shukla et al., 2015; Dilthey et al., 2016; Xie et al., 2017; Hayashi et al., 2018; Lee and Kingsford, 2018). With these methods, information of both somatic mutations and HLA genotypes can be obtained from the entire sequence, which can facilitate investigations on the relationship between cancer and the immune system. In particular, methods that can specifically call germline or somatic mutations in HLA genes (Shukla et al., 2015; Hayashi et al., 2018; Lee and Kingsford, 2018) are valuable, since these mutations have potential to change immune responses, including tumor immune escape. However, the low coverage of WGS data makes it challenging to detect HLA germline and somatic mutations.
Previously, we developed a Bayesian model, called ALPHLARD (Hayashi et al., 2018), which identifies HLA genotypes and germline mutations from WGS data. ALPHLARD can also call HLA somatic mutations by comparing HLA sequences determined from normal and tumor samples. However, the specificity of the HLA somatic mutation calling is insufficient because ALPHLARD conducts the analyses of normal and tumor samples independently. To resolve this issue, we extended ALPHLARD to construct a new model named ALPHLARD-NT for accurately identifying both HLA germline and somatic mutations as well as HLA genotypes from WGS data. ALPHLARD-NT was validated from WES and WGS data sets from 343 and 25 colon cancer samples, respectively, which demonstrated its good performance in HLA genotyping, along with the ability to call HLA germline and somatic mutations, even from low-coverage data.
2. Methods
2.1. Human leukocyte antigen reference data
We used the IPD-IMGT/HLA Database (Robinson et al., 2015) as HLA reference sequences in our method. Since the database provides incomplete sequences for most HLA types, we replaced the unknown bases with those of the most similar HLA type. To this end, similarity was determined by measuring the hamming distance in multiple sequence alignments (MSAs) across HLA types obtained from the IPD-IMGT/HLA Database. We used the Allele Frequency Net Database (González-Galarza et al., 2015) for prior information on HLA type frequencies.
2.2. Human leukocyte antigen read filtering and realignment
Filtering of HLA reads must be carefully performed for various reasons. First, it is insufficient to use only a human genome reference such as GRCh37 or GRCh38 owing to the high polymorphism of HLA genes. Therefore, a specific HLA database is required, such as the IPD-IMGT/HLA Database. Second, HLA genes and pseudogenes are paralogs and are, therefore, quite similar. Hence, when performing HLA genotyping, it is essential to distinguish reads from an HLA gene of interest from those of other HLA genes and pseudogenes.
In our HLA genotyping pipeline, a BAM file whose reference is the human genome is used as input data. First, sequence reads in the BAM file are filtered by extracting the HLA region, which is defined by chr6:28,477,797–33,448,354 for GRCh37 and chr6:28,510,120–33,480,577 for GRCh38, and covers the HLA-A, -B, -C, -DPA1, -DPB1, -DQA1, -DQB1, and -DRB1 genes. Next, the extracted reads are mapped to all HLA reference sequences using BWA-MEM (version 0.7.17) with the option to obtain information on all identified alignments. Each read is classified based on whether or not the HLA genes produced the read, and if so, which specific gene was involved. This classification is made using alignment scores, which we call HLA read scores (HR scores), and are calculated as follows. Let xi be the 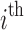 read pair that consists of two single reads
read pair that consists of two single reads 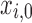 and
and  . In the case of single-end sequence data, xi consists of one read,
. In the case of single-end sequence data, xi consists of one read,  . In addition, tk is defined as the
. In addition, tk is defined as the  HLA type. If the read
HLA type. If the read 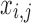 is unmapped to the HLA type tk, then the HR score
is unmapped to the HLA type tk, then the HR score  for
for  and tk is
and tk is 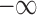 . Otherwise,
. Otherwise,  and
and 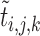 are the aligned sequences of
are the aligned sequences of 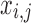 and tk, while
and tk, while  and
and 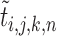 are the
are the 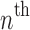 bases or gaps of
bases or gaps of  and
and  , respectively. Moreover, the mismatch probability
, respectively. Moreover, the mismatch probability 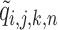 of
of  and
and  can be calculated by
can be calculated by
 |
where 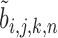 is the Phred base quality of
is the Phred base quality of 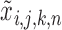 . Using the aforementioned definitions, the HR score
. Using the aforementioned definitions, the HR score  is given by
is given by
 |
where
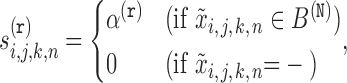 |

Here,  and
and 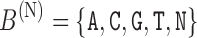 .
.  is a reward for the length of the read, and
is a reward for the length of the read, and 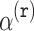 is a positive hyperparameter for one base. By contrast,
is a positive hyperparameter for one base. By contrast,  is a penalty for mismatches between the read and the HLA type, and
is a penalty for mismatches between the read and the HLA type, and  ,
, 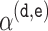 ,
, 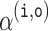 ,
,  , and
, and  are negative hyperparameters for deletion opening, deletion extension, insertion opening, insertion extension, and an unknown base N in the read or the HLA type, respectively.
are negative hyperparameters for deletion opening, deletion extension, insertion opening, insertion extension, and an unknown base N in the read or the HLA type, respectively.
Then, for each read pair xi and each HLA locus l, the score  is defined by
is defined by
 |
where Tl is a set of HLA types of the HLA locus l. When xi is a paired-end read, it is used for genotyping the HLA locus l if the following two criteria are satisfied:
 |
 |
Here, 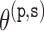 is a hyperparameter of a threshold for the maximum HR score of the locus and
is a hyperparameter of a threshold for the maximum HR score of the locus and  is a hyperparameter of a threshold for the difference between the maximum HR scores of the locus and other loci. However, if xi is a single-ended read, different thresholds are used; in other words, xi is used for genotyping the HLA locus l if
is a hyperparameter of a threshold for the difference between the maximum HR scores of the locus and other loci. However, if xi is a single-ended read, different thresholds are used; in other words, xi is used for genotyping the HLA locus l if
 |
The former criterion is necessary to collect reads that are likely to be produced by the locus, whereas the latter criterion is needed to exclude reads that might be produced by other loci.
Next, all of the read pairs that satisfy the conditions are realigned to the MSAs of the HLA types of the HLA locus l. Realignment of the read  is performed using the best HLA type whose index is given by
is performed using the best HLA type whose index is given by
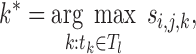 |
and the realigned read  is obtained by aligning
is obtained by aligning  to the MSA
to the MSA 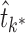 of the HLA type
of the HLA type  to match the alignment
to match the alignment  . This is done by simply translating the positions of bases and gaps in
. This is done by simply translating the positions of bases and gaps in  into those in
into those in  .
.
2.3. Bayesian model for human leukocyte antigen analysis
We applied a Bayesian model for HLA genotyping and HLA somatic mutation detection, with basically the same structure as our previous method (Hayashi et al., 2018) except for some additional parameters. Figure 1 shows the graphical model. Hereafter, we suppose that the sequence reads are paired-ended for simplicity, and the model for single-ended sequence reads is the same except that the reads are unpaired.
FIG. 1.
Graphical representation of our method.
Input data of the model include both the normal and tumor realigned reads. Let  be the
be the  normal realigned read pair, and
normal realigned read pair, and 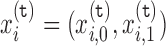 be the
be the 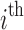 tumor realigned read pair, where
tumor realigned read pair, where  and
and  indicate parameters for the normal and tumor sample, respectively. For each
indicate parameters for the normal and tumor sample, respectively. For each  , we define
, we define  as the
as the 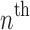 base of
base of  , and
, and  as the mismatch probability of
as the mismatch probability of  . Note that the first position of each realigned read is not the beginning of the read but rather that of the MSAs, and
. Note that the first position of each realigned read is not the beginning of the read but rather that of the MSAs, and  and
and  are undefined if the
are undefined if the  position is not covered by the read. We define
position is not covered by the read. We define  as a set of positions covered by the read
as a set of positions covered by the read  and
and  as
as  .
.
We denote HLA types of the sample by  and
and  , normal HLA sequences by
, normal HLA sequences by  and
and 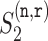 , and tumor HLA sequences by
, and tumor HLA sequences by  and
and  . Here, the sequences of
. Here, the sequences of 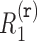 and
and 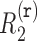 are the MSAs of the HLA types.
are the MSAs of the HLA types. 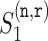 and
and 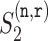 are used to consider germline variants in
are used to consider germline variants in 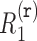 and
and  , and
, and  and
and  are used to reflect somatic mutations. We also introduce decoy HLA types
are used to reflect somatic mutations. We also introduce decoy HLA types  , decoy normal HLA sequences
, decoy normal HLA sequences 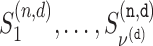 , and decoy tumor HLA sequences
, and decoy tumor HLA sequences 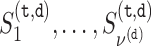 , where
, where  is a hyperparameter of the number of the decoy parameters. These parameters are essential to make a robust inference, because their presence can reduce the influence of misclassified reads at the previous filtering step that were actually produced by other HLA genes or pseudogenes. For convenience, we sometimes use
is a hyperparameter of the number of the decoy parameters. These parameters are essential to make a robust inference, because their presence can reduce the influence of misclassified reads at the previous filtering step that were actually produced by other HLA genes or pseudogenes. For convenience, we sometimes use  ,
,  , and
, and  instead of
instead of  ,
,  , and
, and 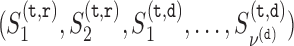 , respectively. In addition, in some cases,
, respectively. In addition, in some cases,  is used instead of
is used instead of  . Similar to the notation for read pairs,
. Similar to the notation for read pairs,  and
and  are defined as the
are defined as the  base of Rm and Sm, respectively.
base of Rm and Sm, respectively.
Next, let  and
and 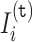 be parameters that indicate the specific HLA sequence that produced
be parameters that indicate the specific HLA sequence that produced  and
and  , respectively. In other words,
, respectively. In other words, 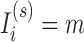 means that
means that  was produced by Sm. Note that
was produced by Sm. Note that 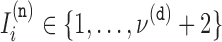 because tumor HLA sequences cannot produce normal sequence reads, and that
because tumor HLA sequences cannot produce normal sequence reads, and that 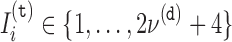 because the tumor sample might also contain normal cells.
because the tumor sample might also contain normal cells.  is independently generated from a distribution governed by
is independently generated from a distribution governed by 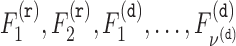 , G, and
, G, and  . Again, we sometimes use convenient notations of
. Again, we sometimes use convenient notations of  and
and  instead of
instead of  , and (
, and (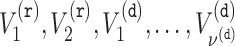 ). Fm is a positive real parameter that expresses the likelihood that a read is produced by
). Fm is a positive real parameter that expresses the likelihood that a read is produced by  and
and  . G is also a positive real parameter and expresses the ratio of normal cells contained in the tumor sample. Vm is a tuple
. G is also a positive real parameter and expresses the ratio of normal cells contained in the tumor sample. Vm is a tuple  , where N is the length of MSAs and
, where N is the length of MSAs and  is a parameter of 0 or 1, which indicates whether
is a parameter of 0 or 1, which indicates whether  and
and  are valid, as described in more detail hereunder.
are valid, as described in more detail hereunder.
The posterior probability of the parameters is given by
 |
where 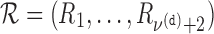 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 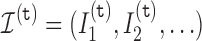 ,
,  , and
, and 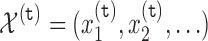 .
.
The likelihoods of sequence read pairs are given by
 |
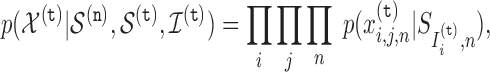 |
where

Here,  ,
, 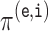 , and
, and  are hyperparameters of probabilities of a deletion error, insertion error, and
are hyperparameters of probabilities of a deletion error, insertion error, and  in a sequence read, respectively.
in a sequence read, respectively.
The prior probability of tumor HLA sequences is given by
 |
where

Here,  ,
,  ,
,  , and
, and  are hyperparameters of probabilities of a somatic substitution, somatic deletion, somatic insertion, and
are hyperparameters of probabilities of a somatic substitution, somatic deletion, somatic insertion, and 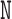 in a tumor HLA sequence, respectively.
in a tumor HLA sequence, respectively.
The prior probability of normal HLA sequences is given by
 |
where


Here,  ,
,  ,
,  , and
, and  are hyperparameters of probabilities of a germline substitution, germline deletion, germline insertion, and
are hyperparameters of probabilities of a germline substitution, germline deletion, germline insertion, and  , respectively, in a nondecoy normal HLA sequence at the position where the reference is an original base. The other hyperparameters are also defined in a similar way. The probabilities for an imputed reference base should be larger than those for an original base to reduce the influence of misimputation. In addition, the probabilities for a decoy normal HLA sequence should also be larger than those for a nondecoy normal HLA sequence to achieve robustness against misclassified reads.
, respectively, in a nondecoy normal HLA sequence at the position where the reference is an original base. The other hyperparameters are also defined in a similar way. The probabilities for an imputed reference base should be larger than those for an original base to reduce the influence of misimputation. In addition, the probabilities for a decoy normal HLA sequence should also be larger than those for a nondecoy normal HLA sequence to achieve robustness against misclassified reads.
The prior probability of HLA types is given by
 |
where
 |
 |
Here, pt is a prior probability of the HLA type t, which was calculated using the Allele Frequency Net Database.
The prior probability of normal indicator variables is given by
 |
where
 |
This formula means that the read cannot be produced by an HLA sequence without a valid position covered by the read, which is controlled by  . Similarly, the prior probability of tumor indicator variables is given by
. Similarly, the prior probability of tumor indicator variables is given by
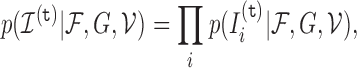 |
where
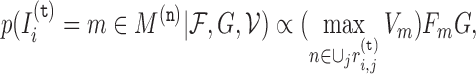 |
 |
 |
 |
Note that 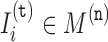 indicates that the read was derived from a normal cell, and
indicates that the read was derived from a normal cell, and 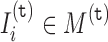 indicates that the read was derived from a tumor cell. Furthermore, matched normal-tumor HLA sequences
indicates that the read was derived from a tumor cell. Furthermore, matched normal-tumor HLA sequences 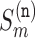 and
and  share Vm and Fm.
share Vm and Fm.
The prior probability of  is given by
is given by
 |
where
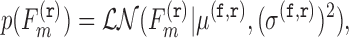 |
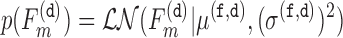 |
Here,  is a log-normal distribution,
is a log-normal distribution,  and
and  are hyperparameters of the mean and variance for the nondecoy parameters, and
are hyperparameters of the mean and variance for the nondecoy parameters, and  and
and  are hyperparameters of the mean and variance for the decoy parameters.
are hyperparameters of the mean and variance for the decoy parameters.  should be smaller than
should be smaller than 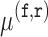 because sequence reads mapped to decoy HLA sequences should be removed at the filtering step.
because sequence reads mapped to decoy HLA sequences should be removed at the filtering step.
The prior probability of G is given by
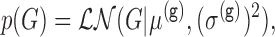 |
where  and
and  are hyperparameters of the mean and variance for normal contamination.
are hyperparameters of the mean and variance for normal contamination.
The prior probability of  is given by
is given by
 |
where

Here,  and
and 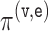 are hyperparameters of probabilities of a validity flag opening and a validity flag extension, respectively. Note that
are hyperparameters of probabilities of a validity flag opening and a validity flag extension, respectively. Note that  must always be 1.
must always be 1.
2.4. Markov chain Monte Carlo-based parameter sampling
The parameters are sampled from the Bayesian model using Markov chain Monte Carlo. Gibbs sampling is primarily used to sample all parameters except for Fm and Vm.
A candidate parameter, 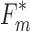 , is first sampled using the Metropolis–Hastings algorithm whose proposal distribution is given by
, is first sampled using the Metropolis–Hastings algorithm whose proposal distribution is given by
 |
where  is a hyperparameter of the variance of the proposal distribution. The acceptance ratio
is a hyperparameter of the variance of the proposal distribution. The acceptance ratio  is calculated by
is calculated by
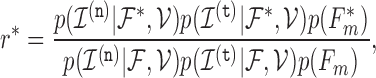 |
where  . A candidate parameter,
. A candidate parameter,  , is sampled using the Metropolis–Hastings algorithm whose proposal distribution is analogous to the Wolff algorithm (Wolff, 1989), which is used for sampling of the Ising model.
, is sampled using the Metropolis–Hastings algorithm whose proposal distribution is analogous to the Wolff algorithm (Wolff, 1989), which is used for sampling of the Ising model. 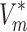 is generated by Algorithm 1. Then,
is generated by Algorithm 1. Then,  and
and 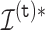 are also sampled using Gibbs sampling given
are also sampled using Gibbs sampling given  . The acceptance ratio
. The acceptance ratio  is calculated by
is calculated by
 |
 |
Algorithm 1 Generate a candidate parameter  using the Wolff algorithm using the Wolff algorithm |
|---|
| Input: |
| V: the current parameter |
| N: the length of V |
 : probability for 0-cluster extension : probability for 0-cluster extension |
 : probability for 1-cluster extension : probability for 1-cluster extension |
| Output: |
 : candidate parameter : candidate parameter |
1: functionWolff
|
| 2: Sample a position p uniformly |
3: 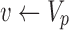
|
4: 
|
5: while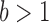 and and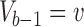 do do
|
6: break with probability 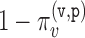
|
7: 
|
| 8: end while |
9: 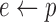
|
10: while and and do do
|
11: break with probability 
|
12: 
|
| 13: end while |
14: 
|
15: for to edo to edo
|
16: 
|
| 17: end for |
18: return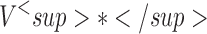
|
| 19: end function |
We set 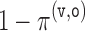 and
and  to
to  and
and  , respectively, so that the acceptance ratio can be calculated by
, respectively, so that the acceptance ratio can be calculated by

 |
2.5. Efficient sampling from multimodal posteriors
In addition to the standard sampling approaches mentioned earlier, we applied some additional elaborate sampling schemes to prevent the parameters from becoming stuck in a local optimum. One such scheme swaps parts of the nondecoy and decoy HLA sequences. First, a nondecoy index  , decoy index
, decoy index  , and interval i such that
, and interval i such that  are sampled uniformly. Next,
are sampled uniformly. Next,  and
and  , and
, and  and
and  are swapped for all
are swapped for all 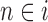 . Finally,
. Finally,  ,
,  ,
,  , and
, and 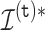 are sampled using Gibbs sampling given
are sampled using Gibbs sampling given 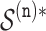 and
and  , which are the normal and tumor HLA sequences after swapping. Consequently, the acceptance ratio
, which are the normal and tumor HLA sequences after swapping. Consequently, the acceptance ratio  is given by
is given by
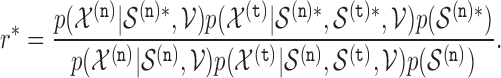 |
This sampling method helps to determine which HLA sequences should be decoys.
Another scheme involves sampling an HLA type and matched normal-tumor HLA sequences simultaneously. For all  ,
, 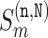 and
and  are defined by
are defined by
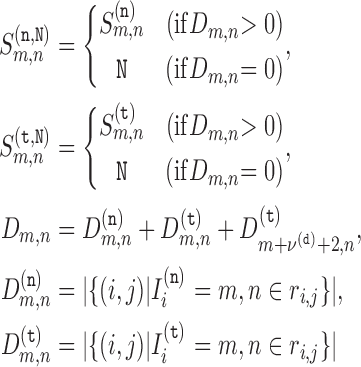 |
In other words, 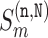 and
and 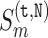 are basically the same as
are basically the same as  and
and  , and bases not covered by any read are replaced with Ns. Next,
, and bases not covered by any read are replaced with Ns. Next,  is sampled given
is sampled given  ,
,  is sampled given
is sampled given  and
and  , and
, and  is sampled given
is sampled given  in order. Then, the acceptance ratio
in order. Then, the acceptance ratio 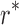 is given by
is given by

This sampling functions in a similar way to blocked Gibbs sampling of Rm,  , and
, and 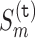 . This blocked Gibbs sampling requires substantial computation time because
. This blocked Gibbs sampling requires substantial computation time because 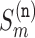 and
and  must be integrated out for each HLA type. By contrast, our scheme requires much less time because
must be integrated out for each HLA type. By contrast, our scheme requires much less time because  and
and  are integrated out only for Rm and
are integrated out only for Rm and  .
.
Other strategies were further used to obtain better parameters. First, reference sequences are periodically copied to HLA sequences. Second, sequence reads are assigned to decoy sequences if there are mismatches between the sequence reads and the reference sequences. These approaches help to reduce the incidence of false-positive mutations and retain only the mutations that seem true. The multistart method is also used to obtain better initial parameters. Moreover, parallel tempering is used to move parameters from mode to mode.
2.6. Human leukocyte antigen analysis from sampled parameters
HLA analysis is conducted based on the sampled parameters. HLA genotyping is performed by counting the number of sampled HLA types, and germline or somatic mutations are identified by finding different bases between HLA types and normal HLA sequences, or between normal and tumor HLA sequences, respectively.
3. Results
3.1. Human leukocyte antigen genotyping from whole-genome sequencing data
We first evaluated the accuracy of this method for HLA genotyping from a WGS data set. For comparison, we applied ALPHLARD-NT, ALPHLARD (Hayashi et al., 2018), and POLYSOLVER (Shukla et al., 2015) to WGS data of 25 colon cancer samples, which were used by Hayashi et al. (2018). The performance comparison is summarized in Table 1. Overall, ALPHLARD-NT outperformed POLYSOLVER at all resolutions for all HLA loci. ALPHLARD-NT also achieved slightly higher accuracy than ALPHLARD because ALPHLARD-NT can use information from both normal and tumor samples, whereas ALPHLARD can only use information from normal samples.
Table 1.
Comparison of the Accuracy of Whole-Genome Sequencing-Based Human Leukocyte Antigen Genotyping with ALPHLARD-NT, ALPHLARD, and POLYSOLVER
| ALPHLARD-NT | ALPHLARD | POLYSOLVER | |
|---|---|---|---|
| HLA-A | |||
| First | 100% (50/50) | 100% (50/50) | 100% (50/50) |
| Second | 100% (50/50) | 98.0% (49/50) | 98.0% (49/50) |
| Third | 98.0% (49/50) | 98.0% (49/50) | 90.0% (45/50) |
| HLA-B | |||
| First | 100% (48/48) | 100% (48/48) | 91.7% (44/48) |
| Second | 100% (48/48) | 100% (48/48) | 85.4% (41/48) |
| Third | 97.9% (47/48) | 95.8% (46/48) | 81.3% (39/48) |
| HLA-C | |||
| First | 100% (50/50) | 100% (50/50) | 100% (50/50) |
| Second | 100% (50/50) | 98.0% (49/50) | 90.0% (45/50) |
| Third | 100% (50/50) | 98.0% (49/50) | 86.0% (43/50) |
| HLA-DPA1 | |||
| First | 100% (24/24) | 100% (24/24) | N/A |
| Second | 100% (24/24) | 100% (24/24) | N/A |
| Third | 100% (24/24) | 100% (24/24) | N/A |
| HLA-DPB1 | |||
| First | 100% (22/22) | 100% (22/22) | N/A |
| Second | 100% (22/22) | 100% (22/22) | N/A |
| Third | 100% (22/22) | 100% (22/22) | N/A |
| HLA-DQA1 | |||
| First | 100% (24/24) | 100% (24/24) | N/A |
| Second | 95.8% (23/24) | 95.8% (23/24) | N/A |
| Third | 95.8% (23/24) | 95.8% (23/24) | N/A |
| HLA-DQB1 | |||
| First | 100% (18/18) | 100% (18/18) | N/A |
| Second | 94.4% (17/18) | 94.4% (17/18) | N/A |
| Third | 94.4% (17/18) | 94.4% (17/18) | N/A |
| HLA-DRB1 | |||
| First | 100% (24/24) | 100% (24/24) | N/A |
| Second | 100% (24/24) | 100% (24/24) | N/A |
| Third | 100% (24/24) | 100% (24/24) | N/A |
| Total | |||
| First | 100% (260/260) | 100% (260/260) | 97.3% (144/148) |
| Second | 99.2% (258/260) | 98.5% (256/260) | 91.2% (135/148) |
| Third | 98.5% (256/260) | 97.7% (254/260) | 85.8% (127/148) |
N/A indicates that the method does not support the HLA locus.
HLA, human leukocyte antigen.
Bold values indicate that the method achieved the highest accuracy for the HLA locus at the resolution.
3.2. Detection of human leukocyte antigen mutations from whole-genome sequencing data
We also searched for HLA class I somatic mutations among the WGS data from the 25 colon cancer samples using ALPHLARD-NT, POLYSOLVER, and EBCall (Shiraishi et al., 2013), which is a standard mutation caller. ALPHLARD-NT called one substitution, two insertions, and two deletions, all of which were verified by the TruSight HLA Sequencing Panels (Weimer et al., 2016). All four indels called are known to lead to the loss of function of the HLA alleles, and might contribute to immune escape. However, POLYSOLVER and EBCall detected no and one mutation, respectively, which was likely due to the low coverage of the data set.
3.3. Detection of human leukocyte antigen mutations from whole-exome sequencing data
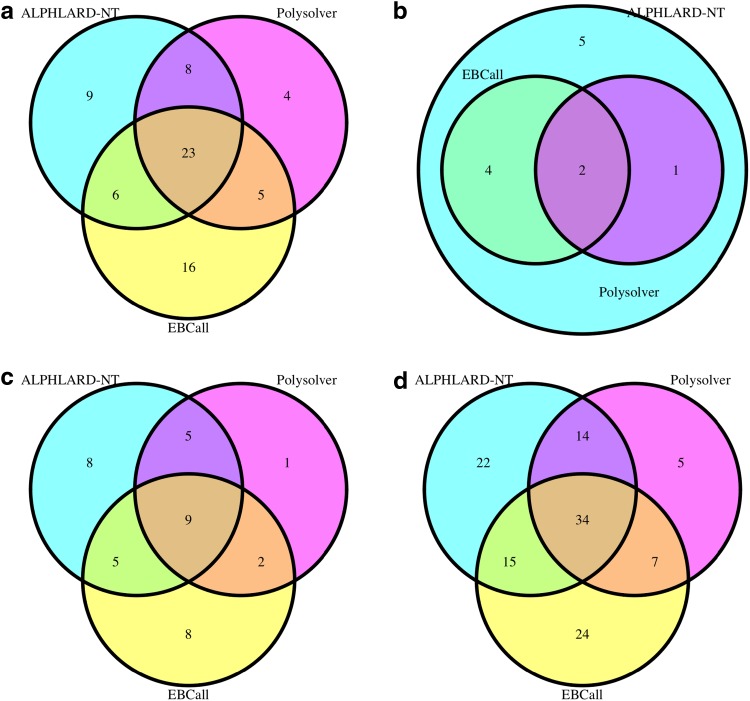
Next, we applied ALPHLARD-NT, POLYSOLVER, and EBCall to a WES data set of 343 colon adenocarcinoma cases from The Cancer Genome Atlas (TCGA). Figure 2 shows the Venn diagrams of the identified HLA class I somatic mutations with each method. This figure demonstrates the high sensitivity of ALPHLARD-NT (88 mutations) compared with POLYSOLVER (60 mutations) and EBCall (80 mutations), which is especially remarkable for insertions. ALPHLARD-NT detected seven insertions at the beginning of exon 4 of HLA class I genes, which is a known hotspot of indels (Mizuno et al., 2018), whereas POLYSOLVER and EBCall identified no and three insertions at this hotspot, respectively. ALPHLARD-NT also identified 12 deletions at the same position. These recurrent frameshift indels seemed to be positively selected for immune escape caused by loss of function of the HLA alleles.
FIG. 2.
Venn diagrams of the number of HLA somatic mutations identified by ALPHLARD-NT, POLYSOLVER, and EBCall for (a) substitutions, (b) insertions, (c) deletions, and (d) all mutations. HLA, human leukocyte antigen.
In addition, ALPHLARD-NT detected a novel HLA-B allele whose exon sequence is the same as HLA-B*35:08:01 except that the 25th base is C rather than G, which changes the 9th amino acid from V to L. The protein produced by the new allele is also novel and not registered in the IPD-IMGT/HLA Database, indicating that the allele defines a new HLA type name at the second field.
4. Conclusion
In this article, we have presented a new Bayesian method, ALPHLARD-NT, which identifies HLA germline and somatic mutations as well as HLA genotypes. Comparison of the performance of ALPHLARD-NT clearly demonstrated its higher accuracy than existing methods for WGS-based HLA genotyping. ALPHLARD-NT also detected HLA somatic mutations from both WES and WGS data. In general, HLA mutation calling is difficult mainly due to the similarity of HLA genes and pseudogenes. We dealt with this problem by applying sophisticated filtering criteria and using decoy-related parameters that reduced the influence of misclassified reads at the filtering step. Although these approaches work well for HLA class I mutation calling, identification of HLA class II mutations remains a challenge, since databases tend to be relatively incomplete for identifying class II genes and pseudogenes compared with class I genes.
With the continuous accumulation of large amounts of WES and WGS data, HLA mutation calling from these data sets is a fundamental step in cancer immunogenomics. Thus, we expect that our method will be an essential tool for comprehensive analyses of HLA genes from WES and WGS data.
Acknowledgment
The super-computing resource was provided by Human Genome Center, the Institute of Medical Science, the University of Tokyo.
Author Disclosure Statement
The authors declare there are no competing financial interests.
References
- Bai Y., Ni M., Cooper B., et al. 2014. Inference of high resolution HLA types using genome-wide RNA or DNA sequencing reads. BMC Genomics. 15, 325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boegel S., Löwer M., Schäfer M., et al. 2012. HLA typing from RNA-Seq sequence reads. Genome Med. 4, 102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dilthey A.T., Gourraud P.-A., Mentzer A.J., et al. 2016. High-accuracy HLA type inference from whole-genome sequencing data using population reference graphs. PLoS Comput. Biol. 12, e1005151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giannakis M., Mu X.J., Shukla S.A., et al. 2016. Genomic correlates of immune-cell infiltrates in colorectal carcinoma. Cell Rep. 15, 857–865 [DOI] [PMC free article] [PubMed] [Google Scholar]
- González-Galarza F.F., Takeshita L.Y., Santos E.J., et al. 2015. Allele frequency net 2015 update: New features for HLA epitopes, KIR and disease and HLA adverse drug reaction associations. Nucleic Acids Res. 43, D784–D788 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grivennikov S.I., Greten F.R., and Karin M. 2010. Immunity, inflammation, and cancer. Cell 140, 883–899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayashi S., Yamaguchi R., Mizuno S., et al. 2018. ALPHLARD: A Bayesian method for analyzing HLA genes from whole genome sequence data. BMC Genomics 19, 790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H.J., and Pourmand N. 2013. HLA haplotyping from RNA-seq data using hierarchical read weighting. PLoS One 8, e67885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreiter S., Vormehr M., Van de Roemer N., et al. 2015. Mutant MHC class II epitopes drive therapeutic immune responses to cancer. Nature 520, 692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee H., and Kingsford C. 2018. Kourami: Graph-guided assembly for novel human leukocyte antigen allele discovery. Genome Biol. 19, 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu C., Yang X., Duffy B., et al. 2013. ATHLATES: Accurate typing of human leukocyte antigen through exome sequencing. Nucleic Acids Res. 41, e142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marty R., Kaabinejadian S., Rossell D., et al. 2017. MHC-I genotype restricts the oncogenic mutational landscape. Cell 171, 1272–1283 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGranahan N., Rosenthal R., Hiley C.T., et al. 2017. Allele-specific HLA loss and immune escape in lung cancer evolution. Cell 171, 1259–1271 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizuno S., Yamaguchi R., Hasegawa T., et al. 2018. Immuno-genomic PanCancer landscape reveals diverse immune escape mechanisms and immuno-editing histories. bioRxiv, 285338 [Google Scholar]
- Nariai N., Kojima K., Saito S., et al. 2015. HLA-VBSeq: Accurate HLA typing at full resolution from whole-genome sequencing data. BMC Genomics 16, S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olerup O., and Zetterquist H. 1992. HLA-DR typing by PCR amplification with sequence-specific primers (PCR-SSP) in 2 hours: An alternative to serological DR typing in clinical practice including donor-recipient matching in cadaveric transplantation. Tissue Antigens 39, 225–235 [DOI] [PubMed] [Google Scholar]
- Robinson J., Halliwell J.A., Hayhurst J.D., et al. 2015. The IPD and IMGT/HLA database: Allele variant databases. Nucleic Acids Res. 43, D423–D431 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rooney M.S., Shukla S.A., Wu C.J., et al. 2015. Molecular and genetic properties of tumors associated with local immune cytolytic activity. Cell 160, 48–61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saiki R.K., Bugawan T.L., Horn G.T., et al. 1986. Analysis of enzymatically amplified β-globin and HLA-DQα DNA with allele-specific oligonucleotide probes. Nature 324, 163. [DOI] [PubMed] [Google Scholar]
- Santamaria P., Boyce-Jacino M.T., Lindstrom A.L., et al. 1992. HLA class II “typing”: Direct sequencing of DRB, DQB, and DQA genes. Hum. Immunol. 33, 69–81 [DOI] [PubMed] [Google Scholar]
- Schreiber R.D., Old L.J., and Smyth M.J. 2011. Cancer immunoediting: Integrating immunity's roles in cancer suppression and promotion. Science 331, 1565–1570 [DOI] [PubMed] [Google Scholar]
- Shiraishi Y., Sato Y., Chiba K., et al. 2013. An empirical Bayesian framework for somatic mutation detection from cancer genome sequencing data. Nucleic Acids Res. 41, e89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shukla S.A., Rooney M.S., Rajasagi M., et al. 2015. Comprehensive analysis of cancer-associated somatic mutations in class I HLA genes. Nat. Biotechnol. 33, 1152–1158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szolek A., Schubert B., Mohr C., et al. 2014. OptiType: Precision HLA typing from next-generation sequencing data. Bioinformatics 30, 3310–3316 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Testoni M., Zucca E., Young K., et al. 2015. Genetic lesions in diffuse large B-cell lymphomas. Ann. Oncol. 26, 1069–1080 [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Network. 2015. Comprehensive genomic characterization of head and neck squamous cell carcinomas. Nature 517, 576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network. 2014. Comprehensive molecular characterization of gastric adenocarcinoma. Nature 513, 202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren R.L., Choe G., Freeman D.J., et al. 2012. Derivation of HLA types from shotgun sequence datasets. Genome Med. 4, 95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weimer E.T., Montgomery M., Petraroia R., et al. 2016. Performance characteristics and validation of next-generation sequencing for human leucocyte antigen typing. J. Mol. Diagn. 18, 668–675 [DOI] [PubMed] [Google Scholar]
- Wolff U. 1989. Collective Monte Carlo updating for spin systems. Phys. Rev. Lett. 62, 361. [DOI] [PubMed] [Google Scholar]
- Xie C., Yeo Z.X., Wong M., et al. 2017. Fast and accurate HLA typing from short-read next-generation sequence data with xHLA. Proc. Natl Acad. Sci. U. S. A. 114, 8059–8064 [DOI] [PMC free article] [PubMed] [Google Scholar]