Differential network enrichment analysis reveals novel lipid pathways in chronic kidney disease

Abstract

Motivation

Functional enrichment testing methods can reduce data comprising hundreds of altered biomolecules to smaller sets of altered biological ‘concepts’ that help generate testable hypotheses. This study leveraged differential network enrichment analysis methodology to identify and validate lipid subnetworks that potentially differentiate chronic kidney disease (CKD) by severity or progression.

Results

We built a partial correlation interaction network, identified highly connected network components, applied network-based gene-set analysis to identify differentially enriched subnetworks, and compared the subnetworks in patients with early-stage versus late-stage CKD. We identified two subnetworks ‘triacylglycerols’ and ‘cardiolipins-phosphatidylethanolamines (CL-PE)’ characterized by lower connectivity, and a higher abundance of longer polyunsaturated triacylglycerols in patients with severe CKD (stage ≥4) from the Clinical Phenotyping Resource and Biobank Core. These finding were replicated in an independent cohort, the Chronic Renal Insufficiency Cohort. Using an innovative method for elucidating biological alterations in lipid networks, we demonstrated alterations in triacylglycerols and cardiolipins-phosphatidylethanolamines that precede the clinical outcome of end-stage kidney disease by several years.

Availability and implementation

A complete list of NetGSA results in HTML format can be found at http://metscape.ncibi.org/netgsa/12345-022118/cric_cprobe/022118/results_cric_cprobe/main.html. The DNEA is freely available at https://github.com/wiggie/DNEA. Java wrapper leveraging the cytoscape.js framework is available at http://js.cytoscape.org.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The development and application of high-resolution analytical methods has advanced metabolic profiling of complex biological samples, including lipids, considerably. Current high-resolution analytic methods have also prompted the development of innovative computational data analysis methods and tools. A common approach to interpreting the results of metabolomic and lipidomic experiments is to map and visualize experimentally measured metabolites in the context of known biochemical pathways. A number of tools that support this process have been developed (Friedman et al., 2008; Lancichinetti and Fortunato, 2012; Meinshausen and Bühlmann, 2010). Several of these tools utilize functional enrichment testing methods, originally developed for gene expression data, for the analysis of metabolomic and lipidomic data (Ma et al., 2016; Shojaie and Michailidis, 2009, 2010). Functional enrichment testing techniques help reduce data comprising hundreds of altered metabolites (or genes) to smaller and more interpretable sets of altered biological ‘concepts’ and help generate testable hypotheses. However, the pathway mapping techniques commonly used for secondary analysis of metabolomic data rarely provide sufficient power or resolution, especially when analyzing lipids, primarily due to scarce coverage of lipid metabolism in pathway databases (Barupal et al., 2012), and is a major limitation of current lipidomic studies.

An alternative to these knowledge-based data analysis methods is to infer meaningful associations between measured lipids and metabolites from experimental data and build data-driven molecular networks to help generate biological insights. Pearson’s correlations can be used to establish linear marginal associations between biomolecules, although they do not differentiate between direct and indirect associations (Basu et al., 2017). In contrast, partial correlations that correspond to conditional dependencies allow identification of direct associations between metabolites, such as lipids (de la Fuente et al., 2004). However, in order to calculate the exact partial correlation network for p lipids, it is required that the number of samples, n, is greater than or comparable with p, which is rarely the case in lipidomic studies.

Taking into account the sparse structure of biochemical networks (Gardner et al., 2003; Jeong et al., 2001; Leclerc, 2008), many regularized estimation methods have been proposed to recover a sparse partial correlation network from high-dimensional observations, when n ≪ p. For example, the graphical lasso (Friedman et al., 2008) is one approach for reconstructing sparse partial correlation networks using the framework of Gaussian graphical models. Recent work in this area provided rigorous statistical methodology for building data-driven partial correlation networks equipped with appropriate statistical guarantees regarding performance (Janková and van de Geer, 2015) that take advantage of recent developments in sparse regression and graphical modeling (Bühlmann and van de Geer, 2011). A refinement of the graphical lasso approach that controls for statistical uncertainty in the estimated partial correlation network (Basu et al., 2017) was implemented as part of the CorrelationCalculator tool that enables estimating such networks from metabolomic and lipidomic datasets from a single group of samples (http://metscape.umich.edu).

Most metabolomic and lipidomic studies, including biomarker discovery and investigation of molecular mechanisms of disease or biological phenomena, involve differential analysis of two or more clinical or experimental conditions. Univariate approaches examining each compound individually are commonly used for data analysis. The downside of univariate approaches is that they ignore compound interactions, and thus can miss orchestrated impacts on disease phenotypes. From a technical standpoint, when compounds or any other biomolecules are analyzed by univariate methods, they might not exceed the critical threshold for statistical significance and thus would not be included in further analysis. Importantly, the interactions between compounds may reflect known biological pathways or novel interactions (Creixell et al., 2015). Extracting more meaningful groups of lipid metabolites and analyzing how their interactions are altered between experimental conditions can provide important insights and assistance in understanding the phenotype of interest (Ideker and Krogan, 2012).

In this study, we present a novel differential network-based enrichment analysis method (DNEA) that allows identification of biologically meaningful networks altered between different groups (e.g. different disease status or experimental conditions). To demonstrate the utility of DNEA, we applied it to elucidate lipid networks involved in the progression of chronic kidney disease (CKD). We identified differential lipid networks characteristic of advanced-stage CKD (stages 4 and 5) versus early-stage CKD (stage 2 and 3) in patients with CKD from the Clinical Phenotyping Resource and Biobank Core (CPROBE). We then compared the differential networks in patients with CKD who progressed to end-stage kidney disease (ESKD; progressors) to those with CKD who did not develop ESKD (non-progressors) in an independent cohort, the Chronic Renal Insufficiency Cohort (CRIC). To our knowledge, this is the first demonstration of data-driven identification of novel differential lipid regulatory networks in two independent human cohorts without a priori pathway knowledge.

2 Materials and Methods

Study cohorts

The previously published lipidomic datasets of CKD patients from the CPROBE (Afshinnia et al., 2018) and CRIC (Afshinnia et al., 2016) studies were used for this study. In brief, the lipidomic-CPROBE is a cross-sectional study of 214 patients across the entire range of CKD stages aimed at comparing lipidome changes with CKD progression. For this study, we selected two groups of patients: those with stage 4 or 5 CKD (n = 79)—advanced CKD—and those with stage 2 or 3 CKD (n = 135)—early-stage CKD. The CRIC lipidomic data come from a case-control study of 200 patients, nested in the parent CRIC study with longitudinally ascertained outcome of progression of CKD to ESKD over a mean duration of 6 years, aimed at identification of lipidomic signature of CKD progression at baseline. It includes 121 non-progressors (those who did not develop ESKD) and 79 progressors to ESKD.

Analysis workflow

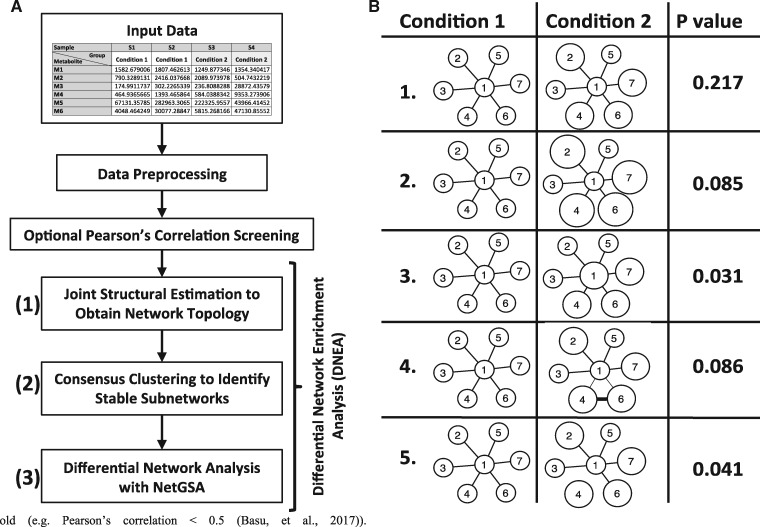
The analysis workflow is shown in Figure 1A. The analysis starts with pre-processing of the input data. Depending on the nature of a specific dataset, pre-processing may involve elimination of compounds from any further analysis due to an excessive number of missing values, and imputation of missing values for the remaining compounds. Pre-processing also includes data normalization and standardization [e.g. log-transformation and autoscaling (Xia and Wishart, 2016)]. The next step, namely, Pearson’s correlation screening is optional and can be used to reduce the number of metabolites included in DNEA analysis by eliminating metabolites whose correlations with other compounds are below a pre-specified thresh old [e.g. Pearson’s correlation <0.5 (Basu et al., 2017)].

Fig. 1.

Differential Network Enrichment Analysis (DNEA) and Proof of Concept. (A) Workflow for DNEA. The workflow includes pre-processing of input data, followed by optional Pearson’s correlation. Main DNEA analysis includes joint structural network estimation, consensus clustering and differential network analysis. (B) NetGSA results using simulated data. The first three scenarios have DE nodes, whereas the last two scenarios have both DE nodes and differential edges

In this study, we applied this general strategy as follows. First, we selected a subset of 285 lipids that were present both in the CPROBE and CRIC datasets. The data were examined for batch effects using visualization tools and by comparing distribution of internal standards and their inter-batch coefficient of variations in reference samples across all batches. We applied the cross-contribution compensating multiple internal standard normalization method (Redestig et al., 2009) to correct for a negligible batch effect. Data were log transformed first and then autoscaled (mean centering and scaling by standard deviation, often referred to as z-scoring or standardization in the literature). Next, we used DNEA to compare advanced CKD patients with early-stage CKD patients in the CPROBE dataset and progressors with non-progressors in the CRIC dataset, wherein all patients were at a CKD stage comparable with the early-stage CKD patients in the CPROBE cohort. The rationale for analyzing these two cohorts was to investigate whether the differential subnetworks identified by comparing advanced CKD with early-stage CKD in CPROBE were also present when comparing progressors with non-progressors in the independent CRIC cohort.

Algorithm

The DNEA algorithm. The main DNEA algorithm includes the following three steps: (i) joint network estimation based on lipidomic profiles across disease groups, (ii) consensus clustering of the resulting network and (iii) enrichment of strongly connected network components based on the NetGSA procedure (Ma et al., 2016), that are described in detail in the following sections.

(i) Network estimation. While the network for each disease group (or biological condition) can be estimated separately, this would lead to employing only the samples available in each group. However, growing experimental evidence suggests that many of the interactions (edges) in each condition-specific network tend to be conserved or not be present (Kling et al., 2015). To take advantage of these observations, we developed a joint estimation method (JEM) to reconstruct partial correlation networks for two or more experimental conditions or disease subtypes. The technical aspects of the method are described next.

To begin the description of JEM, we suppose that we have $\text{n}$ observations on $p$ metabolites organized in an $n\times p$ data matrix, where the first $n_1$ rows come from group/condition 1 and the remaining $n_2=n-n_1$ rows are from group/condition 2. We denote the $n_{\text{k}}\times p$ matrix for condition $k$ ($k=$1, 2) by $X^{(k)}$ and further assume without loss of generality that the data are centered and standardized, so that each column of $X^{(k)}$ has mean 0 and unit variance. Note that the method generalizes in a straightforward manner to K conditions.

Under the assumption that the concentration levels of the $p$ metabolites in the population (after transformation) come from a multivariate normal distribution with covariance ${\text{Σ}}^{\left(k\right)}$ for condition $k$, the partial correlation between metabolites $i$ and $j$ is non-zero, if and only if ${\text{Θ}}_{ij}^{\left(k\right)}\ne 0$, where ${\text{Θ}}^{\left(k\right)}={({\text{Σ}}^{\left(k\right)})}^{-1}$ is the precision matrix. Given the observed data $X^{(k)}$, we can estimate the partial correlation network for each condition $k$ using the graphical lasso estimator (Friedman et al., 2008):

$${\widehat{\text{Θ}}}^{(k)}=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}{\mathrm{n}}_{{\text{Θ}}^{(k)}\succ 0}\left\{tr\left(S^{\left(k\right)}{\text{Θ}}^{\left(k\right)}\right)-\log \det \left({\text{Θ}}^{\left(k\right)}\right)+\lambda {\displaystyle \sum }_{i\ne j}\left|{\text{Θ}}_{ij}^{\left(k\right)}\right|\right\},$$

where $tr(·)$ denotes the matrix trace operator, $S^{\left(k\right)}={(X^{\left(k\right)})}^{\text{prime}}{X}^{\left(k\right)}/n_k$ is the sample covariance matrix for condition $k$, and $\lambda$ is the regularization parameter. The penalty term uses the ${\ell }_1$ norm to introduce sparsity in the estimated partial correlation network, namely that the connectivity between metabolites/lipids is relatively low, as argued in Gardner et al., (2003). Because many connections (edges) across different disease conditions are preserved or are simultaneously absent, the JEM capitalizes on this fact and hence solves the following optimization problem (Guo et al., 2011):

$$\underset{{\{{\text{Θ}}^{(k)}\succ 0\}}_{k=1}^K}{\min }{\displaystyle \sum }_{k=1}^K\left\{tr(S^{\left(k\right)}{\text{Θ}}^{\left(k\right)})-\log \det ({\text{Θ}}^{\left(k\right)})\right\}+\lambda {\displaystyle \sum }_{i\ne j}\sqrt{{\displaystyle \sum }_{k=1}^K\left|{\Theta }_{ij}^{(k)}\right|}.$$

where $K$ is the total number of groups/conditions considered. The penalty term penalizes each edge in the partial correlation networks ${\left\{{\text{Θ}}_{ij}^{\left(k\right)}\right\}}_{k=1}^K$ as a group, thus leading to similar structures across all networks. At the technical level, the above modification enables the use of all samples for estimation of shared presence or absence of edges across multiple network structures, thus enhancing the ability of the method to identify a larger number of connections, vis-à-vis methods that estimate the network for each condition separately. The implementation of JEM uses an iterative algorithm outlined next:

Step A: Initialize ${\widehat{\text{Θ}}}^{(k)}={\left(S^{\left(k\right)}+\text{ν}{I}_{\text{p}}\right)}^{-1}$for $k=1,\dots ,K$, where $I_{\text{p}}$ is the $\text{p}$-identity matrix and $\text{ν}$ is a constant chosen such that $S^{\left(k\right)}+\text{ν}{I}_{\text{p}}$ is positive definite.

Step B: At the $\left(t+1\right)$th iteration, update ${({\widehat{\text{Θ}}}^{(k)})}^{(t+1)}$as${({\widehat{\text{Θ}}}^{(k)})}^{(t+1)}=\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}{\mathrm{n}}_{{\text{Θ}}^{(k)}\succ 0}\left\{tr(S^{\left(k\right)}{\text{Θ}}^{\left(k\right)})-\log \det \left({\text{Θ}}^{\left(k\right)}\right)+\text{λ}{\displaystyle \sum }_{i\ne j}{\text{τ}}_{ij}^{(t)}\left|{\text{Θ}}_{ij}^{\left(k\right)}\right|\right\},$where ${\text{τ}}_{ij}^{(t)}={\left\{{\displaystyle \sum }_{k=1}^K\left|{({\widehat{\text{Θ}}}_{ij}^{(k)})}^{(t)}\right|\right\}}^{-1/2}$.

Step C: Repeat Step B until convergence.

In the above implementation, the tuning parameter $\lambda$ controls the sparsity of the resulting estimates and can be selected by minimizing the Bayesian information criterion (Guo et al., 2011). Note that the optimization in Step B considers estimation of a single sparse precision matrix with penalty parameters weighted according to the joint estimates from the $t$-th iteration and can thus be solved by the graphical lasso algorithm to speed up the calculations. For numerical stability purposes, if ${\left\{{\displaystyle \sum }_{k=1}^K\left|{({\widehat{\text{Θ}}}_{ij}^{(k)})}^{(t)}\right|\right\}}^{1/2}$ becomes smaller than ${10}^{-10}$, it is truncated at that value.

To ensure robust recovery of the partial correlation networks, the JEM algorithm is further coupled with stability selection (Meinshausen and Bühlmann, 2010; Shah and Samworth, 2013) to obtain the selection probabilities of edges in the partial correlation networks. Stability selection is a general algorithm that is based on subsampling of metabolic profiles (from the $X^{(k)}$ matrices) to improve the performance of selecting the most robust network edges. When combined with JEM, it enables finding the stability path, i.e. the probability for each edge to be selected when randomly subsampling the data. In the current context, we refit the partial correlation network under each condition using the graphical lasso algorithm (Friedman et al., 2008) with regularization parameters weighted according to these selection probabilities.

(ii) Consensus clustering to extract stable subnetworks. The second step of DNEA is consensus clustering. A network $G$ is defined as the union of the $K$ partial correlation networks such that there is an edge between metabolite $i$ and $j$, if there is at least one ${\text{Θ}}_{ij}^{\left(k\right)}\ne 0$ for $k=1,\dots ,K$. Given the consolidated network $G$ with $p$ nodes, densely connected subnetworks are first extracted using consensus clustering (Lancichinetti and Fortunato, 2012). The advantage of consensus clustering is that it combines a collection of partitions from different community detection algorithms to help reveal a stable subnetwork structure. The procedure can be briefly summarized as follows. In the first step, $M$ clustering algorithms are applied to $G$ consecutively, to yield $M$ partitions (clusters). In the second step, we construct the consensus matrix $D$, which is a $p$ by $p$ matrix whose ($ij)$-th entry is the percentage of nodes $i$ and $j$ assigned to the same cluster amongst all $M$ partitions. All entries of $D$ that are below a chosen threshold η, which was set to 0.5 in this study, are set to zero in order to focus on large weights in $D$. The same $M$ clustering algorithms are again applied to $D$ to yield another $M$ partitions. If these partitions are all equal, then the consensus matrix would be block diagonal and the procedure stops. Otherwise, we re-evaluate the consensus matrix and repeat the second step.

The consensus matrix $D$ is a weighted matrix, thus the chosen clustering algorithms must be capable of handling weighted networks, which is feasible for most available community detection algorithms. Following suggestions in Lancichinetti and Fortunato (2012), we considered clustering algorithms suitable for weighted networks and based on fast greedy modularity optimization (Clauset et al., 2004), edge betweenness (Newman and Girvan, 2004), the Walktrap method (Pons and Latapy, 2006), leading eigenvectors of the network adjacency matrix (Newman, 2006a,b), the label propagation method (Raghavan et al., 2007), the Louvain method (Blondel et al., 2008) and Infomap (Rosvall and Bergstrom, 2008), all implemented in the R package igraph (Cs´ardi and Nepusz, 2006). In addition, the procedure requires a threshold η to discard small weights in the consensus matrix. This threshold may affect the number of iterations that the procedure takes to reach convergence, but in general we have found in our analysis that the final consensus clusters are not sensitive to the choice of the threshold. Consensus clustering and its numerical performance have been discussed in detail (Lancichinetti and Fortunato, 2012).

(iii) Enrichment of strongly connected network components. The third and final step of DNEA is assessing the enrichment of the identified consensus subnetworks based on changes in both levels of individual metabolites and changes in their network structure. To accomplish this we used a previously published NetGSA method (Ma et al., 2016; Shojaie and Michailidis, 2009, 2010). NetGSA is a network-based method for detecting differential subnetworks when comparing molecular concentration profiles between two conditions. A distinguishing feature of NetGSA is its ability to evaluate enrichment of specified subnetworks based on differential expression of the nodes (metabolites/lipids) and the underlying network structure. The primary advantage of NetGSA is that it does not require pre-defined pathways or other biological concepts to determine enrichment.

3 Results

3.1 Synthetic networks

The main DNEA algorithm used for analysis has three steps (Fig. 1A): joint network estimation based on lipidomic profiles across disease groups, consensus clustering of the resulting network, and enrichment of strongly connected network components based on a network-based gene-set analysis (NetGSA) procedure (Ma et al., 2016). To illustrate how NetGSA evaluates the enrichment of a set of biomolecules, we created a synthetic network that contained seven nodes and compared five different scenarios (Fig. 1B).

For the first three cases, the network structure underlying conditions 1 and 2 was identical. The first case considered the scenario where nodes 2, 4, 6 and 7 were differentially expressed (DE). The enrichment of the network in this case was driven by differential expression of these four DE nodes and would be similarly detected by other enrichment methods, such as gene-set analysis (Efron and Tibshirani, 2007), that consider only differential expression of the nodes. The enrichment P-value under the second scenario was smaller due to greater changes in the expression of nodes 2, 4, 6 and 7. The P-value in the third scenario was also smaller than that in the first scenario due to the change in the expression of a ‘hub’ node 1 that exerts influence on other nodes in the network. Scenarios 4 and 5 considered differential network edges in addition to differential expression of the nodes. In scenario 4, there was an additional edge that connected nodes 4 and 5, and the edge weights associated with edges (1, 4) and (1, 6) were smaller in condition 2. In scenario 5, the edge between nodes 1 and 4 was missing. These changes lead to changes in the P-values for enrichment analysis when compared with the first scenario. Together, the five scenarios demonstrated that NetGSA considers the presence of DE nodes, edges and the overall network topology, all of which contribute to the significance of enrichment of the network under consideration.

3.2 Cohort characteristics

The baseline characteristics of the participants in the two cohorts are shown in Table 1. Overall, there were no significant clinical differences in the demographic variables, comorbidities, use of lipid lowering agents, anthropometric measures or laboratory values of the patients in the two cohorts. The only notable difference was the higher proportion of participants with white race (70%) in the CPROBE cohort as compared with the CRIC study (50%).

Table 1.

Baseline characteristics of the patients by study cohort

Variables	CPROBE	CRIC
N	214	200
Age, in years, ±SD	60 ± 16	59 ± 10
Sex
Male, n (%)	110 (51.4)	112 (56.0)
Female, n (%)	104 (49.6)	88 (44.0)
Race
White, n (%)	150 (70.1)	100 (50.0)
Black, n (%)	64 (29.9)	100 (50.0)
Comorbidities
Hypertension, n (%)	176 (82.2)	178 (89.0)
Diabetes, n (%)	89 (41.6)	100 (50.0)
CAD, n (%)	81 (37.9)	50 (25.0)
Medications:
Statins, n (%)	114 (53.3)	124 (62.0)
Other lipid lowering, n (%)	24 (11.2)	39 (19.5)
Height, in m, ±SD	1.7 ± 0.1	1.7 ± 0.1
Weight, in kg, ±SD	90 ± 21	94 ± 24
BMI, in kg/m2, ±SD	31.0 ± 6.9	32.7 ± 7.9
SBP, in mmHg, ±SD	135 ± 22	129 ± 21
DBP, in mmHg, ±SD	75 ± 11	71 ± 14
Albumin, in g/dl, ±SD	4.0 ± 0.4	4.0 ± 0.4
Cholesterol, in mg/dl, ±SD	169 ± 52	180 ± 47
LDL, in mg/dl, ±SD	86 ± 40	100 ± 36
HDL, in mg/dl, ±SD	39 ± 18	48 ± 15
Triglycerides, in mg/dl, ±SD	163 ± 110	151 ± 94
eGFR, in ml/min, ±SD	41 ± 23	44 ± 12

Note: BMI, Body mass index; CAD, Coronary artery disease; CPROBE, Clinical Phenotyping Resource and Biobank Core; CRIC, Chronic Renal Insufficiency Cohort; DBP, Diastolic blood pressure; eGFR, estimated glomerular filtration rate; HDL, High density lipoprotein; LDL, Low density lipoprotein; SBP, Systolic blood pressure; SD, Standard deviation.

3.3 Comparative analysis of non-differential partial correlation networks derived from the CPROBE and CRIC lipidomic datasets

Before we proceeded with DNEA analysis, we wanted to assess the reproducibility of non-differential partial correlation networks derived from the two independent lipidomic datasets. We reconstructed partial correlation lipid networks from the CPROBE and CRIC datasets using a debiased sparse partial correlation algorithm implemented with the CorrelationCalculator tool (Basu et al., 2017). To accomplish this, we selected 135 patients from CPROBE cohort who had stage 2 or 3 CKD and 200 patients from the CRIC with comparable CKD stages. The CPROBE and CRIC datasets contained 330 and 510 lipids, respectively. We used identical CorrelationCalculator parameters for both datasets. Both datasets were pre-filtered to exclude features that did not correlate with any other lipid features in the dataset with Pearson’s correlation coefficient at least 0.7 (Basu et al., 2017). After pre-filtering, the CPROBE dataset contained 183 lipids, and the CRIC dataset contained 277 lipids. Notably, in both networks, the number of inter-class correlations (edges) exceeded the number of intra-class correlations, resulting in distinct subnetworks that represented different lipid classes.

In both datasets, the network structures within individual lipid classes were not random. In fact, the order of the nodes reflected the number of carbons and the number of double bonds in the molecule. For example, in the CPROBE dataset, the following triacylglycerols (TAGs) were linked sequentially: TAG 54: 1, TAG 54: 2, TAG 54: 3, TAG 54: 4, TAG 54: 5, TAG 54: 6, TAG 54: 7. This order was preserved in the CRIC dataset, where some of these nodes had additional edges. It is highly likely that we were able to see more edges in the CRIC data using the same adjusted P-value threshold, because the CRIC dataset contained more samples than the CPROBE dataset from patients with CKD stage 2 or 3.

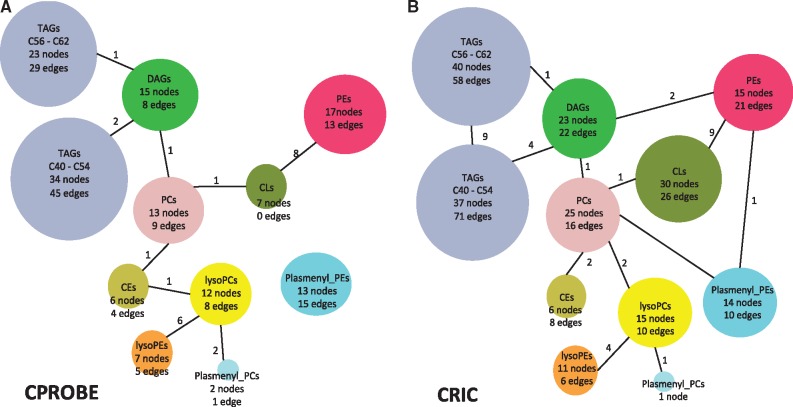
In addition to within-class similarities, we also observed global similarities between the two networks. An overview of the partial correlation networks is illustrated in patients with CKD stage 2 or 3 in the CPROBE (Fig. 2A) and CRIC (Fig. 2B) datasets. The TAGs, a large and abundant lipid class, formed two distinct subnetworks in both datasets, one containing shorter chain TAGs (C40–C54) and one with longer chain TAGs (C56–C62). In the CPROBE dataset, these subnetworks were not linked, whereas in the CRIC dataset they were connected by nine edges (Fig. 2A and B). We believe that the smaller number of CKD stage 2 and 3 samples available in the CPROBE dataset is likely responsible for this difference. In both datasets, the TAG subnetworks were connected to diacylglycerols (DAGs), which in turn were connected to phosphatidylcholines (PCs). In the CRIC dataset, the DAG subnetwork was also connected to phosphatidylethanolamines (PEs) (Fig. 2B). Connectivity between TAGs and DAGs is not unexpected given that DAGs serve as a precursor in TAG biosynthesis. Similarly, the connectivity between DAGs and PCs and DAGs and PEs can be attributed to the fact that DAGs are both a precursor and the product of degradation of these two lipid classes.

Fig. 2.

An overview of the partial correlation networks. (A) Partial correlation network derived from the CPROBE dataset. (B) Partial correlation network derived from the CRIC dataset. The number of lipids (nodes) in each class is shown within each bubble along with the number of intra-class correlations (edges). The numbers next to the edges indicate the number of inter-class correlations. CE, cholesteryl ester; CL, cardiolipin; CoA, coenzyme A; CPROBE, Clinical Phenotyping Resource and Biobank Core; CRIC, Chronic Renal Insufficiency Cohort; DAG, diacylglycerol; FA, fatty acids; PC, phosphatidylcholine; PE, phosphatidylethanolamine; PG, phosphatidylglycerol; TAG, triacylglycerol; TCA, tricarboxylic acid/citric acid

Additional inter-class correlations observed in both datasets include those between lysoPEs and lysoPCs, as well as between lysoPCs and plasmenylPCs. Other classes of lipids that were measured in both datasets included sphingomyelins (SMs), phosphatidylinositol (PIs) and phosphatidylglycerols (PGs). SMs formed their own cluster that was not connected to any other classes (data not shown). PIs and PGs were connected to each other, but not to any other classes (data not shown). Thus, the CPROBE and CRIC lipid partial correlation networks had similar overall topology and were consistent with our knowledge of lipid metabolism (Fig. 3). Equipped with this knowledge, we proceeded to apply our DNEA strategy for further analysis of the CPROBE and CRIC datasets.

Fig. 3.

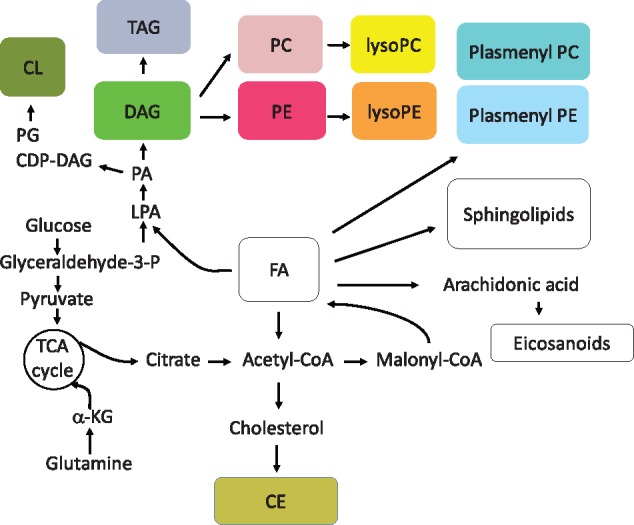
An overview of lipid biosynthesis. CDP, Cytidine diphosphate; CE, cholesteryl ester; CL, cardiolipin; CoA, coenzyme A; DAG, diacylglycerol; FA, fatty acids; PC, phosphatidylcholine; PE, phosphatidylethanolamine; PG, phosphatidylglycerol; TAG, triacylglycerol; TCA, tricarboxylic acid/citric acid

3.4 Application of differential network enrichment to identify lipid pathways altered in CKD progression

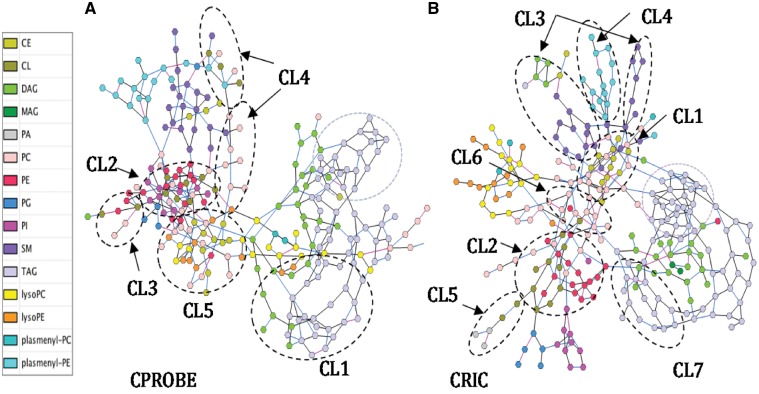
We generated differential networks for patients with early-stage versus late-stage CKD in the CPROBE and for progressors versus non-progressors of CKD in CRIC (Fig. 4). Similar to the four separately estimated networks described above, the differential networks that were generated had more edges within the same lipid class than between classes. In both datasets, TAGs with lower carbon numbers (C40–C54) formed distinct subnetworks, while TAGs with higher carbon numbers (C56–C62) clustered together. In both networks, TAGs were co-clustered with DAGs. Cardiolipins (CLs) and PEs were co-clustered with PIs and PCs, whereas SMs and plasmenylPEs formed their own clusters.

Fig. 4.

Differential partial correlation networks for the CPROBE and CRIC datasets. (A) CPROBE subnetworks. (B) CRIC subnetworks. The legend shows the color code for different lipid classes. The most significant clusters in both datasets (padj <0.05) are circled by the dotted lines. The purple dotted line circles show the clusters of lower carbon number TAGs (C40–C54). The edges that are equally likely to be present in both conditions are shown in black; those that are more likely to be present in early-stage CKD (CPROBE) and in non-progressors (CRIC) are shown in blue and those that are more likely to be present in advanced-stage CKD (CRPOBE) and in progressors (CRIC) are shown in pink. CPROBE, Clinical Phenotyping Resource and Biobank Core; CRIC, Chronic Renal Insufficiency Cohort. This cluster illustrates a higher abundance of long-chain polyunsaturated TAGs in advanced CKD along with a higher number of edges in early-stage CKD. Similarly, in the CRIC, the corresponding replicated cluster showed a higher number of edges

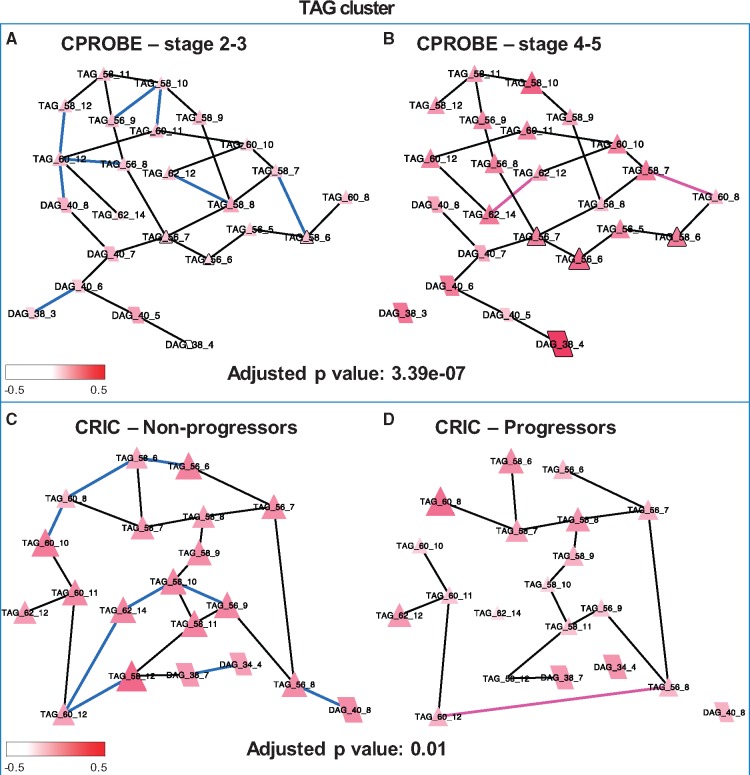
An important feature of our method is the ability to identify differential edges. We identified edges that were equally likely to be present in both conditions, edges that were more likely to be present in early-stage CKD (CPROBE) and in non-progressors (CRIC), and edges that were more likely to be present in advanced-stage CKD (CRPOBE) and in progressors (CRIC) (Fig. 4). Notably, fewer edges were associated with advanced-stage CKD and with disease progression. Differential network activity in both datasets was associated with parts of the TAG subnetworks, SM, PE, CL and other lipid classes. To further explore the significance of these network changes we performed consensus clustering followed by NetGSA. Supplementary Tables S1 and S2 show the significance values for the enriched subnetworks found in CPROBE and CRIC datasets, respectively. The top ranking cluster in the CPROBE dataset contained high-carbon-number TAGs that have been previously shown to be more abundant at the advanced-stages of CKD (Fig. 5) (Afshinnia et al., 2018).

Fig. 5.

TAG cluster lipid pathways altered in CKD progression. (A) Stages 2 and 3 in CPROBE. (B) Stages 4 and 5 in CPROBE. (C) Non-progressor in CRIC. (D) Progressor in CRIC. Blue edges are more likely to be present in early-stage disease (CPROBE) and in non-progressors (CRIC). Pink edges are more likely to be present in late-stage CKD (CPROBE) and in progressors (CRIC). Black edges are equally likely to be present in both conditions. CPROBE, Clinical Phenotyping Resource and Biobank Core; CRIC, Chronic Renal Insufficiency Cohort; DAG, diacylglycerol; TAG, triacylglycerol

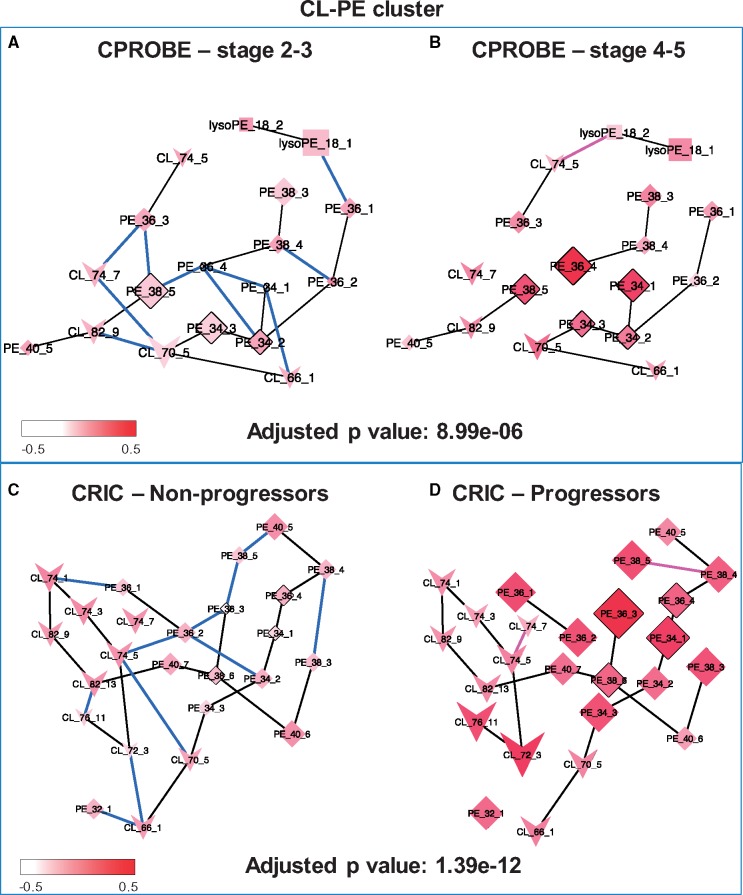
This cluster illustrates a higher abundance of long-chain polyunsaturated TAGs in advanced CKD along with a higher number of edges in early-stage CKD. Similarly, in the CRIC, the corresponding replicated cluster showed a higher number of edges. The second most significant cluster found in both datasets contained the PEs (C34–C40) and the CLs (C66–C82 in CPROBE and C70–C82 in CRIC) (Fig. 6). Similarly, the CL–PE cluster showed a higher number of edges in early-stage CKD than in late-stage CKD in the CPROBE dataset and in non-progressors than in progressors in the CRIC. There were fewer edges in late-stage disease and progressors (Fig. 6).

Fig. 6.

CL-PE cluster lipid pathways altered in CKD progression. (A) Stages 2 and 3 in CPROBE; (B) stages 4 and 5 in CPROBE; (C) non-progressor in CRIC; (D) progressor in CRIC. Blue edges are more likely to be present in early-stage disease (CPROBE) and in non-progressors (CRIC). Pink edges are more likely to be present in late-stage CKD (CPROBE) and in progressors (CRIC). Black edges are equally likely to be present in both conditions. CPROBE, Clinical Phenotyping Resource and Biobank Core; CRIC Chronic Renal Insufficiency Cohort; CL, cardiolipin; PE, phosphatidylethanolamine

4 Discussion

In this study, we present a new, data-driven enrichment analysis method called DNEA that infers differential networks from experimental metabolomic or lipidomic data. To validate the DNEA and demonstrate its utility, we identified alterations in lipid metabolism relevant to CKD progression that could not be identified by application of traditional univariate analysis methods. In the CPROBE dataset, DNEA revealed two significant subnetworks: TAGs and CLs–PEs. The TAG subnetwork was characterized by a significantly higher abundance of long-chain polyunsaturated TAGs in advanced CKD, whereas the CL–PE subnetwork was characterized by disruption of CL–PE edges in advanced CKD. Analysis of the independent CRIC cohort of CKD patients with DNEA demonstrated TAG and CL–PE subnetworks that discriminated between progressors and non-progressors with stage 2 or 3 CKD. In these patients, the presence of the differential TAG and CL–PE subnetworks preceded the clinical outcome of ESKD by several years.

One of the reasons for the wide popularity of knowledge-based methods for the analysis of high throughput data is the inherent ability to relate the experimental results to prior biological knowledge. However, the ability to obtain novel biological insights can be limited by the availability of relevant information (e.g. well-curated biological pathways). Thus, the application of data-driven approaches instead of and in addition to knowledge-based methods may reveal novel relationships and generate additional hypotheses amenable to further confirmatory studies. DNEA overcomes many limitations of existing enrichment analysis programs that rely on prior knowledge of biological pathways. While our study focused on lipidomic datasets, where there is a critical need to identify novel lipid pathways, DNEA can be broadly applied to any metabolomic or lipidomic datasets. It should be noted that DNEA requires a relatively large sample size. Because the number of significant edges depends on the sample size, the training cohort and independent validating cohort should be fairly equal in size. Similarly, the methods of identification and quantification applied in the lipidomic platform for data generation should be identical.

Many pathophysiological processes likely account for the high abundance of polyunsaturated long-chain TAGs in advanced CKD. Progression of CKD is associated with a higher abundance of saturated free fatty acids, which have detrimental effects on the integrity of podocytes and the tubulointerstitial compartments (Afshinnia et al., 2018; Chan et al., 2017). Contributing factors may include diminished dietary intake of polyunsaturated fatty acids (Friedman et al., 2006; Saifullah et al., 2007) and increased in vivo synthesis and diminished catabolism of free fatty acids with progression of CKD (Kim et al., 2009). Palmitate, as the prototype saturated free fatty acid, activates the AMP-activated protein kinase and mammalian target of rapamycin complex-1 signaling pathways, contributes to mitochondrial superoxide generation, augments endothelial reticulum stress, heightens insulin resistance, increases the intracellular abundance of DAGs which in turn activate protein kinase-C, promotes autophagy and eventually triggers apoptosis and cell death. These events all contribute to CKD progression (Jiang et al., 2017; Lee et al., 2017; Lennon et al., 2009; Martinez-Garcia et al., 2015; Sieber et al., 2010; Soumura et al., 2010; Xu et al., 2015; Yasuda et al., 2014). Factors, such as chronic inflammation and oxidative stress, contribute to insulin resistance via increased intracellular DAG and fatty acyl coenzyme A, activation of serine/threonine kinases, increased phosphorylation of serine residues on insulin receptor substrate-1 and inhibition of insulin-induced PI 3-kinase activity, reduced insulin-stimulated AKT2 activity and decreased insulin-induced glucose uptake (Chan et al., 2017; Morino et al., 2006; Teta, 2015; Xu and Carrero, 2017). These abnormalities, along with impairment of β-oxidation, lead to further accumulation of intracellular lipids. In parallel, the palmitate-induced upregulation of acyl coenzyme A: diacylglycerolacyltransferase1 and stearoyl-CoA desaturases-1 and -2 contribute to further synthesis of polyunsaturated TAGs (Afshinnia et al., 2018; Sieber et al., 2013). The higher number of edges between TAGs with a successive number of carbon or double bonds in the TAG subnetworks in early-stage CKD and in non-progressors may reflect the efficient functioning of desaturation-elongation processes early in the CKD disease process, which may mitigate progression of CKD after reaching maximum levels of polyunsaturated long TAGs. Altogether, these processes translate to a higher abundance of longer polyunsaturated TAGs in patients with advanced-stage CKD.

Another finding in our study was a significantly lower number of edges in CL–PE subnetworks in advanced CKD and in patients whose CKD progressed to ESKD (progressors). CL is a cone-shaped, non-bilayer lipid, which is almost exclusively synthesized by and resides in mitochondria (Tatsuta and Langer, 2017). In humans, it is synthesized by the action of CL synthase and via condensation of the precursors cytidine diphosphate diacylglycerol and PG (Chen et al., 2006; Houtkooper et al., 2006). CL comprises about 18% of the inner membrane mitochondrial lipids (Ikon and Ryan, 2017), where it plays an important role in electron transportation and ATP synthesis (Bazan et al., 2013; Haines and Dencher, 2002; Mileykovskaya and Dowhan, 2014; Mileykovskaya et al., 2005; Moser et al., 2014), stabilizes numerous protein complexes (Friedman et al., 2015; Horvath and Daum, 2013; Tatsuta and Langer, 2017) and contributes to the asymmetric distribution of phospholipids in monolayer leaflets necessary for the integrity of mitochondrial cristae membranes (Ikon and Ryan, 2017). Alterations in CL biosynthesis lead to altered cristae morphology, accumulation of aberrant mitochondria, augmentation of proton leak and alterations in membrane potential (Ikon and Ryan, 2017; Jiang et al., 2000; Koshkin and Greenberg, 2002; Pfeiffer et al., 2003; Xu et al., 2005). PE is also a non-bilayer lipid that constitutes about 34% of the lipids in the inner mitochondria membrane (Ikon and Ryan, 2017). In eukaryotes, it is synthesized mostly in the mitochondria from phosphatidylserine by the action of phosphatidylserine decarboxylase (Tatsuta and Langer, 2017). Unlike CL, which is exclusively synthesized in the mitochondria, PE may also be synthesized outside the mitochondria via the Kennedy pathway with a smaller contribution toward the total cellular supply of PE (Birner et al., 2001; Tatsuta and Langer, 2017; Vance and Vance, 2009). PE plays crucial roles in cellular lipid metabolism by stabilizing the negatively curved monolayer leaflet of mitochondrial inner membrane, maintaining the membrane potential, importing pre-proteins across the inner membrane, and serving as a precursor lipid for synthesis of PC in the endoplasmic reticulum (Birner et al., 2001; Bottinger et al., 2012; Ikon and Ryan, 2017; Tatsuta and Langer, 2017). Reduced formation of PE is associated with complete inhibition of its conversion to PC in the endoplasmic reticulum (Aaltonen et al., 2016), impairment of cristae morphology, and oxidative impairment (Tasseva et al., 2013). PE and CL both are required for full activity of the mitochondrial respiratory chain (Bottinger et al., 2012), so the loss of both lipids may lead to decreased mitochondrial fusion and fragmented mitochondria (Joshi et al., 2012). On the other hand, growing evidence suggests that mitochondrial damage and dysfunction might be a highly prevalent abnormality in CKD as early as CKD stage 3. This evidence includes, but is not limited to, elevated long-to-intermediate chain acylcarnitine ratio in CKD stage 3 (Afshinnia et al., 2018), a higher likelihood of mitochondrial DNA damage, low carnitine levels and elevated plasma malonate, methylmalonate and malate in dialysis patients (Lim et al., 2002; Liu et al., 2001; Rhee et al., 2010; Rossato et al., 2008). Mitochondrial dysfunction in CKD is likely associated with impairment in the function and synthesis of the mitochondrial CL–PE complex and may be the key underlying mechanism for the observed differences in the number of edges reflecting the CL–PE complex captured by DNEA as early as CKD stage 3.

This study has several strengths. It presents an innovative method of identifying novel biological subnetworks, beyond the scope of existing prior knowledge-based methods (e.g. standard pathway enrichment techniques). Our base differential networks were generated using a cross section of CKD patients across all stages of CKD and revealed alterations inherent to advanced CKD. We demonstrated that similar subnetworks can be identified in an independent cohort of CKD patients at earlier stages with a longitudinally ascertained outcome of CKD progression. This similarity not only validates the methodology, but also helps to underscore the importance of the CL–PE subnetwork. Abnormalities in the CL–PE subnetwork preceded the outcome of CKD progression by several years. Rigorous quality control, negligible batch-to-batch variability, negligible missing data and outstanding reproducibility provided a high-quality robust dataset (Afshinnia et al., 2016, 2018). A limitation of this work is that the new regulatory networks that were discovered are still associative, because DNEA, like any computational method, should be considered a hypothesis-generating tool. Careful mechanistic model system studies are warranted to test the validity of these hypotheses to confirm biological relevance of these new lipid regulatory networks. In conclusion, DNEA is an innovative method, capable of highlighting novel pathways relevant to the pathophysiology of disease and potentially capable of identifying targets amenable to therapeutic interventions.