A regression framework to uncover pleiotropy in large-scale electronic health record data

Abstract

Objective

Pleiotropy, where 1 genetic locus affects multiple phenotypes, can offer significant insights in understanding the complex genotype–phenotype relationship. Although individual genotype–phenotype associations have been thoroughly explored, seemingly unrelated phenotypes can be connected genetically through common pleiotropic loci or genes. However, current analyses of pleiotropy have been challenged by both methodologic limitations and a lack of available suitable data sources.

Materials and Methods

In this study, we propose to utilize a new regression framework, reduced rank regression, to simultaneously analyze multiple phenotypes and genotypes to detect pleiotropic effects. We used a large-scale biobank linked electronic health record data from the Penn Medicine BioBank to select 5 cardiovascular diseases (hypertension, cardiac dysrhythmias, ischemic heart disease, congestive heart failure, and heart valve disorders) and 5 mental disorders (mood disorders; anxiety, phobic and dissociative disorders; alcohol-related disorders; neurological disorders; and delirium dementia) to validate our framework.

Results

Compared with existing methods, reduced rank regression showed a higher power to distinguish known associated single-nucleotide polymorphisms from random single-nucleotide polymorphisms. In addition, genome-wide gene-based investigation of pleiotropy showed that reduced rank regression was able to identify candidate genetic variants with novel pleiotropic effects compared to existing methods.

Conclusion

The proposed regression framework offers a new approach to account for the phenotype and genotype correlations when identifying pleiotropic effects. By jointly modeling multiple phenotypes and genotypes together, the method has the potential to distinguish confounding from causal genotype and phenotype associations.

INTRODUCTION

Genome-wide association studies (GWAS) have identified numerous single nucleotide polymorphisms (SNPs) that are associated with human traits and diseases.¹ While single variant associations have provided broad overviews of the genetic architectures underlying the phenotypes, more sophisticated analytical approaches are needed to model the complexity of the genotype–phenotype associations.^2,3 The growing availability of electronic health record (EHR)-linked genetic data has enabled unprecedented interrogation of the complex genetic architectures of phenotypes.⁴ In particular, the discovery of pleiotropic effects, where 1 variant is associated with multiple phenotypes, are achievable using EHR data.^5,6

Many existing studies have identified pleiotropic effects across complex traits.^7,8 These complex associations not only enhance our understanding of the relationship between traits, but can also shed light on the underlying causal mechanisms of the biological processes that lead to the manifestation of those traits.⁹ The current most common approach to identify pleiotropy in high-throughput genetic data is through combining the results from multiple single genetic variant and phenotype association tests. As such, the univariate test is well suited to combine existing GWAS results. A notable example of the univariate variant tests is the Phenome-Wide Association Analysis (PheWAS), which utilizes a regression framework to test the effect of a single variant on multiple phenotypes.¹⁰ In contrast, multivariate approaches can be utilized when individuals are phenotyped on all traits.⁹ Standard multivariate analysis of variance can be used when all phenotypes are normally distributed. Methods that can model other distributions or correlated phenotypes have been developed in the Bayesian framework^11,12 as well as in the setting of general estimating equations.^13,14 To circumvent the distribution assumption of the phenotypes, the proportional odds model has been used to analyze the phenotypes jointly by using a genotype as the outcome and phenotypes as independent variables.¹⁵ However, methods that can simultaneously identify pleiotropic effects between multiple genotypes and multiple phenotypes are currently lacking.

While candidate genes or loci can help to prioritize the search space for pleiotropy, EHRs with linked genetic data are an ideal setting to study pleiotropy because of the availability of a large number of matched patients’ clinical records with their complete genotyped or sequenced genetic data. Because the patients are phenotyped for a large number of traits and diseases, EHR data enable the interrogation of the inter-correlations among the phenotypes. In addition, the complete genetic information of the patients allows methods to take into consideration the dependencies among genetic variants, most commonly reflected through linkage–disequilibrium within a genomic region. Thus, in order to strengthen the causal inference in observational EHR data,¹⁶ it is imperative to account for dependencies among both the phenotypes and the genetic variants.

Thus, we propose a novel use of reduced rank regression (RRR) to simultaneously analyze multiple phenotypes and multiple SNPs to identify pleiotropic effects. RRR has been developed as a dimension reduction technique that can identify important patterns in the data by restricting the rank, or linearly independent columns, of the coefficient matrix.^17–19 Through detecting the overall association between 1 SNP and multiple phenotypes conditioning on other SNPs, RRR can be used to identify candidate genetic variants that are most likely to have pleiotropic effects. In order to demonstrate the utility of RRR to identify pleiotropic effects, we selected patients with both genetic data and clinical EHR information from the Penn Medicine BioBank (PMBB) EHR as our data source. As proof of concept, we restricted our analysis to mental disorders and cardiac diseases because of the existing evidence of pleiotropy between these 2 families of phenotypes.²⁰ Thus, we selected 5 cardiovascular diseases and 5 mental disorders that are the most prevalent in the PMBB as targets for identifying pleiotropic effects. Our results showed that SNPs that are known to be associated with the 10 phenotypes have better power to be detected by RRR compared with existing methods. In addition, genome-wide gene-based analysis has shown that RRR has the potential to identify novel pleiotropic signals. Taken together, RRR is a flexible approach that could overcome the limitation of the existing “one-genotype-at-a-time” analysis of pleiotropy. Partnered with large-scale EHR data, RRR has the potential to identify novel pleiotropic genetic variants that can add to our understanding of the genetic architecture of complex diseases.

MATERIALS AND METHODS

Penn Medicine BioBank EHR data

The PMBB recruits patients through the University of Pennsylvania Health System. Currently, over 60 000 individuals are enrolled in PMBB. The average age for the patients is 66 years old with the predominant ethnicities being European (72%), African (19%), and Asian (1%). For a subset of individuals (∼12 000), genetic information is also available. Patients’ disease statuses were derived from their clinical International Classification of Diseases (ICD) codes. We extracted ICD9 and ICD10 data for 11 345 individuals from the EHRs, consisting of 2.6 million records. Of those, 2.2 million records were ICD9 based, and 390 000 records were ICD10 based. As PheCodes are derived from ICD9, we successfully back-converted 7180 ICD10 codes to ICD9 using 2017 general equivalency mapping. The ICD10 conversions were combined with the ICD9 codes to create a data set with 8390 unique ICD9 codes. Using PheCode definitions,¹⁰ ICD9 codes were aggregated to create 1812 PheCodes to inform each patients disease status. Individuals are considered cases for the phenotype if they have at least 2 instances of the PheCode, controls if they have no instance of the PheCode, and “NA” if they have 1 instance or a related PheCode. As the method used for this analysis required no missing data, we coded NA as 0.5 to reflect an intermediate risk for diseases. For the current analysis, we utilized a subset of 7420 patients of European American descent. Using disease prevalence, we selected the top 5 cardiovascular diseases and mental disorders (Table 1). To validate the results, we also repeated the analysis using the top 10 cardiovascular diseases and top 5 mental disorders (Supplementary File 4).

Table 1.

Selected cardiovascular diseases and mental disorders based on prevalence

Disease	PheCode	ICD-9 codes	Number of cases
Hypertension	401	401, 997	6797
Cardiac dysrhythmias	427	427	5784
Ischemic heart disease	411	411	5008
Congestive heart failure	428	428	3695
Heart valve disorders	395	424	3193
Mood disorders	296	293, 296, V11.1	1353
Anxiety, phobic and dissociative disorders	300	300, 313	1322
Neurological disorders	292	781, 799	489
Alcohol-related disorders	317	291, 303, 790, 980, E869	314
Delirium dementia	290	290, 294, 797	123

Abbreviation: ICD, International Classification of Diseases.

Patients were genotyped using the Illumina QuadOmni chip and imputed to the 1000 Genomes reference panel (1000G Phase3 v5) using the Michigan Imputation Server. Before imputation, standard quality control of genotyping data was carried out by removing individuals who failed sex-check, or have > 5% missingness or heterozygosity (> 3 SD), or are related with others in the data set (IBD > 0.185).²¹ Variant level quality control was performed by removing markers with missing rate > 2%, minor allele frequency < 1%, or Hardy-Weinberg equilibrium > 10⁻⁶. Imputation accuracy, measured by the comparison of expected vs actual allele frequency, was high (R² = 0.992). In total, 47 873 914 variants were imputed, of which 27 139 012 (43.3%) were polymorphic.

Reduced rank regression

RRR is an extension of regularized univariate regression to the regularized multivariate regression that models the relationship between multiple outcome variables and 1 or more predictor variables.^22–26 In the setting of identifying pleiotropic effects, we formulate RRR with a logit link function as follows: given $n$ individuals in the data set with $q$ phenotypes $y_i\in \mathrm{}{\{0,\mathrm{}0.5,\mathrm{}1\}}^q$ and p SNPs $x_i\mathrm{}ϵ{\{0,\mathrm{}1,\mathrm{}2\}}^p$ from the subject $i$, a RRR model can be formulated as

$$\mathit{log}\mathrm{}\frac{E\mathrm{}\left(y_i|x_i\right)}{1-E\mathrm{}\left(y_i|x_i\right)}=c_0+{C^{T}x}_i$$

where C is a p x q coefficient matrix, and $c_0$ is the q x 1 vector representing the intercepts for q phenotypes. The coefficient matrix can be represented using singular value decomposition as a sum of r unit rank matrices

$$C=\mathit{UD}{V}^T=\sum _{k=1}^r{d}_k{u}_k{v}_k^T$$

where $d_k$ is the k_th largest positive singular value of C, $u_k$ is the corresponding orthonormal left singular vector with dimension p, and $v_k$ is the corresponding orthonormal right singular vector with dimension q.

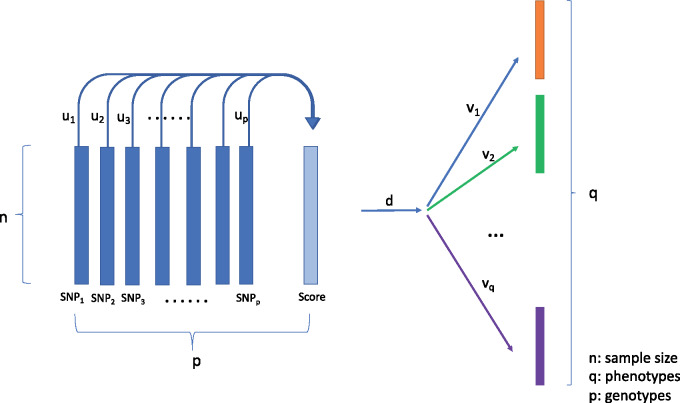
As Figure 1 shows, the vector $u_k$ ($u_{k1},u_{k2}$, … $u_{\mathit{kp}})$ models the joint effect from p SNPs. Thus, $u_k$ can be considered as the coefficient vectors for each SNP conditioned on all other SNPs from the k_th rank. The linear combination of the SNP coefficients, a score vector, represents the joint effect of all SNPs. Similarly, the vector $v_k$ ($v_{k1},v_{k2}$, … $u_{\mathit{kq}})$ consists of each phenotype’s specific association to the score vector from all p SNPs. The parameter $d_k$ indicates the k_th strongest common association between all SNPs and phenotypes. In this study, we limited k = 1 so that the regression has a rank-one structure. Without prior knowledge about the underlying structures of pleiotropic effects, the rank-one structure provides a parsimonious model while maintaining the flexibility to allow for different coefficients for different SNPs and different phenotypes (Figure 1).

Figure 1.

Schematic overview of rank-one RRR method. RRR estimates the coefficient matrix C that can be decomposed into UDV matrices. The U matrix contains the coefficients of SNPs conditioned on all other SNPs. The D matrix represents the common link between all SNPs and phenotypes, which is limited to the unit rank of 1. The V matrix contains the association of each phenotype conditioned on other phenotypes.

Abbreviations: RRR, reduced rank regression; SNP, single-nucleotide polymorphism.

The coefficient matrix can be estimated by minimizing the following objective function

$$\sum _{i=1}^n\sum _{j=1}^q\{\log \{1+\exp ({c_0,}_j+x_i^T{\mathit{UVD}}_j^T)\}-y_{i,j}{x}_i^T{\mathit{UVD}}_j^T\}+\rho \mathrm{}(\mathit{UD}{V}^T,W,\lambda )\},$$

where ${c_0,}_j$ is the j-th element of vector $c_0$, $y_{i,j}$ is the j-th element of vector $y_i$, and ${\mathit{UVD}}_j^T$ is the j-th column of matrix C. The penalty function $\mathrm{\rho }$ is the adaptive elastic net penalty.^27,28$\lambda$ is the tuning parameter controlling the penalty strength on the rank of the coefficient matrix, and it can be chosen using cross-validations. W is a weighting matrix obtained from elastic net estimates.

$$\rho \left(\mathit{UD}{V}^T;\mathrm{}\lambda \right)=\alpha \lambda \parallel W\circ \mathit{UD}{V}^T{\parallel }_1+(1-\alpha )\lambda \parallel \mathit{UD}{V}^T{\parallel }_F^2$$

The detailed estimation procedure can be found in the references.^19,22,29

MultiPhen

As a comparison, we included another method for detecting pleiotropy, MultiPhen, to benchmark against RRR.¹⁹ The reasons for selecting MultiPhen as the benchmark are: 1) It is 1 of the most commonly used and readily available software packages for detecting pleiotropic effects. 2) It is 1 of the few methods that can simultaneously test for pleiotropy for multiple phenotypes. 3) MultiPhen does not assume the phenotypes to have normal or multivariate normal distributions. To circumvent the need to model the distribution of multiple phenotypes, MultiPhen reverses the logistic regression by treating the phenotypes as independent variables and a SNP as the outcome. Then, MultiPhen uses the following proportional odds regression to identify pleiotropic associations¹⁵:

$$P\left(X_i\le m\right)=\frac{1}{1+e^{(-{\alpha }_m-\sum _{k=1}^K{\beta }_k{Y}_{\mathit{ik}})}}$$

where $Y_i=\left\{Y_{i1},\dots ,Y_{\mathit{iK}}\right\}$ denotes K phenotypes for an individual i$,$ and${\mathrm{}X}_i$ is the genotype for individual i, $X_iϵ\left\{0,\mathrm{}1,\mathrm{}2\right\}$. We note that in contrast to the RRR method, the model of MultiPhen only considers 1 SNP at a time.

Candidate SNPs associated with cardiovascular and mental diseases

For each phenotype, previously reported genome-wide associated SNPs were obtained from the NHGRI catalog (https://www.ebi.ac.uk/gwas/).³⁰ To ensure consistency of signals, only SNPs that were reported in the European American population were retained. After removing duplicated SNPs, overall, there were 730 unique SNPs as our candidate SNPs (Supplementary File 1).

The performance of the RRR model, or MultiPhen, is quantified by the ability to prioritize SNPs based on the strength of association with the selected phenotypes. For MultiPhen, the method provides an overall P value for each SNP, and the SNP prioritization is based on the P values (ie, smaller P values indicate stronger associations between the SNP and the multiple phenotypes). For the RRR model, the strength of associations is reflected in the magnitude of the estimated coefficient (vector u), that is, SNPs with the larger absolute value of coefficients are considered to have stronger associations with the outcomes.

Based on these, we designed the comparison to compare the performance of the 2 methods on a group of candidate SNPs against the same number of random SNPs. For each candidate SNP, a matching random SNP was selected from the genome as a negative control. A matching SNP had to have the same minor allele frequency (MAF) as the candidate SNP, but located on a different chromosome. The candidate SNPs, random SNPs, and 10 phenotypes were jointly analyzed by RRR. To minimize biases raised by the differences in MAF, RRR analysis were stratified by the following SNP MAF intervals: MAF < 10%, 10% < MAF < 20%, 20% < MAF < 30%, and 40% < MAF < 50%. Thus, 5 different RRR analyses were carried out for 1 complete analysis and the analyses were repeated 30 times, each time using a different set of random SNPs. The coefficient vector U for the SNPs was recorded. As a comparison, MultiPhen was also applied to the same data set. Because MultiPhen cannot simultaneously model multiple SNPs, the analysis was carried out 1 SNP at a time. The resulting P value for each candidate and random SNP was recorded. The MultiPhen analysis was also stratified by MAF and repeated 30 times.

A method should be able to distinguish the 2 groups (candidate and random) based on the metric it uses for the prioritization. For MultiPhen, known SNPs are expected to have smaller P values than the random SNPs. And for RRR, the estimated coefficient u should be larger in the known SNPs, and closer to 0 in the random SNPs. In order to rigorously compare the results from RRR and MultiPhen methods, SNP coefficients from RRR or P values from MultiPhen were ranked for all SNPs in each MAF stratification. The one-sided Wilcoxon rank test was then applied to formally test whether the candidate SNPs have larger coefficients than random SNPs for RRR. For MultiPhen, the test was for whether the candidate SNPs have lower P values than random SNPs. The P value from this one-sided Wilcoxon rank test can serve as a quantitative measure of the ability for a method in separating signals (ie, the candidate SNPs) from manually added noises (ie, random SNPs).

Genome-wide gene-based analysis

RefSeq gene annotations for the candidate SNPs were downloaded from University of California Santa Cruz genome browser.³¹ Plink 1.9 was then used to extract SNPs within protein-coding genes present in the PMBB. The gene-based analysis was limited to genes with a minimum of 10 SNPs and a maximum of 500 SNPs to assure reasonable power and computational time. For each gene, all SNPs within the gene region and the 10 phenotypes were jointly analyzed by RRR and the resulting coefficients for the SNPs were ranked. Similarly, MultiPhen was applied to each gene, and the analysis was performed on each SNP individually. The P values output by MultiPhen were also ranked within each gene. The rankings from RRR and MultiPhen were compared for each gene using the Wilcoxon two-sided rank test.

For genes that showed significant differences between the 2 methods (p < .01), allele frequency information from the Exome Aggregation Consortium³² was used to determine the relationship between the SNP rankings and their frequencies. We also evaluated whether any of the SNPs within the genes are likely to be the deleterious variants using the Combined Annotation Dependent Depletion (CADD) score.³³

RESULTS

Enrichment of signals from known associated SNPs

In order to compare RRR and MultiPhen on their power to discern signal from noise, both methods were applied to the same set of SNPs, including previously reported SNPs and an equal number of random SNPs. To minimize the influence from SNP variance, the analysis was stratified by 5 nonoverlapping MAF intervals. Generally, across 30 repetitions within each MAF, the fixed real SNPs have resulted in similar SNP rankings as shown by the vertical stripes in the left panel, while the random SNPs have shown no consistent patterns (Figure 2). In addition, across different MAF ranges, RRR showed better performance in distinguishing previously associated SNPs from random SNPs (Figure 2a–e). That is, the coefficients of known SNPs have a higher magnitude than that of random SNPs. The enrichment of signals from known SNPs was highest for SNPs with MAF < 10% (Figure 2a). The output from both methods can be found in Supplementary File 2.

Figure 2.

Ranking of SNPs for RRR and MultiPhen. The ranks of candidate SNPs (left panels) and random SNPs (right panels) for RRR (top panels) and MultiPhen (bottom panels) are shown. There is an equal number of candidate (real) SNPs and random SNPs for each analysis. The ranking is based on the magnitude of SNP coefficients for RRR (darker color for larger coefficients) and P values of SNPs for MultiPhen (darker color for lower P value). Analysis based on different stratifications of SNP MAF are shown in a) MAF $\le$ 10% b) 10% < MAF $\le$ 20% c) 20% < MAF $\le$ 30% d) 30% < MAF $\le$ 40% e) 40% < MAF $\le$ 50%.

Abbreviations: MAF, minor allele frequency; RRR, reduced rank regression; SNP, single-nucleotide polymorphism.

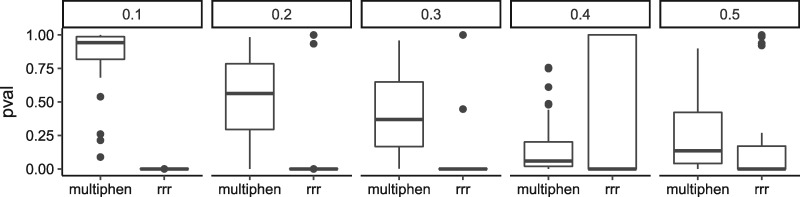
To quantify this difference, the ranks of known SNPs were compared with that of random SNPs using Wilcoxson one-sided test for each method. Compared to MultiPhen, RRR showed more significant differences between the 2 sets of SNPs across different MAF stratification (Figure 3). For MAF < 10%, RRR has consistently resulted in significantly higher rankings for the known SNPs, as indicated by the small P values in the boxplot. At the same time, MultiPhen showed little power to distinguish the 2 sets of SNPs, with mean P value > 0.9 across 30 repetitions. MultiPhen showed improvement of power as the MAF of the known SNP increases, while RRR’s power was consistently higher.

Figure 3.

Statistical test for the SNP rankings of RRR and MultiPhen. For each MAF stratification (vertical panels), Wilcoxon test was used to compare the ranks between candidate SNPs and random SNPs. Each boxplot contains 30 p-values corresponding to 30 analysis repetitions. Abbreviations: MAF, minor allele frequency; RRR, reduced rank regression; SNP, single-nucleotide polymorphism.

Genome-wide scan of potential pleiotropic effects

To investigate whether RRR can detect different pleiotropic signals than the existing method, we systematically applied all methods to genome-wide SNPs to detect pleiotropic effects. We prioritized our analysis to SNPs within gene regions for more interpretable results.

Using the 10 phenotypes, RRR and MultiPhen were separately used to scan all processed RefSeq protein-coding genes for pleiotropic effects. For each gene, the ranking of SNPs produced by RRR was compared with that of MultiPhen using the Wilcoxon two-sided rank test. Table 2 shows that the 2 methods have identified a number of RefSeq genes that have significant differences in their SNPs ranking.

Table 2.

Genes with differential pleiotropic effects under RRR and MultiPhen (p < 01). Genes are sorted from the largest to the smallest differential effects

RefSeq ID	Gene name
NM_001303096	WDR75
NM_001350521	PDE4DIP
NM_001002812	PDE4DIP
NR_026789	FAM66A
NM_001355197	ZNF66
NM_001350520	PDE4DIP
NM_001347717	CHRNB3
NM_001291368	ZNF534
NR_151707	LINC02018
NM_001287585	NUP35
NR_026567	ESPNP
NM_001127394	TSEN15
NM_024109	METTL22
NM_001303281	ZNF18
NM_144680	ZNF18
NM_138330	ZNF675
NM_001198832	PDE4DIP
NM_001145998	SLC15A2

For genes that have available allele frequencies and scores in Exome Aggregation Consortium and CADD, RRR has shown that common SNPs are generally more likely to have pleiotropic effects. The RRR rankings for common alleles (MAF > 10%) are much higher for ZNF534, ZNF66, METTL22, SLC15A2, and TSEN15 genes. Additionally, higher ranking SNPs in SLC15A2 and TSEN15 genes identified by RRR also contain more deleterious variants (Supplementary File 3).

DISCUSSION

Pleiotropy provides a plausible explanation for the observations of shared heritability and comorbidity between many complex traits.⁹ Identifying pleiotropy marks an essential step towards a better understanding of the underlying biological mechanism that may not be fully explained by the single variant–single disease associations. In addition, the advent of large-scale biobank-linked EHR systems has enabled the systematic investigation of pleiotropic effects. In this study, we presented an investigation of pleiotropic effects between 5 cardiovascular diseases and 5 mental disorders in the PMBB. We utilized reduced ranked regression to model 10 phenotypes and multiple SNP genotypes simultaneously and found that it has better power to distinguish real from spurious associations than existing methods. Also, genome-wide scanning of pleiotropic effects showed that RRR has the potential to identify new associations.

Previous efforts to identify pleiotropy has been challenged by both limitations in methodology as well as a lack of suitable data. Currently, methods to detect pleiotropy are typically limited to 1 individual SNP at a time. As a result, we investigated the promise of modeling multiple phenotypes and multiple SNPs at the same time by considering a recently proposed reduced ranked regression method.¹⁹ In addition, we utilized PMBB EHR data that contains a large number of genotyped patients who have extensive clinical records to validate our method.

RRR can jointly model the associations between multiple SNPs and multiple phenotypes to detect genotype and phenotype associations. Due to the conditional dependencies between SNPs and phenotypes, the associations represent overall effects between all SNPs and phenotypes. When more than 1 phenotype is associated with the SNPs, the associations can be interpreted as pleiotropic effects (more in limitation below). The strength of the association is reflected in the magnitude of the coefficients. A higher magnitude of the SNP coefficient (ie, lower rank relative to other SNPs) indicates the SNP are more likely to be associated with 1 or more phenotypes. As Figure 2 shows, across different MAF ranges, RRR produced a lower rank for SNPs with known associations than randomly selected SNPs from the genome. The differences are especially evident in the lower 0%–20% MAF range (Figure 2a, b). The higher efficiency for the low MAF range was also corroborated by a previous study, which found an inverse relationship between MAF and effect size.³⁴ MultiPhen was also able to distinguish known SNPs from random SNPs; however, the separation was not as clear as RRR (Figure 2). The observation was confirmed by the one-sided Wilcoxon rank test, where the ranks of known SNPs were compared with the ranks of random SNPs. If the known SNPs have lower ranks than random SNPs, the Wilcoxon test will result in a lower P value. Figure 3 showed that across 30 different analysis, RRR on average resulted in lower P values than MultiPhen. Additionally, we investigated whether RRR could identify different pleiotropic signals compared to MultiPhen. Using the RefSeq gene definition, we performed genome-wide detection of pleiotropic effects using both RRR and MultiPhen. We identified 18 gene transcripts that showed potential differences between the 2 methods in terms of the ranking of SNPs within a gene (Table 2). Compared with Multiphen, RRR has found common SNPs in ZNF534, ZNF66, METTL22, SLC15A2, and TSEN15 to be more likely to have pleiotropic effects. The prospect of common SNPs influencing phenotypic changes was supported by the infinitesimal model, where common variants of small effect drive phenotypic changes.^35,36 Additionally, within the SLC15A2 and TSEN15 genes, RRR has identified several high-ranking SNPs that have high CADD scores, which reflects a high potential to cause changes to a protein.

In this study, we presented a new regression framework that has the potential to be more potent than existing approaches in detecting pleiotropic signals. However, there are several limitations that are specific to the current study that is worthy for follow-up investigations. First, there is not a comprehensive set of gold standard pleiotropic loci that can be used for validation. Thus, we used NHGRI GWAS catalog’s curated loci for the 10 phenotypes as a surrogate for the gold standard because pleiotropic loci are required to have a marginal effect for at least 1 phenotype. However, this approach is still affected by sample heterogeneity across different studies as some of the known loci were not replicated by either method (Figure 2). Second, further works are required to derive proper statistical inference for RRR. Similar to the least absolute shrinkage and selection operator method, we used RRR to perform point estimation for SNP coefficients, which in turn are used to select important SNPs. In order to obtain proper P values for RRR, we plan to derive the valid statistical procedures for obtaining debiased point estimation and variance estimation. To minimize the effect of different variances on SNP coefficients comparison, we stratified our analysis by the SNPs’ MAF in order to make the SNPs comparable within each stratum. Finally, computational optimizations are needed for RRR to handle large-dimensional genetic data. We had to limit our analysis to protein-coding genes with less than 500 SNPs to satisfy the computational requirements. While gene-based analysis can reveal the most appealing evidence for pleiotropy, many intergenic and non-coding regions have been associated with human phenotypes.^37,38 Thus, further optimizations are needed to perform genome-wide unbiased analysis of pleiotropy. Additionally, there is a limitation that affects RRR and pleiotropic analysis in general. Most of the commonly used methods to detect pleiotropic effects can detect an overall association between phenotypes and genotypes. However, the association could be dominated by 1 or a few phenotype-to-genotype associations. To elucidate the individual associations between phenotypes and genotypes, additional tests are needed. Because of this, associations identified by RRR have high potentials to be pleiotropic; however, they cannot be directly attributed to specific SNPs and phenotypes combinations. In exchange for specificity, the pleiotropic test by RRR or other methods operates in a similar manner as analysis of variance in that they can provide a preliminary detection of the overall effect. The main advantage of the detection of an overall effect is that it is very effective in reducing the search space. In the standard pleiotropic analysis, where each pairwise SNP and phenotype combination is evaluated for an association, the search space, SNPs x Phenotypes, grows very quickly, which incurs a large multiple hypothesis penalty.

CONCLUSION

In this study, we presented a new regression framework, RRR, that could jointly detect overall pleiotropic effects between multiple phenotypes and multiple genotypes. We utilized patient diagnoses of cardiovascular diseases and mental disorders stored in PMBB EHR to demonstrate that our method has a better power to detect pleiotropic effects than existing methods. In addition, genome-wide analysis of pleiotropic effects showed that the method has identified different pleiotropic effects in a number of genes. Further works in RRR include developing proper statistical inference and improved algorithm efficiencies to accommodate high-dimensional data.

FUNDING

This work is supported by National Institutes of Health grants AI116794, DK112217, ES013508, HL134015, LM010098, LM011360, LM012601, and TR001263. This research is also supported in part by the Institute for Translational Medicine and Therapeutics’ (ITMAT) Transdisciplinary Program in Translational Medicine and Therapeutics, and, in part, by the National Center for Advancing Translational Sciences of the National Institutes of Health, award number UL1TR001878. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH. SMD is supported by the US Department of Veterans Affairs (IK2-CX001780). This publication does not represent the views of the Department of Veterans Affairs or the United States government.

AUTHOR CONTRIBUTIONS

RL, RD, RK, YC, and JHM conceived of the study. RK performed the EHR data processing. RL performed data analyses. RL, YC, and JHM wrote the manuscript, and all authors revised and approved the final manuscript.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.

CONFLICT OF INTEREST STATEMENT

None declared.