Abstract
Objective:
To compare field measure differences in simulations of transcranial electrical stimulation (tES) generated by variations in finite element (FE) models due to boundary condition specification, use of tissue compartment smoothing filters, and use of free or structured tetrahedral meshes based on magnetic resonance imaging (MRI) data.
Approach:
A structural MRI head volume was acquired at 1 mm3 resolution and segmented into ten tissue compartments. Predicted current densities and electric fields were computed in segmented models using modeling pipelines involving either an in-house (block) or a commercial platform commonly used in previous FE tES studies involving smoothed compartments and free meshing procedures (smooth). The same boundary conditions were used for both block and smooth pipelines. Differences caused by varying boundary conditions were examined using a simple geometry. Percentage differences of median current density values in five cortical structures were compared between the two pipelines for three electrode montages (F3-right supraorbital, T7-T8 and Cz-Oz).
Main results:
Use of boundary conditions commonly used in previous tES FE studies produced asymmetric current density profiles in the simple geometry. In head models, median current density differences produced by the two pipelines, using the same boundary conditions, were up to 6% (isotropic) and 18% (anisotropic) in structures targeted by each montage. Tangential electric field measures calculated via either pipeline were within the range of values reported in the literature, when averaged over cortical surface patches.
Significance:
Apparently equivalent boundary settings may affect predicted current density outcomes and care must be taken in their specification. Smoothing FE model compartments may not be necessary, and directly translated, voxellated tissue boundaries at 1 mm3 resolution may be sufficient for use in tES FE studies, greatly reducing processing times. The findings here may be used to inform future current density modeling studies.
Keywords: tDCS, finite element simulation, current density, electric field
INTRODUCTION
Finite element (FE) simulations are frequently used to predict current density distributions inside the human head caused by transcranial electrical stimulation (tES) therapies such as transcranial direct current stimulation (tDCS) or transcranial alternating current stimulation (tACS). Patient-specific FE modeling of tES typically uses structural and diffusion information gathered in MRI scans to generate realistic head models [1–4]. Use of high resolution scans (ca. 1 mm in-plane resolution), inclusion of large numbers of tissue types and white matter anisotropy have been considered important factors affecting modeling accuracy [5, 6]. Tissue conductivity values are typically assigned based on literature referenced values [7–10] or direct scaling of diffusion tensor information [11–13]. Segmented head models are then meshed into desired element sizes and types (hexahedral or tetrahedral elements). Commercial platforms [2, 14–16] or specialized software [5, 16–18] have typically been used to solve FE [19–21], finite difference or boundary element method [22] simulations.
Many FE predictions of fields in realistic human head models were initially developed for inverse EEG/MEG applications [13, 23–25]. In these cases, simulations were performed on volume meshes containing either hexahedral or tetrahedral elements. For hexahedral meshes, voxel-based MRI structural data were directly transformed into regular hexahedral meshes [13] or converted into geometry-adapted hexahedral meshes using isoparametric FE approaches [18, 24, 26]. Hexahedral models were determined in studies by Wagner et al. [27] and Vorwerk et al. [28] to produce accurate results, but cautioned that the method of generating the hexahedral mesh must be chosen carefully to avoid leakage or artificially closed compartments. Tetrahedral elements have been constructed by compartmentalizing individual voxel-based hexahedral elements into multiple tetrahedral elements [22] or into free meshes using constrained Delaunay tetrahedralization (CDT) approaches [25, 29]. To simulate EEG data, meshed head models and electrodes are typically assigned homogeneous (insulating) Neumann boundary conditions on the head surface, and zero potential at ground electrodes [23]. Internal sources mimicking an active cortex are approximated as dipolar current sources and voltage differences caused by current dipoles are calculated using the reciprocity principle [30]. These forward problems have often been implemented using in-house or freely available FE software such as NeuroFEM [31], SimBio [13, 23, 24, 32, 33], SCIRun [22, 34].
In tES FE modeling studies, while in-house or freely available FE software [10, 18, 35] have been used, commercial platforms have been much more widely employed than in EEG modeling. COMSOL [2, 4, 14–16, 36–46] has been the most commonly used commercial package used in tES modeling studies. FE software packages such as Abaqus [7, 47, 48], and ANSYS (Ansys Inc., PA, USA) [49] have also been employed. Companion software packages such as ScanFE Simpleware (Synopsys, CA, USA) [15, 16, 37–39, 42–44] or Mimics (Materialise, Belgium) [2, 4, 45, 46] have often been required to mesh the complex geometry of head models for use with COMSOL, Abaqus and ANSYS, because their output formats are compatible with these packages. ScanFE constructs tetrahedral volume meshes using a combination of Delaunay and Advancing front approaches. The conversion process from voxel based MRI volumes into tetrahedral elements that can be successfully imported into commercial software requires a series of smoothing operations to avoid meshing complications [2, 7]. Pre-processing steps are also required to eliminate gaps between subdomains [50].
Previous tES FE studies have used a variety of electrode boundary conditions. Conventional transcranial stimulation protocols use a single pair of electrodes, with one electrode assigned as the anode and the other the cathode [51]. In tES clinical studies, electrical currents of 2 mA or below [51] are applied between the anode and cathode using a controlled constant current source. Multiple FE simulations of tES studies have been performed with boundary conditions assigned with positive normal current density at the anode, and setting the cathode boundary condition to ground voltage [7, 14, 16, 36–38, 40, 42, 43, 47, 48, 52, 44]. Other FE tES studies assigned voltage values at the anode and cathode such that the voltage difference across the electrodes was equivalent to the desired current magnitude [2, 4, 17, 18, 35]. Boundary conditions specifying equal and opposite total current magnitudes applied at the anode and the cathode, respectively, with a reference voltage within the models, have also been employed [10, 21].
Variations in tES FE simulation configurations, such as choices of software, volume meshing types and boundary condition assignments across FE tES studies may cause inconsistencies, rendering comparisons of individual study outcomes difficult. Therefore, there is a need to benchmark existing tDCS FE simulation studies to ensure consistency. In this paper, we present comparisons of results from tES FE models executed using two modeling pipelines. The first pipeline involved a pair of commonly used commercial platforms, ScanFE and COMSOL, while the second pipeline used in-house software [5, 10]. In particular, we investigated the effects of mesh type, segmented model smoothing performed before meshing, and use of different boundary condition settings on outcomes in complex human head geometry simulations. Quadratic basis functions were used in both FE formulations as this is the default used by COMSOL software. The specific outcomes modeled were percentage differences of median current density between block and four levels of smoothing, for both isotropic and anisotropic conductivity distributions. Different levels of smoothing were achieved by applying a recursive Gaussian filter multiple times. White matter tissue anisotropy information was obtained from the diffusion weighted imaging (DWI) scan of the subject and was included in both block and smoothed model pipelines. Three different electrode montages were employed: left frontal-right supraorbital (F3-RS), left-right temporal cortex (T7-T8) and midline central–midline occipital cortex (Cz-Oz), with the first named electrodes in each pair selected as the anode. Distributions formed using either formulation were compared within target, deep and peripheral brain structures. The intended stimulation target structures were the inferior frontal gyrus (IFG) for F3-RS [5, 53], the anterior superior temporal gyrus (ASTG) for T7-T8 [54] and the occipital lobe (OCC) for Cz-Oz [17]. While this study investigated head models derived from a single subject using one set of material properties, we consider our findings indicative of differences that may be introduced using a variety of model workflows. We anticipate that these results will be useful in informing future tES modeling studies.
MATERIALS AND METHODS
All head models were derived from a single subject T1-weighted MRI dataset. White matter conductivity tensor information was calculated from DWI data collected from the subject in the same imaging session. Block models were constructed directly from the segmented head volumes. Four degrees of recursive Gaussian smoothing were employed in constructing smooth models, and these were compared to block model results for the three electrode montages. Details of modeling and simulation processes are described in the following subsections.
T1-weighted and DWI data acquisition
T1-weighted and high angular resolution diffusion weighted imaging (HARDI) MRI datasets from a healthy human subject were collected using a 3T Achieva Phillips MRI system (the McKnight Brain Institute, University of Florida). HARDI data sets were acquired in 64 at high b-value (1000 s/mm2) and 6 directions at low b-value (100 s/mm2) using a 2D multislice spin echo sequence (TE=86.0 ms, TR=9022.8 ms) with a matrix size 112×112 and a total of 70 sagittal slices, each slice being 2 mm thick. T1 data was acquired using a 3D turbo spin echo pulse sequence (TE=3.69 ms, TR=8.057 ms) with a matrix size of 256 × 256 and 0.9375 mm resolution, with 160 axial slices of 1 mm thickness.
Head model construction
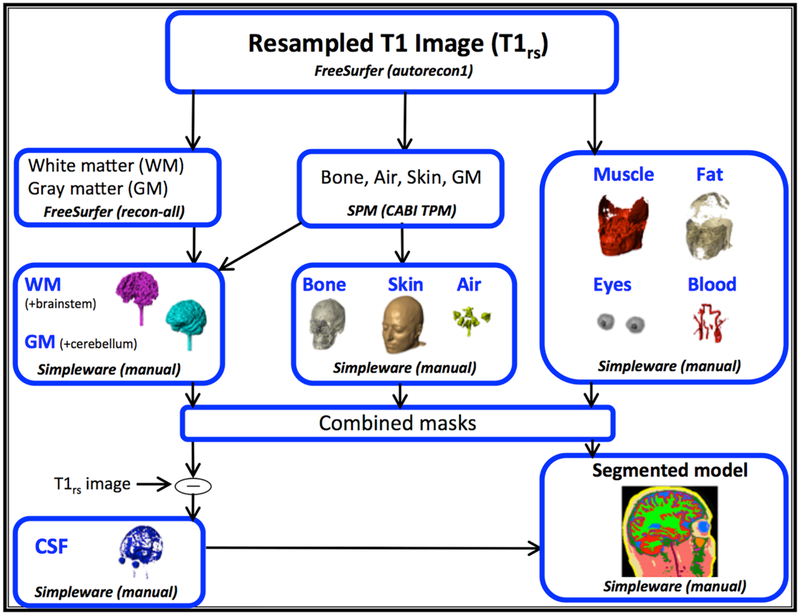
Prior to segmentation, the T1-weighted image was resampled to 256 × 256 × 256, 1 mm3 isotropic resolution using FreeSurfer (Cambridge, MA). Resampled T1-weighted images were segmented into ten tissue types using a combination of manual and automatic segmentation processes. Automatic segmentation of white and gray matter was performed in FreeSurfer, while segmentation for bone, air, and skin were done in SPM (Wellcome Trust Centre for Neuroimaging, London, UK) using an improved tissue probability map developed at CABI [7]. Masks obtained from automatic segmentation software were then imported into ScanIP (Simpleware, Synopsys, Exeter, UK) and corrected. Brainstem, gray matter, and remaining tissue compartments (muscle, fat, eyes, blood and CSF) were completed manually in ScanIP with reference to an anatomical atlas [55]. Figure 1 summarizes the segmentation pipeline used to categorize a single head model into ten final tissue types: white matter, gray matter, CSF, bone, muscle, fat, blood, air and skin. Literature sourced conductivity values were assigned to these ten tissue types, based on available values reported below 1 kHz, as shown in Table 1. While conductivities measured at lower frequencies (closer to 10 Hz) would be preferred, existing literature values are scant, and prone to measurement error [56].
Figure 1.
The segmentation pipeline involved both manual and automatic segmentation processes. The pipeline is shown in terms of the three major operation types (Freesurfer, SPM and manual). Results from each operation type were finally combined to produce a single head model containing ten tissue types.
Table 1.
Literature-referenced conductivity values for ten tissue types for measurement frequency under 1kHz [10]. Bone conductivity (combined) was computed as (where σcan was cancellous bone and σcor was the average of cortical bone conductivity reported in the reference. Isotropic white matter conductivity was simulated using the formula where σl was longitudinal and σt was transverse conductivity.
| Tissue types | σ (S/m) | Reference |
|---|---|---|
| Air | 1.0×10−9 (Smooth Pipeline) | - |
| Blood | 6.7×10−1 | Geddes and Baker (1967) [57] |
| Bone | 214 × 10−3 (cancellous) 5.52 × 10−3 (cortical) 10.9 × 10−3 (combined) |
Akhtari et al. (2002) [58] |
| Cerebrospinal fluid | 1.8 | Baumann et al. (1997) [59] |
| Fat | 2.5×10−2 | Gabriel et al. (1996) [60] |
| Gray matter | 1.0×10−1 | Gabriel et al. (1996) [60] |
| Muscle | 1.6×10−1 | Geddes and Baker (1967) [57] |
| Sclera, lens | 5.0×10−1 | Gabriel et al. (1996) [60] |
| Skin | 4.3×10−1 | Holdefer et al. (2006) [20] |
| White matter | 1.2×10−1 (trans.) 1.2 (long.) |
Geddes and Baker (1967) [57] |
The FSL FDT module was used to calculate diffusion tensor (DT) and fractional anisotropy (FA) maps from HARDI DWI data [61]. Anisotropic conductivity tensors were assigned to portions of white matter compartments that had FA values greater than 0.5. White matter conductivity tensors were calculated from DT principal eigenvector components (V1x, V1y, V1z) as described below.
An initial conductivity tensor, Sw was re-oriented to S*w by pre- and post-multiplying Sw with a product of rotational matrices, R and RT respectively, such that
| (1) |
where
| (2) |
| (3) |
Ax, Ay, and Az were rotation matrices about x, y and z axes, respectively, for angles α, β, γ calculated from normalized V1x, V1y and V1z vectors (, and ) such that
| (4) |
| (5) |
The diffusion free (S0) reference image of DWI data was used to co-register diffusion and T1-weighted data, and all T1-weighted data were resampled to the same resolution as diffusion images before performing tensor calculations. A large white matter anisotropy ratio (σl/σt = 10) was used to illustrate maximal effects. Results from both anisotropic and isotropic white matter models were compared.
TDCS electrode montages
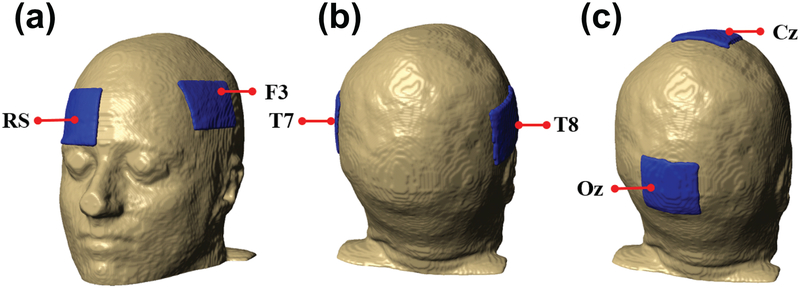
All model results were calculated for three different electrode montages (F3-RS, T7-T8 and Cz-Oz). Current was injected at the anode site, which was the first named electrode in each montage pair. Each electrode had 35 cm2 surface area and 1 mm thickness. This electrode size was typical of conventional tES electrode sizes [51]. Figure 2 shows locations of the three electrode montages with respect to the head model.
Figure 2.
Electrode placements on head models used in this study. From left to right: (a) F3-RS, (b) T7-T8 and (c) Cz-Oz montages.
Block Model Construction
The block model mesh was constructed directly from segmented T1-weighted data. However, hexahedral meshes were not used. Instead, each voxel was transformed into six tetrahedral mesh elements. Each of these tetrahedra was assigned the same conductivity as others within the same voxel. We used this configuration because we anticipated that at sufficiently high resolution (e.g. 1 mm3 voxels or below) this approach could be used to avoid any time and possible inaccuracies introduced by meshing steps, while not greatly increasing the size of the problem (each set of 6 quadratic basis function tetrahedra had 24 nodes, compared to the 20 nodes required to specify a quadratic basis function hexahedral element covering the same region).
Any tissue overlap in the block model was eliminated manually in MATLAB with the following tissue priority: white matter, gray matter, eyes, blood, air, CSF, fat, bone, muscle and skin. The final block model had approximately four million tetrahedral elements. Air voxels were not included in finite element stiffness matrix assembly, and it was assumed that the slightly different air conductivity values in the two pipelines would not contribute to differences in modeling results.
Smooth Model Construction
All tissue masks in smooth models were overlapped to prevent gaps in the final mesh, a process referred to as mask solidifying. Smooth models were constructed by applying a recursive Gaussian smoothing filter to the segmented head model. During this process, individual pixels within the image were multiplied by a Gaussian kernel function and original pixels were replaced by a weighted averaged of the result. The width of the Gaussian kernel was specified as 1 mm in x, y and z directions, to match the underlying data resolution. The smoothing filter only affected the outside boundary of individual tissue compartments. Additional preprocessing was performed on white matter masks in smooth models by applying morphological close and cavity fill operations in ScanIP prior to smoothing, to preserve thin structures [7]. Smooth models were meshed using the Simpleware ScanFE module after all masks were solidified, using the same tissue prioritization as used for the block model. In ScanFE, free tetrahedral mesh type (+FE Free) was selected with compound coarseness of −25 (maximum edge length of 2–5 mm). The meshing process started by forming a surface mesh of triangular elements then replacing the triangular with tetrahedral elements by using a combination of Delaunay and Advancing Front approaches.
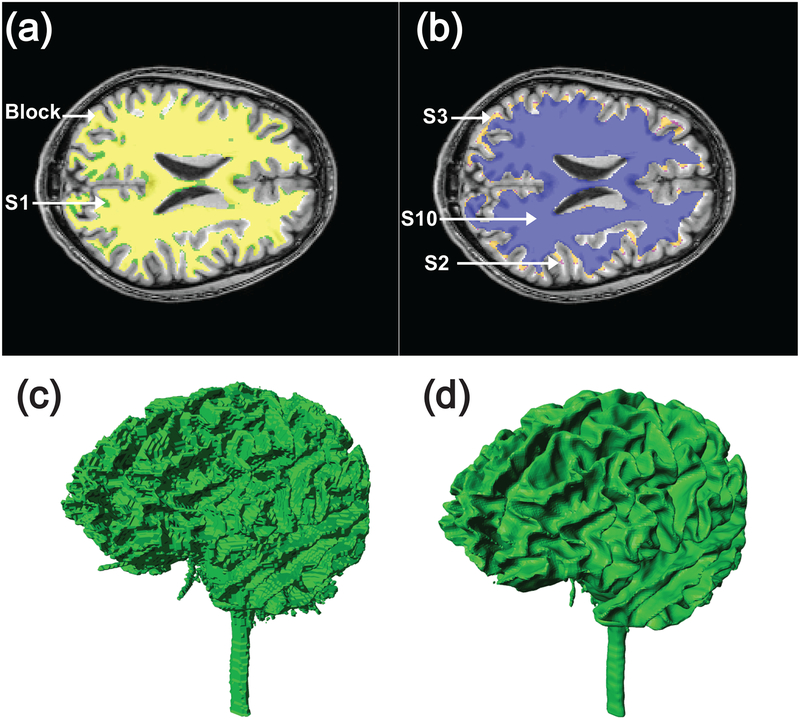
Four levels of smoothing were tested, resulting in four comparisons of block versus smooth models. The first smoothed model was constructed by applying the ScanIP recursive Gaussian smoothing filter to each of the ten tissue masks over a 1 pixel neighborhood in x, y, and z directions, to form model S1. Subsequent smoothed models were obtained by applying the same filter multiple times, to form S2, S3 and S10 i.e. the second level of smoothing (S2) was achieved by applying the smoothing filter twice, the third (S3) by applying the smoothing filter three times, and tenth level (S10) by smoothing ten times. Figure 3 illustrates effects of applying the recursive Gaussian smoothing filter on cross sections of white matter structures. Note that the smoothing filters distorted original boundaries. Smooth model meshes contained approximately 4.5 million tetrahedral elements. Finally, each meshed volume of the smoothed models was exported in COMSOL format. Only results from smoothed models S1, S2, S3 and S10 were used in this study. Figure 3 (C and D) illustrates the different geometric features of block and smooth models (model S1) at the white matter surface.
Figure 3.
Illustration of differences between block and smoothed models in white matter compartment. (A) S1 white matter compartment (green) and segmented block (yellow) compartments overlaid on one slice of T1 model; (B) Overlay of S2 (purple), S3 (orange) and S10 (blue) models of white matter compartment on T1-weighted model. Differences between white matter compartments are shown in as a volume for (C) block and (D) smoothed models.
Finite element modeling
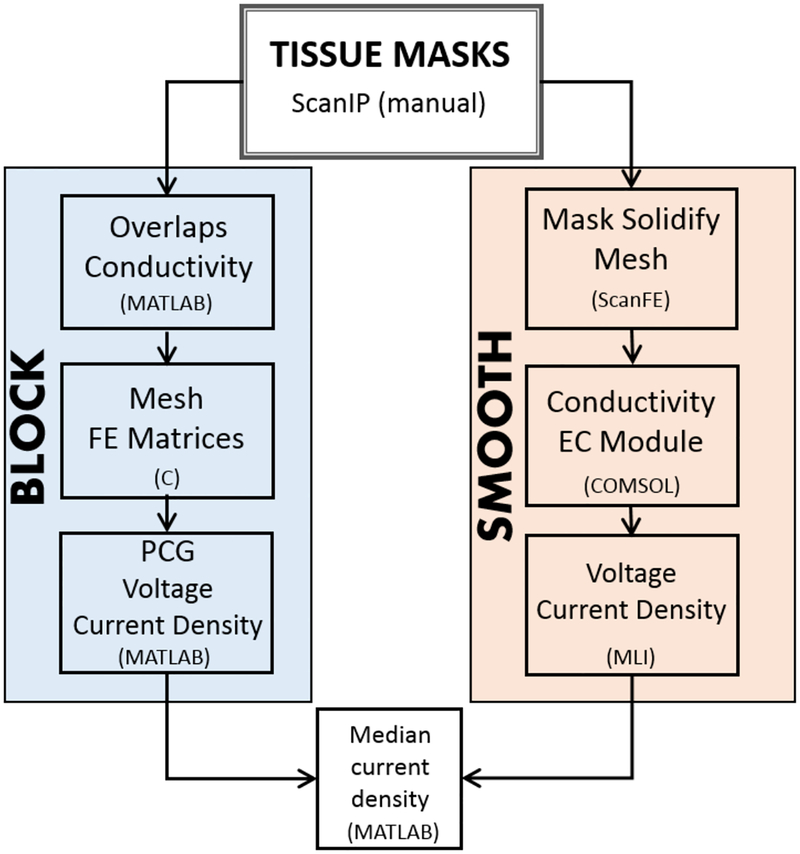
FE formulations, using quadratic basis functions, were used to solve the Laplace equation inside the head volume with mixed boundary conditions applied on head or electrode surfaces. Block models were meshed and simulated using in-house C software and MATLAB, while smooth model meshes were exported to COMSOL as tetrahedral meshes. A total of 1 mA current magnitude was injected at each anode site in all models. Element numbers, solver types and solver tolerances were matched as closely as possible between block and smooth pipelines. The model processing workflows are summarized in Figure 4, and are described below.
Figure 4.
Simulation pipelines for block (left) and smooth (right) head model construction and finite element computation. Block models were processed using C and MATLAB, while smooth models were meshed using ScanFE and solved using COMSOL-MLI. Results from both pipelines were analyzed in MATLAB.
Block Pipeline FE models
In block models, the stiffness and boundary condition matrices for the block-based tetrahedral mesh were formulated with a Continuous Galerkin finite element framework in C code using quadratic shape functions [62]. For anisotropic models, the three components of V1 in DTI data were exported as three volumes matched to the segmented volume, and anisotropic conductivity tensors were computed as each element of the global FE stiffness matrix was assembled. Normal current densities were specified at both anode and cathode, such that the required total current was obtained, and a zero-volt reference node was placed near the model center. Voltage solutions for the block formulation were then calculated using the preconditioned conjugate gradient (pcg) command in MATLAB and a solution tolerance of 10−6. Current densities, J were calculated from voltage gradients, ∇ϕ, and voxelwise conductivity tensors, Dw such that
| (6) |
Smooth Pipeline FE models
FE simulations for smooth models were performed using the electric current (EC) module with the default quadratic element type, and analyzed using the COMSOL-MATLAB livelink interface (MLI). For anisotropic models, the six unique entries in each white matter S*w matrix were exported to individual volumes matched to the imported mesh, and white matter compartment conductivities in the mesh were specified via an interpolation function based on these components. Equal and opposite total current values were specified on electrode surfaces, with positive values assigned at the anode and negative values at the cathode. A reference voltage was assigned at one internal node of the model. A stationary iterative (conjugate gradient) solver was then used to solve Laplace’s equation over the domain using a relative tolerance of 10−6. Voltage and current density results were exported to MATLAB using the function mphinterp over a 256 × 256 (in plane) × 216 (slice) volume with 1 mm3 isotropic voxel resolution.
Model parameter and focus cortical structures
Median current density values within selected cortical structures were compared to quantify differences between block and smooth model results. Median values were used because we anticipated that block models may be affected by partial volume effects, and medians would be less affected by outlier current density values. Current density distributions were evaluated in five cortical structures. Three structures were target structures for each montage, namely the inferior frontal gyrus (IFR) for F3-RS, anterior superior temporal gyrus (ASTG) for T7-T8 and occipital lobe (OCC) for Cz-Oz configuration. The final two structures: hippocampus (HIP) and pre-central gyrus (PRC) were selected as representative deep and peripheral cortical structures, respectively.
Model Verifications and Comparisons
A verification study was performed to confirm that block and COMSOL finite element calculations produced identical results, and to compare the results produced by block and smoothed pipeline in a very simple model where the only differences were due to surface voxellation and boundary conditions. This cross-platform comparison was performed using two models. The first confirmatory model (C1) consisted of a 10 × 10 × 10 cm3 box. The second model (C2) was based on the first model with a 5 cm diameter sphere placed at its center. In both cases, boundary conditions assigning anode and cathode electrodes were applied to opposite faces of the box. Prior to comparisons, a mesh refinement study was performed for each model type to verify that each pipeline’s results did not vary with respect to element size.
Both models (C1 and C2) were initially constructed using the COMSOL drawing interface. Model C1 had a uniform conductivity of 1.8 S/m. In model C2 the sphere had a conductivity of 0.01 S/m. The models were assigned two types of boundary conditions: normal current densities of an equal and opposite value assigned at the anode and cathode (BC-1) with a zero-voltage reference node placed in the center of the model, or, a normal current density equivalent (normal current density times face area) of 1 mA specified at the anode and zero-voltage (ground) at the cathode (BC-2).
The conductivity distribution of both models C1 and C2 was then exported from COMSOL into MATLAB on a uniform 1 mm3 grid and used to compute solutions for each model using the block pipeline. The 1 mm stencil used in block models produced 6 million tetrahedral elements. A boundary condition specifying 1 mA current flow through the electrodes was applied in each case. The voltage drop computed across the electrode faces was examined to determine how well calculations agreed between the two approaches for each model. COMSOL results for model C1 were calculated using the surface average derived value output, while C-code average voltages were obtained by averaging voltages computed on electrode nodes on each face. Model C2 results were also compared in terms of voltage distributions, current density profiles in a central slice, and current density distributions within the sphere and surrounding regions.
Comparison of block and smoothed pipeline results
Comparisons of block and smoothed pipeline results for head models were performed as follows. Medians of simulated current density values (Jmedian) were normalized against adjusted resistance values (ΔRadj) prior to comparisons [8], and percentage differences (PD) between median normalized current density values were computed as
| (7) |
| (8) |
Electric field calculation
Tangential electric field components were calculated on the left anterior temporal gyrus of both block and smooth models and the isotropic, T7-T8 montage case, following [3]. In block models, electric fields E were computed from samples of local voltages, ϕ, such that
| (9) |
Eight small regions (patches) with an area of ~50 mm2 each were isolated on the surface of the left anterior temporal gyrus and analyzed individually. Normal components of these local electric fields, En, were calculated in each patch as a product of E and the averaged normal vectors calculated over the patch surface. Finally, the component of the electric field tangent to the surface patches, Etan, were computed as
| (10) |
Median values for Etan magnitudes were calculated in each patch and averaged to obtain a single median value for block and smooth models. The averaged median values were then compared to similar experimentally measured values reported in the literature [3, 63].
In smooth models, electric fields for the entire model computed using BC-1 were exported on the same grid as used for block models using COMSOL-MLI, and the gridded S1 cortical surface was manually registered to the block cortical surface in ScanIP. The normal component of the electric field in S1 was then calculated on the cortical surface using the same method as used for block models, with Etan magnitudes also calculated using equation (10). Finally, Etan distributions in each patch were translated into histograms for comparison between the two pipelines.
RESULTS
Model cross-comparisons
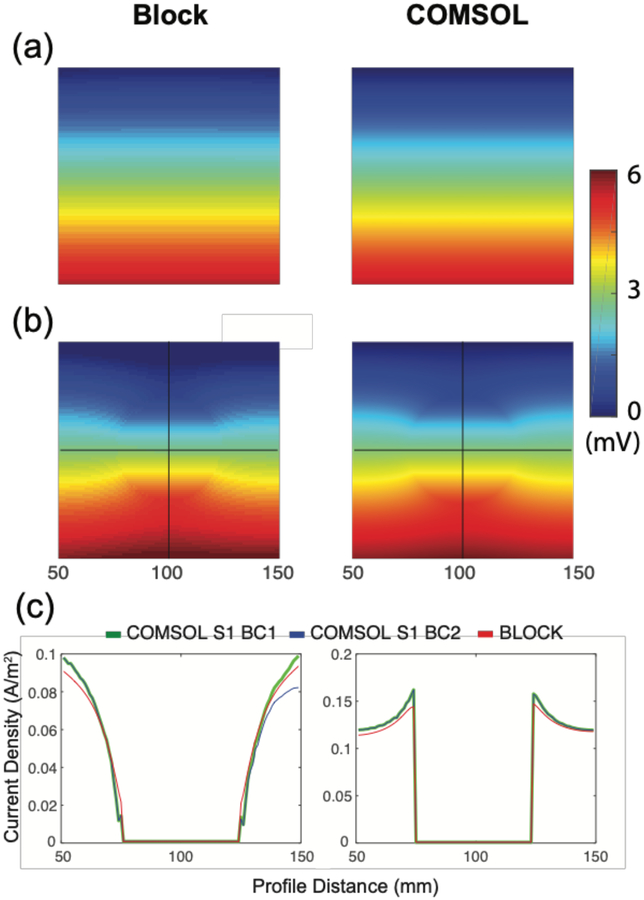
The simple box test calculation resulted in negligible differences between results generated by block and COMSOL BC-1 workflows, while results produced by COMSOL BC-2 showed a discrepancy in vertical current density profiles. Figure 5a shows the voltage distributions for model C1, while Figure 5b shows the voltage distribution along a central slice of model C2. The color gradients in block models were discrete while in smooth models were more continuous, because COMSOL displays were interpolated in post-processing steps. The voltage drop across the electrodes in C1 models was found to be 5.55 mV for both block and COMSOL versions (values were less than 0.1% different), and as predicted by analytic calculations. Voltage solutions for the two C2 models were slightly offset due to the necessary differences in locations of zero volt reference points in the two models (Figure 5b). Current density norm profiles for C2 models are shown in in Figure 5c. In model C2, vertical current density profiles (from anode to cathode) produced by COMSOL BC-2 were asymmetric while the same profiles for COMSOL BC-1 and block models were symmetric. Horizontal current density profiles showed a slight asymmetry in COMSOL and block C2 models. As expected, measures of central tendency were less different. Mean current density norms within the sphere ROI were at most 2% different (medians were at most 1% different), and at most 0.5% different (medians identical) in the bulk of model C2.
Figure 5.
Cross sections of voltage distributions and current density profiles in two of confirmatory models. Block, and COMSOL BC-2 model voltage results for (A) box only model (C1) and (B) box with added sphere (C2). Block, COMSOL BC-1 and COMSOL BC-2 for (C) Vertical (left) and Horizontal (right) current density norm profiles for model C2 along profile lines marked in (B).
Tissue volumes and modeling time comparisons
PD in volumes and normalized median current densities were calculated between block head models and the four smoothed head models (S1, S2, S3 and S10), producing a total of 24 comparisons over the three electrode montages and white matter anisotropy conditions.
Table 2 shows the volumes for each of the ten tissues included in each model. Total volumes of block and smooth models differed by a maximum of around 2%. The largest difference between focus structure volumes was found to be 22%. The solidifying steps involved in constructing smoothed models caused compartments to be differently shaped compared to original T1-weighted images. Solidification steps produced large increases in fat and gray matter compartment volumes (58% and 20% respectively), and decreases in bone and CSF (−16% and −35% respectively). While white matter volume did not change greatly, the shape of this compartment was markedly different after multiple smoothing steps (Figure M3).
Table 2.
Volumes (cm3) of each tissue type within the segmented head model for block, S1, S2, S3 and S10 models. Sums of individual tissue volumes are shown in the last row.
| Structure | Block volume (cm3) |
S1 volume (cm3) |
S2 volume (cm3) |
S3 volume (cm3) |
S10 volume (cm3) |
|---|---|---|---|---|---|
| White matter | 512 | 554 | 544 | 536 | 497 |
| Gray matter | 647 | 777 | 786 | 794 | 833 |
| Eyes | 12 | 12 | 11 | 11 | 10 |
| Air | 68 | 66 | 63 | 62 | 54 |
| Blood | 14 | 12 | 11 | 9 | 3 |
| CSF | 324 | 210 | 210 | 211 | 213 |
| Fat | 218 | 346 | 328 | 315 | 259 |
| Bone | 793 | 665 | 654 | 666 | 708 |
| Muscle | 888 | 865 | 869 | 873 | 900 |
| Skin | 635 | 635 | 628 | 629 | 629 |
| Total | 4111 | 4140 | 4105 | 4106 | 4105 |
Table 3 shows volumes of focus structures as well as percentage differences between smoothed and block models. While overall gray matter volumes were larger in S1 than for the original block model, solidification and meshing for COMSOL steps resulted in focus structures being smaller by 10–20%.
Table 3.
Focus structure volumes for block and S1 model, including percentage differences.
| Structure | Block (cm3) | S1 (cm3) | Difference (%) |
|---|---|---|---|
| ASTG | 7.3 | 6.2 | −15 |
| HIP | 7.7 | 6.9 | −10 |
| IFR | 12.5 | 10.4 | −17 |
| OCC | 41.1 | 32.0 | −22 |
| PRC | 28.7 | 23.9 | −17 |
Computed modeling times were the sum of times required for post-segmentation model processing, meshing and finite element solution and were approximately 200 minutes and 400 minutes for isotropic block and smooth models, respectively. In isotropic models, computed modeling times were 40 minutes for block and 120 minutes for smooth pipelines. Block models were found to require half the time of smooth models to solve for anisotropic cases and a third of the time for isotropic cases.
Median Current Density Comparisons
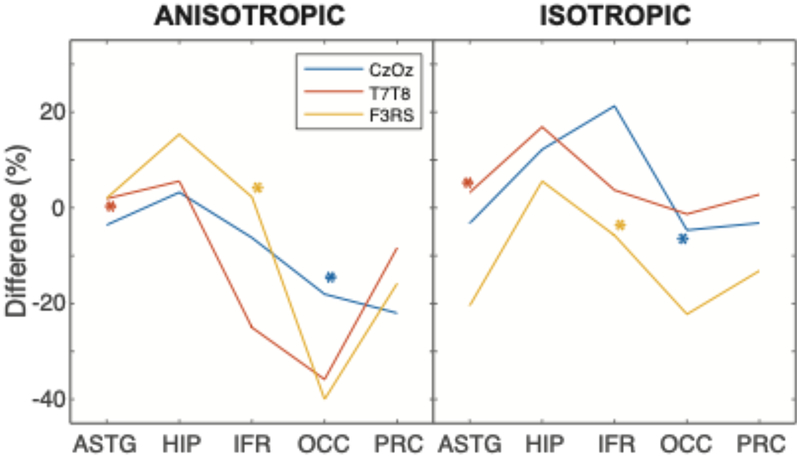
Cross-sectional images showing current density values in a single slice of block and smooth models are shown in Figure 6. Normalized median current density PD values between block and S1 models in cortical structures for the three electrode montages are summarized in Figure 7. PD values in comparisons of anisotropic models were generally larger than for isotropic cases for T7-T8 and F3-RS montages, and smaller than isotropic cases for the Cz-Oz montage. The largest absolute PD values over all three electrode montages and structures were found to be 35.2% for anisotropic and 21.1% for isotropic cases. The corresponding smallest absolute PD values were 0.8% and 1.1% for anisotropic and isotropic cases, respectively. Median current density PD values in structures presumed targeted by each montage were at most around 10% (for the IFR structure with F3-RS).
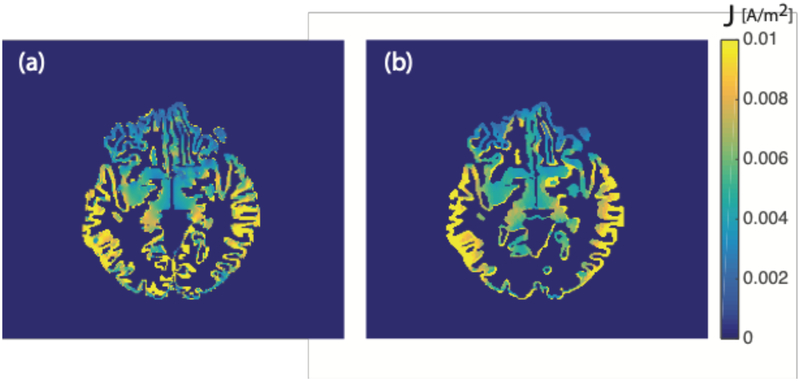
Figure 6.
Axial cross-sections of predicted current density distributions in the cortex. Predicted current densities for T7T8 montage are masked in gray matter structures for isotropic A) block and B) S1 models.
Figure 7.
Normalized median current density percentage difference (PD) values in five focus structures for block and S1 BC-1 models. Negative values indicated that normalized current density values in smooth models were larger than those in block models. Presumed target structures for each montage are indicated with asterisks.
Effects of Additional smoothing
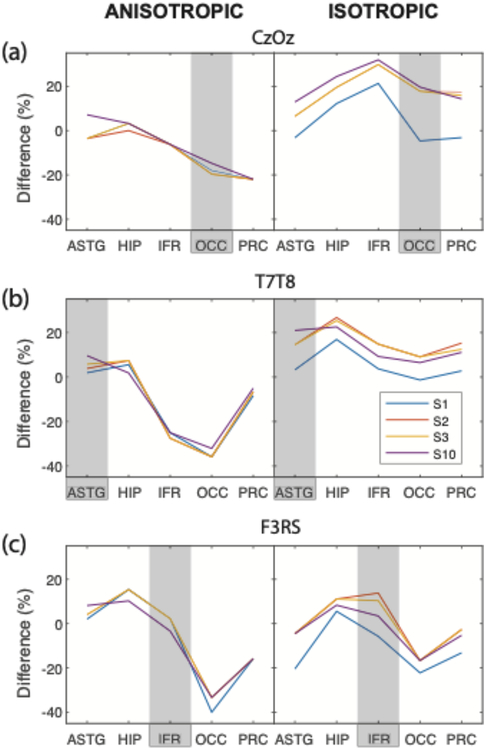
Figure 8 shows current density PD values in focus structures between block models and all smooth models, for each montage. The largest and smallest PD absolute values were observed in S1 models, and were 35.2% and 0.8%, respectively. Models S2 and S3 showed very similar median current density PD values for almost all structures, as expected, and almost always overlapped. There was no overall clear trend between the current density PD values and smoothing level for all electrode montages and tissue anisotropy assignments. In some cases, PD values were smaller in focus structures in more smoothed models than for S1. As also shown in Figure 7, the largest PD values in structures targeted by each montage were less than 6% in isotropic and 18% in anisotropic models.
Figure 8.
Normalized median current density percentage differences (PD) for block and smooth BC-1 (S1, S2, S3, S10) models. Plots show PD values obtained in A) CZ-OZ B) T7-T8 and C) F3-RS electrode montages for (left) anisotropic and (right) isotropic cases. Negative values indicated that normalized current density values computed in smooth models were larger than in block models.
Tangential Electric Fields in Block and Smooth Models
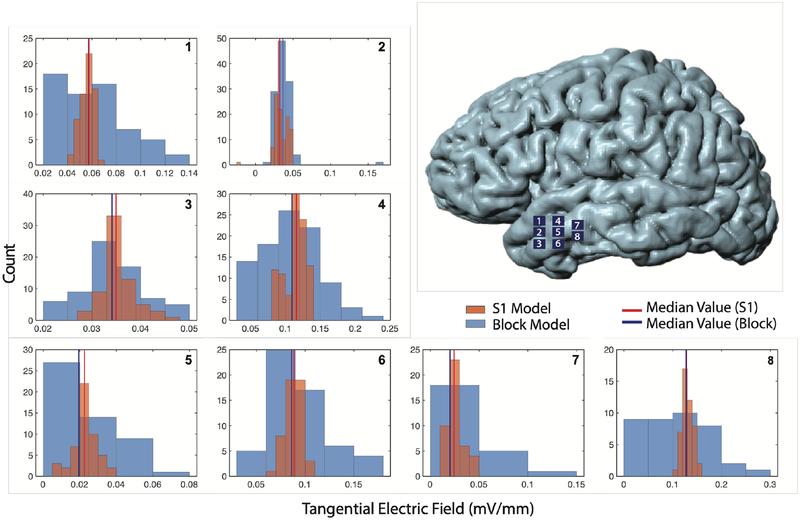
Tangential electrical field distributions were calculated on each of the eight sample patches on the left anterior temporal gyrus for the T7-T8 montage. Histograms of tangential electric field magnitudes are shown in Figure 9. Averaged median tangential electric field magnitudes were found to be 0.064 mV/mm and 0.069 mV/mm (7% different) for block and S1 models, respectively.
Figure 9.
Histograms of tangential electric field (Etan) magnitudes of distributions on the surface of the left anterior temporal gyrus for isotropic block and S1 BC-1 models using the T7-T8 montage. Locations of the eight surface patches are shown on the isosurface model (top right). Plots show Etan magnitude distributions over patches 1–8. Blue lines denote median Etan magnitude values in each patch for the block model while red lines show the same quantity for the S1 BC-1 model.
DISCUSSION
Summary of Findings
In this study, structure volumes, current density and electrical field were calculated to quantify the difference produced by block and smooth pipelines. Major differences between different pipeline results could have been caused by any combination of:
finite element solution differences
boundary conditions
differences in compartment voxellation, or
compartment smoothing and solidification steps
In the sections below, we summarize findings for the different model types in terms of structure shape and volume, current densities and electric fields, first for the cross-platform validation models and then for head models. We assumed that if different pipelines produced differences less than 20% this was an acceptable correspondence.
Cross-Platform Validation Comparisons
The first cross-platform validation step (C1) showed there were no differences between finite element solutions, since differences were less than 0.1%, and both solutions agreed with analytical values. In the second validation model (C2) it was found that mean and median values were at most 2% or 1% respectively different, in the internal sphere ROI. This indicated that while voxellation of the sphere surface produced some differences, they were small. As expected, there were large (up to 70%) differences between current density measures at the sphere boundary. Current density profiles drawn from the anode to cathode (vertical) were asymmetric for the COMSOL BC-2 model, but the same profiles were symmetric in block and COMSOL BC-1 models. COMSOL BC-2 simulations assigned positive current density at the anode and set the cathode to ground voltage, a setting which is frequently used in tES FE studies [7, 14, 16, 36–38, 40, 42, 43, 47, 48, 52, 44]. However, these settings may result in asymmetry, as constant voltage boundary conditions do not necessitate constant normal current density distributions. This observation must be considered carefully in future studies, as it may have been assumed that these settings give the same results as total current or voltage only boundary conditions without needing to specify potential at a separate point. Use of either equal and opposite normal current density (if compensated to give the correct total current), equal and opposite total current, or voltage only boundary conditions should produce results closer to actual experimental conditions. Specification of boundary conditions using total current or fixed voltage boundary conditions is recommended.
In summary, findings from the confirmation models reflected effects of differences between meshes, sphere voxellation and boundary condition specifications, as well as possible registration errors between the two methods.
Head Model Comparisons
A total of 24 comparisons of median current density PD values were investigated for four levels of tissue smoothing (S1, S2, S3, S10), three electrode configurations (Cz-Oz, T7-T8, F3-RS), and two types of white matter (isotropic or anisotropic). Relationships between model construction and solution times, structure volumes, calculated current densities, surface electric fields, and effects of additional smoothing levels are discussed relative to electrode placements and tissue anisotropy for both pipelines in the subsections below.
Overall Model Construction Differences and Times
Because of the need to perform smoothing and mask solidification for successful volume meshing in Simpleware for export to the COMSOL platform, the smooth model pipeline took much longer to solve. Since anisotropic smoothed models took three times as long as matching block versions, while isotropic smoothed models took twice as long, block models may have a distinct advantage if rapid modeling is required.
Smoothing Distortion Effects and Cortical Structure Differences
Overall model volume was preserved after mask solidification and meshing. White matter volumes were also preserved upon smoothing. However, the white matter compartment shape was distorted. Other internal compartments changed volume markedly, with volume increases in fat and gray matter being balanced by decreases in bone and CSF volumes. This indicated that even though the smoothing neighborhood used was minimized, the effect of solidification and smoothing with multiple compartments could produce a very different tissue distribution than represented in original MRI data. There was no distinct relationship between cortical structure size and volumetric changes on processing block models to smooth models. Instead, the complexity of individual cortical structures (e.g., folds and ridges on the surface of the cortex) and tissue prioritization choice was most likely the major contributor to volumetric differences between the modeling pipelines.
Current density Distributions with Different Electrode Montages
While PD values may have been affected by volume changes in target structures (between 10 and 20%), location of structures relative to electrodes was probably the most important determinant of current density PD values. In targets for each montage, median current density PD values for target structures were in the range of ±6% for isotropic and ±18% for anisotropic cases. This indicated that the two pipelines produced similar values for target structures. Comparable observations were obtained for model comparisons between block and additional smoothing levels. These findings suggest that the majority of brain regions surrounding target structures were least affected by meshing choice, most likely due to the higher current densities in brain regions nearby electrode locations.
Effects of Additional Smoothing
The three additional degrees of smoothing (S2, S3 and S10) did not affect changes of normalized median current densities in a predictable manner. For instance, normalized median current density PD values mostly increased from S2 to S10 in isotropic cases for T7-T8 and F3-RS, but decreased in isotropic cases for Cz-Oz. This was most likely because of shape changes produced by each additional smoothing step. Similar current density PD values were observed for S2 and S3 models throughout, as expected, because of the similarities in structure volumes and shapes (Table 2).
Tissue Anisotropy Effects
The anisotropy ratio used here, σl/σt = 10, was large. We included this value to illustrate maximal effects. Results derived from diffusion tensor imaging studies indicate that white matter anisotropy may be modeled more appropriately with anisotropy ratios closer to 3 [13]. Inclusion of white matter anisotropy altered normalized current density PD values for some electrode configurations as shown in Figure 8. Tissue anisotropy reduced PDs in focus structures in T7-T8 and F3-RS montages from ±6% to ±3%. OCC current density PD values were larger for anisotropic cases than isotropic cases for the Cz-Oz montage. This suggests that white matter fiber orientations in and or surrounding OCC contributed to the current flow patterns from Cz to Oz. A similarly large difference was observed for median current density PDs in the PRC for the Cz-Oz montage. The current density PD value was larger in the Cz-Oz anisotropic model than for the Cz-Oz isotropic model. In addition, based on Table 3, OCC and PRC were the largest of the five focus structures. The size factor might also contribute to the largest changes in calculated current density PD between anisotropic and isotropic cases with respect to electrode placements. Therefore, a combination of white matter fiber orientation, the large anisotropy ratio used, the smoothed tissue boundary, structure size and electrode locations affected current density distributions in individual cortical structures and resulted in the 12% differences observed between isotropic and anisotropic cases.
Electric Field Comparisons
Averaged maximum and median local electrical field values on the cortical surface nearby stimulating electrodes calculated for both block and smooth models were within the range of local electric fields observed during TES reported in the literature [3, 63]. For instance, in the study reported by Opitz et al. [3] the median calculated projected electric field along the brain surface near the anode (T7) ranged between 0.059 and 0.098 mV/mm with a maximum value of 0.37 mV/mm. Huang et al. [63] reported a maximum projected electric field of 0.25 mV/mm in the fronto-lateral location for an M1-SO configuration. These reported values were derived from electric potentials measured by surface cortical electrode arrays during TES injections of 1 mA. Averaged tangential electric field measures were around 7% different between block and smoothed models. Averaging therefore reduced the differences between voxellated and smoothed results. Therefore, these comparisons served as a model validation for both pipelines, and a confirmation that either pipeline was suitable to predict TES field quantities, as long as surface measures were averaged.
Result Accuracy
We can only consider differences between the two modeling pipelines here, not absolute accuracy, although we can compare smoothed compartments with source T1 data in volumetric comparisons. Model accuracy determinations can only be evaluated using independent measurements of electric fields and current densities in vivo. This may be possible using (tangential, surface) electric field measurements [3, 63] or measures of internal current density distributions [64–66]. Since conductivities used in models are taken from excised tissue [66], it is also necessary to obtain estimates of in-vivo conductivity values at frequencies typical of stimulation frequencies to perform full validations.
Finally, it is not clear if tissue conductivities may change during tDCS or tACS administration. In particular, it may be the case that properties of tissues immediately under electrodes may change due to presence of wetting electrolytic materials. This could be explored further using sensitivity studies to reconcile model conductivity against gold standard data obtained using cortical arrays or magnetic resonance phase imaging [45, 63, 67].
Further Observations
This study has demonstrated that block-based tetrahedral models provide acceptable results in simulations and that smoothing may not be necessary to obtain good simulation quality. The quadratic element order used here may not be necessary to obtain accurate solutions, particularly at high resolution (voxels smaller than 1 mm3) and linear models may be sufficient. Further study would be necessary to establish this. Differences between meshes may have been responsible for some measure of the differences between results, but this was not rigorously analyzed in this study. Future work may involve consideration of mesh density distribution effects when comparing the two approaches. Use of block-based tetrahedral models, possibly including adjustment of node locations to accommodate tissue features, as in [68–70] may overall improve model formation time, while avoiding leakage effects that may result from usage of hexahedral models [71].
CONCLUSION
Benchmarking tES FE studies is crucial to ensure accurate and consistent predictions of current density distribution in realistic head models of tES. Many factors need to be considered before performing FE tES studies. Care must be taken to ensure boundary conditions are consistent. For instance, assigning normal current density at the anode and set the cathode to ground in a simple geometry may produce asymmetric current density profiles across the anode and cathode. Many tES FE studies in the present literature use commercial platforms requiring subdomain smoothing. However, smoothing steps require additional processing times and may distort original structural information. At 1 mm3 image resolution, FE models constructed from direct conversion of segmented MRI volumes may produce comparable averaged field distributions caused by tES, as demonstrated here. Therefore, modeling pipelines involving direct conversion from imaging voxels to FE models may be desirable to use in tES FE studies.
ACKNOWLEGEMENTS
We gratefully acknowledge the Mareci Laboratory (University of Florida) for providing access for the source images used in constructing models used in this study. Research reported in this publication was supported by the National Institute of Neurological Disorders and Stroke and the National Institute of Mental Health of the National Institutes of Health under Award Numbers R21NS081646 and RF1MH114290 to RJS.
Footnotes
Disclosure: The authors report no conflicts of interest.
REFERENCES
- [1].Laakso I, Tanaka S, Koyama S, De Santis V and Hirata A 2015. Inter-subject Variability in Electric Fields of Motor Cortical tDCS Brain Stimul 8 906–13 [DOI] [PubMed] [Google Scholar]
- [2].Miranda PC, Mekonnen A, Salvador R and Ruffini G 2013. The electric field in the cortex during transcranial current stimulation Neuroimage 70 48–58 [DOI] [PubMed] [Google Scholar]
- [3].Opitz A, Falchier A, Yan CG, Yeagle EM, Linn GS, Megevand P, Thielscher A, Deborah AR, Milham MP, Mehta AD and Schroeder CE 2016. Spatiotemporal structure of intracranial electric fields induced by transcranial electric stimulation in humans and nonhuman primates Scientific Reports 6 31236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Ruffini G, Fox MD, Ripolles O, Miranda PC and Pascual-Leone A 2014. Optimization of multifocal transcranial current stimulation for weighted cortical pattern targeting from realistic modeling of electric fields Neuroimage 89 216–25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Sadleir RJ, Vannorsdall TD, Schretlen DJ and Gordon B 2012. Target optimization in transcranial direct current stimulation Front Psychiatry 3 90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Datta A, Zhou X, Su Y, Parra LC and Bikson M 2013. Validation of finite element model of transcranial electrical stimulation using scalp potentials: implications for clinical dose J Neural Eng 10 036018. [DOI] [PubMed] [Google Scholar]
- [7].Huang Y, Dmochowski JP, Su Y, Datta A, Rorden C and Parra LC 2013. Automated MRI segmentation for individualized modeling of current flow in the human head J Neural Eng 10 066004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Indahlastari A, Chauhan M, Schwartz B and Sadleir RJ 2016. Changing head model extent affects finite element predictions of transcranial direct current stimulation distributions J Neural Eng 13 066006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Parazzini M, Fiocchi S, Rossi E, Paglialonga A and Ravazzani P 2011. Transcranial direct current stimulation: estimation of the electric field and of the current density in an anatomical human head model IEEE Trans Biomed Eng 58 1773–80 [DOI] [PubMed] [Google Scholar]
- [10].Sadleir RJ, Vannorsdall TD, Schretlen DJ and Gordon B 2010. Transcranial direct current stimulation (tDCS) in a realistic head model Neuroimage 51 1310–8 [DOI] [PubMed] [Google Scholar]
- [11].Tuch DS, Wedeen VJ, Dale AM, George JS and Belliveau JW 2001. Conductivity tensor mapping of the human brain using diffusion tensor MRI Proc Natl Acad Sci U S A 98 11697–701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Kwon OI, Sajib SZ, Sersa I, Oh TI, Jeong WC, Kim HJ and Woo EJ 2016. Current Density Imaging During Transcranial Direct Current Stimulation Using DT-MRI and MREIT: Algorithm Development and Numerical Simulations IEEE Trans Biomed Eng 63 168–75 [DOI] [PubMed] [Google Scholar]
- [13].Rullmann M, Anwander A, Dannhauer M, Warfield SK, Duffy FH and Wolters CH 2009. EEG source analysis of epileptiform activity using a 1 mm anisotropic hexahedra finite element head model Neuroimage 44 399–410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Datta A, Baker JM, Bikson M and Fridriksson J 2011. Individualized model predicts brain current flow during transcranial direct-current stimulation treatment in responsive stroke patient Brain Stimulation 4 169–74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Shahid SS, Wen P and Ahfock T 2014. Assessment of electric field distribuion in anisotropic cortical and subcortical regions under the influence of tDCS Bioelectromagnetics 35 41–57 [DOI] [PubMed] [Google Scholar]
- [16].Datta A, Truong D, Minhas P, Parra LC and Bikson M 2012. Inter-Individual Variation during Transcranial Direct Current Stimulation and Normalization of Dose Using MRI-Derived Computational Models Front Psychiatry 3 91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Neuling T, Wagner S, Wolters CH, Zaehle T and Herrmann CS 2012. Finite-Element Model Predicts Current Density Distribution for Clinical Applications of tDCS and tACS Front Psychiatry 3 83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Wagner S, Rampersad SM, Aydin U, Vorwerk J, Oostendorp TF, Neuling T, Herrmann CS, Stegeman DF and Wolters CH 2014. Investigation of tDCS volume conduction effects in a highly realistic head model J Neural Eng 11 1–14 [DOI] [PubMed] [Google Scholar]
- [19].Wagner T, Fregni F, Fecteau S, Grodzinsky A, Zahn M and Pascual-Leone A 2007. Transcranial direct current stimulation: A computer-based human model study NeuroImage 35 1113–24 [DOI] [PubMed] [Google Scholar]
- [20].Holdefer RN, Sadleir R and Russell MJ 2006. Predicted current densities in the brain during transcranial electrical stimulation Clin Neurophysiol 117 1388–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Suh HS, Lee WH and Kim TS 2012. Influence of anisotropic conductivity in the skull and white matter on transcranial direct current stimulation via an anatomically realistic finite element head model Phys Med Biol 57 6961–80 [DOI] [PubMed] [Google Scholar]
- [22].Hyde DE, Dannhauer M, Warfield SK, MacLeod R and Brooks DH. 2016. Evaluation of numerical techniques for solving the current injection problem in biological tissues. Proc. IEEE Int. Symp. Biomed. Imaging pp 876–880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Wolters CH, Anwander A, Tricoche X, Weinstein D, Koch MA and MacLeod RS 2006. Influence of tissue conductivity anisotropy on EEG/MEG field and return current computation in a realistic head model: a simulation and visualization study using high-resolution finite element modeling Neuroimage 30 813–26 [DOI] [PubMed] [Google Scholar]
- [24].Dannhauer M, Lanfer B, Wolters CH and Knosche TR 2011. Modeling of the human skull in EEG source analysis Hum Brain Mapp 32 1383–99 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Vorwerk J, Clerc M, Burger M and Wolters CH 2012. Comparison of boundary element and finite element approaches to the EEG forward problem Biomed Tech (Berl) 57 Suppl 1 795–98 [DOI] [PubMed] [Google Scholar]
- [26].Lau S, Gullmar D, Flemming L, Grayden DB, Cook MJ, Wolters CH and Haueisen J 2016. Skull Defects in Finite Element Head Models for Source Reconstruction from Magnetoencephalography Signals Front Neurosci 10 141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Wagner S, Lucka F, Vorwerk J, Herrmann CS, Nolte G, Burger M and Wolters CH 2016. Using reciprocity for relating the simulation of transcranial current stimulation to the EEG forward problem Neuroimage 140 163–73 [DOI] [PubMed] [Google Scholar]
- [28].Vorwerk J, Engwer C, Pursiainen S and Wolters CH 2017. A Mixed Finite Element Method to Solve the EEG Forward Problem IEEE Trans Med Imaging 36 930–41 [DOI] [PubMed] [Google Scholar]
- [29].Cho JH, Vorwerk J, Wolters CH and Knosche TR 2015. Influence of the head model on EEG and MEG source connectivity analyses Neuroimage 110 60–77 [DOI] [PubMed] [Google Scholar]
- [30].Ziegler E, Chellappa SL, Gaggioni G, Ly JQM, Vandewalle G, Andre E, Geuzaine C and Phillips C 2014. A finite-element reciprocity solution for EEG forward modeling with realistic individual head models Neuroimage 103 542–51 [DOI] [PubMed] [Google Scholar]
- [31].Wolters CH, Anwander A, Tricoche X, Weinstein D, Koch MA, Macleod RS. 2006. Influence of tissue conductivity anisotropy on EEG/MEG field and return current computation in a realistic head model: a simulation and visualization study using high-resolution finite element modeling. NeuroImage. 30 813–26. [DOI] [PubMed] [Google Scholar]
- [32].Vorwerk J, Cho JH, Rampp S, Hamer H, Knosche TR and Wolters CH 2014. A guideline for head volume conductor modeling in EEG and MEG Neuroimage 100 590–607 [DOI] [PubMed] [Google Scholar]
- [33].Fingberg J, Berti G, Hartmann H, Basermann A, Wolters CH, Anwander A, McCarthy A, Woods S. 2003. Bio-numerical simualtions with SimBio. NEC Research and Development. 44 140–5 [Google Scholar]
- [34].MacLeod RS, Weinstein OM, de St Germain JD, Brooks DH, Johnson CR, Parker SG. 2004. SCIRun/BioPSE: Integrated problem solving environment for bioelectric field problems and visualization. Proc. IEEE Int. Symp. on Biomedical Imaging: Nano to Macro pp. 640–643 [Google Scholar]
- [35].Opitz A, Paulus W, Will S, Antunes A and Thielscher A 2015. Determinants of the electric field during transcranial direct current stimulation NeuroImage 109 140–50 [DOI] [PubMed] [Google Scholar]
- [36].Datta A, Bansal V, Diaz J, Patel J, Reato D and Bikson M 2009. Gyri-precise head model of transcranial direct current stimulation: improved spatial focality using a ring electrode versus conventional rectangular pad Brain Stimul 2 201–7, 7 e1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Truong DQ, et al. 2013. Computational Modeling of Transcranial Direct Current Stimulation (tDCS) in Obesity: Impact of Head Fat and Dose Guidelines NeuroImage Clinical 2 759–66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Kessler SK, Minhas P, Woods AJ, Rosen A, Gorman C and Bikson M 2013. Dosage Considerations for Transcranial Direct Current Stimulation in Children: A Computational Modeling Study Plos One 8 1–15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Bai SW, Dokos S, Ho KA and Loo C 2014. A computational modelling study of transcranial direct current stimulation montages used in depression Neuroimage 87 332–44 [DOI] [PubMed] [Google Scholar]
- [40].Shahid S, Wen P and Ahfock T 2013. Numerical investigation of white matter anisotropic conductivity in defining current distribution under tDCS Comput Methods Programs Biomed 109 48–64 [DOI] [PubMed] [Google Scholar]
- [41].Xu J, Healy SM, Truong DQ, Datta A, Bikson M and Potenza MN 2015. A Feasibility Study of Bilateral Anodal Stimulation of the Prefrontal Cortex Using High-Definition Electrodes in Healthy Participants Yale J Biol Med 88 219–25 [PMC free article] [PubMed] [Google Scholar]
- [42].Seibt O, Brunoni AR, Huang Y and Bikson M 2015. The Pursuit of DLPFC: Non-neuronavigated Methods to Target the Left Dorsolateral Pre-frontal Cortex With Symmetric Bicephalic Transcranial Direct Current Stimulation (tDCS) Brain Stimul 8 590–602 [DOI] [PubMed] [Google Scholar]
- [43].Alam M, Truong DQ, Khadka N and Bikson M 2016. Spatial and polarity precision of concentric high-definition transcranial direct current stimulation (HD-tDCS) Phys Med Biol 61 4506–21 [DOI] [PubMed] [Google Scholar]
- [44].Galletta EE, Cancelli A, Cottone C, Simonelli I, Tecchio F, Bikson M and Marangolo P 2015. Use of Computational Modeling to Inform tDCS Electrode Montages for the Promotion of Language Recovery in Post-stroke Aphasia Brain Stimulation 8 1108–15 [DOI] [PubMed] [Google Scholar]
- [45].Santos L, Martinho M, Salvador R, Wenger C, Fernandes SR, Ripolles O, Ruffini G and Miranda PC 2016. Evaluation of the Electric Field in the Brain during Transcranial Direct Current Stimulation: a Sensitivitiy Analysis In: IEEE-EMBC, (Orlando, Florida: IEEE; ) pp 1778–81 [DOI] [PubMed] [Google Scholar]
- [46].Fischer DB, Fried PJ, Ruffini G, Ripolles O, Salvador R, Banus J, Ketchabaw WT, Santarnecchi E, Pascual-Leone A and Fox MD 2017. Multifocal tDCS targeting the resting state motor network increases cortical excitability beyond traditional tDCS targeting unilateral motor cortex Neuroimage 157 34–44 [DOI] [PubMed] [Google Scholar]
- [47].Dmochowski JP, Datta A, Bikson M, Su Y and Parra LC 2011. Optimized multi-electrode stimulation increases focality and intensity at target J Neural Eng 8 046011. [DOI] [PubMed] [Google Scholar]
- [48].Haufe S, Huang Y and Parra LC 2015. A highly detailed FEM volume conductor model based on the ICBM152 average head template for EEG source imaging and TCS targeting Conf Proc IEEE Eng Med Biol Soc 2015 5744–7 [DOI] [PubMed] [Google Scholar]
- [49].Suh HS, Kim SH, Lee WH and Kim T-S 2009. Realistic simulation of transcranial direct current stimulation via 3-D high-resolution finite element analysis: effect of tissue anisotropy In: 2009 Annual International Conference of the IEEE Engineering in Medicine and Biology Society: IEEE; ) pp 638–41 [DOI] [PubMed] [Google Scholar]
- [50].Huang Y and Parra LC 2015. Fully automated whole-head segmentation with improved smoothness and continuity, with theory reviewed PLoS One 10 e0125477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Woods AJ, Antal A, Bikson M, Boggio PS, Brunoni AR, Celnik P, Cohen LG, Fregni F, Herrmann CS, Kappenman ES, Knotkova H, Liebetanz D, Miniussi C, Miranda PC, Paulus W, Priori A, Reato D, Stagg C, Wenderoth N and Nitsche MA 2016. A technical guide to tDCS, and related non-invasive brain stimulation tools Clin Neurophysiol 127 1031–48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Antal A, Bikson M, Datta A, Lafon B, Dechent P, Parra LC and Paulus W 2014. Imaging artifacts induced by electrical stimulation during conventional fMRI of the brain Neuroimage 85 Pt 3 1040–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Pena-Gomez C, Sala-Lonch R, Junque C, Clemente IC, Vidal D, Bargallo N, Falcon C, Valls-Sole J, Pascual-Leone A and Bartres-Faz D 2012. Modulation of large-scale brain networks by transcranial direct current stimulation evidenced by resting-state functional MRI Brain Stimul 5 252–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Turkeltaub PE, Benson J, Hamilton RH, Datta A, Bikson M and Coslett HB 2012. Left lateralizing transcranial direct current stimulation improves reading efficiency Brain Stimul 5 201–7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Spitzer VM and Whitlock DG 1997. National Library of Medicine Atlas of the Visible Human Male: Reverse Engineering of the Human Body (Burlington, MA: Jones & Bartlett Learning; ) [Google Scholar]
- [56].Grimnes S and Martinsen OG 2000. Bioimpedance & Bioelectricity Basics (London, San Diego: Academic Press; ) [Google Scholar]
- [57].Geddes LA and Baker LE 1967. The specific resistance of biological material--a compendium of data for the biomedical engineer and physiologist Med Biol Eng 5 271–93 [DOI] [PubMed] [Google Scholar]
- [58].Akhtari M, Bryant HC, Mamelak AN, Flynn ER, Heller L, Shih JJ, Mandelkern M, Matlachov A, Ranken DM, Best ED, DiMauro MA, Lee RR and Sutherling WW 2002. Conductivities of three-layer live human skull Brain Topogr 14 151–67 [DOI] [PubMed] [Google Scholar]
- [59].Baumann SB, Wozny DR, Kelly SK and Meno FM 1997. The electrical conductivity of human cerebrospinal fluid at body temperature IEEE Trans Biomed Eng 44 220–3 [DOI] [PubMed] [Google Scholar]
- [60].Gabriel C, Gabriel S and Corthout E 1996. The dielectric properties of biological tissues: I. Literature survey Phys Med Biol 41 2231–49 [DOI] [PubMed] [Google Scholar]
- [61].Ashburner J and Friston KJ 2005. Unified Segmentation NeuroImage 26 839–51 [DOI] [PubMed] [Google Scholar]
- [62].Davies AJ 1980. The finite element method: a first approach (New York: Oxford University Press; ) e18834 [Google Scholar]
- [63].Huang Y, Liu AA, Lafon B, Friedman D, Dayan M, Wang X, Bikson M, Doyle WK, Devinsky O and Parra LC 2017. Measurements and models of electric fields in the in vivo human brain during transcranial electric stimulation Elife 6 e35178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Jog MV, Smith RX, Jann K, Dunn W, Lafon B, Truong D, Wu A, Parra LC, Bikson M and Wang DJJ 2016. In-vivo imaging of magnetic fields induced by transcranial direct current stimulation (tDCS) in human brain using MRI Scientific Reports 6 34385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Kasinadhuni AK, Indahlastari A, Chauhan M, Schär M, Mareci TH and Sadleir RJ 2017. Imaging of Current Flow in the Human Head During Transcranial Electrical therapy Brain Stimulation 10 764–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [66].Chauhan M, Indahlastari A, Kasinadhuni AK, Schär M, Mareci TH and Sadleir RJ 2018. Low-Frequency Conductivity Tensor Imaging of the Human Head in vivo using DT-MREIT: First Study IEEE Transactions on Medical Imaging 37 966–76 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Parazzini M, Fiocchi S, Rossi E, Paglialonga A and Ravazzani P 2011. Transcranial direct current stimulation: estimation of the electric field and of the current density in an anatomical human head model IEEE Transactions on Biomedical Engineering 58 1773–80 [DOI] [PubMed] [Google Scholar]
- [68].Camacho DLA, Hopper RH, Lin GM and Myers BS 1997. An improved method for finite element mesh generation of geometrically complex structures with application to the skullbase. Journal of Biomechanics 30 1067–70 [DOI] [PubMed] [Google Scholar]
- [69].Wolters CH, Anwander A, Berti G and Hartmann U 2007. Geometry-adapted hexahedral meshes improve accuracy of finite-element-method-based EEG source analysis IEEE Transactions on Biomedical Engineering 54 1446–53 [DOI] [PubMed] [Google Scholar]
- [70].Aydin U, Vorwerk J, Küpper P, Heers M, Kugel H, Galka A, Hamid L, Wellmer J, Kellinghaus C, Rampp S and Wolters CH 2014. Combining EEG and MEG for the reconstruction of epileptic activity using a calibrated realistic volume conductor model PLoS ONE 9 e93154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Engwer C, Vorwerk J, Ludewic J and Wolters CH 2017. A discontinuous galerkin method to solve the EEG forward problem using the subtraction approach SIAM Journal of Scientific Computing 39 B138–B64 [Google Scholar]