Dynamic nonlinearities enable direction opponency in Drosophila elementary motion detectors

Abstract

Direction-selective neurons respond to visual motion in a preferred direction. They are direction-opponent if they are also inhibited by motion in the opposite direction. In flies and vertebrates, direction opponency has been observed in second-order direction-selective neurons, which achieve this opponency by subtracting signals from first-order direction-selective cells with opposite directional tunings. Here, we report direction opponency in Drosophila that emerges in first-order direction-selective neurons, the elementary motion detectors T4 and T5. This opponency persists when synaptic output from these cells is blocked, suggesting that it arises from feedforward, not feedback, computations. These observations exclude a broad class of linear-nonlinear models that have been proposed to describe direction-selective computations. However, they are consistent with models that include dynamic nonlinearities. Simulations of opponent models suggest that direction opponency in first-order motion detectors improves motion discriminability by suppressing noise generated by the local structure of natural scenes.

Introduction

Stimulus opponency is an essential feature of many sensory neurons and behaviors. An opponent neuron can encode both positive and negative values of a given stimulus feature. In visual circuits, cells are direction-selective (DS) if they respond differently to stimuli moving in different directions. The direction yielding the largest response is termed the preferred direction (PD). Cells are direction-opponent (DO) if they are also inhibited by stimuli moving in the opposite direction, termed the null direction (ND). Opponency often occurs in second-order, wide-field DS neurons that receive inputs from upstream, first-order DS cells^1,2.

In primate cortex, direction opponency is broadly observed in medial temporal area (MT), where cells integrate small-field motion signals from cortical area V1^1,3,4. In fly motion vision pathways, DO signals are produced by the lobula plate tangential horizontal system (HS) and vertical system (VS) cells^2,5,6. These cells combine motion information over broad portions of the visual field by integrating local motion signals from the upstream first-order DS neurons T4 and T5^7,8. Circuit dissections have shown that T4 and T5 provide tangential cells with DS excitatory input and with indirect DS inhibitory input mediated by inhibitory interneurons⁶ (Fig. 1a). In this study, we applied a protocol that combines PD and ND stimuli to show that direction opponency can arise in the T4 and T5 neurons themselves. Their opponency is tuned to both stimulus direction and speed, and is not strongly influenced by silencing their synaptic output. This suggests that opponency in T4 and T5 arises de novo and does not result from lateral inhibition between these first-order DS cells with opposite direction preferences.

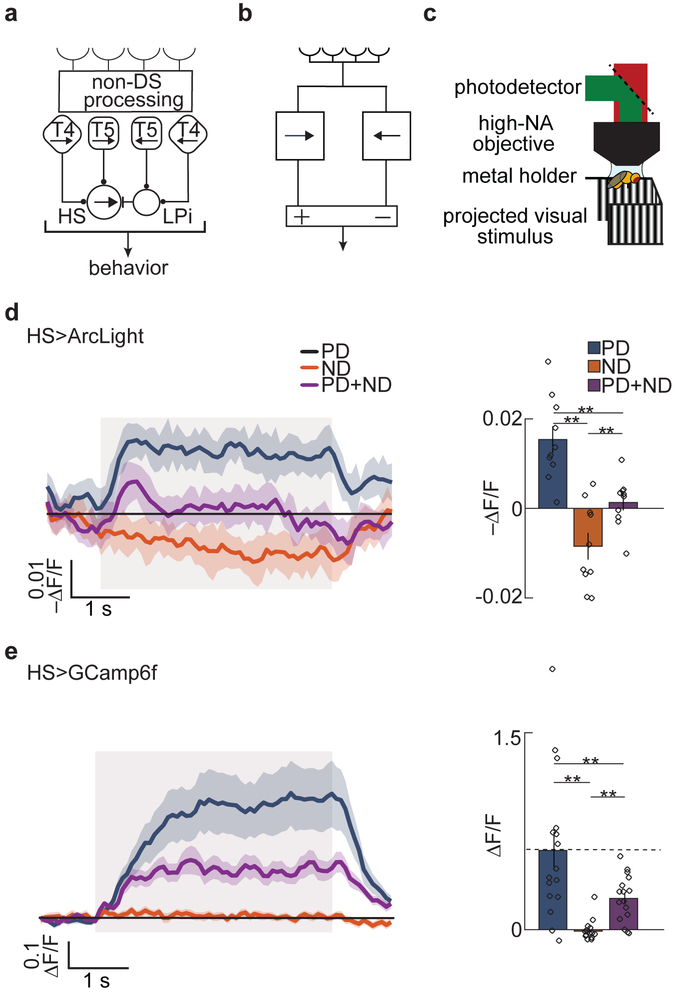
Fig 1. Measurements of opponency and linear-nonlinear models for motion detection.

a) Schematic of first- and second-order DS cells in the fly visual system. HS neurons become opponent by subtracting signals from the first-order DS cells, T4 and T5, with opposite preferred directions. This subtraction is mediated by inhibitory LPi neurons.

b) Schematic of a generic DO model.

c) Schematic of the two-photon microscope set up and panoramic visual display.

d) Fluorescent intensity trace (left) and mean intensity over the stimulus presentation time. (right) of HS neurons expressing the voltage indicator Arclight in response to PD (blue), ND (orange), and PD + ND (purple) sinusoidal gratings. Throughout, bar graphs show mean ± SEM. Shaded region indicates stimulus duration. (** p < 0.01, by a paired two-sided Wilcoxon signed-rank test; p_PD,ND = 0.0020, p_PD,PD+ND = 0.0039, p_ND,PD+ND = 0.0098; n = 10 flies)

e) Fluorescent intensity trace (left) and mean intensity over the stimulus presentation time (right) of HS neurons expressing the calcium indicator GCaMP6f in response to PD (blue), ND (orange), and PD + ND (purple) sinusoidal gratings. Shaded region indicates stimulus duration. (** p < 0.01, by a paired two-sided Wilcoxon signed-rank test; p_PD,ND = 0.0013, p_PD,PD+ND = 0.0013, p_ND,PD+ND = 0.0027; n = 16 flies)

(See also Figure S1 for intuition about opponency and for behavioral results.)

We next addressed what models can account for the opponency in first-order direction-selective (T4 and T5) neurons. Classical models such as the Hassenstein-Reichardt correlator (HRC) model⁹ and the motion energy model¹⁰ (Supp. Fig. 1) account for the opponent properties observed in second-order neurons by subtracting two oppositely-tuned DS signals (Fig. 1b), which could represent the upstream T4 and T5 cells. In these models, the key to opponency is the subtraction step. However, if opponency could only arise through the subtraction of upstream DS inputs, then T4 and T5 could not be opponent since they are thought to be the most peripheral DS neurons in the fly’s eye. These subtractive models therefore do not account for DO responses in T4 and T5 neurons.

Studies of membrane potential in both T4 and T5 neurons have reported that the voltage is approximately equal to a linear transformation of the stimulus contrast^11,12. To many, this has suggested that DS signals in T4 and T5 neurons could be accounted for by a linear filtering step followed by a static nonlinearity^11-13. Similar models have been proposed for mammalian retina in DS starburst amacrine cells¹⁴. Here, we show analytically that opponency is inconsistent with a wide class of linear-nonlinear (LN) models, but instead could be explained by models that include multiplicative interactions, dynamic gain, or divisive nonlinearities.

Opponency can make neurons more selective for specific visual cues, like wide-field motion patterns⁶, and may permit perception of transparent motion⁴. However, the potential computational benefits of opponency remain less well-understood. To investigate this, we presented naturalistic inputs to simple opponent models. These simulations suggest that opponency in the earliest stages of motion detection can cancel out noise in the DS signal that is induced by the statistical structure of natural scenes. Thus, direction opponency in first-order DS neurons may improve the fidelity of motion coding in local motion detectors and in downstream circuits that receive their signals.

Results

Direction-selectivity is often assessed by measuring responses to drifting sinusoidal gratings. In classical direction opponency, neurons depolarize in response to gratings moving in the PD and hyperpolarize in response to gratings moving in the ND^9,10. However, in cells with low baseline activity, such as a low spontaneous firing rate or low basal intracellular calcium concentrations, it may not be possible for ND stimuli to reduce activity further, thereby masking inhibition by ND motion. In such cases, we might still observe opponency by adding ND motion to a stimulus that increases the activity of the system, such as a PD motion stimulus (Supp. Fig. 1)^1,4. When we add PD and ND contrast gratings, the result is a composite stimulus called a counterphase grating (Supp. Video 1). If the response to a counterphase grating is smaller than the response to a PD grating alone, then ND motion has suppressed the response, and the system is DO. This protocol offers a general definition of opponency, since it cannot be masked by low baseline activity rates.

Direction opponency is observable using a calcium indicator

We first applied this protocol to characterize opponency in second-order DS neurons, using the voltage indicator Arclight¹⁵ expressed in the HS neurons; its fluorescence indicates the cell’s membrane potential. We used in vivo two-photon microscopy to measure the fluorescence while we presented the fly with panoramic visual motion stimuli (Fig. 1c)¹⁶. Consistent with previous measurements^2,5, HS neurons depolarized to PD gratings and hyperpolarized to ND gratings (Fig. 1d). Moreover, when flies were presented with both PD and ND gratings summed together, HS neurons responded minimally, with only small transients at stimulus onset and offset. Thus, ND motion strongly suppressed the PD responses in HS neuron membrane potential. In behavior, flies rotated in the direction of visual motion, and did not rotate in response to counterphase gratings, so their rotational responses were also opponent (Supp. Fig. 1).

To characterize opponency in calcium signals in HS neurons, we expressed the calcium indicator GCaMP6f¹⁷. Strong calcium signals were elicited by PD sinusoidal gratings, but there was no decrease relative to the baseline calcium signal elicited by ND gratings (Fig. 1e). Nonetheless, opponency in HS neurons resulted in a suppression in the response when ND sinusoidal gratings were added to the PD gratings. Thus, regardless of the origin of rectification in the calcium signal (Ca²⁺ dynamics or indicator rectification), this assay allows us to detect direction opponency when the responses are non-negative^1,3,4.

First-order direction-selective cells are direction-opponent

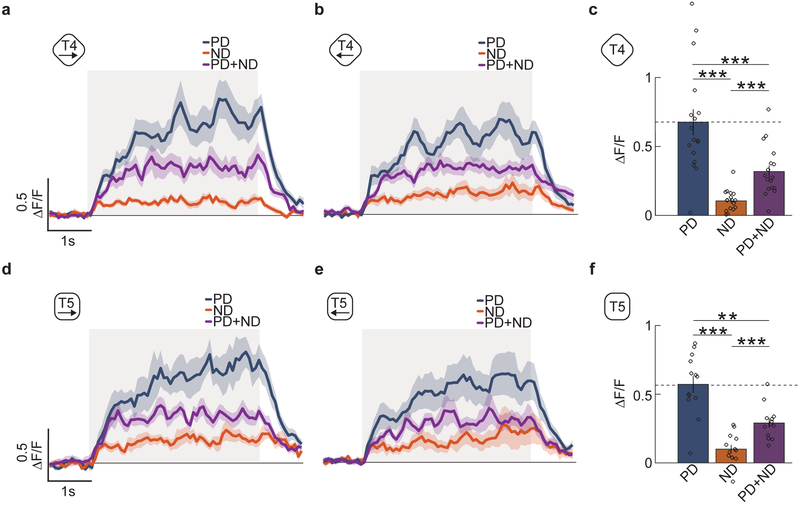
In T4 and T5 cells, calcium indicators show positive responses to PD motion and do not drop below baseline to ND motion^7,13. There are two populations of T4 and T5 neurons that detect motion in the horizontal plane: those whose PD is front-to-back, and those whose PD is back-to-front. We confirmed that all four of these cell types responded positively to PD motion and very little to ND motion (Fig. 2abde). However, when we presented the counterphase grating, all four cell types reduced their responses by about one-half compared to motion in the PD alone. We quantified this reduction by averaging the responses in T4 and T5 cells over the stimulus presentation time (Fig. 2cf). The reduced responses in the presence of ND stimuli mean that both T4 and T5 exhibit direction opponency. Though the mean calcium signals measured in T4 and T5 neurons resemble those measured in HS cells (Figs. 1-2), this does not imply that T4 and T5 must hyperpolarize in response to ND motion.

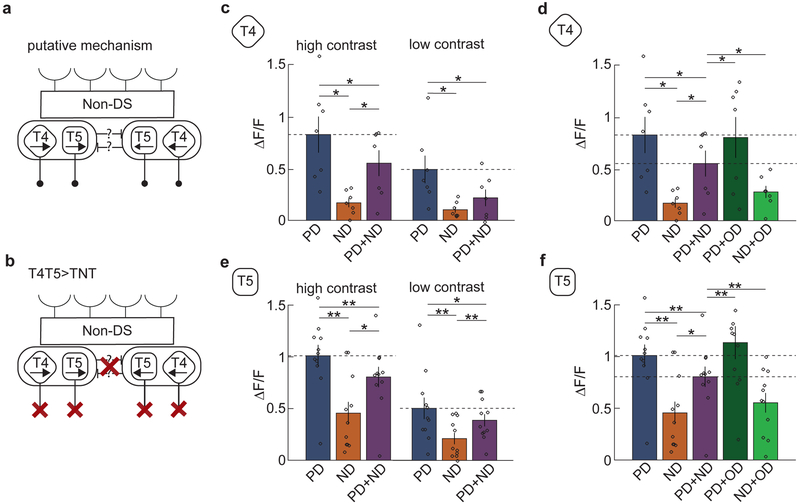
Fig 2. The first-order direction-selective neurons T4 and T5 exhibit opponent responses.

a) Average time trace of the response of T4 axon terminals in lobula plate layer 1 to PD, ND and PD+ND stimuli. These are front-to-back, (blue line), back-to-front (orange line), and the combined (purple line) sinusoidal gratings with wavelength 45° and temporal frequency of 1 Hz. Shaded region indicates stimulus duration. (n = 17 flies)

b) Average time trace of the response of T4 axon terminals in lobula plate layer 2 to PD (blue line), ND (orange line) and PD+ND (purple line) stimuli. Shaded region indicates stimulus duration. (n = 13 flies)

c) The responses of T4 in both layers are averaged and their responses are averaged over time to generate a single mean response over flies. (** p < 0.01, *** p < 0.001, by a paired two-sided Wilcoxon signed-rank test; p_PD,ND = 0.0003, p_PD,PD+ND = 0.0004, p_ND,PD+ND = 0.0003; n = 17 flies)

(d-f) As in (a-c) but for T5 cells. (** p < 0.01, *** p < 0.001, by a paired two-sided Wilcoxon signed-rank test; p_PD,ND = 0.0007, p_PD,PD+ND = 0.0024, p_ND,PD+ND = 0.0005; n = 13 flies)

Opponency persists under changes of contrast and stimulus type

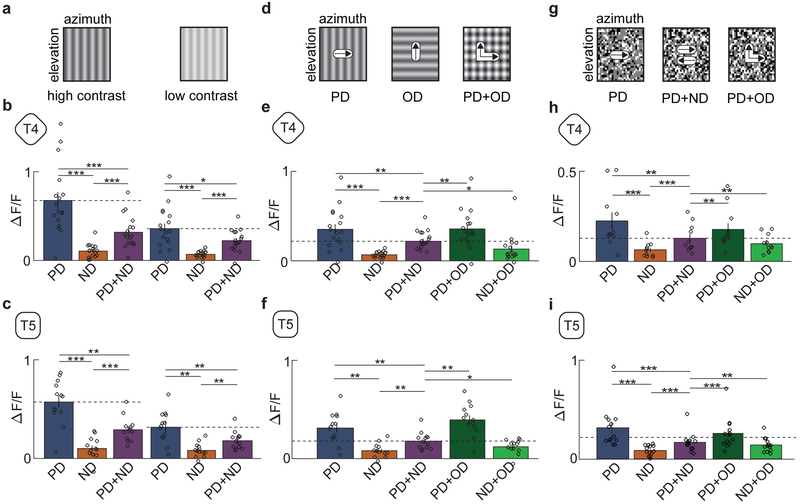
Because the observed direction opponency in T4 and T5 cells was unexpected, we conducted a series of control experiments. We first noted that the contrast of the counterphase grating is double that of the individual sinusoidal gratings, so the suppression could have been a result of some saturation effect of the neurons in the visual pathway. To test this, we lowered the contrast of the PD and ND gratings by a factor of 2, from 0.5 to 0.25 (Fig. 3a). Even with the reduction in contrast, T4 and T5 neurons continued to exhibit the same degree of suppression when ND gratings were added (Fig. 3b,c), suggesting that the observed opponency was not generated by saturation.

Fig 3. Opponency persists under changes of contrast and stimulus type.

a) Intensity plots of a sinusoidal grating at high and low contrast (contrast 0.5 and 0.25).

b) Average responses of T4 to high- (left) and low-contrast (right) sinusoidal gratings. (* p < 0.05, ** p < 0.01, *** p < 0.001, by a paired two-sided Wilcoxon signed-rank test; for high-contrast (left) p-values refer to Fig 2. caption; for low-contrast (right) p_PD,ND = 0.0003, p_PD,PD+ND = 0.0352, p_ND,PD+ND = 0.0004; n = 17 flies)

c) Average responses of T5 to high- (left) and low-contrast (right) sinusoidal gratings. (* p < 0.05, ** p < 0.01, *** p < 0.001, by a paired two-sided Wilcoxon signed-rank test, for high-contrast (left) refer to Fig 2. caption; for low-contrast (right) p_PD,ND = 0.0007, p_PD,PD+ND = 0.0024, p_ND,PD+ND = 0.0005; n = 13 flies)

d) Intensity plots of rightwards and upwards moving sinusoidal gratings and the two combined. The composite stimulus consists of sinusoidal gratings moving in the PD and in the orthogonal direction (OD).

e) Average responses of T4 to stimuli composed of gratings in the PD, ND, PD+ND, PD+OD, and ND+OD. (* p < 0.05, ** p < 0.01, *** p < 0.001, by a paired two-sided Wilcoxon signed-rank test; p_OD+PD,PD+ND = 0.0019, p_OD+ND,PD+ND = 0.0148; n = 17 flies)

f) Average responses of T5 to stimuli composed of gratings in the PD, ND, PD+ND, PD+OD, and ND+OD. (* p < 0.05, ** p < 0.01, *** p < 0.001, by a paired two-sided Wilcoxon signed-rank test; p_OD+PD,PD+ND = 0.0012, p_OD+ND,PD+ND = 0.0215; n = 13 flies)

g) Random dot stimulus made of 5°×5° white and black dots moving in one direction (left panel). The stimulus was combined with one moving in the opposing direction to produce a denser stimulus with containing dots moving in both direction (middle panel). A second composite stimulus was generated by adding a second dot pattern moving in an OD (right panel).

h) Average responses of T4 to dots moving in the PD, ND, PD+ND, PD+OD, and ND+OD. (* p < 0.05, ** p < 0.01, *** p < 0.001, by a paired two-sided Wilcoxon signed-rank test; p_PD,ND = 0.0019, p_PD,PD+ND = 0.0020, p_ND,PD+ND = 0.0010, p_OD+PD,PD+ND = 0.0048, p_OD+ND,PD+ND = 0.010; n = 11 flies)

i) Average responses of T5 to dots moving in the PD, ND, PD+ND, PD+OD, and ND+OD. (* p < 0.05, ** p < 0.01, *** p < 0.001, by a paired two-sided Wilcoxon signed-rank test; p_PD,ND = 0.0007, p_PD,PD+ND = 0.0010, p_ND,PD+ND = 0.0002, p_OD+PD,PD+ND = 0.0010, p_OD+ND,PD+ND = 0.033; n = 13 flies)

(See also Figure S2 for a comparison of the contrast distributions of PD, PD+ND, and PD+OD.)

We next tested whether the measured suppression was DS. We generated stimuli composed of the PD grating and separate gratings moving in an orthogonal direction, either up or down (Fig. 3d). These stimuli, whose contrast distribution is identical to the PD+ND composite stimuli (Supp. Fig. 2), did not suppress the PD response amplitude. Thus, the suppression of the PD responses in both T4 and T5 occurred specifically when the added stimulus was in the ND (Fig. 3e,f). This is further evidence that the opponency does not arise through a contrast-dependent effect (see Methods).

Finally, we tested whether the observed suppression was related to the single spatial and temporal frequencies of sinusoidal gratings. We presented stimuli consisting of random black and white dots moving in the PD, in the ND, or summed together (Fig. 3g). This is a broad-band stimulus, containing many spatial and temporal frequencies. Adding ND motion reduced the response to PD motion by about one-half in both T4 and T5 (Fig. 3h,i), while the addition of dots moving orthogonally did not show the same suppression. Therefore, the observed direction opponency is not specific to sinusoid grating stimuli.

Opponent suppression has tuning similar to the preferred direction response

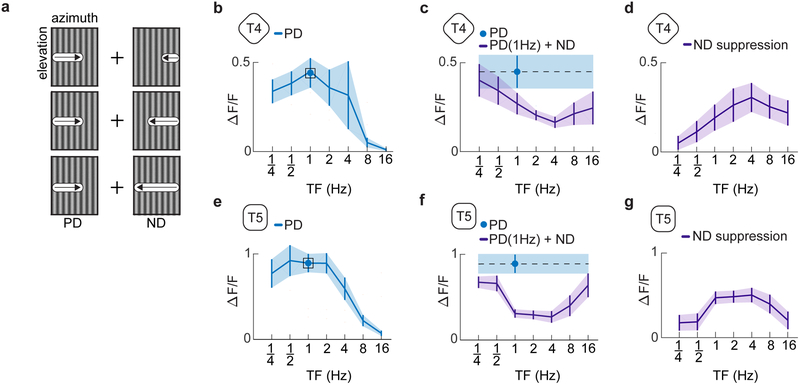
We then measured whether the suppression was tuned to specific temporal frequencies. We presented a composite stimulus in which we fixed the frequency of the PD sinusoid grating at 1Hz but varied the frequency of the ND sinusoid from .25 to 16 Hz (Fig. 4a). With these stimuli, we found that the degree of suppression varied with the frequency of the ND grating (Fig. 4b-g) and peaked at frequencies just above the 1 Hz peak of the PD component alone (Fig. 4d,g). Previous studies using correlated and uncorrelated stochastic stimuli showed little evidence of opponent responses¹⁶, but slowing the timescale of those stimuli revealed stronger ND modulation (Supp. Fig. 3). The responses to slow timescale correlations are qualitatively consistent with the opponent responses to sinusoids reported here.

Fig 4. Temporal tuning of opponent suppression.

a) Intensity plots of the two individual sinusoidal components of the composite stimuli tested. Sinusoidal gratings of differing temporal frequencies moving in the ND were added to a base sinusoid moving in the PD with a temporal frequency of 1 Hz.

b) The temporal frequency tuning curve of T4 cells in response to PD motion.

c) Average response of T4 cells to a 1 Hz sine wave moving in the PD (blue). The response of T4 cells to a stimulus composed of a 1 Hz sinusoid moving in the PD and sinusoid moving in the ND with varying temporal frequency (purple). Plots show mean ± SEM.

d) Suppressive effect of the added ND sinusoid equal to the bare PD sinusoidal response minus the response to the summed gratings at each frequency. Plots show mean ± SEM. (n = 12 flies for panels (b-d))

e-g) As in (b-d) but for T5. (n = 6 flies)

(See also Figure S3 for null direction suppression with other stimuli.)

Opponency in T4 and T5 does not depend on their chemical synaptic transmission

The opponency we observed could be explained by an antagonistic interaction between the populations of T4 and T5 neurons tuned to front-to-back motion and back-to-front motion (Fig. 5a). To investigate this, we expressed tetanus toxin, which blocks chemical synaptic transmission¹⁸, in T4 and T5 cells (Fig. 5b). The silencing was effective, since it suppressed optomotor turning responses in behaving flies (Supp. Fig. 4)^7,16. Nevertheless, the suppression of the response when the ND stimulus was added was similar to that observed in the wild-type experiments. This demonstrates that the chemical synaptic outputs of T4 and T5 are not necessary for opponency (Fig. 5cdef). Thus, it is likely that the opponency in T4 and T5 arises from a feedforward process.

Fig 5. T4 and T5 cells with silenced synapses continue to show opponency.

a) Suggested putative circuit for T4 and T5 feedback onto T4 and T5, which could generate opponency.

b) Schematic of T4 and T5 chemical synaptic output suppressed by expression of tetanus toxin (TNT).

c) Average responses of T4 cells expressing TNT to PD (blue), ND (orange), and PD+ND (purple) sinusoidal gratings at high and low contrast. The addition of ND stimuli continued to suppress the response. (* p < 0.05, ** p < 0.01, by a paired two-sided Wilcoxon signed-rank test; at high contrast, p_PD,ND = 0.0156, p_PD,PD+ND = 0.0313, p_ND,PD+ND = 0.0156; at low contrast, p_PD,ND = 0.0156, p_PD,PD+ND = 0.0156, p_ND,PD+ND = 0.2188; n = 7 flies)

d) Average responses of T4 cells expressing TNT to composite stimuli moving in the PD, ND, PD+ND, PD+OD, and ND+OD. (* p < 0.05, ** p < 0.01, by a paired two-sided Wilcoxon signed-rank test; p_OD+PD,PD+ND = 0.0313, p_OD+ND,PD+ND = 0.0156; n = 7 flies)

(e-f) As in (c) and (d) but with T5 cells. (At high contrast, p_PD,ND = 0.0010, p_PD,PD+ND = 0.0020, p_ND,PD+ND = 0.0186, p_OD+PD,PD+ND = 0.0049, p_OD+ND,PD+ND = 0.0020; at low contrast, p_PD,ND = 0.001, p_PD,PD+ND = 0.042, p_ND,PD+ND = 0.0068, n = 11 flies in both panels) Note in (f) that a single outlying point of value 2.3 is not shown in the PD+OD condition.

(See also Figure S4 for behavioral results validating TNT expression.)

Direction opponency strongly constrains LN models of direction-selectivity

So far, the results show that T4 and T5 are direction-opponent (Fig. 6a), in addition to being direction-selective. What model(s) could account for this? We began by investigating LN models for direction-selectivity, which have been proposed for T4 and T5^11-13. Supplementary Note 1 shows an analytical proof that LN models with expansive nonlinearities cannot generate DO signals in response to summed sinusoidal gratings. This result is independent of the choice of linear filter and expansive nonlinearity. Expansive nonlinearities, which are convex and non-decreasing, are commonly used in models describing DS computations. Nonlinearities in this class of functions include the quadratic nonlinearity used in the motion energy model, as well as the half-quadratic, half-wave rectified, exponential, and soft rectified nonlinearities^13,19-22 (Supp. Fig. 5).

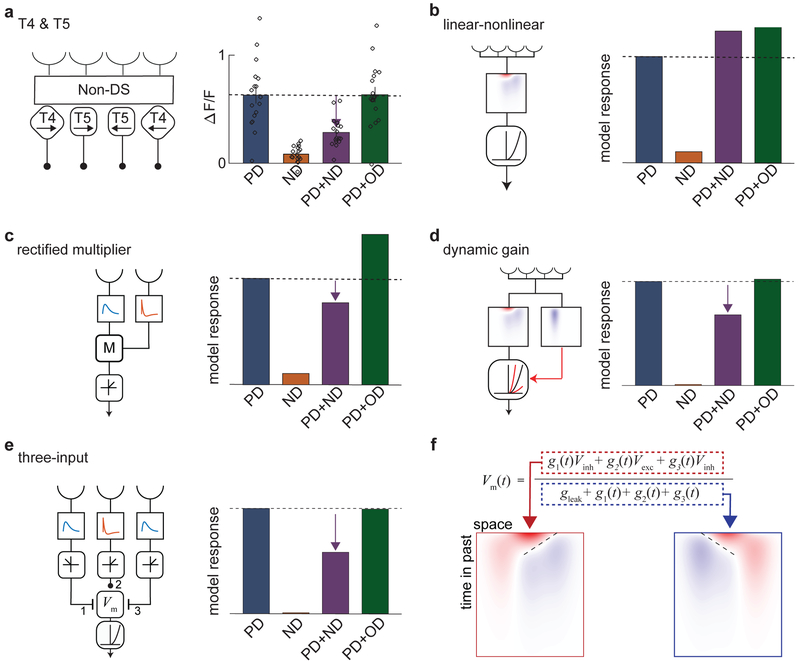
Fig 6. Feedforward models can produce direction-opponent responses.

a) Schematic of T4 and T5 (left), and mean responses of T4 and T5 (right) to sinusoidal gratings moving in the PD (blue), ND (orange), PD+ND (purple), and PD+OD (green). (n = 17 flies)

b) Schematic of linear-nonlinear (LN) model with specified spatiotemporal filter and an expansive nonlinearity. Regardless of the specific choice of filter or expansive nonlinearity, such LN models cannot generate DO responses to sinusoidal gratings (see Supp. Notes 1 and 2).

c) A two-input multiplicative model with rectified output (rectified HRC half-correlator) in which one temporal filter is the derivative of the other. This model is opponent, but shows stronger PD+OD enhancement than T4 and T5. (See Methods for details on this and subsequent models, as well as Supp. Note 3.)

d) A dynamic gain model in which a second linear filter controls the gain of a half-quadratic nonlinearity acting on the output of an oriented linear filter. This model shows opponency with only weak PD+OD enhancement.

e) Three-input model with a center ON excitatory input and flanking delayed ON and OFF inhibitory inputs. The voltage-to-calcium transformation is modeled as a half-quadratic. This model shows strong opponency and little change with the addition of OD stimuli.

f) The equation for membrane potential used in the three-input model shown in (e). The composite linear receptive fields of the numerator (outlined in red) and denominator (outlined in blue) have opposite directional tunings.

(See also Figure S5 and S6 for more details on the models.)

This incompatibility of LN models remains when we consider the calcium indicator. We modeled the nonlinearity of the calcium indicator as a second LN transformation in series with the first. We treated the indicator as a low-pass linear filter of calcium concentration followed by a convex nonlinearity²¹. This system is described by an LNLN model¹³, which also cannot generate opponent signals with the sinusoidal inputs used here (Supp. Note 2). These two derivations imply that if a system produces DO calcium signals in response to sinusoidal gratings, its responses cannot be accounted for by LN models with expansive nonlinearities (Fig. 6b).

Previous studies of calcium indicators in T4 and T5 neurons have reported both PD enhancement and ND suppression relative to purely linear transformations of the stimulus contrast^13,23,24. These properties are not equivalent to opponency and do not provide a similar constraint on models of the DS computation. An LN model with a convex nonlinearity, for example, can generate both PD enhancement and ND suppression, yet is not DO (Supp. Fig. 5).

Several models can account for the observed opponent properties of T4 and T5

Since LN models with convex nonlinearities cannot account for the observed DO signals, we looked for feedforward models that could. In principle, an LN model with a saturating nonlinearity could generate opponent responses, but it is difficult to design one that is opponent at multiple contrasts, since changing the contrast changes the degree of saturation (Supp. Fig. 5). Moreover, the T4 and T5 responses to the sinusoidal gratings used here do not appear to be near saturation, since high-contrast moving edges generate larger peak responses (Supp. Fig. 5).

A single multiplicative interaction between two spatially-separated inputs, equal to one multiplier of the HRC model, is perfectly DO for all stimuli if one input filter is the temporal derivative of the other (Fig. 6c, Supp. Note 3). This property may be understood by supposing that the delay line filter is monolobed and its partner is biphasic, with an initial positive and subsequent negative lobe (Supp. Fig. 6). In this case, the positive lobe precedes the monolobed filter, while the negative lobe is delayed relative to the monolobed filter. This single multiplier can therefore be viewed as the difference of two multipliers with opposite direction tunings. Opponency is still present even if the response is half-wave rectified after the multiplication (Fig. 6c).

Rather than using an LN model with a static nonlinearity, one can construct a model consisting of a linear filter followed by a dynamic nonlinearity. In this model, the gain changes dynamically, since it depends on the stimulus via a second, separate linear filter (Fig. 6d, see Methods). It is plausible that such gain changes could result from metabotropic GABA_B receptors that modulate calcium conductances²⁵. This adaptive gain model can generate DO signals consistent with those measured in T4 and T5 for a broad range of parameters (Fig. 6d, Supp. Fig. 6). Furthermore, mean time traces of this model’s responses to PD, ND, and PD+ND sinusoids are similar to responses measured in T4 and T5 (Supp. Fig. 6).

We also considered an anatomically-inspired three-input model based upon the spatial configuration, timing, and polarity of known synaptic inputs to T4 (Fig. 6e, Supp. Fig. 6, see Methods)^26,27. In this model, three neurons reported visual contrast at three points in space and acted as synaptic inputs to the cell. The two flanking inputs responded to stimuli with opposite polarities. Moreover, the flanking inputs were both inhibitory and their responses were delayed relative to the center input. The effects of the synaptic inputs on postsynaptic membrane potential were modeled by changes in the conductances of excitatory and inhibitory currents in the model cell. This model generates robust DO responses consistent with those measured in T4 and T5 neurons (Fig. 6e, Supp. Fig. 6), even when its parameters are varied over several orders of magnitude (Supp. Fig. 6).

To understand how this model generates DO responses, one may consider how the synaptic inputs affect the membrane potential. Following previous work^11,28, we approximated the membrane potential as the ratio of synaptic driving currents over the total conductance of the cell (Fig. 6f). Since each synaptic input has its own receptive field, we can construct a composite receptive field for both the numerator and the denominator in the membrane voltage equation (see Methods). The spatiotemporal receptive fields of the numerator and denominator are tuned in opposite directions (Fig. 6f). These opposing tunings contribute to DO responses in the model. Since the denominator need not be large to generate DO signals, the model voltage responses can appear reasonably linear (Supp. Fig. 6).

Opponent response properties increase fidelity of motion coding

The last issue we addressed was how direction opponency might improve local motion signals. We asked how well the velocity of rigidly-translating natural stimuli could be inferred from the response of DO and non-DO models (Fig. 7a)^29,30. To make valid comparisons, we changed the filters used in the multiplicative model from Figure 6c such that it could not generate DO responses, and subtracted a spatially anti-symmetric multiplier with the same inputs and filters to create the opponent signal (Fig. 7b i,ii). The fully anti-symmetric DO model is the HRC model, while the non-DO individual multiplier represents one subunit of the HRC. This pair of models allowed us to compare DO and non-DO signals without changing the temporal elements of the models. A distribution of velocities was used to generate a full probability distribution of velocity-response pairings sampled over all scenes in our database (Supp. Fig. 7, Methods). The models were evaluated by asking how much variance in the stimulus velocity can be accounted for by the model signal^29,31,32.

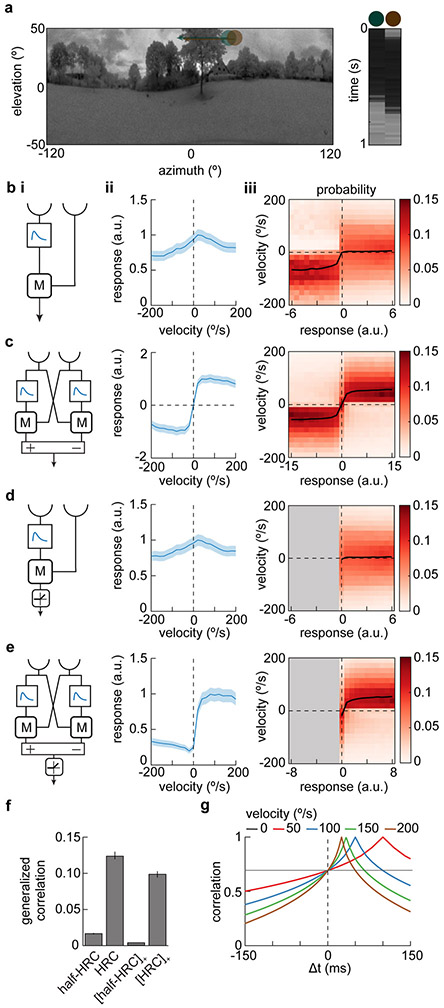
Figure 7. Opponency improves velocity discriminability in elementary motion detectors.

a) A natural scene from the database (left) with two photodetector inputs to an elementary motion detector shown in green and brown. The scene moves at a constant velocity of 50°/s from left to right which is equivalent to the photodetectors moving from right to left. The response over time of the two detectors is shown (right). Natural scene image is from Meyer HG, Schwegmann A, Lindemann JP, Egelhaaf M. (2014): ‘Panoramic high dynamic range images in diverse environments.’ Bielefeld University. doi:10.4119/unibi/2689637.

b) Model responses to natural scenes. (i) Schematic diagram of one half of a Hassenstein-Reichardt Correlator (half-HRC). This model is identical to the multiplicative model shown in Figure 6c, but with filters chosen such that it does not generate DO responses. (ii) Mean response of this model averaged over the database of natural scenes moving at different velocities. Error patches show ±1 SEM. (iii) Distribution of scene velocities given different model responses.

c) As in (b), but for a full, opponent HRC model. This model consists of two copies of the model in (b), but subtracted to generate an opponent model.

d) As in (b), but for a half-wave rectified half-HRC model.

e) As in (b), but for a half-wave rectified full, opponent HRC model.

f) Generalized correlation between model response and the velocity of the natural scenes. Error bars show 99% confidence intervals estimated by bootstrapping.

g) Time-lag cross-correlation in contrast between two points 5° apart while natural scenes move at different constant velocities. Moving natural scenes are positively correlated at 5° even without a temporal delay.

(See also Figure S7 for the full distributions of input velocities and responses for the opponent and non-opponent models.)

The non-DO model detector showed a peak response to stimuli moving at 50°/s in the PD, with responses decaying back to zero at higher stimulus speeds (Fig. 7b). Previous work has shown that natural scenes introduce non-directional noise into correlation-based motion estimates²⁹. Therefore, for each model, we asked how well the image velocity could be inferred from the response. In the single multiplier model, positive responses corresponded to both positive and negative velocities, so that only (rare) negative responses contained strong information about image velocity (Fig. 7b). This is consistent with the finding that inputs of opposite contrast can improve motion estimation^29,33,34. In the DO model, velocities could be inferred from responses with relative ease, since each model response corresponded to a smaller range of input velocities (Fig. 7c). This benefit of opponency was not simply due to the positive-negative symmetry or to the expanded dynamic range of the DO model, since when each model was rectified, the DO model (Fig. 7e) still showed a more reliable relationship between the response and the stimulus velocity than the non-DO model (Fig. 7d).

We quantified the relationship between response and velocity by computing the generalized correlation coefficient between the two (Fig. 7f)³⁵. This metric quantifies how much variance in the velocity is accounted for by the mean velocity given each response. A coefficient of 0 corresponds to no information about the stimulus velocity in the response, while a value of 1 means that, given a response, the stimulus velocity is known exactly. Using this metric, the opponent models (shown in Fig. 7c and Fig. 7e) outperformed their non-opponent counterparts (Fig. 7f). The responses in opponent models accounted for roughly 10% of the variance in input velocities, a value consistent with other simulations that are not averaged over time or space²⁹.

Correlations between spatially-separated points in visual space at non-zero delays can be used to infer motion direction and speed. However, the spatial correlations in scenes induce substantial correlations at zero delay in moving natural scenes (Fig. 7g)²⁹, and these act as uninformative noise when included in motion estimates. Opponent models can improve motion detection by subtracting out this noise.

Discussion

We have provided evidence that direction opponency arises in the first-order DS cells in Drosophila, T4 and T5 (Fig. 2). In these cells, responses to PD motion are suppressed by the addition of ND motion, but not by motion orthogonal to the PD-ND axis (Fig. 3). The suppression arises with spatiotemporally broad-band stimuli and at a range of contrasts and temporal frequencies (Fig. 3 and 4). The opponency appears to arise de novo, in a feedforward manner, since the silencing of T4 and T5 synaptic release does not affect their DO properties (Fig. 5). The opponency we observed in calcium signals rules out a class of LN models that are often used to describe direction-selectivity, but is consistent with models that employ dynamic gain or divisive nonlinearities (Fig. 6). Finally, simulations suggest that opponency improves the ability to discriminate the velocity of moving natural scenes (Fig. 7). This helps explain why small-field motion detectors might employ this property.

Direction-opponent signals can represent vector components of motion

Moving scenes generally include local motion that is oriented differently from the motion of the entire scene³⁶. Cells that respond to the local directed motion are termed component-selective, while those that respond to the direction of the larger scene are termed pattern-selective. In vertebrate cortex, first-order DS cells in V1 are component-selective, and it is the second-order DS cells in MT that are pattern-selective^22,37. In flies, second-order DS cells are pattern-selective to varying degrees³⁸. They respond to optic flow fields⁸ by weighting T4 and T5 signals. In this view, T4 and T5 responses are component-selective and not pattern-selective. In our experiments, the response suppression was selective for the ND, rather than just any non-preferred direction (Fig. 3). This distinguishes the suppression from non-DS changes in the gain of motion signals, which have also been observed in flies³⁹. This sort of DS opponency might be useful if T4 and T5 signals represent vector components of local motion, since they are relatively unaffected by orthogonal motion.

Opponency in T4 and T5 arises in the direction-selective computation

In VS and HS neurons in flies⁶ and MT neurons in cortex^1,4, opponency arises via the subtraction of oppositely tuned DS inputs. In contrast, the opponency we observed appears to arise de novo in T4 and T5, the earliest DS signals in the visual circuit. It remained even when we silenced synaptic release in T4 and T5 (Fig. 5). Apparently, the opponency here results not from inhibitory interactions between populations of T4 and T5 cells, but from the same feedforward processing in T4 and T5 that results in direction-selectivity. We add two caveats to this interpretation. First, it is possible that there are undiscovered DS cell types responsible for the observed opponency. Second, T4 and T5 activity could be transmitted to inhibitory circuits via gap junctions, which would not be affected by tetanus toxin.

The opponency we observed in T4 and T5 neurons may also explain their spatiotemporal tuning. In classical HRC models, single multipliers are tuned to stimulus velocity, independent of spatial structure and temporal frequency⁴⁰. In comparison, the fully opponent HRC model is tuned to the stimulus temporal frequency, which depends on both stimulus velocity and spatial structure⁴¹. Measurements of T4 and T5 neurons have shown that they are tuned to temporal frequency and not to velocity⁴², which is reminiscent of a fully opponent HRC motion signal.

One-step opponency constrains implementations of the direction-selective computation

We should point out three caveats to our proof that rules out a class of LN models when opponency is observed (see Supp. Notes 1 and 2). First, the proof relies on composite sinusoidal stimuli with the same spatial and temporal frequencies in the PD and the ND. Second, it applies to the mean response, which requires averaging over the phases of the PD and ND sinusoids. Since this involves averaging over time, calcium indicator kinetics that smooth responses do not affect the validity of this analysis. Last, we assumed that the indicator fluorescence we measured could be viewed as the output of one LN model in series with a second, i.e., an LNLN model¹³.

With these caveats in mind, the opponency in the calcium signals in T4 and T5 cells cannot result from LN models with convex nonlinearities (Fig. 6, Supp. Fig. 5). Such LN models for DS responses have been favored in primates¹⁰ and have been suggested to explain T4 and T5 responses^11-13. Motion energy models are often used to describe the computations in V1⁴³. And yet, while some studies have observed little direction opponency in V1³, others have found V1 cells that show substantial opponency⁴. LN models have also been proposed to explain direction-selectivity in mouse cortex⁴⁴ and in starburst amacrine cells¹⁴. In these cells, the sinusoidal opponency protocol could act as a test of the validity of LN models. Indeed, in both cortical DS cells and starburst amacrine cells, there is inhibition between cells with opposite direction tuning^45,46, and that could generate opponency and prevent simple LN models from accurately describing their responses. The protocol used here allows for the exploration of similarities between the algorithms in the first-order DS cells in flies and mammals⁴⁷.

We constructed three models in which DO signals are accounted for through feedforward computations (Fig. 6). In one model, DO signals are generated by a two-input multiplicative model with correctly chosen filters, and in another, they are generated by dynamically modulated gain. In a third, three-input synaptic model, suggested by electron microscopy reconstruction, experimental observations, and theoretical studies^23,26,27,29, opponency could be produced with modest saturation. In all three models, the non-suppression of orthogonal motion imposes a strong constraint, since some model parameters generate strong suppression when orthogonal motion is added (Supp. Fig. 6).

Opponency provides an explanation for ON and OFF inputs to T4

The three-input model we examined may explain the synaptic organization of inputs to T4. The three-input organization of the model mirrors the three-input structure of inputs to T4: a central excitatory ON-center neuron is flanked by two delayed inhibitory inputs, one an ON-center neuron displaced in the PD and the other an OFF-center neuron displaced in the ND^26,27 (Supp. Fig. 6). According to previous work, T4 cells combine contrast increments and decrements in their responses³⁴. Still, it is not clear what advantages there are for the combined ON-OFF organization of the inputs to T4. In fact, the ON-OFF organization of the three-input model generates divisive suppression that is tuned to the model’s ND (Fig. 6f). This provides an elegant mechanism for single step opponency. Models with similar structures have been suggested for cortical motion detection⁴⁸, so this conception of ND suppression might apply broadly. The inputs to T5, unlike those to T4, all appear to be OFF-center cells⁴⁹, so a different explanation may be required for the opponency observed in T5.

Direction opponency has benefits for local motion detectors

In Drosophila, the DO encoding of motion in T4 and T5 cells propagates to downstream DO cells, like HS, VS, and LPLC2. For instance, HS and VS cells subtract T4 and T5 signals with opposite direction tuning and integrate over a large visual field. This sharpens their selectivity to specific widefield visual flow fields and reduces their response when there is both PD and ND motion in different regions of the visual field⁶. Since T4 and T5 themselves are already DO, downstream cells that subtract signals from oppositely-tuned T4 and T5 cells are performing a second serial opponent operation.

T4 and T5 cells are local motion detectors with small fields of view, so their opponency cannot achieve the same type of selectivity as opponency in second-order DS neurons. Instead, opponency in T4 and T5 cells improves motion discriminability by rejecting noise induced by the local structure of natural scenes (Fig. 7). Opponency, therefore, acts as a method of common-mode rejection¹⁶. With this rejection, the cell is able to devote its full dynamic range to transmitting informative signals. Rejecting noise in first-order DS cells should also improve signal quality in second-order DS cells with large or small receptive fields. The observed direction opponency, then, bears similarities to the well-understood property of center-surround antagonism⁵⁰. That antagonism occurs in systems where the center and surround signals are correlated, so that the surround inhibition subtracts out redundant information about the environment. With this surround subtraction, the cell is able to devote its full dynamic range to transmitting informative signals. The direction opponency in T4 and T5 is analogous. It rejects non-informative signals generated by the structure of the natural world.

Online Methods

Fly strains and husbandry

Flies for behavioral experiments were grown in a 12-hour light-dark cycle at 20°C, and tested during either the 3-hour period following lights-on or the 3 hours prior to lights-off. Flies used for imaging were grown at 29°C, with the exception of TNT strains or crosses, which were grown at 20°C. All flies were females and 24–72 hours old when tested. Experimental genotypes are listed in Table S1.

Further details on animal handling, data analysis, and statistical testing may be found in the Life Sciences Reporting Summary.

Quantitative optomotor behavior

Behavioral responses to visual stimuli were collected as in previous studies^16,42,51. Flies were fixed to a metallic pin using UV-cured epoxy and placed on an air-suspended ball positioned in the middle of three screens subtending 270° azimuthally and 106° vertically of visual space. Stimuli were projected onto the screens, appearing as a virtual cylinder surrounding the fly. Behavior was inferred by measuring the rotations of the ball. Visual stimuli used green light (peak 520 nm) with mean luminance of 100 cd/m². The temperature of the behavioral chamber was set at 34-36°C. The results were averaged over each recurring stimulus presentation.

In vivo 2-photon imaging

Two-photon imaging was performed with the methods described previously^16,51. Flies were fixed with a metallic holder, exposing the posterior face of their heads. The cuticle over their right eye was surgically removed. Oxygenated solution was perfused over the exposed brain⁵². Flies were placed at the center of panoramic screens, similar to those used for behavior, below a two-photon microscope (Scientifica, UK). The screens had an identical spatial and temporal resolution to the behavioral setup, but covered 270° in azimuth and 69° in elevation. The virtual cylinder was pitched forward 45° to match the pitch of the fly’s head in the holder. Projector light was filtered to avoid detection by the photomultiplier tube (PMT) by applying a bandpass filter. The femtosecond laser (SpectraPhysics, Santa Clara, CA, USA) was set to 930 nm with power <30 mW. Images were acquired at ~13 Hz using ScanImage⁵³ and analyzed using custom Matlab code.

To identify T4 and T5 signals from calcium imaging movies, we used a protocol identical to previously published experiments¹⁶. Briefly, a baseline fluorescence level for each pixel was found by fitting a single exponential to the value of the pixel’s fluorescence through the presentation of gray epochs during the whole experiment. Then, at each pixel, the fluorescence was transformed into a ΔF/F value as ΔF/F = (F-F₀)/ F₀. Candidate groups of pixels were found by performing independent component analysis on probe stimulus responses⁵⁴, with subsequent processing of the independent components to yield small regions of interest (ROIs)¹⁶. The procedure led to candidate ROIs that were of the same size as individual axon terminals.

To classify each of the extracted ROIs as T4 and T5, their edge selectivity (light vs. dark edges), and direction selectivity (right vs. left) was computed from a probe stimulus containing light and dark edges moving both front-to-back and back-to-front. Here, we followed previously described criteria¹⁶. ROIs were only considered if they showed reliable responses to multiple presentations of the probe stimulus. In particular, ROIs were excluded from analysis if the correlation between the responses to the probe presentations was not greater than 0.4. The responses of each ROI to progressive moving light edges (r_ProLight), regressive moving light edge (r_RegLight), progressive moving dark edges (r_ProDark), and regressive moving dark edges (r_RegDark), were used to calculate a direction selectivity index (DSI) and an edge selectivity index (ESI):

$$\text{DSI}=\frac{r_{\mathit{pro}}-r_{\mathit{reg}}}{r_{\mathit{pro}}+r_{\mathit{reg}}}\text{and}\text{ESI}=\frac{r_{\mathit{light}}-r_{\mathit{dark}}}{r_{\mathit{light}}+r_{\mathit{dark}}}.$$

where r_pro is the average of r_proLight and r_reg, and r_light, and r_dark were computed similarly by averaging the probe responses sharing that attribute. ROIs with a DSI > 0.4 (<−0.4) were classified as progressive (regressive) sensitive, likewise ROIs with ESI > 0.3 (<−0.3) were classified as light (dark) edge selective.

Stimuli

All stimuli were programmed in Matlab, using the Psychophysics Toolbox^55-57. Stimuli were projected onto a virtual cylinder that was placed on three flat screens using Lightcrafter DLP (Texas Instruments, Texas, USA). The spatial resolution of the screens was ~ 0.3° and the screen update rate was 180 Hz. The mean luminance for stimuli during functional imaging was 70 cd/m². Image acquisitions were aligned to the stimulus by presenting periodic flashes measured with a photodiode. All stimuli were presented in 4-second durations separated by 4-second gray interleaves.

Sinusoidal gratings

Sinusoidal gratings had contrast computed as follows:

$$c(x,t)=c_0\sin (\kappa x+\omega t+\varphi )$$

The contrast value c(x, t) depends upon contrast c₀, temporal frequency ω, spatial frequency κ, and phase offset ϕ. The contrast value was independent of y-position. Our experiments used a temporal frequency of 1 Hz and spatial wavelength of 45°. The contrast of the sinusoids was 0.5 or 0.25. The direction of motion was reversed by inverting the sign of the grating’s spatial frequency. For both PD and ND stimuli, the phase ϕ was randomly sampled from the uniform distribution on [, 2π).

Composite sinusoidal gratings

The counterphase grating used was composed of two sinusoids at spatial wavelength of 45°, contrast of 0.5, and temporal frequency of 1 Hz traveling in opposite directions.

$$c(x,t)=c_0\sin (\kappa x+\omega t+\varphi )+c_0\sin (-\kappa x+\omega t+\delta )$$

The phases ϕ and δ were independently randomly sampled from the uniform distribution on [0, 2σ). For the sweep of null-direction temporal frequencies, we used 1 Hz PD sinusoids added to variable frequency null-direction sinusoids.

We also generated composite stimuli composed of two sinusoids traveling in orthogonal directions. Those included every combination of two orthogonally moving sinusoids (right and left combined with both up and down).

$$c(x,t)=c_0\sin (\kappa x+\omega t+\varphi )+c_0\sin (\omega t+\delta )$$

The phases ϕ and δ were independently randomly sampled from the uniform distribution on [0, 2π).

The amplitudes of these composite stimuli are higher than that of their component sinusoids (Fig. S3). If a compressive nonlinearity or any form of contrast saturation preceded the elementary motion detector, then the composite sinusoid amplitude would be reduced. In effect, this would be equivalent to reducing the amplitude of the component sinusoids, including the PD component. This effect would hold for composite sinusoids constructed with any two cardinal directions.

Moving random dot stimuli

In addition to sinusoidal gratings, we tested moving dot stimuli. The dots were 5° × 5° black or white squares moving at 100°/s horizontally, placed at random on a gray background with a 40% density. When combining stimuli in two directions, the density of the overall stimulus rises to 64% but their specific contrast did not increase (two white dots add to white, two black dots sum to black, and a white and black dot sum to gray).

Data Analysis and Statistical Testing

Data collection and analysis were not performed blind to the conditions of the experiments. The responses of T4 cells and T5 cells with progressive and regressive PDs were grouped together by combining their respective responses. Each response was indexed by its source fly to avoid double-counting. The responses were averaged over ROIs within each fly and then over flies. Flies were considered to be the independent samples for statistical purposes. No statistical methods were used to pre-determine sample sizes, but our sample sizes are similar to those reported in previous publications^11-13,16,34. The average responses could then be plotted as time traces or integrated over the stimulus duration and presented as the final mean response.

Non-parametric paired two-sided Wilcoxon signed-rank tests were used to test for statistically significant differences between responses⁵⁸. The difference of a response from the response of interest (PD or PD+ND) was calculated per ROI and averaged per fly. With the assumption that individual flies constitute independent samples, our data satisfy the assumptions of the signed-rank test.

Numerical modeling (Fig. 6 & Supp. Fig. 6)

Computation of average model responses

Average responses for each EMD model were computed as expectation values taken over time. For composite sinusoidal gratings, the expectation value in time is dependent on the spatial phase of the stimulus, hence, for those stimuli, expectation values were taken both over time and over phase offsets. The timeseries in Supp. Fig 6 were computed by first averaging model responses over spatial phase. Then, to simulate the temporal dynamics of the GCaMP6f calcium indicator, timeseries were smoothed with a first-order low-pass Butterworth filter with a time constant of 200 ms¹⁷.

Spatiotemporal filters for model inputs

The inputs for all EMD models we considered were implemented as three spatially separated branches. Each input branch had a Gaussian spatial filter, with centers 5° apart and 5° full-widths-at-half-maximum⁵⁹. The temporal filters of the left and right arms were implemented as first-order low-pass Butterworth filters, and that of the center arm, a first-order high-pass Butterworth filter. To smooth the response characteristics of each filter, both low-pass and high-pass filters were composed with an additional first-order low-pass Butterworth filter. Given this choice of temporal filters, the temporal filter of the center branch was the temporal derivative of those of the flanking branches. All temporal filters had a time constant of 150 milliseconds. All filters acted on stimulus contrast. Throughout the following discussion, we denote the left, center, and right inputs, after filtering, as s₁, s₂, and s₃, respectively.

The spatial organization of the branches follows electron-microscopy circuit reconstructions²⁶. The delay vs. non-delay structure of these inputs follows measurements of the T4 inputs^27,60. The timescale is comparable to previous modeling⁶¹ and to measurements of inputs to T4^60,62,63. The timescales were chosen to yield a peak response to sinusoids with ~1 Hz temporal frequency, in agreement with T4 and T5 measurements^7,42. Parameters beyond timescale were swept for various models to investigate robustness (Supp. Fig. 6).

Model parameter evaluation

A subset of the EMD models we considered contain one or more free parameters. To quantify the dependence of model behavior on the values of those parameters, we considered the DSI and analogous indices of opponency and orthogonal direction suppression, defined as

$$I_{PD+ND}=\frac{r(PD+ND)-r(PD)}{r(PD+ND)+r(PD)}$$

and

$$I_{PD+OD}=\frac{r(PD+OD)-r(PD)}{r(PD+OD)+r(PD)}$$

respectively.

Linear-nonlinear model with a compressive nonlinearity

The linear-nonlinear model in Supp. Fig. 6 has a sigmoidal nonlinearity of the form

$$g(x)=[1+\text{exp}(-k_1(x-k_2)){]}^{-1}$$

where K₁ = 20 and k₂ = 0.4 are positive parameters that set the scale and the center of the sigmoid, respectively. These parameters were tuned such to generate DO responses at contrast ½. The linear stage of the LN model was implemented by linearly combining the three spatially offset inputs to yield a spatiotemporally oriented linear filter. The model response was then computed as

$$r=\langle g(s_1+s_2-s_3)\rangle$$

Two-input multiplicative model

The two-input model in Fig. 6c is a rectified Hassenstein-Reichardt correlator (HRC) half-detector. The average response of the two-input half-correlator was computed as

$$r=\langle [s_1\cdot s_2{]}_{+}\rangle$$

See also Supp. Fig. 6 and Supp. Note 3 for analysis of opponency in HRC half-detectors.

Dynamic gain model

The model in Fig. 6d has a dynamic nonlinearity that uses a second linear filter to scale the gain of an LN model. This model can exhibit rich response properties, like other models that employ nonlinear interactions between two linear filters⁶⁴. Here, we chose the LN model to interact divisively with the second filtered quantity:

$$r=\langle \frac{[\alpha s_2-\beta s_3{]}_{+}^2}{1+[-\gamma s_1{]}_{+}^2}\rangle$$

where α, β and γ are positive parameters. This parameterization was chosen because our analysis considers only relative differences between responses rather than their absolute magnitudes. To set the values of the parameters α, β and γ, we swept the values of each between 5 and 400. There exists a large domain of parameter space for which the model displays reasonable directional opponency while keeping the response to PD+OD comparable to the PD response (Supp. Fig. 6). We therefore set α = 300, β = 100, and γ = 50, a set of parameters that falls well within that domain.

Three-input model

The functional structure of the three-input visual motion detector illustrated in Fig. 6e is based on the fly connectome and the signs of responses in neurons upstream of the T4 cells^26-28. We model the effects of the synaptic inputs on membrane potential by changes in the conductances of excitatory and inhibitory currents in the postsynaptic cell. In particular, we define the postsynaptic conductances as threshold-linear functions of the presynaptic filtered inputs:

$$g_1(t)=g_{\text{inh}}[-s_1(t){]}_{+,}{g}_2(t)=g_{\text{exc}}[s_2(t){]}_{+,}\text{and}{g}_3(t)=g_{\text{inh}}[s_3(t){]}_{+}$$

where [·]₊ denotes positive rectification and the parameters g_inh and g_exc are constants that scale the magnitudes of postsynaptic conductances of inhibitory and excitatory driving potentials. The membrane voltage dynamics of this model are given as²⁸

$$c_{\mathrm{m}}{\stackrel{.}{V}}_{\mathrm{m}}(t)+V_{\mathrm{m}}(t)\left(g_{\text{leak}}+g_1(t)+g_2(t)+g_3(t)\right)=g_1(t)V_{\text{inh}}+g_2(t)V_{\text{exc}}+g_3(t)V_{\text{inh}}$$

where c_m is the membrane capacitance and the reversal potentials for inhibitory, excitatory, and leak currents are V_inh, V_exc, and V_leak respectively. We defined our voltage so that E_leak = 0 mV. Because the capacitance of T4 cells has been measured to be very small¹¹, we neglect capacitive currents and solve for the membrane voltage^28,65, yielding

$$V_{\mathrm{m}}(t)=\frac{g_1(t)V_{\text{inh}}+g_2(t)V_{\text{exc}}+g_3(t)V_{\text{inh}}}{g_{\text{leak}}+g_1(t)+g_2(t)+g_3(t)}$$

Only the ratios of the postsynaptic conductances to the leak conductance, rather than the absolute magnitudes of those conductances, influence this analysis. We therefore express the parameters governing the magnitudes of the postsynaptic conductances as nondimensional quantities in units of the leak conductance g_leak. Finally, we model the transformation from the membrane voltage V_m to the calcium concentration as a positively-rectifying quadratic:

$$r(t)=[V_{\mathrm{m}}(t){]}_{+}^2$$

To gain intuition into the operation of this model, we consider its expansion in the limit of small-input contrasts. To do so, we follow previous work²⁹ to make use of an analytic approximation for the rectifier. This smooth rectifier is more biologically plausible than one that is infinitely sharp, and agrees with available measurements⁶². The smooth rectifier has an everywhere-defined first order expansion proportional to x, which leads us to expand both the numerator and the denominator to lowest order (Fig. 6f). Denoting the linear filters of the left, center, and right inputs as f₁, f₂, and f₃, respectively, the effective linear receptive field (up to constant overall scaling factors) of the numerator is

$$-V_{\text{inh}}{g}_{\text{inh}}{f}_1+V_{\text{exc}}{g}_{\text{exc}}{f}_2+V_{\text{inh}}{g}_{\text{inh}}{f}_3$$

and that of the denominator is

$$-g_{\text{inh}}{f}_1+g_{\text{exc}}{f}_2+g_{\text{inh}}{f}_3$$

Since g_exc and g_inh are non-negative, the sign difference between the excitatory and inhibitory reversal potentials gives these receptive fields opposite orientations in spacetime. The opposite directional tuning of the numerator and denominator provides an intuitive explanation for how this model becomes opponent.

We fixed the reversal potentials for excitatory, inhibitory, and leak currents to values that are plausible based on electrophysiological experiments: V_leak = 0 mV, V_exc = 60 mV, and V_inh = −30 mV. To set g_exc and g_inh, we swept values of each between 0.05 and 4 g_leak, and evaluated the behavior of the models using the indices defined above. There exists a broad region of parameter space in which this model displays directional opponency without significantly enhancing or suppressing the response to PD+OD compared to the PD response (Supp. Fig. 6). We set g_exc + 2 g_leak and g_inh = 3g_leak. Following a protocol used to judge linearity in T5 neurons¹², we performed a linearity analysis of the simulated voltage response of this model, the results of which are shown in Supp. Fig. 6.

Modeling opponency with natural scene inputs (Fig. 7)

Calculating elementary motion detector response probabilities

To demonstrate one benefit of opponency in elementary motion detectors (EMDs) we considered 4 models:

Hassenstein-Reichardt Correlator half-detector:

This model (‘half-HRC’) consists of two inputs separated in space by 5 degrees which are multiplied after asymmetric temporal filtering (Fig. 7b). One input filter was modeled as a delta function while the other was implemented as a first order low-pass Butterworth filter with a time constant of 150 ms.

HRC:

This model consists of two spatially mirror-symmetric half-HRCs, the outputs of which are subtracted from one another (Fig. 7c).

Rectified half-HRC:

This model consists of a half-HRC followed by positive rectification (Fig. 7d).

Rectified HRC:

This model consists of an HRC followed by positive rectification. (Fig. 7e).

Stimuli were generated by rigidly translating natural scenes from a database³⁰. Each natural scene was converted from luminance values to contrast to represent early processing in the fly eye. Contrast was computed as $C=\frac{L_{\mathit{local}}-L_{\mathit{mean}}}{L_{\mathit{mean}}}$, where L_local was computed by filtering the image with a Gaussian filter with a standard deviation of 2.5° and L_mean was computed by filtering the image with a Gaussian filter with a standard deviation of 10°. This surround is consistent with measurements in Drosophila⁶⁶.

Models were presented with stimuli drawn at random from the image database, with a random location chosen in each image. The image was rigidly translated with a horizontal velocity drawn from a Gaussian distribution with a mean of 0 °/s and a standard deviation of 100 °/s. In this manner, each model was presented with 10,000 stimuli from each of 421 natural scenes. The model responses and velocities were binned to create the joint probability distribution p(v, r). To avoid empty bins, the bins were chosen to include the center 95% of model responses and the center 95% of velocities. This exclusion means that our modeling does not include tail events, and likely overestimates slightly the accuracy with which each model estimates scene velocity. The expected value of the response, given the velocity of the natural scene, was calculated as E_r[r∣v] = E_r[r p(r∣v)], where $p(r\mid v)=\frac{p(v,r)}{p(v)}$ and E_r[r∣v] is the conditional expectation of the response r given the velocity v. The probability that a natural scene is moving at a particular velocity given the response of a model was computed similarly.

Generalized correlation

The generalized correlation³⁵ between model response and scene velocity was calculated as

$$\text{GMC}[v\mid r]=1-\frac{E_r\left[\text{var}[v\mid r]\right]}{\text{var}[v]}$$

where var[x] is the variance of x. Confidence intervals for the generalized correlation (Fig. 7f) were calculated by bootstrapping model responses across natural scenes using the bias-corrected and accelerated percentile method in Matlab⁶⁷.

Data and code availability

Code for all modeling is available at https://github.com/ClarkLabCode/OpponencyModels. The data that support the findings of this study are available from the corresponding author upon request.