Abstract
We used a terrestrial single-station seismometer to quantify the uncertainty of InSight (INterior explorations using Seismic Investigations, Geodesy and Heat Transport) data for determining Martian core size. To mimic Martian seismicity, we formed a catalog using 917 terrestrial earthquakes, from which we randomly selected events. We stacked ScS amplitudes on modeled arrival times and searched for where ScS produced coherent seismic amplitudes. A core detection was defined by a coherent peak with small offset between predicted and user-selected arrival times. Iterating the detection algorithm with varying signal-to-noise (SNR) ranges and quantity of events determined the selection frequency of each model and quantified core depth uncertainty. Increasing the quantity of events reduced core depth uncertainty while increasing the recovery rate, while increasing event SNR had little effect. Including ScS2 multiples increased the recovery rate and reduced core depth uncertainty when we used low quantities of events. The most-frequent core depths varied by back azimuth, suggesting our method is sensitive to the presence of mantle heterogeneities. When we added 1° in source distance errors, core depth uncertainty increased by up to 11 km and recovery rates decreased by <5%. Altering epicentral distances by 25% added ~35 km of uncertainty and reduced recovery rates to <50% in some cases. From these experiments, we estimate that if InSight can detect five events with high location precision (<10 % epicentral distance errors), that there is at least an 88% chance of core depth recovery using ScS alone with uncertainty in core depth approaching 18 km and decreasing as more events are located.
Plain Language Summary
We used a seismometer on Earth to study how well the NASA mission, InSight (INterior explorations using Seismic Investigations, Geodesy and Heat Transport) could detect the Martian core. We created a catalog of earthquakes from which we randomly selected events to mimic the seismic events (marsquakes) InSight is expected to detect. Several models of Earth’s interior were tested to see which best predicted the arrival of seismic waves reflecting off the core. We found utilizing more events allowed us to determine the core size better than using a limited number of events. Using an additional seismic phase also helped us recover a more accurate core depth if there were not a lot of events. We were also able to find variations in the mantle by using events within certain location ranges. Since the InSight team may not be able to locate marsquakes as accurately as we locate earthquakes, we changed the location of the earthquakes. When changes in location were small, we were still able to determine the size of the core. Larger changes in location prevented us from finding an accurate core depth. If InSight detects at least five events with high location accuracy, we will be able to determine the Martian core size.
1. Introduction
Seismology is a vital tool for investigating Earth’s deep interior. Despite a limited number of seismic stations, early seismologists were able to determine the basic internal structure of Earth and constrain the size of the outer core (Oldham, 1906), the physical properties of the boundary between the outer core and mantle (Gutenberg, 1913), and the size of the inner core (Lehmann, 1936). These studies were achieved by noting arrival times of core traversing or interacting seismic phases and measuring the travel-time versus epicentral distance moveouts to identify these body waves. Body wave studies have been essential for the creation of one-dimensional models of the seismic velocity layering, density, and shear and bulk moduli throughout the Earth (Dziewonski and Anderson, 1981).
More recently, travel time observations of body waves such as P (Dziewonski, 1984; Dziewonski et al., 1977; Wysession et al., 1992), PcP (Garcia and Souriau, 2000; Morelli and Dziewonski, 1987; Tanaka, 2010), PKP (Creager & Jordan, 1986; Morelli & Dziewonski, 1987; Schlaphorst et al., 2015), PKKP (Doornbos and Hilton, 1989), S, SS, and ScS (Garnero, 2000; Russell et al., 1999; Su et al., 1994) indicated that the core-mantle boundary (CMB) may have topography of up to ± 4 km and exhibit variations from a one-dimensional velocity model. These studies compared the arrival times of body waves to predicted arrivals or used the residual times between seismic phases from the same event. In addition to travel time deviations, normal mode investigations indicated the presence of large-scale variations in seismic velocities in the mantle above the CMB (Ishii and Tromp, 2004; Krüger et al., 1995; Li et al., 1991; Mégnin and Romanowicz, 2000; Moulik and Ekstrom, 2014).
The seismic phase ScS wave has been used extensively to study the core-mantle boundary region of Earth (Mitchell and Helmberger, 1973; Wysession et al., 1992; Young and Lay, 1987) placing constraints on anisotropy (Fukao, 1984; Kendall and Silver, 1996; Russell et al., 1999), thermal structure (Hernlund et al., 2005; van der Hilst et al., 2007), the fate of subducted slabs (Hutko et al., 2006), and the source of mantle plumes (Lay et al., 1998; Schubert et al., 2004; Yuan and Romanowicz, 2017). These studies investigated anomalies by comparing ScS-S arrival times, and how ScS arrivals differed from predictions by one-dimensional seismic models (e.g. Preliminary Reference Earth Model) (Dziewonski and Anderson, 1981). Waveform studies of precursory and postcursory scattered arrivals near ScS have also been used to investigate the mantle above the CMB. For example, delayed precursors, reduction in amplitude of the main phase, and delayed postcursors indicated the presence of low-velocity zones. ScS is sensitive to the properties of ultra-low velocity zones (ULVZs) lying above the CMB (Li et al., 2017; Simmons & Grand, 2002; Thorne & Garnero, 2004), the shape and properties of large low-shear velocity provinces (LLSVPs) (Burke et al., 2008; Garnero and McNamara, 2008) and other layered features such as the thickness of the thermal boundary layer, or deposits of denser material above the core (Buffett et al., 2000). In addition to studies on LLSVPs and ULVZs, ScS has been used to investigate the fate of subducted lithosphere “slabs” in the deep mantle (Hutko et al., 2006; Rost et al., 2008). Seismic velocities constrained by ScS have led to better constraints of the Earth’s chemical composition (Kellogg et al., 1999), dynamics (Garnero and McNamara, 2008; Lay et al., 1998) and structure (Lay & Garnero, 2004) of the CMB. Although ScS provides extensive evidence for complex structure and dynamics in the Earth, the interiors of the other terrestrial bodies in our Solar System remain virtually unknown.
We can investigate the interiors of other terrestrial bodies, by placing seismometers on their surface. Even a single-station seismometer can detect and locate seismicity, measure internal layers, and be used to determine the depth to the CMB. From 1969-1972, five of NASA’s Apollo missions installed seismometers on the lunar surface enabling both active and passive experiments (Nakamura et al., 1982). The lunar experiments revealed seismic waves with unusually long codas compared to those on Earth (Latham et al., 1970a). This effect was explained by scattering in the lunar near surface layer (Toksöz et al., 1974) that is heavily cratered and without atmosphere or currently active plate tectonics. The lunar megaregolith is highly porous and fractured creating large velocity gradients in the upper 20 km of the crust (Toksöz et al., 1974). Diffusive scattering effects played a strong role on the Moon owing to the lack of sufficient atmosphere (Pandit and Tozer, 1970), and are weaker on Earth and presumably Mars. Despite the difficulties in identifying body waves the passive experiment found clusters of deep moonquakes that coincided with tides from the Earth and Sun (Bulow et al., 2007; Kawamura et al., 2017; Weber et al., 2011). Rarer, shallower events (<200 km) were thought to be tectonic or meteoritic in origin (Binder and Oberst, 1985; Oberst, 1987). Although only five stations were installed, seismologists were able to invert travel times to begin constraining the shallow internal structure of the moon (Hartmann, 1973; Latham et al., 1970a; Latham et al., 1970b). Owing to the strong scattering in the near surface, constraining the deep interior of the Moon required the stacking of numerous core-reflected phases with additional constraints from geophysical data (Garcia et al., 2011; Weber et al., 2011). These investigations revealed layering within the lunar core that would not have been observed using tidal or gravity data alone. As on Earth, seismology is a vital tool for constraining the deep lunar interior, and seismology will be essential to investigate the Martian deep interior.
In 2018, NASA launched the Interior explorations using Seismic Investigations, Geodesy and Heat Transport (InSight) a Discovery class mission with the goal of investigating the interior structure and processes of Mars (Banerdt et al., 2017; Lognonné et al., 2012). The mission payload included a short period seismometer, the Seismic Experiment for Interior Structure (SEIS-SP) and a 3-component very broadband seismometer (SEIS-VBB) to record seismic waves across a range of frequencies (~1 mHz to 10 Hz) (Panning et al., 2017). The data from these seismometers are used to constrain the interior structure of Mars. With an array of seismometers, a single event can yield several seismograms from multiple distances which help constrain the location and depth of the event. A single-station will only yield a single set of 3 component seismograms; thus, the location and depth of the event is more difficult to determine. Despite difficulties, terrestrial single-stations have detected events and determined their locations (Magotra et al., 1987; Roberts et al., 1989) and magnitudes (Wu et al., 2006) and have also been studied for use in early warning systems (Lockman and Allen, 2005). In preparation for InSight’s landing, several studies have examined InSight’s ability to identify events from impacts (Schmerr et al., 2016; Teanby, 2015; Teanby and Wookey, 2011) or tectonic events (Bose et al., 2017; Khan et al., 2016; Panning et al., 2015), and determine interior structure (Banerdt and Landis, 2010; Lognonné et al., 2012; Panning et al., 2015, 2017). This study aims to build on previous work and determine the efficacy of a single-station in detecting the core and investigating the deep interior.
Currently the interior of Mars is only constrained by a few geophysical parameters and geochemical measurements. Smrekar et al. (2018) present a comprehensive discussion on interior structure constraints and models for Mars. Interior structure models (Folkner et al., 1997; Gudkova and Zharkov, 2004; Khan et al., 2017) and seismic velocity models (Nimmo and Faul, 2013; Okal and Anderson, 1978;Rivoldini et al., 2011; Sohl and Spohn, 1997) rely on tidal dissipation measurements (Bills et al., 2005; Smith & Born, 1976), moment of inertia (Yoder and Standish, 1997), gravity data (Konopliv et al., 2016, 2011), and geochemical constraints from the recent rover missions (Gellert et al., 2004; Hecht et al., 2009; McLennan et al., 2014; McSween et al., 2009) and Martian meteorites (McSween, 1985; McSween, 1994). These models utilized assumptions for the deep interior composition and inferred core depths ranging between 1470-1860 km. For example, Sohl and Spohn (1997) presented two possible end-member models of the Martian interior. One model was optimized to fit the Fe/Si ratio of 1.71, and the second was optimized to fit a moment of inertia equal to 0.366. The first model has a core depth of 1922 km while the other has a core depth of 1723 km. Since then, the moment of inertia measurements have improved and tidal love numbers have been measured (Konopliv et al., 2016), but the estimates of core depth still range between 1531-1797 km (Khan et al., 2017; Nimmo and Faul, 2013; Rivoldini et al., 2011). Numerous forthcoming seismic studies are expected to provide additional constraints on internal layering and better resolve the deep interior to within several tens of kilometers.
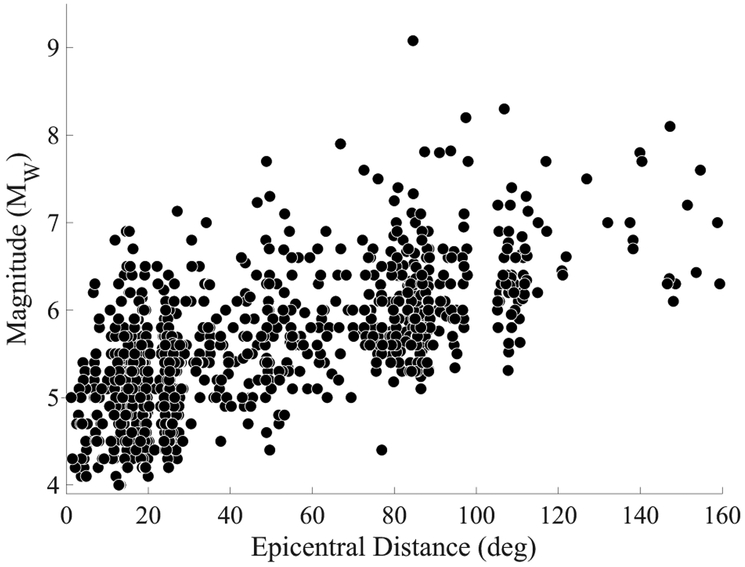
To seismically image the core and explore the possible uncertainty in core size, we used the seismic phases; S, ScS and ScS multiples. The ScS phase is a shear wave (S) that travels down to the core (c) where it reflects and returns to the surface as a shear wave (S) (Fig. 1). ScS is particularly sensitive to the impedance contrasts at the CMB and has been used to constrain the lunar CMB (Weber et al., 2011). Its multiples include ScSScS (ScS2), ScSScSScS (ScS3) and ScSScSScSScS (ScS4), which reflect off the core at multiple points and are observed over a larger range of epicentral distances. To quantify the uncertainty in obtaining core depth with only InSight, we implemented a terrestrial single-station analog of seismic events to test a ScS-S stacking method for constraining the depth to the terrestrial CMB. Our study utilized a database of seismic events recorded at the Black Forest Observatory (BFO) (Fig. 2) to 1) investigate the quality and quantity of events required to identify core reflected ScS arrivals sensitive to the size of the terrestrial core, 2) estimate the uncertainty in core size obtained from a plausible Mars-like distribution of events, 3) investigate if the single-station InSight can detect mantle heterogeneities and deviations from a one-dimensional velocity structure.
Figure 1.
Travel paths of S (black), ScS (red), ScS2 (blue), ScS3 (purple) and ScS4 (green) through Earth. Sources (black stars) occur 80° from the receiver (black triangle). Raypaths were generated using the TauP toolkit (Crotwell et al., 1999).
Figure 2.
Distribution of the 917 events based on a) Magnitude, b) Distance and c) on an epicentral distance map projected with equal azimuths centered at BFO. The smallest Mw magnitude shown is 4.0 where the greatest is 9.08 (2011 Tohoku). The blue star at the center of the map represents BFO.
2. Dataset
2.1. Constructing a Mars-like Database
We built our analog database using earthquake data collected from the Incorporated Research Institutions for Seismology (IRIS) Data Management Center. We select events from those identified in the National Earthquake Information Center, Preliminary Determination of Epicenters (NEIC PDE) catalog (Guy et al., 2015). BFO was chosen as our single-station seismometer because 1) it has previously been used as an analog station for InSight (Bose et al., 2017; Panning et al., 2015) and 2) its intraplate location in Germany approximates InSight’s landing site on Mars due to BFO’s location far from plate boundaries, large population centers, and the coast/ocean, the main producer of microseism noise on Earth (Ardhuin et al., 2001; Stutzmann et al., 2009).
BFO’s local seismicity was modeled to be on the same order of magnitude as Mars (Golombek, 2002; Knapmeyer et al., 2006; Plesa et al., 2018) due the scarcity of local events that the catalog reports. The SEIS VBB instrument has an observational limit of about 10−9m/s2/√Hz in the 0.01-1 Hz range (Lognonné et al., 2019). This range allows for potential observations of multiple orbit surface waves on Mars for events with moments greater than 1016-1017 Nm (Mw 4.6-5.3) and regional (distance < 60°) detection of events with moments as low as 1013 Nm (Mw 2.5) (Mimoun et al., 2017; Panning et al., 2017). To have an observable S and ScS phase, the minimum required moment is estimated to be about 1016Nm. From seismicity estimates (Knapmeyer et al., 2006; Panning et al., 2017; Plesa et al., 2018) this would translate to ~10 detectable ScS events over the duration of InSight’s mission lifetime (one Martian year or approximately two Earth years).
Although Mars will experience fewer seismic events than Earth, Mars has less noise due to the absence of oceans and thick atmosphere, which will improve signal-to-noise for the detectability of body wave phases (Panning et al., 2015). Attenuation effects are expected to be smaller owing to the smaller planet radius and travel path lengths (Panning et al., 2015). For example, core-reflecting waves (e.g. ScS) from an event at an epicentral distance of 60° on Earth travel about 6700 km, while on Mars they would only travel about 3900 km, or −40% less than the Earth distance. Although the Martian mantle is expected to have lower seismic quality factors (Q) than Earth (Lognonné et al., 1993; Nimmo and Faul, 2013) overall attenuation could be lower than Earth due to the thicker Martian thermal lithosphere with higher Q and the smaller planetary radius (Panning et al., 2015). Lower attenuation, or higher Q, would allow InSight to detect smaller magnitude events at greater distances than would be detected on Earth. For this reason, we began searching for terrestrial events with a minimum moment magnitude (Mw) of 4.0.
To build our ScS database, all seismograms from teleseismic events occurring between 2010 and 2016 with Mw> 4.0 and depths less than 100 km were downloaded and individually visually inspected using the Seismic Analysis Code (Goldstein et al., 2003). We do not expect deep events on Mars due to the lack of plate tectonics that produce deep subduction zones on Earth (Barazangi and Isacks, 1976). Due to the scarcity of events that occur within 80° of BFO, we further downloaded events from 2000-2009 to create a more robust catalog. Since we designed our algorithm to pick events based on distance bins, we preferred a larger number of events of similar magnitude within those bins. Initially we found that the selection algorithm (Fig. 6, Section 3.1) had limited options for choosing smaller events (i.e. tended to select the same event in every iteration), which could have created a bias during our analysis. By adding more events, specifically those with low magnitudes (Mw< 5), we were able to create a more diverse dataset that could help remove biases from source location and travel paths (Fig. 3).
Figure 6.
Diagram of event selection algorithm. The desired quantity, SNR, and back azimuth of event were predetennined and used to refine which and how many events were picked from the Mars-like database.
Figure 3.
Our event catalog plotted by distance and magnitude. At distances greater than 169°, we did not identify any events due to the lack of detectable seismic activity in that region. This plot also demonstrates that the catalog was biased to high magnitude events (Mw 5.0) at large distances.
Our chosen station, BFO, has an STS-2 seismometer, that recorded events in three components; vertical (BHZ), East (BHE) and North (BHN). We converted the horizontal components to radial and transverse orientations using the source location published in the NEIC PDE catalog to rotate the horizontal components to the back azimuth of the event. We chose to use acceleration, rather than displacement or velocity, to avoid issues with the polarity of the S and ScS signals. We take advantage of a phase shift relative to displacement, that can produce a coherent positive peak. We used a time window that began 600 seconds before the start of the event and ended up to 10,000 seconds after the source origin time to capture any ScS multiples reverberations in our analysis. We immediately excluded seismograms with multiple earthquake signals within this time window and those with signal-to-noise ratios (SNR) below 0.5, on the assumption that the Martian database would not include such events in a core depth analysis due to poor signal quality. Here we defined the SNR ratio as the maximum amplitude of the first arriving S wave divided by the absolute value of the maximum background noise measured in a window 30-80 seconds prior to the S wave arrival.
2.2. Event SNR Determination
We visually inspected the transverse component of each event in the initial catalog of 12,754 events to determine if body waves could be identified and used in our analysis. To enhance the S and ScS signals, we applied a bandpass filter of 0.05-0.1 Hz (Loper and Lay, 1995). Our first visual criterion in event selection was the presence of a distinct S wave. Without a well-formed reference S phase, ScS will be difficult to identify, thus we excluded these events from our database. Next, we made a preliminary travel time pick on S and ScS (where possible) based upon the PREM predicted arrival time window for each phase. We then assigned the events a SNR rank based on the SNR ratio and whether ScS was identified to assess their quality for stacking. We excluded events from ScS stacking if the event occurred beyond the propagation distance of ScS or another wave obscured ScS. In particular, we did not stack ScS for events located between −18-30° where the ScS arrival coincides with the arrival of surface waves. However, we are still able to use these events for stacking ScS multiples, thus we assigned a ranking to the multiples; either low (SNR < 4.0) or high-SNR (SNR > 4.0) rank and directed our algorithm to select these events only when investigating ScS multiples. The same quality ranking system applied where the S and ScS waves merge around 100°, with S beginning to interfere with ScS around 80°. Another important constraint on the size of the core is where S and ScS merge, but identification of this distance would require events to have sufficient distance sampling near the merging of S and ScS. Our shallow core models predict a merger at ~98° while deeper core models predicted the merger at ~106°, thus Mars would need to produce multiple events that sample approximately every degree from 95-110° to properly distinguish between models.
To determine approximate distance ranges where ScS and its multiple could be utilized, we generated synthetics using the GEMINI code (Friederich and Dalkolmo, 1995) (Fig. 4). The synthetics show that ScS cannot be stacked between ~18-30° and beyond ~80°. The synthetics also show that ScS2 is useable up to epicentral distances of 145° before other body waves such as S multiples (SS, SSS, etc.) interfere. We excluded distances of 60-115° where there was interference between surface wave trains and the multiple. We stacked ScS3 up to 150° before the phase is interfered with by multiple body waves, with an additional exclusion zone of ~85-140° due to surface waves. ScS4 was stacked up to 110° before a combination of body and surface waves interact with ScS4. We were not able to use multiples ScS5 and higher due to the low amplitudes of the phase.
Figure 4.
Moveout of ScS and its multiples relative to S arrival time illustrating the windows used to study ScS and its multiples. Synthetic seismograms based on PREM (Dziewonski & Anderson, 1981) with depths of 0 km and moment magnitude (Mw) of 6.0 were generated using the GEMINI code (Friederich & Dalkomo, 1995). Solid black lines near ScS moveout indicates the range of predicted arrival times from 22 velocity models.
In cases where we observed ScS, we categorized the events as low, average, or high SNR events. Low SNR events were defined by low SNR ratios (< 3), with a median value for this category of 1.4 (Fig. 5a). These events had an emergent ScS that can be difficult to distinguish from background noise. Average SNR events were defined by a larger SNR ratio (3-6), with a mean value for this category of 3.4 (Fig. 5b). ScS was more readily identified, with low uncertainty (<8 seconds) in the arrival time. High SNR events were classified by having large SNR ratios (> 5), with a mean SNR ratio for this category of 8.5, and a maximum of 62 (Fig. 5c). In these events the ScS waveform was evident in the seismogram and emerged above the background noise; these waveforms represented the top 10% of SNR values. Our final database contained 917 events. Through visual inspection and our criteria above, we found 502 events where ScS was not identified (289 were low SNR, 213 were high SNR). Among the remaining events where ScS was identified, 254 were low SNR, 78 average SNR, and 83 high SNR. Each event was assigned a quantitative signal quality factor equal to the square root of the SNR ratio.
Figure 5.
Examples of a) Low, b) Average, and c) High SNR events in our seismicity catalog. The events occur at about the same distance but have different amplitude ranges. Arrows indicate the S wave arrival and brackets indicate the ScS time window.
2.3. Core Models
We created 22 models based on the PREM ID model (minus the ocean) (Dziewonski and Anderson, 1981) with core depths between 2791 km and 2991 km (true core depth ± 100 km) in increments of 10 km. PREM was selected as the reference model because it was built around geochemical and geophysical constraints similar to those that will be used for construction of a reference model for Mars (Panning et al., 2017). These constraints include moment of inertia, mean mass, and mean radius (Khan et al., 2017; Mocquet et al., 1996). PREM is one-dimensional, with seismic velocities constrained by arrival times of both seismic body waves, surface waves, and normal modes. PREM also represents one of the first self-consistent models that was widely accepted as a reference model. Newer models (e.g. ak135 (Kennett et al., 1995)) were similar to PREM and vary most in the inner core with ScS travel times varying by ± 0.2 seconds between the models. This variation is low enough to not affect our analysis of ScS. Finally, PREM has also been invoked in previous terrestrial analog studies for constraining Martian uncertainties (Bose et al., 2017; Khan et al., 2016; Panning et al., 2015), making our results readily comparable to those in the literature. To determine the moveout of ScS relative to S for each model, we used the TauP toolkit (Crotwell et al., 1999) (Fig. 4). For shallower cores, we preserved gradients in PREM's shear wave velocity and density and extended the core to shallower depths. For the deeper cores, we linearly extrapolated the shear velocity and density gradients in PREM to approximate what those properties would be for a deeper CMB. The extrapolation used the deepest 200 km, near the PREM CMB, and resulted in a maximum shear wave velocity of 7.26486 km/s. The change in velocity at the base of the terrestrial mantle is very minor but helps mimic Martian models where deeper cores tend to exhibit faster seismic velocities in the mantle at the CMB (Smrekar et al., 2018).
3. Methods
To determine the size of the core, we stacked seismograms on the model predicted moveout of the ScS phase relative to the S phase. We chose to use ScS only, as the phase has an amplitude ~10-40% of the S wave and was greater than PcP (Garnero, 2000; Woodward and Masters, 1991). PcP was not used because it is a low amplitude phase and is poorly detected on Earth. Furthermore, ScS does not rely on us knowing the core velocity like PKP or SKS to determine core depth. Our stacking process aligns individual wavelets along the predicted moveout based on the interior structure model to produce a higher signal-to-noise ratio than using a single event (Lay et al., 2004; Vidale & Benz, 1992). To avoid errors from using absolute travel time, we chose to stack along the ScS-S moveout rather than ScS relative to the origin time moveout. This helps remove any error caused by onset time and local crustal geology and removed the need for an accurate source onset time. Since S and ScS have similar travel paths through the crust and upper mantle, their travel times were similarly affected by the event depth and local crustal thickness, thus isolating travel time differences to the lowermost mantle.
The algorithm began by drawing events from our database to simulate a Martian, or intraplate, distribution of earthquake seismicity. We selected events using our weighted probability designed to mimic the range of magnitudes and epicentral distances for a planet without the strong signature of plate tectonics (Knapmeyer et al., 2006) (Fig. 3).
3.1. Event Selection
Since our terrestrial database of ScS events was not complete in magnitude or distance, we developed an algorithm to populate the Mars seismicity catalog with the desired number of events for analysis (Fig. 6). We first specified the number of events (N) produced by Mars. This parameter was arbitrary and will be dependent upon the quality of data returned from Mars, and we explore it in more detail in Section 4. We then broke our database into subpopulations of events, separated into bins of 10° in epicentral distance. The bin size was chosen to provide a sufficient number of events at each magnitude. We randomly selected N source location distance bins and used this to determine which subpopulation to draw the events from. We then selected events from the distance bins the Gutenberg-Richter law assuming a b value of 1.05 (Ceylan et al., 2017; Knapmeyer et al., 2006). The b-value for Mars is still speculative, but 1.05 serves as a good approximation. The Gutenberg-Richter law states that for every decrease in magnitude, the number of observed events increases roughly tenfold, thus smaller magnitude events are more likely to be selected than larger magnitude events. For a given moment (Mw) the selection weight (W) was equal to 10−(6.37+1.05Mw). In the circumstance that a subpopulation was exhausted, we redrew the remaining number of events from other distance bins. With this algorithm, we were able to create and evaluate a dataset with mixed SNR events, examine subsets of events based on SNR range or source location, and discern back azimuth or location bias.
Initially we evaluated five events with any SNR and no added source location errors, but we adjusted the algorithm to choose three, ten and then fifteen events to see the effect quantity of events had on the algorithm’s ability to constrain core depth. We based the quantity of events on lower estimates of Martian seismicity (Plesa et al., 2018), the probability of those events occurring at useable distances, and empirical tests. For the ScS multiple study that could utilize all distance bins, the number of events was set at 9, 15, 30 and 45. The average number of ScS events was 3, 6, 12, and 18, respectively, which we rounded to 3, 5, 10, and 15 events. We tested three ScS events to determine the minimum number of events required for core recovery.
3.3. Stacking
The algorithm chose a set of seismograms based on the desired quantity, SNR restrictions, and the selection weights. We then normalized each seismogram by the S wave amplitude and multiplied the amplitude of each seismogram by its quality factor (square root of the SNR ratio). This ensured higher SNR data were weighted more heavily than poor SNR data during stacking. We used the square root instead of just the SNR ratio to prevent a single event from dominating the analysis. Once the quality factor was applied, the algorithm isolated a section of the seismogram based on the visually inspected arrival of S and the predicted time of ScS and/or its multiples (Fig. 7B).
Figure 7.
a) Example of selected events plotted along the moveout of ScS relative to the predicted arrival of S. The distances of the events are the cited distances in the catalog. The shaded region indicates the range in arrival times from the models. Please note two events have similar distances (~ 4 °) and overlap on the plot, b) Same events plotted in panel a) after a taper and window has been applied. The time on the horizontal axis is time from predicted arrival time (Tpred). The plots are labeled by their distances.
For each model, the algorithm applied a Gaussian taper to 40 seconds surrounding the predicted time of ScS relative to the S arrival to decrease the amplitude as it got further from the predicted arrival time of ScS (Fig. 7b). The taper reduced ambient noise and other waveforms that occurred near this interval. The same method applied to ScS multiple arrivals, but Sdiffwas used as the reference phase instead of S if the event occurred within the shadow zone of the core.
We distinguished the ScS arrival from other seismic energy by aligning on predicted travel time (Tpred) and used the phase-weighted stacking approach (Schimmel and Paulssen, 1997) to produce stacked amplitudes for each model (Fig. 8). In this approach we raised the phase coherence to the power of 2 so that higher SNR seismograms are weighted more. Stacked amplitudes that constructively interfere were indicative of a seismic phase arrival at the predicted moveout. We calculated the offset time (Toff) of each model by subtracting the time between Tpred and the visually selected arrival time of ScS (Tvs). This calculation was repeated for each event, then averaged to calculate the mean value of Toff.
Figure 8.
Examples of ScS stacked amplitudes (red lines) and uncertainties (pink shaded regions) using the bootstrap technique. The events are the same as those in the previous plots, and no ScS multiples were stacked in this example. As expected, the model with a core depth of 2891 km, PREM's core depth, has a large peak centered near the estimated time of arrival.
We determined confidence bounds on the stacked amplitudes and derived the uncertainty in amplitudes using the bootstrap technique (Efron and Tibshirani, 1997) with 100 resamples. Because we squared the phase coherence during the phase-weighted stack, some resamples produced anomalously large amplitudes that would skew the mean and standard values. To avoid this, we took the square root of the absolute value of each resample and multiplied by the sign of the original resample. This produced stacks that had a more normal or Gaussian distribution, thus calculating uncertainty using mean and standard deviation was appropriate.
In Fig. 8, the PREM model produced a coherent peak in amplitude of ScS at Tpred and had a small mean Toff, while perturbed core models defocused the stacked ScS arrivals. Fig. 9 shows the mean stacked amplitudes with uncertainty at Tpred for all 22 models with uncertainties equal to the shaded region of Fig. 8. The model with a core depth of 2891 (the correct value) had the greatest amplitude (Fig. 9A) and the smallest mean Toff (Fig. 9B).
Figure 9.
Criteria for evaluating core detection. Panel a) shows the mean stacked amplitude with certainty at Tpred for each model. Panel b) shows the average time between Tpred the visually selected ScS arrival Tvs. The dashed line indicates the PREM core depth for reference and the red points indicate the maximum amplitude (a) and smallest mean offset time (Toff) (b). The green line indicates the bounds for the models that can be considered. Errors bars must fall above green line (a) and offset times must fall between the green lines representing ± 8 seconds (b).
3.4. Core Recovery
A robust detection of the core had a large peak at Tpred with relatively low uncertainty, such that lower bound of uncertainty was still above zero at the 95% confidence bound, and a small value for mean Toff. We therefore selected the core depth using the maximum amplitude of models with amplitude certainty above zero with the additional criterion that the absolute value of Toff be less than 8 seconds. By ensuring lower uncertainty bounds were positive, we can be confident there is an arrival at Tpred. We used a cutoff Toff of 8 seconds because it typically eliminated about half of the model outliers left in consideration and corresponded to about half the width of the ScS waveform. This avoided spurious selection of ScS sidelobes and arrivals at the edge of the stacked predicted ScS time window. The cutoff also ensured we did not consider models that consistently failed to predict the arrival time of ScS. We could recover a core depth using only the maximum amplitude, but we found that by adding the time criterion, we reduced the uncertainty in the core depth by nearly half in some cases. The combination of time and amplitude restrictions typically left fewer than five core depth models for consideration. Using this combination of criteria also eliminated all models in some iterations, meaning the algorithm failed to recover a core depth, returning a null value for core depth.
We repeated this algorithm in over 1000 iterations to explore how data SNR, quantity, and location uncertainty each affected the outcomes. During each iteration, the event database was resampled for the desired criteria. Some events were rarely or never selected, like the large Mw 9.0 Tohoku, Japan event, because of low selection weights. We selected some smaller events more frequently but verified that an event was never selected in more than 50% of the iterations so each iteration would represent a mostly unique combination of events. This was only a problem when selecting many events from a more restricted database (i.e. 15 high SNR ScS events) but the median event selection rate was always below 70 out of 1000 iterations.
4. Results
We used the 1000-fold ensemble of stacked ScS data to generate histograms showing the selection frequency of each core depth model and derived the mean core depth and uncertainty, here defined as the 1 sigma (σ) value assuming a Gaussian distribution (Fig. 10, Table 1). In addition to varying the number of events, we also investigated event SNR, using 1) only low SNR events or, 2) any SNR events or, 3) average SNR events or 4) excluding low SNR events or 5) only the highest SNR events.
Figure 10.
Selection Frequency based on SNR of events. Dashed Grey lines indicate the PREM core depth for reference. These plots represent core recovery using five ScS stacks. Results are without added source location errors.
Table 1.
Table showing the recovery rate (%), mean core depth, and the 1σ confidence level based on SNR and quantity of seismograms. No source location errors were added.
| SNR | 3 events | 5 events | 10 events | 15 events | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Recovery Rate (%) |
Mean – PREM Core Depth- [km] |
Uncertainty[km] | Recovery Rate (%) |
Mean – PREM Core Depth- [km] |
Uncertainty[km] | Recovery Rate (%) |
Mean – PREM Core Depth- [km] |
Uncertainty[km] | Recovery Rate (%) |
Mean – PREM Core Depth- [km] |
Uncertainty[km] | |
| Low | 94.8 | 0.9 | 26.7 | 93.4 | 1.8 | 26.1 | 96.4 | 1.1 | 22.2 | 96.4 | 2.8 | 20.3 |
| Average | 94.9 | 7.5 | 25.9 | 90.9 | 7.8 | 24.1 | 90.3 | 9.3 | 23.7 | 90.9 | 7.8 | 24.1 |
| High | 86.8 | 5.1 | 30.1 | 87.7 | 6.7 | 27.9 | 92.5 | 6 | 25.8 | 93.8 | 6.4 | 23.4 |
| All | 95.1 | 2.9 | 25.9 | 95.5 | 3.4 | 24.3 | 94.7 | 2.4 | 20 | 96.4 | 1.82 | 18 |
| No Low | 93.1 | 6 | 25.5 | 90.8 | 7.4 | 23.3 | 88.6 | 7.4 | 21.7 | 91.3 | 8.5 | 21.5 |
4.1. Synthetic Tests
In addition to terrestrial events, we created PREM synthetic seismograms using the GEMINI code (Friederich and Dalkolmo, 1995). This allowed us to independently quantify how noise and source location errors affected core recovery while eliminating errors from mantle heterogeneities, crustal variations, and source location errors. To test how SNRs may affect our results we added noise to the synthetic seismograms. White noise was added using a random number generator and adding the resulting values to the amplitude of the seismogram. We used white noise because a Martian noise model is currently unavailable. The white noise model assumed equal amounts of energy at all frequencies, which for our purposes allowed us to evaluate the detectability of the synthetics for a given SNR without having to establish a noise model at each frequency. We always recovered the PREM core depth when the maximum value of added noise was comparable to the ScS amplitude. When noise increased to about half of the S amplitude (SNR ~ 2, comparable to the lowest event SNR we used) the algorithm still recovered a core, but the core depths had an uncertainty of ± 14 km.
We altered the location of events to test the effects of location uncertainty and origin time using five ScS events. It should be noted that InSight is predicted to have less location uncertainty (−0.5-1°) compared to terrestrial single-stations owing to the lack of oceans and anthropogenic noise (Bose et al., 2017; Khan et al., 2016). Changes in source location caused changes in the expected arrival time of the models such that a now closer event (i.e. 29° versus 30°) had greater time differences between S and ScS arrivals (Fig. 4). This results in a mismapping of the visually selected time (Tvs) and an incorrect value for the offset time between Tvs and the predicted arrival time (Tpred). The rotation of BHE and BHN components to radial and transverse required a precise source location, meaning source location errors will cause the radial component to contaminate the transverse.
We attempted to quantify location uncertainties here by randomly changing the epicentral distance by up 1° (Bose et al., 2017; Khan et al., 2016; Panning et al., 2015) representing low source location errors, 10% epicentral distance, a moderate source location error, and 25% of the epicentral distance, corresponding to larger errors in location but still meeting the mission goals of InSight (NASA, 2018). We also altered the back azimuth by up to 10° (Panning et al., 2015). During an iteration of the algorithm, we altered the source location of each event which modified the predicted arrival times of S and ScS and affected the rotation of the horizontal components. The new location was not permanent; we recalculated an adjustment in the location for subsequent iterations. For example, a source location could be closer in one iteration, but farther in another iteration. The errors were randomized such that the error function could select a value between −1 and 1 (for 1° error) and add that value to the cited epicentral distance, then select a value between −10 and 10 and add that value to the cited back azimuth value. When we added ±1° errors in distance, the core depth uncertainties increased by ~ 8 km. When we altered epicentral distances by ± 25%, the algorithm only recovered a core in ~ 61% of the iterations, and the uncertainty in core depth was over 55 km. Since most of these errors were smaller than our terrestrial data errors (discussed in the following paragraphs), this suggests that a combination of factors affected our algorithm’s ability to recover the core depth.
4.2. Quantity and SNR effects of Real Events
Event SNR had less effect on core recovery than anticipated (Fig. 11). Low SNR events had higher recovery rates, more accurate core depths, and tended to have lower core depth uncertainties than high SNR data. This suggests that any event where S and ScS can be identified is useful in core detection. It also implies that by applying our signal-quality index and using phase-weighted stacking, as opposed to linear stacking, we are sufficiently weighting higher SNR data. Higher SNR events tended to be from larger Mw events, and as a result may be limited in their event locations. For a lengthier discussion on the effects of location biases see Section 4.4. Increasing the quantity of events reduced the core depth uncertainty but did not necessarily increase recovery rate or improve core depth accuracy. When stacking events with no SNR limitations, the core depth uncertainty dropped from 25.9 to 18.0 km.
Figure 11.
The effects of different SNR and quantity of events for a) recovery rate of a core depth b) mean core depth recovered with uncertainty and c) uncertainty in core depth. The dashed line in panel b) represents the PREM core depth for reference.
4.3. Location Alteration of Real Events
For the purposes of this study we assumed the distances reported in the NEIC PDE catalog are accurate (minimal location error), thus we considered any alterations to the cited distance and/or back azimuth as errors in locating the source. Smaller magnitude events inherently were less constrained than larger events on Earth because fewer stations detected them. Since InSight will be a single-station seismometer, this effect is absent on Mars.
We attempted to quantify location uncertainties here by randomly changing the cited epicentral distance by up 1° (Bose et al., 2017; Khan et al., 2016; Panning et al., 2015) representing low source location errors, 10% epicentral distance, a moderate source location error, and 25% of the epicentral distance, corresponding to larger errors in location but still meeting the mission goals of InSight (NASA, 2018). We also altered the back azimuth, as cited by the catalog, by up to 10° (Panning et al., 2015). During an iteration of the algorithm, we altered the source location of each event which modified the predicted arrival times of S and ScS and affected the rotation of the horizontal components. The new location was not permanent; we recalculated an adjustment in the location for subsequent iterations. For example, a source location could be closer in one iteration, but farther in another iteration. The errors were randomized such that the error function could select a value between −1 and 1 (for 1° error) and add that value to the cited epicentral distance, then select a value between −10 and 10 and add that value to the cited back azimuth value.
Adding error to the location affected the selection frequency of core models and the uncertainty in core depth (Fig. 12). In contrast to results from synthetic seismograms, but in line with real events, event SNR did not have any affect but increasing the quantity of events increased core depth recovery and decreased core depth uncertainty. When we altered the source epicentral distance by ±1°. In contrast to results from synthetic seismograms, but in line with real events, event SNR the core recovery rate dropped by 0-3% depending on the quantity and SNRs of events stacked (Table 2.0). The uncertainty in core depth increased by up to 11 km. Increasing source errors to up to ±10% epicentral distance further reduced recovery rates by ~4-19% and increased uncertainty in core depth by 14-28 km compared to using cited locations.
Figure 12.
The effects of added 1° (red), 10% epicentral distance (black) and 25% epicentral distance errors compared to known locations (blue). The known core depth (2891 km) is indicated by the dashed vertical line. Five, ScS only, events were used to generate to recover the core depth.
Table 2.0.
Effects of adding source location errors. Both have ±10° back azimuth errors and either ± 1°, ± 10 % or ± 25% epicentral distance errors.
| SNR | Source Distance Error |
3 Events | 5 events | 10 events | 15 events | ||||
|---|---|---|---|---|---|---|---|---|---|
| Recovery Rate (%) |
Uncertainty(km) | Recovery Rate (%) |
Uncertainty(km) | Recovery Rate (%) |
Uncertainty(km) | Recovery Rate (%) |
Uncertainty(km) | ||
| Low | 1° | 93.9 | 37.4 | 95.3 | 32.5 | 95.8 | 30.7 | 95.9 | 29.4 |
| 10% | 75.8 | 53.4 | 75.0 | 47 | 71.8 | 44.2 | 71.7 | 38.7 | |
| 25% | 50.0 | 64.3 | 56.1 | 57.7 | 67.6 | 53.8 | 70.2 | 53.8 | |
| Average | 1° | 92.6 | 35.5 | 92.5 | 31.4 | 91.2 | 29.2 | 90.0 | 25.9 |
| 10% | 86.0 | 51.7 | 86.4 | 46.3 | 86.7 | 39.2 | 87.4 | 35.9 | |
| 25% | 52.6 | 62.3 | 63.4 | 60.5 | 73.8 | 54.2 | 75.5 | 52.6 | |
| High | 1° | 88.0 | 37.5 | 88.6 | 31.3 | 88.4 | 28.1 | 89.4 | 26.7 |
| 10% | 80.5 | 50.9 | 83.7 | 46.6 | 84.0 | 39.6 | 83.9 | 37.4 | |
| 25% | 47.6 | 62.7 | 56.5 | 59.4 | 68.2 | 55.2 | 71.1 | 53.9 | |
| All | 1° | 93.4 | 36 | 94.3 | 32 | 94.4 | 29.2 | 95.8 | 28.0 |
| 10% | 79.5 | 53.2 | 80.3 | 48.3 | 77.4 | 40.4 | 76.8 | 39.0 | |
| 25% | 49.0 | 62.5 | 57.4 | 60.4 | 71.1 | 57.3 | 70.3 | 51.0 | |
| No Low | 1° | 92.0 | 34 | 91.3 | 31 | 89.3 | 27.7 | 89.6 | 26.3 |
| 10% | 85.2 | 52.3 | 83.7 | 45.7 | 84.1 | 39.4 | 85.1 | 35.7 | |
| 25% | 52.9 | 59 | 59.7 | 59.4 | 71.1 | 54.3 | 74.6 | 54.5 | |
When we modified the epicentral by ± 25%, the recovery rate dropped to 40-75%. The selection frequency distribution no longer resembled a Gaussian distribution; all models had similar selection rates until 15 events were used, and then accurate core depth become the most selected model. Increasing the number of events increased the recovery rate and allowed some models to become selected more frequently than others, but the uncertainty in core depth was still greater than 50 km.
These experiments indicate that if the number of events recorded by InSight is limited, then source location errors will need to be low to accurately recover a core depth through stacking ScS. Higher quantities of events produce stacks that are more resistant to the effects of source location errors. InSight may be limited by the number of events it can observe, but more data can be made available if ScS multiples are also stacked.
4.3. ScS Multiples
In addition to the ScS wave, we also investigated if the addition of ScS multiples to the stacked data could aid in the recovery of the core depth. Based on synthetics, we found that the amplitude ratio of ScS to its multiples was distance-dependent. For example, at a distance of 16° the ratio of ScS:ScS2 was 5.2:1, but at 56°, the ratio was 3.1:1. Synthetics also indicated that the multiples should decrease in amplitude. The ScS2:ScS3 amplitude ratio was typically around 3:1, while the ScS2:ScS4 was about 7:1. This was caused by the loss of energy when reflecting off the CMB and due to attenuation in the crust and mantle. In addition to the loss of energy, background noise also affected amplitudes of multiples. In many cases, the background noise of terrestrial events caused the amplitudes of ScS2, ScS3, and ScS4 to become comparable. Unlike ScS, the arrival times of most multiples could not be uniquely visually identified on individual seismograms due to poor signal-to-noise at the time of their arrival. ScSn multiples also see the crust 2*n times, meaning ScS2 sees the crust 4 times, while ScS4 sees the crust 8 times. The crust can create offset in travels times that our stacking algorithm does not take into account, defocusing the ScSn arrival. For these reasons, we determined mean offset times (Toff) using only ScS events and did not attempt to visually select the arrival of multiples.
The addition of ScS2 slightly increased recovery rates when the number of events was limited (<15 events) (Fig. 13a) and reduced core depth uncertainty (Fig 13c). Stacking beyond ScS2 reduced the recovery rate, especially when stacking numerous events. Multiples did not have a consistent effect on recovering an accurate core (Fig. 13b) or reduction in core depth uncertainty (Fig 13c). As mentioned earlier, multiples had much lower signal-to-noise ratios than ScS and S. After stacking, the stacked amplitude tended to remain above zero, but the poor signal of the multiple meant the uncertainty in the stack was relatively large, thus a coherent peak was not formed. The very low signals of the multiples had insufficient signals to create a coherent stack with 95% confidence bounds. If the number of ScS events is limited to less than five, then ScS2 could be used to recover the core depth, but there is no advantage to stacking additional multiples.
Figure 13.
Results from ScS multiples experiments with the dataset. Comparison of (a) Recovery Rate (b) Mean Core Depth and (c) Uncertainty using different ScS multiples. Algorithm was not limited by event SNR.
For ScS multiples, we also investigated how SNR and quantity affected the recovery of the core (Table 3.0). To investigate SNR effects, we only selected events that we considered average or above SNR and thus were more likely to have stronger multiple signals compared to the background noise. Like ScS, SNR did not have a significant effect on recovery rate or mean core depth. However, using high SNR data did tend to reduce core depth uncertainty, especially once more than 15 events were stacked. However, the recovery rate for those quantities were still below the recovery rates using only ScS. Thus, we maintain, ScS2 is only beneficial if there are less than 5 stackable ScS events.
Table 3.
Results of stacking ScS multiples. *ScS values are given for comparison, but refer to 3, 5, 10 and 15 events using only ScS.
| ScS Multiple | 9 events | 15 events | 30 events | 45 events | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Recovery Rate (%) | Mean – PREM Core Depth- [km] |
Uncertainty[km] | Recovery Rate (%) | Mean – PREM Core Depth- [km] |
Uncertainty[km] | Recovery Rate (%) | Mean – PREM Core Depth- [km] |
Uncertainty[km] | Recovery Rate (%) | Mean – PREM Core Depth- [km] |
Uncertainty[km] | ||
| ScS* | All SNR | 95.1 | 2.9 | 25.9 | 95.5 | 3.4 | 24.3 | 94.7 | 2.4 | 20 | 96.4 | 1.82 | 18 |
| No Low SNR | 93.1 | 6 | 25.5 | 90.8 | 7.4 | 23.3 | 88.6 | 7.4 | 21.7 | 91.3 | 8.5 | 21.5 | |
| ScS2 | All SNR | 96.1 | −3.3 | 24.4 | 90.6 | −5.6 | 22.2 | 66.1 | −0.6 | 23.8 | 52.1 | −2.9 | 20.4 |
| No Low SNR | 97 | −6.2 | 24.2 | 87.6 | −0.2 | 18.4 | 76.6 | −0.4 | 16.3 | 51.3 | 1.2 | 16.7 | |
| ScS3 | All SNR | 88.8 | 7 | 31.4 | 80.2 | −1.32 | 24.8 | 61 | −3.1 | 19.9 | 30.3 | −4.5 | 16.7 |
| No Low SNR | 90.1 | −2.9 | 26.2 | 70.4 | 2.8 | 23.5 | 59.1 | 4 | 10.4 | 32.8 | −3 | 8.8 | |
| ScS4 | All SNR | 74.7 | −1.3 | 30.7 | 49.4 | −1.3 | 27.9 | 25.7 | 4.6 | 16.7 | 8.7 | −0.2 | 17.5 |
| No Low SNR | 72.3 | 0.7 | 28.3 | 51.1 | −0.7 | 24 | 17 | −0.2 | 17.4 | 5.7 | −2.9 | 16.6 | |
We also tested source location errors when including multiples to see if they were still beneficial. When quantities of events were limited (<15 events), ScS2 increased the recovery rate and decreased core depth uncertainty compared to using only ScS. For 9 events (~3 could stack ScS) the recovery rate increased by 1%, 9%, and 9% and core depth uncertainty was reduced by 5km, 5km, and 3 km for 1°, 10%, and 25% errors, respectively. Stacking ScS3 produced similar results to stacking only ScS but stacking ScS4 greatly reduced the recovery rate. For 15 events, ScS2 reduced the recovery rate, but for 10% and 25% distance errors, also reduced core depth uncertainty. As with no added source location errors, once there were more than 5 ScS events, there were no benefits of stacking ScS2 or any additional multiples. The recovery rates were much lower than using ScS alone.
4.4. Mantle Heterogeneities
A key result of our investigations is that the core was not always found to be at the PREM depth, and the mean core depth could be up to 9 km from the PREM core depth (Fig. 10). There are several possible causes for this discrepancy 1) the presence of mantle shear velocity heterogeneities within the Earth, 2) source location errors, including event depth, 3) crustal thickness variations, and 4) possible CMB topography. As previously discussed, using the ScS-S differential travel times eliminated many travel time perturbations from source origin times, as well as crustal thickness variations on the source and receiver sides of the ScS path. The S and ScS waves have similar raypaths, especially for large epicentral distances, and thus both were affected similarly by event depth and crustal variations. For local and regional events (within 30°) where the S raypath is shallow, and ScS travels nearly vertically, crustal variations are still able to affect travel times. Thicker continental crust would exhibit slower velocities than the PREM average crustal values and cause ScS to arrive later than predicted (Christensen and Mooney, 1995; Rudnick et al., 1998). If the source locations cited in the catalog (NEIC PDE) are accurate to within 1° then the travel time uncertainty from source location errors translates to ~15 km in core depth errors. Furthermore, topography at the CMB can vary up to 2 km (Morelli and Dziewonski, 1987; Schlaphorst et al., 2016; Tanaka, 2010), adding to the uncertainty in core depth.
To determine if there were any systematic effects arising from mantle heterogeneity, we stacked events as a function of back azimuth quadrant and examined variations in core depth and recovery. Seismic waves traveling through an area with velocities higher than PREM resulted in the core reflected phase arriving earlier than predicted. This translates in our analysis of the ScS travel times to a shallower core depth. We used a tomographic shear-wave velocity model (S362ANI+M) of the mantle (Moulik and Ekstrom, 2014) to determine travel time heterogeneities along our sampled paths. We first computed the raypaths of ScS through the earth using the TauP Toolkit for each of our events. We used the tomographic velocity model along the path to compare the travel time delay or advance relative to the PREM one-dimensional travel time. We then show the location where the reflection off the core occurs, to determine the amount velocity varied from the average (Fig. 14a). Many of the travel paths in our dataset reflected off the CMB where shear velocities are relatively high (+1-2%).
Figure 14.
Possible sources of discrepancies in core depth measurements, a) Tomographic map of shear velocities heterogeneity near the CMB (2800 km) from (Moulik & Ekstrom, 2014). White points indicate points where ScS bounce points at the CMB for 8 common paths in our ScS dataset, b) Back azimuth (BA) stacks of the ScS dataset using five ScS events with any SNR.
The algorithm was re-run using only events within certain back azimuth ranges (Fig. 14b) and we compared the results to a tomography map of Vs near the core-mantle boundary. Although the map indicated that the northern hemisphere exhibits predominately faster velocity zones, we found that the most common bounce points (where ScS reflects off the core) tended to occur where the shear velocity was close to average. Therefore, the algorithm for 0-90° (blue in Fig. 14b) selected core depths only 10 km shallower than PREM most often and the overall mean was 7.5 km shallower than PREM. The quadrant of 90-180° produced similar results where common bounce points occur in regions of faster than average shear velocities, thus result in a mean core depth of 5 km shallower than PREM. The tomography model suggested that events with origins near the Mediterranean (Greece, Turkey, Italy) should have travel times that arrived ~4 seconds earlier than PREM corresponding to a ~15 km shallower core depth model. Events originating near the East African Rift passed through regions that closely matched PREM’s velocities resulting in travel time distances that were within 1 second of PREM. However, CMB topography and crustal variations could have caused the selection of PREM or deeper core depth models. The CMB was deeper than average (~2.5 km) underneath Northeast Africa and the Mediterranean Sea where many of the bounce points occur (Morelli and Dziewonski, 1987). A 2.5 km deeper core would cause errors of 1 s or about 4 km. The fast area around the Mediterranean has also been disputed (Lekic et al., 2012), thus the region may experience velocities closer to average values than suggested in the figure. These combinations of effects would explain why a deeper core depth was recovered, despite the faster than average velocities in Figure 14a.
In the 270-360° quadrant (green dashed), the algorithm selected many models deeper than PREM, but also selected a handful of models much shallower than PREM. Many events in this range originated in the Pacific Northwest with a bounce point in a relatively fast shear velocity area while events that occurred along the Mid-Atlantic Ridge tended to reflect off in regions of average or slower than average velocities. An event originating in Aleutians would recover a core depth nearly 70 km shallower than PREM but events originating near Iceland or the Mid-Atlantic Ridge would pick core depths within 10 km of PREM.
In the 180-270° region (solid black), some bounce points occurred in or around the large-low shear velocity province (LLSVP) situated beneath Africa which slowed the ScS wave causing the algorithm to select deeper core depths. For example, an event that occurs along the Mid-Atlantic Ridge (near approximately 0°N, 30°W) would pick a core about 30 km deeper than PREM. As indicated in Fig. 14B, that back azimuth range consistently picked deep core depths and the most selected core depth range was 40 km deeper than PREM. Core topography could also have influenced our results by up to 5 km (Morelli and Dziewonski, 1987; Schlaphorst et al., 2016; Tanaka, 2010). The CMB under the South Atlantic had slower than average velocities combined with a deeper core depth, both of which would cause delays in the ScS arrival, leading to the recovery of a deeper core depth.
5. Analysis and Discussion
Our experiments showed that the depth of the terrestrial core was recovered by stacking at least three ScS recordings on a single-station, with an uncertainty in core depth of less than 31 km. This requires that the sources are well located (<1° error in distance), and the velocity model derived from other types of data is reasonably constrained. Increasing the quantity of events consistently led to decreases in core depth uncertainty and tended to increase the recovery rate. We found that low SNR events were able to recover the core better than requiring only high SNR events. For InSight, this implies that any event where S and ScS can be identified will be invaluable for core depth analysis. Small source location errors (<1°) caused core depth uncertainty to increase by <10 km and decreased the chances of recovering a core depth by <3 %. Larger uncertainties (25%) in source location reduced the chances of core recovery down to a minimum of 49%. The addition of ScS2 helped reduced the effects of source location errors when the number of ScS events was limited. However, ScS multiples should be avoided once there are more than 5 ScS events. The following section delineates how to extrapolate our terrestrial results to Mars.
5.1. Comparison to Mars
We chose PREM as our Earth reference model because it is a relatively simple one-dimensional velocity model with a single average crustal thickness and no topography at the CMB, which are the same assumptions made by existing Martian models (Sohl et al., 2005; Sohl and Spohn, 1997; Zheng et al., 2015). More importantly, PREM was based on seismological and geodetic constraints including seismic velocity, attenuation, and density, the same constraints that InSight will provide. The InSight team plans to produce an initial model of Mars as velocity information from seismic events becomes available during the science monitoring phase of the mission (Panning et al., 2017). Impacts with known source locations will provide Vp-Vs differential profiles, and large events will provide Rayleigh and Love wave group velocities that constrain S velocity. Multiple surface wave orbits allow for more precise source locations that reduce error during velocity inversions. The dispersion of surface waves from small events may not be as precise but can still provide data for inversion of Martian crustal structure. A Bayesian inversion approach (Drilleau et al., 2013; Khan & Connolly, 2008; Khan et al., 2000; Panning et al., 2015) will be implemented with a limited dataset of arrival times and surface wave dispersions to derive shear and compressional wave velocities at greater depths. The inversions will use additional constraints from mineral physics modeling and geophysical constraints such as moment of inertia and tidal love numbers (Khan et al., 2016; Rivoldini et al., 2011). As more data is collected, it is anticipated that the interior structure model can be updated and refined to become more accurate. If the scientific goal for interior models is met (within 5% accuracy) (NASA, 2018) then the velocity models would be comparable to the variation of velocities seen in tomographic models on Earth (~3% velocity variation) (Moulik and Ekstrom, 2014). The recovery of the Martian core will rely on the InSight mission’s ability to produce an accurate model of the crust and mantle velocities.
The recovery of the Martian core using ScS stacking is dependent upon the SNR of the ScS waveforms. We anticipate that many of the sources we stack will come from double-couple events with identifiable S wave energy. For Mars, we assume scattering will be less than that of the Moon due to the lack of megaregolith. As exemplified by the lunar data, even highly scattered signals can produce a result. If the scattering effects are closer to the Moon than Earth, our approach still resembles the approach used by Weber et al. (2011) that recovered the lunar core. If scattering on Mars is large, recovery of the core will likely be more difficult and may require a larger number of events that can be stacked. The addition of a polarization filter, similar to what was used for the Apollo seismic data on the Moon (Weber et al., 2011) could be implemented to mitigate scattering effects if present on Mars.
Core recovery will also be more difficult if attenuation on Mars is higher than on Earth. On Earth, mantle attenuation has been constrained using ScS and ScS multiples (Kovach and Anderson, 1964; Lawrence & Wysession, 2006; Yoshida & Tsujiura, 1975) and ScS or ScS multiples may be used to constrain Martian mantle attenuation. Seismic quality factor (Q) on Mars will be lower in the mantle compared to Earth’s (130 compared to Earth’s 312) (Lognonné et al., 1993; Nimmo and Faul, 2013) but higher in the crust compared to Earth (Panning et al., 2015). Mars has a radius equal to about half of Earth’s thus greatly reducing the travel path length, and consequently reducing the geometric spreading, overall attenuation, and scattering of raypaths. The decay of the ScS (or its multiples) amplitude is a function of the depth of each layer divided by the product of the layer’s velocity and seismic quality factor. On Mars, the lithosphere is thicker than on Earth while the Q is greater, and the reverse is true for the mantle. Core reflected waves will be more affected by attenuation in the mantle than the crust, but since the mantle of Mars is about half the thickness of Earth’s mantle, Q of Mars would have to be less than half of Earth’s Q to begin degrading ScS. This agrees with Panning et al., (2017) who found attenuation can be an order of magnitude higher than expected without significant detriment to the recovery of Vs and the detection of events.
Ultimately, the recovery of the core may depend on the number of detected events, and core phases. If InSight records several high SNR events in which scattering is minimal and source locations are well constrained, then not only will the core be recoverable, but we will also be able to investigate the lowermost mantle. Although impacts would provide numerous sources with low location errors, their source mechanism is not well suited for producing SH energy for stacking purposes (Banks et al., 2015; Schmerr et al., 2016). Our experiments show that core retrieval requires non-impact events with Mw > 4.0. Ideally, we need several large events for core retrieval, but Martian seismicity estimates indicate InSight is unlikely to record any events with MW>6.0 (Panning et al., 2017), thus we avoided selection of large events in our algorithm. Furthermore, in our analysis, we assume events occurred at the surface and further excluded deep seismicity events from our catalog. For Mars, we expect many of the marsquakes will be relatively shallow (<100 km) compared to deep terrestrial events. On Earth, deep quakes are caused by subducting slabs, a feature more than likely absent on Mars. On the Moon, deep moonquakes were caused by tides from the Earth and Sun (Bulow et al., 2007; Kawamura et al., 2017). Mars is unlikely to experience similar tidal effects due to the smaller size of its moons; Deimos and Phobos, although the thicker lithosphere would expand the brittle/ductile transition to great depths (Montési and Zuber, 2003).
5.2. Detecting mantle heterogeneities
The back-azimuth study revealed that a range in the core may be indicative of the presence of crustal and mantle heterogeneities as the core would occur at similar depths around the planet, barring significant CMB topography (small for the Earth). For example, if InSight detects events originating in both the northern and southern hemispheres of Mars, it is possible to compare the travel times for each direction to determine if the surface dichotomy extends deeper into the planet. On Mars the crustal thickness varies greatly between the Northern and Southern hemisphere possibly due to mantle convection or from a giant impact (Andrews-Hanna et al., 2008; Golabek et al., 2011; Smith & Zuber, 1996; Thiriet et al., 2018; Wilhelms & Squyres, 1984; Zuber, 2001). If the events from different hemispheres retrieve different best fitting models for the core, this could indicate core topography, but such discrepancies are more likely caused by mantle heterogeneities.
On Earth, temperature and density increases reduce seismic velocities and are the implied mechanism for Large Low Shear Velocity Provinces (LLSVPs). Ultra-Low Velocity Zones (ULVZs) may further reduce seismic velocities due to increased melt, enhancement of MgO concentrations, core leakage, or other compositional variations. Alternatively, cold material from sinking slabs increases seismic velocities. In our back-azimuth study, the most frequently selected core depth was up to 40 km deeper than the PREM depth but in the region of 90-270° (which contains the African LLSVP) less than 10% of the recovered core depths were 50km or deeper than PREM. This suggests few raypaths sampled the LLSVP. The identification of such features on Mars would require careful study of pre and post-cursory waveform effects. For example, the postcursors, Scd and Sab (Thorne et al., 2007), along with precursors from reflections off D” (Hernlund et al., 2005) have been used to investigate the thermal boundary layer above the CMB.
Investigations into the lower mantle of Mars will have important implications in understanding the thermal evolution of Mars. A layer of bridgmanite might exist if lowermost Martian mantle temperatures are high enough and the core is sufficiently small (Elkins-Tanton et al., 2003; Nimmo and Stevenson, 2000; Ruedas et al., 2013). Such a feature would have a shear velocity 4-5% higher than the shallower mantle in similar fashion to the Earth’s seismic discontinuity at depths of 660 km. Like Earth, a high temperature plume source region beneath Tharsis and/or Elysium would produce seismic velocities slower than the rest of the planet. Alternatively, sinking cold material would create regions of faster than average velocities. With sufficient seismicity and good source locations, these lowermost mantle features could be identified using the same back azimuth approach we used for ScS in this study. InSight would need to detect 3-5 events located over multiple back azimuths to examine the existence of any travel time heterogeneity.
5.3. Benefits/Negatives of using Multiples
ScS2 was helpful in increasing the recovery rate and reducing core depth uncertainty when there was a limited number of events or source locations were uncertain. ScS3 and ScS4 had weak signals that created large uncertainties in the stacked amplitude. These uncertainties prevented the recovery of the core and for that reason, stacking ScS3 and ScS4 should be avoided unless a method is developed to correct for their defocusing. ScS2 also stopped being beneficial once there were five or more ScS events for similar reasons. Since the multiple can occur at a wider range of distances, and can also occur when ScS occurs, it was not uncommon for the number of ScS2 stacks to outnumber ScS stacks.
5.4. Blind Test
In preparation for the data collected by InSight, a blind test was constructed using synthetic seismogram for expected Martian seismicity and noise (Ceylan et al., 2017; Clinton et al., 2017; Van Driel et al., submitted). This blind test consisted of one year of continuous seismic data calculated using one of postulated fourteen internal structure models with core depths ranging from 1539-1870.4 km (Table 4). The input model, EH45Tcoldcrust1b, had a core depth of 1671.5 km. The seismic data were disturbed with seismic noise as predicted by Mimoun et al. (2017). The test was designed so that participants could attempt to detect, locate, and identify sources of seismicity and ultimately try to determine which interior model was used to construct the blind test. The creators of the blind test have since released the interior model used to create the synthetic series, which allowed us to verify if our method worked. We used the InSight blind test data to determine if our method could recover the correct internal structure model. We used the true source locations to select onset times to pick S, and if possible, ScS arrivals. The blindtest source locations were publicly released after the end of the test, and during the mission the Mars Quake Service will provide source location estimates (Panning et al., 2017) with the expected uncertainty discussed above. We used the geographic locations to compute source receiver azimuths, and rotate the three component seismograms into radial, transverse and vertical components. We initial used a bandpass filter mimicking that of Earth (10-20 s) but tested additional filters. The sampling rate of the blind test (2 Hz) is lower than BFO’s sampling rate (1000 Hz) but is the same as that of the continuous data channel from Mars and reduces the Nyquist frequency to 1 Hz. Reducing the lower bandpass below 10 s allowed high frequency noise that can make it more difficult to identify S. Longer periods beyond 25 s tend to make it more difficult to separate S from ScS when they get close to merging. Therefore, we chose to adjust our filter from 10-20 seconds for terrestrial data to 10-25 seconds for synthetic Martian data. This allowed us the opportunity to stack events over a larger distance range and enhanced the S arrival relative to the background. We can further adjust our filters and tapers once the background noise of Mars has been established. Of the 204 events in the blind test, we were able to identify S in 7 events and ScS in 3 of those events (Fig. 15), knowing the true event location. ScS2 and ScS3 are predicted to appear without coincident phases in 3 events and 6 events, respectively. We used the provided models to determine a range over which S was predicted to occur. We then selected S based on the waveform and picked the amplitude maximum. The range of predicted time of arrivals was calculated for ScS. If any of the predicted times fell within the arrival of the surface wave, we did not use the event for ScS stacking. We also chose not to stack for ScS if the arrival windows of S and ScS overlapped. This was caused when shallow core depths would predict an early ScS arrival compared to slower moving S waves of other models.
Table 4.
Possible Interior Models for the blind test constructed by Clinton et al. 2017.
| Model Name | Source | Core Depth fkml | Moho Depth [km] |
|---|---|---|---|
| DWAK | Khan et al. (2016) | 1704 | 66 |
| EH45ThotCrust2 | Rivoldini et al. (2011) | 1594 | 85 |
| EH45Tcold | Rivoldini et al. (2011) | 1539 | 90 |
| EH45TcoldCrust1 | Rivoldini et al. (2011) | 1671.5 | 85 |
| EH45TcoldCrust1b | Rivoldini et al. (2011) | 1671.5 | 85 |
| EH45ThotCrust2b | Rivoldini et al. (2011) | 1594 | 85 |
| DWThot | Rivoldini et al. (2011) | 1634 | 90 |
| DWThotCrust1 | Rivoldini et al. (2011) | 1584 | 90 |
| DWThotCrust1b | Rivoldini et al. (2011) | 1584 | 90 |
| Gudkova | Zharkov and Gudkova (2005) | 1591 | 50 |
| LEAK | Khan et al. (2016) | 1659 | 56 |
| MAAK | Khan et al. (2016) | 1808 | 69 |
| SANAK | Khan et al. (2016) | 1870 | 32 |
| TAYAK | Khan et al. (2016) | 1597 | 77 |
Fig. 15.
Transverse component seismograms from the InSight blind test aligned on the where we picked the S or Sdiff phases. The shaded regions indicate the range of arrival times for ScS across the 14 potential interior structure models of Mars calculated using TauP. Seismograms were nonnalized for viewing purposes.
One complication of the Martian blind test compared to the terrestrial test is the presence of shadow zones. In Fig. 16b, many models don’t show smooth ScS-S arrival times. Part of this is due to triplication of the S wave following an immediate shadow zone. As with the terrestrial data, if triplication occurred, we chose the first arriving S wave as our S arrival time. To compensate for the shadow zone, we linearly interpolated to approximate when S would have arrived for the purposes of plotting the anticipated time difference. Some models like EH45ThotCrust had large shadow zones spanning over 40°, while models like Gudkova had shadow zones smaller than 5°. To avoid selecting SS or another body wave instead of S we chose not to stack events that occurred within any model’s shadow zone.
Fig. 16.
a) S velocities through the crust, mantle and core. Figure is adapted from (Clinton et al., 2017). b) We used TauP to generate arrival times of ScS relative to S for each of the 14 models. When triplication of S occurred, the first arriving S time was chosen. If TauP predicted a shadow zone for S, we interpolated the S time arrival.
We followed our terrestrial algorithm by applying a bandpass filter (10-25 seconds, instead of 10-20 seconds for reasons stated above) and calculating a signal quality factor using the same procedure in Section 3.3. We stacked along the predicted moveout of ScS and ScS2 relative to S for each velocity model. Following our terrestrial analog results, when only three ScS events are available, ScS2 aids in core depth recovery. When stacking ScS alone, six out of the fourteen models produced positive amplitudes within the bootstrap derived uncertainty (Fig. 17). The model with the greatest stacked amplitude was EH45TColdCrust1b followed by EH45TColdCrust1, DWThot, DWAK, EH45Tcold, and TAYAK. Note that EH45TColdCrust1b and EH45TColdCrust1 vary only in the crust where 1b has a 1km thick slow velocity zone at the surface. The accurate core depth was 1671.5 km, and the models with coherent peaks had core-depths ranging from 1539 km - 1704 km. If we also considered a maximum value of Toff (average time between visually selected arrival and model’s predicted arrival) then only DWThot, EH45TcoldCrust1 and Eh45TcoldCrust1b could be considered. This would reduce the range in core depths down to 1634-1671.5 km. When ScS2 was added, EH45TColdCrust1 and TAYAK no longer had positive amplitudes within uncertainty. DWThot now had the greatest stacked amplitude.
Fig. 17.
Stacked amplitudes of InSight blind test data along the predicted moveouts for 14 interior structure models. The mean stacked amplitude (red) and 95% confidence intervals (shaded in pink) are derived from a bootstrap resample of the data. The reference distance is 45° and only ScS was used for stacking.
We used the six models with positive values at Tpred to quantify the uncertainty in core depth. We found the width of the signal peak at Tpred and converted time to core depth. By assuming the reference velocity model used to create the stacks, we converted the time at our reference distance to a core depth. This reference model would need to be derived from other seismic phases, including body waves that sample the crust and mantle (Panning et al., 2017). For each model we were able to recover a range of core depths that would create a coherent ScS peak (Fig. 17). The distribution of core depths results in an overall recovery rate of 1630.9 ± 58.2 km. The core depth range of 1670-1680 km including the inputted (accurate) depth of 1671.5km, was the most selected core depth, suggesting recovery of the core depth. The uncertainty of 58 km is larger than our predicted core depth uncertainty of 26 km for 3 events. Using ScS2, would have increased the uncertainty to 66 km and retrieved a shallower core depth (1639 km).
The main difference between the terrestrial analog study, and the blind test is the use of accurate interior models. When the inputted interior model was used in the blind test stack, a clear coherent peak was present at the time of arrival. In addition to changes in the core depth, the models also had variations in Moho depths and velocities within the crust and mantle (Fig. 18). For example, SANAK has a Moho depth of 32 km with S velocities ranging from 1.9-3.4 km/s. At 45° it takes ScS about 23.1 seconds, versus 52.6 seconds it takes EH45TcoldCrust1b, to travel through the crust. SANAK also has a much deeper core (1870 versus 1671 km). It takes about 884 seconds for ScS to travel through the mantle based on the SANAK model, but only 762 seconds based on the correct model. Because the models vary in crustal and mantle velocities, the moveouts of the different models can cross each other. For example, at 10° the model DWThot predicts ScS should arrive ~580 seconds after S, about 5 seconds after than the correct model. However, at 45° the model DWThot predicts ScS should arrive ~220 seconds after S, about 12 seconds sooner than the correct model. Depending on the epicentral distance of the event, more than one model may accurately predict the arrival of ScS relative to S. For the reason, it is important to consider the moveout of ScS and not just the arrival of a single event.
Fig. 18.
Recovered core depths using models with coherent stacks around Tpred Most recovered models fall within the red lines indicating the maximum and minimum core depths of all interior models. The dashed line indicates the input model’s core depth (1671.5 km). In addition to the mean and standard deviation we also report the median with 15th and 85th percentiles, as the distribution is not a normal gaussian.
6. Conclusions
Our approach shows that it is possible to correctly recover the size of the terrestrial core with as few as three ScS events recorded at a single-station seismometer, assuming relatively precise source locations (<1°) and an accurate reference background 1D crust and mantle velocity model. Given estimates of Martian seismicity and uncertainty in mantle structure we anticipate we can recover the Martian core within 40 km if the errors in source location are small (<10% epicentral distance). Larger source location errors (>25%) would require larger quantities of events to constrain the core depth. A blind test of synthetic Martian seismograms indicated core depth uncertainties could be larger by 20 km if inaccurate internal models are used.
In addition to locating the depth of the CMB, our analysis shows how the single-station seismometer provided by InSight can be used to infer mantle heterogeneities on Mars. Both topography at the CMB and velocity heterogeneities in mantle would cause changes in travel times and waveforms for seismic phases traveling along different raypaths. Investigating these variations based on back-azimuth could reveal if the Martian mantle and CMB are more or less heterogeneous than the Earth.
Acknowledgments
AGM, MEB, ID and NCS were supported by NASA MFRP grant: NNX14AQ92G and 80NSSC18K1628. A portion of this research (ID) was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with the National Aeronautics and Space Administration. We thank S. Ceylan, M. Drilleau, M. van Driel and B. Kendar for their work on preparing the blindtest dataset. We also thank Jessica Irving, Simon Stähler, and Renee Weber for their helpful comments and discussions. This paper is InSight contribution number 90.
Footnotes
Declarations of interest: none
Dataset
Terrestrial Events were downloaded from IRIS DMC using National Earthquake Information Center, Preliminary Determination of Epicenters (NEIC PDE) catalog (Guy et al., 2015). Blindtest data and internal models were downloaded from http://blindtest.mars.ethz.ch/ .
References
- Andrews-Hanna JC, Zuber MT, Banerdt WB, 2008. The Borealis basin and the origin of the martian crustal dichotomy. Nature 453, 1212–1215. 10.1038/nature07011 [DOI] [PubMed] [Google Scholar]
- Ardhuin F, Stutzmann E, Schimmel M, Mangeney A, 2001. Ocean wave sources of seismic noise. J. Geophys. Res. Ocean. 116 10.1029/2011JC006952 [DOI] [Google Scholar]
- Banerdt B, Landis ME, 2010. Getting Under Mars’ Skin: The InSight Mission to the Deep Interior of Mars, in: American Geophysical Union; San Francisco, pp. DI52B–06. [Google Scholar]
- Banerdt WB, Smrekar SE, Hoffman T, Spath S, Lognonné P, Spohn T, Stone H, Willis J, Feldman J, De Paula R, Turner R, Asmar S, Banfield D, Christensen U, Clinton J, Dehant V, Folkner W, Garcia RF, Giardini D, Golombek MP, Grott M, Hudson TL, Johnson C, Kargl G, Knapmeyer-endrun B, Maki JN, Mimoun D, Mocquet A, Morgan P, Panning MP, Pike WT, Russell CT, Teanby NA, Tromp J, Weber RC, Wieczorek MA, Hurst K, Barrrett E, Team TI, 2017. The InSight Mission for 2018. LPSC 48 1896 10.1029/2007JE002905. [DOI] [Google Scholar]
- Banks ME, Daubar IJ, Schmerr NC, Golombek MP, 2015. Predicted Seismic Signatures of Recent Dated Maritan Impact Events: Implications for the InSight Lander. LPSCXLVI. [Google Scholar]
- Barazangi M, Isacks BL, 1976. Spatial distribution of earthquakes and subduction of the Nazca plate beneath South America. Geology 4, 686 [DOI] [Google Scholar]
- Bills BG, Neumann GA, Smith DE, Zuber MT, 2005. Improved estimate of tidal dissipation within Mars from MOLA observations of the shadow of Phobos. J. Geophys. Res. 110, E07004 10.1029/2004JE002376 [DOI] [Google Scholar]
- Binder AB, Oberst J, 1985. High stress shallow moonquakes: evidence for an initially totally molten moon. Earth Planet. Sci. Lett, 10.1016/0012-821X(85)90018-4 [DOI] [Google Scholar]
- Bose M, Clinton J, Ceylan S, Euchner F, vanDriel M, Khan A, Giardini D, Lognonne P, Banerdt B, 2017. A probabilistic framework for single-station location of seismicity on Earth and Mars. Phys. Earth Planet. Inter. 262, 48–65. 10.1016/j.pepi.2016.11.003 [DOI] [Google Scholar]
- Buffett BA, Garnero EJ, Jeanloz R, 2000. Sediments at the Top of Earth’s Core. Science. 290, 1338 LP–1342. [DOI] [PubMed] [Google Scholar]
- Bulow RC, Johnson CL, Bills BG, Shearer PM, 2007. Temporal and spatial properties of some deep moonquake clusters. J. Geophys. Res. E Planets 112, 1–12. 10.1029/2006JE002847 [DOI] [Google Scholar]
- Burke K, Steinberger B, Torsvik TH, Smethurst MA, 2008. Plume Generation Zones at the margins of Large Low Shear Velocity Provinces on the core-mantle boundary. Earth Planet. Sci. Lett. 265, 49–60. 10.1016/j.epsl.2007.09.042 [DOI] [Google Scholar]
- Ceylan S, van Driel M, Euchner F, Khan A, Clinton J, Krischer L, Böse M, Stähler S, Giardini D, 2017. From Initial Models of Seismicity, Structure and Noise to Synthetic Seismograms for Mars. Space Sci. Rev. 211, 595–610. 10.1007/s11214-017-0380-6 [DOI] [Google Scholar]
- Christensen NI, Mooney WD, 1995. Seismic velocity structure and composition of the continental crust: A global view. J. Geophys. Res. Solid Earth 100, 9761–9788. 10.1029/95JB00259 [DOI] [Google Scholar]
- Clinton JF, Giardini D, Lognonné P, Banerdt B, van Driel M, Drilleau M, Murdoch N, Panning M, Garcia R, Mimoun D, Golombek M, Tromp J, Weber R, Bäse M, Ceylan S, Daubar I, Kenda B, Khan A, Perrin L, Spiga A, 2017. Preparing for InSight: An Invitation to Participate in a Blind Test for Martian Seismicity. Seismol. Res. Lett. 88, 1290–1302. 10.1785/0220170094 [DOI] [Google Scholar]
- Creager KC, Jordan TH, 1986. Aspherical structure of the core-mantle boundary from PKP travel times. Geophys. Res. Lett. 13, 1497–1500. 10.1029/GL013i013p01497 [DOI] [Google Scholar]
- Crotwell HP, Owens TJ, Ritsema J, 1999. The TauP Toolkit: Flexible Seismic Travel-time and Ray-path Utilities. Seismol. Res. Lett. 70, 154–160. 10.1785/gssrl.70.2.154 [DOI] [Google Scholar]
- Doornbos DJ, Hilton T, 1989. Models of the core-mantle boundary and the travel times of internally reflected core phases. J. Geophys. Res. Solid Earth 94, 15741–15751. 10.1029/JB094iB11p15741 [DOI] [Google Scholar]
- Drilleau M, Beucler É, Mocquet A, Verhoeven O, Moebs G, Burgos G, Montagner J-P, Vacher P, 2013. A Bayesian approach to infer radial models of temperature and anisotropy in the transition zone from surface wave dispersion curves. Geophys. J. Int. 195, 1165–1183. 10.1093/gji/ggt284 [DOI] [Google Scholar]
- Dziewonski AM, 1984. Mapping the lower mantle: Determination of lateral heterogeneity in P velocity up to degree and order 6. J. Geophys. Res. Solid Earth 89, 5929–5952. 10.1029/JB089iB07p05929 [DOI] [Google Scholar]
- Dziewonski AM, Anderson DL, 1981. Preliminary Reference Earth Model. Phys. Earth Planet. Inter. 25, 297–356. [Google Scholar]
- Dziewonski AM, Hager BH, O’Connell RJ, 1977. Large-scale heterogeneities in the lower mantle. J. Geophys. Res. 82, 239–255. 10.1029/JB082i002p00239 [DOI] [Google Scholar]
- Efron B, Tibshirani R, 1997. Improvements on Cross-Validation: The 632+ Bootstrap Method. J. Am. Stat. Assoc. 92, 548–560. 10.1080/01621459.1997.10474007 [DOI] [Google Scholar]
- Elkins-Tanton LT, Parmentier EM, Hess PC, 2003. Magma ocean fractional crystallization and cumulate overturn in terrestrial planets: Implications for Mars. Meteorit. Planet. Sci 38, 1753–1771. [Google Scholar]
- Folkner WM, Yoder CF, Yuan DN, Standish EM, Preston RA, 1997. Interior structure and seasonal mass redistribution of Mars from radio tracking of Mars Pathfinder. Science (80-, ). 278, 1749–1752. 10.1126/science.278.5344.1749 [DOI] [PubMed] [Google Scholar]
- Friederich W, Dalkolmo J, 1995. Complete synthetic seismograms for a spherically symmetric earth by a numerical computation of the Green’s function in the frequency domain. Geophys. J. Int 122, 537–550. 10.1111/j.1365-246X.1995.tb07012.x [DOI] [Google Scholar]
- Fukao Y, 1984. Evidence from Core-Reflected Shear-Waves for Anisotropy in the Earths Mantle. Nature 309, 695–698. 10.1038/309695a0 [DOI] [Google Scholar]
- Garcia R, Souriau A, 2000. Amplitude of the core-mantle boundary topography estimated by stochastic analysis of core phases. Phys. Earth Planet. Inter 117, 345–359. 10.1016/S0031-9201(99)00106-5 [DOI] [Google Scholar]
- Garcia RF, Gagnepain-Beyneix J, Chevrot S, Lognonne P, 2011. Very preliminary reference Moon model. Phys. Earth Planet. Inter 188, 96–113. 10.1016/j.pepi.2011.06.015 [DOI] [Google Scholar]
- Garnero EJ, 2000. Heterogeneity of the Lowermost Mantle. Annu. Rev. Earth Planet. Sci 28, 509–537. 10.1146/annurev.earth.28.1.509 [DOI] [Google Scholar]
- Garnero EJ, McNamara AK, 2008. Structure and dynamics of Earth’s lower mantle. Science. 320, 626–628. 10.1126/science.1148028 [DOI] [PubMed] [Google Scholar]
- Gellert R, Rieder R, Anderson RC, Brückner J, Clark BC, Dreibus G, Economou T, Klingelhöfer G, Lugmair GW, Ming DW, Squyres SW, d'Uston C, Wänke H, Yen A, Zipfel J, 2004. Chemistry of Rocks and Soils in Gusev Crater from the Alpha Particle X-ray Spectrometer. Science. 305, 829 LP–832. 10.1126/science.1099913 [DOI] [PubMed] [Google Scholar]
- Golabek GJ, Keller T, Gerya TV, Zhu G, Tackley PJ, Connolly JAD, 2011. Origin of the martian dichotomy and Tharsis from a giant impact causing massive magmatism. Icarus 215, 346–357. 10.1016/J.ICARUS.2011.06.012 [DOI] [Google Scholar]
- Goldstein P, Dodge D, Firpo M, Lawrence LM, 2003. SAC2000: Signal Processing and Analysis Tools for Seismologists and Engineers. [Google Scholar]
- Golombek MP, 2002. A revision of Mars seismicity from surface faulting. LPSCXXXIII. [DOI] [PubMed] [Google Scholar]
- Gudkova TV, Zharkov VN, 2004. Mars: interior structure and excitation of free oscillations. Phys. Earth Planet. Inter. 142, 1–22. 10.1016/j.pepi.2003.10.004 [DOI] [Google Scholar]
- Gutenberg B, 1913. Uber die Konstitution des Erdinnern, erschlossen aus Erdbebenbeobachtungen. Phys. Z 14, 1217–1218. [Google Scholar]
- Guy MR, Patton JM, Fee J, Hearne M, Martinez E, Ketchum D, Worden C, Quitoriano V, Hunter E, Smoczyk G, Schwarz S, 2015. National Earthquake Information Center systems overview and integration, Open-File Report. Reston, VA. 10.3133/ofr20151120 [DOI] [Google Scholar]
- Harry Y McSween J, 1994. What we have learned about Mars from SNC meteorites. Meteoritics 29, 757–779. [Google Scholar]
- Hartmann WK, 1973. Ancient lunar mega-regolith and subsurface structure. Icarus 18, 634–636. 10.1016/0019-1035(73)90066-3 [DOI] [Google Scholar]
- Hecht MH, Kounaves SP, Quinn RC, West SJ, Young SMM, Ming DW, Catling DC, Clark BC, Boynton WV, Hoffman J, DeFlores LP, Gospodinova K, Kapit J, Smith PH, 2009. Detection of Perchlorate and the Soluble Chemistry of Martian Soil at the Phoenix Lander Site. Science. 325, 64 LP–67. 10.1126/science.1172466 [DOI] [PubMed] [Google Scholar]
- Hernlund JW, Thomas C, Tackley PJ, 2005. A doubling of the post-perovskite phase boundary and structure of the Earth’s lowermost mantle. Nature 434, 882–886. 10.1038/nature03472 [DOI] [PubMed] [Google Scholar]
- Hutko AR, Lay T, Garnero EJ, Revenaugh J, 2006. Seismic detection of folded, subducted lithosphere at the core-mantle boundary. Nature 441, 333–336. 10.1038/nature04757 [DOI] [PubMed] [Google Scholar]
- Ishii M, Tromp J, 2004. Constraining large-scale mantle heterogeneity using mantle and inner-core sensitive normal modes. Phys. Earth Planet. Inter. 146, 113–124. 10.1016/J.PEPI.2003.06.012 [DOI] [Google Scholar]
- Kawamura T, Lognonné P, Nishikawa Y, Tanaka S, 2017. Evaluation of deep moonquake source parameters: Implication for fault characteristics and thermal state. J. Geophys. Res. Planets 122, 1487–1504. https://doi.org/10,1002/2016JE005147 [Google Scholar]
- Kellogg LH, Hager BH, van der Hilst RD, 1999. Compositional Stratification in the Deep Mantle. Science 283, 1881–1884. 10.1126/science.283.5409.1881 [DOI] [PubMed] [Google Scholar]
- Kendall J-M, Silver PG, 1996. Constraints from seismic anisotropy on the nature of the lowermost mantle. Nature 381, 409. [Google Scholar]
- Kennett BLN, Engdahl ER, Buland R, 1995. Constraints on seismic velocities in the Earth from traveltimes. Geophys. J. Int. 122, 108–124. 10.1111/j.1365-246X.1995.tb03540.x [DOI] [Google Scholar]
- Khan A, Connolly JAD, 2008. Constraining the composition and thermal state of Mars from inversion of geophysical data. J. Geophys. Res. Planets 113 [Google Scholar]
- Khan A, Liebske, Rozel A, Rivoldini A, Nimmo F, Connolly JAD, Plesa A-C, Giardini D, 2017. A geophysical perspective on the bulk composition of Mars. J. Geophys. Res. Planets. 10.1002/2017JE005371 [DOI] [Google Scholar]
- Khan A, Mosegaard K, Rasmussen KL, 2000. A new seismic velocity model for the Moon from a Monte Carlo inversion of the Apollo lunar seismic data. Geophys. Res. Lett. 27, 1591–1594. 10.1029/1999GL008452 [DOI] [Google Scholar]
- Khan A, van Driel M, Bose M, Giardini D, Ceylan S, Yan J, Clinton J, Euchner F, Lognonne P, Murdoch N, Mimoun D, Panning M, Knapmeyer M, Banerdt WB, 2016. Single-station and single-event marsquake location and inversion for structure using synthetic Martian waveforms. Phys. Earth Planet. Inter. 258, 28–42. 10.1016/j.pepi.2016.05.017 [DOI] [Google Scholar]
- Knapmeyer M, Oberst J, Hauber E, Wahlisch M, Deuchler C, Wagner R, 2006. Working models for spatial distribution and level of Mars’ seismicity. J. Geophys. Res. 111 [Google Scholar]
- Konopliv AS, Asmar SW, Folkner WM, Karatekin Ö, Nunes DC, Smrekar SE, Yoder CF, Zuber MT, 2011. Mars high resolution gravity fields from MRO, Mars seasonal gravity, and other dynamical parameters. Icarus 211, 401–428. [Google Scholar]
- Konopliv AS, Park RS, Folkner WM, 2016. An improved JPL Mars gravity field and orientation from Mars orbiter and lander tracking data. Icarus 274, 253–260. 10.1016/J.ICARUS.2016.02.052 [DOI] [Google Scholar]
- Kovach RL, Anderson DL, 1964. Attenuation of shear waves in the upper and lower mantle. Bull. Seismol. Soc. Am. 54, 1855–1864. [Google Scholar]
- Krüger F, Weber M, Scherbaum F, Schlittenhardt J, 1995. Evidence for normal and inhomogeneous lowermost mantle and core-mantle boundary structure under the Arctic and northern Canada. Geophys. J. Int. 122, 637–657. 10.1111/j.1365-246X.1995.tb07017.x [DOI] [Google Scholar]
- Latham G, Ewing M, Dorman J, Press F, Toksoz N, Sutton G, Meissner R, Duennebier F, Nakamura Y, Kovach R, Yates M, 1970. Seismic Data from Man-Made Impacts on the Moon. Science. 170, 620–626. 10.1126/science.170.3958.620 [DOI] [PubMed] [Google Scholar]
- Latham GV, Ewing M, Press F, Sutton G, Dorman HJ, Nakamura Y, Toksöz MN, Lammlein D, Duennebier F, Dorman J, Nakamura Y, Toksöz N, Wiggins R, Derr J, Duennebier F, 1970. Passive Seismic Experiment. Science. 167, 455–457. 10.1126/science.167.3918.455 [DOI] [PubMed] [Google Scholar]
- Lawrence JF, Wysession ME, 2006. QLM9: A new radial quality factor (Qμ) model for the lower mantle. Earth Planet. Sci. Lett. 241, 962–971. 10.1016/J.EPSL.2005.10.030 [DOI] [Google Scholar]
- Lay T, Garnero EJ, 2004. Core-mantle boundary structures and processes, in: Geophysical Monograph Series. American Geophysical Union (AGU), pp. 25–41. 10.1029/150GM04 [DOI] [Google Scholar]
- Lay T, Williams Q, Garnero EJ, 1998. The core-mantle boundary layer and deep Earth dynamics. Nature 392, 461–468. 10.1038/33083 [DOI] [Google Scholar]
- Lehmann I, 1936. P’. Bur. Cent. Seismologique Int. Strasbg. Publ. du Bur. Cent. Sci 14, 87–115. [Google Scholar]
- Lekic V, Cottaar S, Dziewonski A, Romanowicz B, 2012. Cluster analysis of global lower mantle tomography: A new class of structure and implications for chemical heterogeneity. Earth Planet. Sci. Lett. 357–358, 68–77. 10.1016/J.EPSL.2012.09.014 [DOI] [Google Scholar]
- Li X-D, Giardini D, Woodhouses JH, 1991. Large-scale three-dimensional even-degree structure of the Earth from splitting of long-period normal modes. J. Geophys. Res. 96, 551 10.1029/90JB02009 [DOI] [Google Scholar]
- Li M, McNamara AK, Garnero EJ, Yu S, 2017. Compositionally-distinct ultra-low velocity zones on Earth’s core-mantle boundary. Nat. Commun. 8, 177 10.1038/s41467-017-00219-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lockman AB, Allen RM, 2005. Single-station earthquake characterization for early warning. Bull. Seismol. Soc. Am. 95, 2029–2039. 10.1785/0120040241 [DOI] [Google Scholar]
- Lognonné P, Banerdt WB, Giardini D, Pike WT, Christensen U, Laudet P, de Raucourt S, Zweifel P, Calcutt S, Bierwirth M, Hurst KJ, Ijpelaan F, Umland JW, Llorca-Cejudo R, Larson SA, Garcia RF, Kedar S, Knapmeyer-Endrun B, Mimoun D, Mocquet A, Panning MP, Weber RC, Sylvestre-Baron A, Pont G, Verdier N, Kerjean L, Facto LJ, Gharakanian V, Feldman JE, Hoffman TL, Klein DB, Klein K, Onufer NP, Paredes-Garcia J, Petkov MP, Willis JR, Smrekar SE, Drilleau M, Gabsi T, Nebut T, Robert O, Tillier S, Moreau C, Parise M, Aveni G, Ben Charef S, Bennour Y, Camus T, Dandonneau PA, Desfoux C, Lecomte B, Pot O, Revuz P, Mance D, tenPierick J, Bowles NE, Charalambous C, Delahunty AK, Hurley J, Irshad R, Liu H, Mukherjee AG, Standley FM, Stott AE, Temple J, Warren T, Eberhardt M, Kramer A, Kiihne W, Miettinen E-P, Monecke M, Aicardi C, André M, Baroukh J, Borrien A, Bouisset A, Boutte P, Brethomé K, Brysbaert C, Carlier T, Deleuze M, Desmarres JM, Dilhan D, Doucet C, Faye D, Faye-Refalo N, Gonzalez R, Imbert C, Larigauderie C, Locatelli E, Luno L, Meyer J-R, Mialhe F, Mouret JM, Nonon M, Pahn Y, Paillet A, Pasquier P, Perez G, Perez R, Perrin L, Pouilloux B, Rosak A, Savin de Larclause F, Sicre J, Sodki M, Toulemont N, Vella B, Yana C, Alibay F, Avalos OM, Balzer MA, Bhandari P, Blanco E, Bone BD, Bousman JC, Bruneau P, Calef FJ, Calvet RJ, D’Agostino SA, de los Santos G, Deen RG, Denise RW, Ervin J, Ferraro NW, Gengl HE, Grinblat F, Hernandez D, Hetzel M, Johnson ME, Khachikyan L, Lin JY, Madzunkov SM, Marshall SL, Mikellides FG, Miller EA, Raff W, Singer JE, Sunday CM, Villalvazo JF, Wallace MC, Banfield D, Rodriguez-Manfredi JA, Russell CT, Trebi-Ollennu A, Maki JN, Beucler E, Böse M, Bonjour C, Berenguer JL, Ceylan S, Clinton J, Conejero V, Daubar F, Dehant V, Delage P, Euchner F, Estève F, Fayon L, Ferraioli L, Johnson CL, Gagnepain-Beyneix J, Golombek M, Khan A, Kawamura T, Kenda B, Labrot P, Murdoch N, Pardo C, Perrin C, Pou L, Sauron A, Savoie D, Stähler S, Stutzmann E, Teanby NA, Tromp J, van Driel M, Wieczorek M, Widmer-Schnidrig R, Wookey J, 2019. SEIS: Insight’s Seismic Experiment for Internal Structure of Mars. Space Sci. Rev. 215, 12 10.1007/s11214-018-0574-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lognonné P, Banerdt WB, Hurst K, Mimoun D, Garcia R, Lefeuvre M, Gagnepain-Beyneix J, Wieczorek M, Mocquet A, Panning M, Beucler E, Deraucourt S, Giardini D, Boschi L, Christensen U, Goetz W, Pike T, Johnson C, Weber R, Larmat K, Kobayashi N, Tromp J, 2012. InSight and single-station broadband seismology: From signal and noise to interior structure determination. Lunar Planet. Sci. Conf. 43. [Google Scholar]
- Lognonné P, Mosser B, Lognonne P, Mosser B, 1993. Planetary seismology. Surv. Geophys. 14, 239–302. [Google Scholar]
- Loper DE, Lay T, 1995. The core-mantle boundary region. J. Geophys. Res. Solid Earth 100, 6397–6420. 10.1029/94JB02048 [DOI] [Google Scholar]
- Magotra N, Ahmed N, Chael E, 1987. Seismic event detection and source location using single-station (three-component) data. Bull. Seismol. Soc. Am. 77, 958–971. [Google Scholar]
- McLennan SM, Anderson RB, Bell JF, Bridges JC, Calef F, Campbell JL, Clark BC, Clegg S, Conrad P, Cousin A, Des Marais DJ, Dromart G, Dyar MD, Edgar LA, Ehlmann BL, Fabre C, Forni O, Gasnault O, Gellert R, Gordon S, Grant JA, Grotzinger JP, Gupta S, Herkenhoff KE, Hurowitz JA, King PL, Le Mouélic S, Leshin LA, Léveillé R, Lewis KW, Mangold N, Maurice S, Ming DW, Morris RV, Nachon M, Newsom HE, Ollila AM, Perrett GM, Rice MS, Schmidt ME, Schwenzer SP, Stack K, Stolper EM, Sumner DY, Treiman AH, VanBommel S, Vaniman DT, Vasavada A, Wiens RC, Yingst RA, 2014. Elemental Geochemistry of Sedimentary Rocks at Yellowknife Bay, Gale Crater, Mars. Science. 343, 1244734 10.1126/science.1244734 [DOI] [PubMed] [Google Scholar]
- McSween HY, 1985. SNC meteorites: Clues to Martian petrologic evolution? Rev. Geophys 23, 391 10.1029/RG023i004p00391 [DOI] [Google Scholar]
- McSween HY, Taylor GJ, Wyatt MB, 2009. Elemental Composition of the Martian Crust. Science (80-, ). 324, 736 LP–739. 10.1126/science.1165871 [DOI] [PubMed] [Google Scholar]
- Mégnin C, Romanowicz B, 2000. The three-dimensional shear velocity structure of the mantle from the inversion of body, surface and higher-mode waveforms. Geophys. J. Int. 143, 709–728. 10.1046/j.1365-246X.2000.00298.x [DOI] [Google Scholar]
- Mimoun D, Murdoch N, Lognonné P, Hurst K, Pike WT, Hurley J, Nébut T, Banerdt WB, 2017. The Noise Model of the SEIS Seismometer of the InSight Mission to Mars. Space Sci. Rev. 211, 383–428. 10.1007/s11214-017-0409-x [DOI] [Google Scholar]
- Mitchell BJ, Helmberger DV, 1973. Shear velocities at the base of the mantle from observations of S and ScS. J. Geophys. Res. 78, 6009–6020. 10.1029/JB078i026p06009 [DOI] [Google Scholar]
- Mitsuru Y, Tsujiura M, 1975. Spectrum and attenuation of multiply reflected core phases. J. Phys. Earth 23, 31–42. 10.4294/jpe1952.23.31 [DOI] [Google Scholar]
- Mocquet A, Vacher P, Grasset O, Sotin C, 1996. Theoretical seismic models of Mars: The importance of the iron content of the mantle. Planet. Space Sci. 44, 1251–1268. 10.1016/S0032-0633(96)00086-4 [DOI] [Google Scholar]
- Montési LGJ, Zuber MT, 2003. Clues to the lithospheric structure of Mars from wrinkle ridge sets and localization instability. J. Geophys. Res. Planets 108 10.1029/2002JE001974 [DOI] [Google Scholar]
- Morelli A, Dziewonski AM, 1987. Topography of the core-mantle boundary and lateral homogeneity of the liquid core. Nature 325, 678–683. 10.1038/325678a0 [DOI] [Google Scholar]
- Moulik P, Ekstrom G, 2014. An anisotropic shear velocity model of Earth’s mantle using normal modes, body waves, surface waves and long-period waveforms. Geophys. J. Int. 199, 1713–1738. [Google Scholar]
- Nakamura Y, Latham GV, Dorman HJ, 1982. Apollo lunar seismic experiment-final summary, in: Lunar and Planetary Science Conference Proceedings, pp. A117–A123. [Google Scholar]
- NASA, 2018. Mars InSight Launch Kit.
- Nimmo F, Faul UH, 2013. Dissipation at tidal and seismic frequencies in a melt-free, anhydrous Mars. J. Geophys. Res. Planets 118, 2558–2569. 10.1002/2013JE004499 [DOI] [Google Scholar]
- Nimmo F, Stevenson DJ, 2000. Influence of early plate tectonics on the thermal evolution and magnetic field of Mars. J. Geophys. Res. Planets 105, 11969–11979. 10.1029/1999JE001216 [DOI] [Google Scholar]
- Oberst J, 1987. Unusually high stress drops associated with shallow moonquakes. J. Geophys. Res. 10.1029/JB092iB02p01397 [DOI] [Google Scholar]
- Oldham RD, 1906. The Constitution of the Interior of the Earth, as Revealed by Earthquakes. Q. J. Geol. Soc. 62, 456–475. [Google Scholar]
- Okal EA, Anderson DL, 1978. Theoretical-Models for Mars and Their Seismic Properties. Icarus 33, 514–528. [Google Scholar]
- Panning MP, Beucler E, Drilleau M, Mocquet A, Lognonne P, Banerdt WB, 2015. Verifying single-station seismic approaches using Earth-based data: Preparation for data return from the InSight mission to Mars. Icarus 248, 230–242. 10.1016/j.icarus.2014.10.035 [DOI] [Google Scholar]
- Panning MP, Lognonné P, Bruce Banerdt W, Garcia R, Golombek M, Kedar S, Knapmeyer-Endrun B, Mocquet A, Teanby NA, Tromp J, Weber R, Beucler E, Blanchette-Guertin J-F, Bozdağ E, Drilleau M, Gudkova T, Hempel S, Khan A, Lekić V, Murdoch N, Plesa A-C, Rivoldini A, Schmerr N, Ruan Y, Verhoeven O, Gao C, Christensen U, Clinton J, Dehant V, Giardini D, Mimoun D, Thomas Pike W, Smrekar S, Wieczorek M, Knapmeyer M, Wookey J, 2017. Planned Products of the Mars Structure Service for the InSight Mission to Mars. Space Sci. Rev. 211, 611–650. 10.1007/s11214-016-0317-5 [DOI] [Google Scholar]
- Pandit BI, Tozer DC, 1970. Anomalous Propagation of Elastic Energy within the Moon. Nature 226, 335–335. 10.1038/226335a0 [DOI] [PubMed] [Google Scholar]
- Plesa A-C, Knapmeyer M, Golombek MP, Breuer D, Grott M, Kawamura T, Lognonné P, Tosi N, Weber RC, 2018. Present-Day Mars’ Seismicity Predicted From 3-D Thermal Evolution Models of Interior Dynamics. Geophys. Res. Lett. 10.1002/2017GL076124 [DOI] [Google Scholar]
- Rivoldini A, VanHoolst T, Verhoeven O, Mocquet A, Dehant V, 2011. Geodesy constraints on the interior structure and composition of Mars. Icarus 213, 451–472. 10.1016/j.icarus.2011.03.024 [DOI] [Google Scholar]
- Roberts RG, Christoffersson A, Cassidy F, 1989. Real-Time Event Detection, Phase Identification and Source Location Estimation Using Single Station Three-Component Seismic Data. Geophys. J. Int. 97, 471–480. 10.1111/j.1365-246X.1989.tb00517.x [DOI] [Google Scholar]
- Rost S, Garnero EJ, Williams Q, 2008. Seismic array detection of subducted oceanic crust in the lower mantle. J. Geophys. Res. Earth 113 [Google Scholar]
- Rudnick RL, McDonough WF, O’Connell RJ, 1998. Thermal structure, thickness and composition of continental lithosphere. Chem. Geol. 145, 395–411. 10.1016/S0009-2541(97)00151-4 [DOI] [Google Scholar]
- Ruedas T, Tackley PJ, Solomon SC, 2013. Thermal and compositional evolution of the martian mantle: Effects of phase transitions and melting. Phys. EARTH Planet. Inter. 216, 32–58. 10.1016/j.pepi.2012.12.002 [DOI] [Google Scholar]
- Russell SA, Lay T, Garnero EJ, 1999. Small-scale lateral shear velocity and anisotropy heterogeneity near the core-mantle boundary beneath the central Pacific imaged using broadband ScS waves. J. Geophys. Res. Solid Earth 104, 13183–13199. 10.1029/1999JB900114 [DOI] [Google Scholar]
- Schimmel M, Paulssen H, 1997. Noise reduction and detection of weak, coherent signals through phase-weighted stacks. Geophys. J. Int. 130, 497–505. 10.1111/j.1365-246X.1997.tb05664.x [DOI] [Google Scholar]
- Schlaphorst D, Thomas C, Holme R, Abreu R, 2016. Investigation of core-mantle boundary topography and lowermost mantle with P4KP waves. Geophys. J. Int. 204, 1060–1071. 10.1093/gji/ggv496 [DOI] [Google Scholar]
- Schmerr NC, Banks ME, Daubar IJ, 2016. The Seismic Signatures of Impact Events on Mars: Implications for the InSight Lander. Lunar Planet. Sci. Conf. [Google Scholar]
- Schubert G, Masters G, Olson P, Tackley P, 2004. Superplumes or plume clusters? Phys. Earth Planet. Inter 146, 147–162. 10.1016/j.pepi.2003.09.025 [DOI] [Google Scholar]
- Simmons NA, Grand SP, 2002. Partial melting in the deepest mantle. Geophys. Res. Lett. 29, 1552 10.1029/2001GL013716 [DOI] [Google Scholar]
- Smith DE, Zuber MT, 1996. The shape of Mars and the topographic signature of the hemispheric dichotomy. Science. 271, 184. [Google Scholar]
- Smith JC, Born GH, 1976. Secular acceleration of Phobos and Q of Mars. Icarus 27, 51–53. 10.1016/0019-1035(76)90183-4 [DOI] [Google Scholar]
- Smrekar SE, Lognonné P, Spohn T, Banerdt WB, Breuer D, Christensen U, Dehant V, Drilleau M, Folkner W, Fuji N, Garcia RF, Giardini D, Golombek M, Grott M, Gudkova T, Johnson C, Khan A, Langlais B, Mittelholz A, Mocquet A, Myhill R, Panning M, Perrin C, Pike T, Plesa A-C, Rivoldini A, Samuel H, Stähler SC, van Driel M, Van Hoolst T, Verhoeven O, Weber R, Wieczorek M, 2018. Pre-mission InSights on the Interior of Mars. Space Sci. Rev. 215, 3 10.1007/s11214-018-0563-9 [DOI] [Google Scholar]
- Sohl F, Schubert G, Spohn T, 2005. Geophysical constraints on the composition and structure of the Martian interior. J. Geophys. Res. 110 [Google Scholar]
- Sohl F, Spohn T, 1997. The interior structure of Mars: Implications from SNC meteorites. J. Geophys. Res. 102, 1613–1635. [Google Scholar]
- Stutzmann E, Schimmel M, Patau G, Maggi A, 2009. Global climate imprint on seismic noise. Geochemistry, Geophys. Geosystems 10 10.1029/2009GC002619 [DOI] [Google Scholar]
- Su W, Woodward RL, Dziewonski AM, 1994. Degree 12 model of shear velocity heterogeneity in the mantle. J. Geophys. Res. 99, 6945 10.1029/93JB03408 [DOI] [Google Scholar]
- Tanaka S, 2010. Constraints on the core-mantle boundary topography from P 4 KP-PcP differential travel times. J. Geophys. Res. 115, B04310 10.1029/2009JB006563 [DOI] [Google Scholar]
- Teanby NA, 2015. Predicted detection rates of regional-scale meteorite impacts on Mars with the InSight short-period seismometer. Icarus 256, 49–62. 10.1016/j.icarus.2015.04.012 [DOI] [Google Scholar]
- Teanby NA, Wookey J, 2011. Seismic detection of meteorite impacts on Mars. Phys. Earth Planet. Inter. 186, 70–80. 10.1016/j.pepi.2011.03.004 [DOI] [Google Scholar]
- Thiriet M, Michaut C, Breuer D, Plesa A-C, 2018. Hemispheric Dichotomy in Lithosphere Thickness on Mars Caused by Differences in Crustal Structure and Composition. J. Geophys. Res. Planets. 10.1002/2017JE005431 [DOI] [Google Scholar]
- Thorne MS, Garnero EJ, 2004. Inferences on ultralow-velocity zone structure from a global analysis of SPdKS waves. J. Geophys. Res. Solid Earth 109 10.1029/2004JB003010 [DOI] [Google Scholar]
- Thorne MS, Lay T, Garnero EJ, Jahnke G, Igel H, 2007. Seismic imaging of the laterally varying D” region beneath the Cocos plate. Geophys. J. Int. 10.1111/j.1365-246X.2006.03279.X [DOI] [Google Scholar]
- Toksöz MN, Dainty AM, Solomon SC, Anderson KR, 1974. Structure of the Moon. Rev. Geophys. 12, 539–567. 10.1029/RG012i004p00539 [DOI] [Google Scholar]
- van der Hilst RD, de Hoop MV, Wang P, Shim S-H, Ma P, Tenorio L, 2007. Seismostratigraphy and Thermal Structure of Earth’s Core-Mantle Boundary Region. Science. 315, 1813–1817. 10.1126/science.1137867 [DOI] [PubMed] [Google Scholar]
- Vidale JE, Benz HM, 1992. A sharp and flat section of the core–mantle boundary. Nature 359, 627–629. 10.1038/359627a0 [DOI] [Google Scholar]
- Weber RC, Lin PY, Garnero EJ, Williams Q, Lognonne P, 2011. Seismic Detection of the Lunar Core. Science. 331, 309–312. 10.1126/science.1199375 [DOI] [PubMed] [Google Scholar]
- Wilhelms DE, Squyres SW, 1984. The martian hemispheric dichotomy may be due to a giant impact. Nature 309, 138–140. 10.1038/309138a0 [DOI] [Google Scholar]
- Woodward RL, Masters G, 1991. Lower-mantle structure from ScS-S differential travel times. Nature 352, 231–233. [Google Scholar]
- Wu M, Yen H-YH, Zhao L, Huang BB-S, Liang W-TW, Wu Y, Taiwan, N.T.U.D. of G.T., Yen H-YH, Taiwan, N.T.U.D. of G.T., Zhao L, Taiwan, A.S I. of E.S.T., Huang BB-S, Taiwan, A.S.I. of E.S.T., Liang W-TW, Taiwan, A.S.I. of E.S.T., 2006. Magnitude determination using initial P waves: A single-station approach. Geophys. Res. Lett. 33 10.1029/2005GL025395 [DOI] [Google Scholar]
- Wysession ME, Okal EA, Bina CR, 1992. The structure of the core-mantle boundary from diffracted waves. J. Geophys. Res. Solid Earth 97, 8749–8764. 10.1029/92JB00511 [DOI] [Google Scholar]
- Yoder CF, Standish EM, 1997. Martian precession and rotation from Viking lander range data. J. Geophys. Res. Planets 102, 4065–4080. 10.1029/96JE03642 [DOI] [Google Scholar]
- Young CJ, Lay T, 1987. The Core-Mantle Boundary. Annu. Rev. Earth Planet. Sci. 15, 25–46. [Google Scholar]
- Yuan K, Romanowicz B, 2017. Seismic evidence for partial melting at the root of major hot spot plumes. Science. 357, 393–397. 10.1126/science.aan0760 [DOI] [PubMed] [Google Scholar]
- Zheng Y, Nimmo F, Lay T, 2015. Seismological implications of a lithospheric low seismic velocity zone in Mars. Phys. Earth Planet. Inter. 240, 132–141. 10.1016/j.pepi.2014.10.004 [DOI] [Google Scholar]
- Zuber MT, 2001. The crust and mantle of Mars. Nature 412, 220–227. 10.1038/35084163 [DOI] [PubMed] [Google Scholar]