Assessing Tuning Parameter Selection Variability in Penalized Regression

Abstract

Penalized regression methods that perform simultaneous model selection and estimation are ubiquitous in statistical modeling. The use of such methods is often unavoidable as manual inspection of all possible models quickly becomes intractable when there are more than a handful of predictors. However, automated methods usually fail to incorporate domain-knowledge, exploratory analyses, or other factors that might guide a more interactive model-building approach. A hybrid approach is to use penalized regression to identify a set of candidate models and then to use interactive model-building to examine this candidate set more closely. To identify a set of candidate models, we derive point and interval estimators of the probability that each model along a solution path will minimize a given model selection criterion, for example, Akaike information criterion, Bayesian information criterion (AIC, BIC), etc., conditional on the observed solution path. Then models with a high probability of selection are considered for further examination. Thus, the proposed methodology attempts to strike a balance between algorithmic modeling approaches that are computationally efficient but fail to incorporate expert knowledge, and interactive modeling approaches that are labor intensive but informed by experience, intuition, and domain knowledge. Supplementary materials for this article are available online.

1. Introduction

Penalized estimation is a popular means of regression model fitting that is quickly becoming a standard tool among quantitative researchers working across nearly all areas of science. Examples include the Lasso (Tibshirani 1996), SCAD (Fan and Li 2001), Elastic Net (Zou and Hastie 2005), and the adaptive Lasso (Zou 2006). One appealing feature of these methods is that they perform simultaneous model selection and estimation, thereby automating model-building at least partially. This is especially beneficial in settings where the number of predictors is large, precluding manual inspection of all possible models. However, a consequence is that the analyst becomes increasingly dependent on an estimation algorithm that has neither the subject-matter knowledge nor the intuition that might guide a less automated and more interactive model-building process (Henderson and Velleman 1981; Cox 2001). A hybrid approach is to use penalized estimation to construct a small subset of models, for example, the sequence of models occurring on a solution path, and then to apply interactive model-building techniques to choose a model from among these. We develop and advocate such a hybrid approach wherein a set of candidate models are identified using a solution path, and then models along this path are prioritized using their conditional probability of selection according to one or more tuning parameter selection methods. We envision this approach as being useful in at least two ways: (i) it facilitates interactive, expert-knowledge-driven exploration of high-quality candidate models even when the initial pool of models is large; and (ii) it provides valid conditional prediction sets for a data-driven tuning parameter given the observed design matrix and solution path, which is applicable for a large class of tuning parameter selection methods.

There is a vast literature on tuning parameter selection methods. Classical methods include Mallow’s C_p (Mallows 1973), Akaike information criterion (AIC; Akaike 1974), Bayesian information criterion (BIC; Schwarz 1978), cross-validation, and generalized cross-validation (Golub, Heath, and Wahba 1979). More recent work on tuning parameter selection, driven by interest in high-dimensional data, includes new information-theoretic selection methods (Chen and Chen 2008; Wang, Li, and Leng 2009; Zhang, Li, and Tsai 2010; Wang and Zhu 2011; Kim, Kwon, and Choi 2012; Fan and Tang 2013; Hui, Warton, and Foster 2015) as well as resampling-based approaches (Hall, Lee, and Park 2009; Meinshausen and Bühlmann 2010; Feng and Yu 2013; Sun, Wang, and Fang 2013; Shah and Samworth 2013). The foregoing methods select a single tuning parameter and hence a single fitted model. Our goal is to quantify the stability of these methods by constructing conditional prediction sets for data-driven tuning parameters and to use these prediction sets to prioritize models for further, expert-guided exploration. Given one or more tuning parameter selection methods, we identify all models with sufficiently large conditional probability of being selected given the design matrix and observed solution path.

In Section 2, we review penalized linear regression. In Section 3, we derive exact and asymptotic estimators of the sampling distribution of a data-driven tuning parameter. We examine the performance of the proposed methods through simulation studies in Section 4. In Section 5, we illustrate the proposed methods using two data examples. A concluding discussion is given in Section 6. Technical details are relegated to the supplement materials.

2. Penalized Linear Regression

We assume that the data are generated according to the linear model $Y_i={\mathbf{X}}_i^{⊺}{\beta }_0+{ϵ}_i$, for i = 1, … , n, where ϵ₁, … , ϵ_n are independent, identically distributed errors with expectation zero, β₀ = (β₀₁, … , β_0p)^⊺, and X₁, … ,X_n are predictors that can be regarded as either fixed or random. Let Y = (Y₁, Y₂, … , Y_n)^⊺ be the vector of responses and X = (X₁, X₂, … , X_n)^⊺ the design matrix with the first column equal to 1^n×1. Let ${\mathbb{P}}_n$ denote the empirical distribution. We consider penalized least-square estimators

$$\widehat{\beta }(\lambda )=\underset{\beta \in {ℝ}^p}{\text{argmin}}\left\{\frac{1}{2}\Vert \mathbf{Y}-\mathbf{X}\beta {\Vert }^2+\lambda \sum _{j=2}^p{f}_j({\beta }_j;{\mathbb{P}}_n)\right\},$$

where f_j(·), j = 2, … , p are penalty functions. For example,$f_j({\beta }_j;{\mathbb{P}}_n)=\mid {\beta }_j\mid$ corresponds to the Lasso, and $f_j({\beta }_j;{\mathbb{P}}_n)=\mid {\beta }_j\mid \mid {\widehat{\beta }}_{\mathrm{ols},j}{\mid }^{-\gamma }$ corresponds to the adaptive Lasso, where ${\widehat{\beta }}_{\mathrm{ols},j}$ is the ordinary least-square estimator and γ > 0 is a constant.

For any Λ ⊆ [0, ∞) define the solution path along Λ as $\widehat{S}(\Lambda )=\{\widehat{\beta }(\lambda ):\lambda \in \Lambda \}$; we write $\widehat{S}$ to denote $\widehat{S}\{[0,\infty )\}$. While the solution path along Λ may contain a continuum of coefficient vectors, it is commonly viewed as containing a finite set of unique models corresponding to each unique combination of nonzero elements of coefficients in $\widehat{S}(\Lambda )$, that is, the set of models $\mathcal{M}\{\widehat{S}(\Lambda )\}=\{\mathbf{M}\in \left\{0,1{\}}^p:\mathbf{M}={𝟙}_{\widehat{\beta }(\lambda )\ne 0},\text{for some}\lambda \in \Lambda \right\}$. The number of models in $\mathcal{M}\{\widehat{S}\}$ is typically much smaller, for example, O_p{min(n, p)}, than the set of all of 2^p possible models. Thus, the set of models along the solution path are a natural and computationally manageable subset ofmodels for further investigation. Standard practice is to choose a single value of the tuning parameter, say $\widehat{\lambda }$, that optimizes some prespecified criterion and subsequently a single model $\mathcal{M}[\widehat{S}\{(\widehat{\lambda })\}]$]. However, the selected tuning parameter is a random variable and there may be multiple models along the solution path where the support of the selected tuning parameter is large, for example, $\mathcal{M}\{\widehat{S}({\mathcal{L}}_{\tau })\}$ where ${\mathcal{L}}_{\tau }$ is a τ upper-level set of the conditional distribution of $\widehat{\lambda }$ given $\widehat{S}$ and X. If these models can be identified from the observed data, then they can be reported as potential candidate models or a single model can be chosen from among them using expert judgment and other factors not captured in the estimation algorithm. Also, unlikely models can be ruled out. To formalize this procedure, we consider selection methods within the framework of generalized information criterion.

Define the generalized information criterion as

$${\text{GIC}}_{\lambda }=\log ({\widehat{\sigma }}_{\lambda }^2)+w_n{\widehat{\mathit{df}}}_{\lambda },$$ (1)

where ${\widehat{\sigma }}_{\lambda }^2=n^{-1}{\sum }_{i=1}^n{\{Y_i-{{\mathbf{X}}_{\mathbf{i}}}^{⊺}\widehat{\beta }(\lambda )\}}^2$, ${\widehat{\mathit{df}}}_{\lambda }={\sum }_{j=1}^p{𝟙}_{\mid {\widehat{\beta }}_j(\lambda )\mid >0}$, and w_n is a sequence of positive constants, with w_n = log(n)/n and w_n = 2/n yielding BIC and AIC, respectively. We consider data-driven tuning parameters of the form ${\widehat{\lambda }}_{\mathrm{GIC}}={\mathrm{argmin}}_{\lambda }\{\log ({\widehat{\sigma }}_{\lambda }^2)+w_n{\widehat{\mathit{df}}}_{\lambda }\}$ We focus primarily on the setting where n > p as the GIC is not well-defined if p ≥ n However, we provide an illustrative example in Section 5 where p > n wherein our method is applied after an initial screening step; this two-stage procedure is in line with our vision for using automated methods to identify a small set of candidate models for further consideration. We also present extensions of key distributional approximations to the setting where p diverges with n in the Appendix.

3. Estimating the Conditional Distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}$

In this section, we characterize and derive estimators of the conditional distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}$ given $\widehat{S}$ and X. We first show that conditioning on $\widehat{S}$ and X is equivalent to conditioning on X^⊺Y and X. We then show that ${\widehat{\lambda }}_{\mathrm{GIC}}$ is a nondecreasing function of the sum of squares error of the full model ${\widehat{\sigma }}_0^2=n^{-1}{\sum }_{i=1}^n{(Y_i-{\mathbf{X}}_{\mathbf{i}}^{⊺}{\widehat{\beta }}_{\mathrm{ols}})}^2$. Therefore, the conditional distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}$ is completely determined by the conditional distribution of ${\widehat{\sigma }}_0^2$.

3.1. Conditioning on the Solution Path

We assume that f_j(β_j, ℙ_n), j = 2, … , p depends on the observed data only through X^⊺Y and X^⊺X; this assumption is natural as X^⊺X and X^⊺Y are sufficient statistics for the conditional mean of Y given X under the assumed linear model. Under this assumption, $\widehat{\beta }(\lambda )={\mathrm{argmin}}_{\beta }\{\frac{1}{2}{\beta }^{⊺}{\mathbf{X}}^{⊺}\mathbf{X}\beta -{\mathbf{Y}}^{⊺}\mathbf{X}\beta +\lambda {\sum }_{j=2}^p{f}_j({\beta }_j;{\mathbb{P}}_n)\}$, from which it can be seen that the solution path is completely determined by X^⊺X and X^⊺Y. On the other hand, given $\widehat{S}$ and X, we can recover X^⊺Y using ${\mathbf{X}}^{⊺}\mathbf{X}\widehat{\beta }(0)={\mathbf{X}}^{⊺}\mathbf{X}\{({\mathbf{X}}^{⊺}\mathbf{X}{)}^{-1}{\mathbf{X}}^{⊺}\mathbf{Y}\}={\mathbf{X}}^{⊺}\mathbf{Y}$. Therefore, conditioning on solution path and design matrix is equivalent to conditioning on X^⊺Y and X (see Lemma C.1 in the Appendix).

In the case of adaptive Lasso, we assume that X is full column rank so that f_j(β_j; ℙ_n), which depends on ${\widehat{\beta }}_{\mathrm{ols},j}$, is well-defined. It can be seen that if X is full column rank, then the entire solution path is determined by X^⊺X and ${\widehat{\beta }}_{\mathrm{ols}}$ Conditioning on the solution path is also practically relevant because it is consistent with the common practice wherein an analyst is presented with a full solution path and then proceeds to identify a model as a point along this path.

3.2. Exact Distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}\mid (\widehat{S},\mathbf{X})$

We assume that the models along the solution path are determined by the sequence of tuning parameters ${\widehat{\lambda }}_{(1)}<{\widehat{\lambda }}_{(2)}<\cdots <{\widehat{\lambda }}_{(\widehat{m})}$, so that $\widehat{m}$ is the total number of tuning parameters to be considered. The following lemma characterizes the conditional distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}$.

Lemma 1.

The selected tuning parameter, ${\widehat{\lambda }}_{\mathrm{GIC}}$, is completely determined by $(\widehat{S},\mathbf{X},{\widehat{\sigma }}_0^2)$. Furthermore, assume ${\mid \mid \mathbf{Y}-\mathbf{X}\widehat{\beta }(\lambda )\mid \mid }^2$ is a nondecreasing function of λ, write ${\widehat{\lambda }}_{\mathrm{GIC}}=\lambda (\widehat{S},\mathbf{X},{\widehat{\sigma }}_0^2)$, then for each fixed $\widehat{S}=s$ = s and X = x, the map σ² ↦ λ(s, x, σ²) is nondecreasing.

The assumption that ${\mid \mid Y-X\widehat{\beta }(\lambda )\mid \mid }^2$ is nondecreasing function of λ holds under mild conditions, for example, if ${\sum }_{j=2}^p{f}_j\{\widehat{\beta }(\lambda );{\mathbb{P}}_n\}$ is a decreasing function of λ and the original penalized problem can be recast as constrained minimization problem of the form minimize ||Y − X β||² subject to the constraint ${\sum }_{j=2}^p{f}_j({\beta }_j;{\mathbb{P}}_n)\le {\sum }_{j=2}^p{f}_j\{\widehat{\beta }(\lambda );{\mathbb{P}}_n\}$. It is well known that Lasso satisfies this property. If the error is normally distributed, then $(n{\widehat{\sigma }}_0^2)∕{\sigma }_0^2$ is independent of ($\widehat{S}$, X) and follows a chi-square distribution with n − p degrees of freedom. Therefore, the preceding lemma shows that, under normal errors, the conditional distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}$ given $(\widehat{S},\mathbf{X})$ is a nondecreasing function of a chi-square random variable. The remaining results stated in this section do not require the assumption that ${\mid \mid Y-X\widehat{\beta }(\lambda )\mid \mid }^2$ is nondecreasing in λ; rather, the results are stated in terms of a finite but arbitrary sequence of tuning parameter values.

Define ${\widehat{D}}_{\lambda }=\{{\widehat{\beta }}_{\mathrm{ols}}-\widehat{\beta }(\lambda ){\}}^{⊺}{\mathbf{X}}^{⊺}\mathbf{X}\{{\widehat{\beta }}_{\mathrm{ols}}-\widehat{\beta }(\lambda )\}$. For k = 1, … , $\widehat{m}$, define ${\widehat{A}}_k=\{i:{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}}<{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}\}$, ${\widehat{B}}_k=\{i:{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}}>{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}\}$, ${\widehat{C}}_k=\{i:i\ne k,\text{and}{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}}={\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}\}$, and

$$\begin{array}{cc}\hfill {\widehat{\ell }}_{i,k}& =\frac{{\widehat{D}}_{{\widehat{\lambda }}_{(k)}}\text{exp}\{w_n({\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}-{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}})\}-{\widehat{D}}_{{\widehat{\lambda }}_{(i)}}}{1-\text{exp}\{w_n({\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}-{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}})\}},\hfill \\ \hfill & \text{for}1\le i,k\le \widehat{m},\hfill \end{array}$$

where w_n is from Equation (1). The quantities in the foregoing definitions are all measurable with respect to X and $\widehat{S}$ and thus, for probability statements conditional on X and $\widehat{S}$, they are regarded as constants.

The following proposition gives the exact conditional distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}$ given $\widehat{S}$ and X.

Proposition 1.

Define ${\widehat{I}}_k=𝟙({\widehat{D}}_{{\widehat{\lambda }}_{(k)}}<{\widehat{D}}_{{\widehat{\lambda }}_{(i)}},\text{for all}i\in {\widehat{C}}_k)$ with the convention that ${\widehat{I}}_k=1$ if ${\widehat{C}}_k$ is empty, and $p_k=P({\max }_{i\in {\widehat{B}}_k}{\widehat{\ell }}_{i,k}\le n{\widehat{\sigma }}_0^2\le {\min }_{i\in {\widehat{A}}_k}{\widehat{\ell }}_{i,k}\mid \widehat{S},\mathbf{X})$. Then,

$$P({\widehat{\lambda }}_{\text{GIC}}={\widehat{\lambda }}_{(k)}\mid \widehat{S},\mathbf{X})=\text{min}(p_k,{\widehat{I}}_k).$$

Provided that the conditional distribution of ${\widehat{\sigma }}_0^2$ given ($(\widehat{S},\mathbf{X})$ is known or can be consistently estimated, the preceding proposition can be used to construct conditional prediction sets for ${\widehat{\lambda }}_{\mathrm{GIC}}$. A (1 − α) × 100% conditional prediction set is $\{{\widehat{\lambda }}_{(i)}:i\in \Gamma \}$, where ${\sum }_{i\in \Gamma }P({\widehat{\lambda }}_{\mathrm{GIC}}={\widehat{\lambda }}_{(i)}\mid \widehat{S},\mathbf{X})\ge 1-\alpha$. Alternatively, as discussed previously, one can construct the τ upper-level set ${\mathcal{L}}_t=\{{\widehat{\lambda }}_{(i)}:P({\widehat{\lambda }}_{\mathrm{GIC}}={\widehat{\lambda }}_{(i)}\mid \widehat{S},\mathbf{X})>\tau \}$, for any τ ∈ (0, 1).

Define ${\widehat{a}}_k={\min }_{i\in {\widehat{A}}_k}{\widehat{\ell }}_{i,k}$ and ${\widehat{b}}_k={\max }_{i\in {\widehat{B}}_k}{\widehat{\ell }}_{i,k}$. If the errors are normally distributed then

$$p_k=F_{{\chi }_{n-p}^2}\left(\frac{{\widehat{a}}_k}{{\sigma }_0^2}\right)-F_{{\chi }_{n-p}^2}\left(\frac{{\widehat{b}}_k}{{\sigma }_0^2}\right),\text{for}{\widehat{a}}_k\ge {\widehat{b}}_k.$$ (2)

Plugging ${\widehat{\sigma }}_0^2$ into this expression yields an estimator ${\widehat{p}}_k$ for p_k.

Define $g_k(t)=F_{{\chi }_{n-p}^2}({\widehat{a}}_k∕t)-F_{{\chi }_{n-p}^2}({\widehat{b}}_k∕t)$. Then a (1 − α) × 100% projection confidence interval (Berger and Boos 1994) for p_k (Equation (2)) is

$$\left(\underset{t\in \mathcal{C}}{\text{inf}}{g}_k(t),\underset{t\in \mathcal{C}}{\text{sup}}{g}_k(t)\right),$$ (3)

Where $C=(n{\widehat{\sigma }}_0^2/{\chi }_{\alpha /2,n-p}^2,n{\widehat{\sigma }}_0^2/{\chi }_{1-\alpha /2,n-p}^2)$ is a (1−α) × 100% confidence interval for ${\sigma }_0^2$. Thus, an estimator of ${\mathcal{L}}_{\tau }$ is

$${\widehat{\mathcal{L}}}_{\tau }=\left\{{\widehat{\lambda }}_{(k)}:\underset{t\in \mathcal{C}}{\text{sup}}{g}_k(t)>\tau \right\}.$$ (4)

Remark 1. The assumption that X is full rank is not necessary for Proposition 1. Note that the conclusions depend only on the quantities $\mathbf{X}{\widehat{\beta }}_{\mathrm{ols}}$, $\mathbf{X}\widehat{\beta }(\lambda )$, and ${\widehat{\sigma }}_0^2$, which are computable even when X is not full rank.

3.3. Limiting Conditional Distribution of ${\widehat{\sigma }}_0^2$

As discussed above, if the errors are assumed tobe normally distributed then exact distribution theory for ${\widehat{\lambda }}_{\mathrm{GIC}}$ is possible using a transformed chi-square random variable. Here, we consider asymptotic approximations that apply more generally.

Denote the third and fourth moment of ϵ as μ_3,ϵ and μ_4,ϵ respectively. Define

$$\Sigma =\left(\begin{array}{cc}\hfill {\sigma }_0^2{C}^{-1}\hfill & \hfill {\mu }_x{\mu }_{3,ϵ}\hfill \\ \hfill {\mu }_x^{⊺}{\mu }_{3,ϵ}\hfill & \hfill {\mu }_{4,ϵ}-{\sigma }_0^4\hfill \end{array}\right),$$

where $C={\lim }_{n\to \infty }{n}^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i{\mathbf{X}}_i^{⊺}$. And write Φ_p+1 (t) to denote the cumulative distribution function of a standard (p + 1 )-dimensional multivariate normal distribution evaluated at t. For u, v ∈ ℝ^p+1 write u ≤ v to mean component-wise inequality. The following are standard results from ordinary linear regression under common regularity conditions summarized in Section C in the Appendix (see the proof of Proposition 2).

Proposition 2.

The asymptotic joint distribution of ${\widehat{\beta }}_{\mathrm{ols}}-{\beta }_0$ and ${\widehat{\sigma }}_0^2-{\sigma }_0^2$ is multivariate normal with mean zero and covariance Σ, that is,

$$\underset{\mathbf{t}\in {ℝ}^{p+1}}{\text{sup}}\mid P\left\{\sqrt{n}{\Sigma }^{-1∕2}\left(\begin{array}{c}\hfill {\widehat{\beta }}_{ols}-{\beta }_0\hfill \\ \hfill {\widehat{\sigma }}_0^2-{\sigma }_0^2\hfill \end{array}\right)\le \mathbf{t}\right\}-{\Phi }_{p+1}(\mathbf{t})\mid \to 0.$$

Because we assume that X is full column rank, conditioning on ($\widehat{S}$, X) is equivalent to conditioning on (${\widehat{\beta }}_{\mathrm{ols}}$, X) (in the sense that they generate the same σ-algebra). Therefore to approximate the conditional distribution of ${\widehat{\sigma }}_0^2$ given ($\widehat{S}$, X), we construct an estimator of Σ, say $\widehat{\Sigma }$, and then use the above proposition to form a plug-in estimator of the distribution of ${\widehat{\sigma }}_0^2$ given $({\widehat{\beta }}_{\mathrm{ols}},\mathbf{X})$. Define

$${\widehat{e}}_i=Y_i-{\mathbf{X}}_{\mathbf{i}}^{⊺}{\widehat{\beta }}_{ols},i=1,2,\dots ,n,$$ (5)

and subsequently ${\widehat{\sigma }}_0^2=n^{-1}{\sum }_{i=1}^n{\widehat{e}}_i^2$, ${\widehat{\mu }}_{3,ϵ}=n^{-1}{\sum }_{i=1}^n{\widehat{e}}_i^3$, ${\widehat{\mu }}_{4,ϵ}=n^{-1}{\sum }_{i=1}^n{\widehat{e}}_i^4$, ${\widehat{\mu }}_x=n^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i$, and $\widehat{C}=n^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i{\mathbf{X}}_i^{⊺}$. The estimated conditional distribution of ${\widehat{\sigma }}_0^2$ is

$$N\left[{\widehat{\sigma }}_0^2,\frac{1}{n}\left\{({\widehat{\mu }}_{4,ϵ}-{\widehat{\sigma }}_0^4)-\frac{{\widehat{\mu }}_{3,ϵ}^2}{{\widehat{\sigma }}_0^2}{\widehat{\mu }}_x^{⊺}\widehat{C}{\widehat{\mu }}_x\right\}\right].$$ (6)

This approximation, coupled with Proposition 1, can be used to approximate the conditional distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}$ when a chi-squared approximation is not feasible.

Henceforth, we assume that the errors are symmetric about zero, in which case the third moment of ϵ_i, μ_3ϵ, is zero, which implies ${\widehat{\sigma }}_0^2$ is asymptotically independent of ${\widehat{\beta }}_{\mathrm{ols}}$. Therefore,

$$\begin{array}{cc}\hfill p_k& =P({\widehat{b}}_k\le n{\widehat{\sigma }}_0^2\le {\widehat{a}}_k\mid \widehat{S},\mathbf{X})\hfill \\ \hfill & =\Phi \left(\frac{\sqrt{n}({\widehat{a}}_k∕n-{\sigma }_0^2)}{\sqrt{{\mu }_{4,ϵ}-{\sigma }_0^4}}\right)-\Phi \left(\frac{\sqrt{n}({\widehat{b}}_k∕n-{\sigma }_0^2)}{\sqrt{{\mu }_{4,ϵ}-{\sigma }_0^4}}\right)\hfill \\ \hfill & +o_p(1),\text{for}{\widehat{a}}_k\ge {\widehat{b}}_k,\hfill \end{array}$$ (7)

where μ_4,ϵ is the fourth moment of ϵ_i. Define

$$h_k(t_1,t_2)=\Phi \left(\frac{\sqrt{n}({\widehat{a}}_k∕n-t_1)}{\sqrt{t_2}}\right)-\Phi \left(\frac{\sqrt{n}({\widehat{b}}_k∕n-t_1)}{\sqrt{t_2}}\right).$$

Suppose that ${\mathcal{E}}_y$ is a (1 − α) x 100% asymptotic confidence region for μ_4,ϵ − ${\sigma }_0^4$ and ${\sigma }_0^2$, then

$$\left[\underset{(t_1,t_2)\in {\mathcal{E}}_y}{\text{inf}}{h}_k(t_1,t_2),\underset{(t_1,t_2)\in {\mathcal{E}}_y}{\text{sup}}{h}_k(t_1,t_2)\right],$$ (8)

is an approximate (1 − α) × 100% projection confidence interval for p_k (see Proposition C.1 in Section C of the Appendix.).

We construct the confidence set ${\mathcal{E}}_y$ using Wald confidence region:

$$\begin{array}{cc}\hfill {\mathcal{E}}_y=& \{(t_1,t_2):{\left(\begin{array}{c}\hfill t_1-{\widehat{\sigma }}_0^2\hfill \\ \hfill t_2-{\widehat{\mu }}_{4,ϵ}+{\widehat{\sigma }}_0^4\hfill \end{array}\right)}^{⊺}\phantom{\}}\hfill \\ \hfill & \times {\widehat{V}}^{-1}\phantom{\{}\left(\begin{array}{c}\hfill t_1-{\widehat{\sigma }}_0^2\hfill \\ \hfill t_2-{\widehat{\mu }}_{4,ϵ}+{\widehat{\sigma }}_0^4\hfill \end{array}\right)\le {\chi }_{1-\alpha ,2}^2\},\hfill \end{array}$$

where $\widehat{V}$ is the estimated covariance matrix of ${({\widehat{\sigma }}_0^2,{\widehat{\mu }}_{4,ϵ}-{\widehat{\sigma }}_0^4)}^{⊺}$. Then the optimization problem in Equation (9) is solved using an augmented Lagrangian method (Bertsekas 2014). An estimator of ${\mathcal{L}}_{\tau }$ is

$${\widehat{\mathcal{L}}}_{\tau }=\left\{{\widehat{\lambda }}_{(k)}:\underset{(t_1,t_2)\in {\mathcal{E}}_y}{\text{sup}}{h}_k(t_1,t_2)>\tau \right\}.$$ (9)

Proposition 2 is stated in terms of fixed p and diverging n. We show in the Appendix that the approximation in Equation (7) remains valid in the setting $p=o(\sqrt{n})$ as well as the setting where $p=O\{\exp (n^c)\}$ provided that an appropriate screening step is applied as a first step. We illustrate this screening approach with a high-dimensional example in our simulation experiments.

3.4. Bootstrap Approximation to the Distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}\mid (\widehat{S},\mathbf{X})$

In small samples, it may be preferable to estimate the conditional distribution of ${\widehat{\sigma }}_0^2$ using the bootstrap. Let γ^(b) = (γ₁^(b), … , γ_n^(b))^⊺ be a sample drawn with replacement from $\{{\widehat{e}}_1,\dots ,{\widehat{e}}_n\}$. Define ${\mathbf{Y}}^{(\mathbf{b})}=\mathbf{X}{\widehat{\beta }}_{\mathrm{ols}}+(\mathbf{I}-{\mathbf{P}}_{\mathbf{x}}){\gamma }^{(b)}$, where P_x = X(X^⊺X)⁻X^⊺. This bootstrap method differs from the usual residual bootstrap in ordinary linear regression because our goal is to estimate the conditional distribution of ${\widehat{\sigma }}_0^2$. We accomplish this by multiplying the error vector by (I − P_x), which ensures that ${\widehat{\beta }}_{\mathrm{ols}}^{(b)}={({\mathbf{X}}^{⊺}\mathbf{X})}^{-1}{\mathbf{X}}^{⊺}{\mathbf{Y}}^{(b)}={\widehat{\beta }}_{\mathrm{ols}}$ so that Y^(b) produces the same solution path as the original sample Y. The conditional distribution of the tuning parameter is estimated by generating b = 1,…, B bootstrap samples and calculating the corresponding tuning parameter for each bootstrap sample. See Proposition C.2 in Section C of the Appendix for a statement of the asymptotic equivalence between the proposed bootstrap method and the normal approximation given in Equation (6).

4. Simulation Studies

In this section, we investigate the finite-sample performance of the proposed methods using a series of simulation experiments. We focus on the Lasso tuned using BIC. Simulated datasets are generated from the model $Y_i={\mathbf{X}}_i^{⊺}{\beta }_0+{ϵ}_i$, where ϵ_i, i = 1, … , n are generated independently from a standard normal distribution and X_i, i = 1, … , n are generated independently from a multivariate normal distribution with mean zero and autoregressive covariance structure, C_j,k = ρ^|j−k|, with ρ = 0 or 0.5 and 1 ≤ j, k ≤ 20, or 200. For the regression coefficients β₀, we consider the following four settings:

Model 1: β₀ = c₁×(1, 1, 1, 1, 0, 0, 0, 0, … , 0)^⊺;

Model 2: β₀ = c₂×(1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, … , 0)^⊺;

Model 3: β₀ = c₃×(3, 2, 1, 0, 0, 0, 0, … , 0)^⊺;

Model 4: β₀ = c₄×(3, 2, 1, 0, 0, 0, 0, 0, 3, 2, 1, 0, … , 0)^⊺;

where c₁, … , c₄ are constants chosen so that the population R² of each model is 0.5 under the definition R² = 1 − var(Y|X)/var(Y). For each combination of parameter settings, 10,000 datasets were generated; the bootstrap estimator was constructed using 5000 bootstrap replications.

For estimating the τ upper-level set, ${\mathcal{L}}_{\tau }=\{\lambda :P({\widehat{\lambda }}_{\mathrm{GIC}}=\lambda \mid \widehat{S},\mathbf{X})>\tau \}$, we consider:

1. (AsympNor) the plug-in estimator based on the normal approximation to the distribution of p_k;

2. (Bootstrap) the estimator based on the bootstrap approximation to the sampling distribution of p_k as described in Section 3.4;

3. (UP1) the estimator based on a 90% projection confidence set as in Equation (4);

4. (UP2) the estimator based on a 90% projection confidence set as in Equation (10);

5. (Akaike) the estimator based on Akaike weights: ${\widehat{\mathcal{L}}}_{\tau }=\{{\lambda }_i:\frac{\exp (-0.5n{\mathrm{GIC}}_{{\lambda }_i})}{{\sum }_{i=1}^{\widehat{m}}\exp (-0.5n{\mathrm{GIC}}_{{\lambda }_i})}>\tau \}$, with w_n = 2/n (Burnham and Anderson 2003);

6. (ApproxPost) the estimator based on approximate posterior distribution: ${\widehat{\mathcal{L}}}_{\tau }=\{{\lambda }_i:\frac{\exp (-0.5n{\mathrm{GIC}}_{{\lambda }_i})}{{\sum }_{i=1}^{\widehat{m}}\exp (-0.5n{\mathrm{GIC}}_{{\lambda }_i})}>\tau \}$, with W_n = log(n)/n (Burnham and Anderson 2003).

We define the performance of these estimators in terms of their true and false discovery rates. Provided that ${\mathcal{L}}_{\tau }$ is nonempty, define the true discovery rate of an estimator ${\widehat{\mathcal{L}}}_{\tau }$ as

$$\text{TDR}({\widehat{\mathcal{L}}}_{\tau })=𝔼\left[\frac{\#\{{\widehat{\mathcal{L}}}_{\tau }\cap {\mathcal{L}}_{\tau }\}}{\#{\mathcal{L}}_{\tau }}\right],$$

where # denotes the number of elements in a set. Provided ${\widehat{\mathcal{L}}}_{\tau }$ is nonempty with probability one, define the false discovery rate of an estimator ${\widehat{\mathcal{L}}}_{\tau }$ as

$$\text{FDR}({\widehat{\mathcal{L}}}_{\tau })=1-𝔼\left[\frac{\#\{{\widehat{\mathcal{L}}}_{\tau }\cap {\mathcal{L}}_{\tau }\}}{\#{\widehat{\mathcal{L}}}_{\tau }}\right].$$

Here, we present results for τ = 0.05; results for τ = 0.1 and τ = 0.2 are presented in the supplemental materials. The results for p = 20, n = 50 and p = 100, n = 200 are presented in Tables 1 and 2, respectively. AsympNor and the Bootstrap perform similarly with a TDR above 0.9 and an FDR below 0.10. As expected, methods based on the upper bound of the confidence interval achieve higher TDR but at the price of higher FDR. Methods based on Akaike weights and approximate posterior have the worst performances in terms of discovery rate of ${\mathcal{L}}_{\tau }$. The poor performance is not surprising as these methods were not designed for conditional inference.

Table 1.

Discovery rate for p = 20, n = 50.

		AsympNor		Bootstrap		UP1		UP2		Akaike		ApproxPost
Model	ρ	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR
	0	0.90	0.10	0.90	0.10	1.00	0.32	0.99	0.36	0.54	0.83	0.90	0.58
1	0.5	0.92	0.09	0.92	0.09	1.00	0.29	0.99	0.34	0.61	0.83	0.95	0.58
	0	0.88	0.11	0.88	0.10	0.99	0.30	0.99	0.34	0.46	0.83	0.82	0.59
2	0.5	0.89	0.10	0.90	0.10	1.00	0.35	0.99	0.36	0.55	0.82	0.89	0.59
	0	0.92	0.09	0.92	0.09	1.00	0.29	0.99	0.34	0.57	0.84	0.94	0.58
3	0.5	0.93	0.08	0.93	0.08	1.00	0.27	0.99	0.32	0.64	0.83	0.96	0.57
	0	0.89	0.11	0.90	0.10	0.99	0.32	0.99	0.36	0.50	0.84	0.88	0.59
4	0.5	0.91	0.10	0.91	0.09	0.99	0.33	0.99	0.35	0.58	0.83	0.92	0.58

Table 2.

Discovery rate for p = 100, n = 200.

		AsympNor		Bootstrap		UP1		UP2		Akaike		ApproxPost
Model	ρ	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR
	0	0.97	0.03	0.97	0.03	1.00	0.12	1.00	0.13	0.11	0.98	1.00	0.58
1	0.5	0.98	0.03	0.98	0.02	1.00	0.09	1.00	0.10	0.24	0.95	1.00	0.56
	0	0.95	0.04	0.95	0.04	1.00	0.17	1.00	0.18	0.05	0.99	0.98	0.59
2	0.5	0.96	0.03	0.96	0.03	1.00	0.14	1.00	0.15	0.12	0.97	0.99	0.58
	0	0.97	0.03	0.97	0.03	1.00	0.12	1.00	0.13	0.16	0.97	1.00	0.57
3	0.5	0.98	0.02	0.98	0.02	1.00	0.09	1.00	0.10	0.28	0.94	1.00	0.56
	0	0.96	0.04	0.96	0.04	1.00	0.14	1.00	0.16	0.07	0.98	0.99	0.59
4	0.5	0.97	0.03	0.97	0.03	1.00	0.12	1.00	0.13	0.16	0.97	1.00	0.57

We also evaluated the coverage of the proposed confidence intervals based on assumption of normality assumption as well as the asymptotic approximation. In calculating the coverage probabilities, we restricted calculations to the set (λ : 0.9999 > $P({\widehat{\lambda }}_{\mathrm{GIC}}=\lambda \mid \widehat{S},\mathbf{X})$ > 0.0001}. Nominal coverage is set at 0.90. The results are presented in Table 3. The confidence intervals based on normality (Equation (3)) achieve nominal coverage in all cases. The confidence intervals based on an asymptotic approximation undercover slightly, though coverage approaches nominal levels as n increases.

Table 3.

Coverage probability. Results are based on 10,000 replicated datasets.

	ρ	Approximate		Normality
		0	0.5	0	0.5
	Model 1	0.86	0.85	0.92	0.91
n = 50	Model 2	0.86	0.85	0.91	0.91
p = 20	Model 3	0.85	0.85	0.91	0.91
	Model 4	0.86	0.85	0.92	0.91
	Model 1	0.88	0.88	0.91	0.90
n = 200	Model 2	0.87	0.88	0.91	0.91
p = 100	Model 3	0.87	0.87	0.91	0.90
	Model 4	0.87	0.88	0.91	0.90

5. Illustrative Data Examples

In this section, we apply the proposed methods to two datasets. The first dataset informs the relationship of pollution and other factors related to urban-living, and to age-adjusted mortality (McDonald and Schwing 1973; Luo, Stefanski, and Boos 2006); and the second regards the relationship between gene mutations and drug resistance level (Rhee et al. 2006). We demonstrate that reporting a single model may not be appropriate in these two examples and that the proposed methods have the potential to identify interesting models warranting further examination. As in the simulation experiments, we consider the Lasso estimator tuned using BIC.

5.1. Pollution and Mortality

As our first illustrative example we consider data on mortality rates recorded in 60 metropolitan areas. Prior analyses of these data focused on the regression of age-adjusted mortality on 15 predictors that are grouped into three broad categories: weather, socioeconomic factors, and pollution. A copy of the dataset and a detailed description of each predictor are provided in the supplemental materials.

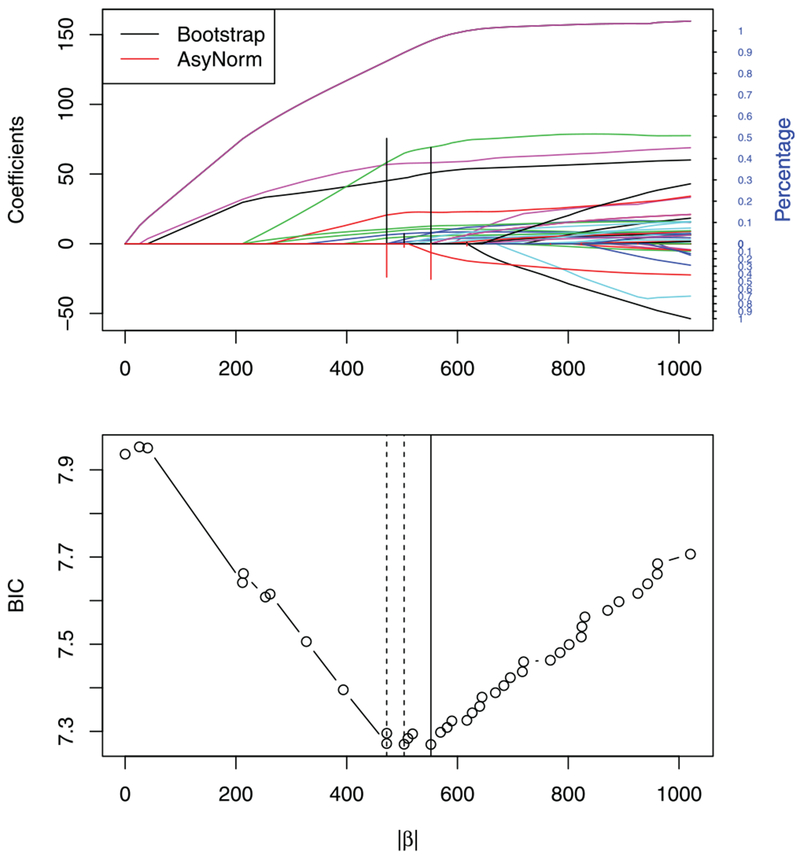
Ignoring uncertainty in the tuning parameter selection, the LASSO estimator tuned using BIC leads to a model with six variables, Percent Non-White, Education, SO₂ Pollution Potential, Precipitation, Mean January Temperature, and Population Per Mile. However, the estimated conditional sampling distribution of the tuning parameter indicates that a larger model with eight predictors is approximately equally probable. Figure 1 displays the solution path with the estimated selection probabilities using both the asymptotic normal and bootstrap approximations. The estimated conditional distribution of the tuning parameter is displayed in Table 4; 90% confidence intervals based on Equations (3) and (9) are presented. The LASSO coefficient estimates are presented in Table B.1 of the Appendix.

Figure 1.

The top figure shows LASSO solution path of mortality rates data; The vertical lines above and belowx-axis correspond to the distribution estimated by bootstrap and asymptotic normal approximation, respectively. The bottom figure shows BIC values for candidate models along solution path. The solid vertical line corresponds to the model with six variables and smallest BIC value. The dashed vertical line corresponds to a model with eight variables.

Table 4.

Estimated conditional distribution of the tuning parameter for the mortality rates data. Both the asymptotic normal approximation and the bootstrap had only two support points, {124.21,288.20}.

λ	288.20	124.21
Model size	6	8
Probability mass normal	0.51	0.49
Probability mass bootstrap	0.48	0.52
90% CI based on normality	(0.052,0.950)	(0.048, 0.948)
90% Approximate CI	(0.009,0.848)	(0.154, 1.000)

We further investigate the model with eight predictors. The eighth predictor added to the model is Mean July Temperature. Fitting a simple linear regression of mortality on Mean July Temperature yields a p-value of 0.03 compared with a p-value of 0.81 in the regression of mortality on Mean January Temperature. This is in line with Katsouyanni et al. (1993) who concluded that high temperatures are related to the mortality rate. It can be seen that in this case, reporting a single model may not be appropriate. Rather, it may be more informative to report the two models that contain essentially all of the mass of the conditional distribution of the tuning parameter.

For comparison, results from forward stepwise regression are presented in Figure 2. The smallest BIC value corresponds to Step 5 of the procedure which corresponds to a model with the five predictors: Percent Non-White, Education, Mean January Temperature, SO₂ Pollution Potential, and Precipitation. This model is smaller than the model selected by LASSO tuned using BIC. This may be because forward stepwise regression is greedy in that at each step it seeks a variable that captures maximum variation in the residuals. Thus, if a candidate variable is correlated with those selected in previous steps, it may be difficult to see the improvement in the fitted model. In such cases, it might be preferable to use the solution path to generate a candidate set of models.

Figure 2.

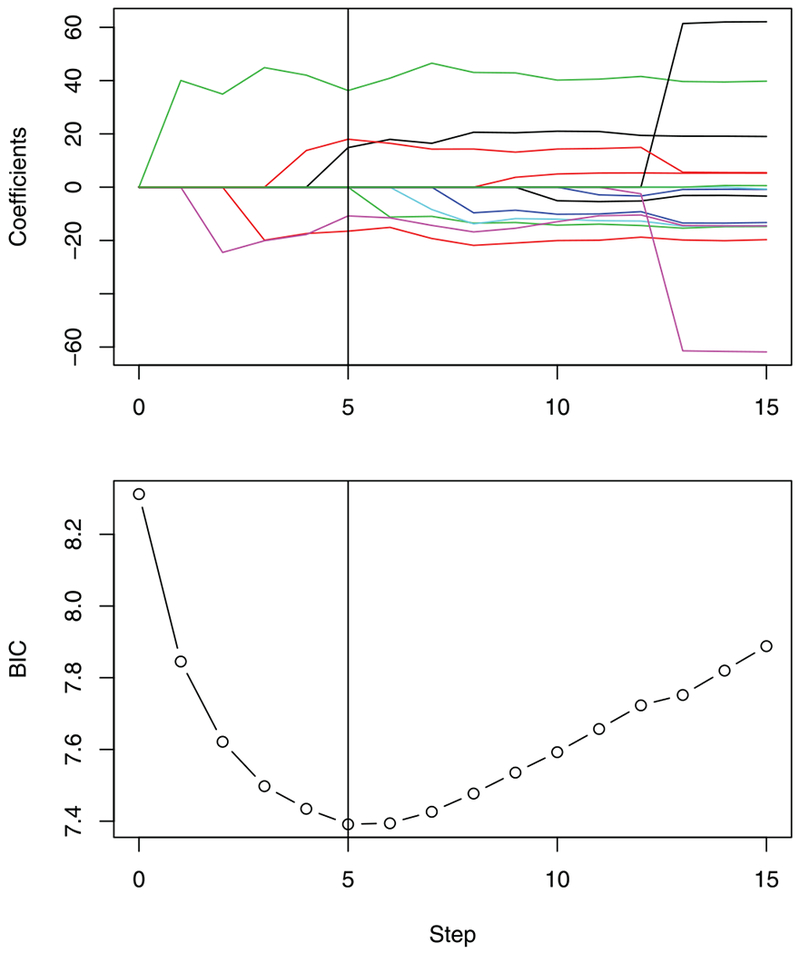
The top figure shows forward stepwise regression solution path of mortality rates data; The vertical line corresponds to the model which minimizes BIC. The bottom figures show BIC values for candidate models along solution path. The solid vertical line corresponds to the smallest BIC value.

5.2. ATV Drug Resistance

Our second example considers mutations that affect resistance to Atazanavir (ATV), a protease inhibitor for HIV (Rhee et al. 2006; Barber et al. 2015). After preprocessing, the dataset contains 328 observations and 361 predictors of gene mutations. The response is a measure of drug resistance for ATV. Because p > n in this example, we use 100 observations for screening 50 important predictors, ranked by Pearson correlation with response. We then fit a linear model using the Lasso applied to the remaining 228 observations with the 50 important predictors selected at screening.

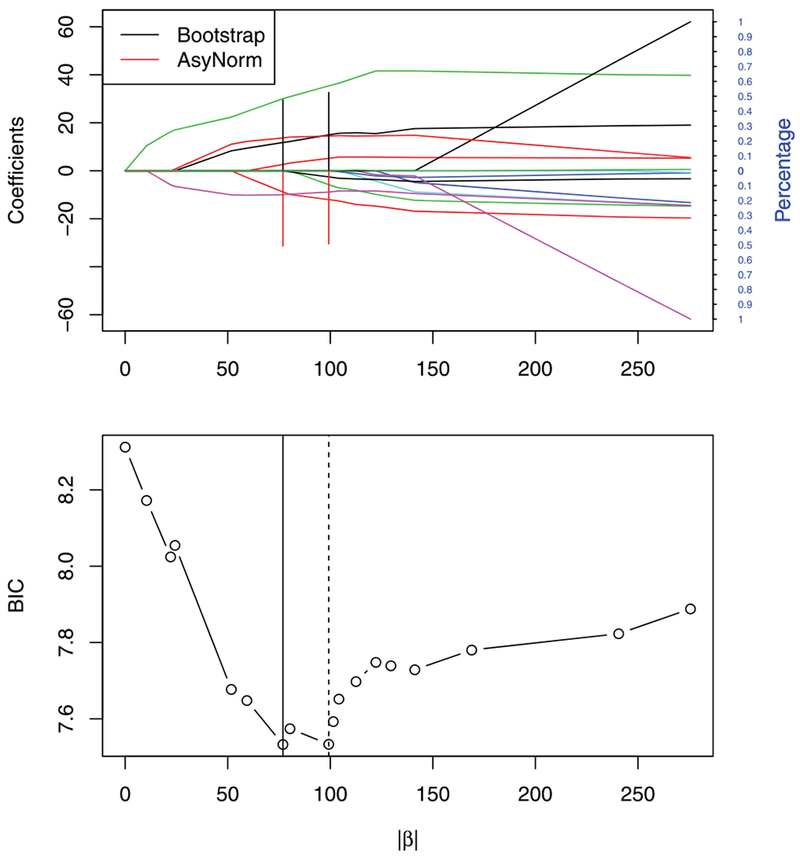
The estimated conditional distribution of the tuning parameter and 90% confidence intervals are presented in Table 5; the estimated distribution is overlaid on the solution path in Figure 3. It can be seen that the estimated distribution of the tuning parameter mainly favors two models.

Table 5.

Estimated conditional distribution of the tuning parameter for ATV drug resistance data.

λ	1347.92	1101.71	805.53
Model size	10	12	15
Probability mass normal	0.443	0.045	0.472
Probability mass bootstrap	0.494	0.047	0.454
90% CI based on normality	(0.019, 0.896)	(0.026,0.127)	(0.059, 0.959)
90% Approximate CI	(0.000, 0.751)	(0.020, 0.064)	(0.020, 1)

Figure 3.

The top figure shows LASSO solution path of ATV drug resistance data; The vertical lines above and below x-axis correspond to the distribution estimated by bootstrap and asymptotic normal approximation, respectively. The bottom figure shows BIC values for candidate models along solution path. The solid vertical line corresponds to the model with 15 variables and smallest BIC value. The dashed vertical lines correspond to model with 12 and 10 variables.

Similar to Barber et al. (2015), we evaluate candidate models based on treatment selected mutations (TSM) panels, which provide a surrogate for the true important mutations. The model minimizing BIC contains 15 variables, while two of them correspond to the same mutation. This leads to 14 unique mutation locations, and four locations are potential false discoveries (as assessed by TSM); see Table 5. Therefore, the surrogate-based estimated false discovery rate is 4/14 ≈ 0.29. For tuning parameter λ = 1101.71, 11 unique positions are identified, and two locations are potential false discoveries. Tuning parameter λ = 1347.92 leads to nine unique locations with one potential false discovery. The corresponding surrogate-based estimated false discovery rate is 1/9 ≈ 0.11, a decrease of 20% compared with the model minimizing BIC. Thus, in this case it might not be appropriate to report the single model selected by BIC.

6. Conclusion

We proposed two simple procedures for estimating the conditional distribution of a data-driven tuning parameter in penalized regression given the observed solution path and design matrix. Our objective was to quantify the stability of selected models and thereby identify a set of potential models for consideration by domain experts. A plot of the solution path with the estimated selection probabilities or upper confidence bounds overlaid, for example, Figures 1 and 3, is one means of easily conveying uncertainty in the tuning parameter and identifying models that warrant additional investigation. It is noteworthy that in both examples the identified sets of likely models are not contiguous in size. Thus, our methods provide a theoretically motivated, confidence-set-based alternative to the practice of considering models near in size to the BIC-chosen LASSO model.

Appendix A: Simulation Results

Table A.1.

Discovery rate for p = 20, n = 50; τ = 0.1.

Model	ρ	AsympNor		Bootstrap		UP1		UP2		Akaike		ApproxPost
		TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR
	0	0.90	0.10	0.90	0.10	1.00	0.33	0.99	0.37	0.42	0.80	0.89	0.48
1	05	0.92	0.08	0.92	0.08	1.00	0.30	0.99	0.33	0.48	0.78	0.93	0.48
	0	0.87	0.11	0.88	0.11	0.99	0.33	0.99	0.36	0.35	0.81	0.81	0.48
2	05	0.89	0.10	0.89	0.11	1.00	0.35	0.99	0.36	0.45	0.78	0.87	0.47
	0	0.91	0.09	0.92	0.09	1.00	0.29	0.99	0.34	0.44	0.80	0.93	0.48
3	05	0.92	0.07	0.93	0.08	1.00	026	0.99	0.30	0.50	0.78	0.96	0.49
	0	0.89	0.10	0.90	0.10	1.00	0.34	0.99	0.37	0.39	0.80	0.87	0.48
4	05	0.90	0.10	0.91	0.10	1.00	0.34	0.99	0.35	0.46	0.79	0.91	0.48

Table A.2.

Discovery rate for p = 100, n = 200; τ = 0.1.

Model	ρ	AsympNor		Bootstrap		UP1		UP2		Akaike		ApproxPost
		TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR
	0	0.97	0.03	0.97	0.03	1.00	0.13	1.00	0.14	0.07	0.97	0.99	0.42
1	0.5	0.97	0.02	0.97	0.02	1.00	0.10	1.00	0.10	0.15	0.93	1.00	0.40
	0	0.95	0.04	0.95	0.04	1.00	0.17	1.00	0.18	0.03	0.99	0.98	0.42
2	0.5	0.96	0.04	0.96	0.04	1.00	0.14	1.00	0.15	0.07	0.97	0.99	0.42
	0	0.97	0.03	0.97	0.03	1.00	0.12	1.00	0.13	0.09	0.96	0.99	0.42
3	0.5	0.98	0.02	0.98	0.02	1.00	0.09	1.00	0.10	0.17	0.93	1.00	0.40
	0	0.96	0.04	0.96	0.04	1.00	0.14	1.00	0.15	0.04	0.98	0.99	0.42
4	0.5	0.97	0.03	0.97	0.03	1.00	0.12	1.00	0.13	0.09	0.96	0.99	0.42

Table A3.

Discovery rate for p = 20, n = 50; τ = 0.2.

Model	ρ	AsympNor		Bootstrap		UP1		UP2		Akaike		ApproxPost
		TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR
	0	0.89	0.11	0.89	0.11	0.99	0.34	0.99	0.39	0.25	0.69	0.84	0.22
1	0.5	0.91	0.08	0.91	0.08	1.00	0.29	0.99	0.34	0.29	0.65	0.90	0.22
	0	0.86	0.13	0.86	0.13	0.99	0.36	0.99	0.41	0.22	0.73	0.77	0.23
2	0.5	0.88	0.11	0.88	0.12	0.99	0.37	0.99	0.40	0.28	0.65	0.83	0.23
	0	0.91	0.09	0.91	0.09	1.00	0.30	0.99	0.35	0.26	0.68	0.89	0.23
3	0.5	0.92	0.07	0.92	0.08	1.00	0.26	0.99	0.31	0.31	0.64	0.92	0.23
	0	0.88	0.11	0.88	0.11	0.99	0.35	0.99	0.40	0.23	0.71	0.83	0.22
4	0.5	0.89	0.10	0.90	0.10	0.99	0.34	0.99	0.38	0.28	0.66	0.86	0.23

Table A.4.

Discovery rate for p = 100, n = 200; τ = 0.2.

Model	ρ	AsympNor		Bootstrap		UP1		UP2		Akaike		ApproxPost
		TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR	TDR	FDR
	0	0.97	0.03	0.97	0.03	1.00	0.13	1.00	0.13	0.03	0.94	0.98	0.22
1	0.5	0.97	0.03	0.97	0.03	1.00	0.10	1.00	0.11	0.07	0.88	0.99	0.21
	0	0.95	0.05	0.95	0.05	1.00	0.17	1.00	0.18	0.01	0.98	0.96	0.21
2	0.5	0.96	0.04	0.96	0.04	1.00	0.14	1.00	0.15	0.03	0.93	0.98	0.21
	0	0.97	0.03	0.97	0.03	1.00	0.12	1.00	0.12	0.04	0.91	0.99	0.21
3	0.5	0.98	0.03	0.98	0.03	1.00	0.09	1.00	0.10	0.09	0.86	0.99	0.20
	0	0.96	0.04	0.96	0.04	1.00	0.15	1.00	0.16	0.02	0.96	0.97	0.21
4	0.5	0.97	0.03	0.97	0.03	1.00	0.12	1.00	0.13	0.04	0.92	0.99	0.21

Appendix B: Additional Results for Real-Data

Table B.1.

Coefficient estimates for pollution and mortality data; columns BIC-8 and BIC-6 correspond to lasso estimateswith eight and six predictors, respectively; columns Refit-8 and Refit-6 correspond to refitting coefficient with eight and six predictors; column FS-5 corresponds to model selected by forward stepwise regression.

Variable	Lasso				FS-5
	BIC-8	Refit-8	BIC-6	Refit-6
Mean annual precipitation	14.95	17.76	11.78	14.85	14.86
Mean January temperature	−12.04	−14.26	−8.80	−16.61	−16.50
Mean July temperature	−5.80	−11.71	0	0	0
Median school years	−8.89	−8.05	−9.99	−9.75	−10.80
Pct of housing units with facilities	−2.55	−4.69	0	0	0
Population per square mile	5.15	7.11	2.62	6.039	0
Pct of non-White	35.38	39.98	30.04	36.98	36.27
Pollution potential of sulfur dioxide	14.47	14.92	13.66	15.51	18.00

Appendix C: Proof and Technical Details

Lemma C.1.

If the penalty function f_j(β_j; ℙ_n) depends on the data only through X^⊺Y and X, then the distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}$ conditional on $\widehat{S}$ and X is equal to the distribution of ${\widehat{\lambda }}_{\mathrm{GIC}}$ conditional on X^⊺Y and X.

Proof. $\widehat{\beta }(\lambda )={\mathrm{argmin}}_{\beta }\{\frac{1}{2}{\beta }^{⊺}{\mathbf{X}}^{⊺}\mathbf{X}\beta -{\mathbf{Y}}^{⊺}\mathbf{X}\beta +{\sum }_{j=2}^p{f}_j({\beta }_j;{\mathbb{P}}_n)\}$, from which it can be seen that the solution path is completely determined by X^⊺X and X^⊺Y. On the other hand, given $\widehat{S}$ and X, we can recover X^⊺Y using ${\mathbf{X}}^{⊺}\mathbf{X}\widehat{\beta }(0)$ = X^⊺X{(X^⊺X)⁻¹X^⊺Y} = X^TY. □

Lemma C.2.

Suppose that b(·) and c(·) are nonnegative valued functions defined on [0, ∞] such that b(λ) is a nondecreasing for λ ≥ 0 with b(0) = 0. For x ≥ 0, define

$$H(x,\lambda )=\log \{x+b(\lambda )\}+c(\lambda )$$

and

$$\lambda (x)=\underset{\lambda }{\text{argmin}}H(x,\lambda ).$$

Then λ(x) is nondecreasing in x ≥ 0.

Proof of Lemma C.2. Supposed x₁ ≤ x₂, we need to show that λ(x₁) ≤ λ(x₂). First, consider the difference of H(x₂, λ) and H(x₁, λ)

$$\begin{array}{cc}\hfill H(x_2,\lambda )-H(x_1,\lambda )& =\log \{x_2+b(\lambda )\}-\log \{x_1+b(\lambda )\}\hfill \\ \hfill & =\log \left\{1+\frac{x_2-x_1}{x_1+b(\lambda )}\right\},\hfill \end{array}$$

which is nonnegative for every λ and nonincreasing in λ. Therefore if λ(x₁) = argmin_λ H(x₁, λ), it follows that

$$\begin{array}{cc}\hfill \lambda (x_2)& =\underset{\lambda }{\text{argmin}}H(x_2,\lambda ),\hfill \\ \hfill & =\underset{\lambda }{\text{argmin}}\left[H(x_1,\lambda )+\log \left\{1+\frac{x_2-x_1}{x_1+b(\lambda )}\right\}\right]\hfill \\ \hfill & \ge \lambda (x_1).\hfill \end{array}$$

The last inequality follows from that log{1 + (x₂ − x₁ )/(x₁ + b(λ))} is nonnegative and nonincreasing with respect to λ. □

Proof of Lemma 1. Recall that the information criterion can also be expressed as

$$\begin{array}{cc}\hfill {\text{GIC}}_{\lambda }& =\log \left(\frac{\Vert \mathbf{Y}-\mathbf{X}\widehat{\beta }(\mathbf{\lambda }){\Vert }^2}{n}\right)+w_n{\widehat{\mathit{df}}}_{\lambda }\hfill \\ \hfill & =\log \left(\frac{\Vert \mathbf{Y}-\mathbf{X}{\widehat{\beta }}_{\text{ols}}+\mathbf{X}{\widehat{\beta }}_{\text{ols}}-\mathbf{X}\widehat{\beta }(\mathbf{\lambda }){\Vert }^2}{n}\right)+w_n{\widehat{\mathit{df}}}_{\lambda }\hfill \\ \hfill & =\log \left({\widehat{\sigma }}_0^2+\frac{D_{\lambda }}{n}\right)+w_n{\widehat{\mathit{df}}}_{\lambda },\hfill \end{array}$$

where $D_{\lambda }=\{{\widehat{\beta }}_{\mathrm{ols}}-\widehat{\beta }(\lambda ){\}}^{⊺}{\mathbf{X}}^{⊺}\mathbf{X}\{{\widehat{\beta }}_{\mathrm{ols}}-\widehat{\beta }(\lambda )\}$.

Because D_λ is a deterministic function of λ conditional on the solution path and design matrix, the only variability in ${\widehat{\lambda }}_{\mathrm{GIC}}$ is due to ${\widehat{\sigma }}_0^2$. Therefore, ${\widehat{\lambda }}_{\mathrm{GIC}}\mid ({\widehat{\beta }}_{\mathrm{ols}},\mathbf{X})$ is a function of ${\widehat{\sigma }}_0^2$.

Then monotonicity comes immediately by observing that D_λ is a non-decreasing function for λ ≥ 0 with D(0) = 0 and invokng Lemma C.2. □

Lemma C.3.

Let $\widehat{S}$ and X be fixed. If ${\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}<{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}}$, then ${\mathrm{GIC}}_{{\widehat{\lambda }}_{(i)}}\le {\mathrm{GIC}}_{{\widehat{\lambda }}_{(k)}}$ iff $n{\widehat{\sigma }}_0^2\le {\widehat{\ell }}_{i,k}$ and if ${\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}>{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}}$, then ${\mathrm{GIC}}_{{\widehat{\lambda }}_{(i)}}\le {\mathrm{GIC}}_{{\widehat{\lambda }}_{(k)}}$ iff $n{\widehat{\sigma }}_0^2\ge {\widehat{\ell }}_{i,k}$.

Proof of Lemma C.3. Consider the case ${\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}<{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}}$,

$$\begin{array}{cc}\hfill p({\text{GIC}}_{{\widehat{\lambda }}_{(i)}}& \le {\text{GIC}}_{{\widehat{\lambda }}_{(k)}}\mid \widehat{S},\mathbf{X})\hfill \\ \hfill & =P[\log \left\{{\widehat{\sigma }}_0^2+\frac{D_{{\widehat{\lambda }}_{(i)}}}{n}\right\}\phantom{]}+w_n{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}}\hfill \\ \hfill & \le \log \phantom{[}\left\{{\widehat{\sigma }}_0^2+\frac{D_{{\widehat{\lambda }}_{(k)}}}{n}\right\}+w_n{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}\mid \widehat{S},\mathbf{X}]\hfill \\ \hfill & =P[\log \left\{{\widehat{\sigma }}_0^2+\frac{D_{{\widehat{\lambda }}_{(i)}}}{n}\right\}-\log \left\{{\widehat{\sigma }}_0^2+\frac{D_{{\widehat{\lambda }}_{(k)}}}{n}\right\}\phantom{]}\hfill \\ \hfill & \le w_n\phantom{[}\left\{{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}-{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}}\right\}\mid \widehat{S},\mathbf{X}]\hfill \\ \hfill & =P\left[\frac{n{\widehat{\sigma }}_0^2+D_{{\widehat{\lambda }}_{(i)}}}{n{\widehat{\sigma }}_0^2+D_{{\widehat{\lambda }}_{(k)}}}\le \text{exp}\{w_n({\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}-{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}})\}\mid \widehat{S},\mathbf{X}\right]\hfill \\ \hfill & =P\left(n{\widehat{\sigma }}_0^2\le \frac{D_{{\widehat{\lambda }}_{(k)}}\text{exp}\{w_n({\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}-{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}})\}-D_{{\widehat{\lambda }}_{(i)}}}{1-\text{exp}\{w_n({\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}-{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}})\}}\mid \widehat{S},\mathbf{X}\right).\hfill \end{array}$$

The case ${\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(k)}}>{\widehat{\mathit{df}}}_{{\widehat{\lambda }}_{(i)}}$ follows by a similar argument. □

Proof of Proposition 1. The proof follows from the fact that

$${\text{GIC}}_{{\widehat{\lambda }}_{(k)}}<{\text{GIC}}_{{\widehat{\lambda }}_{(i)}}\text{for}\text{all}i\in A_k\cup B_k\text{if}\text{and}\text{only}\text{if}\underset{i\in {\widehat{B}}_k}{\text{max}}{\widehat{\ell }}_{i,k}\le n{\widehat{\sigma }}_0^2\le \underset{i\in {\widehat{A}}_k}{\text{max}}{\widehat{\ell }}_{i,k}.$$

□

To prove Proposition 2, we assume:

(A1F): under a fixed design ${\lim }_{n\to \infty }{n}^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i{\mathbf{X}}_i^{⊺}=C$, ${\lim }_{n\to \infty }{n}^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i={\mu }_x$, where C ∈ ℝ^p×p is nonnegative definite and μ_xx ∈ ℝ^p;

(A1R): under a random design, with probability one, ${\lim }_{n\to \infty }{n}^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i{\mathbf{X}}_i^{⊺}=C$, and ${\lim }_{n\to \infty }{n}^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i={\mu }_x$, where C ∈ ℝ^p×p is nonnegative definite and μ_x ∈ ℝ^p;

(A2): $𝔼{ϵ}_i^4<\infty$.

Under assumptions (A1F) and (A2), we have the following well-known results, which facilitate the proof of Proposition 2.

Lemma C.4.

$$\begin{array}{c}\hfill {\widehat{\beta }}_{\text{ols}}\stackrel{\text{as}}{\to }{\beta }_0;\hfill \\ \hfill \sqrt{n}({\widehat{\beta }}_{\text{ols}}-{\beta }_0)\stackrel{d}{\to }N({\mathbf{0}}_{p\times 1},C^{-1}).\hfill \end{array}$$

Proof of Proposition 2. First consider the fixed design model. Let

$$\psi (Y_i,{\mathbf{X}}_i,\beta ,{\sigma }^2)=\left(\begin{array}{c}\hfill (Y_i-{\mathbf{X}}_i^{⊺}\beta ){\mathbf{X}}_i\hfill \\ \hfill {(Y_i-{\mathbf{X}}_i^{⊺}\beta )}^2-{\sigma }^2\hfill \end{array}\right).$$

Then ${({\widehat{\beta }}_{\mathrm{ols}}^{⊺},{\widehat{\sigma }}^2)}^{⊺}$ is a solution to the equation

$$\sum _{i=1}^n\psi (Y_i,{\mathbf{X}}_i,\beta ,{\sigma }^2)=0.$$

A Taylor series expansion around the true value (β₀, ${\sigma }_0^2$) results in

$$\begin{array}{cc}\hfill & \underset{i=1}{\overset{n}{\Sigma }}\psi (Y_i,{\mathbf{X}}_i,{\widehat{\beta }}_{\text{ols}},{\widehat{\sigma }}^2)=\underset{i=1}{\overset{n}{\Sigma }}\psi (Y_i,{\mathbf{X}}_i,{\beta }_0,{\sigma }^2)\hfill \\ \hfill & +\underset{i=1}{\overset{n}{\Sigma }}{\psi }^{\prime }(Y_i,{\mathbf{X}}_i,{\beta }_0,{\sigma }^2)\left(\begin{array}{c}\hfill {\widehat{\beta }}_{ols}-{\beta }_0\hfill \\ \hfill {\widehat{\sigma }}^2-{\sigma }_0^2\hfill \end{array}\right)+R_n,\hfill \end{array}$$

where ψ′ is the derivative of ψ and

$$R_n=\sum _{i=1}^n\left(\begin{array}{c}\hfill 0_{p\times 1}\hfill \\ \hfill ({\widehat{\beta }}_{\text{ols}}-{\beta }_0{)}^{⊺}{\mathbf{X}}_i{\mathbf{X}}_i^{⊺}({\widehat{\beta }}_{\text{ols}}-{\beta }_0)\hfill \end{array}\right).$$

Rearranging it leads to

$$\begin{array}{cc}\hfill & \left\{-\frac{1}{n}\underset{i=1}{\overset{n}{\Sigma }}{\psi }^{\prime }(Y_i,{\mathbf{X}}_i,{\beta }_0,{\sigma }_0^2)\right\}\sqrt{n}\left(\begin{array}{c}\hfill {\widehat{\beta }}_{\text{ols}}-{\beta }_0\hfill \\ \hfill {\widehat{\sigma }}^2-{\sigma }_0^2\hfill \end{array}\right)\hfill \\ \hfill & =\left\{\frac{1}{\sqrt{n}}\underset{i=1}{\overset{n}{\Sigma }}\psi (Y_i,{\mathbf{X}}_i,{\beta }_0,{\sigma }_0^2)\right\}+R_n∕\sqrt{n}.\hfill \end{array}$$

Because −${\psi }^{\prime }(Y_i,{\mathbf{X}}_i,{\beta }_0,{\sigma }_0^2)=(\begin{array}{cc}\hfill {\mathbf{X}}_i{\mathbf{X}}_i^{⊺}\hfill & \hfill 0_{p\times 1}\hfill \\ \hfill 2{\mathbf{X}}_i^{⊺}(Y_i-{\mathbf{X}}_i^{⊺}{\beta }_0)\hfill & \hfill 1\hfill \end{array})$, it follows that

$$-\frac{1}{n}\sum _{i=1}^n{\psi }^{\prime }(Y_i,{\mathbf{X}}_i,{\beta }_0,{\sigma }_0^2)\stackrel{p}{\to }\left(\begin{array}{cc}\hfill \mathrm{C}\hfill & \hfill {\mathbf{0}}_{p\times 1}\hfill \\ \hfill {\mathbf{0}}_{1\times p}\hfill & \hfill 1\hfill \end{array}\right)$$

by consistency of ${\widehat{\beta }}_{\mathrm{ols}}$.

Then by the multivariate Lindberg–Feller CLT,

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n\psi (Y_i,{\mathbf{X}}_i,{\beta }_0,{\sigma }_0^2)\stackrel{d}{\to }N\left[\left(\begin{array}{c}\hfill 0_{p\times 1}\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\sigma }_0^2\mathrm{C}\hfill & \hfill {\mu }_x{\mu }_{3,ϵ}\hfill \\ \hfill {\mu }_x^{⊺}{\mu }_{3,ϵ}\hfill & \hfill {\mu }_{4,ϵ}-{\sigma }_0^4\hfill \end{array}\right)\right].$$

Finally, $R_n∕\sqrt{n}$ is o_p(1) as of

$$\begin{array}{cc}\hfill & \frac{1}{\sqrt{n}}\underset{i=1}{\overset{n}{\Sigma }}({\widehat{\beta }}_{\text{ols}}-{\beta }_0{)}^{⊺}{\mathbf{X}}_i{\mathbf{X}}_i^{⊺}({\widehat{\beta }}_{\text{ols}}-{\beta }_0)\hfill \\ \hfill & =\sqrt{n}({\widehat{\beta }}_{\text{ols}}-{\beta }_0{)}^{⊺}\left\{\frac{1}{n}\sum _{i=1}^n{\mathbf{X}}_i{\mathbf{X}}_i^{⊺}\right\}({\widehat{\beta }}_{\text{ols}}-{\beta }_0).\hfill \end{array}$$

Therefore by Slutsky’s theorem,

$$\sqrt{n}\left(\begin{array}{c}\hfill {\widehat{\beta }}_{\text{ols}}-{\beta }_0\hfill \\ \hfill {\widehat{\sigma }}_0^2-{\sigma }_0^2\hfill \end{array}\right)\stackrel{d}{\to }N\left[\left(\begin{array}{c}\hfill 0_{p\times 1}\hfill \\ \hfill 0\hfill \end{array}\right),\left(\begin{array}{cc}\hfill {\sigma }_0^2{\mathrm{C}}^{-1}\hfill & \hfill {\mu }_x{\mu }_{3,ϵ}\hfill \\ \hfill {\mu }_x^{⊺}{\mu }_{3,ϵ}\hfill & \hfill {\mu }_{4,ϵ}-{\sigma }_0^4\hfill \end{array}\right)\right].$$ (C.1)

Then, for the random design, because ${\lim }_{n\to \infty }{n}^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i{\mathbf{X}}_i^{⊺}=C$ and ${\lim }_{n\to \infty }{n}^{-1}{\sum }_{i=1}^n{\mathbf{X}}_i={\mu }_x$ almost surely, assumption A1F holds for almost every sequence x₁, x₂, …. Therefore Equation (C.1) holds for almost every sequence x₁, x₂,…. □

Lemma C.5.

Suppose ϵ₁, ϵ₂, … , ϵ_n are normally distributed with mean zero and variance ${\sigma }_0^2$, then plugging estimator ${\widehat{p}}_k=F_{{\chi }_{n-p}^2}({\widehat{a}}_k∕{\widehat{\sigma }}_0^2)-F_{{\chi }_{n-p}^2}({\widehat{b}}_k∕{\widehat{\sigma }}_0^2)$ need not be a consistent estimator for p_k, where ${\widehat{a}}_k$ and ${\widehat{b}}_k$ are defined in Section 3.2.

Proof. We show that there exist sequences for which ${\widehat{p}}_k$ is not consistent for p_k. Considering the case X^⊺X = n × I₂ with X₁ = 1^n×1 and ${\sigma }_0^2$ = 1, then

$$\begin{array}{cc}\hfill p_1& =P\left({\text{GIC}}_{+\infty }>{\text{GIC}}_0\mid {\widehat{\beta }}_{\text{ols}},\mathbf{X}\right)\hfill \\ \hfill & =P\left(\frac{{\widehat{\beta }}_{\text{ols},2}^2}{\text{exp}(w_n)-1}>{\widehat{\sigma }}_0^2\mid {\widehat{\beta }}_{\text{ols}},\mathbf{X}\right)\hfill \\ \hfill & =\varphi \left(\frac{{\widehat{a}}_1-n}{\sqrt{2n}}\right)+o_p(1),\hfill \end{array}$$

where ${\widehat{a}}_1=n{\widehat{\beta }}_{\mathrm{ols},2}^2∕\{\exp (w_n)-1\}$ and ${\widehat{\beta }}_{\mathrm{ols},2}$ corresponds least-square estimate for X₂. And

$${\widehat{p}}_1=\Phi \left(\frac{{\widehat{a}}_1∕{\widehat{\sigma }}_0^2-n}{\sqrt{2n}}\right)+o_p(1).$$

For the sequence of ${\widehat{\beta }}_{\mathrm{ols},2}=\sqrt{(\exp (w_n)-1)(1+{\mathit{cn}}^{-1∕2})}$, where c is any constant, it follows that ${\widehat{a}}_1=n+c\sqrt{n}$. And then

$$\begin{array}{cc}\hfill \frac{{\widehat{a}}_1-n}{\sqrt{2n}}-\frac{{\widehat{a}}_1∕{\widehat{\sigma }}_0^2-n}{\sqrt{2n}}& =\frac{{\widehat{a}}_1({\widehat{\sigma }}_0^2-1)}{\sqrt{2n}{\widehat{\sigma }}_0^2}\hfill \\ \hfill & =\frac{(n+c\sqrt{n})({\widehat{\sigma }}_0^2-1)}{\sqrt{2n}{\widehat{\sigma }}_0^2},\hfill \end{array}$$

which is not o_p(1). Therefore, ${\widehat{p}}_1$ is not a consistent estimator for p₁. □

Proposition C.1.

Assume the distribution of ϵ_i, i = 1, … , n is symmetric about zero, then for any ϵ > 0,

$$P\left\{\underset{(t_1,t_2)\in {\mathcal{E}}_y}{\text{inf}}\mid p_k-h_k(t_1,t_2)\mid >ϵ\right\}\le \alpha +o(1),$$ (C.2)

where ${\mathcal{E}}_y$ is an asymptotically (1 − α) × 100% confidence region for μ_4,ϵ − ${\sigma }_0^4$ and ${\sigma }_0^2$.

Proof. Denote the event that $({\sigma }_0^2,{\mu }_{4,ϵ}-{\sigma }_0^4)\in {\mathcal{G}}_y$ as A,

$$\begin{array}{cc}\hfill P& (\underset{(t_1,t_2)\in {\mathcal{E}}_y}{\inf }\mid p_k-h_k(t_1,t_2)\mid >ϵ)\hfill \\ \hfill & \le P(\underset{(t_1,t_2)\in {\mathcal{E}}_y}{\inf }\mid p_k-h_k(t_1,t_2)\mid >ϵ\mid A)P(A)+P(A^c)\hfill \\ \hfill & \le 0(1-\alpha )+\alpha +o(1)\hfill \\ \hfill & =\alpha +o(1).\hfill \end{array}$$

□

Lemma C.6.

For any s ≥ 1, assume $n^{-1}{\Sigma }_{i=1}^n{\mid \mid X_i\mid \mid }^s=O(1)$, then

$$n^{-1}\sum _{i=1}^n{\mid {\widehat{e}}_i\mid }^s\stackrel{\text{as}}{\to }{m}_s,$$

where m_s = E|ϵ₁|^s.

Proof of Lemma C.6.

$$\begin{array}{cc}\hfill {\left\{{\left(n^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\mid {\widehat{e}}_i\mid }^s\right)}^{1∕s}-{\left(n^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\mid {ϵ}_i\mid }^s\right)}^{1∕s}\right\}}^s& \le n^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\mid {\widehat{e}}_i-{ϵ}_i\mid }^s\hfill \\ \hfill & =n^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\mid X_i^{⊺}({\widehat{\beta }}_{\text{ols}}-{\beta }_0)\mid }^s\hfill \\ \hfill & \le n^{-1}\underset{i=1}{\overset{n}{\Sigma }}{\Vert X_i\Vert }^s{\Vert {\widehat{\beta }}_{\text{ols}}-{\beta }_0\Vert }^s.\hfill \end{array}$$

But ${\widehat{\beta }}_{\mathrm{ols}}\stackrel{\text{as}}{\to }{\beta }_0$ and $n^{-1}{\sum }_{i=1}^n{\mid \mid X_i\mid \mid }^s=O(1)$, so that ${(n^{-1}{\sum }_{i=1}^n{\mid {\widehat{e}}_i\mid }^s)}^{1∕s}-{(n^{-1}{\sum }_{i=1}^n{\mid {ϵ}_i\mid }^s)}^{1∕s}\stackrel{\text{as}}{\to }0$. Then by Strong Law of Large Numbers, $n^{-1}{\sum }_{i=1}^n{\mid {ϵ}_i\mid }^s\stackrel{\text{as}}{\to }E{\mid {ϵ}_1\mid }^s$. And thus $n^{-1}{\sum }_{i=1}^n{\mid {\widehat{e}}_i\mid }^s\stackrel{\text{as}}{\to }E{\mid {ϵ}_1\mid }^s$. □

Lemma C.7.

Assume (A1F) and (A2), then

$$\frac{1}{\sqrt{n}}{\gamma }^{{(b)}^{⊺}}{\mathbf{P}}_{\mathbf{x}}{\gamma }^{(b)}\stackrel{p}{\to }0,$$

conditionally almost surely.

Proof of Lemma C.7. Denote ${\widehat{\beta }}_{\mathrm{ols}}^{\ast }={({\mathbf{X}}^{⊺}\mathbf{X})}^{-1}{\mathbf{X}}^{⊺}(\mathbf{X}{\widehat{\beta }}_{\mathrm{ols}}+{\gamma }^{(b)})$, then we have

$$\frac{1}{\sqrt{n}}{\gamma }^{{(b)}^{⊺}}{\mathbf{P}}_{\mathbf{x}}{\gamma }^{(b)}=\sqrt{n}{({\widehat{\beta }}_{\text{ols}}^{\ast }-{\widehat{\beta }}_{\text{ols}})}^{⊺}(\frac{1}{n}{\mathbf{X}}^{⊺}\mathbf{X})({\widehat{\beta }}_{\text{ols}}^{\ast }-{\widehat{\beta }}_{\text{ols}}).$$

Then by noting $\sqrt{n}({\widehat{\beta }}_{\mathrm{ols}}^{\ast }-{\widehat{\beta }}_{\mathrm{ols}})\stackrel{d}{\to }N(0,C^{-1})$ conditionally almost surely (Theorem 2.2 of Freedman 1981), $\frac{1}{\sqrt{n}}{\gamma }^{(b{)}^{⊺}}{\mathbf{P}}_{\mathrm{x}}{\gamma }^{(b)}$ is o_p(1) conditionally almost surely. □

Proposition C.2.

Under the assumptions (A1F) and (A2), and further assuming that E|ϵ_i|^4+δ < ∞ and $n^{-1}{\sum }_{i=1}^n\mid \mid X_i\mid {\mid }^{4+\delta }<\infty$ for any δ > 0, then $\sqrt{n}({\widehat{\sigma }}_{\ast }^2-{\widehat{\sigma }}_0^2)\stackrel{d}{\to }N(0,{\mu }_{4,ϵ}-{\sigma }_0^4)$ conditionally almost surely. □

Proof of Proposition C.2. Recall

$$\begin{array}{cc}\hfill {\widehat{\sigma }}_{\ast }^2& =\frac{1}{n}{\gamma }^{{(b)}^{⊺}}(\mathbf{I}-{\mathbf{P}}_{\mathbf{x}}){\gamma }^{(b)}\hfill \\ \hfill & =\frac{1}{n}{\gamma }^{{(b)}^{⊺}}{\gamma }^{(b)}-\frac{1}{n}{\gamma }^{{(b)}^{⊺}}{\mathbf{P}}_{\mathbf{x}}{\gamma }^{(b)}.\hfill \end{array}$$

Because $n^{-1∕2}{\gamma }^{(b{)}^{⊺}}{\mathbf{P}}_{\mathrm{x}}{\gamma }^{(b)}\underrightarrow{p}0$ almost surely by Lemma C.7, ${\widehat{\sigma }}_{\ast }^2$ has the same asymptotic distribution as n⁻¹γ^(b)⊺γ^(b). Then because the γ₁^(b), γ₂^(b), … , γ_n^(b) are sampled from different distribution for every n, the Lindberg central limit theorem is used to obtain the asymptotic distribution. The conditional mean of ${({\gamma }_i^{(b)})}^2$ is

$$E({\{r_1^{(b)}\}}^2\mid \mathbf{Y})=\frac{1}{n}\sum _{i=1}^n{({\widehat{e}}_i)}^2={{\widehat{\sigma }}_0}^2.$$

The conditional variance is

$$\text{var}({\{r_1^{(b)}\}}^2\mid \mathbf{Y})=\frac{1}{n}\sum _{i=1}^n{({\widehat{e}}_i)}^4-{\left\{\frac{1}{n}\sum _{i=1}^n{({\widehat{e}}_i)}^2\right\}}^2.$$

Use Lemma C.6, $n^{-1}{\sum }_{i=1}^n{(\widehat{e})}^4\stackrel{\text{as}}{\to }{\mu }_{4,ϵ}$ and ${\{n^{-1}{\sum }_{i=1}^n{({\widehat{e}}_i)}^2\}}^2\stackrel{\text{as}}{\to }{\sigma }_0^4$. So the conditional variance converges to ${\mu }_{4,ϵ}-{\sigma }_0^4$ almost surely.

Then to verify the Lyapunov condition,

$$\begin{array}{cc}\hfill & \frac{1}{{\{\text{var}({\{r_1^{(b)}\}}^2\mid \mathbf{Y})\}}^{2+\delta }}\underset{i=1}{\overset{n}{\Sigma }}E\left\{{\mid {(r_1^{(b)})}^2∕\sqrt{n}\mid }^{2+\delta }\mid \mathbf{Y}\right\}\hfill \\ \hfill & =\frac{1}{{\{\text{var}({\{r_1^{(b)}\}}^2\mid \mathbf{Y})\}}^{2+\delta }}\frac{1}{n^{\delta ∕2}}E\left\{{\mid r_1^{(b)}\mid }^{4+2\delta }\mid \mathbf{Y}\right\}\hfill \\ \hfill & =\frac{1}{{\{\text{var}({\{r_1^{(b)}\}}^2\mid \mathbf{Y})\}}^{2+\delta }}\frac{1}{n^{1+\delta ∕2}}\underset{i=1}{\overset{n}{\Sigma }}{\mid {\widehat{e}}_i\mid }^{4+2\delta },\hfill \end{array}$$

which is o(1) almost surely by invoking Lemma C.6. And thus $\sqrt{n}({\widehat{\sigma }}_{\ast }^2-{\widehat{\sigma }}_0^2)\stackrel{d}{\to }N(0,{\mu }_{4,ϵ}-{\sigma }_0^4)$ conditionally almost surely. □

C1. Theoretical Results for High Dimensions

Proposition C.3.

If p = o(n^1/2), then

$$\sqrt{n}({\widehat{\sigma }}_0^2-{\sigma }_0^2)\stackrel{d}{\to }N(0,{\mu }_{4,ϵ}-{\sigma }_0^4).$$

Proof of Proposition C.3. We know ${\widehat{\sigma }}_0^2=n^{-1}{ϵ}^{⊺}ϵ-n^{-1}{ϵ}^{⊺}{P}_xϵ$, where $\sqrt{n}(n^{-1}{ϵ}^{⊺}ϵ-{\sigma }_0^2)$ converges to $N(0,{\mu }_{4,ϵ}-{\sigma }_0^4)$ in distribution. It remains to prove $n^{-1∕2}{ϵ}^{⊺}{P}_xϵ\stackrel{p}{\to }0$.

By expectation of quadratic form, we have $n^{-1∕2}E({ϵ}^{⊺}{P}_xϵ)=n^{-1∕2}\mathrm{tr}(P_x\times I)\le n^{-1∕2}p=o(1)$. Therefore, $n^{-1∕2}{ϵ}^{⊺}{P}_xϵ\stackrel{p}{\to }0$. This completes the proof. □

Now we study the distribution of variance estimator after screening. First, we restate Theorem 1 from Fan and Lv (2008) with slight modification. Denote A₀ to be the true index of nonzero regression coefficients, and S to be the screened subset. Assume Conditions 1–4 in Fan and Lv (2008) hold for some 2κ + τ < 1/2, then we have the following result.

Theorem C.1 (Accuracy of SIS). Under Conditions 1–4 in Fan and Lv (2008), if 2κ + τ < 1/2, there exists θ > 1/2, we have

$$P(A_0\in S)=1-O(\text{exp}(-C{n}^{1-2\kappa }∕\log n)),$$

where C is a positive constant, and the size of S is O(n^1−θ).

From above result, we have a screening approach to reduce number of predictors from huge scale, O(exp(n^c)), to a smaller scale, $o(\sqrt{n})$. Denote Denote X = (X^(1)⊺, X^(2)⊺)^⊺, X⁽¹⁾, X⁽²⁾ are corresponding to the first and second half of design matrix, respectively. Similarly, define Y⁽¹⁾, Y⁽²⁾. Then the variance estimator is defined as

$${\widehat{\sigma }}_0^2=1∕m{\left\{{\mathbf{Y}}^{(2)}\right\}}^{⊺}\left(I-P_{{\mathbf{X}}_s^{(2)}}\right){\mathbf{Y}}^{(2)},$$

where m = n/2, and $P_{{\mathrm{X}}_S^{(2)}}$ is the projection matrix constructed from screened subset S and second half of design matrix, X⁽²⁾.

Proposition C.4.

Under Conditions 1–4 in Fan and Lv (2008), if 2κ + τ < 1/2, then

$$\sqrt{m}({\widehat{\sigma }}_0^2-{\sigma }_0^2)\stackrel{d}{\to }N(0,{\mu }_{4,ϵ}-{\sigma }_0^4).$$

Proof of Proposition C.4.

$$\begin{array}{cc}\hfill \sqrt{m}{\widehat{\sigma }}_0^2& =1∕\sqrt{m}{\{{\mathbf{Y}}^{(2)}\}}^{⊺}\left(I-P_{{\mathbf{X}}_s^{(2)}}\right){\mathbf{Y}}^{(2)}\hfill \\ \hfill & =1∕\sqrt{m}{\{{\mathbf{X}}^{(2)}{\beta }_0+{ϵ}^{(2)}\}}^{⊺}\left(I-P_{{\mathbf{X}}_s^{(2)}}\right)\{{\mathbf{X}}^{(2)}{\beta }_0+{ϵ}^{(2)}\}\hfill \\ \hfill & =1∕\sqrt{m}{\{{ϵ}^{(2)}\}}^{⊺}{ϵ}^{(2)}-1∕\sqrt{m}{\{{ϵ}^{(2)}\}}^{⊺}{P}_{{\mathbf{X}}_s^{(2)}}{ϵ}^{(2)}\hfill \\ \hfill & +1∕\sqrt{m}{\{{\mathbf{X}}^{(2)}{\beta }_0\}}^{⊺}\left(I-P_{{\mathbf{X}}_S^{(2)}}\right)\{{\mathbf{X}}^{(2)}{\beta }_0\}\hfill \\ \hfill & +2∕\sqrt{m}{\{{\mathbf{X}}^{(2)}{\beta }_0\}}^{⊺}\left(I-P_{{\mathbf{X}}_S^{(2)}}\right)\{{ϵ}^{(2)}\}.\hfill \end{array}$$

For the first term, we know $\sqrt{m}(1∕m{\{{ϵ}^{(2)}\}}^{⊺}{ϵ}^{(2)}-{\sigma }_0^2)$ converges to $N(0,{\mu }_{4,ϵ}-{\sigma }_0^4)$. It remains to prove the remaining term are o_p(1). For the second term, we know

$$E(1∕\sqrt{m}\{{ϵ}^{(2)}{\}}^{⊺}{P}_{{\mathbf{X}}_S^{(2)}}{ϵ}^{(2)})=1∕\sqrt{m}E(P_{{\mathbf{X}}_S^{(2)}})=1∕\sqrt{m}\times O(\sqrt{n}).$$

Therefore it is o_p(1). For the third term,

$$\begin{array}{cc}\hfill & 1∕\sqrt{m}E({\{{\mathbf{X}}^{(2)}{\beta }_0\}}^{⊺}(I-P_{{\mathbf{X}}_S^{(2)}})\{{\mathbf{X}}^{(2)}{\beta }_0\})\hfill \\ \hfill & =1∕\sqrt{m}E({\{{\mathbf{X}}^{(2)}{\beta }_0\}}^{⊺}(I-P_{{\mathbf{X}}_S^{(2)}})\{{\mathbf{X}}^{(2)}{\beta }_0\}\mid A_0\in S)P(A_0\in S)\hfill \\ \hfill & +1∕\sqrt{m}E({\{{\mathbf{X}}^{(2)}{\beta }_0\}}^{⊺}(I-P_{{\mathbf{X}}_S^{(2)}})\{{\mathbf{X}}^{(2)}{\beta }_0\}\mid A_0\notin S)P(A_0\notin S)\hfill \\ \hfill & =0+1∕\sqrt{m}E({\{{\mathbf{X}}^{(2)}{\beta }_0\}}^{⊺}(I-P_{{\mathbf{X}}_S^{(2)}})\{{\mathbf{X}}^{(2)}{\beta }_0\}\mid A_0\notin S)P(A_0\notin S)\hfill \\ \hfill & \le 1∕\sqrt{m}E({\{{\mathbf{X}}^{(2)}{\beta }_0\}}^{⊺}\{{\mathbf{X}}^{(2)}{\beta }_0\})P(A_0\notin S)\hfill \\ \hfill & =\sqrt{m}{{\beta }_0}^{⊺}C{\beta }_{0}P(A_0\notin S)\hfill \\ \hfill & \le \sqrt{m}\text{var}(Y)P(A_0\notin S)\hfill \\ \hfill & =O(\sqrt{n}\text{exp}(-C{n}^{1-2\kappa }∕\log n)),\hfill \end{array}$$

where the last inequality follows Condition 3 in Fan and Lv (2008), var(Y ) = O(1). And thus it is o_p(1). For the last term,

$$\begin{array}{cc}\hfill & \text{var}(2∕\sqrt{m}{\{{\mathbf{X}}^{(2)}{\beta }_0\}}^{⊺}(I-P_{{\mathbf{X}}_S^{(2)}}){\{ϵ}^{(2)}\})\hfill \\ \hfill & =4∕mE({\{{\mathbf{X}}^{(2)}{\beta }_0\}}^{⊺}(I-P_{{\mathbf{X}}_S^{(2)}})\{{\mathbf{X}}^{(2)}{\beta }_0\})\hfill \end{array}$$

which is o(1). This completes the proof. □