Magnesium(II) d-Gluconate Complexes Relevant to Radioactive Waste Disposals: Metal-Ion-Induced Ligand Deprotonation or Ligand-Promoted Metal-Ion Hydrolysis?

Abstract

The complexation equilibria between Mg²⁺ and d-gluconate (Gluc^–) ions are of particular importance in modeling the chemical speciation in low- and intermediate-level radioactive waste repositories. NMR measurements and potentiometric titrations conducted at 25 °C and 4 M ionic strength revealed the formation of the MgGluc⁺, MgGlucOH⁰, MgGluc(OH)₂^–, and Mg₃Gluc₂(OH)₄⁰ complexes. The trinuclear species provides indirect evidence for the existence of multinuclear magnesium(II) hydroxido complexes, whose formation was proposed earlier but has not been confirmed yet. Additionally, speciation calculations demonstrated that MgCl₂ can markedly decrease the solubility of thorium(IV) at low ligand concentrations. Regarding the structure of MgGluc⁺, both IR spectra and density functional theory (DFT) calculations indicate the monodentate coordination of Gluc^–. By the potentiometric data, the acidity of the water molecules is higher in the MgGluc⁺ and MgGlucOH⁰ species than in the Mg(H₂O)₆²⁺ aqua ion. On the basis of DFT calculations, this ligand-promoted hydrolysis is caused by strong hydrogen bonds forming between Gluc^– and Mg(H₂O)₆²⁺. Conversely, metal-ion-induced ligand deprotonation takes place in the case of calcium(II) complexes, giving rise to salient variations on the NMR spectra in a strongly alkaline medium.

Short abstract

Combining potentiometric, NMR spectroscopic, and density functional theory quantum-chemical methods, we gained a detailed understanding about the complexation equilibria between magnesium(II) and d-gluconate ions. The thermodynamic aspect of the results is that, under the conditions of radioactive waste disposals, MgCl₂ may lower the solubility of thorium(IV). Regarding the structural implications, we found that deprotonation of the magnesium(II) gluconate complexes takes place on the metal-bound water molecule(s) and is promoted by the formation of strong hydrogen bonds.

Introduction

The chemical behavior of actinides in aqueous solutions is of general importance for the disposal of nuclear waste in underground salt mines. The solubility of actinide hydroxides in the so-called pore water is determined by various factors, such as the pH, ionic strength, presence of complexing agents, etc. Portland cement, used for the formulation of cementitious materials,¹ has a large impact on the solution pH. The pH of the pore water is known to increase from neutral to ca. 12.5 because of the dissolution of Ca(OH)₂(s).² In underground salt mines, concentrated MgCl₂- or NaCl-containing salt brines are supposed to form as a result of the incidental intrusion of water.³ Bube and co-workers reported that, for brines containing ≈3.8 M MgCl₂, the pH increases to ≈12, while most of the Mg²⁺ ions are replaced by Ca²⁺ ions.³ In leachant solutions containing ≈5.4 M NaCl, the pH becomes as high as 13.

In principle, a highly caustic medium leads to the precipitation of radionuclides, thereby lowers their mobility as well as their release to the geosphere. The presence of various organic molecules, however, may result in an increase of the solubility through the formation of stable metal complexes. d-Gluconate (Gluc^–; Scheme 1), being used as an additive in cement,⁴ is likely to be present in underground repositories; thus, it is regarded as a general model compound for organic contaminants. Gluc^– is known to chelate thorium(IV),^5,6 uranium(IV),⁷ uranium(VI),^8,9 neptunium(IV),¹⁰ plutonium(IV),^11,12 and americium(III)¹³ in an alkaline medium.

Scheme 1. Structural Formula of Gluc^–

In a caustic medium, one of the OH groups of Gluc^– undergoes deprotonation:

1

The corresponding concentration stability constant, K_a, reads as

2

where c^⌀ is the standard molar concentration, 1 mol·dm^–3. In concentrated electrolyte solutions, the pK was found to be 13.7 (I = 1 M)^14,15 and 14.1 (I = 4 M).¹⁶ Additionally, the deprotonation reaction was invoked to explain the solubility curve of UO₂(OH)₂(s)⁹ as well as Th(OH)₄(s)^5,17 in the presence of Gluc^–. The pK of the ThGluc(OH)₄^– aqueous species was calculated to be 9.2 (at infinite dilution).¹⁷ In conclusion, deprotonation of Gluc^– occurs more readily in its metal-bound form compared to the free ligand.

The solubility of actinides can be affected by CaCl₂ and/or MgCl₂; both salts are expected to be present at high concentrations.³ First, stable binary complexes forming between Ca²⁺ or Mg²⁺ and Gluc^– ions may suppress the formation of actinide gluconate species, resulting in a decrease of the solubility. For calcium(II), the formation of CaGlucOH⁰ was detected above pH ≈ 11, while the multinuclear Ca₂Gluc(OH)₃⁰ and Ca₃Gluc₂(OH)₄⁰ complexes are the predominant ones at higher CaCl₂ and ligand concentrations.¹⁵

Second, the formation of ternary species consisting of calcium(II), actinide(IV), and gluconate ions increases the solubility. For thorium(IV), the CaThGluc₂(OH)₄⁰ complex was proposed to elucidate the sorption properties of thorium(IV) onto calcite at pH = 13.3.¹³ The formation of this ternary species can be promoted via the mononuclear CaGlucOH⁰:

3

Ternary complexes with similar stoichiometry and stability might be formed with Mg²⁺ ions as well. Contrary to Ca²⁺/Gluc^– complexes, the literature concerning Mg²⁺/Gluc^– interactions is sporadic. In an early paper, the MgGluc⁺ species was reported to form at neutral pH.¹⁸ Using IR and ¹H NMR spectroscopic means at 25 °C, it was found that the interaction with Mg²⁺ mainly localizes to the carboxylate group of Gluc^–.¹⁹ Above ≈35 °C, ¹³C NMR relaxation studies indicated the additional participation of the terminal hydroxymethyl group (C6-OH; Scheme 1).²⁰ Alteration of the coordination mode was interpreted in terms of conformational changes: at T < 30 °C, Gluc^– exists in solution as a mixture of the planar (zigzag) and bent-chain forms. With increasing temperature, however, the bent-chain conformer becomes predominant,²⁰⁻²³ rendering the simultaneous coordination of COO^– and C6-OH possible.

In contrast to Ca²⁺, the complexation equilibria between Mg²⁺ and Gluc^– ions in the alkaline pH regime were not studied. The formation of such coordination compounds may have a marked influence on the solubility of actinides in the presence of Gluc^–. Thus, for modeling the solubility and aqueous speciation of these metal ions in MgCl₂-containing solutions, a quantitative description of the Mg²⁺/Gluc^–/OH^– system is indispensable. Furthermore, to reveal the binding sites of the ligand and to make reliable comparisons with the calcium(II) complexes, structural analysis of the magnesium(II) species is necessary.

In this Article, we report on the solution equilibria of magnesium(II) gluconate complexes forming in a neutral-to-alkaline medium. The complexation reactions were studied by potentiometry, IR as well as ¹H and ¹³C NMR spectroscopies. Additionally, the experiments were augmented with quantum-chemical computations. The results are discussed with respect to (1) the effect of MgCl₂ on the solubility of thorium(IV) and (2) the possible structures of the magnesium(II) gluconate complexes in comparison with the calcium(II) ones.

Experimental Section

Reagents and Solutions

NaGluc (≥98%, Acros Organics), MgCl₂·6H₂O (ACS grade, VWR Chemicals), CaCl₂·2H₂O (ACS grade, VWR Chemicals), and NaCl (analytical reagent grade, VWR Chemicals) were used without further purification. Stock solutions of NaGluc, MgCl₂, and CaCl₂ were prepared by dissolving the salts in Milli-Q Millipore water. The exact concentration of the Mg²⁺ or Ca²⁺ ions was determined by ethylenediaminetetraacetic acid titration.

A 1 M stock solution of NaOH was prepared by diluting a carbonate-free 50% (w/w) NaOH prepared by the procedure reported in ref (24). The NaOH solution was then standardized against HCl. The 1 M stock solution of HCl was made by volumetric dilution of ≈37% (w/w) HCl (analytical reagent grade, VWR Chemicals), and its concentration was determined via titration of a KHCO₃ solution.

Potentiometric Titrations

The potentiometric titrations were carried out using a Metrohm Titrando 888 titration instrument in a double-jacketed glass cell. Each solution was stirred continuously, while the temperature was kept at 25.0 ± 0.1 °C by a Julabo F12-MB thermostat. The equilibrium cell potentials were measured by a Jenway 3540 Bench pH and conductivity meter using a SenTiX-62 combined glass electrode (from WTW). The ionic strength was adjusted to 4 M with NaCl.

During the course of electrode calibration, a weak acid (0.200 M malonic acid) and, subsequently, a strong acid (0.196 M HCl) were titrated with ≈1 M NaOH. These titration curves were evaluated with the pHCali(25) software. The program applies a nonlinear-fitting procedure, allowing for calculation of the electrode slope and intercept, the pK_w, the first and second protonation constants of the malonate ion, the exact concentration of the titrant, and the carbonate content. For log K_w, a value of –14.26 was used (determined previously by applying a platinized platinum electrode),¹⁶ while the two protonation constants of CO₃^2– were taken from the literature.²⁶

As a result, the electrode response was found to be linear in the range of 1.8 < pH_c < 12.2, where pH_c is defined as −log([H⁺]/c^ø). The linear relationship is demonstrated in Figures S1 and S2. Furthermore, the ratio of CO₃^2– relative to NaOH was found to be <0.5 mol %, while the slope and intercept (±3SE) were calculated to be 58.1 ± 0.2 and 456.3 ± 1.1 mV, respectively. On the basis of the latter parameter, the error in pH_c is ±0.02, which we consider to be the minimum error of the equilibrium constants determined.

To investigate the protonation of Gluc^–, two series were studied: 70 mL solutions containing [Gluc^–]_T = 0.100 and 0.200 M were titrated with 0.246 and 0.496 M HCl solutions, respectively. For component X, hereafter [X]_T,0 or [X]_T represents its initial total (at V = 0 for titrations) or simply its total concentration (for NMR and IR measurements), while [X] is referred to as the equilibrium concentration.

To study the complex formation between Mg²⁺ and Gluc^– ions, two titration series were undertaken. First, 70 mL solutions with [Gluc^–]_T,0 = 0.100–0.200 M, [Mg²⁺]_T,0 = 0.051–0.203 M, and [HCl]_T,0 = 0.005 M were titrated with 0.050 M NaOH. Second, 70 mL samples containing [Gluc^–]_T,0 = 0.100–0.200 M and [OH^–]_T,0 = 0.005–0.100 M or [HCl]_T,0 = 0.096 M were titrated with 1.017 M MgCl₂.

NMR Spectroscopic Measurements

¹H and ¹³C NMR spectra were recorded with a Bruker Ascend 500 MHz NMR spectrometer equipped with a 5 mm inverse broad-band probe head furnished with z-oriented magnetic-field-gradient capability. The magnetic field was stabilized by locking it to the ²D signal of the solvent prior to spectral acquisition. The sample temperature was set to 25 ± 1 °C for measurements at a constant temperature and to 7–47 °C during the temperature-dependent experiments. 10% (v/v) D₂O was added to each sample, and 32 or 256 interferograms were collected to obtain the ¹H or ¹³C NMR spectra. For comparison, the spectra were baseline-corrected and normalized.

The pH values of the solutions were set using the SenTix-62 electrode, which was calibrated with buffers (obtained from WTW). Conversely, the activity coefficient of H⁺ in the buffers is considerably different from that in the samples because of the more concentrated ionic media and use of D₂O in the latter. Thus, the nominal pH adjusted in the solutions is referred to as pH* hereafter, and its deviation from the real pH can be estimated as ±0.2 units. Nevertheless, this difference is acceptable for qualitative purposes.

To study the complex formation between Mg²⁺ and Gluc^– at neutral pH, solutions with [Gluc^–]_T = 0.200 M and [Mg²⁺]_T = 0.000–0.492 M were prepared. The ionic strength was adjusted to 4 M. It has to be noted that incidental variations in the pH may affect the chemical shifts of Gluc^–. For this series, however, the pH* was found to be 6.7–6.9; thus, the formation of HGluc can be ruled out. Consequently, the observed changes in the chemical shifts were solely due to complex formation.

To study the pH dependence of the spectra, sample sets with [Gluc^–]_T = 0.2 M as well as [Gluc^–]_T = 0.2 M and [Mg²⁺]_T or [Ca²⁺]_T = 0.1 M were prepared at pH* = 6–13. The temperature dependence of a solution containing [Gluc^–]_T = 0.2 M and [Mg²⁺]_T = 0.1 M was studied in the range of 7–47 °C, and the pH* was adjusted to 10.0 at T = 22 °C. In each case, the pH* was set by HCl or NaOH solutions (right before the measurements), and the ionic strength was not adjusted.

IR Spectroscopic Measurements

The IR spectra were recorded at room temperature, using a Bio-Rad Digital Division FTS-65 A/896 Fourier transform infrared instrument with a spectral resolution of 4 cm^–1. The measurements were performed in transmittance mode in the 750–4000 cm^–1 range, and 256 scans were collected for each sample. The spectra were baseline-corrected and normalized.

To investigate the effect of Mg²⁺ ions on the IR absorption of gluconate, a series with [Gluc^–]_T = 0.2 M and [Mg²⁺]_T = 0–1.0 M was prepared by applying D₂O as the solvent. The pH* values of the solutions were checked and found to be neutral.

Computations

Data Evaluation and Speciation Calculations

The potentiometric and NMR spectroscopic data were evaluated with the aid of PSEQUAD.²⁷ The general complexation reaction and corresponding conditional stability product, β_pqr, read as

4

5

During fitting, the stability product, log β_pqr, was refined by minimizing the so-called fitting parameter, FP, which reads as

6

where Y_i,calc and Y_i,meas pertain to the calculated and measured data (pH_c or chemical shift), while n and k represent the number of the measured data and fitted parameters, respectively. The log K_w value was set to −14.26¹⁶ throughout the calculations.

For homogeneous systems, speciation calculations were carried out utilizing the MEDUSA(28) program. For heterogeneous systems, where the solubility is controlled by Th(OH)₄(s), PSEQUAD(27) was applied by setting the Th(OH)₄(aq) complex as the primary species. The stability product of Th(OH)₄(s) and those of the various hydrolysis species, Th(OH)_r^(4–r)+, were taken from the respective NEA-TDB review.²⁹ No formation constant was selected for the Th(OH)₃⁺ complex; hence, it was taken from ref (30). Concerning the gluconate complexes of thorium(IV),^5,6 the equilibrium constants were taken from ref (17). All of these values are presented in Table S1.

In order to perform speciation calculations for the Th⁴⁺/Mg²⁺/Gluc^–/OH^– system, the literature data of the thorium(IV)-containing species were converted to I = 4 M. For this purpose, the specific-ion-interaction theory (SIT)³¹⁻³⁴ was applied. The SIT introduces ion-interaction parameters (ε_ij) to describe short-range ion interactions and the ionic strength dependence of the mean activity coefficient. It is worth mentioning that, in general, the Pitzer approach³⁵ or the modified SIT³⁶ is known to be more accurate at higher ionic strength. The literature data, however, are insufficient (especially for the gluconate complexes) to perform accurate calculations with these models. Nonetheless, the SIT approach was found to be applicable at I > 4 M in numerous cases, a also for different background electrolytes,³⁷⁻³⁹ including NaCl.^40,41 Hence, we used this model following the approach of the standard NEA-TDB review.²⁹

The respective ε_ij coefficients (Table S2) were taken from refs (29) and (42). The stability constants calculated using the SIT equation are listed in Table S1. For further details, the reader is referred to the Supporting Information and to refs (29)–³⁴.

Quantum-Chemical Calculations

To model the structure of the complexes, in vacuo calculations were performed using the M11 range-separated hybrid meta-generalized gradient approximation density functional theory (DFT) functional⁴³ coupled with the cc-pVDZ basis set. The recently developed M11 functional was shown to provide excellent performance for main-group energies, proton and electron affinities, barrier heights, bond dissociation, and noncovalent interaction energies. The computations were coupled with conformational analysis by varying the freely rotating HCCH dihedral angles of Gluc^–.

Subsequent geometry optimizations of all structures were carried out utilizing the same functional and the aug-cc-pVTZ basis set. These calculations with the higher basis set were undertaken by taking solvent effects into account with the aid of the conductor-like polarizable continuum model (CPCM)⁴⁴ (where water was considered to be the solvent). All calculations were carried out using the Gaussian09(45) software package.

Results and Discussion

Complexation between Mg²⁺ and Gluc^– in a Neutral Medium

With increasing [MgCl₂]_T in solutions containing [Gluc^–]_T = 0.2 M, the H2 and H3 NMR signals of Gluc^– show a gradual downfield shift (Figure 1). Simultaneously, the position of the C1 signal shifts upfield. Such variations indicate complex formation as in the case of Ca²⁺ binding, which was confirmed by 2D ¹H–⁴³Ca NMR measurements.⁴⁶ Moreover, no additional peaks appear on the spectra, which stems from fast ligand-exchange processes between free and complexed Gluc^–.

Figure 1.

¹H and ¹³C NMR chemical shifts as a function of [Mg²⁺]_T. Experimental conditions: I = 4 M (NaCl) and T = 25 ± 1 °C; [Gluc^–]_T = 0.200 M. Symbols represent measured data, while solid lines were calculated assuming the formation of MgGluc⁺. The chemical shifts were normalized to the neat Gluc^– ion for better visualization.

The experimentally obtained chemical shifts were fitted as a function of [Mg²⁺]_T, assuming formation of the 1:1 complex.¹⁸ The relationship between the observed chemical shift (δ_obs) and the equilibrium concentrations of Gluc^– and MgGluc⁺ is as follows:

7

where δ_Gluc^– and δ_MgGluc⁺ are the limiting chemical shifts of Gluc^– and MgGluc⁺, respectively.

When solely the ¹³C chemical shifts are fitted, log β₁₁₀ was determined to be 0.25–0.33, with FP (eq 6) being 0.002–0.006 ppm. When only the ¹H chemical shifts are fitted, log β₁₁₀ ranged from 0.46 to 0.60 (FP = 0.0006–0.0012 ppm). When both the ¹H and ¹³C shifts were taken into account, log β₁₁₀ was found to be 0.25 on average (FP = 0.002 ppm). The best fitting from each set is shown in Table 1, while the calculations considering all chemical shifts are depicted in Figure 1.

Table 1. Stability Products, log β_pqr, for Equilibria Taking Place in the Mg²⁺/Gluc^–/H₃O⁺/OH^– System^a.

reaction	log βpqr ± 3SE	methodb	ref
H2O = H+ + OH–	–14.26	H2-Pt POT	(16)
HGluc = Gluc– + H+	–3.73 ± 0.05	GLE POT	p.w.
Gluc– = GlucH–12– + H+	–13.92 ± 0.06	GLE POT	p.w.
	–14.08 ± 0.03	H2-Pt POT	(16)
	–13.90 ± 0.03	13C NMR	(16)
Mg2+ + H2O = MgOH+ + H+	–12.33 ± 0.18	GLE POT	(47)
Ca2+ + H2O = CaOH+ + H+	–13.92 ± 0.36	ISE POT	(48)
Mg(OH)2(s) + 2H2O = Mg2+ + 2H+	17.64 ± 0.20c,d	SOL/ICP-OES	(49)
Ca(OH)2(s) + 2H2O = Ca2+ + 2H+	24.00 ± 0.09c	ISE POT	(48)
Mg2+ + Gluc– = MgGluc+	0.47 ± 0.05	1H NMR	p.w.
	0.25 ± 0.02	13C NMR	p.w.
	0.25 ± 0.05	1H/13C NMR	p.w.
	0.33 ± 0.04	GLE POT	p.w.
	0.4 ± 0.2e		p.w.
	0.70d	GLE POT	(18)
Ca2+ + Gluc– = CaGluc+	0.85 ± 0.15	13C NMR	(46)
	1.21d	GLE POT	(18)
Mg2+ + Gluc– + H2O = MgGlucOH0 + H+	–10.20 ± 0.01	GLE POT	p.w.
Ca2+ + Gluc– + H2O = CaGlucOH0 + H+	–11.73 ± 0.03	H2-Pt POT	(16)
Mg2+ + Gluc– + 2H2O = MgGluc(OH)2– + 2H+	–21.66 ± 0.06	GLE POT	p.w.
3Mg2+ + 2Gluc– + 4H2O = Mg3Gluc2(OH)40 + 4H+	–38.52 ± 0.10	GLE POT	p.w.
3Ca2+ + 2Gluc– + 4H2O = Ca3Gluc2(OH)40 + 4H+	–43.80 ± 0.03	H2-Pt POT	(16)

^aFor comparison, analogous constants for the Ca²⁺/Gluc^–/H₃O⁺/OH^– system are presented. The constants correspond to T = 25 °C and I = 4 M (NaCl), unless indicated differently.

^bH₂-Pt, GLE, ISE POT: potentiometry applying hydrogen (platinized platinum), glass or calcium ion-selective electrode. ¹H and ¹³C NMR: nuclear magnetic resonance spectroscopy. SOL/ICP-OES: solubility determined with inductively coupled plasma optical emission spectroscopy.

^cHere the solubility product (log K_sp) is given.

^dThe experiments were performed at T = 22.5 °C in ref (49) and at I = 0.2 M (KCl) in ref (18).

^eRecommended value for log β₁₁₀ (see the text for discussion).

The difference in the formation constants obtained by ¹H and ¹³C nuclei is not unusual for weak complexes because β₁₁₀ and the actual limiting chemical shifts are highly correlated. Hence, on the basis of the NMR results, we suggest 0.4 ± 0.2 for log β₁₁₀; this value is in reasonable agreement with log β₁₁₀ = 0.70 determined potentiometrically at I = 0.2 M.¹⁸ Using log β₁₁₀ = 0.4, 50% of the ligand molecules are complexed at the highest [MgCl₂]_T (Figure S3).

Although the uncertainty of the formation constant of MgGluc⁺ is rather high, it seems to be less stable than CaGluc⁺. This difference is unambiguous in Cannan and Kibrick’s work: they determined log β₁₁₀ = 0.70 for MgGluc⁺ and 1.21 for CaGluc⁺.¹⁸ In general, the stability order of 1:1 complexes forming between alkaline-earth metal and glycolate, lactate, or glycerate ions is as follows: Mg²⁺ < Ca²⁺ > Sr²⁺ > Ba²⁺.^18,50,51 From Ca²⁺ to Ba²⁺, the decreasing order follows from the decreasing charge density of the cation.

Conversely, other thermodynamic factors may play important roles in the complex formation reactions of Mg²⁺. First, Mg²⁺ prefers 6-fold coordination, while the first coordination sphere of Ca²⁺ is rather flexible, with the hydration number being 6–8.⁵²⁻⁵⁹ As a result, binding of the COO^– group requires the loss of (at least) one solvent molecule for Mg²⁺, while Ca²⁺ can accommodate it without dehydration, yielding more stable calcium(II) complexes. Moreover, if dehydration occurs in both cases, it is again more favorable for Ca²⁺: the enthalpy of dehydration was found to be 16.8–17.7 kJ·mol^–1 for Ca(H₂O)₇²⁺, while 23.4–24.2 kJ·mol^–1 was determined for Mg(H₂O)₆²⁺.⁶⁰

It is important to note that the release of water molecules would result in higher disorder, thereby favoring the formation of MgGluc⁺. The higher stability constant of CaGluc⁺, however, indicates that enthalpy effects dominate the formation of 1:1 complexes.

Coordination Mode of Gluc^– in the MgGluc⁺ Complex

The variations of the NMR chemical shifts do not allow one to decide whether Gluc^– is bound in a mono- or a bidentate manner to the metal ion. To unravel the coordination mode in the 1:1 complex, a solution series of [Gluc^–]_T = 0.2 M and [Mg²⁺]_T = 0–1 M was studied via IR spectrosopy, applying D₂O as the solvent.

Upon the addition of Mg²⁺ ions, the region of O–H stretching vibrations (3000–3700 cm^–1) does not exhibit any significant changes upon metal-ion coordination. In conclusion, the metal–ligand interactions are localized to the region of carboxylate stretching vibrations, in agreement with a previous IR study.¹⁹ Therefore, only this region is presented (Figure 2) and discussed.

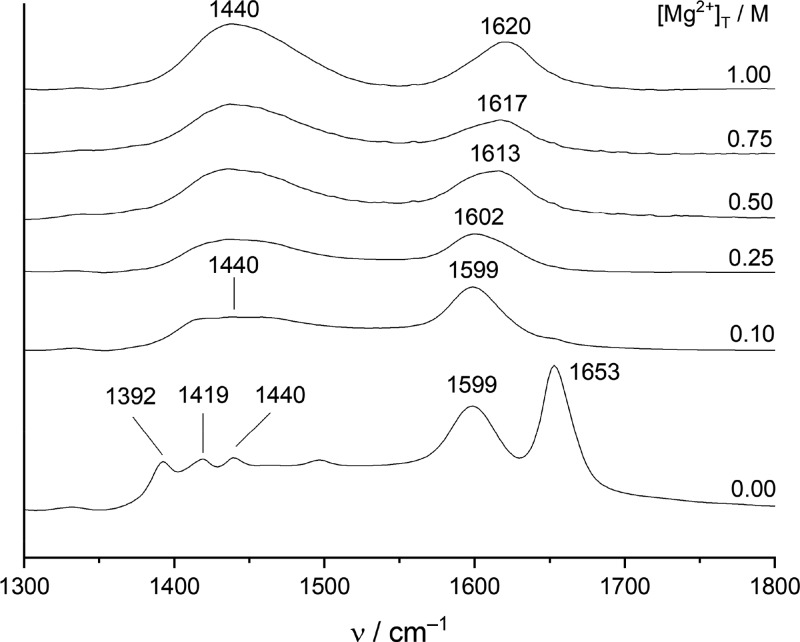
Figure 2.

Traces of IR spectra of a solution series of [NaGluc]_T = 0.2 M and [MgCl₂]_T = 0–1 M at room temperature.

Assignment of the symmetric and asymmetric stretching vibrations of Gluc^– is rather difficult. The asymmetric vibration mode is obviously split into two components (1599 and 1653 cm^–1), which was also previously observed on the spectrum of the solid NaGluc salt.¹⁶ Such a splitting is an indicative of two different coordination modes between the metal ion and ligand, as was proposed for the cobalt(II) acetate dihydrate and calcium succinate trihydrate salts.^61,62 Conversely, given that Na⁺ is a weekly binding cation, the degree of association between Na⁺ and Gluc^– is probably low; therefore, it cannot completely account for the observed splitting. An analogous interpretation can be the dynamic equilibrium between the planar and bent-chain conformations of the free ligand;²⁰⁻²³ however, none of these two scenarios can be unambiguously confirmed or ruled out. Nevertheless, the symmetric vibration mode must be split as well, giving rise to the appearance of two peaks in the region of 1350–1450 cm^–1. Furthermore, this region coincides with the C–O–H bending modes,^19,63 which explains the presence of a third peak in this frequency range.

Upon the addition of Mg²⁺ ions, the spectra simplify to two broad peaks, known as the symmetric and asymmetric COO^– regions.⁶³⁻⁶⁵ Two important conclusions can be drawn from the observed variations. First, the disappearance of the splitting seen for Gluc^– implies one coordination mode. Second, the distance between the peak maxima of the symmetric and asymmetric modes increases with increasing [Mg²⁺]_T, as a token of complex formation. At [MgCl₂]_T = 1 M, ca. 70% of the ligand is bound in the 1:1 complex, where the distance is 180 cm^–1. On the basis of IR analysis of numerous solid complexes,^64,65 such a difference refers to the so-called pseudobridged monodentate coordination, where one oxygen atom of the COO^– group is bound to the metal ion, while the other establishes hydrogen bonding of a neighboring OH group.

Solely on the basis of the IR spectra, participation of the OH groups in ligand coordination is still uncertain. To address this problem, quantum-chemical computations were undertaken. The following scenarios were taken into consideration: (1) monodentate binding, (2) bidentate coordination of COO^–, and (3) monodentate binding of COO^– and the adjacent OH group. During calculations, octahedral geometry around Mg²⁺ was assumed.

For bidentate coordination modes, the binding of both oxygen atoms of the COO^– group (Figure S4) yields a less stable complex than monodentate coordination of both the COO^– and OH groups (Figure S5). The difference in energy is 13.5 kJ·mol^–1, significantly higher than the energy of thermal motion (≈2.5 kJ·mol^–1 at 25 °C). Thus, bidentate coordination of COO^– can be excluded, in agreement with the outcome of the IR experiments.

To compare the stabilities of the chelate (Figure S5) and monodentate species, the number of water molecules must match. Hence, a water molecule was added to the chelate complex, and its position was varied around the metal ion and along the gluconate backbone. The most stable structure is depicted in Figure S6. Alternatively, this complex represents the product of the reaction

8

Its energy, however, is higher by 6.2 kJ·mol^–1 than that of Mg(H₂O)₅Gluc⁺ (Figure S7). In conclusion, the bidentate coordination of Gluc^– is not favored because of the strong hydration of Mg²⁺. Additionally, one oxygen atom of COO^– establishes strong hydrogen bonding with an axial metal-bound water molecule (dashed line in Figure S7), resulting in pseudobridged monodentate coordination.^64,65 The discussion of the role of hydrogen bonding is deferred to the Role of Hydrogen Bonds in the MgGluc⁺ and MgGlucOH⁰ Complexes section.

In summary, both IR measurements and structure computations suggest that Gluc^– acts as a monodentate ligand in the MgGluc⁺ complex. Conversely, chelate formation is preferred for CaGluc⁺.⁴⁶

Effect of the pH on the Complexation between Mg²⁺ and Gluc^– Ions

In order to examine the complex formation between Mg²⁺ and Gluc^– as well as protonation of the ligand, a series of potentiometric titrations were performed in the pH_c range of 1.9–12.1. To demonstrate the pH changes caused by complex formation, several comparative titration curves are shown in Figure 3.

Figure 3.

Equilibrium pH_c values as a function of the added titrant volume. Experimental conditions: T = 25 ± 1 °C, I = 4 M (NaCl), and V₀ = 70 mL; [HCl]_T,0 = 0.005 M, while [Gluc^–]_T and [Mg²⁺]_T are listed in the legend. The titrant was 0.050 M NaOH in each case. Hollow circles indicate the range of precipitation of Mg(OH)₂(s). Inset: Zoomed region of the acidic and alkaline pH regimes.

The red curve depicts the pH_c values of a slightly acidic solution of 0.2 M NaGluc titrated with NaOH. Upon the addition of MgCl₂ (0–0.2 M), the shapes of the curves resemble that of 0.2 M NaGluc. The pH_c, however, is much lower after the equivalence point, indicating complex formation.

Furthermore, the titration curves of solutions with [Gluc^–]_T,0 = 0.1 M and [Mg²⁺]_T,0 = 0.1 M (orange curve) and [Gluc^–]_T,0 = 0.2 M and [Mg²⁺]_T,0 = 0.05 M (blue curve) are essentially the same in the alkaline region. According to the Guldberg–Waage mass action law, the equilibrium concentration of the complex(es) formation must be proportional to that of [Mg²⁺]^α·[Gluc^–]^β and, hence, to that of [Mg²⁺]_T^α·[Gluc^–]_T^β. Because in both cases [Mg²⁺]_T·[Gluc^–]_T ≈ 0.01, the similar values of pH_c imply that α = β = 1, i.e., the formation of 1:1 species. It is also worth mentioning that, with increasing [Mg²⁺]_T,0, a small but significant decrease in pH_c is discernible in the acidic region, which follows from the reaction

9

When the titration curve of the solution containing only 0.1 M MgCl₂ (black curve) is compared to those containing Gluc^–, it is seen that the increase of pH_c is less steep for the latter, indicating a stronger buffering capacity and, thus, complexation between the Mg²⁺ and Gluc^– ions in the alkaline regime. This is strongly supported by the fact that, in contrast to the solution with 0.1 M MgCl₂, precipitation of Mg(OH)₂(s) cannot be observed in the presence of Gluc^–.

Expectedly, titrations performed with 1 M MgCl₂ as the titrant (Figure S8) exhibit a remarkable pH_c decrease (ΔpH_c = 2) upon the addition of 5 mL of titrant. Starting with the titrations from the acidic region ([HCl]_T,0 = 0.1 M), a lower but still pronounced pH_c decrease (ΔpH_c ≈ 0.3) is seen as a token of the formation of MgGluc⁺ (eq 9).

During data evaluation, the pH- and MgCl₂-dependent titrations as well as the protonation measurements of Gluc^– were fitted simultaneously. Assuming the formation of HGluc, GlucH_–1^2–, MgGluc⁺, and its two deprotonated forms, MgGluc(OH)⁰ and MgGluc(OH)^2–, the FP was found to be 0.024 (in pH_c units).

Further improvement of the FP (0.017) could be achieved by taking the formation of Mg₃Gluc₂(OH)₄⁰ into consideration. Expectedly, the two curves, starting from the alkaline region and with MgCl₂ as the titrant, are the most affected ones. That is, the individual FP decreased from 0.034 to 0.021 (Figure S8, red curve) as well as from 0.040 to 0.015 (Figure S8, blue curve). Given that the calcium(II) analogues were detected in the presence of Gluc^–,^15,16 the presence of such a trinuclear magnesium(II) complex seems to be realistic.

In conclusion, the proposed chemical model for the Mg²⁺/Gluc^–/OH^–/H⁺ system consists of HGluc, GlucH_–1^2–, MgGluc⁺, MgGlucOH⁰, MgGluc(OH)₂^–, and Mg₃Gluc₂(OH)₄⁰. The calculated potentials are depicted in Figures S8–S10, while the respective stability products are listed in Table 1. To the best of our knowledge, the deprotonation constant of HGluc (at I = 4 M NaCl) is the only one to date. Regarding GlucH_–1^2–, the reliability of its stability constant (−13.92) is justified by the excellent agreement with that (−13.90) determined previously via ¹³C NMR at the same ionic strength.¹⁶ As for MgGluc⁺, log β₁₁₀ = 0.33 agrees well with that proposed from the NMR results (0.4 ± 0.2).

Comparing the stability products of the calcium(II) and magnesium(II) analogues (i.e., the 1:1:1 and 3:2:4 species), it is evident that more stable complexes are formed with Mg²⁺. This striking difference can be explained by the fact that Mg²⁺ ions undergo hydrolysis more readily. In fact, the stability of MgOH⁺ is higher by roughly 1.5 orders of magnitude than that of CaOH⁺.^47,48 Similarly, the solubility product of Mg(OH)₂(s) is smaller by more than 6 orders of magnitude than that of Ca(OH)₂(s).^48,49

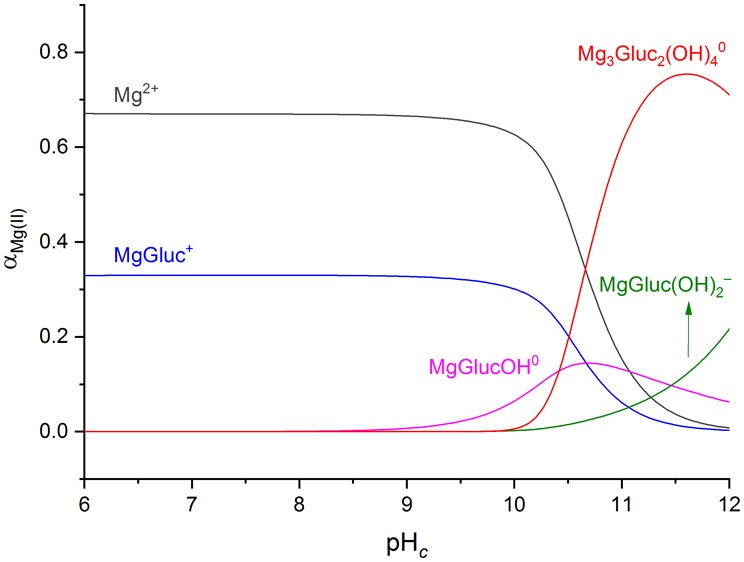
Figure 4 shows the concentration distribution diagram of magnesium(II) for the most concentrated solution used in our studies ([Gluc^–]_T = 0.2 M and [Mg²⁺]_T = 0.1 M). It is seen that the Mg₃Gluc₂(OH)₄⁰ species is the predominant one in the pH_c range of 10.5–12.0. As for the stoichiometry of Mg₃Gluc₂(OH)₄⁰, it shows a pronounced similarity with both the Mg₃(OH)₄²⁺ and Mg₄(OH)₄⁴⁺ polynuclear species that were invoked in previous studies.^47,66,67 These complexes, however, were not accepted in a later critical review⁶⁸ because their formation coincides with the onset of the precipitation of Mg(OH)₂(s). Nevertheless, the formation of Mg₃Gluc₂(OH)₄⁰ can be indirect evidence of the existence of these hydroxido complexes because they might be stabilized by Gluc^– through the following reactions:

Figure 4.

Speciation diagram with respect to magnesium(II) as a function of pH_c. The calculations were based on equilibrium constants corresponding to T = 25 °C and I = 4 M (NaCl). Total concentrations: [Mg²⁺]_T = 0.100 M and [Gluc^–]_T = 0.200 M.

10

11

Effect of MgCl₂ on the Solubility of Thorium(IV)

The impact of MgCl₂ on the solubility of Th(OH)₄(s) in the presence of Gluc^– was assessed via calculation of the solubility curve of thorium(IV) using the solubility and stability products listed in Tables 1 and S1. The pH_c ranged from 7 to 10, [Gluc^–]_T was set to 10^–5 to 10^–2 M, and [Mg²⁺]_T was adjusted to 0, 0.1, 0.2, 0.3, 0.5, and 1 M. It has to be mentioned that the last two concentrations are too high compared to that of the background electrolyte; therefore, the ionic interaction coefficients (Table S2) are only approximate. Thus, these calculations are considered to be semiquantitative.

It is known that thorim(IV) has a high affinity to form multinuclear hydroxido complexes. For the formation of these species, however, reasonably high concentrations of thorium(IV) (>10^–6 M) and acidic solutions (pH < 5) are prerequisites.^29,30,68 Given the pH range of the present simulations, these complexes were neglected. Furthermore, because of the presence of MgCl₂, precipitation of Mg(OH)₂(s) is expected to occur. The only literature data with respect to 4 M NaCl was obtained by the solubility method at 22.5 °C.⁴⁹ Although it was later not accepted in Ekberg and Brown’s critical review, it was used here to estimate the onset of precipitation.

Figure 5 shows the solubility curve of thorium(IV) in the absence and presence of 10^–5 M NaGluc and the increasing amount of MgCl₂. At [MgCl₂]_T = 0 M and pH_c < 9, log([Th^IV]_T/c^ø) increases by 0.1–0.2 units because of the ThGluc(OH)₄^– complex.^5,6,17 The increase is significantly higher at pH_c = 10, where the ThGluc(OH)₅^2– (or the ThGlucH_–1(OH)₄^2–) complex^5,17 is formed to a significant extent.

Figure 5.

Solubility of thorium(IV) hydroxide as a function of pH_c. The calculations were based on equilibrium constants corresponding to T = 25 °C and I = 4 M (NaCl). Total concentrations: [Gluc^–]_T = 0 M (black line) and 0.00001 M (colored lines). [Mg²⁺]_T: listed in the legend. In the pH ranges depicted with dashed lines, Mg(OH)₂(s) is expected to precipitate.

Increasing [MgCl₂]_T lowers the solubility of thorium(IV) dramatically because of the formation of magnesium(II) gluconate complexes proposed in this work (Table 1). That is, at high concentrations of MgCl₂, their formation partially suppresses that of the thorium(IV) gluconate species. The direction of this variation would be the opposite if a ternary complex such as CaThGluc₂(OH)₄⁰ was also formed with Mg²⁺. This kind of species, however, was not reported so far.

At higher concentrations of gluconate (Figures 6 and S11 and S12), however, the decrease of the solubility becomes less pronounced, which stems from the extremely high stability of both the ThGluc(OH)₄^– and ThGluc(OH)₅^2– species. For instance, at pH_c = 7, log([Th^IV]_T/c^ø) is −8.3 at [Gluc^–]_T = 0 M, while it increases to −6.3 at [Gluc^–]_T = 0.01 M (Figure 6). Upon the addition of 1 M MgCl₂, this value decreases only to −6.8. In conclusion, the formation of thorium(IV) gluconate complexes cannot be completely suppressed even at high [Mg²⁺]_T/[Gluc^–]_T ratios. On the other hand, the effect of the Mg²⁺ ions might be expected to be more significant under the conditions of radioactive waste disposals, with [MgCl₂]_T being as high as 4 M.³

Figure 6.

Solubility of thorium(IV) hydroxide as a function of pH_c. The calculations were based on equilibrium constants corresponding to T = 25 °C and I = 4 M (NaCl). Total concentrations: [Gluc^–]_T = 0 M (black line) and 0.01 M (colored lines). [Mg²⁺]_T: listed in the legend. In the pH ranges depicted with dashed lines, Mg(OH)₂(s) is expected to precipitate.

As any speciation model, this one should also be justified experimentally via solubility measurements, albeit carrying out such experiments in the alkaline pH range is a difficult endeavor even for the experts of this field. First, solubility equilibria of actinide hydroxides are usually established very slowly (if at all) because of the formation of more soluble amorphous precipitates or amorphous layers on the surface of the thermodynamically stable, crystalline phases.³⁰ Namely, the transformation of such metastable phases to crystalline phases is kinetically hindered. Second, because the concentrations to be detected are extremely low (<10^–8–10^–7 M), the scattering range of the data is often 1 order of magnitude or higher, even upon application of state-of-the art instrumentation. The predicted effects of MgCl₂ are within this uncertainty and, hence, difficult to detect experimentally. Thus, we believe that our calculations serve as a good first estimation for modeling the solubility of thorium(IV) in the presence of NaGluc and MgCl₂.

Effect of the pH and Temperature on the NMR Spectra of Gluc^– in the Presence of MgCl₂

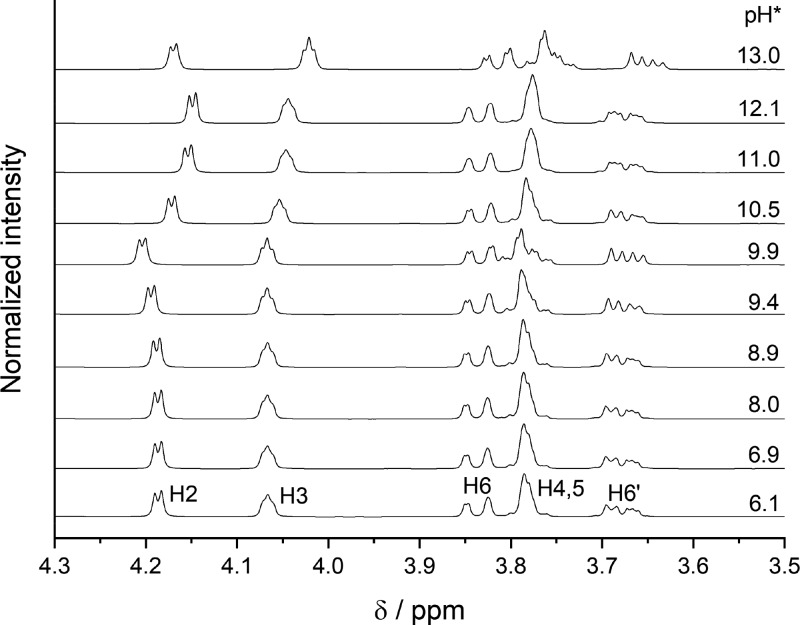
To gain further insights concerning the structures of the complexes formed, a series of NMR spectra were recorded. Figure 7 shows the pH dependence of the ¹H spectra of Gluc^– in solutions containing [Gluc^–]_T = 0.2 M and [Mg²⁺]_T = 0.1 M. At pH* = 6, ca. 14% of [Gluc^–]_T is bound in the MgGluc⁺ complex. [It has to be noted that only a semiquantitative comparison is possible because the formation constants of the present samples are somewhat different (I < 1 M) from those used for the speciation calculations (I = 4 M).]

Figure 7.

¹H NMR spectra of solutions containing [Gluc^–]_T = 0.200 M and [Mg²⁺]_T = 0.100 M as a function of the nominal pH* at T = 25 ± 1 °C.

At pH* = 6–9, the spectra remain unchanged, while at pH* = 9.5–10, the H2 peak is shifted slightly downfield; furthermore, the H4–H5 signals become more resolved. These minor variations probably result from the formation of MgGlucOH⁰, which is supported by the speciation diagram (Figure 8): the formation of this species starts at pH_c = 9. Interestingly, the shape of the spectra above pH* = 10 returns to those observed at pH* < 9. This is a hint that another complex is formed that suppresses the formation of MgGlucOH⁰. Indeed, these reverse spectral changes coincide well with the Mg₃Gluc₂(OH)₄⁰ species, which appears at pH_c = 10 and becomes the dominant one up to pH_c = 12 (Figure 8). In parallel, the amount of free ligand drops to approximately 60%, yet the spectra resemble those of the free ligand (at pH* = 6). This similarity implies that the interactions between Mg²⁺ and Gluc^– are weaker in the trinuclear complex than in MgGlucOH⁰; hence, Mg₃Gluc₂(OH)₄⁰ might be the ligand-stabilized form of the Mg₃(OH)₄²⁺ or Mg₄(OH)₄²⁺ unit.^47,66,67

Figure 8.

Speciation diagram with respect to gluconate as a function of pH_c. The calculations were based on equilibrium constants corresponding to T = 25 °C and I = 4 M (NaCl). Total concentrations: [Mg²⁺]_T = 0.100 M and [Gluc^–]_T = 0.200 M.

Above pH* ≈ 13, the H3–H6′ peaks are slightly shifted upfield because of the formation of GlucH_–1^2–. Conversely, the same downfield shift is seen on the H2 signal, indicating that the structures of the MgGlucOH⁰ and the newly-formed MgGluc(OH)₂^– species are similar. This conclusion is corroborated by the ¹³C NMR spectra as well (Figure S13), on which the same trend is seen. Additionally, the C1 signal (Figure S14) exhibits the highest variation: its chemical shift increases by 0.8 ppm at pH* = 10, while it merges to the baseline at pH* = 13. Hence, the COO^– group is likely to be bound to Mg²⁺ in these complexes, similarly to MgGluc⁺.

On the other hand, it is not obvious where the deprotonation takes place: on an alcoholic OH group of the ligand or on a coordinated water molecule. Although potentiometry is in general not suitable to distinguish between these processes, comparing pK values of the ligand and aqua complexes of a given metal ion might help. In this respect, Van Duin and co-workers proposed a general ionization scheme for the complexation reactions occurring between metal ions and poly(hydroxycarboxylates).⁶⁹ Accordingly, deprotonation of MGluc⁺ can be attributed to ionization of the α-hydroxy (C2–OH) group because the respective pK is lower by ≈2 units than that of the first hydrolytic step of the aqua complex (pK_h). The same conclusion was drawn by analyzing the formation constants of the gluconate complexes of aluminum(III)^70,71 and praseodymium(III),⁷² respectively. This so-called metal-ion-induced ligand deprotonation is driven by the formation of very stable, five-membered chelate complexes.

The pK_h of the Mg²⁺ aqua ion (i.e., −log β₁₀₁) was reported to be 12.33.⁴⁷ For MgGluc⁺, using log β₁₁₀ = 0.33, pK₁ is 10.53 (i.e., log β₁₁₀ – log β₁₁₁), while pK₂ is 11.46 (i.e., log β₁₁₁ – log β₁₁₂). Given that pK₁ < pK₂ < pK_h, even the second deprotonation of the 1:1 complex can occur on the alcoholic OH groups of Gluc^–. Because displacement of an alcoholic proton has already been established for the calcium(II) gluconate complexes,¹⁵ comparative NMR measurements were undertaken for the Gluc^–, Mg²⁺/Gluc^–, and Ca²⁺/Gluc^– systems. The ¹H NMR spectra are displayed in Figure 9, while the ¹³C NMR spectra are depicted in Figures S15 and S16.

Figure 9.

¹H NMR spectra of solutions containing (a) [Gluc^–]_T = 0.200 M, (b) [Gluc^–]_T = 0.200 M and [Mg²⁺]_T = 0.100 M, and (c) [Gluc^–]_T = 0.200 M and [Ca²⁺]_T = 0.100 M as function of the nominal pH* at T = 25 ± 1 °C.

From pH* = 6 to 10, only small spectral variations are discernible for both metal-ion-containing solutions compared to the spectra of free Gluc^–. These changes are caused by formation of the mononuclear species, discussed in detail in the previous sections as well as in ref (46). Conversely, the spectrum of the Ca²⁺/Gluc^– system exhibits salient changes at pH* = 12. That is, the ¹H peaks are broadened, especially the H2 and H3 ones, indicating their substantial role in the formation of two deprotonated complexes, CaGlucOH⁰ and Ca₃Gluc₂(OH)₄⁰, which is visualized on the distribution diagram of this system (Figure S17). (To calculate the species distribution, formation constants were obtained from refs (16), (46), and (48).) The dramatic changes seen on the ¹H NMR spectra appear on the ¹³C NMR spectra as well: the peaks of C1–C4 are merged to the baseline, while those of C5 and C6 are widened (Figures S15 and S16).

Such marked changes can be interpreted in terms of metal-ion-induced ligand deprotonation. Namely, the simultaneous coordination of Ca²⁺ and deprotonation of the OH group(s) lead to the formation of alcoholate binding site(s) and therefore much stronger coordinative bonds than those present in the CaGluc⁺ species. As a result, the rate of ligand exchange between bound and free Gluc^– slows down, becoming commensurate to the NMR relaxation rates. This, in turn, results in an increase of the signal half-widths, especially of those belonging to the coordination sites. Such a spectral feature was detected for the Ca²⁺/Gluc^– system, and the shift from slow to fast complexation dynamics was attested by temperature-dependent measurements.¹⁵

Conversely, only marginal changes can be observed for Mg²⁺ at the same pH*. Given that the concentrations of the magnesium(II) gluconate complexes are higher than those of the calcium(II) complexes (Figure 8 vs Figure S17), this difference is striking. Obviously, there is no sign of metal-ion-promoted deprotonation of Gluc^–, indicating that, similarly to MgGluc⁺, the alcoholic OH groups are not directly bound to the metal ion. The lack of ligand deprotonation is also supported by the temperature-dependent ¹H and ¹³C NMR experiments (Figures S18–S20). At pH* = 10 (at T = 22 °C), where the concentration of MgGlucOH⁰ is the highest, the characteristic transition between the slow and fast exchange rates is absent. Furthermore, the monotonous shift of the C6 peak position provides no sound evidence of coordination of the C6–OH group, which was proposed in a previous ¹³C NMR relaxation study.²⁰ A possible reason is that the chemical shift is a less sensitive quantity compared to the relaxation time.

In conclusion, deprotonation in the magnesium(II) gluconate species takes place not on the ligand side but on one of the coordinated water molecules. Still, proton displacement occurs more readily in the MgGluc⁺ complex (pK₁ ≈ 10.5) than in the Mg(H₂O)₆²⁺ aqua ion (pK_h ≈ 12.3).⁴⁷ Hence, this apparent ligand-promoted hydrolysis of Mg²⁺ in the 1:1 species probably arises from other structural features that are invisible for NMR spectroscopy.

Role of Hydrogen Bonds in the MgGluc⁺ and MgGlucOH⁰ Complexes

The structure of MgGluc⁺ was optimized by assuming octahedral coordination geometry around Mg²⁺ and monodentate binding of the COO^– group. The optimum geometry is depicted in Figure 10, while the metal–oxygen distances and hydrogen bonds are listed in Table 2.

Figure 10.

Optimized structure of the Mg(H₂O)₅Gluc⁺ complex at the M11 level, applying the aug-cc-pVTZ basis set. The solvation effects were taken into account by utilizing the CPCM. Dashed lines indicate the hydrogen-bonding system.

Table 2. Selected Bond Lengths and Hydrogen Bond Distances (in Å) in the Optimized Structures of the Mg(H₂O)₅Gluc⁺ and MgGluc(H₂O)₄(OH)⁰ Complexes^a.

		d(Mg–O)	Db	H	Ab	d(D–H)	d(H···A)
MgGluc+
Mg	O1B	2.044	O1W	H(O1W)	O1A	0.995	1.687
Mg	O1W	2.069	O3W	H(O3W)	O3	0.986	1.746
Mg	O2W	2.094	O3	H(O3)	O4	0.969	2.172
Mg	O3W	2.083	O2	H(O2)	O1A	0.974	1.951
Mg	O4W	2.071	O4	H(O4)	O2	0.972	1.920
Mg	O5W	2.093	O6	H(O6)	O4	0.968	1.961
MgGlucOH0
Mg	O1B	2.081	O1W	H(O1W)	O1A	0.994	1.694
Mg	OH	1.967	O3W	H(O3W)	O3	0.982	1.765
Mg	O1W	2.115	O3	H(O3)	O4	0.969	2.192
Mg	O2W	2.180	O2	H(O2)	O1A	0.974	1.939
Mg	O3W	2.095	O4	H(O4)	O2	0.973	1.902
Mg	O5W	2.130	O6	H(O6)	O4	0.968	1.956
			O2W	H(O2W)	O(OH)	0.991	1.758

^aThe calculations were performed at the M11/aug-cc-pVTZ level of theory, while solvation effects were considered by applying the CPCM.

^bD: donor oxygen atom. A: acceptor oxygen atom.

First, it is seen that the Mg–O1B distance (2.04 Å) is lower only by 0.03–0.05 Å than the respective Mg–O1W bond lengths, implying that the Mg²⁺–^–OOC and Mg²⁺–OH₂ interactions are of similar strengths. Second, two OH groups of Gluc^– interact with the hydrating water molecules; namely, very strong hydrogen bonds are established between O1A and O1W (1.69 Å) as well as O3 and O3W (1.75 Å). (In general, strong hydrogen bonds are considered when d < 2.5 Å.⁷³) Meanwhile, the respective O1W–H and O3W–H covalent bond lengths are more elongated (0.99–1.00 Å) than those for the other water molecules (≈0.96 Å). Interestingly, those structures that are less stable but whose differences in energy are lower than the energy of thermal motion (≈2.5 kJ·mol^–1 at 25 °C) exhibit the same coordination motif.

Structure optimization of the MgGlucOH⁰ species was based on the most stable geometry of MgGluc⁺ as the input, and the site of deprotonation was varied from O1W to O5W. The lowest-energy complex is shown in Figure 11, and the corresponding bond distances are listed in Table 2.

Figure 11.

Optimized structure of the Mg(H₂O)₄(OH)Gluc⁰ complex at the M11 level, applying the aug-cc-pVTZ basis set. The solvation effects were taken into account by utilizing the CPCM. Dashed lines indicate the hydrogen-bonding system.

Deprotonation on the equatorial 4W water molecule results in slight weakening of the Mg–O1B (2.08 Å) and of the Mg–OH₂ (2.10–2.18 Å) bonds, while the formation of a hydroxide ion establishes strong interaction with the metal ion (1.97 Å) as well as a hydrogen bond with O2W (1.76 Å). (It is worth mentioning that a complex hydrogen-bonding network is present in MgGluc⁺ and MgGlucOH⁰, respectively. Such intramolecular interactions were found in the NaGluc and CaGluc₂⁰ solid complexes as well.^74,75) More importantly, strong hydrogen bonding is seen between O1A and O1W as well as O3 and O3W, as for MgGluc⁺.

Concerning the hydrogen bonding in these species, this unique feature at the molecular level can be related to our macroscopic findings. That is, elongation of the water O–H bonds results in the increased acidity of these H₂O molecules compared to those in the Mg(H₂O)₆²⁺ ion. Hence, coordination of Gluc^– leads to the “ligand-promoted” hydrolysis of Mg²⁺, and the order of pK₁ < pK₂ < pK_h can be elucidated qualitatively. Additionally, such hydrogen bonds in metal complexes are difficult to discern by conventional NMR measurements.

Furthermore, the formation of both MgGluc(OH)⁰ and MgGluc(OH)₂^– is facilitated by these hydrogen bonds by lowering the pK value of the ligand. Consequently, Gluc^– is able to keep Mg²⁺ ions in solution without precipitation. To prove this effect, two samples were prepared with [Mg²⁺]_T = 0.08 M, [OH^–]_T = 0.006 M, and [L^–]_T = 0.17 M, where L^– is gluconate or acetate (Ac^–). For comparison, Ac^– was chosen because it has no OH groups, and the stability of MgAc^+ 18,50 is similar to that of MgGluc⁺. For Gluc^–, the formation of Mg(OH)₂(s) was not observed. Conversely, the precipitate was detected right after the addition of NaOH in the case of Ac^–. Because hydrogen bonding between COO^– and H₂O is also possible in the MgAc⁺ species, the different behavior of Gluc^– highlights the importance of ligand OH groups in the stabilization of Mg²⁺.

Conclusions

The complex formation between Mg²⁺ and Gluc^– was studied in neutral-to-alkaline aqueous solutions at 25 °C and 4 M ionic strength. The formation of the MgGluc⁺ complex was observed and quantitatively described via ¹H and ¹³C NMR spectroscopic measurements. It was proven by additional IR measurements and quantum-chemical computations that the preferred coordination mode is a pseudobridged monodentate, where one oxygen atom of COO^– is bound to the metal ion, while the other is in hydrogen-bonding interaction with an adjacent OH group.

Further potentiometric titrations revealed the formation of stable, deprotonated complexes, namely, the MgGlucOH⁰, MgGluc(OH)₂^–, and Mg₃Gluc₂(OH)₄⁰ species; the calcium(II) analogue of the latter was reported earlier. Furthermore, the presence of such a trinuclear complex may be indirect proof for the existence of multinuclear hydroxido complexes of magnesium(II) proposed in the literature.

Because concentrated MgCl₂ salt brines might contact with underground radioactive waste disposals, the effect of Mg²⁺ ions on the solubility of actinides is a key factor in the long-term stability assessment of these repositories. Using the stability products obtained in the present work, we calculated the solubility curve of thorium(IV) as a function of pH_c by varying the concentrations of Gluc^– and MgCl₂. It was found that, with an increase in the concentration of MgCl₂, the solubility of thorium(IV) decreases, which stems from binary complexes forming between the Mg²⁺ and Gluc^– ions. These processes can effectively suppress complexation between Th(OH)₄(s) and Gluc^– at low ligand concentrations.

Additional pH-dependent ¹H and ¹³C NMR experiments showed that deprotonation does not significantly affect the spectrum of Gluc^–. Comparing these spectra with those of the Ca²⁺/Gluc^– system revealed that, for the magnesium(II) complexes, deprotonation takes place on the coordinated water molecules rather than on the OH groups of the ligand. The main reason for the difference between the two metal complexes is that, in contrast to Ca²⁺, the OH groups are not directly attached to Mg²⁺.

On the basis of the titration data, hydrolysis of Mg²⁺ is facilitated by the coordination of Gluc^–; this phenomenon can be interpreted on the basis of molecular structures of the MgGluc⁺ and MgGlucOH⁰ complexes. DFT calculations showed that, in parallel to ligand binding, two strong hydrogen bonds are established between the COO^– and C3–OH groups of Gluc^– and two metal-bound water molecules, leading to increased acidity of these O–H bonds. Macroscopically, this yields lower pK values for the complexes compared to the aqua ion.

In conclusion, ligand-promoted metal-ion hydrolysis appears to be the result of strong hydrogen bonding between the ligand and hydrating water molecules, while the direct binding of ligand OH groups gives rise to metal-ion-induced ligand deprotonation.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.inorgchem.9b00289.

• Detailed description about conversion of the stability/solubility products of the Th_pGluc_q(OH)_r^{(4p–q–r)+} species applying the SIT model, tables listing the converted equilibrium constants and ion interaction parameters, graphical representation of the electrode calibration curves and fitted titration data, optimized structures for the MgGluc⁺ complex with varying coordination modes, additional speciation diagrams for the Mg²⁺/Gluc^– and Ca²⁺/Gluc^– systems, additional solubility curves of thorium(IV), pH-dependent ¹³C NMR, and temperature-dependent ¹H and ¹³C NMR spectra (PDF)

The authors declare no competing financial interest.