Abstract
We investigate system-size effects on the rotational diffusion of membrane proteins and other membrane-embedded molecules in molecular dynamics simulations. We find that the rotational diffusion coefficient slows down relative to the infinite-system value by a factor of one minus the ratio of protein and box areas. This correction factor follows from the hydrodynamics of rotational flows under periodic boundary conditions and is rationalized in terms of Taylor–Couette flow. For membrane proteins like transporters, channels, or receptors in typical simulation setups, the protein-covered area tends to be relatively large, requiring a significant finite-size correction. Molecular dynamics simulations of the protein adenine nucleotide translocase (ANT1) and of a carbon nanotube porin in lipid membranes show that the hydrodynamic finite-size correction for rotational diffusion is accurate in standard-use cases. The dependence of the rotational diffusion on box size can be used to determine the membrane viscosity.
Introduction
Diffusion in molecular dynamics (MD) simulations under periodic boundary conditions (PBC) depends on the size and shape of the simulation box due to hydrodynamic self-interactions with the periodic images.1−3 In cubic boxes of increasing size, both the translational3 and the rotational diffusion coefficients4,5 converge with increasing box volume as predicted by hydrodynamic theory. However, for asymmetrically increased box volumes, translational diffusion becomes anisotropic and either does not converge or converges to values different from the correct infinite-system limit.6−10 This problem especially affects membrane simulations for which practicable corrections have been provided.9,11,12 In contrast to translational diffusion, the finite-size behavior of rotational diffusion in the membrane has remained largely unstudied, even though corrections may be required for meaningful comparisons to experiment.13,14
Here, we investigate the influence of the simulation box width on the rotational diffusion coefficient of membrane proteins and other membrane-embedded macromolecules. In the Theory section, we present three different hydrodynamic models that give consistent expressions for the finite-size correction of the rotational diffusion coefficient. The first model extends the original derivation of Saffman and Delbrück15 to two-dimensional (2D) rotational flow under PBC. The second model considers the 2+1 dimensional hydrodynamic problem of the membrane and the water layers by constructing a periodic “rotlet” using the Oseen tensor of Camley et al.8 The third model is an approximate hydrodynamic description in terms of the Taylor–Couette flow model that rationalizes the finite-size correction. The hydrodynamic theory suggests a significant dependence of the apparent rotational diffusion coefficient on the box width and a negligible dependence on the box height. By performing MD simulations of the protein adenine nucleotide translocase (ANT1) and by reanalyzing earlier simulations of ANT112 and carbon nanotube porins,16 we show that the hydrodynamic description quantitatively captures the finite-size effects. The rotational diffusion coefficient is shown to converge to the infinite-system limit as the reciprocal 1/A of the membrane area A. This explicit functional dependence makes it possible to estimate a box size at which size effects drop below a certain threshold for molecules of a given size.
Theory
Diffusion in Membranes
The thermally induced random rotation θ(t) of an ideal cylindrical inclusion in a membrane as a function of time t is described by the rotational diffusion coefficient D around the main axis normal to the membrane. At long times t, we expect that the mean squared displacement (MSD) grows as ⟨(θ(t + t0) – θ(t0))2⟩t0 ≈ a + 2Dt for a continuous trajectory of the angle θ(t), with ⟨···⟩t0 denoting the average over all possible starting times and a as a constant offset that accounts for local molecular dynamics at short times. The expression for the MSD in rotational diffusion is thus much simpler in 2D than in 3D because a 2D rotation unfolds on a line, whereas a 3D rotation requires more involved representations, for example, in terms of quaternions.4
For membrane proteins of nearly cylindrical shape, the Saffman–Delbrück model15,17 predicts a rotational diffusion coefficient
| 1 |
where kB is the Boltzmann constant, T the absolute temperature, η the viscosity of the membrane, h its height, and RH the hydrodynamic radius of the protein. For later use, we also define the membrane surface viscosity as ηm = ηh because, here, η and h always appear as a product.
The Saffman–Delbrück law is valid for radii RH that are small compared to the Saffman–Delbrück length
| 2 |
which is usually the case for membrane proteins. ηf is the viscosity of the fluid surrounding the membrane. For larger membrane inclusions or solid domains, an extended version18 and a useful interpolation19 are available.
Periodic Saffman–Delbrück Model for Rotational Diffusion
Following Saffman and Delbrück’s original derivation,15 we first model the rotational diffusion of a membrane protein in the plane of the membrane by assuming that the friction contributions of the highly viscous membrane dominate, exceeding those of the more fluid water layers above and below. As for rotational diffusion in three dimensions (3D),5 we concentrate on the lowest-order correction and ignore protein shape effects. Under these assumptions, we can treat the problem as the rotational diffusion of a 2D periodic array of infinite cylinders in the Stokes limit of hydrodynamics, combining the linearized Navier–Stokes equation
| 3 |
with the condition of incompressibility
| 4 |
where η is the viscosity of the membrane, p(r) is the pressure as a function of position r = (x, y)T, v(r) is the periodic fluid velocity field, and ∇ = ∂/∂r. On the surface of the cylinder with radius RH, the boundary condition is a flow with a constant angular velocity Ω
| 5 |
We simplify this hydrodynamic problem by writing the 2D velocity field in the membrane in terms of the stream function ψ(x, y)20
| 6 |
which ensures that the condition of incompressibility is satisfied. Substitution of eq 6 into eq 3 and multiplication from the left with the row vector (∂/∂y, – ∂/∂x) eliminates the pressure field and reduces the hydrodynamic problem to finding a periodic solution of the biharmonic equation
| 7 |
Because lines of constant
ψ are streamlines,20 the boundary
condition on the rotating cylinder is ψ(x, y) = const for 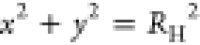 , which we combine with the condition of
periodicity of ψ in the domain outside the rotating cylinder.
, which we combine with the condition of
periodicity of ψ in the domain outside the rotating cylinder.
For cylinder radii RH ≪ L that are small compared to the (characteristic) box dimension L = A1/2 defined in terms of the 2D box area A, the hydrodynamic problem of flow in an infinite lattice of periodic rotating cylinders can be solved by mapping it onto the problem of 2D electrostatics under PBC. The Green’s function in 2D electrostatics under PBC is the periodic solution to
| 8 |
where the term −1/A is subtracted from the delta source to ensure overall charge neutrality. Without neutrality in each box, the overall potential would be infinite. As in 3D electrostatics,21 we can write the 2D Green’s function as a sum of (i) the direct Coulomb interaction in 2D, −ln r, and (ii) the potential created by the neutralizing background, πr2/2A, and an infinite sum of harmonic functions
| 9 |
where r2 = x2 + y2. Here, the origin is at the center of the simulation box, which has a 2D inversion symmetry about this point. The pk(x, y) are harmonic polynomials in x and y of order k that satisfy the 2D symmetry of the periodic simulation box and are solutions to the Laplace equation, ∇2pk(x, y) = 0. In the Supporting Information, we list the first four “square harmonic functions”, which satisfy the symmetry of the square, together with their coefficients ak, as determined by rapidly converging lattice sums22 for square-shaped boxes.
For RH ≪ L,
the 2D electrostatic Green’s function φ(x, y) defines our hydrodynamic stream function ψ(x, y) up to a constant factor. By construction,
φ(x, y) is periodic, ∇2φ = const for r > 0, and φ(x, y) ≈ const for 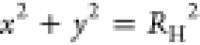 and RH ≪ L.
Therefore, ∇4φ(x, y) = 0 and deviations from the boundary condition
φ = const on the cylinder, r = RH, are of order RH4/A2 and thus negligible for RH ≪ L. We determine the constant
factor by matching the rotational velocity, vy(x = RH, y = 0) = – ∂ψ/∂x = ΩRH. In this way, we obtain
and RH ≪ L.
Therefore, ∇4φ(x, y) = 0 and deviations from the boundary condition
φ = const on the cylinder, r = RH, are of order RH4/A2 and thus negligible for RH ≪ L. We determine the constant
factor by matching the rotational velocity, vy(x = RH, y = 0) = – ∂ψ/∂x = ΩRH. In this way, we obtain
| 10 |
for r2 = x2 + y2 ≪ A. Figure 1 shows the flow field around a rotating cylinder in a square-shaped simulation box under PBC calculated according to the full 2D ψ(x, y) evaluated with rapidly converging lattice sums.22
Figure 1.
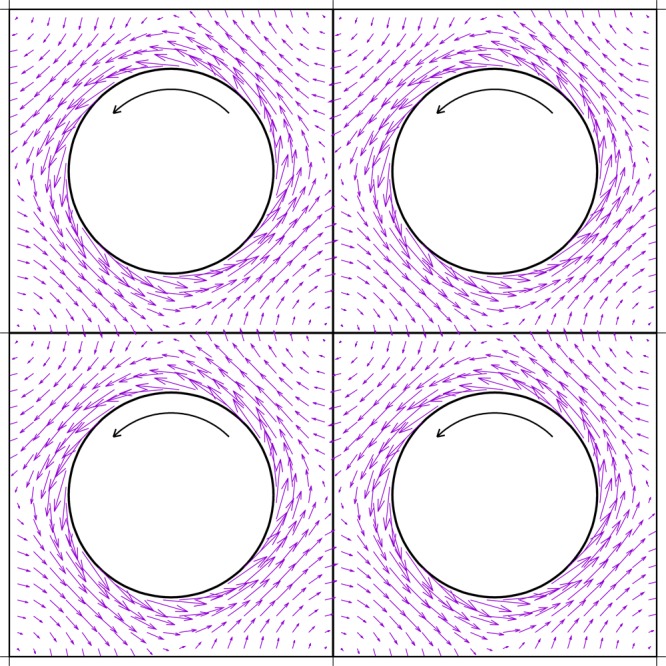
Hydrodynamic
flow around a rotating cylinder of radius 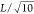 under periodic boundary conditions. The
stream function was obtained by Lekner summation.22 A top-down view on four equivalent periodic boxes is shown.
Periodicity requires the flow to stall at the points of symmetry between
two periodic images.
under periodic boundary conditions. The
stream function was obtained by Lekner summation.22 A top-down view on four equivalent periodic boxes is shown.
Periodicity requires the flow to stall at the points of symmetry between
two periodic images.
From the corresponding velocity field, we calculate the friction on the rotating cylinder by following the derivation in ref (20) (par. 18). In the limit of r2 ≪ A, we ignore deviations of the flow field from the axial symmetry and write the relevant stress tensor element in cylindrical coordinates in terms of the circumferential velocity vθ(r) ≡ v(r) as a function of the distance r from the cylinder axis
| 11 |
where
| 12 |
We obtain the torque τ required to drive the rotation of a cylinder of height h by integrating the negative stress times the axial distance over the cylinder surface. This integral corresponds to multiplying the negative stress by the circumference 2πRH, the “lever arm” RH, and the height h,
| 13 |
By the Stokes-Einstein relation, the torque and the angular velocity are related via the rotational diffusion coefficient D,
| 14 |
In this way, we arrive at an expression for the apparent rotational diffusion coefficient DPBC in a periodic simulation box
| 15 |
where A is the box area, and h is the cylinder height and thus typically the membrane thickness. D0 is the infinite-system rotational diffusion coefficient, which is given by the Saffman–Delbrück expression (eq 1), and the second term in parentheses is the lowest-order correction for periodic boundary conditions. In the limit of an infinite box, A → ∞, our hydrodynamic model therefore leads directly to the Saffman–Delbrück rotational diffusion coefficient, eq 1.
For finite simulation boxes, eq 15 predicts that the apparent rotational diffusion coefficient decreases linearly with the ratio of the areas of the molecule, πRH2, and the box, A. This lowest-order correction of the rotational diffusion coefficient is independent of the shape of the simulation box, as was found previously for 3D rotation.2 However, for odd-shaped boxes, we expect that higher-order terms gain in importance as the radius RH is increased.
Hydrodynamic Correction from the Periodic Rotlet
We now extend our hydrodynamic analysis from the quasi-2D description to the 2 + 1 dimensional system of the membrane and water layers. To construct a periodic rotational flow in a membrane under 3D PBC, we use the Oseen tensor of Camley et al.8
| 16 |
where the sum is over the nonzero vectors k of the 2D reciprocal lattice corresponding to the PBC in the membrane plane of the simulation system, and H is the height of the water layer, with 2H + h = Lz as the height of the simulation box. A rotational periodic flow is generated by adding two orthogonal “dipolar” flow fields
| 17 |
with c being a constant that will later be defined to match the boundary condition on the surface of the rotating cylindrical molecule in the membrane. This rotlet form of the hydrodynamic flow eliminates the “stresslet” associated with a single dipolar flow field. In the first step, we recognize that typical simulation boxes are much smaller than the Saffman–Delbrück length, L ≪ LSD and H ≪ LSD. We can then ignore the second term in the denominator of the Oseen tensor because tanh(kH) ≤ 1 ≪ 2πLSD/L ≤ kLSD. In the second step, we approximate the 2D lattice sums in eq 17 by 2D integrals, which we write in polar coordinates
| 18 |
where 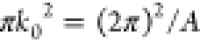 is the area corresponding to the k = 0 term left out from the lattice sums. The integrals over
the polar angle θ of the k vector give a rotational
flow of
is the area corresponding to the k = 0 term left out from the lattice sums. The integrals over
the polar angle θ of the k vector give a rotational
flow of
| 19 |
The integral over the Bessel function of the first kind and order 1 evaluates to
| 20 |
where the approximation is
valid for small k0. We obtain the circumferential
velocity by projecting (vx, vy) in eq 19 onto the unit vector (−y, x)/r. Using the approximation eq 20 for the integral and 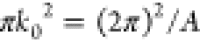 , we find
, we find
| 21 |
We determine the proportionality factor by matching v(r = R) to the rotational velocity ΩR. In this way, we recover exactly the circumferential velocity profile (eq 12) derived above. Consequently, if we determine the friction by integrating the stress over the outer surface of the cylindrical particle, as in the preceding derivation, we also recover the correction term in eq 15. To the leading order, the derivation for 2+1 dimensions in the limits of RH ≪ L ≪ LSD and H ≪ LSD thus gives the same correction for rotational diffusion as the above derivation for a strictly 2D periodic flow under the Saffman–Delbrück approximation. In addition, we find that for L ≪ LSD, the finite-size correction for the rotational diffusion coefficient does not depend significantly on the height H of the water layer because tanh(kH) ≪ 2πLSD/L in this case. For large boxes, L > LSD, the small height dependences could be estimated numerically or perturbatively by using the full denominator in the 2D lattice sums and their integral approximations or by performing a series expansion.
Hydrodynamic Correction from the Taylor–Couette Model
In the following,
we motivate the finite-size correction derived
above for the rotational diffusion coefficient using the simpler model
of the Taylor–Couette flow between two rotating cylinders.
The primary effect of PBC is that, by symmetry, the lipid rotational
flow around a protein centered in the membrane stalls at the points
of symmetry on the box boundaries (see Figure 1). Following earlier descriptions for translation23 and rotation in three dimensions,5 we therefore approximate the boundary where the
rotational flow stalls by a cylinder whose cross-sectional area matches
that of the box. The inclusion and the box then correspond to the
two coaxial cylinders in the theory of Taylor–Couette flow
(Figure 2). The radii
of the two cylinders are R1 = RH and 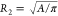 . In the laminar regime
for angular velocities
Ω1 = Ω and Ω2 = 0 of the inner
and outer cylinders of length h, respectively, the
required torque on the inner cylinder is20
. In the laminar regime
for angular velocities
Ω1 = Ω and Ω2 = 0 of the inner
and outer cylinders of length h, respectively, the
required torque on the inner cylinder is20
| 22 |
consistent with eq 13. For A → ∞, we again recover the Saffman–Delbrück formula (eq 1) by using the Stokes-Einstein relation (eq 14). For simulation boxes of finite area A, we recover eq 15
| 23 |
which relates the
rotational
diffusion coefficient DPBC in periodic
boundary conditions to its counterpart D0 in an infinite system in terms of the effective areas 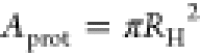 and A = L2 of the protein and the box, respectively.
and A = L2 of the protein and the box, respectively.
Figure 2.
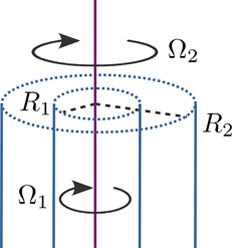
Taylor–Couette flow20 between rotating coaxial cylinders separated by a viscous fluid. The inner and outer cylinders have radii R1 and R2 and rotate around the central axis with angular velocities Ω1 and Ω2, respectively.
We can use eq 1 for D0 to obtain another formulation of the size correction
| 24 |
which can be used even when the exact value of the hydrodynamic radius RH is unknown.
Choice of Box Size
Our correction, eq 15 (eq 23), allows us to estimate how large a box should be chosen to limit the finite-size effects to an upper bound. We recommend using a box edge with
| 25 |
when the relative error (DPBC – D0)/D0 is desired to be smaller than ε. As an example, consider a small inclusion (RH = 1 nm) and a large one (RH = 3 nm). For the small one, the relative error drops below 10% already at L = 5.6 nm. However, for the large inclusion, it drops below 10% only at a box width of 16.8 nm. At a typical box width (2RH + 3 nm), the error would be 12% for the small inclusion and 35% for the large one. The effects are thus substantial in typical simulations of large membrane proteins such as transporters, channels, and receptors.
Simulation Methods
Molecular Dynamics Simulations
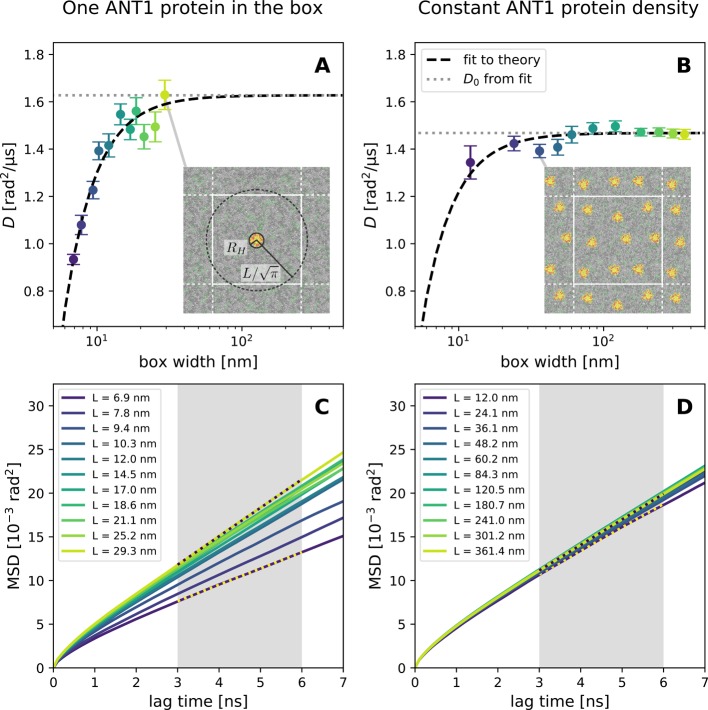
To test the hydrodynamic theory of rotational diffusion, we simulated single ANT1 proteins in model mitochondrial membranes of different areas using the MARTINI coarse-grained force field24 following the setup and simulation protocols of earlier such simulations.12,25 The initial box size was varied from 7 to 28 nm at a constant initial box height of 10 nm by adding lipids and water, approaching the limit of ANT1 at infinite dilution (Figure 3A). Additionally, we varied the initial box height from 7.5 to 20 nm for boxes of width L = 7 nm. We set up six replicas of each simulation and ran them for 2 μs each.
Figure 3.
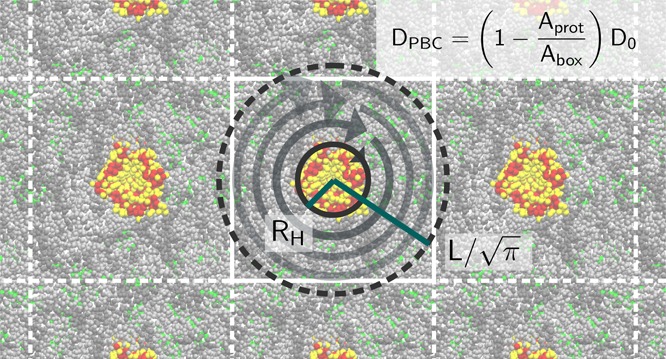
Rotational diffusion of ANT1 proteins in lipid membranes. (A) Diffusion coefficients from MD simulations of systems containing one protein per simulation box (symbols) with fit (dashed line) to hydrodynamic theory (eq 15) and the infinite-system value D0 (dotted line) obtained from this fit. The inset shows a top view on the system at L = 29.3 nm with the cylindrical approximations of the protein and simulation box. (B) Diffusion coefficients from MD simulations of systems containing ANT1 proteins at a constant area density with the corresponding fit. The inset shows a top view on the system at L = 36.1 nm. Error bars denote 1 SE. (C, D) MSD curves corresponding to (A) and (B), respectively. Gray regions indicate the fitting range.
We also reanalyzed earlier simulations of multiple ANT1 proteins diffusing in the membrane,12 simulated in boxes of varying widths at a fixed height and a constant protein area density (Figure 3B). This setup has the advantage of a constant membrane viscosity but imposes an upper limit to the smallest box size. The setups of the two studies coincide for a box width of L = 12 nm. Only one simulation per box size was available here, but we could average over the several proteins in the box. We complemented this study by simulations with an initial box height from 7.5 to 15 nm for a box width of 48 nm and 16 ANT1 proteins in the membrane.
In addition, we extended and reanalyzed trajectories from an earlier study on atomistic molecular dynamics simulations of a carbon nanotube (CNT) porin in a POPC membrane in boxes of varying widths.16
The details on all individual simulations can be found in the Supporting Information. Parameter files, analysis scripts, and raw diffusion data are available at https://github.com/bio-phys/rotmemdiff.
Diffusion Analysis
We calculated diffusion coefficients for the rotation θ(t) in the membrane plane. The lateral rotation angle δθτ between two subsequent frames at times τ – δτ and τ was calculated from the rotation matrix of a root-mean-square distance (RMSD) fit of the backbone bead coordinates from the latter frame to those in the previous frame, projected to the membrane plane. The total rotation θ(t) was then calculated as the cumulative sum over δθτ with θ(0) ≡ 0 as
| 26 |
The rotational diffusion coefficient D was determined from least-squares fits of linear functions a + 2Dt to the MSD in a time window from t0 to t1. The intercept a is a fitting constant accounting for the initial regime where local molecular events dominate the dynamics, before entering into a long-time diffusive regime. The MSD was calculated using an efficient Fourier-based algorithm.26 The fitting range for all ANT1 simulations is 3 to 6 ns. We chose the fitting region as a compromise between small noise in the MSD and small systematic errors from its nonlinear initial behavior. A model for harmonically coupled diffusion rationalizes this initial regime. Comparisons for fits at a later interval show that our choice of fitting range does not change the results significantly. See the Supporting Information for details.
Uncertainties were estimated as standard errors (SE) over the six runs of each box size for the new simulations of ANT1. For the dilute-limit simulations of ANT1, we used block averaging over 10 blocks to estimate errors. For the CNT porin, we chose the fitting range as 3 to 7 ns and estimated uncertainties using a variable number of blocks of lengths 60 to 80 ns, depending on the length of each simulation.
Results and Discussion
Coarse-Grained Simulations of ANT1
In both simulation setups, the rotational diffusion of the ANT1 protein follows the hydrodynamic prediction (Figure 3). A fit of eq 15 with D0 and the hydrodynamic radius RH of the protein as free parameters gives RH = 2.3(2) nm for the constant-density simulations and RH = 2.5(2) nm for the dilute-limit simulations (where numbers in parentheses indicate the SE of the last digit or digits). These values are within one SE of the hydrodynamic radius of 2.1(4) nm obtained for ANT1 translational diffusion and consistent with the value of 2.3 nm obtained from the convex hull in the xy plane.12
Additional simulations at varying box heights show no dependence on the height of the simulation box (Figure 4), consistent with the prediction obtained for the 2+1 dimensional hydrodynamic model for L ≪ LSD. In both narrow boxes with only one protein and in wider boxes with 16 proteins, we find no significant change in the diffusion coefficient. For translational diffusion,12 we found earlier a height dependence in wide boxes, L > LSD.
Figure 4.
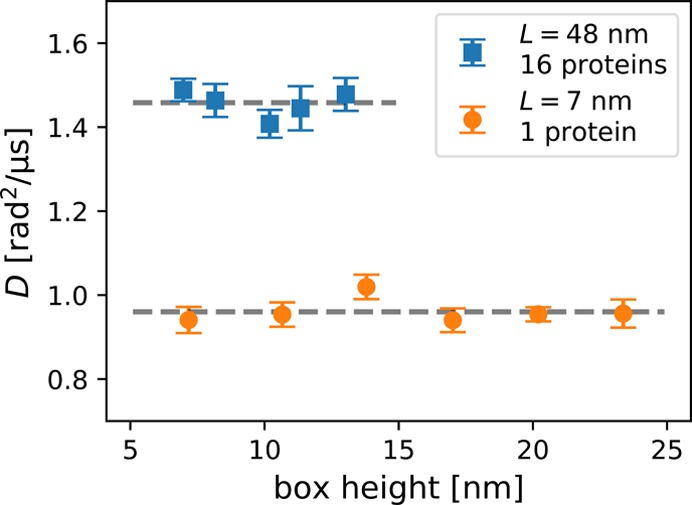
Box-height dependence of the rotational diffusion coefficient of coarse-grained ANT1 proteins in lipid membranes.
Even though the deviation of D from the infinite-system limit D0 caused by finite-size effects decreases with increasing box width in a well-behaved manner, it is still substantial for typical simulation-box sizes. A typical box width for a simulation of a membrane protein of the size of ANT1 would be 7 to 10 nm, amounting to a 20 to 30% reduction in rotational diffusivity. With our model, one can correct for these effects or give an estimate on how large a box should be chosen to avoid significant size effects (using eq 25).
The box-size dependence of rotational diffusion can be used to obtain the effective membrane viscosity. In the constant-density case, we obtain via eq 1 a membrane surface viscosity of ηm = ηh = 4.28 × 10–11 Pa·s·m, close to the value of ηm = 4.36 × 10–11 Pa·s·m obtained from the translational diffusion coefficient.12 This agreement further corroborates the consistency of the Saffman–Delbrück model of rotational diffusion with its translational version.15 In the dilute case, we obtain in the same way a lower membrane surface viscosity (ηm = 3.28 × 10–11 Pa·s·m). Using eq 2 with the fluid viscosity ηf = 8.4 × 10–4 Pa·s of MARTINI water at 310 K,12 we obtain Saffman–Delbrück lengths of 26 and 20 nm for the constant-density and dilute systems, respectively. These are an order of magnitude larger than the radius of ANT1, justifying the use of the Saffman–Delbrück model. For atomistic simulations, the Saffman–Delbrück length is usually much larger, extending the range of applicability even further.
The result for the membrane viscosity in the constant-density case is 30% larger than that in the dilute case. To compare to theoretical predictions for the dependence of the membrane viscosity on the area fraction ϕ occupied by membrane proteins,27,28 we calculate ϕ assuming a hydrodynamic radius of RH = 2.3(2) nm and LSD = 20(2) nm. The theory by Henle and Levine27 predicts an increase of [3 + 8RH/(πLSD)] ϕ, for which we obtain 37(7)%, whereas the expression used by Oppenheimer and Diamant,28 2ϕ, predicts 23(4)% (uncertainties, signifying 1 SE, were calculated with Monte Carlo error propagation). The observed increase is between the two predictions and within 2 SE of both values, precluding a simple decision between the models. Both models have been derived for very small area fractions, but earlier simulations by Camley and Brown29 indicate that this approximation works surprisingly well up to ∼10%. Thus, even though a decision on the exact functional dependence on the protein area fraction is not possible, the apparent membrane viscosity evidently decreases with increasing box width in single-protein simulations, approaching the pure-lipid value in the limit.
The limiting value of the diffusion coefficient in our simulations differs significantly between the study with a constant area density (D0 = 1.4 rad2·μs–1) and the dilute-limit study with only one protein in the box (D0 = 1.63 rad2·μs–1). This difference can be explained by the difference in viscosities in the limiting case of an infinite system, as discussed above. We note that the proteins in the constant-density simulations do not form clusters during the time of our simulation. Nevertheless, the presence of the ANT1 proteins increases the apparent membrane viscosity ηm = ηh. The possibility to describe the observed effects by a single value of an effective viscosity shows that rotational diffusion is not only determined by the local surrounding of the protein but also by long-ranged hydrodynamic effects.
Atomistic Simulations of a CNT Porin
Rotational diffusion of the CNT porin in atomistic simulations shows a very quick convergence to the infinite-system value, as predicted by our theory (Figure 5). The slightly lower value at 4 nm is in accordance with the prediction. The CNT has a small radius (0.72 nm), and therefore a strong finite-size effect is only predicted for unreasonably small boxes. Much longer simulations would be necessary to reach the precision that is required to detect them, as can be seen from the noisy behavior of the MSD (Figure 5B). At boxes smaller than 5 nm, the periodic images would be separated by less than 3.5 nm, and it is likely that effects other than hydrodynamics would dominate, for example, lipid ordering.16 This quick convergence shows that at least for small membrane inclusions (such as single transmembrane helices) in typical simulations, rotation is only slightly affected by the box size. However, one has to keep in mind that the relative effect grows with the square of the hydrodynamic radius.
Figure 5.
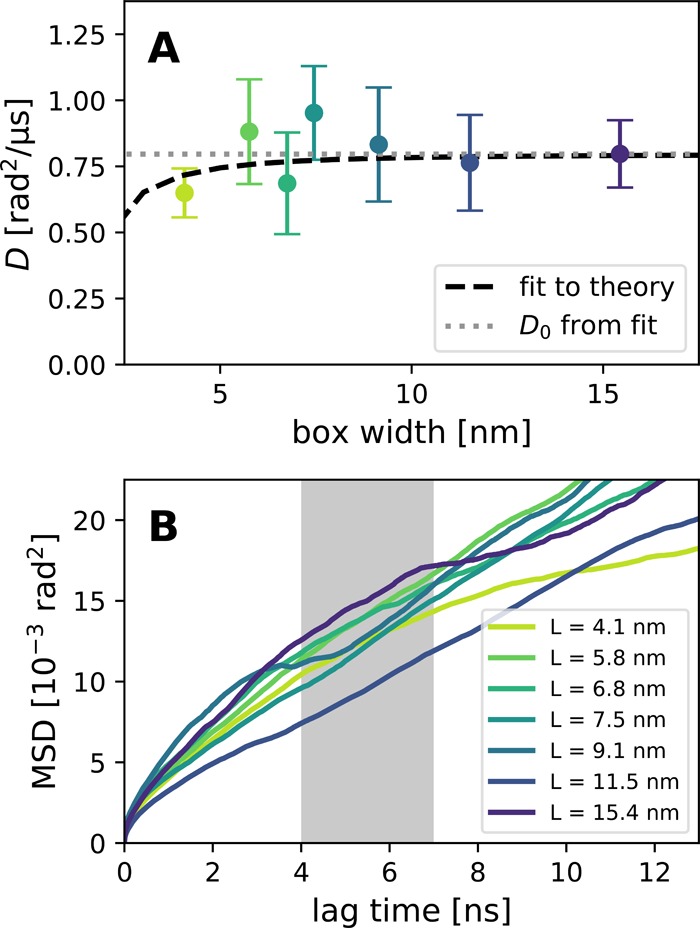
Rotational diffusion of a CNT porin in a POPC membrane. (A) Diffusion coefficients from MD simulations (symbols) and a fit (dashed line) to hydrodynamic theory eq 15 with D0 (dotted line) as the only free parameter and the hydrodynamic radius fixed at RH = 0.72 nm. (B) MSD curves. The gray region indicates the fitting range.
Conclusions
We showed that hydrodynamic theory for 2D periodic flows in membranes describes the finite-size effects on rotational diffusion in membranes. In contrast to lateral membrane diffusion, the rotational diffusion coefficient converges as the box width is increased. The relative size of the effect depends on the ratio of the protein area and the box area and is substantial for small to medium-sized boxes or medium-sized to large membrane proteins. From the corresponding correction, we derive an estimate for how large boxes should be to keep size effects below a chosen limit. In our analysis, we assume that the boxes are small relative to the Saffman–Delbrück length, L ≪ LSD, as is typically the case in membrane simulations. Moreover, we use the Saffman–Delbrück rotational diffusion coefficient15 in eq 1 as the infinite-system reference value, valid for RH ≪ LSD, and not the extended version of Hughes, Pailthorpe, and White.18 The finite-size analysis of rotational diffusion also leads to an estimate of the membrane viscosity by fitting eq 24, which is difficult to calculate otherwise.12,30 For both dense and dilute ANT1 membrane proteins in cardiolipin-containing mitochondrial membranes,12,25 we found the corrected rotational diffusion coefficients to be consistent with the Saffman–Delbrück model15,17 using values for the membrane viscosity and hydrodynamic radius determined previously from ANT1 translational diffusion data.12
Acknowledgments
We acknowledge PRACE for access to Mare Nostrum at the Barcelona Supercomputing Center. We also acknowledge the Max Planck Computing and Data Facility, Garching, where we performed additional simulations. This work was supported by the Max Planck Society.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.9b01656.
Details on hydrodynamic finite-size correction for rotational diffusion, analysis of the mean squared displacement, simulation details (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Hasimoto H. On the Periodic Fundamental Solutions of the Stokes Equations and Their Application to Viscous Flow Past a Cubic Array of Spheres. J. Fluid Mech. 1959, 5, 317–328. 10.1017/S0022112059000222. [DOI] [Google Scholar]
- Dünweg B.; Kremer K. Molecular Dynamics Simulation of a Polymer Chain in Solution. J. Chem. Phys. 1993, 99, 6983–6997. 10.1063/1.465445. [DOI] [Google Scholar]
- Yeh I. C.; Hummer G. System-Size Dependence of Diffusion Coefficients and Viscosities from Molecular Dynamics Simulations with Periodic Boundary Conditions. J. Phys. Chem. B 2004, 108, 15873–15879. 10.1021/jp0477147. [DOI] [Google Scholar]
- Linke M.; Köfinger J.; Hummer G. Fully Anisotropic Rotational Diffusion Tensor from Molecular Dynamics Simulations. J. Phys. Chem. B 2018, 122, 5630–5639. 10.1021/acs.jpcb.7b11988. [DOI] [PubMed] [Google Scholar]
- Linke M.; Köfinger J.; Hummer G. Rotational Diffusion Depends on Box Size in Molecular Dynamics Simulations. J. Phys. Chem. Lett. 2018, 9, 2874–2878. 10.1021/acs.jpclett.8b01090. [DOI] [PubMed] [Google Scholar]
- Kikugawa G.; Ando S.; Suzuki J.; Naruke Y.; Nakano T.; Ohara T. Effect of the Computational Domain Size and Shape on the Self-Diffusion Coefficient in a Lennard-Jones Liquid. J. Chem. Phys. 2015, 142, 024503 10.1063/1.4905545. [DOI] [PubMed] [Google Scholar]
- Kikugawa G.; Nakano T.; Ohara T. Hydrodynamic Consideration of the Finite Size Effect on the Self-Diffusion Coefficient in a Periodic Rectangular Parallelepiped System. J. Chem. Phys. 2015, 143, 024507 10.1063/1.4926841. [DOI] [PubMed] [Google Scholar]
- Camley B. A.; Lerner M. G.; Pastor R. W.; Brown F. L. H. Strong Influence of Periodic Boundary Conditions on Lateral Diffusion in Lipid Bilayer Membranes. J. Chem. Phys. 2015, 143, 243113. 10.1063/1.4932980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vögele M.; Hummer G. Divergent Diffusion Coefficients in Simulations of Fluids and Lipid Membranes. J. Phys. Chem. B 2016, 120, 8722–8732. 10.1021/acs.jpcb.6b05102. [DOI] [PubMed] [Google Scholar]
- Simonnin P.; Noetinger B.; Nieto-Draghi C.; Marry V.; Rotenberg B. Diffusion under Confinement: Hydrodynamic Finite-Size Effects in Simulation. J. Chem. Theory Comput. 2017, 13, 2881–2889. 10.1021/acs.jctc.7b00342. [DOI] [PubMed] [Google Scholar]
- Venable R. M.; Ingólfsson H. I.; Lerner M. G.; Perrin B. S. Jr.; Camley B. A.; Marrink S. J.; Brown F. L.; Pastor R. W. Lipid and Peptide Diffusion in Bilayers: The Saffman–Delbrück Model and Periodic Boundary Conditions. J. Phys. Chem. B 2017, 121, 3443–3457. 10.1021/acs.jpcb.6b09111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vögele M.; Köfinger J.; Hummer G. Hydrodynamics of Diffusion in Lipid Membrane Simulations. Phys. Rev. Lett. 2018, 120, 268104. 10.1103/PhysRevLett.120.268104. [DOI] [PubMed] [Google Scholar]
- Awosanya E. O.; Nevzorov A. A. Protein Rotational Dynamics in Aligned Lipid Membranes Probed by Anisotropic T1ρ NMR Relaxation. Biophys. J. 2018, 114, 392–399. 10.1016/j.bpj.2017.11.3740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paulino J.; Pang X.; Hung I.; Zhou H. X.; Cross T. A. Influenza A M2 Channel Clustering at High Protein/Lipid Ratios: Viral Budding Implications. Biophys. J. 2019, 116, 1075–1084. 10.1016/j.bpj.2019.01.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saffman P. G.; Delbrück M. Brownian Motion in Biological Membranes. Proc. Natl. Acad. Sci. U. S. A. 1975, 72, 3111–3113. 10.1073/pnas.72.8.3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vögele M.; Köfinger J.; Hummer G. Molecular Dynamics Simulations of Carbon Nanotube Porins in Lipid Bilayers. Faraday Discuss. 2018, 209, 341–358. 10.1039/C8FD00011E. [DOI] [PubMed] [Google Scholar]
- Saffman P. G. Brownian Motion in Thin Sheets of Viscous Fluid. J. Fluid Mech. 1976, 73, 593–602. 10.1017/S0022112076001511. [DOI] [Google Scholar]
- Hughes B. D.; Pailthorpe B. A.; White L. R. The Translational and Rotational Drag on a Cylinder Moving in a Membrane. J. Fluid Mech. 1981, 110, 349–372. 10.1017/S0022112081000785. [DOI] [Google Scholar]
- Petrov E. P.; Petrosyan R.; Schwille P. Translational and Rotational Diffusion of Micrometer-Sized Solid Domains in Lipid Membranes. Soft Matter 2012, 8, 7552–7555. 10.1039/c2sm25796c. [DOI] [Google Scholar]
- Landau L.; Lifshitz E.. Course of Theoretical Physics, vol. 6, Fluid Mechanics ;Butterworth-Heinemann: Oxford, 1987. [Google Scholar]
- Hummer G.; Soumpasis D. M. Correlations and Free Energies in Restricted Primitive Model Descriptions of Electrolytes. J. Chem. Phys. 1993, 98, 581–591. 10.1063/1.464600. [DOI] [Google Scholar]
- Grønbech-Jensen N. Summation of Logarithmic Interactions in Nonrectangular Periodic Media. Comput. Phys. Commun. 1999, 119, 115–121. 10.1016/S0010-4655(99)00200-3. [DOI] [Google Scholar]
- Fushiki M. System Size Dependence of the Diffusion Coefficient in a Simple Liquid. Phys. Rev. E 2003, 68, 021203 10.1103/PhysRevE.68.021203. [DOI] [PubMed] [Google Scholar]
- Marrink S. J.; Risselada H. J.; Yefimov S.; Tieleman D. P.; De Vries A. H. The MARTINI Force Field : Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- Hedger G.; Rouse S. L.; Domański J.; Chavent M.; Koldsø H.; Sansom M. S. P. Lipid-Loving ANTs: Molecular Simulations of Cardiolipin Interactions and the Organization of the Adenine Nucleotide Translocase in Model Mitochondrial Membranes. Biochemistry 2016, 55, 6238–6249. 10.1021/acs.biochem.6b00751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calandrini V.; Pellegrini E.; Calligari P.; Hinsen K.; Kneller G. R. nMoldyn - Interfacing Spectroscopic Experiments, Molecular Dynamics Simulations and Models for Time Correlation Functions. Collect. SFN 2011, 12, 201–232. 10.1051/sfn/201112010. [DOI] [Google Scholar]
- Henle M. L.; Levine A. J. Effective Viscosity of a Dilute Suspension of membrane-bound Inclusions. Phys. Fluids 2009, 21, 033106 10.1063/1.3086831. [DOI] [Google Scholar]
- Oppenheimer N.; Diamant H. Correlated Diffusion of Membrane Proteins and Their Effect on Membrane Viscosity. Biophys. J. 2009, 96, 3041–3049. 10.1016/j.bpj.2009.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camley B. A.; Brown F. L. H. Fluctuating Hydrodynamics of Multicomponent Membranes with Embedded Proteins. J. Chem. Phys. 2014, 141, 075103 10.1063/1.4892802. [DOI] [PubMed] [Google Scholar]
- Den Otter W. K.; Shkulipa S. A. Intermonolayer Friction and Surface Shear Viscosity of Lipid Bilayer Membranes. Biophys. J. 2007, 93, 423–433. 10.1529/biophysj.107.105395. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.