Abstract
Background:
Standard segmentation of high-contrast electron micrographs (EM) identifies myelin accurately but does not translate easily into measurements of individual axons and their myelin, even in cross-sections of parallel fibers. We describe automated segmentation and measurement of each myelinated axon and its sheath in EMs of arbitrarily oriented human white matter from autopsies.
New methods:
Preliminary segmentation of myelin, axons and background by machine learning, using selected filters, precedes automated correction of systematic errors. Final segmentation is done by a deep neural network (DNN). Automated measurement of each putative fiber rejects measures encountering pre-defined artifacts and excludes fibers failing to satisfy pre-defined conditions.
Results:
Improved segmentation of three sets of 30 annotated images each (two sets from human prefrontal white matter and one from human optic nerve) is achieved with a DNN trained only with a subset of the first set from prefrontal white matter. Total number of myelinated axons identified by the DNN differed from expert segmentation by 0.2%, 2.9%, and −5.1%, respectively. G-ratios differed by 2.96%, 0.74% and 2.83%. Intraclass correlation coefficients between DNN and annotated segmentation were mostly >0.9, indicating nearly interchangeable performance.
Comparison with Existing Method(s):
Measurement-oriented studies of arbitrarily oriented fibers from central white matter are rare. Published methods are typically applied to cross-sections of fascicles and measure aggregated areas of myelin sheaths and axons, allowing estimation only of average g-ratio.
Conclusions:
Automated segmentation and measurement of axons and myelin is complex. We report a feasible approach that has so far proven comparable to manual segmentation.
Keywords: myelin, g-ratio, segmentation, white matter, electron microscopy, deep learning, convolutional networks
1. Introduction
In a nerve fiber, the thickness of the myelin sheath is critical to the function of the ensheathed axon. Thicker myelin increases conduction velocity by maintaining the high potential between the nodes of Ranvier. However, if total diameter for a bundle of fibers is limited, myelin thickness increases at the expense of axonal diameter, which decreases conductivity. Balancing these effects, in peripheral nerve, conduction velocity is maximized when the ratio of axonal diameter to outer diameter of myelin, the g-ratio, is approximately 0.6; in human sural nerve the average measured g-ratio is 0.581. In CNS, the relationship between axon diameter and myelin thickness is more complex. In human peripheral nerve, the smallest myelinated axons have a diameter of 2 microns2, while in CNS, axons as thin as 0.16 microns are myelinated3. In peripheral nerve, neuregulin 1, type 3 has an important role in determining myelin thickness4; in CNS, this is ambiguous5. Extensive interactions between proteins of the axolemma and those of myelin6 imply additional functions of the myelin sheath. The recent discovery by several laboratories7, 8 that very short axons of interneurons are myelinated further suggests that myelin serves additional purposes besides insulating the axon and enabling saltatory conduction. Myelin thickness in the brain can be clinically relevant. For instance, when CNS axons are demyelinated, as in multiple sclerosis, they often remyelinate, but the new myelin sheaths are generally thinner than the original ones9, which may help to explain why remissions of multiple sclerosis are often incomplete.
Morphological study of myelinated axons requires the ability to measure the diameters of axons and the thickness of each axon’s myelin sheath. For example, aging is associated with a loss of small myelinated axons10 and with thinning of myelin sheaths11, neither of which is apparent on qualitative inspection of electron micrographs nor on measurement of a few fibers. To identify such changes, one must measure many fibers. Human-operated computerized measurement of digital images is already much faster than manual measurement, but completely automated measurement requires automated segmentation of the axons and myelin sheaths, as well as an algorithm for associating specific myelin pixels with the axon that they surround. Since the smallest fibers are near the refraction-limited resolution of the light microscope (~200 nm), precise histological quantitation of myelin sheath thickness typically requires electron microscopy (EM). We describe here a computational workflow to segment electron micrographs and determine axonal diameter and myelin thickness of hundreds to thousands of fibers. The workflow employs both traditional machine learning and deep learning to segment the image, followed by a measurement algorithm that is resistant to small inaccuracies in segmentation. The system is operable by users without training in neuroanatomy. Compared with a “ground truth” segmentation by a neuroanatomist and a neuropathologist, the workflow accurately and rapidly measured thousands of axons and their myelin sheaths both from fibers in parallel fascicles cut in cross section or in fields without regular patterns, in which the orientations are largely oblique.
Semi-automated myelin measurement protocols, requiring continuous interaction between computer and trained anatomist to outline axons and myelin and to exclude non-fibers, have been in use since digitized images became routinely available over 30 years ago. These interactive methods accelerated analysis tremendously when applied, as they generally were, to peripheral nerves cut in or close to cross section12, 13, and modeled as circular or ellipsoid cross-sections. Recent work has continued to employ interactive procedures and extended parametric control14, 15. On the other hand, accurate, fully automated measuring has so far required accurate and reproducible automated segmentation of myelinated fibers. This is especially difficult in EM images of subcortical white matter, which is not usually organized into bundles of parallel fibers. Myelin in such images is easily recognized (and segmented) by its dark staining with osmium and uranium. Once the myelin sheaths are defined, they are automatically filled with axons, and any remaining pixels are classified as “background”. However, typical obstacles to correct segmentation (Fig. 1) include: (i) Densely stained nuclei or artifacts that can be interpreted as myelin, (ii) Especially in autopsy tissue, spaces between artefactually separated myelin lamellae that can be misclassified as axons and that must be avoided when measuring thickness of myelin, (iii) Non-axonal tissue surrounded by mutually apposed myelin sheaths, and (iv) Segmentation of axons as background when there is a defect in the surrounding myelin.
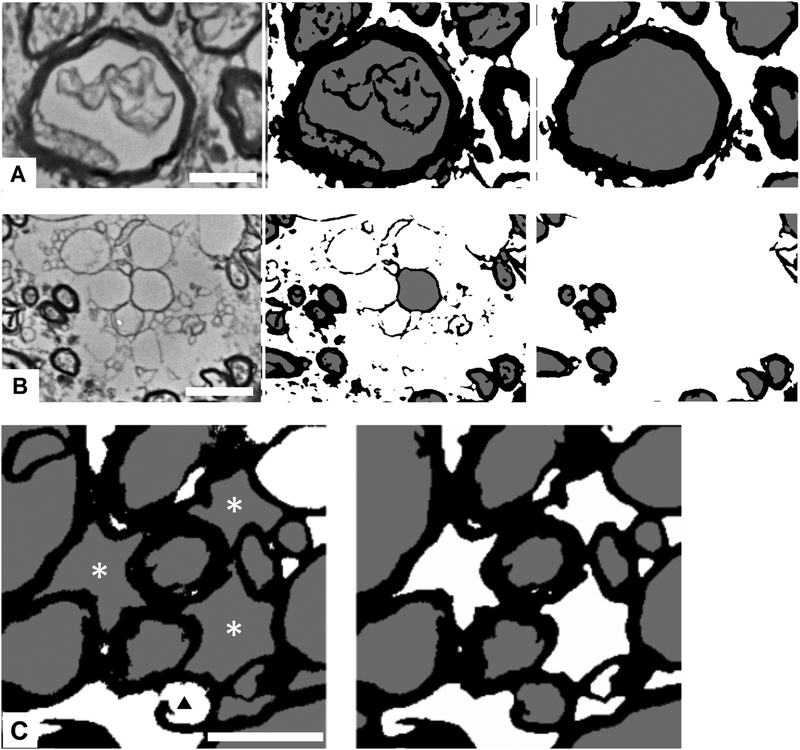
Figure 1 -.
Examples of typical errors of 3-class segmentation with Visiomorph, common to all pixel classifiers. (A) segmenting nuclei or dark debris as myelin, (B) segmenting artificial gaps in myelin as axons, (C) segmenting regions surrounded by a ring of myelinated axons as axons, and (D) segmentation of axons as background when there is a defect in the surrounding myelin. Scale bar = 1 micron.
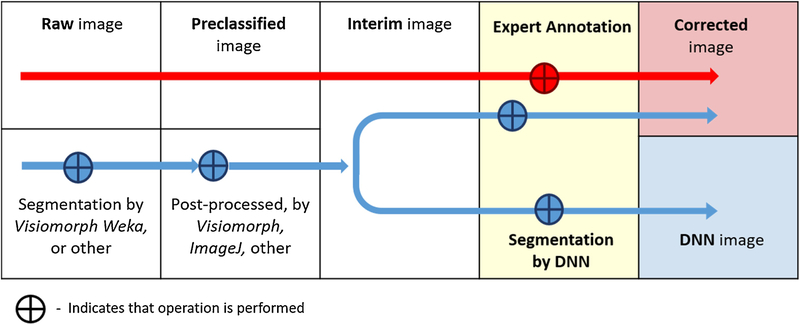
Our protocol (Fig. 2) sidesteps some of these difficulties with a measurement-oriented approach that is insensitive to classification errors in regions that the measurement tool is designed to exclude.
Figure 2 -.
Nomenclature of image processing steps
Segmentation based on Machine learning (ML) is widely available in packages (e.g., Visiomorph, ImageJ Weka Segmenter, various MATLAB add-ins) Commonly, such packages also provide processing toolboxes for large volumes of images and filters and definitions that detect a wide range of features16. These result in less bias and greater reproducibility than do manual or interactive segmentation. However, commercial segmentation packages typically try to limit the overall computational cost, which has restricted those tools to semi-supervised machine learning and statistical inference. Typically, these programs require the user to select manually only a few labeled sample regions corresponding to each class. The program then uses the examples to define filters or kernels that it applies to outline clusters or to detect boundaries. Recognition is best for statistically very similar structures, like peripheral nerve fibers. For very complex forms and great tissue variability at the relevant spatial scales, as in the case of primate subcortical white matter, such purely computational, non-learning or unsupervised learning methods17 typically saturate at a pixel-based accuracy of 55–65% (see18 or19 for a short survey).
Since 2010, the use of deep neural networks (DNN)20 in machine learning has grown rapidly, fueled by commercial GPU multiprocessing devices. Responses to tissue segmentation challenges21 have demonstrated the utility of typical DNN architectures based on error back-propagation neural networks of the 1980’s. The latter, also known as multi-layer perceptrons, have proven very efficient tools for supervised learning of various classification tasks. Our DNN architecture for segmentation of white matter combines 2-dimensional arrays of simple processing logical units. Each unit computes a convolution of the input image fragment over a small pixel window to self-extract features. Such 2-dimensional feature maps are then stacked in a deep, interconnected multi-layered 3-dimensional structure, reminiscent structurally of mammalian visual sensory processing22. The whole structure is trained in a supervised learning framework using a set of ground-truth images, annotated with a segmentation representing the consensus of several experts. The use of such convolutional neural networks (CNN) as 3-dimensional feature detection layers21, 23 has enabled the deep networks, as computational and learning structures, to scale to large, high-resolution images. Very recently, commercial software has begun to apply deep learning to histopathological diagnosis24.
2. Materials and Methods
2.1. Image acquisition
All tissue was from 17 sudden deaths autopsied at the Institute for Forensic Medicine at the University of Saints Cyril and Methodius, Skopje, North Macedonia. The study was performed with the approval of the Institutional Review Boards of the New York State Psychiatric Institute and the Macedonian Academy of Sciences and Arts. Since this methodological study was in preparation for a larger study to compare axonal diameters and g-ratios in psychiatric diseases, we included cases with history of schizophrenia or major depressive disorder, as well as cases without history of serious mental illness (Table S7, Supplementary Information 7). Because of the small number of brains in each clinical group, preliminary determination of statistical effects of psychiatric or medical history, demographics, medications, cause of death, or interval from death to autopsy (postmortem interval), any of which could have an influence on the dependent measures, could easily be misleading, so such preliminary analyses were eschewed.
At autopsy, a coronal block of the unfixed superior frontal gyrus, approximately 5 mm thick, containing cortex and underlying white matter (Fig. 3), and a transverse section of the optic nerve were placed at 4°C in fixative containing 1% glutaraldehyde, 4% paraformaldehyde, 0,9% NaCl, and 100 mM sodium phosphate, pH 7.4, until further processing. The fixed tissues were cut on a vibrating microtome to a thickness of 0.2 mm. The tissues were stained with 1% osmium tetroxide in 0.1 M phosphate buffer, pH7.2, for 15 minutes and rinsed with phosphate buffer. Afterwards, the tissues were dehydrated in graded ethanol solutions from 50% to 95%, followed by propylene oxide for 15 minutes. They were then impregnated with a 1:1 mixture of propylene oxide and Durcupan on a shaker. Once the impregnation was finished, the tissues were placed on glass slides and covered with undiluted Durcupan for 4 hours. The Durcupan was gently removed and a fresh small quantity of it poured over the tissues again. Coverslips, treated with Liquid Release Agent, were placed on top of the slides, and the tissues left in an oven at 55–60°C for 36 hours. Small sections, approximately 0.25 × 0.25 mm, predominantly containing white matter, were removed with a blade from the Durcupan-embedded slices and placed on Durcupan blocks. They were trimmed by hand and ultramicrotome (with glass knives), and cut with a diamond knife into ultra-thin sections (uts) of 80 nm, which were placed on mesh grids. The uts were stained, first with uranyl acetate and then with lead citrate. The mesh grids were loaded into the holding chamber of the EM and the magnification set to 5000x. The microscopist visually confirmed regions of white matter by the presence of myelinated axons and the absence of more than an occasional neuron) and recorded images with a 2048 × 2048 pixel digital camera at a resolution of 0.011 micron/pixel.
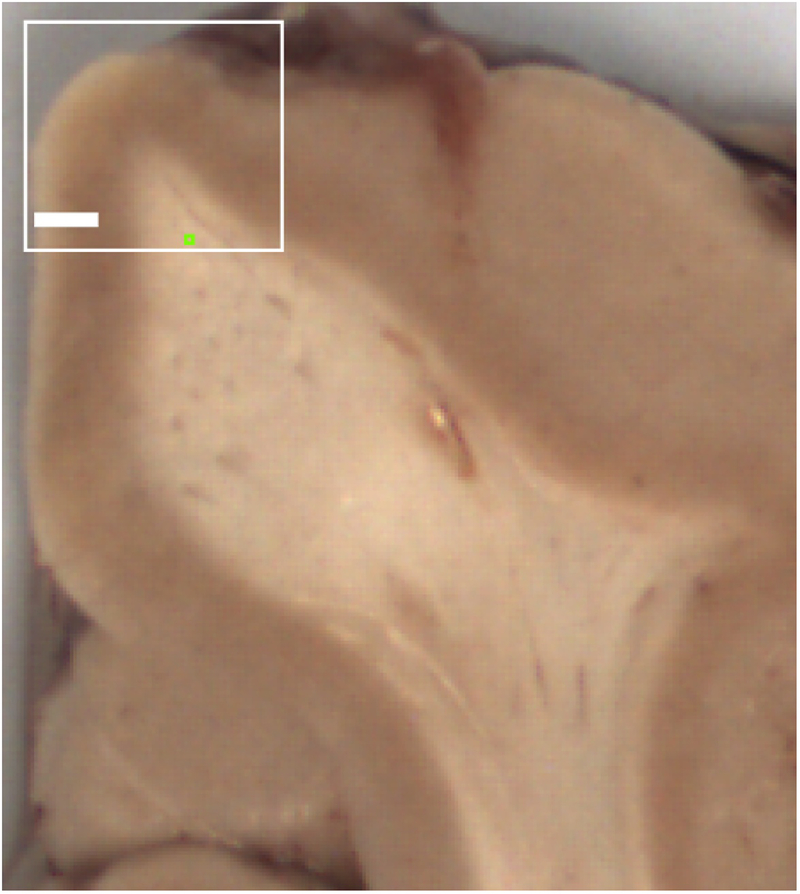
Figure 3 -.
Superior frontal gyrus from formalin-fixed coronal slice of an autopsy brain. White box represents the location of a typical sample collected at autopsy (from an unfixed slice) for electron microscopy. Green box indicates typical location selected for thin sections of white matter. Bar = 2 mm.
2.2. Generation of DNN input by preliminary segmentation and post-processing –
Basic features of the white matter lend themselves to a preliminary classification of all pixels in the original EM images to 3 values: 1=myelin, represented herein as black, 2=axon, represented as gray and 3 = anything else (“background”), represented as white. For cerebral white matter, this initial segmentation (henceforth, pre-segmentation) is obtained in a semi-supervised ML environment (e.g., Visiomorph, ImageJ Trainable Weka Segmenter). Typically, a few examples of each class are annotated and a different number of user-selected features are computed for each pixel. Based on them, a conventional segmentation algorithm, such as decision trees (random forest) or naïve Bayes finally classifies each pixel in the image. Classification of myelin is generally accurate because of its dark color and sharp edges, although artifacts and nuclei with these properties may be misclassified as myelin (Fig. 1). While the classification does not meaningfully distinguish between axons and background, a 3-class segmentation usually labels myelin more accurately than does a 2-class segmentation. In theory, were it not for artefacts, the measurements of axonal diameter and myelin thickness could be made on this classified image by measuring the inner and outer diameters of each myelin sheath. (However, defining a myelin sheath as an object for measurement is not trivial.)
The pre-classified image, in which only myelin is meaningfully classified, is processed to an interim image in several steps (Fig. 2) that operate on the entire image: (i) All pixels classified as axon are re-classified as background, creating an image with only two classes. (ii) Fields of background pixels completely surrounded by myelin pixels are re-classified as axon pixels. (iv) Contiguous groups of myelin pixels completely surrounded by axon pixels are re-classified as axon pixels. (v) Contiguous groups of myelin pixels completely surrounded by background pixels are re-classified as background pixels. (vi) Contiguous groups of axon pixels completely surrounded by background pixels are re-classified as background pixels. Described post-processing can be adapted to the tissue at hand. For example, when analyzing optic nerve, with generally thicker fibers and more artefactual separations of myelin lamellae, steps iv and v are modified to: (iv) Contiguous groups of axon pixels in groups smaller than 1,000 are re-classified as background pixels. (v) Myelin pixels in groups smaller than 1000 are re-classified to the class of the surrounding pixels. A circle of area 1000 pixels has a diameter slightly less than 400 nm; in optic nerve we find no myelinated axons smaller than this, so axons below this size can be assumed safely to be artifacts, most commonly from separations of the myelin lamellae. On the other hand, smaller fibers are common in prefrontal white matter, so a size filter cannot be used.
These pre-segmented, post-processed 3-value images are the input for the DNN enhanced segmentation protocol. Similar approaches of initial pre-segmentation followed by segmentation improvement based on machine learning have been reported in studies of histologically more uniform and much more ordered tissue, such as biopsy samples of cat and rat peripheral nerve (at low magnification)15 and human sural nerve25. We considered pre-segmentation as a trade-off between too much structural detail in the original EM images, which typically causes supervised ML methods to over-fit, and loss of original information, which causes the post-processing to create structured noise (i.e., various forms of artifacts and debris interpreted as structure by the classifier) (Fig. 4). The newly introduced structured noise consisted mainly of spurious fibers or ROIs most typically debris or other non-fiber structures in the original EM images that were mapped to mixtures of pixels with values of 1 or 2.
Figure 4 -.
Limitations of pre-segmentation, which maps the original electron micrograph (EM) to a 3-class image. (A) and (B), triads comprising (left) fragment of original EM image, (center) pre-segmented image, and (right) fully corrected (3-class annotated) image. (A) Typical appearance of spurious structures, pre-classified as myelin, inside axons. (B) External debris and structures spuriously assigned to fiber ROIs. Some types of spurious objects are removed by post-processing and others by the subsequent segmentation protocol. (C) Examples of defects in (left) initially presegmented, and (right) corrected/annotated image. Defect in myelin sheath leads to pre-classification of axon as background (black triangle). Engulfed background is pre-classified as axoplasm (asterisks). Although the non-circularity of profiles, this large, should exclude them from segmentation as axons, we were unable to find a combination of size and circularity that consistently distinguished between axons and such spaces; hence, this task was left for the deep neural network. Scale bar = 1 micron.
The initial two steps are critical, because they replace the difficult problem, once myelin is defined, of distinguishing axoplasm and background in the original image, where each has a complex and variable appearance in a similarly rich range of grey values, with the relatively simple problem of determining whether a non-myelin pixel is inside or outside a boundary defined by the myelin sheath. These two steps redefine the fiber structures. The task of the DNN then becomes to correct the errors of the pre-segmentation and post-processing that will affect the count of myelinated axons or the measurement of axon diameter or myelin thickness.
With these interventions completed, each 3-class image is designated an interim image and saved in TIFF format (nominally an 8-bit image, but actually only 2 bits deep, since there are only 3 possible grey values) and. Such images are later fragmented to create input sets for the DNN segmentation protocol.
2.3. Annotation –
An initial segmentation of 3 sets of 30 images from 17 cases (6, 7, and 12 cases per set), into 3 pixel classes were post-processed, as described below. Errors in the post-processed initial segmentation were manually corrected by the electron microscopist (BD). The neuropathologist (AJD) and neuroanatomist (JS) then independently compared the segmented images with the originals and made corrections. The two annotations (anatomist’s and pathologist’s) were compared; any disagreements were discussed, and a consensus was achieved, yielding a final, “corrected” segmentation. Two sets of images were from samples of pre-frontal white matter, while the third set was from the optic nerve.
2.4. Sampling and fragmentation –
To train the DNN to classify a pixel according to its context (i.e., the pattern of the pixels surrounding it) we systematically fragmented the images into overlapping, 45 × 45 pixel “patches,” which became the input to the ML tool (~4 million from a single image). The input patches overlap, because each fragment is an input context for its central pixel. The size was chosen to present enough local context for a learning tool to learn to classify the central pixel correctly. Fragment size is of course a critical parameter, which depends on the imaging context and should be selected from a range of values to reach a trade-off with later computing costs.
Extensive preliminary experimentation with our class and type of images showed that the main machine learning difficulties come from (i) variations of form at the boundary between axon and myelin in all possible spatial configurations and variations of the form of myelinated fibers, and (ii) various non-fiber, debris forms encountered in pre-classified images. It is important to note that these issues occur on different scales, depending on the size of the fiber. We therefore selectively sampled the images so that input datasets for machine learning contain ample representation of different categories of fiber size. First, all regions of interest (ROI) were defined in ImageJ as each region corresponding to an axonal profile, i.e., the particles outlined by (and including) the outermost pixels of each axon (particles of class 2, color coded gray in segmented images). For small fibers, where axon area contains between 112 and 800 pixels, center points of the 45 × 45 pixel patches were chosen randomly from the region defined by a series of 25 × 25 pixel squares, each centered on an outer pixel of the ROI. For medium and large fibers (areas above 800 pixels) center points of 45 × 45 pixel patches were chosen randomly from a series of 45 × 45 pixel squares centered on the axonal boundary. In both cases, 10% of the pixels in the series of tiled squares around each axon were chosen randomly as the center points for the 45 × 45 pixel input patches. Both fiber size classes were represented in their natural frequency of occurrence. Debris objects were all small clusters with fewer than 112 pixels in area, classified either as myelin, axon, or a mixture of those classes that were not present in the corresponding fragment of the annotated copy of the image. Sampling of those small clusters was done randomly at 15% of them, by sparsely selecting the central pixel of an 11 × 11 pixel window to avoid always having a debris pixel in the center of final sample fragment. This sampling procedure, on 20 out of 30 images of the training set, produced close to 2 million patches from both fiber sizes combined, and 4 to 5.5 million samples of background regions that contained debris objects (with fiber ROIs masked).
2.5. Machine learning –
Pixel-based classification of irregular, stochastic forms is in principle a demanding task, especially when the goal is to measure the classified object, rather than just to recognize or count it. This is especially true when accuracy should be on the scale of 1 or 2 pixels. In most applications on biological tissue, the goal is achieved by supervised workflows26 using multi-layer networks16, 19, 27–30. Deep, multi-layer networks learn by adjusting connection weights between blocks of 2-d feature maps in consecutive layers (Fig. 6). For our convolutional DNN, each pixel in the feature-maps is produced by mapping a 4 × 4 pixel convolution over each input patch, by a suitable activation function. The resulting map is sub- sampled (downsized) by [2×2 → 1] max-pooling. Different maps within a block result from different initial weights from the input field, randomized by probabilistic sampling.
2.5.1. Pre-training of feature maps –
Learning in deep networks means computing a massive volume of weights for each of millions of patches introduced at the input layer. This poses the issue of initialization of interconnection weights between the maps of each layer and the preceding one. A typical random selection of initial weights may affect learning error convergence due to inherent capacity of the deep neural networks to overfit, and in the early stages of training assign parameters in such a way that corresponding local minima generalize rather poorly. This is the result of a trap effect, typical for statistical gradient descent methods, where early in the training, small training perturbations may cause the learning state to switch from one local minimum to another, which is less likely to happen deeper in the descent. It is now known that a pre-training epoch, during which the network learns the initial weights of feature maps, can improve learning31. Out of several structures suggested for this purpose, we tested two (Fig. 5): (i) a two-layer, unsupervised generative graphical model consisting of restricted Boltzmann machines, (RBMs)32, 33, and (ii) a supervised denoising auto-encoder in deep network architecture34. In both cases, pre-trained weights of the first, input-layer of maps produced features much better resembling the forms seen in sample input fragments, compared to initially randomized weights (see Results).
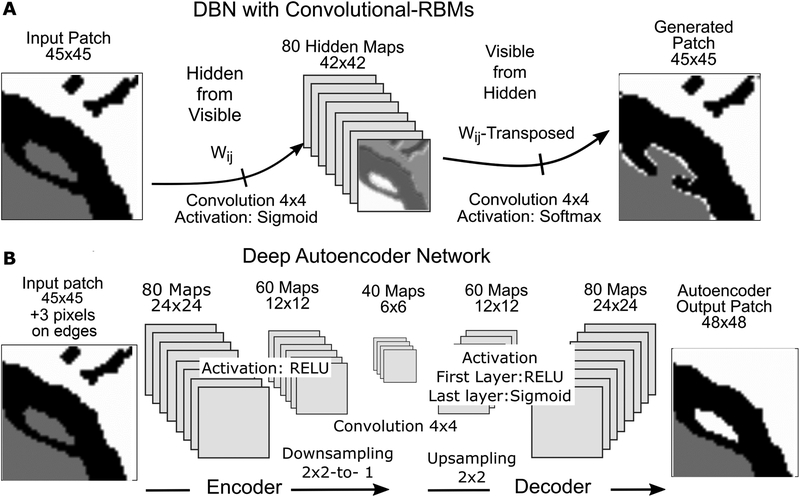
Figure 5 -.
Pre-training architectures for initializing weights to the first DNN layer. (A) A 2-layer Deep Belief Network (DBN) is an unsupervised ML architecture implemented as a Bayesian network of convolutional Restricted Boltzmann Machines (cRBM) in the inner, hidden layer. Weight tensor W is updated so that it maximizes the probability of local features in the generated image to have come from the presented inputs. We bias the pre-training by introducing patches from annotated, ground-truth images, although this is not a requirement. Final weights to the hidden layer are then re-used as the initial set of weights for the input layer of the deep neural network (DNN). (B) Alternative pre-training architecture using a fully supervised DNN as the initialization stage to the main DNN workflow. It represents a de-noising encoder/decoder where convolution & downsizing reduce the input image to one where certain statistically marginal local relationships among pixels (like noise and rare artifacts) are lost with downsizing to a 6×6 element feature map. This feature map is then decoded back, by a mirror of the encoding architecture, to scale up to a map connected to the corresponding annotated output patch. Again, the weight tensor W to the first inner layer is reused for initializing the input layer of the main DNN. It contains weights to the full 48×48 arrays (downsizing step from 48×48 to 24×24 element maps not shown). All image samples in (A) and (B) are from actual pre-training experiments.
In unsupervised, generative 2-layer RBM networks (also known as belief networks or deep belief network (DBN) when multiple layers are used), the input field is connected to a block of “hidden” maps of convolutional RBM elements, (Fig. 5A). Each node within the RBM is restricted to convolution of a 4 × 4 pixel kernel over the input fragment. No lateral connections are allowed between elements within each 2-d map. The convolution is mapped by a sigmoid function into probability of activation of the corresponding node in each hidden map. Those maps in parallel connect to a single output 2d array of the same size, where a “best match” or strongest belief of the given input generates the output. The connection weights to both layers are learned after forward and backward updating steps, using probabilistic sampling, for large numbers of presented input patches35. The structure represents a Bayesian network, computing and learning the likelihood that the observed output was generated by the given input as prior. After many examples, activation probabilities of hidden units attain some stationary distribution. When pre-training using these structures, we are presenting a slightly modified, annotated, ground-truth version of the image fragments at the input, visible layer, to bias the learning towards weights that would resemble better the ground truth forms. Scattered noise and small artifacts, obtained from the actual interim images, were added to those patches as described above. Having such synthetic input is not a requirement, but its inclusion in the training set is advantageous because it improves training convergence. Comparable improvement should be expected if fragments are generated directly from interim pre-segmented image sets.
A de-noising auto-encoder (DAE) architecture (Fig. 5B), as a pre-training stage, represents itself a full convolutional DNN network, implemented in a supervised workflow. It uses convolution + sub-sampling with local de-noising criteria to compress the whole input fragment down to a 6 × 6 map, thus encoding dominant local relationships on a small scale. The resulting compressed map is then used to decode the presented input, by up-scaling the maps to the full fragment size. Using the input weights from such a fully trained, converged DAE as input weights in the main DNN can be seen as adding a de-noising layer to the main DNN. Although the DAE is computationally more massive than the DBN, we benefit from using the same computational environment as that in which the main DNN is implemented, which simplifies its development. This architecture allows an efficient workflow in terms of overall performance, flexibility of implementation and modification, and computational efficiency. This way, all computations reuse the same set of input patches prepared for one working set of images. Both DNNs, pre-training and main network, use the same convolutional and sub-sampling layers21 (More detail on the architecture and actual implementation of de-noising constraints in pre-training DNNs can be found in Vincent et al.34). We have implemented the DAE architecture shown in Fig. 5B with the layer structure as illustrated. Input patches of 45 × 45 pixels were padded with 3 additional pixels to adjust the size of the maps in downsizing and upsizing. Binary pixel representation was used: (1,0,0) – myelin, (0,1,0)-axon, (0,0,1)-background. Convolution was uniformly done with a 4 × 4 kernel, using a stride (or pace) of one pixel, while max-pooling used a 2 × 2 window. The number of maps per layer is (80,60,40,60,80) with connection dropout rates of (0.5, 0.33,0.33,0.33,0.33,0.5) at each step, respectively. Random dropout of connections and neural elements between layers adds some stochastic sparsity, which perturbs the weight tensor, improving the gradient-based learning by preventing overfitting36. Linear node activation function ReLU F(x) = x+ = max(0, x) is used in all layers except in the last (decoding branch), where sigmoid activation f(x) = 1/(1 + e−x) was used. DAE training typically runs in a single epoch.
2.5.2. Deep CNN architecture (main segmentation flow) and training –
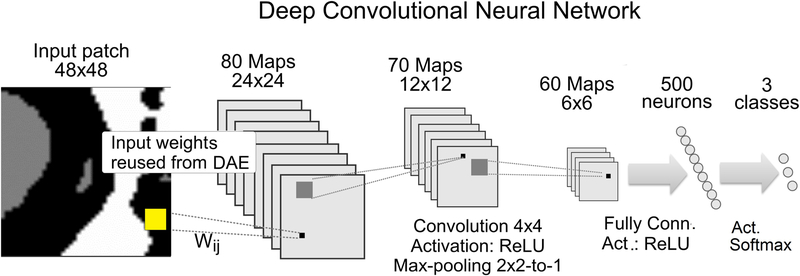
The main segmentation workflow consists of a two-stage structure, where we train a DAE and reuse the input weights to initialize input weights of a 3-layer CNN, (Fig. 6). The CNN architecture in Çiresan et al.21 was used as an initial model network. It takes a 45 × 45 pixel input patch to predict the value of the central pixel. Three convolutional layers use 80, 70, and 60 feature maps each, with a uniform 4 × 4 convolutional kernel, [2×2 → 1] max-pooling layer. After the last convolution, 60 feature maps of size 6 × 6 are fully connected to a single layer of 500 neurons that vote for the class of the central pixel. The network was trained using Adadelta learning rate optimizer37. ReLU activation function in all layers, except at the output classifier, where the probabilistic softmax activation was used, (xi) = exp(xi) / Σj exp(xj), j = 0,1,2. . k, in which the sum is over all instances so that Σi f(xi) = 1.
Figure 6 -.
DNN Architecture. Deep convolutional neural network (CNN) architecture for improved segmentation is composed of three layers of convolution mapping & max-pooling to blocks of 80, 70 and 60 feature maps subsequently. The last convolutional layer connects fully to output layer which vote for the class of the central pixel of input patches. See text for more details
A processing batch size of 500 input-output pairs was used, and their back-propagation offset was averaged to produce a single correction of the weights. Thus, the same batch size was used for both pre-training and the main DNN. Dropout rates of 0.25 for convolutional layers and 0.5 for the fully connected layer were used in training. The training typically converged quickly within a single epoch and then was stopped, since continuing it only increased the variance and worsened generalization of the model. The model was implemented with the Keras framework, running on a Tensorflow backend on an Intel Core i7 workstation equipped with a single NVidia GeForce GTX1080 (8GB) or GTX980 (4GB) GPU processor.
Of the thirty 2048 × 2048 pixel images in a working set, twenty were fragmented for generating training input, 5 were used for validation, and 5 images constituted the testing set. Of the full set of 84 million different training patches (~4 million per image), ~ 6 million were randomly selected for training. Ten percent (approximately 2 million) of all the patches from validation and testing subsets were randomly selected to validate error convergence and to do the intermediate testing. In a typical segmentation study to achieve replicability of the DNN accuracy, we suggest evaluating the tools with two or more sets of non-overlapping images, to detect whether the performance shows notable sensitivity to the input data.
2.6. Measurement of axon and myelin size (Ray-measurement tool) –
The segmentation protocol is supplemented with a measurement routine, specifically tailored to address the measurement of myelinated axons in nearly random orientations. The ray-measurement tool (RMT) evaluates the intersection, at each pixel of the axon-myelin boundary, of a radial ray from the centroid of an elliptical approximation of the axon-myelin boundary. Similar radial scanning of fiber ROIs has been proposed for myelin segmentation itself within a semiautomatic protocol for EM images14 and an automated protocol for coherent anti-Stokes Raman scattering (CARS) microscopy38, Both reports were restricted to fairly circular profiles in fiber bundles sectioned transversely.
Our ray measurement procedure assures that we obtain the maximum possible number of valid radial measurements of axon and axon + myelin for each fiber. The tool selects only measurements that fulfill a set of conditions that exclude possible errors due to structural ambiguity.
The axonal centroid, the axonal minor axis, and the axon-myelin boundary are determined in ImageJ by setting an upper and lower threshold of grey value 2 (axon) and running “analyze particles” with particles touching the edge excluded, and boundary co-ordinates are written to the ROI Manager Tool in ImageJ. They are extracted using JavaScript code that we run as an ImageJ plugin. We then define a set of rays extending from that centroid through each point on the boundary. Along each ray, we measure axon radius and myelin thickness. Multiple stopping conditions applied to each ray measurement robustly detect myelin holes, contacts between adjacent sheaths, and myelin ruptures. Measurements along a ray meeting one or more specific stopping conditions are disqualified (Fig. 7). Measurements can also be restricted to certain azimuthal angles around the minor axis if the ratio of major to minor axis is above a certain value, indicating a very oblique cut. However while the minor axis is the only true diameter of an axon cut obliquely, oblique cutting should not affect the ratio of axon radius (A2) and fiber radius (A2 + M) along any ray (and in general g = A2/(M + A2) ). The final output measures for each ROI (axon) are the minor axis of the axon (which we define as its diameter) and the g-ratio derived from the average of the g-ratios measured on all non-excluded rays. Myelin thickness (which is also measured along each valid ray) can then be defined more rigorously as:〈M〉 = (minor/〈g〉)(1 − 〈g〉), where 〈g〉 represents g-ratio averaged across all of the valid rays for that fiber.
Figure 7 -.
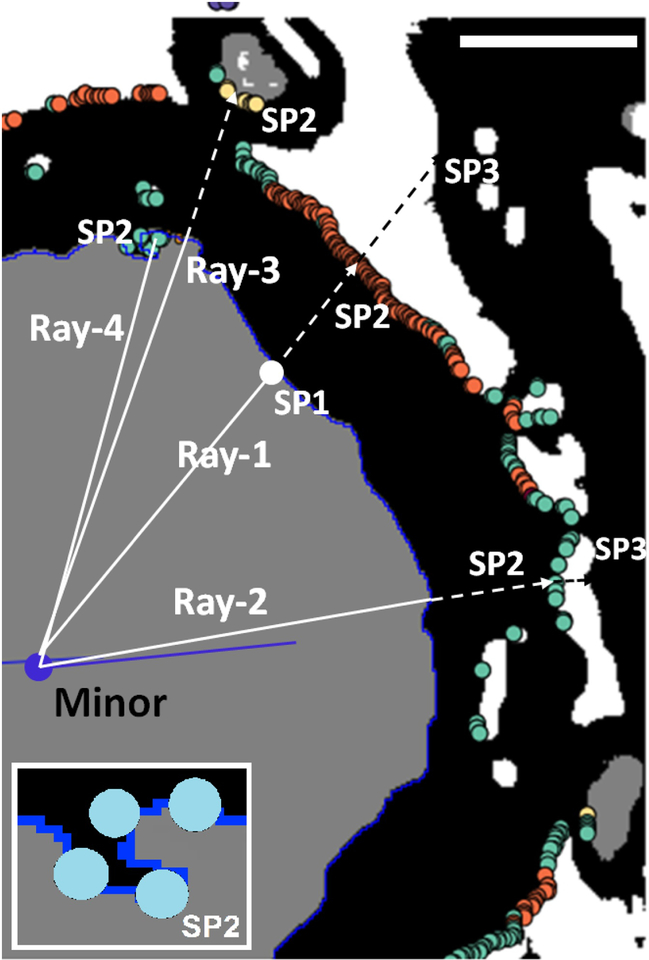
Examples of ray measurements. The grey area is part of an axon as segmented by the deep neural network (DNN) and here defined as a region of interest (ROI). Black represents pixels segmented as myelin by the DNN. White lines are examples of potential ray measurements. The ROI boundary (blueline) is obtained from the ROI Manager Tool in ImageJ as a set of pixels representing the outer edge of the axon. The center of the axon (blue circle) is computed as the centroid of the ellipse most closely approximating this boundary. Three possible stopping points (SP) are defined for each ray originating from the center. After SP1 (stopping-point 1) which is always on the boundary (blue), Ray-1 encounters a background pixel at SP2 (orange) and a myelin pixel at SP3 sufficently distant to qualify the measurements from the centroid to SP1 and from SP1 to SP2 as a valid. Ray-2 encounters background at SP2, but myelin at SP3 and background on SP4 (not shown) which indicates a gap ipn the myelin sheath. Ray-3 encounters axoplasm at SP2 which indicates that the thickness of the myelin includes the sheath of a touching fiber. Ray-4 picks myelin pixels from the same ROI at SP1, SP2 and SP3 (see inset), which indicates an incursion of myelin pixels into the axon. Rays 2, 3, and 4 all represent discarded measurements. Scale bar (upper rignt corner) = 1 micron.
In addition to setting inclusion criteria for ray measurements, we formulated additional conditions, which serve to detect myelin assigned to more than one axon, which is not measured. These also disqualify spurious ROIs, which RMT recognizes by: (i) A very high ratio of myelin thickness to axon size. This could result from the inclusion of myelin from touching fibers in the measurement of myelin thickness. Although most rays passing through two fibers would be eliminated by the stopping conditions (see Ray-3 in Fig. 7), the ray would escape exclusion if it did not pass through a second axon. An unrealistically high ratio of myelin thickness to axon size could also appear in the case of a fiber whose longitudinal axis runs parallel to the plane of section but passes above or below it. (ii) A large percentage of rays for one ROI suggesting extensive artefactual disruption of the myelin sheath, also disqualify the ROI. For definition of the full set of single-ray conditions in the RMT, including the additional conditions applied to whole ROIs, see Supplementary Information 1. As output, the RMT stores all the ray measurements for each ROI together with other ROI measures, in separate text files for each image. The script also generates the g-ratio data for the scatter plots of Fig. 9.
3. Results
Of the three working sets of images, we trained the DNN tool using the first set of 30 images of prefrontal white matter (WM_Set_01) while we tested and evaluated the segmentation and measurement tools on all three sets: WM_Set_01 and WM_Set_02, representing white-matter, and the third, ON_Set_01, from optic nerve, each containing 30 images. The DNN tool was trained only on fragments from a subset of 20 images from WM_Set_01, as described above. DNN segmentation performance was then tested on all three complete sets. All presented DNN segmentation results were obtained with pre-training of feature maps.
3.1. DNN segmentation performance –
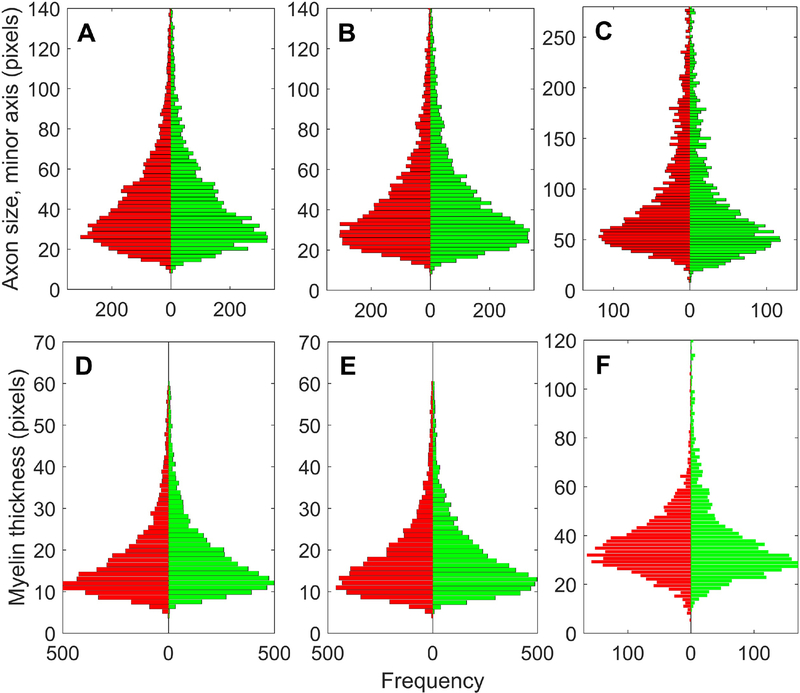
First, DNN performance was evaluated by comparison of DNN and Interim images with the corresponding Corrected images. The averaged pixel-based accuracy of DNN segmentation was superior to the interim image, improving from 64% in the Interim images to 86% – 92% after DNN segmentation. (See Discussion and Supplementary Information 2 for comparisons with other segmentation tools.) We observed that targeted attempts to increase input sample to improve accuracy of one class often reduced accuracy of another class. For example, increasing the sample size of background debris fragments deteriorated classification of axon pixels close to the boundary. Therefore, we do not rely only on the averaged pixel-based accuracy for validating performance. Fig. 8 shows the quality of segmentation by comparing histograms of axon sizes and myelin thickness on all fiber ROIs. On both PFCWM sets, the DNN demonstrated almost equal performance, producing only a 1%–3% gap between the number of ROIs identified in the DNN segmentations and the Corrected segmentations in each set. This is illustrated in the shape of both pairs of histograms in Fig. 8A and Fig. 8B for axon size, and in Fig. 8D and Fig. 8E for myelin thickness. The third 30-image sample, from the optic nerve, was introduced to challenge the segmentation capability of the DNN on a somewhat different white matter cytoarchitecture, with notably different frequencies of axon, myelin and background classes of pixels.
Figure 8 -.
Comparison of DNN segmented images (green) with Corrected (expert-annotated) images (red). (A) Histograms of axon sizes, in pixels, measured as the length of the minor axis of the ellipse fitted within the ROIs obtained by thresholding on pixel class Axon (ImageJ - Analyze Particles) on the first set of 30 images (WM_Set_01), each 2,048 × 2,048 pixels. Green bars give the counts from images segmented by the deep neural network DNN workflow trained on the same set WM_Set_01, while the red bars represent the same image set annotated by experts after pre-segmentation and post-processing. (B), (C) Same as (A) but on different sets of 30 images that the DNN tool has not seen before, coming from (B) the same cases sampled in the same PFWM area (WM_Set_02), and (C) optic nerve (ON_Set_01). (D),(E),(F) Histograms of myelin thickness, in pixels, as directly measured by the ray measurement (RM) tool on the same sets used for (A),(B) and (C).
The gap in number of ROIs from DNN and CORR segmentations increased to 5% when segmenting the ON set. This could be the result of a similar number of errors on images with less than half the total number of fibers. Nonetheless, the main features of the histograms are preserved (Fig. 8C and Fig. 8E). Such performance was expected, because the DNN learns very local features, since it is trained only on 45 × 45 pixel fragments. On such a fine scale, it appears that the extracted features represent common patterns that are present in different regions of white matter.
Statistical similarity of the histograms was checked by the chi-squared distance measure39, where xi, yi represent the frequency counts of ROIs in n bins of each histogram, within DNN and CORR images respectively. The denominator (xi + yi) has been chosen so that the distance measure is symmetric, dxy = dyx, with the second index representing the reference set. Using yi as denominator (analogous to the Chi-square test) gives roughly twice larger distances, for similar data. The following distances, as percentages, were obtained on normalized histograms Σn = 1, for WM_Set_01: daxon = 0.85%, dmyelin = 4.6%, for WM_Set_02: daxon = 0.56%, dmyelin = 4.0%, for ON_Set_01: daxon = 1.78%, dmyelin = 7.3%.
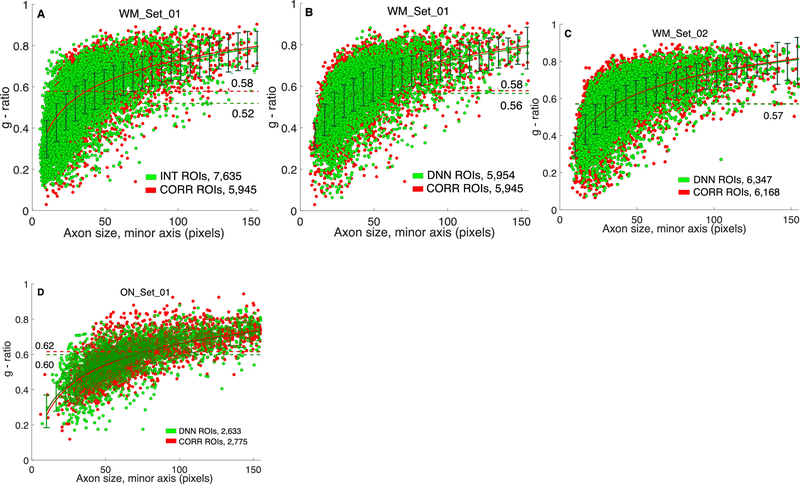
Measurement-oriented DNN performance is shown in Fig. 9, which contains scatter-plots of g-ratio plotted against axonal diameter. Both measurements are derived by the RMT as described above.
Figure 9 -.
Axonal g-ratio estimated from different segmentations. Scatter-plots of average g-ratio for each ROI: , where ai is axonal radius along ray-i, and mi is myelin “length” along the same ray-i, where ray-i does not meet any exclusion criterion and n is the number of valid measurement rays for the ROI, are compared between segmented (green) and annotated (red) sets. The number of ROIs produced after different segmentation and filtering conditions used in the Ray Measurement Tool are given in the lower right field of each plot, (A) On WM_Set_01 of 30 images, with ROIs obtained from the interim version of the images, prior to deep neural network (DNN) segmentation. (B) with DNN-segmentation of the same WM_Set_01, (C), (D) same comparison as in (B), on WM_Set_02, and ON_Set_01 from optic nerve, respectively, which the DNN workflow had not seen. The same DNN tool, trained only on WM_Set_01, was used in all experiments. Log fit (red and dark green solid lines in all plots) describes best the dependence of g-ratio on axon size, when looking for the most uniform variance (error-bars) over the whole range (in (A), 〈g〉 = 0.16 log(A) – 0.22), where A is the axon diameter. Mean values of g-ratio over all ROIs, are given on each plot next to dashed lines corresponding to the mean. Relative errors of the mean, |MEANseg – MEANcorr|/MEANcorr are: 10,17%, 2,96%, 0.74% and 2.83% for (A)-(D) respectively. Pre-segmentations and clean-up post-processing were done using Visiomorph (see text for details).
The eventual goal is to compare subjects for effects of independent variables (e.g., age, sex, diagnosis) on axonal diameter, myelin thickness, and g-ratio. It is important to confirm that, compared with expert-annotated (CORR) segmentation, the DNN reliably reproduces the dependent variables on a subject-by-subject basis. Such inter-rater reliability can be quantified by the intraclass correlation coefficient (ICC)40. For each of the 3 image sets, we used SPSS to perform three univariate two-way ANOVAs with rater (CORR or DNN, each followed by RMT) and subject as independent variables, and axon diameter, myelin thickness, or g-ratio as the single dependent variable. We then used the values from the ANOVA summary to compute ICC(2,1) which tests for agreement of the raters, i.e., whether CORR and DNN are interchangeable40.
For comparison, we determined the ICCs for CORR and INT (both followed by RMT) as the dependent variables. We find (Table 1) excellent agreement between DNN and CORR, with all but 2 values above 0.9. Agreement between INT and CORR is much weaker, with good agreement only for myelin thickness. Measures of consistency, ICC(3,1) are stronger yet (data not shown). Fig. S3 in Supplementary Information 3, displays mean and confidence intervals by subject for all dependent variables. Although axon size was averaged over qualified ray measurements within azimuthal range around the minor axis of the best fitted ellipse, and should be very close to the minor axis, we present ICCs for both quantities as those are computed independently.
Table 1 -.
Interclass correlations comparing measurements on DNN or INT segmentation with annotated, CORR dataset, with the cases as independent variables. See ref. [39] Psychological Bull. for definitions of different interclass correlation coefficients. CORR - corrected, DNN - deep neural network, INT - interim.
| Dependent var. in different image sets | ICC(2,1) DNN vs. CORR | ICC(2,1) INT vs. CORR | |
|---|---|---|---|
| WM_Set_01 | axon | 0.98 | 0.53 |
| myelin | 0.92 | 0.90 | |
| minor | 0.98 | 0.45 | |
| g-ratio | 0.70 | 0.07 | |
| WM_Set_02 | axon | 0.97 | 0.54 |
| myelin | 0.98 | 0.97 | |
| minor | 0.98 | 0.45 | |
| g-ratio | 0.96 | 0.30 | |
| ON_Set_01 | axon | 0.59 | 0.12 |
| myelin | 0.96 | 0.88 | |
| minor | 0.47 | 0.32 | |
| g-ratio | 0.91 | 0.23 | |
We achieved the best segmentation and measurement performance with the DNN tool trained on WM_Set_01, while segmenting the WM_Set_02 (Fig. 9C). Comparison of Fig. 9A with Fig. 9B illustrates the gain in segmentation accuracy between the preliminary (INT) segmentation and the subsequent improvement by the DNN, with the RMT applied identically to both. DNN improved segmentation, reducing the gap in mean g-ratio by 71%. The major difference is that the DNN reduced the number of spurious axons from 1,690 (22% of observed) to 9 (0.015% of observed). The same DNN tool performed reasonably well on an image set from optic nerve, ON_Set_01 (Fig. 9D) where cytoarchitecture differs, while fine structure presents common local patterns of axon-myelin and myelin-background boundaries. These results suggest that in a typical application on electron micrographs of myelinated fibers, a much smaller number of images need to be annotated for training, as long as the bulk of the images share comparable microscopy-related parameters. For comparison, previously reported25 area similarity metric (AS) averaged over all axons, defined using the Sørensen–Dice coefficient as AS = 2(A ∩ B)/(A + B), where A and B are axon areas in pixels, gave 0.966 and 0.982 for WM_Set_01 and WM_Set_02 datasets respectively.
3.2. Pre-training of feature maps
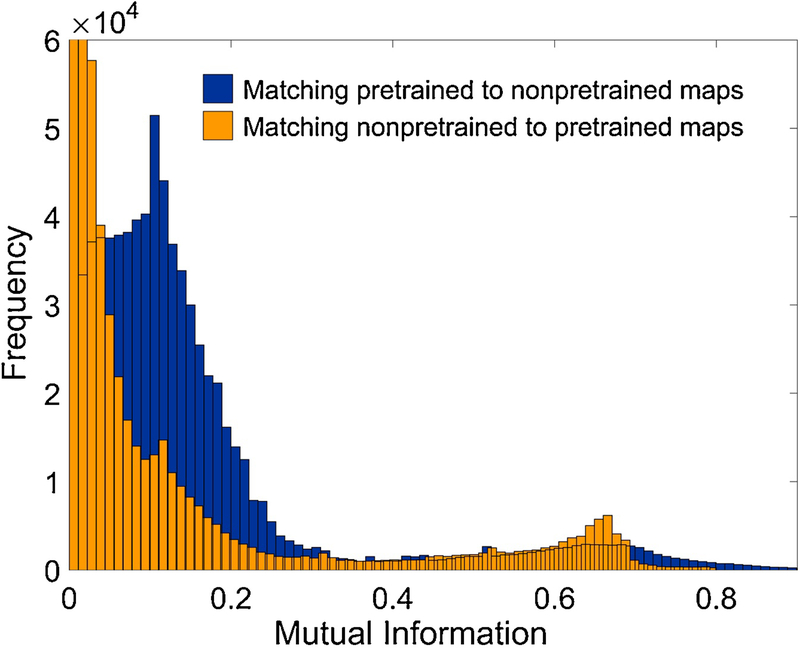
Fig. 10 illustrates the benefit of pre-training of the weights to the first layer of DNN feature maps, in this example using DEA architecture (see Materials and Methods, Pre-training of feature maps, Fig. 5B). Mutual information (M) between a pair of maps was used as a statistical measure of shared content between the two DNN layers of activated maps, for a certain volume of input fragments. M was computed over two sets of 80 feature maps, 48 × 48 pixels, of the initial hidden layer of the DNN (prior to first max-pooling) – one set of maps with randomly initialized weights from input fragment to the maps, while the other obtained after pre-training the weights with the DEA tool as described above. A test set of 10,000 randomly sampled input fragments were used for map activation. Pixel values in activated feature maps represent real-valued random variables, because the initial discrete values (of the three classes) are mapped through convolution followed by weighted ReLU activation. Fig. 10 shows the histogram of maximal M when matching an activated map from either set to all maps in the other set (for example, a map from the pre-trained block matched with all 80 from the random block, for 10,000 input image fragments). The M value for each pair of maps (X, Y) as random variables for a single given input fragment is computed using:
| (1) |
where we calculate joint probability p(x, y) and the marginal probabilities p(x), p(y) and sum over all elements of a feature map, which corresponds to single pixel activation by one input patch (see Supplementary information 4 for examples of feature maps).
Figure 10 -.
Pre-training of DNN layer-1 weights. Blue histogram counts the maxima of mutual information (M) over all pairs (PT, RND), PT - map with pre-trained weights, RND - map with randomly initialized weights, where the pre-training has been done using de-nosing auto-encoder (DAE) architecture. The yellow histogram shows the counts of M in the opposite case (RND, PT) when for each randomly initialized feature map, the maximal M match has been searched within PT maps.
Notably higher counts for larger mutual information in blue histogram M (pretrained matched to non-pretrained), indicates that activated layer-1 maps of pretrained layer share more information with input fragments, than the maps in non-pretrained layer.
4. Discussion
4.1. Validity
Invariance to reflection or rotation –
The training images are presented at input as 45 × 45 pixel, (500 × 500 nm) fragments, centered near the axon-myelin boundary. They rarely come close to containing an entire cross section of a myelinated axon. Therefore, since all center points around the boundary have an equal probability of being selected, it follows that the orientations of the patches are also random; e.g., from left to right bkg-myelin-axon and axon-myelin-bkg are equally likely.
Near invariance to enlargement or reduction –
Input fragments of 45 × 45 pixels typically carry part of the fiber structure centered along the axon-myelin boundary, to focus the learning on the neighboring relations of the central pixel. Even in statistically rarer cases of very small fibers, the fragment will not show most of the fiber ROI because with the biased sampling (see Materials and Methods), the fragment will be centered at the axon-myelin boundary and capture part of the background as well, because fibers typically have proportionally thick sheaths. With such sampling, additionally augmenting the geometrical forms captured in the fragments using any affine transformation does not introduce any new geometry or neighboring relationship, so it should not alter context-based learning. If the toolbox is applied to: (i) lower magnifications images and fragment size containing more than one fiber, or (ii) in cases where not many fiber ROIs are available in the whole working set, then augmenting the input dataset with rotation, reflection and stretching could generate more data without additional annotation cost, while achieving a certain degree of robustness to such deformations.
The critical dependence of machine learning on the quality of the input data makes the pre-segmentation and the initial post-processing steps necessary. Any initial segmentation (we compared customized ImageJ Trainable Weka Segmenter and Visiopharm’s VIS segmenting tool, see Supplementary Information 2 for illustrative example) leaves large areas of background misclassified as axons, and leaves various structural details, labeled as myelin or background, inside many axons. This suggested that either for producing the annotated set, or for producing a working/ training set, an initial cleanup, primarily of the axons, is necessary.
Any approach selected requires defining axonal outer contours (or myelin internal contours, 1 pixel centrifugal, which is what we actually detect in the pre-segmentation step) as ROIs. This is because, in the true structure, without artifact, myelin and background surrounding one axon are often contiguous with their counterparts surrounding adjacent axons. Even with perfect segmentation and without artefact, not all myelin is obviously associated with particular axons. In that perfect case, the myelin thickness should be the shortest of all distances from each point on the outer contour of an axon to the nearest non-myelin pixel outside of that contour. If such nearest pixel is classified as axon, some portion of the measured myelin thickness belongs to that axon (shared myelin, Fig. 7), and since the boundary between apposed myelin sheaths cannot be detected without much greater magnification, we discard the measurement. If the nearest non-myelin pixel is background, the measurement is acceptable. It could be possible to develop a strategy in which measurement begins at the boundaries between myelin and background, but it appears to us that such a strategy would be much more complicated, with only the one possible advantage of interpolating boundaries between apposed myelin sheaths.
Defining axon contours makes at least the cleanup of the interior straightforward. We formulated and tested a software-agnostic routine for the initial cleanup based on topological contour hierarchy (See: Supplementary Information 5) over pre-segmented images, which, combined with additional conditions, also manages to clean the background to a large extent. Some additional conditions detect spurious ROIs in the form of closed regions, surrounded by the outer myelin boundaries of several touching fibers (Fig. 4C), and allows them to be cleaned of any form of misclassified patterns and particularly of debris initially classified as myelin. Different processing environments should offer different sequences of steps that will produce comparable effects. For illustration of comparable performance of such clean-up in terms of g-ratio measurements, see Fig. S5, Supplementary Information 2, showing the same g-ratio scatter-plots (as in Fig. 9C) and axon size and myelin histograms (as in Fig. 8B and 8E) from the full experiment on ML_Set_01 processed with a contour hierarchy approach for cleaning. Compared with the corresponding plots in Fig. 8 and Fig. 9, obtained using pre-segmentation and cleaning in Visiomorph, they show satisfactory reproducibility. The main challenge in this computational study, the structural complexity of deep white matter in EM images, makes the quality of final segmentation dependent on pre-segmentation and the initial cleanup. In different applications of the suggested workflow, the investigator will decide on the benefit of such steps, depending on the extent to which the local features have been preserved, so that annotation is straightforward and accordingly the training of convolutional network is unambiguous.
4.2. Utility
The full image processing and computational protocol have been tailored to come as close as possible to axon size and myelin thickness measured in annotated images. For that reason we used neither pixel error which is too general and very variable among the three pixel classes, nor any topologically defined accuracy measure like warping error17. Those do not explain accuracy of single linear measures like thickness, but rather reflect matching of shapes and boundary relationships. A critical feature of myelin in EM data is that the contrast on both myelin boundaries is almost always good enough to have the ROIs well defined, so most of the main causes of fiber damage, like myelin holes, ruptures and spurious patterns do not notably damage the boundary. This has guided us in formulating the ray measurement tool to complement the segmentation tool.
As mentioned earlier, after observing saturated performance of classical ML approaches in segmentation of myelinated axons, either using pre-defined feature extractors or pixel clustering, few studies have applied deep CNNs in histological studies of peripheral nerves. Mesbah et al.19 report comparison of segmentation performance of two deep CNN architectures with several traditional parametric feature extraction methods, in two- and three-class images of mouse spinal cord. Naito et al.25 used ML clustering for two subsequent segmentations, and then used deep CNNs for identifying and outlining fiber ROIs, combined with splitting of fiber clumps. Leveraging on their previous semi-automated workflow15, Zaimi et al.41 have developed a deep learning protocol and tool trained on low-magnification images of mouse spinal cord and splenium of the mouse corpus callosum, and they report additionally results from a single image of macaque corpus callosum. Apart from the generic CNN segmentation architecture for classifying the central pixel21, U-net architecture, or encoder-decoder (or downsampling-upsampling) architecture has also been tested19, 41 where the standard deep CNN track of reduction of feature maps is followed by upsampling or reconstruction of the whole set of image fragments. Faced with the enormous structural complexity of deep white matter in primate brain, while aiming at extracting very local boundary features, we do not think that learning to decode a whole input fragment can add more generalization capacity in statistical, measurement-oriented studies. Although typically the pixel classifier is central in quantitative microscopy of myelin, there are many more study- specific steps and tools, essentially producing very different protocols that are difficult to compare. From that perspective, despite the similarity of our CNN architecture and others already reported, we suggest that overall usefulness should be judged based on how the specific steps address specific imaging issues, and their relevance to the specific morphometry in images typically coming from unique experimental designs and microscopy setups.
The critically-minded potential user may still dwell over the utility and feasibility of our suggested pre-processing, which starts with a mapping of the EM originals into an interim, segmented dataset, which our goal is to improve. We emphasize here that our measurement ambitions take us to a 3-class segmentation problem, where the central feature, the myelin sheath, appears in the same gray-scale and contrast range as major artifacts. The three classes appear typically in direct apposition at varying scale due to varying size of myelinated axons and local variability of form in very large fibers. This leaves us with no automated ML approach that can retain the interim version images with the major structural artifacts and debris removed. For example, application of U-net architectures, attractive due to much less redundant computation compared with central-pixel segmentation, are essentially ambiguous even in 2-class problems of detecting cell-to-cell boundaries when complex forms appear on the boundary, e.g., synaptic structure42. We therefore suggest the preliminary segmentation as a necessary step, focusing on the measurement oriented, morphometric features of myelination for final adjustments of the workflow including the interventions within the RMT routine.
The RMT is designed so that after we generate the ray measurements on DNN segmented images, additional conditions detect heavily damaged and spurious, non-fiber ROIs as already described (for details see Supplementary Information 1). Table 2 lists the ROI counts at different stages of processing for comparison with the annotated dataset.
Table 2 -.
Total ROI counts at different stages of segmentation workflow. Thresholding and assigning of ROIs at axon myelin boundary is done on preliminary segmented images, Interim dataset, for control purposes. Improved segmentation reduces the number of ROIs in white matter images. After measurements by the ray measurement tools (RMT), a final cleanup of non-fiber ROIs and notably damaged fibers is obtained by suitably formulated conditions on exit from the RMT. See Supplementary Information 3, for specification of additional conditions and examples of spurious ROIs. Counts for all three image sets were obtained using deep neural network tool trained only on 20 images from WM_Set_01.
| ROI number / Image set | WM_Set_01 | WM_Set_02 | ON_Set_01 | comment |
|---|---|---|---|---|
| ROI num. at INTERIM stage | 11,277 | 10,977 | 3,932 | After pre-segmentation and post-processing |
| ROI num. in DNN segmented | 7,897 | 9,379 | 6,762 | |
| Num. ROI discarded in RMT by ray measurements | 522 | 1,661 | 2,122 | ROIs are discarded due to no usable rays |
| Num. ROI discarded in RMT by add. conditions | 1,421 | 1,370 | 2,017 | |
| Final ROI num. after RMT | 5,954 (7,635)* | 6,347 (7,851)* | 2,623 (3,000)* | * remaining ROIs when RMT is applied at INTERIM |
| ROI num. CORRECTED data | 5,945 | 6,168 | 2,775 | ROIs in the annotated set |
Written in JavaScript as a plug-in for ImageJ, the RMT is connected to ROI Manager Tool and ImageJ Measurements in a manner fully transparent to the user. It thresholds at axon edges, providing ROI border at axon-myelin boundary, and the other ROI parameters like ROI area, centroid coordinates of the best fitted ellipse, minor/major axes, are all fetched from ImageJ measurements. Here, we threshold for the second time on DNN outputs, as we did initially on the INT images, which was for the purpose of region-constrained sampling of the input patches for the ML workflow. A separate workflow window receives the inputs from the user, activates the measurements and generates the output measures.
4.3. Feasibility
Our segmentation protocol is computationally intensive. Extensive testing of different variants of algorithms for the different steps complementing the DNN segmentation has led to the design of the final workflow. In addition to the DNN segmentation, two additional, computationally involved steps: (i) cleaning of pre-segmented images prior to DNN segmentation, and (ii) pre-training of DNN feature maps, provided major improvements to the protocol. The workflow was developed and executed on an Intel Core i7 class workstation with 16GB RAM, equipped with NVIDIA GTX-1080/4GB GPU, using standard development environments like Keras with Tensorflow backend. Table 3 shows the typical execution times for 30-image 2,048 × 2,048 pixel 8-bit images. It is important to remind the user that preparatory steps (shaded yellow) are performed only once for a working bulk of images.
Table 3 -.
Examples of execution times. Note that the yellow shaded steps are done only once for a given bulk of working images. The workflow here starts with an interim (pre-segmented - post-processed) image-set. Image size and fragment size are the critical parameters determining the time needed for computations.
| Processing step | Description | Execution Time |
|---|---|---|
| Sampling of input fragments | Creating 6.3M input fragments, as number arrays, 5.8M fiber, and ~0.5M debris fragments | 5.2 min |
| Creation of DNN fragment DB | Fragments are allocated in batches of 500K, as RAM DB, to be accessed efficiently between CPU/RAM and GPU. More GPU RAM and using max. batch size shorten the execution | 22.4 min. |
| Creation of DEA fragment DB | Same as above, with additional space allocated to CORR fragments | 33.7 min. |
| DEA pre-training | Single epoch, including validation | 61.8 min. |
| DNN training, main flow | 6.3M fragments, single epoch, including validation | 36.6 min |
| Producing DNN segmented set | Recreation of 3-class DNN-segmented TIFF image in the native 2,048 × 2,048 pixel resolution. | 15 min / image |
Apart from ImageJ, used in the measurement routine and user-selected tools (e.g., ImageJ Weka, Visiomorph) for the initial segmentation and cleaning no additional software is needed besides the tools provided within the software package. All code libraries used within the DNN design and measurement scripts are public. The whole package is freely available on https://github.com/K5rovski/dnn_seg. Description of all processing steps is provided in Supplementary Information 6 – Workflow Description. Descriptions of pure software details accompany the code.
Stronger GPUs would allow higher batch-sizes, and more RAM and SSD drives will allow processing whole data sets without HDD access, which will altogether shorten total execution time of the training phase. Duration of the initial image fragmentation and final generation of output images depend linearly on the size of working image sets and are typical for all protocols doing pixel-based processing and not specific or excessive for our measurement-oriented segmentation. Depending on the application, imaging design, and final appearance of the myelinated fibers, some steps could be modified or excluded.
We have demonstrated the generalization capacity of a trained DNN to segment myelinated fibers in images it has not seen. Since the histological appearance of myelin is similar in most areas of cerebral white matter, we assume that our solution would easily generalize to most other areas of cerebral white matter. Thus, the proposed computational cost and complexity matches well the challenge of accurate segmentation of structurally complex human cortical white matter in autopsy samples.
Supplementary Material
Highlights.
Concatenated machine learning protocols improve segmentation of myelin and axons.
Convolutional networks learn to segment the central pixel of small input fragments.
Automated routine assigns radial measurements to each axon and its myelin sheath.
Statistically, results are interchangeable with those of a trained human.
Acknowledgements –
Authors acknowledge the initial guidance on DNN implementation using the common GPU software environments provided by Gjorgji Strezoski and Ivica Dimitrovski, from the Faculty of Computer Science and Engineering, Ss. Cyril and Methodius University, Skopje.
Funding: This work was supported by National Institute of Mental Health and the Fogarty International Center (MH098786, MH060877, MH064168).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Mohseni S, Badii M, Kylhammar A, Thomsen NOB, Eriksson KF, Malik RA, Rosen I, Dahlin LB: Longitudinal study of neuropathy, microangiopathy, and autophagy in sural nerve: Implications for diabetic neuropathy. Brain Behav 2017, 7:e00763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Schmidt RE, Bilbao JM: Diseases of Peripheral Nerves. Greenfield’s Neuropathology. Edited by Love S, Budka H, Ironside JS, Perry A. Ninth ed Boca Raton: Taylor and Francis Group, 2015. p. 1418. [Google Scholar]
- [3].Liewald D, Miller R, Logothetis N, Wagner H-J, Schüz A,: Distribution of axon diameters in cortical white matter: an electron-microscopic study on three human brains and a macaque. Biol Cybern 2014, 108:541–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Michailov GV, Sereda MW, Brinkmann BG, Fischer TM, Haug B, Birchmeier C, Role L, Lai C, Schwab MH, Nave KA: Axonal neuregulin-1 regulates myelin sheath thickness. Science 2004, 304:700–3. [DOI] [PubMed] [Google Scholar]
- [5].Brinkmann BG, Agarwal A, Sereda MW, Garratt AN, Muller T, Wende H, Stassart RM, Nawaz S, Humml C, Velanac V, Radyushkin K, Goebbels S, Fischer TM, Franklin RJ, Lai C, Ehrenreich H, Birchmeier C, Schwab MH, Nave KA: Neuregulin-1/ErbB signaling serves distinct functions in myelination of the peripheral and central nervous system. Neuron 2008, 59:581–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Rasband MN, Tayler J, Kaga Y, Yang Y, Lappe-Siefke C, Nave KA, Bansal R: CNP is required for maintenance of axon-glia interactions at nodes of Ranvier in the CNS. Glia 2005, 50:86–90. [DOI] [PubMed] [Google Scholar]
- [7].Stedehouder J, Kushner SA: Myelination of parvalbumin interneurons: a parsimonious locus of pathophysiological convergence in schizophrenia. Mol Psychiatry 2017, 22:4–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Micheva KD, Wolman D, Mensh BD, Pax E, Buchanan J, Smith SJ, Bock DD: A large fraction of neocortical myelin ensheathes axons of local inhibitory neurons. Elife 2016, 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Duncan ID, Marik RL, Broman AT, and, Heidari M: Thin myelin sheaths as the hallmark of remyelination persist over time and preserve axon function. PNAS 2017, 114:E9685–E91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Marner L, Nyengaard JR, Tang Y, Pakkenberg B,: Marked loss of myelinated nerve fibers in the human brain with age. J Comp Neurol 2003, 462:144–52. [DOI] [PubMed] [Google Scholar]
- [11].Peters A: The effects of normal aging on myelin and nerve fibers: a review. J Neurocytol 2002, 31:581–93. [DOI] [PubMed] [Google Scholar]
- [12].Friede RL: Computer editing of morphometric data on nerve fibers. An improved computer program. Acta Neuropathol (Berlin) 1986, 72:74–81. [DOI] [PubMed] [Google Scholar]
- [13].Auer RN: Automated nerve fibre size and myelin sheath measurement using microcomputer-based digital image analysis: theory, method and results. JNeurosciMeth 1994, 51:229–38. [DOI] [PubMed] [Google Scholar]
- [14].More HLCJ, Gibson E, Maxwell Donelan J. Beg MF,: A semi-automated method for identifying and measuring myelinated nerve fibers in scanning electron microscope images. J Neurosci Methods 2011, 201:149–58. [DOI] [PubMed] [Google Scholar]
- [15].Zaimi ADA, Gasecka A,, Côté D, Stikov N, Cohen-Adad J,: AxonSeg: Open Source Software for Axon and Myelin Segmentation and Morphometric Analysis. Front Neuroinform 2016, 10:37. doi: 10.3389/fninf.2016.00037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Madabhushi ALG: Image analysis and machine learning in digital pathology: Challenges and opportunities. Med Image Anal 2016, 33:170–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Jain VSS, Turaga SC,: Machines that learn to segment images: a crucial technology for connectomics. Current Opinion in Neurobiology 2010, 20:653–66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Busk J: Support Vector Machines for Pixel Classification Application in Microscopy Images. Kongens Lyngby DTU - Technical University of Denmark, 2014. [Google Scholar]
- [19].Mesbah RMB, and Mills S,: Deep convolutional encoder-decoder for myelin and axon segmentation. International Conference on Image and Vision Computing New Zealand (IVCNZ): ieeexplore.ieee.org, 2016. [Google Scholar]
- [20].LeCun YB Y; Hinton G, : Deep learning. Nature 2015, 521:436–44. [DOI] [PubMed] [Google Scholar]
- [21].Ciresan D, Giusti A, Gambardella LM, Schmidhuber J: Deep neural networks segment neuronal membranes in electron microscopy images 2012 Advances in Neural Information Processing Systems (NIPS 2012). Edited by Pereira F, Burges CJC, Bottou L, Weinberger KQ, 2012. [Google Scholar]
- [22].Eickenberg MGA, Varoquaux G, Thirion G,: Seeing it all: Convolutional network layers map the function of the human visual system. Neuroimage 2017, 152:184–94. [DOI] [PubMed] [Google Scholar]
- [23].Krizhevsky A, Sutskever I, Hinton G,: Imagenet classification with deep convolutional neural networks 2012 Advances in Neural Information Processing Systems (NIPS 2012). Edited by Pereira F, Burges CJC, Bottou L, Weinberger KQ, 2012. pp. 1097–105. [Google Scholar]
- [24].Visiopharm Becomes a Technology Leader in Deep Learning and AI Image Analysis for Digital Pathology. Visiopharm 2018. [Google Scholar]
- [25].Naito T, Nagashima Y, Taira K, Uchio N, Tsuji S, Shimizu J: Identification and segmentation of myelinated nerve fibers in a cross-sectional optical microscopic image using a deep learning model. J Neurosci Methods 2017, 291:141–9. [DOI] [PubMed] [Google Scholar]
- [26].Kotsiantis S: Supervised Machine Learning: A Review of Classification Techniques. Informatica 2007, 31:249–68. [Google Scholar]
- [27].Esteva AKB, Novoa RA, Ko J, Swetter SM, Blau HM, Thrun S,: Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542:115–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Wang W, Cruz Roa A, Basavanhally AN, Gilmore HL, Shih N, Feldman M, Tomaszewski J, Gonzalez F, Madabhushi A, : Mitosis detection in breast cancer pathology images by combining handcrafted and convolutional neural network features. J of Medical Imaging 2014, 1:034003, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Ertosun MG. RD: Automated grading of gliomas using deep learning in digital pathology images: A modular approach with ensemble of convolutional neural networks. 2015 Annual Symp AMIA (American Medical Informatics Association) 2015. pp. 1899–908. [PMC free article] [PubMed] [Google Scholar]
- [30].Havaei HDA, Warde-Farley D, Biard A, Courville A, Bengio Y, Pal C, Jodoin P-M, Larochelle H,: Brain tumor segmentation with Deep Neural Networks. Med Image Analysis 2017, 35:18–31. [DOI] [PubMed] [Google Scholar]
- [31].Erhan DBY, Courville, Manzagol P-A, Vincent P, Bengio S: Why Does Unsupervised Pre-training Help Deep Learning? J Machine Learning Res 2010, 11: 625–60. [Google Scholar]
- [32].Hinton G: A practical guide to training restricted Boltzmann machines Toronto: Department of Computer Science, University of Toronto, 2010. pp. 1–21. [Google Scholar]
- [33].Hinton J, Osindero S, Teh Y- W,: A Fast Learning Algorithm for Deep Belief Nets. Neural Computation 2006, 18:1527–54. [DOI] [PubMed] [Google Scholar]
- [34].Vincent PLH, Lajoie I, Bengio Y, Manzagol AP,: Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. J Machine Learning Res 2010, 11:3371–408. [Google Scholar]
- [35].Lee H, Grosse R, Ranganath R, Ng AY,: Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations 2009 Annual Conference on Machine Learning. Montreal, Canada, 2009. pp. 609–16. [Google Scholar]
- [36].Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R, : Dropout: a simple way to prevent neural networks from overfitting. J Machine Learning Res 2014, 15:1929–58. [Google Scholar]
- [37].Zeiler M: ADADELTA: An Adaptive Learning Rate Method. [Google Scholar]
- [38].Begin S, Dupont-Therrien O, Belanger E, Daradich a, Laffray S, De Koninck Y, Cote DC: Automated method for the segmentation and morphometry of nerve fibers in large-scale CARS images of spinal cord tissue. Biomed Optics Express 2014, 5(12):4145–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Greenacre M: Correspondence Analysis in Practice. 2nd edition ed: Chapman & Hall/CRC Press, 2007. [Google Scholar]
- [40].Shrout PE, Fleiss JL: Intraclass correlations: Uses in assessing rater reliability. Psychological Bull 1979, 86(2):420–8. [DOI] [PubMed] [Google Scholar]
- [41].Zaimi AWM, Herman V, Antonsanti P-L, Perone CS, Cohen-Adad J,: AxonDeepSeg: automatic axon and myelin segmentation from microscopy data using convolutional neural networks. Sci Reports 2018, 8, Article number: 3816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Ronneberger O, Fischer P, Brox T,: U-Net: Convolutional Networks for Biomedical Image Segmentation MICCAI 2015: Medical Image Computing and Computer-Assisted Intervention. Edited by Navab N, Hornegger J, Wells W, Frangi A (eds) Springer, 2015. pp. 234–41. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.