Uniaxial Extension and Compression in Stress-Strain Relations of Rubber

Abstract

A survey of experimental data from the literature in cases where the deformation of a specimen is varied continuously from uniaxial compression to tensile deformation shows that Young’s Modulus M, defined as the limit of stress to strain in the undeformed state, is independent of the direction of approach to the limit. The normalized stress-strain relation of Martin, Roth, and Stiehler (MRS, 1956) is F/M = (L⁻¹ − L⁻²) exp A (L − L⁻¹) where F is the stress on the undeformed section, L is the extension ratio, and M and A are constants. Values of M and A are obtained from the intercept and slope of a graph of experimental observations of log F/(L⁻¹ − L⁻²) against (L − 1⁻¹) including observations of uniaxial compression if available. They found the value of A to he about 0.38 for pure-gum vulcanizates of natural rubber and several synthetics.

In later work several observers have now found that the equation is also valid for vulcanizates containing a filler, but A is higher, reaching a value of about 1 for large amounts of filler. In extreme cases A is not constant at low deformations. The range of applicability in many cases now is found to extend from the compressive region where L = 0.5 up to the point of tensile rupture or to a point where A increases abruptly because of crystallization. Taking A as a constant parameter in the range 0.36 to 1, graphs are presented showing calculated values of (1) F/M as a function of L and (2) the normalized Mooney-Rivlin plot of F/[2M(L − L⁻²)] against L⁻¹. Each of the latter graphs has only a limited region of linearity corresponding to constant values of the Mooney-Rivlin coefficients C₁ and C₂. Since this region does not include the undeformed state, where L = 1, or any of the compression region, the utility of the Mooney-Rivlin equation is extremely limited, since it can not be used at low elongations. The coefficients are dramatically altered for rubbers showing different values of the MRS constant A. For rubbers showing the higher values of A, the coefficients are radically altered and the region of approximate linearity is drastically reduced.

1. Introduction

The form of the stress-strain relation of rubber has been the subject of several previous investigations at the National Bureau of Standards [1].¹ An empirical equation was developed by Martin, Roth, and Stiehler [2] in 1956 to describe the behavior of a typical pure-gum rubber vulcanizate after a given period of creep. They showed it to be valid up to 200 percent elongation for the first extension of pure-gum vulcanizates of natural rubber, styrene-butadiene rubber (SBR), butyl rubber (IIR), and chloroprene rubber (CR) over a 10-fold range of times of vulcanization and for constant times of creep (isochrones) from 1 to 10,000 min. Another paper [3] showed that the equation could be applied to the compression region with the same constants as in the extension region. This conclusion is especially significant because it means that the equation is valid at low deformations, where it is difficult to obtain good experimental data. It also means that the slope of the stress-strain curve shows no discontinuity on passing from uniaxial compression to tension. As discussed later, this is in accordance with direct experimental observations.

The present paper extends consideration to published experimental data regarding the nature of the stress-strain relation at elongations above 200 percent up to the point of rupture. The discussion includes the effects of crystallization when present and the effects of filler content. Here one must consider values of the parameter A in the Martin, Roth, and Stiehler equation which are larger than that utilized originally.

A discussion is given of the limited regions of linearity of the Mooney-Rivlin plot and the relation of the constants C₁ and C₂, obtained from that plot, to the modulus (the limit of the ratio of stress to strain in the undeformed state).

2. Continuity of Slope of Stress-Strain Curves

Over many years there has been general agreement with the experimental observation that the slope of the stress-strain curve shows no discontinuity on passing from uniaxial compression to extension [4–8]. In other words the modulus, M defined as the limit of the ratio of stress, F, to strain at L = 1 is independent of the direction of approach to the limit, where L is the extension ratio.

The validity of this conclusion has been questioned by van der Hoff and Glynn [9], who have presented data on polybutadiene vulcanizates. However, they did not make measurements on the same specimens in extension and compression. Data of Blokland [10, 11] on lightly cross-linked polyure-thane networks have sometimes been quoted in support of a discontinuity. However Blokland [10] himself states that the data on compression are not very satisfactory because of friction arising from tackiness of the specimens.

Direct experimental studies involving a single specimen in the two regions have been rare. R. H. Taylor, [12] in unpublished work in our laboratories in 1942, utilized the central section of a cylindrical specimen of pure-gum natural rubber in a balanced beam arrangement to pass in continuous fashion from compression to extension. When L was varied from 0.9 to 1.1, a plot of FL against L yielded a single straight line. Linearity of this plot indicates that the ratio of stress calculated on the deformed cross-section to strain is a constant over this range of deformation [3], and that there is no discontinuity.

In more extensive recent work Wolf [13] accomplished the same result by metal springs counterbalanced by weights. As the extension ratio L increased from 0.88 to 1.18, the ratio of F, the stress on the initial section, to the strain decreased continuously, showing no evidence of discontinuity at L = 1.

3. Form of Stress-Strain Relation

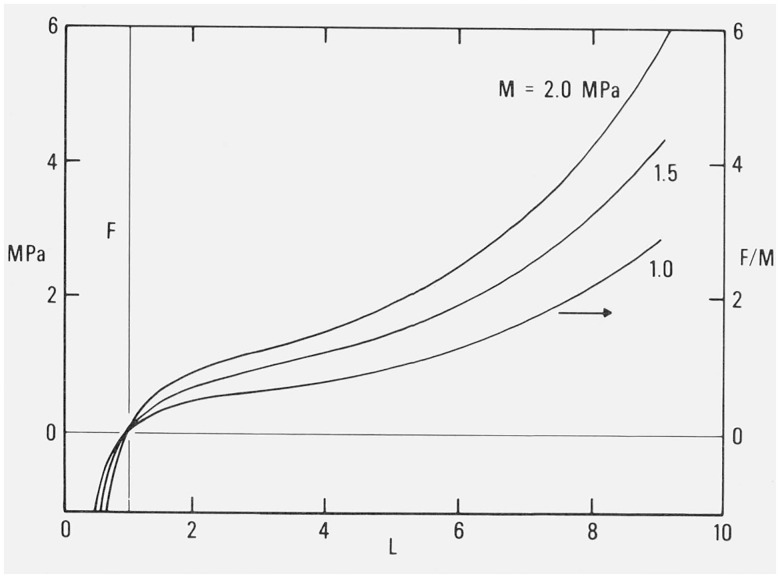
Three typical curves in figure 1 show the relation of stress F (based on undeformed cross-sectional area) to the extension ratio L, the ratio of stressed length to unstressed length. The figure includes a short section of the compression region where L < 1. The values of Young’s modulus M, the slope of each curve for the unstressed state (where L = 1), are 1, 1.5, and 2 MPa respectively, normal values for a pure-gum vulcanizate at different increasing degrees of cross-linking.

Figure 1. Relation of stress F (based on undeformed cross-section) to extension ratio L.

Modulus M-1, 1.5, or 2 MPa. Lowest modulus curve is also normalized relation between F/M and L.

The similarity of shape of the curves is obvious and suggests immediately a normalized plot in which the ordinate is F/M, the ratio of the stress to the modulus. Such a plot of course is identical with the lowest curve, (where M = 1), if one utilizes the ordinate scale on the right.

Thus the stress-strain relation for all three rubbers is represented by the single plot of F/M. Consequently attention can be concentrated on the shape of the curve without regard to variations in modulus. The modulus itself will vary with the nature of the rubber, the extent of vulcanization, the temperature, the time of creep or relaxation and possibly other factors. However, the relation of stress to strain does not appear to depend on what particular combination of these factors leads to a given modulus.

Martin, Roth, and Stiehler [2] developed the following empirical equation to represent the normalized relation up to L = 3.

$$F/M=\left(L^{-1}-L^{-2}\right)\text{\hspace{0.17em}exp\hspace{0.17em}}A\left(L-L^{-1}\right)$$ (3.1)

where A is a parameter equal to about 0.38. The lowest value they reported was 0.32 and the highest 0.42.

The slope of the normalized equation, readily obtained by differentiation of eq 3.1 is

$$\partial \left(F/M\right)/\partial L=L^{-1}\left[\text{exp\hspace{0.17em}}A\left(L-L^{-1}\right)\right]\left[A\left(\text{l}-L^{-1}+L^{-2}-L^{-3}\right)-L^{-1}+2L^{-2}\right].$$ (3.2)

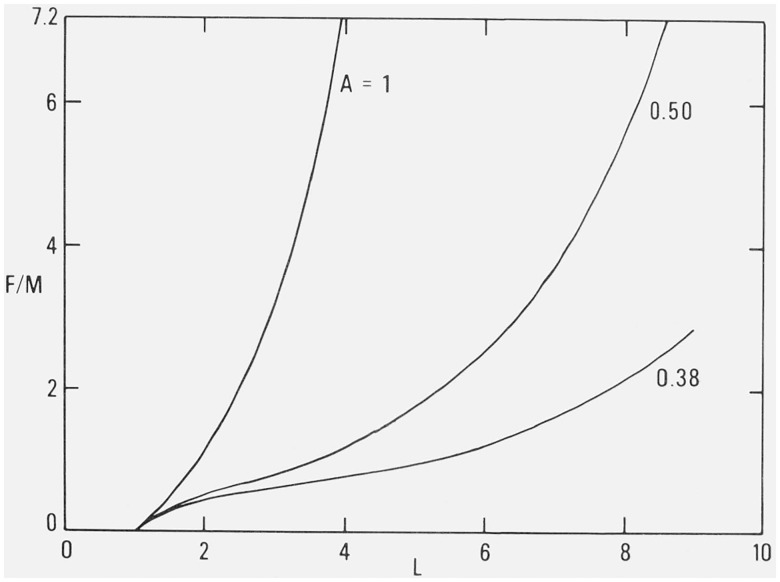
With A = 0.38 there is a region of decreasing slope beginning at L = 0.26, passing through unit slope at L = 1 and having a point of inflection at L = 2.91. Beyond this the slope increases up to the point of rupture. The equation represents the previously-mentioned data of Martin, Roth, and Stiehler [2] for pure-gum rubbers reasonably well over the interval from L = 0.5 to about L = 3.5. As described more fully in the next section, in recent years other observers [14–17] have reported measurements on rubbers containing fillers, where the value of A was larger than 0.38, in some cases becoming as much as 1.1. Figure 2 is therefore drawn to represent the generalized normalized Martin, Roth and Stiehler equation where the parameter A can assume values other than 0.38. The lowest curve is the same as that shown in figure 1.

Figure 2.

Relation of normalized stress F/M (ratio of stress to modulus) to extension ratio L, as calculated by Martin, Roth, and Stiehler equation with coefficient A = 0.38, 0.50, or 1.0.

The additional curves maintain unit slope at L = 1, but the point of inflection is displaced downwards with increasing values of A. When A = 0.5 the point of inflection is at L = 1.77. When A = 1.0 the slope obtained from eq (3.2) is unity within 0.6 percent for 1.0 < L < 1.2. with an increasing slope at higher elongations.

4. Application of MRS Equation to Experimental Data

The validity of the representation of any stress-strain data by eq (3.1) can be ascertained by a plot of log F/(L⁻¹ − L⁻²) against (L − L⁻¹). If the data conform to the equation the plot will be linear. The modulus M can be obtained from the intercept (which is log M), and the parameter A from the slope (which is 0.4343 A for base-10 logarithms). For brevity a graph with these co-ordinates will be called an MRS plot.

4.1. Pure-Gum Vulcanizates

Landel and Stedry [18] reported excellent adherence to linearity in plots of this sort for samples of polyurethane. The data were obtained at a constant strain rate (0.325 min⁻¹ in one case), rather than being isochronal as in the studies of Martin, Roth, and Stiehler [2], The values of A, reasonably constant for a given rubber, varied between 0.4 and 0.5. Linearity was obtained up to the breaking strain of 225 percent. Similar studies with styrene-butadiene rubber (SBR) showed values of A varying from 0.35 to 0.45 at temperatures from −5 to 60 °C for times from 1 to 10,000 min. An average value of 0.40 was utilized in later calculations. Both constant strain rate and stress relaxation measurements were made with this rubber. At the lowest temperature the measured strain was as high as 550 percent.

In later work Landel and Fedors [19] utilized the equation with a value A = 0.40 to represent very well the form of the stress-strain relation for the failure envelope of a master curve with experimental data for 12 different rubbers.

T. L. Smith [20] studying the response of pure gum SBR vulcanizates at widely different constant strain rates and temperatures obtained data which gave an equilibrium stress-strain curve represented by the MRS equation with A = 0.47 or 0.49 [21]. In later work [22] the ultimate values of stress and strain were also found to lie along the same curve.

Harwood and Schallamach [23, 24] made isochronal plots of data from constant-strain-rate experiments for a pure-gum vulcanizate of natural rubber. They obtained good agreement with the straight lines predicted by the MRS plot. At −45 °C the value of A was 0.56 for constant times from 0.2 to 1000 s. Over this time range the modulus M decreased from 41 to 13 kg/cm⁻² (4.0 to 1.27 MPa). The same value of A was obtained at other temperatures.

Bartenev and Vishnitskaya [25] report values of A and M determined by MRS plots for several different rubbers. With measurements in their own laboratories they report 0.356 and 10.0 kg/cm² (0.98 MPa) respectively, for a natural rubber vulcanizate as well as 0.371 and 7.24 kg/cm² (0.710 MPa) for a styrene-butadiene rubber. In concluding that the equation is fairly satisfactory up to the point of rupture they also report values obtained from MRS plots of data obtained by other observers [26–30].

Other stress-strain data in the literature which we have found to show good approximations to linearity in an MRS plot include observations by Shepard and Clapson [4], Treloar [6], Rivlin and Saunders [31], Smith, Greene, and Cifferi [32], and Obata et al. [33]. The MRS plots for the first three sets of observations have been presented in a previous paper [3].

J. F. Smith [34] has noted an abrupt increase in the slope of some MRS plots at a high elongation. He ascribes this discontinuity of slope to the onset of crystallization. From its location he and his co-workers [35] have drawn conclusions regarding the critical elongation as it is affected by different types of vulcanization. We have also found that some of the data presented by Smith, Greene and Cifferi [32] likewise show this abrupt increase in slope associated with crystallization.

4.2. Rubber-Filler Systems

Data obtained by Becker and Rademacher [15] on vulcanized rubber containing different amounts of titanium dioxide filler are suitable for this type of analysis. Values read from their figure 8 for the unfilled rubber are almost identical with those shown in the lowest curve of figure 1 of the present paper. Values for the filled rubbers lie above this curve.

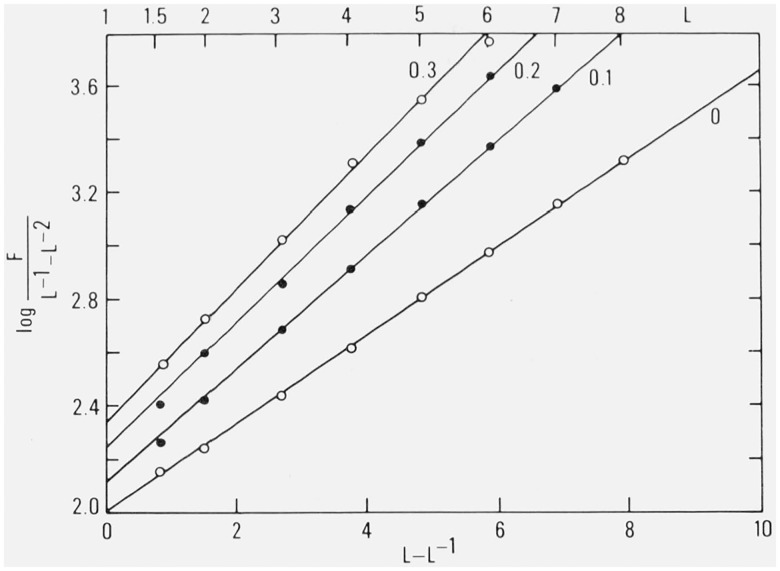
Figure 3 presents a plot of Becker and Rademacher data (as read from the curves of their fig. 8) in the form used to test the validity of eq (3.1). The points are in excellent agreement with straight lines. The values of A increased from 0.38 for the pure gum rubber to 0.50, 0.55, and 0.58 as the fractional filler content was increased from 0 to 0.1, 0.2, and 0.3 respectively. Values of the modulus M, as read from the intercept, increased from 1.03 MPa for the pure-gum rubber to 1.26, 1.71, and 2.15 MPa respectively.

Figure 3. MRS plot – Relation of log F/(L⁻¹ − L⁻²) to (L − L⁻¹) for four volume-fractions of TiO₂ filler from 0 to 0.3 in natural rubber.

Data of Becker and Rademacher [15] (their fig. 8).

Similar results were obtained in unpublished studies by Nakayama [14] on rubber containing carbon black. He found somewhat higher values of A and some deviations from linearity at low elongations, with low values of A, for rubbers containing large amounts of filler. The values of A obtained were 0.495, 0.587, 0.732, and 0.951 for natural rubber containing 0, 10, 30, and 50 percent carbon black. Experimental details regarding his method of measurement and the type of black are not available. Harwood and his co-workers [16, 17] have found linear MRS plots for isochronal data on styrene-butadiene rubber. The value of A for a pure-gum vulcanizate was 0.384 and did not vary with temperature (240 to 420 K). For an SBR vulcanizate containing 30 phr of HAF carbon black the values of A decreased from about 1.1 at 250 K to 0.83 at 425 K. Here, as with Nakayama’s results, there were some deviations at low elongations. For each vulcanizate, A was independent of the rate of extension over the range 0.1 to 1000 percent/s. In a natural rubber containing mainly polysulfide cross-links the value of A was found to increase, from 0.39 to 0.61 as the cross-linking was increased.

5. Young’s Modulus from Experimental Observations of Uniaxial Extension and Compression

Young’s Modulus M is defined as the limit of the ratio of stress to strain in the undeformed state (where L = 1). For the data considered here it will be equal to 3G where G is the shear modulus. We consider it highly desirable to reserve the word modulus for the limit of the ratio, not using it for the ratio itself or for F/(L − L⁻²) as several previous workers have done.

In a previous paper [3] consideration was given to the various methods of obtaining M from observations of stress and strain. The paper concluded that the most satisfactory method was to measure the intercept of an MRS plot (e.g., as in fig. 3), since a linear extrapolation from finite deformations to the unstressed state can include observations over a greater range than with other methods. Furthermore data on uniaxial compression can be included in the determination. This makes possible a determination of the modulus from the intercept obtained by interpolation of observed values of positive and negative uniaxial stress rather than by extrapolation of positive stress values only.

A simpler form involving the plotting of F/(L⁻¹ − L⁻²) against L or the elongation (L − 1) was also found to be satisfactory (0.5%) when L is between 0.5 and 2.0.

Previous papers [36, 37] have already called attention to the fact that the modulus as obtained by the use of the MRS equation in uniaxial extension is in excellent agreement with the modulus obtained directly by an indentation technique with specimens cross-linked by varying amounts of dicumyl peroxide [38]. Good agreement was also obtained with the modulus on similar specimens measured by a torsion pendulum [39].

6. Mooney-Rivlin Equation

Two different independent types of theoretical approach by Mooney [40] and by Rivlin [41] lead to an equation which may be written

$$F/2=S_1\left(L-L^{-2}\right)+S_2\left(l-L^{-3}\right)$$ (6.1)

where S₁ and S₂ are, in general, functions of L. It is of interest to examine experimental stress-strain data to see whether there are certain regions where S₁ and S₂ are found to have constant values.

The usual procedure to locate these regions is to put the equation into the form

$$F/\left[2\left(L-L^{-2}\right)\right]=S_1+S_2{L}^{-1}$$ (6.2)

In those regions where S₁ and S₂ are constant, a plot of the left-hand member F/[2(L − L⁻²)] against L⁻¹ will yield a straight line with an intercept S₁ and a slope S₂. Let us denote these constant values as C₁ and C₂ respectively and call a graph with these coordinates a Mooney-Rivlin plot.

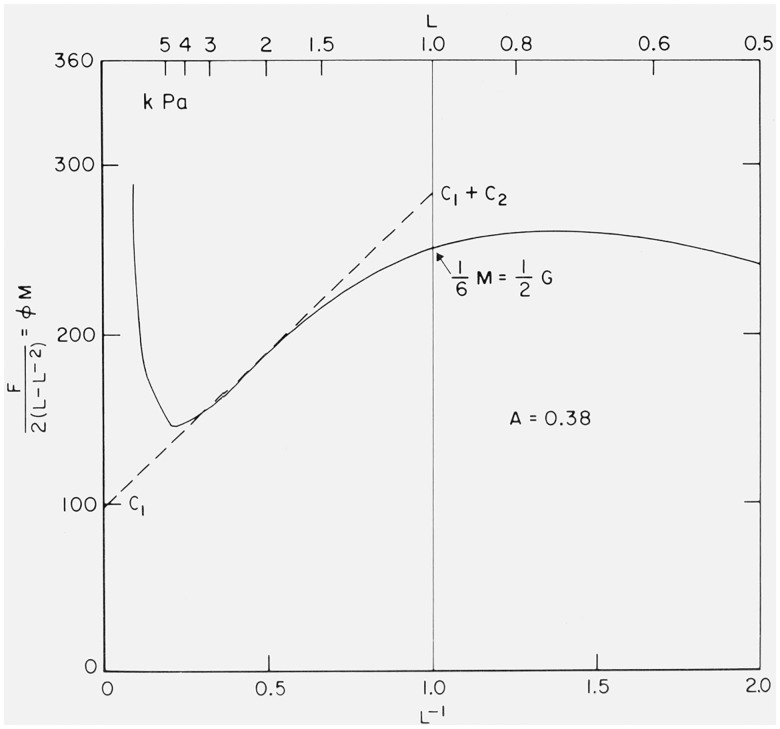
Figure 4 shows such a plot for the stress-strain data for the typical pure-gum vulcanizate exemplified by the middle curve of figure 1, where M = 1.5 MPa. It can be seen that in extension there is indeed a region of linearity where the curve coincides with the dashed line shown. This region includes values of L⁻¹ between 0.3 and 0.7, namely where L is between about 1.5 and 3.5. However there is increasing divergence between the curve and the straight line on approach to the undeformed state, where L⁻¹ = 1.

Figure 4.

Mooney-Rivlin plot – Relation of F/[2(L − L⁻²)] to L⁻¹ for rubber conforming to MRS equation with A = 0.38.

The curve represents experimental data, which conform to eq (3.1), the MRS equation. In terms of the ordinate of figure 4 the equation is:

$$\frac{F}{2\left(L-L^{-2}\right)}=\frac{M\left(L^{-1}-L^{-2}\right)}{2\left(L-L^{-2}\right)}\text{\hspace{0.17em}exp\hspace{0.17em}}A\left(L-L^{-1}\right)$$ (6.3)

The equation of the straight line is

$$\frac{F}{2\left(L-L^{-2}\right)}=C_1+C_2{L}^{-1}.$$ (6.4)

The straight line represents experimental data only in the region where it coincides with the curve.

It is evident from figure 4 that

$$C_1<\underset{L=1}{\text{lim}}\frac{F}{2\left(L-L^{-2}\right)}=\frac{M}{6}<\left(C_1+C_2\right).$$ (6.5)

The shear modulus G = ⅓ M is often calculated by cross-linking considerations [42, 43]. It is clear that it should not be regarded as directly correlated with either C₁ [44] or with (C₁ + C₂) [45]. The value of M/6, always intermediate between the two, can best be determined by the method given in Section 5. The Mooney-Rivlin equation with constant coefficients certainly does not agree with the experimental data (represented by the curve) in the region where L⁻¹ is greater than 0.7 - namely where L is less than 1.5.

At L = 1 the ordinate of the curve, namely the ratio F/[2(L − L⁻²)], has both numerator and denominator zero, but its value may be obtained by differentiating them both and applying the rule of de l’Hopital. The ratio of the derivatives gives the ordinate of figure 4 at L = 1 as M/6 where M is [∂F/∂L]_L=1. The actual value is 250 kPa in this case.

The values of C₁ and C₂ may be read from figure 4. Subjective variations in drawing the line may be avoided by using the analytical expression of the MRS equation with A = 0.38 to represent the stress F. As outlined in more detail previously [3] the analysis shows that there is a point of inflection in the curve near L⁻¹ = 0.42 and a minimum at L⁻¹ = 0.24. If the straight line is drawn as the tangent at the point of inflection, it will be found that C₁ = 0.64 M = 96 kPa and C₂ = 0.124 M = 186 kPa, with the ratio C₂/C₁ = 1.94. Thus the ordinate of the straight line at L = 1, namely (C₁ + C₂) is 282 kPa. As expected this is definitely greater than 250 kPa, the ordinate of the curve at this point. If the straight line is drawn to be tangent to the curve at a point where the abscissa L⁻¹ is greater than 0.42, somewhat lower values of C₂ will be obtained, but poorer agreement is found below 0.42.

Many previous authors have assumed the constancy of the Mooney-Rivlin coefficients S₁ = C₁, and S₂ = C₂ in the region where L⁻¹ is between 0.7 and 1, (1.0 < L < 1.5). The fallacy in this assumption, (at least for a rubber with A = 0.38) is shown by an examination of figure 4, where the curve representing experimental values deviates from the dotted line representing the Mooney-Rivlin equations.

In the compression region, where L⁻¹ > 1, there is general agreement that experimental data do not conform to eq (6.2) with the values of C₁ and C₂ applicable in the extension region. Instead the value of F/[2(L − L⁻²)] is approximately constant with a value of about (1/6)M as predicted by the statistical theory of rubber elasticity. In terms of the Mooney-Rivlin equation, C₁/M = 0.167 and C₂/M = 0 in this region.

The value of F/[2(L − L⁻²)] predicted by the MRS equation, eq (3.1), with A = 0.38 shows only a small variation between L⁻¹ = 1 and L⁻¹ = 2 as can be noted in figure 4. In the normalized form the calculated value of F/M in this region differs from that calculated from the statistical theory, namely ⅓ (L − L⁻²), by less than 4 percent [3], Since the precision of the available experimental data in this region is no better than this figure, the MRS equation may be regarded as an adequate representation of the data for compressions as large as those in which the thickness is reduced to half the original thickness (L = 0.5).

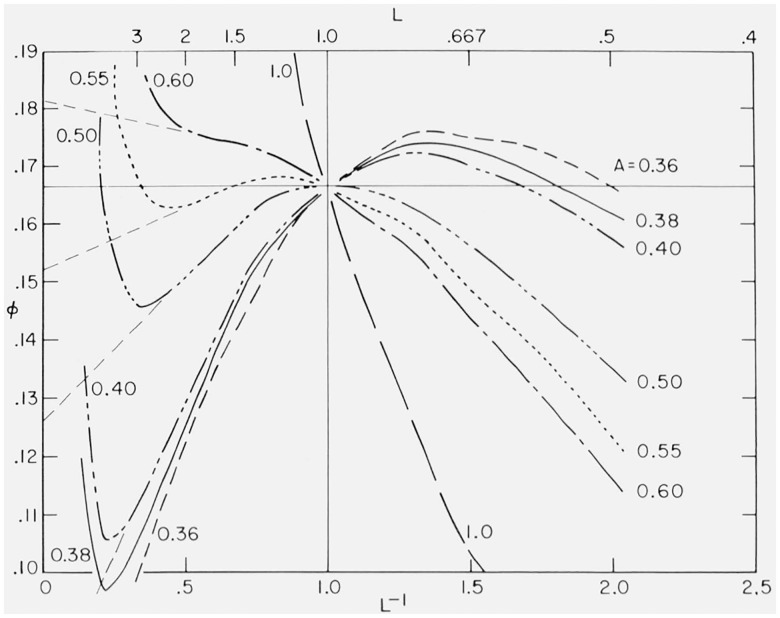
A normalized Mooney-Rivlin plot is shown in figure 5 where the ordinate of figure 4 has been divided by the modulus M to give the curve marked A = 0.38. This curve can be utilized for all values of modulus including those which differ from the value (1.5 MPa) represented in figure 4.

Figure 5.

Normalized Mooney-Rivlin plot – Relation of F/[2M(L − L⁻²)] to L⁻¹ for rubbers conforming to MRS equation with A = 0.36, 0.38, 0.40, 0.50, 0.55, 0.60, or 1.0.

Figure 5 also shows normalized Mooney-Rivlin plots for stress-strain data represented by several different arbitrary values of A in the generalized MRS equation. It can be seen that C₁/M increases and C₂/M decreases as A is raised above 0.38, with C₂/M becoming zero when A is near 0.55. C₂/M is negative when A is still higher. The point of inflection and the sum (C₁ + C₂) both show little change with increase of A, but the minimum (“upturn”) moves upward. In all cases the ordinate of the curve at L = 1 is ⅙, while the ordinate of the straight line at this point is (C₁ + C₂)/M.

In the compression region of figure 5 the near-constancy of ordinate is soon lost as the value of A is increased above 0.4. For elastomers exhibiting this type of stress-strain behavior, the statistical theory of elasticity would not be even approximately valid in compression. However, this conclusion has not been checked experimentally by a study of compression data on rubbers containing a filler.

7. Previous Use of Mooney-Rivlin Plots

During the past quarter century experimental values of stress and strain have been presented in the form of Mooney-Rivlin plots for hundreds of different elastomer systems. The conclusions of the present paper up to this point have been applicable to only those systems which conform to the generalized Martin, Roth and Stiehler equation, where A and M may have any values. The conformity in any particular case can be determined by the linearity of an MRS plot like figure 3. Mention has already been made in Section 4 of many cases in which this conformity has been found.

It will be remembered that in the original formulation the MRS equation was stated to be applicable to isochronal data – that each point of a given curve was obtained at the same time after the application of the stress. Some of the later work has found the relation valid also at constant rates of strain. In other work the stress has been measured after a specified program of prestretching – often a program suggested by Gumbrell, Mullins, and Rivlin [46]. It is not certain to what extent these deviations from isochronal data may cause deviations from linearity in the MRS plots and resulting invalidation of the conclusions just drawn regarding the Mooney-Rivlin plots.

With the foregoing qualification one can make several general statements about the literature results, many of which have been summarized by Blokland [10]. For example, in many cases the upper limit of linearity lies above L⁻¹ = 0.7. Sometimes it is as high as 0.9. However only rarely do the observations themselves extend above 0.85. In a number of instances the experimental points fall below the straight line for the highest values, as would be predicted from figure 4. In all the literature we have found at the higher values an almost complete absence of points lying above the line. Equal numbers above and below would be expected if the deviation arose from random errors of measurement of strain – the cause often assigned to this deviation [47, 48].

Figure 4 shows the lower limit of linearity of the Mooney-Rivlin plot as about L⁻¹ = 0.3 with a minimum at 0.24. In the literature many different values can be found but there is always an upturn immediately below the linear region, if the observations extend to high enough elongations. Mullins [44] found values of the upturn region as high as 0.6. The higher values are obtained as the cross-linking is increased or when measurements are made on a swollen specimen. He ascribes the upturn to an approach to the limited extensibility of a network, in contrast with some others [49] who consider it to be due to crystallization. Smith, Greene, and Cifferi [32] consider it as arising initially from the first and then from the second cause. It can be seen from figure 5 that increasing values of A, which might be produced by the increase of filler content or by crystallization, cause the upturn to appear at higher values of L⁻¹.

In some instances metnioned in section 3, J. F. Smith [34, 35] found the onset of crystallization giving rise to an abrupt increase of slope of the MRS plot corresponding to an increase in A at high elongations. In these instances the upturn in the Mooney-Rivlin plot would be still more pronounced than that in figure 4.

The ratio C₂/C₁ is often found to be less than 1.94, the value obtained when MRS coefficient A = 0.38. In many instances the ratio is found to be near 1. The ratio is a very sensitive function of A, as can be seen in figure 5. The ratio is expected to be near zero when A is near 0.55 as already noted. The ratio often depends on molecular weight of the rubber and on previous thermal and mechanical history.

In view of the inability of previous workers to relate the Mooney-Rivlin constants C₁ and C₂ to molecular considerations and the failure of the equation to represent experimental data in the region of low elongations or compression as shown here, we think that Mooney-Rivlin plots have only very limited utility. It seems futile to try to ascribe much significance to C₂ after noting the wide variations shown in figure 5.

Jones and Treloar [47] have recently shown that C₁ and C₂ do not furnish significant information about the strain energy, and that (contrary to Mooney’s assumption [40]) the shear stress-strain curve is not linear. They show a curve very similar to figure 4 with a maximum near L⁻¹ = 2 and extending smoothly into the region of low extensions. Their experimental data are represented by a stress-strain relation much more complex than the generalized MRS equation.

8. Conclusions

A comprehensive literature survey shows the general applicability of the generalized normalized Martin, Roth, and Stiehler equation to uniaxial stress-strain data in extension and compression on rubber vulcanizates. The equation can be expressed as F/M = (L⁻¹ − L⁻²) exp A (L − L⁻¹) where F is the stress on the undeformed section and L the ratio of stressed to unstressed length. The equation contains two constants – M, Young’s Modulus, the slope of the stress-strain curve at L = 1, and A an empirical constant.

The conformity of stress-strain data to the equation can readily be determined by a plot of log F/(L1 —L⁻²) against (L − L⁻¹).

In almost every case a straight line is obtained, from the slope and intercept of which both the constants can be determined. The range of validity of the equation usually begins near L = 0.5 (in the compression region) and continuing through the region of low deformations often extends to the region of rupture in extension. If uniaxial compression data are available the modulus can thus be obtained by interpolation through the region of low deformations, where experimental data are often somewhat unreliable. The value of the modulus M varies with the nature of the rubber, the extent of vulcanization, and the time and temperature of creep or stress relaxation. The value of the constant A is near 0.4 for pure-gum vulcanizates, increasing to values near 1.0 with increasing filler content, and showing an abrupt increase when crystallization occurs. Direct experimental observations where the deformation of a single specimen is varied continuously from compressive to tensile deformation are cited to show that M, defined as the limit of the ratio of stress to strain, is independent of the direction of approach to the limit at L = 1.

The normalized Mooney-Rivlin plots show F/[2M(L − L⁻²)] against L⁻¹. These graphs have only limited regions of linearity corresponding to constant values of the coefficients C₁ and C₂. Since these regions do not include the undeformed state the Mooney-Rivlin equation can not be used at low elongations or in compression. The values of C₁ and C₂ show very wide fluctuations for the Mooney-Rivlin plots of experimental data, which are themselves usually well represented by the Martin, Roth, and Stiehler equation with different values of the constant A.

In view of all these considerations the conclusion of the present study confirms that of Treloar in his recent publications [7, 50] in failing to find much utility in making Mooney-Rivlin plots. The failure to represent the experimental data at low elongations and the inability to correlate the constants with theoretical predictions based on strain energy or statistical theory considerations are the most serious objections.