Abstract
A survey of published experimental work on the modulus of natural rubber cross-linked by dicumyl peroxide permits a comparison with the results and molecular interpretations obtained in recent NBS work [J. Res. NBS 76A, No. 1, 51 (1972), 77A, No. 1, 171 (1973) and 80A, No. 3, 451 (1976)]. Excellent agreement was found among values of the shear modulus G at the same cross-linking when the cross-linking is calculated from the amount of decomposed dicumyl peroxide. The types of deformation included torsion as well as uniaxial extension and compression. G increases linearly with cross-linking (except at the lowest degrees) with a slope from 5 to 15 percent greater than that predicted by the simple statistical theory. Data of Mullins demonstrated that at each degree of cross-linking the value of G is intermediate between 2C1 and 2(C1 + C2) where C1 and C2 are the Mooney-Rivlin constants. Measurements of equilibrium swelling at a given degree of cross-linking are in reasonable agreement with each other. However the entropy components of the modulus and the sub-chain density calculated from swelling measurements are appreciably greater than those calculated from cross-linking or from direct mechanical measurements. They increase linearly with cross-linking. It is concluded that the number of sub-chains effective in limiting swelling is greater than that effective in direct mechanical measurements.
Keywords: Cross-linking of rubber; dicumyl peroxide; elasticity theory of rubber; modulus of rubber; Mooney-Rivlin constants; rubber elasticity theory; rubber, natural; swelling of rubber network
1. Introduction
In recent years extensive investigations have been made of the mechanical properties of natural rubber cross-linked by dicumyl peroxide. Because the basic mechanism appears to be relatively simple and free from side reactions, this system is particularly suitable for fundamental studies. The amount of cross-linking can readily be calculated from the quantity of peroxide decomposed and not otherwise wasted by reaction with impurities. The calculation assumes that each molecule of unwasted decomposed dicumyl peroxide gives rise to one cross-link. This assumption has found extensive experimental verification in recent years [1–9].1 Dicumyl peroxide is thus a quantitative cross-linking agent for natural rubber. It seems quite surprising that with only a few exceptions previous investigators have not calculated the amount of decomposed dicumyl peroxide from the time and temperature of cure and used it to calculate the cross-linking. In the present study this calculation has been made utilizing the times and temperatures of cure reported in the original publications.
In previous studies at the NBS, experimental observations, Part I [10], were compared with theory, Part II [11], and given a more detailed molecular interpretation, Part III [12]. The present paper presents a survey of other published experimental work in this field and makes a detailed comparison with the NBS studies. The experimental observations of directly observed quantities show only small discrepancies which can probably be explained simply in terms of differences in purity or molecular weight of the rubber. A much wider variation exists with respect to calculated molecular quantities, particularly the calculated number of effective sub-chains.
2. Modulus and Cross-Linking
The shear modulus G as determined by an indentation technique in our previous work [10] is represented by the equation
| (2.1) |
S, B, H, and A are constants having the values shown, while G is the shear modulus (in kPa) at a temperature T (in kelvins) for natural rubber crosslinked by adding p parts of dicumyl peroxide per hundred of rubber and heating until a fraction f of the peroxide is decomposed.
The fraction f of the dicumyl peroxide molecules decomposed during cure can be calculated from the relation [10].
| (2.2) |
where t is the time of cure and t1/2 is the half-life, the time required for half of the molecules to decompose. This in turn is related to T, the temperature of cure, by the equation
| (2.3) |
based on the dicumyl peroxide studies of Hummel, Scheele, and Hilmer [1].
A graph representing eq (2.1) at 25 °C is given as figure 5 of our original work, Part I [10]. The straight line shown, corresponding to G = 183.5 fp + 187, gives good agreement with our experimental points obtained with values of fp as high as 23.8 phr (parts per hundred of rubber), corresponding to a modulus G of about 4400 kPa.
A similar graph representing the equation at 30 °C was also given as figure 8 in Part I [10]. Here G = 186.4 fp + 186 and the scales were magnified about five-fold.
When the tensile stress at some arbitrary elongation is reported, the modulus can be calculated by multiplying by a factor calculated from the empirical equation of Martin, Roth, and Stiehler [13–15]. For example the equation yields F50/M = 0.3050 where F50 is the stress at 50 percent elongation and M is Young’s Modulus. Thus the shear modulus G = (1/3)M = F50/0.915 = 1.093 F50. Likewise F100/M = 0.4421, where F100 is the stress at 100 percent elongation, and G = F100/1.3263 = 0.7549F100.
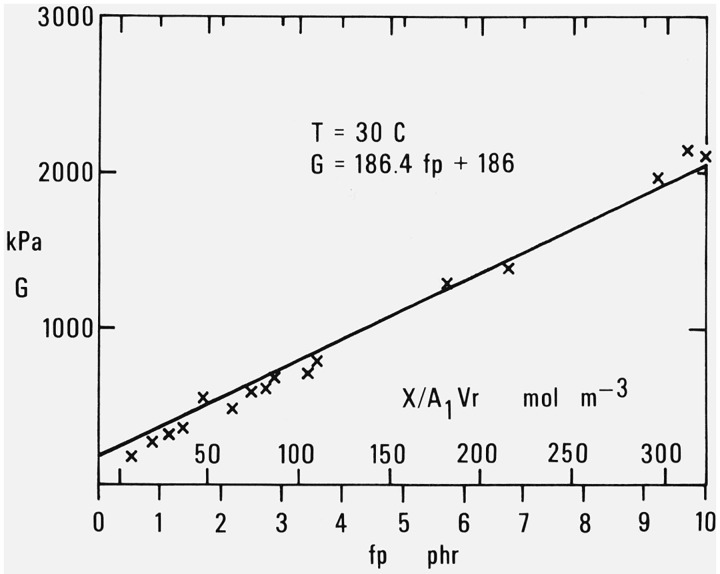
Figure 8 of Part I shows that modulus values at 30 °C obtained as just described from the observations of Chasset and Thirion [16] on stretched specimens or those of Plazek [17] with a torsion pendulum agree very well with the line obtained from eq (2.1). A more complete discussion has already been given [10]. Figure 1 of the present paper is a plot of the data of Tamura and Murakami [18] in extension for another comparison with the straight line representing eq. (2.1) at 30 °C. Here again there is good agreement with the results obtained by the indentation measurements. As previously noted in Part III [12] the observed values of G at low degrees of cross-linking fall below the line. Values shown for fp (lower abscissa scale) are based on the application of eqs (2.2) and (2.3) to the curing conditions specified by the authors.
Figure 1. Modulus at 30 °C as a function of decomposed dicumyl peroxide or added cross-linking.
Data of Tamura and Murakami [18].
An alternate scale of abscissas (upper scale) has been added to this figure to show X/(A1Vr) the number of moles of added cross-links per unit volume. This is based on eq. (2.2.2) of Part III [12].
| (2.4) |
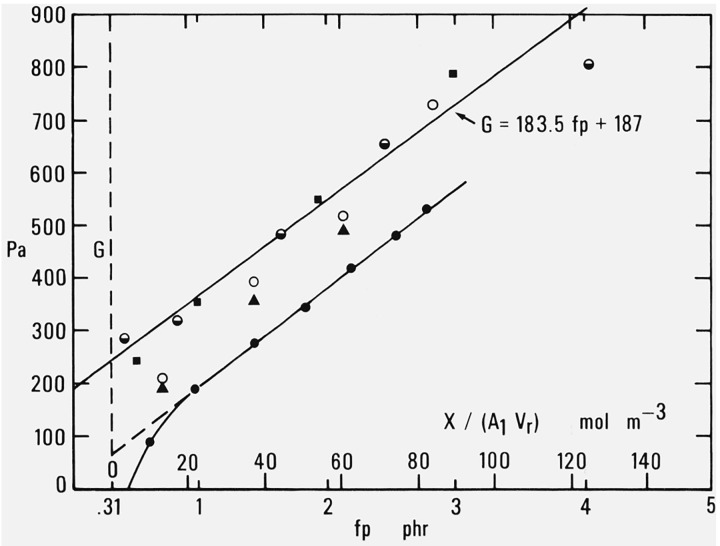
Additional data from four other more recent publications are shown in figure 2 together with the line representing eq (2.1) at 25 °C. In each case the values taken for the lower abscissa scale are derived as before by applying eqs (2.2) and (2.3) to the compounding and curing conditions reported by the respective authors.
Figure 2. Modulus at 25 °C as a function of decomposed dicumyl peroxide or added cross-linking.
Several different types of measurement are represented here. Extension measurements on unswollen rubber were made by Wood and Bullman [19] and by Melley and Stuckey [20]. Compression measurements on swollen rubber were made by Melley and Stuckey and by Redding and Smith [21]. Torsion measurements on unswollen rubber were reported by Gent and Kuan [22]. In all cases the results are expressed in terms of the shear modulus G of the unswollen rubber.
The intercepts corresponding to the data of Melley and Stuckey and of Redding and Smith are somewhat smaller than that given by the line representing eq (2.1). This probably reflects differences in purity or molecular weight of the rubber. The change of modulus with cross-linking however is in very good agreement with the other data.
Figures 1 and 2 thus confirm with additional data the figures given in Part I [10] and the results represented by eq (2.1). One would expect deviations only if there are appreciable deviations from the normal experimental conditions, such as differences in molecular weight or purity of the rubber.
We consider it highly desirable to follow this practice of first dealing as nearly as possible with directly observed quantities. Thus we prefer to plot as ordinate the time-dependent modulus rather than any other related mechanical property and to relate it to the amount of decomposed dicumyl peroxide as abscissa. Other quantities often used implicity assume the validity of the statistical theory of rubber elasticity or a particular form of stress-strain relation.
It is sometimes desirable to break down the modulus G into two parts – a component G* independent of temperature and a component G − G* varying with temperature [11]. For systems in which the internal energy does not vary significantly with temperature these components may be identified as an energy component and an entropy component respectively. For systems conforming to eq (2.1) with the constants found in earlier work [10].
| (2.5) |
and
| (2.6) |
At T = 298.15K
| (2.7) |
3. Mooney-Rivlin Coefficients C1 and C2
Many previous investigators have expressed experimental results in terms of the Mooney-Rivlin equation
| (3.1) |
where F is the stress (based on undeformed cross-sectional area) and L is the extension ratio, the ratio of stressed length to unstressed length. The Mooney-Rivlin equation with constant coefficients C1 and C2 is sometimes found to describe rubber behavior in uniaxial extension over certain limited regions [14, 15] but it is generally found experimentally that the constants cannot be uniquely correlated with derivatives of the strain energy function [23–27]. In a recent paper [15] the present author has pointed out the limited applicability of the equation and in particular its lack of validity in the region of low elongations and compressions, which are important in determining the shear modulus G and Young’s Modulus M. The only quantitative conclusion drawn was that
| (3.2) |
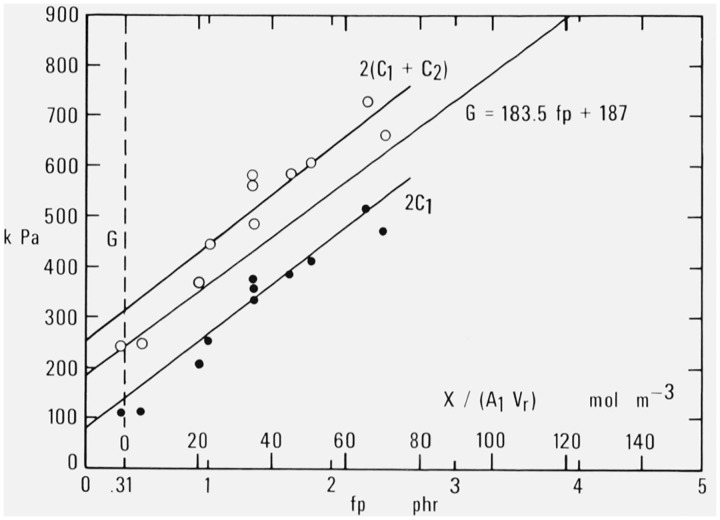
This conclusion is tested in figure 3, which shows a plot of experimental Mooney-Rivlin coefficients at 25 °C obtained by Mullins [28] by extension for natural rubber cross-linked by dicumyl peroxide. The values of 2(C1 + C2) are read from figures 2, 3, and 4 of Mullins’s paper, while the values of 2C1 are read from the same figures and given in his Table II. Mullins made no report of values of the modulus G itself.
Figure 3. Mooney-Rivlin constants and modulus at 25 °C as a function of decomposed dicumyl peroxide or added cross-linking.
Data of Mullins [28].
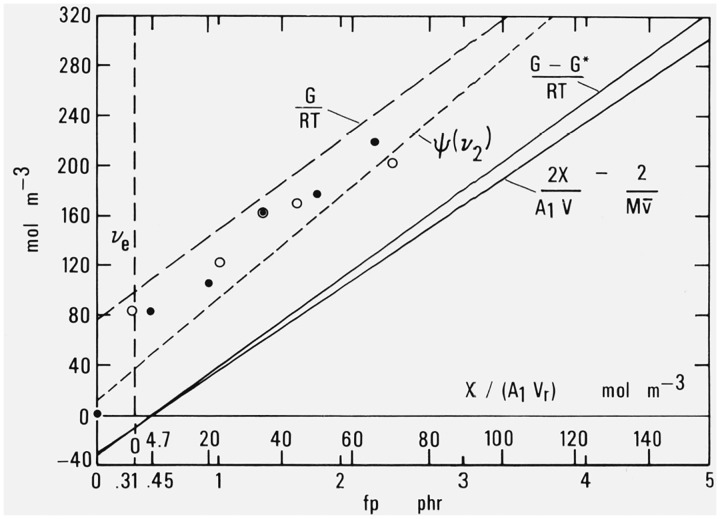
Figure 4. Effective sub-chain density (moles of effective sub-chains per unit volume) as a function of decomposed dicumyl peroxide or added cross-linking.
Lines from data summarized by Wood [12]
(G − G*)/RT = 71.26 fp − 32.1
ψ(v2) = 82.70 fp + 14.0
G/RT = 74.02 fp + 75.4
Flory-Rehner equation
ψ(v2) = [− ln(1 − v2) − v2 − μv22][V1−1][v21/3 − v2/2]−1
Experimental points from data of Mullins [28].
A comparison with the solid line representing eq (2.1) obtained in the NBS studies shows that G obtained there is indeed intermediate between 2C1 and 2(C1 + C2) as obtained by Mullins at each degree of cross-linking represented by the different specimens. The range of values for fp = 1.365 phr corresponds to a systematic variation in the molecular weight of the rubber before cross-linking from to 323,000. Thus it is not possible to equate the modulus G to either 2C1 or 2(C1 + C2), as has sometimes been suggested. Since the slopes of all three lines in figure 3 are nearly the same it appears that G differs from each of these quantities by a constant amount (roughly equal to about ± C2) over the range of cross-linking studied.
4. Swelling and Cross-Linking
An extensive literature survey in Part III [12] has considered 28 published papers reporting values of equilibrium swelling volume as a function of cross-linking for the dicumyl peroxide system.
In accordance with the practice of plotting a directly-observed quantity plots were made of equilibrium swelling volume as ordinate against cross-linking as abscissa. Different graphs were obtained with different swelling liquids. The slope decreased with increase of cross-linking. Flory and Rehner utilized statistical considerations to derive the following relation for the calculation of [G − G*]sw, the enthropy component of the modulus as determined from the equilibrium swelling.
| (4.1) |
Here v2 is the measured equilibrium volume fraction of rubber in the swollen material, V1 is the molar volume of the swelling liquid and μ is the Flory-Huggins interaction parameter characteristic of the rubber and the liquid. Its value is normally near 0.4. We denote the right hand member of the equation as RTψ(v2) for brevity.
Values of RTψ(v2) calculated from v2 data reported by five different observers showed reasonable agreement with each other. When plotted against the cross-linking in figure 2 of Part III [12] they all lay close to a single straight line, independent of the swelling liquid. The equation of the line with T = 298.15 K was
| (4.2) |
where the units of G are kPa. The previous paper [12] concluded that any differences among the remaining 23 reports of experimental results were small and could probably be explained in terms of minor differences in the specimens.
By a comparison of eq (4.2) with eq (2.7) it can be seen that the entropy component of the modulus obtained by the Flory-Rehner equation from equilibrium swelling measurements is considerably larger than that obtained from direct mechanical measurements at all degrees of cross-linking. It also increases about 16 percent more rapidly with increase of cross-linking. This is evident in figure 2 of our paper [12] where reference is made to earlier workers who also reported similar results.
5. Number of Effective Sub-Chains
As demonstrated in the preceding sections, there has been no serious disagreement among previous investigators regarding values of the modulus on its entropy component as measured by direct experiments at a given degree of cross-linking. Likewise there has been reasonably good agreement among investigators who have made swelling measurements. However the resulting entropy component of the modulus, calculated by the Flory-Rehner equation, is considerably larger than the corresponding component measured directly.
The difference in modulus components just mentioned leads immediately to a difference in calculated values of ve, the number of moles of effective sub-chains per unit volume. This is demonstrated in figure 4 where the modulus ordinates shown in figure 2 of Part III have merely been divided by the constant factor RT to give corresponding numbers of effective sub-chains.
The lowest line in figure 4 represents the number of added effective sub-chains when calculated from the number of added cross-links, making allowance for chain ends but not for entanglements. This line is simply based on the assumption that each added cross-link gives rise to exactly two effective sub-chains.
The next line, with slightly greater slope, represents values calculated from the direct modulus observations of many observers described in section 2, after making allowance for G*, the energy component. The equation used is the fundamental equation of the statistical theory of rubber elasticity.
| (5.1) |
The difference in slopes between the two lines is ascribed to the effect of entanglements [12].
The next higher line represents values of ve obtained from the investigations of equilibrium swelling volume discussed in section 4. The relation used is
| (5.2) |
and is based on the Flory-Rehner relation eq (4.1).
The highest line is that calculated from modulus observations without regard to the energy component G*, thus taking ve = G/RT.
The four lines shown are derived from a consensus of experimental results obtained in the previous NBS work [10–12] and in the literature. Reference should be made to the earlier papers for experimental points. As in the previous sections of this paper, all abscissa values are based on reported temperatures and times of cure.
The differences in the calculated values of ve shown in figure 4 can now be explained as arising from different causes. We first consider that the lowest line (based on cross-linking considerations) gives the value usually regarded as the most unambiguous calculation of the number of effective sub-chains. If one adds to this a number of pseudo sub-chains arising from entanglements he obtains the next line representing the number effective in direct measurements of modulus. The difference in any event is not large. The term effective has been thus broadened to include the effect of entanglements in this case.
Accepting the validity of the Flory-Rehner relation used in calculating the number of sub-chains effective in limiting swelling, we conclude from figure 4 that the number of sub-chains limiting swelling is indeed larger than twice the number of added cross-links as calculated from the amount of decomposed dicumyl peroxide or its approximately equivalent number effective in mechanical measurements.
The highest line, with ordinate G/RT, is drawn only for the purpose of comparison with the other lines. It is not useful for any other purpose, since it is not expected that this uncorrected quantity should bear any direct relationship to a number of cross-links or sub-chains. G includes an energy component not correlatable with a number of sub-chains. (G − G*), the entropy component is the correlatable quantity. G/RT is merely the number of sub-chains that would be calculated if the energy component of the modulus is assumed to be zero. Previous papers in the literature have often erroneously presented this ratio as ve.
The individual experimental points plotted in figure 4 are based on data reported by Mullins [28] in a widely-quoted systematic study of the dicumyl peroxide system. The Mooney-Rivlin coefficients C1 and C2 for the same specimens have already been presented in figure 3.
Mullins did not report values of cross-linking and so the abscissa values, like those in figure 3, are obtained from the reported conditions of cure. The ordinates in figure 4 are obtained from Mullins’ list [28, Table II] of values of Mc phys, the effective molecular weight of the sub-chains. These values were based on measurements of both equilibrium swelling and the Mooney-Rivlin constant C1 with several corrections and modifications previously developed [29–31].
We have utilized the relation
| (5.3) |
to give the values of ve plotted in figure 4.
It can be seen that the number of effective sub-chains calculated by the complicated procedures of Mullins, Moore and Watson [28–31] is appreciably greater than that obtained by the other calculations at a given cross-linking. However this number increases with increase of cross-linking at about the same rate.
6. Conclusions
Previous work [10–12] at the National Bureau of Standards led to the development of eq (2.1).
This predicts linearity of modulus with temperature at constant cross-linking. A careful search of the literature on the dicumyl peroxide system did not reveal any satisfactory modulus-temperature data at constant cross-linking for comparison with that in the original NBS work [10]. Consequently comparisons of modulus had to be limited to values at 25 or 30 °C.
The equation also predicts linearity of modulus with cross-linking at constant temperature. Numerous studies at room temperature in other laboratories confirmed this linearity (except at low degrees of cross-linking) and gave satisfactory agreement with the constants previously given. The slope of the line, (ST + H) given in the NBS work was about 10.5 percent greater than that calculated from molecular considerations, disregarding entanglements [11]. The values found in the literature were in fairly good agreement with slopes ranging from 5 to 31 percent greater. The intercept of the plot of modulus against cross-linking was found to range from 15 to 200 kPa (with most data near the higher value) in good agreement with the value 187 kPa found in the NBS work. This would be expected to vary with differences in initial molecular weight and purity of the rubber used. In the original work [11] it was concluded that the molecular weight (assuming monodispersity) was about 200,000, and that the impurities rendered unavailable for cross-linking about 0.31 phr of the added dicumyl peroxide [5].
Values of the Mooney-Rivlin coefficients C1 and C2 obtained in a study by Mullins [28] showed that the modulus G obtained from eq (2.1) is indeed intermediate between 2C1 and 2(C1 + C2) at a given degree of cross-linking. All three quantities increased with increase of cross-linking at approximately the same rate.
The number of moles of sub-chains effective in mechanical measurements is found to be essentially twice the number of cross-links calculated from the amount of decomposed dicumyl peroxide (especially when the necessary small corrections are made for chain ends, wasted peroxide and entanglements). For a given amount of cross-linking, the number of moles of sub-chains effective in limiting swelling is appreciably greater than that effective in mechanical measurements. The increase in this number with increase of cross-linking is about 16 percent greater than the corresponding increase for mechanical measurements.
Footnotes
Figures in brackets indicate literature references at the end of this paper.
7. References
- [1].Hummel K., Scheele W., and Hillmer K. H., Vulcanization of natural rubber by dicumyl peroxide in the absence of additives, Kautschuk und Gummi 14 (6) WT 171 (1961). [Google Scholar]
- [2].Lorenz O. and Parks C. R., Cross linking efficiency of some vulcanizing agents in natural rubber, J. Polymer Sci. 50, 299 (1961). [Google Scholar]
- [3].Thomas D. K., Cross linking efficiency of dicumyl peroxide in natural rubber, J. Applied Polymer Sci. 6, 613 (1962). [Google Scholar]
- [4].Loan L. D., Cross linking efficiencies of cumyl peroxide in unsaturated synthetic rubbers, J. Applied Polymer Sci 7, 2259 (1963); Rubber Chem Technol 38, 573 (1965). [Google Scholar]
- [5].van der Hoff B.M.E., Reactions between peroxide and diolefins, I. & E. C. Product Research & Development 2, 273 (1963); Rubber Chem Technol 38, 560 (1965). [Google Scholar]
- [6].Bristow G. M., Estimation of chain scission during vulcanization, III Temperature effects in the peroxide vulcanization of natural rubber, J. Applied Polymer Sci. 9, 3255 (1965). [Google Scholar]
- [7].Bristow G. M., Moore C. G., and Russell R. M., Determination of degree of cross-linking in natural rubber vulcanizates, VII Cross linking efficiencies of di-tert-butyl and dicumyl peroxides in the vulcanization of natural rubber and their dependence on the type of rubber, J. Polymer Sci. A3, 3893 (1965). [Google Scholar]
- [8].Loan L. D., Mechanism of the peroxide vulcanization of elastomers, Rubber Chem Technol, 40, 149 (1967). [Google Scholar]
- [9].Manik S. P. and Banerjee S., Determination of chemical cross-links in rubbers, Angew. Makromol. Chem. 6, 171 (1969). [Google Scholar]
- [10].Wood Lawrence A., Bullman George W., and Decker George E., Modulus of natural rubber cross-linked by dicumyl peroxide, I Experimental Observations, J. Res. Nat. Bur. Stand. (U.S.), 76A (Phys. and Chem.), No. 1, 51–59 (January-Feb 1972); Rubber Chem. Technol. 45, 1388 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Wood Lawrence A., Modulus of natural rubber cross-linked by dicumyl peroxide, II Comparison of theory, J. Res. Nat. Bur. Stand. (U.S.), 77A (Phys. and Chem.), No. 1, 171–177 (January-Feb 1973); Rubber Chem. Technol. 45, 1287 (1973). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Wood Lawrence A., Modulus of natural rubber cross-linked by dicumyl peroxide, III Some molecular interpretations, possible refinements of theory, and conclusions, J. Res. Nat. Bur. Stand. (U.S.) 80A, (Phys. and Chem.), No. 3, 451–463 (May-Jun 1976); Rubber Chem. Technol. 50, 233 (1977). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Martin G. M., Roth F. L., and Stiehler R. D., Behavior of pure-gum rubber vulcanizates in tension, Trans. Inst. Rubber Industry 32 (6) 189 (1956); Rubber Chem. Technol 30, 876 (1957). [Google Scholar]
- [14].Wood Lawrence A., Stress-strain relation of pure-gum rubber vulcanizates in compression and tension, J. Res. Nat. Bur. Stand. (U.S.) 60, No. 3, 193–199 (March 1958); Rubber Chem. Technol. 32, 1 (1959). [Google Scholar]
- [15].Wood Lawrence A., Uniaxial extension and compression in stress-strain relations in rubber, J. Res. Nat. Bur. Stand. (U.S.), 82, No. 1, 57–63 (Jul-Aug 1977); Rubber Chem. Technol. 51, 840 (1978). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Chasset R. and Thirion P., Viscoelastic relaxation of rubber vulcanizates between the glass transition and equilibrium, Proc. Int. Conf. (Non-crystalline Solids Delft 1964) J. A. Prins, Ed. p. 345 (North Holland Publishing Co. Amsterdam, Interscience New York 1965); Rubber Chem Technol 39, 870 (1966), Rev. Gen. Caoutchouc 44, 1041 (1967). [Google Scholar]
- [17].Plazek D. J., Effect of crosslink density on the creep behavior of natural rubber vulcanizates, J. Polymer Sci. A-2 4 745 (1966). [Google Scholar]
- [18].Tamura S. and Murakami K., Determination of network chain density and the chemical stress relaxation of cross linked polymers, J. Applied Polymer Sci. 16 1149 (1972); Rubber Chem. Technol 46, 477 (1973). [Google Scholar]
- [19].Wood L. A. and Bullman G. W., Creep and other tensile properties of rubber cross-linked by dicumyl peroxide, J. Polymer Sci A-2 10, 43 (1972). [Google Scholar]
- [20].Melley R. E. and Stuckey J. E., Determination of crosslink density from compression modulus data, J. Applied Polymer Sci 14, 2327 (1970). [Google Scholar]
- [21].Redding R. B. and Smith D. A., Rapid measurement of the chemical contribution to network chain density for natural rubber, J. Polymer Sci. C30, 491 (1970). [Google Scholar]
- [22].Gent A. N. and Kuan T. H., Thermoelasticity of stretched elastomers under small torsions: effects of crosslinking, extension and swelling, J. Polymer Sci. Phys. Ed. 11, 1723 (1973). [Google Scholar]
- [23].Rivlin R. S. and Saunders D. W., Large elastic deformations of isotropic materials, VII Experiments on the deformation of rubber, Phil. Trans. Roy. Soc London A 243, 251 (1951). [Google Scholar]
- [24].Wood Lawrence A., The elasticity of rubber, J. Washington Acad. Sci. 47, 281 (1957); Rubber Chem Technol. 31, 959 (1958). [Google Scholar]
- [25].Jones D. F. and Treloar L. R. G., The properties of rubber in pure homogeneous strain, J. Phys. D. Applied Phys. 8, 1285 (1975). [Google Scholar]
- [26].Penn R. W. and Kearsley E. A., The scaling law for finite torsion of elastic cylinders, Trans. Soc. Rheology 20:2, 227 (1976). [Google Scholar]
- [27].Kawabata S. and Kawai H., Strain energy density functions of rubber vulcanizates from biaxial extension, Advances in Polymer Science (Fortschritte der Hochpolymeren Forschung) 24, 89 (1977). [Google Scholar]
- [28].Mullins L., Determination of degree of cross-linking in natural rubber vulcanizates, IV Stress-strain behavior at large extensions, J. Applied Polymer Sci. 2, 257 (1959), Rubber Chem Technol 34, 290 (1961). [Google Scholar]
- [29].Mullins L, Determination of degree of cross-linking in natural rubber vulcanizates I, J. Polymer Sci. 19, 225 (1956). [Google Scholar]
- [30].Moore C. G. and Watson W. F., Determination of degree of cross linking in natural rubber vulcanizates, II, J. Polymer Sci 19, 237 (1956). [Google Scholar]
- [31].Mullins L., Determination of degree of cross-linking in natural rubber vulcanizates III, J. Applied Polymer Sci. 2, 1 (1959), Rubber Chem Technol 34, 279 (1961). [Google Scholar]