Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2019 Apr 3;180(3):1406–1417. doi: 10.1104/pp.19.00094

The Spatial Distribution of Chlorophyll in Leaves1,[OPEN]

Aleca M Borsuk 1, Craig R Brodersen 1,2,3
PMCID: PMC6752913  PMID: 30944156

Relative chlorophyll concentration as a function of leaf depth is a remarkably conserved trait across a wide diversity of plant taxa and can be described by a simple mathematical model.

Abstract

Measuring and modeling the spatial distribution of chlorophyll within the leaf is critical for understanding the relationship between leaf structure and carbon assimilation, for defining the relative investments in leaf tissues from the perspective of leaf economics theory, and for the emerging application of in silico carbon assimilation models. Yet, spatially resolved leaf chlorophyll distribution data are limited. Here, we used epi-illumination fluorescence microscopy to estimate relative chlorophyll concentration as a function of mesophyll depth for 57 plant taxa. Despite interspecific variation due to differences in leaf thickness, mesophyll palisade fraction, and presence of large intercellular airspaces, the spatial distribution of chlorophyll in laminar leaves was remarkably well conserved across diverse lineages (ferns, cycads, conifers, ginkgo, basal angiosperms, magnoliids, monocots, and eudicots) and growth habits (tree, shrub, herbaceous, annual, perennial, evergreen, and deciduous). In the typical leaf, chlorophyll content increased gradually as a function of depth, peaking deep within the mesophyll. This chlorophyll distribution pattern is likely coupled to adaxial and abaxial intraleaf light gradients, including the relative enrichment of green light in the lower leaf. Chlorophyll distribution for the typical leaf from our dataset was well represented by a simple mathematical model (R2 = 0.94). We present chlorophyll distribution data and model equations for many ecologically and commercially relevant species and plant functional types (defined according to chlorophyll profile similarity, clade, and leaf thickness). These findings represent an advancement toward more accurate photosynthesis modeling and increase our understanding of first principles in intraleaf physiology.

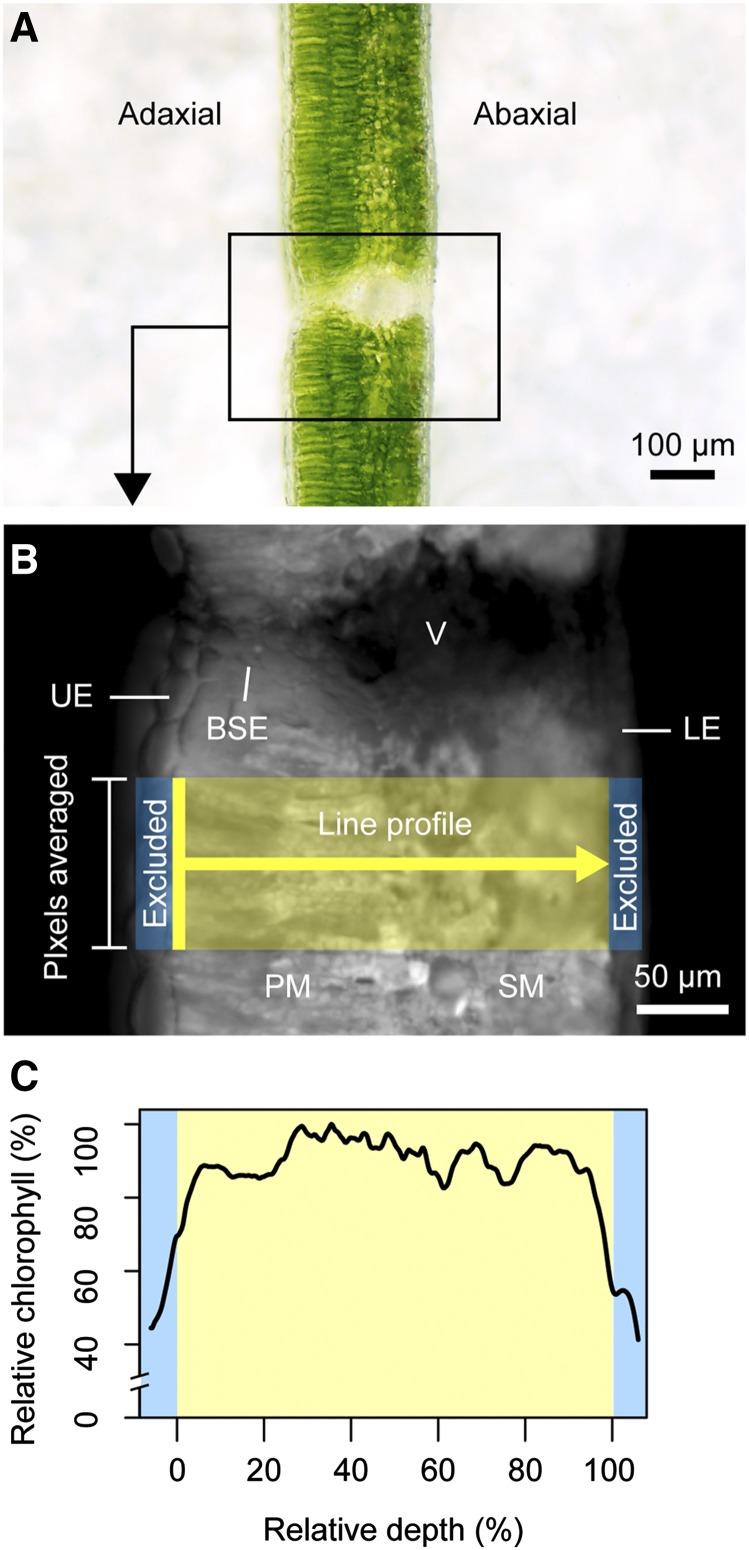
The biochemistry of photosynthesis and biophysical processes that constrain it are intrinsically linked within the landscape of the inner leaf. Because leaf tissue is heterogeneous in structure as well as photosynthetic capacity (Smith et al., 1997; Adams and Terashima, 2018; Earles et al., 2019), it follows that chlorophyll may also be spatially heterogeneous. Yet, while bulk chlorophyll content of leaves can be readily measured (Porra et al., 1989; Palta, 1990), fewer studies have systematically dissected the leaf to determine how chlorophyll content is partitioned across the photosynthetic domain or mesophyll (Vogelmann and Evans, 2002; Johnson et al., 2005; Evans and Vogelmann, 2006; Brodersen and Vogelmann, 2010; Slattery et al., 2016). The paucity of spatially resolved chlorophyll distribution data available at present is likely due to the historically labor- and time-intensive processes of obtaining such data, requiring extraction of chlorophyll from thin paradermal sections (Bornman et al., 1991; Cui et al., 1991; Nishio et al., 1993) or counting chloroplasts with a light microscope (e.g. Aalto and Juurola, 2002). However, epi-illumination chlorophyll fluorescence offers a simple and rapid method of measuring relative chlorophyll distribution within cell layers of a leaf (Vogelmann and Evans, 2002). In this method, a fresh leaf is cut transversely, placed under a microscope (Fig. 1A), and irradiated with an excitation wavelength orthogonal to the cut surface. Autofluorescence emitted from chlorophyll is captured with a charge-coupled device (CCD) camera with a bandpass filter to collect only light generated from fluorescence. Pixel intensity in the grayscale images derived from this method is proportional to relative chlorophyll content according to a 1:1 relationship, as reported in detail by Vogelmann and Evans (2002). Relative chlorophyll content can then be measured directly from images using image analysis software (Fig. 1B) to obtain chlorophyll distribution (Fig. 1C). To the best of our knowledge, the epi-illumination fluorescence technique has only been used to measure leaf chlorophyll distribution for seven species—spinach (Spinacia oleracea; Vogelmann and Evans, 2002), Rhododendron catawbiense, Abies fraseri, Picea rubens (Johnson et al., 2005), Eucalyptus pauciflora (Evans and Vogelmann, 2006), snapdragon (Antirrhinum majus), and sunflower (Helianthus annuus; Brodersen and Vogelmann, 2010). Using light sheet microscopy, a modified form of this method, Slattery et al. (2016) were able to make similar measurements in a soybean (Glycine max) cultivar and mutant. These studies reported that chlorophyll content in laminar leaves is nonuniform, with the lowest concentration in the palisade mesophyll near the adaxial surface and higher concentrations in the medial and abaxial domains. Johnson et al. (2005) introduced the model equation

Figure 1.

Figure 1.

Open in a new tab

Overview of the epi-illumination method. In brief, leaf samples are dark-adapted for ∼20 min before transverse sections (A) are cut and placed on damp filter paper for imaging. Samples are irradiated (<30 s), and fluorescence from chlorophyll is detected with a CCD camera. Chlorophyll content is proportional to pixel intensity in the resulting grayscale images (B; Vogelmann and Evans, 2002). The 1D chlorophyll distribution is measured in ImageJ using a line profile (line width mean of ∼100 pixels, or ∼60 µm at 20× magnification) drawn through the photosynthetic tissue. Nonphotosynthetic features such as veins (V), bundle sheath extensions (BSE), and upper epidermal (UE) and lower epidermal (LE) cells are excluded from the measurements. The profile begins at the upper edge of the mesophyll (e.g. palisade mesophyll if present; PM) and ends at the lower edge of the spongy mesophyll (SM). Previous studies using this technique included the epidermal cell layer (shown in C; blue bars), potentially making chlorophyll profiles look more bell-shaped than with this method. Chlorophyll profiles are normalized as a function of maximum intensity to allow for comparison (absolute fluorescence intensity varies across samples because of slight differences in exposure parameters and signal decay over time) and are represented as a function of relative depth (C; 0%, upper edge of mesophyll; 100%, lower edge of mesophyll).

graphic file with name PP_201900094DR2_equ1.jpg

to express relative chlorophyll content (y) as a function of leaf depth (x) in vertical profiles of R. catawbiense and A. fraseri (both laminar or relatively flattened) leaves. Yet, because of the lack of chlorophyll distribution data in the literature and the wide variability in leaf form, it is unclear whether this characterization represents the rule or the exception.

In theory, as a light-harvesting molecule, chlorophyll should be well coordinated spatially with intraleaf light availability. Yet, Nishio et al. (1993) showed that carbon fixation gradients in S. oleracea leaves do not follow leaf internal light gradients, which decrease exponentially through the leaf. Instead, carbon fixation was higher in the middle of the leaf, with spongy mesophyll contributing significantly (40%) to total carbon reduction. This is largely counter-intuitive, assuming that carbon fixation should be highest at the upper leaf surface, where there is the most light available. Yet, observed increases in chlorophyll within the middle of leaves has been observed in multiple species (using paradermal sectioning; Bornman et al., 1991; Cui et al., 1991), with the suggestion that this would balance the decline in the amount of available light from the adaxial and/or abaxial surfaces. Here, we note that light gradients, and therefore chlorophyll distribution, could be altered by palisade mesophyll, which may propagate light deeper into the leaf (Smith et al., 1997; Johnson et al., 2005). Studies have also demonstrated the importance of different rates of light extinction through the leaf between strongly absorbed (e.g. blue, red) and weakly absorbed (e.g. green) wavelengths. Cui et al. (1991) found that while strongly absorbed wavelengths such as blue and red are 90% attenuated in the upper 20% of leaves, medial and deep leaf tissues remain relatively enriched in green light. Interestingly, Sun et al. (1998) reported that green light drove more CO2 fixation than red or blue light in deep leaf tissues of S. oleracea. Evans and Vogelmann (2003) also reported that photosynthetic capacity matched the profile of green but not white light absorption in S. oleracea leaves. Taken together, studies such as these have contributed to the growing understanding of the role of green light in driving photosynthesis deep within leaf tissues (Terashima et al., 2009; Smith et al., 2017). These reports are also consistent with the concept of the intraleaf environment as an analog to a canopy, with vertical gradients in light quantity and quality. Terashima et al. (2009) noted, for example, that chloroplasts acclimate to the local light environment, resulting in a gradient of sun and shade characteristics. Terashima et al. (2009) also reported that chloroplasts in the lowermost part of S. oleracea leaves exhibit 20% to 40% of the maximal photosynthetic capacity of the chloroplasts closest to the adaxial surface. These data were used by Tholen et al. (2012) to model the fraction of chlorophyll in palisade versus spongy mesophyll and the photosynthetic rate that could be sustained by green light. Assuming that S. oleracea chloroplasts in the lowermost part of the leaf exhibit 20% of the maximal photosynthetic capacity of those in the uppermost part, photosynthetic capacity was maximized by a roughly equal (∼50%) distribution of chlorophyll between palisade and spongy mesophyll tissues.

Based on these precedents, in a laminar leaf receiving irradiation primarily from the adaxial surface we anticipate that relative chlorophyll content would increase toward the abaxial domain as a response to the decline in available light and/or the relative enrichment of weakly absorbed green light and would be well characterized by the model equation y = y0 + ax + bx2 proposed by Johnson et al. (2005). Yet, carbon assimilation requires more than light, namely CO2 and water. Interestingly, leaf veins represent a nexus of distribution of these resources. Specifically, leaf vein-to-vein and vein-to-evaporative surface spacing is highly conserved (Noblin et al., 2008; Zwieniecki and Boyce, 2014), especially in derived taxa. Thus, we also anticipated that chlorophyll content might peak at a depth coincident with leaf veins.

The aim of this study was to describe the spatial distribution of chlorophyll as a function of leaf depth in bulk mesophyll domains of laminar leaves across broad levels of phylogenetic diversity. These observations were intended to expand the number of species for which empirical chlorophyll distribution data are available, articulate any common scheme(s) in chlorophyll distribution within bulk mesophyll domains, and initiate an understanding of associations between chlorophyll distribution, light environment, leaf anatomy, and the optimization of photosynthesis relative to the multiple competing biophysical demands placed on a leaf.

Toward this, we used epi-illumination fluorescence microscopy to measure chlorophyll distributions within vertical (transverse) leaf profiles of 57 species from eight major terrestrial plant clades (ferns, cycads, conifers, ginkgo, basal angiosperms, magnoliids, monocots, and eudicots), representing a diversity of growth habit, habitat, and leaf form (e.g. tree, shrub, herbaceous, annual, perennial, evergreen, and deciduous plant species; Supplemental Table S1). Seven congeneric pairs (Acer, Arenga, Begonia, Dioon, Encephalartos, Quercus, and Zamia) were included in this dataset to explore variability within a genus in basal and derived groups. Hierarchical cluster analysis and mean model approaches were used to articulate patterns in chlorophyll distribution. We also characterized leaf thickness, vein depth, and palisade fraction of mesophyll to examine possible relationships between patterns in chlorophyll content and major anatomical traits (Supplemental Table S1). In a subset of species, we measured monochromatic light absorption profiles following the methods of Brodersen and Vogelmann (2010) to characterize the relationship between intraleaf light environment and chlorophyll distribution.

The results of this work could be used for research focused on the relative investments in leaf tissues from the perspective of leaf economics theory (Shipley et al., 2006; Reich, 2014) or the relationship between leaf structure and carbon assimilation (Terashima et al., 2011; Earles et al., 2019). This information is also relevant to the emerging application of in silico carbon assimilation models for testing first principles in plant physiology and toward engineering increased performance and resiliency in agricultural crops (Tholen et al., 2012; Ort et al., 2015). While such models may incorporate fine-scale phenomena such as intraleaf CO2 diffusion (Pieruschka et al., 2006; Morison et al., 2007; Terashima et al., 2011; Tholen et al., 2014; Ho et al., 2016; Earles et al., 2018), hydraulics (Noblin et al., 2008; Zwieniecki and Boyce, 2014), and light propagation (Smith et al., 1997, 2017; Sun et al., 1998; Vogelmann and Gorton, 2014; Ichiro et al., 2016), similarly resolved chlorophyll distribution data are not yet widely available or well understood. This is evident from the multiple approaches used for parameterizing chlorophyll distribution in leaf carbon assimilation models, including as a homogeneous biochemical domain (Oguchi et al., 2011; Tholen and Zhu, 2011; Earles et al., 2017).

RESULTS

Chlorophyll Profiles of Individual Species

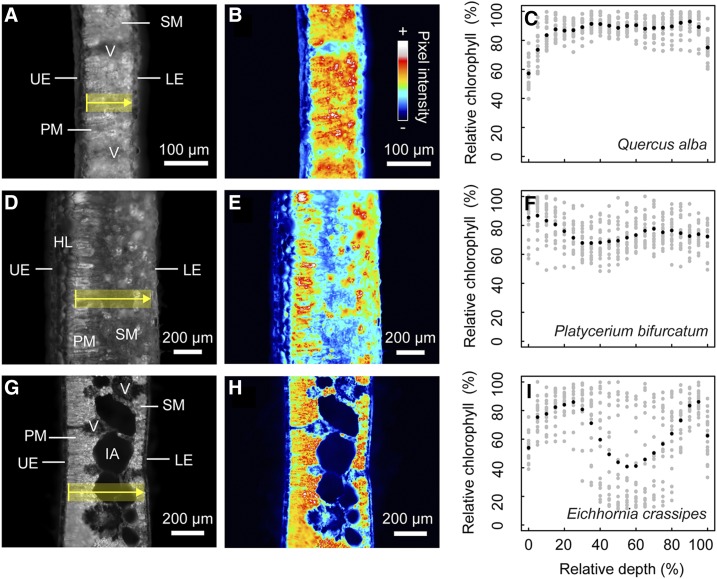
To visually assess the chlorophyll distribution, or chlorophyll profiles, of individual species, mean chlorophyll content was plotted as a function of mesophyll depth (n = 3 profiles were collected for each leaf, and n = 2–6 leaves were collected for each species; Supplemental Fig. S1). The profile expressed by Quercus alba is representative of many of the species in this study, where chlorophyll content was relatively uniform or increased slightly toward the abaxial surface (Fig. 2, A–C). In some species, such as the fern Platycerium bifurcatum (Fig. 2, D–F), chlorophyll content was clearly partitioned into two domains, concentrating chlorophyll in either palisade and/or spongy mesophyll just below the epidermis (Fig. 2E). Yet, for most species, it was unclear whether mesophyll tissue type was coordinated with changes in relative chlorophyll content (e.g. Dioon merolae, Amorphophallus titanum, Arenga engleri; Supplemental Fig. S1) or whether chlorophyll content was relatively uniform across the leaf, i.e. did not change despite differentiation of mesophyll (e.g. Q. alba, Fig. 2,A–C; Acer saccharum, Drimys winteri, Robinia pseudoacacia; Supplemental Fig. S1). The presence of large intercellular airspaces depressed local chlorophyll content in some leaves, such as with the aquatic plant Eichhornia crassipes (Fig. 2, G–I), and the spatial heterogeneity of these intercellular airspaces led to increased variability compared to areas of the leaf with lower porosity (Fig. 2H). Where congeneric pairs were measured, the chlorophyll profiles were remarkably similar, particularly in the cases of Acer and Quercus from the derived eudicot clade (Supplemental Fig. S1).

Figure 2.

Figure 2.

Open in a new tab

Differences in chlorophyll distribution for three representative species. Q. alba (A–C), P. bifurcatum (D–F), and E. crassipes (G–I). At left, a typical grayscale fluorescence image is shown for each species (A, D, and G), where the yellow transect indicates the section of tissue in a single measurement; chlorenchyma domains such as palisade (PM) and spongy mesophyll (SM) are included in the measurements, whereas nonphotosynthetic structures such as veins (V), upper epidermal (UE) and lower epidermal (LE) layers, and hypodermal layers (HL) are excluded. Intercellular airspaces (IA) in E. crassipes are included in the measurements and increase local variability in mean profiles. Heat maps (B, E, and H) of the same images help to highlight trends in chlorophyll distribution. Multiple (n > 6) line profiles are measured (gray points; C, F, and I) to describe the mean chlorophyll profile (black points; C, F, and I) for an individual species. Chlorophyll content (as a percentage of the absolute chlorophyll maximum) is displayed as a function of relative depth (percentage depth from upper to lower edge of mesophyll).

Major Patterns in Chlorophyll Distribution

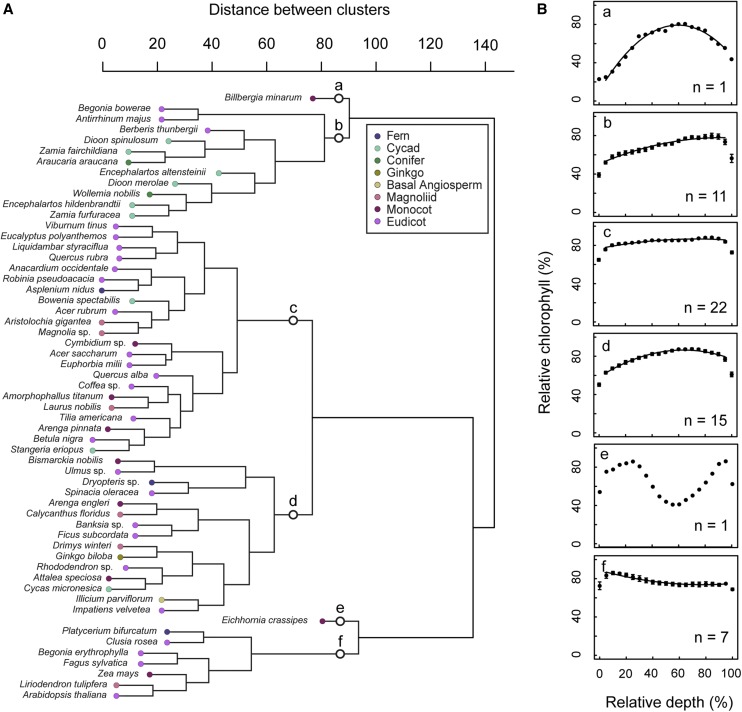
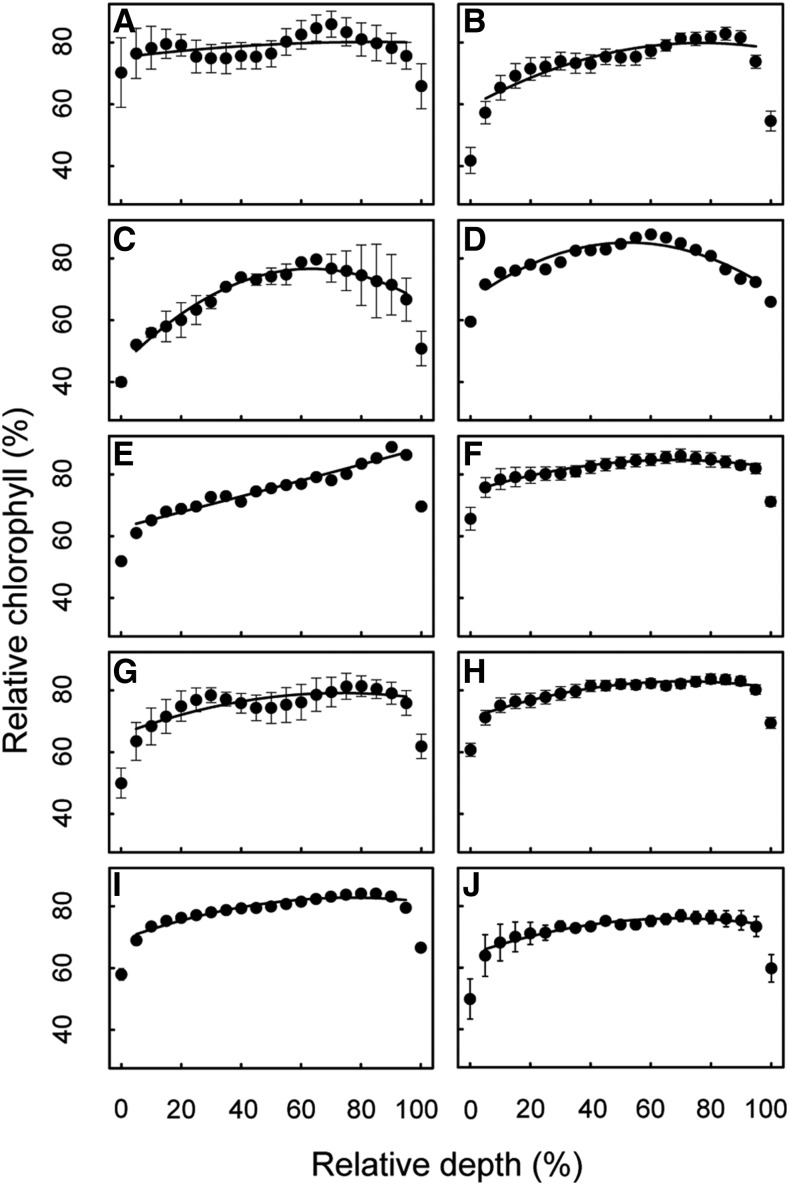
A hierarchical cluster analysis was used to identify common patterns in the chlorophyll profiles without imposing a priori classification. This indicated the presence of six clusters or groups of species with similar chlorophyll profiles (Fig. 3A, a–f). To aid in comparing the major patterns, the mean chlorophyll profile of each group was analyzed according to the model equation (Eq. 1) using quadratic regression (Fig. 3B). Numerical coefficients for the regression curves are found in Table 1. As discussed in detail in the “Materials and Methods” section, the first and last relative depth values (relative depth = 0, 100) or where mesophyll was bordered by epidermal layers are not part of the photosynthetic domain and are excluded from all regressions. Group (a) contained a single species, the bromeliad Billbergia minarum. This species had an atypical leaf form in our dataset due to a multiple-layer hypodermis (which was not included in measurements but may have influenced chlorophyll distribution indirectly). B. minarum had markedly lower chlorophyll content in the adaxial chlorenchyma (n = 1, R2 = 0.98, F(2,16) = 426.5, P < 0.000). Group (b) was dominated by gymnosperms (predominantly cycads; mean = 0.482 mm, se = 0.051). Species in group (b) exhibited a gradual increase in chlorophyll from the adaxial side and maxima shifted heavily to the abaxial domain (n = 11, R2 = 0.96, F(2,16) = 172, P < 0.000). Group (c) was the largest group. This group was phylogenetically diverse, containing fern, cycad, magnoliid, monocot, and eudicot taxa and was typified by a uniform distribution (n = 22, R2 = 0.86, F(2,16) = 48.9, P < 0.000). Group (d) was also phylogenetically diverse, with a typical profile similar to groups (b) and (c), but with a gradual tapering of chlorophyll content at both adaxial and abaxial edges (n = 15, R2 = 0.98, F(2,16) = 363.9, P < 0.000). The outlier E. crassipes comprised group (e). This was separated from the other groups because of a local depression in the center of the mesophyll reflective of large intercellular airspaces. The model equation was not applied to this profile because of its divergence from the typical parabolic shape. Group (f) was unique in that it contained profiles with chlorophyll maxima in the adaxial domain (n = 7, R2 = 0.93, F(2,16) = 100.7, P < 0.000), also from diverse lineages (i.e. fern, eudicot, monocot, magnoliid).

Figure 3.

Figure 3.

Open in a new tab

Clustered display of chlorophyll profile data for 57 species. Dendrogram showing the relationship among species chlorophyll profiles (A). The presence of six major profile schemes (groups a–f) is indicated. Mean chlorophyll profiles of the species in each cluster are shown in B. Chlorophyll content (as a percentage of the absolute chlorophyll maximum) is displayed as a function of relative depth (percentage depth from upper to lower edge of mesophyll). Points and error bars represent mean ± se. se bars less than ∼3.0 are below resolution.

Table 1. Numerical Coefficients for the Equation y = y0 + ax + bx2 for Models Based on Cluster Analysis, Clade, and Leaf Thickness.

NA, Model equation could not be fitted to data.

Model y0 a b
Cluster a 10.50834 2.31279 −0.01941
Cluster b 50.45836 0.59300 −0.00321
Cluster c 76.51942 0.27804 −0.00191
Cluster d 58.27920 0.88874 −0.00699
Cluster e NA NA NA
Cluster f 88.74845 −0.38816 0.00250
Fern NA NA NA
Cycad 59.28052 0.53491 −0.00348
Conifer 45.26811 0.99436 −0.00787
Ginkgo 66.61461 0.70577 −0.00672
Basal angiosperm 61.51000 1.24990 0.00160
Magnoliid 74.46951 0.30182 −0.00223
Monocot 65.78703 0.36470 −0.00249
Eudicot 71.05103 0.33471 −0.00236
Thin leaf 69.24298 0.35299 −0.00229
Thick leaf 64.36971 0.33783 −0.00245
Open in a new tab

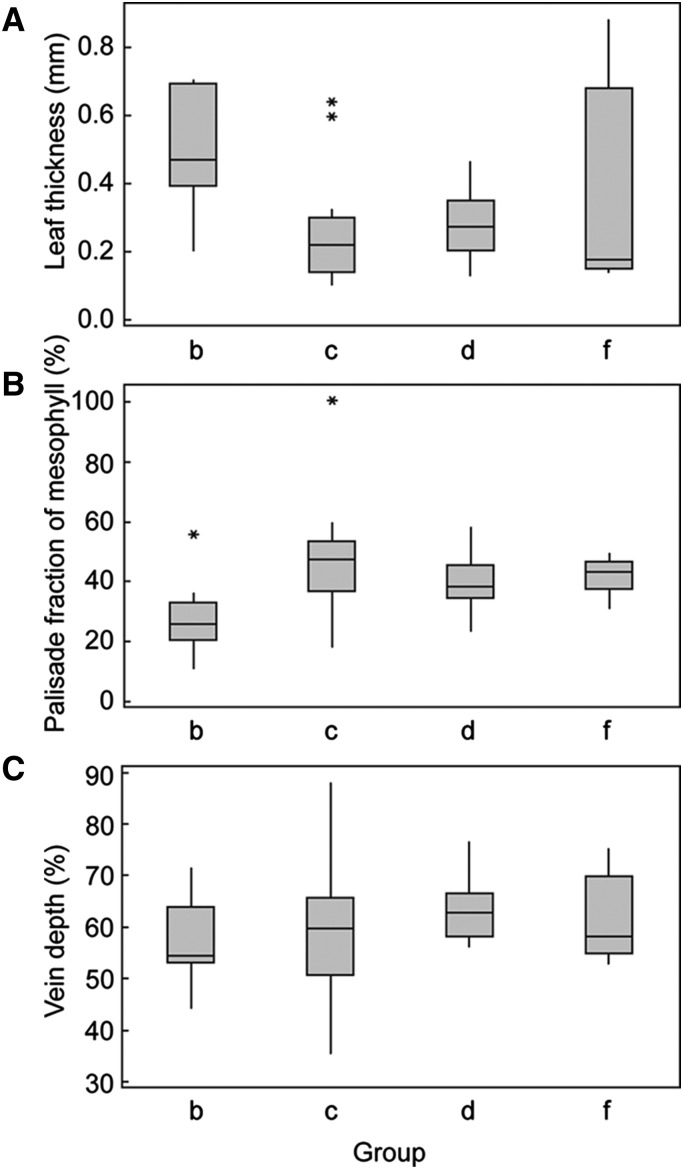
One-way ANOVAs were conducted to determine if groups of species with similar chlorophyll profiles (groups derived from the cluster analysis) differed in anatomical traits anticipated to influence chlorophyll distribution (i.e. leaf thickness, palisade fraction of mesophyll, and vein depth). Groups (a) and (e) with only one species were excluded from the analyses. Boxplots illustrating the differences in traits by group are shown in Figure 4. There was a statistically significant difference in leaf thickness between groups [R2 = 0.25, F(3,54) = 5.65, P = 0.002] as determined by one-way ANOVA. A Tukey post-hoc test revealed that leaves from the taxonomically diverse groups (c; mean leaf thickness = 0.2449 ± 0.1386 mm, P = 0.002) and (d; mean leaf thickness = 0.2788 ± 0.1002 mm, P = 0.020) were significantly thinner compared to leaves from group (b), which was dominated by gymnosperms (mean leaf thickness = 0.4835 ± 0.1780 mm). One-way ANOVA analysis indicated a statistically significant difference in the palisade fraction of mesophyll between groups [R2 = 0.23, F(3,47) = 4.38, P = 0.009]; a Tukey post-hoc test showed that this difference was only significant (P = 0.004) between groups (b; mean palisade fraction of mesophyll = 27.56% ± 12.07%) and (c; mean palisade fraction of mesophyll = 46.81% ± 17.68%). There were no statistically significant differences in vein depth between groups.

Figure 4.

Figure 4.

Open in a new tab

Differences in traits among groups with distinct chlorophyll profiles. Box plots of leaf thickness (A), palisade fraction of mesophyll (B), and relative vein depth (C) by group derived from hierarchical cluster analysis. Excludes groups a and e with single species. Boxes represent interquartile range and lines across boxes represent group median. Whiskers extend from the upper and lower quartiles to the group maximum and minimum, respectively. Asterisks represent sample outliers.

A General Model for Chlorophyll Distribution in Laminar Leaves

Quadratic regression was applied to the mean chlorophyll profile of the 57 species in our study, resulting in the following general model of relative chlorophyll distribution for the mean or typical leaf:

graphic file with name PP_201900094DR2_equ2.jpg

(R2 = 0.94, F(2,16) = 127.3, p < 0.001; Fig. 5). Thus, for the typical leaf from our dataset, chlorophyll increased gradually as a function of leaf depth, with minor depressions in chlorophyll content at the outermost edges of the mesophyll. The highest chlorophyll concentration occurred at 83% (se = 1.0) relative mesophyll depth, which is highly shifted towards the abaxial surface and deeper than the mean vein position (∼60% relative mesophyll depth) and mean transition point between the palisade and spongy tissue layers (∼38% relative mesophyll depth). This extends the work of Johnson et al. (2005) who first introduced a model equation (Eq. 1) to describe chlorophyll distribution in leaves of two species, R. catawbiense and A. fraseri.

Figure 5.

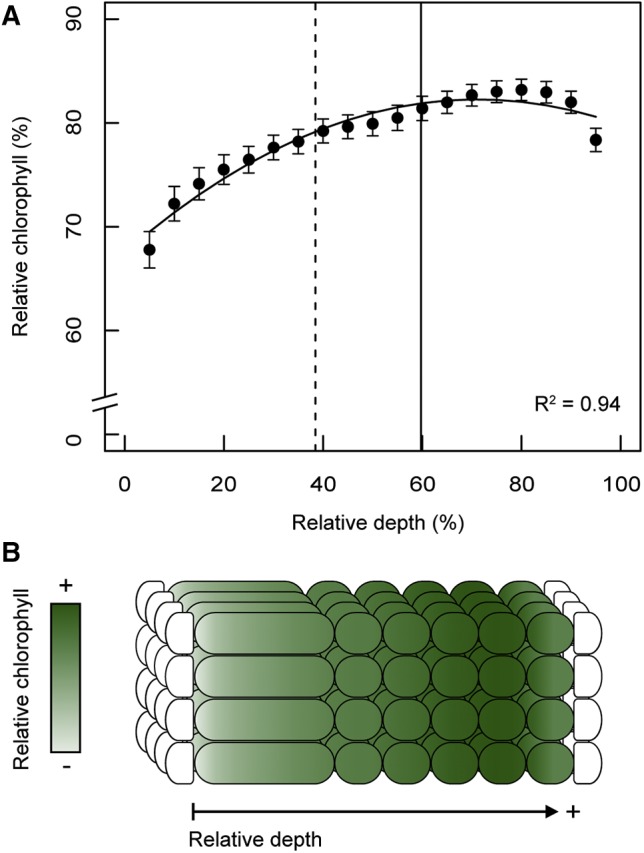
Figure 5.

Open in a new tab

General model of chlorophyll distribution. Mean chlorophyll distribution of 57 species as a function of mesophyll depth (A). Chlorophyll content (as a percentage of the absolute chlorophyll maximum) is displayed as a function of relative depth (percentage depth from upper to lower edge of mesophyll). Quadratic regression is shown by the solid black curve. Points and error bars represent mean ± se. The dashed, vertical line indicates the relative depth of the transition between palisade and spongy mesophyll cell layers (38.64% ± 1.60% se.). The solid, vertical line indicates the mean vein depth relative to the adaxial edge of leaf mesophyll (59.76% ± 1.27% se.). Schematic of the typical leaf cross section parameterized with approximate chlorophyll content according to the general model (B).

Chlorophyll Distribution Models by Clade

Quadratic regression was applied to the mean chlorophyll profile of categorical sets of plants based on clade (fern, cycad, conifer, ginkgo, basal angiosperm, magnoliid, monocot, eudicot; Fig. 6, A–H). While mesophyll depth was not a significant predictor of chlorophyll distribution for the clade-wise group of ferns (n = 3, R2 = 0.17, F(2,16) = 1.687, P = 0.216), it was a significant predictor and explained a high degree of variance in chlorophyll distribution for the sampled groups of cycads (n = 9, R2 = 0.84, F(2,16) = 42.57, P < 0.001), conifers (n = 2, R2 = 0.96, F(2,16) = 211.7, P < 0.001), ginkgo (Ginkgo biloba; n = 1 species [mean of n = 6 leaves and n = 3 profiles per leaf], R2 = 0.85, F(2,16) = 46.51, P < 0.001), basal angiosperm (n = 1 species [mean of n = 6 leaves and n = 3 profiles per leaf], R2 = 0.96, F(2,16) = 170.2, P < 0.001), magnoliids (n = 6, R2 = 0.92, F(2,16) = 95.72, P < 0.001), monocots (n = 9, R2 = 0.69, F(2,16) = 17.47, P < 0.001), and eudicots (n = 26, R2 = 0.94, F(2,16) = 122, P < 0.001). Numerical coefficients for the regression curves are shown in Table 1.

Figure 6.

Figure 6.

Open in a new tab

Chlorophyll distribution by clade and leaf thickness. Chlorophyll content (as a percentage of the absolute chlorophyll maximum) is displayed as a function of relative depth (percentage depth from upper to lower edge of mesophyll) for cladistic and leaf thickness subgroups: fern, n = 3 (A); cycad, n = 9 (B); conifer, n = 2 (C); ginkgo, n = 1 (D); basal angiosperm, n = 1 (E); magnoliid, n = 6 (F); monocot, n = 9 (G); eudicot, n = 26 (H); thin leaf, n = 47 (I); thick leaf, n = 10 (J). Regressions shown in the form 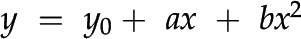Inline graphic for the respective datasets. Points and error bars represent mean ± se.

Chlorophyll Distribution Models by Leaf Thickness

Quadratic regression was applied to the mean chlorophyll profile of categorical sets of plants based on leaf thickness (Fig. 6, I and J). Mesophyll depth was a significant predictor of chlorophyll distribution for species with both categorically thin leaves (<0.5 mm; n = 47, R2 = 0.92, F(2,16) = 88.46, P < 0.001) and species with categorically thick leaves (≥0.5 mm; n = 10, R2 = 0.91, F(2,16) = 85.83, P < 0.001). Numerical coefficients for the regression curves are shown in Table 1.

General Model Predictions versus Clade/Leaf Thickness Model Predictions

Chlorophyll content predictions made by the clade and leaf thickness model equations, which are significant for all but the fern model, correlated strongly with chlorophyll content predictions made by the general model, or Equation 2. The general and subgroup model predictions were most highly correlated for the cycad, magnoliid, monocot, eudicot, thin leaf, and thick leaf subgroups (r = 0.99, P < 0.001), but also strongly correlated for the conifer group (r = 0.97, P < 0.001), ginkgo (r = 0.67, P = 0.0018), and basal angiosperm (r = 0.87, P < 0.001).

Mesophyll Tissue Type and Vein Depth as Predictors of Chlorophyll Content Maxima

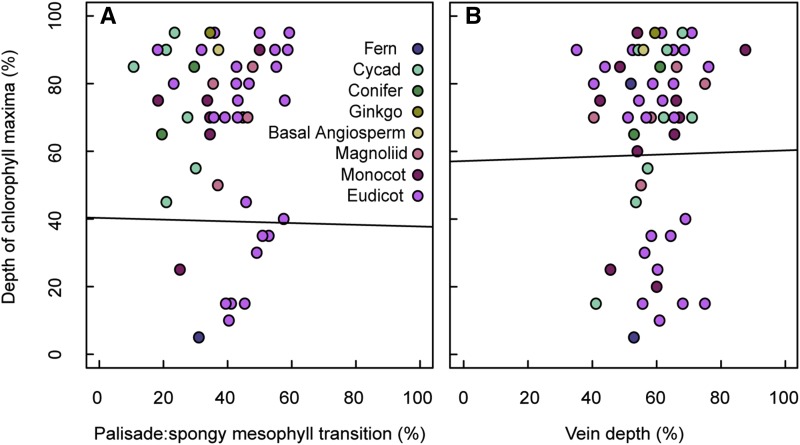
Given that the typical parabolic chlorophyll profile has a distinguishable peak or global maximum, it was anticipated that this peak in chlorophyll content would be associated with anatomical features of the leaf, i.e. at a predictable location relative to the transition from light-guiding palisade to light-diffusing spongy mesophyll or at a depth coincident with leaf veins. Indeed, by observation, some chlorophyll profiles did peak at a similar depth as the veins (e.g. G. biloba; Supplemental Fig. S1). Yet, when linear regression was used to statistically assess the strength of these anatomy-chlorophyll relationships, the spatial associations between anatomical traits and peak chlorophyll content were very weak, and neither mesophyll tissue type transitions (r −0.05, n = 49, P = 0.710; Fig. 7A) nor vein depth (r = 0.08, n = 54, P = 0.956; Fig. 7B) were significant predictors of peak chlorophyll according to Pearson’s test.

Figure 7.

Figure 7.

Open in a new tab

Spatial associations between anatomical traits and peak chlorophyll content. Mesophyll depth corresponding to peak chlorophyll concentration as a function of the palisade to spongy mesophyll transition (A) and vein depth (B). Depth of chlorophyll maxima measured from species chlorophyll profiles as a percentage of mesophyll thickness. Vein depth measured from the adaxial edge of leaf mesophyll as a percentage of mesophyll thickness. Linear fit shown in black (statistically nonsignificant in both cases).

Intraleaf Light Absorption and Chlorophyll Distribution

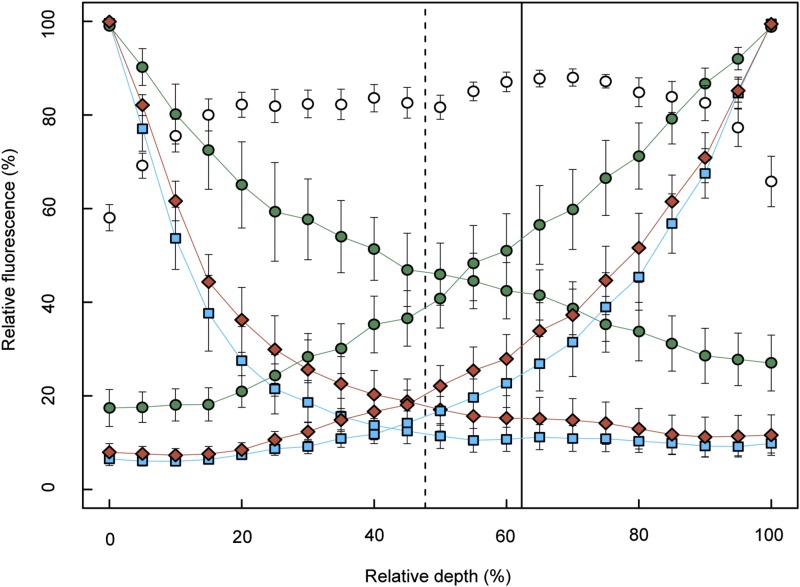
Light absorption profiles and chlorophyll profiles of species from different clades (n = 5 species, Arenga pinnata, Ulmus sp., Dryopteris sp., Coffea sp., and Bowenia spectabilis) were used to examine the relationship between the intraleaf light environment and chlorophyll distribution. Monochromatic (blue, red, and green) light extinction profiles decayed exponentially through the leaf as seen in previous studies (e.g. Vogelmann and Evans, 2002; Johnson et al., 2005; Brodersen and Vogelmann, 2010). As anticipated from previous work by Vogelmann and Han (2000), red and blue light were absorbed strongly near the source of irradiation, while deeper portions of the mesophyll remained enriched in green light (Fig. 8). In an analysis of light absorption profiles generated from light entering opposite sides of the leaf, we found that the overlap of these profiles for red, green, and blue light occurred within a relatively narrow region of the mesophyll, approximately between the mean vein position and the position of the transition between the palisade and spongy mesophyll. Chlorophyll content reached a maximum around this narrow band of tissue (Fig. 8).

Figure 8.

Figure 8.

Open in a new tab

Light absorption profiles and chlorophyll distribution in leaves. Subset of taxa (n = 5 species, with n = 2–3 leaves measured per species): A. pinnata, B. spectabilis, Coffea sp., Ulmus sp., Dryopteris sp. Points and error bars represent species mean ± se. Leaves were irradiated on their adaxial or abaxial surface with blue (squares), red (diamonds), or green (circles) light. Relative chlorophyll content is displayed (open circles) as a function of relative depth (percentage depth from upper to lower edge of mesophyll). The dashed, vertical line represents the mean relative depth of the transition between palisade and spongy mesophyll (n = 3 species, excludes B. spectabilis and Drypoteris sp.; 47.73% ± 5.2% se). The solid, vertical line represents mean vein depth relative to the adaxial edge of leaf mesophyll (n = 4 species, excludes Drypoteris sp.; 62.3% ± 8.9% se).

DISCUSSION

Leaf Thickness, Palisade Fraction of Mesophyll, and Intercellular Airspaces May Influence Chlorophyll Distribution

Although many of the leaves sampled showed chlorophyll distributions that were parabolic, with abaxially shifted maxima, variations on and deviations from this trend were observed, indicating which anatomical traits may alter or influence chlorophyll allocation. Unsurprisingly, we found pronounced localized depressions in chlorophyll content in areas of leaves with high porosity, or large intercellular airspaces, such as in the medial tissue of the aquatic plant E. crassipes (Fig. 2, G–I). Considering the results of the cluster analysis (Fig. 3B), chlorophyll content in group (b) increased sharply across the photosynthetic domain, with a clear minimum in the upper leaf and maximum in the lower leaf. This group was dominated by gymnosperms and had statistically thicker leaves than plants in groups (c) and (d) and less palisade tissue than those in group (c). In contrast, group (c) had members with the thinnest leaves, was dominated by more derived taxa, and had the most uniform or flat chlorophyll distribution across the photosynthetic domain. Taken together, this suggests that a thicker leaf with less developed palisade tissue (e.g. cycad) allocates less chlorophyll near the adaxial leaf surface, while a thinner leaf with more developed palisade tissue (e.g. eudicot) allocates chlorophyll more uniformly throughout the chlorenchyma. Assuming that chlorophyll content increases to balance decreases in available light (Bornman et al., 1991; Cui et al., 1991), then the observed chlorophyll distributions would occur because thinner leaves, particularly with highly developed light-guiding palisade tissue, would experience more of a homogenous internal light environment compared to a thick leaf, which would rapidly attenuate light with increasing depth (Takahashi et al., 1994; Koizumi et al., 1998; Vogelmann and Han, 2000; Johnson et al., 2005; Brodersen and Vogelmann, 2010). Intraleaf gradients in CO2 may also influence the allocation of chlorophyll in bulk mesophyll domains. Assuming most laminar leaves have a higher relative abundance of CO2 near stomata on the underside of the leaf, thick leaves might have a more pronounced CO2 diffusion gradient and therefore less CO2 available for photosynthesis in the upper mesophyll. We also note that the localized depressions in chlorophyll content at both adaxial and abaxial mesophyll edges observed in most leaves could be due to limited mesophyll conductance in these areas (Earles et al., 2018). That is, if a large proportion of the mesophyll cell wall has contact with an epidermal cell, then the diffusion of CO2 would be limited and chloroplasts within this region would underperform. While beyond the scope of this work, future studies are anticipated to show the degree to which variations in mesophyll porosity and/or connectivity influence CO2 availability, chlorophyll distribution, and chloroplast performance.

Common Patterns in Chlorophyll Distribution Indicate That a General Chlorophyll Profile Scheme Is Conserved across Phylogenetic Boundaries

When hierarchical cluster analysis was used to identify common patterns in the chlorophyll profiles without imposing a priori classification (Fig. 3), most species (n = 48/57) were sorted into groups (b), (c), and (d), for which the mean chlorophyll profile converged to a similar pattern; i.e. chlorophyll content increased gradually as a function of mesophyll depth. Thus, a general pattern of chlorophyll distribution is exhibited by plants as phylogenetically diverse as ferns, cycads, conifers, G. biloba, Illicium parviflorum (basal angiosperm), magnoliids, monocots, and eudicots, representing a diversity of growth habits, habitats, and leaf morphologies (e.g. tree, shrub, herbaceous, annual, perennial, evergreen, deciduous, etc.). Considering all species sampled in the study (n = 57), for the typical species, chlorophyll content increased gradually as a function of mesophyll depth from the adaxial surface, peaking deep within the leaf (∼83% relative mesophyll depth). This is quantitatively described by a simple quadratic equation or general model (Eq. 2, R2 = 0.94, F(2,16) = 127.3, P < 0.001; Fig. 5).

Chlorophyll Content Maxima Are Well Positioned to Take Advantage of Relative Enrichment of Green Light in Medial and Abaxial Leaf Tissues and Abaxially Incident Irradiation

Our comparison of intraleaf light absorption profiles and chlorophyll profiles (Fig. 8) also suggests that peak chlorophyll content may respond not only to irradiation incident on the upper leaf, but also to opposing light gradients from both upper and lower leaf surfaces. We found that the red, green, and blue light absorption profiles overlapped within a relatively narrow region of mesophyll that also coincided with the positioning of the palisade to spongy transition, the location of the veins, and maximum chlorophyll content. This region is also relatively enriched in green light compared with blue and red wavelengths, which is consistent with the growing understanding of the role of green light in driving photosynthesis within deep leaf tissue (Terashima et al., 2009; Johkan et al., 2012; Earles et al., 2017; Smith et al., 2017). While further studies are needed, this could point to the optimization of peak chlorophyll content where absorption of strong light from the adaxial surface and weaker light from the abaxial surface is maximized.

Vein Depth and Mesophyll Tissue Type Are Not Predictive of Chlorophyll Content Maxima

We expected to find some coordination between the peak chlorophyll content within the leaf and other anatomical trait patterns that are believed to be important for optimizing photosynthesis. For example, the density and spacing of veins within the leaf has been shown to have a remarkable scaling relationship across evolutionarily diverse species (Noblin et al., 2008), presumably to most efficiently deliver water to the sites of photosynthesis and evaporation from the mesophyll surface exposed to the intercellular airspace (Boyce et al., 2009). However, no statistical evidence for the coordinated positioning of maximum chlorophyll content with vein position was found (Fig. 7). Vein depth was also not statistically different between groups of species with distinctive chlorophyll profiles as identified through cluster analysis, suggesting that vein location is not a driver of major patterns in chlorophyll distribution, at least in the 1D vertical profiles of bulk mesophyll measured in this study. Future studies are anticipated to show if there are additional patterns in chlorophyll distribution in 2- and 3-dimensions in the leaf, including around the vascular tissue in transverse and paradermal planes.

The General Model Predicts Bulk Mesophyll Chlorophyll Distribution in a Broad Range of Plant Lineages and for Leaves with Different Thicknesses

While we report that several variations in leaf form do affect chlorophyll distribution, we also suggest that the general model (Eq. 2) is appropriate for describing chlorophyll distribution in most cases; this is because chlorophyll distribution predictions based strictly on categorical groupings of leaves (i.e. by clade and leaf thickness; Fig. 6) were highly correlated with those given by the general model (r = 0.99, P < 0.001 for cycad, magnoliid, monocot, eudicot, thin leaf, and thick leaf groups).

CONCLUSION

While further studies are warranted to determine the mechanistic underpinnings of the chlorophyll profile schemes characterized in this study, the main trend shared by the majority of species—as well as the deviations from this trend in thick leaves—suggests that fundamental physical constraints, such as intraleaf gradients in light, are central to chlorophyll distribution in laminar leaves. It is worth noting that the leaves in this study were all relatively thin (<1 mm) and most exhibited C3 photosynthesis. Variation in chlorophyll distribution could occur outside these phenotypic parameters; for example, the C4 grass Zea mays (Supplemental Fig. S1) shows a depression in chlorophyll content near the midpoint of the depth profile, potentially due to the highly modified Kranz anatomy of the bundle sheath that occupies a significant portion of the leaf cross sectional area. For our datasets where mesophyll depth failed to predict chlorophyll distribution (e.g. clade-wise for ferns), this could in future studies be retested by increasing the sample size or taxonomic representatives. Expanding the epi-illumination chlorophyll fluorescence dataset, particularly within a genus or species and in two and three dimensions, is an opportunity for further research. For example, the observed similarity between chlorophyll profiles of congeneric pairs points to the possibility of nuanced modification of chlorophyll distribution according to shared traits. The response of these traits and of the spatial allocation of chlorophyll within the leaf to different environmental conditions awaits testing.

In summary, this study provides empirical chlorophyll distribution data and model equations for many ecologically and commercially relevant species, quantitatively defines a common chlorophyll distribution scheme across phylogenetic and functional group boundaries, and initiates an understanding of the mechanisms underlying chlorophyll distribution in bulk mesophyll domains. Taken together, these findings advance our understanding of first principles in intraleaf physiology and move us toward more accurate in silico photosynthesis modeling and a clearer relationship between chlorophyll distribution, the light environment within a leaf, and photosynthetic performance.

MATERIALS AND METHODS

Plant Material

Mature, fully expanded leaves were collected from various environments (Marsh Botanical Garden, New Haven, CT; Yale Marsh Greenhouse, New Haven, CT; Montgomery Botanical Center, Coral Gables, FL; University of Vermont Campus, Burlington, VT; University of Vermont Greenhouse, Burlington, VT; private garden, Monterey, CA; naturalized habitat, New Haven, CT; Supplemental Table S1). Spinacia oleracea and Arabidopsis (Arabidopsis thaliana) wild type were grown in commercial and controlled growth chamber environments, respectively. In outdoor environments, leaves were collected from sun-exposed, south-facing sides of the plant canopy. Highly contrasting leaf phenotypes (i.e. sun or shade) were avoided where distinctive. All species had laminar or flattened leaf forms. Excised leaves were adapted to darkness for a minimum of 20 min before being prepared for chlorophyll fluorescence measurements. This period of dark adaptation was implemented as a control for possible chloroplast movement within cells as a response to the external light environment (Trojan and Gabrys, 1996).

Anatomical Measurements

Leaf thickness, upper epidermis thickness (including hypodermis where present), lower epidermis thickness, mesophyll thickness, percentage of mesophyll cross sectional area occupied by palisade mesophyll, and vein depth (measured from the adaxial edge of leaf mesophyll to the center of the vein) were measured from images of leaf cross sections. All measurements were replicated twice per leaf on 2 to 6 leaves for each species. In three cases (Begonia erythrophylla, Dryopteris sp., Zamia fairchildiana), veins were excluded from or not discernable in the chlorophyll fluorescence images. Mean and se were calculated for all measurements. Species were categorized as having thick or thin leaves subjectively based on the nonuniform distribution of sampled leaf thickness frequencies by 0.05 mm bins (thin < 0.50 mm, thick ≥ 0.50 mm).

Measurement of Relative Chlorophyll Distribution within Leaves

Relative chlorophyll distribution within leaves was measured using epi-illumination fluorescence microscopy similar to the method of Vogelmann and Evans (2002). Transverse hand sections cut several cells thick were mounted on lightly wetted filter paper on top of a glass slide, such that the sample did not dry out during imaging and while preventing the infiltration of intercellular airspaces with mounting liquid (water). The sample was then placed on the stage of a microscope (Olympus BX43, Olympus America) and irradiated with epi-illumination at 490 nm generated from a broad-spectrum LED light source (Lumen 300-LED, Prior Scientific Instruments) after passing through a filter. Light emitted via chlorophyll fluorescence passed through a barrier filter (680 nm, half bandwidth = 16 nm, S10-680F; Corion Filters) and was imaged with a digital Peltier-cooled CCD camera (PIXIS 1024B, Princeton Instruments) using shutter times of 70 to 150 ms. Individual profiles were measured from the images by drawing lines from the adaxial edge of the mesophyll to the abaxial edge of the mesophyll with a line width of 50 to 100 pixels, over which the mean intensity was given; in general 100-pixel width (equivalent to ∼60 µm at 20× magnification or ∼120 µm at 10× magnification) was used; however, thinner widths were used as necessary when nonphotosynthetic features such as veins were spaced less than 100 pixels apart. Measurements excluded epidermal cells, veins, and other conspicuous nonphotosynthetic structures such as hypodermis. Chlorophyll and depth data for each profile were normalized by dividing all values by the global absolute chlorophyll or depth maxima, respectively. The mean of three profiles was measured for each leaf sample, and the mean of 2 to 6 leaf samples was measured per species. Estimates of absolute fluorescence intensity among different samples were not possible. This was due to variability in exposure needed to image differently sized samples at appropriate focal lengths, and additionally the temporal variation in signal due to Kautsky decay, i.e. the decline in fluorescence intensity as a function of exposure time under continuous irradiation. As discussed in Vogelmann and Han (2000), Kautsky decay changes the relative intensity of the fluorescence signal but does not alter the relative distribution of fluorescence imaged from the sample. The entire epi-illumination process for a single sample was completed within approximately 30 s. Differential detection of chlorophyll a and b by the epi-illumination method was considered as a source of bias in the shape of the measured chlorophyll profiles, yet is assumed to be minimal due to precedent by Vogelmann and Evans (2002). These authors found a strong linear relationship for in vivo paradermal chlorophyll concentration as a function of fluorescence detected by the epi-illumination method. Additionally, excitation and emission bands used here were well within peaks for detection of both chlorophyll a and b. Finally, our protocol for normalizing the fluorescence signal for each sample removes potential bias in chlorophyll a/b ratios across species.

Cluster Analysis of Species Chlorophyll Profiles

Hierarchical cluster analysis was used to group species chlorophyll profiles according to similar distribution schemes. Euclidean distances between chlorophyll intensity data points were calculated at 21 loci (0%, 5%, 10%, … 100% relative mesophyll depth) and clusters were agglomerated using complete linkage. Analysis was performed using the R statistical program (R Core Team, 2018). Visual assessment of clustering patterns indicated the presence of six major groups. The small subcluster containing Begonia bowerae and Antirrhinum majus could have been treated as a seventh group; however, to avoid over-splitting, and consistent with observed patterns in the species chlorophyll profiles, this was grouped with its neighboring major cluster. To aid in comparison of major patterns in chlorophyll distribution between groups, a mean model was generated from the individual chlorophyll profiles of species in each group. A regression of the form y = y0 + ax + bx2 was applied to each group mean model and tested for significance and fit (Johnson et al., 2005). Domains where the upper and lower epidermal cell walls met the chlorenchyma cell walls (0%–5% and 95%–100% relative depth, respectively) were excluded from the regression. These domains represent a nonphotosynthetic transition point between tissue types, which is retained in the data as a marker of the transition point in tissue morphology.

General Model of Chlorophyll Distribution

A mean model approach was used to develop a general equation for chlorophyll distribution in laminar leaves. The mean model, or mean species chlorophyll profile, was calculated by averaging relative chlorophyll intensity values at common relative depth values for all 57 species in the study. Mean se was calculated to evaluate the variation in chlorophyll intensity among species as a function of mesophyll depth. A regression curve of the form y = y0 + ax + bx2 was applied to the mean model and tested for fit (Johnson et al., 2005). Domains where the upper and lower epidermal cell walls met the chlorenchyma cell walls (0%–5% and 95%–100% relative depth, respectively) were excluded from the regression. These domains represent a nonphotosynthetic transition point between tissue types, which is retained in the data as a marker of the transition point in tissue morphology.

Measurement of Light Absorption Profiles in Leaves

Chlorophyll fluorescence was also used to estimate the relative absorption of red, green, and blue light through leaf samples using previously reported methods (Takahashi et al., 1994; Koizumi et al., 1998; Vogelmann and Han, 2000; Vogelmann and Evans, 2002; Brodersen and Vogelmann, 2010). Fresh leaf sections were cut to ∼1 cm2 with a razor blade and mounted in a 3D-printed sample holder on the stage of a microscope (Olympus BX43, Olympus America) with the transverse edge normal to the objective. The abaxial or adaxial side of the leaves were irradiated with monochromatic red (660 nm), green (532 nm), or blue (488 nm) light generated by one of three lasers (red solid-state laser, model #BWN-660-10E, BandW Tek; green solid-state laser, model #DY20B, Power Technology; blue solid-state laser, model LRS-473-TM-10-5, LaserGlow Technologies). The laser light was attenuated with neutral density filters such that the light incident on the leaf surface was of equal intensity (1200 µmol m−2s−1) measured by a LI-190 (Li-Cor) light meter mounted in the same position as the leaf sample holder. As the leaf was illuminated with the monochromatic laser light, the transverse (orthogonal) surface of the leaf was observed for fluorescence emitted from the leaf tissue with a Peltier-cooled CCD camera (PIXIS 1024B, Princeton Instruments). The laser spot (1-mm radius) was directed onto the 1-cm2 leaf surface centered on the cut surface being observed. Consequently, the observed fluorescence would only arise from chloroplasts up to 1 mm from the cut transverse surface. Light profiles were measured from the resulting digital images where light absorbance was proportional (1:1) to the imaged fluorescence, or pixel intensity (Vogelmann and Evans, 2002). Measurements were taken from the adaxial edge of the mesophyll to the abaxial edge of the mesophyll and excluded conspicuous nonphotosynthetic structures such as veins. The mean of three profiles was measured for each leaf sample and the mean of 2 to 3 leaf samples was measured per species.

All images were processed using the FIJI (Schindelin et al., 2012) distribution of ImageJ (Rueden et al., 2017) software. All statistical calculations and graphing were performed using R (R Core Team, 2018), with the exception of ANOVA and Tukey analyses, which were performed using Minitab 18 Statistical Software (2017).

Supplemental Data

The following supplemental materials are available.

Acknowledgments

The authors thank Dr. Jay Wason (University of Maine) and Dr. Adam Roddy (Yale University) for discussions, Dr. Jonathan Reuning-Scherer (Yale University) for statistical consultation, and Dr. Joshua Gendron (Yale University), the Marsh Botanical Garden (New Haven, CT) and Montgomery Botanical Center (Coral Gables, FL) for plant materials. The authors declare that there is no conflict of interest.

Footnotes

1

This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under grant no. DGE1752134. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

[OPEN]

Articles can be viewed without a subscription.

References

  1. Aalto T, Juurola E (2002) A three-dimensional model of CO2 transport in airspaces and mesophyll cells of a silver birch leaf. Plant Cell Environ 25: 1399–1409 [Google Scholar]
  2. Adams WW III, Terashima I (2018) The Leaf: A Platform for Performing Photosynthesis, Vol 44 Springer, Dordrecht, the Netherlands [Google Scholar]
  3. Bornman JF, Vogelmann TC, Martin G (1991) Measurement of chlorophyll fluorescence within leaves using a fibreoptic microprobe. Plant Cell Environ 14: 719–725 [Google Scholar]
  4. Boyce CK, Brodribb TJ, Feild TS, Zwieniecki MA (2009) Angiosperm leaf vein evolution was physiologically and environmentally transformative. Proc Biol Sci 276: 1771–1776 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Brodersen CR, Vogelmann TC (2010) Do changes in light direction affect absorption profiles in leaves? Funct Plant Biol 37: 403–412 [Google Scholar]
  6. Cui M, Vogelmann TC, Smith WK (1991) Chlorophyll and light gradients in sun and shade leaves of Spinacia oleracea. Plant Cell Environ 14: 493–500 [Google Scholar]
  7. Earles JM, Théroux-Rancourt G, Gilbert ME, McElrone AJ, Brodersen CR (2017) Excess diffuse light absorption in upper mesophyll limits CO2 drawdown and depresses photosynthesis. Plant Physiol 174: 1082–1096 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Earles JM, Theroux-Rancourt G, Roddy AB, Gilbert ME, McElrone AJ, Brodersen CR (2018) Beyond porosity: 3D leaf intercellular airspace traits that impact mesophyll conductance. Plant Physiol 178: 148–162 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Earles JM, Buckley TN, Brodersen CR, Busch FA, Cano FJ, Choat B, Evans JR, Farquhar GD, Harwood R, Huynh M, et al. (2019) Embracing 3D complexity in leaf carbon-water exchange. Trends Plant Sci 24: 15–24 [DOI] [PubMed] [Google Scholar]
  10. Evans JR, Vogelmann TC (2003) Profiles of 14C fixation through spinach leaves in relation to light absorption and photosynthetic capacity. Plant Cell Environ 26: 547–560 [Google Scholar]
  11. Evans JR, Vogelmann TC (2006) Photosynthesis within isobilateral Eucalyptus pauciflora leaves. New Phytol 171: 771–782 [DOI] [PubMed] [Google Scholar]
  12. Ho QT, Berghuijs HNC, Watté R, Verboven P, Herremans E, Yin X, Retta MA, Aernouts B, Saeys W, Helfen L, et al. (2016) Three-dimensional microscale modelling of CO2 transport and light propagation in tomato leaves enlightens photosynthesis. Plant Cell Environ 39: 50–61 [DOI] [PubMed] [Google Scholar]
  13. Ichiro T, Hiroki O, Takashi F, Riichi O (2016) Light environment within a leaf. II. Progress in the past one-third century. J Plant Res 129: 353–363 [DOI] [PubMed] [Google Scholar]
  14. Johkan M, Shoji K, Goto F, Hahida S, Yoshihara T (2012) Effect of green light wavelength and intensity on photomorphogenesis and photosynthesis in Lactuca sativa. Environ Exp Bot 75: 128–133 [Google Scholar]
  15. Johnson DM, Smith WK, Vogelmann TC, Brodersen CR (2005) Leaf architecture and direction of incident light influence mesophyll fluorescence profiles. Am J Bot 92: 1425–1431 [DOI] [PubMed] [Google Scholar]
  16. Koizumi M, Takahashi K, Mineuchi K, Nakamura T, Kano H (1998) Light gradients and the transverse distribution of chlorophyll fluorescence in mangrove and camellia leaves. Ann Bot 81: 527–533 [Google Scholar]
  17. Minitab 18 Statistical Software (2017) Minitab, Inc., State College, PA: www.minitab.com [Google Scholar]
  18. Morison JIL, Lawson T, Cornic G (2007) Lateral CO2 diffusion inside dicotyledonous leaves can be substantial: Quantification in different light intensities. Plant Physiol 145: 680–690 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Nishio JN, Sun J, Vogelmann TC (1993) Carbon fixation gradients across spinach leaves do not follow internal light gradients. Plant Cell 5: 953–961 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Noblin X, Mahadevan L, Coomaraswamy IA, Weitz DA, Holbrook NM, Zwieniecki MA (2008) Optimal vein density in artificial and real leaves. Proc Natl Acad Sci USA 105: 9140–9144 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Oguchi R, Douwstra P, Fujita T, Chow WS, Terashima I (2011) Intra-leaf gradients of photoinhibition induced by different color lights: implications for the dual mechanisms of photoinhibition and for the application of conventional chlorophyll fluorometers. New Phytol 191: 146–159 [DOI] [PubMed] [Google Scholar]
  22. Ort DR, Merchant SS, Alric J, Barkan A, Blankenship RE, Bock R, Croce R, Hanson MR, Hibberd JM, Long SP, et al. (2015) Redesigning photosynthesis to sustainably meet global food and bioenergy demand. Proc Natl Acad Sci USA 112: 8529–8536 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Palta JP. (1990) Leaf chlorophyll content. Remote Sens Rev 5: 207–213 [Google Scholar]
  24. Pieruschka R, Schurr U, Jensen M, Wolff WF, Jahnke S (2006) Lateral diffusion of CO2 from shaded to illuminated leaf parts affects photosynthesis inside homobaric leaves. New Phytol 169: 779–787 [DOI] [PubMed] [Google Scholar]
  25. Porra RJ, Thompson WA, Kriedemann PE (1989) Determination of accurate extinciton coefficients and simultaneous equations for assaying chlorophylls a and b extracted with four different solvents: Verification of the concentration of chlorophyll standards by atomic absorption spectroscopy. Biochim Biophys Acta Bioenerg 975: 384–394 [Google Scholar]
  26. R Core Team (2018) R: A language and environment for statistical computing. R Foundation, Vienna, Austria: https://www.r-project.org/ [Google Scholar]
  27. Reich PB. (2014) The world-wide ‘fast-slow’ plant economics spectrum: A traits manifesto. J Ecol 102: 275–301 [Google Scholar]
  28. Rueden CT, Schindelin J, Hiner MC, DeZonia BE, Walter AE, Arena ET, Eliceiri KW (2017) ImageJ2: ImageJ for the next generation of scientific image data. BMC Bioinformatics 18: 529. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, et al. (2012) Fiji: An open-source platform for biological-image analysis. Nat Methods 9: 676–682 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Shipley B, Lechowicz MJ, Wright I, Reich PB (2006) Fundamental trade-offs generating the worldwide leaf economics spectrum. Ecology 87: 535–541 [DOI] [PubMed] [Google Scholar]
  31. Slattery RA, Grennan AK, Sivaguru M, Sozzani R, Ort DR (2016) Light sheet microscopy reveals more gradual light attenuation in light-green versus dark-green soybean leaves. J Exp Bot 67: 4697–4709 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Smith HL, McAusland L, Murchie EH (2017) Don’t ignore the green light: Exploring diverse roles in plant processes. J Exp Bot 68: 2099–2110 [DOI] [PubMed] [Google Scholar]
  33. Smith WK, Vogelmann TC, Delucia EH, Bell DT, Shepherd KA (1997) Leaf form and photosynthesis: Do leaf structure and orientation interact to regulate internal light and carbon dioxide? BioScience 47: 785–793 [Google Scholar]
  34. Sun J, Nishio JN, Vogelmann TC (1998) Green light drives CO2 fixation deep within leaves. Plant Cell Physiol 39: 1020–1026 [Google Scholar]
  35. Takahashi K, Mineuchi K, Nakamura T, Koizumi M, Kano H (1994) A system for imaging transverse distribution of scattered light and chlorophyll fluorescence in intact rice leaves. Plant Cell Environ 17: 105–110 [Google Scholar]
  36. Terashima I, Fujita T, Inoue T, Chow WS, Oguchi R (2009) Green light drives leaf photosynthesis more efficiently than red light in strong white light: revisiting the enigmatic question of why leaves are green. Plant Cell Physiol 50: 684–697 [DOI] [PubMed] [Google Scholar]
  37. Terashima I, Hanba YT, Tholen D, Niinemets Ü (2011) Leaf functional anatomy in relation to photosynthesis. Plant Physiol 155: 108–116 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Tholen D, Zhu X-G (2011) The mechanistic basis of internal conductance: A theoretical analysis of mesophyll cell photosynthesis and CO2 diffusion. Plant Physiol 156: 90–105 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Tholen D, Boom C, Zhu X-G (2012) Opinion: Prospects for improving photosynthesis by altering leaf anatomy. Plant Sci 197: 92–101 [DOI] [PubMed] [Google Scholar]
  40. Tholen D, Éthier G, Genty B (2014) Mesophyll conductance with a twist. Plant Cell Environ 37: 2456–2458 [DOI] [PubMed] [Google Scholar]
  41. Trojan A, Gabrys H (1996) Chloroplast distribution in Arabidopsis thaliana (L.) depends on light conditions during growth. Plant Physiol 111: 419–425 [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Vogelmann TC, Evans JR (2002) Profiles of light absorption and chlorophyll within spinach leaves from chlorophyll fluorescence. Plant Cell Environ 25: 1313–1323 [Google Scholar]
  43. Vogelmann TC, Gorton HL (2014) Leaf: Light Capture in the Photosynthetic Organ. Springer, Dordrecht, the Netherlands, pp 363–377 [Google Scholar]
  44. Vogelmann TC, Han T (2000) Measurement of gradients of absorbed light in spinach leaves from chlorophyll fluorescence profiles. Plant Cell Environ 23: 1303–1311 [Google Scholar]
  45. Zwieniecki MA, Boyce CK (2014) Evolution of a unique anatomical precision in angiosperm leaf venation lifts constraints on vascular plant ecology. Proc Biol Sci 281: 20132829. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES