Adaptive learning under expected and unexpected uncertainty

Abstract

Decision outcomes are often uncertain and can frequently change over time. Thus, not every outcome should substantially affect behavior or learning. Successful learning and decision making require a distinction between the range of typically experienced outcomes (expected uncertainty) and variability reflecting real changes in the environment (unexpected uncertainty). Here, we posit that understanding the interaction between these two types of uncertainty, at both computational and neural levels, is crucial for understanding adaptive learning. We re-examine computational models and experimental findings to help reveal computational principles and neural mechanisms used in mammalian brains to achieve adaptive learning under uncertainty.

Introduction

Imagine while in traffic, we decide on the route to our destination based on commute times experienced over many days, months, even years. Experiencing random small delays should not be concerning or prompt us to change our route. Yet unexpectedly slow traffic can signal important events (i.e. accidents, road closures) and this information should be used to update our route. Importantly, what we would consider unexpected delays are very different for the dynamic metropolitan Los Angeles area versus the small town of Hanover. Nonetheless, successful learning necessitates mechanisms to discriminate inconsequential expected variability (expected uncertainty) and distinguish those events from outcomes that signal environmental volatility (often producing unexpected uncertainty), which should instead lead to significant update of value and/or changes in behavior (i.e., a change in route).

Computation and update of expected rewards from selecting stimuli and taking actions, often referred to as stimulus and action values, require integration of signals across multiple brain areas and systems. These include areas involved in making decisions, executing actions, and responding to primary rewards and their motivational and hedonic significance. In addition, update of stored information could involve neuromodulatory systems engaged in processing reward and neural plasticity. Therefore, the amount of updating in stimulus or action values after experiencing an outcome depends on many signals, some of which should be sensitive to uncertainty in the environment. Yet learning in dynamic environments is bounded by a tradeoff between being adaptable (i.e. respond quickly to changes in the environment) and being precise (i.e. update slowly after each feedback to be more accurate), which we refer to as the adaptability-precision tradeoff [1]. There are mechanisms to improve this tradeoff [2, 3] and one such way is to increase the rate of learning after unexpected events and decrease it when the world is stable.

We argue that critical questions about learning under uncertainty are how expected and unexpected uncertainty are computed, interact, and in turn, influence learning. More specifically, what is the relationship between stimulus/action values and expected and unexpected uncertainty, and how does expected uncertainty contribute to the computation of unexpected uncertainty? Moreover, it is not yet fully understood whether and how different forms of uncertainty are generalized across stimuli and actions in order to control an overall rate of learning. We use these questions as a framework to survey existing computational models and re-examine recent experimental findings in order to identify neural evidence that may serve to validate or refute the predictions and basic principles of these models. At the end, we offer ideas for future directions to pinpoint the neural substrates and mechanisms of adaptive learning.

Expected versus unexpected

Expected uncertainty.

Specific definitions of expected uncertainty in the laboratory typically depend on both the nature of the learning or decision-making task and the model used by the organism to perform the task. In the case of estimating reward expected from a stimulus (or action) that upon selection results in different amounts of reward with different probabilities (outcome m_i with probability p_i), expected uncertainty can be equated with the variance (or standard deviation) of reward outcome in terms of magnitude or delay (see Box 1). The notion of uncertainty as the variance of probabilistic reward outcomes is linked to the “risk” of not getting reward that the decision maker perceives [4, 5]. However, expected uncertainty is limited to cases when probabilities have to be estimated and do not change over time; that is, in stable conditions/environments. It is deemed “expected” because it is thought to reflect variability or stochasticity that is ubiquitous and unavoidable. In theory, encountering this kind of uncertainty should not be surprising nor promote learning or behavioral adjustment over time, but in practice, it is difficult for the subject to verify that probabilities are stationary and do not change over time.

Box 1. Key Terms.

Reward environment = A collection of stimuli and actions wherein selection of a stimulus or execution of an action based on the presented stimuli bring about reward with certain magnitudes and probabilities. Reward obtained after selection of a stimulus allows assigning stimulus value. Reward obtained following execution of an action can result in forming a stimulus-action association or assigning action values. Reward attributes such as magnitudes and probabilities can be fixed or change over time resulting in a stable or volatile environment, respectively.

Learning rate = The rate at which stimulus/action values are updated after each reward feedback. In error-driven models, the learning rate is a parameter between 0 and 1 that is multiplied by RPE to determine the size of update, or equivalently, how observed reward should be weighted relative to previous stimulus/action values to update these values. In more mechanistic models, the learning rate can be seen as the rate of transition between different synaptic states [32, 104, 105]. Dynamic environments require learning to be adjusted constantly and this adjustment often is translated to time-dependent learning rates, rendering the concept of learning rate futile. Instead, we suggest using the “gain” of learning to refer to the modulation of the overall amount of update.

Expected uncertainty = Uncertainty in reward outcome due to its probabilistic nature even with fixed probabilities for different outcomes. For the stimulus/action that can result in reward m_i with probability p_i, the expected uncertainty can be defined as the variance over n possible outcomes

$$ExpectedUncertainty=\sum _{i=1}^n{p}_i\times {\left(m_i-EV\right)}^2$$

where EV is the expected value $\left(={\mathrm{\sum }}_{i=\mathrm{1}}^n{p}_i\times m_i\right)$. In the simple case of binary reward (reward m with probability p_R and zero otherwise) the variance or expected uncertainty is equal to p_R × (1 − p_R) × m². The corresponding standard deviation also can be estimated by the average absolute deviations from the mean, ${\mathrm{\sum }}_{i=\mathrm{1}}^n{p}_i\times |m_i-EV|$. Importantly, for binary outcome and m equal 1, the mean absolute deviation can be computed by averaging unsigned reward prediction error (RPE) over a large enough number of trials because the best estimate of EV is the expected reward resulting from selection of a stimulus or action. This suggests that unsigned RPE can directly contribute to the computation of expected uncertainty for a given stimulus/action.

Volatility = Volatility refers to uncertainty due to “actual” changes in reward magnitude and/or probability associated with stimuli or actions over time. In the context of the two-alternative probabilistic reversal learning task with complementary probabilities for two possible actions, it is proportional to (2p_R - 1)/L where L is the block length, capturing the overall rate of change per time. Volatility can be local (i.e., related to one stimulus/action) or global implying that volatility is generalized and shared between sets of (or all) stimuli/actions in the reward environment. It is reasonable that volatility is computed locally since unexpected changes about one stimulus/action could be independent of those on other stimuli/actions. On the other hand, it is beneficial to estimate an overall level of volatility in the environment in order to adjust learning and decision making globally.

Unexpected uncertainty = Uncertainty due to subjective perceived changes in reward probabilities, magnitudes, and/or delays associated with stimuli or actions over time. Unexpected uncertainty could only be read from the subject’s responses (choice behavior, estimation report, etc.) and thus strongly depends on the assumptions of the computational model used to explain subjects’ behavior. Unexpected uncertainty could be local or global.

Most error-driven models of learning rely on prediction error, equal to the difference between what is expected and what is obtained, modulated by the so-called learning rates (see Box 1) to update stimulus or action values. Because dynamic environments require learning to be adjusted constantly and this adjustment is often translated to time-dependent learning rates, the concept of learning rate becomes rather futile. In addition, it is unclear how the learning rates are set neuronally. Therefore, instead we suggest using the “gain” of learning to refer to the modulation of the overall amount of update in stimulus/action values. It has been suggested that expected uncertainty can be used to scale the learning rates in order to reduce the influence of prediction error when reward outcomes are more variable [6, 7]. This strategy is only useful if the environment is stable enough that the variance can be estimated reliably. A large variance, however, could also reflect a real change in the environment, which should instead enhance learning. Finally, expected uncertainty can be estimated by averaging unsigned RPE over time (e.g., trials) because the latter approximates the standard deviation of reward outcomes. This provides a plausible mechanism for computation of expected uncertainty based on the difference between stimulus/action values and observed reward. Together, these suggest that instead of directly scaling down the gain of learning, expected uncertainty could indirectly influence learning by providing a “baseline” level of variability for detection of surprising events that should increase the gain of learning (see below).

Unexpected uncertainty.

Though definitions do differ, unexpected uncertainty occurs due to changes in reward probabilities, magnitudes, and/or delays over time. Nonetheless, to accurately estimate unexpected uncertainty, the subject should take into account what is known about the variability in outcomes, or expected uncertainty. On theoretical grounds, it has been suggested that only the first violation of an expected outcome, such as the first reversal of previously-learned reward contingencies, constitutes unexpected uncertainty and all subsequent reversals yield expected uncertainty because they could be expected [8, 9]. In other words, there is no unexpected uncertainty if changes are predictable. This definition, however, is not practical because it is unclear when the ‘unexpectedness’ of changes degrades. Moreover, the subject can also learn in a single trial, as in epiphany learning [10], pointing to possible detection/perception of drastic changes in the environment. It also has been argued that to capture “surprise” correctly, commitment to a belief needs to be considered as well [11]. Together, these suggest that unexpected uncertainty could primarily be subjective and possibly not follow actual changes in the environment.

To reconcile different definitions, we equate unexpected uncertainty with the “subjective” perceived uncertainty due to changes in reward probabilities, magnitudes, or delays over time (see Box 1). In contrast, we refer to volatility as uncertainty due to actual changes in reward probabilities, magnitudes, or delays over time. Therefore, volatility depends on how quickly changes occur in the environment independently of whether it is detected by the decision maker or not, whereas unexpected uncertainty could only be read from the subject’s responses (choice behavior, estimation report, etc.). Considering that unexpected uncertainty strongly depends on the assumptions of the computational model used to explain subjects’ behavior (and adopting such a model could take a long time), it is necessary to test whether volatility is computed and signaled by neural elements and how it subsequently influences learning.

Finally, to make the relationship between expected and unexpected uncertainty more tractable, here we focus on tasks in which unexpected uncertainty is caused by changes in parameters that determine the model of the environment and not the model itself. This also helps avoid situations in which unexpected uncertainty could significantly deviate from volatility due to internal models of the subject, which are very difficult to pinpoint at the neuronal level. Similarly, perceptual uncertainty introduces another layer of complexity because it requires interaction between internally stored information and sensory input/representation. Such “model-based” and perceptual uncertainties have been reviewed elsewhere [12–16] and are outside the focus of this Opinion.

Computational models

For the purpose of this Opinion article, we categorize computational models of learning under uncertainty into normative models such as Bayesian or statistical models that prescribe how learning should adjust to uncertainty in the environment, approximation to these normative models (approximate-normative models) that aim to provide plausible update rules that could be implemented in the brain, and finally but not the least, mechanistic models aiming to elucidate how necessary computations can be performed by neural elements.

Normative models.

To be able to use Bayes’ rule as the learning or update rule and simulate behavior of an ideal observer [9, 17, 18], Bayesian and statistical models of learning make certain assumptions about the environment in order to determine what regularities to expect and to learn from in the environment [9, 12, 13, 18–22]. These models assume that the decision-maker or learner constructs a “model” of the environment and how it changes over time, and accordingly adjusts the parameters of this model based on reward feedback. Parameters of the Bayesian models could represent different properties of the environment such as the probability of reward, the width of distribution from which reward is drawn (i.e. expected uncertainty), and the probability that any of the underlying parameters may change over time (i.e. unexpected uncertainty) [9, 18–21]. Therefore, Bayesian models not only estimate stimulus or action values but also expected and unexpected uncertainty associated with those values, which is very useful for localizing corresponding neural correlates.

Many Bayesian models of learning under uncertainty assume a hierarchical structure for estimating the state of environment and how transition between these states happen [19–21]. This assumption is usually made for mathematical convenience and may not reflect the type of uncertainty in the natural environment. For example, the hierarchical model of Behrens and colleagues (2007) assumes three separate systems for estimating the following quantities: reward probability (r), volatility (v), and the rate of change in volatility (k). Transitions between different values of r and v are affected by the parameter in the system above it (v and k, respectively). Using this structure, the Bayes rule can be applied to compute posteriors (posterior probability distributions) or the belief about all three parameters given the data. This model has been successfully used to explain choice behavior and identify neural correlates of unexpected uncertainty in humans, and moreover, sparked the development of many models of learning under uncertainty. Despite logical simplicity, however, the actual computations necessary for estimating posteriors are very complex and thus, it is unclear how these computations are performed in the brain. Most relevant to our discussion, due to the interconnected nature of the update rules in the Bayesian models, it is challenging to use these models to make predictions about the exact relationship between expected and unexpected uncertainty [21].

One common normative approach for tackling learning under uncertainty is the Kalman filter that can formalize the predictive relationship between stimuli/actions and reward outcome and how this relationship is assumed to change over time [12]. The Kalman filter model lends itself well to learning under uncertainty because it keeps track of not only the estimated state of the system (predicted state estimates, e.g., reward probability) but also the variance or uncertainty of the estimates (predicted error covariance) [12, 13]. An important concept in this model is the optimal Kalman gain that determines the amounts of update for both state and error covariance [12]. Similar to Bayesian models, the Kalman filter requires an assumption about state transitions (more specifically, a state-transition model) and the most common form of state transitions follow a hierarchical structure [12, 13]. Both Bayesian models and Kalman filter have been instrumental in formalizing alternative solutions to tackle uncertainty.

Approximate-normative models.

Although optimal and quite generalizable, computations required in the normative models are rather complex and cannot be easily mapped to neural processes. Moreover, because normative models are mainly concerned with describing optimal learning, these models are sometimes limited in accounting for choice and learning behaviors [1, 20]. Different approaches have been used to overcome these issues to provide a better link to neural processes and/or account for the behavior. This includes incorporating additional components to the Bayesian models or approximations to those models. For example, Payzan LeNestour and colleagues (2011) [20] propose a forgetting Bayesian algorithm that allows introduction of an explicit learning rate. Using this model, this group was able to estimate the effects of different types of uncertainty on the learning rate and identify multiple brain regions (including anterior and posterior cingulate cortex, intraparietal sulcus, locus coeruleus) that display blood oxygen level-dependent (BOLD) responses correlated with different types of uncertainty [23]. As another example, Dayan et al. (2000) note the Kalman filter model assumes that predictive values of all stimuli are simply added to compute “net prediction” even though those stimuli could have different degrees of reliability due to abrupt changes in the environment. To resolve this issue, they propose a competitive combination mechanism that uses the inverse of the standard deviation of the difference between the actual value of reward and the prediction associated with each stimulus (as a measure of reliability for each stimulus) to combine predictions. To solve a similar problem, Courville et al. (2006) [13] suggest that whereas the update of Bayesian model parameters or beliefs about them inversely depends on uncertainty in the environment, surprising events or outcomes should signal changes and the need for faster or new learning.

There are other approximate Bayesian models that arguably provide better fit to behavior and links to its neural substrates [18, 21, 24]. For example, Wilson et al. (2013) show how the optimal Bayesian model can be replaced with a mixture of error-driven ‘delta’ rules (i.e. update based on the difference between actual and estimated outcomes) that can capture human behavior in a predictive-inference task. A related study proposed a delta-rule approximation of the ideal-observer [18]. In this model, the influence of newly experienced outcomes is adjusted according to ongoing estimates of (expected) uncertainty and the probability of a fundamental change in the environment (unexpected uncertainty). These approximate models tend to provide a good fit of behavioral data (mainly for continuous and not binary reward feedback) and have been used to identify neural correlates of belief updating [25]. The most direct testable prediction of these models is in how they describe changes in the learning rates, or equivalently how RPE is modulated by environmental factors.

Classic models of learning based on RPE (e.g., Rescorla-Wagner and various reinforcement learning, or RL, models [26]) assume fixed learning rates and thus, do not have specific mechanisms for adjusting the learning rate according to uncertainty in the environment. In contrast, the Pearce-Hall (PH) model provides a built-in mechanism for adjusting the learning rate for each stimulus based on how surprising the outcome is; surprising reinforcement (or non-reinforcement) can result in increased associabilities and faster learning [27]. This is why many hybrid models have been proposed in which RPE is multiplied by a variable that measures surprise, which could signal uncertainty [28]. In the PH model surprise is computed based on the mean value of unsigned RPE but in other models this variable could resemble variance of the RPE [6, 13]. Nonetheless, all these models suggest that RPE, based on the same “expected” stimulus/action values that drive choice behavior, can also be used in multiple ways to control the gain of learning. For example, Preuschoff and Bossaerts (2007) have suggested that the standard deviation of the RPE, which they refer to as the prediction risk, can be used to adjust the learning rates by scaling down the RPE. Another study proposes a model with a dynamic learning rate based on the slope of the change in the smoothed unsigned RPE over trials [29]. Such scaling of learning with expected uncertainty and dynamic learning rates using RPE have been combined to account for human learning better than classic RL models [7]. Although the notion of variable learning rates based on unsigned RPE has been adopted in many models to deal with uncertainty [12, 13, 30], the unsigned RPE does not tease apart expected from unexpected errors per se. Therefore, additional computations are necessary for proper estimation of surprising outcomes and the underlying neural mechanisms are currently unknown.

Mechanistic models.

Mechanistic models of learning under uncertainty aim to explain how necessary computations are performed by neural elements and thus, their components can be more easily mapped onto brain circuits and substrates.

Error-driven models often use RPE modulated by the learning rate as the teaching signal that is assumed to be mediated by dopamine [31, 32]. Therefore, adjustments of learning in these models translate to the adjustment of RPE or the learning rates, or both. However, there is a wealth of evidence for the role of dopamine in other processes that also influence choice behavior including incentive salience or desirability [33], effort [34]), and novelty and salience [35]. Thus, it is unclear whether required computations for adjustments of learning in error- driven models can be mapped uniquely onto the modulation of a functionally-multifaceted dopaminergic system.

We have recently proposed a mechanistic model for adaptive learning under uncertainty in which synapses endowed with metaplasticity (i.e., the ability to change synaptic states without measurable changes in synaptic efficacy) can self-adjust to reward statistics in the environment without any optimization or knowledge of the environment [1, 3]. In this model, the changes in the activity of neurons that encode stimulus/action values can be used by another system to compute volatility in the environment. The volatility signal can be used subsequently to increase the gain of learning when volatility passes a threshold set by expected uncertainty. Therefore, the extended model predicts a direct two-way interaction between neurons encoding stimulus/action values and neurons computing volatility, modulated by input from a circuit computing expected uncertainty. We think that such interactions between value-encoding and expected- and uncertainty-monitoring systems can enhance adaptability required in dynamic environments, and metaplasticity [36] provides a crucial mechanism for this interaction to be beneficial. In addition, we propose that that expected uncertainty may not directly modulate the gain of learning but instead may be involved in setting a baseline to compute unexpected uncertainty.

In another recent study, Iigaya (2016) [2] proposed a model for learning under uncertainty that consists of two networks. The first network exploits reward-based metaplasticity to estimate stimulus/action values. The second network, compares the current differences in reward rates over pairs of timescales (referred to as unexpected uncertainty) with the means of these differences (referred to as expected uncertainty) to detect “surprise” on a specific timescale, and subsequently update corresponding plasticity (learning) rate in the first network. Therefore, unlike our model [1], this model proposes that completely separate systems are involved in estimating stimulus/action values for making decisions and for computing uncertainty. In addition, this model predicts that only the surprise detection system should influence the valuation system whereas our model predicts two-way interactions between systems encoding stimulus/action values and volatility. These alternative predictions can be tested by pathway-specific inactivation of brain regions involved in computations of different types of uncertainty (see below) and measuring the effect on learning.

Neural substrates of uncertainty

Next, we examine recent experimental findings to identify neural evidence that may serve to validate or refute the predictions of aforementioned computational models. With few exceptions [37], most experimental paradigms probing the neural substrates of uncertainty rarely involve clear distinctions between different types of uncertainty studied here (Boxes 2 and 3). Thus, we re-interpret recent experimental findings in terms of: 1) any specialization in the circuit in terms of encoded signals while distinguishing between different variables related to uncertainty; 2) links between stimulus/actions values, unsigned RPE, and expected uncertainty; and 3) connectivity between cortical and subcortical areas involved in valuation and uncertainty computations. In addition, due to space constraints, we do not discuss learning from aversive stimuli [38] and emphasize corticolimbic contributions to this learning rather than the supporting neuromodulatory systems. Several studies and reviews have already outlined the important contributions of dopamine [39, 40], acetylcholine and norepinephrine [8], and serotonin [41, 42] to learning and decision making under uncertainty. Finally, we consider studies that examine neural correlates and those that aim to reveal causal roles using different interference methods. Findings to date point to a distributed network that includes regions of the prefrontal cortex (PFC), striatum, hippocampus, basolateral amygdala (BLA), and mediodorsal thalamus (MD), which we briefly summarize here (Figure 1).

Box 2. Behavioral paradigms used to study expected and unexpected uncertainty.

Learning and decision-making paradigms with probabilistic outcomes that manipulate the variance in reward outcome can be used to study expected uncertainty and its influence on learning [65, 106]. A popular approach for studying expected uncertainty on learning and choice is to require animals to select between a probabilistic (uncertain) large magnitude reward versus a certain small magnitude reward, while the probability of the uncertain reward has to be learned [66, 107–109]. A related concept, risk, is often used to refer to cases in which reward probabilities are known and thus, do not involve learning. Another way that some groups have attempted to study expected uncertainty is to introduce variability in reward magnitudes or delays-to-reward [7, 18, 57, 67, 110]. In such paradigms, subjects are typically required to select between stimuli associated with different delay variance or estimate reward magnitudes for stimuli associated with different probability distributions, but each with the same mean value and with the same reward rate over the session. Existing evidence suggests that both primates [18, 57] and rodents [67, 110] are able to infer the standard deviation of a reward distribution, or expected uncertainty.

Most experimental paradigms for studying unexpected uncertainty involve learning of frequently changing associations between stimuli/actions and reward outcomes [9, 17, 59, 111–113]. A commonly used paradigm is probabilistic reversal learning (PRL) where the subject selects between two alternative options (e.g., visual stimuli) that each result in probabilistic delivery of reward. The probabilities of reward on the two options can switch after a certain number of trials (L, or block length) that could be fixed [19, 112] or drawn from a distribution [17]. Alternatively, a switch in reward probabilities could be determined based on when performance reaches a certain level, but such design is not ideal because it makes volatility contingent on choice. In the case of fixed block length L, a combination of reward probability on the two options and L collectively define the reward environment, with a specific value of unexpected uncertainty (Box 1). PRL is challenging due to two factors: (1) the probabilistic nature of reward assignment or expected uncertainty; and (2) frequent switches in reward probabilities between blocks of trials (reversals), resulting in volatility and thus unexpected uncertainty. In more general “bandit tasks”, reward probabilities on two or more options/actions can be allowed to change over time (often based on a diffusion or random-walk process, or experimenter predetermined change points [114–117].

Box 3. Example experimental paradigm to dissociate expected and unexpected uncertainty.

Components of probabilistic reversal learning tasks can be used for a new experimental paradigm to dissociate expected and unexpected uncertainty, and to study their interaction. In this task, the subject concurrently learns stimulus-action associations for multiple visual stimuli via reward feedback, as in a natural environment. Stimuli could have similar features and could be associated with similar or different sets of actions. The reward outcomes for actions associated with each stimulus can be probabilistic or deterministic, and reverse on a specific time scale (or block length, L, drawn from a normal distribution with a specific mean and variance; e.g., N(20,6)). A stimulus with a fixed, probabilistic stimulus-action association (no reversal) involves expected uncertainty but not unexpected uncertainty. A stimulus with deterministic outcomes and reversal involves only unexpected uncertainty. Other stimuli with probabilistic reward outcomes and reversal involve both types of uncertainty. Neural response to such stimuli with different levels of expected and unexpected uncertainty can be used to dissociate the neural correlates of different types of uncertainty. Moreover, the subject could construct models of the environment to predict reversals resulting in a divergence between “objective” volatility and “subjective” unexpected uncertainty (see Box 1). In addition to stimulus-specific (“local”) volatility or unexpected uncertainty, global volatility or unexpected uncertainty could be computed over sets of stimuli, actions, or both in order to determine an overall gain of learning in the environment. To compute global volatility, the inverse of expected uncertainty could be used to differentially weigh volatility from different stimuli or actions. These alternatives can be dissociated using different levels of similarity between stimuli and between sets of actions. Finally, this paradigm allows studying the interaction between expected and unexpected uncertainty in terms of: 1) how expected uncertainty is used to compute volatility (or unexpected uncertainty) about each stimulus or sets of actions; 2) if and how expected uncertainty is used to combine volatility across stimuli and/or sets of actions; 3) how expected and unexpected uncertainty influence learning.

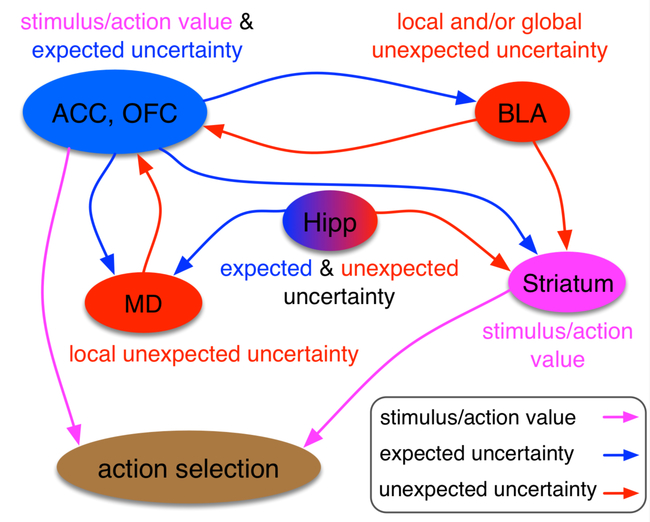
Figure 1. Major nodes of expected and unexpected uncertainty computations.

Based on existing data, these are a few cortical and subcortical areas that could be involved in the computations (and representations) of expected and unexpected uncertainty as well as stimulus or action values. We do not include all anatomical connections for simplicity. The uncertainty network includes Anterior Cingulate Cortex (ACC), Basolateral amygdala (BLA), Hippocampus (Hipp), Mediodorsal thalamus (MD), and Orbitofrontal Cortex (OFC). Most of these are areas are highly reciprocally connected to other areas in this network, which could explain the overlap in the information/variable each of these areas represent and compute. This suggests that learning under uncertainty involves inherent interactions between expected and unexpected uncertainty signals.

Prefrontal cortex.

Neural correlates of uncertainty have been found in many species in different regions of PFC including the anterior cingulate cortex (ACC) [43]. Relevant to our discussion here, Hayden and colleagues [44] have shown that not only do ACC neurons represent unsigned RPE, but this signal is correlated with some behavioral adjustment in a gambling task. In a more recent study, Monosov (2017) [45] found neurons in ACC signal both expected value and expected uncertainty but in a valence-specific manner. Moreover, of the populations of neurons that signaled uncertainty, fewer neurons signaled RPEs than variability in reward outcomes (expected uncertainty). Thus, encoding of RPE in ACC, previously observed by several groups [46–48] could contribute to uncertainty computations in this area. Encoding of RPE alone does not qualify a brain area for uncertainty computations, but signaling of unsigned RPE can provide strong evidence for approximation of expected uncertainty.

Unlike ACC, there is debate on whether orbitofrontal cortex (OFC) signals RPEs [49–51], and whether and how these signals may contribute to different forms of uncertainty. Electrophysiological recording studies in rat OFC provide convincing evidence that activity in this region correlates with both stimulus value and expected uncertainty [52, 53] similar to ACC. This encoding depends on the stability of the environment (Riceberg and Shapiro 2017) suggesting a contribution of OFC to expected uncertainty and perhaps even volatility (Riceberg and Shapiro 2012). Most of the functions described above in rats [54] have been realized in the nonhuman primate brain as well: representations of expected outcomes can also be decoded from monkey OFC during value-based choice [55, 56] and OFC neurons signal both stimulus value and expected uncertainty [57]. In monkeys, activity of OFC neurons rapidly updates in response to changes in reward magnitude via cues and activity in this region, like in rat, and is modulated by reward history [58]. For example, Massi and colleagues [59] demonstrated that signals relevant to task performance can be decoded better in both OFC and ACC in a volatile environment. Taken together, the evidence in rat and primate OFC points to conserved functions in learning under uncertainty.

Learning under uncertainty ostensibly involves multiple areas of PFC across species, but which of these regions are causally-involved in uncertainty computations? Both anatomical and functional data support the idea that ACC may function as a key integrator of reward, cognitive, and action plans across species [60–64]. Similarly, lesions or transient/reversible pharmacological inactivation of OFC across species also result in learning and/or performance decrements in conditions of risk and uncertainty [54, 65–71]. An important follow-up question is how these regions contribute to uncertainty computations. OFC (and perhaps also ACC) has access to volatility to construct stable representations of stimulus/action values under expected uncertainty [52, 67]. Yet computations of volatility or unexpected uncertainty likely occur outside PFC (e.g., BLA) with access to both cortical and subcortical regions to enable modulation by these factors. Based on the available evidence, we speculate that OFC and ACC may have dissociable and complementary roles in learning under uncertainty and in mitigating the adaptability-precision tradeoff. Specifically, OFC may support slow updates of stimulus values and estimation of expected uncertainty over multiple trials to provide a baseline for computing unexpected uncertainty. The ACC may instead carry a spectrum of learning or transition rates [1, 72] to not only estimate expected uncertainty but also to allow computation of unexpected uncertainty in another area and subsequently, faster updates if unexpected events are detected. Thus, OFC and ACC could provide parallel signals necessary for computations of unexpected uncertainty elsewhere, where these signals can be compared.

Does the functional connectivity support this possibility? Anatomical studies in rodents and primates point to a topographic map of connectivity from various subcortical to cortical structures. Specifically, in lateral-to-medial sectors of rat OFC there is increasing innervation by affective/motivational systems and decreasing innervation by sensory integration areas (reviewed in [54]). In ACC there is a similar pattern of connectivity but along the dorsal-ventral plane, with dorsal areas better connected with sensorimotor and association areas, and ventral areas connected to amygdala [73]. This results in largely redundant information to both OFC and ACC that could be used to compute different quantities (i.e. stimulus/action values, unsigned RPE, etc.) required for uncertainty computations. Additionally, it is important not to neglect cortico-cortical connectivity and ‘crosstalk’ in forming representations of value and uncertainty. There is dense labeling of fibers from both medial and ventral OFC to both dorsal and ventral ACC [74], suggesting that the ACC receives both direct and ‘OFC-filtered’ information about rewards, and may represent reward information very differently [75]. Moving forward, it will be crucial to discern conditions and timing wherein ACC and OFC may be differentially engaged in learning about reward, and to compare their contributions directly on the same task(s).

Striatum.

Correlates of expected uncertainty, as defined here, and related to stimulus-outcome associations have been found in the dorsal striatum in monkeys [76], but there is evidence that the striatum may also be causally involved in learning under expected uncertainty. Lesion studies do indeed support its role in learning during probabilistic, rather than deterministic, reward schedules in both rodents and nonhuman primates [77, 78]. The striatum is also involved in contexts where reward rate and delay-to-reward must be encoded for appropriate task performance [77, 79], thereby implicating this region in flexible learning (and responding to) changes in individual outcomes, since it receives inputs about both expected and unexpected uncertainty (Figure 1).

Hippocampus.

Expected uncertainty signals associated with probabilistic outcomes have been found in the septum [80], which in turn may aid learning via innervation of GABAergic interneurons in the hippocampus [81]. Conversely, unexpected uncertainty correlates have also been found in the hippocampus, mostly reported in primates. For example in humans, there are correlates of change detection and “mismatch” computations in hippocampus [82]. Additionally, negative event-related potentials in hippocampus covary with unexpected uncertainty in outcome, irrespective of valence [83]. Further, BOLD signal in hippocampus correlates negatively with unexpected uncertainty at the time of outcome [23]. Both hippocampus and OFC have been implicated in cognitive maps that could provide predictions about choice outcomes [84, 85]. Given this overlap, it is conceivable that the hippocampus also signals expected uncertainty in addition to unexpected uncertainty. To our knowledge, there has been no direct test of a causal role for hippocampus in learning under the different forms of uncertainty we consider here, in either rodents or primates.

Basolateral Amygdala.

A large body of data in rodents and primates points to the basolateral amygdala (BLA) in detecting surprising changes, leading to quick updating [86, 87], that supports flexible learning [77, 88]. Indeed, BLA activity changes in response to the internal (motivational) state, typically probed via reinforcer devaluation paradigms [89]. However, its role also extends to changes beyond the motivational state, signaling changes in the (external) environment as both positive and negative RPEs, when expectations are repeatedly violated [89, 90]. This previously has been explained in the context of attentional salience and “associability” signals (as in the PH model) both of which could contribute to computations of unexpected uncertainty. For the BLA to facilitate rapid updating, this region must also receive information about expected uncertainty.

Newer evidence points to BLA critically involved in supporting learning of actual changes (i.e. volatility) in the expected value of rewards as signaled externally [67], not necessarily by shifts in (internal) motivational state. Based on neuroanatomical connectivity, BLA may directly influence value learning under uncertainty via projections to/from ACC [91, 92], OFC [93, 94], and/or dopaminergic circuitry [95]. These projections could allow BLA to compute unexpected uncertainty by comparing changes in stimulus-action values to baselines from expected uncertainty (see Mechanistic models).

Mediodorsal Thalamus.

The mediodorsal thalamus (MD) is an important node for value processing [96, 97], but has also been explored for its involvement in rapid learning in changing environments [98–100]. For example, monkeys with MD lesions exhibit an increased tendency to switch, even after a win trial [99], suggesting MD is required for maintaining a representation of recent reward modulated by choice, which could facilitate learning when there are multiple stimuli in the environment. In support of this [101] suggested that the architecture of thalamocortical and corticothalamic pathways may be particularly important in supporting the maintenance and rapid update of cortical representations, making MD a candidate region for volatility computations.

In summary, current experimental evidence points to the following. First, it is clear that there may be some bias (likely not “specialization”) for encoding and computing different variables related to uncertainty in the reward environment. However, uncertainty computations and perhaps representations of uncertainty signals are distributed. Second, there are close links between stimulus/actions values, unsigned RPE, and expected uncertainty both anatomically and behaviorally, suggesting that computations of uncertainty may not require separate estimation of stimulus/action values. Finally, although there are connections from cortical areas involved in valuation and uncertainty computations to subcortical areas, it is unclear whether dopaminergic systems receive and can integrate different types of uncertainty information to modulate the learning rates, as has been widely proposed.

Future perspectives

To allow effective learning, the brain must achieve a balance of ‘scaling down’ learning when expected uncertainty is high vs. ‘scaling up’ learning when unexpected uncertainty is high. Moreover, we suggest that volatility could be shared and generalized across individual stimuli/actions in order to compute an environmental or global estimate of volatility. Expected uncertainty could be used for differential weighting of volatility across stimuli/actions to estimate such global volatility, which in turn, could set an overall gain of learning in the environment. Above, our discussion of computational models and experimental data suggests that understanding interactions between expected and unexpected uncertainty is crucial for understanding learning and choice under uncertainty (see Box 4 for remaining questions and how they can be addressed).

Box 4. Outstanding questions about the computation of expected and unexpected uncertainty.

In our opinion, the following are critical remaining questions for future research in learning under uncertainty and understanding underlying neural substrates and mechanisms.

1. How do uncertainty computations in ACC/OFC and BLA (or MD) interact to support learning?

   • (1.1)
     Do uncertainty computations rely on separate estimates of stimulus/action values than those used to make decisions?
   • (1.2)
     Is expected uncertainty used as a baseline for comparison, in order to detect unexpected outcomes/events?
   • (1.3)
     Does expected and unexpected uncertainty directly influence the gain of learning?
2. How does updating of stimulus/action values in striatum and ACC/OFC depend on expected and unexpected uncertainty signals from BLA, Hipp, and MD?

   • (2.1)
     Do surprising events and unexpected uncertainty ‘scale up’ the gain of learning and if so how?
   • (2.2)
     Does expected uncertainty help detection of unexpected outcomes or instead, only ‘scale down’ the gain of learning?

3. Are signed and unsigned RPE signals (found in many brain areas) used for the computation of expected uncertainty?

4. Are expected and unexpected uncertainty generalized across stimuli/actions in the reward environment, and if so how?

   • (4.1)
     Is expected uncertainty used to combine uncertainty across different stimuli/actions to compute a global level of volatility in the environment?

Some of these questions can be tested currently by pathway-specific manipulations in rodents, multi-area recoding in nonhuman primates, and behavioral manipulations using novel paradigms in humans and other species (see Box 3). In vivo imaging in target PFC regions while specific pathways and cell-populations are activated or silenced during learning with specific designs would be especially revealing in this regard. In addition, answering these questions requires understanding interactions between neural elements across multiple levels (synaptic and circuit- level), which is not possible without detailed computational modeling.

Although neural correlates of expected uncertainty signals have been found in many species’ brains, we still do not know how these signals contribute to the computations of unexpected uncertainty (volatility) and subsequent learning. We also lack an understanding of how unexpected uncertainty is encoded in the brain (e.g. single-cell vs. population level) or how it is computed, but metaplasticity may provide a promising mechanistic framework for its computation [1, 36].

The importance of the nonhuman primate work on this general topic cannot be overstated; it is the crucial link to understanding how the human brain copes with and learns under uncertainty. The lack of behavioral paradigms and accompanying models in rodents that are designed with the nonhuman primate work in mind, we think, has slowed progress in understanding the causal, systems-level neural mechanisms that support such adaptive learning and choice under different forms of uncertainty. Part of this is a methodological issue: the circuit dissection technology is more advanced in rodents, but the behavioral paradigms rarely are designed to mimic nonhuman primate studies. Moreover, custom and novel tasks are needed to examine nuances of interactions between expected and unexpected uncertainty systematically (Box 3).

Value-based learning is assumed to happen at the synaptic level whereas interactions between expected and unexpected uncertainty relies on circuit-level mechanisms. This indicates that revealing mechanisms of learning under uncertainty requires understanding interactions between neural elements across multiple levels (synaptic and circuit- level), which is not possible without detailed computational modeling. Such models are also instrumental to computational psychiatry: various psychiatric conditions (including behavioral and substance addictions, anxiety disorders) lead to failures either in generating accurate models of the reward environment [102] or inabilities in using those models to flexibly guide behavior [103]. We hope that this Opinion outlines some important considerations for identifying the basic underlying mechanisms that may go awry in several neuropsychiatric disorders. Ultimately, a combination of novel behavioral paradigms, detailed mechanistic models, multi-area recording, and circuit- level manipulations are required to answer critical lingering questions about learning under uncertainty (Box 4).