Computational Studies of Catalytic Loop Dynamics in Yersinia Protein Tyrosine Phosphatase Using Pathway Optimization Methods

Abstract

Yersinia Protein Tyrosine Phosphatase (YopH) is the most efficient enzyme amongst all known PTPases and relies on its catalytic loop movements for substrate binding and catalysis. Fluorescence, NMR and UV resonance Raman (UVRR) techniques have been used to study the thermodynamic and dynamic properties of the loop motions. In this study, a computational approach based on the pathway refinement methods Nudged Elastic Band (NEB) and Harmonic Fourier Beads (HFB) has been developed to provide structural interpretations for the experimentally observed kinetic processes. In this approach, the minimum potential energy pathways for the loop open/closure conformational changes were determined by NEB using a one dimensional global coordinate (ΔRMSD). Two dimensional data analyses of the NEB results were performed as an efficient method to qualitatively evaluate the energetics of transitions along several specific physical coordinates. The free energy barriers for these transitions were then determined more precisely using the HFB method. Kinetic parameters were estimated from the energy barriers using transition state theory and compared against experimentally determined kinetic parameters. When the calculated energy barriers are calibrated by a simple “scaling factor”, as have been done in our previous vibrational frequency calculations to explain the ligand frequency shift upon its binding to protein, it is possible to make structural interpretations of several observed enzyme dynamic rates. For example, the ns kinetics observed by fluorescence anisotropy may be assigned to the translational motion of the catalytic loop and μs kinetics observed in fluorescence T-jump can be assigned to the loop backbone dihedral angle flipping. Furthermore, we can predict that a Trp354 conformational conversion associated to the loop movements would occur on the tens of ns timescale, to be verified by future UVRR T-jump studies.

Graphical Abstract

Introduction

Protein tyrosine phosphatases (PTPase) comprise a large and structurally diverse family of signaling enzymes with a unique signature (H/V)C(X)₅R(S/T) motif. It is estimated that more than 100 PTPases are encoded in the human genome. In humans, the protein tyrosine phosphatases, in combination with protein tyrosine kinases, regulate cellular protein tyrosine phosphorylation levels, thus regulating many intracellular signal transduction pathways. Malfunctions of the PTPases have been associated with a number of cancers and also metabolic diseases, including non-insulin dependent diabetes (cf. ^1–3). Yersinia pestis is the causative agent of human diseases from gastrointestinal syndromes to the plague.^4–5 It directly injects cytotoxic effector proteins, including YopH, a PTPase, into the cytosol of mammalian cells. YopH is hyperactive compared to human PTPases, and interferes with mammalian cellular pathways to achieve the pathogenicity of Yersinia.

The high activity of YopH has made it a model system for detailed mechanistic studies of the PTPases.⁶ PTPase catalysis is achieved at its substrate binding site which is composed of a phosphate binding loop including the nucleophilic cysteine in the signature motif ((H/V)C(X)₅R(S/T)). The reaction mechanism involves two main chemical steps (reviewed in ^5–7), and Scheme 1 shows the first step of the reaction. After substrate binding, a protein conformational change involving the so-called WPD loop motion brings the essential Asp356 residing on the loop from almost 8 Å away to the scissile oxygen of the phosphorylated tyrosine (see Scheme 1 and Figure 1 inset for the loop movements). In the first chemical step, Asp356 is proposed to act as a general acid to transfer a proton to the scissile oxygen of the substrate to initiate the tyrosine leaving group dissociation. The active site Cys403 becomes (or already is) deprotonated to serve as a nucleophile to accept the phosphoryl group dissociated from phosphotyrosine substrate. The completion of the first reaction step results in a phosphocysteine intermediate. After fast dissociation of the substrate leaving group, the side chain of Gln446 flips into the active site to form a hydrogen bond to Gln357 on the WPD loop and to stabilize a water molecule that is positioned along the S-P bond direction for the next hydrolysis step. ^8–9

Scheme 1.

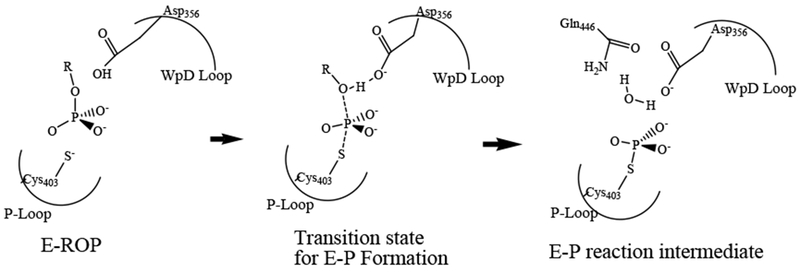
The first chemical step in PTPase catalyzed reaction.

Figure 1.

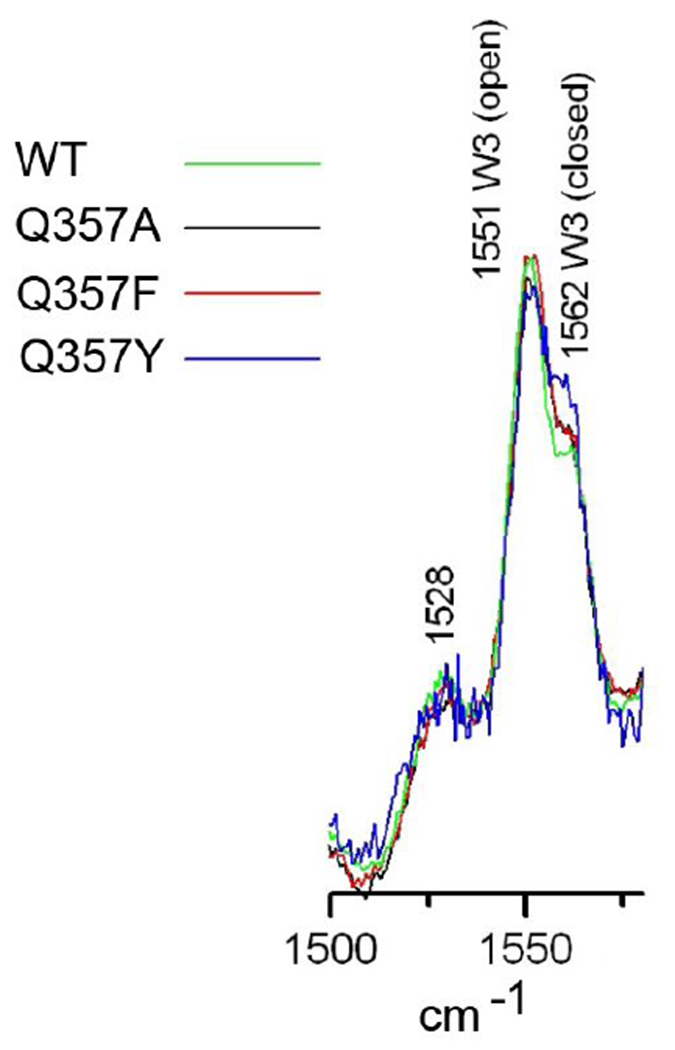
UVRR spectra of YopH and Q357X mutants. 0.4 ml of each sample is taken in quartz NMR tube and the tube was spun and solution was mixed with stirrer and kept ~10 C during the UVRR measurement. The 229 nm UVRR beam was used at the power level of ~ 1 mw. Each UVRR spectrum is average of 10 mins except Y-mutant, which was averaged for 20 mins. All samples are in 50 mM citrate buffer, pH 6.5 with 0.15 M NaCl. Sample concentrations were 0.34 mM for wt, 0.08 mM for Q357A, 0.08 mM for Q357F, and 0.015 mM for Q357Y.

The importance of the WPD loop structure and dynamics to YopH catalysis is implied in this proposed reaction mechanism and is the subject in a number of spectroscopic and computational studies. The study on the thermodynamic characterization of the WPD loop structures by UVRR measurement of Trp354 and the WPD loop dynamics by Trp354 fluorescence anisotropy measurements showed that there are two similarly populated loop structures in the apo YopH and ns to tens of ns protein motions are present.¹⁰ A study by MD computational simulations showed that the observed ns dynamics is likely due to the translational motions of the WPD loop. ¹¹

The enzyme system under current study is the catalytic domain of YopH (residues 162-468), which contains a single tryptophan (Try354) at the hinge of the WPD loop (loop sequence WPDQTAVS). In previous fluorescence T-jump studies on apo YopH, ~3 μs kinetics was observed. ¹² Since the T-jump signal is from Trp354, the observed kinetic process was believed to be associated with the loop dynamics. In addition, fluorescence T-jump studies of YopH bound to an inhibitor (p-nitrocatechol sulfate, pNCS) showed ~200 μs kinetics in WPD loop motions. ¹² In a series of mutations to WPD loop residue Q357 (Q357F/Q357Y/Q357A), WPD loop dynamics in the tens to hundreds of μs range were observed when bound to pNCS. The faster kinetics in the Q357 mutants were attributed to destabilization of the closed conformation by preventing formation of hydrogen bonds between Gln446 and Gln357. The X-ray structural studies of Q357F showed that the disruption of the Gln446-Gln357 hydrogen bond changes the active site hydrogen bonding network in the loop closed conformation, resulting in the observation of both loop open and loop closed conformations in the crystal form of Q357F/pNSC complex (3U96). ¹³

Recently, the WPD loop dynamics of two PTPases, PDP1B and YopH, were determined by NMR methods, in which a close correlation between the k_cat and the loop closure of these PTPases was demonstrated.¹⁴ For YopH, the NMR studies were focused on the relaxation properties of Ala359 and Ser361 ¹⁵N resonances, located at the C-terminal end of the WPD loop. 22 μs kinetics was observed in apo YopH, slower than the 3 μs kinetics observed by fluorescence T-jump. Furthermore, −500 μs kinetics was observed for a YopH/peptide (Ac-DADEXLIP-NH₂) complex, which is also slower than the −200 μs kinetics observed by T-jump studies on YopH/pNCS complex. The difference in the kinetics of the ligand binding was explained by very different ligands used in these two studies. However, the different kinetics observed in apo YopH by these two different spectroscopic studies were not easily understood and one possible explanation was that the T-jump results report on the environmental change of the indole ring of Trp354 at the N-terminal end of the WPD loop and NMR results report on the motions of the back bone nitrogen atoms near the C-terminal end of the loop.¹⁴

Such observations raise the possibility that the loop opening and closing motions are not uniform and different sections of the loop may follow different kinetics. Furthermore, the NMR studies also determined that the loop opening movement is 34 times faster than the loop closure in apo YopH, so that the loop closed conformation is the dominate species in solution.¹⁴ This is in clear contrast with the UVRR results which suggested that the loop open and closed conformations in the apo YopH are almost equally populated.¹⁰

In our view, the apparent contradictory spectroscopic observations by different techniques are at least partially due to the limitations in these spectroscopic methods in describing complex processes such as ligand binding. In ligand binding, at least three events occur: the ligand approaches the active site, the catalytic loop opens and closes, and the enzyme structure reorganizes after ligand reaches the active site. Any of these events may show complex kinetic behavior. Thus any of the spectroscopic methods may only be able to characterize certain specific aspects of the ligand binding process.

For example, in fluorescence T-jump relaxation and fluorescence anisotropy studies, the observed relaxation signal is related to the environmental change of the Trp354, which can be caused by ligand approaching to the active site, enzyme catalytic loop movements and subsequent enzyme structural reorganizations after ligand reaches the active site. The observed kinetics may be fitted by one or more kinetic rates, corresponding to two-state or multiple-state kinetic transitions related to these three events that occur during ligand binding. ^15–16 To associate the observed kinetic rates to specific events is generally a challenge and often requires additional knowledge from other experimental studies.

In the cited PTPase dynamic studies by NMR relaxation methods, ¹⁴ the results were analyzed using a two-state model to determine the exchange rate between the two states. Compared to the fluorescence relaxation methods, the NMR relaxation methods can be applied to the atoms on the catalytic loop to determine the dynamics associated to the loop motions directly. On the other hand, it may be difficult to resolve multiple transitions due to the two-state model used in the analysis. The exact structures for these two states, typically labeled as the “loop open” and “loop closed” forms, may not be well defined in such studies, especially when the loop motion during ligand binding is not a simple uniform translational movement but follows complex pattern involving multiple stages.

In UVRR studies, the two observed YopH Trp354 W3 bands with similar intensities indicate that there are two equally populated protein conformations. ¹⁰ Separate X-ray structural studies suggested that they are associated to the “loop open” and “loop closed” forms and the population of the “loop open” form is reduced significantly when ligand is bound. ^{10, 13} Apparently, the two loop conformations determined by the UVRR studies may not be the same as the two conformations referenced from the NMR relaxation studies. Likewise, the enzyme dynamics determined from the UVRR T-jump relaxation studies on the Trp354 W3 bands will report on the Trp354 conformational change rather than the Trp354 environmental change as reported by fluorescence techniques, or the loop motions as reported by NMR relaxation methods.

Thus, the inherent limitations of these spectroscopic methods prevent full understanding of a complex process such as ligand binding. In general, structural and functional interpretations of the spectroscopically determined enzyme kinetic results, which may be observed in all times scales from sub ps to ms and beyond, are difficult. For example, ps-ns protein loop motions may be detected by NMR methods but the relative atomic movements within the loop are not well defined (for a recent review, see ¹⁷). This is in part due to the fact that if and how the observed kinetics may associate to enzyme functions in most cases are not well understood, except in a few cases where sub ms enzyme motions may be correlated to substrate turnover in enzyme (e. g. ¹⁴). On the other hand, the chemical bond breaking/forming events in enzyme occur in the time period of a few bond vibrations, in the fs to sub μs time scales (e. g. see ¹⁸). How the sub ms loop motions are coupled to the faster (from μs to ps) motions of the enzyme to facilitate the fs chemical event is unknown.

To develop a tool to study such coupled motions in enzyme, a computational approach is described to quickly survey the enzyme kinetics associated to enzyme catalytic loop open and close movements. Our results indicate that the loop closure is not a uniform translational motion as generally assumed. Furthermore, multiple kinetics associated to specific structural features have been identified in ns to μs time scales and these kinetics are believed to be detectable by laser spectroscopic methods.

The high spatial and temporal resolution available in MD simulations can provide a relatively complete dynamic picture for ligand binding and structural reorganization of the enzyme, provided the models can be shown to agree with experimentally determined features of the system. In this study, we are able to provide structural interpretations for the spectroscopically observed kinetics such that the results from experimental and computational studies may be cross validated. Since our model can recapitulate certain experimentally observed features, we have a degree of confidence in predicting features which have not been experimentally measured, and hope the predictions will stimulate the effort and innovation to study these properties.

In this study, UV resonance Raman measurements on Q357F/Q357Y/Q357A mutants were performed to determine how the disruption of the Gln446-Gln357 hydrogen bond affects the loop conformational distribution in the apo enzymes. To gain a better structural understanding of the loop dynamics, we developed a computational approach based on molecular dynamics simulation techniques to assign the experimentally observed kinetics to motions of specific structural features of the loop. Nudged elastic band (NEB)^19–20 and Harmonic Fourier beads (HFB) methods²¹ were used to determine minimum potential energy pathways between loop open and closed conformations. The free energy profiles along these pathways can be calculated by umbrella sampling in multidimensional conformational space. The free energy barriers along specific coordinates can then be compared to the experimentally determined reaction rates via the Eyring equation to correlate experimentally observed kinetic processes with the specific enzyme conformational transformations. Our results suggest that our computational approach has the potential to provide a complete molecular picture for the spectroscopically observed ns to sub millisecond kinetic processes.

Materials and Methods

Enzyme Preparation.

The catalytic domain (residues 162–468) of Yersinia PTPase (referred as YopH) and its Q357A, Q357F and Q357Y mutants were prepared according to our previously published procedure. ¹³ Briefly, YopH and its Q357X mutants were expressed under the control of the T7 promoter in E. coli BL21(DE3) cells. Two columns, CM Sepharose FF 50 mL homemade column and a gel filtration column (Superdex 200) were used to purify the enzymes to >95% purity as determined by SDS-PAGE. The purified enzyme was stored in the presence of 1 mM DTT and 1 mM EDTA at 4 °C until use.

UVRR experiments.

Briefly, Raman excitation wavelength at 229 nm (0.5–0.8 μJ/pulse, 20 ns, 1 kHz) was obtained by frequency quadrupling a second Ti:sapphire laser. About 0.4 ml of sample solution was contained in a suprasil quartz NMR tube and spun and translated while stirring the solution using a stationary magnetic spin-bar for vertical mixing of the sample. Spectra were obtained by averaging for 10 minutes. Scattered light was collected at ~135° with a pair of fused quartz lenses, f-matched to a 1.26 m spectrograph (Spex 1269), which was equipped with a holographic grating (3600 groove mm) and UV enhanced liquid nitrogen cooled CCD detector (Roper Scientific). The measured spectra were calibrated using the standard Raman spectrum of acetone.

Typically, 0.4 ml of each sample is taken in quartz NMR tube and the tube was spun and solution was mixed with stirrer and kept ~10 C during the UVRR measurement. The 229 nm UVRR beam was used at the power level of ~ 1 mw.

Computational methods.

In this study, NEB/HFB methods were used to characterize apo YopH loop closure conformational transition pathways and to find possible physical changes associated with the experimentally observed transitions. NEB ²² methods implemented in CHARMM ²³ were used to determine the minimum potential energy path between loop open and loop closed conformations obtained from X-ray structures.; c35b1 version of CHARMM with force field parameter set CHARMM22 ²⁴was used for these calculations. SHAKE ²⁵ was used to constrain the covalent bond to hydrogen so that 2 fs integration time steps can be used in MD simulations. Several YopH (and its mutants) X-ray structures with WPD loop open and closed conformations, and with or without a bound ligand from PDB were used. These include Q357F/pNCS in both loop open and loop closed conformations (PDBID: 3U96), C403S mutant in loop closed conformation (PDBID: 1YTS), wt YopH in loop open conformation (PDBID: 1YPT), and wt YopH/pNCS in loop closed conformation (PDBID: 1PA9). For NEB calculations, we prepared two endpoint structures, one with loop open and one with loop closed conformations, based on the corresponding X-ray structures using CHARMM.^{19, 26} Hydrogens are added by HBUILD, with the experimental input that all carboxyl groups are ionized. The procedure described by Arora and Brooks ²⁷ is followed to determine the minimal potential path between these two enzyme conformations using NEB methods with 52-64 intermediate images, and to construct the free energy profile along this path by umbrella sampling using ΔRMSD from all protein atoms as the order parameter. ΔRMSD is the difference between the two RMSDs calculated with respect to the two endpoint starting structures.

To set up initial endpoint structures for NEB calculations, the loop open and the loop closed X-ray structures were relaxed by energy minimization. During minimization, the harmonic force constraint on all heavy atoms of the catalytic loop is reduced gradually from 200 to 5 kcal/mol/Ų in 4 stages, using 200 steepest decent (SD) followed by 1000 (ABNR) minimization steps for each harmonic force constraint. The minimized structures were then used to start NEB calculations to search for the minimum potential energy path between these two endpoint structures. In NEB calculations, the spring force constant was reduced from 10,000 to 1,000 kcal/mol/Ų in three stages, with 200 SD steps followed by 2000 ABNR minimization steps in each stage. The RMS off-path force of 0.002 kcal/mol/Ų was reached for the final NEB structures.

To quantify the free energy surface 1D-Umbrella sampling simulations using Langevin dynamics along the NEB determined pathways were performed. The biasing coordinate was the same coordinate that was used in NEB, which was ΔRMSD. The force constants for the bias potentials along the conformational transformation pathway were adjusted when necessary to ensure the proper sampling in MD simulations to achieve overlapping distributions of neighboring simulation windows. The free energies of the separate simulation windows along the reaction coordinate were combined using the weighed histogram analysis method (WHAM) ²⁸ to remove the contributions of biasing potentials. The solvent effects were modeled by a low dielectric implicit solvent using the GBMV module implemented in CHARMM; ²⁹ This generalized born implicit solvent models have been shown to accurately reproduce Poisson-Boltzmann solvation energies. ³⁰ 2D free energy surfaces were constructed by monitoring a 2^nd degree of freedom, which was unrestrained in the umbrella sampling simulations. 2D WHAM was used to construct the 2D surfaces under the assumption that the 2^nd coordinate is uncoupled from the ΔRMSD coordinate.

The harmonic Fourier bead (HFB) method was also used as a pathway refinement method to evolve an initial naive pathway (string) to a low energy pathway. Initial pathways for the apo YopH enzyme were created using HFB in CHARMM to interpolate between the open and closed configurations in the reactive coordinate space (RCS). The RCS is the set of atoms which characterize the transition of interest, in all of our HFB calculations the RCS was chosen as the backbone Cα, C, N atoms of Asp356, the backbone N atom of residue Gln357 and the Cα atom of residue Cys403. This 5-atom RCS captures the 356-357 backbone amide flip, and the Cα - Cα separation between residues 356 and 403. Each of the initial pathways consisted of 64 structures (beads). The initial strings were then evolved using HFB; in each iteration of HFB the RCS atoms were restrained with a 20 kcal/mol*Ų harmonic restraint to their current position and then minimized for 1000 SD steps, followed by 2000 ABNR steps. The minimization was performed using the GBMV implicit solvent model and the non-bonded interactions were switched off between 12 and 14 Å. Following the minimization procedure, the string is reparameterized using 48 Fourier basis functions, in order to keep the beads equally spaced in the RCS. The cycles of minimization and reparameterization are repeated until the string stabilizes, indicating a minimum energy pathway has been reached. 36 iterations of HFB were applied to the pathway, by which time the string displayed convergence as monitored by a cumulative RMSD metric.

The HFB refined pathway was subsequently used in 2D umbrella sampling simulations to calculate the free energy profiles. In one set of 2D umbrella sampling simulations, restraints were applied to the Cα-Cα distance between residues 356 and 403, and to the backbone dihedral ψ angle of residue 356. A second set of umbrella sampling simulations were performed using the same distance restraint, but also restraining the Chi2,1 dihedral angle (defined by Cα-Cβ-Oγ-Cδ1) on Trp354. The restraint spring constant for all dihedral angles used in umbrella sampling was 20 kcal/mol/rad². The umbrella sampling simulations were run for 1 ns, using Langevin dynamics and GBMV implicit solvent. The final 800 ps, where used to construct the free energy surfaces using the 2D WHAM program from Alan Grossfield (http://membrane.urmc.rochester.edu/content/wham).

Results

Trp354 conformational distributions in apo YopH and Q357X mutants.

WPD loop is the signature motif in PTPase family and the mutation of this invariant Trp residue in WPD loop reduces the catalytic efficiency by 3 to 4 orders of magnitude. ⁷ While only YopH in this enzyme family contains a single Trp residue, our spectroscopic studies may be extended to the other members of the PTPase family by mutating non-essential Trp residues. The mutations of these Trp residues may have little effects on the catalytic efficiency, as demonstrated by the NMR and fluorescence T-jump studies on a mutant of triosephosphate isomerase, in which only the Trp at the hinge of the loop was reserved.^31–32

Figure 1 shows UV resonance Raman spectra of apo YopH and its Q357X mutants in the tryptophan W3 mode region. W3 mode has been assigned to the Cγ=Cδ1 stretch of the tryptophan and its frequency is sensitive to the tryptophan conformation (also see below).³³ This W3 mode shows two peaks at 1551 and 1562 cm⁻¹, respectively, in wt and all Q357X mutants, suggesting two Trp354 conformations in the apo form of these YopH variants. Curve fittings of the W3 bands showed the population ratios of 68:32, 67:33, 68:32 and 60:40 for wt, Q357A, Q357F and Q357Y, respectively. In the ligand bound form of YopH, the W3 band typically shows only a single band near 1560 cm⁻¹ (data not shown). ¹⁰ The disappearance of the band intensity near 1550 cm-1 in the UVRR spectrum of YopH upon ligand binding is consistent with the X-ray structural studies of YopH/ligand complexes, in which the loop is in closed conformation. ^10–13

Previous studies have shown that the W3 band frequency is correlated with the tryptophan Chi2,1 dihedral angle (defined by Cα-Cβ-Cγ-Cδ1).³⁴ W3 frequency near 1550 cm⁻¹ and 1560 cm⁻¹ correspond to Chi2,1 values near ±60 degrees and 0 degrees, respectively. A number of X-ray structures of YopH and its mutants in both WPD loop open and closed forms have been determined. For example, in the structures with PDB code 1YTS,³⁵ 3F9A,³⁶ 2142,³⁷, 1YTW/1YTN,³⁸ and pNCS complexes 1PA9,³⁹ and 3U96, Q357F/pNCS,¹³ Chi2,1 is typically near 0 degrees in the loop open conformation, and near 60 degrees in the loop closed conformation. Based on these correlations, and the UVRR results shown in Figure 1, we can conclude that the loop open conformation is slightly favored over the loop closed conformation in the apo YopH and its Q357X mutants.

UVRR results on Trp354 clearly capture the conformational distribution of its indole ring in the apo YopH, and likely also report on the conformational distribution of the WPD loop near the N-terminal end. This conclusion has been generalized to the conformation distribution of the entire WPD loop in a number of previous studies.^12–13,34 However, recent NMR studies on the dynamics of the backbone NH resonances near the C-terminal end of the WPD loop in apo YopH suggested that the loop structure is dominated by one conformation which was interpreted as the loop open conformation.¹⁴ The apparent discrepancies on the loop conformations from UVRR and NMR studies raised an interesting possibility that the WPD loop follows not a uniform, rigid body motion but instead complex dynamics in its open-closure movements.

Experimentally observed protein dynamics near the WPD loop by spectroscopic methods.

Some of the time constants, either observed directly by spectroscopic measurements or derived from model building in the analysis of the experimental data from fluorescence or NMR spectroscopic studies of the YopH WPD loop dynamics are listed in Table 1.

Table 1,

Summary of observed time constants by spectroscopic techniques in apo YopH and YopH/ligand complexes.

Enzymes	Observed time constant	Loop open	Loop close	Detection method
Apo YopH	4 and 30 ns	4 ns#	4 ns#	1, #: 5
Apo YopH	~3 μs	~5 μs*	~7 μs*	2, *: 4
Apo YopH	23 μs	23 μs	800 μs	3
YopH/Arsinate	4 and 50 ns			1
YopH/PNCS	20 - 110 μs	130 μs	11 μs	2
Q357F/PNCS	35 - 250 μs	380 μs	26 μs	2
Q357A/PNCS	13 - 60 μs	100 μs	9 μs	2
YopH/peptide	550 μs	550 μs	50 μs	3

1. Fluorescence Anisotropy; ¹⁰ 2. Fluorescence T-jump (Observed values for E/PNCS are concentration dependent. Loop open/closed values are derived from a four-state model); ^12,13 3. NMR (all values are derived from a two-state model), ¹⁴ 4. UVRR (this work) and 5. MD simulations. ¹¹

pNCS is a YopH specific inhibitor structurally similar to the small molecule substrate pNPP.³⁹

In fluorescence anisotropy studies of the apo YopH, two correlations times, 3.8 and 30.6 ns, were obtained from the curve fitting of the anisotropy decay spectra. 30.6 ns motion was assigned to the overall rotation of the protein and 3.8 ns motion was assigned to the protein shape change, which was assigned to the loop motions.¹⁰ Since the loop population ratio was near one as determined by UVRR results on W3 bands, the loop open and loop closure time constants should be similar.¹⁰ In fluorescence T-jump measurements of the YopH, a time constant of ~3 μs was determined from the curve fitting of the original kinetic spectra.¹² In T-jump experiments, the observed kinetics was the exchange rate, which equals to the sum of the loop open and loop closure rates in a two-state model. Since the populations of the two loop conformations are not exactly the same (see Figure 1), the time constants for loop open and loop closure are slightly different as listed in Table 1. In NMR measurements, the time constants and the population ratio were determined simultaneously by curve fitting of the relaxation data using a two-state kinetic model.¹⁴

For comparisons and future studies, the kinetic parameters from some spectroscopic studies of ligated YopH are also listed in Table 1. The kinetic parameters determined by fluorescence T-jump studies were based on a four-state ligand binding model^12–13 while those by NMR relaxation studies were based on a two-state model.¹⁴ It can be seen that the experimentally observed protein dynamics cover a wide range of timescales from nanoseconds to milliseconds. All these motions are believed to be associated with the structural changes of the WPD loop and they were loosely assigned to loop open/closure changes. However the assignment of these rates to open/closing motions were done in the absence of resolution of molecular details and therefore could be capturing different dynamical processes. One exception to those studies was a molecular dynamics simulation study in which the translational motions of the loop backbone was directly observed to be occurring on a timescale around 4 ns.¹¹

Computational studies of loop open/closure pathway by NEB methods.

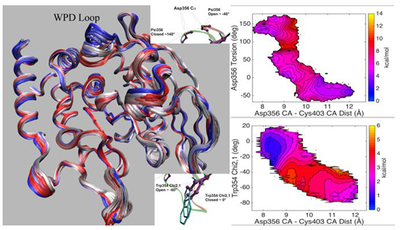
Although equilibrium MD simulations have been used for structural characterization of observed ns kinetic processes, the kinetic processes in the μs and longer time range are not practical for brute force equilibrium MD. Therefore, enhanced sampling/pathway refinement NEB methods were used to characterize apo YopH loop closure conformational transition pathways and to identify structural changes which have transition rates consistent with the experimentally observed kinetic processes. A number of NEB calculations were performed on apo wt YopH and its Q357F mutant using different starting structures. These starting structures have been prepared from the X-ray structures according to the procedures describe in Methods section. The loop open conformations were prepared from PDB structures 1YPT and 3U96 with bound ligand removed. The loop closed conformations were prepared from PDB structures 1YTS, 1PA9 and 3U96 with bound ligand removed. For the structure from 1YTS (a C403S mutant), the active site residue S403 was changed back to the native C403. The missing residues in 1PA9 were built in using CHARMM according to standard procedures. Different starting conformations for NEB calculations were used to find out if the conformational transition pathways for the loop closure are sensitive to slight differences in the end point structures. Besides the starting conformations, different ionic states of active site residues Cys403 and Asp356 were also varied to determine their effects on the loop movements. Our results indicate that while there are some differences in the calculated conformational exchange pathways between loop open and closed forms, no free energy barrier separating open from closed conformations has been detected in any of our NEB/umbrella sampling calculations in which ΔRMSD was used as the reaction coordinate. The lack of a barrier was consistently observed in all of these calculations no matter which starting structures or ionic states were used. A typical energy profile along the ΔRMSD coordinate by NEB calculations is shown in Figure 2, along with the corresponding conformation exchange images for the YopH loop open/closure movements.

Figure 2.

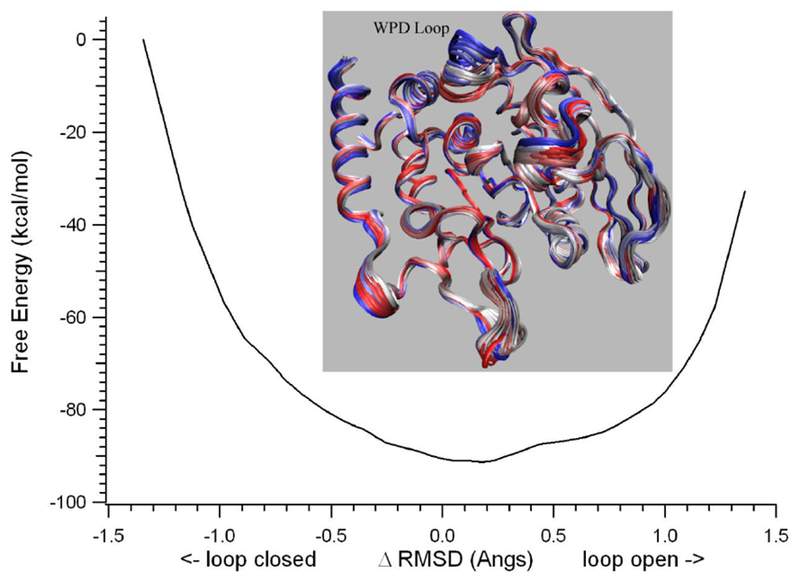
The free energy profile along the ΔRMSD coordinate by NEB computations and WHAM analysis of the umbrella sampling data for apo YopH. The inset shows the NEB determined structural evolution images along the loop open-closure conformational exchange pathway. The two end starting structures were prepared from 1YTS and 1YPT according to the procedure described in Methods section.

The advantages to using ΔRMSD as the reaction coordinate are that it is a global coordinate, which does not require detailed knowledge of the pathway or for assumptions to be made by the user; typically this results in a pathway which is easily converged in the optimization process. Thus, this coordinate has been used by several research groups to study the transition barriers for the conformational changes in a number of enzyme systems. In such studies, NEB or similar string methods were used to determine the minimum potential pathways between two enzyme conformations and followed by 1D umbrella sampling along the ΔRMSD coordinate to determine the free energy profile along the pathways. However, in these studies, the free energy barriers along the ΔRMSD coordinate are either absent or too low to explain the experimentally observed kinetic processes associated to the enzyme conformational changes. ^27,40–43 Apparently, this is due to the uneven nature of the phase space volumes along the ΔRMSD coordinate such that the resolution is often not sufficient to locate the transition barrier or to determine it accurately.

This is also the case in our NEB/umbrella sampling calculations for the YopH loop motions as demonstrated in Figure 2. The barrier-less feature along the ΔRMSD coordinate is obviously inconsistent with the ns to sub ms kinetics observed in previous experimental studies listed in Table 1. To solve this problem, a second coordinate that describe one of the three specific physical transitions as shown in Scheme 2 was used along with ΔRMSD coordinate in our 2D data analysis of the umbrella sampling results.

Scheme 2.

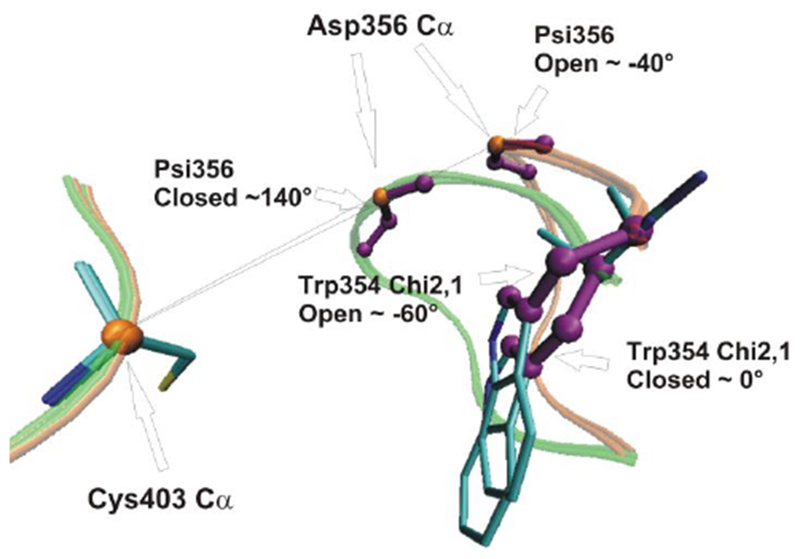
The active site of YopH in loop open and loop closed conformations. Three parameters used in our calculations are depicted: The distances between Cys403 Cα and Asp356 Cα; Psi356 as defined by the loop backbone rotation around the Asp356 C-Cα bond; and Trp354 Chi2,1 as defined by the side chain rotation around the Trp354 Cβ-Cγ bond. The two endpoint structures were prepared from PDBID:3U96 (Y357F mutant, containing both loop open and closed structures).

Energy barriers associated to the loop translational motion.

To provide structural explanations for experimentally observed kinetic processes, an understanding of the specific experimental techniques is desired. For fluorescence anisotropy experiments, one possible source for the anisotropy decay is due to the environmental changes near the Trp354 indole ring and such changes can be brought about by the translational motion of the WPD loop. Thus, the data from umbrella sampling along the minimum potential path obtained by NEB methods were analyzed using 2D WHAM to produce the free energy surface, along a second dimension that could relate to the experimentally observed kinetics. Therefore we projected out the umbrella sampling data onto the 2D space using ΔRMSD as one coordinate and the distance between Cys403 Cα and the Asp356 Cα as the second coordinate. By constructing 2D potentials of mean force (PMFs), which included both a global (ΔRMSD) and local (Cys403-Asp356 distance) coordinate we anticipated we might be able to obtain an energy landscape that was consistent with the observed experimental results, namely the nearly equal energies for loop open and loop closed conformations in the apo YopH (slightly in favor of the loop open conformation with the difference <0.5 kcal/mol) and a transition barrier corresponding to the experimentally observed loop dynamics. Although many different starting X-ray structures and different ionic states have been used to perform these NEB calculations, none of the results were able reproduce these experimentally observed features simultaneously. While the lack of quantitative agreement may not be surprising considering the accuracy required (< 0.5 kcal/mol) to match the experimental observations, the lack of qualitative agreement was somewhat unexpected. With different starting and ending structures, the 2D PMFs displayed different characteristics, where some calculations showed ΔRMSD < 0 states to be favored, while other calculations showed ΔRMSD > 0 regions to be favored. We will present one in each case to show how the starting and ending structures may affect the qualitative features of the 2D PMFs.

The 2D PMFs computed from the wild type apo YopH X-ray structures is shown in Figure 3. In this case, the energy minimum is slightly biased towards ΔRMSD < 0 (corresponding to loop closed conformation). This energy surface shows two loop movement pathways along the Cys403 Cα - Asp356 Cα distance coordinate, one with no barrier along a path near ΔRMSD ~ 0 and another with a small barrier around 13 Å along the distance coordinate at ΔRMSD ~0.5.

Figure 3.

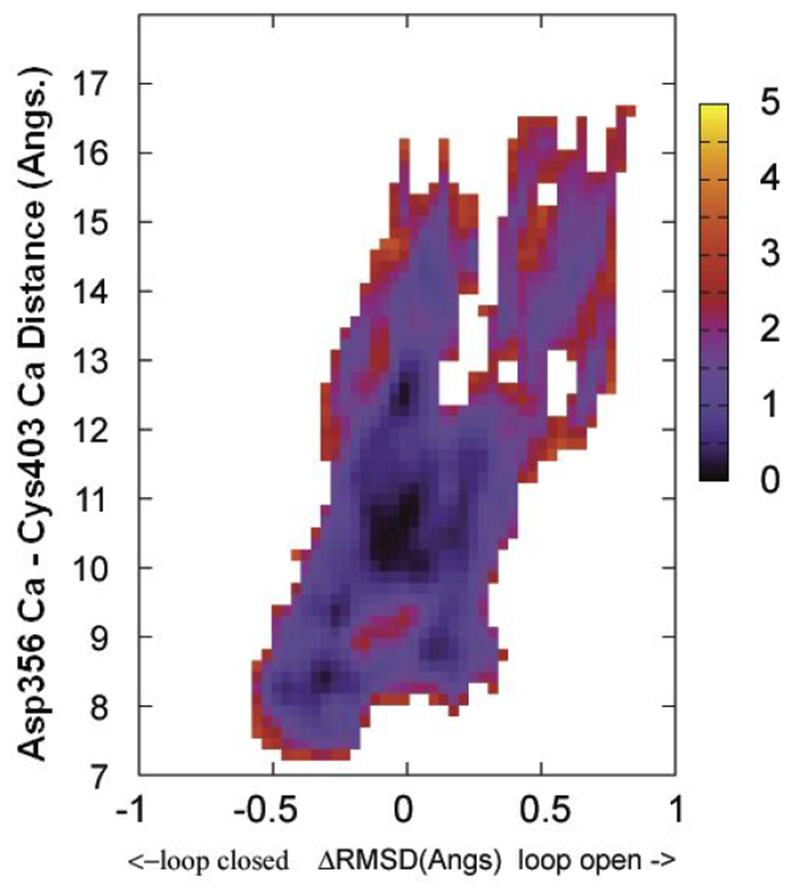
The free energy landscape as determined by 2D WHAM analysis of the umbrella sampling data on NEB determined structural evolution images along the loop open-closure conformational exchange pathway. ΔRMSD is the X coordinate and the distance between Cys403 Cα and the Asp356 Cα is the Y coordinate. The two endpoint starting structures were prepared from PDBID:1PA9 and PDBID:1YPT according to the procedure described in Methods section. The side bar shows the color coded energy levels (kcal/mol).

The 2D PMF computed from the apo Q357F mutant YopH X-ray structures is shown in Figure 4. This 2D figure clearly shows a barrier near 13 Å along the distance coordinate. The barrier height is −3.0 kcal/mol in the loop closure direction or is ~3.5 kcal/mol in the loop open direction. It is interesting to note here that the results shown in Figures 3 and 4 indicate that there are multiple pathways for the loop closure movements and these pathways may not have crossover connections. Such results are very similar to those in a recent MD studies on the catalytic loop movements in triosephosphate isomerase. ⁴⁴

Figure 4.

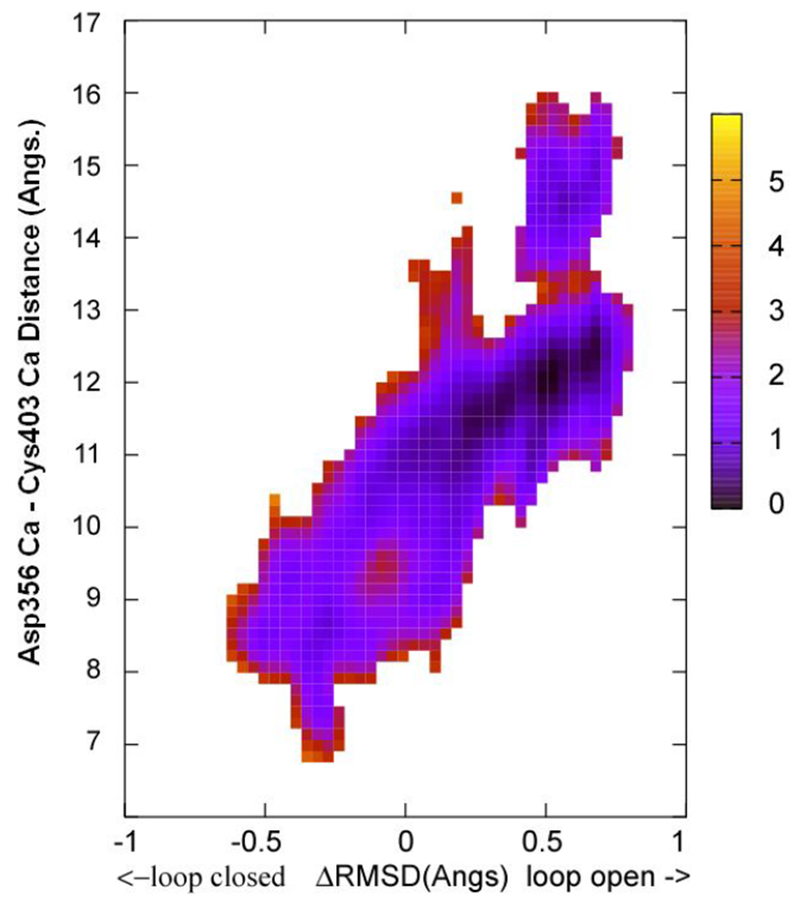
The free energy landscape as determined by 2D WHAM analysis of the umbrella sampling data on NEB determined structural evolution images along the loop open-closure conformational exchange pathway. ΔRMSD is the X coordinate and the distance between Cys403 Cα and the Asp356 Cα is the Y coordinate. The two endpoint starting structures were prepared from PDBID:3U96 (Y357F mutant, containing both loop open and closed structures) according to the procedure described in Methods section. The side bar shows the color coded energy levels (kcal/mol).

Energy barriers associated to the loop backbone dihedral angle flip.

The structural evolution images along the loop closure conformational exchange pathway in apo YopH (Figure 2 inset) show a kink in the middle of the transition, demonstrating non-uniform loop movements. Examinations of the loop open and loop closed structures reveal a loop backbone dihedral angle flip near the N-terminal end. The dihedral angle Psi356 (defined by the backbone N356-Cα356-C356-N357) changes from ~−40 degrees in the loop open conformation to ~140 degrees in the loop closed conformation (also see Scheme 2). The kink in the image series shown in Figure 2 occurs when this angle flips and one consequence is that the loop at the C-terminal end moves in the opposite direction compared with the N-terminal end during the flip. The flipping of dihedral Psi356 is expected to affect the Trp354 environments thus its fluorescence intensity, the kinetic signal observed in fluorescence T-jump studies, should reflect the motions along this coordinate. To evaluate the connection between Psi356 angle and WPD loop motions 2D WHAM analyses of the ΔRMSD NEB/umbrella sampling were performed by projecting onto the Psi356 angle. This analysis was performed for apo wt YopH and apo Q357F mutant YopH and the results are shown in Figure 5 and Figure 6, respectively. In both cases, a discontinuous energy surface is obtained along the Psi356 coordinate, indicating a large energy barrier is present along this direction. However, due to the incomplete sampling along the Pis356 coordinate an estimate of the barrier height cannot be obtained.

Figure 5.

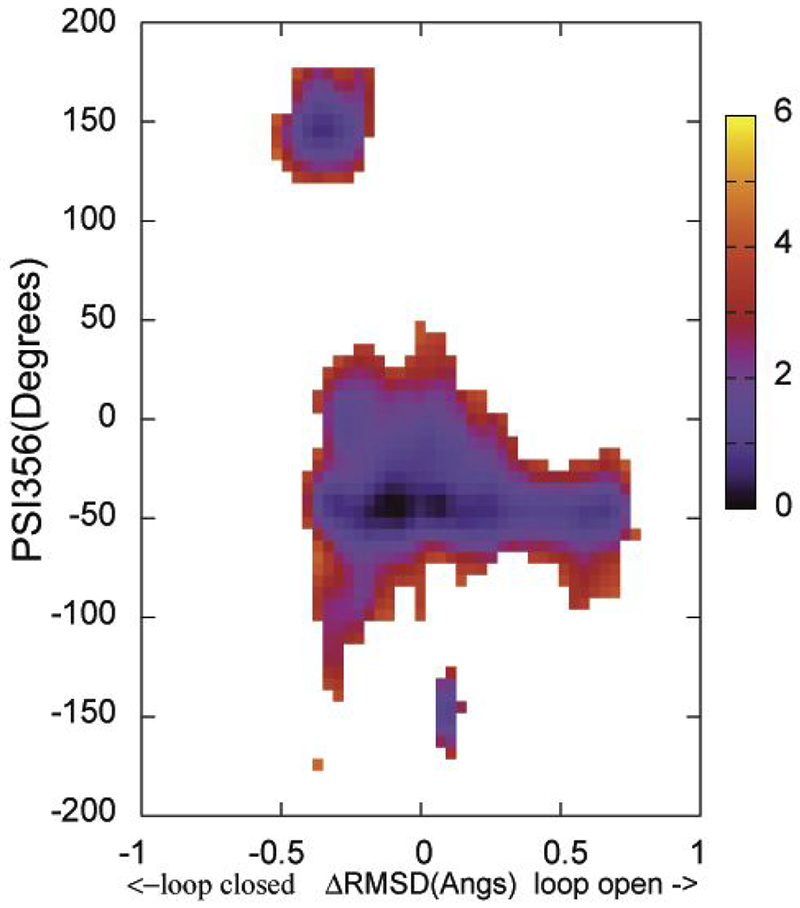
The free energy landscape as determined by 2D WHAM analysis of the umbrella sampling data on NEB determined structural evolution images along the loop open-closure conformational exchange pathway. ΔRMSD is the X coordinate and Psi356 is the Y coordinate. The two endpoint starting structures were prepared from PDBID:1PA9 and PDBID:1YPT according to the procedure described in Methods section. The side bar shows the color coded energy levels (kcal/mol).

Figure 6.

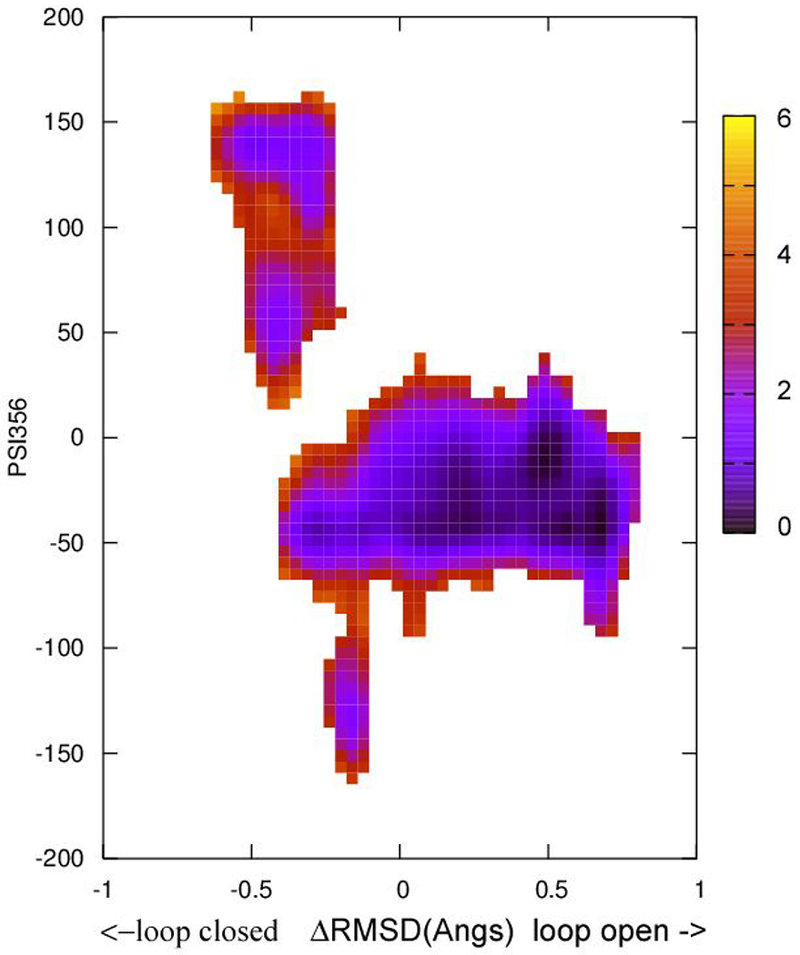
The free energy landscape as determined by 2D WHAM analysis of the umbrella sampling data on NEB determined structural evolution images along the loop open-closure conformational exchange pathway. ΔRMSD is the X coordinate and Psi356 is the Y coordinate. The two endpoint starting structures were prepared from PDBID:3U96 (Y357F mutant) according to the procedure described in Methods section. The side bar shows the color coded energy levels (kcal/mol).

To improve the resolution of our calculations along the Psi356 coordinate, we employed an alternative pathway refinement method (HFB)²¹ in which a more localized reaction coordinate can be specified. HFB is a variant of the string method,⁴⁵ which has been employed by Brooks and co-workers to study conformational dynamics in several systems including activation of rhodopsin and maturation of the bacteriophage HK97.^46–47 By employing a localized reaction coordinate in HFB, which captures both the Psi356 and the Cα403-Cα356 distance a continuous energy surface. The free energy landscape as determined by the HFB based calculations, using Cα403-Cα356 distance as the first coordinate and Psi356 as the second, are shown in Figure 7, with contour lines drawn at 0.5 kcal/mol increments. The results show that the energy barrier from the loop closed to loop open direction is about 5.0 kcal/mol and about 6.0 kcal/mol in the opposite direction. The saddle point is near Psi356 at ~75 ° and Cα403-Cα356 distance at ~9.2 Å.

Figure 7.

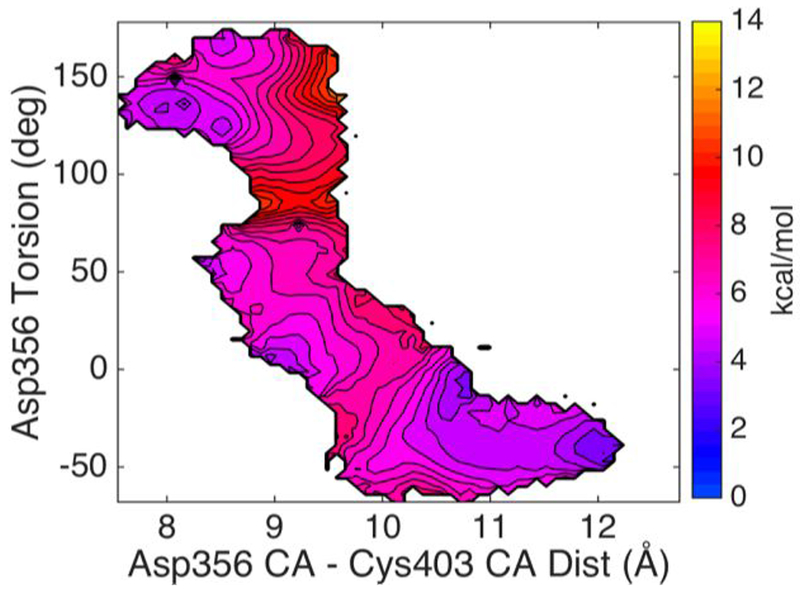
The free energy landscape as determined by HFB computations. The distance between Cys403 Cα and the Asp356 Cα is the X coordinate and Psi356 is the Y coordinate. The two endpoint starting structures were prepared from PDBID:1PA9 and PDBID:1YPT according to the procedure described in Methods section. The side bar shows the color coded energy levels (kcal/mol). Contour lines, drawn at 0.5 kcal/mol increments, are added to the energy surface to allow convenient estimation of the barrier heights.

Relate free energy barriers to the experimentally observed kinetics.

Previous MD simulations showed that the WPD loop of YopH is intrinsically flexible and fluctuates between the open and closed conformation with exchange time of ~4 ns for the apo, native protein. ¹¹ The results are consistent with the experimental observation in fluorescence anisotropy measurements.^10–11 Since the simulations were performed with standard MD procedures for 10 to 20 ns starting from the loop open conformation, they could not capture the WPD loop backbone dihedral angle flip. Comparing to our NEB results, a fast process with a 4ns timescale should correspond to a small energy barrier.

Our results show small barriers (3 to 3.5 kcal/mol) for the transition barriers near Cα403-Cα356 distance at ~ 13 Å in Figures 3 and 4, which are due to loop translational motions. However, using the Erying equation, a 3.5 kcal/mol barrier height converts to a kinetic rate of ~1.8×10¹⁰/s, much higher than the experimentally observed or previously calculated rates from MD. This disagreement suggests that our NEB calculations underestimate the free energy barrier for the loop translational motion.

There are a number of possible reasons for the inaccuracy of the magnitudes of our calculated free energy barriers. Previous studies suggest that it is still possible to make use of our computational results by focusing on the trend of these calculated values and by assuming that the errors are systematic and may be alleviated by introducing a “scaling factor”. For example, in previous MD studies on protein folding dynamics, an empirical pre-exponential factor was introduced in the Erying equation in order to match the experimentally observed kinetics from the calculated free energy barriers. ⁴⁸ The concept of scaling has also been used in our vibrational frequency calculations with ab initio quantum mechanics methods to interpret the ligand frequency shifts upon binding to protein (cf. ⁴⁹). In such calculations, the observed frequency shifts of the ligand can be quantitatively interpreted by using various models for the ligand-protein interactions. When the calculated ligand frequencies and their shifts (with the correction of a scaling factor) upon binding to protein are consistent with experimental observation, the correct model for the ligand-protein interactions can then be determined. ^50–57 Typically, a single scaling factor can be applied to the same type of group frequencies such as C=O stretch. Since the successful application of the scaling factor in frequency calculations, and since the energy is directly proportional to frequency, we propose to use a single scaling factor to change the calculated free energy barriers and then use the scaled free energy in the Erying equation to calculate the rate of the transition kinetics.

Since both fluorescence anisotropy and MD simulations showed a 4 ns transition time for loop movements, ^10–11 we can use this value as our reference point to obtain the scaling factor we are going to use for determining the corrected energy barriers calculated by NEB/HFB. 4 ns corresponds to ~ 6 kcal/mol energy barrier and the NEB calculated barrier for the loop translational motions (Figures 3 and 4) is ~ 3.5 kcal/mol. Therefore, the scaling factor is ~ 1.7. For the energy barrier associated to the loop backbone dihedral angle flipping in the loop open-closure movements, the HFB calculated value is ~ 6 kcal/mol (Figure 7). After correction by 1.7 scaling factor, the energy barrier is ~ 10 kcal/mol, corresponding to ~ 3 μs transition time, consistent with the μs kinetics observed in the fluorescence T-jump studies of the apo YopH (see Table 1).¹²

An alternative approach to scaling the energies is to consider that the Erying rate equation uses a pre-exponential of k₀ = k_BT/h, where k_B is Boltzmann’s constant, Tis the temperature and h is Planck’s constant. This pre-exponential factor sets a speed limit for gas-phase chemical reactions, but protein dynamics occurring in solvent happen on a slower timescale. Given the unsealed free energy barriers we have calculated (3.5 and 6 kcal/mol), smaller pre-exponential factors of 9x10¹⁰ s⁻¹ and 7x10⁹ s⁻¹ would be required to match the experimental rates of 4 ns and 3 μs, respectively. k₀’s in this range are reasonable given that fast-folding proteins have been shown to be characterized by a k₀ ≈10⁶ S⁻¹.^40,58

A prediction for the UVRR T-jump studies on the Trp354 W3 bands in apo YopH.

Due to the complexity of the factors that can influence Trp354 fluorescence properties, ambiguities exist as to which enzyme conformational changes can contribute to the observed kinetics from fluorescent measurements. For example, the fluorescence anisotropy studies of the apo YopH showed kinetics from sub ns to tens of ns, and the observed sub ns signal was not explained.^10–11 On the other hand, UVRR studies of the apo YopH and its Q357X mutants identified two Trp354 conformations as shown by the two W3 bands at 1551 and 1562 cm⁻¹. Since the correlations between tryptophan W3 frequency and the Chi2,1 angles are well established,^33–34 we can safely relate these two W3 band intensities to the populations of the enzyme conformations in which Trp354 Chi2,1 angles are at 0 degree and ~60 degrees, respectively. In proposed UVRR T-jump studies, the probe frequencies will be on the two W3 bands at 1551 and 1562 cm⁻¹ in apo YopH, the observed kinetics associated with the intensity changes at these two frequencies can then be correlated to the exchange of the two Trp354 conformations.

Figures 8 and 9 show the results from 2D WHAM analysis of the NEB calculations on apo YopH and Q357F mutant, respectively, using delta ΔRMSD as the first coordinate and Trp354 Chi2,1 as the second coordinate. In both cases, a small barrier near Chi2,1 ~ −40 degrees is present. For apo YopH, the barrier is about 2.0-3.0 kcal/mol, and for Q357F, the barrier is about 3.0 – 4.0 kcal/mol. To determine this barrier height more accurately, HFB calculations were conducted.

Figure 8.

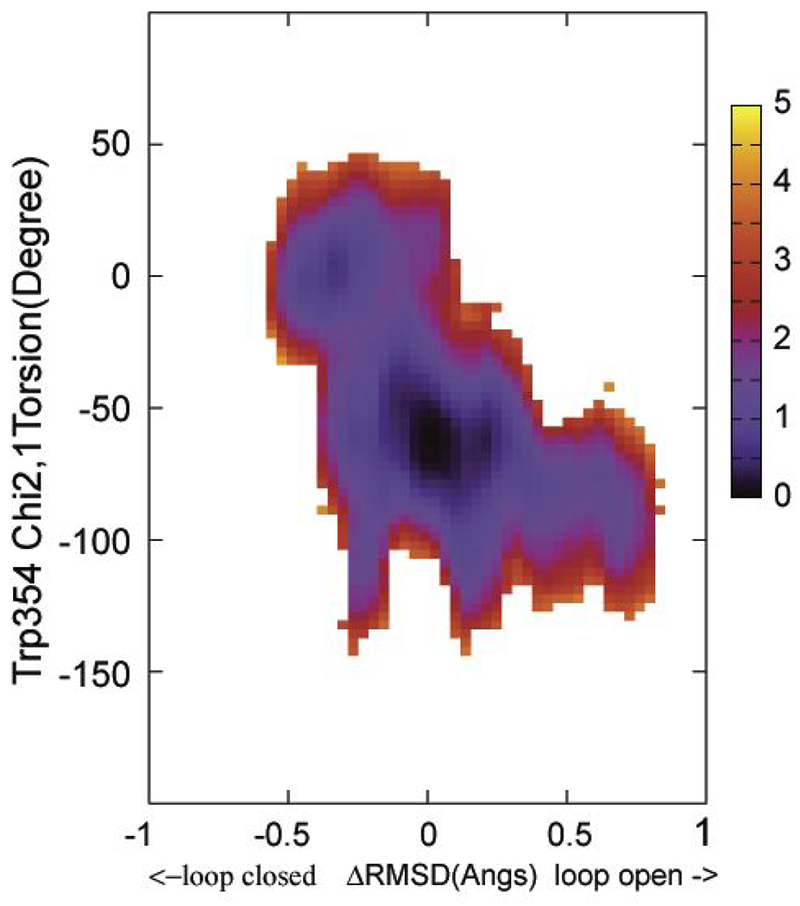
The free energy landscape as determined by 2D WHAM analysis of the umbrella sampling data on NEB determined structural evolution images along the loop open-closure conformational exchange pathway. ΔRMSD is the X coordinate and Chi2,1 is the Y coordinate. The two end starting structures were prepared from PDBID:1PA9 and PDBID:1YPT according to the procedure described in Methods section. The side bar shows the color coded energy levels (kcal/mol).

Figure 9.

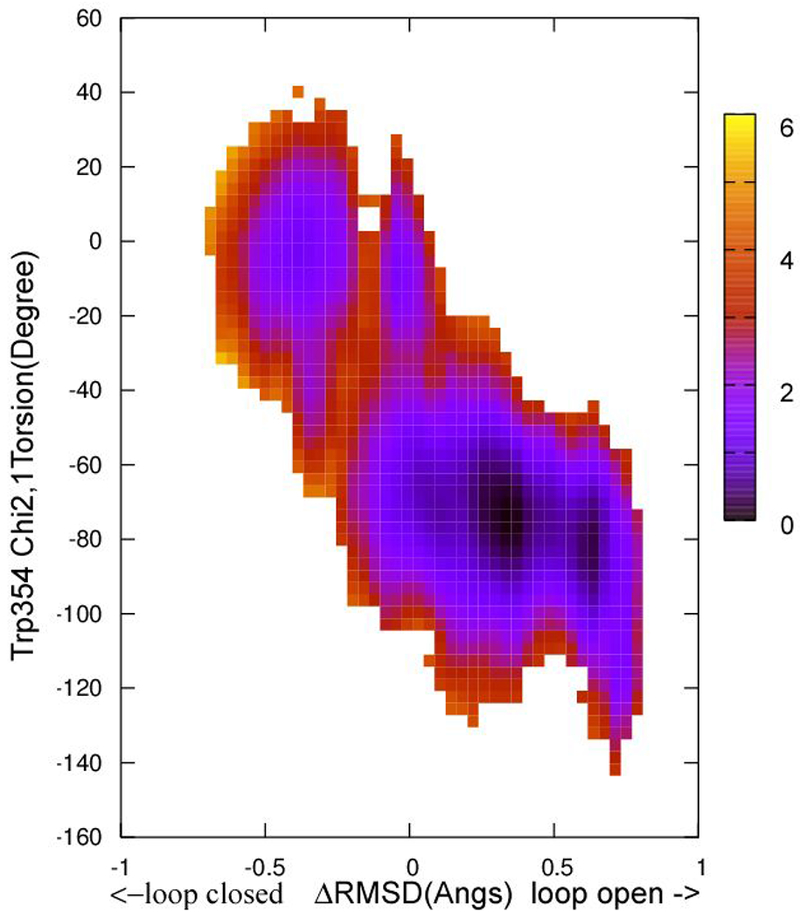
The free energy landscape as determined by 2D WHAM analysis of the umbrella sampling data on NEB determined structural evolution images along the loop open-closure conformational exchange pathway. ΔRMSD is the X coordinate and Chi2,1 is the Y coordinate. The two end starting structures were prepared from PDBID:3U96 (Y357F mutant) according to the procedure described in Methods section. The side bar shows the color coded energy levels (kcal/mol).

Figure 10 shows the results of from umbrella sampling the HFB refined pathway using Cα403-Cα356 distance as the first coordinate and Trp354 Chi2,1 as the second biasing coordinate. In this coordinate space, the loop closed form is slightly favored and the energy barriers are 2.0-3.0 kcal/mol but the higher barrier is in the loop open direction, opposite of the results by NEB calculations on Q357F mutant. Although none of the calculations precisely reproduced the loop open and loop closed conformation ratio determined by UVRR studies of the apo YopH and its mutants, the calculated transition barriers may be used to predict the time range of the observed kinetics for future UVRR T-jump measurements (a technique described in ref⁵⁹) on the apo YopH. In T-jump studies, the observed kinetics is related to the exchange rate between the two Trp354 conformations with Chi2,1 angle at 0 and −40 degrees, respectively. This exchange rate is equal to the sum of the two transition rates in both directions in a two-state model. Thus, our calculation results (after scaling factor corrections) suggest that in UVRR T-jump measurements with probes on the two W3 bands of apo YopH Trp354 at 1551 and 1562 cm⁻¹, the observe kinetic transition signals should be ~ one ns for wild type YopH and ~15 ns for Q357F mutant.

Figure 10.

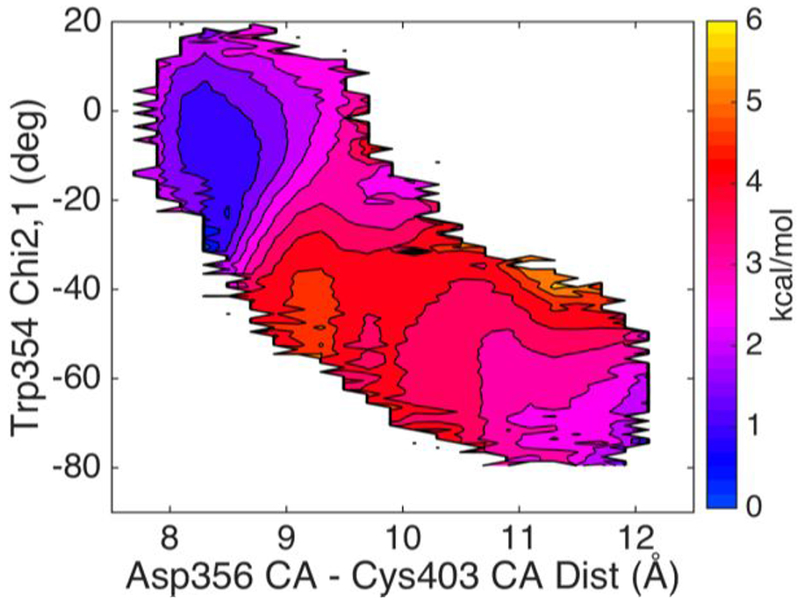
The free energy landscape as determined by HFB computations. The distance between Cys403 Cα and the Asp356 Cα is the X coordinate and Chi2,1 is the Y coordinate. The two end starting structures were prepared from PDBID:1PA9 and PDBID:1YPT according to the procedure described in Methods section. The side bar shows the color coded energy levels (kcal/mol). Contour lines, drawn at 0.5 kcal/mol increments, are added to the energy surface to allow convenient estimation of the barrier heights.

Discussion and Conclusion

A number of spectroscopic kinetic studies have been focused on the catalytic loop dynamics of YopH to find its relationships with ligand binding and catalysis. The experimentally observed kinetic processes cover a wide time range, from ns to ms, and they are all believed to be related to loop open/closure movements. X-ray structural studies have shown that the loop closure brings the Asp356 carboxyl group, pointing away from the active site in the loop open conformation, towards the scissile oxygen of the substrate. Two kinds of motions are involved to bring the Asp356 carboxyl group into the active site to initiate the catalysis: the loop translational motion and the twist of loop backbone as reflected by the dihedral angle change around the Asp356 back bone Cα356-C356 bond. In this study, NEB and HFB computations have been used to investigate the free energy profiles along these two coordinates in apo YopH, where the application of a two-state kinetic model is appropriate. Since these motions are expected to change the environments of Trp354, the calculated free energy barriers along these two coordinates should be correlated to the observed kinetics by Trp fluorescence anisotropy and T-jump techniques.

Our computational approach includes the following steps: 1) Initial NEB pathway refinement was used to determine the minimum potential pathway for the WPD loop closure using a global ΔRMSD order parameter for its ease of use and rapid convergence properties; 2) 2D WHAM analysis of the umbrella sampling data on the converged NEB images can then be used to quickly estimate the free energy profile along various coordinates of interest; 3) To overcome the poor resolution along ΔRMSD coordinate, HFB methods were utilized to enhance the resolution along specified coordinates by employing a local order parameter to focus the refinement on the specific region of the enzyme. This allowed for a more accurate energy profile to be calculated as well as the mechanistic sequence of the events along these coordinates. Our results from this computational approach show that the ns and μs kinetics observed in fluorescence anisotropy and T-jump measurements of the apo YopH may be assigned to the translational and twist motions of the WPD loop near Asp356. Furthermore, the results from HFB suggest that in the loop closure movement, the translational motions happen first and the twist motions (the Asp356 backbone flip) do not happen until the translational motion is practically completed (Figure 7).

Besides the structural interpretations of the experimentally observed kinetics, our computational approach also allows us to make predictions which can inform the design of future spectroscopic experiments. This is demonstrated in the proposed UVRR T-jump studies of apo YopH on the two Trp354 W3 bands observed in the static UVRR studies. It is interesting to note that the predicted kinetics will be observed in hundreds of ns, a time range different from the observations by other spectroscopic methods.

Although the focus of our current computational studies is on the kinetics observed in apo YopH by spectroscopic methods, the computational approach described here can also be applied to other more complex cases, such as the multiple-step kinetic processes that occur in the ligand binding to YopH as described in our previous fluorescence T-jump studies.^12–13 In addition, the computational approach developed here can serve as a fast screen method for the structural interpretations of the experimentally observed protein dynamic processes. For example, NEB and related string methods have been used to study the catalytic loop dynamics in some enzymes including lactate dehydrogenase,⁴⁰ and adenylate kinase.²⁷ In such studies, all-atom ΔRMSD has been used as reaction coordinate for its unbiased nature and its easy convergence properties. However, one problem with the results using ΔRMSD coordinate is that no energy barriers are present along this coordinate, so that it cannot provide direct interpretations for the experimental observations of various kinetic processes associated to the loop dynamics in a wide range of time scales. Our current study indicates that the absence of the energy barriers along ΔRMSD coordinate in such studies is likely due to insufficient resolution. When the NEB results are analyzed using 2D method with additional coordinates, the energy barriers associated with the loop motion/protein conformational change can then be identified to provide structural evolution assignments to the experimentally observed kinetic data. This approach provides a fast and convenient way for the initial screening of potentially important order parameter/degrees of freedom. The initial NEB-based results can provide a semi-qualitative analysis of the proteins dynamics. Identification of these key order parameters can then be analyzed through additional pathway refinement methods using localized coordinates, in our case using HFB on a small set of atoms which describe both a residue pair separation distance and a residue torsional angle. We can then determine the energy barriers associated specific physical coordinates and compare those rates with experimentally determined kinetics.