Standardization of Cesium-137 Gamma-Ray Sources in Terms of Exposure Units (Roentgens)

Abstract

¹³⁷Cs γ-ray sources, which have been proposed by the Public Health Service as a substitute for radium in the treatment of malignant diseases, require suitable calibration if consistency is to be achieved in radiation treatment.

Several ¹³⁷Cs sources were calibrated using a graphite cavity ionization chamber in an open-air geometry. The contribution of scatter from the room surfaces was calculated and the source measurements corrected for this effect.

A large-volume aluminum-walled ionization chamber was designed and fabricated for use in routine calibrations. This chamber will be used as a means for intercomparison of the source to be calibrated with one of the standards.

1. Introduction

Gamma radiation has been used successfully for many years in the treatment of malignant disease. Extensive use of radium has brought about the development of many treatment plans, and much dosimetry data has been accumulated. Attendant on the use of radium are some serious problems which derive from the fact that its first daughter product is the gas radon which, if introduced into the body and retained, has serious toxic effects. Because of the difficulties associated with the use of radium, the Public Health Service has proposed [1]¹ that ¹³⁷Cs be used as a substitute in cancer therapy. Some source leakage had been experienced in the early use of ¹³⁷Cs, but, with improved encapsulation techniques, this problem has largely been solved. In addition, the isotope can now be incorporated into physiologically inert material. ^l37Cs is inexpensive, has a relatively long half-life, good characteristics as a radium substitute, and requires less shielding than radium.

The Public Health Service proposal of ¹³⁷Cs as a substitute for radium has had favorable acceptance, though both suppliers and users have lacked satisfactory standards for determining source exposure rates. The National Bureau of Standards has been requested on various occasions to provide source calibrations, and, with the support of the Public Health Service, has carried out the work required to establish such a service.

Several small ¹³⁷Cs sources were measured in an open-air geometry using a graphite cavity ionization chamber. The effect of scattering from the room surfaces was computed and the measured exposure rates reduced accordingly. The standardized sources are to be used for comparison with unknowns submitted for calibration. A specially designed spherical, aluminum-walled ionization chamber of large volume has been fabricated and will be used for intercomparison calibrations.

Calibrations of ¹³⁷Cs sources will be performed for exposure rates ranging from a few to a few hundred milliroentgens per hour at 1 m.

2. Exposure Measurements Using Cavity Ionization Chambers

The instrument ordinarily used for measurements of x or gamma radiation, in terms of exposure units (roentgens), is the standard free-air ionization chamber. The chamber presently available at the National Bureau of Standards is designed for measurements of radiation generated by x-ray tube potentials of up to 250 kv, and is inadequate for measurements of the 662-keV gamma rays of ¹³⁷Cs. Therefore it was necessary to use the principle of cavity ionization for these measurements and a cavity chamber which fulfills the requirements of the Bragg-Gray theory. Briefly, these are (1) the chamber must be small with respect to the distance between the source and chamber to minimize the variation of radiation intensity over the chamber dimensions; (2) the chamber gas cavity must be small to ensure that only a small fraction of the electron energy is dissipated in traversing the cavity, and to minimize the contribution to the ionization by direct interaction of the gamma rays with the gas; and (3) the chamber wall material must be sufficiently thick to establish electronic equilibrium and exclude electrons generated from other sources.

Consider a graphite chamber of volume V with air of density ρ. If a charge Q is collected, the specific ionization in the chamber is Q/ρV charge per unit mass. The corresponding energy deposited in the air of the cavity is found by multiplying by W, the average energy per ion pair (or per unit charge). Using the Bragg-Gray cavity principle, the energy absorbed in the graphite wall is obtained by multiplying by ${}_{m}S{}_{\text{air}}^C,$ the ratio of the mass stopping power of carbon to that of air. Then the corresponding energy which would be absorbed in the wall if it were air instead of graphite is obtained by multiplying by ${\left[{\mu }_{en}/\rho \right]}_c^{\text{air}},$ the ratio of the mass energy-absorption coefficient of air to that of carbon. The corresponding ionization in air is obtained by dividing by W. So the ionization per unit mass of free air, in the absence of the chamber, is given by

$$\frac{Q}{\rho V}{}_{m}S{}_{\text{air}}^C{\left[{\mu }_{en}/\rho \right]}_C^{\text{air}}.$$

Since 1 roentgen = 2.578 × 10⁻⁴ C/kg of free air at STP, and the density of air is 1.293 kg/m³ at STP, the exposure rate in roentgens per second is given by

$$\dot{X}=\frac{3\times {10}^{3}I}{V}\frac{T}{273.2}\frac{1.013}{P}{}_{m}S{}_{\text{air}}^C{\left[{\mu }_{en}/\rho \right]}_{\mathcal{C}}^{air}R/s$$

where I is the chamber current in amperes, V is the volume in m³, T is the temperature in degrees Kelvin, and P is the pressure in bar (1.013 bar = 760 mm Hg.)

Several corrections must be applied to the measurements in order to comply with the requirements of an experimental realization of the roentgen. For the cavity chamber, these corrections account for wall absorption, saturation, and stem scatter.

3. Cavity Chamber Description and Corrections

The cavity ionization chamber, used to measure the exposure rates from the ¹³⁷Cs sources, is spherical in shape with an external diameter of 20.7 mm. This chamber is one of three spherical graphite chambers designed by Wyckoff [2], all of which have the same outer diameter but different inner diameters. The wall absorption correction is determined by measuring for each chamber the ionization per unit volume at a constant gamma-ray exposure rate, and plotting it against wall thickness. These data, supplemented by absorption data available from other types of graphite chambers, are extrapolated to a zero wall condition to determine the wall-absorption correction for each chamber.

The intermediate-volume chamber (designated as VIII), used for these measurements, has a wall thickness of 4 mm and its derived wall correction is 2.5 percent. This value is reduced slightly since extrapolation to a zero wall condition actually over-estimates the correction, and the extrapolation should be only to the mean center of electron production. An estimate of the reduction required in the absorption correction has been provided by Wyckoff [3]. From measurements of electronic equilibrium requirements for ⁶⁰Co and ¹³⁷Cs gamma rays in a parallel-plate pressure chamber, and the calculations of Roesch [4] and Aglintsev [5], he computed the required reduction in the absorption correction to be 0.2 percent for ¹³⁷Cs gamma rays and carbon-walled cavity chambers. The saturation correction for the exposure rates encountered in these measurements is 0.2 percent and the correction for scatter from the supporting stem and shank of the chamber is 0.1 percent.

The mean mass stopping power ratio, ${}_{m}S{}_{\text{air}}^C,$ used in the calculation of exposure rate is 1.010. This value was computed for ¹³⁷Cs gamma rays by Burlin [6] using an average exitation potential of 78.4 eV for carbon and the Spencer-Attix theory.

The ratio of the mass energy-absorption coefficients for air and carbon [7] differs from unity by less than 0.1 percent for the gamma rays of ¹³⁷Cs and is taken to be unity in the calculations.

The air volume of chamber VIII was determined by differential weighing using water to fill the cavity. The volume determined in this manner includes the small volume in the neck of the chamber. The value for the volume used in the computations is this measured volume minus the volume of the collection electrode. For the electrode used at the time of these measurements, the net chamber volume was 1.130 cm³.

4. ¹³⁷Cs Sources

Eight sources were used in this project. Three sources were designed primarily for nondestructive testing of materials, density gauging, and research projects. The nominal activities of these three sources are 5, 50, and 500 mCi. The sources are doubly encapsulated in stainless steel with both inner and outer capsules sealed by heliarc welding. The outer capsule is 13.5 mm long with an outer diameter of 7.1 mm. The inside active diameter is 4.3 mm with the active length varying with the activity of the source. The end wall thickness is 1.0 mm.

Since this same capsule design is used for source strengths up to one curie, it was necessary to determine the acutal length of each source. The sources were radiographed and it was found that the lengths of the active volumes were about 4, 6, and 7 mm for the 5, 50, and 500 mCi sources respectively. These results are uncertain by about 1 mm due to fogging of the x-ray film by the source radiation. While the active material of the 5-mCi source appears to be localized in the active volume to three distinct particles, the larger sources seem to be uniformly filled although the fogging precludes an examination in detail.

Five sources of a medical type were obtained for study, calibration, and in order to provide a complete range of source activities as standards for routine calibrations. These sources are doubly sealed in nickelplated stainless-steel capsules and needles, with nominal activities of 2.5, 7.5, 25, 60, and 100 mCi. Radiographs of these sources indicate they are all uniformly filled. A detailed study using densitometric methods however was not carried out for confirmation.

5. Open-Air Geometry Source Measurements

The exposure-rate measurements were carried out in an open-air geometry to minimize the contribution of scattered radiation to the measured ionization. The room was 9 m long, 6 m wide, and 4.5 m high. To minimize scattering from the supporting devices, the source was laid in a thin plastic trough which was supported above the floor by a long thin-walled plastic tube. The chamber was supported horizontally above the source by a plastic rod which extended approximately 1.3 m out from a ring stand. Mirror-image measurements with another ring stand and support rod showed no significant scatter contribution to the chamber reading from the stand.

Most of the exposure measurements were carried out for a source-to-chamber distance of approximately 0.5 m. For this geometry, the source and chamber were located symmetrically in the room, the chamber being 2 m from the ceiling and the source 2 m from the floor. In subsequent measurements, where there was a distance of 1 m between source and chamber, the chamber position remained the same and the source trough was lowered.

The distance between the source and ion chamber was determined by means of a cathetometer placed about 3 m from the source-detector line and supported by sturdy steel tables 1.5 m above the floor. The preamplifier of the vibrating-reed electrometer was located about 2.5 m from the source and protected from the radiation by a lead house. The operator and the measurement equipment were protected from the radiation by mobile lead shields.

Table 1.

Summary of ¹³⁷Cs open air exposure-rate measurements with all data corrected to August 24, 1967

Measurement No.	Nominal source activity (mCi)	Nominal chamber-to-source distance (meters)	Measured $\dot{X}$ multiplied by D2 (mR · m2 · h−1)	A verage $\dot{X}{D}^2$ (mR · m2 · h−1)	Avg. $\dot{X}{D}^2$ corrected for room scatter (mR · m2 · h−1)
1	500	0.5	137.94
2	500	.5	137.62	137.83	137.20
3	500	.5	137.92
4	500	.5	137.36
5	500	.5	136.82	137.14	136.51
6	500	.5	137.24
7	500	1.0	139.58
8	500	1.0	140.03	139.80	137.27
10	50	0.5	15.05
11	50	.5	14.89	14.97	14.90
12	5	.5	1.34		1.33
13	100	.5	36.11		35.94

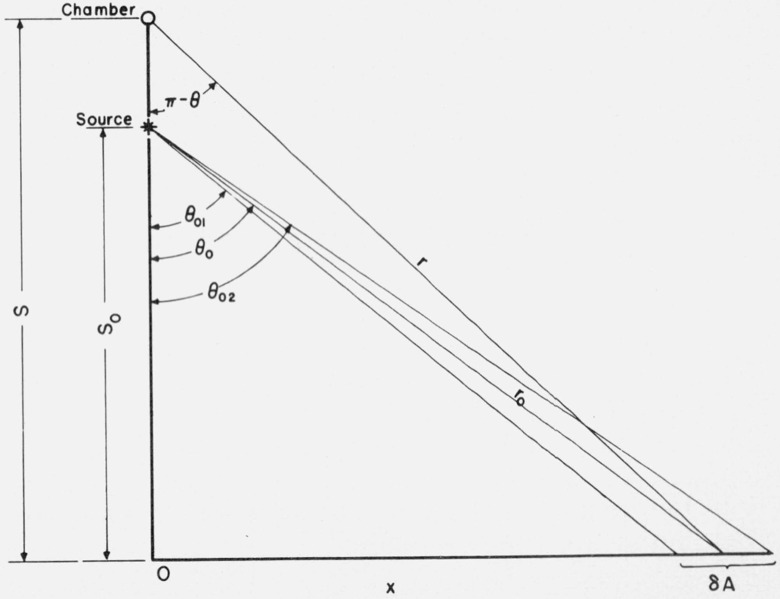
Part of the measured ionization is caused by radiation scattered from the walls, ceiling, and floor of the laboratory, and an estimate of its effect must be made in order to make an absolute determination of the direct exposure rate from the source. The scatter contribution can be calculated using data published by Berger [8], which provides dose-reflection coefficients for gamma rays incident on concrete slabs. The reflected dose D_r, from the concrete floor of the laboratory, was computed using the equation

$$D_R=\frac{N{E}_0{\mu }_{en}{R}_d}{r^2}$$

where R_d = R_d(θ, φ/E₀, θ₀) is Berger’s reflection coefficient, a dimensionless number;

$$N=N_0\text{cos}{\theta }_0\text{δ}A/4\pi r_0^2;$$

and μ_en is the mass energy-absorption coefficient for air at the gamma-ray energy E₀. N₀ is the number of photons emitted per second by an isotropic source located a distance r₀ from the scattering area δA, while r is the distance from δA to the detector (see fig. 1). Berger’s data are tabulated in terms of the cosine of the source obliquity angle θ₀, the cosine of the obliquity of emergence θ, and the azimuthal variable φ which is measured with respect to the direction of incidence in the plane of the floor.

Figure 1. Relationship of angles of y-ray incidence on the area δA and scatter from δA back to the cavity chamber.

The particular geometry of source and detector with respect to the floor allows a simplification of the computations, since the azimuthal angle φ is always 180 degrees. The data for the reflection coefficient may therefore be plotted versus the cosine of the emergence obliquity with the cosine of the incidence obliquity as a parameter.

The differential area δA is a ring on the floor, with its center on the vertical through the chamber and source. For computational purposes, it was useful to develop an analytical solution for δA in terms of the vertical distance to the floor S₀, and the source obliquity angle θ₀. With reference to figure 1 it can be shown that

$$\text{δ}A=2\pi S_0^2{\left[\frac{{\text{sec}}^2{\theta }_0}{2}\right]}_{{\theta }_{01}}^{{\theta }_{02}}.$$

In addition, it is convenient to solve for r₀ and r in terms of S₀, θ₀, and S.

Then for the reflecting area defined by angles θ₀₁ and θ₀₂

$$D_R=\frac{N_0{E}_0{\mu }_{en}{R}_d}{4S_0^2}\frac{\left({\text{sec}}^2{\theta }_{02}-{\text{sec}}^2{\theta }_{01}\right){\text{cos}}^3{\theta }_0}{{\text{tan}}^2{\theta }_0+\frac{S^2}{S_0^2}}.$$

The appropriate R_d factor can be read from a plot of Berger’s tabulated data when the cos θ is found from

$$\theta =\pi +{\text{tan}}^{-1}\left(\frac{S_0\text{tan}{\theta }_0}{S}\right).$$

The computation was made for five-degree intervals out to a distance on the floor equal to the radius of a circle of area equal to the area of the rectangular floor. The scattered radiation contribution from the floor area was found to be 0.14 percent for the 0.5 m source-to-chamber distance. The same approach was used for calculating the contributions from each sidewall, even though in this case the azimuthal angle is not exactly 180 degrees. The sum of the percentage scatter contributions from all room surfaces is 0.46 percent.

As an independent check on the above calculations, an upper limit to the scatter contribution can be estimated using a method proposed by Eisenhauer [9] in which an image source technique is used for calculating the reflection of gamma rays from concrete slabs. The ratio of the scattered dose to the primary dose is given as a function of the ratio of the distance of the source from the detector to the distance of an image source from the detector, and a constant which is dependent on the properties of the medium and the energy of the radiation. Thus

$$\frac{D_s}{D_0}=\frac{{\left(S-S_0\right)}^2}{{\left(S+S_0\right)}^2}{R}_{PT}.$$

For the detector-source-floor geometry of this experiment S − S₀ = 0.50 m and S + S₀ = 4.50 m. The scatter contribution, calculated from these data and Chilton’s [10] R_PT value of 0.161 for ¹³⁷Cs gamma rays, is 0.2 percent. This value compares favorably with the value of 0.14 percent derived from Berger’s data for the same geometry.

The percentage contribution to the chamber reading, due to scattered radiation from the floor, was also computed from Berger’s data for a source-to-chamber distance of 1 m in the above-described geometry. The calculation showed that the scatter contribution to the chamber reading was essentially unchanged by this slight change in geometry, as a result of which the percentage scatter contribution increased by a factor of 4 for the 1-m separation.

6. Measurement Procedure

The ionization currents produced in the cavity chamber were measured by the rate-of-drift method. The measurement consists of determining, by means of a null method, the time Δt required for the charge buildup on a known capacitor C to produce a known change in potential ΔV. Each of these quantities can be precisely determined and the ionization current computed from the equation

$$I=C\frac{\mathrm{\Delta }V}{\mathrm{\Delta }t}.$$

To reduce source handling, the measurement procedure was to determine the background current (which includes leakage) at the collection potential and polarity to be used, and then take sightings on the top and bottom of the ion chamber with the cathetometer. The cathetometer was lowered to the expected position of the source, the source placed in the trough and then sightings taken on the top and bottom of the source with the cathetometer. Eight current measurements were performed and the polarity of the collection potential was then reversed. After a sufficient time lapse to allow for soakage at the new polarity, another eight measurements were made. The source was then returned to its container and the background current measured for the polarity last used. Averaging of the background drift rates, determined for both positive and negative collection potentials, eliminates background ionization produced in those extracameral volumes where the current does not change sign.

Four sources were measured for a distance of 0.50 m between source and chamber and the largest source was measured at a distance of 1 m. The data resulting from all these measurements are given in table 1.

Measurements 1 through 3 in table 1 were performed approximately one year before the 4 through 6 measurements. The elapsed time between measurements 10 and 11 was nine months. The decay corrections used to correct all the data to the August 24, 1967 date were computed on the basis of a 26.68-year half-life [11]. The good agreement between measurements made at such long intervals of time indicates that ¹³⁴Cs contamination is insignificant. The agreement between the two groups of measurements for the “500” source at 0.5 m is within 0.5 percent, and the ratio of the average value for the “500” source at one meter to the average value for 0.5 m is 1.003.

In order to correlate source measurements at 0.5 and 1 m distances, it is necessary to account for air attenuation and scatter. For 0.6-Mev gamma rays and short source-to-detector distances, the buildup factor equals 1 + μD ~ e^μD [12], where μ is the linear attenuation coefficient and D is the distance from the source. At the same time the attenuation of the primary radiation goes as e^−μD. The product of these two corrections is not significantly different from unity.

7. Ion Chambers for Routine Measurements

A 2.5 liter ionization chamber was fabricated from aluminum alloy with the insulators designed to minimize charge soakage and extracameral effects. The chamber consists of two spun aluminum hemispheres welded together with a hole 6 mm in diameter at one point in the weld to allow entrance of a copper collection electrode 3 mm in diameter. The inside diameter of the spherical chamber is approximately 170 mm, and the wall thickness is 1.6 mm. The collection electrode is about 140 mm long.

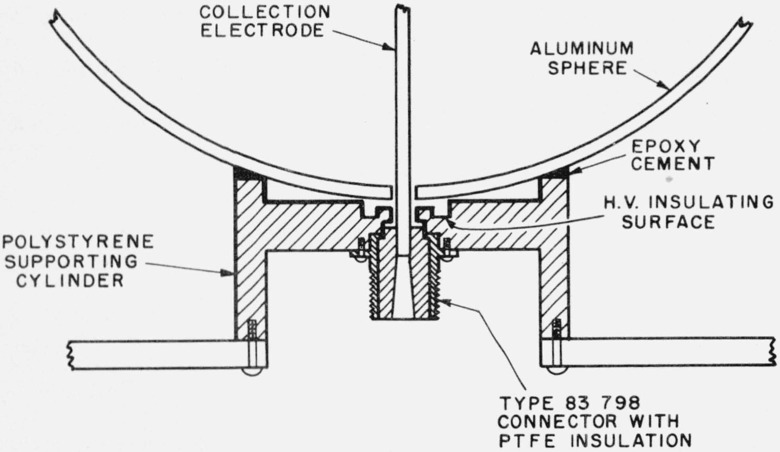
The large spherical chamber is supported by a polystyrene cylinder, shown in figure 2, which also serves as the high-voltage insulator. The high-voltage connection is made through a phosphor-bronze spring (not shown) inserted between the sphere and the high-voltage insulator. The sphere and cylinder are cemented together with an epoxy resin. In the high-voltage insulator all surfaces which can be “seen” by the collection electrode have been made conducting with colloidal graphite. The high-voltage insulating surface is recessed behind the conducting surfaces. A type-83 connector with high-quality insulation is used for mounting the collection electrode and as the guard ring. No charge soakage effects have been observed in this chamber.

Figure 2. Polystyrene cylinder which serves as (1) a support for the spherical aluminum chamber, (2) a high-voltage insulator, and (3) a means for mounting the guard ring and collection electrode.

The heavy lines indicate where the polystyrene surfaces have been coated with colloidal graphite to make them conductive.

The large air volume of the aluminum chamber is required to allow measurement of low-activity sources. The chamber background current is about 10⁻¹⁴ A which is consistent with the radiation background of about 0.03 mR/h. For the “5” source located one meter from the chamber, the background current is about 3 percent of the reading.

The chamber is mounted on a steel plate which is supported on a track in the radium range. The source to be intercompared, and the standard, are alternately placed in a plastic trough at the same height as the center of the chamber and at an appropriate distance away. The trough can be rotated through 180° to test for possible nonuniform source loading and this is ordinarily done in the course of a calibration.

8. Calibration of Working Standards

When sources are submitted for calibration, it is convenient to use working standards of approximately the same activity for the comparison-type measurements. These working standards should be self consistant so that subsequent intercomparisons of calibrated sources will show no discrepancy beyond the estimated uncertainty when consideration is given to the precision of the combined measurements. Therefore, although several sources were measured in the open-air geometry, the “500” source was chosen to be the reference source for all the working standards since the relatively large ion current it generated allowed the most precise measurements. The average of the eight “500” source measurements, appropriately corrected for room scatter, was 136.9₆mR · m² · h⁻¹ on the reference date and this value was used for calibration of the working standards. The intercomparisons were carried out using the large aluminum chamber and a vibrating-reed electrometer. The same source-to-chamber distance was used for all the measurements although the source activities differed by a factor of about 100. This was made possible by changing the feedback capacitance of the vibrating-reed electrometer by the addition of accurately calibrated air capacitors.

The results of these intercomparisons are given in table 2. For those sources which were calibrated in open-air condition, the ratios of the two calibration values are also given in table 2. The agreement between the calibrations for the larger sources is within one percent but there is a large difference for the “5” source. The calibration of the “5” source using the aluminum chamber, with the “500” source as the reference, is believed to be the more reliable since the background and leakage correction under these conditions is a smaller fraction of the reading.

Table 2.

Comparison of source calibrations referenced to “500” source, using the aluminum chamber, and open-air calibrations

Source	Working standard calibrations referenced to “500” source (mR · m2 · h−1)	$\text{Ratio}:\frac{\text{ open-air cal }}{"500"\text{ ref cal }}$
500	136.96	1.000
50	14.79	1.007
5	1.276	1.04
100	36.15	0.994
60	9.48
25	8.23

Seven intercomparisons of the “500” and “50” sources were carried out using the aluminum chamber and electrometer system. Using these data an estimate of the standard deviation of the ratios of the ion currents developed in the chamber, is computed to be 0.7 percent.

The calibration of a ¹³⁷Cs source for the range of exposure rates considered here is believed to have an overall uncertainty of 3.2 percent. The contribution of systematic errors to this percentage, computed from the values given in table 3, is 1.2 percent. This value is equal to the square root of the sum of the squares of the estimated maximum uncertainties for the quantities given in the table.

Table 3.

Estimated maximum uncertainties in the cavity chamber calibration of a ¹³⁷Cs Source

Factor	Est. max. uncertainty
	Percent
Wall absorption correction	1.0
Stopping power correction	0.5
Capacity, potential and time	.1
Recombination	.1
Temperature	.1
Pressure	.1
Chamber volume	.3
Center of electron production correction	.1
Room scattering correction	.1

The largest uncertainties given in table 3 are for the stopping power correction, the wall absorption correction and the volume determination. In the case of the stopping power correction the calculations of Burlin [6] produce values for the carbon-to-air ratio which are identical with those of Spencer-Attix and both agree with the experimental determinations of Whyte [13] for ⁶⁰Co gamma rays. The accuracy of Whyte’s measurements is 0.5 percent and Burlin’s calculated values are within his experimental uncertainty of 2 percent. Therefore an uncertainty of 0.5 percent is assigned to this correction.

The wall absorption correction, determined experimentally, is 0.6 percent per mm and 0.8 percent per mm for one-cm³ and 50-cm³ spherical chambers respectively. These corrections are determined from data for a set of three chambers each. Therefore 1 percent is taken as the estimated uncertainty for this correction since this is approximately the difference in the percentage corrections for a 4-mm wall.

The cavity chamber volumes were determined by differential weighing of the chambers, using water to fill the cavity. The range of the volume determinations for these chambers is 0.3 percent.

Each of the other quantities contributing to the systematic error, and entering into the cavity chamber measurement of the “500” source exposure rate, is believed to be known to 0.1 percent.

The random error contribution to the overall uncertainty is computed from three times the square root of the sum of the squares of the percent standard deviations of the various measurements. This includes the cavity chamber measurements of the “500” source, the intercomparison of the “500” source with the working standard sources and finally, the intercomparison of a working standard with a source to be calibrated for the user. In the case of the working standard calibrations the percent standard deviation is for the mean of several sets of measurements whereas the percent standard deviation for the calibration of the user’s source is for one set of measurements.

$$\begin{gathered} \text{Overall uncertainty = }\sqrt{1.4}+3\sqrt{{0.11}^2+{0.26}^2+{0.6}^2} \\ =3.2\text{ percent} \end{gathered}$$

where the values given under the square root signs are in the order described above.