Abstract
Two-dimensional (2D) materials with intrinsic ferromagnetism provide unique opportunity to engineer new functionalities in nano-spintronics. One such material is CrI3, showing long-range magnetic order in monolayer with the Curie temperature (Tc) of 45 K. Here we study detailed evolution of magnetic transition and magnetic critical properties in response to systematic reduction in crystal thickness down to 50 nm. Bulk Tc of 61 K is gradually suppressed to 57 K, however, the satellite transition at T * = 45 K is observed layer-independent at fixed magnetic field of 1 kOe. The origin of T * is proposed to be a crossover from pinning to depinning of magnetic domain walls. The reduction of thickness facilitates a field-driven metamagnetic transition around 20 kOe with out-of-plane field, in contrast to the continuous changes with in-plane field. The critical analysis around Tc elucidates the mean-field type interactions in microscale-thick CrI3.
Subject terms: Ferromagnetism, Magnetic properties and materials
Introduction
Layered materials, when thinned to atomic limits in 2D exhibit novel properties, different from the bulk counterpart. Recent discoveries of intrinsic 2D ferromagnetism in atomically thin CrI3 and Cr2Ge2Te6 open up new opportunities for studying fundamental 2D magnetism and show great potential in spintronic applications1–3. CrI3 and Cr2Ge2Te6 are ferromagnetic (FM) below Tc ~ 61 K in bulk4–6. First-principle calculations predict a robust 2D ferromagnetism with Tc ~ 57.2 or 106 K in monolayer Cr2Ge2Te67,8, However, the scanning magneto-optic Kerr microscopy experiment shows that the Tc monotonically decreases with decreasing thickness, showing 30 K in bilayer and the absence of Tc in monolayer3.
In bulk CrI3, the Cr atoms in each layer form a honeycomb structure, and each Cr atom is surrounded by six I atoms in an octahedral coordination [Fig. 1(a)]. In contrast to Cr2Ge2Te6, ferromagnetism in CrI3 persists in monolayer with Tc of 45 K2. Intriguingly, the magnetism in CrI3 is layer-dependent, from FM in monolayer to antiferromagnetic (AFM) in bilayer, and back to FM in trilayer, providing great opportunities for designing magneto-optoelectronic devices2. The monolayer CrI3 can be described by the Ising model2,9. Remarkably, the electrostatic doping can modify the saturation magnetization, the coercive force, and the Tc in monolayer as well as change the interlayer magnetic order in bilayer CrI310,11. In addition, giant tunneling magnetoresistance is observed in few-layer CrI3, exhibiting multiple states as a function of magnetic field12–15. This highlights CrI3 as a potential magnetic tunnel barrier for van der Waals heterostructure spintronic devices and also shows demand for magnetic order investigation at all length scales from bulk to monolayer.
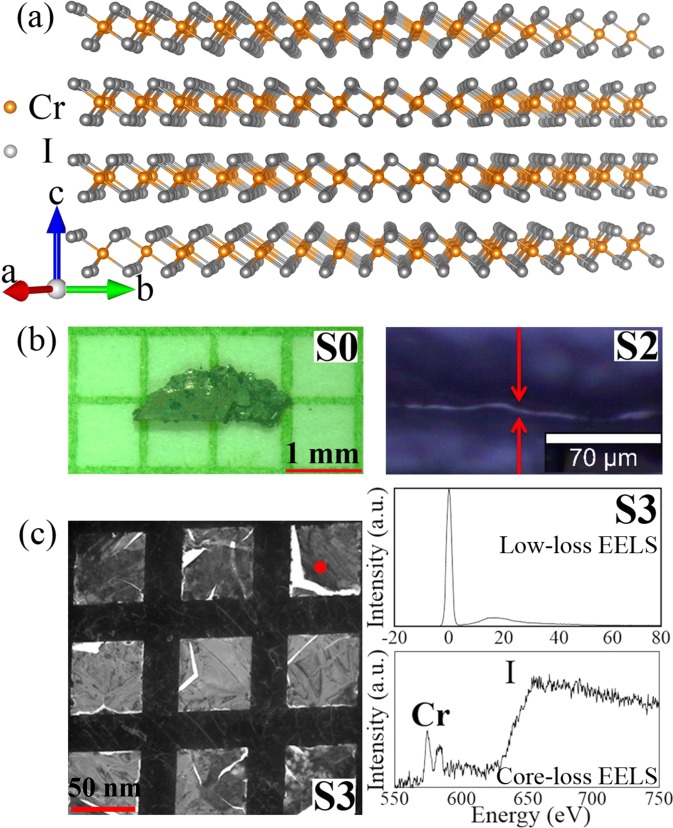
Figure 1.
(a)Low temperature structure of CrI3 in the space group. (b) Optical microscopy of bulk S0 sample (thickness ~100 μm) and cross-section of S2 sample (thickness ~2 μm). (c) Transmission electron microscopy (TEM) image of S3 sample in Cu grid along with the low-loss and core-loss electron energy loss spectra (EELS) taken from top right area marked by red circle. The thickness of S3 was calculated from the low-loss EELS based on log-ratio method in Digital Micrograph program to be 44 nm. The average thickness for many areas measured is 49 ± 8 nm.
Here we report a detailed study of thickness-dependent magnetic transition and critical behavior in CrI3. An additional satellite transition at T* was observed just below Tc. The value of T* is found thickness-independent at fixed magnetic field, in contrast to gradually suppressed Tc with reduction in thickness. Thin CrI3 crystals show an increase in coercive field and distinct field-driven metamagnetic transition around 20 kOe with out-of-plane field but not in-plane field. The critical behavior suggests the long-range mean-field type interactions in mesoscale-thick CrI3 crystals.
Methods
Bulk CrI3 single crystals were fabricated by the chemical vapor transport method and characterized as described previously16. A series of thicknesses were obtained step-by-step mechanical exfoliating bulk crystal down to nanometer scale [Fig. 1(b,c)]. Considering the reactivity of thin CrI3 flakes, all the samples were prepared in an argon-filled glove-box and protected using scotch tape on both sides when transferring for magnetization measurement. The dc magnetization was measured in Quantum Design MPMS-XL5 system. An optical microscopy equipped with 100× objective lens in Witec alpha 300 confocal Raman microscope was used for imaging the cross-section of S2 sample to determine its thickness. Transmission electron microscopy (TEM) sample of S3 was prepared by putting the exfoliated S3 sample in Cu grid. The thickness (t) of S3 sample was measured by the low loss EELS spectrum in JEM-ARM200F microscope [Fig. 1(c)], t = ln(It/I0) × λ, where I0 and It are integrated EELS signal intensity under the zero-loss peak and the total spectrum, respectively; λ is a total mean free path for all inelastic scattering which can be calculated based on the composition of the sample17.
Results and Discussion
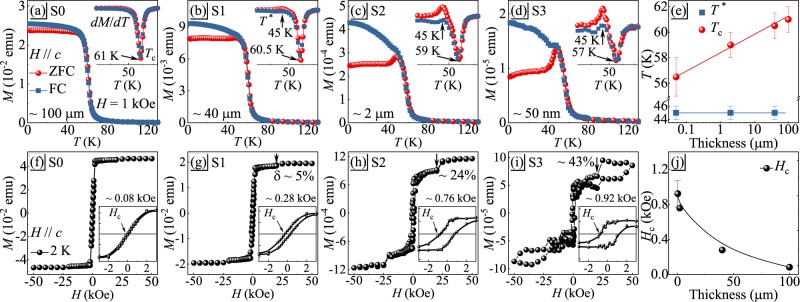
Figure 2(a–d) present the temperature-dependent magnetization M(T) with zero-field cooling (ZFC) and field-cooling (FC) modes measured in out-of-plane field H = 1 kOe for the samples (S0–S3) with typical thickness from 100 μm to 50 nm. There is an apparent increase in M(T), in line with the paramagnetic (PM) to FM transition1. The Tc can be determined from the minima of the first derivative of the M(T) curves [insets in Fig. 2(a–d)]. Given the large magnetocrystalline anisotropy in CrI318, the divergence of ZFC and FC curves is observed below Tc in H = 1 kOe. With subsequent reduction of crystal thickness this discrepancy tends to be larger, indicating an increasing anisotropy in thin crystals. Intriguingly, an additional satellite transition T* just below Tc is observed. A similar phenomenon was also observed in Fe3GeTe2, arising from the emergence of antiparallel spin arrangement along the c axis between different Fe3Ge layers19. This satellite transition T* is defined by the maxima of the first derivative of the M(T) curves [insets in Fig. 2(b–d)], which is more apparent in thinner crystal. The thickness dependence of Tc and T* is summarized in Fig. 2(e). The Tc shows linear decrease with logarithm of thickness. In contrast, the T* seems thickness-independent and shows a value of 45 K identical to the Tc in monolayer measured by magneto-optic Kerr microscopy in H = 1.5 kOe2. The isothermal magnetization at T = 2 K for the corresponding samples is shown in Fig. 2(f–i). With H//c, the magnetization of bulk CrI3 crystal saturates at a relatively low magnetic field H ~ 2 kOe and in line with the previous reports1,16. With reduction of thickness, there is an increase of coercive field Hc as shown in insets of Fig. 2(f–i), from about 80 Oe for S0 sample to 920 Oe for S3 sample, still identified as a relatively soft ferromagnet. It is interesting to note that an apparent magnetization jump around H ~ 20 kOe is observed in thin crystals. The calculated value δ = [M(25kOe) − M(20kOe)]/M(20kOe) increases from 5% for S1 to 43% for S3. This field-driven metamagnetic transition is first identified by the step-like change of magnetization in the hysteresis curves, which is similar with the giant tunneling magnetoresistance step around the same field observed in few-layer devices15. The tunneling magnetoresistance step in few-layer devices is attributed to spin filtering effect arising from collapse of interlayer AFM in thin CrI312–15. Above this critical field, a fully spin polarized FM state is reached in S0–S2 samples, however, a large hysteresis is observed in S3 sample.
Figure 2.
(a–d) Temperature dependence of magnetization for CrI3 at various crystal thicknesses measured with H//c at 1 kOe. Insets show the first derivative of the M(T) curves. (e) Thickness-dependent T* and Tc. (f–i) Isothermal magnetization at T = 2 K for corresponding S0-S3 samples. Insets show the enlarged low field part and the derived coercive field Hc. (j) Thickness dependence of Hc.
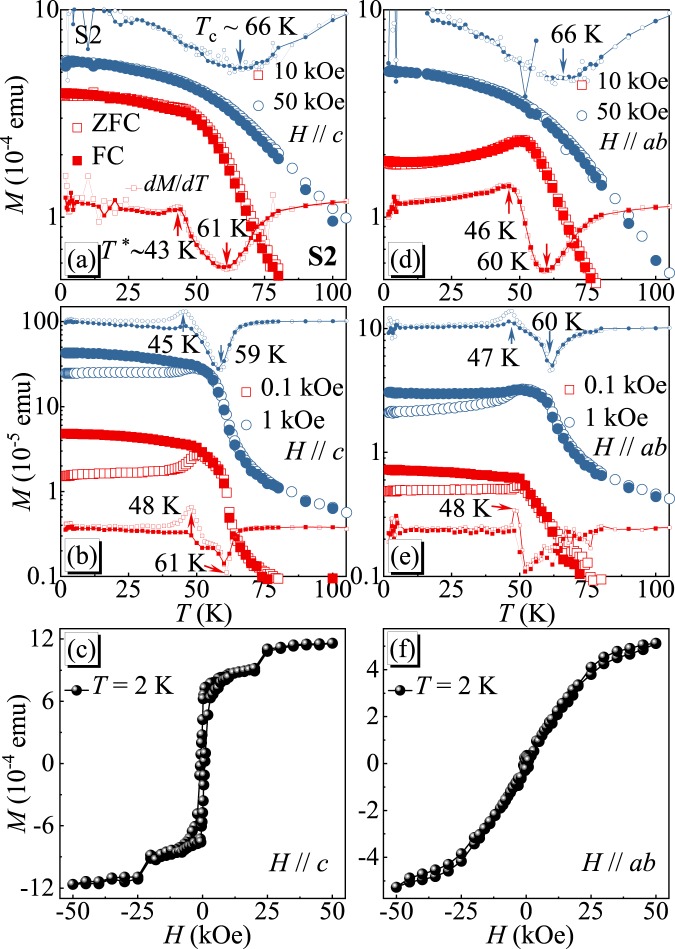
To well understand the nature of magnetism in CrI3 and its properties from bulk to monolayer, we then focus on the S2 sample with mesoscale thickness of 2 μm. Figure 3 shows the temperature- and field-dependent magnetization M(T,H) with out-of-plane and in-plane fields, respectively. The M(T) is nearly isotropic in H = 50 kOe, whilst anisotropic magnetic response is observed in low fields. In H = 10 kOe, a monotonic increase of M(T) with decreasing temperature is observed for H//c [Fig. 3(a)], however, the M(T) decreases with decreasing temperature below 50 K for H//ab [Fig. 3(d)]. Similar feature was also observed in bulk CrI3 crystal, associated with its temperature dependent magnetocrystalline anisotropy18,20. The satellite transition T* reveals itself by the emergence of a weak kink in the dM/dT curve with H = 10 kOe. With decreasing field, the magnetic anisotropy results in larger divergence between ZFC and FC magnetization and a more abrupt satellite transition, as shown in Fig. 3(b,e). Both Tc and T* are field-dependent but with an opposite tendency, i.e., with decreasing field the Tc decreases whereas the T* gradually increases. The isothermal magnetization at 2 K increases discretely for out-of-plane field [Fig. 3(c)], but monotonically for in-plane field [Fig. 3(f)]. Although an A-type AFM ground state was proposed in few-layer devices15, a FM ground state is still expected in S2 sample with thickness ~2 μm. Therefore, the field-driven metamagnetic transition is most likely caused by a movement or depinning of magnetic domains, rather than flipping the spins from an antiparallel to a parallel configuration. A crossover from pinning to depinning of magnetic domain walls is also proposed as the reason for the satellite T* kink. When the sample is cooled in zero field, the magnetic domains start to be pinned below the crossover temperature T*. Small applied field at base temperature is insufficient to move the pinned domains. With increasing temperature, thermal fluctuations gradually weaken the pinning force and finally completely depin the domains above T*. This also explains why the T* kink is more apparent in the ZFC curves. In the FC process the domains are always pinned with the effective FM moment aligned along the cooling field.
Figure 3.
(a,b)Temperature-dependent magnetization measured at various magnetic fields and (c) field-dependent magnetization measured at T = 2 K for H//c. (d,e) Temperature-dependent magnetization measured at various magnetic fields and (f) field-dependent magnetization measured at T = 2 K for H//ab.
Near a second-order phase transition, the free energy of a ferromagnet . By ∂Fm(M)/∂M = 0, the equation of state is obtained as H/M = a + bM2 for the behavior of magnetization near Tc. According to the scaling hypothesis, the spontaneous magnetization Ms below Tc, the inverse initial susceptibility H/M above Tc, and the M(H) at Tc can be characterized by a series of critical exponents21:
| 1 |
| 2 |
| 3 |
where M0, h0/m0, D and ε = (T − Tc)/Tc are the critical amplitudes and the reduced temperature, respectively22.
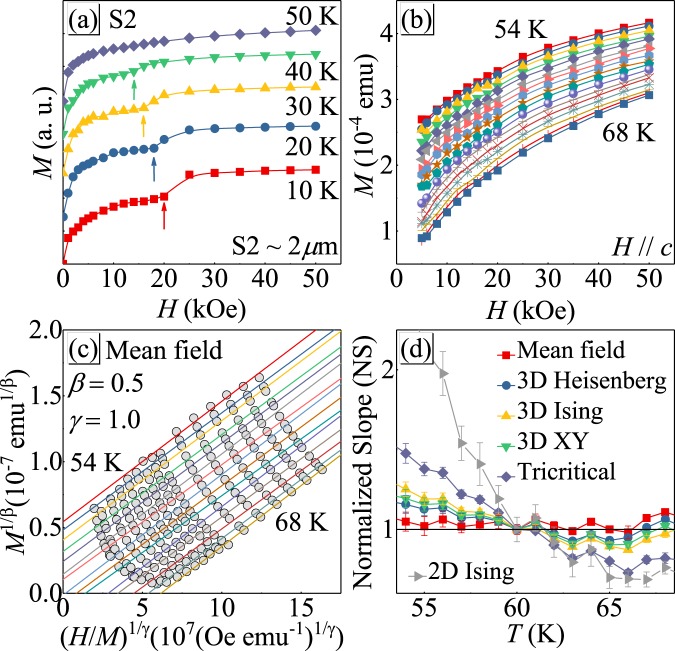
The isothermal magnetization curves with out-of-plane field are depicted in Fig. 4(a,b). The magnetization jump gradually moves to lower field and finally disappears at 50 K for S2. The Arrott plot of M2 vs H/M [Fig. 4(c)], with β = 0.5 and γ = 1.023,24, gives a set of quasi-straight lines and the isotherm at Tc pass through the origin, suggesting the mean-field type magnetic interactions in S2 sample. In addition, the positive slope of the straight lines indicates that it is a second-order transition based on the Banerjee’s criterion25. The Arrot-Noaks equation of state gives a general modified Arrott plot (H/M)1/γ = aε + bM1/β, where a and b are constants26. Taking into consideration the three-dimensional (3D) critical behavior in bulk CrI3 (S0 sample)16, and 2D Ising-like in monolayer2, a set of possible exponents belonging to different models are used to build the modified Arrott plots27. Comparison the normalized slope (NS = S(T)/S(Tc)) with ideal value “1” can determine the most suitable model, where S(T) = dM1/β/d(H/M)1/γ. Figure 4(d) presents the NS vs T curves for indicated models, confirming that the mean-field model is the best and the 2D Ising model shows the largest deviation. That is to say, the critical behavior of mesoscale S2 sample is quite different when compared to bulk and monolayer2,16.
Figure 4.
(a,b) Initial isothermal magnetization at various temperatures with out-of-plane field. (c) The Arrott Plot of S2 sample with β = 0.5 and γ = 1.0. (d) Temperature-dependent NS = S(T)/S(Tc) for indicated models.
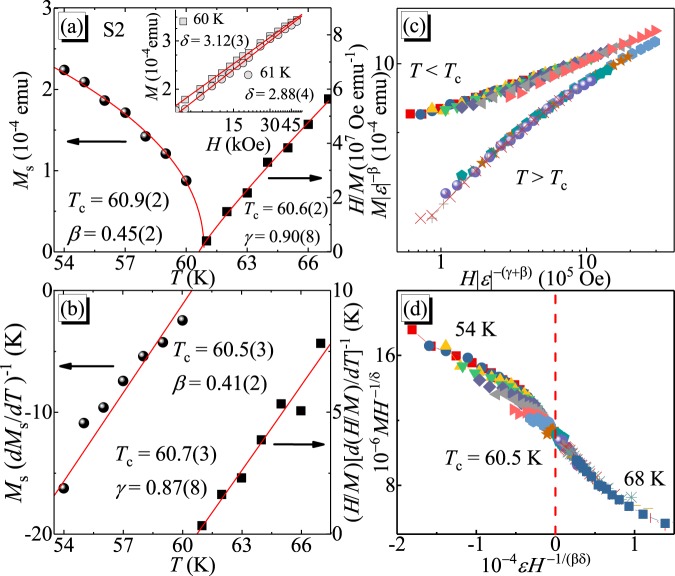
The linearly extrapolated Ms and H/M are plotted from in Fig. 5(a). The solid lines are fitted lines according to Eqs (1) and (2). The precise critical exponents β = 0.45(2), with Tc = 60.9(2) K, and γ = 0.90(8), with Tc = 60.6(2) K, are obtained, close to the parameters of mean-field model. According to Eq. (3), the M(H) at Tc should be a straight line in log-log scale with the slope of 1/δ [inset in Fig. 5(a)]. Such fitting yields δ = 3.12(3) for T = 60 K and 2.88(4) for T = 61 K, respectively. The Kouvel-Fisher (KF) method can be used to double check the obtained critical exponents,
| 4 |
| 5 |
where Ms/(dMs/dT) and (H/M)/[d(H/M)/dT] are linear in T and the slopes are 1/β and 1/γ, respectively28. Such fitting gives β = 0.41(2), with Tc = 60.5(3) K, and γ = 0.87(8), with Tc = 60.7(3) K, respectively, in line with the values obtained by the modified Arrott plot.
Figure 5.
(a)Temperature-dependent Ms (left) and H/M (right) with solid fitting curves. Inset shows the isotherms M(H) in log-log scale near Tc with linear fitting curves. (b) Temperature-dependent Ms(dMs/dT)−1 (left) and (H/M)[d(H/M)/dT)]−1 (right) with linear fitting curves. (c) Scaling plot of m vs h with m ≡ ε−βM(H, ε) and h ≡ ε−(β+γ)H, respectively. (d) MH−1/δ vs εH−1/(βδ).
The reliability of obtained critical exponents β, γ, δ, and Tc can be further checked by a scaling analysis. Near the critical region, the magnetic equation of state can be expressed as
| 6 |
where f± is the regular function with f− for T < Tc, and f+ for T > Tc, respectively. This equation can be further expressed as m = f± (h), where m ≡ ε−β M (H, ε) and h ≡ ε−(β+γ) H are the rescaled magnetization and magnetic field, respectively. Figure 5(c) presents the scaled m vs h in log-log scale, falling on two separate branches above and below Tc, confirming the true scaling treatment and the intrinsic critical values of β, γ, and δ. The scaling equation of state can also be expressed as
| 7 |
where the MH−1/δ vs εH−1/(βδ) should collapse into a single curve with the Tc locating at horizontal zero point [Fig. 5(d)].
The critical exponents of CrI3 (S0 and S2) with different thickness are listed in Table 1 for comparison with the theoretical models2,16,21,27,29. For a 2D magnet, the value of critical exponent β should be within a window ~0.1 ≤ β ≤ 0.2530. As we can see, the critical exponents of bulk CrI3 crystal (S0) are between the values of theoretical tricritical mean-field and 3D Ising model, exhibiting a clear 3D critical phenomenon, in contrast to Cr2(Si,Ge)2Te6 showing 2D Ising-like behavior31,32. The monolayer CrI3 is claimed as a 2D Ising-like ferromagnetism as a result of large magnetic anisotropy removing the Mermin-Wagner restriction2,33. However, the critical exponents of β, γ, and δ for mesoscale CrI3 (S2) are well fit with the mean-field model (Table 1), which is quite different from the behavior in bulk and monolayer. It should be noted that the precise value of Tc for S2 almost equals to Tc = 61 K for S0 based on the critical analysis, in contrast to the strong thickness dependence of β, γ, and δ. We assume that the Tc of 45 K in monolayer is most likely stabilized by the satellite transition (T* ~ 45 K) in bulk CrI3, calling for further in-depth theoretical study.
Table 1.
The critical exponents of CrI3 (S0 and S2) with different thickness obtained by various methods such as the modified Arrott plot (MAP), the Kouvel-Fisher plot (KFP), the critical isotherm (CI) and the magneto-optical Kerr (MOK) effect, in comparison with different theoretical models.
| Thickness | Theoretical model | Reference | Technique | Tc (K) | β | γ | δ |
|---|---|---|---|---|---|---|---|
| S0 ~100 μm | 16 | MAP | 60.45 (3)/60.38 (6) | 0.284 (3) | 1.146 (11) | 5.04 (1) | |
| 16 | KFP | 60.05 (13)/60.43 (4) | 0.260 (4) | 1.136 (6) | 5.37 (4) | ||
| 16 | CI | 60 | 5.32 (2) | ||||
| 3D Heisenberg | 29 | Theory | 0.365 | 1.386 | 4.8 | ||
| 3D XY | 29 | Theory | 0.345 | 1.316 | 4.81 | ||
| 3D Ising | 29 | Theory | 0.325 | 1.24 | 4.82 | ||
| Tricritical mean field | 27 | Theory | 0.25 | 1.0 | 5 | ||
| S2 ~2 μm | This work | MAP | 60.9 (2)/60.0 (2) | 0.45 (2) | 0.90 (8) | 3.00 (9) | |
| This work | KFP | 60.5 (3)/60.7 (3) | 0.41 (2) | 0.87 (8) | 3.12 (9) | ||
| This work | CI | 60 | 2.88 (4) | ||||
| This work | CI | 61 | 3.12 (3) | ||||
| monolayer | Mean field | 21 | Theory | 0.5 | 1.0 | 3.0 | |
| 2 | MOK | 45 | |||||
| 2D Ising | 27 | Theory | 0.125 | 1.75 | 15 |
Conclusion
In summary, we have investigated the thickness-dependent magnetism in CrI3 from bulk to 50 nm thickness. In addition to suppression of bulk Tc, we observe an additional satellite transition T* at 45 K which is independent of thickness and corresponds to the Tc observed in monolayer. Analysis of critical behavior shows mean-field interactions in mesoscale-thick CrI3, in contrast to that in bulk and monolayer, which is helpful to understand the nature magnetism in in CrI3 and is of great importance for future magneto-optoelectronic devices.
Acknowledgements
Work at Brookhaven National Laboratory was supported by US DOE, Office of Science, Office of Basic Energy Sciences under contract DE-SC0012704.
Author Contributions
C.P. initiated the study, designed research and supervised the project. Y.L. synthesized crystals and performed magnetization measurements. X.T. performed optical microscopy study. L.W., J.L., J.T. and Y.Z. contributed TEM and EELS measurements. Y.L. and C.P. organized and wrote the paper with input from all collaborators. This manuscript reflects the contribution and ideas of all authors.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Change history
1/24/2020
An amendment to this paper has been published and can be accessed via a link at the top of the paper.
Contributor Information
Yu Liu, Email: yuliu@bnl.gov.
C. Petrovic, Email: petrovic@bnl.gov
References
- 1.McGuire MA, Dixit H, Cooper VR, Sales BC. Coupling of Crystal Structure and Magnetism in the Layered, Ferromagnetic Insulator CrI. Chem. Mater. 2015;27:612. doi: 10.1021/cm504242t. [DOI] [Google Scholar]
- 2.Huang B, et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature. 2017;546:270. doi: 10.1038/nature22391. [DOI] [PubMed] [Google Scholar]
- 3.Gong C, et al. Discovery of intrinsic ferromagnetism in two-dimensional van der Waals crystals. Nature. 2017;546:265. doi: 10.1038/nature22060. [DOI] [PubMed] [Google Scholar]
- 4.Carteaux V, Brunet D, Ouvrard G, André G. Crystallographic, magnetic and electronic structures of a new layered ferromagnetic compound Cr Ge Te. J. Phys.: Condens. Matter. 1995;7:69. doi: 10.1088/0953-8984/7/1/008. [DOI] [Google Scholar]
- 5.Casto LD, et al. Strong spin-lattice coupling in CrSiTe. APL Mater. 2015;3:041515. doi: 10.1063/1.4914134. [DOI] [Google Scholar]
- 6.Zhang X, et al. Magnetic anisotropy of the single-crystalline ferromagnetic insulator Cr Ge Te. Jpn. J. Appl. Phys. 2016;55:033001. doi: 10.7567/JJAP.55.033001. [DOI] [Google Scholar]
- 7.Li XX, Yang JL. CrXTe (X = Si, Ge) nanosheets: two dimensional intrinsic ferromagnetic semiconductors. J. Mater. Chem. C. 2014;2:7071. doi: 10.1039/c4tc01193g. [DOI] [Google Scholar]
- 8.Sivadas N, Daniels MW, Swendsen RH, Okamoto S, Xiao D. Magnetic ground state of semiconducting transition-metal trichalcogenide monolayers. Phys. Rev. B. 2015;91:235425. doi: 10.1103/PhysRevB.91.235425. [DOI] [Google Scholar]
- 9.Griffiths RB. Peierls Proof of Spontaneous Magnetization in a Two-Dimensional Ising Ferromagnet. Phys. Rev. 1964;136:A437. doi: 10.1103/PhysRev.136.A437. [DOI] [Google Scholar]
- 10.Jiang S, Li L, Wang Z, Mak KF, Shan J. Controlling magnetism in 2D CrI by electrostatic doping. Nat. Nanotech. 2018;13:549. doi: 10.1038/s41565-018-0135-x. [DOI] [PubMed] [Google Scholar]
- 11.Huang B, et al. Electrical control of 2D magnetism in bilayer CrI. Nat. Nanotech. 2018;13:544. doi: 10.1038/s41565-018-0121-3. [DOI] [PubMed] [Google Scholar]
- 12.Song T, et al. Giant tunneling magnetoresistance in spin-filter van der Waals heterostructures. Science. 2018;360:1214. doi: 10.1126/science.aar4851. [DOI] [PubMed] [Google Scholar]
- 13.Klein DR, et al. Probing magnetism in 2D van der Waals crystalline insulators via electron tunneling. Science. 2018;360:1218. doi: 10.1126/science.aar3617. [DOI] [PubMed] [Google Scholar]
- 14.Wang Z, et al. Very large tunneling magnetoresistance in layered magnetic semiconductor CrI. Nat. Commun. 2018;9:2516. doi: 10.1038/s41467-018-04953-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kim HH, et al. One Million Percent Tunnel Magnetoresistance in a Magnetic van der Waals Heterostructure. Nano Lett. 2018;18:4885. doi: 10.1021/acs.nanolett.8b01552. [DOI] [PubMed] [Google Scholar]
- 16.Liu Y, Petrovic C. Three-dimensional magnetic critical behavior in CrI. Phys. Rev. B. 2018;97:014420. doi: 10.1103/PhysRevB.97.014420. [DOI] [Google Scholar]
- 17.Egerton, R. F. Electron Energy-Loss Spectroscopy in the Electron Microscope (Plenum Press, New York, 1996).
- 18.Richter N, et al. Temperature-dependent magnetic anisotropy in the layered magnetic semiconductors CrI and CrBr. Phys. Rev. Materials. 2018;2:024004. doi: 10.1103/PhysRevMaterials.2.024004. [DOI] [Google Scholar]
- 19.Yi J, et al. Competing antiferromagnetism in a quasi-2D itinerant ferromagnet: Fe GeTe. 2D Mater. 2016;4:011005. doi: 10.1088/2053-1583/4/1/011005. [DOI] [Google Scholar]
- 20.Liu Y, Petrovic C. Anisotropic magnetocaloric effect in single crystals of CrI. Phys. Rev. B. 2018;97:174418. doi: 10.1103/PhysRevB.97.174418. [DOI] [Google Scholar]
- 21.Stanley, H. E. Introduction to Phase Transitions and Critical Phenomena (Oxford U. P., London and New York, 1971).
- 22.Fisher ME. The theory of equilibrium critical phenomena. Rep. Prog. Phys. 1967;30:615. doi: 10.1088/0034-4885/30/2/306. [DOI] [Google Scholar]
- 23.Arrott A. Criterion for Ferromagnetism from Observations of Magnetic Isotherms. Phys. Rev. B. 1957;108:1394. doi: 10.1103/PhysRev.108.1394. [DOI] [Google Scholar]
- 24.Lin JC, et al. Unusual ferromagnetic critical behavior owing to short-range antiferromagnetic correlations in antiperovskite Cu NMn (0.1 ≤ x ≤ 0.4) Sci. Rep. 2015;5:7933. doi: 10.1038/srep07933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Banerjee BK. On a generalised approach to first and second order magnetic transitions. Phys. Lett. 1964;12:16. doi: 10.1016/0031-9163(64)91158-8. [DOI] [Google Scholar]
- 26.Arrott A, Noakes JE. Approximate Equation of State For Nickel Near its Critical Temperature. Phys. Rev. Lett. 1967;19:786. doi: 10.1103/PhysRevLett.19.786. [DOI] [Google Scholar]
- 27.LeGuillou JC, Zinn-Justin J. Critical exponents from field theory. Phys. Rev. B. 1980;21:3976. doi: 10.1103/PhysRevB.21.3976. [DOI] [Google Scholar]
- 28.Kouvel JS, Fisher ME. Detailed Magnetic Behavior of Nickel Near its Curie Point. Phys. Rev. 1964;136:A1626. doi: 10.1103/PhysRev.136.A1626. [DOI] [Google Scholar]
- 29.Kaul SN. Static critical phenomena in ferromagnets with quenched disorder. J. Magn. Magn. Mater. 1985;53:5. doi: 10.1016/0304-8853(85)90128-3. [DOI] [Google Scholar]
- 30.Taroni A, Bramwell ST, Holdsworth PCW. Universal window for two-dimensional critical exponents. J. Phys.: Condens. Matter. 2008;20:275233. doi: 10.1088/0953-8984/20/27/275233. [DOI] [PubMed] [Google Scholar]
- 31.Liu Y, Petrovic C. Critical behavior of quasi-two-dimensional semiconducting ferromagnet Cr Ge Te. Phys. Rev. B. 2017;96:054406. doi: 10.1103/PhysRevB.96.054406. [DOI] [Google Scholar]
- 32.Lin GT, et al. Critical behavior of two-dimensional intrinsically ferromagnetic semiconductor CrI. Appl. Phys. Lett. 2018;112:072405. doi: 10.1063/1.5019286. [DOI] [Google Scholar]
- 33.Mermin ND, Wagner H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966;17:1133. doi: 10.1103/PhysRevLett.17.1133. [DOI] [Google Scholar]