Multiplexed protein force spectroscopy reveals equilibrium protein folding dynamics and the low-force response of von Willebrand factor

Significance

The physiological function of proteins is often critically regulated by mechanical forces acting on them. Single-molecule manipulation techniques such as atomic force microscopy or optical tweezers have enabled unprecedented insights into the molecular mechanisms underlying such force regulation. Current limitations include the resolution at low forces and low throughput. We here introduce a versatile, modular approach for force measurements on proteins in magnetic tweezers that allows for probing dozens of single molecules in parallel, in a wide force range including very low forces <1 pN. We demonstrate the utility of this assay by elucidating regulatory low-force transitions within von Willebrand factor, a vascular protein that is activated for its critical role in hemostasis by hydrodynamic forces in the bloodstream.

Abstract

Single-molecule force spectroscopy has provided unprecedented insights into protein folding, force regulation, and function. So far, the field has relied primarily on atomic force microscope and optical tweezers assays that, while powerful, are limited in force resolution, throughput, and require feedback for constant force measurements. Here, we present a modular approach based on magnetic tweezers (MT) for highly multiplexed protein force spectroscopy. Our approach uses elastin-like polypeptide linkers for the specific attachment of proteins, requiring only short peptide tags on the protein of interest. The assay extends protein force spectroscopy into the low force (<1 pN) regime and enables parallel and ultra-stable measurements at constant forces. We present unfolding and refolding data for the small, single-domain protein ddFLN4, commonly used as a molecular fingerprint in force spectroscopy, and for the large, multidomain dimeric protein von Willebrand factor (VWF) that is critically involved in primary hemostasis. For both proteins, our measurements reveal exponential force dependencies of unfolding and refolding rates. We directly resolve the stabilization of the VWF A2 domain by Ca²⁺ and discover transitions in the VWF C domain stem at low forces that likely constitute the first steps of VWF’s mechano-activation. Probing the force-dependent lifetime of biotin–streptavidin bonds, we find that monovalent streptavidin constructs with specific attachment geometry are significantly more force stable than commercial, multivalent streptavidin. We expect our modular approach to enable multiplexed force-spectroscopy measurements for a wide range of proteins, in particular in the physiologically relevant low-force regime.

Mechanical forces acting on proteins or ligand–receptor pairs are an integral part of many biological processes. Often the physiological functions of proteins are critically regulated by force: Examples include the mechano-activation of enzymes, force-regulated exposure of cryptic binding sites, and force-dependent unfolding and refolding of protein domains as “strain absorbers” to dissipate mechanical stress (1, 2). A well-studied protein “strain absorber” is the 4th domain of the F-actin cross-linking filamin rod of Dictyostelium discoideum (ddFLN4), which exhibits extraordinarily fast refolding, facilitated by an intermediate state along the refolding pathway (3, 4). Another remarkable example of physiological force regulation occurs in the large, multimeric glycoprotein von Willebrand factor (VWF) in the vasculature. VWF’s hemostatic function is regulated by increased hydrodynamic forces occurring upon blood vessel injury. Activation of VWF relies on a complex interplay of force-induced conformational changes, both of single domains and of the large-scale protein conformation (5–7), while down-regulation of VWF is based on mechano-enzymatic cleavage at a cryptic binding site only accessible upon unfolding of VWF’s A2 domain (8). While many of the individual transitions in VWF have been probed in detail, their interplay, and thus our understanding of how full-length VWF reacts to external forces in the bloodstream, remains incomplete. Since hydrodynamic peak forces grow as the square of the contour length (5, 8), transitions that release contour length at low forces are expected to be particularly relevant for VWF’s physiological function, as they will initiate a cascade of increasing forces that trigger additional transitions with further contour length release. Recent work using atomic force microscopy (AFM) imaging has suggested large-scale transitions in the VWF C-domain stem that, however, could not be detected in AFM-based force spectroscopy, due to its limited force resolution (9, 10).

Most insights into the mechanical properties and regulation of proteins and their complexes at the single-molecule level have been obtained from force-spectroscopy experiments using atomic force microscopes or optical tweezers (OT). While AFM and OT force-spectroscopy measurements have provided unprecedented insights, they also have important shortcomings (11). AFM measurements cannot resolve forces below ∼10 pN; OT provide excellent spatiotemporal resolution even for forces down to ∼1 pN, but are not capable of measuring many molecules in parallel (11). In addition, both AFM and OT intrinsically control position and not force, such that constant-force measurements require active feedback (12). A passive force-clamp mode of operation for OT has been demonstrated, but is limited to a narrow range of molecular extensions (13).

Magnetic tweezers (MT) are a single-molecule force-spectroscopy technique that can overcome these shortcomings. In MT, molecules of interest are tethered between a surface and superparamagnetic beads (11, 14, 15) (SI Appendix, Fig. S1). External magnetic fields exert precisely controlled forces (16) in the range of ∼0.01–100 pN, and previous work has demonstrated camera-based tracking for tens to hundreds of nucleic acid-tethered beads simultaneously (17–19) in (x, y, z) with ∼1-nm spatial resolution and, recently, also up to ≤1-ms temporal resolution (20–22). MT naturally operate in constant force mode, i.e., the applied force is constant during the measurement (to within 0.01%; SI Appendix, Fig. S2), as long as the external magnetic field is not actively changed, with excellent sensitivity in particular at low forces. In addition, MT enable long-term, stable, and robust measurements, as they do not suffer from heating or photo-damage and as instrument drift can be compensated by using nonmagnetic beads immobilized to the surface as references (11, 21, 23, 24).

Despite these advantages, MT so far have mainly been employed to investigate nucleic acid tethers. A key challenge in applying MT to protein force spectroscopy remains to tether approximately nanometer-sized proteins between much larger, ∼1-µm-sized beads and the surface, while avoiding unspecific surface interactions and ideally with a large number of usable tethers in each field of view. Previous MT studies on proteins, therefore, mostly employed large protein constructs, often engineered as polyproteins with repeats of, e.g., titin Ig or protein L domains (23, 25–29). Both covalent and noncovalent strategies have been utilized for attaching proteins to the surface in MT. Noncovalent approaches are either based on antibodies (30–34) or His-tag Cu²⁺-NTA chemistry (35, 36), but have the disadvantage of limited force stability compared to covalent attachment. High force stability is especially desirable for measurements over extended periods of time—for instance, in order to study protein folding and unfolding dynamics at equilibrium. The most common covalent immobilization strategy, based on linking Halo-tagged proteins directly to a surface coated with Halo-tag amine ligands (23, 25, 26, 28, 29, 37), has the problem that unfolding of the tag can contribute undesired signals in addition to specific signals of the protein of interest (25). Recent studies have circumvented this by replacing the Halo-tag system with the Spy-tag–SpyCatcher system (27, 38). Still, as the protein is immobilized onto the surface without a linker, this approach may be prone to unspecific interactions or bias (re)folding (39). Recently, fusion proteins—including, e.g., titin I27 domains flanking the protein of interest or a short DNA tether attached to the protein of interest—have been used as linkers to increase the distance between magnetic bead and surface (27). The use of large fusion proteins not only requires major protein modification, but also again has the disadvantage that the spacer domains potentially complicate the analysis due to their unfolding and refolding transitions. Similarly, double-stranded DNA undergoes an overstretching transition around 65 pN (40), giving a large extension signal in this force range. In summary, currently employed approaches suffer from a low number of usable tethers, as so far there are no reports of multiplexed protein unfolding and refolding measurements in MT.

Here, we present a versatile, modular protein attachment strategy for single-molecule MT force spectroscopy. Our tethering protocol uses an elastin-like polypeptide (ELP) linker (41) that ensures efficient attachment to the surface while minimizing unspecific interactions, both critical prerequisites for high-throughput parallel measurements. In our approach, the protein of interest requires only short [1 and 11 amino acids (aa)] peptide tags for coupling to the linker and bead, respectively, avoiding the need for large fusion proteins and providing a general attachment protocol that is independent of protein size. We demonstrate the versatility of our attachment strategy by applying it to a small, single-domain protein, ddFLN4 (100 aa), and a very large, multidomain protein, dimeric full-length VWF (∼4,000 aa). For both proteins, we achieve a high yield of specific tethers—that is, a large number of single-molecule tethers that exhibit characteristic unfolding and refolding signatures and can be measured in parallel in a single field of view. Our highly parallel, ultra-stable measurements of repeated unfolding and refolding resolve outstanding questions about the respective folding pathways and stabilities and reveal how forces in the range of 1 pN are sufficient to open up the VWF C-domain stem. In addition, we leverage the ability of our assay to apply constant forces over extended periods of time to many molecules in parallel to probe the stability of the biotin–streptavidin receptor–ligand system. We anticipate our tethering strategy to be applicable to a wide range of proteins and, furthermore, expect it to be of immediate use for other parallel force-spectroscopy techniques, such as single-molecule centrifugation (42, 43) or acoustic force spectroscopy (44), extending their capabilities toward protein force spectroscopy.

Results

Site-Specific and Efficient Tethering of Proteins with ELP Linkers.

Our attachment strategy uses an unstructured ELP linker (41, 45) with a contour length of ∼120 nm (∼300 aa) and functional groups at its termini that we utilize as spacers for immobilizing the protein of interest to the bottom glass slide of the flow cell and to reduce unspecific protein–surface (41) and bead–surface interactions (Fig. 1A).

Fig. 1.

Attachment protocol for highly parallel force spectroscopy on proteins in MT. (A) Schematic of the strategy for tethering a protein of interest between the bottom glass slide of the flow cell and a magnetic bead (not to scale). An ELP linker with a single cysteine at its N terminus is coupled to the amino-silanized glass slide via a small-molecule NHS–maleimide cross-linker. After covalent coupling of CoA–biotin to the ybbr-tag at the C terminus of the protein in a bulk reaction catalyzed by sfp phosphopantetheinyl transferase, the protein is covalently ligated to the ELP linker via one (or more) glycines at its N terminus in a reaction mediated by sortase A, which selectively recognizes the C-terminal LPETGG motif of the ELP linker. Finally, a streptavidin-coated magnetic bead is bound to the biotinylated protein via the high-affinity biotin–streptavidin interaction. Red and gray double arrows indicate covalent and noncovalent bonds, respectively. Forces are exerted on the magnetic bead by permanent magnets positioned above the flow cell. Nonmagnetic polystyrene beads baked onto the surface are used as reference beads for drift correction. (B) Representative field of view. Yellow boxes indicate ∼60 beads marked for tracking. (B, Inset) The enlarged image of 1 bead shows the diffraction ring pattern used for 3D bead tracking. (C) Example tether extension time traces showing the characteristic 3-state unfolding pattern of ddFLN4. All traces shown were recorded in parallel from different beads within the same field of view at a constant force of 21 pN.

We chose the ELP peptide linkers over polyethylene glycol (PEG) linkers, which are widely used in AFM-based force spectroscopy (9, 46–48), and over DNA linkers, as typically used for OT measurements (49–51) and in a recent MT study (27), for several reasons. During systematic tests with PEG-coated surfaces, unspecific binding of beads remained a major problem, even in the absence of the protein of interest (SI Appendix, Fig. S3), severely limiting the number of useable tethers per field of view. In contrast, we found the ELP linkers to provide excellent passivation (SI Appendix, Fig. S3), in line with AFM-based measurements comparing PEG- and ELP-based linkers (41). Disadvantages of DNA linkers include 1) the fact that covalent DNA–protein coupling schemes typically provide only low yields (52, 53); 2) the DNA overstretching transition around 65 pN that severely complicates measurements in this force range, in contrast to ELP linkers (compare SI Appendix, Figs. S2B and S4); and 3) the observation that DNA interacts with many proteins; in particular, VWF has been reported to directly interact with DNA via its A1 domain (54). Compared to peptide tethers, DNA linkers—or even engineered DNA bundles (55)—provide a lower level of intrinsic Brownian fluctuations at high forces due to their stiffness. However, at forces <1 pN, peptide linkers have a significantly lower level of intrinsic extension fluctuations (SI Appendix, Fig. S5).

In our attachment scheme, the ELP linker is attached to a glass slide functionalized with thiol-reactive maleimide groups via an N-terminal cysteine (see Materials and Methods for details of the coupling protocol). The ELP linker carries a C-terminal LPETGG motif that allows for site-specific and covalent ligation to the protein of interest via an N-terminal glycine residue in a reaction catalyzed (56) by the enzyme sortase A. For coupling to the bead, the protein of interest is further engineered to carry an 11-aa ybbR-tag (57) at its C terminus that is covalently attached to CoA–biotin in the sfp phosphopantetheinyl transferase reaction. Finally, the biotin label forms a high-affinity noncovalent bond to streptavidin-functionalized beads. Our approach requires only short peptide tags on the protein of interest that can readily be introduced by standard molecular cloning methods and have been shown to be compatible with expression and folding of a large range of proteins (46, 56–59). The coupling can also be inverted, by coupling a protein with an N-terminal ybbR-tag and a C-terminal LPETGG sequence to an ELP linker with an N-terminal glycine and a C-terminal cysteine (SI Appendix, Fig. S6).

Here, we apply our tethering protocol to 2 very different protein systems: the small ddFLN4 domain and large, full-length dimeric VWF. We obtained comparable and efficient tethering of beads with a large number of specific, single-molecule tethers in both cases. Typically, in a single field of view (∼440 × 330 μm²) of our MT setup (Fig. 1B; see Materials and Methods and SI Appendix, Figs. S1 and S2 for details on the setup), 50–100 tethered beads are tracked in parallel, of which 30–50 tethers exhibit characteristic unfolding and refolding signatures (Fig. 1C). The beads that do not show characteristic signatures are likely anchored to the surface by multiple protein tethers, since in control measurements without the protein of interest added, there is essentially no unspecific binding of beads to the surface (0–1 beads per field of view; SI Appendix, Fig. S3). The fraction of specific tethers attached via a single protein can be increased by decreasing the density of proteins immobilized on the surface. However, decreasing the protein concentration will also result in a decrease of the number of single-tethered beads. Optimizing our conditions, we achieved fractions of up to ∼60% specific, single-protein tethers, while still obtaining a large number of tethered beads at the same time. The most efficient flow cell exhibited 50 specific out of 85 beads within the single field of view measured.

Three-State Folding and Unfolding of ddFLN4.

We first applied our tethering protocol to the Ig-fold ddFLN4 domain (Fig. 2A), which exhibits a characteristic 3-state unfolding pattern that has been extensively studied in AFM experiments (3, 4) and is routinely employed as a molecular fingerprint in AFM force-spectroscopy experiments (47, 60, 61). To characterize unfolding and (re)folding in our MT assay, we recorded time traces of tether extension under different, constant forces. In a typical measurement (Fig. 2B), the force was increased from an initial low value (0.5 pN) that allows for (re)folding, to a high value (25 pN in Fig. 2B) that promotes unfolding, and subsequently decreased to a moderate value (6.5 and 7.5 pN in Fig. 2B) to directly monitor refolding. Subsequently, this cycle was repeated multiple times with variable force levels to collect statistics. Unfolding and refolding of ddFLN4 were observed as clear double steps in the traces—i.e., as an increase or decrease of the tether extension in 2 separate steps that we interpret as transition between the native (N) and intermediate (I) and between the intermediate and unfolded (U) states, respectively (Fig. 2 B, Insets). We analyzed the changes in extension for the transitions N ↔ I and I ↔ U as well as for the full transition N ↔ U for many different clamped forces (Fig. 2C). The resulting force–extension profiles are well described by fits of the worm-like chain (WLC) model with a fixed persistence length of 0.5 nm, yielding contour length values (mean ± SD) of 15.0 ± 0.1, 18.3 ± 0.1, and 31.9 ± 0.2 nm, in excellent agreement with values reported from AFM (3, 4).

Fig. 2.

Three-state folding and unfolding of ddFLN4 at constant force. (A) Structure of ddFLN4 [Protein Data Bank ID code 1KSR (83), rendered using VMD (84)], with strands A and B rendered in blue and strands C–G forming the structured portion of the intermediate state, in red. Arrows indicate the direction of force acting on ddFLN4’s termini during MT experiments. (B) Extension vs. time trace of a ddFLN4 tether subjected to alternating intervals of high force (here 25 pN) allowing for ddFLN4 unfolding, intermediate force (here 6.5 or 7.5 pN) allowing for direct observation of refolding, and low force (0.5 pN) to ensure refolding before the next cycle. Unfolding and refolding of ddFLN4 via the mandatory intermediate state are observed as upward or downward double steps in the traces, respectively. Dashed lines in B, Insets indicate extension levels corresponding to the native (N), intermediate (I), and unfolded (U) states, respectively. (C) Force-extension profiles of ddFLN4 for the transitions N ↔ I (blue) and I ↔ U (red) and for full (un)folding N ↔ U (black). Data points are obtained by Gaussian fits to step extension histograms (C, Insets) at each constant force. Data points above 8 pN are from unfolding (based on 68–131 events obtained from 27–36 independent tethers), and data points up to 8 pN from refolding (54–159 events from 26–39 independent tethers). Error bars correspond to the full width at half maximum (FWHM) of Gaussian fits, divided by the square root of counts. Lines are fits of the WLC model. (D) Rates of unfolding at different constant forces for the 3 transitions. Color code is as in C. Error bars correspond to 95% CIs of exponential fits to the fraction of observed events as a function of time (Materials and Methods and SI Appendix, Fig. S8). Lines are fits of a single-barrier kinetic model. (E) Rates of refolding at different constant forces. Color code, error bars, and fits are analogous to D. (F) Fitted rates at zero force k₀ and distances to the transition state Δx for the unfolding and refolding transitions as determined from the fits of a single-barrier kinetic model shown in D and E.

Our data are fully consistent with previous work that found unfolding of the ddFLN4 domain to proceed via a mandatory, short-lived intermediate state: In a first unfolding step, strands A and B (42 aa; blue in Fig. 2A) detach and unfold, with strands C–G (58 aa; red in Fig. 2A) forming a less stable intermediate state (3), which quickly unfolds in the second unfolding step. Folding of ddFLN4 was also suggested to proceed via an intermediate state that is most likely structurally identical or very similar to the intermediate populated during unfolding (4). In our dataset, unfolding (data points > 8 pN) and refolding (data points ≤ 8 pN) are well described by a single WLC curve, confirming that the intermediate states populated during unfolding and folding are structurally very similar or identical. Importantly, no other features except the double steps originating from ddFLN4 were observed in the force range probed (SI Appendix, Fig. S7), showing that the other components of our tethering strategy do not interfere with the measurements.

Our force-clamp measurements allowed us to directly determine the rates of all transitions (Materials and Methods and SI Appendix, Fig. S8). For unfolding (Fig. 2D), we observed the rate for the first transition, N → I, to increase with increasing force from ∼0.001 s⁻¹ at 9 pN to ∼0.2 s⁻¹ at 31 pN. We fitted the rates to a single-barrier kinetic model, in which the rate is given by k(F) = k₀ exp(F⋅Δx/k_BT), where F is the applied force, k₀ the rate at zero force, Δx the distance to the transition state, k_B the Boltzmann constant, and T the absolute temperature (62). We find k_{0,N → I} = 1.5 ×10⁻⁴ s⁻¹ (1.3–1.8 × 10⁻⁴ s⁻¹) and Δx_{N → I} = 0.99 ± 0.03 nm (mean ± SD for all rates and Δx values). The measured rates for full unfolding N → U are essentially identical to those for the transition N → I (Fig. 2D), owing to the fact that the rates for the second transition, I → U (k_{0,I → U} = 0.25 s⁻¹ [0.19–0.32 s⁻¹]; Δx_{I → U} = 0.32 ± 0.04 nm), are at least 1 order of magnitude faster (Fig. 2D), implying that the transition N → I is the rate-limiting step for unfolding.

For refolding in the force range from 2 to 8 pN (Fig. 2E), the rates for the first substep U → I (k_{0,U −> I} = 0.52 s⁻¹ [0.34–0.79 s⁻¹]; Δx_{U −> I} = 3.6 ± 0.3 nm) are again essentially identical to the rates for full refolding U → N (Fig. 2E), and rates for the second transition I → N (1,500 s⁻¹ [950–2,500 s⁻¹]; Δx_{I −> N} of 3.5 ± 0.3 nm) are at least 3 orders of magnitude higher compared to the first transition, implying that again the first transition, U → I, is rate-limiting (Fig. 2F). For forces below 6 pN, the intermediate state was too short-lived to be reliably detected, so that rates were determined separately only for forces ≥6 pN.

We compared our force clamp results to the rates at zero force reported from fits of a single barrier kinetic model to constant pulling speed AFM measurements (4). For unfolding, the rates for the second step k₀,_{I −> U} are in excellent agreement (0.25 and 0.33 s⁻¹ in MT and AFM, respectively), yet the zero force rates for the first step k₀,_{N −> I} appear, in contrast, to differ significantly (1.5 × 10⁻⁴ vs. 0.28 s⁻¹). However, in AFM measurements with low pulling speeds of 1 nm/s, a markedly higher mechanical strength of ddFLN4 has been observed and explained by switching to a second unfolding pathway (63). The reported zero-force rate (for full unfolding) from AFM of 1.4 × 10⁻⁴ s⁻¹ agrees with our results. Thus, our data support the existence of a second unfolding pathway and suggest that differences between the 2 pathways can be largely attributed to the first unfolding step N → I.

For refolding, a direct comparison is less straightforward, as refolding in AFM experiments has been measured at zero force and not under load (4). The rates obtained from MT and AFM differ significantly (k₀,_{U −> I}: 0.52 vs. 55 s⁻¹; k₀,_{I −> N}: 1,500 vs. 179 s⁻¹), which might indicate different folding pathways in the presence and absence of force. Intriguingly, however, in both cases, the same intermediate state appears to be populated during folding. Whereas the first step of folding—and thereby also full folding—is markedly slowed down by force, the second step of folding is almost 10-fold sped up, suggesting a prealignment of the structured portion of the intermediate state by force that allows for faster folding of strands A and B in the second folding step. Since ddFLN4 in vivo is positioned within actin-cross-linking filamin and under tensile load, it appears plausible that a force-induced prealignment of the intermediate state might play a physiological role.

Ultra-Stable Equilibrium Measurements of ddFLN4 Unfolding and Refolding.

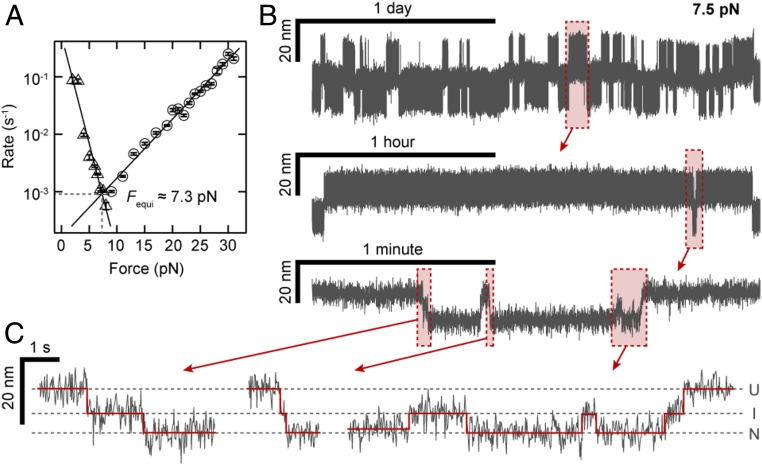
By determining the force for which the fitted rates for full unfolding and refolding (Fig. 2 D and E; black lines) intersect, we predicted the equilibrium force at which the probabilities of ddFLN4 being in the unfolded and folded states are equal to ∼7.3 pN (Fig. 3A). We tested this prediction by measuring at constant forces close to the predicted equilibrium force. Since the predicted rates at equilibrium are only ∼3 h⁻¹ (Fig. 3A), we performed very long measurements (55 h in Fig. 3B and 144 h in SI Appendix, Fig. S9), harnessing the excellent force and drift stability of MT. We observed repeated transitions between the unfolded and folded states, with the system spending approximately half of the time in each of the 2 states (Fig. 3B), as expected for a measurement close to equilibrium. Examining the traces close to equilibrium in detail, we observed repeated transitions not only N ↔ U via the I state (Fig. 3C, left and center traces), but also from the U and N states into the I state that return to the initial state (Fig. 3C, right trace, and SI Appendix, Fig. S9, Inset), again strongly suggesting that the same intermediate state is populated during unfolding and folding. Finally, we note that even for the very long measurements reported here, no significant change of ddFLN4’s force response over time was observed, indicating reliable, correct refolding of the domain without any hysteresis effects, both for the long equilibrium measurement at constant force and for repeated cycles of unfolding and refolding under varying load (SI Appendix, Fig. S10). The long-term stability combined with its very characteristic 3-state unfolding signature make ddFLN4 an ideal fingerprint for the identification of single-molecule tethers.

Fig. 3.

Long and stable ddFLN4 folding and unfolding traces close to equilibrium. (A) Force dependence of the rates for complete unfolding (circles) and refolding (triangles) as determined in Fig. 2 D and E. The intersection of the linear fits predicts the equilibrium force F_equi ∼ 7.3 pN, at which the probabilities of ddFLN4 being in the folded and unfolded state are equal. (B) 55-h-long extension vs. time trace of a ddFLN4 tether subjected to a constant force of 7.5 pN and zooms into indicated segments of the trace. (C) Zooms show not only full unfolding and folding transitions, but also transitions from the native to the intermediate state and back. Dashed lines indicate average extension levels corresponding to the native (N), intermediate (I), and unfolded (U) states, respectively. Red lines indicate positions of transitions between states and extension levels in each state, as determined by the step-finding algorithm employed for the analysis.

Lifetime of Biotin–Streptavidin Interactions for Multivalent and Monovalent Streptavidin.

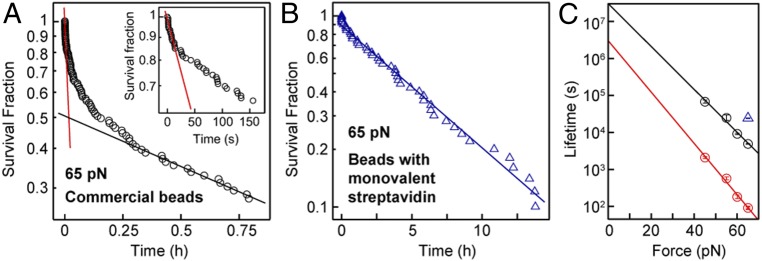
Having established ddFLN4 as an ideal fingerprint and having demonstrated the ability to apply constant forces over extended periods of time to multiple tethers in parallel, we utilized our assay to investigate not only protein folding and refolding, but also ligand–protein receptor interactions. As a proof-of-concept measurement, and to validate our tethering approach, we directly probed the stability of the high-affinity, noncovalent biotin–streptavidin interaction under constant force. Since all other linkages in our tethering protocol consisted of mechanically stable covalent bonds, we used ddFLN4-tethered beads to apply different high forces (45–65 pN) to the biotin–streptavidin bond and monitored the time until bead rupture. In the analysis, we only took into account beads that showed the specific ddFLN4 unfolding signature in 2 short force plateaus of 25 pN at the beginning of the measurement. Importantly, the number of beads that ruptured already during these initial short plateaus was small (<3.5%). For commercially available streptavidin-coated beads (Dynabeads M-270 Streptavidin; Invitrogen), we found the survival fraction to decay with time in a complex, multiexponential fashion (Fig. 4A) for all forces probed, suggesting the existence of several populations of the biotin–streptavidin interaction with different lifetimes. To quantify the lifetimes involved, we fit the fastest and slowest decaying populations by linear regression to the logarithm of the first and last 20% of data points, respectively (lines in Fig. 4A). Over the studied force range, the lifetime of the fastest decaying population ranged from ∼100 s at 65 pN to ∼2,100 s at 45 pN, whereas the lifetime of the slowest decaying population was ∼50-fold higher, increasing from ∼5,000 s at 65 pN to ∼68,000 s at 45 pN (Fig. 4C). For both populations, the lifetime was found to increase exponentially with decreasing force (Fig. 4C). Already for a force of 20 pN, extrapolated lifetimes were well above a day, and off-rates at zero force were in the range of 10⁻⁷ to 10⁻⁸ s⁻¹, consistent with the fact that beads remained stably bound for hours or days in our force-spectroscopy measurements at forces ≤20 pN (Figs. 2, 3, and 5).

Fig. 4.

Bond lifetimes of beads functionalized with different streptavidin variants. (A) Survival fraction as a function of time for commercially available beads coated with tetravalent streptavidin (Dynabeads M-270 Streptavidin; Invitrogen), tethered by ddFLN4 and subjected to a constant force of 65 pN. The survival fraction decays in a complex, multiexponential fashion, suggesting the existence of several populations of biotin–streptavidin interactions with different lifetimes. Red and black lines are linear fits to the logarithm of the first and last 20% of data points, respectively, to estimate off-rates of the fastest-decaying (A, Inset) and slowest-decaying populations. (B) Survival fraction as a function of time for ddFLN4-tethered beads functionalized with a monovalent streptavidin variant, measured at 65 pN. The blue line is a linear fit to the natural logarithm of all data points. Note the markedly different scale of the time axis. (C) Estimated lifetime of the biotin–streptavidin interaction at different constant forces for the fastest- and slowest-decaying population of commercial beads with tetravalent streptavidin (red and black circles, respectively) and for beads with monovalent streptavidin (blue triangle). Error bars correspond to 1 SD; lines are fits of a single-barrier kinetic model. The number of measured, specifically tethered beads per condition was between 44 and 118, of which 35–86 ruptured during the duration of the measurement. The measurement duration was 15 h for beads with monovalent streptavidin and for the commercial beads 1 h at 65 pN, 3 h at 55 and 60 pN, and 15 h at 45 pN.

Fig. 5.

Folding and unfolding of A2 domains within VWF dimers. (A) Schematic structure of a VWF dimer, consisting of 2 ∼65-nm, multidomain monomers C-terminally connected by disulfide bonds. The 2 A2 domains, which can unfold under force (A, Inset), are shown in blue. Arrows indicate the direction of force acting on the 2 N termini during MT experiments. (B) Segments from a ∼30-h-long extension vs. time trace of a VWF dimer tether subjected to alternating intervals of high force (here 12 pN), allowing for A2 unfolding; of intermediate force (here 3, 4, or 5 pN), allowing for direct observation of A2 refolding; and of low force (0.5 pN) to ensure refolding. Unfolding and refolding of the 2 A2 domains are observed as 2 independent positive or negative steps in the trace, respectively. Dashed lines in B, Insets indicate extension levels with none, one, or both of the A2 domains unfolded. (C) Force–extension curves of A2 (un)folding, in near-physiologic buffer containing Ca²⁺ (black) and in buffer without Ca²⁺ and with 10 mM EDTA (red). Data points are obtained by Gaussian fits to step extension histograms (C, Lower Right Inset) at each constant force. Data points above 5 pN are from unfolding (based on 62–632 and 40–747 events for the near-physiologic and EDTA case, respectively, obtained from 13–53 independent tethers), and data points up to 5 pN are from refolding (41–120 and 49–158 events for the near-physiologic and EDTA case, respectively, obtained from 10–19 independent tethers). Error bars correspond to the FWHM of Gaussian fits, divided by the square root of counts. Lines are fits of the WLC model. C, Upper Left Inset shows a global WLC fit to all data points. (D) Rates of unfolding (circles) and refolding (triangles) at different constant forces for near-physiologic (black) and EDTA (red) buffer. Error bars correspond to 95% CIs of exponential fits to the fraction of observed events as a function of time (Materials and Methods). Lines are fits of a single-barrier kinetic model, yielding rates at zero force k₀ and distances to the transition state Δx for unfolding and refolding as indicated.

We hypothesized that the different populations and multiexponential lifetimes for commercially available streptavidin-functionalized beads originate from the biotin–streptavidin complex being loaded with force in different geometries that result from the tetravalency of streptavidin (61). Indeed, for measurements with custom-made beads functionalized with a monovalent version of streptavidin (61) in a well-defined geometry using a C-terminal tag (48), the survival fraction was well described by a single-exponential decay (Fig. 4B). We chose immobilization of the monovalent streptavidin construct via the C terminus of its functional subunit, as it has been recently demonstrated in AFM force-spectroscopy measurements that the monovalent streptavidin–biotin complex can withstand markedly higher forces when loaded with force from the C terminus as compared to pulling from the N terminus (48). Indeed, we found the lifetime of the custom-made monovalent streptavidin beads to be 24,000 s (∼6.7 h) at 65 pN (Fig. 4B), similar to and even exceeding that of the 20% longest-lived commercially available beads (Fig. 4C).

Force-Clamp Measurements on Full-Length VWF Dimers.

Having demonstrated our attachment approach on a small, well-characterized protein, we next applied it to large (∼500 kDa) dimeric constructs of full-length VWF. Dimers, the smallest repeating subunits of VWF multimers, consist of 2 multidomain monomers that are C-terminally linked via disulfide bonds and have a contour length of ∼130 nm between their N termini (5, 64) (Fig. 5A). Since different peptide tags at the 2 N termini are required for attaching dimers in the desired pulling geometry (Fig. 5A), we genetically engineered heterodimers consisting of 2 different monomers that are N-terminally modified with a ybbR-tag or a sortase motif GG, respectively (Materials and Methods). After tethering in the MT, we recorded time traces of VWF dimers with alternating plateaus of high force (Fig. 5B, 6–20 pN) and moderate force (Fig. 5B, 2–5 pN). In most cases, we observed 2 unfolding and 2 refolding steps in the high and moderate force traces, respectively, with extension values matching the expected values for unfolding of the A2 domains (∼180 aa each) that have been previously probed in isolation in OT (8, 52). Observation of domain (un)folding only for the 2 A2 domains is consistent with the prediction that all domains of VWF except A2 are protected against unfolding by long-range disulfide bonds (64, 65) and with the results of recent AFM studies (9, 10).

In addition to the steps attributed to A2 unfolding and refolding, we less frequently observed larger steps (SI Appendix, Fig. S11; 70–80 nm at ∼11 pN), which we attributed to the dissociation of a strong intermonomer interaction mediated by the D4 domains that has recently been identified in AFM force measurements in approximately one-half of all VWF dimers under near-physiologic conditions (9, 10). Consistent with their assignment to the D4-mediated intermonomer interaction, the large unfolding steps occurred much less frequently in the absence of divalent ions, which have been shown to be critical for the intermonomer interaction (9, 10), and were absent for mutant constructs lacking the D4 domain (delD4; SI Appendix, Figs. S11 and S12). The dissociation of the intermonomer interaction was in some cases—after intermittent relaxation to a low force—observed repeatedly for the same molecule, implying reversibility of the interaction (SI Appendix, Fig. S11). Whereas in the constant pulling speed AFM measurements dissociation of this interaction had always occurred at much higher forces than—and therefore after—A2 unfolding, in our constant force measurements, we observed dissociation of the D4-mediated intermonomer interaction in the same force range as A2 unfolding, suggesting a steep force-loading rate dependence for the intermonomer interaction. In fact, in the constant-force measurements, we repeatedly observed dissociation of this interaction, even before unfolding of one or both of the A2 domains (SI Appendix, Fig. S11). Opening of the D4-mediated intermonomer interaction in the same force range as A2 unfolding suggests that it might play an important role for regulation of VWF’s hemostatic activity at physiologically relevant forces in the bloodstream.

Calcium Binding Stabilizes the VWF A2 Domain.

We next used our assay to elucidate the controversial impact of calcium on A2 stability (52, 66, 67). We performed measurements both in buffer mimicking the physiological pH and salt concentrations of the vasculature (“near-physiologic”; pH 7.4, 150 mM NaCl, 1 mM MgCl₂, and 1 mM CaCl₂) and in buffer lacking divalent ions and supplemented with 10 mM EDTA. First, we analyzed the change in extension upon A2 unfolding and refolding for different constant forces. For both buffer conditions, the resulting force–extension profiles (Fig. 5C), combining data from unfolding (data points > 6.5 pN) and from refolding (data points < 5 pN), are well described by a single WLC curve. The WLC fits yielded values for contour length and persistence length of 75.0 and 0.42 nm (95% CI: 70.8–79.2 and 0.37–0.46 nm) for near-physiologic buffer, and of 68.5 and 0.50 nm (62.7–74.3 and 0.41–0.58 nm) for the EDTA buffer, and thus showed no significant difference, indicating that calcium has no effect on the extension of the unfolded state. A WLC fit to the combined data from both buffer conditions (Fig. 5 C, Inset) yielded contour and persistence length values of 71.9 and 0.45 nm (68.3–75.4 and 0.41–0.50 nm). The contour length increments determined from the MT measurements on full-length dimeric VWF are in excellent agreement with OT unfolding studies on isolated A2 domains (8, 52, 66), suggesting that complete A2 unfolding is not obstructed by the presence of other domains. Control measurements using the same attachment protocol and ddFLN4 under the same buffer conditions found no difference in the force response for the different buffer conditions (SI Appendix, Fig. S13).

Next, we studied the kinetics of A2 unfolding and refolding. In the case of unfolding, rates were approximately 2- to 4-fold higher for the EDTA buffer in the force range probed, 6.5–17 pN (Fig. 5D, circles). For both buffer conditions, rates increased exponentially with increasing force, with a slightly stronger dependence on force for the EDTA condition. Fitting a single-barrier kinetic model yielded values for the unfolding rate at zero force k_unf,0 = 3.6 × 10⁻⁵ s⁻¹ (1.8–7.1 × 10⁻⁵ s⁻¹) and 7.8 ×10⁻⁵ s⁻¹ (5.1–12 ×10⁻⁵ s⁻¹) and distances to the transition state Δx_unf = 2.45 ± 0.22 and 2.60 ± 0.15 nm in the presence and absence of Ca²⁺, respectively. The rates measured in our constant force assay were 2 orders of magnitude slower than the rates determined in near-physiologic buffer in OT measurements on isolated A2 domains. While in principle, this difference might indicate stabilization of A2 by neighboring domains, we deem it likely that it at least partially results from the transformation of rupture force distributions measured in the OT by using the Dudko–Hummer–Szabo method (68), which is sensitive to the elastic response of employed flexible linkers. In our traces, we did not observe any features that corresponded to dissociation of potential interactions of A2 with neighboring domains. For refolding against external forces of 2–5 pN, rates were approximately 2- to 6-fold higher in the presence of Ca²⁺ (Fig. 5D, triangles) and decreased exponentially with force, with a more pronounced force dependence in the presence of Ca²⁺, which was reflected by the higher value of Δx of 6.80 ± 0.56 nm compared to 4.73 ± 0.26 nm in the absence of Ca²⁺. The refolding rate at zero force in the presence of Ca²⁺ k_ref,0 = 5.1 s⁻¹ (2.9–8.7 s⁻¹) was 20-fold higher than in the absence of Ca²⁺, k_ref,0 = 0.23 s⁻¹ (0.18–0.28 s⁻¹), indicating that calcium substantially speeds up folding of A2.

Taken together, our results demonstrate that A2 is stabilized by the presence of Ca²⁺ by increasing the refolding rate and stabilizing against unfolding compared to the conditions without Ca²⁺. The observed increases in the refolding rates in our experiments are in quantitative agreement with a previous report using OT on isolated A2 domains (52). Importantly, we directly observed refolding under mechanical load, even in the absence of Ca²⁺ (SI Appendix, Fig. S14), in contrast to a previous study (66). The role of Ca²⁺ in the stabilization against unfolding is controversial: We observed a modest reduction in the unfolding rate by Ca²⁺, which is consistent with the low-force data found in a previous OT study (52), which, however, reported no statistically significant change in the unfolding rate with and without Ca²⁺ overall, possibly as their assay might have lacked the sensitivity to resolve small differences. In contrast, we found no evidence for a long-lived intermediate in the unfolding pathway in the presence of Ca²⁺ that was reported by another study using OT (66). Finally, we occasionally observed tethers that only showed the unfolding and refolding signal of one A2 domain (SI Appendix, Fig. S15). In such tethers, refolding of one A2 domain may be inhibited due to cis–trans isomerization of a cis-proline, as reported in a previous OT study (8).

Transitions in the VWF Stem at Low Forces.

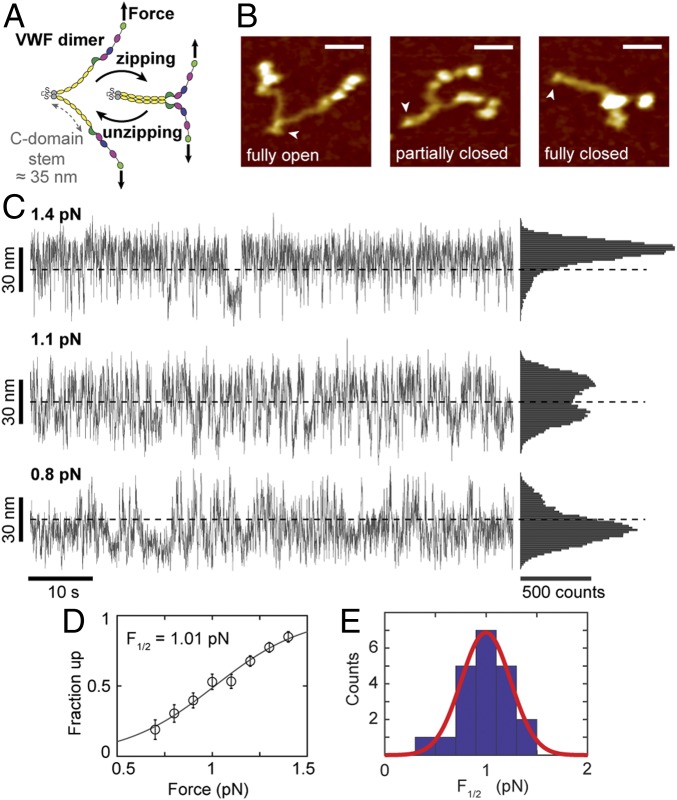
AFM imaging (9, 10) and electron microscopy (69) suggest that the VWF stem consisting of 6 C domains can open and close in a zipper-like fashion (Fig. 6 A and B). However, transitions of the VWF stem have not been observed directly. To probe for interactions in the VWF stem, we subjected dimeric VWF tethers that had shown the characteristic A2 unfolding pattern to different levels of low forces. At forces of ∼1 pN, we observed repeated, reversible transitions with a maximum contour length increase of ∼50 nm that were consistent with fully unzipping and rezipping the VWF stem (Fig. 6C and SI Appendix, Fig. S16). Increasing force in the range 0.5–1.5 pN systematically shifted the population toward higher tether extensions, which we interpreted as less compact “unzipped” conformations of the VWF stem. Control measurements with ddFLN4-tethered beads using the same linkers, attachment protocols, and buffer conditions never exhibited such transitions (SI Appendix, Fig. S7). In addition, the large change in extension at low forces makes it highly unlikely that the observed transitions originated from domain unfolding events (for comparison, a tether extension of <5 nm would be expected for unfolding of an A2 domain at a force of ∼1 pN, due to the WLC stretching behavior of the unfolded protein chain).

Fig. 6.

Unzipping and (re)zipping of the C-domain stem in VWF dimers. (A) Schematic of closing and opening of the stem (domains C1–C6, yellow) of VWF dimers in a zipper-like fashion due to interactions between the C domains. (B) AFM images of single VWF dimers adsorbed onto a surface under near-physiologic buffer conditions. Arrowheads indicate C-terminal ends of dimers, where the 2 constituting monomers are linked. In thermal equilibrium and in the absence of force, dimer stems exhibit conformations ranging from fully open to fully closed. It should be noted that in approximately one-half of all dimers, the stem region is firmly closed by the D4-mediated intermonomer interaction (9, 10) (Scale bars: 20 nm; height range of color scale: 2.4 nm.) (C) Extension vs. time traces of VWF dimer constructs subjected to low forces in MT. Fast reversible transitions between a maximum and minimum value of extension, ∼50 nm apart, are observed that we attribute to closing and opening of the C-domain stem. Dashed lines indicate the midpoint between the 2 extreme values of extension. Traces are raw data recorded at 58 Hz. (D) Fraction of data points in the up state, i.e., above the midpoint lines indicated in C as a function of applied force. The black line is a fit of the expression {1 + exp[−Δx⋅(F − F_1/2)/(k_BT)]}⁻¹ with F_1/2 the midpoint force and Δx a length-scale parameter characterizing the cooperativity of the transition. (E) Histogram of F_1/2 values determined from fits as shown in D. The red line is a Gaussian fit with mean ± SD = 1.00 ± 0.24 pN. The fitted values for Δx gave 28.6 ± 15.9 nm (mean ± SD from 21 molecules).

To characterize the overall force response of the VWF stem, we carried out a simple 2-state analysis and determined the fraction of data points above and below the midpoint between the 2 extreme values of extension (Fig. 6C, dashed lines). The fraction in the high-extension “up” state increased systematically with increasing force, and the data are well described by a simple 2-state model (Fig. 6D) with a midpoint force of F_1/2 = 1.00 ± 0.24 pN (mean ± SD from 21 molecules; Fig. 6E). The fitted F_1/2 is very close to the value for the onset of VWF multimer elongation predicted by Brownian hydrodynamics simulations (70).

While the 2-state analysis enables direct determination of the characteristic forces required to open the stem, a close inspection of the extension time traces (Fig. 6C) suggests that the stem does not behave as a strict 2-state system, but that, instead, the extension takes a range of values with fast transitions between different levels of extension. This multistate behavior with different levels of stem zipping is fully consistent with observations from AFM imaging that show that the stem frequently populates partially open configurations with different numbers of C-domains interacting (Fig. 6B and refs. 9 and 10). In order to quantify the rapid transitions in the VWF stem, we analyzed extension time traces close to F_1/2 with a step-finding algorithm developed for detecting transitions in single-molecule time traces (71) (Fig. 7A). The analysis revealed a broad distribution of step sizes with a maximum around 15 nm (Fig. 7B and SI Appendix, Fig. S17 A and B). Interestingly, steps >40 nm were rare (2.6% of all steps); similarly, small steps were also relatively rare (e.g., 5.8% of steps are <7 nm). Analysis of AFM images has shown that the unzipped VWF stem shows WLC behavior with a contour length of 70 nm and a bending persistence length of 6.4 nm (9), which implies a total extension change upon unzipping of ∼42 nm at 1 pN, in good agreement with the overall extension changes observed in the time traces (Fig. 6C). The fact that steps >40 nm were only rarely observed suggests that direct transitions between the fully open and completely closed conformations are rare and that most transitions pass through partially zipped intermediate configurations. We note that the most common step size of ∼14 nm was consistent with the expected length increase for pairs of C domains on each monomer zipping and unzipping.

Fig. 7.

Step sizes and time scale of VWF dimer stem transitions. (A) Segment of an extension vs. time trace of the VWF dimer construct at a stretching force of 1.1 pN. Raw data were recorded at 58 Hz (thin gray line), and steps were fit to the raw data by using a step-finding algorithm (71) (thick orange lines). (B) Distribution of the magnitude of step sizes determined from the data analysis schematically shown in A. (C) Distribution of dwell times between steps (orange dots) and maximum-likelihood fit of a single exponential model (solid black like). (B and C) Data for 7,659 steps from 12 independent molecules, all analyzed close to the 50–50 point. The maximum-likelihood fit gives a mean dwell time of τ = 0.28 ± 0.006 s (mean ± 95% CI). Maximum-likelihood fits to the individual datasets give τ = 0.28 ± 0.05 s (mean ± SD). The logarithmic y axis emphasizes bins with low counts at long times; however, dwell times >2 s only comprise 0.4% of all events. (D) Segment of an extension vs. time trace at 1.3 pN (same tether as in Fig. 6C) recorded at 1 kHz.

The dwell times between steps were exponentially distributed, with a characteristic time of τ = 0.28 s ± 0.006 s (mean ± 95% CI; Fig. 7C). The fact that the dwell times were well described by a single exponential suggests that the transitions occur between substates of similar individual lifetimes. To investigate the transitions in the VWF stem at high resolution, we recorded extension time traces of the VWF dimer constructs using high-speed, camera-based tracking at 1 kHz (Fig. 7D). The high-speed data revealed overall extension changes, step sizes, and dwell times that were in good agreement, within experimental error, with the results from tracking at 58 Hz (SI Appendix, Fig. S17 C–F). Importantly, molecular interactions that break and release contour length at low forces are expected to be particularly relevant for VWF’s physiological function, as these are likely the first interactions to open under shear flow and to set off a cascade of increased contour length and increased force, since hydrodynamic peak forces grow as the square of the contour length (5, 8).

Discussion

We have introduced an approach for single-molecule force-spectroscopy measurements on proteins using MT. Our protocol enables multiplexed measurements through high-yield, ultra-stable tethering of proteins requiring only short peptide tags. As a proof-of-concept measurement, we probed the 3-state unfolding and refolding of ddFLN4. Our measurements at constant force are overall in excellent agreement with constant pulling-speed AFM experiments and confirm the existence of a low-loading rate pathway for unfolding (4, 63). While for ddFLN4, we observed exponential force dependencies of unfolding and refolding rates, we note that the precise determination of rates at low, constant forces afforded by our assay should allow detection of deviations from such exponential Bell model-type behavior (72) expected for other systems and testing of more complex models, e.g., involving transitions from catch-bond to slip-bond behavior (73, 74), switching between different protein unfolding or receptor–ligand dissociation pathways (75–77), or taking into account structural–elastic properties of the investigated molecules (73, 78).

Applying our method to the large, force-regulated protein VWF confirmed several structural transitions previously observed in AFM and OT force-spectroscopy measurements, including D4 and A2 unfolding. In addition, our data show how Ca²⁺ stabilizes the A2 domain by reducing the unfolding and increasing the refolding rate. Finally, our measurements reveal transitions between multiple extension levels in the VWF stem at forces of ∼1 pN, which likely constitute critical first steps in the stretch response of VWF under physiological shear flow. Future measurements under a range of solution conditions, in particular varying pH, and using VWF mutants should help to further identify the distinct contributions and roles of the different C domains.

Using the ability of our assay to apply constant forces over long periods of time to multiple tethers in parallel, we probed the stability of streptavidin–biotin bonds, a widely used ligand–receptor system. We found that commercially available, multivalent streptavidin (far) exceeds the requirements of typical constant force force-spectroscopy measurements (with lifetimes ≥1 d at forces ≤20 pN), but has a multiexponential lifetime distribution. Monovalent, site-specifically attached streptavidin, in contrast, exhibits a single-exponential lifetime distribution with extremely high force stability, making it an attractive approach for force spectroscopy on systems that require high forces over extended periods of time. Ultimately, one could also replace the biotin–streptavidin bond with a covalent linkage to even further enhance the force and also chemical stability of the attachment protocol.

In conclusion, we have demonstrated the versatility and power of single-molecule protein force-spectroscopy measurements using MT. Our method provides a high yield of ultra-stable specific single-molecule tethers that can be probed in parallel at constant forces over extended periods of time. Given ongoing improvements in camera technology, we expect that the number of protein tethers that can be measured in parallel will further increase by at least an order of magnitude in the near future. In addition, we anticipate that our tethering strategy will enable multiplexed protein force spectroscopy using other single-molecule methods such as acoustic and centrifugal force spectroscopy as well. Since the approach is modular and only requires minimal modifications to the protein of interest, we anticipate it to be applicable to a wide range of proteins. We expect MT force spectroscopy to, in particular, give access to the physiologically relevant low force (<1 pN) regime and to provide a wealth of insights into the mechanics and force regulation of proteins.

Materials and Methods

Experimental Procedures, Data Analysis, and Engineering of Recombinant Proteins.

Please refer to the SI Appendix for details of how tagged ddFLN4, hetero-bifunctional VWF dimer constructs, regular and inverted ELP linkers, and monovalent streptavidin were prepared, purified, and coupled. Measurements used a custom-built MT setup described in ref. 79; forces in the MT were calibrated by analysis of transverse fluctuations using long DNA tethers (80). The largest source of force uncertainty was the bead-to-bead variation, which we found to be on the order of ≤10% for the beads used in this study (SI Appendix, Fig. S2), in line with several reports (16, 81, 82). Details of the MT assay, AFM imaging, and data analysis are given in SI Appendix.

Buffers.

Measurements on ddFLN4 and measurements on VWF dimers under “near-physiologic” conditions were performed in buffer containing 20 mM Hepes, 150 mM NaCl, 1 mM MgCl₂, 1 mM CaCl₂, and 0.1% Tween-20, at pH 7.4. Measurements without calcium were performed in EDTA buffer containing 20 mM Hepes, 150 mM NaCl, 10 mM EDTA, and 0.1% Tween-20, at pH 7.4. Before measurements in the absence of calcium, the flow cell was incubated with EDTA buffer for 2 h. Control measurements at acidic pH were performed in 20 mM sodium-acetate, 150 mM NaCl, 1 mM MgCl₂, 1 mM CaCl₂, and 0.1% Tween-20, at pH 5.5.